Study on the Causes of Cracking in Concrete Components of a High-Pile Beam Plate Wharf

Abstract

The high-pile beam slab structure is a commonly employed design for riverbank wharves; however, the wharf structure may incur damage due to various factors during long-term operation, resulting in potential safety concerns. To illustrate this, an investigation was conducted on a high-pile beam slab wharf, which included on-site examination, testing, and large-scale three-dimensional numerical simulation. The effects of gravity, ship impact, earthquake, lateral impact, water, and crane change were considered to explore the causes of cracking in the wharf concrete components. The results indicated that crane modification significantly augmented loads, precipitating notable deformation (92% increase in maximum vertical displacement), and the maximum tensile stress exceeded concrete tensile strength. The inadequate thickness of the steel reinforcement protective layer caused concrete carbonation, steel exposure, and corrosion, reducing structural capacity. The presence of defects in the pile foundation has been shown to result in high stress concentrations, which can lead to deformation and damage. There was a 58% increase in vertical displacement in the concrete components above the affected area compared to intact piles. Based on analysis of the results, appropriate measures for strengthening and correction have been proposed to ensure the safety and durability of the wharf. A comprehensive multifactor evaluation and 3D simulation of the actual dimensions are recommended to ensure the safety of wharf structures.

1. Introduction

High-pile wharves are extensively used in coastal areas of China and the Yangtze River due to their advantages of small structural displacement, small amount of sand and gravel, and suitability for deep water and soft soil foundation conditions [1]. However, the long-term operation of these wharves can cause damage to concrete components, which can affect the safety and durability of the wharves [2].

The load on a wharf structure is categorized into three main types: horizontal load, which includes ship berthing load and wave load; vertical load, which includes gravity of self-weight, stacked goods, and upper machinery; and environmental load, which includes seismic load and corrosion. Under these loads, the thickness of the concrete protective layer decreases, leading to concrete carbonation, corrosion of exposed steel bars, and the development and expansion of cracks in concrete members [3,4,5,6,7]. Numerous experimental and analytical studies have been carried out on the deformation and failure of high-piled wharf structures under various loads. Zheng and Zhang [6] conducted a model test to evaluate the damage caused by horizontal impact loads on bent structures. The study compared the extent of damage caused by different loads and concluded that ship collisions are the main cause of wharf damage. Xie et al. [8] established formulas for single-pile and pile-supported platform force–displacement for determining the horizontal load-bearing capacity of a high-pile wharf using numerical simulation. Zhang et al. [9] developed a three-dimensional finite element model of a high-piled beam-slab wharf and simulated its dynamic response to horizontal loads. This showed that the frame structure had the weakest bearing capacity at the joints of the members. Yuan [10] developed a model for a beamless high-piled wharf to analyze the effect of post-stack loading on the deformation of a pile–soil system. Zheng et al. [11] proposed a damage identification method based on stiffness, natural vibration period, and experimental acceleration data, which can effectively improve the health monitoring of high-piled wharves. Zhu et al. [12] proposed a method to extract the effective component of dynamic response under wave excitation. The robustness and sensitivity of the new damage index were verified by finite element simulation and an experimental model of a high-piled wharf, which is expected to assist the daily health monitoring of pile foundations of high-piled wharves. Xu et al. [13] used FLAC 3D 6.0 version to carry out dynamic calculations under ship impact load, and effectively identified locations of damage to a high-piled wharf. You et al. [14] investigated the 3D bearing characteristics of a high-piled beam slab wharf under an upper mechanical load. Xiao and Li [15] proposed models for chloride penetration, crack initiation, and crack propagation in reinforced concrete (RC) structures under different stages of marine environments. Li et al. [16] investigated the stress characteristics of a coastal port wharf structure in a special environment with high salt and high humidity, and proposed a health inspection index for the wharf structure. Li et al. [17] established a three-dimensional finite element model of an integral high-piled wharf structure with pile–soil interaction, and revealed the failure mechanism of lateral bearing deformation and the degradation mode of lateral bearing performance under the combined action of chloride attack and ship berthing impact. Coelho and Araújo [18] demonstrated that in instances of intricate geometric configurations, the finite element model is capable of accurately predicting the structural behavior of the beam–column connection. Furthermore, the finite element model can accurately simulate and analyze the structural performance of reinforced concrete components, which demonstrates its good applicability [19,20,21,22].

The existing literature has mainly studied the mechanical behavior of wharf structures under single loads. Numerical simulations and laboratory tests have been conducted using small models, such as single piles and bent piles. However, for high-pile beam plate wharves, the foundation, high piles, and superstructure interact and influence various external loads, resulting in a more complex stress and deformation response. This paper presents a study on the causes and failure mechanisms of cracks in concrete components of a high-pile beam slab wharf with a large number of cracks during operation. The study was conducted through on-site investigation, detection, and large-scale 3D numerical simulation. The effects of various loads, including gravity load, ship impact load, seismic load, lateral impact load, water load, and crane load, were considered.

2. Characteristics of Cracks in Concrete Components

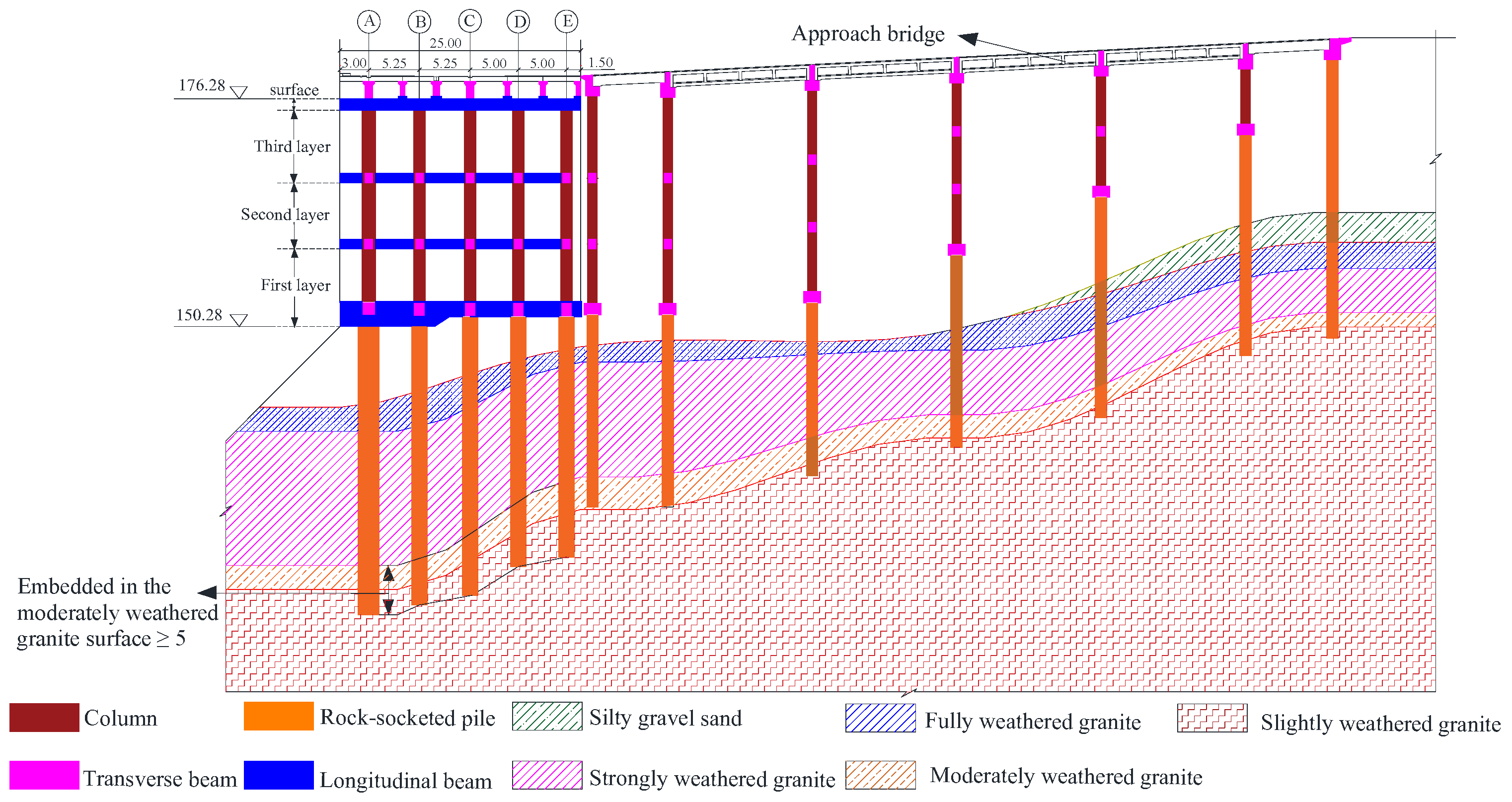
2.1. Project Overview

Zigui Port is located in Yinxingtuo Village, Maoping Town, Zigui County, Yichang City, about 8.0 km upstream of the Three Gorges Dam on the Yangtze River. It functions as an emergency and long-term transportation hub for the Three Gorges Reservoir area. The project for protecting the reservoir bank covers a length of approximately 1262.00 m and a width of 130.00 m. It is divided into two areas: a RO–RO terminal area and a miscellaneous terminal area. Figure 1 illustrates that the wharf comprises a wharf platform and four approach bridges. This is a supporting project of Zigui Three Gorges Overturned Dam Logistics Industrial Park. The wharf platform measures 315.00 m in length and 25.00 m in width, with a top elevation of 176.28 m and a bottom elevation of 150.28 m. It is divided into three 3000 t-class miscellaneous berths to meet the import and export requirements of 1.40 million tons of groceries per year.

Figure 2 illustrates a stratigraphic sequence composed of silty gravel, sand, and granitic materials exhibiting varying degrees of weathering. The basal unit consists of slightly weathered granite with a thickness ranging from approximately 1.0 m to 5.0 m, which is conformably overlain by moderately weathered granite. Overlying this unit is a 4.1–11.2 m-thick layer of strongly weathered granite, followed by the uppermost stratum of completely weathered granite with a vertical extent of 0.5–4.3 m. Additionally, localized lens-shaped deposits of silty gravelly sand are present near the terrestrial margin, occupying a sub-horizontal zone with a maximum thickness of 3.0 m.

The foundation for the rock-socketed pile was designed to take advantage of the high strength and rigidity of granite. The bearing layer is made of moderately and slightly weathered granite, and the pile must be embedded in the weathered rock surface of the granite, at a depth of no less than 5.00 m. The piles are arranged in five columns (A–E) and 40 rows (1–40). Figure 2 illustrates that the spacing between columns A and B and between columns B and C is 5.25 m and the spacing between columns C and D and between columns D and E is 5.00 m. The spacing of each row is 8.00 m. The diameter of the piles in columns B to E was designed to be 1600.00 mm. To consider the effects of ship berthing and wave loads during operation, the diameter of the pile foundation for column A near the river side was increased slightly to 2200.00 mm. The final design of the rock-socketed pile length ranges from 23.00 m and 43.00 m due to the variation in the thickness of the moderately weathered granite.

The structure above was a frame type consisting of cast-in-place columns, longitudinal and transverse foundation connecting beams, cast-in-place crossbeams, prefabricated longitudinal beams, prefabricated panels, cast-in-place surface layers, and wearing layers. The framework comprised three layers (excluding the surface layer). The distribution of columns was consistent with the pile foundation, with one column arranged at the top of each rock-socketed pile. The diameter of columns in columns B to E was 1200 mm. To ensure high impact strength on the river side, the diameter of column A had been increased to 1400 mm. The longitudinal beams measured 2400 mm × 1600 mm, while the transverse beams measured 1200 mm × 1600 mm. The cast-in-place crossbeam measured 800 mm × 1000 mm, and the prefabricated longitudinal beam measured 1400 mm × 1000 mm. The prefabricated panel was 1000 mm thick.

2.2. Characteristics of Cracks

The on-site investigation, carried out after three years of operation, revealed that multiple cracks had appeared in the concrete surface layer, columns, and beams of the wharf (Figure 3).

Some components were severely damaged, affecting the normal use of the wharf. The cracks in the surface layer were primarily in a network pattern, with the longest crack measuring 21.80 m and the largest network crack measuring 1.50 m × 7.60 m. The column exhibited numerous axial cracks, some of which combined with circumferential cracks to form mesh cracks. In severe cases, the steel bars were corroded and the hoops were exposed. The maximum crack width in the column was 12 mm, with a depth ranging from 111 mm to 209 mm. The connecting beams had cracks with a maximum width of 2.38 mm and a depth ranging from 139 mm to 144 mm. Additionally, some of the top surfaces of the connecting beams were covered with mesh cracks. The connecting beam developed multiple symmetric cracks on both the upstream and downstream sides, with a maximum width of 12 mm and a depth of 125 mm to 186 mm. Some of these cracks extended to the top surface of the foundation beam, forming a network of cracks. The connecting beams are severely damaged and show signs of exposed reinforcement corrosion.

Li et al. [23] concluded that concrete cracks with a width of less than 0.20 mm generally do not require specialized control measures. For cracks between 0.20 and 3.00 mm, significant deformation occurs, and repair and reinforcement measures are necessary. If the crack width exceeds 3 mm and the degree of deformation is significant, complex repair and reinforcement measures are required. The concrete components are classified into four categories based on crack width: Class A represents components without cracks, Class B represents components with minor cracks that have a width of less than 0.3 mm, Class C represents components with obvious cracks that have a width between 0.3 and 3 mm, and Class D represents components with severe cracks that have a width greater than 3 mm.

Figure 4a–c display the distribution of cracks in columns and connecting beams. The column cracks were mainly concentrated downstream between rows 21 to 40. Out of the 102 columns in this interval, 82 columns had cracks, accounting for 80.4%. The most severe D-class cracks were all present on the downstream side. On the upstream side, out of the 102 columns in rows 1 to 40, 21 columns had cracks, accounting for 20.6%. Moreover, the cracks in the columns were mainly distributed vertically, with over 80% of them appearing on the first layer. The most severe D-class cracks were also concentrated on the first layer. Furthermore, D-class cracks were found to be distributed in all four directions of the column. It is worth noting that all cracks were on the water-facing side.

The cracks in the connecting beams were mainly concentrated in the first layer, with relatively few cracks in the second and third layers. Furthermore, the connecting beams with C-class and D-class cracks were primarily located in the first layer and concentrated in rows 1 to 20. In the first layer of connecting beams, 20% of the total was found to be cracked D-class beams, while 12.5% and 5% were cracked C-class and B-class beams, respectively.

The cracks on the columns were mostly located on the river side and were concentrated on the downstream side (rows 21 to 40) and the first layer. The cracks in the connecting beams were concentrated in rows 1 to 20 of the first layer. The wharf structure was severely damaged, with reduced bearing capacity and durability that no longer meets the design service life requirements. The maximum width of cracks in the wharf and approach bridge was 12 mm, which poses serious peeling problems and does not meet the requirements for use.

3. Cause Investigation

3.1. Potential Causes

Possible causes of cracking in concrete components were investigated on-site. (1) Operational errors were made by waiting vessels during three months of operation at the wharf due to the influence of strong winds. These errors caused impacts on the structures of rows 1 to 5 of the wharf, resulting in the peeling and chipping of some concrete component protective layers. (2) Two blasting operations were carried out near the wharf during its operation. Earthwork blasting was conducted at the Xiongjialing site behind the wharf, with the closest distance to the wharf being 50 m. Underwater blasting construction was also carried out to excavate the harbor pool, with a minimum distance of 100 m from the wharf. (3) A 4.5 magnitude earthquake occurred in Zigui County (31.03° N, 110.47° E), where the wharf is located, with a depth of 7 km, after two years of operation at the wharf. Local residents reported the earthquake as strong. The horizontal loads generated by earthquakes may have an impact on the wharf structure. (4) The elevation of the bedrock varies significantly, with the moderately weathered bedrock layer ranging from 77.6 to 195.4 m and the slightly weathered bedrock layer ranging from 75.4 to 192.9 m. This uneven distribution of the bearing rock layer may result in differential deformation of the pile foundation. (5) Due to functional requirements, the initially designed lifting equipment had undergone changes. Figure 4d illustrates the layout before and after the change of lifting equipment. The lifting equipment of Berth 1 had been altered from two 40 t–30 m gantry cranes to one 45 t–26 m shore container crane. Similarly, the lifting equipment of Berth 2 had been altered from two 16 t–30 m gantry cranes to one 45 t–26 m shore container crane. The lifting equipment of Berth 3 had been modified from two 16 t–30 m gantry cranes to two 40 t–30 m multipurpose gantry cranes. The substitution of the lifting apparatus has the consequence of an augmented load on the lower structure, which may have an effect on the overall stability of the structure. (6) In addition to the influence of external loads, the strength of concrete is of crucial importance. Insufficient strength can readily result in cracking and deformation of concrete components under external loads. (7) A site investigation revealed that the concrete components lacked sufficient thickness of the steel reinforcement protection layer, which directly affected the durability of the concrete components and could lead to corrosion of the steel reinforcement, thereby reducing the load-bearing capacity of the components. (8) The integrity of the pile was found to be defective. The embedded rock pile serves to transfer the load of the upper structure to the stable bedrock. The strength, stiffness, and stability of the pile directly affect the load transfer, while the integrity of the pile also affects the vertical compression, pull-out, and horizontal bearing capacity.

3.2. Cause Elimination

The incident occurred in the early stages of the construction of the wharf, when the wharf was at a high water level and a ship collided with the upper frame structure. Following the collision at the wharf, the concrete components of rows 1 to 5 were significantly damaged, and the external steel reinforcement protection layer was damaged. The steel reinforcement was exposed, but no fracture or damage was found. The damage statistics of all columns, beams, and surface layers at the impact location indicated that there was no structural damage to the main structure. Furthermore, the inspection results of the surface layer, upper structure, track, and ancillary facilities also demonstrated that there was no significant damage. Figure 4e shows the locations of 22 settlement monitoring points that were set at the top of the pile foundation. Figure 5 illustrates the settlement variation curves of four monitoring points (MP1–MP4) situated in rows 1 to 5 following a three-month period after collision. According to the “Engineering survey standards” [24], the settlement displacements of the monitoring points exhibited a very slight increase (0.01 mm/d–0.04 mm/d), and the settlements at each monitoring point after three months were also very small, ranging from 0.5 mm to 0.7 mm. This indicates that the impact of the ship collision on the overall structure of the wharf was minimal.

The Xiongjialing site earthwork blasting was conducted using a loosening blasting technology, with the safe distance of blasting effect calculated using Equation (1) [25]:

$$Q={\displaystyle \frac{eqgL{W}^2{n}_c}{\left(1+n_c\right)}}$$

(1)

where the variables Q, e, g, q, L, and W represent the actual charge of each borehole, the conversion coefficient of explosives, the blockage coefficient of the explosive eye, the amount of explosives required to be installed for media blasting under standard conditions, the length of the borehole, and the distance affected by the explosion, respectively. The action index of blasting, represented by n_c, is also a crucial parameter. In consideration of the site conditions, the values of each parameter were as follows: Q = 15.33 kg, e = 1.5, g = 0.5, q = 0.3 kg, L = 1.5 m, and n_c = 0.6, giving W = 10.5 m.

The closest distance between the site and the wharf was 50 m so there would be no significant impact on the wharf structure.

The following equation for millisecond delayed loosening blasting is used to analyze the effects of underwater blasting [26]:

$$R={\left({\displaystyle \frac{\mu P{\sigma }_{\mathrm{t}}}{1-\mu }}\right)}^{{\displaystyle \frac{1}{a}}}{r}_b$$

(2)

where R is the radius of the crack zone after blasting, μ is the Poisson’s ratio of the rock mass, σ_t is the tensile strength of the rock mass, a is the stress attenuation value and a = (2 − μ)/(1 − μ), and r_b is the radius of the hole. P is the initial impact value on the hole wall during blast, and it can be calculated as follows:

$$P={\displaystyle \frac{1}{8}}{\rho }_e{D}^2{\left({\displaystyle \frac{r_c}{r_b}}\right)}^{6}n$$

(3)

where ρ_e is the density of explosives, D is the explosive velocity, r_c is the radius of the explosive, and n is the pressure increase coefficient. Based on the actual situation on-site, each parameter was taken as μ = 0.25, σ_t = 5.8 MPa, γ_b = 23 mm, ρ_e = 1.07 × 10³ kg/m³, D = 3600 m/s, r_c = 19.5 mm, and n = 11, respectively. Thus, R = 10.1 m was obtained, which was well below the minimum distance (100 m) from the blast site to the wharf, so it would not have had an impact on the structure.

According to the Seismic Ground Motion Parameter Zoning Map of China [27], the construction of the wharf was designed with seismic intensity of VI, while the 4.6 magnitude earthquake that occurred was calculated to be only II–III. Apparently, this earthquake was not strong enough to cause damage to the wharf structure.

The monitoring of the 22 points at the top of the pile revealed that the final settlement of the MP5 monitoring point was the highest (1.12 mm) due to the upper part bearing the load of the 45 t–26 m-type lifting equipment. In contrast, the settlement of the MP3 monitoring point at the edge of the wharf was the lowest, at −0.79 mm. This resulted in a settlement difference of 1.91 mm between the two points. In accordance with the pertinent Chinese standard, the Code for Design of Building Foundations (GB 50007–2011) [28], the typical standard value for the settlement difference between adjacent pile foundations is 0.002 l₀, where l₀ represents the distance between the adjacent pile foundations. The distance between the adjacent piles in the miscellaneous wharf was 8 m, which permitted a settlement difference of 16 mm. It can be observed that the uneven settlement of the wharf structure was minimal, and thus it can be concluded that it was not the primary factor contributing to the cracking of the concrete components.

In accordance with the Standard for Test Methods of Concrete Physical and Mechanical Properties (GB/T 50081-2019) [29], concrete samples with dimensions of 150 mm × 150 mm × 150 mm were cured under standard conditions for 28 days (Figure 6), during which the temperature was maintained at 20 ± 2 °C and the relative humidity was ≥95%. Strength tests were then conducted, and the average strength of three samples per group was calculated. Individual sample strengths were required to deviate from the group average by no more than 15%. The test results demonstrated an average strength of 44.84 MPa and a minimum strength of 42.20 MPa, which met the design requirements. A random selection of components from the construction site was subjected to the rebound method to test the strength of the sampled concrete components. The test data indicated that the average rebound of the concrete components at 28 days was distributed between 41 and 53. After angle correction and pouring surface correction, it was estimated that the average strength of this batch of concrete components was not less than 40 MPa and not more than 50 MPa, which meets the design requirements. Consequently, the strength of the concrete components was not the primary factor in their cracking.

3.3. Exact Causes

The inspection results of the steel reinforcement protection layer for the column and foundation connecting beam indicated that the qualification rates of the column were 25.6%, 55.6%, and 31.1%, respectively. The qualification rates of foundation connecting beams were 16.7%, 58.9%, and 30.0%, respectively. The maximum negative deviation of the unqualified point in the thickness of the steel reinforcement protective layer was greater than 1.5 times the allowable deviation value. This was due to insufficient thickness, which resulted in multiple connecting beams being exposed and corroded. Therefore, it can be determined that the inadequate thickness of the steel reinforcement protective layer was an important cause of cracking in concrete components.

Two further factors that should be considered to have an impact were changes in the lifting equipment and defects in the integrity of the piles. Figure 4a–c clearly demonstrate the presence of significant cracks in the structure below the location of the lifting equipment. In particular, for rows 30–32 and 36–38, the originally designed 16-ton crane was replaced with a larger 40-ton crane, resulting in the emergence of significant cracks in the three-story structure below. The on-site investigation also revealed that there were integrity defects in the piles at C-3, B-7, C-7, E-7, E-8, E-9, C-10, E-10, and D-11. Furthermore, the C-type and D-type cracks in the foundation connecting beam were primarily concentrated in rows 3, 7, 8, 9, 10, and 11, and their distribution was largely consistent. It is evident that alterations in the lifting apparatus were directly correlated with the occurrence of pile defects, as well as with the emergence of structural cracks.

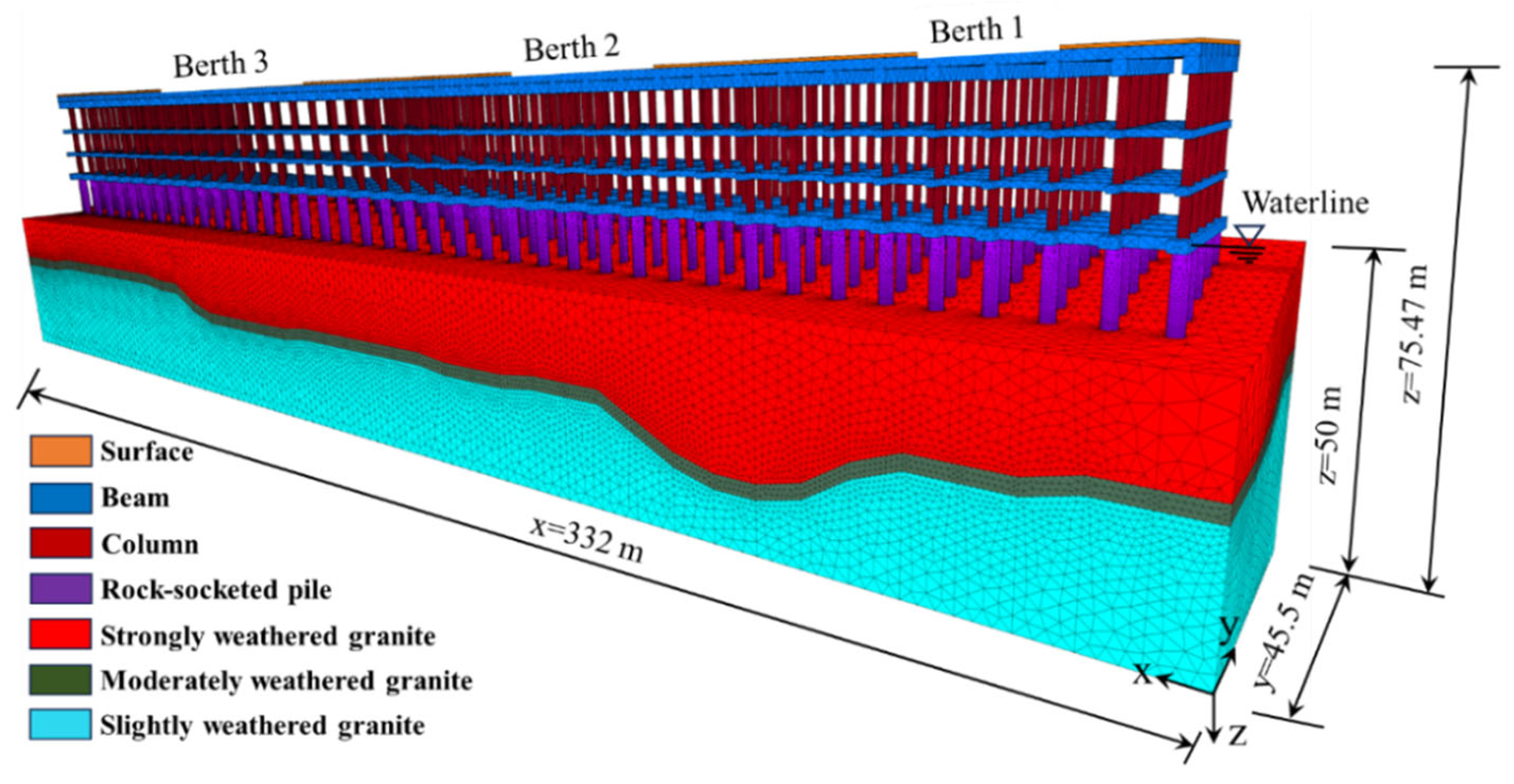
4. Numerical Simulation

4.1. Numerical Model and Loading Cases

To further investigate the specific impact of changes in lifting equipment and pile defects on the wharf structure, the finite-difference code FLAC^3D version 6.0 was employed for numerical simulation. A numerical model of the three-layer frame beam column structure and foundation of the miscellaneous wharf platform was established based on the terrain and geological conditions. The upper structure comprises 40 rows of beams and 204 columns, in addition to a concrete surface layer. The foundation comprises medium to slightly weathered bedrock and a strong weathered zone of upper granite. Each pile foundation is embedded in medium to slightly weathered bedrock to a depth of 5 m. All the upper structures, piles, and foundation were all simulated using solid elements. Given that tetrahedral meshes enable efficient local refinement of fine boundary layers while effectively preventing mesh distortion, they were better suited for the nonlinear large-scale structural model used in this study. The mesh size was determined based on component geometry: cylindrical columns were assigned a 0.5 m mesh, beams and top slabs adopted 1 m elements, and the foundation mesh size was optimized according to its distribution width: larger widths utilized moderately expanded meshes, while narrower regions employed smaller meshes, maintaining an overall range of 0.5–1 m. As illustrated in Figure 7, the model has a length of 332 m, a width of 45.5 m, and a height of 75.47 m. The model comprised a total of 10,409,112 zones and 1,876,477 grid points.

For the boundary conditions, the four side boundaries and the bottom boundary were fixed with hinges and the top of the foundation was free. The “zone attach” command is used to connect the beams, slabs and columns, so that their translational degrees of freedom are coupled. When subjected to forces, axial forces and shear forces are transmitted, while bending moments are not transmitted. The wharf studied in this paper belongs to the prefabricated assembled structure, which is consistent with its hinged connection mode.

A total of four cases were subjected to simulation. In Case I, the potential impact of pile defects and modified lifting equipment was evaluated. In Case II, the loading of the initial lifting equipment was considered. In Case III, the effects of modified lifting equipment were considered. In Case IV, the impact of pile defects was considered.

All the structures, including the beams, columns and piles, and the rock materials were assumed to obey the Mohr–Coulomb failure criterion. In the calculation of the four cases, a water level of 50 m was considered to apply load to the model, with the foundation and piles below the water level assumed to be saturated. The results of concrete strength testing indicated that the parameters of C40 concrete were employed for concrete beams, piles, and surface layers, while the parameters of C45 concrete were used for concrete columns. The mechanical property parameters of the concrete material were mainly determined by the relevant parameters in the project report during the construction of the wharf and the test results of the concrete curing in Section 3.2. Three types of granite rock layers with varying degrees of weathering were reduced according to the comprehensive granite material parameters outlined in the engineering geological survey report. The three categories of weathering were classified as slight, medium, and strong, with the respective proportions of granite material parameters being 90%, 75%, and 35% [30]. The calculated parameters are presented in

Table 1. Numerical model material parameters.

Model Construct	Material Type	Bulk Modulus/GPa	Shear Modulus/GPa	Density (kg/m3)	Saturation Density (kg/m3)	Internal Friction Angle (°)	Cohesion (MPa)	Tensile Strength (MPa)
Basis of bedrock layer	Granite	23.81	21.74	2600	2860	51	12	10
beams, piles, and surface layers	C40 concrete	18.00	13.54	2500	2750	45	1.51	1.51
Columns	C45 concrete	18.61	13.96	2500	2750	45	1.6	1.6

.

To validate the applicability of tetrahedral elements and mesh discretization, numerical simulations under identical loading conditions (considering gravitational load only) were initially conducted using tetrahedral and hexahedral meshes, respectively. Subsequent numerical model computations under Case I were performed with mesh sizes of 0.5 m and 1 m. The comparison of final simulation results presented in

Table 2. Sensitivity analysis of grid element and mesh size.

Categories		Vertical Displacement/mm	Maximum Tension Stress/MPa	Maximum Compressive Stress/MPa
Mesh Types	Hexahedral mesh	0.029	1.60	1.00
	Tetrahedral mesh	0.022	1.62	1.04
Mesh Sizes	1 m	4.35	1.65	1.47
	0.5 m	4.04	1.65	1.44

indicates negligible discrepancies, thereby confirming the rationality of the selected modeling approach.

The loads of three types of lifting equipment, namely 45 t–26 m, 40 t–30 m, and 16 t–30 m, were calculated based on their maximum operating weights of 595 t, 540 t, and 256 t. The lifting equipment shown in Figure 8 had a length of 9 m and a width of 0.5 m for each track. The contact area between the lifting equipment and the two tracks on the ground was 9 m². In the simulation, the position of the lifting equipment load is consistent with the actual situation, with two tracks located between y = 3 and y = 3.5, as well as between y = 13.5 and y = 14 of the surface layer (Figure 9). The estimated stress applied to the surface layer was calculated based on the maximum weight of the lifting equipment and the contact area with the track. The results were 648 kPa, 589 kPa, and 279 kPa, respectively.

A total of nine piles, C-3, B-7, C-7, E-7, E-8, E-9, C-10, E-10, and D-11, were simulated in the model based on the actual situation of piles. This was achieved by removing grid elements at their corresponding positions to simulate actual pile.

Before analyzing the impacts of the crane load and pile defects, the verification analysis was first carried out using working condition 1. Since the actual load conditions endured by the wharf are the same as those of working condition 1, the plastic damage and deformation generated during the operation of working condition 1 can be compared and analyzed with the actual distribution positions of the concrete cracks. If the two are consistent, it indicates that the numerical model is reliable and can be applied to the subsequent load analysis.

4.2. Simulation Results

As illustrated in Figure 10, the wharf structure in Case I exhibited significant plastic damage, with the plastic zone concentrated in the area affected by the crane and defective of piles. The number of columns with plastic damage on the first, second, and third floors was 36, 10, and 3, respectively. A zone of plastic deformation is evident in the vicinity of the wharf, in proximity to the crane installation location (on the river side) on each floor. In contrast, the opposite side exhibits minimal deformation. The number of beams exhibiting plastic failure in the first, second, and third layers is 53, 62, and 12, respectively. Similarly, there are numerous plastic zones on the riverside of each layer, with a high concentration in the area of the first layer comprising defect-embedded rock. This indicates that the plastic zone of columns and beams is primarily located on the first floor of the wharf structure and the riverside. This is consistent with the distribution of damage to columns and beams under actual working conditions. This suggests that the established model can be used for subsequent cases involving crane and pile defects.

As illustrated in Figure 11, analysis of displacement contour plots and stress distribution diagrams for Case I reveals significant structural responses at the crane installation location. A maximum displacement amplitude of 4.35 mm was recorded at the installation site, accompanied by pronounced tensile stress concentrations at the pier margin reaching 1.65 MPa. The resultant asymmetric structural deformation of the wharf system demonstrates direct correlation with the geometric configuration of crane placement.

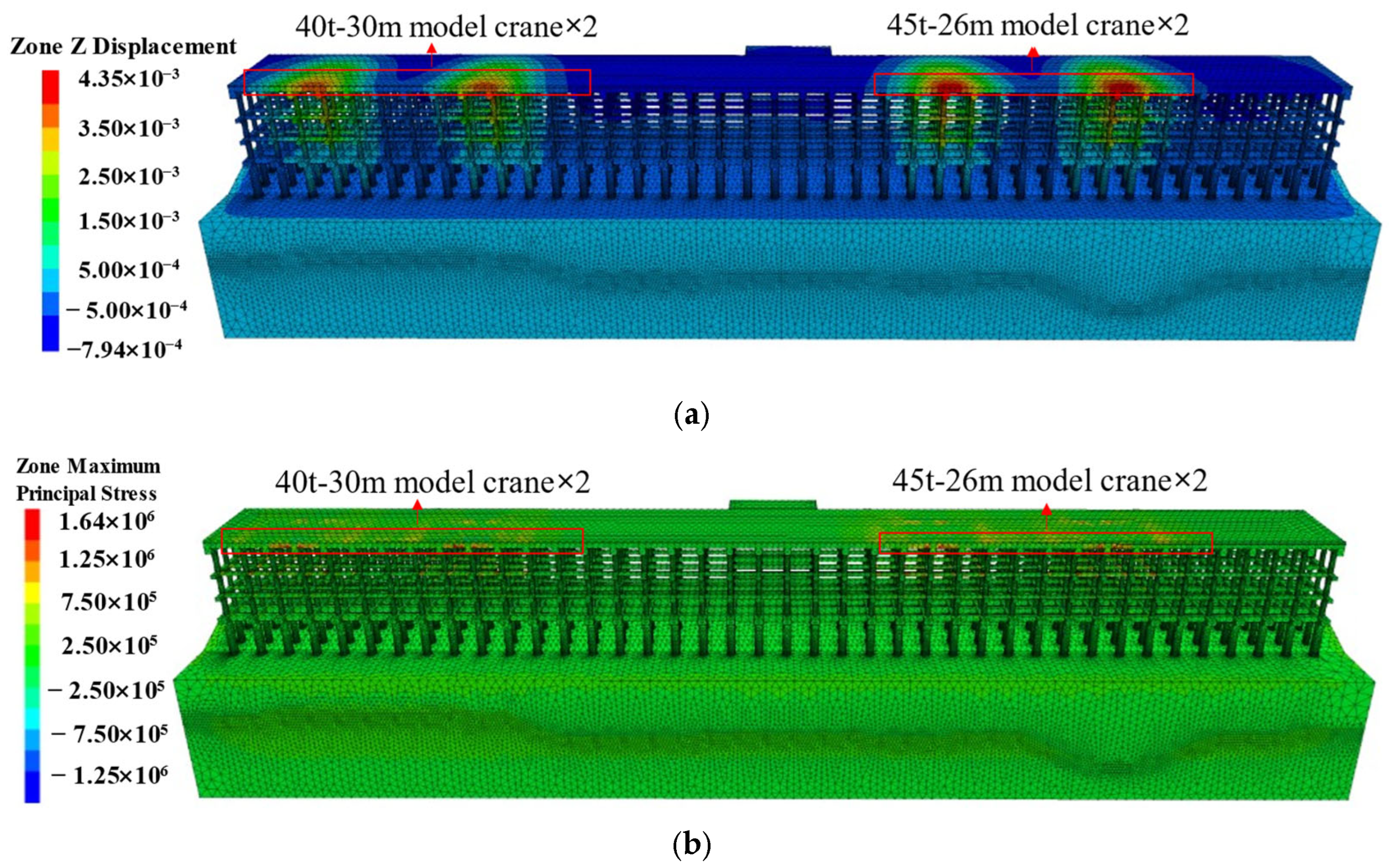
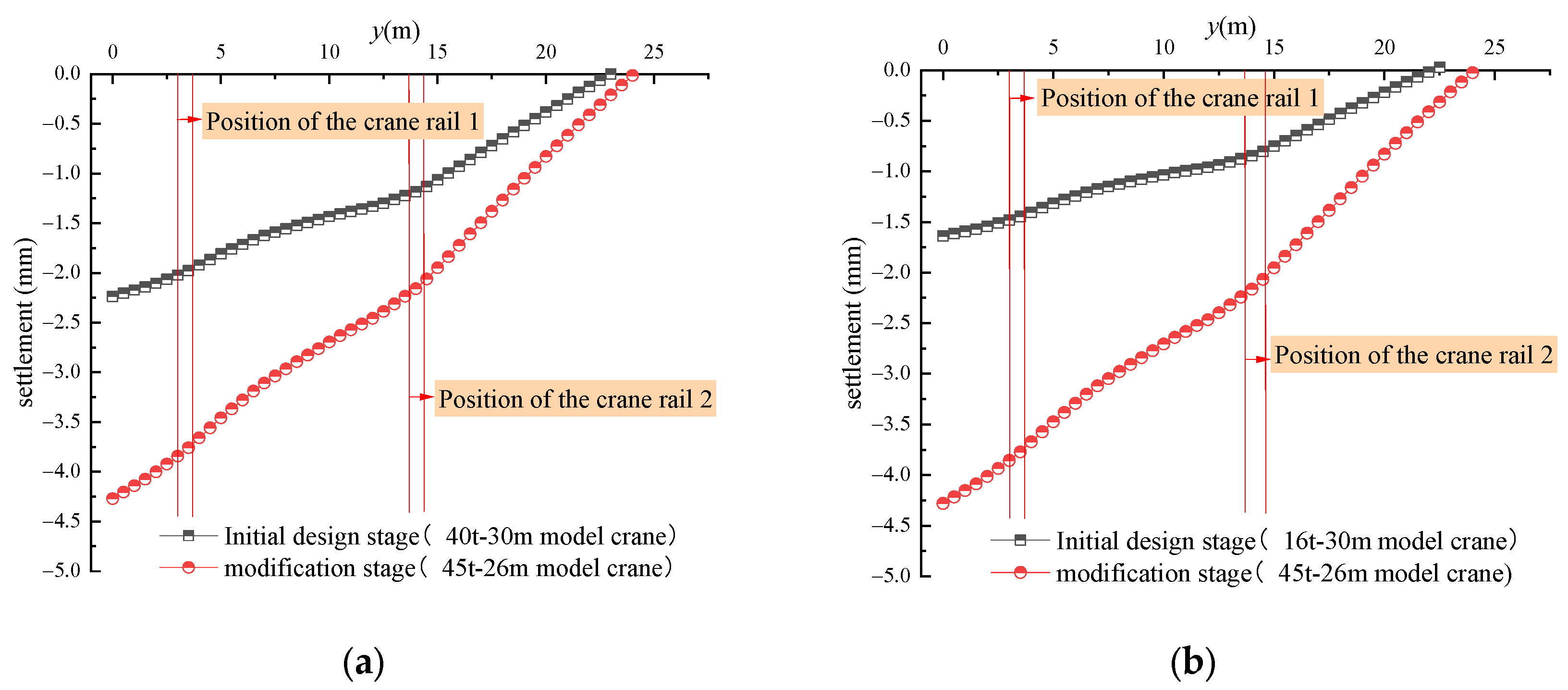
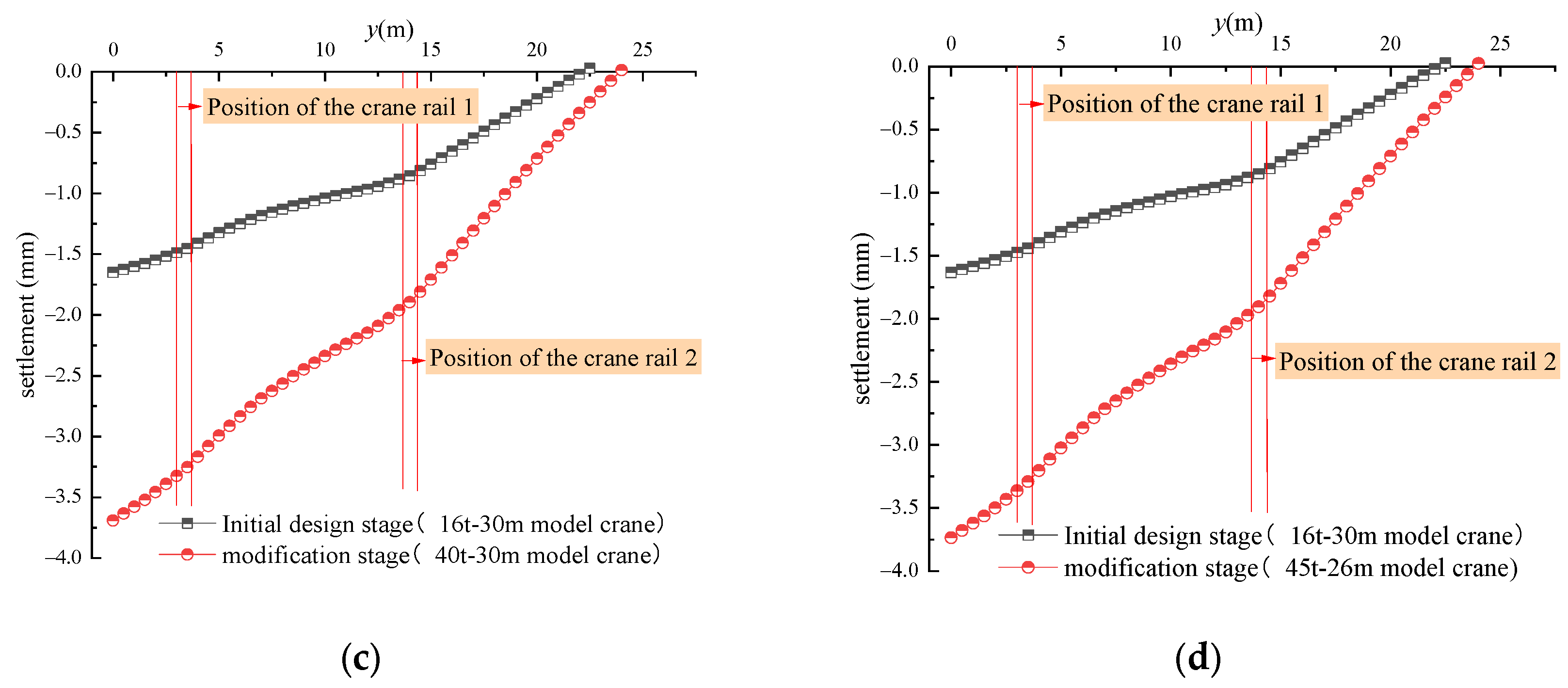
4.2.1. The Impact of Crane Changes

Figure 12 illustrates the vertical displacement of the wharf structure under Cases II and III. As a consequence of the crane’s weight, a significant settlement was observed at its location, with the maximum occurring at the surface layer and gradually decreasing towards the next layer. The maximum vertical displacement was observed at the maximum tonnage of the crane, with maximum values of 2.27 mm and 4.35 mm, respectively. Furthermore, due to the crane’s non-central position within the panel, asymmetric pressure is generated on the panel as a result of its larger self-weight, resulting in a certain upward bulge deformation on the side away from the crane. The maximum bulge deformation under the three working conditions is 0.70 mm and 0.84 mm, respectively.

Figure 13 shows the vertical displacement at the same installation position (x = 60 m, 116 m, 188 m, and 240 m) before and after the crane change in Cases II and III. Following the change of the crane, there was a notable increase in vertical displacement, with the greatest vertical displacement increment occurring at the edge of the wharf structure (on the river side). As the value of y increased, the vertical displacement increment exhibited a gradual decrease. A significant turning point was observed at the second crane track, with a rapid decrease in the vertical displacement increment. The maximum vertical displacement increment was observed at x =116 m, with a displacement increment of 2.64 mm and an increase of 161%. The minimum value was generated at x = 60 m, with a displacement increment of 0.58 mm and an increase of 24%. This is due to the inconsistency in the weight increase of the crane following two changes. The weight of the crane at x = 116 m increased by 181.25%, while the weight of the crane at x = 60 m increased by 12.5%. This demonstrates that cranes have a significant impact on the deformation of wharf structures, and that their weight is an important factor affecting structural deformation.

The asymmetric deformation caused by the installation position of the crane results in the generation of significant tensile stress on both sides of the track (orange and yellow distribution in Figure 14), while compressive stress is observed at the track position. The maximum tensile stresses under Cases II and III are 1.49 MPa and 1.65 MPa, respectively. These values are below the designed tensile strength of C40 concrete for the wharf, which is 1.51 MPa. This implies that the introduction of a new crane position may result in the formation of cracks in the concrete.

4.2.2. The Impact of Pile Defects

In Case IV, which considers the influence of pile defects alone, both the defective pile and its corresponding upper components have undergone significant deformation (Figure 15a). This is primarily attributable to the presence of defects in the pile, which has resulted in a reduction in its strength, thereby leading to an uneven distribution of stress on the upper structure and a notable degree of settlement. The greatest vertical displacement is observed at the E-7 rock-socketed pile and connecting beam, where there are significant and dense pile defects, with a maximum vertical displacement of 0.63 mm. It can be observed that the vertical displacement caused by pile defects is comparatively minor in comparison to the displacement caused by changes in the crane, which is 2.08 mm. Local defects in some rock-socketed piles result in significant stress concentration at their corresponding positions, with a maximum tensile stress of 1.1 MPa (Figure 15b). The occurrence of such high tensile stress concentrations in rock-socketed piles renders them susceptible to deformation and failure, which in turn affects the stability of the upper structure.

Compare the maximum stress and vertical displacement of the wharf structure in four different cases. As illustrated in Figure 16, the maximum tensile stress, compressive stress, and vertical displacement were 1.65 MPa, 1.47 MPa, and 4.35 mm, respectively, in Cases I and III due to the presence of a maximum-tonnage crane. Due to the relatively low tonnage of the crane in the initial design stage, the maximum stress and displacement generated in Case II are smaller than those in Cases I and III, with reductions of 10%, 30%, and 48%, respectively. In the presence of pile defects, Case IV exhibited minimal stress and displacement values of 1.10 MPa, 0.63 MPa, and 0.63 mm, respectively. These values were 33%, 57%, and 85% lower than those observed in Case I.

In comparison, it can be observed that the impact of crane changes is most significant, resulting in notable deformation of the wharf structure. The impact of defective piles is relatively minor, but nevertheless merits consideration. The high stress concentration at the defect site poses considerable harm, and its bearing capacity directly affects the stability of the upper structure. When the two factors are considered together, the deformation and damage at the defect of the pile body are more severe. Consequently, in operational conditions, the combined effect of various loads on the wharf structure results in a more severe situation, necessitating the strengthening and treatment of concrete components to prevent further deterioration.

5. Treatment Measures

In light of the aforementioned analysis, the following treatment measures have been implemented.

• It is necessary to repair and reinforce the concrete cracks existing on the wharf site. For the repair of shallow cracks or irregular cracking in concrete, it should be noted that these will not directly affect the structural load capacity. Cement, asphalt oil, and other similar materials can be applied directly to the surface of the concrete for repair. In cases where deep or penetrating cracks are more severe, grouting can be employed using pressure equipment to inject bonding materials into the cracks, thereby forming a unified whole and effectively improving the overall stability of the concrete. Distinct repair strategies should be implemented based on crack width. For cracks ≤0.2 mm, no intervention is typically required. Microcracks in concrete (0.2 < w ≤ 0.3 mm) may be treated using low-viscosity epoxy resin, which penetrates and solidifies within the fissures. Medium cracks (0.3–3 mm) necessitate high-pressure grouting with cementitious or polymeric materials, followed by surface sealing with elastomeric coatings. In cases where grouting is infeasible, structural reinforcement via steel mesh-reinforced shotcrete (C25 fine-aggregate concrete) is recommended. For cracks >3 mm, damaged concrete should be excavated and replaced with non-shrinkage, high-strength concrete to restore load-bearing capacity.
• Implement construction treatment in instances where the thickness of the steel reinforcement protective layer is not deemed to be adequate. In instances where the protective layer’s thickness is inadequate, remeasurement and reconstruction are necessary to augment the layer’s thickness and ensure compliance with the specified requirements. Conversely, in cases where the protective layer’s thickness is excessive, mechanical cleaning can be employed to eliminate the surplus layer. In instances where the steel reinforcement protection layer is not deemed to be of an acceptable standard, it is imperative to consider reconstruction in accordance with standard construction methods. Otherwise, it will reduce the bearing capacity of the wharf structure and accelerate the damage of the wharf structure.
• The lifting equipment is to be replaced in accordance with the actual requirements of the wharf. The installation method combining small and large lifting equipment in Case II is significantly more reasonable than the distribution of overly dense large lifting equipment in Case III. Furthermore, this method will not cause deformation or damage to the local structure of the wharf due to excessive load. Consequently, in order to guarantee the safe operation of the wharf, comprehensive selection, comparison, and optimization analysis of lifting equipment change plans must be conducted, and the most suitable lifting equipment installation plans must be selected for change processing.
• It is necessary to repair the defects in the piles and to adopt a new method for the daily testing of the pile foundations. This method should be capable of identifying damage to the pile foundation at an early stage and should enable timely measures for repair to be taken, thus avoiding greater losses.
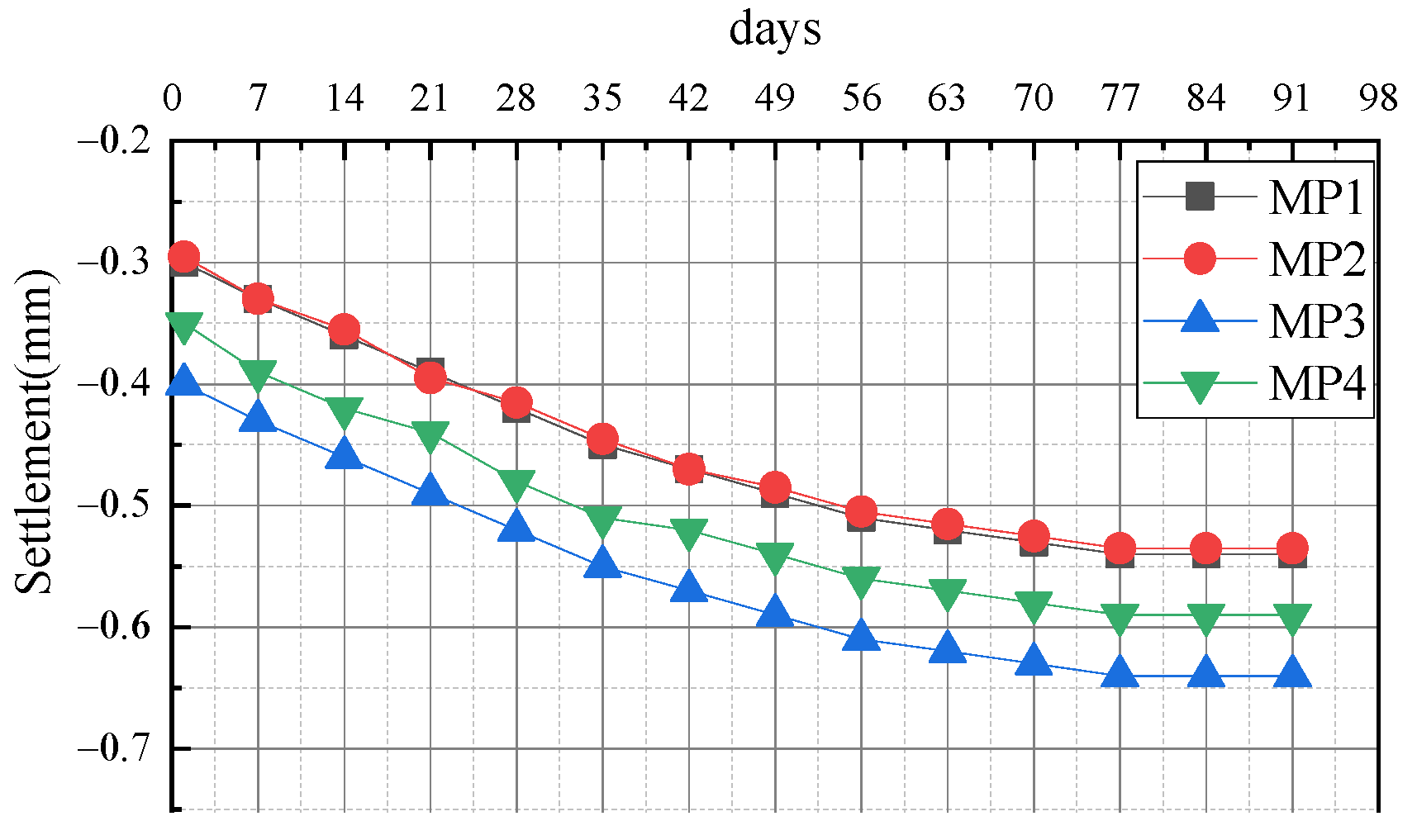
• It is recommended that information technology be combined with the establishment of a wharf monitoring system to monitor the horizontal displacement and settlement deformation of hydraulic structures in real time. A wharf monitoring and early-warning system should be constructed to provide support and guarantee the construction and operation safety of emergency reinforcement and subsequent system reinforcement.

6. Conclusions

A wharf structure is subject to a number of factors during its operational lifetime. This study employed a potential cause analysis and elimination methodology to elucidate the primary causes of cracking in a high-pile beam plate wharf and proposes corresponding reinforcement measures. Based on the results, the following conclusions can be drawn.

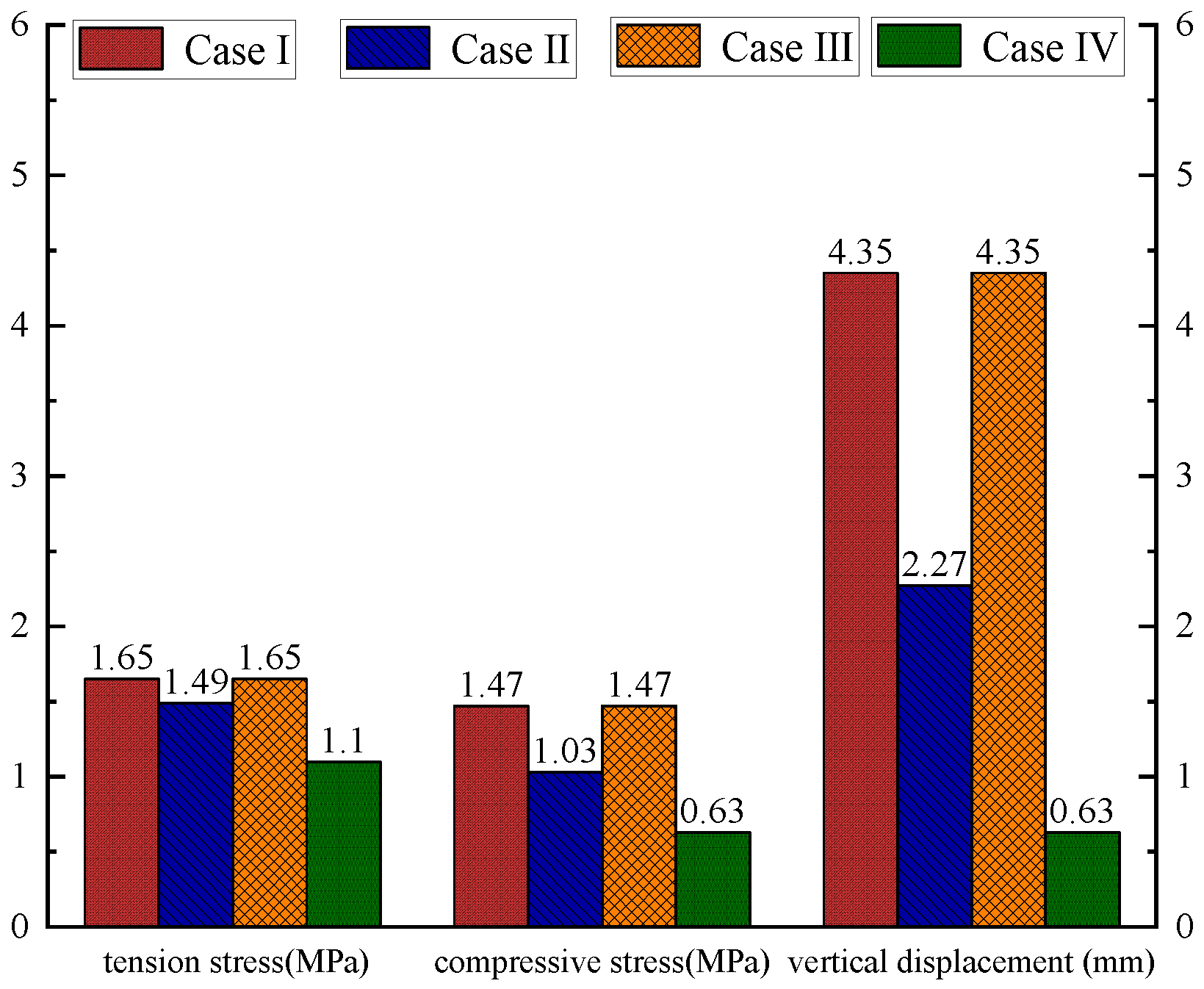
• The primary cause of the cracking observed in concrete components is the result of alterations made to the crane. Following the modification of the crane, the maximum tensile and compressive stresses of the wharf structure increased by 0.16 MPa and 2.58 MPa, respectively, in comparison to the initial design stage. This represents increases of 11% and 44%, respectively. This resulted in a maximum vertical displacement increase of 2.08 mm, representing a 92% increase. Furthermore, the maximum tensile stress generated by the crane following the modification exceeded the tensile strength of the concrete, leading to the formation of cracks.
• The impact of pile defects on the stability of wharf structures is relatively minor, yet it is nonetheless a significant factor that cannot be overlooked. The tensile stress at the defect site of the pile is high, with a maximum tensile stress of 1.1 MPa. This makes the defective pile prone to deformation and damage, thereby affecting the stability of the upper structure. The more intact pile resulted in greater deformation of the upper components of the defective pile, with a maximum vertical displacement increase of 0.23 mm, an increase of 58%.
• A three-dimensional numerical model of a high-pile beam plate wharf was constructed in order to ascertain the complex stress and deformation response of the structure under the combined action of gravity load, water load, crane load, and pile defects. Thus, an effective approach was provided. Given the multitude of factors that influence the safety of wharf structures in practice, it is highly effective and imperative to establish a comprehensive three-dimensional numerical model that aligns with the actual scale for analysis.
• In this paper, a large-scale three-dimensional numerical simulation was carried out by modeling according to the actual dimensions. It took into account the deformation and damage of the wharf under the combined action of multiple loads. The simulation results are consistent with the actual situation, which has great reference significance. However, regarding the accurate identification of the existing damage to the wharf structure, since the simulation did not consider the effects of wave loads, wind loads, or water erosion, there still exists a slight difference between the position of the plastic damage obtained from the numerical simulation and the actual damage position. As a result, it is unable to achieve the health monitoring of the wharf structure, and further research on this is still needed.