Comprehensive Design Optimization Framework for Prestressed Concrete Continuous Beam Bridge Using Genetic Algorithm and Backpropagation Neural Network

Abstract

Prestressed concrete (PC) continuous beam bridges are widely used in transportation infrastructure. However, their construction involves substantial material consumption, raising sustainability concerns amid increasing environmental pressures. This study aims to address the urgent need for resource-efficient bridge design by developing a comprehensive optimization framework that minimizes material usage while ensuring structural safety, durability, and compliance with engineering standards. The proposed methodology integrates a Genetic Algorithm (GA) with a Backpropagation (BP) neural network to optimize both the cross-sectional geometry and the overall alignment of PC continuous beam bridges. The GA is utilized to identify optimal cross-sectional parameters within regulatory constraints, while the BP neural network, trained on extensive design data, refines the bridge bottom height profile to enhance structural performance. The integrated GA-BP framework is validated through a case study of a continuous beam bridge, demonstrating a 94% improvement in design efficiency, a 14% reduction in concrete consumption, and a 34% reduction in prestressed steel usage during the preliminary design stage. These results highlight the framework’s significant potential in advancing sustainable and intelligent bridge design, offering a novel approach to combining artificial intelligence with structural optimization for practical engineering applications.

1. Introduction

The prestressed concrete (PC) continuous beam bridges pre-apply the internal tension of prestressing steel reinforcement to enhance the load-bearing capacity of the structure. This design performs admirably under various environmental conditions, especially in extreme climates and geographical conditions such as high temperatures, high humidity, strong winds, and earthquakes [1]. However, with the continuous increase in traffic loads and environmental pressures, countries worldwide are increasingly focusing on sustainability issues arising from environmental and resource consumption concerns [2]. In the construction industry, steel and concrete are the most commonly used building materials, accounting for over 30% of the global construction industry’s energy consumption [3] and over 70% of energy consumption among all building materials [4]. Effective alleviation of sustainability issues in the construction industry can be achieved by reducing material consumption while meeting functional and structural requirements. Therefore, continuous research and innovation are indispensable to further enhance the design and construction techniques of such bridges to meet future challenges. According to Zhou, et al. [5], improvements in structural designs can play a crucial role in enhancing the sustainability of these bridges, ensuring their long-term operation under more demanding conditions.

PC continuous beam bridges are widely used in bridge construction, with numerous completed projects providing valuable data and experience for both design and construction. However, determining design parameters for these bridges often relies on subjective and restrictive criteria, prompting engineers to engage in iterative calculations and adjustments during the design phase. For instance, engineers may adjust parameters such as beam dimensions and reinforcement distribution until they comply with the design codes. This method, though practical, often results in conservative design choices, leading to oversized cross-sections or excessive reinforcement, thereby causing material wastage. In projects with similar engineering conditions, designers frequently refer to standard design formulas, tables, and charts provided by regulations and standards. These references guide the selection of design parameter values, like dimensions and load-bearing capacity, based on the project’s specific requirements. However, the drawback of this approach lies in its dependence on generalized design formulas and empirical values, which may not account for the unique needs of individual projects. As a result, the conventional approach usually causes design redundancy and material wastage, while fully satisfying the load requirements.

The optimization of bridge structures must begin with a focus on efficient material usage [6]. This includes refining design parameters [7], reducing construction costs [8], enhancing construction efficiency [9], and minimizing energy consumption and carbon emissions [10,11]. As designs become increasingly complex, the number of parameters involved in the optimization process grows, transforming the problem from a singular to a multi-objective challenge. Therefore, balancing material costs with energy consumption has become essential [12,13]. Traditional mathematical modeling and single-objective optimization methods are inadequate for addressing these complexities.

In response, researchers have integrated metaheuristic algorithms into the optimization process. These algorithms have been employed to optimize reinforcement quantities [14] and reduce overall construction costs [15], demonstrating significant potential in optimizing large, complex bridge structures [16]. By facilitating more efficient and sustainable designs, these algorithms overcome limitations in optimization, particularly when addressing multiple objectives [17,18]. To achieve optimal design and performance, engineers must consider factors such as the shape and dimensions of various sections of the continuous beam and the corresponding prestressing reinforcement. A multi-objective optimization approach is crucial to meet diverse engineering requirements and performance indicators in the optimization of continuous beam bridges. Previous studies have explored the optimization of partially and fully prestressed concrete bridges using genetic algorithms to enhance sustainability and reduce implicit carbon emissions and costs [7,10]. However, previous studies have focused on optimizing each segment individually, which can significantly complicate the overall process and increase the workload. Currently, there is a lack of comprehensive solutions that simultaneously address the optimization of both the overall bridge curve design and the cross-sectional dimensions. This highlights a gap in holistic optimization approaches for continuous beam bridges.

Given these challenges, this study employs a GA-BP approach to predict the optimal geometric variations of continuous beam sections, deriving the best overall bridge curve based on these optimization variables. By addressing the limitations of conventional design methods, this research integrates advanced optimization techniques into a comprehensive framework. The framework has two main components: optimizing sectional dimensions using genetic algorithms and predicting the overall bridge curve through a GA-BP neural network. Structural analysis and verification are then conducted to ensure safety and performance. The primary goal of this study is to provide a systematic and efficient methodology for the design and optimization of continuous beam bridges, emphasizing both precision and sustainability. Although the study utilizes the Chinese reinforced concrete bridge code for validation, the proposed optimization framework is universally adaptable and can be applied to bridge design and optimization in various countries or regions. This approach is expected to contribute significantly to the development of more efficient, durable, and sustainable continuous beam bridge designs.

The remainder of the paper is structured as follows. The Literature Review discusses the current methods of bridge design and optimization, as well as the application of various metaheuristic algorithms in bridge optimization. Section 3 provides a detailed introduction to the optimization framework for PC continuous beam bridges. In Section 4, we present an optimization design based on a real engineering example and perform a comparative analysis to highlight the advantages of our optimization framework. Finally, Section 5 offers a comprehensive conclusion of this study and outlines the future work.

2. Literature Review

In the pursuit of creating safer, more economical, and sustainable bridge structures, optimization research has employed various strategies, including reducing steel consumption by substituting traditional steel with high-strength alternatives, optimizing the cross-sectional dimensions and reinforcement layout of reinforced concrete beams to lower overall bridge costs [19], and employing topology optimization to enhance bridge performance [20]. The optimization process typically involves multiple objectives, such as minimizing costs, maximizing performance, and enhancing sustainability, while considering various constraints like material strength and load requirements. To improve post-optimization performance, researchers have integrated locally optimal search operators based on rigorously derived Optimality Criteria (OC) techniques into their optimization frameworks [21]. Moreover, studies have addressed the impacts of moving traffic loads [19] and environmental forces [22] during optimization, incorporating these factors as constraints to minimize the bridge’s self-weight. In parallel, recent developments in damage identification and stiffness optimization methods, such as the stiffness separation method [23,24], have further advanced the computational efficiency and accuracy in assessing complex bridge structures. As bridge structures grow increasingly complex, with a wider variety of design variables, optimization challenges become more intricate, making metaheuristic algorithms particularly suitable for addressing these issues.

Metaheuristic algorithms have a broad range of applications in engineering optimization. Their main goal is to explore, generate, or select heuristic solutions using local search strategies to identify the best solutions that meet multiple optimization objectives in a complex design space [25]. This approach allows engineers to effectively optimize structures by balancing various objectives and intricate constraints, ensuring that performance and safety requirements are satisfied. For example, Skoglund, et al. [26] employed multi-objective optimization to optimize the steel structure of a steel–concrete composite bridge, considering independent objectives like weight, cost, and environmental factors. Similarly, Abdelkader, et al. [27] developed a multi-objective optimization model using an exponential chaotic differential evolutionary algorithm to maximize the performance level of bridge components, minimize lifecycle maintenance costs, reduce traffic disruption time, and minimize environmental impact. Jahjouh and Erhan [28] proposed an improved harmony search algorithm for optimizing the main beam sections of prestressed concrete bridges. In summary, metaheuristic algorithms have proven highly effective in optimizing bridge structures, allowing for the generation or selection of heuristic solutions that satisfy multiple objectives, including reducing the cost of bridge superstructures, decreasing material usage for reinforced concrete components, and minimizing carbon emissions while integrating performance and safety requirements. Among the heuristic algorithms, the GA is the most common algorithm for multi-objective optimization problems [18]. The GA can be combined with finite element methods to reduce the weight of steel truss arch bridges [22], and can also be combined with visual programming to establish an automation framework that maximizes material consumption reduction [9]. Overall, the GA demonstrates significant advantages in study by effectively addressing multi-objective challenges and rapidly converging to optimal solutions, making it a powerful tool for structural optimization in bridge design.

While optimization of bridge structures has yielded significant results—such as cost reduction, enhanced performance, and decreased carbon emissions—the methods for prestressed concrete (PC) continuous beam bridges may not be directly applicable due to the varying load conditions and structural transformations throughout different construction stages. Achieving optimal design and performance for these bridges requires careful consideration of multiple key factors, including the cross-sectional shape and dimensions of the continuous beam, as well as the design of prestressed reinforcement. Structural analysis and verification are essential to ensure that the bridge meets strength, stiffness, and durability requirements under various loads.

Researchers have addressed these challenges using advanced optimization techniques. For instance, García-Segura, et al. [29] utilized a hybrid harmony search algorithm with threshold optimization for sustainable concrete continuous beam bridge design, minimizing costs and emissions while ensuring safety. García-Segura and Yepes [30] developed a multi-objective optimization method addressing cost, carbon dioxide emissions, and safety for post-tensioned concrete bridge beams, employing a multi-objective harmony search to find optimal solutions for geometry, concrete strength, and reinforcement. Martínez-Muñoz, et al. [31] integrated unsupervised learning with continuous swarm intelligence metaheuristics to optimize the cost and CO₂ emissions of reinforced concrete continuous beams.

Despite recent advancements, many current optimization methods remain limited to the design of individual segments or to isolated components such as concrete volume or prestressing steel quantity, lacking a comprehensive consideration of the bridge as a whole. Such fragmented approaches often fail to capture the interdependence among key design variables, which can result in suboptimal global performance. Therefore, future research should emphasize the integration of global design variables to achieve a more thorough and coordinated optimization of continuous beam bridges. To address this gap, the present study proposes a comprehensive framework that simultaneously optimizes both the critical cross-sectional dimensions and the prestressing reinforcement layout of continuous beam bridges. Additionally, a GA-BP neural network model is developed to optimize the overall bridge curve design. In this model, the genetic algorithm (GA) is employed not only for multi-variable optimization of structural parameters, but also to identify the optimal weights and thresholds of the backpropagation (BP) neural network. This enables the GA-BP model to accurately capture complex nonlinear relationships within the design space and to efficiently determine the optimal solution with minimal prediction error. The final optimization results are validated through structural analysis to ensure full compliance with engineering specifications and operational requirements.

3. Methodology

Based on the mechanical characteristics of continuous beam bridges and engineering practice, the pivot section (maximum negative moment zone) and mid-span section (maximum positive moment zone) are selected as key optimization zones, as their stress states represent over 95% of the most critical conditions along the entire bridge. Seven key design variables are considered: beam height at the pivot and mid-span, total span length, side/mid-span ratios, and the power exponents of the beam height and bottom slab thickness variation curves. These parameters are directly related to the bridge’s geometric configuration and static performance, jointly determining its load-bearing capacity, stiffness distribution, and material consumption. The optimization framework for continuous beam bridges proposed in this study is illustrated in Figure 1, and comprises two main components: the optimization of cross-sectional dimensions and prestressing reinforcement, and the training of a GA-BP neural network model for overall bridge curve design.

In the optimization phase, the pivot section and mid-span section are identified as critical areas for optimization based on actual engineering requirements and specifications. The key design variables are selected as optimization variables. The Genetic Algorithm (GA) generates an initial population of cross-sectional dimensions, followed by the creation of new populations through crossover and mutation operations. Iterative calculations are then performed to determine the minimum cross-sectional area of the continuous beam. The required area for prestressing reinforcement is calculated, and the positive section capacity is verified to ensure compliance with relevant codes.

During the training of the GA-BP neural network for the overall bridge curves, the collected data are first organized and preprocessed. The GA is utilized to encode the weights and thresholds of the initial neural network, with the training error of the Back Propagation (BP) neural network serving as the adaptation value. The optimal combination of weights and thresholds is obtained through the GA, and these parameters are then updated in the neural network to create a training model with minimized error. The processed cross-sectional dimension information is subsequently input into the trained neural network to generate the overall bridge curves. Finally, a structural analysis of the entire bridge is conducted to ensure the safety and performance of the optimized structure.

3.1. GA-Based Optimization for Prestressing Reinforcement and Section Dimensions

3.1.1. Parameter Variables for Cross-Section Optimization of Continuous Beam

The optimization framework selects the mid-span and pivot sections as the primary control sections, based on their distinct mechanical behaviors, prestressing layouts, and loss mechanisms. The mid-span section typically experiences the maximum positive bending moment and must resist tensile stresses; therefore, prestressing tendons are usually arranged along the bottom edge. In contrast, the pivot section is subjected to the maximum negative bending moment and significant shear force, requiring tendons to be concentrated near the upper edge. Additionally, critical nodes or variable cross-section zones may be exposed to complex stress combinations (bending, shear, and torsion), and geometric discontinuities can lead to stress concentrations. Since different sections are characterized by different stress states and corresponding prestress loss mechanisms, the effective prestress must be accurately calculated for each section accordingly. The span and pivot section dimensions of the continuous beam are illustrated in Figure 2. The following seven variables were selected for analysis in this study: continuous beam height h, cantilever plate length d, top plate thickness $e_a$ web plate thickness $e_b$, root plate thickness $e_c$, bottom plate thickness $e_d$, and prestressing reinforcement area Ap [32,33]. The width of the top plate of the continuous beam B needs to be determined according to the actual project engineering requirements. The width of the base plate b depends on the length of the cantilever plate, i.e., $b=B-2d$. The dimensions of the stem axils ($x_1$, $x_2$, $x_3$, $x_4$) of the box chambers in the continuous beam are determined according to the following equations but are not included in the variables of the optimization calculation.

$$x_1=x_3=e_c-e_a$$

(1)

$$x_2=x_4=b/5$$

(2)

The beam height h of the continuous beam should satisfy the range of 1/30 to 1/50 of the maximum span height at the mid-span section and 1/16 to 1/20 of the maximum span height at the pivot section. The length of the cantilever plate d is according to the specification, if it is more than 3 m, transverse prestressing should be set; if no transverse prestressing is set, the length of the cantilever plate is generally 2 to 2.5 m. The top plate of the continuous beam should satisfy the requirements of the bridge deck plate, the thickness of the top plate e_a should not be less than 200 mm, and the specific value should be determined according to the actual project and the specification of the bridge. The specific value should be determined according to the actual project and bridge specification. The thickness of the web of prestressed concrete continuous beam e_b shall be set up as a gradually widening structure from the middle of the span to the pivot according to the specification requirements, the thickness of the web in the middle of the span is generally taken as 300–400 mm, and the thickness of web at the pivot is taken as 500–600 mm. e_c of the thickness of the root of the cantilevered plate of the continuous beam shall be taken as d/4. The thickness of the bottom plate of the continuous beam should satisfy the force characteristics of the continuous beam under the action of positive bending moment and the construction requirements of the force reinforcement. The thickness of the bottom plate will be gradually thickened from the mid-span section to the pivot section with the increase in negative bending moment, and the thickness of the bottom plate at the pivot section is generally 1/10 to 1/12 of the height of the pivot beam, which can satisfy the load requirement of the continuous beam bridge in the construction and operation stages. The thickness of the bottom plate in the span of a continuous beam is generally 200 to 250 mm, to satisfy the change in positive and negative moments in the span of a continuous beam and the structural requirements.

3.1.2. Objective Function

In this study, the objective is to minimize the combined cross-sectional area of the continuous beam and the area of prestressing reinforcement. Therefore, the objective function is the sum of the cross-sectional area of the continuous beam and the prestressing reinforcement area at each corresponding section. This objective is to be minimized, subject to constraints that ensure the design requirements are satisfied. The optimization can be expressed in the following equation:

$$F\left(A\right)={\mathit{min}(A}_c+A_{p\_\mathit{all}})$$

(3)

The area calculation of a continuous beam in a prestressed concrete bridge can be approached by dividing the beam into smaller sections (as shown in Figure 3). The area of each smaller section is then calculated individually. The total area A_c of the continuous beam section is the sum of the areas of these individual subsections, which can be expressed as

$$A_c=\sum _{i=1}^n{A}_i$$

(4)

The area of prestressing reinforcement A_{p_all} for the corresponding optimized section of a continuous prestressed concrete beam is calculated as follows:

$$A_{p\_all}=A_p\left(N_s+N_x\right)$$

(5)

where A_p is the cross-sectional area of a single prestressing reinforcement in the tensile zone of the bridge cross-section. N_s and N_x are the number of prestressing bars required at the top and bottom edges of the continuous beam section.

Prestressing reinforcement number for continuous beam bridges can be considered only to control the tensile stress at the top and bottom edges of the cross-section, and the number of reinforcements at the top and bottom edges of the prestressing reinforcement is calculated according to the following equation:

$$N_s\ge {\displaystyle \frac{M_{\max }\left(e_s-k_x\right)-M_{\min }\left(k_s+e_x\right)}{\left(k_s+k_x\right)\left(e_s+e_x\right)}}\times {\displaystyle \frac{1}{A_p{\sigma }_{pe}}}$$

(6)

$$N_x\ge {\displaystyle \frac{M_{\max }\left(k_x+e_s\right)+M_{\min }\left(k_s-e_x\right)}{\left(k_s+k_x\right)\left(e_s+e_x\right)}}\times {\displaystyle \frac{1}{A_p{\sigma }_{pe}}}$$

(7)

where M_max and M_min are the maximum and minimum bending moments at the optimized cross-section, and the bending moments are calculated according to the specification in accordance with the most unfavorable combination of loads. e_s, e_x is the center of gravity of prestressing reinforcement at the upper edge and the center of gravity of prestressing reinforcement at the lower edge away from the center of gravity of the cross-section (e_s = z_bs − e, e_x = z_bx − e, e is the distance from the center of gravity of the section of the prestressing reinforcement to the edge of the section); k_s and k_x are the core distance above and below the cross-section (k_s = I_yy/(A_c × z_bs), k_x = I_yy/(A_c × z_bx).

In the normal service limit state, prestressed concrete members will produce prestressing loss, called prestressing loss value σ_l. The circumstances leading to prestressing loss include the following six elements: friction between prestressing reinforcement and tube wall; anchorage deformation, rebar retraction, and joint compression; temperature difference between prestressing reinforcement and abutment; elastic compression of concrete; stress relaxation of prestressing reinforcement; and shrinkage creep of concrete. σ_pe is the effective prestressing force of prestressing reinforcement in the tensile zone of the bridge cross-section, calculated as

$${\sigma }_{pe}={\sigma }_{con}-{\sigma }_l$$

(8)

where σ_con is the tension control stress of prestressing in the tension zone, which should not be greater than 0.75 f_pk according to the specification, and f_pk is the standard value of tensile strength of prestressing reinforcement. σ_l is the value of prestress loss in the tension zone, which is the process of reduction or loss of tension in prestressing reinforcement in the prestressed concrete structure, and it may be caused by the creep, transmission, bending, and indirect factors, and the value of prestress loss often needs to be calculated and controlled according to the process maneuvers, etc., in the project. For a continuous beam section, the effective prestressing force of prestressing reinforcement in the tensile zone of the section is calculated as 0.7 σ_con for the main beam bearing section, 0.8 σ_con for the side-span section, and 0.6 σ_con for the mid-span section.

3.1.3. Constraints

To optimize the optimization variables towards the evolution of the objective function so that the optimum solution can be obtained, the positive section capacity of the beam is used as a constraint according to the code requirements. In accordance with the code, the height of the compression zone at the interface is first calculated:

$$x={\displaystyle \frac{f_{pd}{A}_{p\_all}-f_{sd}{A}_s}{f_{cd}B}}$$

(9)

where f_pd is the design value of compressive strength of prestressing steel; f_sd is the design value of tensile strength of ordinary steel; A_{p_all} is the area of prestressing steel; A_s is the area of ordinary steel; f_cd is the design value of compressive strength of concrete.

After the height of the cross-section compression zone of the continuous beam is calculated, it is compared with the equivalent flange plate thickness h_f. If x ≤ h_f, it shows that the cross-section compression zone of the continuous beam is within the range of the flange plate thickness, which satisfies the first type of box cross-section. Then the positive cross-section capacity at this time is

$$M_u=f_{cd}\cdot B\cdot x\cdot \left(h_0-{\displaystyle \frac{x}{2}}\right)$$

(10)

Otherwise, the calculation is based on a second type of box section:

$$M_u=f_{cd}\cdot 2e_b\cdot x\cdot \left(h_0-{\displaystyle \frac{x}{2}}\right)+f_{cd}\cdot \left(B-2e_b\right)\cdot h_f\cdot \left(h_0-{\displaystyle \frac{h_f}{2}}\right)$$

(11)

where h₀ is the effective height of the section (h₀ = h − a, a is the distance from the point of action of the prestressing reinforcement to the top edge of the section), h_f is the equivalent thickness of the flange plate, h_f = e_f + 2 ∗ (A₄ + A₇)/(B − 2e_b).

Once the calculation of the positive section capacity (M_u) is completed, a comparison with the design capacity (M_d) is required. If M_u is greater than M_d, it indicates that the orthotropic section capacity requirement has been satisfied, at which point the calculation should be terminated and the results are output. However, if M_u is less than M_d, the requirement has not been satisfied and the calculation must be repeated.

3.2. GA-BP-Based Optimization for the Overall Bridge Curve Design Optimization

The GA-BP neural network establishes an efficient training model (as shown in Figure 4), accurately predicting the overall bridge curve while accounting for various design parameters and loading conditions. First, the collected continuous beam data are organized and preprocessed. Then, the GA is used to encode the initial neural network weights and thresholds, with the BP neural network’s training error serving as the fitness value. The optimal weight and threshold combinations are obtained through the GA, and these parameters are updated in the neural network to minimize the training error. Finally, the processed section dimension information is input into the trained neural network to obtain the variation curves of the continuous beam bridge’s geometric characteristics.

3.2.1. Data Selection and Processing

Before training the neural network, it is essential to gather sufficient data on continuous beam bridges to ensure the accuracy of the algorithm. Given the numerous parameters associated with these bridges, it is crucial to select appropriate input parameters for the model before establishing the prediction framework. In this study, we have identified pivotal beam height, mid-span beam height, total bridge span length, edge span, mid-span, beam height variation curve exponent, and bottom plate thickness variation curve exponent as the primary variables. These parameters determine the static properties, geometric shape, and structure of the continuous beam bridge. To enhance training effectiveness, we processed these data parameters by incorporating the pivot-to-mid-span beam height ratio (Xh), pivot-to-side span ratio (Hso), mid-span-to-side span ratio (Hsz), and edge-to-mid-span ratio (Bc) as input variables for the model. The two exponents of the variation curves were used as output variables to improve prediction accuracy. The pivot-to-mid-span height ratio (h/L) reflects the distribution of bending stiffness, while the edge-to-mid-span ratio represents the coordination of the main beam’s moment distribution.

Since the selected feature descriptors encompass both qualitative and quantitative aspects, it is essential to quantify these indicators for input into the model. Qualitative indicators must be converted into equivalent numerical values through appropriate quantitative processing. For existing quantitative indicators, such as beam height and total bridge span length, significant differences in scale and magnitude can hinder data integration within the model, adversely affecting predictive outcomes. Therefore, normalization of these quantitative indicators is necessary to mitigate the impact of data disparities before they are utilized as inputs. Regarding the normalization method, since the variables in this study are nonlinear and exhibit clear boundary distributions during the optimization process, the Min-Max normalization method is adopted. This approach can accelerate convergence and enhance training stability. The calculation formula is as follows:

$$x_0={\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(12)

3.2.2. Establishing a Prediction Model Based on GA-BP Neural Network

The BP neural network is a multi-layer feedforward network trained through error backpropagation, drawing inspiration from the structure and function of the human brain’s neural networks. Through multiple training iterations and learning cycles, combined with gradient descent, the BP neural network seeks to minimize the mean square error between the actual input values and the expected output values of the training model.

The network structure typically consists of three components: the input layer, hidden layers, and output layer (as illustrated in Figure 5). The operation begins by mapping the feature data of input signals (x_i) to the hidden layer and subsequently to the output layer to produce the expected output values. By comparing these expected output values with the actual measured values, the error function is computed. Through the error backpropagation mechanism, the weights and thresholds of the BP network are then adjusted using optimization algorithms, such as gradient descent. This iterative process continues until it meets predetermined criteria, such as a target error or a maximum iteration count, thereby completing the network training.

In this study, the GA-BP neural network was primarily used to predict the curve shape of continuous beam bridges, which is a nonlinear modeling problem. Two hidden layers were empirically selected for the model. The key parameters influencing the curve—total span length (S), side-span length (Ls), mid-span length (Lz), beam height at the pivot (h0), and beam height at mid-span (hz)—were used as input nodes, while the output nodes were the height curve (xl) and bottom slab thickness curve (xd) of the continuous beam bridge. In practical engineering design, beam height significantly influences the bottom slab thickness. Mechanically, an increase in beam height enhances the section’s moment of inertia, which reduces bending stress and allows for a thinner bottom slab. However, the bottom slab must still maintain sufficient thickness to resist local stresses and ensure stability, particularly in regions with higher beam height where shear forces and bending moments are greater. In terms of structural coordination, variations in beam height are typically accompanied by adjustments in bottom slab thickness to maintain geometric continuity. For example, at the pivot section where beam height is greater, the bottom slab tends to be thicker to resist high negative moments and shear forces; while at mid-span, a thinner bottom slab is sufficient to reduce self-weight. This coordinated design improves both the structural performance and material efficiency. Therefore, in this study, two separate models are developed to predict each of the curves.

However, when addressing practical problems, the BP neural network faces a challenge: the initial solution generated by its algorithm is randomly produced, directly impacting the overall performance of the algorithm. Consequently, its final results exhibit instability. Furthermore, the BP neural network algorithm employs gradient descent to determine the search direction. Due to the search space containing flat regions and multiple local minima, the BP neural network is prone to slow convergence or being trapped in local minima, impeding convergence. Previous research has revealed that genetic algorithms possess strong adaptability and excellent global search capabilities [34]. Thus, introducing genetic algorithms into the BP neural network algorithm can effectively compensate for its shortcomings. Optimizing weights and thresholds using genetic algorithms within the BP neural network can mitigate the issue of the network easily converging to local minima, thereby enhancing model accuracy. When utilizing genetic algorithms to optimize the BP neural network, the primary issue to address is the encoding problem of genetic algorithms. To obtain the optimal weights and thresholds within the BP neural network more effectively, this study adopts real number encoding, where the encoding length Z_l is calculated based on the number of weights and thresholds between neurons.

$$Z_l=x_i{x}_{h1}+x_{h1}{x}_{h2}+x_{h2}{x}_o+x_{h1}+x_{h2}+x_o$$

(13)

where x_i is the number of nodes in the input layer; x_o is the number of nodes in the output layer; x_h1 is the number of nodes in the first hidden layer; x_h2 is the number of nodes in the second hidden layer.

A set of data is first randomly generated and combined into an initial population based on a predefined population size. The initial weights and thresholds are obtained through BP neural network training, after which the genetic algorithm (GA) is employed to optimize these parameters and obtain a trained model that achieves minimum prediction error. This entire process—including convergence to the minimum error—is treated as a black-box computation. To ensure the reliability and repeatability of the optimization process, the optimized results are verified through crack resistance and deflection checks, in accordance with design codes. This validation confirms the reliability and practical applicability of the GA-BP model. For the calculation of the fitness value of the population, the error between the predicted output and the desired output of the BP neural network is used. The fitness value F is calculated using the following equation:

$$F={\displaystyle \sum _{i=1}^n{\left(o_i-y_i\right)}^2}$$

(14)

where n is the number of samples; o_i is the desired output of the ith node of the BP neural network and y_i is the predicted output of the ith node.

In the sample data, the last 30 sets of data are designated as the test set, while the remaining sets serve as the training set. Subsequently, normalization is applied in the algorithm, and training is conducted within the neural network model, with the parameter configuration detailed in

Table 1. Neural network parameter configuration.

Parameter	Value
Number of iterations	1000
Learning rate	0.01
Target minimum error	0.00001
Momentum factor	0.01
Minimum performance gradient	1 × 10−6
Maximum number of failures	6

[35]. Finally, the algorithm is executed based on the predetermined maximum number of iterations until reaching the set number of rounds, or if the algorithm finds a satisfactory solution during runtime. Through the GA, optimal weight values are identified, updating the weights and thresholds within the BP neural network to train the most accurate model. To acquire a more precise model for the overall bridge curves of continuous beam bridge beam height and bottom plate thickness, it was discovered through research that the bottom plate thickness curve is closely related to the beam height curve, with a tight geometric connection between the beam height and the bottom plate. Consequently, this study separately trains neural network models for these two curves. Unlike the continuous beam height variation curve, in the training model for the continuous beam bottom plate thickness variation curve, the continuous beam height variation curve is utilized as a feature. This approach enables obtaining a more accurate bottom plate thickness variation curve, thus providing a more reliable representation of the continuous beam’s structural characteristics.

4. Experimental Validation

To validate the applicability of the present optimization framework, a real case of a prestressed concrete continuous beam bridge project was selected for illustration. The project used a three-span, one-link prestressed concrete variable cross-section continuous beam structure with a single box and single chamber beam superstructure. The width (B) of the continuous beam was 9.2 m.

Table 2. Technical parameters of the continuous beam bridge.

Parameter Type	Parameters
Total span length	110 m
Middle span length	50 m
Side span length	30 m
Bridge design load	Highway–Class I
Pedestrian load	3.5 kN/m2
Bridge deck width	9.2 m
Prestressed continuous beam	C50 Concrete
Prestressed Reinforcement	Low-relaxation high-strength steel wires with a nominal diameter of 15.2 mm

lists the technical parameters related to the project:

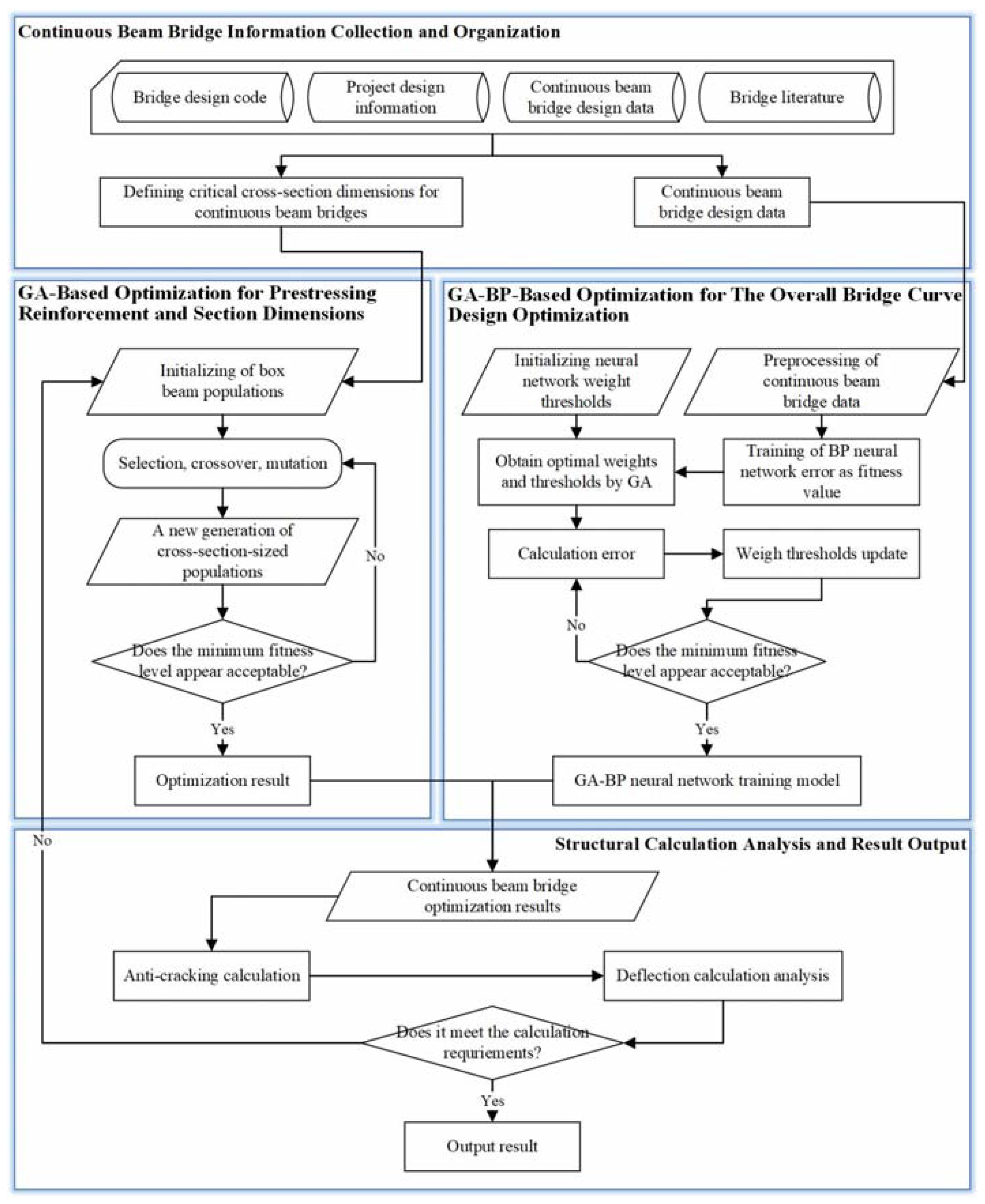
According to the project requirements, continuous beam bridge construction will be carried out by hanging basket cantilever casting. The design optimization calculation was conducted using Matlab 2021b, through which the structural parameters were optimized to improve the safety and economy of the structure. The final results were checked and calibrated by Midas Civil 2022 to ensure the performance and stability of the design solution under various loading conditions.

4.1. Cross-Section Optimization

According to the optimization strategy of this study, the initial focus lies in optimizing the cross-sectional dimensions and prestressed steel bars of the continuous beam bridge. Throughout the optimization process, we designate the mid-span section and the pivot section of the prestressed concrete continuous beam as the primary control sections for optimization. Concerning the steel reinforcement of the continuous beam bridge, the load-bearing capacity of the components of prestressed continuous beams must meet the requirements of the ultimate limit state of the positive cross-section load-bearing capacity. On this basis, the entire bridge only needs to be equipped with longitudinal non-prestressed steel bars according to construction requirements. The range of values for the dimensions of the continuous beam section of the continuous beam bridge should comply with the requirements of bridge specifications. The range of values for the optimization parameters of the cross-sectional dimensions is shown in the

Table 3. Optimization parameter range for prestressed continuous beams.

	Mid-Span Section	Pivot Section
Continuous beam Height h(mm)	1000~1667	2500~3125
Flange Plate Length d(mm)	2000~2500	2000~2500
Top Plate Thickness ea(mm)	200~250	200~250
Web Thickness eb(mm)	200~350	500~600
Root Thickness ec(mm)	400~625	400~625
Bottom Plate Thickness ed(mm)	200~300	300~600
Prestressed Reinforcement Ap(mm2)	0~20,980	0~11,340

.

To enhance the transparency and reproducibility of initial parameter selection for the GA, this study provides a detailed explanation of the selection rationale, range, and tuning methods. Critical parameters, such as population size, crossover rate, and mutation rate, significantly impact optimization performance. Thus, we set these values based on relevant bridge code [32] to determine an appropriate initial parameter range.

During the initial phase of the GA, parameter variables are configured into an initial population. Following iterative calculations for the optimization objective, this study includes the optimization of prestressed steel bar quantities, corresponding to those in the original design. Figure 6 illustrates the iterative optimization process for prestressed concrete continuous beams. Here, the maximum iteration count is set to 300, providing optimal values for parameter variables at both the pivot and mid-span sections, as detailed in

Table 4. Optimization results of pivot section and mid-span section of continuous beam.

	Mid-Span Section	Pivot Section
h(mm)	1450	2550
d(mm)	2100	2100
b(mm)	5000	5000
ea(mm)	200	200
eb(mm)	200	355
ec(mm)	400	400
ed(mm)	200	450
Ap(mm)	17,236	9869

.

4.2. Overall Bridge Curve Design Optimization

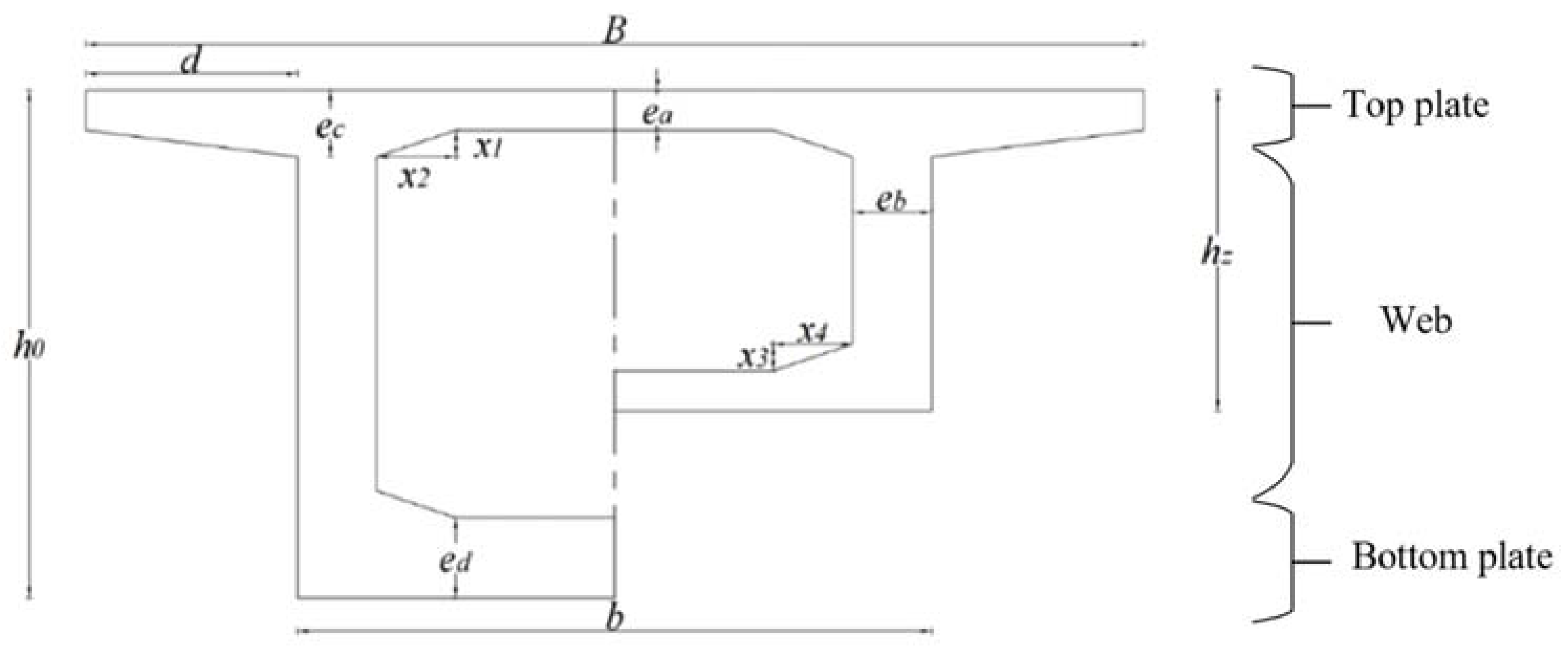
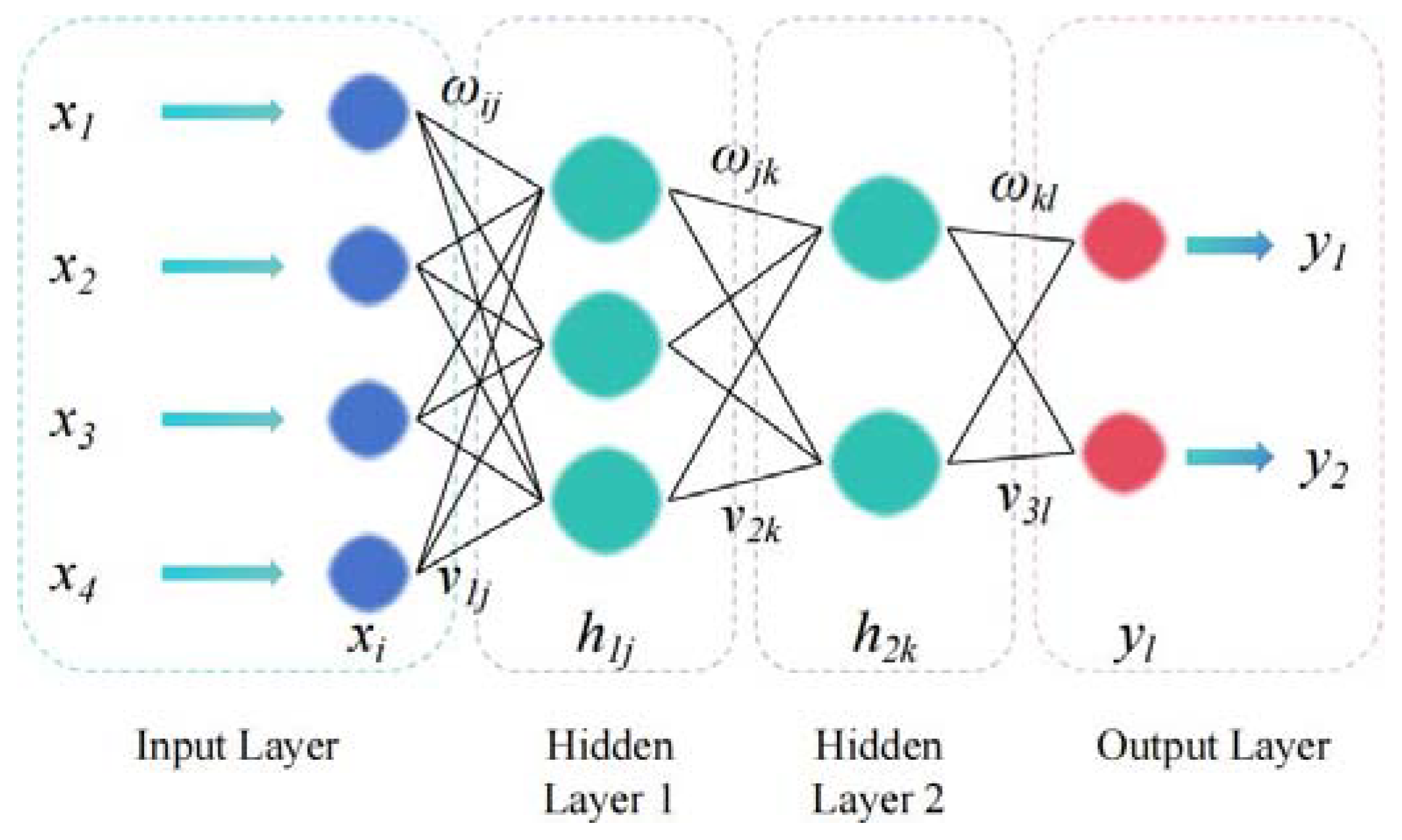
To obtain optimization results for the continuous beam bridge, this study employs a novel approach: using a GA-BP neural network prediction model instead of optimizing designs for multiple sections of the continuous beam bridge. This prediction model forecasts the curves of the beam height and bottom plate thickness of the continuous beam bridge. To ensure the accuracy of the predictions, we gather data from numerous continuous beam bridges domestically and internationally, including total span (S), side span length (L_s), mid-span length (L_z), pivot beam height (h₀), mid-span beam height (h_z), etc., as input data. The beam height curve (x_l) and bottom plate thickness curve (x_d) of the continuous beam are designated as output data. To enhance model accuracy, we extensively collect data from continuous beam bridges as training samples and employ neural network algorithms for learning to obtain precise prediction models. During training, we observe a correlation between the bottom plate thickness curve and the beam height curve of the continuous beam bridge. Consequently, we separately train and predict the exponentials of the two curves to obtain more accurate prediction models. Furthermore, before training begins, we preprocess variables to extract additional data features for training purposes. This study delves into the neural network models of continuous beam height curves and comprehensively evaluates their performance by comparing standard BP neural networks with GA-BP neural networks optimized through genetic algorithms.

Table 5. Parameter configuration of GA-BP for the overall bridge curve.

Parameter Type	The Continuous Beam Height Curve Value	The Continuous Beam Bottom Plate Thickness Curve Value
Number of Input Layer Nodes	9	10
Number of Output Layer Nodes	1	1
Number of Hidden Layer Nodes (Optimized by GA)	13	7
Initial Population Size of GA	100	100
Maximum Evolutionary Generations of GA	200	200
Crossover Probability of GA	0.8	0.8
Mutation Probability of GA	0.1	0.1

shows the parameter configurations used during model training.

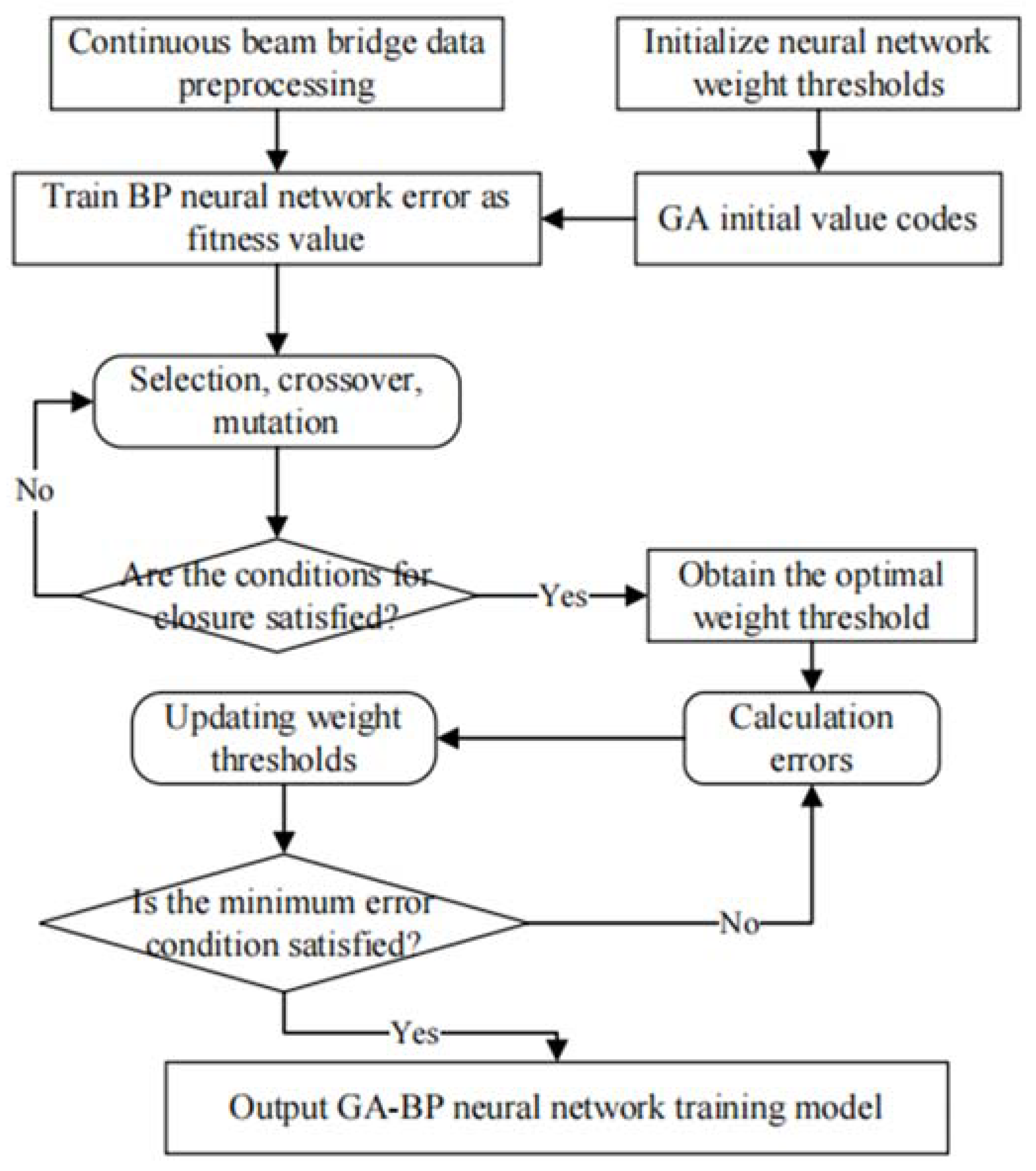
At this stage, the GA-BP neural network training process involves two key steps: first, the convergence of the standard BP neural network training, and second, the optimization of the network using a genetic algorithm (GA). The GA performs crossover and mutation operations, using the error from the BP neural network as the fitness value for optimization. This process identifies the optimal weights and thresholds, which are then used to update and retrain the network for enhanced performance.

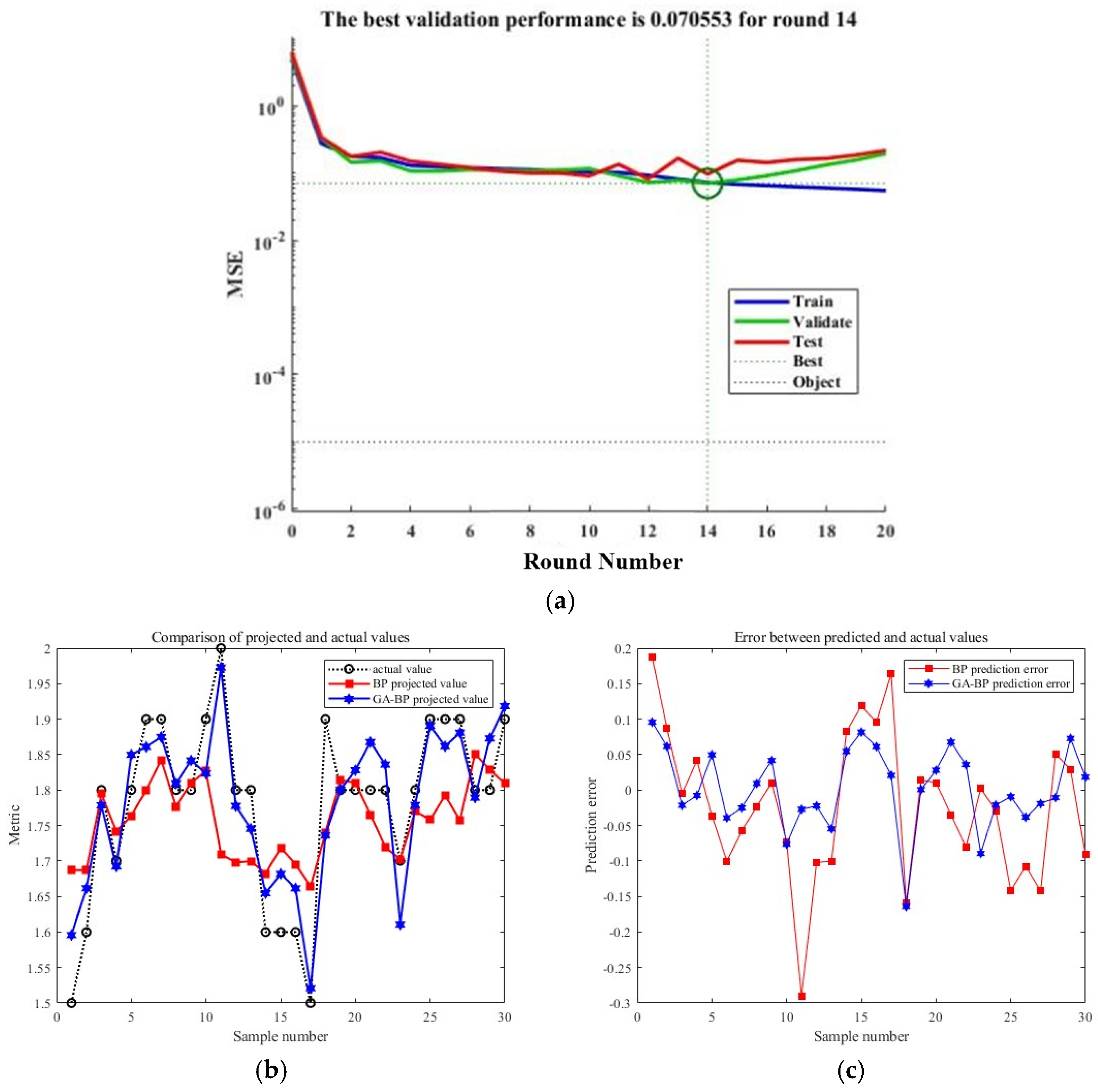
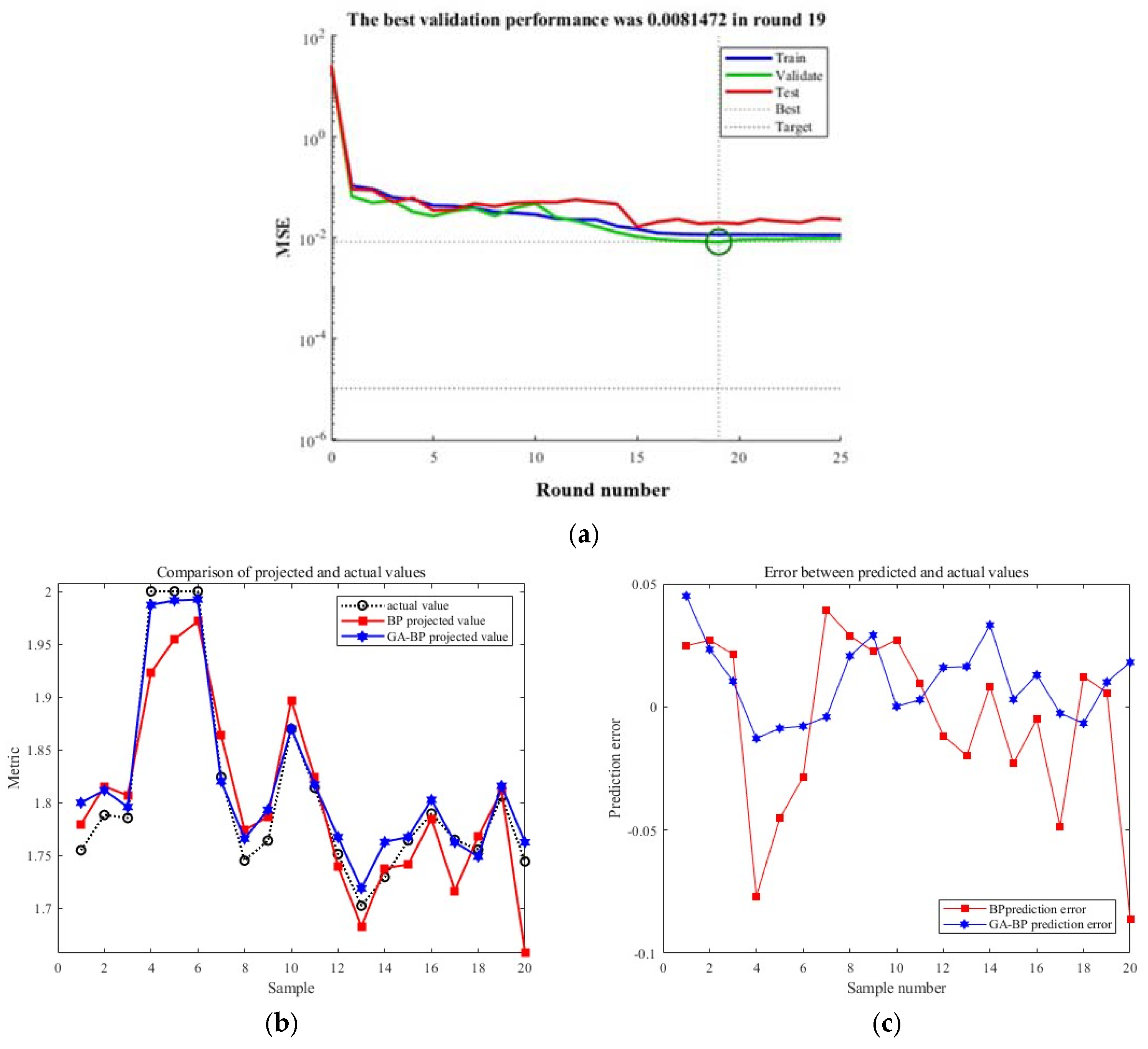
At the current stage, the training process of the GA-BP neural network comprises two key steps: the convergence of the standard BP neural network training and the optimization of the neural network by genetic algorithms. Genetic algorithms utilize operations such as crossover and mutation, using the error obtained from training the standard BP neural network as the optimization fitness value. This process determines the optimal weights and thresholds and subsequently updates and retrains the network accordingly. By the 14th training iteration, the system successfully reaches the predetermined target error, as depicted in Figure 7a. Meanwhile, Figure 7b illustrates the corresponding predictions of the continuous beam height curve. Additionally, it can be observed from Figure 7c that the error range of the GA-BP neural network remains relatively stable. Compared to the standard BP neural network, the GA-BP neural network exhibits a better trend in fitting the actual values. 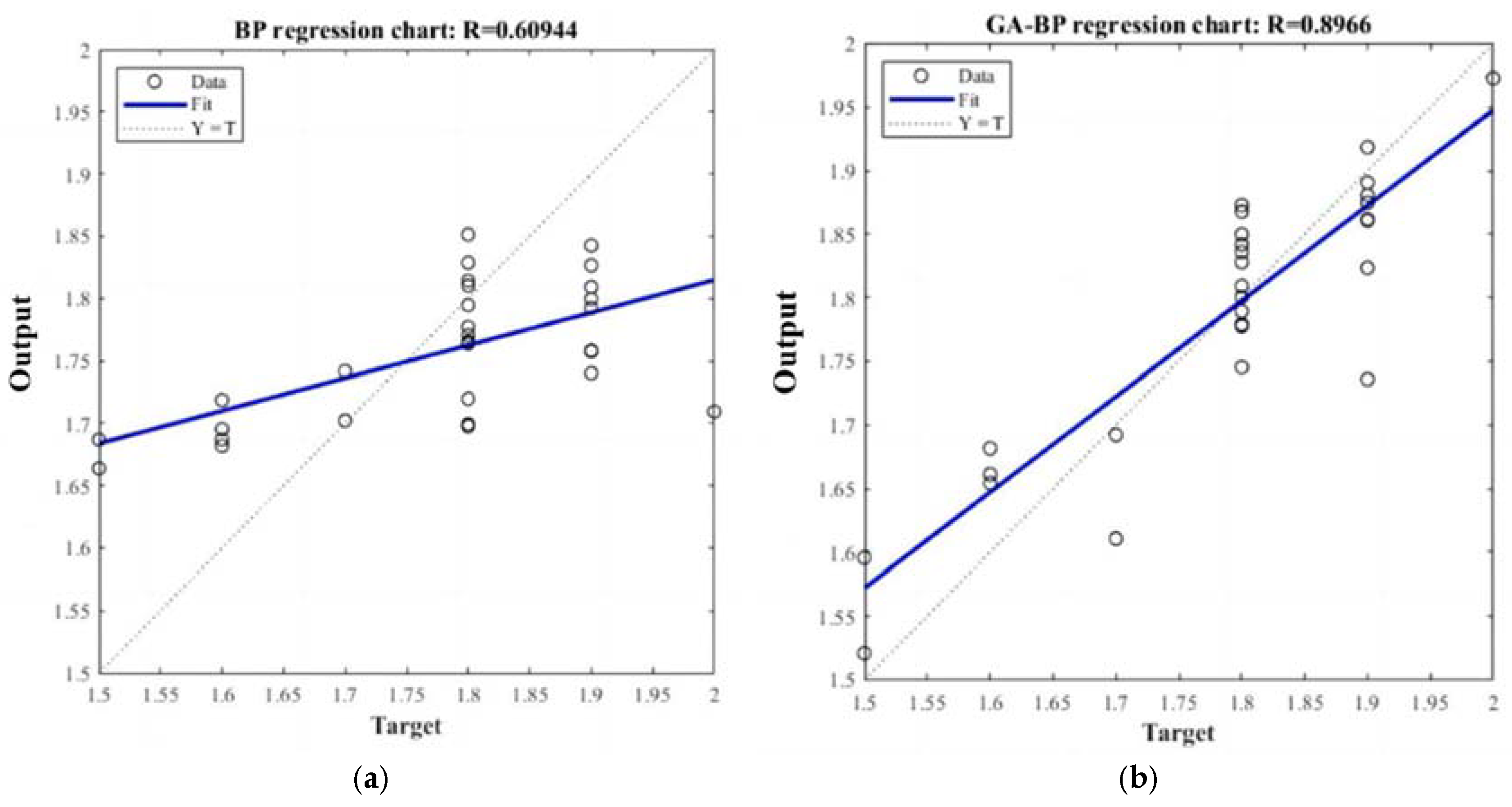The results in Figure 8 demonstrate that the regression coefficient of the GA-BP neural network model improved by 29% compared to the standard BP neural network model.

In this study, a performance comparison between the GA-BP neural network and the traditional BP neural network for predicting the height curve of continuous beams was conducted using 10 test groups (as shown in

Table 6. Performance evaluation of GA-BP neural network in predicting continuous beam height curves.

Group	MAE	MSE	RMSE	MAPE	Predictive Accuracy
1	0.0432	0.0031	0.0550	2.48%	97.52%
2	0.0445	0.0031	0.0558	2.51%	97.49%
3	0.0450	0.0032	0.0566	2.55%	97.45%
4	0.0438	0.0031	0.0553	2.49%	97.51%
5	0.0442	0.0031	0.0556	2.52%	97.48%
6	0.0442	0.0032	0.0561	2.53%	97.47%
7	0.0447	0.0031	0.0559	2.54%	97.46%
8	0.0437	0.0031	0.0552	2.50%	97.50%
9	0.0443	0.0031	0.0557	2.51%	97.49%
10	0.0441	0.0031	0.0560	2.56%	97.44%

and

Table 7. Performance evaluation of GA-BP neural network in predicting continuous beam height curves.

Group	MAE	MSE	RMSE	MAPE	Predictive Accuracy
1	0.0815	0.0105	0.1025	4.55%	95.48%
2	0.0830	0.0110	0.1049	4.65%	95.35%
3	0.0850	0.0115	0.1072	4.75%	95.25%
4	0.0800	0.0102	0.1010	4.50%	95.50%
5	0.0825	0.0108	0.1039	4.60%	95.40%
6	0.0835	0.0112	0.1058	4.70%	95.30%
7	0.0818	0.0106	0.1030	4.58%	95.42%
8	0.0822	0.0109	0.1044	4.62%	95.38%
9	0.0833	0.0111	0.1054	4.68%	95.32%
10	0.0810	0.0104	0.1020	4.53%	95.47%

). The average results, presented in

Table 8. Performance comparison between GA-BP neural network and BP neural network in predicting continuous beam height curves (paired t-test verification).

	GA-BP Neural Networks	BP Neural Networks	Statistical Significance (Paired t-Test)
MAE	0.044209	0.082323	t = 101.33, p < 0.001
MSE	0.0031185	0.010833	t = 61.25, p < 0.001
RMSE	0.055843	0.10408	t = 95.44, p < 0.001
MAPE	2.5265%	4.6578%	t = 94.28, p < 0.001
Predictive accuracy	97.4735%	95.3422%	t = 94.28, p < 0.001

indicate that the GA-BP neural network significantly outperformed the BP model. Specifically, the Mean Absolute Error (MAE) was reduced by 46.3% (from 0.0823 to 0.0442), demonstrating a substantial reduction in average prediction deviation. The Mean Squared Error (MSE) dropped by 71.2% (from 0.0108 to 0.0031), and the Root Mean Squared Error (RMSE) was reduced by 46.4% (from 0.1041 to 0.0558), indicating that extreme prediction error fluctuations were effectively suppressed. Additionally, the Mean Absolute Percentage Error (MAPE) decreased by 45.8% (from 4.6578% to 2.5265%), confirming the model’s enhanced adaptability to beam height curves of different magnitudes.

The prediction accuracy improved to 97.47%, representing a 2.13% increase over the BP network’s 95.34%, highlighting the higher proportion of reliable predictions within the allowable error range. Statistical significance tests using paired t-tests for all evaluation metrics (p < 0.001) rejected the null hypothesis, confirming that the improvements achieved by the GA-BP model are statistically significant. Moreover, a large effect size further validates the practical relevance of the differences observed.

The GA-BP neural network enhances the BP model by optimizing initial weights and structure through a genetic algorithm, effectively avoiding the common issue of local minima in traditional BP models. This results in substantial improvements in both accuracy and stability for predicting continuous beam height curves. The simultaneous reduction in MAE and RMSE demonstrates that the model minimizes average deviation while suppressing extreme errors, and the significant drop in MAPE highlights its robustness across varying data scales. The improved prediction accuracy further supports the GA-BP model’s reliability in engineering applications, providing a solid theoretical foundation for its use in scenarios such as bridge health monitoring.

Upon completion of the training for the exponentials of the continuous beam height curve variations in the previous stage, the parameter configuration for the continuous beam bottom plate thickness curve variations in the GA-BP neural network is outlined in Table 5. Similarly, through comparison between the standard BP neural network and the GA-BP neural network optimized by genetic algorithms, the performance is comprehensively evaluated.

During the current stage of computation, as depicted in Figure 9a, the system achieved the predetermined target error by the 26th training iteration. Simultaneously, Figure 9b illustrates the corresponding predictions of the continuous beam height curve. Figure 9c shows that the error range of the GA-BP neural network remains relatively stable. While the predictions of the standard BP neural network exhibit a reasonable fit with the actual values, those of the GA-BP neural network demonstrate a better trend in fitting the actual values. Moreover, the results from Figure 10 indicate that the regression coefficient of the GA-BP neural network model improved by 7.196% compared to the standard BP neural network model. Additionally, it can be observed from Figure 9c that the error range of the GA-BP neural network is relatively stable.

In this study, ten sets of computations were conducted to compare the performance of the GA-BP neural network and the traditional BP neural network in predicting the height curve of continuous beam bridges (as shown in

Table 9. Performance evaluation of GA-BP neural network in predicting continuous beam floor slab thickness profiles.

Group	MAE	MSE	RMSE	MAPE	Predictive Accuracy
1	0.01410	0.000328	0.01811	0.78%	99.22%
2	0.01430	0.000331	0.01817	0.79%	99.21%
3	0.01425	0.000329	0.01815	0.80%	99.28%
4	0.01415	0.000328	0.01810	0.78%	99.22%
5	0.01435	0.000331	0.01819	0.81%	99.19%
6	0.01420	0.000329	0.01814	0.79%	99.21%
7	0.01428	0.000330	0.01816	0.80%	99.20%
8	0.01432	0.000328	0.01812	0.79%	99.21%
9	0.01422	0.000330	0.01817	0.80%	99.20%
10	0.04410	0.000329	0.01813	0.79%	99.21%

and

Table 10. Performance evaluation of BP neural network in predicting continuous beam floor slab thickness profiles.

Group	MAE	MSE	RMSE	MAPE	Predictive Accuracy
1	0.02845	0.001268	0.03550	1.54%	98.46%
2	0.02870	0.001275	0.03569	1.57%	98.43%
3	0.02865	0.001272	0.03563	1.58%	98.42%
4	0.02850	0.001269	0.03562	1.56%	98.44%
5	0.02880	0.001277	0.03570	1.59%	98.41%
6	0.02855	0.001271	0.03565	1.55%	98.45%
7	0.02872	0.001273	0.03567	1.57%	98.43%
8	0.02860	0.001269	0.03561	1.56%	98.44%
9	0.02875	0.001274	0.03569	1.58%	98.42%
10	0.02858	0.001271	0.03564	1.57%	98.43%

). The final averaged results, presented in

Table 11. Performance comparison between GA-BP neural network and BP neural network in predicting the thickness profile of continuous beam floor slabs (paired t-test verification).

	GA-BP Neural Networks	BP Neural Networks	Statistical Significance (Paired t-Test)
MAE	0.014225	0.028606	t = 317.52, p < 0.001
MSE	0.00032936	0.0012709	t = 210.18, p < 0.001
RMSE	0.018148	0.035649	t = 318.75, p < 0.001
MAPE	0.7944%	1.5671%	t = 295.64, p < 0.001
Predictive accuracy	99.2006%	98.4329%	t = 295.64, p < 0.001

, demonstrate that the GA-BP model significantly outperformed the BP model. Specifically, the mean absolute error (MAE) was reduced by 50.27% (from 0.0286 to 0.0142), indicating a notable decrease in average prediction deviation. The mean squared error (MSE) dropped by 74.08% (from 0.00127 to 0.000329), and the root mean squared error (RMSE) decreased by 49.09% (from 0.0356 to 0.0181), confirming improved overall prediction stability. Furthermore, the mean absolute percentage error (MAPE) was reduced by 49.29% (from 1.5671% to 0.7944%), highlighting the model’s enhanced adaptability to height data across varying magnitudes. The prediction accuracy increased to 99.20%, an improvement of 0.77% over the BP model (98.43%), indicating a higher proportion of reliable predictions in high-precision applications (e.g., within an allowable error margin of δ = 1%). These findings confirm that the GA-BP neural network, by globally optimizing the initial weights and network topology of the BP model through genetic algorithms, effectively overcomes issues such as local minima and unstable convergence commonly seen in traditional BP networks. This significantly improves both the accuracy and robustness of the predicted beam height curves.

The simultaneous reductions in MAE and RMSE indicate that the model not only lowers average error but also suppresses the volatility of extreme errors. The substantial drop in MAPE further underscores its strong adaptability to complex engineering data distributions. The near-perfect prediction accuracy of 99.2%, along with the results of the statistical significance tests (p < 0.001), provides solid evidence for the model’s potential in high-precision applications such as bridge health monitoring and structural safety assessment. Additionally, the substantial reductions in MAE and RMSE (by over 50% and 49%, respectively) indicate a marked improvement in both error control and stability. The exceptionally low MAPE (below 0.8%) further demonstrates the model’s reliability in precision-demanding scenarios, confirming that nearly all predictions fall within acceptable error margins.

Following the optimization results of the continuous beam section dimensions, after data processing, they are inputted into a pre-trained neural network model to obtain the exponentials of the overall bridge curves (detailed in

Table 12. Prediction results of GA-BP for the overall bridge curve.

Parameter Variable	Value
h0(m)	2.55
hz(m)	1.45
S(m)	110
Ls(m)	30
lz(m)	50
Xh	0.57
Hso	0.05
Hsz	0.03
Bc	0.6
xl	2
xd	2

). Through this step, we can derive the mathematical formula for the overall bridge curves. Subsequently, the modeling process of the entire bridge can be conducted using Midas Civil 2021 v2.1 software (as illustrated in Figure 11, the Midas model of the continuous beam bridge), for structural analysis and verification.

According to the computational results from the Midas bridge model, the stress of the continuous beam bridge under long-term and short-term load combinations complies with the requirements of bridge design specifications. Additionally, both the crack resistance performance of the positive section and the inclined section are adequately met. Through meticulous calculations, the deflection of the continuous beam bridge under the standards specified by the regulations is only 34 mm, significantly below the specified L/600 = 81.7 mm in the regulations. This indicates that the deflection values of the continuous beam bridge during operational use, after detailed optimization, fully satisfy the regulatory requirements.

4.3. Comparative Analysis

Compared to conventional design methods, our optimization approach demonstrates significant advantages in both computational efficiency and results. Firstly, in terms of computational efficiency, the design of the entire continuous beam typically involves preliminary planning, conceptual design, and detailed design stages. Our optimization design framework primarily focuses on the preliminary design stage, which is the longest phase in the entire design process. We surveyed five designers with bridge design experience, and their average time spent is approximately 7 days. In contrast, our optimization framework only requires 10 h in the preliminary design stage, including data organization, resulting in a 94% increase in computational efficiency.

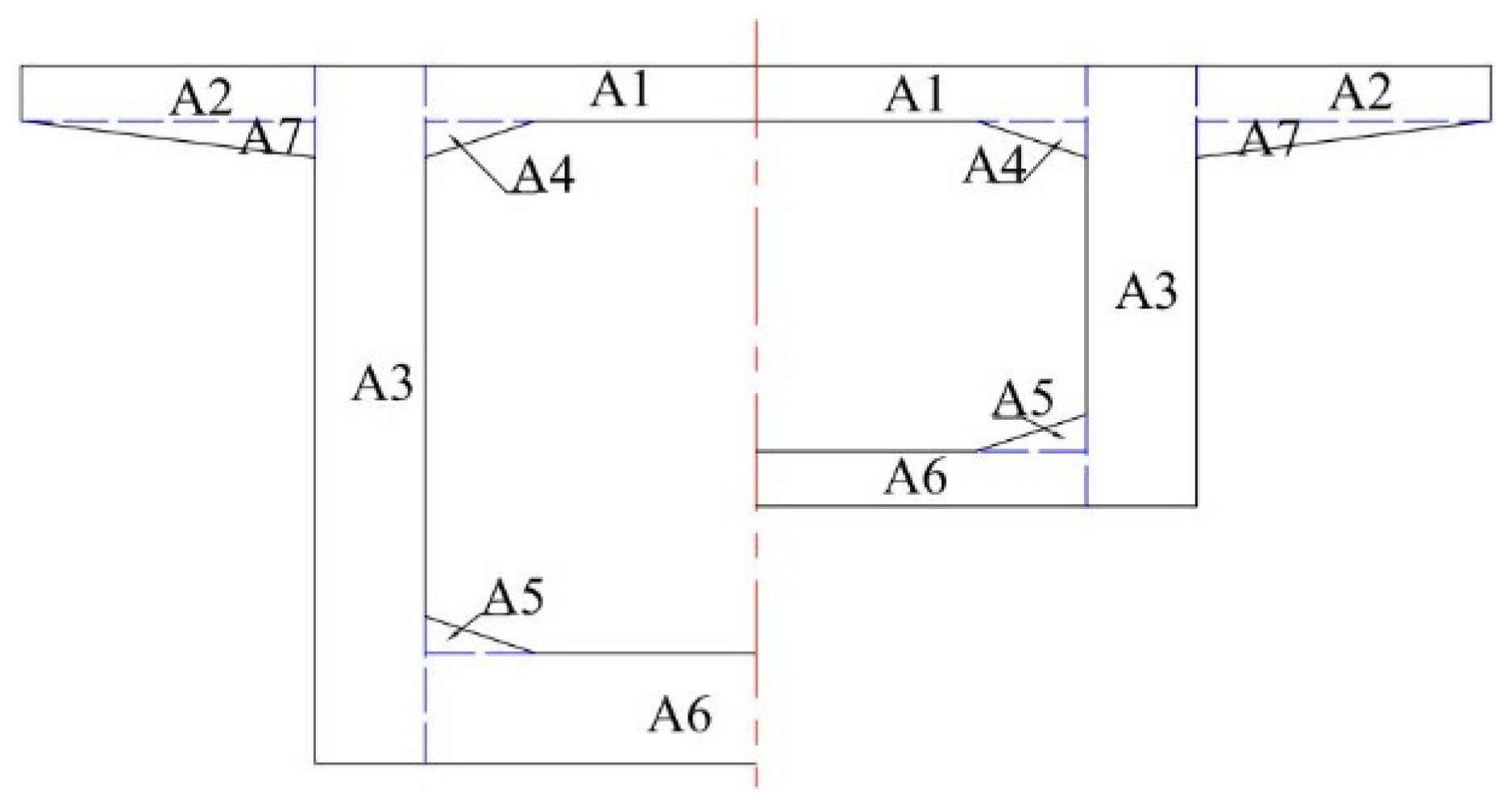
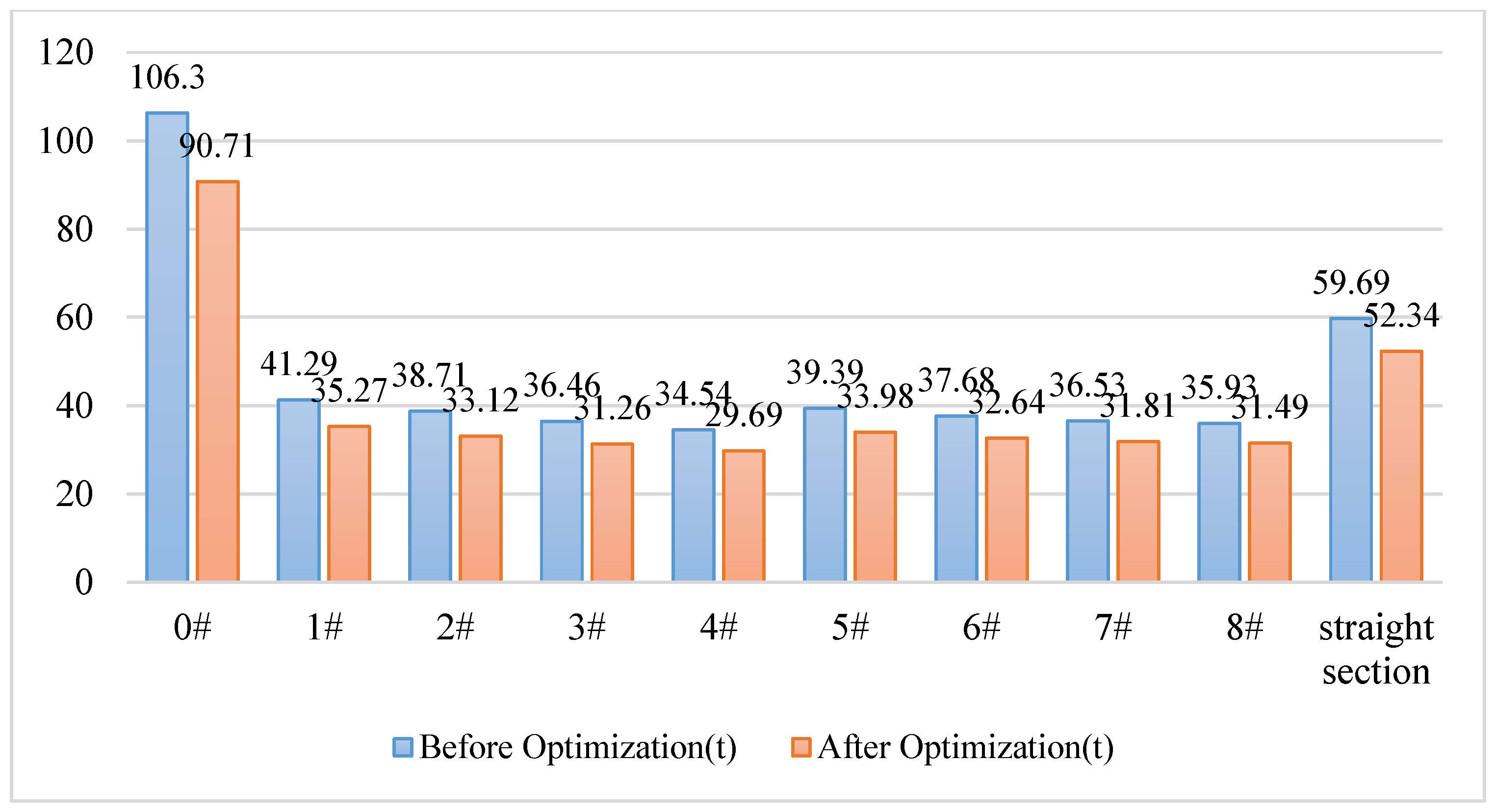
Regarding optimization results, our continuous beam bridge optimization method substantially reduces the consumption of concrete and prestressed steel bars. To show the optimization results more intuitively, the weight of each segment of the continuous beam is counted in this study, which contains 0# block and 8 block segments as well as straight segments (the continuous beam segments are shown in Figure 12). Specifically, the changes in concrete consumption for each segment before and after optimization are illustrated in Figure 13. The data in the figure indicate a significant reduction in concrete consumption for each segment of the continuous beam bridge after optimization. For instance, the concrete consumption of segment 0# decreased by 14.6% after optimization. Similarly, the concrete consumption for other segments also decreased after optimization. This suggests that selecting the pivot section and mid-span section as key sections for calculation in continuous beam bridge optimization yields significant optimization effects overall.

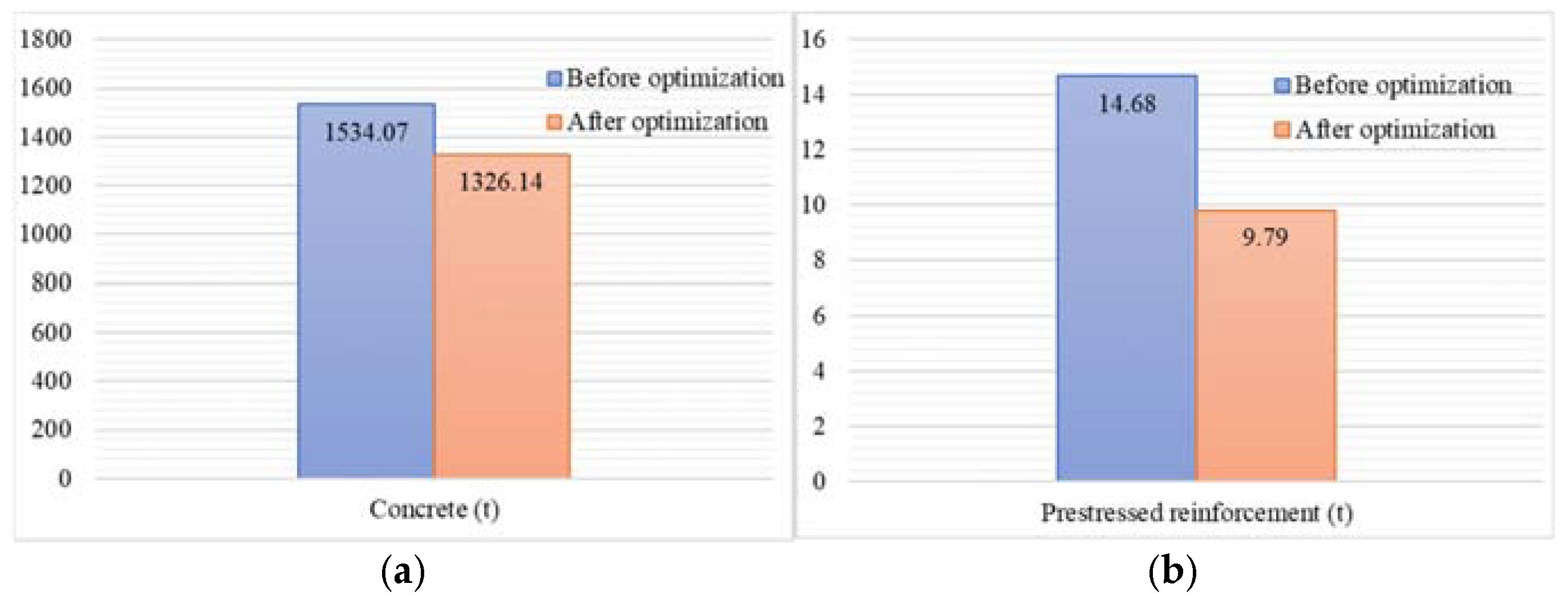
By comparing the total concrete consumption (see Figure 14a) and prestressed steel bar consumption (see Figure 14b) of the entire bridge before and after optimization, we conclude that the total concrete consumption decreased from 1534.07 t to 1326.14 t, a reduction of 14%; while the top and bottom prestressed steel bar consumption decreased from 14.68 t to 9.79 t, a reduction of 34%. This further confirms the effectiveness of our optimization framework in reducing material consumption.

5. Conclusions and Future Work

This study establishes a comprehensive optimization framework for continuous beam bridges, addressing a critical research gap by integrating the optimization of cross-sectional dimensions and prestressed steel bars with the training and prediction capabilities of a GA-BP neural network for overall bridge curve design. Traditional optimization methods have often focused solely on individual segments, overlooking the interconnectedness of various components, which complicates the overall process and increases workload. In contrast, our framework employs a GA to iteratively minimize beam section areas while ensuring compliance with load-bearing requirements. To predict variations in beam height and bottom plate thickness, we utilize a GA-BP neural network, with an input dataset that includes key variables such as span length and beam heights. The output dataset comprises curves for beam height and bottom plate thickness. The GA encodes the initial neural network parameters and updates them to minimize training errors, ultimately generating equations for the overall bridge curve. These equations are then combined with optimized cross-sectional dimensions to create a complete continuous beam bridge. This integrated approach enhances structural efficiency and contributes to sustainable engineering practices by reducing material consumption and improving resource allocation, while also ensuring structural safety and performance through thorough analysis. Through practical engineering applications, our framework demonstrated a 14% reduction in concrete usage and a 34% decrease in the consumption of prestressed steel bars. Additionally, the optimization framework achieved a remarkable 94% increase in computational efficiency during the detailed design stage compared to traditional methods. These enhancements not only improve structural efficiency and safety but also yield significant economic and environmental benefits, underscoring our research’s contribution to sustainability and resource conservation.

Looking ahead, our goal is to integrate Building Information Modeling (BIM) technology into our workflow. In the context of advancing construction industrialization, the integration of BIM should go beyond basic modeling functions and focus on developing an intelligent construction system capable of autonomous decision-making. To meet the demands of this transformation, we propose to build an intelligent collaborative platform driven by BIM-AI integration. This platform will incorporate AI-based structural optimization to establish a comprehensive BIM hub that spans the entire project lifecycle—from conceptual and detailed design to construction management. By enabling seamless task coordination within a unified environment, this system will significantly enhance design and construction efficiency. Furthermore, we plan to develop simulation and validation tools for construction processes and establish a multi-source data fusion framework. This will support the integration of BIM with ERP and IoT systems through a centralized data middleware. Blockchain technology will be employed to ensure transparent and traceable design changes. In addition, the system will enable real-time quantity take-off, embed a material lifecycle database, and implement a dynamic carbon emission model that allows automated tracking of carbon output at each construction stage. These features will ultimately contribute to improved structural performance and greater sustainability. Nevertheless, we recognize that the current optimization framework has certain limitations. Its performance is highly dependent on the quality and availability of training data, which remains limited for continuous beam bridge types. In addition, this framework is currently limited to continuous beam bridges, and its application to other types of bridge structures or building systems would require separate methodological development and validation. To address this, future research will focus on implementing transfer learning. By leveraging established models trained on comparable bridge types, we aim to transfer domain knowledge using existing datasets. This approach is expected to improve the adaptability and robustness of the proposed framework across diverse engineering contexts, even when data resources are limited.