Multi-Criteria Analysis of Steel–Concrete–Steel Slab Performance: Dynamic Response Assessment Under Post-Fire Explosion
Abstract
1. Introduction
2. The Constitutive Model of Materials Under High Temperature and Explosion
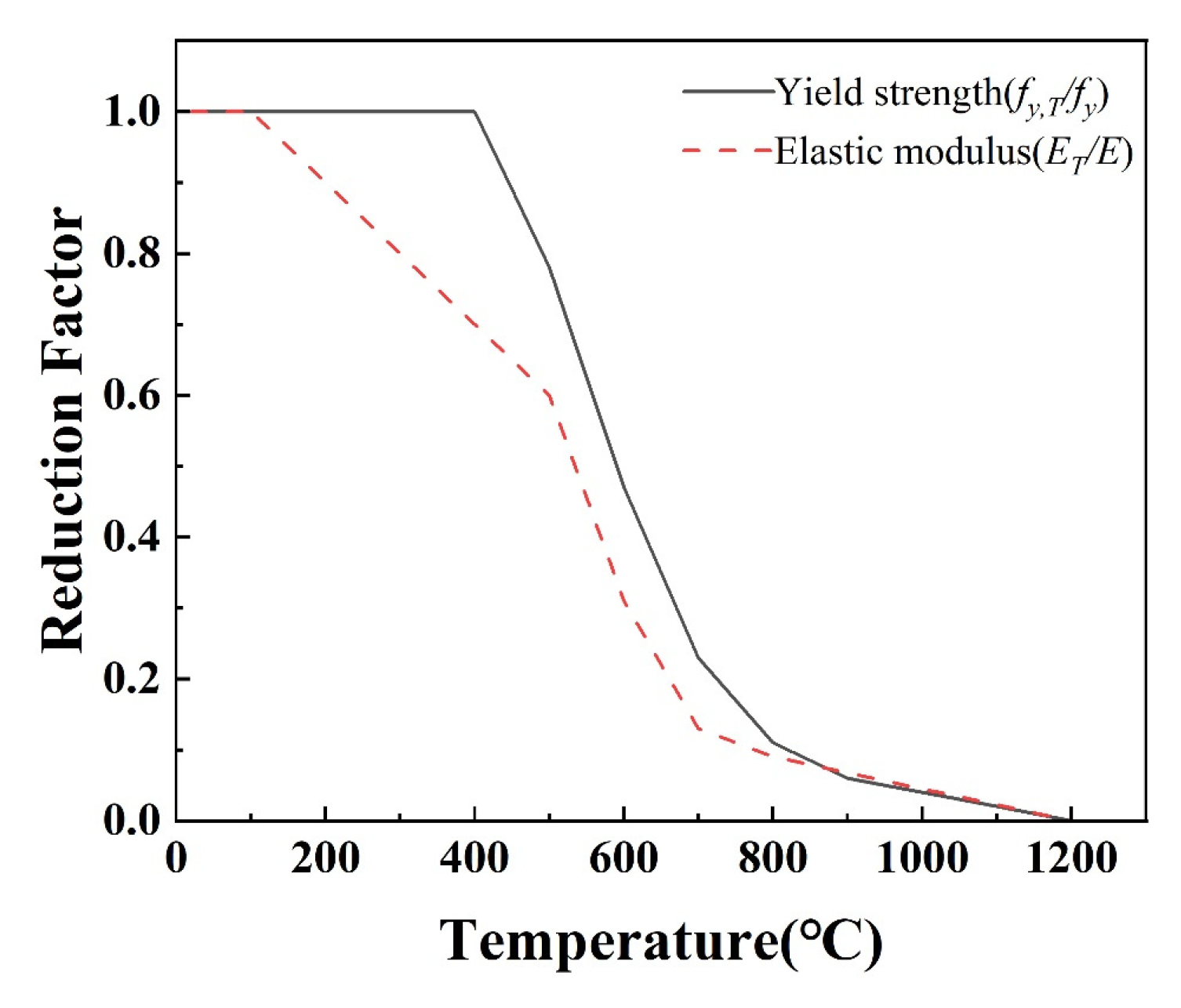
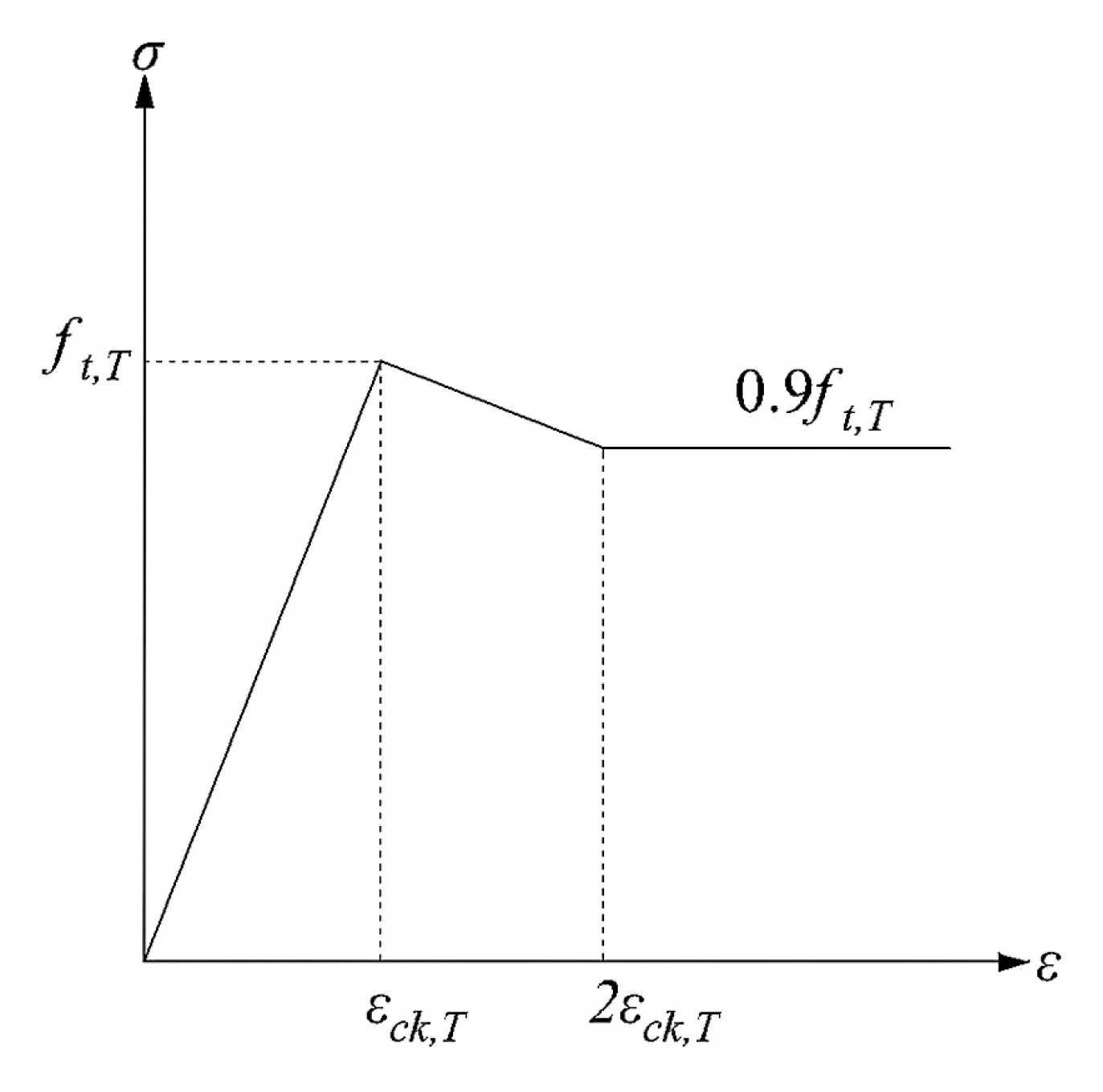
2.1. Thermal Parameters and Constitutive Models of Materials at High Temperatures
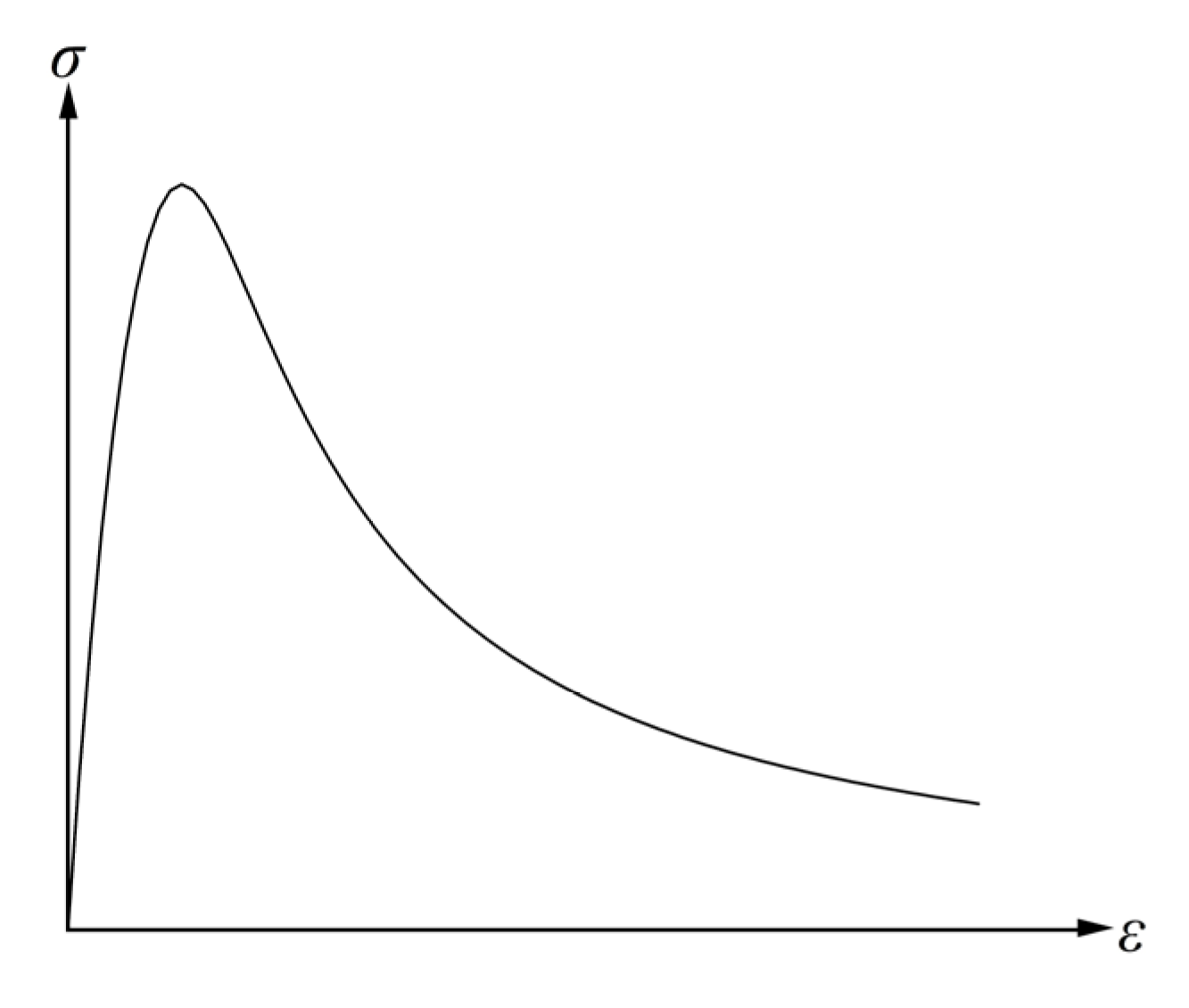
2.2. Strain Rate Effects on Materials Under Explosive Loading
2.3. TNT Explosive and Air Constitutive Equation
3. Finite Element Model Validation
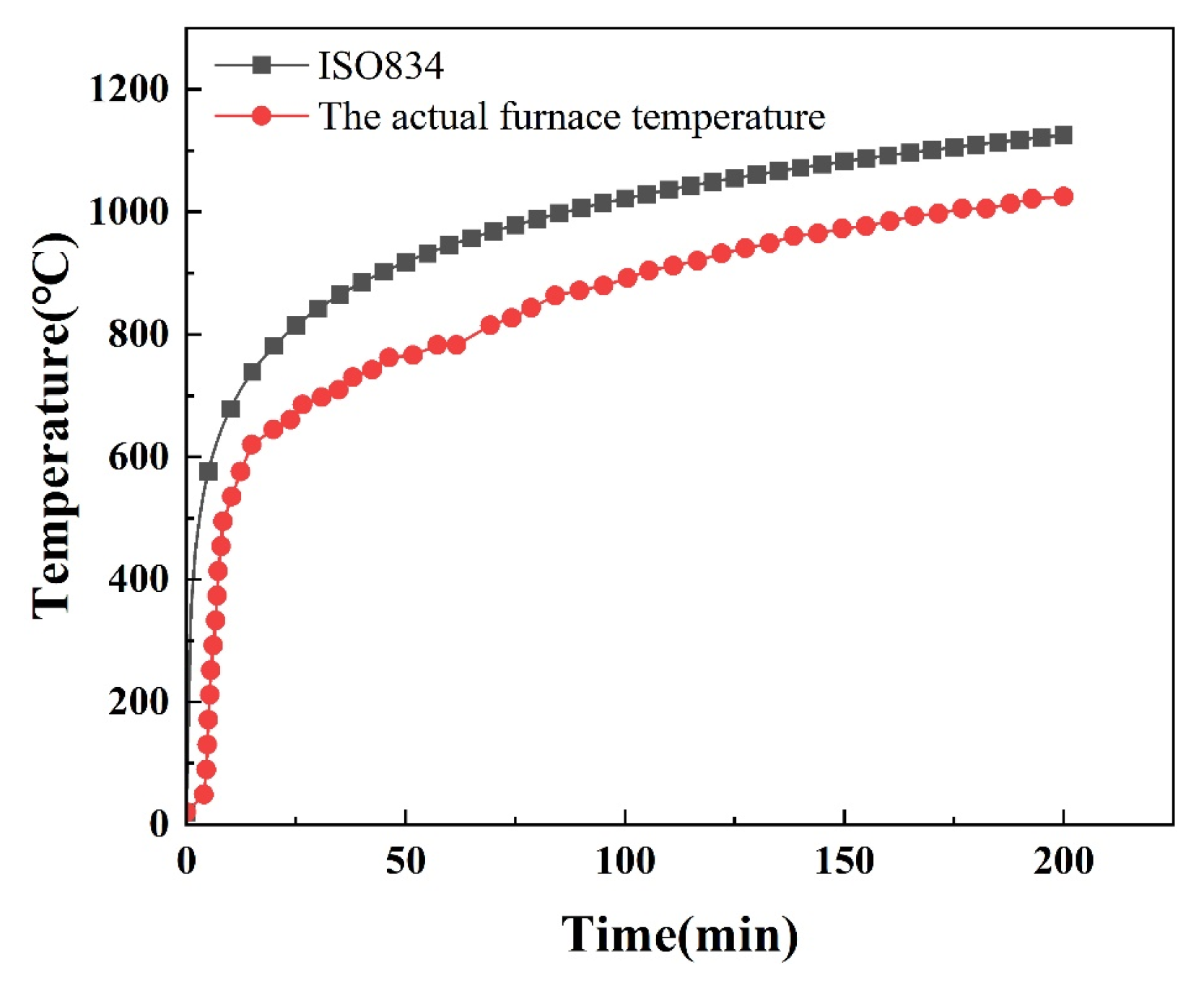
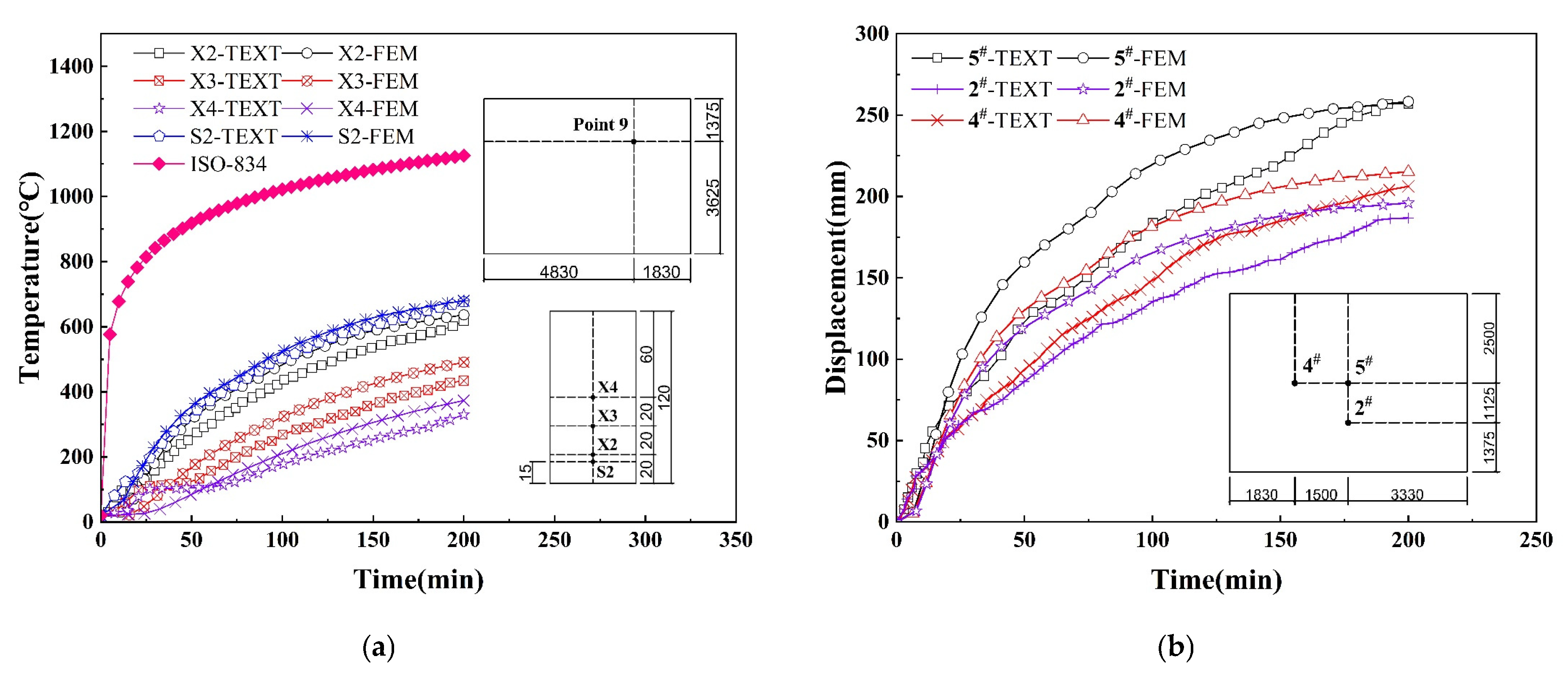
3.1. Experimental Simulation of Fire Performance of RC Slab
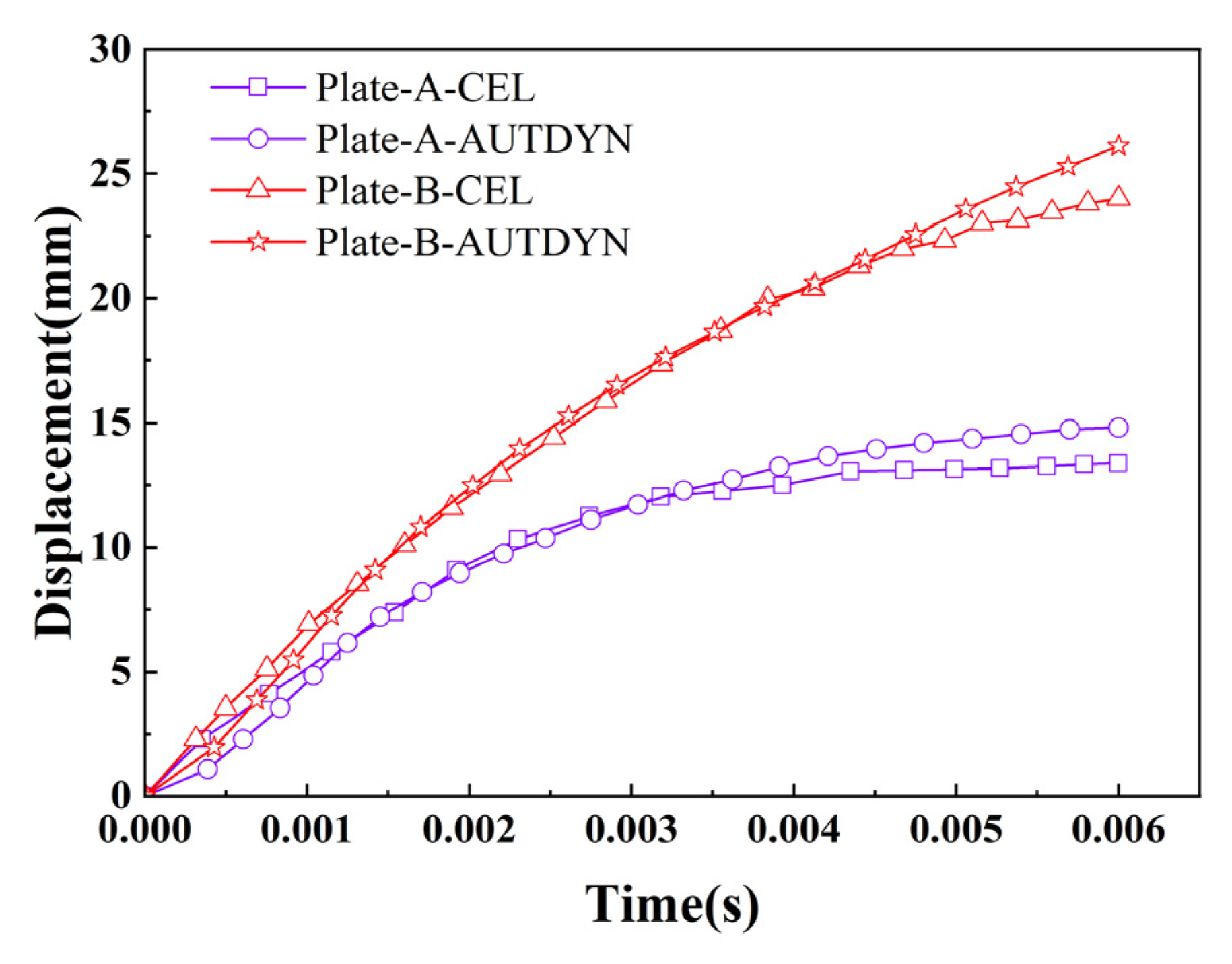
3.2. Reinforced Concrete Slab Explosion Test Simulation
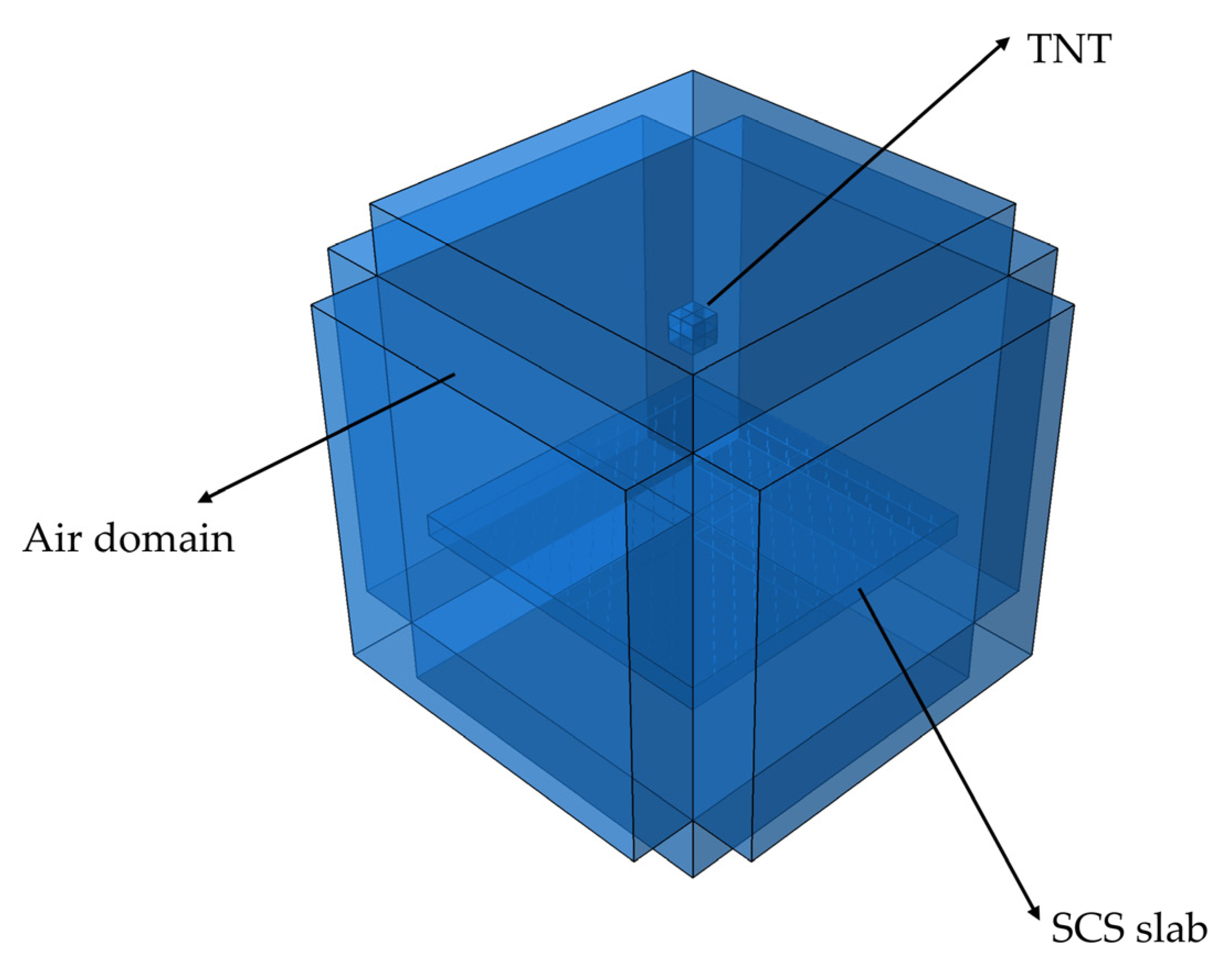
4. SCS Slab Finite Element Modeling
4.1. Material Parameters
4.2. Coupling Conditions
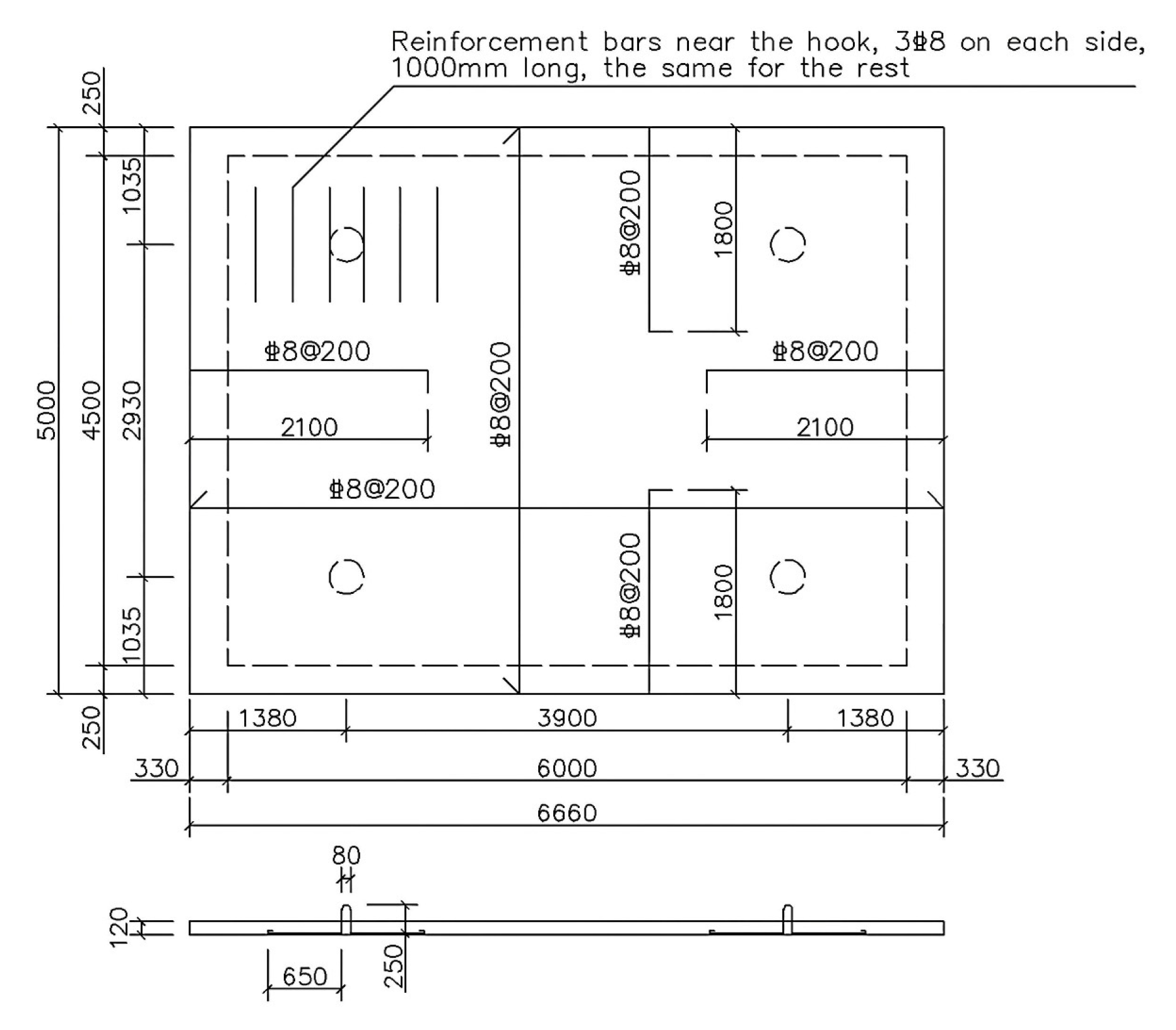
4.3. Model Building
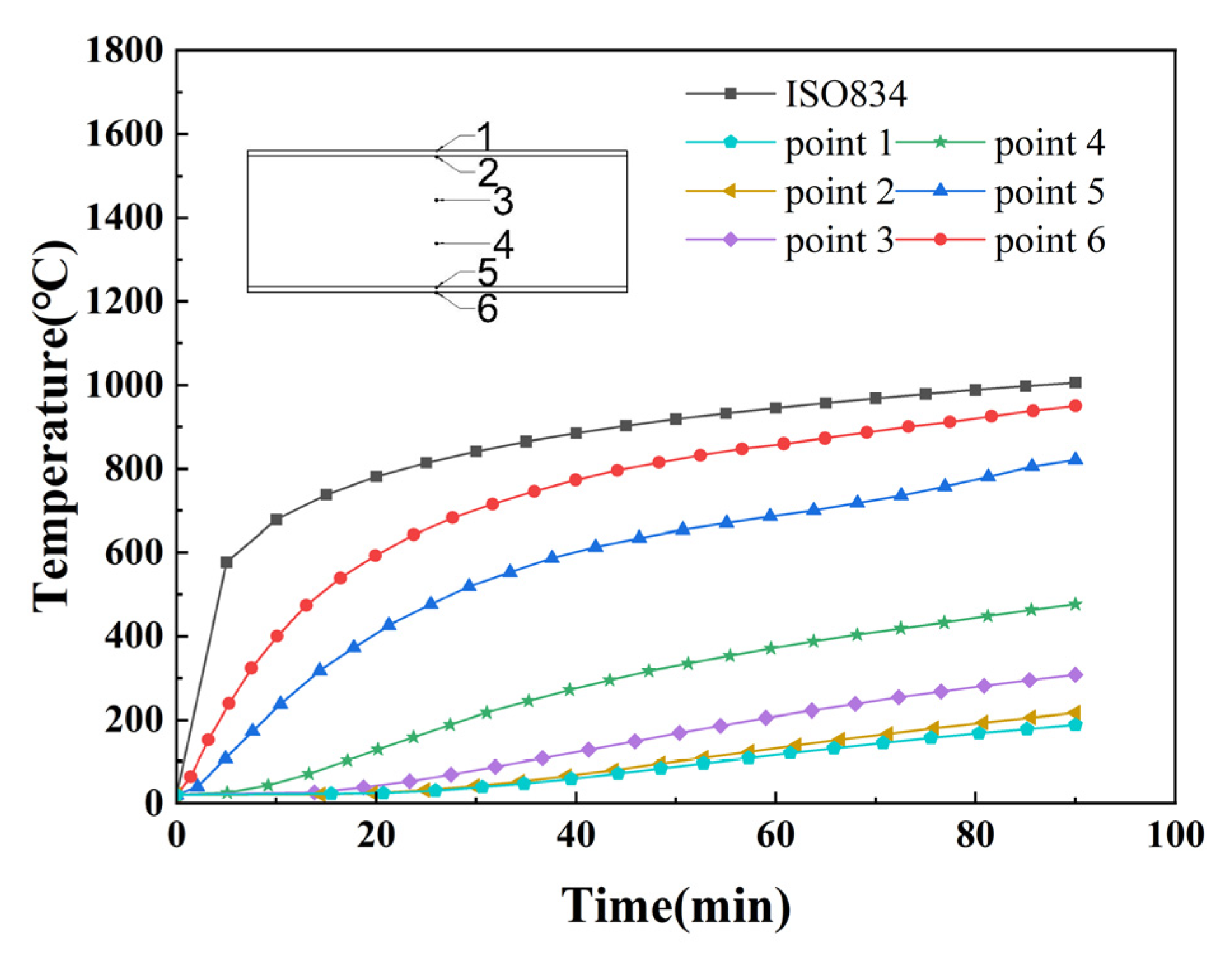
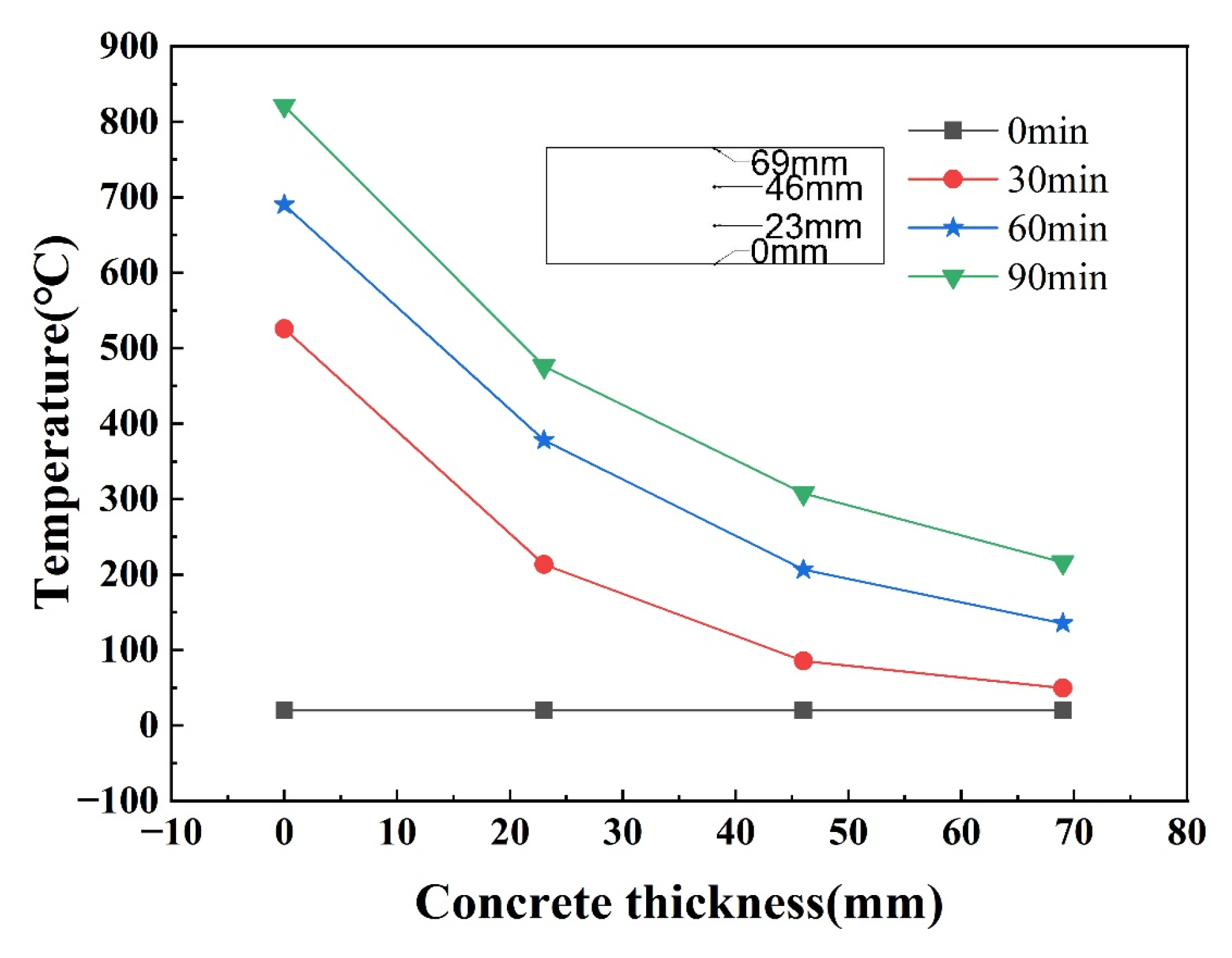
5. Temperature Field Distribution
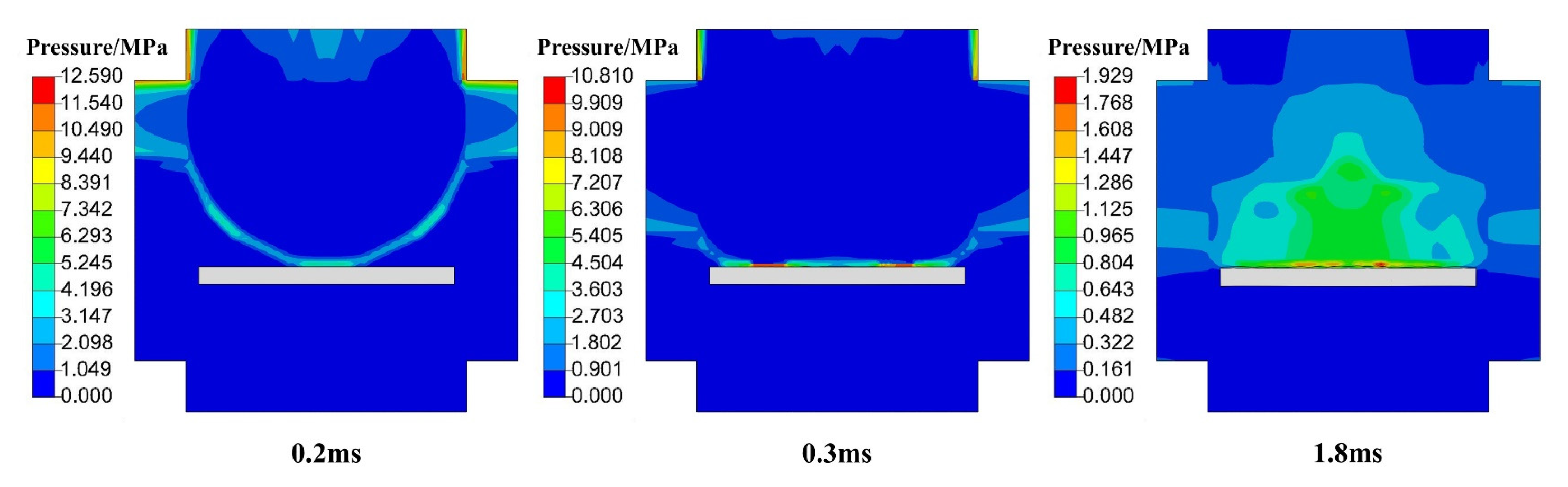
6. The Propagation Characteristics of Blast Shock Waves in Air
7. Dynamic Response Analysis
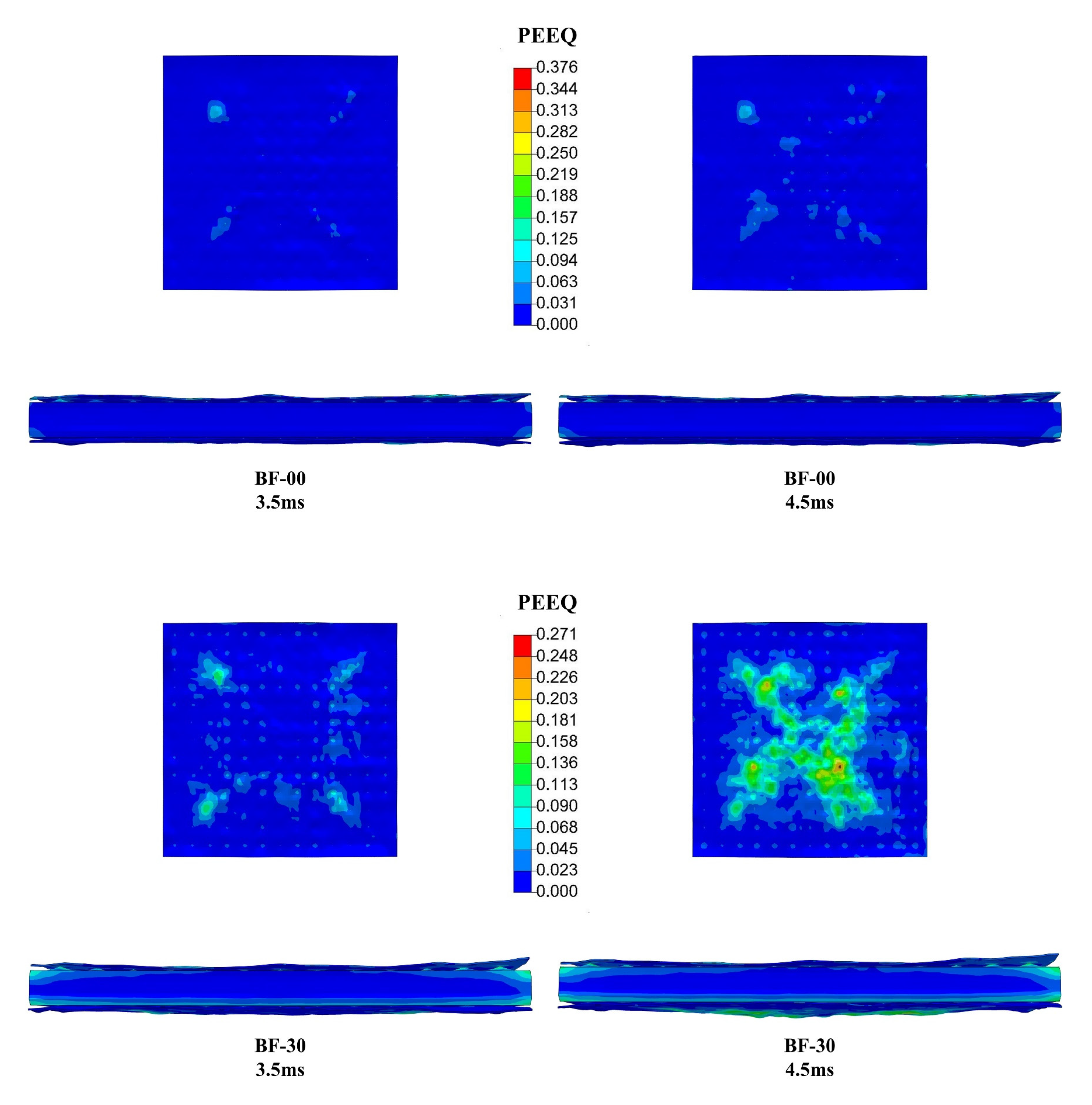
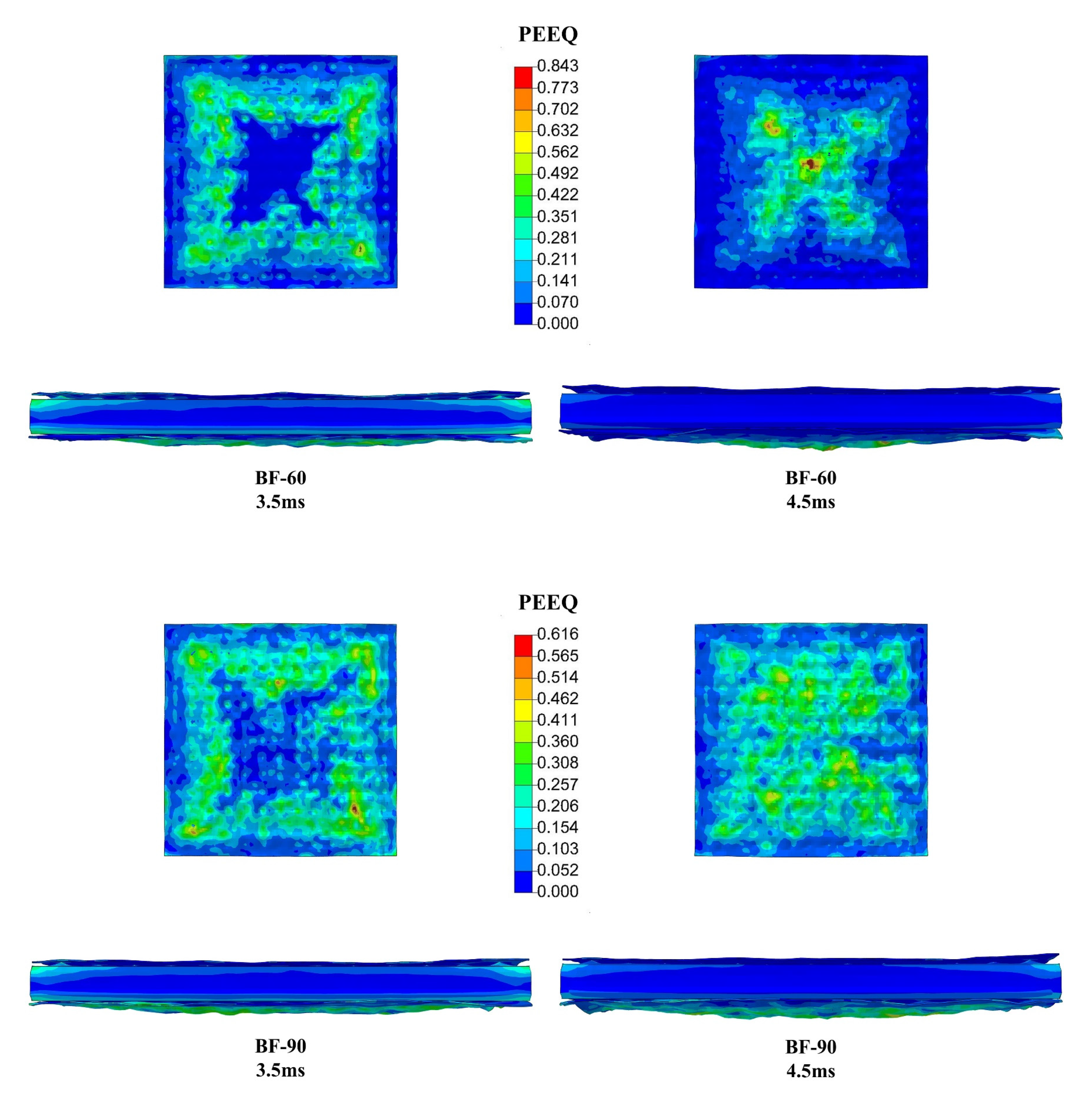
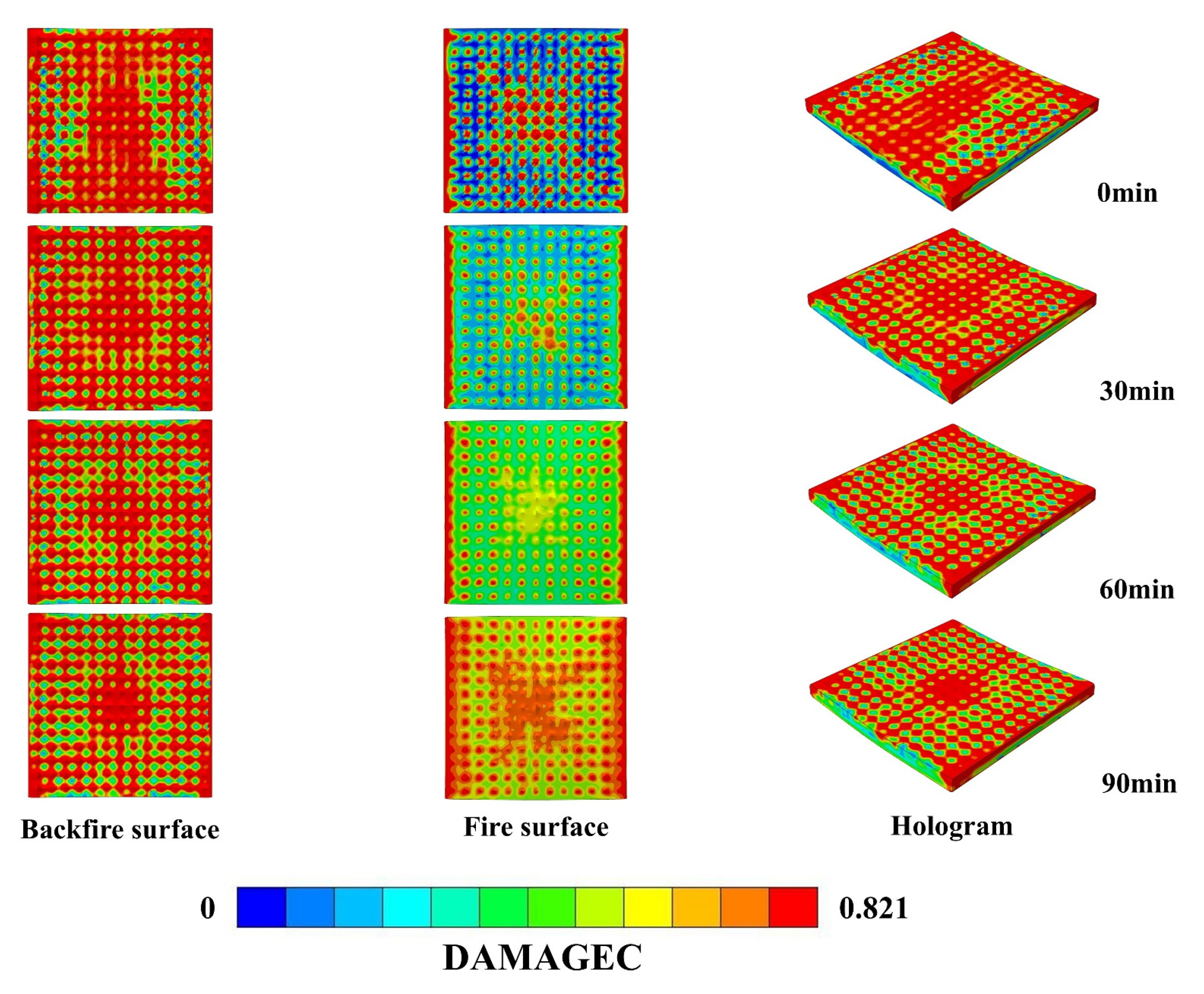
7.1. Destruction State Analysis
7.2. Stress Variation Analysis
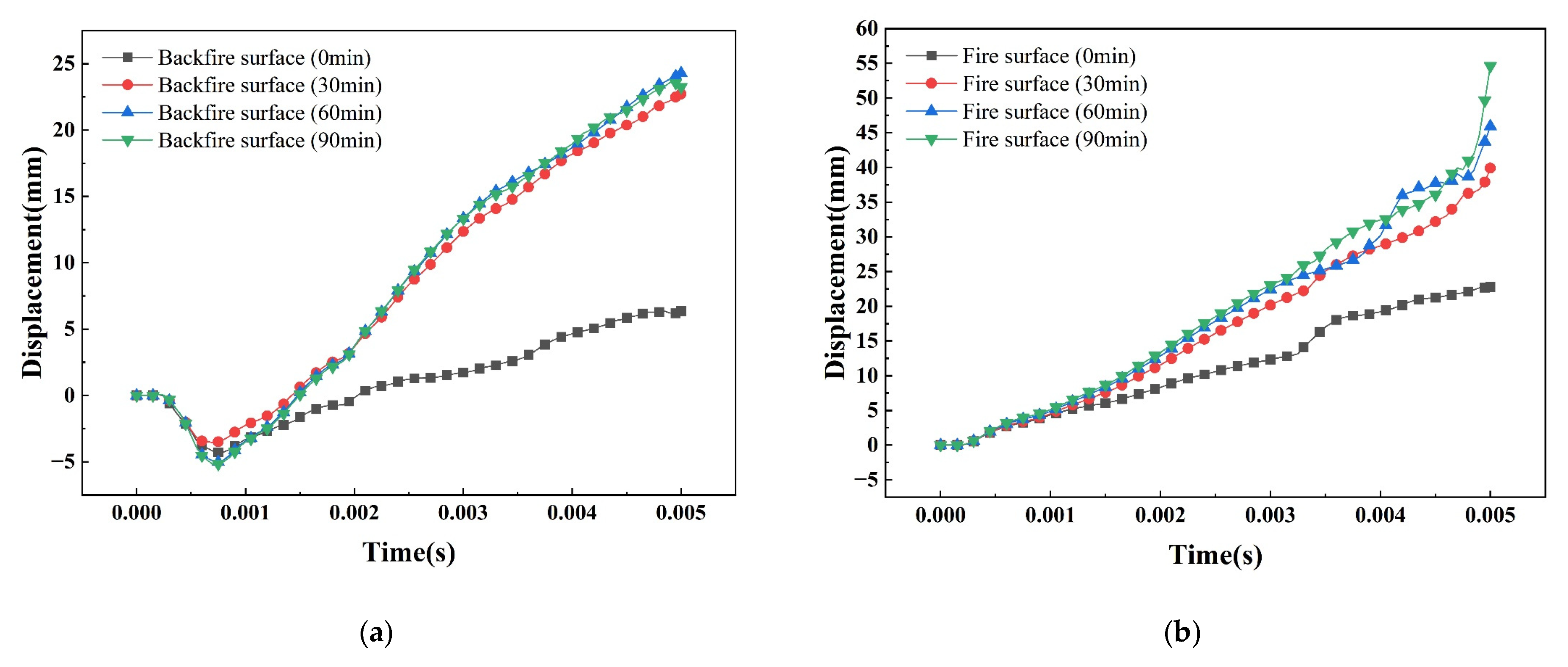
7.3. Displacement Change Analysis
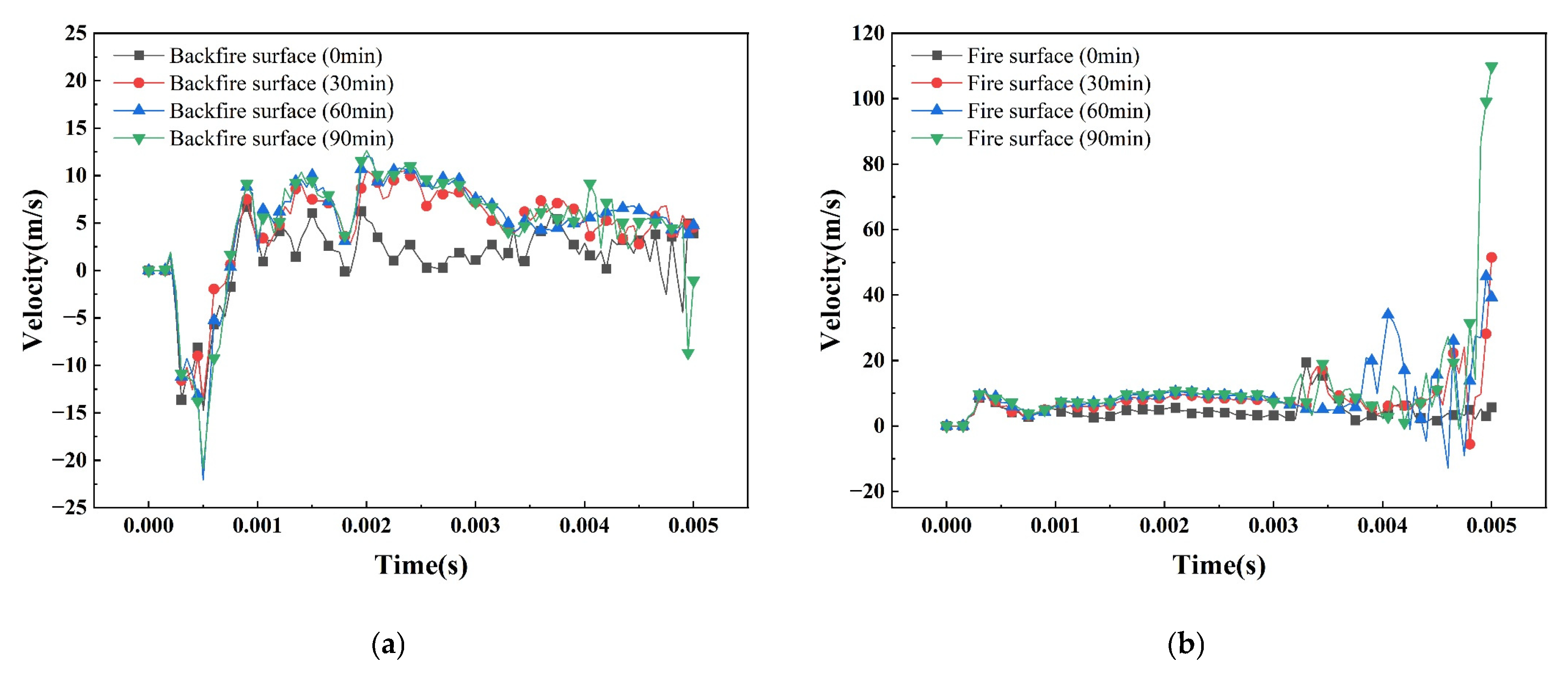
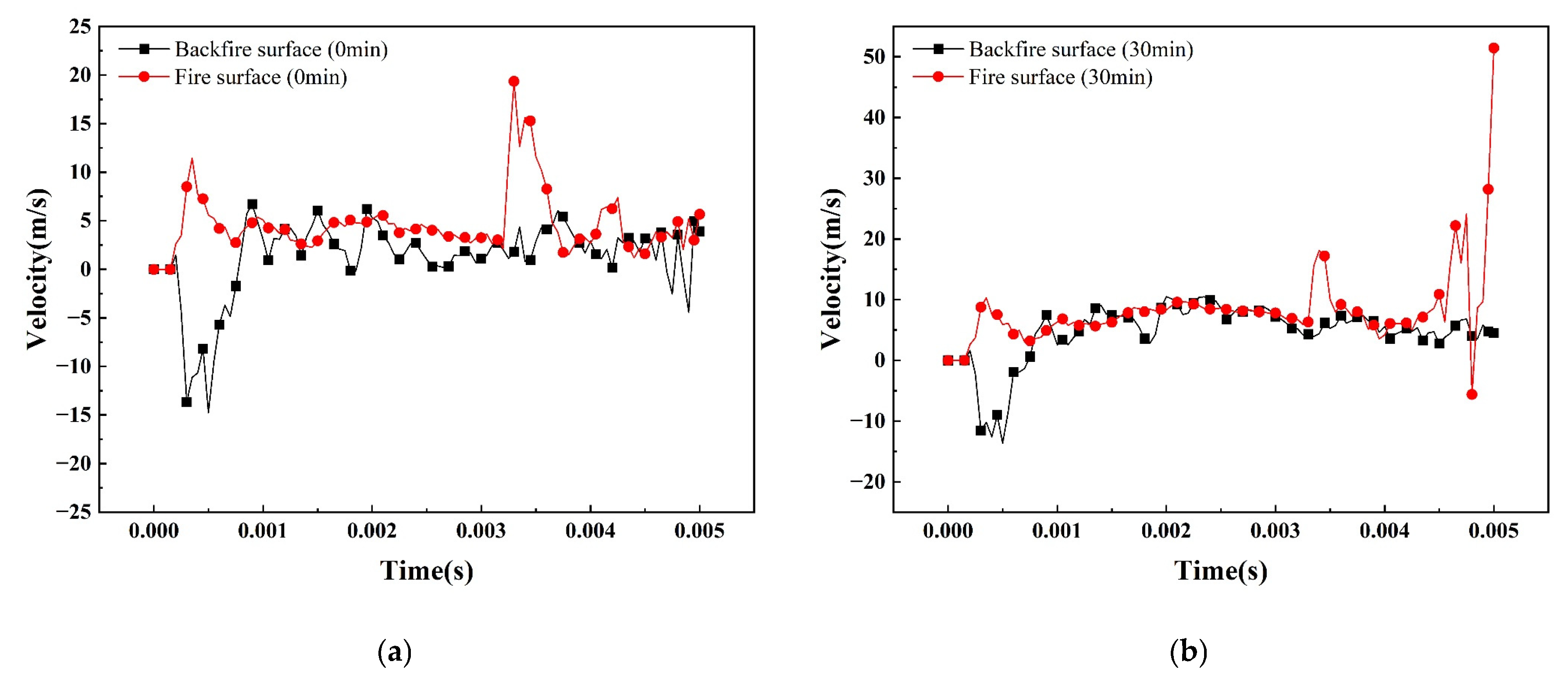
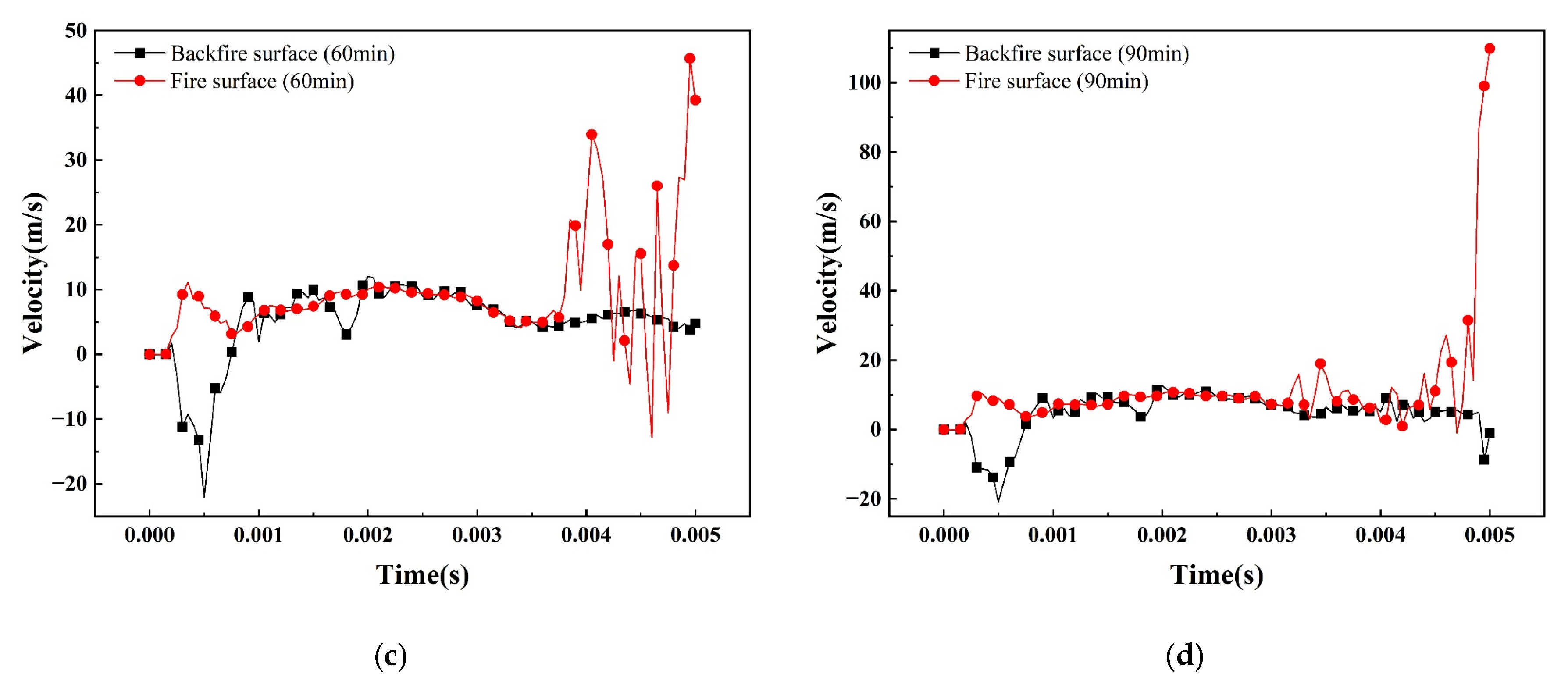
7.4. Analysis of Vibration Velocity Changes
8. Conclusions
- (1)
- There is a contact thermal resistance between the steel plate and the concrete, and there will be a temperature hysteresis at their junction, which will gradually decrease from the fire surface to the back fire surface. When the fire time is 90 min, the temperature difference between the junction of the steel plate and concrete on the fire surface is 128 °C, and the temperature difference between the junction of the steel plate and concrete on the back fire surface is 28 °C. The temperature at each measuring point within the wall panel exhibits a nonlinear increasing trend with prolonged fire exposure time. For the same duration of fire exposure, the concrete section temperature shows a nonlinear decreasing trend with increasing thickness. Consequently, an uneven temperature distribution occurs across the wall panel’s cross-section, inducing non-isothermal deformation of the material and consequently reducing the blast resistance performance of the wall panel.
- (2)
- Under post-fire blast effects, there is a significant warping phenomenon around the back fire surface and the fire-receiving surface of the steel plate. The studs are pulled out of the concrete, and the steel plate and concrete are partially separated. The damage to the fire-receiving surface of the steel plate is relatively severe, and the equivalent plastic strain gradually expands from the periphery to the middle, resulting in bulging and deformation. As the duration of exposure to fire increases, the bulging area and flexural deformation of the steel plate are also increasing; the local damage at the junction of concrete and studs, as well as at the support, becomes increasingly evident; and the damage area on the fire and back fire surfaces gradually expands.
- (3)
- Temperature change and blast shock wave together affect the mechanical properties of the material, but the temperature change throughout the explosion has a greater impact on the mechanical properties of the material. Compared to the fire surface, the back fire surfaces of both concrete and steel plates experience more intense stress fluctuations due to direct exposure to blast shockwaves. When compared to normal temperature conditions, the steel plates and concrete under elevated temperatures exhibit significantly more pronounced stress fluctuations and stress differentials. During the explosion, the steel plates absorbed more energy and endured greater blast wave impact than the concrete, effectively preventing spalling of the core concrete.
- (4)
- The higher the temperature, the greater the tendency to increase the mid-span displacement of the steel plate, and even a steep increase in the phenomenon, the greater the peak displacement; the magnitude of the change in the spanwise displacement of the fire surface is significantly larger than that of the back fire surface, the fire surface and the back fire surface of the peak displacement of 54.59 mm and 24.29 mm, respectively. The peak vibration velocity of the steel plate at high temperature is larger than that at room temperature. Compared with the back fire surface, the steel plate on the fire surface shows more obvious velocity fluctuation at high temperature, and the peak vibration velocities of the fire surface and the back fire surface are 109.83 m/s and −22.07 m/s, respectively, and the fire surface absorbs more kinetic energy, which results in more serious damage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Parameters | Meaning and Unit |
| λs | Thermal conductivity of steel [W/(m·°C)] |
| Cs | Specific heat capacity of steel [J/(kg·°C)] |
| αs | Coefficient of thermal expansion of steel [10−6/°C] |
| λc | Thermal conductivity of concrete [W/(m·°C)] |
| Cc | Specific heat capacity of concrete [J/(kg·°C)] |
| ρc | Density of concrete [kg/m3] |
| αc | Coefficient of thermal expansion of concrete [10−6/°C] |
| fy | Yield strength of the steel at room temperature [Pa] |
| E | Elastic modulus of the steel at room temperature [Pa] |
| fu | Ultimate strength of steel at room temperature [Pa] |
| fc | Compressive strength of concrete at room temperature [Pa] |
| ft | Tensile strength of concrete at room temperature [Pa] |
| Ec | Modulus of elasticity of concrete at room temperature [Pa] |
| fy,T | Yield strength of steel at high temperature [Pa] |
| ET | Elastic modulus of steel at high temperature [Pa] |
| fu,T | Ultimate strength of steel at high temperature [Pa] |
| fc,T | Compressive strength of concrete at high temperature [Pa] |
| ft,T | Tensile strength of concrete at high temperature [Pa] |
| Ec,T | Modulus of elasticity of concrete at high temperature [Pa] |
| T | Temperature [°C] |
| σ0 | Initial yield stress [Pa] |
| β | Hardening parameter |
| Ep | Plastic hardening strain modulus [Pa] |
| εeff | Equivalent plastic strain |
| Strain rate [s−1] | |
| C | Material strain rate parameter |
| P | Material strain rate parameter |
| fc0 | Static compressive strength [Pa] |
| ft0 | Static tensile strength [Pa] |
| Static compressive strain rate [s−1] | |
| Static tensile strain rate [s−1] | |
| p | Burst pressure [Pa] |
| V | Relative volume [m3] |
| E0 | Initial volume internal energy [J] |
| A | Material parameter [Pa] |
| B | Material parameter [Pa] |
| R1 | Material parameter |
| R2 | Material parameter |
| ω | Material parameter |
| c0 | Speed of sound in the fluid [m/s] |
| Γ0 | Gruneisen’s constant |
| ρ0 | Density of the fluid [kg/m3] |
| S | Linear coefficient between the speed of sound and the velocity of propagation of the shock wave |
| Em | Internal energy per unit mass of the fluid [J] |
| η | Coefficient of dynamic viscosity [Pa·s] |
References
- Li, X.; Li, X. Steel Plates and Concrete Filled Composite Shear Walls Related Nuclear Structural Engineering: Experimental Study for out-of-Plane Cyclic Loading. Nucl. Eng. Des. 2017, 315, 144–154. [Google Scholar] [CrossRef]
- Wei, F.; Zheng, Z.; Yu, J.; Wang, Y. Structure Behavior of Concrete Filled Double-Steel-Plate Composite Walls under Fire. Adv. Struct. Eng. 2019, 22, 1895–1908. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, X.; Wang, Q.; Gautam, A.; Wang, J.; Mo, Y.L. Experimental and Numerical Investigation of Steel-Concrete (SC) Slabs under Contact Blast Loading. Eng. Struct. 2019, 196, 109337. [Google Scholar] [CrossRef]
- Bolina, F.L.; Schallenberger, M.; Carvalho, H. Experimental and Numerical Evaluation of RC Ribbed Slabs in Fire Conditions. Structures 2023, 51, 747–759. [Google Scholar] [CrossRef]
- ISO 834-1999; Fire-Resistance Tests—Elements of Building Construction—Part 1: General Requirements. ISO: Geneva, Switzerland, 1999.
- Zhou, T.; Liu, X.; Liu, H.; Li, Y.; Zhang, P.; Chen, H.; Chen, Z. Experimental Study on Fire Resistance Performance of Concrete-Filled Steel Plate Composite Walls. Int. J. Steel Struct. 2023, 23, 389–403. [Google Scholar] [CrossRef]
- Du, E.; Shu, G.; Qin, L.; Lai, B.; Zhou, X.; Zhou, G. Experimental Investigation on Fire Resistance of Sandwich Composite Walls with Truss Connectors. J. Constr. Steel Res. 2022, 188, 107052. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Li, J.; Li, J.; Yan, Y.; Wu, C. Experimental and Numerical Study on Damage Behavior of Air-Backed Steel-Concrete-Steel Composite Panels Subjected to Underwater Contact Explosion. Eng. Struct. 2024, 318, 118744. [Google Scholar] [CrossRef]
- Yu, S.; Wu, H.; Zhang, G.; Wang, Z.; Yao, J.; Li, H.; Liu, C. Experimental Study on Anti-Shallow-Buried-Explosion Capacity of a Corrugated Steel-Plain Concrete Composite Structure. Int. J. Impact Eng. 2023, 172, 104393. [Google Scholar] [CrossRef]
- Zhu, W.; Xiao, Y.; Yu, J.; Jia, J.; Li, Z. Damage Modes and Mechanism of Steel-Concrete Composite Bridge Slabs under Contact Explosion. J. Constr. Steel Res. 2024, 212, 108223. [Google Scholar] [CrossRef]
- Huang, R.; Li, S.; Meng, L.; Jiang, D.; Li, P. Coupled Effect of Temperature and Strain Rate on Mechanical Properties of Steel Fiber-Reinforced Concrete. Int. J. Concr. Struct. Mater. 2020, 14, 48. [Google Scholar] [CrossRef]
- Alogla, S.M.; Kodur, V. Temperature-Induced Transient Creep Strain in Fiber-Reinforced Concrete. Cem. Concr. Compos. 2020, 113, 103719. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Chen, Y.; Chen, R.; Liu, Y.; Zhang, Y. Study on the Dynamic Impact Mechanical Properties of High-Temperature Resistant Ultra-High Performance Concrete (HTRUHPC) after High Temperatures. J. Build. Eng. 2024, 91, 109752. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Y.; Zhai, X.; Zhou, H. Compressive Mechanical Behaviors of Q235B Steel over a Wide Range of Temperatures and Strain Rates. Int. J. Impact Eng. 2025, 198, 105222. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, R.; Zhao, H.; Zhang, H.; Lam, D.; Zhu, Y. Dynamic Compressive Behaviours of Stainless-Clad Bimetallic Steel under High Temperatures. J. Constr. Steel Res. 2023, 210, 108055. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Ji, C.; Gao, F.; Yu, Y.; Cheng, L.; Zhang, K.; Jiang, T.; Wu, J. Damage Effect of Steel Circular Tube Subjected to Fire and Blast. J. Constr. Steel Res. 2021, 176, 106389. [Google Scholar] [CrossRef]
- Al-Thairy, H. Prediction of Behaviour and Failure of Steel Columns Subjected to Blast Followed by Fire Induced by Explosion. Int. J. Steel Struct. 2021, 21, 1431–1453. [Google Scholar] [CrossRef]
- Xi, F. Large Deflection Response of Restrained Steel Beams under Fire and Explosion Loads. Springerplus 2016, 5, 752. [Google Scholar] [CrossRef]
- Ji, S.-H.; Wang, W.-D.; Shi, Y.-L.; Wang, J.-X. Numerical Analysis on Fire Behaviour of Concrete-Filled Steel Tubular Columns after Lateral Impact. Eng. Struct. 2025, 327, 119632. [Google Scholar] [CrossRef]
- Hu, W.W.; Wang, R.; Zhao, H.; Zhang, L. Study on explosion-resistance performance of concrete-filled steel tubular columns considering the influence of elevated temperatures. Explos. Shock Waves 2021, 11, 58–69. [Google Scholar]
- Li, X.; Zhang, R.; Jin, L.; Du, X. Influence of Fire Scenario on Dynamic Behavior of RC Columns in Structures: A Refined Simulation. Structures 2023, 48, 108–124. [Google Scholar] [CrossRef]
- Roy, T.; Matsagar, V. A Probabilistic Framework for Assessment of Reinforced Concrete Wall Panel under Cascaded Post-Blast Fire Scenario. J. Build. Eng. 2022, 45, 103506. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Hao, H. Performance of Reinforced Concrete Slabs Subjected to Simultaneous Fire and Blast Loads. Eng. Struct. 2024, 311, 118133. [Google Scholar] [CrossRef]
- BS EN 1993-1-2:2005; Eurocode 3: Design of Steel Structures—Part 1–2: General Rules—Structural Fire Design. British Standards Institution: London, UK; European Committee for Standardization: Bruxelles, Belgium, 2005.
- Lie, T.T.; Irwin, R.J. Fire Resistance of Rectangular Steel Columns Filled with Bar-Reinforced Concrete. J. Struct. Eng. 1995, 121, 797–805. [Google Scholar] [CrossRef]
- Lie, T.T. Fire Resistance of Circular Steel Columns Filled with Bar-Reinforced Concrete. J. Struct. Eng. 1994, 120, 1489–1509. [Google Scholar] [CrossRef]
- Ding, F.X.; Yu, Z.W.; Wen, H.L. Experimental Research on Mechanical of Q235 Steel after High Temperature Treatment. J. Build. Mater. 2006, 9, 245–249. [Google Scholar]
- Guo, Z.H.; Li, W. Experimental study on strength and deformation properties of concrete under high temperature. J. Build. Struct. 1993, 14, 8–16. [Google Scholar]
- Hong, S.; Varma, A.H. Analytical Modeling of the Standard Fire Behavior of Loaded CFT Columns. J. Constr. Steel Res. 2009, 65, 54–69. [Google Scholar] [CrossRef]
- Zhu, B.L.; Lu, Z.D.; Hu, K.X. Constitutive relationship between concrete and steel reinforcement under high temperature (fire). Sichuan Build. Sci. 1990, 16, 37–43. [Google Scholar]
- Thomas, R.J.; Sorensen, A.D. Review of Strain Rate Effects for UHPC in Tension. Constr. Build. Mater. 2017, 153, 846–856. [Google Scholar] [CrossRef]
- Bischoff, P.H.; Perry, S.H. Compressive Behaviour of Concrete at High Strain Rates. Mater. Struct. 1991, 24, 425–450. [Google Scholar] [CrossRef]
- Qian, K.; Tan, X.Y.; Li, Z.; Yu, X.H. Impact performance and the influence factors of reinforced concrete slabs under high temperatures. Eng. Mech. 2023, 40, 132–143+154. [Google Scholar]
- Abdul Razak, N.S.; Alias, A.; Mohsan, N.M.; Masjuki, S.A. The Influence of Cowper-Symonds Coefficients on the Response of Stiffened Steel Plates Subjected to Close-In Blast Loads. Key Eng. Mater. 2022, 912, 171–184. [Google Scholar] [CrossRef]
- Comité Euro-International du Béton (CEB); the Federation Internationale de la Précontrainte (FIP). CEB-FIP Model Code 1990: Design Code; Thomas Telford Ltd.: London, UK, 1993. [Google Scholar]
- Yang, G.; Wang, G.; Lu, W.; Wu, L.; Yan, P.; Chen, M. Experimental and Numerical Study of Damage Characteristics of RC Slabs Subjected to Air and Underwater Contact Explosions. Mar. Struct. 2019, 66, 242–257. [Google Scholar] [CrossRef]
- Wang, X.H.; Chu, X.S.; Feng, G. Numerical simulation of sphere’s water-entry based on Coupled Eulerian-Lagrangian method. J. Ship Mech. 2018, 22, 838–844. [Google Scholar]
- Wang, B.; Dong, Y.L. Experimental research of four—Edge simple support two—Way reinforced concrete slab under fire. J. Build. Struct. 2009, 30, 23–33. [Google Scholar]
- Wang, B.; Dong, Y.L. Experimental study of two-way reinforced concrete slabs under fire. China Civ. Eng. J. 2010, 43, 53–62. [Google Scholar]
- Bolina, F.L.; Fachinelli, E.G.; Pachla, E.C.; Centeno, F.R. A Critical Analysis of the Influence of Architecture on the Temperature Field of RC Structures Subjected to Fire Using CFD and FEA Models. Appl. Therm. Eng. 2024, 247, 123086. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, D.; Lu, F.Y. Near-field blast resistance of square reinforced concrete slabs. Explos. Shock Waves 2012, 32, 251–258. [Google Scholar]
- Wang, W. Study on Damage Effects and Assessments Method of Reinforced Concrete Structural Members Under Blast Loading. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Zhao, C.F.; He, K.C.; Lu, X. Analysis on the blast resistance of steel concrete composite slab. Explos. Shock Waves 2021, 41, 116–131. [Google Scholar]
- American Society of Civil Engineers. Blast Protection of Buildings; American Society of Civil Engineers: Reston, VA, USA, 2011; ISBN 9780784411889. [Google Scholar]
- Zhao, C.F.; Zhang, L.; Li, X.J. Damage damage and blast resistance of corrugated double steel plate concrete composite wall slabs under near-field explosion. Chin. J. High Press. Phys. 2024, 38, 88–104. [Google Scholar]
- Wang, Y.P.; Wang, W.; Yang, J.C.; Wang, J.H.; Wang, X. Blast resistance of steel plate/POZD composite structures under proximity airburst loading. Chin. J. High Press. Phys. 2023, 31, 74–85. [Google Scholar]
- Han, L.-H.; Yao, G.-H.; Tao, Z. Performance of Concrete-Filled Thin-Walled Steel Tubes under Pure Torsion. Thin-Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
- Yu, J.; Liu, F.Y.; Fang, Q. Distribution pattern and simplified model of blast load for building columns under near-field near-ground explosion. Explos. Shock Waves 2024, 41, 164–180. [Google Scholar]



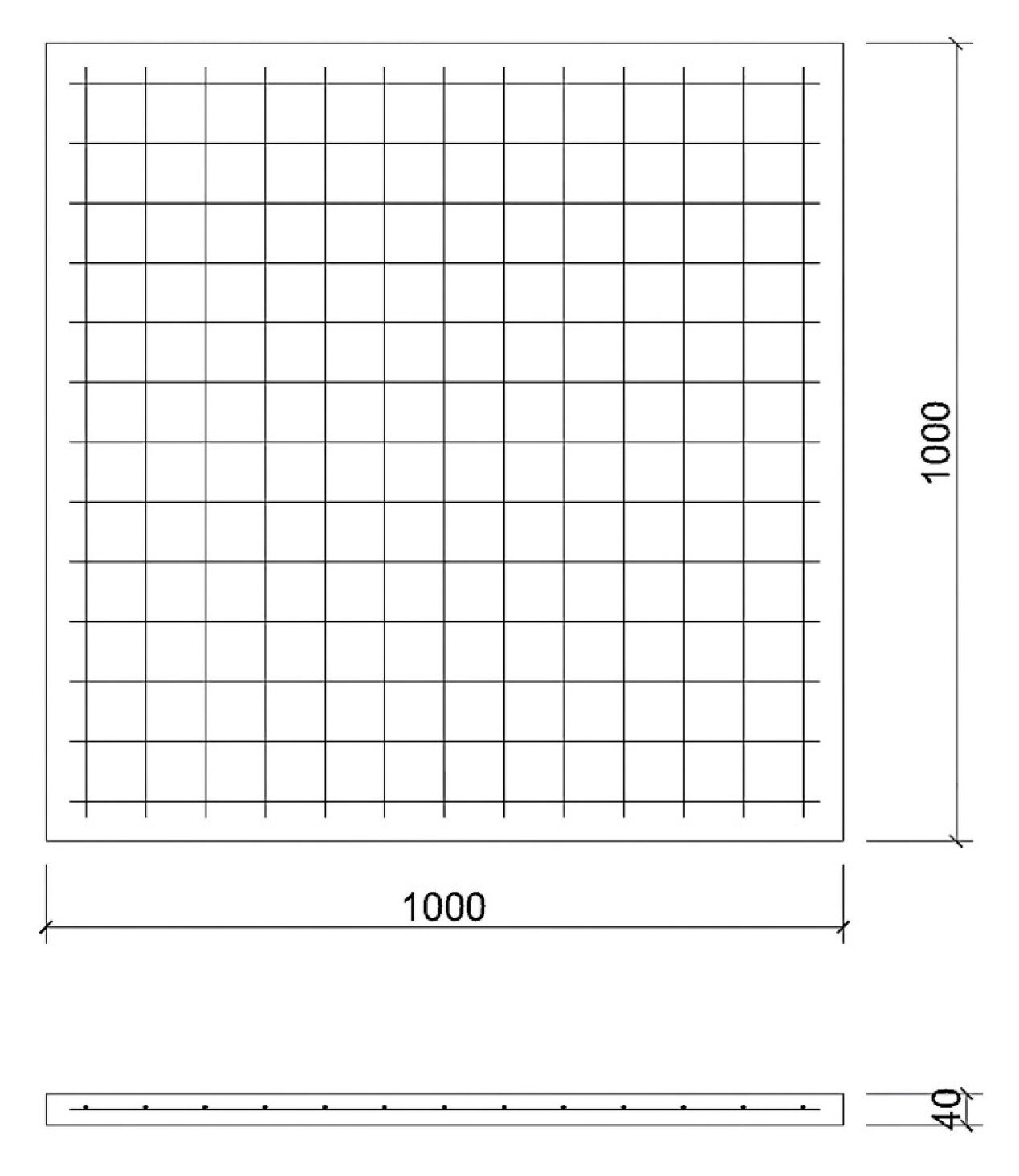







| Material | Model Number | Modulus of Elasticity E/GPa | Compressive Strength fc/MPa | Yield Strength fy/MPa | Tensile Strength ft/MPa |
|---|---|---|---|---|---|
| Concrete | C30 | 30 | 20.6 | 2.06 | |
| Steel plate | Q235 | 200 | 235 | 370 | |
| Welding nail | A2-50 | 200 | 210 | 500 |
| Component Number | W/kg | R/m | Z/(m·kg−1/3) | t/min |
|---|---|---|---|---|
| BF-00 | 1 | 0.65 | 0.65 | 0 |
| BF-30 | 1 | 0.65 | 0.65 | 30 |
| BF-60 | 1 | 0.65 | 0.65 | 60 |
| BF-90 | 1 | 0.65 | 0.65 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Chen, Z.; Liu, Y.; Tao, Q.; Wu, D.; Zou, P. Multi-Criteria Analysis of Steel–Concrete–Steel Slab Performance: Dynamic Response Assessment Under Post-Fire Explosion. Buildings 2025, 15, 1340. https://doi.org/10.3390/buildings15081340
Zhang S, Chen Z, Liu Y, Tao Q, Wu D, Zou P. Multi-Criteria Analysis of Steel–Concrete–Steel Slab Performance: Dynamic Response Assessment Under Post-Fire Explosion. Buildings. 2025; 15(8):1340. https://doi.org/10.3390/buildings15081340
Chicago/Turabian StyleZhang, Shijie, Zhenfu Chen, Yizhi Liu, Qiuwang Tao, Dan Wu, and Pinyu Zou. 2025. "Multi-Criteria Analysis of Steel–Concrete–Steel Slab Performance: Dynamic Response Assessment Under Post-Fire Explosion" Buildings 15, no. 8: 1340. https://doi.org/10.3390/buildings15081340
APA StyleZhang, S., Chen, Z., Liu, Y., Tao, Q., Wu, D., & Zou, P. (2025). Multi-Criteria Analysis of Steel–Concrete–Steel Slab Performance: Dynamic Response Assessment Under Post-Fire Explosion. Buildings, 15(8), 1340. https://doi.org/10.3390/buildings15081340







