A Novel Hybrid Metaheuristic MPA-PSO to Optimize the Properties of Viscous Dampers
Abstract
1. Introduction
2. Modeling and Optimization Methods
2.1. Modeling
2.2. Nonlinear Viscous Damper Optimization Problem
2.2.1. Decision Variables
2.2.2. Objective Function
2.2.3. Problem Constraints
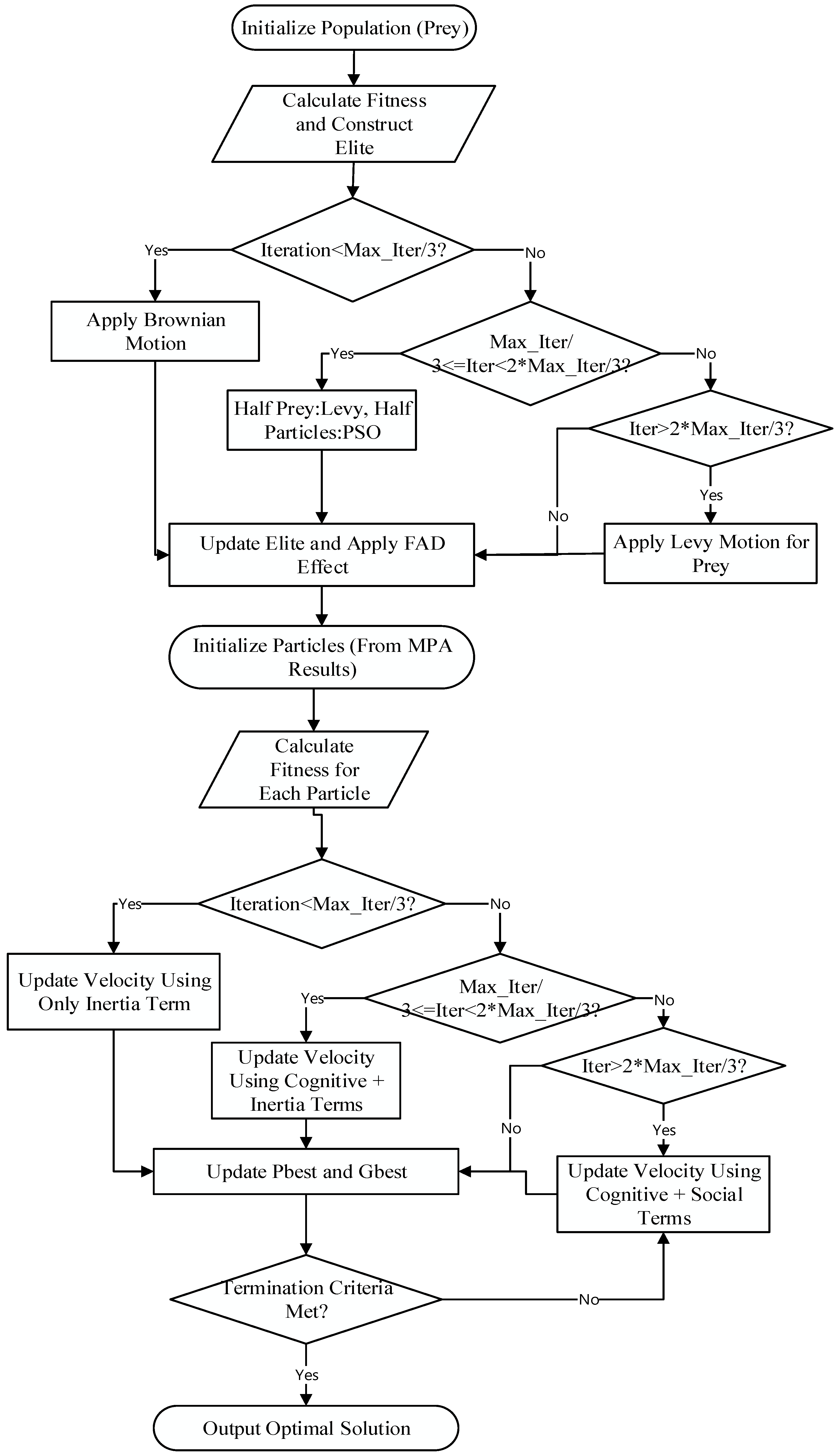
2.3. Methods
2.3.1. Marine Predator Algorithm (MPA)
2.3.2. Combination of MPA and PSO
3. Application
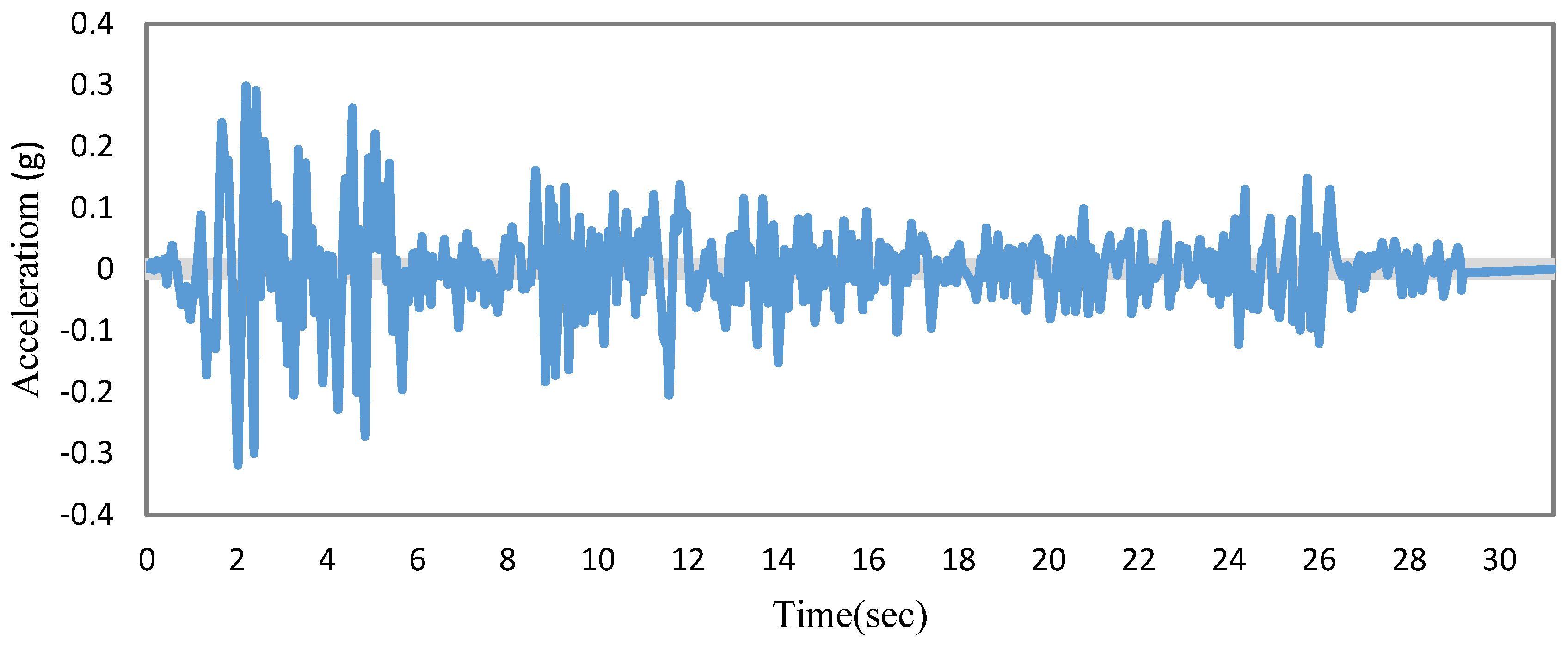
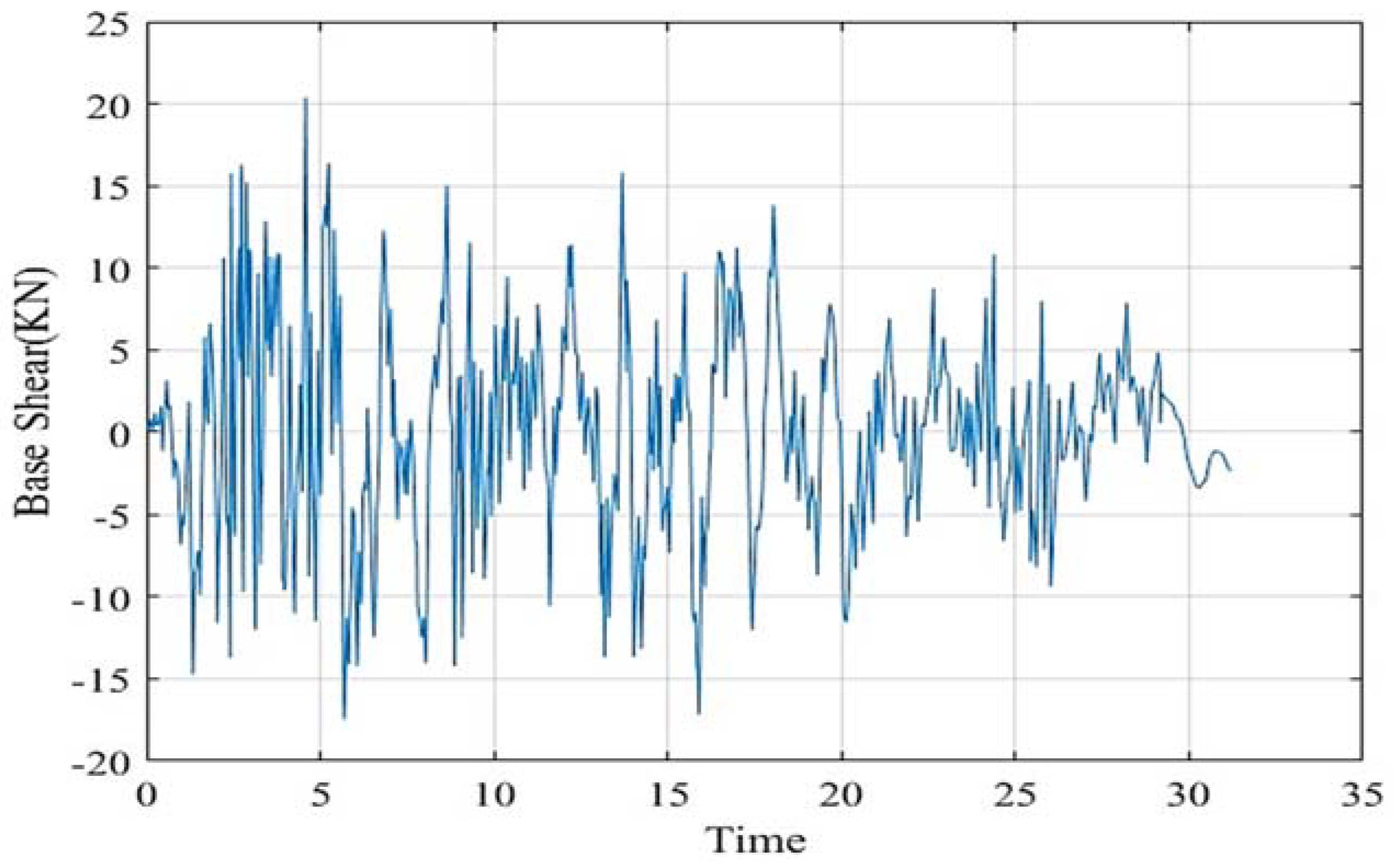
3.1. Scenario 1: Three-Story Concrete Frame
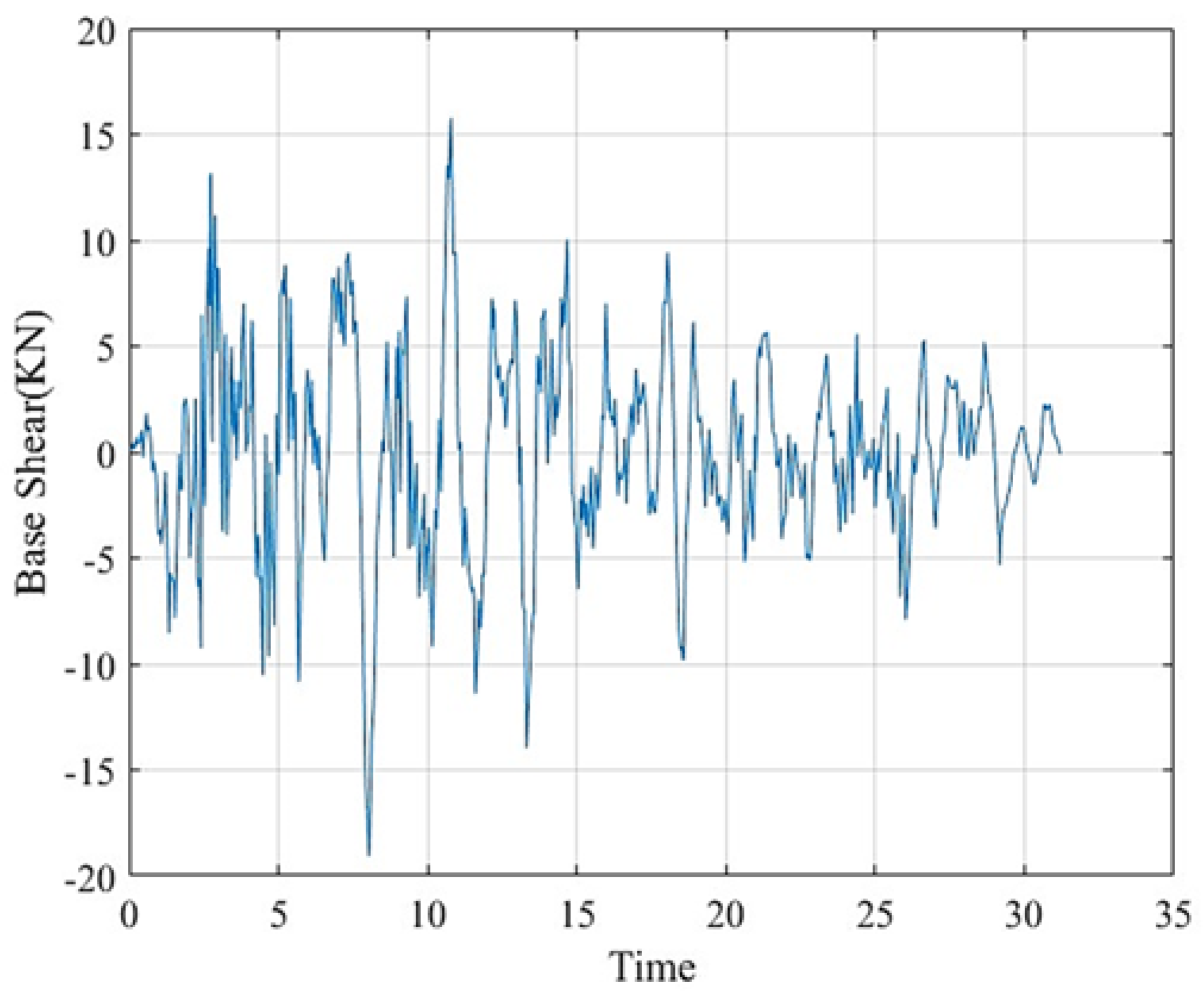
3.2. Scenario 2: Five-Story Concrete Frame
4. Conclusions
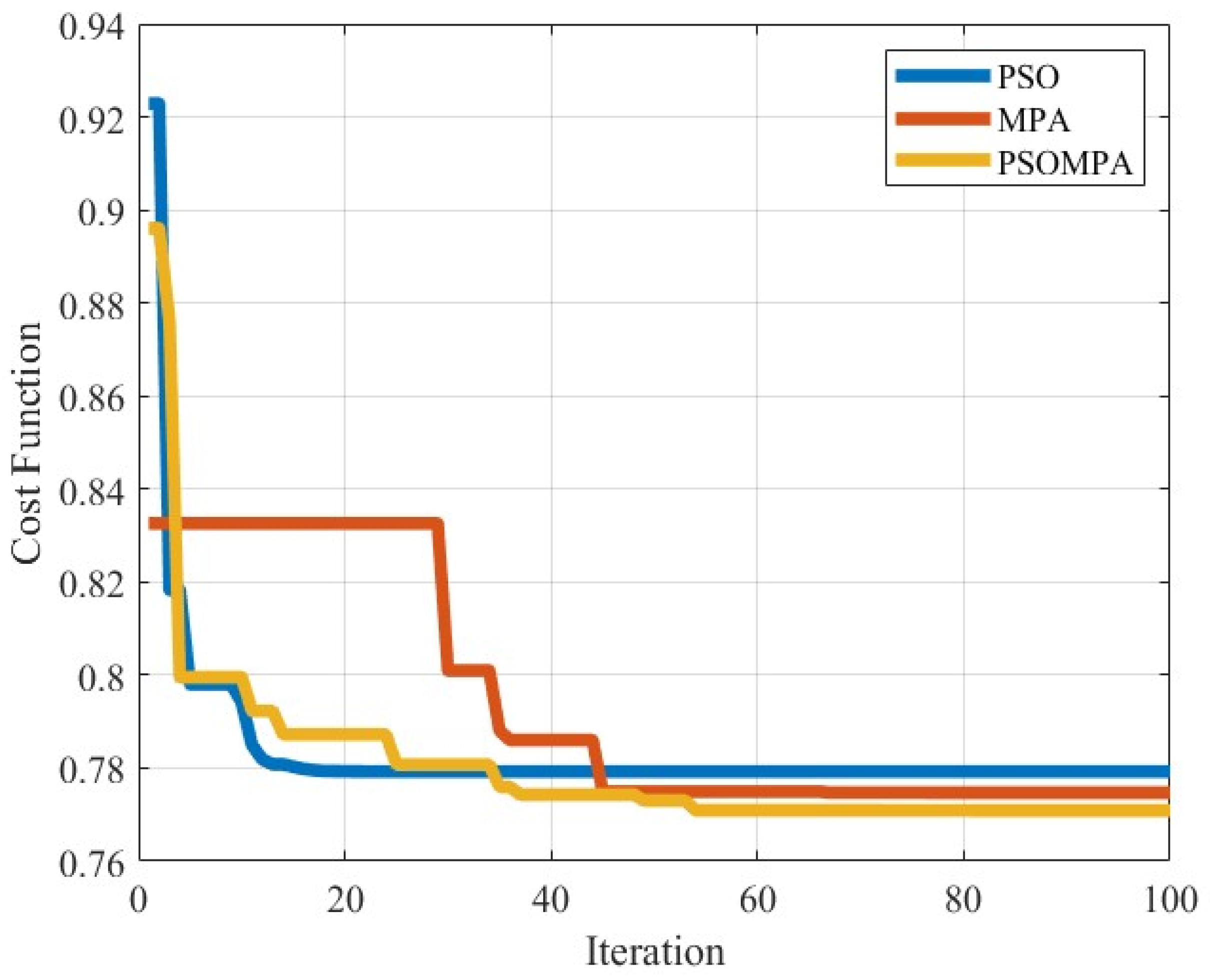
- The hybrid MPA-PSO algorithm demonstrated superior performance in both scenarios, achieving a lower cost function value and faster convergence rates compared to the individual MPA and PSO algorithms. While all algorithms exhibited rapid initial convergence, PSO showed a tendency towards premature convergence, potentially leading to suboptimal solutions. Conversely, MPA displayed a more oscillatory convergence pattern, indicating a thorough exploration of the solution space. MPA-PSO effectively balances these characteristics, leading to robust and efficient optimization;
- The optimal axial stiffness (Ka) of the viscous dampers exhibited sensitivity to the choice of optimization algorithm, particularly in the five-story frame scenario. MPA-PSO achieved comparable performance with significantly lower stiffness values compared to MPA and PSO, suggesting potential material savings and cost-effectiveness. The damping coefficient (Cd) showed less variation across algorithms, indicating a relatively robust optimal value;
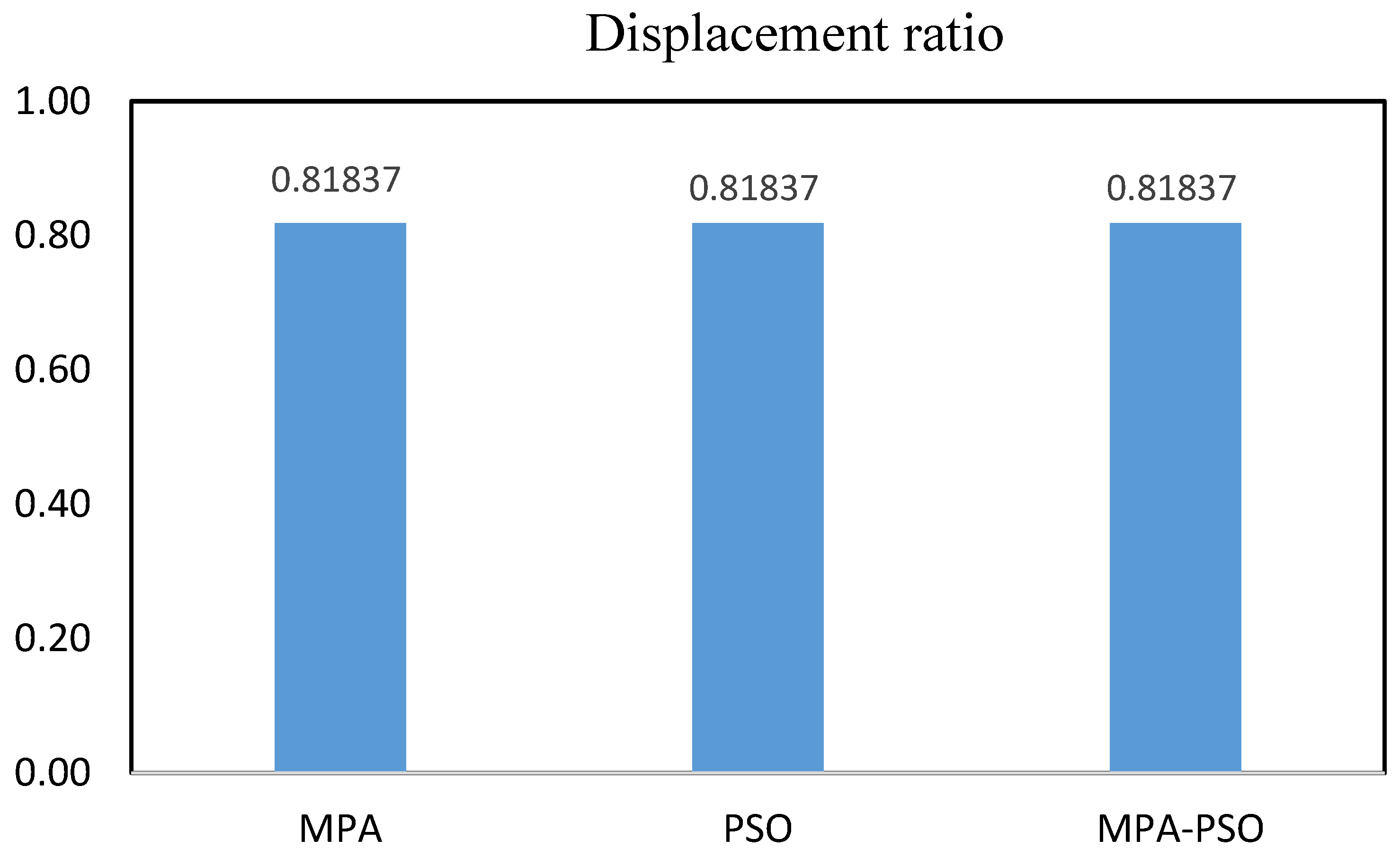
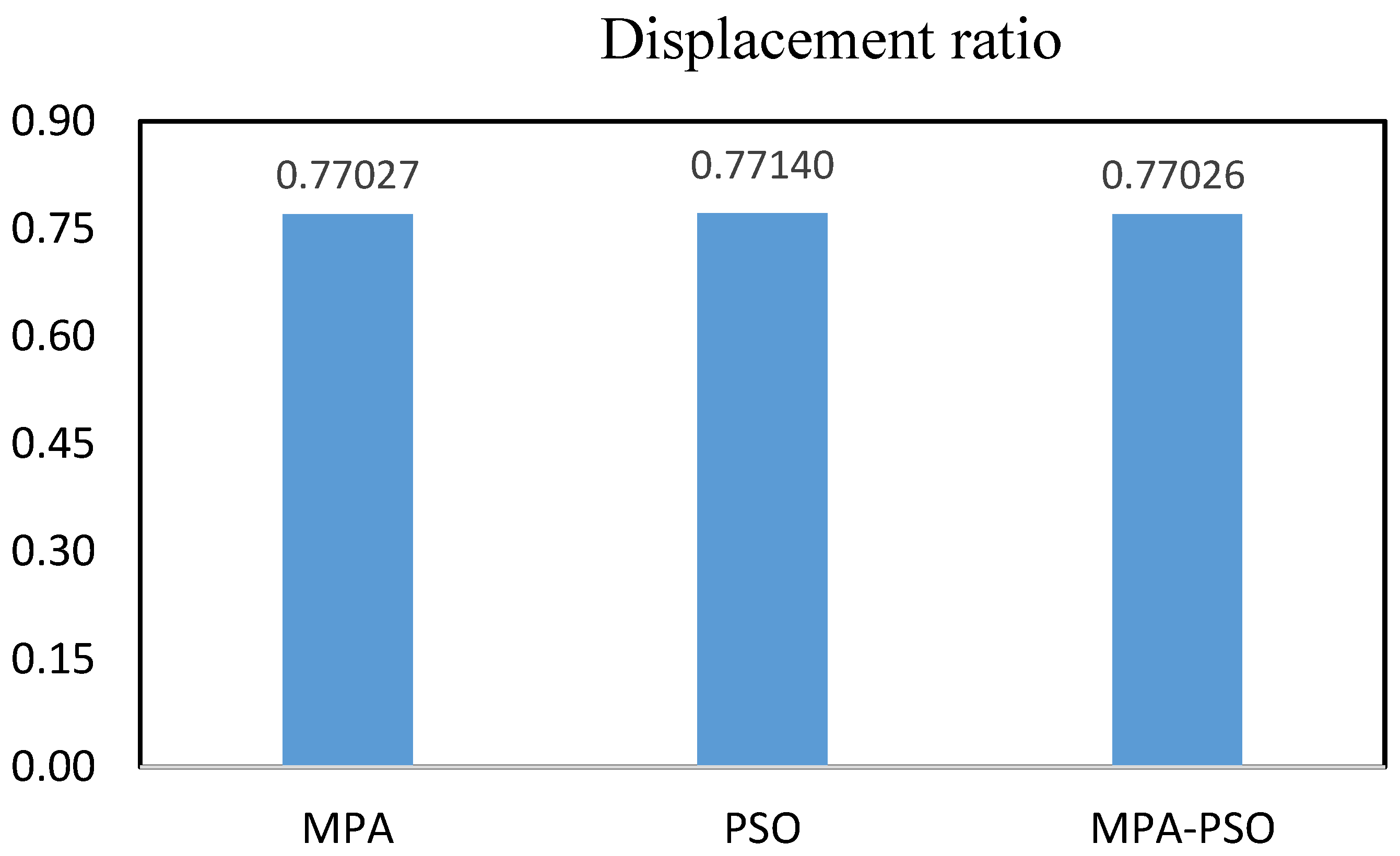
- All three algorithms effectively minimized the maximum roof displacement ratio in both three- and five-story frames, demonstrating their capability to mitigate structural response under seismic loading. In the three-story frame, all algorithms converged to a similar displacement ratio, indicating comparable performance. However, in the five-story frame, MPA-PSO and MPA achieved near-identical displacement ratios, slightly outperforming PSO. This suggests that while all algorithms are effective, MPA-PSO and MPA may offer superior precision in complex structural optimization problems;
- The successful implementation of the MPA-PSO algorithm demonstrates the potential of hybrid metaheuristic approaches for enhancing the efficiency and accuracy of structural optimization. The combination of MPA and PSO effectively leveraged their complementary strengths, resulting in improved convergence rates and solution quality. However, the marginal improvement in displacement ratio observed in the five-story frame suggests that the benefits of hybridization may be problem-dependent. Future research should explore the applicability of MPA-PSO and other hybrid algorithms to a wider range of structural configurations and loading conditions, further elucidating their potential for practical engineering applications;
- The results indicated that the optimal axial stiffness (Kd) for the five-story frame varied based on the optimization algorithm. While both MPA and PSO converged to 200 kN/mm, the MPA-PSO hybrid approach achieved the same stiffness but resulted in a lower displacement ratio (0.77026 compared to 0.77140 in PSO). Furthermore, in the three-story frame, the optimal damping coefficient (Cd) obtained through MPA-PSO was 14.22824 kN·s/mm, which was lower than the value determined by PSO (19.32417 kN·s/mm). This suggests that the hybrid algorithm can achieve effective displacement control with reduced damping requirements without necessitating an increase in structural stiffness;
- For the five-story frame, the MPA-PSO algorithm converged in 4:00 min, whereas PSO and MPA required 2:45 and 3:30 min, respectively. Although the hybrid approach had a slightly higher computational time compared to PSO, it achieved a lower maximum displacement ratio (0.77026) than PSO (0.77140). This finding highlights that in larger and more complex structural systems, a marginal increase in computational time can lead to more precise optimization and improved structural performance. Furthermore, the proposed algorithm was able to converge in all cases, unlike the individual algorithms, which failed to converge in some instances. This demonstrates the higher reliability of the hybrid approach in solving more complex problems, ensuring optimal results even in more challenging structural scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yashinsky, M. Earthquake Damage to Structures, in Earthquake Engineering for Structural Design; CRC Press: Boca Raton, FL, USA, 2005; pp. 2-1–2-58. [Google Scholar]
- Sadeghi-Movahhed, A.; De Domenico, D.; Majdi, A. Structural flexibility impact on pounding severity and seismic performance of adjacent isolated buildings. Soil Dyn. Earthq. Eng. 2024, 181, 108667. [Google Scholar] [CrossRef]
- Sadeghi-Movahhed, A.; Billah, A.H.M.M.; Shirkhani, A.; Mashayekhi, M.; Majdi, A. Vulnerability assessment of tall isolated steel building under variable earthquake hazard levels using endurance time method. J. Struct. Integr. Maint. 2024, 9, 2314816. [Google Scholar] [CrossRef]
- Majdi, A.; Mashayekhi, M.; Sadeghi-Movahhed, A. Effect of Near-Fault Earthquake Characteristics on Seismic Response of Mid-Rise Structures with Triple Friction Pendulum Isolator. J. Rehabil. Civ. Eng. 2024, 12, 47–62. [Google Scholar] [CrossRef]
- Movahhed, A.S.; Zardari, S.; ¸Sadoglu, E. Seismic performance of a building base-isolated by TFP susceptible to pound with a surrounding moat wall. Earthq. Struct. 2022, 23, 723–736. [Google Scholar] [CrossRef]
- Sadeghi-Movahhed, A.; Shirkhani, A.; Zardari, S.; Farsangi, E.N.; Karimi, A. Pour Effective range of base isolation design parameters to improve structural performance under far and near-fault earthquakes. Adv. Struct. Eng. 2023, 26, 52–71. [Google Scholar] [CrossRef]
- Zamani, F.; Alavi, S.H.; Mashayekhi, M.; Noroozinejad Farsangi, E.; Sadeghi-Movahhed, A.; Majdi, A. Optimum design of double tuned mass dampers using multiple metaheuristic multi-objective optimization algorithms under seismic excitation. Front. Built Environ. 2025, 11, 1559530. [Google Scholar] [CrossRef]
- Lee, D.; Taylor, D.P. Viscous damper development and future trends. Struct. Des. Tall Build. 2001, 10, 311–320. [Google Scholar] [CrossRef]
- Majdi, A.; Sadeghi-Movahhed, A.; Mashayekhi, M.; Zardari, S.; Benjeddou, O.; De Domenico, D. On the Influence of Unexpected Earthquake Severity and Dampers Placement on Isolated Structures Subjected to Pounding Using the Modified Endurance Time Method. Buildings 2023, 13, 1278. [Google Scholar] [CrossRef]
- Akcelyan, S.; Lignos, D.G.; Hikino, T. Adaptive numerical method algorithms for nonlinear viscous and bilinear oil damper models subjected to dynamic loading. Soil Dyn. Earthq. Eng. 2018, 113, 488–502. [Google Scholar] [CrossRef]
- Kamgar, R.; Hatefi, S.M.; Majidi, N. A fuzzy inference system in constructional engineering projects to evaluate the design codes for RC buildings. Civ. Eng. J. 2018, 4, 2155–2172. [Google Scholar] [CrossRef]
- Kamgar, R.; Khatibinia, M.; Khatibinia, M. Optimization criteria for design of tuned mass dampers including soil–structure interaction effect. Int. J. Optim. Civil. Eng. 2019, 9, 213–232. [Google Scholar]
- Sadeghi-Movahhed, A.; Shirkhani, A.; Zardari, S.; Mashayekhi, M.; Farsangi, E.N.; Majdi, A. Modified endurance time method for seismic performance assessment of base-isolated structures. J. Build. Eng. 2023, 67, 105955. [Google Scholar] [CrossRef]
- Majdi, A.; Sadeghi-Movahhed, A.; Farsangi, E.N.; Mashayekhi, M.; Almujibah, H.; De Domenico, D. Application of the Modified Endurance Time Method for Predicting Seismic Response of Base-Isolated Structures Under Pounding. J. Earthq. Tsunami 2025, 19, 2450037. [Google Scholar] [CrossRef]
- Foulds, L.; Foulds, L. Classical Optimization. Optimization Techniques: An Introduction; Springer: Berlin/Heidelberg, Germany, 1981; pp. 257–309. [Google Scholar]
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by Direct Search: New Perspectives on Some Classical and Modern Methods. SIAM Rev. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Alavi, S.H.; Mashayekhi, M.; Zolfaghari, M. Optimizing gas pipeline routing considering seismic risk through metaheuristic algorithm. Res. Sq. 2024, preprint. [Google Scholar]
- Yang, X. Metaheuristic optimization. Scholarpedia 2011, 6, 11472. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm-A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Babu, B.; Jehan, M.M.L. Differential evolution for multi-objective optimization. In Proceedings of the 2003 Congress on Evolutionary Computation, 2003, CEC’03, Chicago, IL, USA, 12–16 June 2003; IEEE: New York, NY, USA, 2003. [Google Scholar]
- Fourie, P.; Groenwold, A. The particle swarm optimization algorithm in size and shape optimization. Struct. Multidiscip. Optim. 2002, 23, 259–267. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahar, S. A hybrid particle swarm and ant colony optimization for design of truss structures. Asian J. Civ. Eng. 2008, 9, 329–348. [Google Scholar]
- Selvi, V.; Umarani, R. Comparative analysis of ant colony and particle swarm optimization techniques. Int. J. Comput. Appl. 2010, 5, 1–6. [Google Scholar] [CrossRef]
- Mashayekhi, M.; Shirpour, A.; Sadeghi, R. Finding Optimum Parameters of Passive Tuned Mass Damper by PSO, WOA, and Hybrid PSO-WOA (HPW) Algorithms. J. Soft Comput. Civ. Eng. 2023, 7, 72–92. [Google Scholar]
- Lamberti, L. An efficient simulated annealing algorithm for design optimization of truss structures. Comput. Struct. 2008, 86, 1936–1953. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Akehashi, H.; Takewaki, I. Comparative investigation on optimal viscous damper placement for elastic-plasticMDOF structures: Transfer function amplitude or double impulse. Soil Dyn. Earthq. Eng. 2020, 130, 105987. [Google Scholar] [CrossRef]
- Kargahi, M.; Ekwueme, C.G. Structural optimization of viscous dampers using genetic algorithms for improving seismic performance of existing buildings. In Proceedings of the ATC and SEI Improving the Seismic Performance of Existing Buildings and Other Structures, San Francisco, CA, USA, 10–12 December 2009; pp. 955–966. [Google Scholar]
- Çerçevik, A.E.; Avşar, Ö.; Dilsiz, A. Optimal placement of viscous wall dampers in RC moment resisting frames using metaheuristic search methods. Eng. Struct. 2021, 249, 113108. [Google Scholar] [CrossRef]
- Ayyash, N.; Hejazi, F. Development of hybrid optimization algorithm for structures furnished with seismic damper devices using the particle swarm optimization method and gravitational search algorithm. Earthq. Eng. Eng. Vib. 2022, 21, 455–474. [Google Scholar] [CrossRef]
- Juneja, M.; Nagar, S.K. Particle swarm optimization algorithm and its parameters: A review. In Proceedings of the 2016 International Conference on Control, Computing, Communication and Materials (ICCCCM), Allahbad, India, 21–22 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- MasMashayekhi, M.R.; Mosayyebi, S. A new hybrid Harris hawks optimization (HHO) and particle swarm optimization (PSO) algorithm for the design of castellated beams. Asian J. Civ. Eng. 2023, 24, 2121–2139. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Silwal, B.; Michael, R.J.; Ozbulut, O.E. A superelastic viscous damper for enhanced seismic performance of steel moment frames. Eng. Struct. 2015, 105, 152–164. [Google Scholar] [CrossRef]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Guler, E.; Alhan, C. Effectiveness of nonlinear fluid viscous dampers in seismically isolated buildings. Earthq. Struct. 2019, 17, 191–204. [Google Scholar]
- Kelly, T.E. In-Structures Damping and Energy Dissipation. Design Guidelines; SE Holmes Consulting Group Ltd.: Queenstown, New Zealand, 2001; p. 164. [Google Scholar]
- Yu, Y.; Tsai, K.; Li, C.; Weng, Y.; Tsai, C. Earthquake response analyses of a full-scale five-story steel frame equipped with two types of dampers. Earthq. Eng. Struct. Dyn. 2013, 42, 1301–1320. [Google Scholar] [CrossRef]

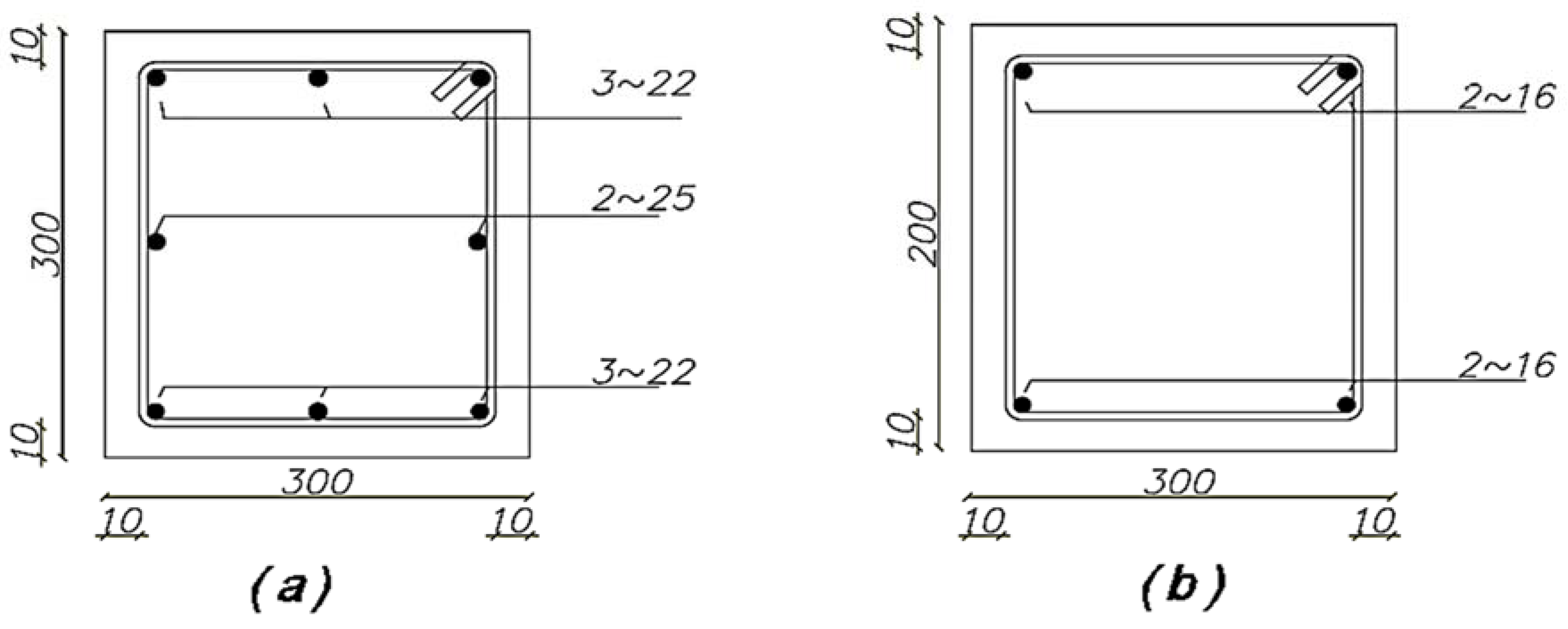


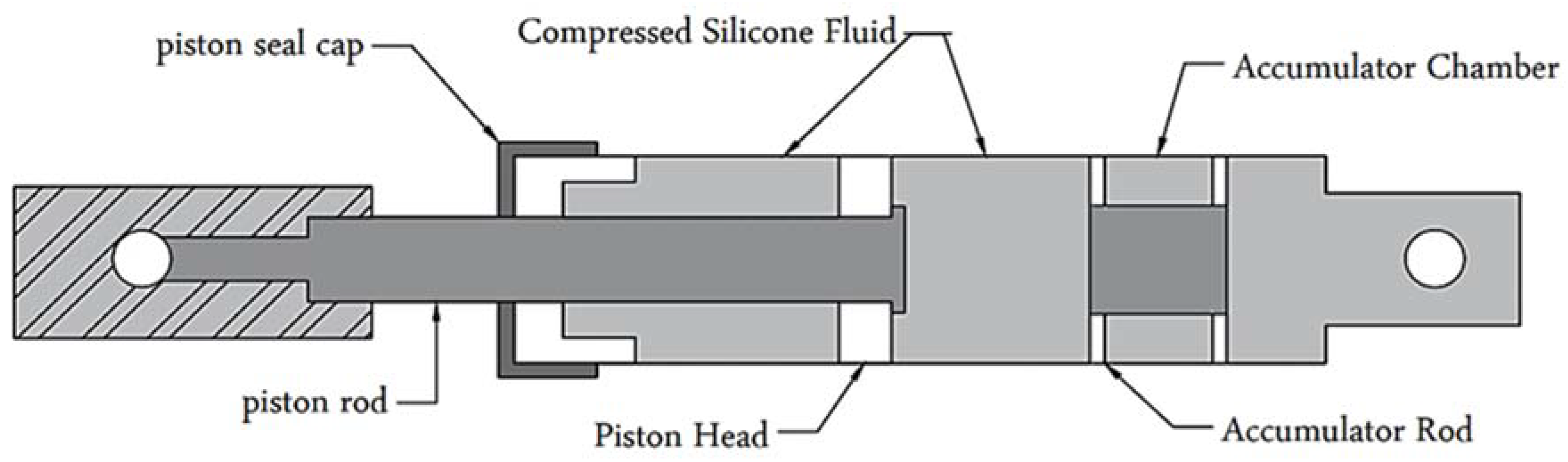

| Dimension (mm) | Rebar Diameter (mm) | Number of Rebar | Yield Stress (MPa) | |
|---|---|---|---|---|
| Columns | 300 × 300 | 22 | 6 | 440 |
| 25 | 2 | 440 | ||
| Beams | 300 × 200 | 16 | 4 | 440 |
| Function | Name | Range | Actual Minimum | |
|---|---|---|---|---|
| Sphere | [−100, 100] | 2.2407 × 10−10 | 0 | |
| Schwefel 2.20 | [−10, 10] | 8.5552 × 10−09 | 0 | |
| Rosenbrock | [−30, 30] | 3.748 × 10−11 | 0 | |
| Step | [−100, 100] | 2.9137 × 10−17 | 0 | |
| Schwefel | [−500, 500] | −1256.9487 |
| Three Floors | Best | Worst | Time |
|---|---|---|---|
| MPA | 0.8183 | 0.8184 | 2:20 |
| PSO | 0.8183 | 0.8183 | 1:50 |
| MPA-PSO | 0.8183 | 0.8183 | 2:40 |
| Three Floors | Kd (kN/mm) | Cd (kN·s/mm) | α | Disp Ratio |
|---|---|---|---|---|
| MPA | 50 | 16.21536 | 0.01000 | 0.81837 |
| PSO | 50 | 19.32417 | 0.01000 | 0.81837 |
| MPA-PSO | 50 | 14.22824 | 0.01000 | 0.81837 |
| Five Floors | Best | Worst | Time |
|---|---|---|---|
| MPA | 0.7702 | did not converge | 3:30 |
| PSO | 0.7714 | did not converge | 2:45 |
| MPA-PSO | 0.7702 | 0.7766 | 4:00 |
| Five Floors | Kd (kN/mm) | Cd (kN·s/mm) | α | Disp Ratio |
|---|---|---|---|---|
| MPA | 200 | 24.99550 | 0.15406 | 0.77027 |
| PSO | 200 | 19.17759 | 0.10363 | 0.77140 |
| MPA-PSO | 200 | 24.99994 | 0.15409 | 0.77026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shemshaki, E.; Haddad, M.H.; Mashayekhi, M.; Aghajanzadeh, S.M.; Majdi, A.; Noroozinejad Farsangi, E. A Novel Hybrid Metaheuristic MPA-PSO to Optimize the Properties of Viscous Dampers. Buildings 2025, 15, 1330. https://doi.org/10.3390/buildings15081330
Shemshaki E, Haddad MH, Mashayekhi M, Aghajanzadeh SM, Majdi A, Noroozinejad Farsangi E. A Novel Hybrid Metaheuristic MPA-PSO to Optimize the Properties of Viscous Dampers. Buildings. 2025; 15(8):1330. https://doi.org/10.3390/buildings15081330
Chicago/Turabian StyleShemshaki, Elmira, Mohammad Hasan Haddad, Mohammadreza Mashayekhi, Seyyed Meisam Aghajanzadeh, Ali Majdi, and Ehsan Noroozinejad Farsangi. 2025. "A Novel Hybrid Metaheuristic MPA-PSO to Optimize the Properties of Viscous Dampers" Buildings 15, no. 8: 1330. https://doi.org/10.3390/buildings15081330
APA StyleShemshaki, E., Haddad, M. H., Mashayekhi, M., Aghajanzadeh, S. M., Majdi, A., & Noroozinejad Farsangi, E. (2025). A Novel Hybrid Metaheuristic MPA-PSO to Optimize the Properties of Viscous Dampers. Buildings, 15(8), 1330. https://doi.org/10.3390/buildings15081330






