Coupled Vibration Mathematical Model of Special-Shaped Column Structure Considering Ground Rotation Effects
Abstract
1. Introduction
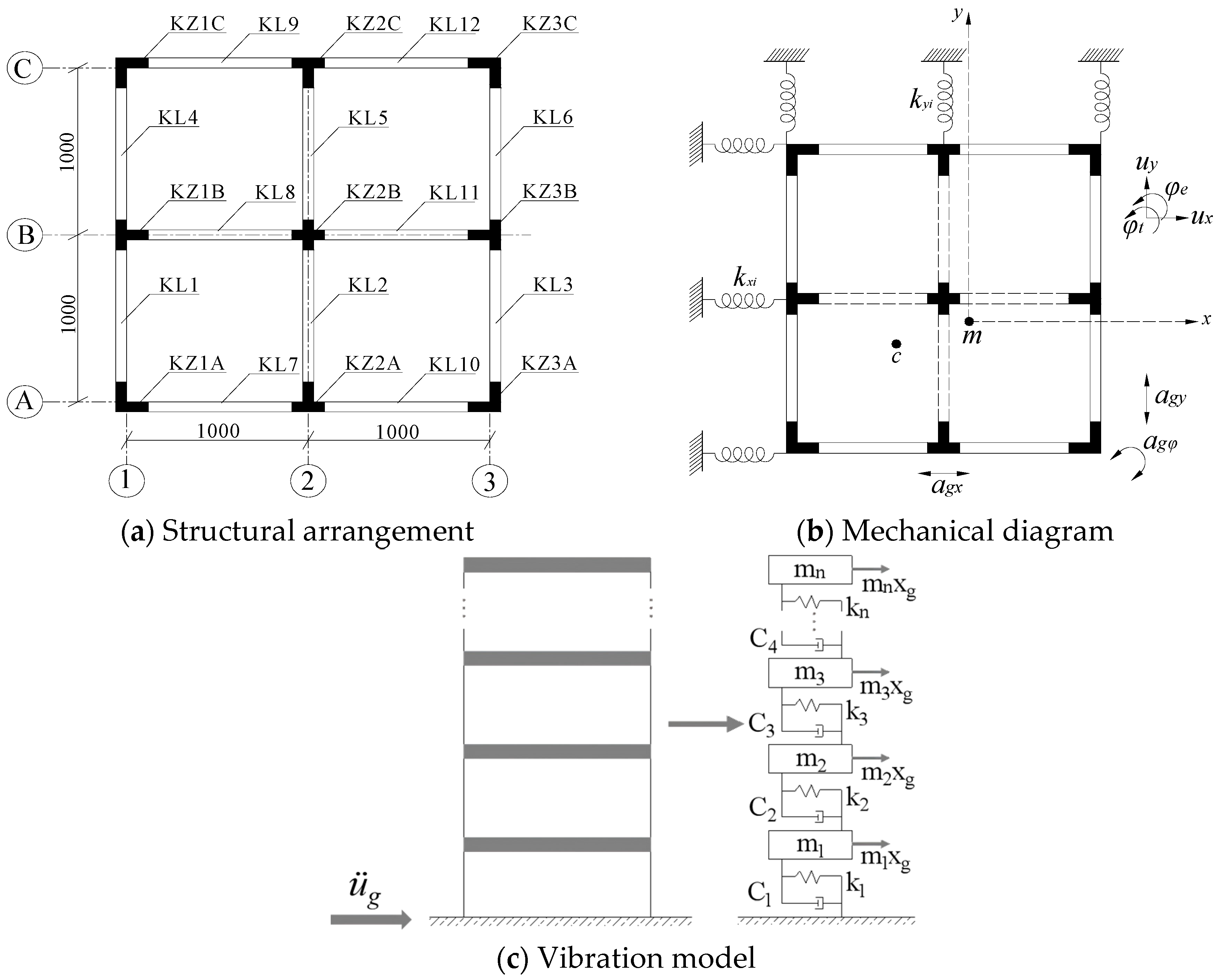
2. Seismic Response Analysis Model Considering Ground Rotational Components
2.1. Dynamics Model Considering Ground Rotational Components
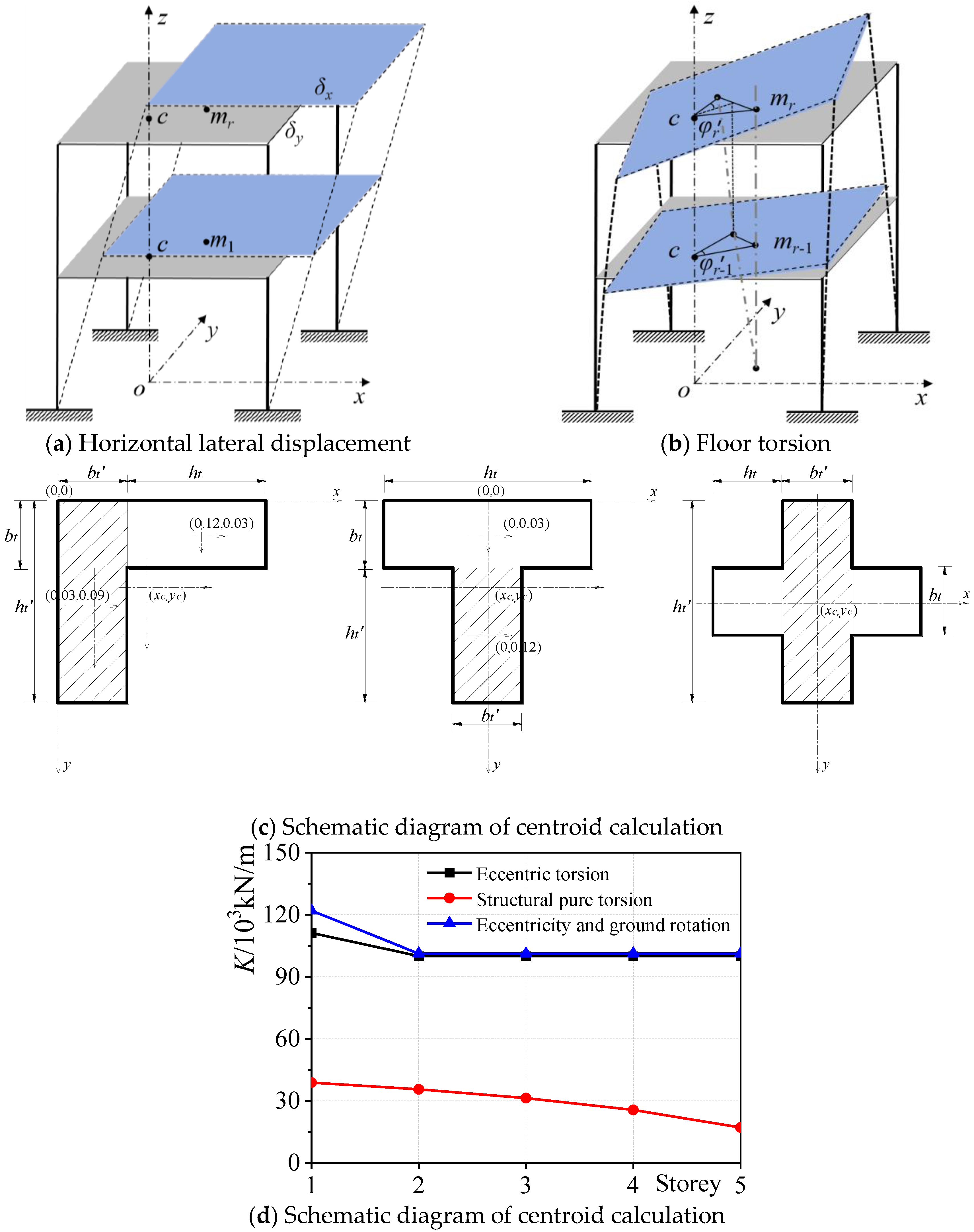
2.2. Determination of Floor Torsional Stiffness
3. Lateral–Torsional Vibration Mathematical Mode
3.1. Establishment of Lateral–Torsional Coupled Motion Equations
3.2. Response Patterns of Lateral–Torsional Coupled Vibration
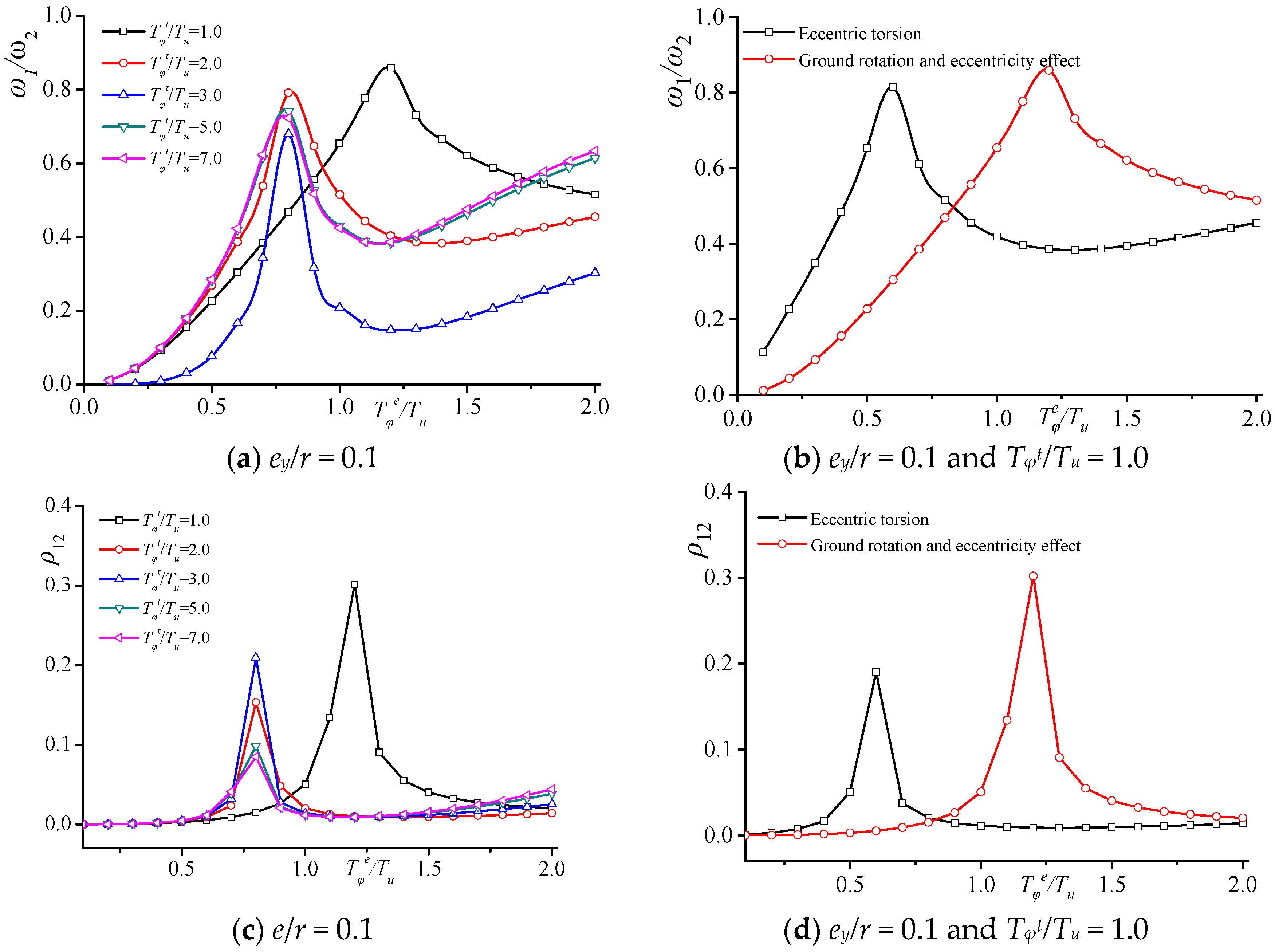
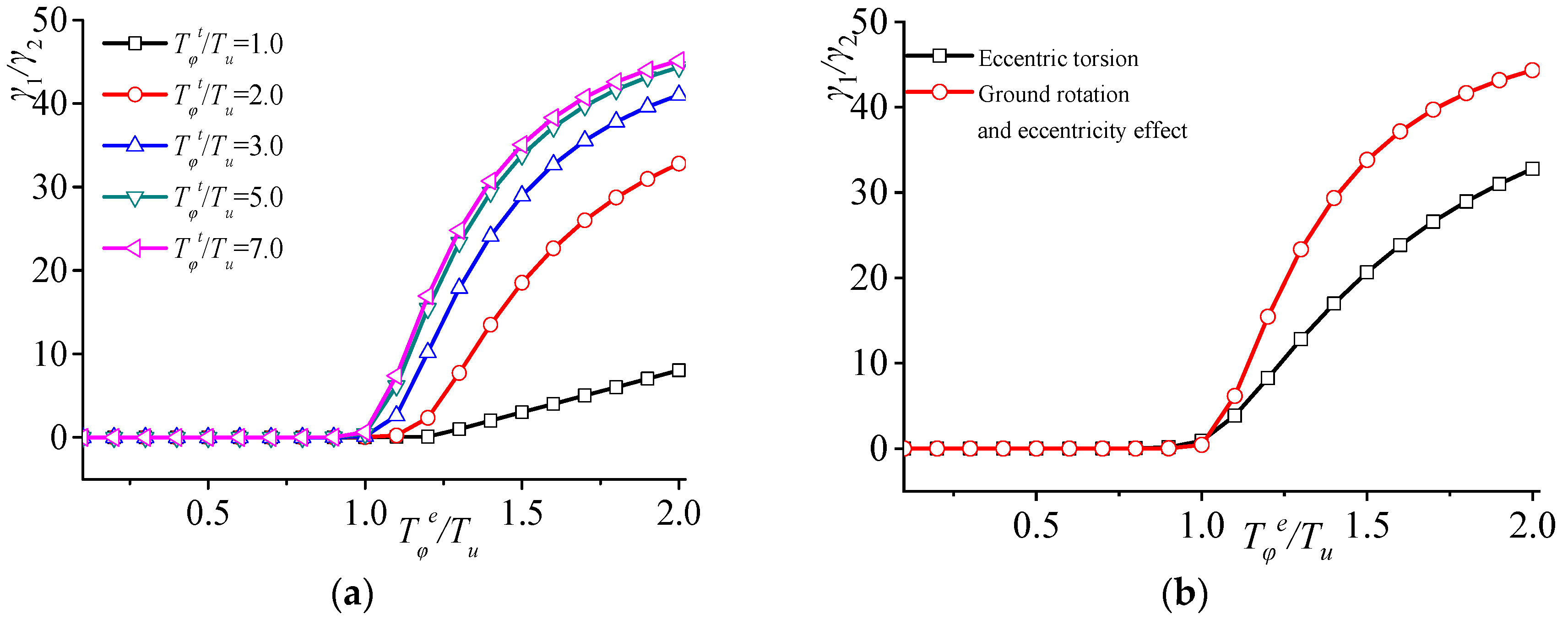
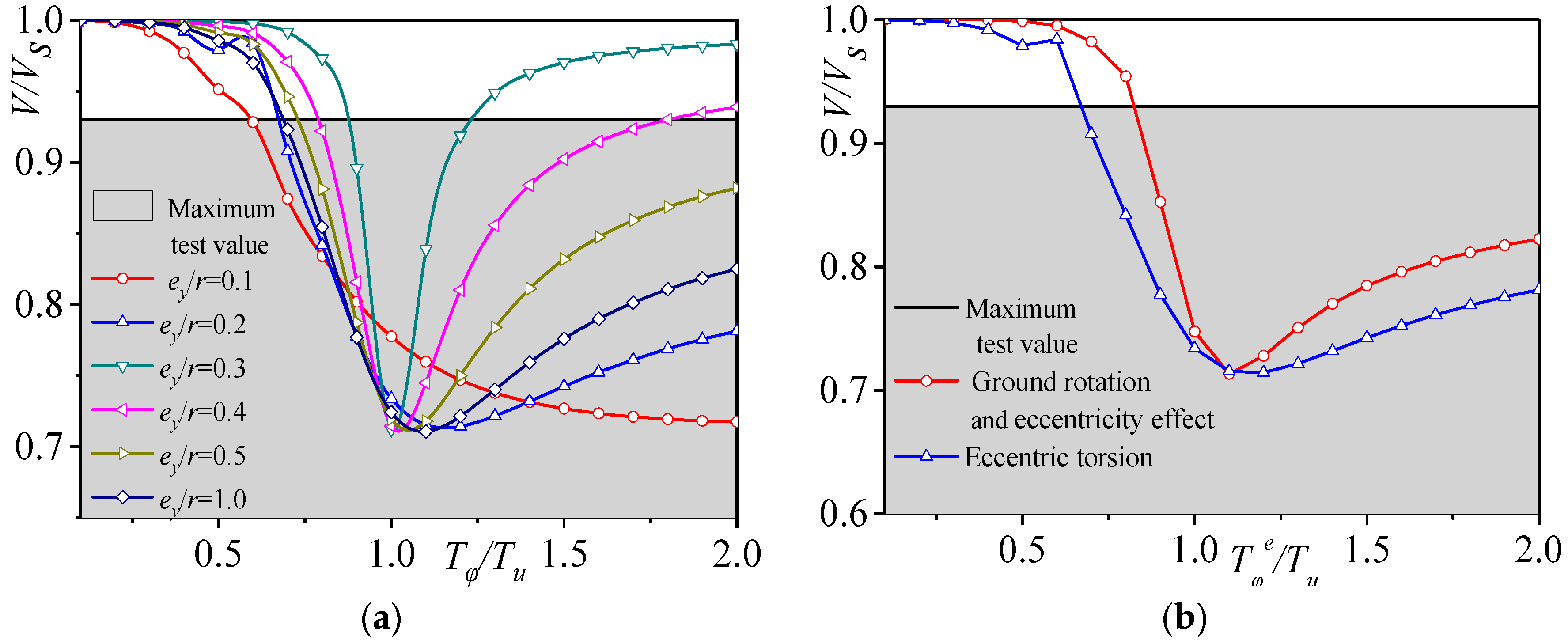
3.2.1. Natural Vibration Frequency Variation
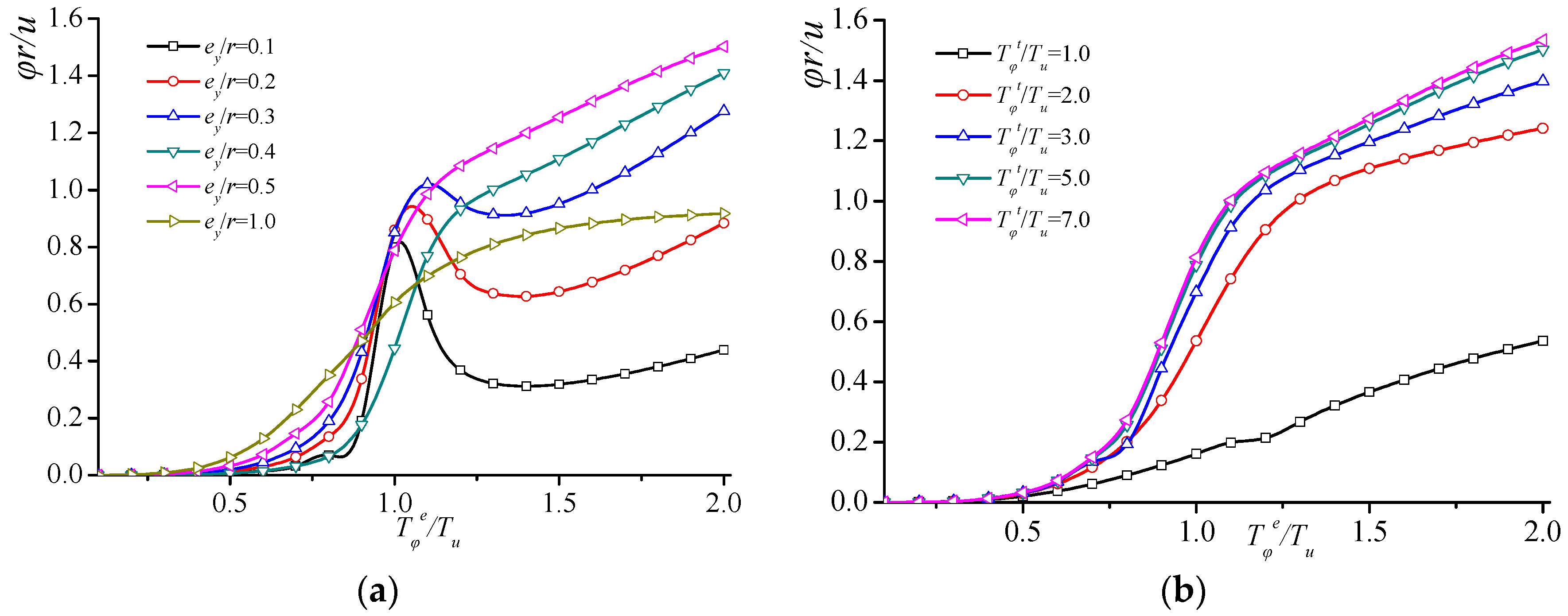
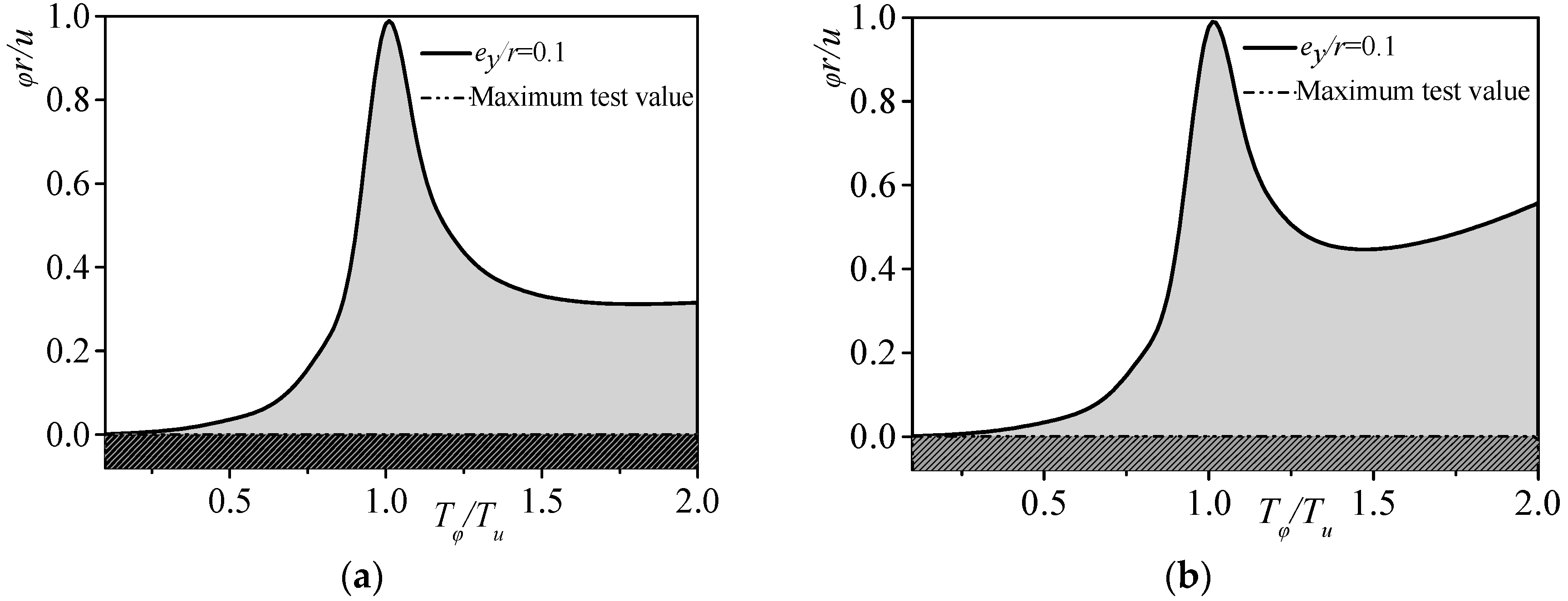
3.2.2. Torsional Amplitude
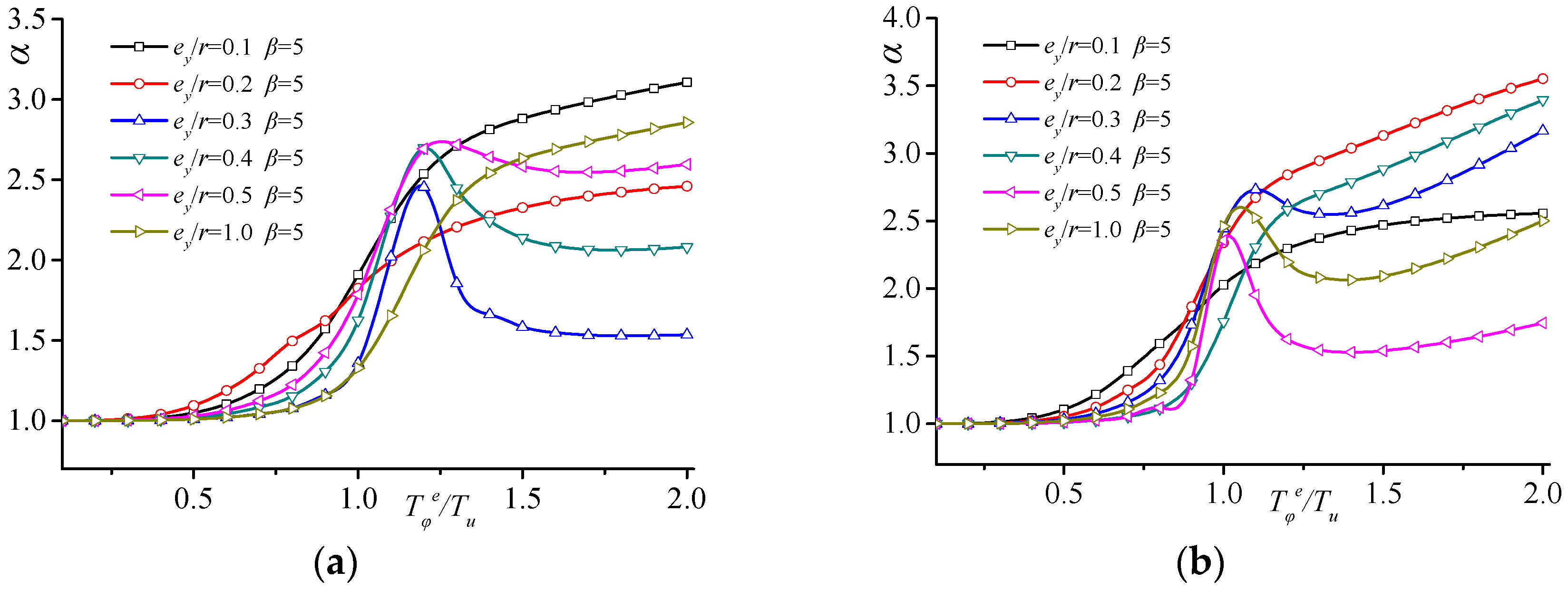
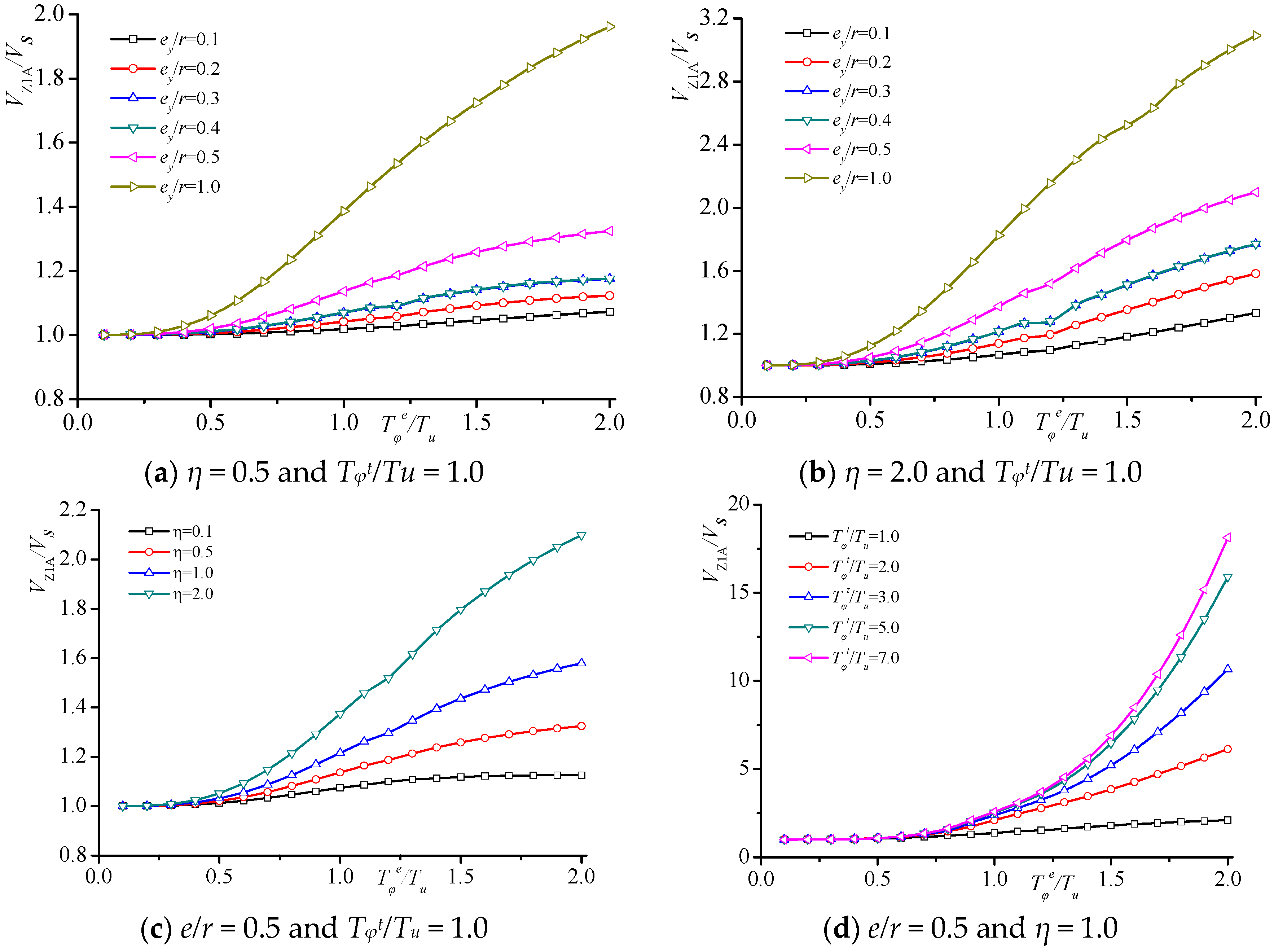
3.2.3. Participation Coefficient
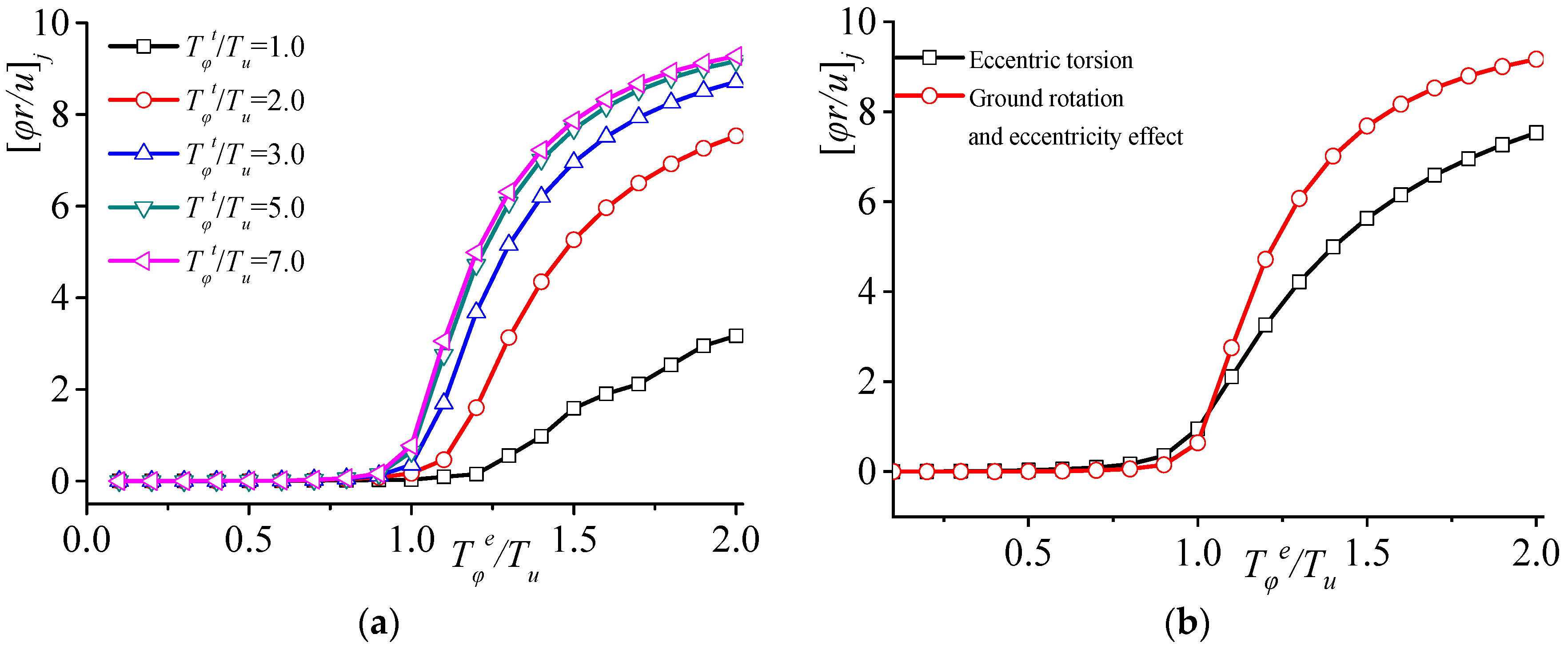
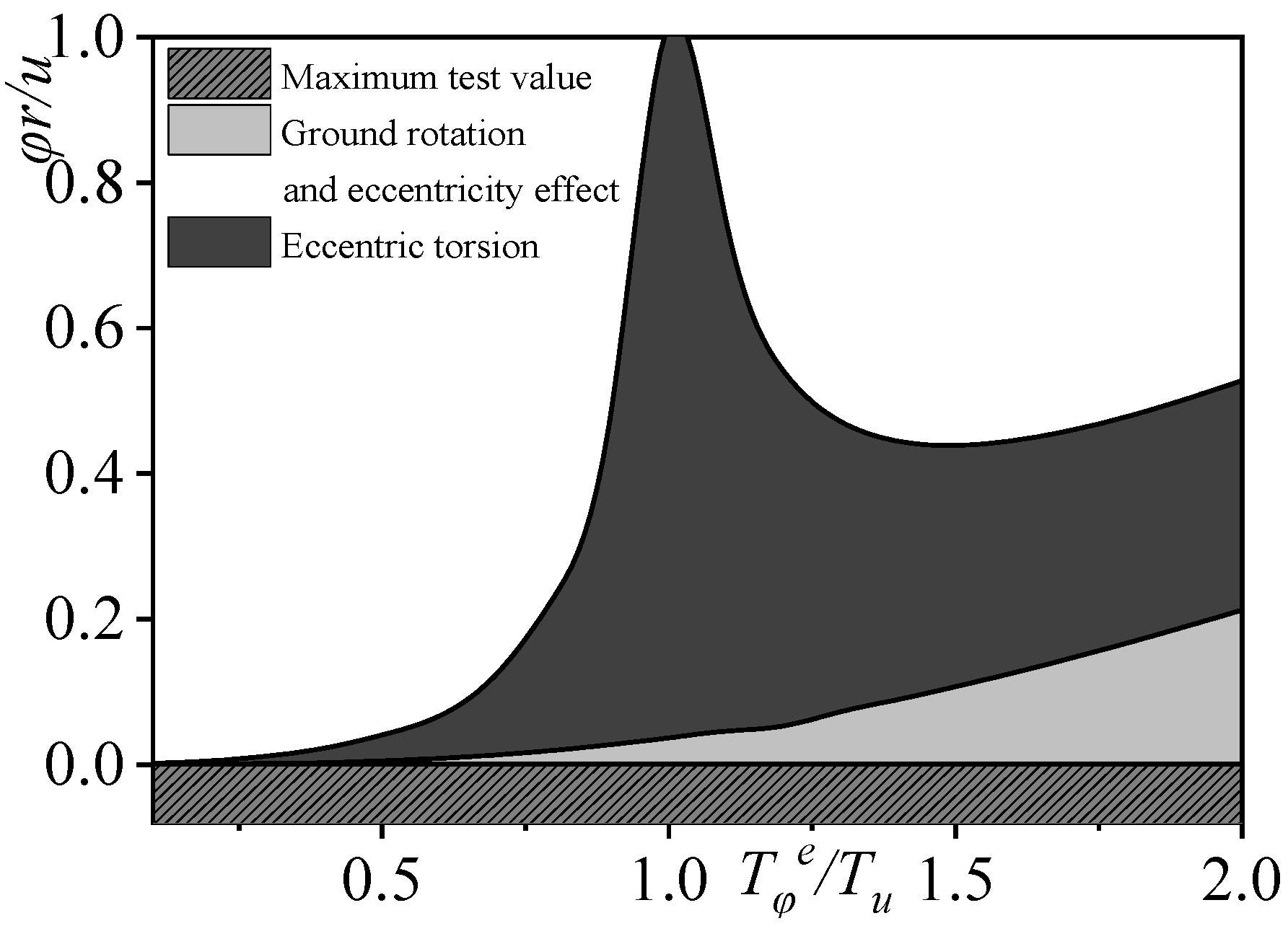
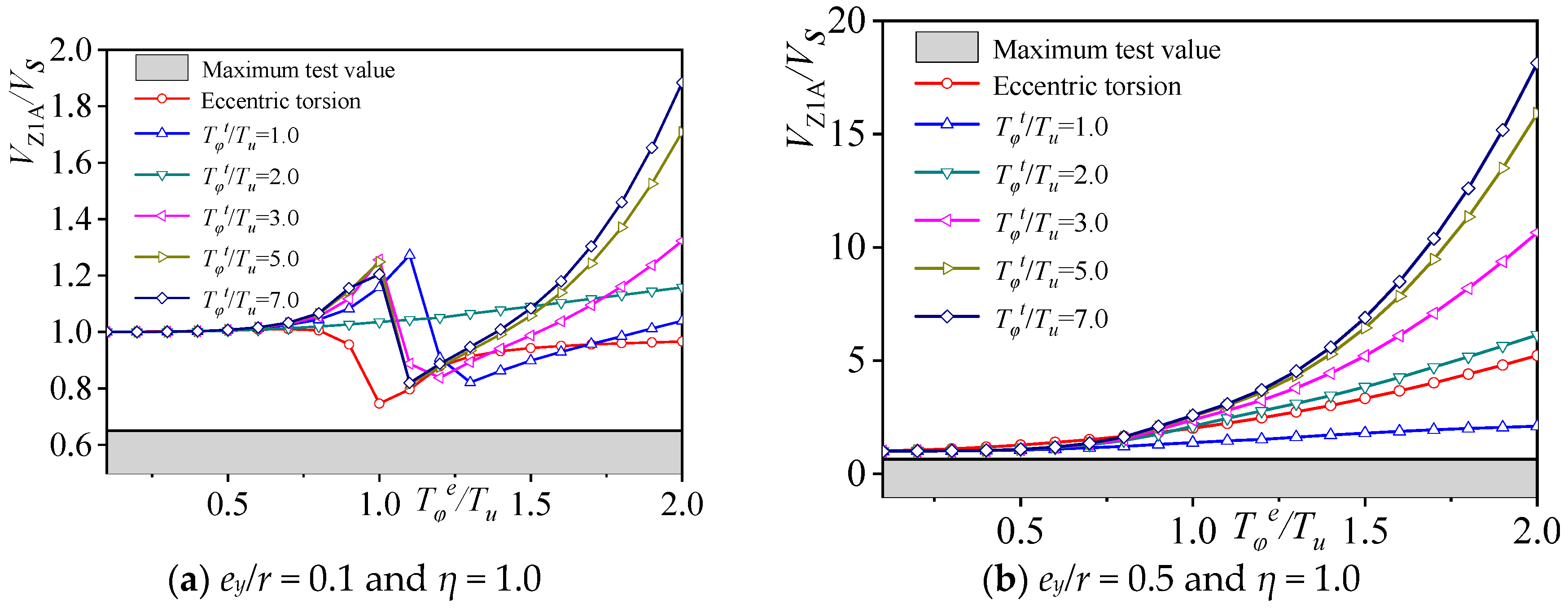
3.2.4. Relative Torsion Effect
3.2.5. Torsional Control Indicator
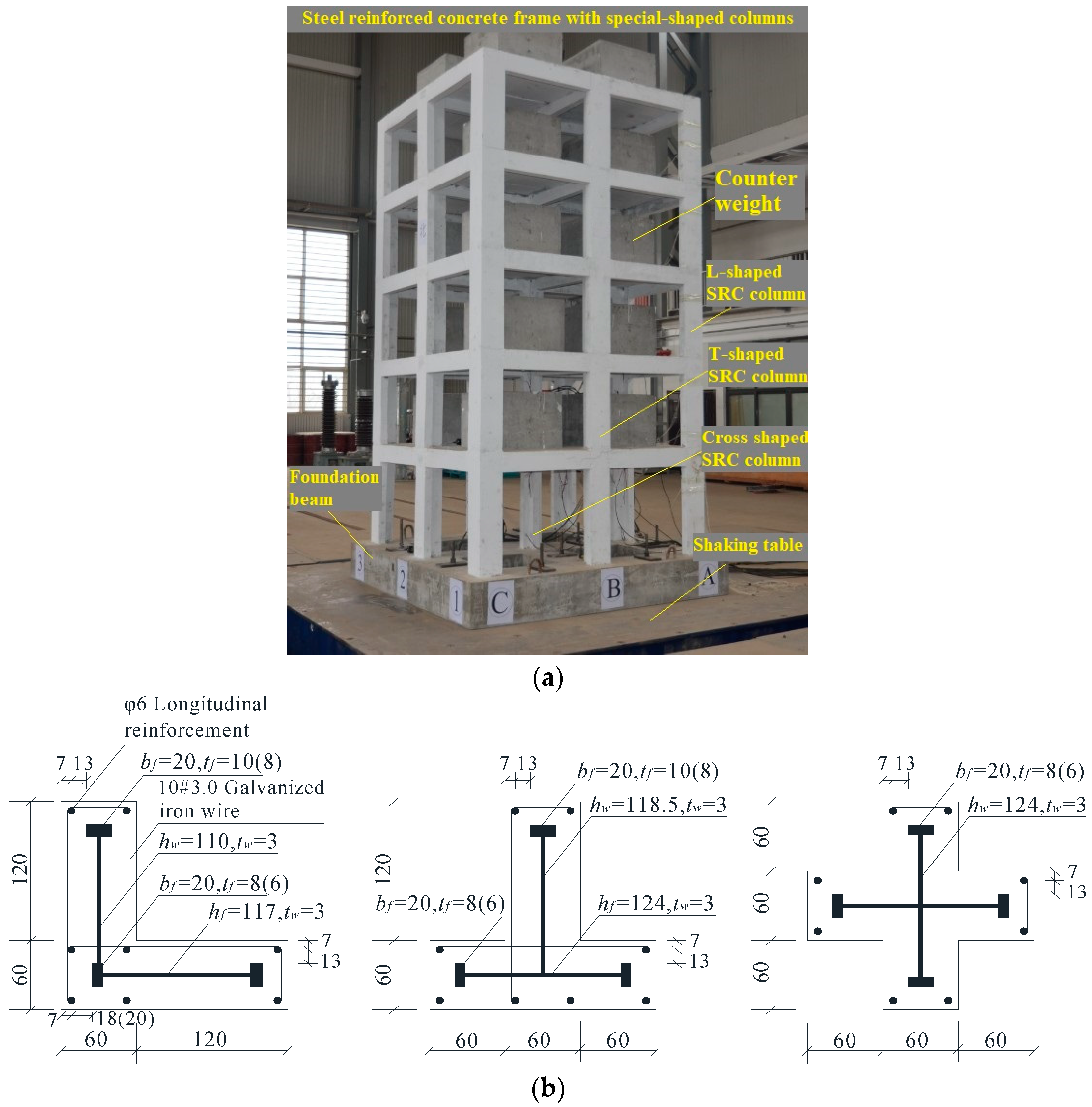
4. Shaking Table Test of the Special-Shaped Column Frame Structure
4.1. Test Survey
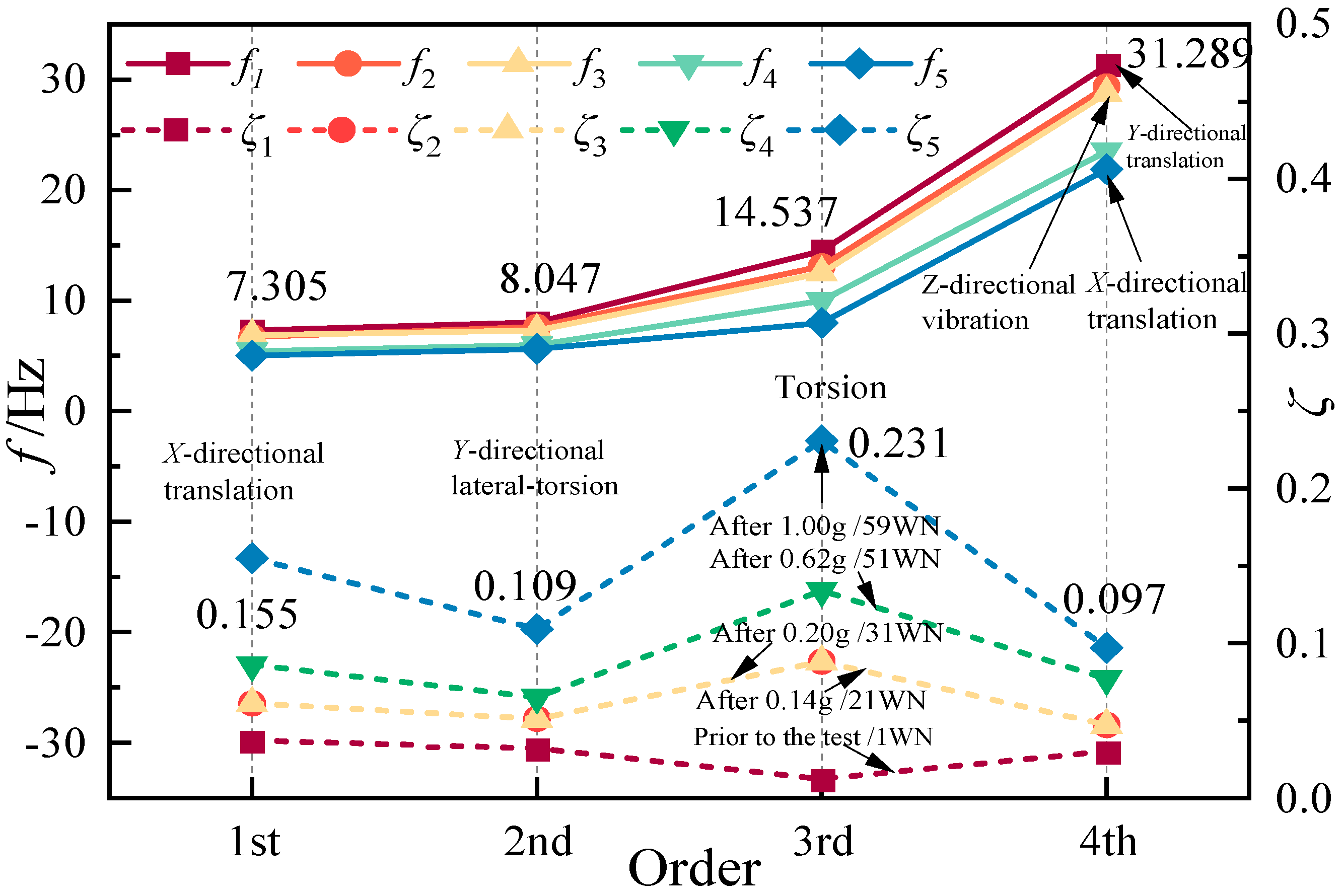
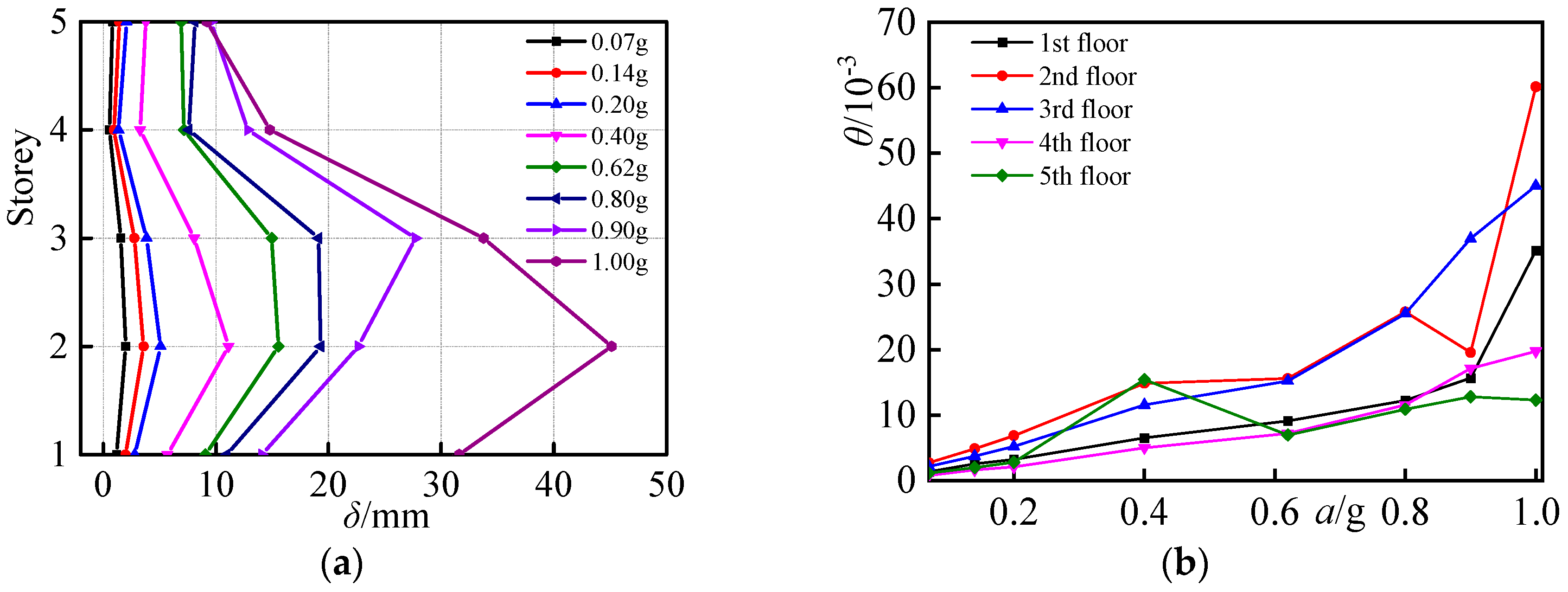
4.2. Lateral Vibration
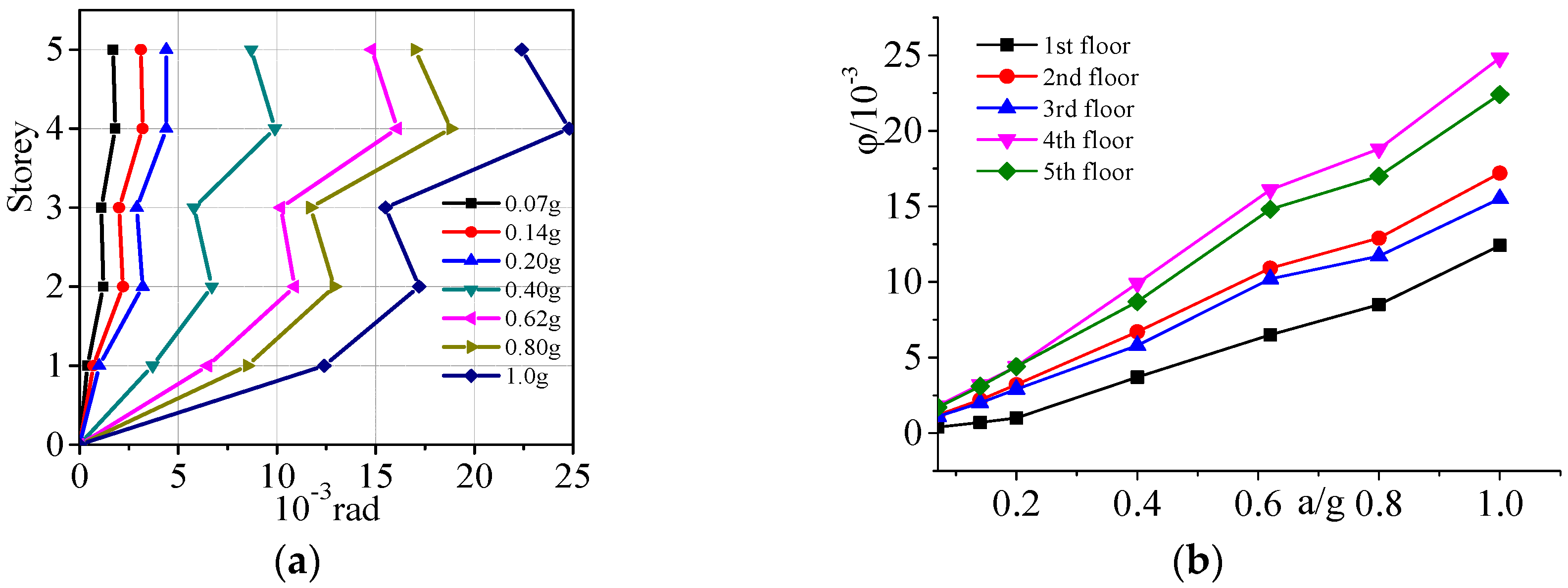
4.3. Torsional Vibration
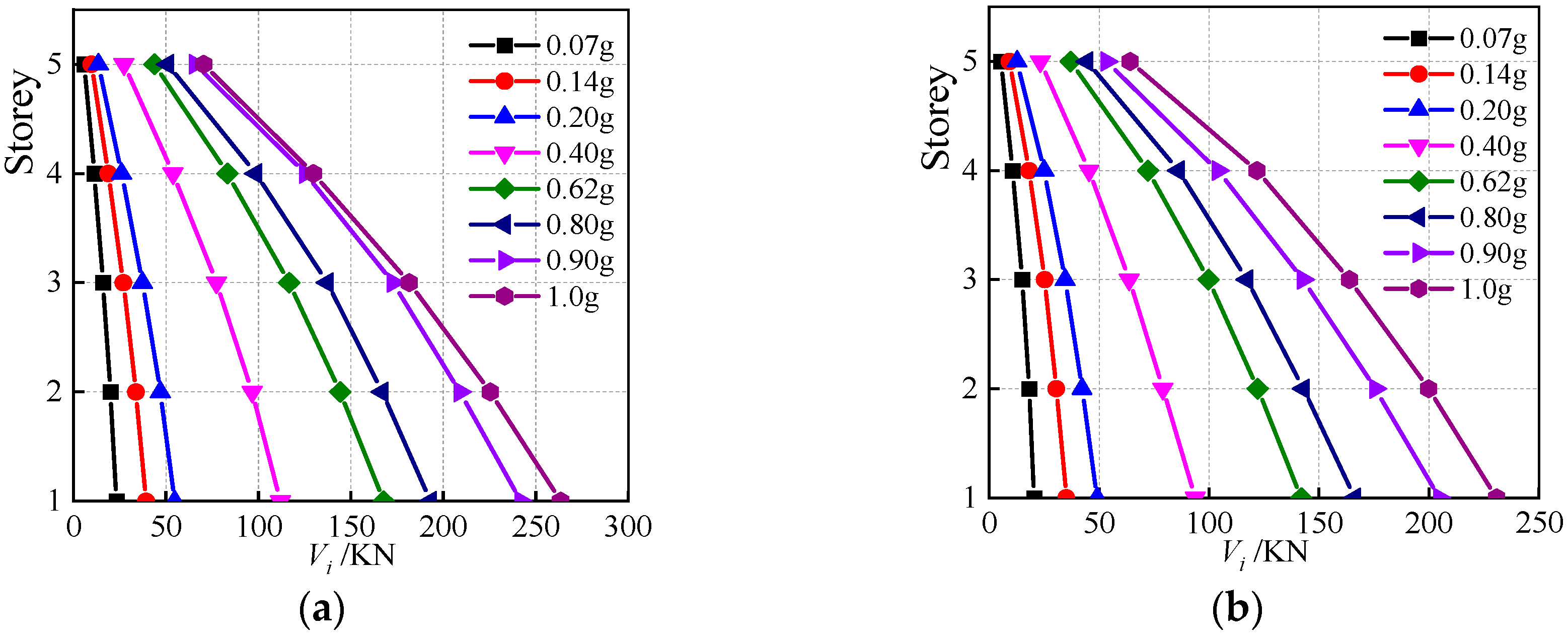
4.4. Seismic Shear
4.5. Column Shear
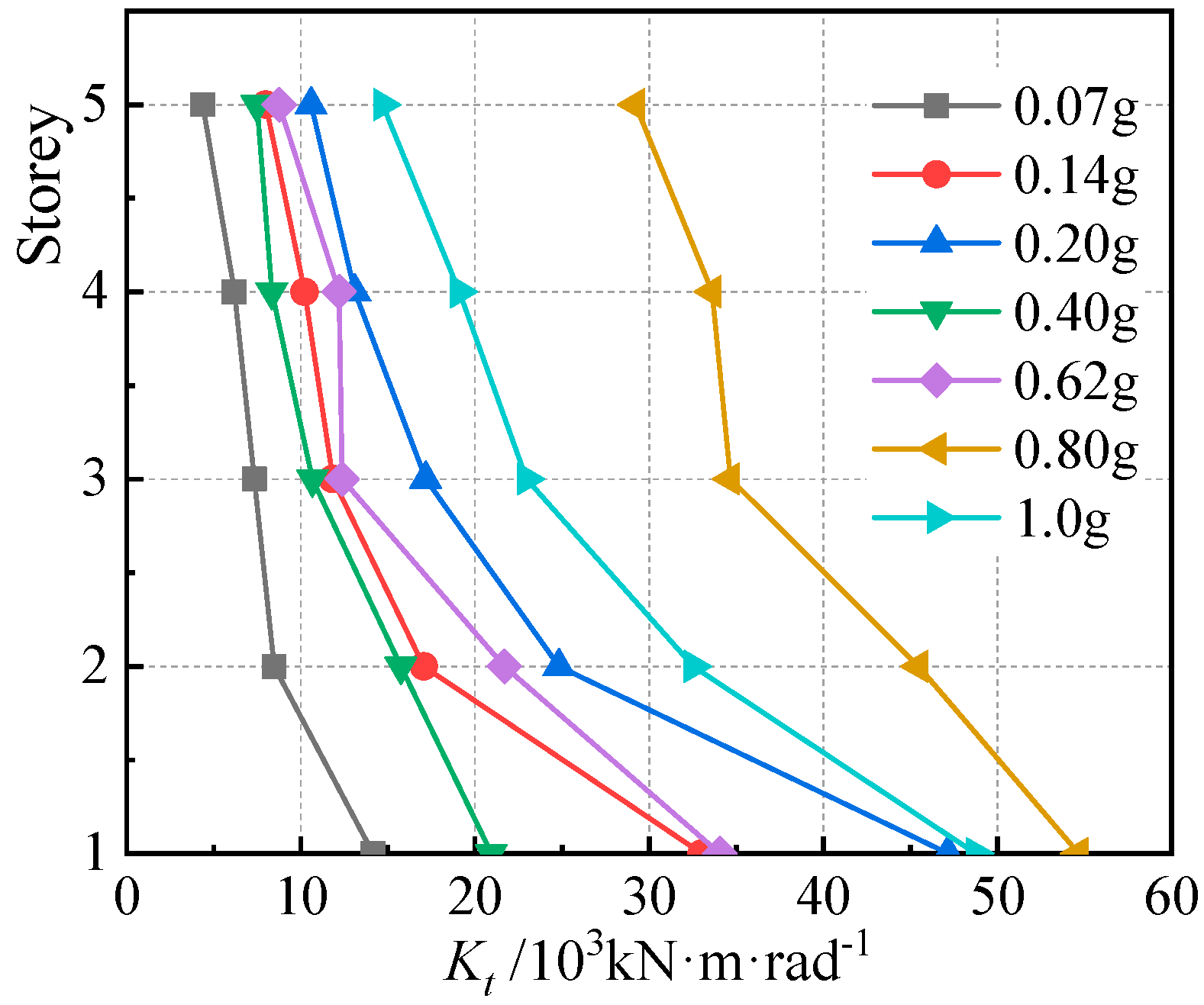
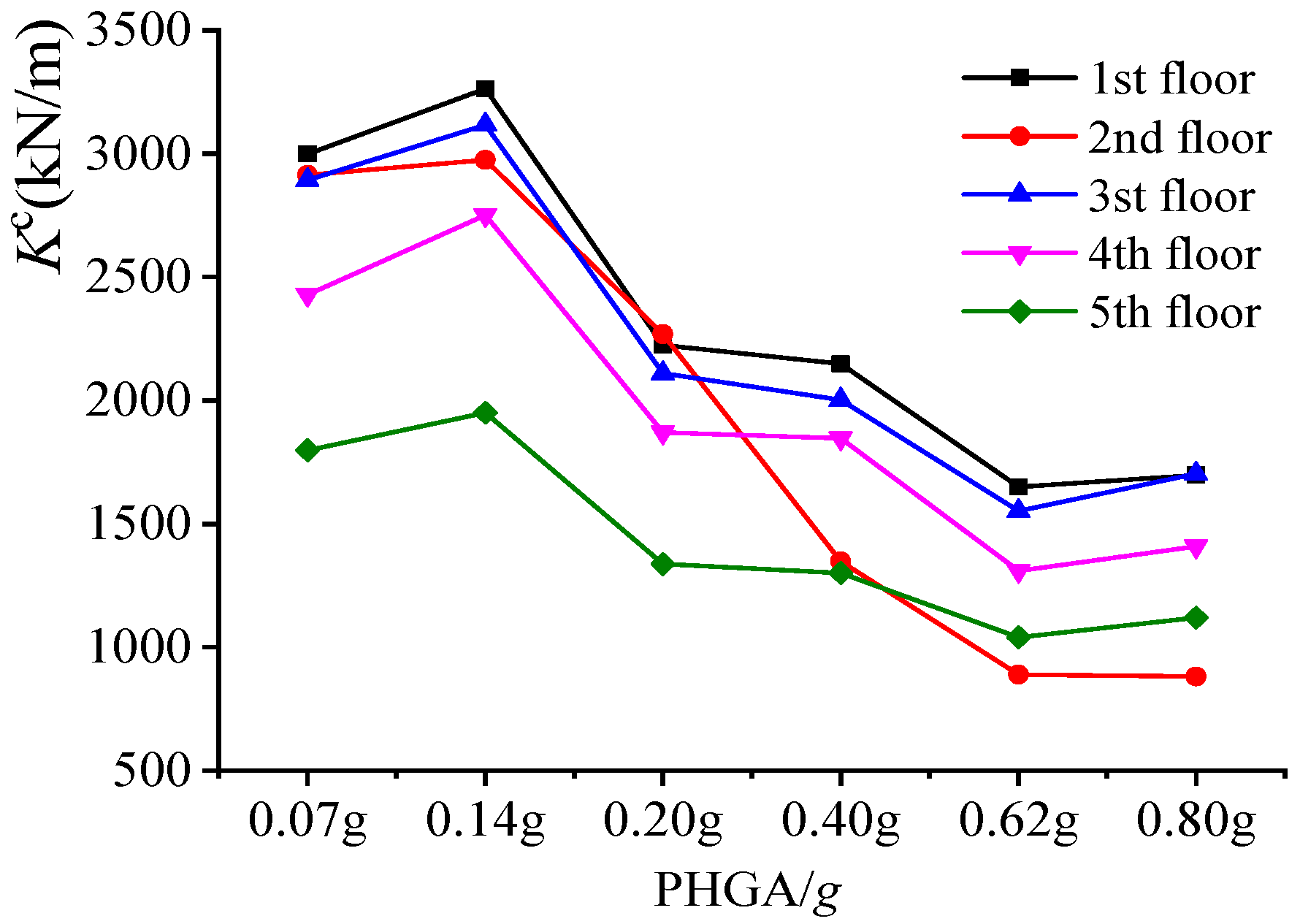
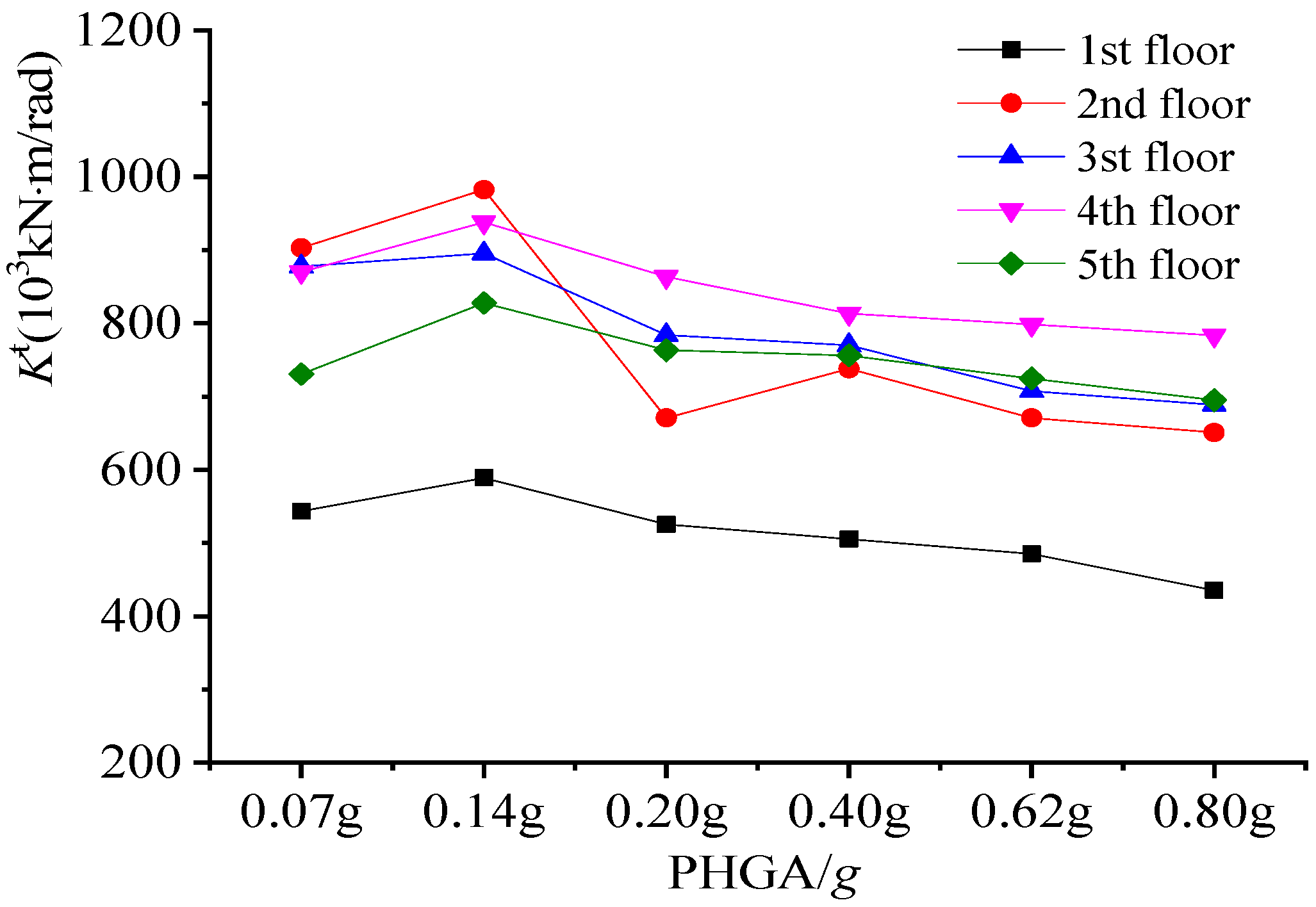
4.6. Column Torsional Stiffness
5. Comparison Between the Experimental Results and Theoretical Calculations
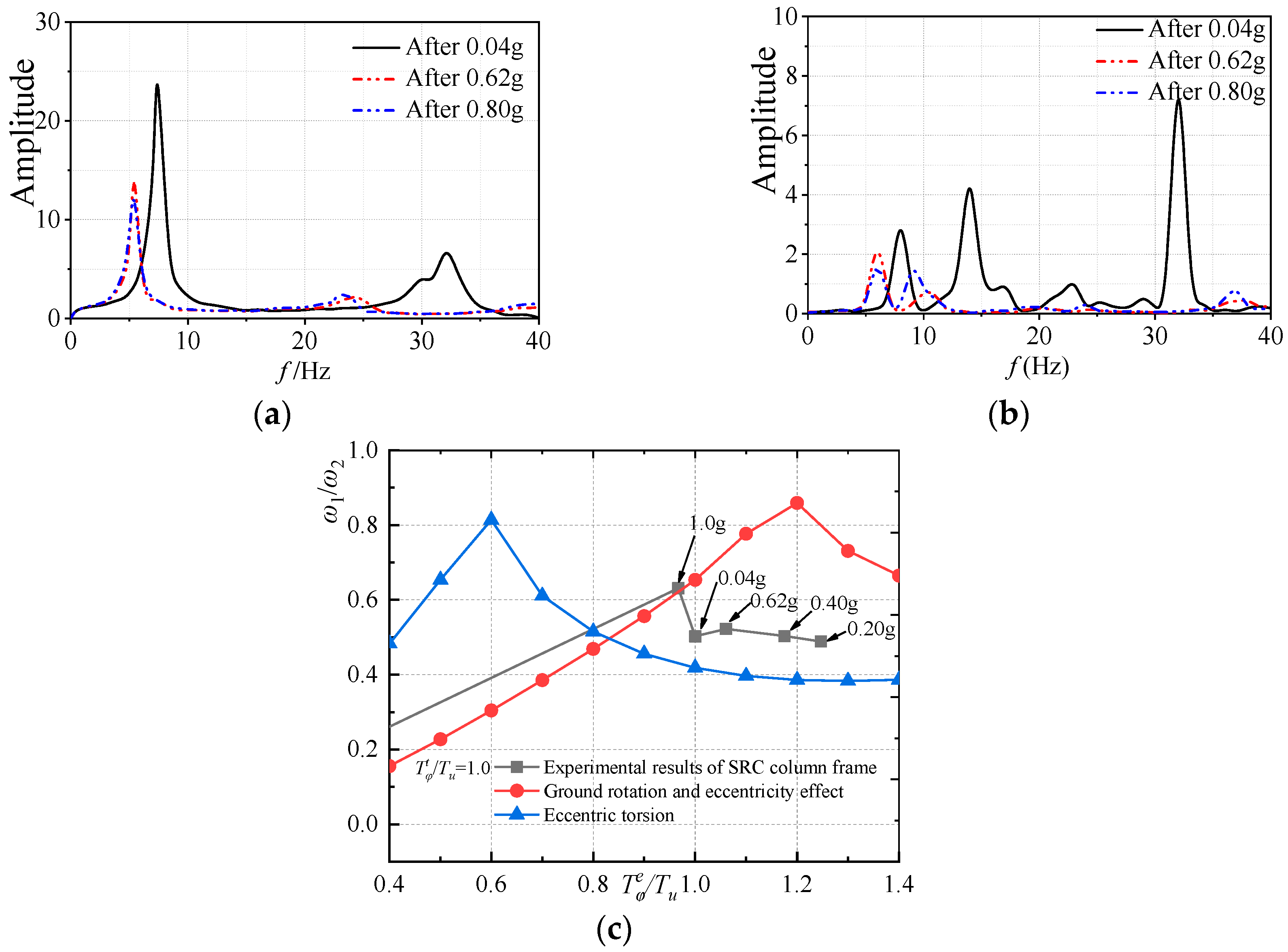
5.1. Comparison of the Natural Frequency Ratio
5.2. Comparison of the Torsional Effect
5.3. Comparison of Base Shear
5.4. Comparison of Special-Shaped Column Shear Force
5.5. Comparison of Torsional Stiffness
6. Conclusions
- (1)
- Considering the influence of ground rotation and eccentric torsion on the model, the lateral displacement of the structure and floor torsion is primarily induced by horizontal seismic components and floor eccentricity. The seismic torsion of the model is attributed to ground rotational components. The floor torsional angle is equivalent to the sum of the inter-story and pure torsional angles caused by eccentric torsion and ground rotation, respectively.
- (2)
- The natural vibration frequency of a structure, considering the influence of ground rotation, is a function of relative eccentricity ey/r, the lateral–torsional period ratio Tφt/Tu caused by ground rotation, and the lateral–torsional period ratio Tφe/Tu considering only eccentric torsion. The following conclusions are drawn from the variation analysis of the natural vibration frequency ratio, torsional amplitude ratio, mode participation factor ratio, and relative torsional index of the structure, considering the influence of ground rotation. When eccentricity ey/r is constant and Tφt/Tu remains unchanged, the peak points of the natural vibration frequency ratio and the lateral–torsional coupling coefficient, considering ground rotation, shift significantly compared to when considering only eccentricity under the same conditions. Once Tφe/Tu surpasses 1.0, the torsional amplitude increases remarkably, and the first vibration mode participation indicates elevated values compared to the scenario where only eccentricity is taken into account. When considering torsional dynamic effects, the accidental relative eccentricity of the SRC special-shaped structure in the Y-axis is less than 0.1.
- (3)
- The shaking table test results facilitate the acquisition of the natural characteristics, translational response, torsional response, and internal force distribution of the SRC special-shaped column frame structure. Under intense earthquake conditions, the inter-story stiffness of the structure degrades rapidly. The maximum displacement angle of the structure is observed to be 1/14, the maximum accidental eccentric torsional angle is measured at 18.8 × 10−7, and the maximum inter-story displacement angle resulting from lateral–torsional coupling is recorded as 1/48. Throughout the experimentation, the torsional response of the SRC special-shaped column remains within the elastic stage. For the special-shaped column structure that meets the height limitation requirement specified in the code, the influence of accidental eccentricity and lateral–torsional coupling on its seismic performance is relatively minimal.
- (4)
- By comparing experimental and theoretical values, the measured structural lateral–torsional natural frequency ratio considering ground rotation is close to the calculated results from the mathematical model. The maximum ratio of torsional displacement at the ground floor to the horizontal displacement in the X direction of the SRC special-shaped column frame structure under three-directional seismic action is 0.0007. The torsional effect, torsional stiffness, and internal force theoretical calculations of the special-shaped column correspond well to the experimental results, indicating that they can be used for analyzing lateral–torsional vibration response patterns of structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shetty, S.; R.M., S.; Bhandary, S.; Shetty, T. Comparative study on seismic performance of specially shaped RC columns with that of rectangular columns in high-rise structures. Int. J. Struct. Integr. 2019, 1, 202–215. [Google Scholar] [CrossRef]
- Patel, D.S. Comparative Seismic Behaviour Study of Special Shaped Column Framed Reinforced Structure. Int. J. Res. Appl. Sci. Eng. Technol. 2020, 8, 714–719. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, J.; Miao, Y.; Zhou, B.; Huang, W.; He, Y.; Lu, Q.; Wang, Y. Performance of T-shaped CFST columns with embedded T-shaped steel skeleton under axial compression. J. Constr. Steel Res. 2024, 215, 108554. [Google Scholar] [CrossRef]
- Salah, A.; Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Behavior of axially loaded L-shaped RC columns strengthened using steel jacketing. J. Build. Eng. 2022, 47, 103870. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Zhou, Z.; Xue, J.; Lai, B.; Xu, J. Experimental and numerical study on seismic performance of steel reinforced concrete spatial frame with irregular section columns. Eng. Struct. 2021, 242, 112507. [Google Scholar] [CrossRef]
- Guo, X.; Yin, P. Study on Seismic Performance of Concrete Special-shaped Columns. Int. Core J. Eng. 2023, 9, 1–6. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, Z.; Liu, X.; Liao, H. Seismic behavior of RC cross-shaped column under combined torsion loading: Experiment and simulation finite element. Structures 2023, 47, 1652–1667. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Niu, Z.Y.; Zhang, A.L.; Liu, X.C. Design method of axial compression stability for cross-section corrugated plate steel special-shaped column. Thin-Walled Struct. 2024, 194, 111243. [Google Scholar] [CrossRef]
- Tao, S.Q.; Liu, Y.; Wang, J.F.; Yu, Q.J.; Zhao, J.H. Experimental investigation and design method of axial compression behavior of T-shaped partially encased steel-concrete composite stub columns. J. Build. Eng. 2024, 85, 108668. [Google Scholar] [CrossRef]
- Zhang, X.; Far, H. Effects of dynamic soil-structure interaction on seismic behaviour of high-rise buildings. Bull. Earthq. Eng. 2021, 20, 3443–3467. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Wang, X.; Chen, Y.F. Test and design of eccentrically-loaded slender circular tubed columns filled with high-strength concrete and reinforcement. Structures 2023, 51, 1461–1473. [Google Scholar] [CrossRef]
- Sunagar, P.; Gowda, R.; Nayak, S.; Sumalatha, J. Seismic vulnerability and resilience of steel-reinforced concrete (SRC) and composite Structures. Des. Eng. 2021, 1, 11455–11469. [Google Scholar]
- Wang, L.; Zhou, Y.; Nagarajaiah, S.; Shi, W. Bi-directional semi-active tuned mass damper for torsional asymmetric structural seismic response control. Eng. Struct. 2023, 294, 116744. [Google Scholar] [CrossRef]
- Ismail, M. New approach to seismic-resistant design and structural torsion mitigation. Eng. Struct. 2020, 207, 110092. [Google Scholar] [CrossRef]
- Kuang, Y.; Liu, Y. Parametric analysis of the whole loading process of translation-torsion coupled vibration characteristics of the multi-layer bi-directional eccentric frame structure. J. Theor. Appl. Mech. 2022, 60, 479–494. [Google Scholar] [CrossRef]
- Hao, H. Torsional response of building structures to spatial random ground excitations. Eng. Struct. 1997, 19, 105–112. [Google Scholar] [CrossRef]
- Lai, X.; He, Z. A generalized hybrid model considering earthquake-induced internal force distribution rules for super high-rise frame-core tube structures. Eng. Struct. 2022, 268, 114745. [Google Scholar] [CrossRef]
- Wen, J.; Xiong, H.; Bu, G.; Xu, C.; Chen, K.; Wen, J. Seismic fragility of vertically irregular gravity column-core tube structure subjected to pulse-like ground motions. Structures 2024, 62, 106217. [Google Scholar] [CrossRef]
- Mao, H.; Yan, X.; Wei, X.; Liu, X. Seismic analysis of a frame structure equipped with displacement-amplified torsional dampers. Structures 2022, 41, 190–202. [Google Scholar] [CrossRef]
- Alam, Z.; Sun, L.; Zhang, C.; Noroozinejad Farsangi, E. Global performance of multi-story stiffness-eccentric RC structures subjected to progressive seismic excitations: Shaking table investigations. J. Build. Eng. 2023, 64, 105582. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Architecture & Building Press: Beijing, China, 2016.
- JGJ149-2017; Technical Specification for Concrete Structures with Specially Shaped Columns. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Architecture & Building Press: Beijing, China, 2017.
- Maheri, M.R.; Chandler, A.M.; Bassett, R.H. Coupled lateral-torsional behaviour of frame structures under earthquake loading. Earthq. Eng. Struct. Dyn. 1991, 20, 61–85. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Xue, J. Coupled Vibration Mathematical Model of Special-Shaped Column Structure Considering Ground Rotation Effects. Buildings 2025, 15, 1300. https://doi.org/10.3390/buildings15081300
Hu Z, Xue J. Coupled Vibration Mathematical Model of Special-Shaped Column Structure Considering Ground Rotation Effects. Buildings. 2025; 15(8):1300. https://doi.org/10.3390/buildings15081300
Chicago/Turabian StyleHu, Zongbo, and Jianyang Xue. 2025. "Coupled Vibration Mathematical Model of Special-Shaped Column Structure Considering Ground Rotation Effects" Buildings 15, no. 8: 1300. https://doi.org/10.3390/buildings15081300
APA StyleHu, Z., & Xue, J. (2025). Coupled Vibration Mathematical Model of Special-Shaped Column Structure Considering Ground Rotation Effects. Buildings, 15(8), 1300. https://doi.org/10.3390/buildings15081300





