A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings
Abstract
1. Introduction
- To identify and quantify the key house features across traditional and modern models that significantly impact energy efficiency;
- To rigorously evaluate the predictive performance and scalability of traditional and modern models in the context of large datasets;
- To assess the robustness of models and address any biases that can affect the analysis.
2. Related Work
3. Methodology
3.1. Description of Dataset
3.2. Feature Transformation
3.2.1. Handling Missing Data
3.2.2. Handling Duplicates
3.2.3. Normalisation
3.2.4. Standardisation
3.2.5. Encoding Categorical Variables
3.3. Features Classification
3.3.1. Building Components
3.3.2. Energy
3.3.3. Environmental Factors
3.3.4. Cost
3.4. Features Selection Process
3.5. Feature Analysis Techniques
3.6. Principal Component Analysis (PCA) Algorithm
Mathematical Model
3.7. Correlation Analysis
Mathematical Model
- and are the sample points for the individual;
- and are the means;
- n is the number of observations.
3.8. Mutual Information Algorithm
Mathematical Model
- is the joint probability distribution function of X and Y;
- and are the marginal probability distribution functions of X and Y, respectively.
3.9. Recursive Feature Elimination (RFE)
Mathematical Model
3.10. Least Absolute Shrinkage and Selection Operator (LASSO)
Mathematical Model
- is the dependent variable;
- are the independent variables;
- is the intercept;
- are the coefficients of the model;
- n is the number of observations;
- p is the number of features;
- is the regularisation parameter.
3.11. Random Forest Algorithm
Mathematical Model
3.12. Gradient Boosting
Mathematical Model
- is the forecast from the -th iteration;
- is the m-th Decision Tree;
- is the learning rate, which helps in applying the regularisation parameter, scaling the contribution of each tree.
3.13. Model Selection
3.14. Linear Regression
Mathematical Model
- Y is the dependent variate;
- are the independent variables;
- is the constant. are the coefficients of the error term, .
3.15. k-Nearest Neighbors (KNNs) Algorithm
Mathematical Model
3.16. Decision Tree
Mathematical Model
3.17. Support Vector Regression (SVR)
Mathematical Model
3.18. Random Forest Algorithm with Extra Trees
3.19. XGBoost and LightGBM
3.20. Hyperparameters Tuning
3.21. Model Evaluation
3.21.1. Mean Squared Error (MSE)
3.21.2. Mean Absolute Error (MAE)
3.21.3. Root Mean Squared Error (RMSE)
3.21.4. R-Squared (R2)
3.21.5. Mean Absolute Percentage Error (MAPE)
3.21.6. Adjusted R-Squared (Adjusted R2)
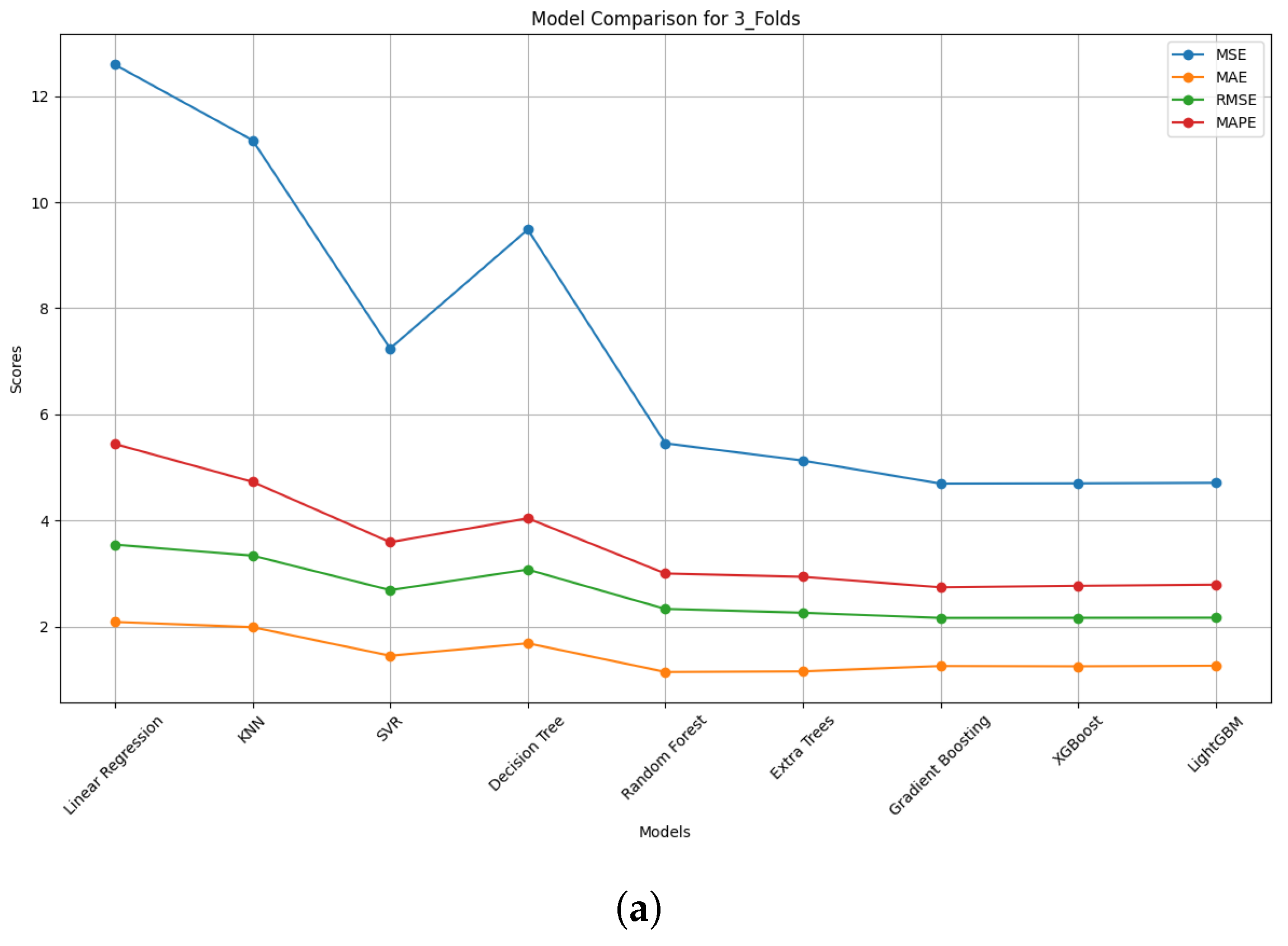
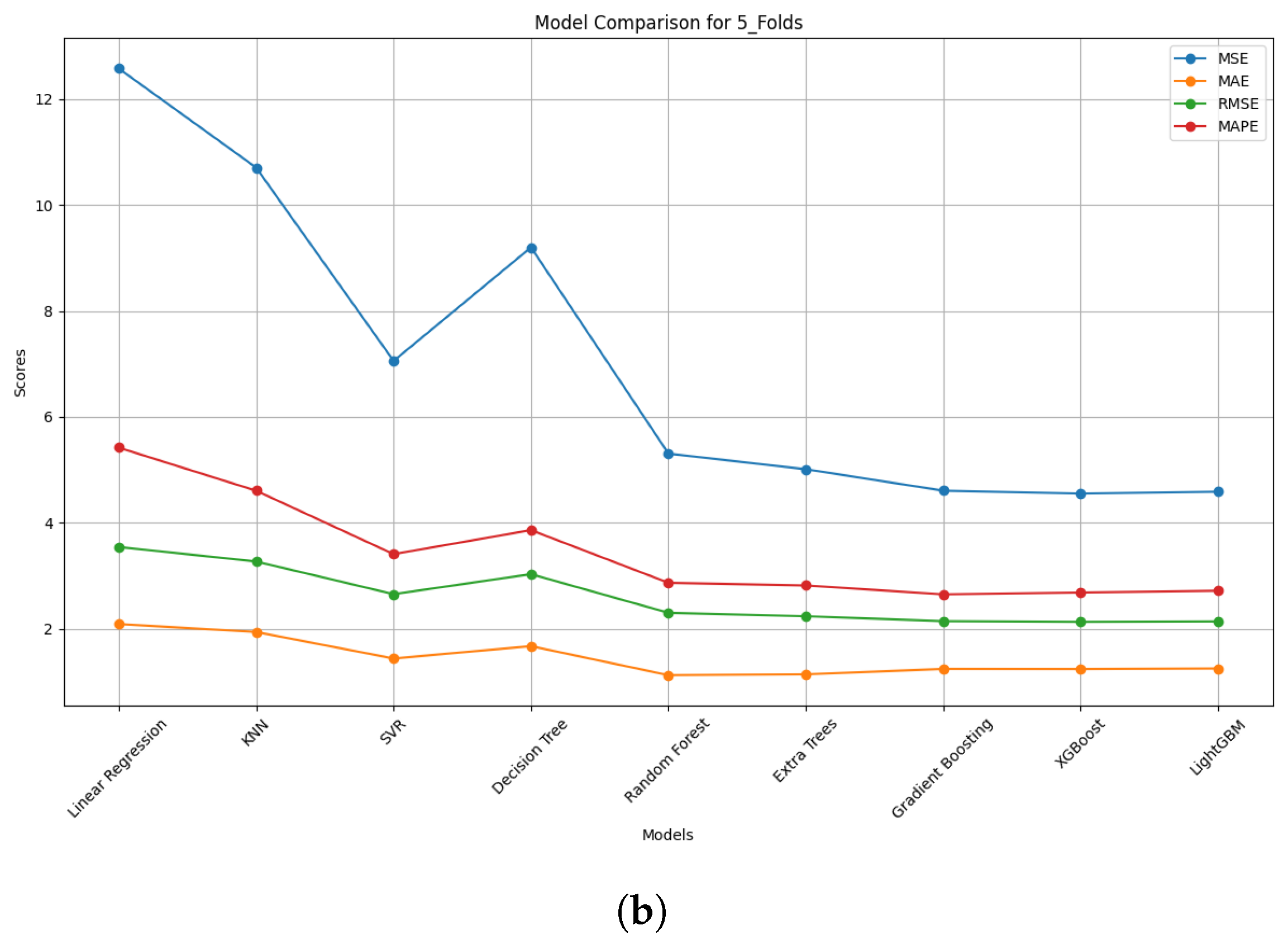
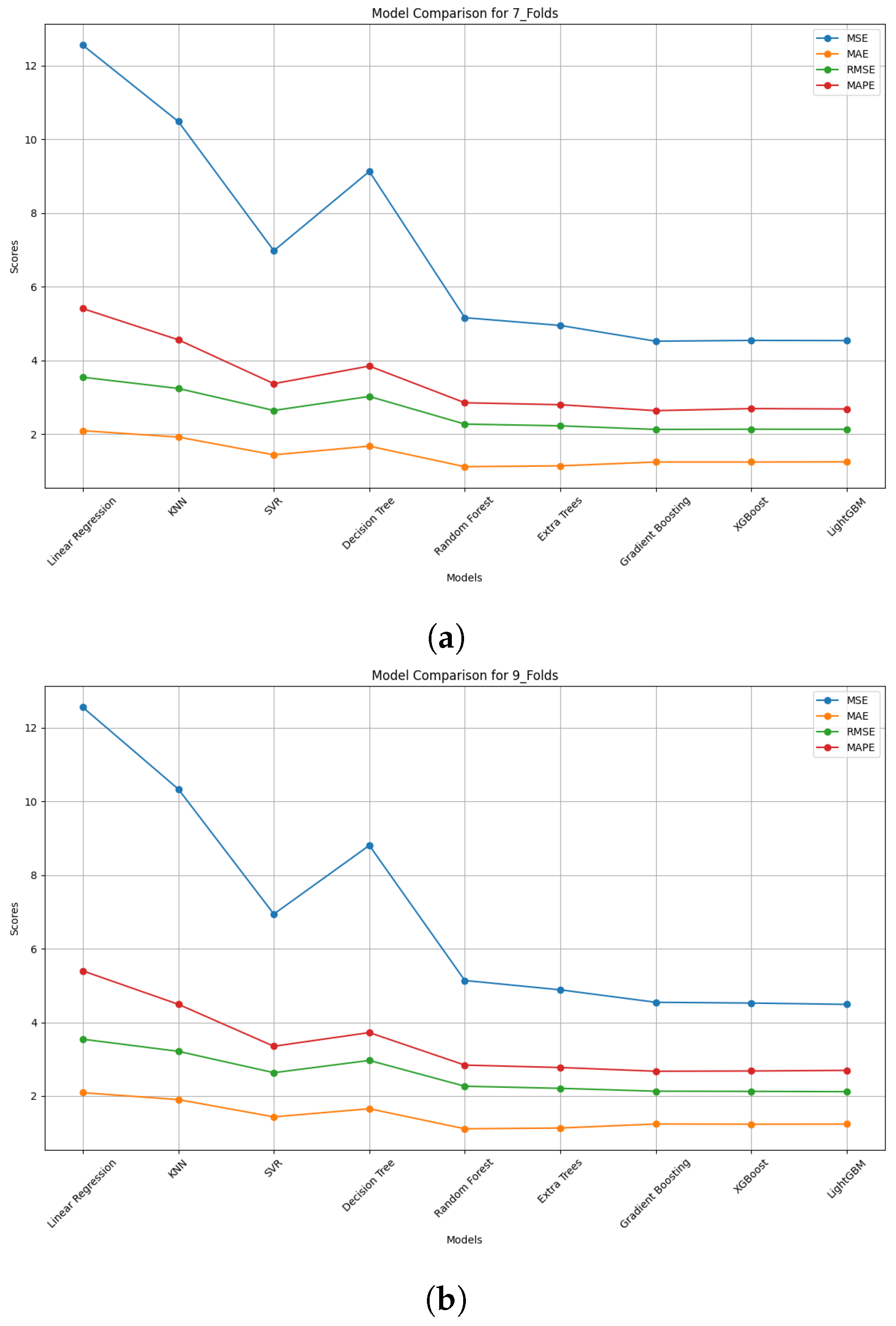
3.22. Cross-Validation
4. Results
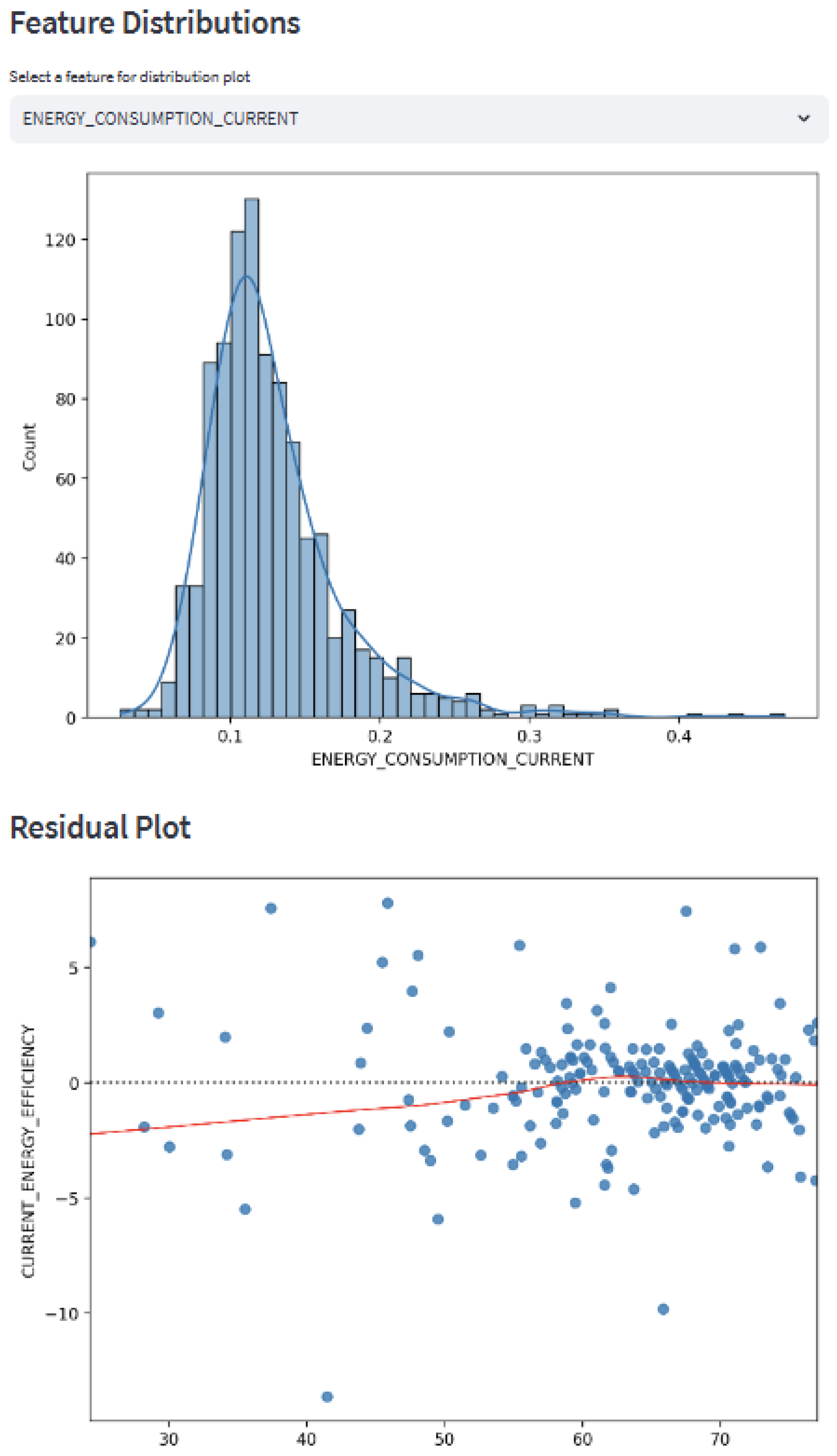
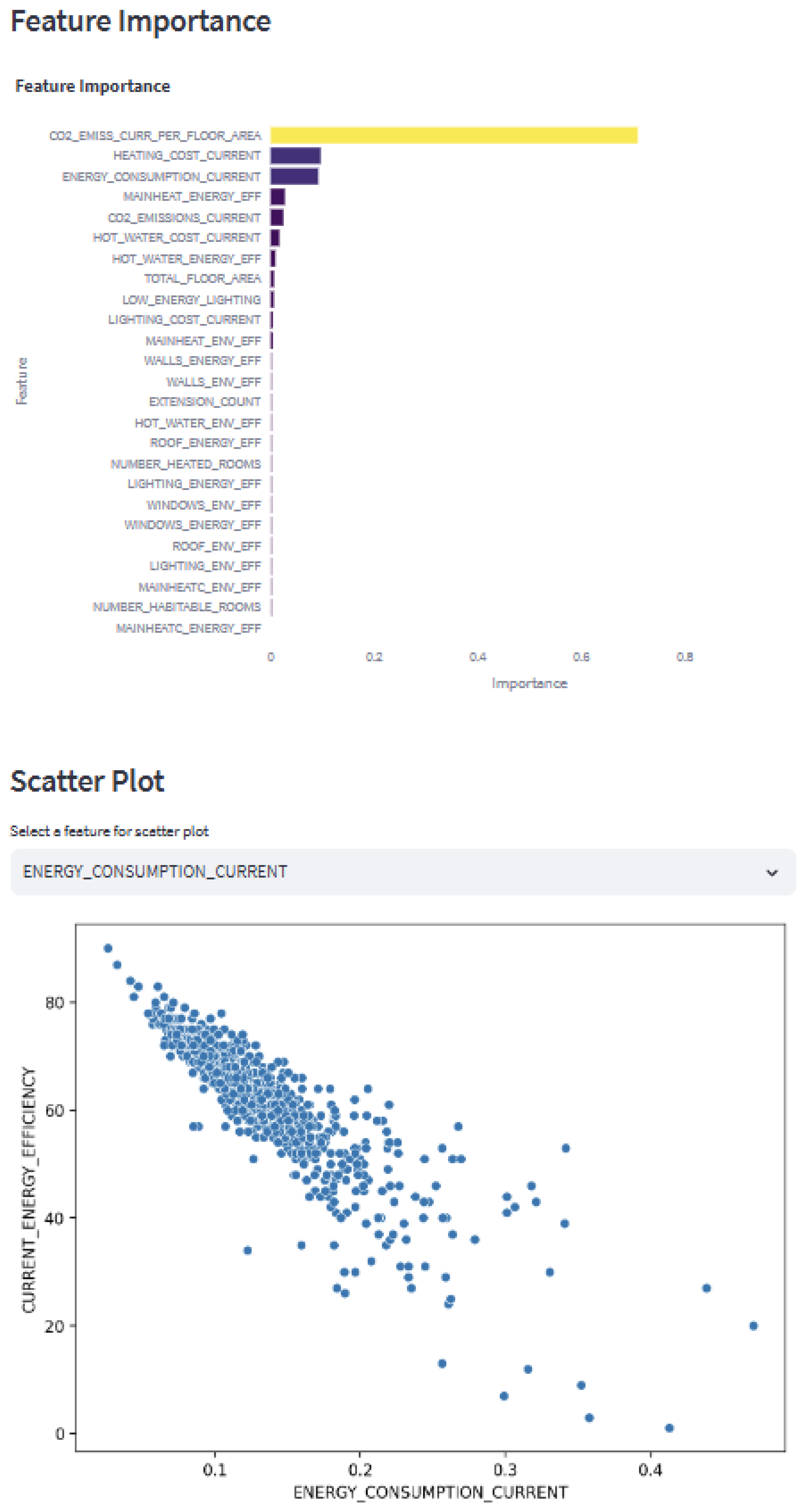
4.1. Key Features
Analysis of Key Feature Contributions
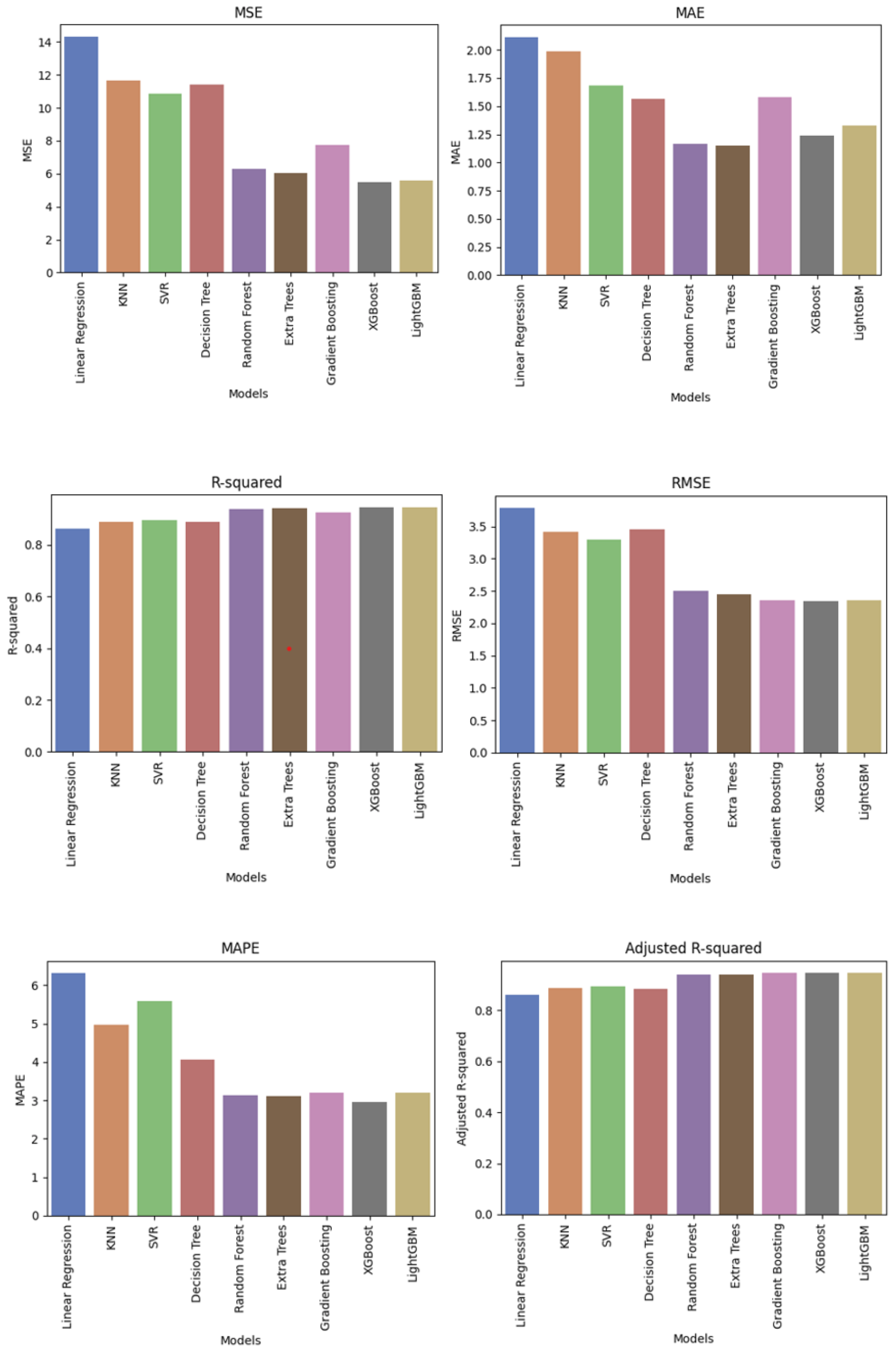
4.2. Model Performance
4.2.1. Performance Metrics
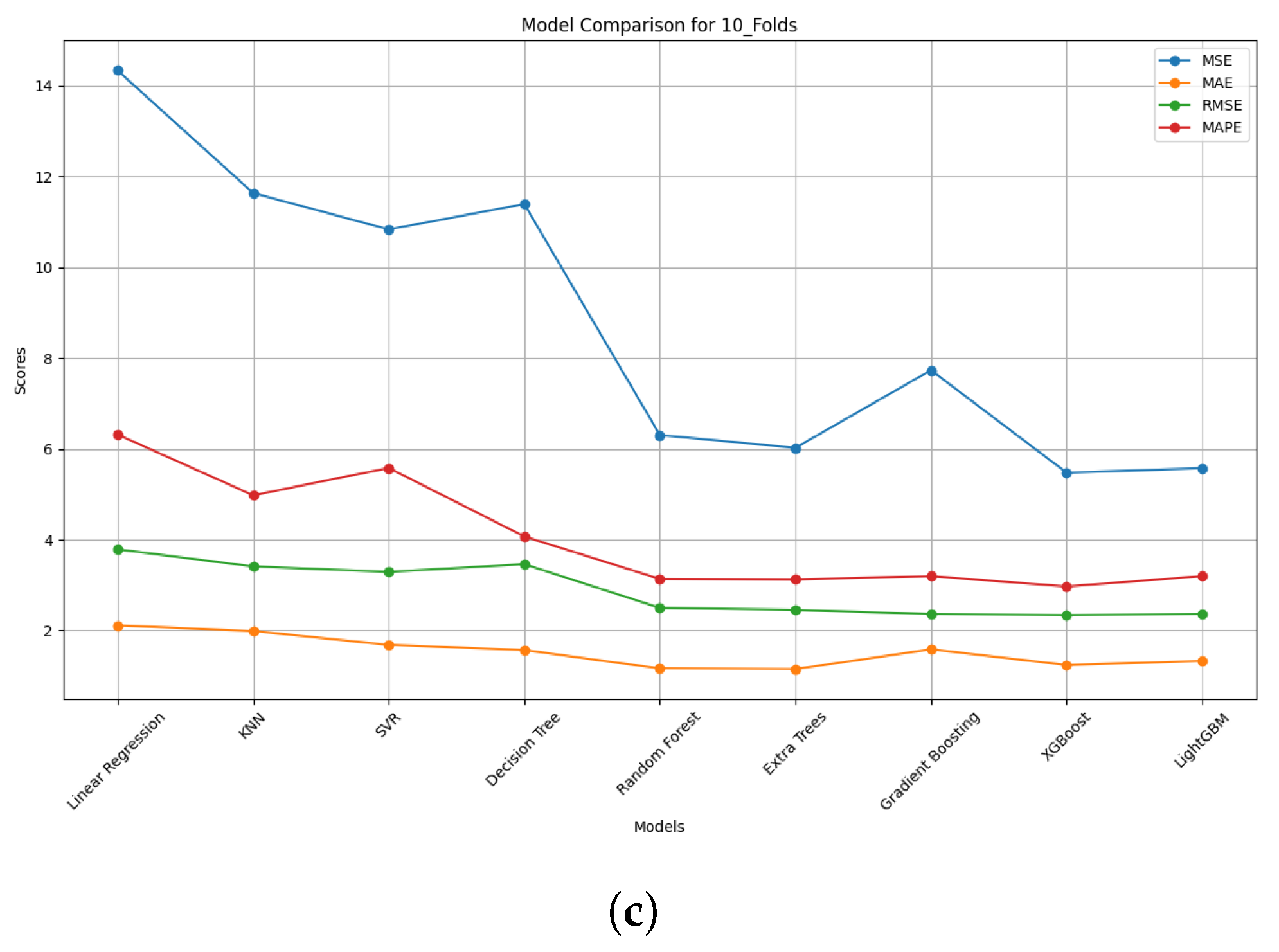
4.2.2. Comparison of Model Performance
4.2.3. Model Performance Discussion
5. Implications of Study
5.1. Theoretical
5.2. Policy
6. Conclusions
6.1. Limitations
6.2. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PCA | Principal component analysis |
| KNNs | k-Nearest Neighbours |
| SVR | Support Vector Regression |
| RF | Random Forest |
| GB | Gradient Boosting |
| XGBoost | Extreme Gradient Boosting |
| LightGBM | Light Gradient Boosting Machine |
| MI | Mutual information |
| RFE | Recursive Feature Elimination |
| HWEE | Hot Water Energy Efficiency |
| HWEVE | Hot Water Environment Efficiency |
| HVAC | Heating, Ventilation, Air Conditioning |
| WIEE | Windows Energy Efficiency |
| WENE | Windows Environment Efficiency |
| WEE | Walls Energy Efficiency |
| WENE | Walls Environment Efficiency |
| REE | Roof Energy Efficiency |
| RENE | Roof Environment Efficiency |
| MHEE | Main Heat Energy Efficiency |
| MHENE | Main Heat Environment Efficiency |
| MHCEE | Main Heat Control Energy Efficiency |
| MHCENE | Main Heat Control Environment Efficiency |
| LEE | Lighting Energy Efficiency |
| LENE | Lighting Environment Efficiency |
| CEE | Current Energy Efficiency |
| EIC | Environment Impact Current |
| ECC | Energy Consumption Current |
| CEC | CO2 Emissions Current |
| CEPFA | CO2 Emissions Current per Floor Area |
| LCC | Lighting Cost Current |
| HCC | Heating Cost Current |
| HWCC | Hot Water Cost Current |
| TFA | Total Floor Area |
| EO | Extension Count |
| NAR | Number of Habitable Rooms |
| NHR | Number of Heated Rooms |
| LEL | Low-Energy Lighting |
| SAP | Standard Assessment Procedure |
| RdSAP | reduced Standard Assessment Procedure |
References
- BRE. The Government’s Standard Assessment Procedure for Energy Rating of Dwellings; Building Research Establishment: Watford, UK, 2012. [Google Scholar]
- Khazal, A.; Sønstebø, O.J. Valuation of energy performance certificates in the rental market—Professionals vs. nonprofessionals. Energy Policy 2020, 147, 111830. [Google Scholar] [CrossRef]
- Anđelković, A.S.; Kljajić, M.; Macura, D.; Munćan, V.; Mujan, I.; Tomić, M.; Vlaović, Ž.; Stepanov, B. Building energy performance certificate—A relevant indicator of actual energy consumption and savings? Energies 2021, 14, 3455. [Google Scholar] [CrossRef]
- Yuan, M.; Choudhary, R. Energy Performance Certificate renewal—An analysis of reliability of simple non-domestic buildings’ EPC ratings and pragmatic improving strategies in the UK. Energy Policy 2023, 178, 113581. [Google Scholar] [CrossRef]
- Brockway, P.E.; Sorrell, S.; Semieniuk, G.; Heun, M.K.; Court, V. Energy efficiency and economy-wide rebound effects: A review of the evidence and its implications. Renew. Sustain. Energy Rev. 2021, 141, 110781. [Google Scholar] [CrossRef]
- Webborn, E.; Few, J.; McKenna, E.; Elam, S.; Pullinger, M.; Anderson, B.; Shipworth, D.; Oreszczyn, T. The SERL Observatory Dataset: Longitudinal smart meter electricity and gas data, survey, EPC and climate data for over 13,000 households in Great Britain. Energies 2021, 14, 6934. [Google Scholar] [CrossRef]
- Sekisov, A.; Ovchinnikova, S.; Schneider, E. Challenges and prospects for energy efficiency development in residential buildings. E3S Web Conf. 2023, 389, 6009. [Google Scholar] [CrossRef]
- Sheina, S.; Girya, L.; Shvets, A.; Larin, N. Methods for increasing energy efficiency during the construction of high-rise residential buildings. Mod. Trends Constr. Urban Plan. Territ. Plan. 2022, 1, 17–23. [Google Scholar]
- Ugli, K.K.B. Improving the energy efficiency of low-rise residential buildings. Int. J. Adv. Sci. Res. 2022, 2, 24–31. [Google Scholar] [CrossRef]
- Akgüç, A.; Yılmaz, A.Z. Determining HVAC system retrofit measures to improve cost-optimum energy efficiency level of high-rise residential buildings. J. Build. Eng. 2022, 54, 104631. [Google Scholar] [CrossRef]
- Riabchuk, V.; Hagel, L.; Germaine, F.; Zharova, A. Utility-based context-aware multi-agent recommendation system for energy efficiency in residential buildings. arXiv 2022, arXiv:2205.02704. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elzarka, H. Advanced machine learning techniques for building performance simulation: A comparative analysis. J. Build. Perform. Simul. 2019, 12, 193–207. [Google Scholar] [CrossRef]
- Zuhaib, S.; Schmatzberger, S.; Volt, J.; Toth, Z.; Kranzl, L.; Maia, I.E.N.; Verheyen, J.; Borragán, G.; Monteiro, C.S.; Mateus, N.; et al. Next-generation energy performance certificates: End-user needs and expectations. Energy Policy 2022, 161, 112723. [Google Scholar] [CrossRef]
- Egwim, C.N.; Alaka, H.; Egunjobi, O.O.; Gomes, A.; Mporas, I. Comparison of machine learning algorithms for evaluating building energy efficiency using big data analytics. J. Eng. Des. Technol. 2024, 22, 1325–1350. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, G.; Xia, X.; Setunge, S.; Shi, L. A review of internal and external influencing factors on energy efficiency design of buildings. Energy Build. 2020, 216, 109944. [Google Scholar] [CrossRef]
- Mo, Y.; Zhao, D. Effective factors for residential building energy modeling using feature engineering. J. Build. Eng. 2021, 44, 102891. [Google Scholar] [CrossRef]
- Buyo, N.; Sheikh-Akbari, A.; Saleem, F. An Ensemble Approach to Predict a Sustainable Energy Plan for London Households. Sustainability 2025, 17, 500. [Google Scholar] [CrossRef]
- Wilfling, S. Augmenting data-driven models for energy systems through feature engineering: A Python framework for feature engineering. arXiv 2023, arXiv:2301.01720. [Google Scholar]
- Ali, P.J.M.; Faraj, R.H.; Koya, E.; Ali, P.J.M.; Faraj, R.H. Data normalization and standardization: A technical report. Mach. Learn. Tech. Rep. 2014, 1, 1–6. [Google Scholar]
- Mohamed, S.; Smith, R.; Rodrigues, L.; Omer, S.; Calautit, J. The correlation of energy performance and building age in UK schools. J. Build. Eng. 2021, 43, 103141. [Google Scholar] [CrossRef]
- Choi, J.H. Investigation of the correlation of building energy use intensity estimated by six building performance simulation tools. Energy Build. 2017, 147, 14–26. [Google Scholar] [CrossRef]
- Hafez, F.S.; Sa’di, B.; Safa-Gamal, M.; Taufiq-Yap, Y.; Alrifaey, M.; Seyedmahmoudian, M.; Stojcevski, A.; Horan, B.; Mekhilef, S. Energy efficiency in sustainable buildings: A systematic review with taxonomy, challenges, motivations, methodological aspects, recommendations, and pathways for future research. Energy Strategy Rev. 2023, 45, 101013. [Google Scholar]
- Zhou, Y. Climate change adaptation with energy resilience in energy districts—A state-of-the-art review. Energy Build. 2023, 279, 112649. [Google Scholar] [CrossRef]
- Dimitroulopoulou, S.; Dudzińska, M.R.; Gunnarsen, L.; Hägerhed, L.; Maula, H.; Visualisation, R.S.; Visualisation, O.T.; Haverinen-Shaughnessy, U. Indoor air quality guidelines from across the world: An appraisal considering energy saving, health, productivity, and comfort. Environ. Int. 2023, 178, 108127. [Google Scholar] [CrossRef]
- Fuerst, F.; McAllister, P.; Nanda, A.; Wyatt, P. Energy performance ratings and house prices in Wales: An empirical study. Energy Policy 2016, 92, 20–33. [Google Scholar] [CrossRef]
- Iram, S.; Shakeel, H.; Farid, H.M.A.; Hill, R.; Fernando, T. A web-based visual analytics platform to explore smart houses energy data for stakeholders: A case study of houses in the area of Manchester. Energy Build. 2023, 296, 113342. [Google Scholar] [CrossRef]
- Department for Business, Energy & Industrial Strategy. Changes to Government’s Standard Assessment Procedure (SAP): Government Response; Technical report; Department for Business, Energy & Industrial Strategy: London, UK, 2023. [Google Scholar]
- Sustainable Energy Authority of Ireland. Building Energy Rating (BER); Sustainable Energy Authority of Ireland: Dublin, Ireland, 2023. [Google Scholar]
- Passive House Institute. What Is a Passive House? Passive House Institute: Darmstadt, Germany, 2023. [Google Scholar]
- United States Environmental Protection Agency. US Green Building Council’s Leadership in Energy and Environmental Design (LEED®); United States Environmental Protection Agency: Washington, DC, USA, 2023. [Google Scholar]
- Spudys, P.; Jurelionis, A.; Fokaides, P. Conducting smart energy audits of buildings with the use of building information modelling. Energy Build. 2023, 285, 112884. [Google Scholar] [CrossRef]
- Ferreira, A.; Pinheiro, M.D.; de Brito, J.; Mateus, R. A critical analysis of LEED, BREEAM and DGNB as sustainability assessment methods for retail buildings. J. Build. Eng. 2023, 66, 105825. [Google Scholar]
- Droutsa, K.G.; Kontoyiannidis, S.; Dascalaki, E.G.; Balaras, C.A. Mapping the energy performance of hellenic residential buildings from EPC (energy performance certificate) data. Energy 2016, 98, 284–295. [Google Scholar] [CrossRef]
- International Energy Agency. Transition to Sustainable Buildings: Strategies and Opportunities to 2050; Organization for Economic Co-Operation & Development, International Energy Agency: Paris, France, 2013. [Google Scholar]
- Iram, S.; Al-Aqrabi, H.; Shakeel, H.M.; Farid, H.M.A.; Riaz, M.; Hill, R.; Vethathir, P.; Alsboui, T. An innovative machine learning technique for the prediction of weather based smart home energy consumption. IEEE Access 2023, 11, 76300–76320. [Google Scholar]
- Lopes, M.A.; Antunes, C.H.; Martins, N. Energy behaviours as promoters of energy efficiency: A 21st century review. Renew. Sustain. Energy Rev. 2012, 16, 4095–4104. [Google Scholar]
- Williams, J.; Mitchell, R.; Raicic, V.; Vellei, M.; Mustard, G.; Wismayer, A.; Yin, X.; Davey, S.; Shakil, M.; Yang, Y.; et al. Less is more: A review of low energy standards and the urgent need for an international universal zero energy standard. J. Build. Eng. 2016, 6, 65–74. [Google Scholar] [CrossRef]
- Fathi, S.; Srinivasan, R.; Fenner, A.; Fathi, S. Machine learning applications in urban building energy performance forecasting: A systematic review. Renew. Sustain. Energy Rev. 2020, 133, 110287. [Google Scholar] [CrossRef]
- Tronchin, L.; Fabbri, K. Energy Performance Certificate of building and confidence interval in assessment: An Italian case study. Energy Policy 2012, 48, 176–184. [Google Scholar] [CrossRef]
- Prieler, M.; Leeb, M.; Reiter, T. Characteristics of a database for energy performance certificates. Energy Procedia 2017, 132, 1000–1005. [Google Scholar] [CrossRef]
- Touzani, S.; Granderson, J.; Fernandes, S. Gradient boosting machine for modeling the energy consumption of commercial buildings. Energy Build. 2018, 158, 1533–1543. [Google Scholar] [CrossRef]
- Walker, S.; Khan, W.; Katic, K.; Maassen, W.; Zeiler, W. Accuracy of different machine learning algorithms and added-value of predicting aggregated-level energy performance of commercial buildings. Energy Build. 2020, 209, 109705. [Google Scholar] [CrossRef]
- Luo, X.; Oyedele, L.O.; Ajayi, A.O.; Akinade, O.O. Comparative study of machine learning-based multi-objective prediction framework for multiple building energy loads. Sustain. Cities Soc. 2020, 61, 102283. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Rahimian, F.P.; Glesk, I.; Roper, M. Machine learning for estimation of building energy consumption and performance: A review. Vis. Eng. 2018, 6, 1–20. [Google Scholar] [CrossRef]
- Al-Shargabi, A.A.; Almhafdy, A.; Ibrahim, D.M.; Alghieth, M.; Chiclana, F. Buildings’ energy consumption prediction models based on buildings’ characteristics: Research trends, taxonomy, and performance measures. J. Build. Eng. 2022, 54, 104577. [Google Scholar] [CrossRef]
- Eker, H. Natural Language Processing Risk Assessment Application Developed for Marble Quarries. Appl. Sci. 2024, 14, 9045. [Google Scholar] [CrossRef]
- Department for Levelling Up, Housing & Communities Energy Performance of Buildings Data: England and Wales. 2023. Available online: https://epc.opendatacommunities.org/ (accessed on 15 March 2024).
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Potdar, K.; Pardawala, T.S.; Pai, C.D. A comparative study of categorical variable encoding techniques for neural network classifiers. Int. J. Comput. Appl. 2017, 175, 7–9. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 69, 66138. [Google Scholar] [CrossRef]
- Chen, X.w.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the Sixth International Conference on Machine Learning and Applications (ICMLA 2007), IEEE, Cincinnati, OH, USA, 13–15 December 2007; pp. 429–435. [Google Scholar]
- Kukreja, S.L.; Löfberg, J.; Brenner, M.J. A least absolute shrinkage and selection operator (LASSO) for nonlinear system identification. IFAC Proc. Vol. 2006, 39, 814–819. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Bansal, M.; Goyal, A.; Choudhary, A. A comparative analysis of K-nearest neighbor, genetic, support vector machine, decision tree, and long short term memory algorithms in machine learning. Decis. Anal. J. 2022, 3, 100071. [Google Scholar] [CrossRef]
- Song, Y.Y.; Ying, L. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar]
- Nemeth, M.; Borkin, D.; Michalconok, G. The comparison of machine-learning methods XGBoost and LightGBM to predict energy development. In Computational Statistics and Mathematical Modeling Methods in Intelligent Systems: Proceedings of 3rd Computational Methods in Systems and Software; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1047, pp. 208–215. [Google Scholar]






| Cite | Techniques Used | Context | Key Findings |
|---|---|---|---|
| [33] | LR | Building features analysis | Assessed the impact of various features on energy performance. |
| [34] | KNN | Residential energy consumption | Predicted historical energy usage and identified characteristic patterns. |
| [36] | KNN | Pre- and post-retrofit energy data | Demonstrated suitability to predicting energy-saving potential. |
| [37] | SVR | Meteorological, material, and occupancy data | Modeled energy performance under heterogeneous conditions. |
| [38] | DT | Historical energy and building characteristics | Effectively identified critical energy-saving areas. |
| [39] | RF | Building size, insulation, and occupancy patterns | Captured complex relationships for accurate energy use prediction. |
| [40] | RF | Historical consumption and building data | Validated RF’s performance in predicting energy demand. |
| [41] | GB | Commercial building energy consumption | Achieved superior forecasting accuracy compared to other approaches. |
| [44] | ANN, SVM, Gaussian-based regressions, clustering | Building energy performance forecasting | Provided a comprehensive analysis of primary ML techniques. |
| [12] | XGBoost, ANN, Degree-Day OLS Regression | Energy model construction | Demonstrated enhanced accuracy and efficiency in energy prediction. |
| [45] | Taxonomy of ML Techniques | Energy consumption prediction | Offered a comparative examination of various ML algorithms. |
| [46] | SGD, NLP | Classification and Prediction by analysing text data | Conducted automatic risk assessment on text data and effectively predicted it. |
| Category | Feature | Description |
|---|---|---|
| Building | Total Floor Area | The total floor area measured in square meters. |
| Number of Extensions | The number of extensions present in the property. | |
| Number of Habitable Rooms | The total number of habitable rooms within the property. | |
| Number of Heated Rooms | The total number of rooms in the property that are heated. | |
| Low-Energy Lighting | The percentage of lighting within the property that utilizes low-energy solutions. | |
| Window Energy Efficiency | The energy efficiency rating of the windows. | |
| Wall Energy Efficiency | The energy efficiency rating of the walls. | |
| Energy | Current Energy Efficiency Rating | The current energy efficiency rating of the property. |
| Current Energy Consumption | The total energy consumption of the property in its current state. | |
| Main Heating System Efficiency | The energy efficiency rating of the primary heating system. | |
| Main Heating Control Efficiency | The energy efficiency rating of the primary heating control system. | |
| Lighting Efficiency | The energy efficiency rating of the lighting system. | |
| Hot Water System Efficiency | The energy efficiency rating of the hot water system. | |
| Roof Energy Efficiency | The energy efficiency rating of the roof. | |
| Window Energy Efficiency | The energy efficiency rating of the windows. |
| Category | Feature | Description |
|---|---|---|
| Environmental | Current Environmental Impact Rating | The environmental impact rating of the property in its current state. |
| Current CO2 Emissions | The total amount of CO2 emissions produced by the property. | |
| CO2 Emissions per Floor Area | The amount of CO2 emissions produced per square meter of floor area. | |
| Main Heating System Environmental Efficiency | The environmental efficiency rating of the primary heating system. | |
| Main Heating Control Environmental Efficiency | The environmental efficiency rating of the primary heating control system. | |
| Lighting Environmental Efficiency | The environmental efficiency rating of the lighting system. | |
| Hot Water System Environmental Efficiency | The environmental efficiency rating of the hot water system. | |
| Roof Environmental Efficiency | The environmental efficiency rating of the roof. | |
| Window Environmental Efficiency | The environmental efficiency rating of the windows. | |
| Cost | Annual Lighting Cost | The estimated annual cost incurred for lighting. |
| Annual Heating Cost | The estimated annual cost incurred for heating. | |
| Annual Hot Water Cost | The estimated annual cost incurred for hot water usage. | |
| Current Energy Consumption | The total energy consumption of the property in its current state. |
| Models | Selected Hyperparameters | Best Hyperparameters |
|---|---|---|
| Linear Regression | {} | {} |
| KNN | {n_neighbors: [3, 5, 7]} | {n_neighbors: 5} |
| SVR | {C: [0.1, 1, 10], gamma: [0.1, 1, ’cale’, ’auto’]} | {C: 10, gamma: ’cale’} |
| Decision Tree | {max_depth: [None, 10, 20], min_samples_split: [2, 5, 10]} | {max_depth: 10, min_samples_split: 10} |
| Random Forest | {n_estimators: [50, 100, 200], max_depth: [None, 10, 20], min_samples_split: [2, 5, 10]} | {max_depth: 20, min_samples_split: 2, n_estimators: 100} |
| Extra Trees | {n_estimators: [50, 100, 200], max_depth: [None, 10, 20], min_samples_split: [2, 5, 10]} | {max_depth: 20, min_samples_split: 2, n_estimators: 100} |
| Gradient Boosting | {n_estimators: [50, 100, 200], learning_rate: [0.01, 0.1, 0.5], max_depth: [3, 5, 10]} | {learning_rate: 0.1, max_depth: 5, n_estimators: 200} |
| XGBoost | {n_estimators: [50, 100, 200], learning_rate: [0.01, 0.1, 0.5], max_depth: [3, 5, 10]} | {learning_rate: 0.1, max_depth: 5, n_estimators: 200} |
| LightGBM | {n_estimators: [50, 100, 200], learning_rate: [0.01, 0.1, 0.5], max_depth: [3, 5, 10]} | {learning_rate: 0.1, max_depth: 5, n_estimators: 200} |
| Ranking | Correlation | Linear Regression | Random Forest | Gradient Boosting | PC1 | Mutual Information | RFE | LASSO |
|---|---|---|---|---|---|---|---|---|
| 1 | CEPFA | ECC | CEPFA | CEPFA | LEE | CEPFA | CEPFA | ECC |
| 2 | ECC | CEC | CEC | CEC | LENE | ECC | ECC | CEC |
| 3 | CEC | CEPFA | HCC | HCC | LEL | CEC | CEC | HWEE |
| 4 | HCC | HCC | ECC | ECC | RENE | HCC | TFA | WEE |
| 5 | HWCC | HWCC | MHEE | MHEE | REE | WENE.1 | HCC | MHEE |
| 6 | EO | NAR | HWCC | HWCC | MHCEE | HWEE | MHEE | REE |
| 7 | LCC | MHCENE | MHENE | MHENE | MHCENE | WEE | MHENE | LEL |
| 8 | TFA | MHCEE | LCC | LCC | WEE | HWEVE | NAR | WIEE |
| 9 | NAR | LEE | TFA | TFA | WENE.1 | HWCC | NHR | MHCEE |
| 10 | NHR | LENE | HWEE | HWEE | WENE | MHEE | HWEE | WENE.1 |
| 11 | LENE | EO | LEL | LEL | WIEE | RENE | LCC | RENE |
| 12 | LEE | LEL | HWEVE | HWEVE | LCC | REE | LEL | LEE |
| 13 | LEL | NHR | WENE.1 | WENE.1 | HWEE | MHCENE | HWCC | MHCENE |
| 14 | WENE | LEE | WEE | WEE | HWEVE | MHCEE | WEE | MHENE |
| 15 | WIEE | MHENE | NHR | NHR | ECC | WIEE | HWEVE | HWEVE |
| 16 | REE | EO | NAR | NAR | CEC | MHENE | MHCEE | WENE |
| 17 | RENE | WIEE | EO | EO | CEPFA | WENE | WENE.1 | NHR |
| 18 | MHCEE | WENE | RENE | RENE | MHEE | LEL | RENE | NAR |
| 19 | MHCENE | REE | REE | REE | MHENE | TFA | MHCENE | EO |
| 20 | MHENE | REE | WENE | WENE | HCC | NHR | REE | TFA |
| 21 | WEE | RENE | WIEE | WIEE | NAR | LENE | WENE | HWCC |
| 22 | WENE.1 | WEE | MHCEE | MHCEE | HWCC | LEE | WIEE | HCC |
| 23 | MHEE | MHENE | MHCENE | MHCENE | TFA | LCC | EO | LCC |
| 24 | HWEVE | WENE.1 | LENE | LENE | NHR | EO | LENE | CEPFA |
| 25 | HWEE | MHEE | LEE | LEE | EO | NAR | LEE | LENE |
| Models | MSE | MAE | R2 | RMSE | MAPE | Adjusted R2 |
| Linear Regression | 12.590 | 2.091 | 0.873 | 3.548 | 5.444 | 0.873 |
| KNN | 11.167 | 1.993 | 0.887 | 3.342 | 4.731 | 0.887 |
| SVR | 7.244 | 1.455 | 0.927 | 2.692 | 3.595 | 0.927 |
| Decision Tree | 9.483 | 1.690 | 0.903 | 3.079 | 4.045 | 0.903 |
| Random Forest | 5.455 | 1.150 | 0.945 | 2.336 | 3.004 | 0.945 |
| Extra Trees | 5.131 | 1.162 | 0.948 | 2.265 | 2.943 | 0.948 |
| Gradient Boosting | 4.698 | 1.261 | 0.953 | 2.167 | 2.744 | 0.953 |
| XGBoost | 4.703 | 1.256 | 0.953 | 2.169 | 2.773 | 0.953 |
| LightGBM | 4.713 | 1.267 | 0.952 | 2.171 | 2.794 | 0.952 |
| (a) Using 3-Fold Data | ||||||
| Models | MSE | MAE | R2 | RMSE | MAPE | Adjusted R2 |
| Linear Regression | 12.574 | 2.091 | 0.873 | 3.546 | 5.421 | 0.873 |
| KNN | 10.704 | 1.942 | 0.892 | 3.272 | 4.608 | 0.892 |
| SVR | 7.057 | 1.442 | 0.929 | 2.656 | 3.411 | 0.929 |
| Decision Tree | 9.200 | 1.675 | 0.907 | 3.033 | 3.865 | 0.907 |
| Random Forest | 5.308 | 1.128 | 0.946 | 2.304 | 2.870 | 0.946 |
| Extra Trees | 5.014 | 1.144 | 0.949 | 2.239 | 2.820 | 0.949 |
| Gradient Boosting | 4.609 | 1.245 | 0.953 | 2.147 | 2.652 | 0.953 |
| XGBoost | 4.555 | 1.243 | 0.954 | 2.134 | 2.687 | 0.954 |
| LightGBM | 4.590 | 1.253 | 0.954 | 2.142 | 2.720 | 0.954 |
| (b) Using 5-Fold Data | ||||||
| Models | MSE | MAE | R2 | RMSE | MAPE | Adjusted R2 |
| Linear Regression | 12.554 | 2.092 | 0.873 | 3.543 | 5.406 | 0.873 |
| KNN | 10.483 | 1.919 | 0.894 | 3.238 | 4.559 | 0.894 |
| SVR | 6.977 | 1.437 | 0.929 | 2.641 | 3.368 | 0.929 |
| Decision Tree | 9.129 | 1.673 | 0.909 | 3.022 | 3.846 | 0.909 |
| Random Forest | 5.159 | 1.115 | 0.948 | 2.271 | 2.850 | 0.948 |
| Extra Trees | 4.948 | 1.138 | 0.950 | 2.224 | 2.797 | 0.950 |
| Gradient Boosting | 4.521 | 1.242 | 0.954 | 2.126 | 2.636 | 0.954 |
| XGBoost | 4.543 | 1.242 | 0.954 | 2.132 | 2.692 | 0.954 |
| LightGBM | 4.538 | 1.246 | 0.954 | 2.130 | 2.682 | 0.954 |
| (c) Using 7-Fold Data | ||||||
| Models | MSE | MAE | R2 | RMSE | MAPE | Adjusted R2 |
| Linear Regression | 12.558 | 2.092 | 0.873 | 3.544 | 5.400 | 0.873 |
| KNN | 10.336 | 1.904 | 0.895 | 3.215 | 4.492 | 0.895 |
| SVR | 6.943 | 1.435 | 0.930 | 2.635 | 3.353 | 0.930 |
| Decision Tree | 8.808 | 1.656 | 0.911 | 2.968 | 3.724 | 0.911 |
| Random Forest | 5.139 | 1.111 | 0.948 | 2.267 | 2.841 | 0.948 |
| Extra Trees | 4.885 | 1.132 | 0.951 | 2.210 | 2.775 | 0.951 |
| Gradient Boosting | 4.547 | 1.241 | 0.954 | 2.132 | 2.674 | 0.954 |
| XGBoost | 4.526 | 1.236 | 0.954 | 2.127 | 2.681 | 0.954 |
| LightGBM | 4.490 | 1.238 | 0.955 | 2.119 | 2.698 | 0.955 |
| (d) Using 9-Fold Data | ||||||
| Models | MSE | MAE | R2 | RMSE | MAPE | Adjusted R2 |
| Linear Regression | 14.334 | 2.115 | 0.862 | 3.786 | 6.316 | 0.862 |
| KNN | 11.634 | 1.986 | 0.888 | 3.411 | 4.979 | 0.888 |
| SVR | 10.834 | 1.685 | 0.896 | 3.291 | 5.580 | 0.896 |
| Decision Tree | 11.391 | 1.568 | 0.890 | 3.460 | 4.071 | 0.884 |
| Random Forest | 6.305 | 1.165 | 0.939 | 2.499 | 3.135 | 0.940 |
| Extra Trees | 6.023 | 1.151 | 0.942 | 2.454 | 3.125 | 0.942 |
| Gradient Boosting | 7.733 | 1.583 | 0.925 | 2.361 | 3.197 | 0.925 |
| XGBoost | 5.477 | 1.242 | 0.947 | 2.340 | 2.970 | 0.947 |
| LightGBM | 5.575 | 1.331 | 0.946 | 2.361 | 3.197 | 0.946 |
| (e) Using whole data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakeel, H.M.; Iram, S.; Hill, R.; Athar Farid, H.M.; Sheikh-Akbari, A.; Saleem, F. A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings. Buildings 2025, 15, 1275. https://doi.org/10.3390/buildings15081275
Shakeel HM, Iram S, Hill R, Athar Farid HM, Sheikh-Akbari A, Saleem F. A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings. Buildings. 2025; 15(8):1275. https://doi.org/10.3390/buildings15081275
Chicago/Turabian StyleShakeel, Hafiz Muhammad, Shamaila Iram, Richard Hill, Hafiz Muhammad Athar Farid, Akbar Sheikh-Akbari, and Farrukh Saleem. 2025. "A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings" Buildings 15, no. 8: 1275. https://doi.org/10.3390/buildings15081275
APA StyleShakeel, H. M., Iram, S., Hill, R., Athar Farid, H. M., Sheikh-Akbari, A., & Saleem, F. (2025). A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings. Buildings, 15(8), 1275. https://doi.org/10.3390/buildings15081275









