Restoration Study of a Masonry Monumental Building in Thrapsano, Greece

Abstract

This study investigates structural integrity and proposes retrofitting solutions for the historical two-storey school building in Thrapsano, Crete, severely impacted by the September 2021 earthquake. An extensive methodology was adopted, incorporating field surveys, material characterization, finite element modeling, and experimental analysis. The assessment is focused on identifying structural damage, such as cracking and delamination in masonry walls, and evaluating the dynamic and static performance of the load-bearing system under seismic loads. Key interventions include grouting for masonry reinforcement, replacement of mortar with compatible materials, stitching of cracks, and the addition of reinforced concrete and metallic tie elements to enhance diaphragm action. Advanced numerical simulations, validated through experimental data, were employed to model the pre- and post-retrofit behavior of the structure. The proposed retrofitting measures align with Eurocodes 6 and 8, and the Greek code for masonry structures (KADET), aiming to restore the structural stability and improve seismic resilience while respecting the building’s historical significance. The results from the finite element analysis confirm the effectiveness of the interventions in reducing tensile stresses and improving load redistribution, ensuring compliance with modern safety standards. This case study offers a framework for the seismic retrofitting of heritage structures in a similar context.

1. Introduction

Static analysis and vulnerability assessment of unreinforced masonry (URM) structures is a topic of practical interest and the focus of many current research investigations. Although an unreinforced masonry element is brittle and linear elastic analysis is expected to be the only acceptable design methodology, some plasticity can still be expected due to the cooperation of various structural elements (walls in different orientations, slabs, and other rigid diaphragms). Modern design codes allow for vulnerability evaluation by using detailed structural analysis models. Static and seismic evaluation, as well as suitable retrofitting measures, will be discussed and applied to a two-storey URM building that hosts a School in Thrapsano village in Crete, Greece. The building suffered severe damage that has been documented in a recent study [1]. Most damage can be attributed to the lack of a rigid diaphragm at the level of the second story, under the wooden roof, and the incomplete composition of the transverse walls. Various interventions have been considered, including the restoration of the transverse wall connections and cracks with stone seams, the strengthening of walls with suitable grouting, and finally, the strengthening of the diaphragmatic function at the level of the crowning of the walls with reinforced concrete beams and additional diaphragms made of steel or reinforced concrete. The results of the investigation will be reported in the present paper.

The vulnerability evaluation and classification of a specific URM building are based on suitable structural models and the assessment of expected stresses or relative displacements (shifts) under prescribed earthquake equivalent loadings. This procedure is described in Greek design codes [2] following the European and international codes [3,4,5,6].

The usage of equivalent beam macro-elements for the evaluation of regular masonry buildings is generally accepted in the relevant literature [7]. Nevertheless, the results of simplified models could be unacceptable and conservative [8,9,10]. Therefore, the more general finite element approach with two and three-dimensional elements has been adopted [11,12,13]. This is critical for irregular buildings [14,15,16]. Comparison of different retrofit measures is, for the time being, the acceptable methodology of the effectiveness of various retrofit measures [17]. Optimal design of retrofit seems to be an open question for future research. In addition, it should be noted that displacement drift quantities during past earthquakes have not been measured and usually are not available. Therefore, adopting a structural model and earthquake data for the estimation of these parameters is proposed in this paper, accompanied by visual inspection and instrumental measurements on the damaged structure. This method can be compared with the visual method proposed in [18] for simple masonry walls tested in the laboratory.

In this paper, two main findings have been drawn. First, simplified models based on macro-elements or beams and columns, as well as push-over analysis, are in principle conservative for irregular URM structures, while finite element models of higher complexity and response spectrum analysis on a three-dimensional model are more reliable. Second, interventions require some creativity in order to create the required effect with less additional mass and change in the structure. The example of a metal diaphragm proposed here, in comparison to a more classical reinforced concrete slab, exemplifies this point.

2. Materials and Methods

2.1. Methodology Overview

This study focuses on the investigation of structural adequacy and the selection of structural interventions for the historical Thrapsano School in Crete, following the earthquake of September 2021. For the needs of this study, data from the “Geotechnical study” (Laboratory of Applied Geophysics, School of Mineral Resources Engineering, Technical University of Crete), the Technical Report concerning the “On-site exploratory works for the assessment of the strength and dynamic mechanical characteristics of the load-bearing structure of the building of the Primary School of Thrapsano Heraklion” as well as the calculation of the mechanical properties of the materials (Laboratory of Applied Mechanics and Strength of Materials, School of Architecture, Technical University of Crete), the “Study of mortars and coatings” (Laboratory of Cultural Heritage Materials and Contemporary Building, School of Architecture, Technical University of Crete) and the Architectural study have been considered [1]. The finite element method was used to assess the mechanical behavior of the structure, as it is well-suited for simulating monumental structures with unique geometry, stiffness, and mechanical behavior that are difficult to model with simplified approaches. Therefore, simulations consisting of three-dimensional hexahedral solid finite elements were created. The final configuration of the finite element network was determined after successive discretization, with the aim of accurately simulating the existing structure and ensuring the precision of the results.

The building was constructed in 1930, in two storeys of an average height of 4.50 m (Figure 1a–c). It consists of vertical load-bearing masonry walls, horizontal reinforced concrete elements on the ground floor level (slabs, beams), and a wooden roof. The vertical forces are taken up by compressive forces from the walls, which have high compressive strength. Horizontal forces caused by the seismic loads lead to the development of tensile stresses that are called upon to be received by the masonry, which always has a reduced tensile strength compared to the compressive strength. Elements that determine seismic behavior are the structure of the masonry, the quality of the materials, and the connection of the transverse walls.

The analysis of the structure was based on the creation of 3D finite element models considering geometric mapping and experimental investigations in terms of materials, the dynamic behavior of the structure, and the bearing conditions. According to the current regulations, the following analyses were conducted to assess the structure’s load-bearing capacity:

• Linear, static analysis
• Eigenvalue analysis
• Response spectrum analysis

2.2. Structural Damages

The structure (Figure 1a) exhibited distinctly different behavior on the two levels (ground floor and first floor) due to the development of the diaphragm function on the ground floor and its absence on the first floor. The development of the diaphragm function is exclusively due to the existence of a reinforced concrete slab on the ground floor roof, while on the first floor, there was a wooden roof supported on a thin layer of mortar on the top of the perimeter walls, so the structure did not act as a diaphragm at this level.

The differing dynamic behavior of the structure at the two individual levels is reflected in the development of distinct pathologies, respectively. On the ground floor, damage is observed in the load-bearing walls, both peripheral and transverse. This damage is primarily limited to the disintegration of coatings and mortar. However, in isolated cases—specifically at one point on the north wall of the shell—stone breakage is also present (Figure 2). On the first floor, the masonry exhibits significant pathological deterioration. The main damage is the detachment of the transverse internal masonry walls (Figure 3) due to their inadequate connection to the load-bearing walls of the shell, suggesting the development of hinge mechanisms at the connection points.

In addition, the formation of diagonal cracks due to the seismic oscillation of the structure, stone failure at the points of severe pathology, and mortar deterioration are observed (Figure 4). As for the reinforced concrete elements, namely the ground floor roof slab and the elements of beams on the top of the external walls (concrete ties), they did not develop damage due to the seismic stress, but neither did they show any deterioration and/or damage related to environmental causes such as reinforcement oxidation. Similarly, the wooden roof did not show any significant deformation, although the wooden elements presented local failures, so it was proposed to replace it with a new one of the same shape. The foundation of the building (Figure 5) behaved adequately against the seismic load, without the development of stresses or differential settlements.

2.3. Experimental Characterization of Materials

For the needs of this study, data of the Technical Report concerning the “On-site exploratory works for the assessment of the strength and dynamic mechanical characteristics of the load-bearing structure of the building of the Primary School of Thrapsano Heraklion” as well as the calculation of the mechanical properties of the materials (Laboratory of Applied Mechanics and Strength of Materials, School of Architecture, Technical University of Crete), were taken into account for the analysis [1]. More specifically, the mechanical characteristics that were used for the characterization of the masonry walls were Ε = 2.83 GPa for the elastic modulus, ν = 0.3 for the Poisson ratio, ρ = 2500 kg/m³ for the density, f_wc = 3.77 MPa compressive strength, and f_wt = 0.30 MPa for the tensile strength.

2.4. Restoration Methodology

The maintenance and strengthening measures proposed are intended to repair structural damage, strengthen the structural bearing system, and prevent the deterioration of the mortar, ensuring the safety and longevity of the structure. The guiding principle of the intervention is to preserve the building’s authenticity by respecting the original materials and minimizing the extent of interventions. More specifically, it is proposed to fully restore the masonry structure by filling and connecting areas with cracks, disorganization, and at the junctions of the transverse walls. Additional measures are recommended to enhance the diaphragm function at the roof level. The removal of coatings will be necessary to conduct these interventions. The proposed interventions are as follows.

Restoration of cracks with stone seams: The cracks that are observed should be repaired by stonewalling, connecting the two sides of the crack using keystones at regular intervals (0.80–1.00 m), i.e., stones of a sufficient length to restore the continuity of the wall. The loose mortar from the walls should be removed from the walls, and areas where the mortar has completely crumbled should be grouted using a mortar that matches the original in strength and contains an appropriately sized aggregate, as proposed by the relevant study. It will also be supplemented with stone where necessary. Application of grouts to strengthen the masonry (due to the low strength of the mortar). The composition of the grouts is suggested by the corresponding material study. Two grouts are proposed, one with lime and metakaolin (compressive strength 4.5 MPa) and one with natural hydraulic lime (compressive strength 1.76 MPa), which equally meet the specifications for the restoration of the masonry. They are grouts with not very high compressive strength, and it is estimated that they will be used to fill the gaps in the masonry. In the case of discrete clay masonry, the percentage of voids in the total thickness of the wall can reach 8%. In this way, we can increase the tensile strength of the masonry to 100%. This includes the placement of a 35 cm high concrete tie in the crown of the perimeter and internal walls with appropriate reinforcement. Metal grating (Figure 6) will reinforce the diaphragm function at roof level consisting of IPE200 sections made of S275 steel.

2.5. Finite Element Modeling

The design model created was the basis for the discretization of the structure using the finite element method and allowed the initial estimation of the mechanical (dynamic) characteristics of the structure and the comparison with the measured (experimental) data. The finite element model of the carrier was sufficiently identified through the consideration of different scenarios regarding the mechanical properties of the material at different locations, depending on the damage state, the comparison with the measurements of specific characteristics, and finally, the assessment of the actual state of the structure. Based on the adaptation of the model using parameter identification techniques, we assume that the masonry structure can be successfully restored, and a monolithic connection of the transverse walls can be established. The final model was then obtained and used in analyses to assess structural adequacy and determine reinforcement methods. For the study of the structural framework, computer programs such as MSC/MARC (V2016) (Figure 7) and Abaqus 6.12-3 (V2012) (Figure 8), which are based on the finite element method, are used. Initially, the geometric model is entered into the program environment, and discretization is performed with three-dimensional finite elements of five or eight nodes with three metamorphic degrees of freedom per node. Then, the materials, connections, supports, and loads applied to the structure are added.

The presence of reinforced concrete beams at the top of the perimeter walls, on which the wooden roof trusses rest, limits the roof’s contribution to the stiffness of the structure. Based on this, the wooden roof was not taken into account in the FE model of the original building.

3. Results

3.1. Finite Element Results

3.1.1. Eigenmodal Analysis

To solve the finite element model for the calculation of the eigenfrequencies and eigenmodes of the structure, an eigenmodal analysis was carried out first on the model with the damage and then on the other models studied. The original model was sufficiently identified by considering different scenarios regarding the mechanical properties of the material at different locations depending on the damage condition, comparing them with the measured eigenmodes, and finally estimating the actual state of the structure. The results of the damage model frequencies (

Table 1. Numerical eigenvalues and eigenfrequencies.

Marc/MSC: Model 1 (Damaged)		Marc/MSC: Model 2 (Non-Damaged)		Abaqus: Model 1 (Damaged)
Eigenvalue	Freq (Hz)	Eigenvalue	Freq (Hz)	Eigenvalue	Freq (Hz)
1	5.153	1	7.948	1	5.1680
2	6.151	2	9.446	2	6.8559
3	7.246	3	11.089	3	7.2662
4	8.207	4	12.113	4	8.2057
5	8.864	5	12.964	5	8.4959
6	9.705	6	14.533	6	9.7079
7	10.759	7	15.205	7	10.845
8	11.249	8	15.943	8	11.238
9	11.477	9	16.848	9	11.324
10	11.629	10	17.199	10	11.662
11	11.784	11	17.749	11	11.784
12	12.081	12	18.100	12	12.117
13	12.653	13	18.368	13	12.683
14	13.287	14	19.509	14	13.120
15	13.47	15	20.347	15	13.331
16	13.683	16	20.347	16	13.587
17	14.071	17	21.014	17	14.088
18	14.619	18	21.853	18	14.565
19	14.706	19	22.025	19	14.719
20	15.107	20	22.089	20	15.066

) lead to a satisfactory comparison with the frequencies identified by the experimental investigations. In Figure 9 and Figure 10, two characteristic deformation shapes of 5.15 Hz and 7.25 Hz for Model 1 (with damages) are presented. The ratio of effective modal mass to total mass is equal to 8.37% (in Y direction) and 4.47% (in X direction) for these eigenmodes, respectively.

From the eigenmodal analysis, the areas of strong oscillation are obvious, namely, the walls of the first floor. The existence of a slab on the ground floor ceiling enhances the diaphragm function and reduces the oscillation of the ground floor walls. The role of the beams connecting the intermediate wall to the north wall is also characteristic, together with the existence of corresponding ribs in the north wall. In the existing structure, they minimized the damage to the north wall while intense stress developed at their connection points with the intermediate wall, where cracking and disorganization of the masonry occurred.

Having finalized the restoration and reinforcement interventions, an eigenmodal analysis of the final model in Abaqus was performed, with the final reinforcement interventions (scaffolding on the crown of all walls and placement of a horizontal metal frame).

Table 2. Numerical eigenvalues and eigenfrequencies of the strengthened model.

Abaqus: Strengthened Model
Eigenvalue	Freq (Hz)
1	2.3224
3	3.2386
7	3.8920
9	4.5995
10	4.7622
16	5.4259
18	5.5276
32	7.2603
34	7.3706
74	11.472

shows 10 eigenfrequencies of the model, while in Figure 11 and Figure 12, the characteristic deformation shapes of 3.23 Hz and 7.26 Hz are present.

3.1.2. Response Spectrum Analysis Result

The seismic loading (design spectrum) was initially assumed to act in the three directions in space, assuming different combinations in terms of participation in the different directions (e.g., main directions, alternatively, the two axes of the structure’s plan view) in accordance with the seismic code:

E = ±Ex ± 0.3 Ey ± 0.3 Ez

E = ±0.3 Ex ± Ey ± 0.3 Ez

E = ±0.3 Ex ± 0.3 Ey ± Ez

The final intensive quantities were obtained by superimposing static and dynamic spectral analysis. The soil class and the depth of masonry walls were estimated by a geophysical study [1]. For the spectral analysis, the Eurocode 8 elastic spectrum (

Table 3. Design spectrum.

Design Spectrum Data	Value
Seismic hazard zone	Z2
Maximum reference ground acceleration at ground level in standard soil A	0.24 g
Design acceleration in class A ground	2.8253 m/s2
Importance factor	1.30
Acceleration of gravity	9.81 m/s2
Soil class	B
Characteristic period below the lower limit of the constant spectral acceleration branch	0.15 s
Upper limit characteristic period of the constant spectral acceleration branch	0.60 s
Characteristic period defining the beginning of the steady-state region of the spectrum	2.50 s
Ground coefficient	1.0
Behavior factor	1.0
Damping z(%)	5

) was used with the following characteristics.

Considering the high level of data reliability, the results of the response spectrum analysis, in terms of stresses, show that the compressive strength of the masonry is fwc,d = 3.14 MPa, and the tensile strength is fwt,d = 0.25 MPa. The maximum and minimum principal stresses for the model before and after the finalized strengthening are shown in Figure 13 and Figure 14. The distribution of stresses across the elements of the entire structure is illustrated in Figure 13a,b and Figure 14a,b, for both the initial and strengthened models. Regarding the mechanical response of the bearing walls, the stress distribution for both the initial and final models is shown in Figure 13c,d and Figure 14c,d. The proposed strengthening reduces the developed stresses of the masonry. The spectral analysis indicates that, in some areas (shown in light gray in Figure 15a), the tensile strength of the masonry is exceeded. By introducing concrete ties at the crown of the walls and a metal horizontal frame, the areas where the tensile strength exceeded its limit were reduced (Figure 15b). The tensile strength of masonry increases due to the filling of voids and discontinuities in the masonry and the improvement of the cohesion at the interfaces. In this sense, and in the absence of more precise data, it is recommended to take into account, where necessary, the tensile strength of the masonry with an increase of approximately 100%. For parametric investigation, various assumptions of increase were studied, and the effects of two cases are shown in Figure 15c,d, with an increase equal to 75% and 100% (an upper limit of tensile strength of 0.375 MPa and 0.50 Mpa). This combination of initial restoration interventions, along with reinforcement measures at the wall crown and grout application, effectively mitigates the issue of tensile strength exceedance. Specifically, a clear limitation of the areas exceeding the maximum tensile strength limit is presented as shown in Figure 16, while no reduction in the maximum value of the tensile stresses is observed. It is important to note that the compressive strength is not exceeded, due to the high strength of the stonework.

3.1.3. Critical Evaluation of Interventions

From the numerical models of the structure before and after interventions, the following conclusions can be drawn.

Without an essential change in the total mass, the stiffness of the structure has been enhanced, see

Table 4. Influence of interventions on mass and inertia properties of the structure.

Quantity	No Strengthened Model	Strengthened Model
Total mass (kg)	2,189,146	2,202,519
Location of the center of mass (x,y,z) (m)	(30.6259, 10.4221, 5.3709)	(30.6201, 10.4548, 5.3762)
Moments of Inertia about origin (m4)	(3.551733 × 108, 2.3600062 × 109, 2.5261936 × 109)	(3.5908524 × 108, 2.3734410 × 109, 2.5423576 × 109)
Moments of Inertia about the center of mass (m4)	(5.4201732 × 107, 2.4355169 × 108, 2.3510423 × 108)	(5.4685894 × 107, 2.4471804 × 108, 2.3655553 × 108)

.

Considering the first 50 eigenmodes, with respect to the effective mass to total mass ratio, one recognizes the dominant role of certain eigenmodes in each direction. For instance, in the X direction, along the highest stiffness of the building, eigenmodes 18 and 60 play a significant role, see

Table 5. Modal contributions in the X direction.

X Direction
No Strengthened Model			Strengthened Model
Frequency	Mode Number	Effective Mass/Total Mass	Frequency	Mode Number	Effective Mass/Total Mass
9.4524	18	0.3390	10.422	60	0.3932
12.14	34	0.0416	10.334	58	0.0665
12.743	35	0.0390	8.3453	43	0.0264
15.084	57	0.0344	10.962	65	0.0186
9.3677	17	0.0217	8.2068	39	0.0134
12.881	37	0.0215	10.513	61	0.0127

.

In the vertical, Y direction, a different figure arises, with eigenmodes 74, 65, and 160, 151 being the leading with respect to the participation factor, see

Table 6. Modal contributions in the Y direction.

Y Direction
No Strengthened Model			Strengthened Model
Frequency	Mode Number	Effective Mass/Total Mass	Frequency	Mode Number	Effective Mass/Total Mass
18.723	74	0.1106	19.927	160	0.0745
17.01	65	0.0315	19.35	151	0.0393
20.327	93	0.0212	19.813	158	0.0177
18.529	73	0.0176	20.205	162	0.0166
19.769	87	0.0068	22.089	183	0.0165
20.089	90	0.0067	17.38	132	0.0137
6.5563	6	0.0056	19.851	159	0.0119
19.602	85	0.0053	17.038	128	0.0118
19.075	78	0.0052	21.22	176	0.0118

.

Finally, in the Ζ direction, perpendicular to the longitudinal direction of the building, a more complex situation arises, and no single eigenmode can be identified to play a higher role, see

Table 7. Modal contributions in the Z direction.

Z Direction
No Strengthened Model			Strengthened Model
Frequency	Mode Number	Effective Mass/Total Mass	Frequency	Mode Number	Effective Mass/Total Mass
7.1136	10	0.0876	7.0434	29	0.3685
7.0885	9	0.0813	7.1819	31	0.0979
6.7554	7	0.0805	14.759	103	0.07413
3.4128	1	0.0746	6.9208	27	0.045589
12.14	34	0.0746	8.3453	43	0.018521
9.0877	16	0.0635	8.2068	39	0.01085
5.6627	3	0.0589	17.641	133	0.010123
11.62	32	0.0462	6.5576	24	0.009308
12.743	35	0.0329	17.82	135	0.006478

.

The effective modal masses in the three directions for various frequencies are plotted in Figure 16, Figure 17 and Figure 18.

3.2. KADET Analysis

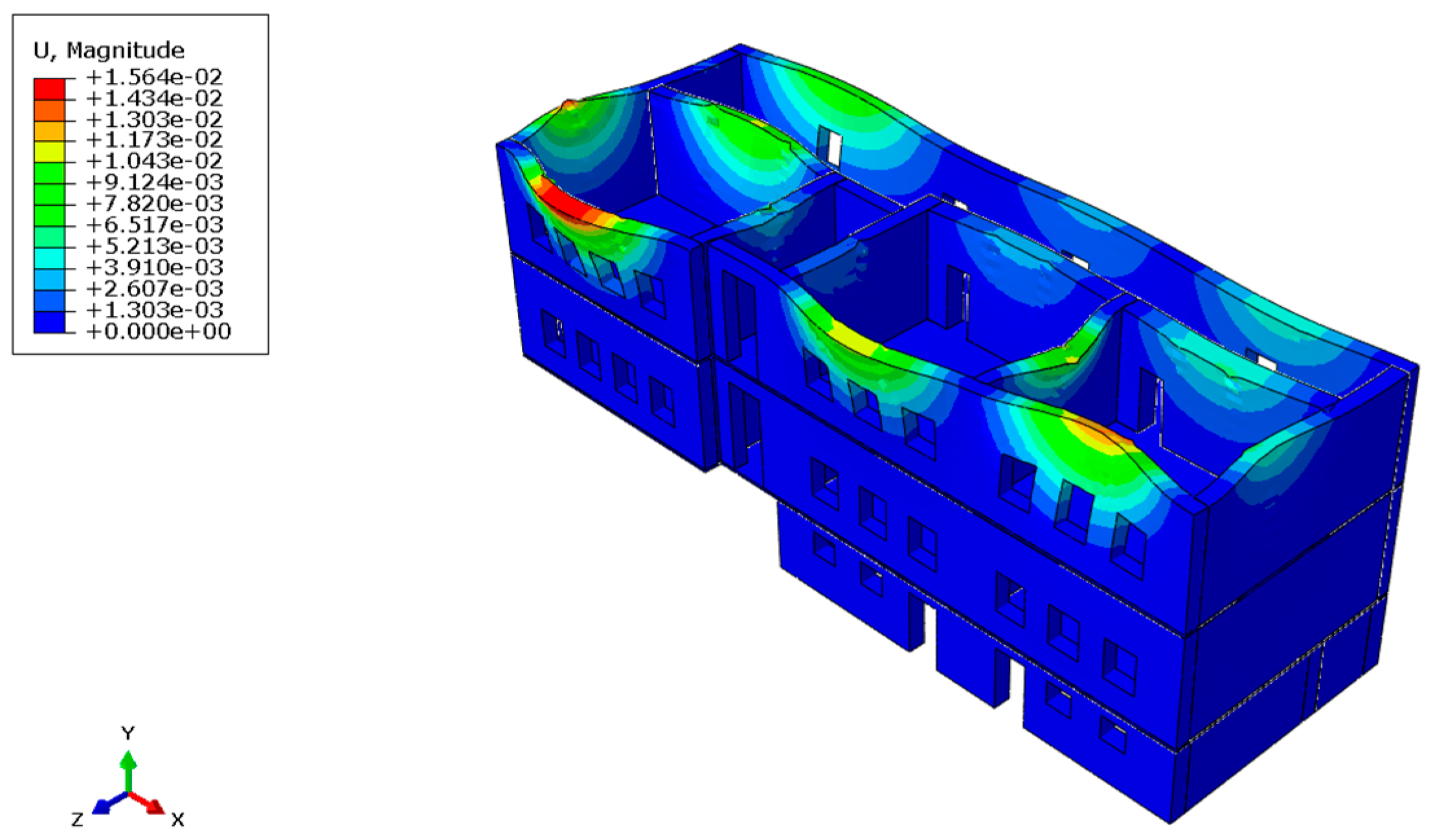
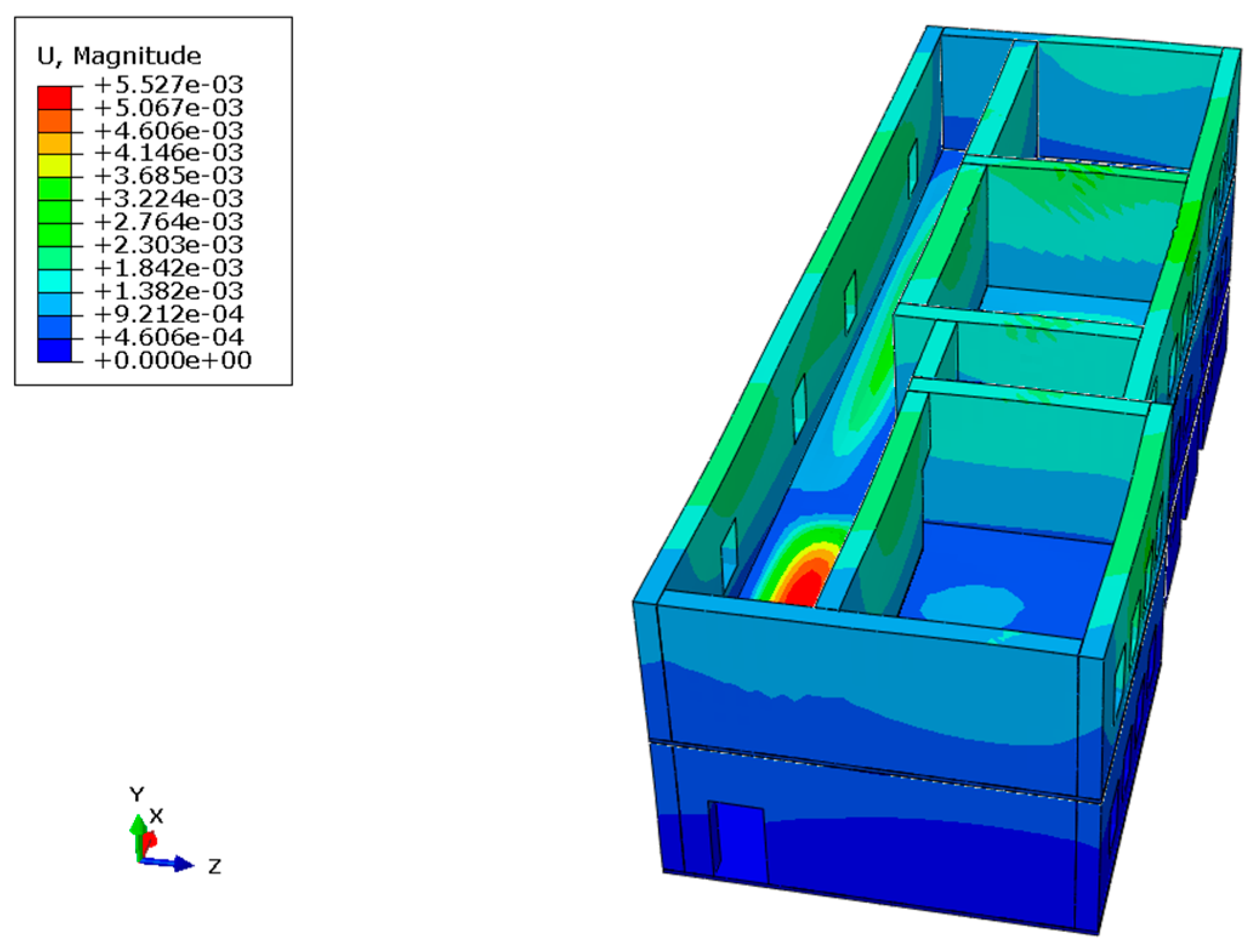
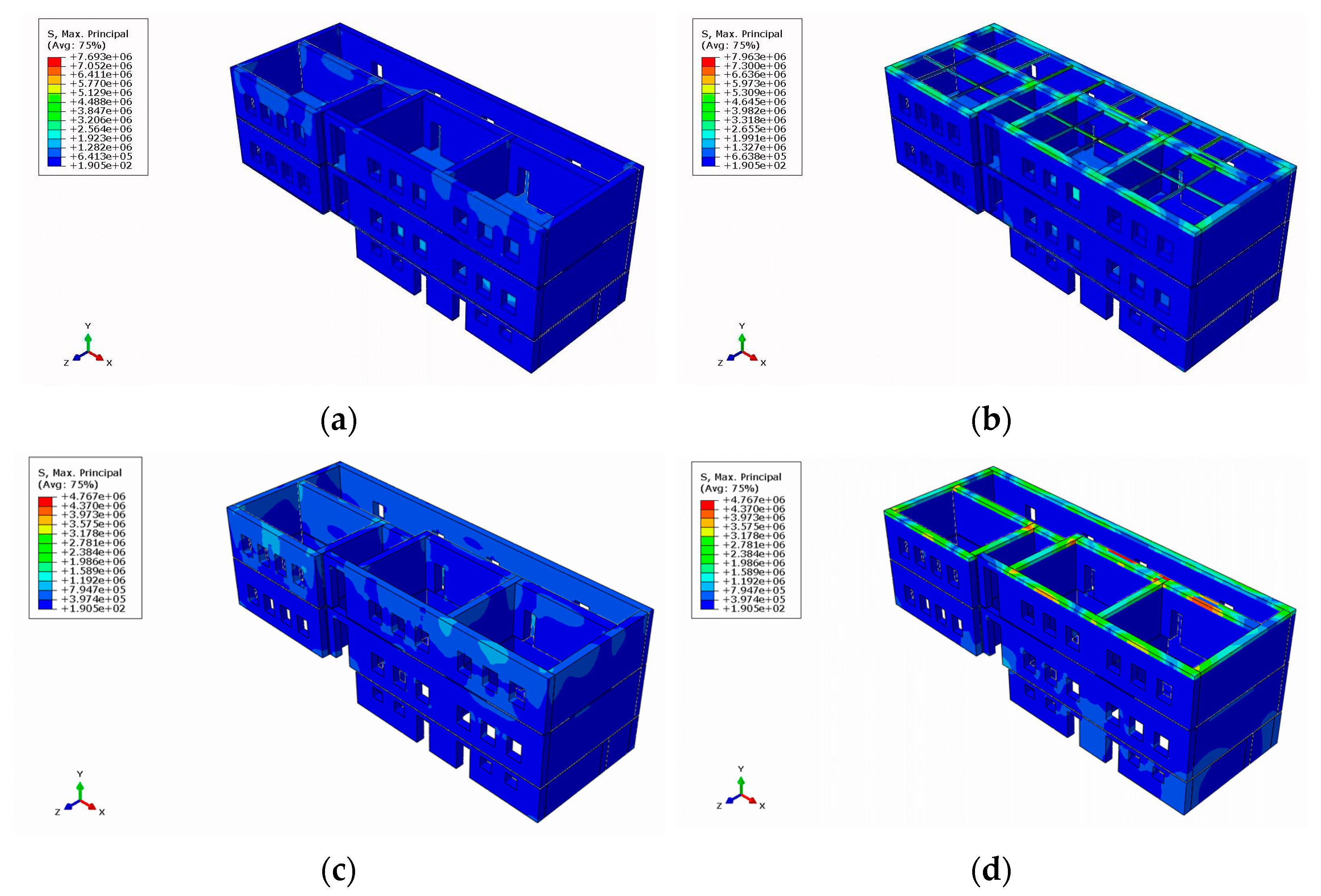
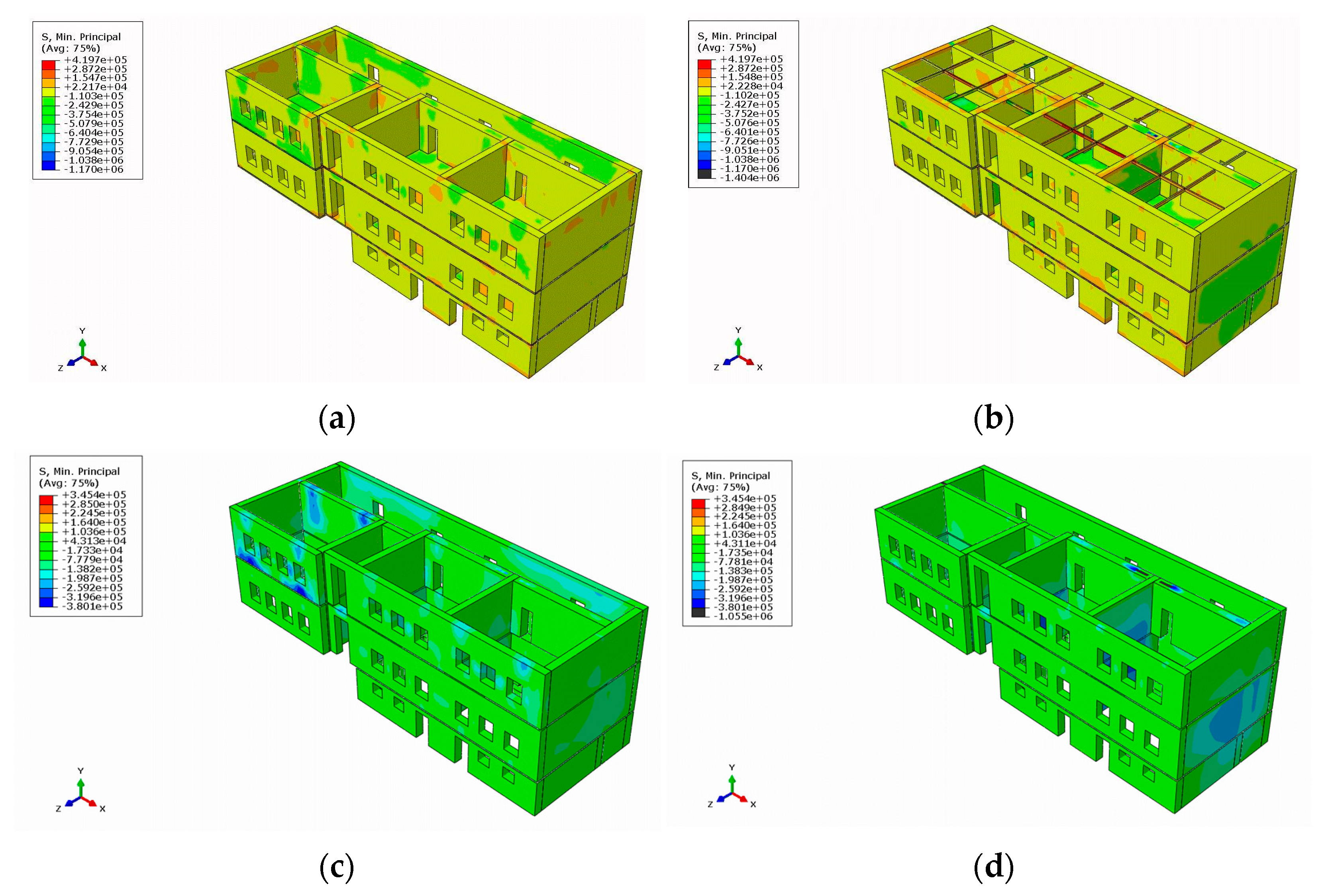
3.2.1. Failure Checks for In- and Out-of-Plane Action According to KADET

For the assessment of the whole structure, the load and the displacement performance-based approach adopted in the Greek Code for Structural Interventions on Masonry Structures [2] is applied to each wall and pier. Wall failure checks are implemented for in- and out-of-plane action. The need for a code of seismic assessment of masonry structures was highlighted many years ago, and some attempts were made by laying out a framework that encompasses performance-based assessment of older traditional or heritage masonry structures with no diaphragms. More details can be found in [19,20,21].

The proposed method, which is the base of the KADET, focuses on estimating the shape of lateral displacement that the structure would assume if subjected to a uniform field of acceleration throughout the building height in the event of an earthquake. The shape is scaled to the spectral displacement associated with the end of the plateau of the total acceleration design spectrum that corresponds to the building site. Drift ratios are quantified to determine seismic demand for the structure from the relative displacements between significant points of the structure after normalizing with the distance between those points of reference. These values are compared with deformation capacities for in-plane and out-of-plane distortion and bending of the walls, associated with critical levels of performance, to assess the level of anticipated damage and the localization of its occurrence in the structure [22]. The practical seismic assessment procedure for masonry buildings consists of two steps. First is the determination of local demands of the examined buildings during seismic excitation in terms of relative drift ratios referring to the in-plane and out-of-plane relative deviation of the piers and wall ends from the member chord. Second is the definition of local member capacities and the acceptance criteria [23,24].

The selected structural analysis method combined with the method of evaluating the load—bearing capacity of the structural elements of the masonry building, which is in accordance with the proposed method for seismic assessment of masonry heritage structures based on the modern Eurocode 8—Part 3 [25] and Greek Code for Interventions of Masonry Structures regulations has been applied for the study of a three-story building with stone and brick masonry, floors with metal and timber beams and a timber roof [26]. The defined performance levels—an important parameter introduced by the modern codes—were used as they determine the level of the applied seismic demands. Both load-based and displacement-based assessments were applied, and it was concluded that the displacement-based method allows for the usage of the nonlinear response of the masonry components, leading to a less conservative evaluation and limiting the extent of the required strengthening schemes, something useful, especially in heritage buildings, where extended interventions are not recommended.

In our case study, based on the results of the spectral analysis method and considering the overestimation of the stresses that this method provides, stress results were collected in selected cross-sections of walls and columns, and then the corresponding vertical and horizontal stresses were calculated. These forces were used to estimate the resistance of the elements to bending and shear, as well as the limit values of deformation. This was followed by a check in terms of forces and deformations according to the KADET. To ensure a sufficient safety margin, the capacity of the wall controlled by bending can be expressed in terms of relative displacement and is taken equal to the corresponding nominal values of δ_u, θ_u, determined for in-plane and out-of-plane bending of the walls. Accordingly, the shear-controlled wall capacity can be expressed in terms of relative displacement or rotation and is taken equal to the corresponding nominal values of δ_u, θ_u, determined for the in-plane and out-of-plane bending action of the walls.

3.2.2. Failure Control for In-Plane Wall Action

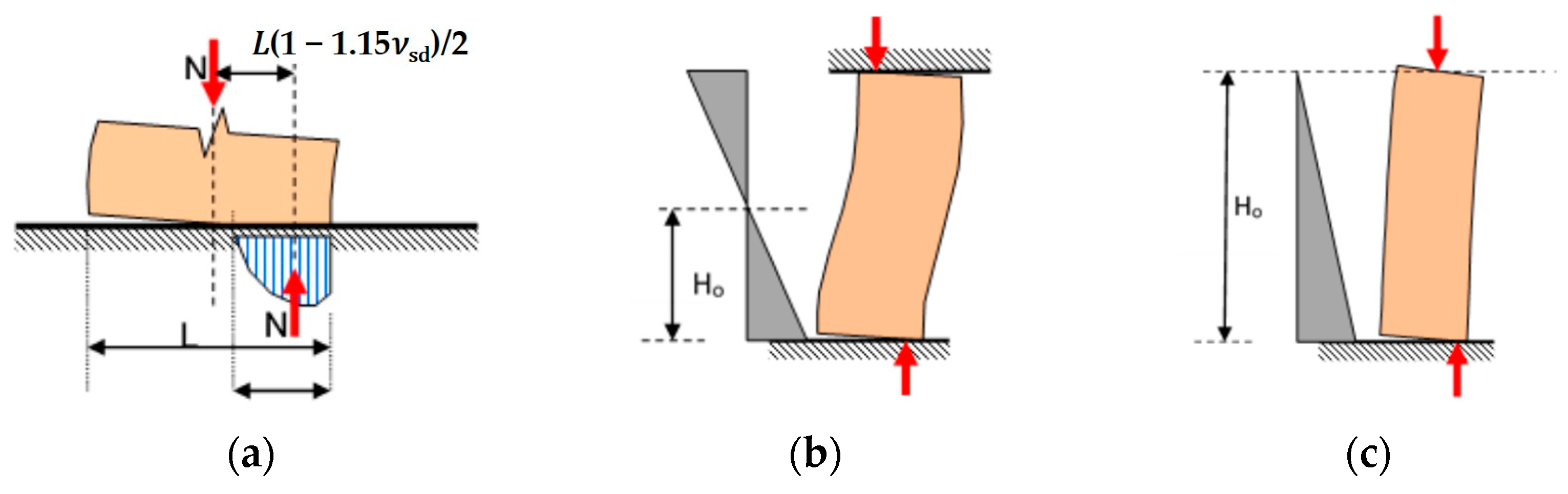
Structural elements such as unreinforced masonry (URM) subjected to vertical axial force and in-plane horizontal shear are considered. When checking a cross-section against in-plane bending, the tensile strength of the masonry is neglected, and, accordingly, an inactive part of the cross-section area is assumed. The bending moment that the cross-section can take depends on the compressive strength of the masonry and on the value of the (beneficial) axial load, according to the following relationship (Figure 19) as follows:

$${\mathrm{M}}_{Rd}=N_{sd}\times (1-1.15{\mathsf{\nu }}_{sd})/2{\mathrm{H}}_o$$

where

N_sd is the axial load of the wall for the seismic combination

L is the horizontal in-plane dimension of the wall (length)

ν_sd = N_sd/(L × t × f_md,c) is the reduced axial load with f_md,c = f_mc/γ_m, where f_mc is the average compressive strength of the masonry as obtained from in situ tests and from additional sources of information, and γ_m is the safety factor for the masonry according to the data reliability level according to [2], t is the wall thickness.

During the shear test, the shear capacity V_f (Figure 20, Figure S7.3 KADET) is calculated from the equation,

$${\mathrm{V}}_f=\mathrm{L}\times N_{sd}\times (1-1.15{\mathsf{\nu }}_{sd})/2{\mathrm{H}}_o$$

where H₀ is the distance between the cross-section at which the maximum moment is developed and the point of zeroing of the moments.

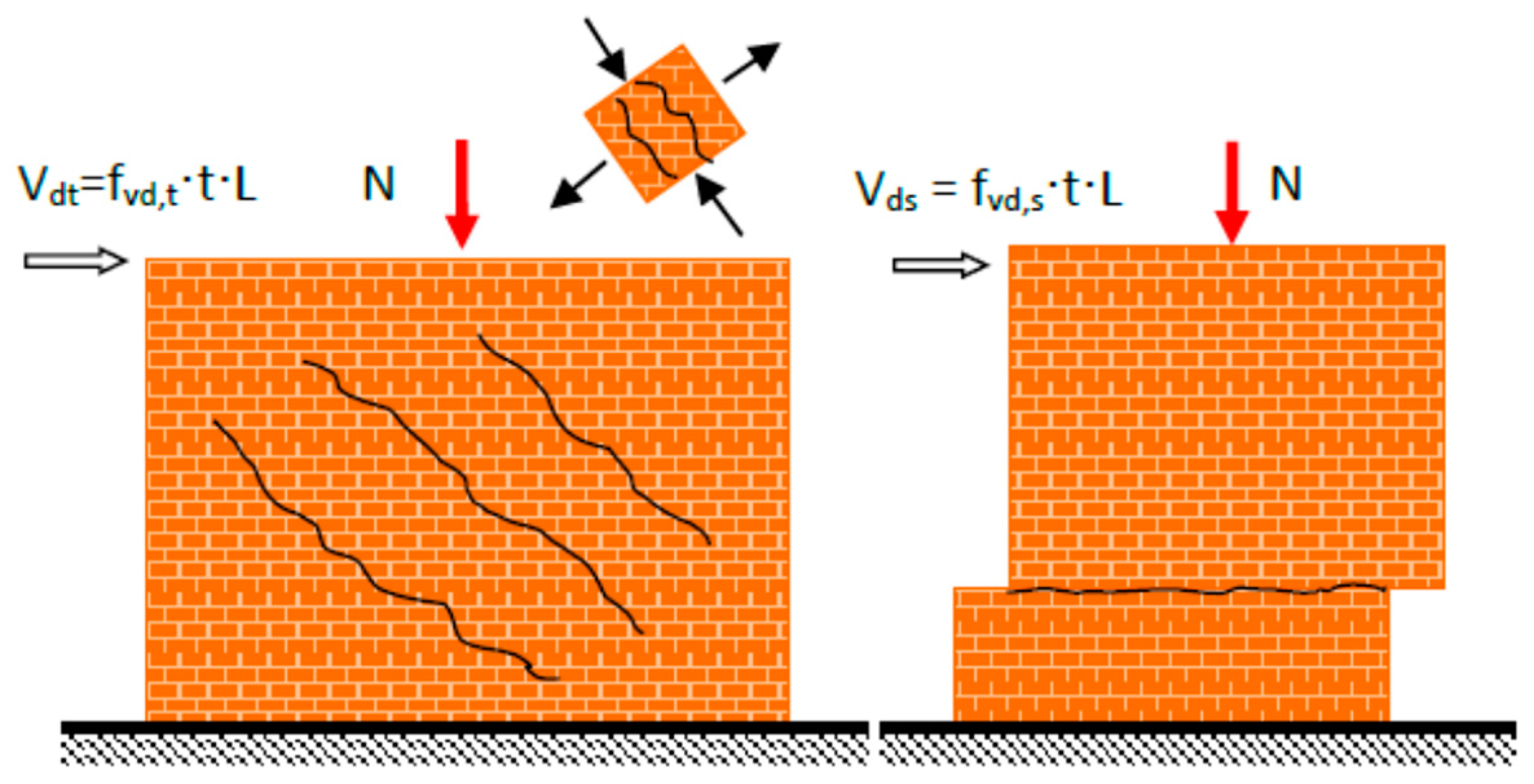
The in-plane shear strength of the wall is defined as the minimum of the following two shear failure mechanisms (Figure 20):

Due to diagonal tensile failure [2]

$$f_{vd,t}=\sqrt{f_{md,t}\times (f_{md,t}+v_{sd}\times f_{md,c})}$$

$$V_{v,t}=f_{vd,t}\times L\times t$$

where

f _vd,t is the shear strength of the masonry related to diagonal tensile cracking.

f _md,t is the representative value of the tensile strength of the masonry.

Due to sliding along horizontal joints, the shear resistance develops on the surface of the wall under compression only [2].

$$f_{vd,s}=f_{vm0}+0.4{\displaystyle \frac{N_{sd}}{L^{\prime }t}}\le 0.065f_{bc}$$

$$V_{v,s}=f_{vd,s}\times L\prime \times t$$

where

L′ is the compressed area of the wall and is calculated as a function of the eccentricity of the load, e_y:

L′ = L when e_y ≤ L/6

L′ = 3 (0.5 − e_y/L) when L/6 < e_y < L/2

L′ = 0.0 when L/2 ≤ e_y

t is the wall thickness

f _vd,_s the shear strength of masonry associated with sliding along a friction surface.

f_vm0 is the cohesion that develops at the mortar–stone interface.

μ is the apparent coefficient of friction along the sliding surface, taken equal to 0.4.

Ultimate shear resistance of the wall: V_v = min (V_v,t, V_v,s)

The wall is controlled by shear if V_v ≤ V_f; otherwise, the wall is considered to be controlled by bending. The yield resistance f_y is obtained as the minimum of the capacity shear V_f, when the moment is critical, and the shear strength V_v when the shear is critical for failure [2]. Therefore, during the adequacy check, the design shear is compared with the minimum of the values V_v and V_f. More details can be found in [19,20,21].

Based on the results of the spectral analysis, the horizontal seismic force has been calculated for the application of the method with a force control criterion.

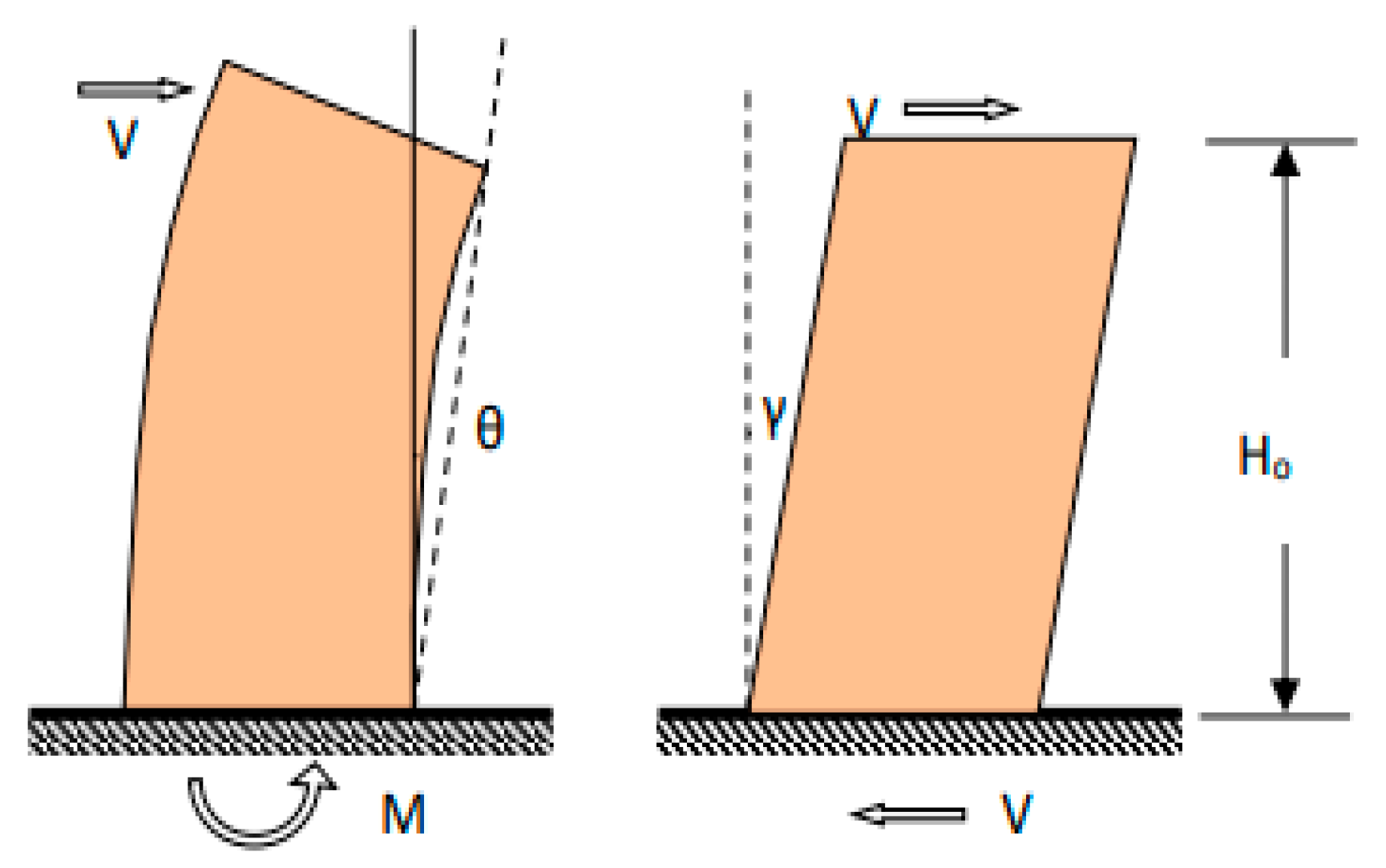
For the displacement-based assessment, the ultimate in-plane failure strain, θu, depends on the shear failure mechanism and on whether the wall is a primary or secondary member (Figure 21). For the control in terms of deformation, we have the following [2]:

(a) The capacity of a wall made of unreinforced masonry, which is controlled by bending, can be expressed in terms of relative displacement and is obtained from the relations:

$$d_u=0.008·H_o/L \mathrm{for} \mathrm{primary} \mathrm{seismic} \mathrm{walls} \mathrm{and} d_u=0.012·H_o/L \mathrm{the} \mathrm{secondary} \mathrm{ones}.$$

where

L is the horizontal in-plane dimension of the wall (length), and H_o is the distance between the cross-section at which the bending capacity is achieved and the point of zeroing of the moments.

(b) The capacity of a wall of unreinforced masonry controlled by shear can be expressed in terms of reduced relative displacement and is taken equal to

θ_u = 0.004 for primary seismic walls and θ_u = 0.006 for secondary

The relative rotation is defined as the deviation of the chord joining two points in the deformed state of the element, compared to the straight line joining these two points before any deformation is imposed (Figure 22). For the definition of this reference line, the rotation of the supports is taken into account as shown in Figure 22b [2].

It should be mentioned that the deformation capacity of a load-bearing element that fails due to in-plane bending depends on many parameters, such as the way the masonry is constructed, the presence of “reinforcement” elements in the masonry body, etc. Therefore, the estimation of appropriate deformation capacity values can be based on appropriate experimental results. In the absence of more precise data, the above-mentioned values for primary and secondary walls can be used, according to KADET.

Furthermore, according to the KADET, the walls that contribute to the load-bearing capacity and stability of the building under seismic loads will be characterized as primary. The remaining load-bearing elements that contribute to the bearing of vertical loads, but do not contribute significantly to earthquake resistance, or their degree of contribution is rather unreliable, due to low stiffness or strength or ductility (or due to uncontrolled construction methods), may be characterized as secondary. Such elements include the so-called ‘tsatmades’, i.e., cases of wall construction with a wooden frame and facade panels (sandwich wall). According to EC 8-1, it is indicated that load-bearing elements that do not satisfy the appropriate limits for the ratios of their geometric dimensions may be characterized as secondary.

The initial shear strength f_vm0 (cohesion) of the masonry may be determined from the evaluation of a database on the results of tests or from the values which are given in Eurocode 6 for various general-purpose mortars and masonry units. In Eurocode 6, cohesion between lime mortar and stone bed is 0.10 MPa [5]

The tension strength of the masonry unit, f_md,t, is the nominal value f_m,t divided by the safety factor, γ_m. According to KADET, the safety factor γ_m is related to the knowledge level regarding the geometric and material properties of the examined building (a higher value of γ_m refers to a lower knowledge level). It takes values 1.35, 1.20, or 1.50 for the load-based method of assessment, and 1.10, 1.00, or 1.20 for the displacement-based method of assessment. According KADET, for stone masonry, in the absence of more precise data, the tensile strength of the masonry, f_m,t, may be taken equal to 0.10 MPa, when the compressive strength of the mortar does not exceed 2.0 MPa, equal to 0.20 MPa, when the compressive strength of the structural mortar is between 2.0 and 5.0 MPa and equal to 0.40 MPa, when the compressive strength of the mortar is greater than 5.0 MPa.

The rotation corresponding to the stage of yield strain of surface elements of load-bearing masonry, θ_y, is the average reduced deviation between the deformed element and its chord at the onset of cracking (Figure 21). This relative movement (drift) within the plane is θ_y = 0.0015 [2].

The ductility index is defined as μ_θ = θ_u/θ_y. If the available value of the ductility index μ_θ of a structural element, a critical area of an element, or a connection of wall elements, exceeds a certain limit, the behavior is characterized as ductile, so its safety inequality will be expressed in terms of deformations δ. The boundary between ductile and brittle behavior is conventionally taken to be equal to 1.5 when referring to an available ductility index value that is based on the reduced relative displacements (i.e., chord rotation) of the walls, μ_θ. The control is carried out in terms of resultant forces and bending moments [2], and specifically is carried out by checking the developed stresses from the three-dimensional analysis of the structure using the finite element method. In fact, based on the expected failure type (brittle or ductile), force- or displacement-based assessments are proposed to use [KADET]. Conventionally, if the available local plasticity, ductility index is ≥1.5, i.e., if the behavior is quasi-ductile, the controls are performed in terms of deformations. Otherwise, if the behavior is quasi-brittle, the controls are performed in terms of forces. Since URM structures are brittle, the ductility index measures mainly the mechanical behavior of the structure as a whole system and not the brittle behavior of one individual element. Nevertheless, it can be used for prioritizing intervention measures on a damaged building.

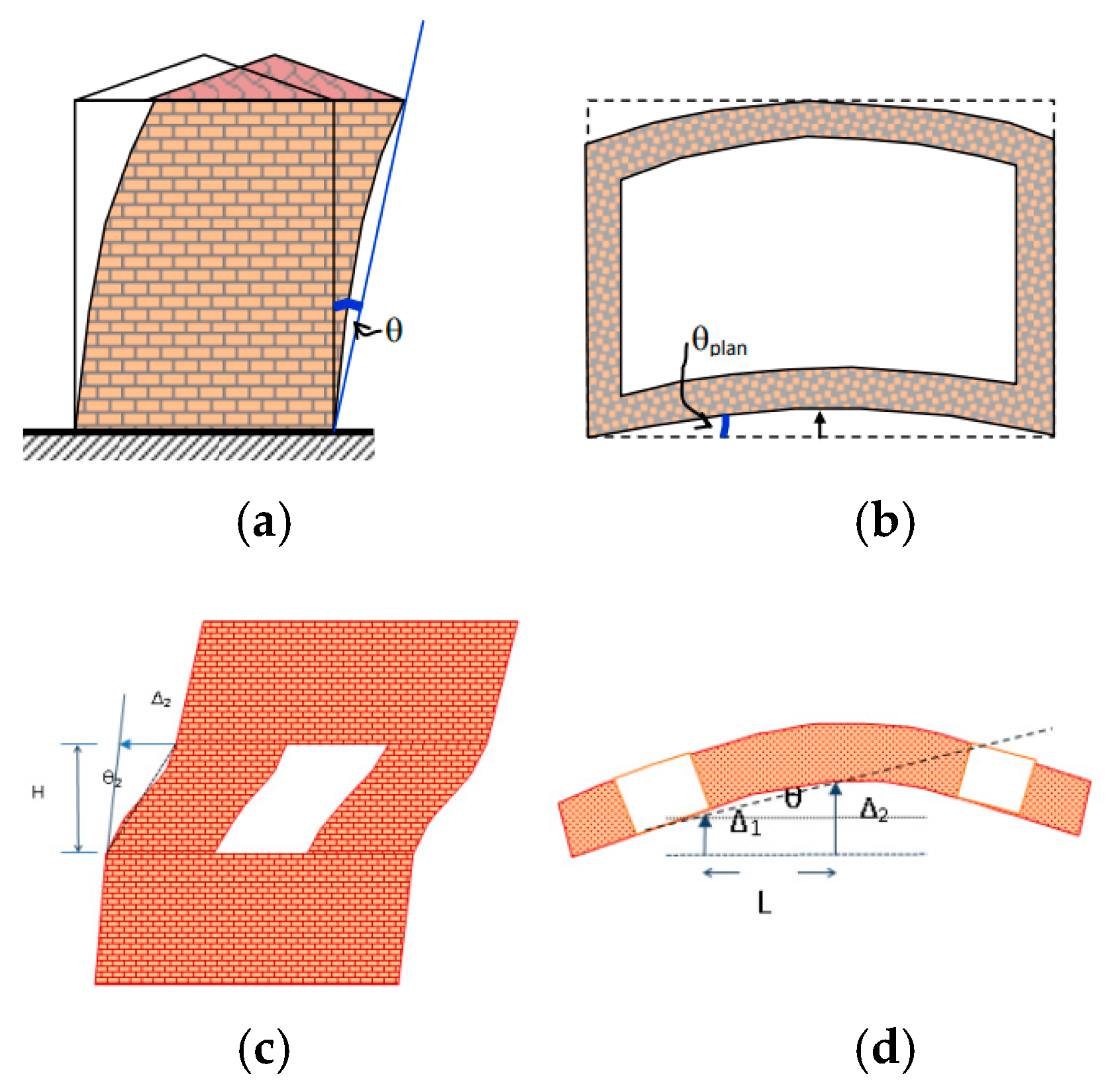
3.2.3. Failure Control for Out-of-Plane Wall Action

The yield resistance F_y of the element (wall or pier) is obtained for out-of-plane bending about a horizontal axis with axial force (Figure 23) as [2]

$$M_R=({\displaystyle \frac{1}{2}})\times l\times t^2\times {\sigma }_o\times (1-{\displaystyle \frac{{\sigma }_o}{f_{mb,c}}})$$

where

${\sigma }_o=({\displaystyle \frac{{\rm N}}{l\times t}})$ is the average compressive stress due to axial action in the control cross-section.

l and t are the length and thickness of the cross-section

f_mb,c is the compressive strength of the masonry

In this case, of the out-of-plane bending moment about the vertical axis, the bending moment that the critical cross-section can take is estimated based on the corresponding tensile strength of the masonry:

$$M_{Rd,2}=\left({\displaystyle \frac{1}{6}}\right)\times \left(f_{md,t}\times t^2\times l\right)$$

where

ℓ and t are the length and thickness of the bent section of the element, respectively; in this case, ℓ corresponds to the height of the wall.

f_md,t the representative tensile strength of the masonry (equal to f_mt/γ_w).

Taking into account the wall support conditions, the resultant force V_f that stresses the wall in out-of-plane action is calculated from the ratio of the corresponding moment to the shear length of the wall, H_o, i.e., the distance from the critical section where the maximum moment is developed, to the point of zeroing of the moment (Figure 24).

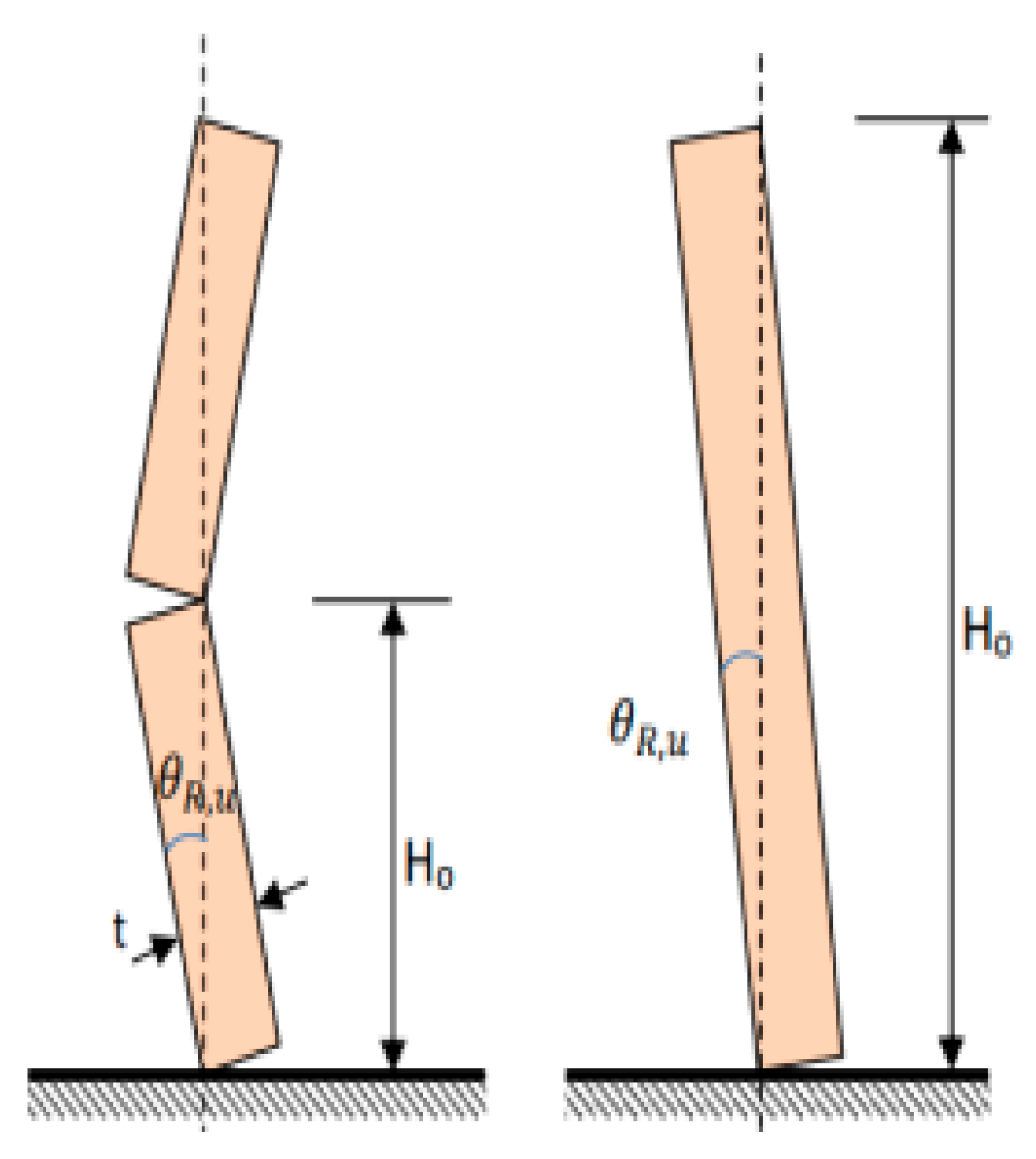
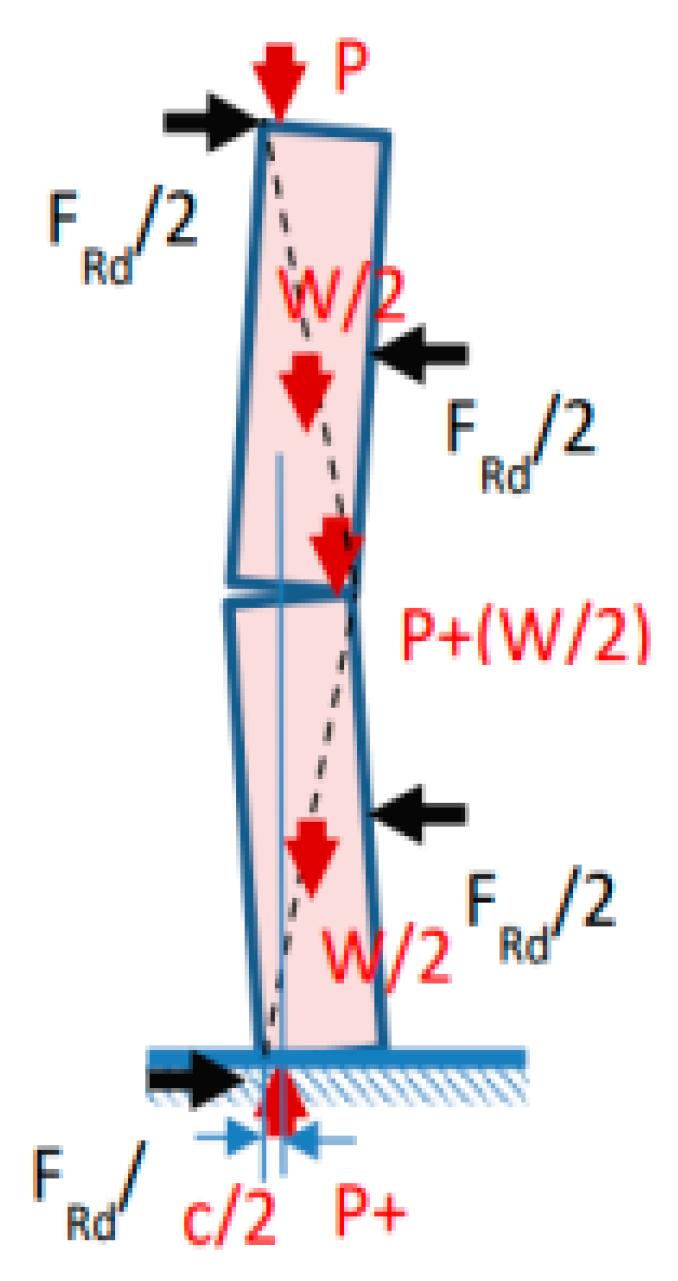
As F_Rd is defined, the resistance of the element against overturning, and it is calculated (Figure 25) as [2]

$$F_{Rd}=\lambda \times W\times \left(1+\Psi \right)\times {\displaystyle \frac{t_w}{H_o}};\Psi =2P/W$$

where

W is the weight

P is the vertical load on the top

λ = 2 for a wall with top and bottom, or left and right support (fixed support)

λ = 1 for all other cases (i.e., cantilever wall)

For the displacement-based assessment, the overturning rotation of a section of the wall that is bent about an axis, the limiting deformation (Figure 24) is taken as

$${\theta }_{Ru}=t/H_o$$

where H_o is the distance of the point of maximum displacement from the failure edge.

(a) For walls controlled by bending in out-of-plane action, the deformation capacity is defined as follows [2]:

The minimum of the values will be taken as the failure angle

$${\Theta }_{u,1}=0.003\times H_o\times t$$

$${\Theta }_{u,2}={\theta }_{Ru}\times (1-{\displaystyle \frac{V_f}{F_{Rd}}})$$

(b) For floors where there are rigid partitions, that is, where a floor shear is defined, the following limits can be used for the relative horizontal movement of a floor from load-bearing unreinforced masonry, based on the method of construction of the masonry:

-

0.7% for masonry with solid bricks;

-

0.45% for masonry with perforated bricks;

-

0.6% for masonry made of adobe.

For the yield strain θ_y, according to [2], the chord rotation angle for out-of-plane bending is θ_y = 0.002

The ductility index is defined as μ_θ = θ_u/θ_y, and if the available value exceeds a certain limit, the behavior is characterized as ductile, so its safety inequality will be expressed in terms of deformations δ.

3.2.4. Performance Levels

The performance levels of the load-bearing structure are defined as a function of the tolerable degree of damage as follows, specifically for the needs of the Greek code for interventions (KADET) [2]:

Performance level (A) “Limited damage”. The structure has only suffered minor damage. The structural elements retain a high degree of load-bearing capacity and stiffness.

Performance level (B), “Significant damage”. The structure has suffered significant damage, some of which may be severe, without local collapse, but it has residual load-bearing capacity and stiffness.

Performance level (C), “Impaired collapse”. The structure has suffered severe damage, most of which is beyond repair. The residual load-bearing capacity and stiffness are low, but the vertical elements are still able to carry the vertical loads.

The check about the performance level in terms of internal forces and deformations is carried out for individual structural members.

For performance level A, acceptance criteria are expressed in terms of elastic forces/deformations, and for levels B and C, performance checks for brittle members/and or failure modes are carried out in terms of forces, whereas checks for nominally ductile members the checks may be expressed preferably in terms of deformation [15].

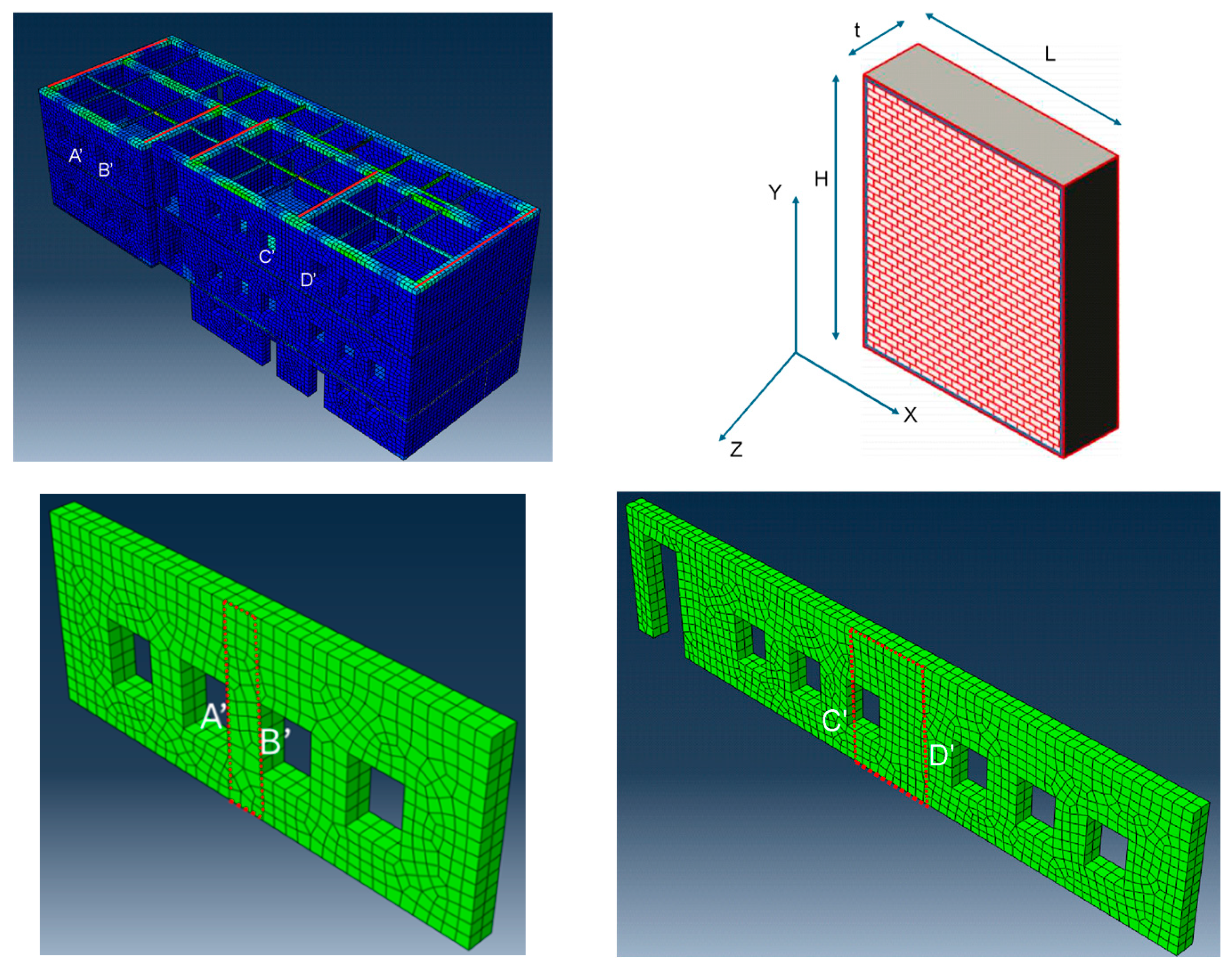
Based on the results of the spectral analysis of the final finite element model, control in terms of forces and deformations according to the KADET of selected piers (facade columns A’B’ and C’D’) is presented indicatively for selected pillars (Figure 26). The results are given in

Table A1. Control of strength to out-of-plane action.

Piers_Plane ΧΥ-Control of Strength to Out-of-Plane Action
Data	Pier C′D′		Pier A′B′
L (m) (Length)	2.930		0.930
L1 (length of the compression zone)	1.480		0.450
tw (m) (Thickness)	0.600		0.600
H (m) (Height)	4.400		4.400
Htotal (m) (Total height of wall)	9.040		9.040
Aw = l × t (m2) (Area of the pier wall cross-section)	1.758		0.558
p (kN/m3) (Density)	25.000		25.000
W = p × H × L × t (κΝ) (Weight)	193.380		61.380
Nroof (N22) (κΝ) (Vertical loads from roof)	76.134		31.344
Nsd = W + Nroof (κΝ) (axial load of the pier)	269.514		92.724
N33 (κΝ) (Horizontal load in plane)	11.385		1.762
Compressive design strength of masonry fmd,c (kN/m2)	3770.000		3770.000
Tensile design strength of masonry fmd,t (kN/m2)	300.000		300.000
Cohesive strength fvm0 = 0.1 (kN/m2)	100.000		100.000
Compressive strength of stone fb,c (kN/m2)	49,800.000		49,800.000
For shear strength
Flexural strength for bending parallel to the horizontal joints
considered inactive area (KADET) 6.5
σο = Nsd/(L × t)	153.307		166.171
MRx = 1/2(L × tw2 × σο(1 − σο/fcw))	77.566		26.591
Flexural strength for bending orthogonal to the horizontal joints
considered inactive area (KADET) 6.5
MRy = 1/6(fwt,d × tw2 × H) (cantilever walls)	79.200		79.200
MRy = 1/6(fwt,d × tw2 × H/2) (walls with fixed supports)	39.600		39.600
MR = min(MRx, MRy)	77.566		26.591
	39.600		26.591
Shear force for out-of-plane bending
Vf = MR/H (cantilever walls)	17.629		6.043
Vf = MR/H × 0.5 (walls with fixed supports)	35.257		12.087
Shearing force against overturning
Ψ = 2 × Nroof/No	0.787		1.021
fRd = 1 × W × (1 + Ψ)tw/Ho (cantilever walls)	47.134		16.918
FRd = 2 × W × (1 + Ψ)tw/Ho (walls with fixed supports)	188.536		67.673
Ved	11.385		1.762
Load-based assessment of masonry (Performance level A (DL))
Vf ≥ Ved ή Vf/Ved ≥ 1.0	1.548	Satisfied	3.429	Satisfied
	3.097	Satisfied	6.858	Satisfied
Displacement-based assessment of masonry (Performance level Β (SD))
For bending characterization
Drift capacity
θRu = tw/Ho (cantilever walls)	0.136		0.136
(walls with fixed supports)	0.068		0.068
θu1 = 0.003 × Ho/tw (cantilever walls)	0.022		0.022
(walls with fixed supports)	0.011		0.011
θu2 = ΘRu × (1 − Vf/FRd) (cantilever walls)	0.085		0.088
(walls with fixed supports)	0.055		0.056
θu = min (θu1, θu2) (cantilever walls)	0.022		0.022
(walls with fixed supports)	0.011	θu relative drift ratio in height	0.011	θu relative drift ratio in height
For shear characterization		0.000471819		0.000252963
θu = 0.6% (adobe masonry)	0.006	θplan relative drift ratio in plan	0.006	θplan relative drift ratio in plan
θy = 0.002	0.002	0.001743988	0.002	0.000665272
	0.002	Satisfied	0.002	Satisfied
Ductility index μθ = θu/θy	0.236	<1.0 elastic behavior	0.126	<1.0 elastic behavior

and

Table A2. Control of Strength to in-plane action.

Piers_Plane ΧΥ-Control of Strength to In-Plane Action
Data	Pier C′D′		Pier A′B′
L (m) (Length)	2.930		0.93
L1 (length of the compression zone)	1.480		0.45
tw (m) (Thickness)	0.600		0.6
H (m) (Height)	2.700		2.7
Htotal (m) (Total height of wall)	9.040		9.040000
Aw = l × t (m2) (Area of the pier wall cross-section)	1.758		0.5580
p (kN/m3) (Density)	25.000		25.0000
W = p × H × L × t (κΝ) (Weight)	118.665		37.6650
Nroof (N22) (κΝ) (Vertical loads from roof)	76.134		3.13 × 101
Nsd = W + Nroof (κΝ) (axial load of the pier)	194.799		69.0086
N11 (κΝ) (Horizontal load in plane)	73.537		57.4191
Compressive design strength of masonry fmd,c (kN/m2)	3770.000		3770.0000
Tensile design strength of masonry fmd,t (kN/m2)	300.000		300.0000
Cohesive strength fvm0 = 0.1 (kN/m2)	100.000		100.0000
Compressive strength of stone fb,c (kN/m2)	49,800.000		49,800.0000
Flexural strength of masonry MR = Nsd(1 − 1.15vsd)L/2	275.735		30.8784
νsd = Νsd/(L × t × fmd,c) (the normalized axial load of the pier)	0.029		0.0328
Eccentricity L/6 < ey = MR/Nsd < 0.5 L	1.415	Valid (no eccentricity)	0.4475	Valid (no eccentricity)
L/6	0.488		0.1550
L/2	1.465		0.4650
L′ = 3 × (0.5 − e/L) × L (length of the compression zone)	0.149		0.0526
Flexural capacity (strength under axial force and flexure)
Vf1 = MR/Ho (cantilever walls)	102.124		11.4365
Vf1 = MR/0.5 × Ho (walls with fixed supports)	204.248		22.8729
Shear strength of masonry
If Vvd > Vf1 (the behavior is controlled by flexure)			Valid
fvd,t = (fmd,t × (fmd,t + vsd fmd,c))0.5 (associated with diagonal tension cracking)	351.059		356.5128
fvd,s = fvm0 + 0.4 × Nsd/(L′ × t) < 0.065 × fb,c (associated with sliding)	974.203		974.2029
0.065 × fb,c	3237.000		3237.0000
Vvd,t = L × t × fvd,t Dagonal shear capacity	21,063.524		21,390.7691
Vvd,s = L′ × t × fvd,s Sliding shear capacity	86.833		30.7610
Vvd = min(Vvd,t, Vvd,s) Shear capacity	86.833		30.7610
If Vf > Vvd, behavior is controlled by shear		Satisfied (walls with fixed supports)
Ved	73.537		57.4191
Load-based assessment of masonry (Performance level A (DL))
Vf ≥ Ved or Vf/Ved ≥ 1.0	1.389	Satisfied (cantilever walls)
	2.777	Satisfied (walls with fixed supports)
Displacement-based assessment of masonry (Performance level Β (SD))
If Vf < Vvd critical failure mode is flexural failure
θu = 0.008 × Ho/L (Drift capacity- Cantilever walls)	0.007		0.0232
θu = 0.008 × Ho × 0.5/L (Drift capacity—walls with fixed supports)	0.004		0.0116
If Vf > Vvd critical failure mode is shear failure		Valid		Valid
θu = 0.004	0.004	0.001234	0.0040	0.0013
		Satisfied		Satisfied
θy	0.002		0.0015
Ductility index μθ = θu/θy	0.823	<1.0 elastic behavior	0.8845	<1.0 elastic behavior

(see “Appendix A”), where for these two piers, the performance level A and B control is presented.

In general, for the walls and piers of the floor on which the control was carried out, cover the deformation check (performance level B). The control in terms of forces (performance level A) is satisfied for all the piers for in-plane behavior and for some of them for out-of-plane behavior. The control in terms of deformation (performance level B) is satisfied for all the piers and the walls for both in-plane and out-of-plane behavior. This is critical to the selection of interventions.

4. Discussion and Conclusions

This study presented a comprehensive seismic assessment and restoration strategy for the two-storey historical masonry school building in Thrapsano, Crete, which suffered significant damage due to the September 2021 earthquake. This research employed a combination of field surveys, material characterization, finite element modeling, and structural analysis to evaluate the building’s pathology and propose effective retrofitting interventions.

Key findings indicate that the primary structural deficiencies were attributed to the absence of a rigid diaphragm at the roof level and the inadequate connection of transverse walls, which led to significant cracking and wall failure. Finite element simulations confirmed that the proposed strengthening measures, including masonry grouting, the introduction of reinforced concrete ties, and the addition of a metal diaphragm on the roof level of the first floor, significantly improved the seismic behavior of the structure. Comparison of stress and drift violations without and with the proposed intervention demonstrates the effectiveness of the intervention.

The proposed restoration approach aligns with Eurocodes 6 and 8 as well as the Greek KADET guidelines, ensuring structural safety while preserving the building’s historical authenticity. The performance-based assessment demonstrated that the reinforced structure meets modern seismic safety standards, achieving an acceptable performance level under in-plane and out-of-plane actions.

This case study provides a framework for the seismic strengthening of unreinforced masonry heritage structures, highlighting the importance of tailored interventions that respect the architectural and historical significance of such buildings. Future research should focus on optimizing restoration methods, particularly through the use of sustainable and reversible materials that enhance structural performance while maintaining heritage integrity. Further optimization and comparison of alternatives is still possible and can be useful for more complicated structures where engineering intuition does not help much.

Consideration of more advanced, nonlinear finite element analysis under earthquake dynamic loadings is a topic of current research, provided that enough confidence in material and structural model data are available, which is not always the case for old structures. In this respect more detailed evaluation of drift limits based on detailed analysis, see, e.g., [27], the effect of cyclic loading [28], and fusion of results from multifidelity models [29], seems to be a viable alternative.

Additionally, advanced monitoring techniques, such as structural health monitoring systems with real-time data collection, should be explored to assess the long-term behavior of the reinforced structure under dynamic loading conditions, see, e.g., [30,31], and eventually replace heavy interventions, as soon as building regulations permit it.