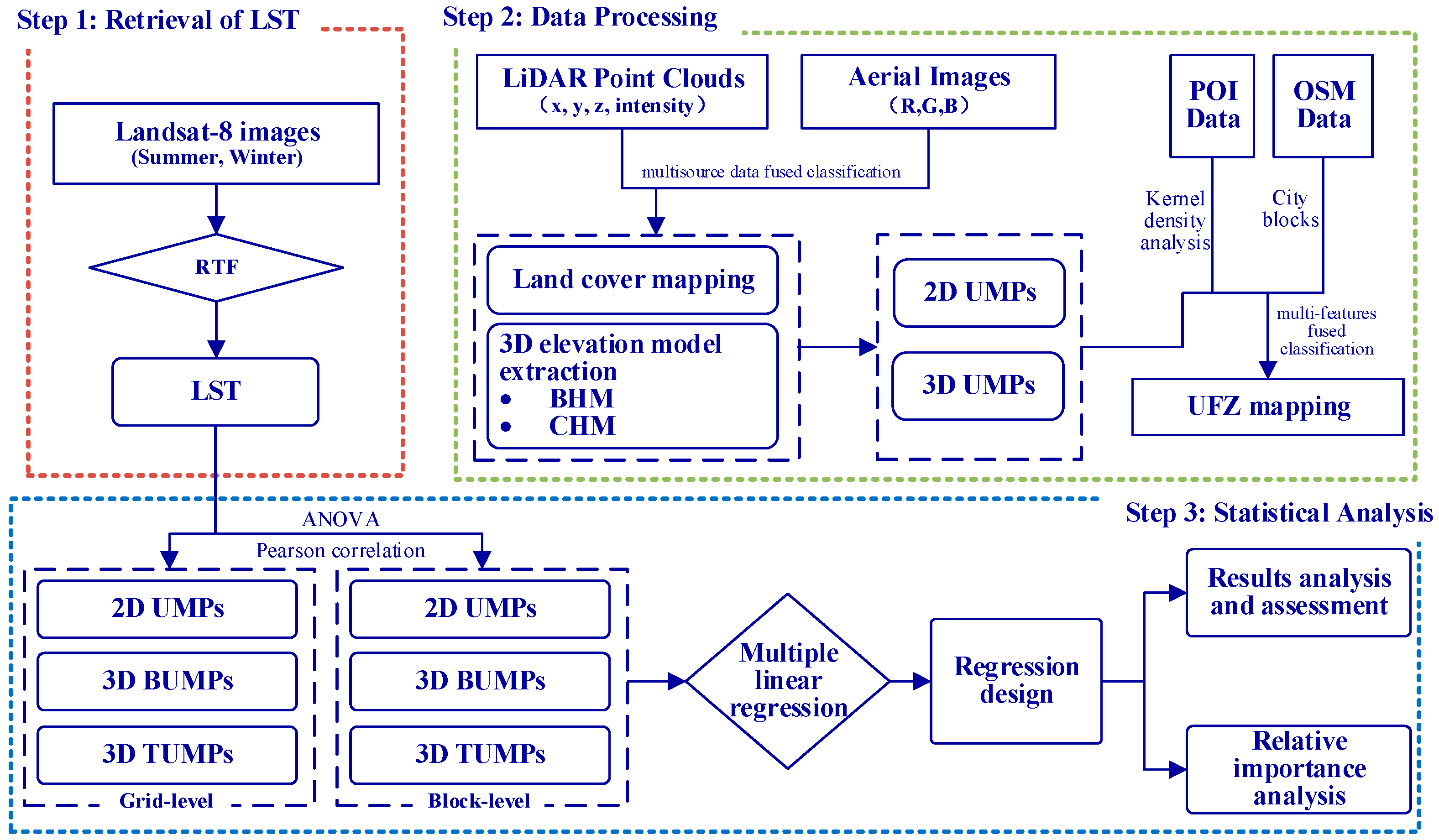
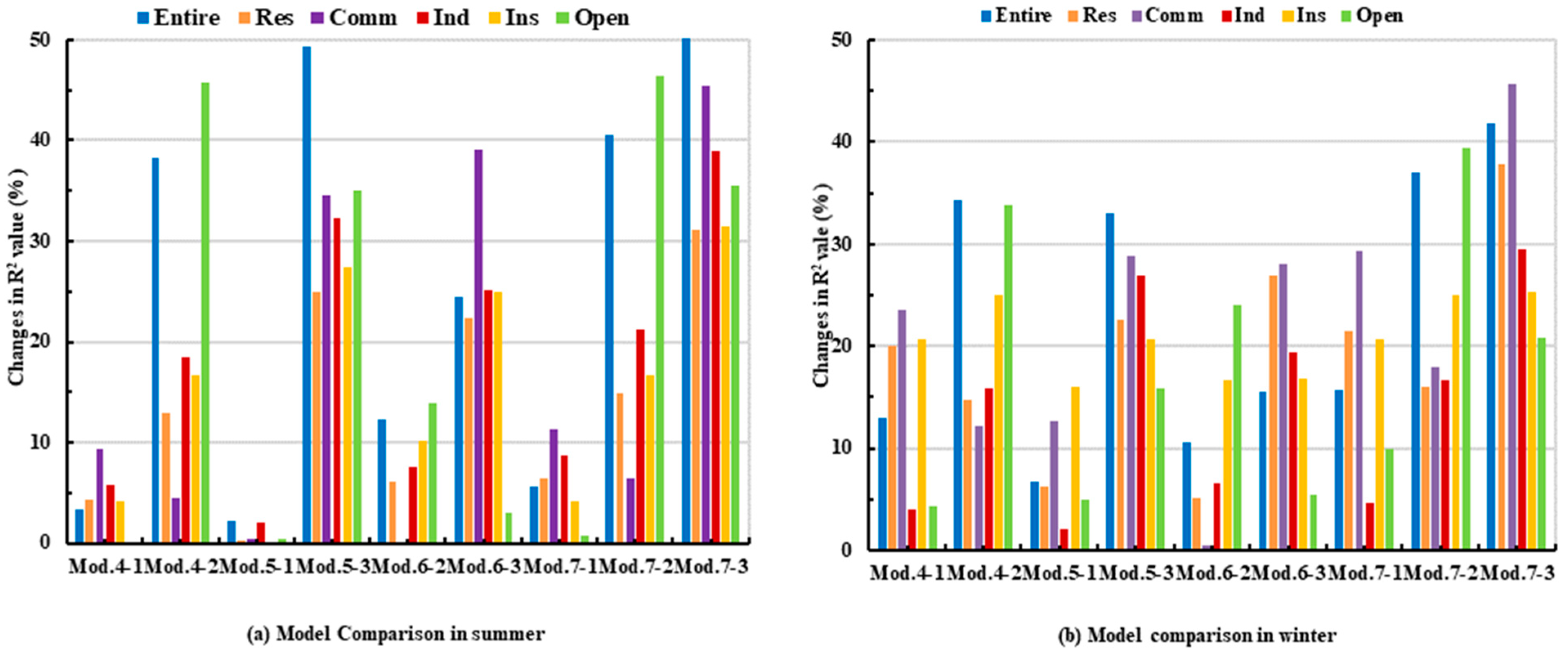
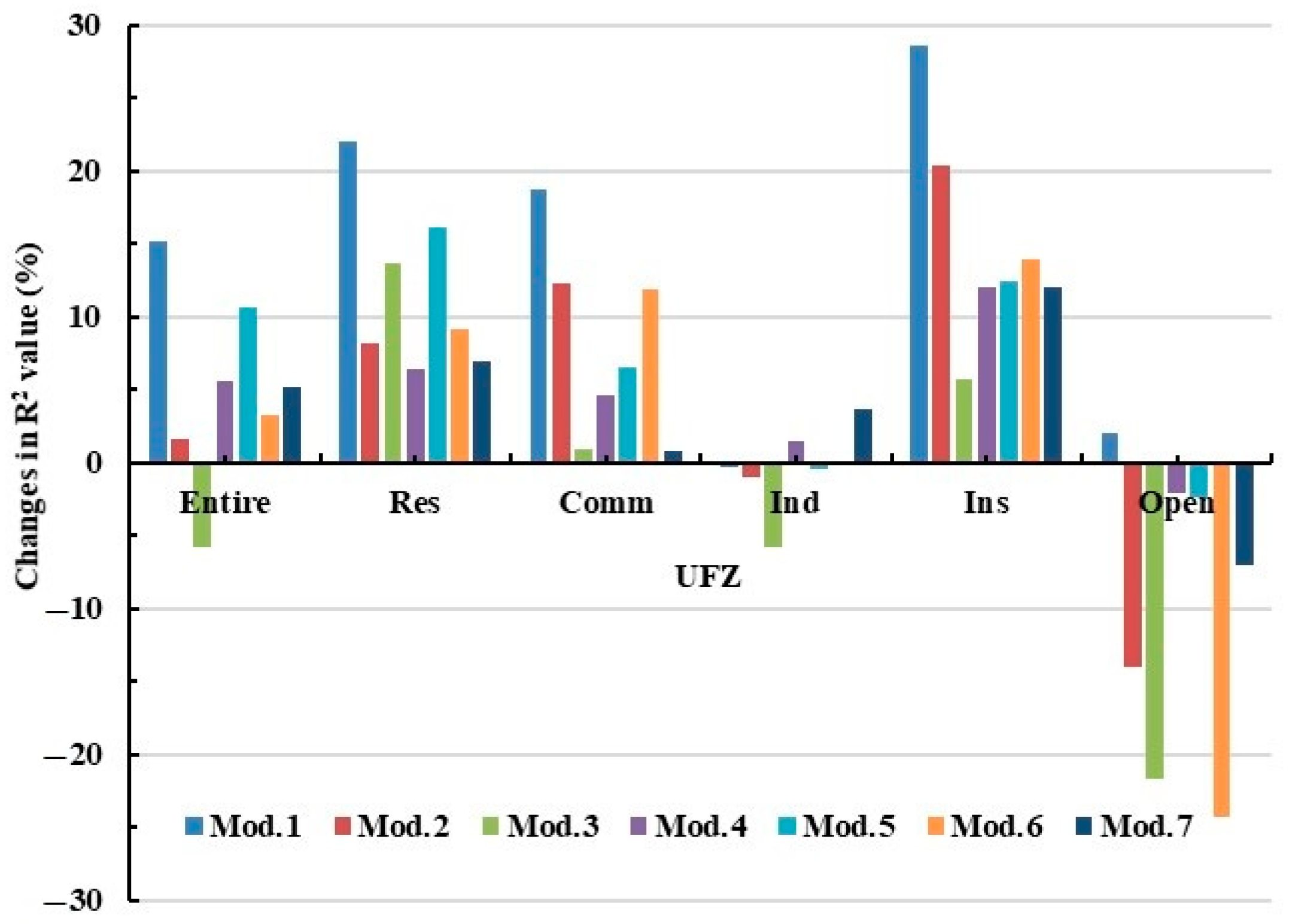
3.2.1. Pearson Correlation Analysis Results Between 2D UMPs and LST at Grid Level and Block Level
Table 5 presents a comprehensive overview of the Pearson correlation analysis conducted between 2D UMPs and LST at the grid level during summer and winter. The statistical results reveal that the majority of 2D UMPs exhibit a noteworthy correlation with LST. During summer, 2D UMPs related to building land and roads display a pronounced positive correlation with LST. Notably, PLAND_BL (r = 0.365,
p < 0.01), COHESION_BL (r = 0.305,
p < 0.01), and FRAC_AM_BL (r = 0.281,
p < 0.01) indicate significant positive correlations. Specifically, a higher proportion of building area, more complex building shapes, and tighter integration of buildings contribute substantially to an increase in LST. FRAC_AM_RD (r = 0.219,
p < 0.01) and COHESION_RD (r = 0.223,
p < 0.01) suggest that more complex road shapes and closer integration of roads are significantly associated with increased LST. Conversely, the 2D UMPs of cropland, grassland, woodland, and water show significant negative correlations with LST. Notably, PLAND_WL (r = −0.186,
p < 0.01), COHESION_WL (r = −0.13,
p < 0.01), PLAND_WT (r = −0.252,
p < 0.01), and PLAND_WT (r = −0.224,
p < 0.01) indicate that larger coverage areas of woodland or water and the closer integration of these patches are more likely to mitigate the rise in summer LST. Although cropland and grassland contribute to reducing LST, their Pearson correlation coefficients are relatively small, indicating a less pronounced effect compared to woodland and water. Additionally, most of the 2D UMPs of bare soil exhibit a significant positive correlation with LST to varying degrees. Although the r values are relatively small, bare soil still has a noticeable effect on increasing LST.
In winter, the 2D UMPs of building land and roads continue to demonstrate a notable warming effect on LST, albeit weaker compared to summer. Among these factors, COHESION_BL (r = 0.107, p < 0.01), FRAC_AM_RD (r = 0.13, p < 0.01), and COHESION_RD (r = 0.13, p < 0.01) exhibit relatively strong correlations, suggesting that a more cohesive or clustered arrangement of buildings or roads is more conducive to increasing LST in winter. The 2D UMPs of bare soil, cropland, and grassland exhibit a notable positive correlation with LST in winter. Specifically, the UMPs of cropland and grassland have a diametrically opposed influence on LST during winter compared to summer. This reversal is attributed to the substantial reduction in vegetation coverage in winter, which reveals bare ground in many cropland and grassland areas. Consequently, these areas absorb more heat during the day in winter. The impact of bare soil and grassland on LST is more significant than that of cropland, as evidenced by the high correlation coefficients such as COHESION_BS (r = 0.252, p < 0.01) and FRAC_AM_BS (r = 0.244, p < 0.01) for bare soil, and COHESION_GL (r = 0.291, p < 0.01) and FRAC_AM_GL (r = 0.288, p < 0.01) for grassland. This suggests that the intricate distribution and tighter clustering of bare soil or grassland patches play a more favorable role in regulating LST. In winter, woodland and water exhibit a significant negative correlation with LST. However, the absolute value of the correlation coefficient (r) for woodland is comparatively smaller, indicating a reduced cooling effect. This attenuation is attributed to the loss of foliage during winter, which allows for increased direct sunlight penetration and weakened transpiration, thereby reducing heat consumption. Conversely, the larger coverage area and tighter clustering of water, as indicated by PLAND_WT (r = −0.218, p < 0.01) and COHESION_WT (r = 0.191, p < 0.01), result in a more significant reduction in LST.
Table 6 shows the Pearson correlation analysis results between 2D UMPs and LST at the block level during summer and winter. Notably, a majority of the 2D UMPs exhibit a significant correlation with LST. Specifically, in summer, the 2D UMPs pertaining to building land and roads maintain a positive correlation with LST, highlighting UMPs such as PLAND_BL (r = 0.567,
p < 0.01) and ED_BL (r = 0.315,
p < 0.01) for building land and PLAND_RD (r = 0.221,
p < 0.01) and ED_RD (r = 0.194,
p < 0.01) for roads. These UMPs indicate that an increased coverage area and density of buildings or roads within a block are likely to contribute to a rise in LST. The 2D UMPs of cropland, grassland, woodland, and water all exhibit a distinct negative correlation with LST. Specifically, LSI_CL (r = −0.256,
p < 0.01) and PLAND_CL (r = −0.243,
p < 0.01) for cropland reveal that the expansion of cropland coverage area and its more dispersed distribution contribute to a reduction in LST. Additionally, LSI_GL (r = −0.244,
p < 0.01) and SHA_AM_GL (r = −0.159,
p < 0.01) for grassland suggest that a fragmented grassland distribution also favors a decrease in LST. Similarly, for woodland, PLAND_WL (r = −0.301,
p < 0.01), LSI_WL (r = −0.235,
p < 0.01), and SHA_AM_WL (r = −0.235,
p < 0.01) display a marked correlation with LST, indicating that a larger woodland coverage area and a more irregular shape effectively mitigate LST. Furthermore, LSI_WT (r = −0.413,
p < 0.01) and SHA_AM_WT (r = −0.389,
p < 0.01) for waterbodies highlight that a more irregular and complex distribution of water significantly enhances their ability to reduce LST. On the other hand, the FRAC_AM and ENN_MN of bare soil do not exhibit a significant correlation with LST at the 0.05 or 0.01 significance levels. However, their LSI, ED, and PD exhibit a strong negative correlation with LST, suggesting that a more fragmented distribution of bare soil is likely to contribute to a decrease in LST.
The influence of 2D UMPs on LST in building land undergoes a notable shift during winter. PLAND maintains a positive correlation, while PD, ED, LSI, and SHA_AM exhibit a negative correlation. Specifically, LSI_BL (r = −0.194, p < 0.01) and ED_BL (r = −0.188, p < 0.01) reveal that more fragmented and irregular building layouts can reduce LST. Conversely, the UMPs of roads have a significantly diminished impact on LST, with PD_RD (r = −0.146, p < 0.01) suggesting that a higher density of road patches in a neighborhood promotes faster heat dissipation, thereby effectively lowering LST. The UMPs of bare soil demonstrate a robust correlation with LST, where PLAND_BS (r = 0.361, p < 0.01) and SHA_AM_BS (r = 0.339, p < 0.01) suggest that a larger coverage area and more complex shape of bare soil in winter enhance its capacity to absorb heat, subsequently raising LST. In cropland, only ED, LSI, SHA_AM, FRAC_AM, and COHESION exhibit significant positive correlations, with ED_CL (r = 0.206, p < 0.01) and SHA_AM_CL (r = 0.166, p < 0.01) indicating that a larger number of cropland patches and more intricate shapes are conducive to increasing LST. In grassland, except for PLAND and PD, which exhibit significant positive correlations, other UMPs do not show a noteworthy relationship with LST. Notably, the 2D UMPs of woodland and water maintain a strong cooling effect in winter, with PLAND and ED remaining the most significant UMPs. This underscores that in winter, a greater coverage area of vegetation or water, along with a higher number of patches, is more effective in reducing LST.
3.2.2. Pearson Correlation Analysis Results Between 3D UMPs and LST at Grid Level and Block Level
Table 7 presents the results of a Pearson correlation analysis between 3D UMPs and LST at the grid level in both summer and winter. Our findings reveal that a significant correlation exists between most 3D BUMPs and 3D TUMPs with LST, regardless of the season. Specifically, in summer, with the exception of BSC, which shows no significant correlation with LST, all other UMPs exhibit significant correlations. Among these, BSVF (r = −0.326,
p < 0.01) indicates that an increase in the open space around buildings during summer favors a decrease in LST. Additionally, PBSA (r = 0.31,
p < 0.01), PBV (r = 0.335,
p < 0.01), and BED (r = 0.31,
p < 0.01) suggest that a larger surface area and volume proportion of buildings in 3D space are conducive to an increase in LST. Further, BSA (r = 0.231,
p < 0.01) and BVR (r = 0.225,
p < 0.01) also exhibit a strong positive correlation with LST, indicating that the surface area and volume of buildings positively impact LST. Regarding the height variation in buildings, BMH (r = 0.215,
p < 0.01), BMaH (r = 0.201,
p < 0.01), and BHR (r = 0.187,
p < 0.01) demonstrate that taller buildings with a greater difference in height are more effective at absorbing solar energy, thereby leading to an increase in LST. Meanwhile, BHV (r = 0.154,
p < 0.01) and NBHV (r = 0.207,
p < 0.01) indicate that a more dispersed height distribution of buildings tends to enhance LST. However, the r values of BHW and BHL, although slightly smaller than other BUMPs, still suggest a positive correlation with LST improvement. However, in winter, the influence of 3D BUMPs on LST is significantly diminished. Specifically, PBV (r = 0.13,
p < 0.01) and BED (r = 0.109,
p < 0.01) exhibit a relatively strong correlation with LST, suggesting that an increased volume proportion and Edge Density of buildings in 3D space contribute positively to the rise in LST. Conversely, the height variation in buildings, including BMaH, BHV, NBHV, and BHR, demonstrates a negative correlation with LST. This indicates that taller buildings with greater height differences and a more unstable height distribution are more effective at reducing heat accumulation and accelerating the convection of cold air in winter, ultimately leading to a decrease in LST. Furthermore, BHW, BHL, BLSI, and BSVF also exhibit a negative correlation with LST, further indicating that taller buildings with more complex shapes in 3D space and wider surrounding views are more conducive to the timely dissipation of LST in winter, thereby reducing heat accumulation and lowering LST. In contrast, BSA and BSC do not show a significant correlation with winter LST at the grid level.
Based on the Pearson correlation analysis results of 3D TUMPs and LST in summer, it is evident that all TUMPs except TSC exhibit a significant negative correlation with LST. Specifically, PTSA (r = −0.189, p < 0.01), PTV (r = −0.19, p < 0.01), TED (r = −0.183, p < 0.01), and TLSI (r = −0.155, p < 0.01) suggest that the larger the proportion of Tree Surface Area and Volume in 3D space, and the more irregular and fragmented the shape, the more effective they are in reducing LST. This is attributed to the fact that the greater the proportion of Tree Surface Area and Volume in 3D space, the higher the vegetation coverage, making them more resistant to direct sunlight during summer days. Additionally, the more irregular and fragmented shapes further contribute to reducing LST. Similarly, TSA (r = −0.182, p < 0.01) and TV (r = −0.161, p < 0.01) also exhibit a strong negative correlation. Moreover, the height variation in trees, including TMH (r = −0.1, p < 0.01), TMAH (r = −0.103, p < 0.01), THV (r = −0.1, p < 0.01), NTHV (r = −0.1, p < 0.01), and THR (r = −0.104, p < 0.01), indicates that taller trees, greater height variation between trees, and a more unstable height distribution are all beneficial for reducing LST. This is because while tree coverage effectively resists direct sunlight, height variation enhances air circulation, further accelerating the dissipation of LST. In winter, despite the fact that all TUMPs, apart from TSC, maintain a significant correlation with LST at the 0.01 level, the magnitude of their influence on LST is notably diminished compared to summer. This suggests that while the parameters retain a certain degree of relevance, their efficacy in modulating LST during the colder season is substantially reduced.
Table 8 presents the comprehensive findings of the Pearson correlation analysis conducted to examine the relationship between 3D UMPs and LST at the block level, spanning both summer and winter. The results highlight a significant correlation between the majority of 3D UMPs and LST. More precisely, in summer, PBSA (r = 0.384,
p < 0.01), BED (r = 0.374,
p < 0.01), and BLSI (r = 0.374,
p < 0.01) emerge as pivotal factors exerting a considerable impact on LST. This underscores the significance of the buildings’ surface area ratio in the 3D space, their fragmented distribution, and the complexity of their shapes in contributing significantly to the rise in LST at the block level during summer. The influence of PBV (r = 0.068,
p < 0.01) has notably diminished. Conversely, BSA (r = 0.178,
p < 0.01) and BVR (r = 0.253,
p < 0.01) continue to exhibit a robust positive correlation with LST. As we delve into the effect of variations in building height, BMH (r = 0.208,
p < 0.01), BMaH (r = 0.117,
p < 0.01), and BHR (r = 0.117,
p < 0.01) suggest that a rise in building height and its heterogeneity tend to exacerbate the increase in LST. While BHV (r = 0.083,
p < 0.01) and NBHV (r = 0.021,
p < 0.01) still have a positive correlation, their impact on LST is substantially less significant. Furthermore, BHL (r = 0.295,
p < 0.01) and FAI (r = 0.254,
p < 0.01) indicate that a larger frontal area of buildings enhances solar energy absorption, thereby contributing significantly to the rise in LST. In contrast, BSVF (r = −0.365,
p < 0.01) shows a marked negative correlation with LST, implying that a more open visual perspective of buildings in a block, coupled with less building aggregation, facilitates faster air convection and significantly mitigates the increase in LST. Notably, BHW and BSC do not demonstrate a significant correlation with LST. During winter, the variation in building height exhibits a stronger correlation with LST compared to other BUMPs. Specifically, BMH (r = −0.223,
p < 0.01), BMaH (r = −0.278,
p < 0.01), BHR (r = −0.278,
p < 0.01), BHV (r = −0.315,
p < 0.01), and NBHV (r = −0.235,
p < 0.01) all indicate that taller buildings, greater height differences, and uneven height distribution enhance the convection of cold air during the day in winter. Even if some solar heat is absorbed, it is quickly dissipated. Additionally, the taller the buildings, the more shadows they cast, blocking solar energy and leading to a decrease in LST. On the other hand, BSVF (r = 0.289,
p < 0.01) exhibits a positive correlation with LST in winter. Meanwhile, PBSA (r = −0.186,
p < 0.01), PBV (r = −0.223,
p < 0.01), BSA (r = −0.167,
p < 0.01), and FAI (r = −0.163,
p < 0.01) suggest that larger surface and frontal areas, as well as a greater proportion of surface area and volume in 3D space, block more solar energy from reaching the interiors of buildings. This, coupled with the smaller solar elevation angle in the northern hemisphere during the daytime in winter, contributes to a reduction in LST within the block. BV, BHL, BED, and BLSI also demonstrate a negative correlation with LST, albeit to a lesser extent. Lastly, BSC does not exhibit a significant correlation with LST.
For 3D TMUPs, during summer, PTV (r = −0.315,
p < 0.01), PTSA (r = −0.286,
p < 0.01), TSA (r = −0.271,
p < 0.01), and TV (r = −0.262,
p < 0.01) show a strong negative correlation with LST. This signifies that the greater the surface area and volume of trees in the block level, along with their larger proportion in 3D space, the more effective they are at blocking direct solar heat. Furthermore, the transpiration process of vegetation accelerates the dissipation of heat. TLSI (r = −0.212,
p < 0.01) suggests that a more irregular distribution of trees in 3D space is favorable for reducing LST. Furthermore, the parameters TMH, TMaH, and THR, as well as the height variations THV and NTHV, also exhibit a strong negative correlation with LST. This indicates that taller trees and a more uneven distribution of tree heights at the block level result in a larger surface area blocking direct sunlight. Additionally, the uneven distribution of tree heights enhances air circulation, further accelerating the dissipation of heat. Based on the Pearson correlation analysis between 3D TUMPs and LST during winter, certain parameters exhibit a greater influence on LST compared to summer, contrasting with the grid-level findings. Specifically, TMH (r = −0.437,
p < 0.01), THV (r = −0.427,
p < 0.01), and TLSI (r = −0.429,
p < 0.01) have the most significant impact on LST. This is attributed to the change in solar elevation angle during winter, which significantly reduces the energy reaching the ground in the northern hemisphere. Trees with a higher average height, more unstable height variation, and a more irregular distribution are more likely to block the weakened winter solar energy, resulting in a shadow effect that reduces LST [
55]. Additionally, TMaH (r = −0.354,
p < 0.01), THR (r = −0.35,
p < 0.01), PTSA (r = −0.354,
p < 0.01), and PTV (r = −0.308,
p < 0.01) also demonstrate a strong negative correlation with LST, indicating that taller trees, greater height differences, and a larger proportion of surface area and volume in 3D space are more likely to a lower LST in winter. In contrast, NTHV, TSA, and TV have a relatively weaker impact on LST, yet they still exhibit a significant negative correlation.