Sulphoaluminate-Aluminate Cement-Based Composites: Mechanical Behaviors and Negative Poisson’s Ratio Mechanism Under Static Loads
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Design and Preparation
2.2.1. Mixing Design
2.2.2. Preparation and Maintenance
2.3. Test Method
2.3.1. Mechanical Property Test
2.3.2. Deformation Behavior Test
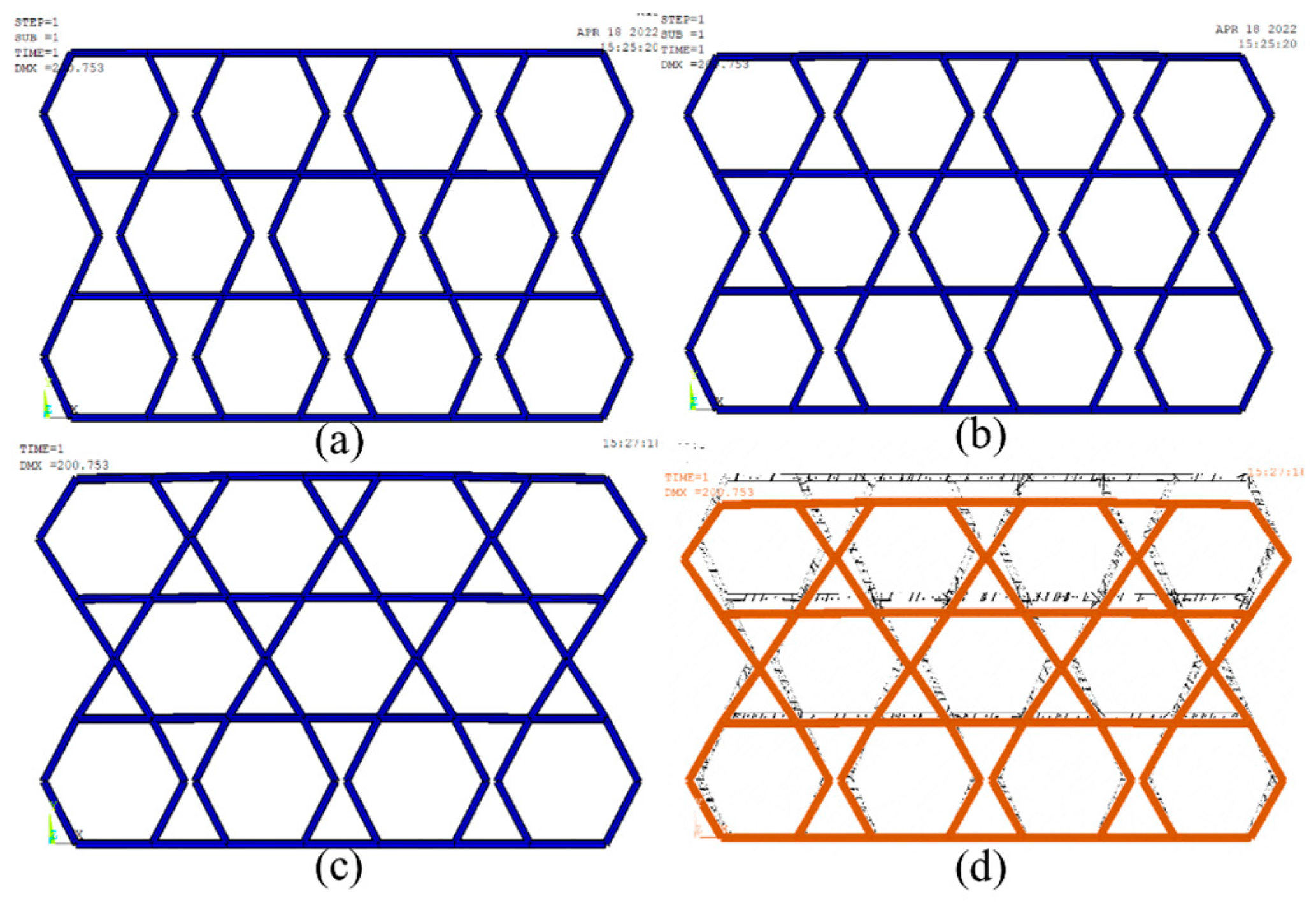
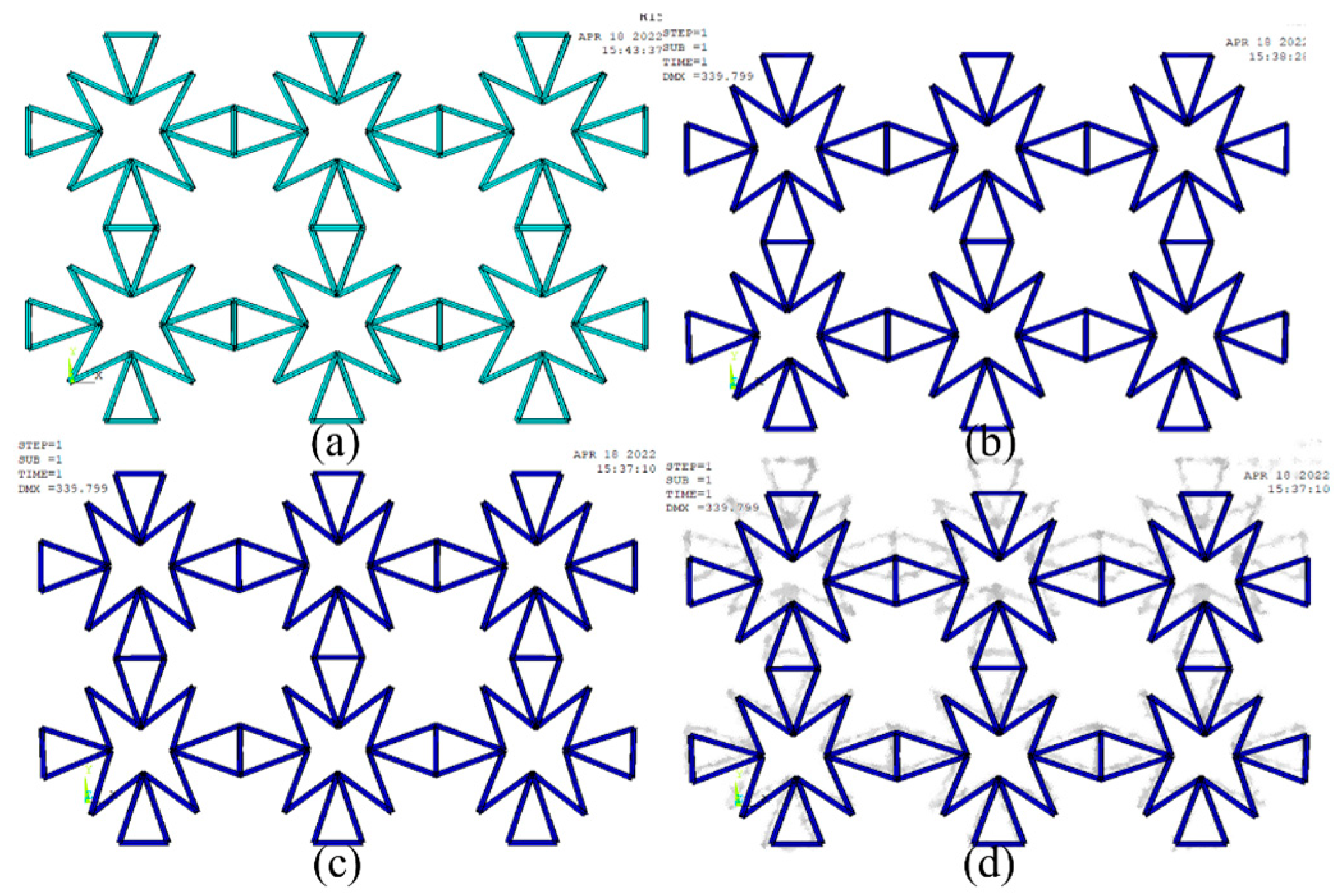
2.3.3. Finite Element Simulation
2.3.4. Microstructure Test
3. Results and Discussion
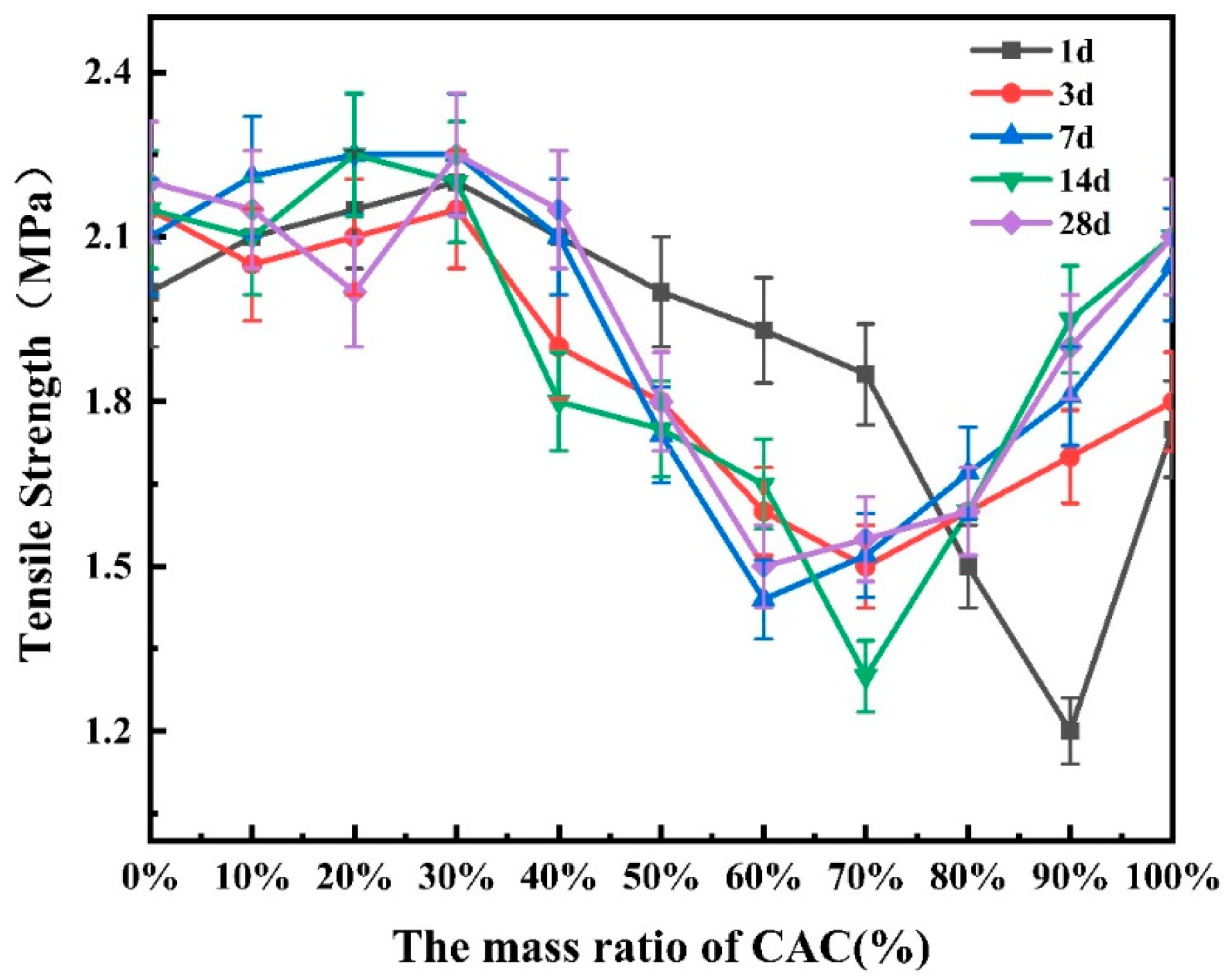
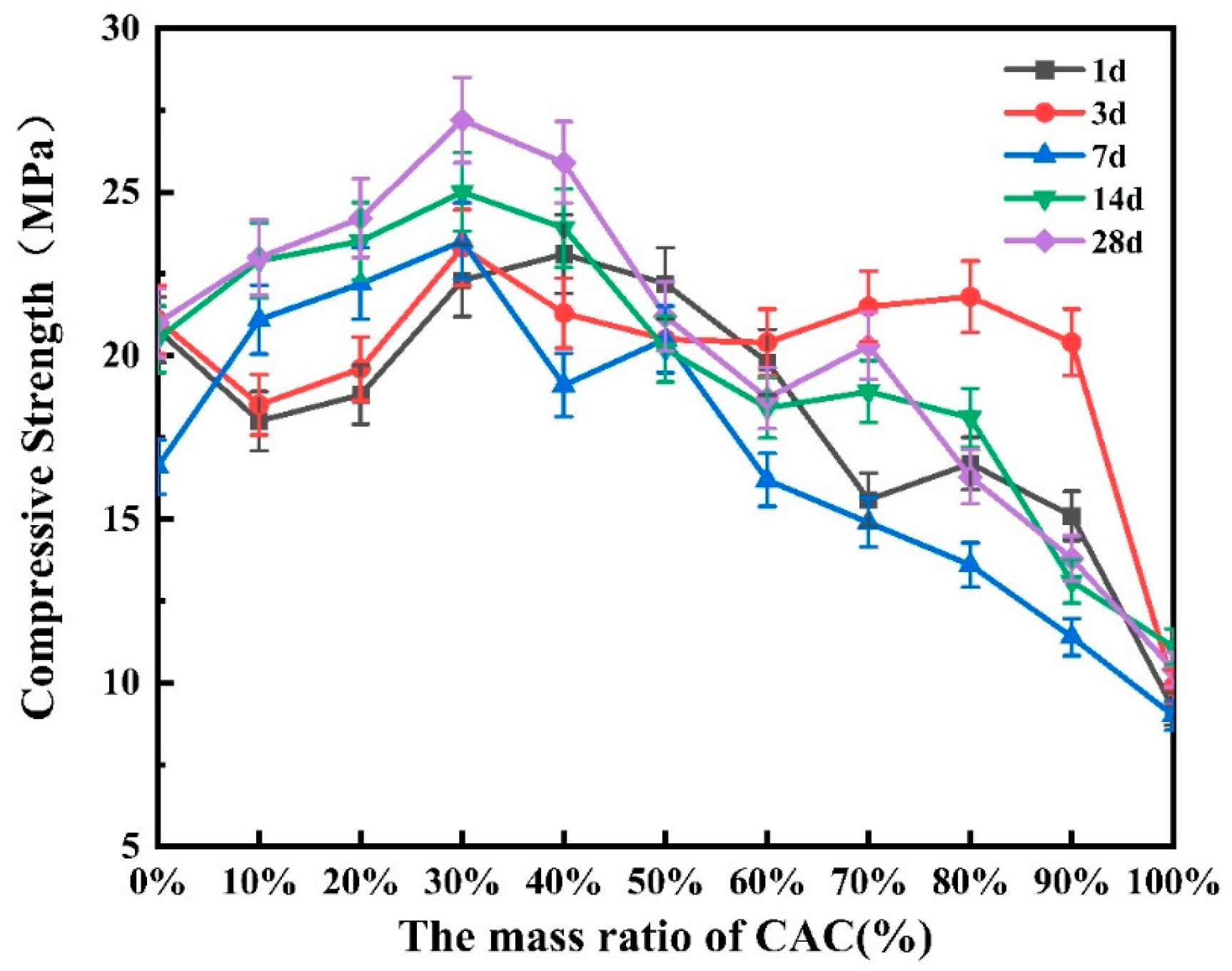
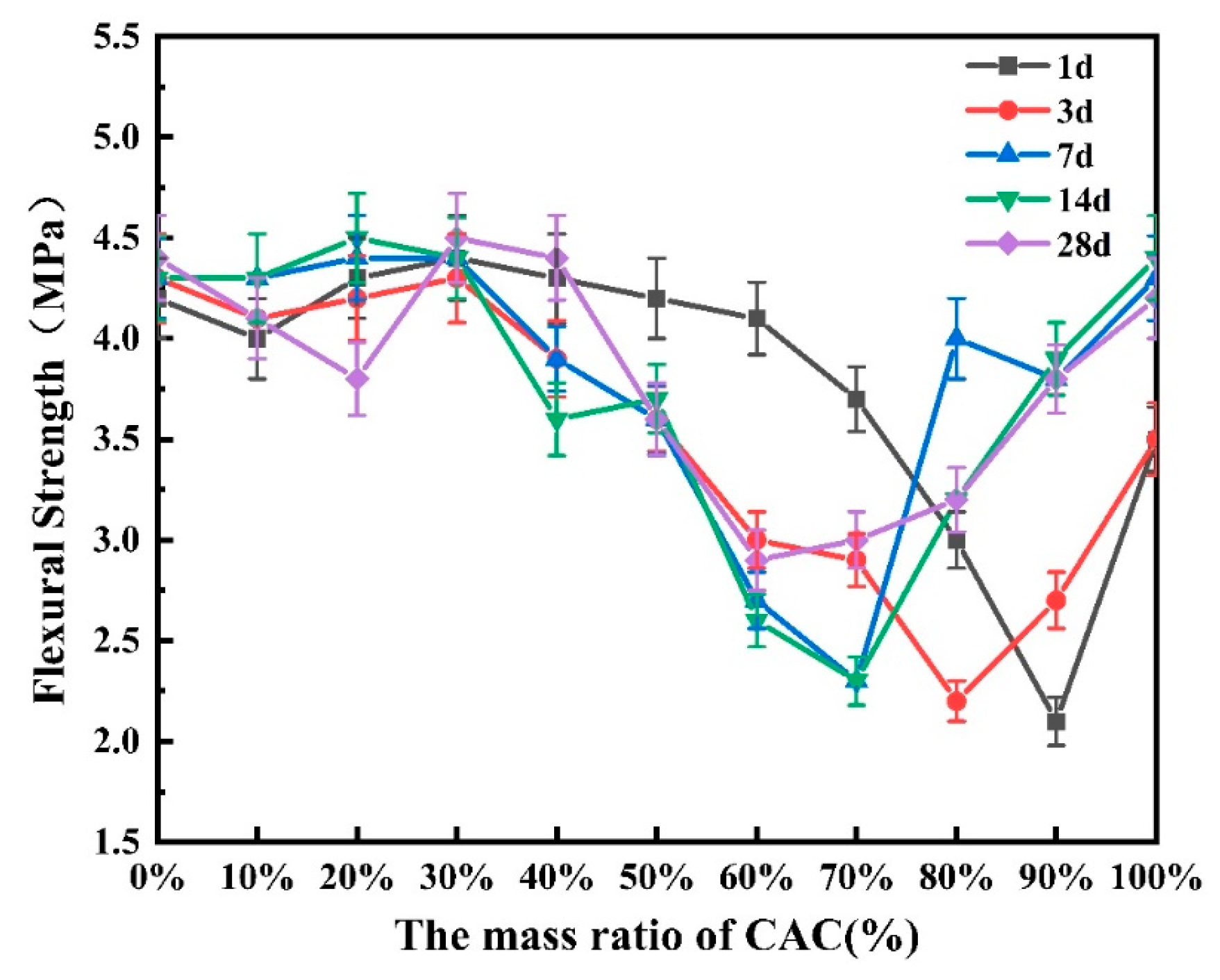
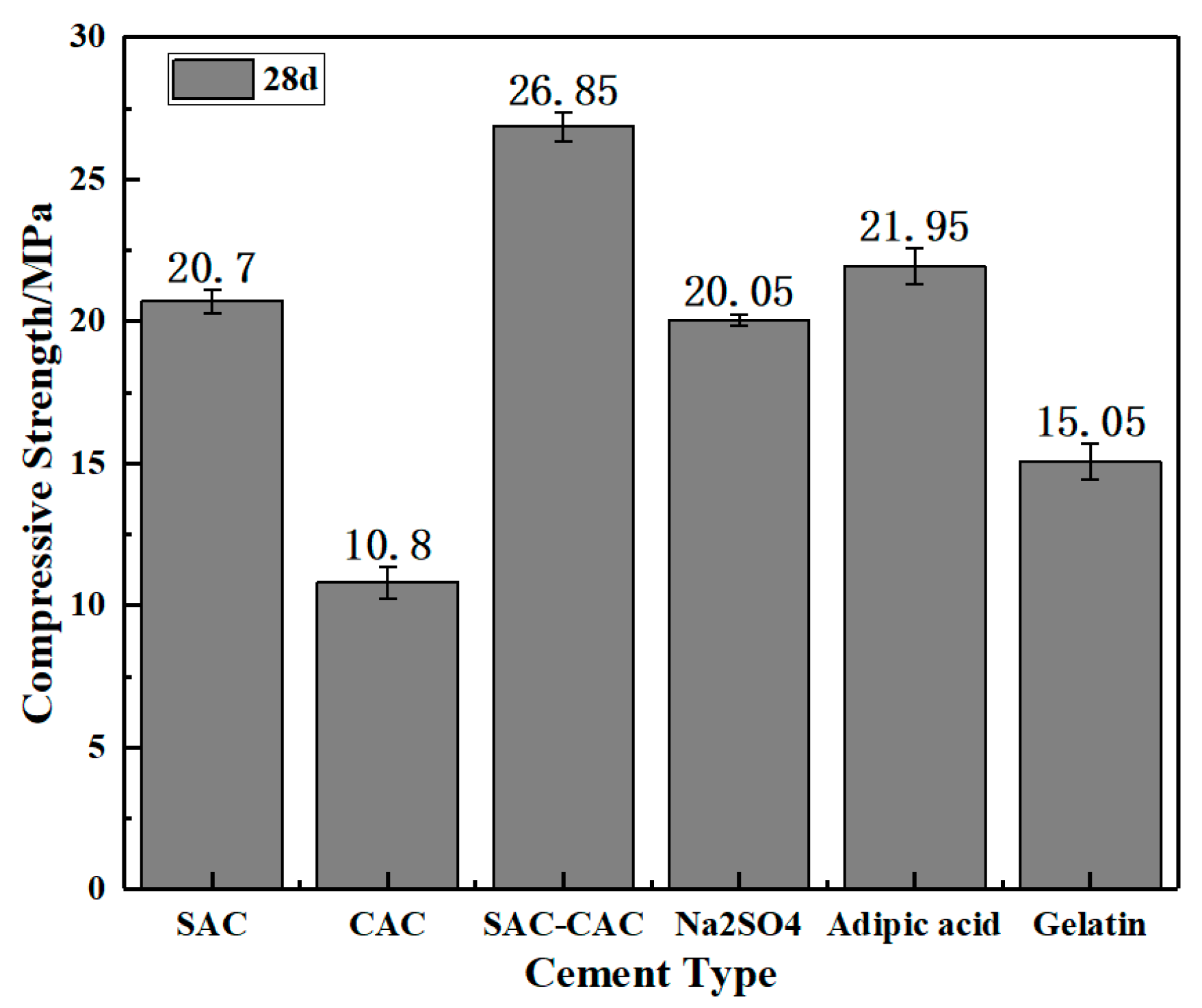
3.1. Mechanical Properties of SAC-CAC Composite Cement Under Different Proportions
3.2. Mechanical Properties of Composite Cement Under Different Crystal Modifiers
3.2.1. Mechanical Properties
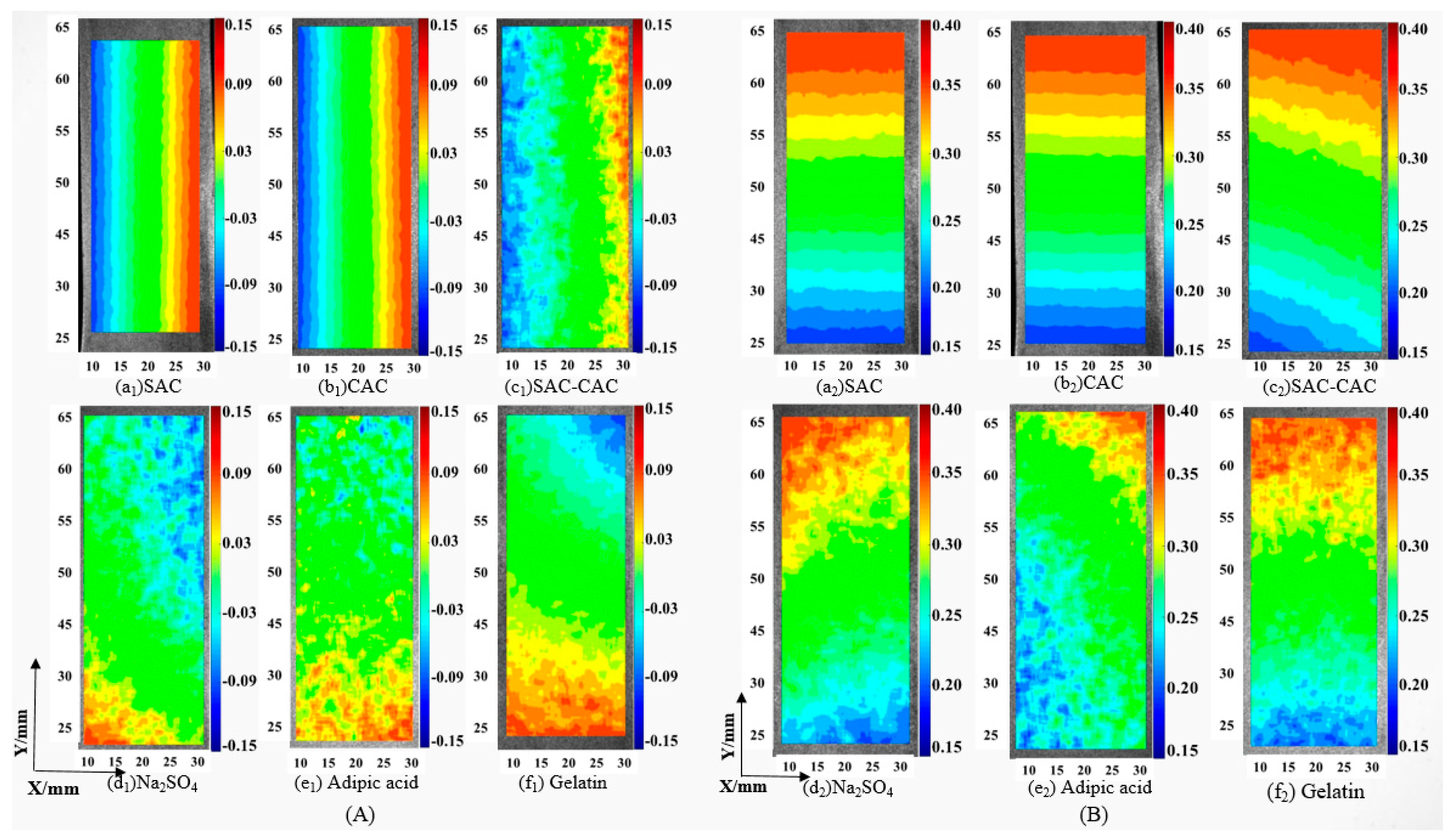
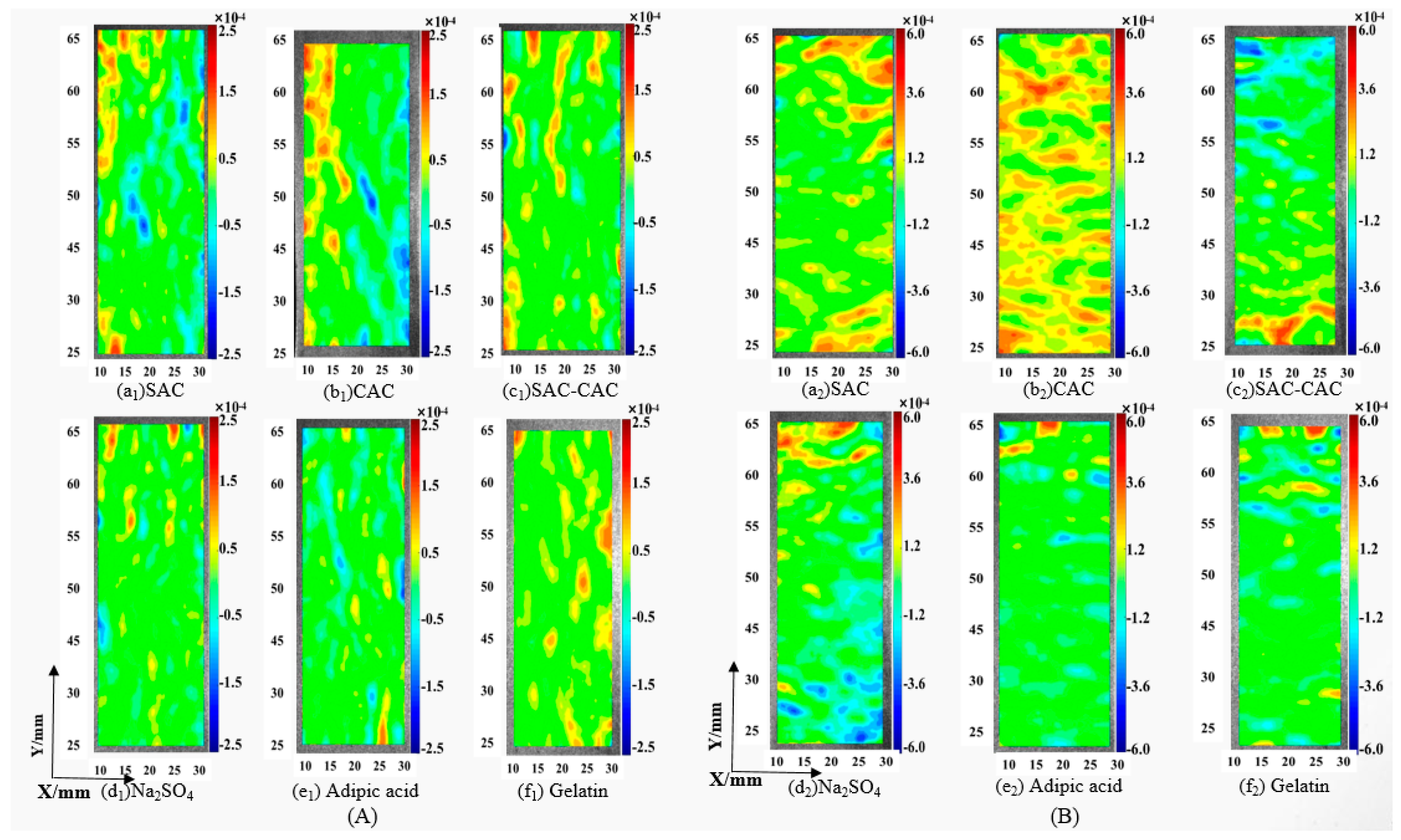
3.2.2. Deformation Behavior
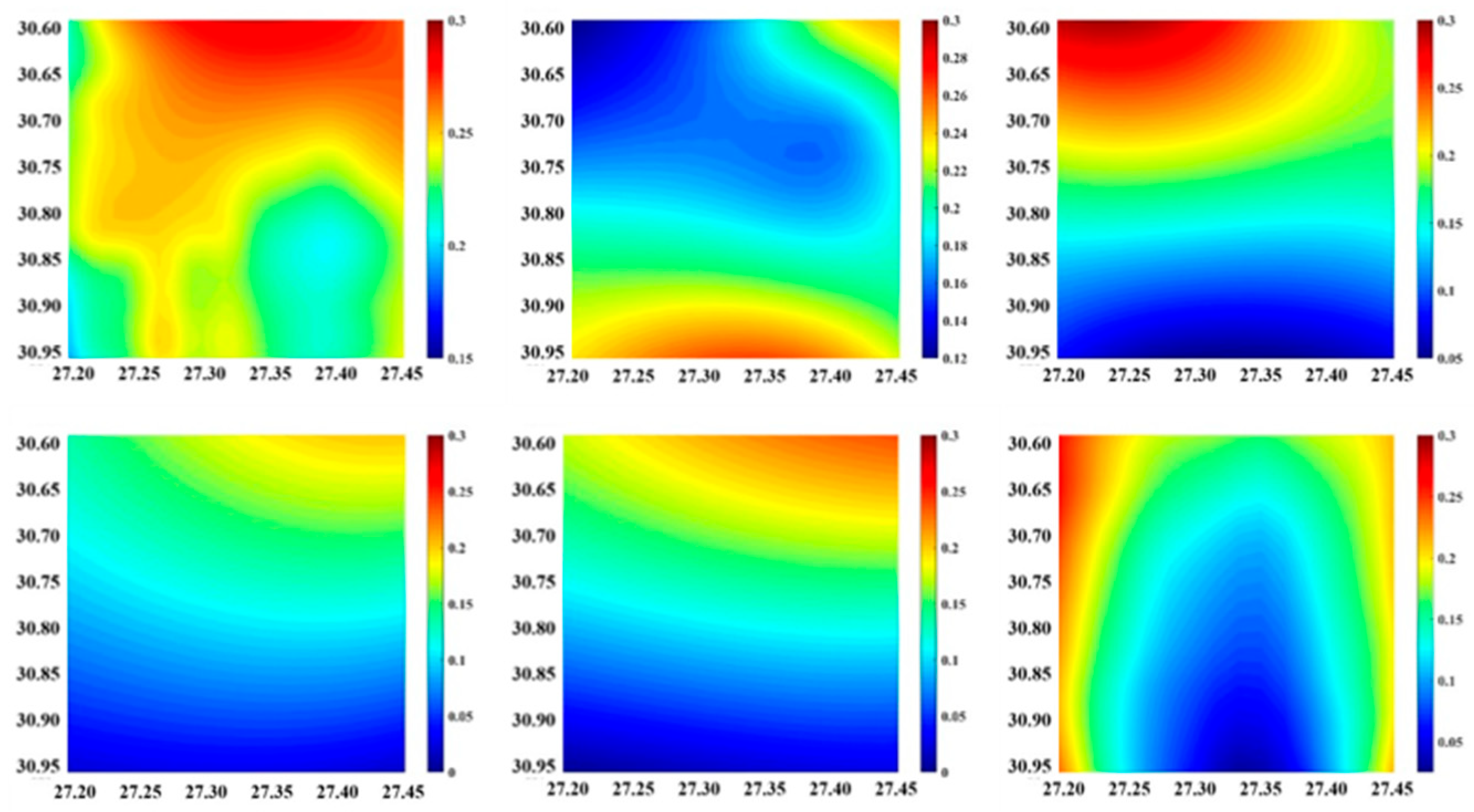
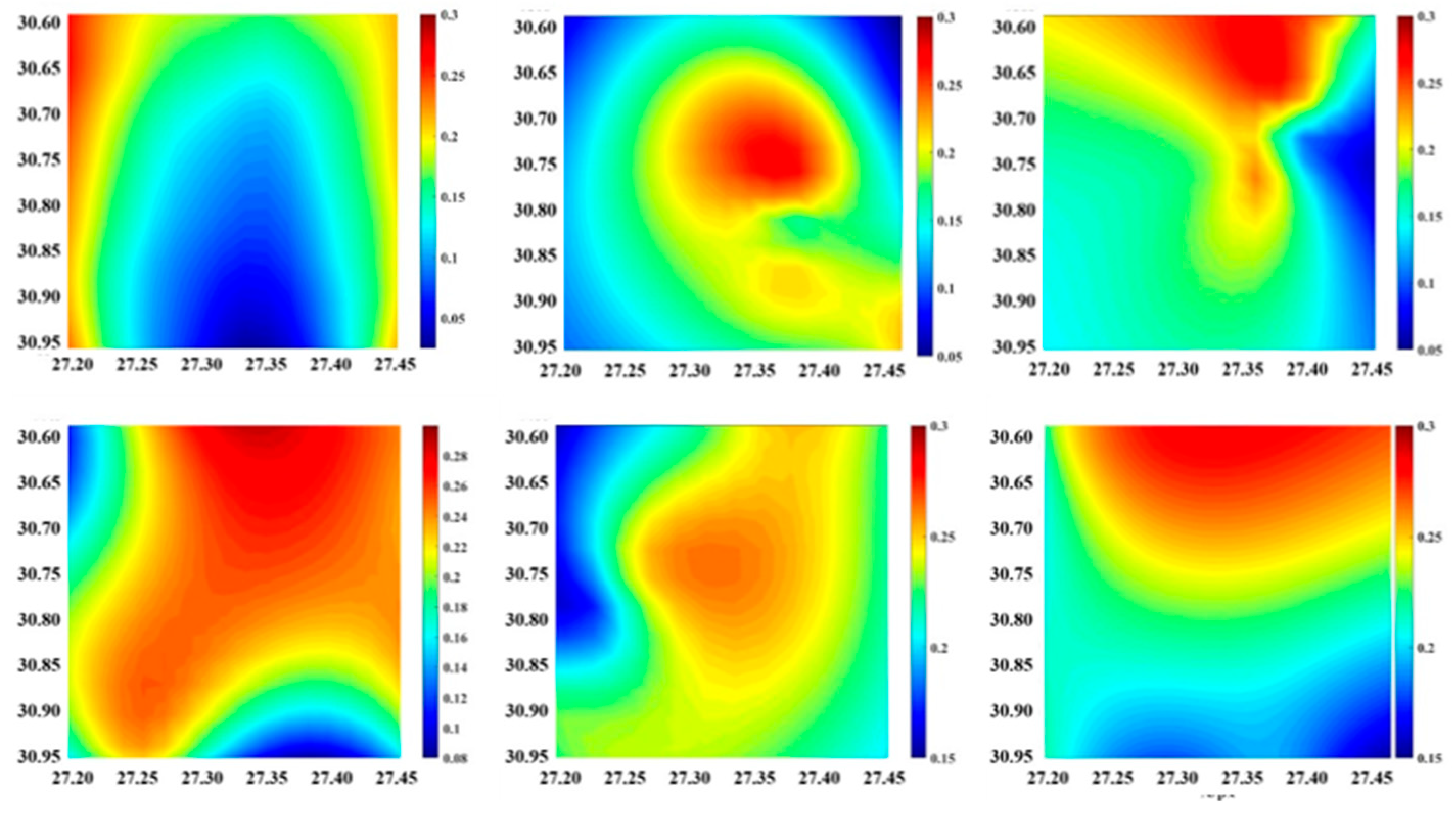
3.2.3. Micro-Area Dynamic Poisson’s Ratio Distribution
3.3. Negative Poisson’s Ratio Constitutive Mechanism
3.3.1. Microstructure Evolution Mechanism of Negative Poisson’s Ratio Effect
3.3.2. Computational Modeling and Finite Element Simulation of Poisson’s Ratio
4. Conclusions
- (1)
- The combination of two kinds of cement improves the compressive, flexural, and tensile strength and reduces the Poisson’s ratio of the structure. The mechanical properties of cement-based composites are the best when the content of SAC is 70% and CAC is 30%. Compared with SAC and CAC, the 28d compressive strength of the formula increased by 28.94% and 161.54%, respectively, the 28d tensile strength increased by 1.82% and 6.67%, respectively, and the 28d flexural strength increased by 2.27% and 7.14%, respectively.
- (2)
- The combination of the two kinds of cement reduces the Poisson’s ratio of the structure. The Poisson’s ratio of composite cement is the smallest when the content of SAC is 70% and CAC is 30%, the addition of a crystal modifier changed the crystal morphology, and the deformation behavior of cementitious materials was improved. The average displacement, average strain, and Poisson’s ratio decreased to different degrees, among which, adipic acid had the best effect on the improvement of deformation behavior.
- (3)
- The addition of different crystal modifiers affects the crystal structure of cement hydration. Two kinds of crystal arrangements are predicted, and an ideal calculation model is given. The deformation process of cement with negative Poisson’s ratio was analyzed by the morphology of hydration products and concave structure. The deformation process of the structure is simulated by the Finite Element Method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.; Yu, X.; Zhao, F.; Liu, J.; Zhu, P.; Zhang, P.; Zhang, J.; Wu, L. Research progress in environmental response of fiber concrete and its functional mechanisms. Adv. Mater. Sci. Eng. 2022, 26, 3059507. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, T.; Liu, H.; Su, S. Improving the sulfate resistance of recycled aggregate concrete (RAC) by using surface-treated aggregate with sulfoaluminate cement (SAC). Constr. Build. Mater. 2021, 297, 123535. [Google Scholar] [CrossRef]
- Liu, G.; Li, M.; Zhang, S.; Zhang, Z.; Wu, Y. Strengthening effect and mechanism of titanium extraction slag on the mechanical property of calcium aluminate cement. Ceram. Int. 2023, 49, 30326–30334. [Google Scholar]
- Xue, Q.; Ni, C.; Wu, Q.; Yu, Z.; Shen, X. Effects of Nano-CSH on the hydration process and mechanical property of cementitious materials. J. Sustain. Cem.-Based Mater. 2022, 11, 378–388. [Google Scholar] [CrossRef]
- Idrees, M.; Ekincioglu, O.; Sonyal, M.S. Hydration behavior of calcium aluminate cement mortars with mineral admixtures at different curing temperatures. Constr. Build. Mater. 2021, 285, 122839. [Google Scholar] [CrossRef]
- Engbert, A.; Plank, J. Impact of sand and filler materials on the hydration behavior of calcium aluminate cement. J. Am. Ceram. Soc. 2021, 104, 1067–1075. [Google Scholar] [CrossRef]
- Fernández-Carrasco, L.; Rius, J.; Miravitlles, C. Supercritical carbonation of calcium aluminate cement. Cem. Concr. Res. 2008, 38, 1033–1037. [Google Scholar] [CrossRef]
- Wang, F.; Chen, P.; Li, X.; Zhu, B. Effect of colloidal silica on the hydration behavior of calcium aluminate cement. Materials 2018, 11, 1849. [Google Scholar] [CrossRef]
- Li, Z.; Tian, B.; Li, L.; Quan, L.; Li, D. Effect of phosphates on early-age hydration process and products of calcium aluminate cement at-10 degrees C. Constr. Build. Mater. 2022, 346, 128405. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Chong, H.; Huang, J. Use of Sulphoaluminate Cement in Grouted Macadam as Sustainable Pavement Material. J. Transp. Eng. Part B Pavements 2020, 146, 04020018. [Google Scholar] [CrossRef]
- Belhadi, R.; Govin, A.; Grosseau, P. Influence of polycarboxylate superplasticizer, citric acid and their combination on the hydration and workability of calcium sulfoaluminate cement. Cem. Concr. Res. 2021, 147, 106513. [Google Scholar] [CrossRef]
- Xu, Q.; Ji, T.; Yang, Z.; Ye, Y. Steel rebar corrosion in artificial reef concrete with sulphoaluminate cement, sea water and marine sand. Constr. Build. Mater. 2019, 227, 116685. [Google Scholar] [CrossRef]
- Wang, W.; Wei, X.; Cai, X.; Deng, H.; Li, B. Mechanical and Microstructural Characteristics of Calcium Sulfoaluminate Cement Exposed to Early-Age Carbonation Curing. Materials 2021, 14, 3515. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.; Xu, W.; Wang, W.; Cheng, S. Thermal expansion regulation and bandgap analysis of a novel dual-constituent negative Poisson’s ratio lattice metamaterial. Mater. Today Commun. 2023, 35, 106311. [Google Scholar] [CrossRef]
- Cui, Y.J.; Liu, C.; Wang, K.F.; Wang, B.L.; Liu, Y. Effect of negative Poisson’s ratio architecture on fatigue life and output power of flexible wearable thermoelectric generators. Eng. Fract. Mech. 2023, 281, 109142. [Google Scholar] [CrossRef]
- Ma, Y.; Yu, X.; Zhao, F.; Liu, J.; Xu, Y.; Zhang, P.; Zhang, J.; Wu, L. Negative Poisson’s ratio design, static mechanical properties and deformation behaviors on PVA-carbon fiber reinforced concrete. J. Mater. Sci. 2023, 58, 1568–1585. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Hao, J.; Wang, Y. Mechanical properties of corrugated structure with negative Poisson’s ratio and its application on energy absorbing box based on parametric modeling method. Mater. Today Commun. 2024, 38, 107921. [Google Scholar] [CrossRef]
- Wallbanks, M.; Khan, M.F.; Bodaghi, M.; Triantaphyllou, A.; Serjouei, A. On the design workflow of auxetic metamaterials for structural applications. Smart Mater. Struct. 2021, 31, 023002. [Google Scholar] [CrossRef]
- Tahir, D.; Zhang, M.; Hu, H. Auxetic materials for personal protection: A review. Phys. Status Solidi (B) 2022, 259, 2200324. [Google Scholar] [CrossRef]
- Gao, D.; Wang, B.; Gao, H.; Ren, F.; Guo, C.; Ma, S.; Cao, T.; Xia, Y.; Wu, Y. Strain Rate Effect on Mechanical Properties of the 3D-Printed Metamaterial Foams With Tunable Negative Poisson’s Ratio. Front. Mater. 2021, 8, 712500. [Google Scholar]
- Gao, S.; Liu, W.; Zhang, L.; Gain, A.K. A New Polymer-Based Mechanical Metamaterial with Tailorable Large Negative Poisson’s Ratios. Polymers 2020, 12, 1492. [Google Scholar] [CrossRef] [PubMed]
- Zhong, R.; Ren, X.; Zhang, X.Y.; Luo, C.; Zhang, Y.; Xie, Y.M. Mechanical properties of concrete composites with auxetic single and layered honeycomb structures. Constr. Build. Mater. 2022, 322, 126453. [Google Scholar] [CrossRef]
- Bouguermouh, K.; Habibi, M.; Laperrière, L. 4D printing of fiber-reinforced auxetic structures: The building blocks: A review. Smart Mater. Struct. 2024, 33, 063001. [Google Scholar]
- Yao, Y.; Ni, Y.; He, L.H. Rutile-mimic 3D metamaterials with simultaneously negative Poisson’s ratio and negative compressibility. Mater. Des. 2020, 200, 109440. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Wang, K.; Yao, S.; Peng, Y. On impact behaviors of 3D concave structures with negative Poisson’s ratio. Compos. Struct. 2022, 298, 115999. [Google Scholar]
- Xu, Y.; Zhang, H.; Schlangen, E.; Luković, M.; Šavija, B. Cementitious cellular composites with auxetic behavior. Cem. Concr. Compos. 2020, 111, 1–11. [Google Scholar] [CrossRef]
- Asad, M.; Zahra, T.; Thambiratnam, D.P.; Chan, T.H.; Zhuge, Y. Geometrically modified auxetic polyurethane foams and their potential application in impact mitigation of masonry structures. Constr. Build. Mater. 2021, 311, 125170. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, Z.; Liu, X.; Ziruo, T.; Zhang, K.; Zhang, P.; Ren, J.; Liu, Z.; Le, G.; Zhong, J. The in-plane stretching and compression mechanics of Negative Poisson’s ratio structures: Concave hexagon, star shape, and their combination. J. Alloys Compd. 2021, 859, 157840. [Google Scholar] [CrossRef]
- Bao, S.; Ren, X.; Qi, Y.J.; Li, H.R.; Han, D.; Li, W.; Luo, C.; Song, Z.Z. Quasi-Static Mechanical Properties of a Modified Auxetic Re-Entrant Honeycomb Metamaterial. Phys. Status Solidi (B) 2022, 159, 2200270. [Google Scholar] [CrossRef]
- Lu, F.; Chen, X.; Zhu, Y.; Zhang, C.; Hou, Y. A Novel Re-Entrant-Type Metamaterial with Tunable Negative Poisson’s Ratios and Coefficients of Thermal Expansion. Int. J. Appl. Mech. 2022, 14, 2250040. [Google Scholar]
- Lee, W.; Jeong, Y.; Yoo, J.; Huh, H.; Park, S.H.; Yoon, J. Effect of auxetic structures on crash behavior of cylindrical tube. Compos. Struct. 2019, 208, 836–846. [Google Scholar]
- Fang, G.; Yuan, S.; Meng, S.; Liang, J. Graded negative Poisson’s ratio honeycomb structure design and application. J. Sandw. Struct. Mater. 2019, 21, 2527–2547. [Google Scholar] [CrossRef]
- Ha, C.S.; Plesha, M.E.; Lakes, R.S. Chiral three-dimensional isotropic lattices with negative Poisson’s ratio. Phys. Status Solidi (B) 2016, 253, 1243–1251. [Google Scholar] [CrossRef]
- Lv, C.; Krishnaraju, D.; Konjevod, G.; Yu, H.; Jiang, H. Origami based Mechanical Metamaterials. Sci. Rep. 2014, 4, 5979. [Google Scholar] [CrossRef]
- Izadifar, M.; Dolado, J.S.; Thissen, P.; Ukrainczyk, N.; Koenders, E.; Ayuela, A. Theoretical elastic constants of tobermorite enhanced with reduced graphene oxide through hydroxyl vs epoxy functionalization: A first-principles study. J. Phys. Chem. C 2023, 127, 18117–18126. [Google Scholar] [CrossRef]
- Momoh, E.O.; Jayasinghe, A.; Hajsadeghi, M.; Vinai, R.; Evans, K.E.; Kripakaran, P.; Orr, J. A state-of-the-art review on the application of auxetic materials in cementitious composites. Thin-Walled Struct. 2024, 196, 111447. [Google Scholar] [CrossRef]
- Li, N.; Liu, Z.; Shi, X.; Fan, D.; Xing, H.; Qiu, J.; Li, M.; Tang, T. Preparing Polypropylene Auxetic Foam by a One-Pot CO2 Foaming Process. Adv. Eng. Mater. 2022, 24, 2100859. [Google Scholar] [CrossRef]
- He, Y. Orientational dependence of Poisson’s ratio in tetragonal γ-TiAl single crystal. MRS Commun. 2023, 13, 431–437. [Google Scholar] [CrossRef]
- Huang, C.W.; Chen, L. Negative Poisson’s Ratio in Modern Functional Materials. Adv. Mater. 2016, 28, 8079–8096. [Google Scholar] [CrossRef]
- Winnefeld, F.; Martin, L.H.; Müller, C.J.; Lothenbach, B. Using gypsum to control hydration kinetics of CSA cements. Constr. Build. Mater. 2017, 155, 154–163. [Google Scholar] [CrossRef]
- Gastaldi, D.; Bertola, F.; Irico, S.; Paul, G.; Canonico, F. Hydration behavior of cements with reduced clinker factor in mixture with sulfoaluminate binder. Cem. Concr. Res. 2021, 139, 106261. [Google Scholar] [CrossRef]
- Liu, C.; Huang, R.; Zhang, Y.; Liu, Z.; Zhang, M. Modelling of irregular-shaped cement particles and microstructural development of Portland cement. Constr. Build. Mater. 2018, 168, 362–378. [Google Scholar] [CrossRef]
- Deng, X.; Guo, H.; Tan, H.; Zhang, J.; Zheng, Z.; Li, M.; Chen, P.; He, X.; Yang, J.; Wang, J. Comparison on early hydration of Portland cement and sulphoaluminate cement in the presence of nano ettringite. Constr. Build. Mater. 2022, 360, 129516. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Yu, J.; Xu, L.; Li, M.; Cheng, J.; Li, Z. Effects of sodium sulfate and potassium sulfate on the properties of calcium sulfoaluminate (CSA) cement based grouting materials. Constr. Build. Mater. 2022, 353, 129045. [Google Scholar] [CrossRef]
- Kartnaller, V.; Ribeiro, E.M.; Venancio, F.; Rosario, F.F.; Cajaiba, J. Preferential incorporation of sulfate into calcite polymorphs during calcium carbonate precipitation: An experimental approach. CrystEngComm 2018, 20, 2241–2244. [Google Scholar] [CrossRef]
- Gao, Y. Effect of crystallization additives on crystal morphology of ammonium sulfate. CIESC J. 2011, 62, 3575. [Google Scholar]
- Zhang, W.; Gong, J.; Dong, W.; Wu, S. Research progress in effect of gel on crystallization process. CIESC J. 2020, 71, 487. [Google Scholar]
- GB/T50081-2016; Standard for Test Method of Mechanical Properties on Ordinary Concrete. China Ministry of Construction: Beijing, China, 2016.
- Ma, Y.; Liu, J.; Zhang, Y.; Ge, Y.; Wu, R.; Song, X.; Zhang, P.; Wu, J. Mechanical behavior and self-healing mechanism of polyurea-based double-walled microcapsule/epoxy composite films. Prog. Org. Coat. 2021, 157, 106283. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Liu, J.; Ge, Y.; Yan, X.; Sun, Y.; Wu, J.; Zhang, P. GO-modified double-walled polyurea microcapsules/epoxy composites for marine anticorrosive self-healing coating. Mater. Des. 2020, 189, 108547. [Google Scholar]
- Buttlar, W.G.; Hill, B.C.; Kim, Y.R.; Kutay, M.E.; Millien, A.; Montepara, A.; Paulino, G.H.; Petit, C.; Pop, I.O.; Romeo, E.; et al. Digital image correlation techniques to investigate strain fields and cracking phenomena in asphalt materials. Mater. Struct. 2014, 47, 1373–1390. [Google Scholar]
- Hao, W.; Ge, D.; Ma, Y.; Yao, X.; Shi, Y. Experimental investigation on deformation and strength of carbon/epoxy laminated curved beams. Polym. Test. 2012, 31, 520–526. [Google Scholar]
- Yan, F.F.; Xu, X.D. Negative Possion’s Ratio Honeycomb Structure and Its Applications in Structure Design of Morphing Aircraft. China Mech. Eng. 2012, 23, 542–546. [Google Scholar]











| Chemical Composition (wt%) | Al2O3 | CaO | SiO2 | Fe2O3 | SO3 | MgO | K2O | TiO2 | Na2O | P2O5 | LOI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CAC | 50.81 | 35.8 | 7.96 | 2.41 | 0.17 | 0.4 | 0.04 | 2.01 | 0.18 | 0.06 | 0.42 |
| SAC | 22.47 | 42.7 | 8.15 | 2.66 | 14.98 | 2.08 | 0.62 | 1.36 | 0.20 | 0.07 | 4.81 |
| Phases (wt%) | CA | Ye’elimite | Gehlenite | Grossite | Mayenite | Spinel | Ferrite | Belite | Gypsum | Dolomite |
|---|---|---|---|---|---|---|---|---|---|---|
| CAC | 71.8 | \ | 23.2 | 2.5 | 1.3 | 0.8 | 0.4 | \ | \ | \ |
| SAC | \ | 65.3 | \ | \ | 8.9 | \ | 0.9 | 22.8 | 1.5 | 0.6 |
| Formula | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SAC | 100% | 90% | 80% | 70% | 60% | 50% | 40% | 30% | 20% | 10% | 0% |
| CAC | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% |
| Sample Number | SAC | CAC | SAC-CAC | Sodium Sulfate | Adipic Acid | Gelatin |
|---|---|---|---|---|---|---|
| SAC | 100% | 0% | 70% | 70% | 70% | 70% |
| CAC | 0% | 100% | 30% | 30% | 30% | 30% |
| Crystal modifier | \ | \ | \ | Sodium sulfate | Adipic acid | Gelatin |
| Formula | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Compression | Average | 0.23 | 0.20 | 0.16 | 0.15 | 0.15 | 0.17 | 0.18 | 0.18 | 0.22 | 0.23 | 0.24 |
| Maximum | 0.28 | 0.26 | 0.25 | 0.20 | 0.23 | 0.25 | 0.25 | 0.26 | 0.26 | 0.26 | 0.30 | |
| Minimum | 0.15 | 0.12 | 0.05 | 0.00 | 0.00 | 0.03 | 0.05 | 0.05 | 0.08 | 0.15 | 0.15 | |
| Tension | Average | 0.23 | 0.20 | 0.17 | 0.13 | 0.15 | 0.18 | 0.20 | 0.21 | 0.22 | 0.23 | 0.24 |
| Maximum | 0.28 | 0.26 | 0.25 | 0.20 | 0.24 | 0.25 | 0.25 | 0.26 | 0.26 | 0.26 | 0.30 | |
| Minimum | 0.15 | 0.10 | 0.04 | −0.05 | 0.00 | 0.02 | 0.05 | 0.09 | 0.12 | 0.14 | 0.15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Q.; Wang, P.; Ma, Y.; Zhang, Z.; Alexandrovich, S.D.; Liu, J.; Zhao, F.; Zhu, P. Sulphoaluminate-Aluminate Cement-Based Composites: Mechanical Behaviors and Negative Poisson’s Ratio Mechanism Under Static Loads. Buildings 2025, 15, 1251. https://doi.org/10.3390/buildings15081251
Chang Q, Wang P, Ma Y, Zhang Z, Alexandrovich SD, Liu J, Zhao F, Zhu P. Sulphoaluminate-Aluminate Cement-Based Composites: Mechanical Behaviors and Negative Poisson’s Ratio Mechanism Under Static Loads. Buildings. 2025; 15(8):1251. https://doi.org/10.3390/buildings15081251
Chicago/Turabian StyleChang, Qin, Peng Wang, Yanxuan Ma, Zhipeng Zhang, Stroev Dmitry Alexandrovich, Jin Liu, Fei Zhao, and Pengfei Zhu. 2025. "Sulphoaluminate-Aluminate Cement-Based Composites: Mechanical Behaviors and Negative Poisson’s Ratio Mechanism Under Static Loads" Buildings 15, no. 8: 1251. https://doi.org/10.3390/buildings15081251
APA StyleChang, Q., Wang, P., Ma, Y., Zhang, Z., Alexandrovich, S. D., Liu, J., Zhao, F., & Zhu, P. (2025). Sulphoaluminate-Aluminate Cement-Based Composites: Mechanical Behaviors and Negative Poisson’s Ratio Mechanism Under Static Loads. Buildings, 15(8), 1251. https://doi.org/10.3390/buildings15081251






