A Comparative Study of Inertial Mass Dampers and Negative Stiffness Dampers for the Multi-Mode Vibration Control of Stay Cables
Abstract
1. Introduction
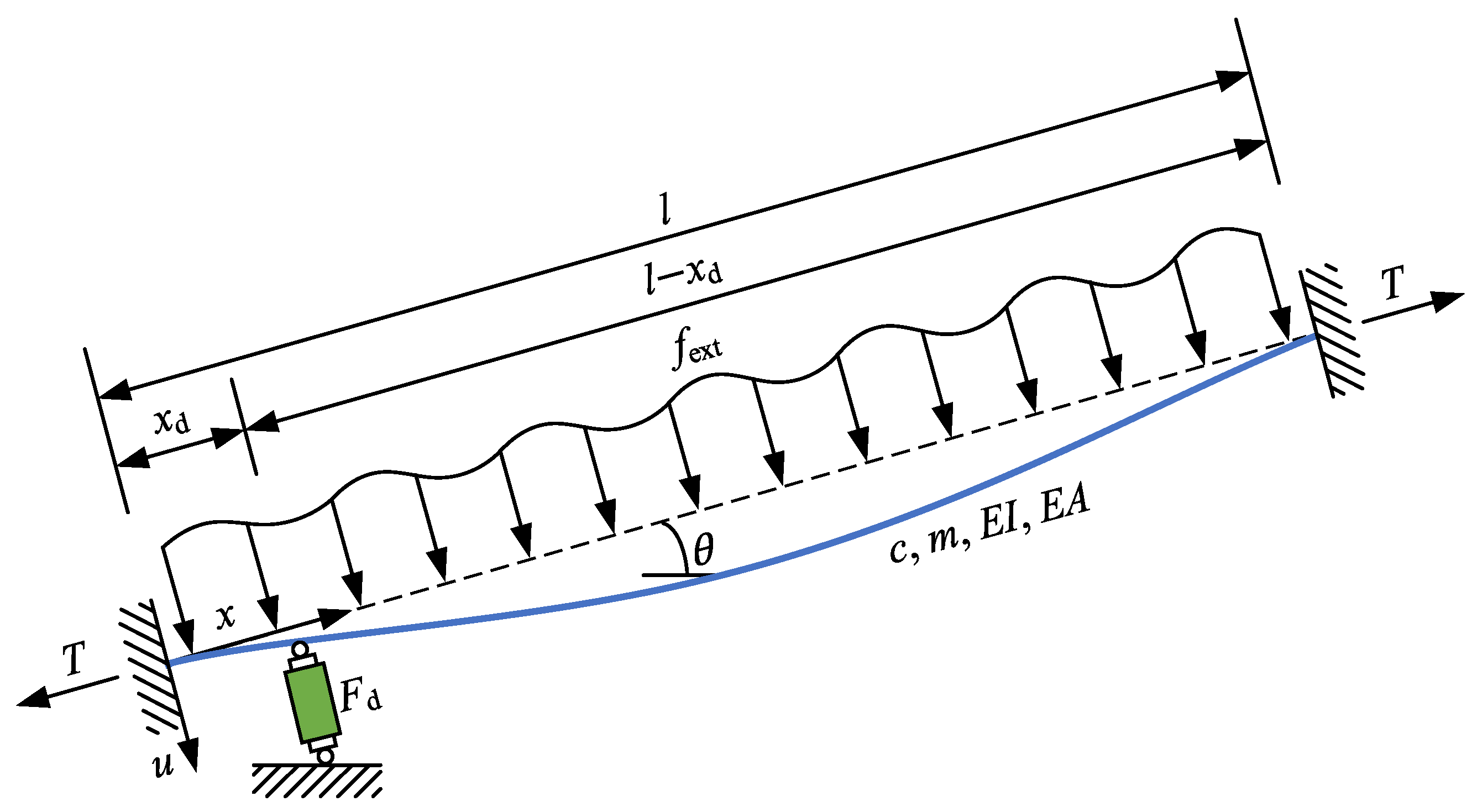
2. Dynamic Formulation of a Stay Cable Equipped with an IMD or a NSD
2.1. Mechanical Models of Typical IMD and NSD
2.2. Numerical Modeling of Two Cable-Damper Systems
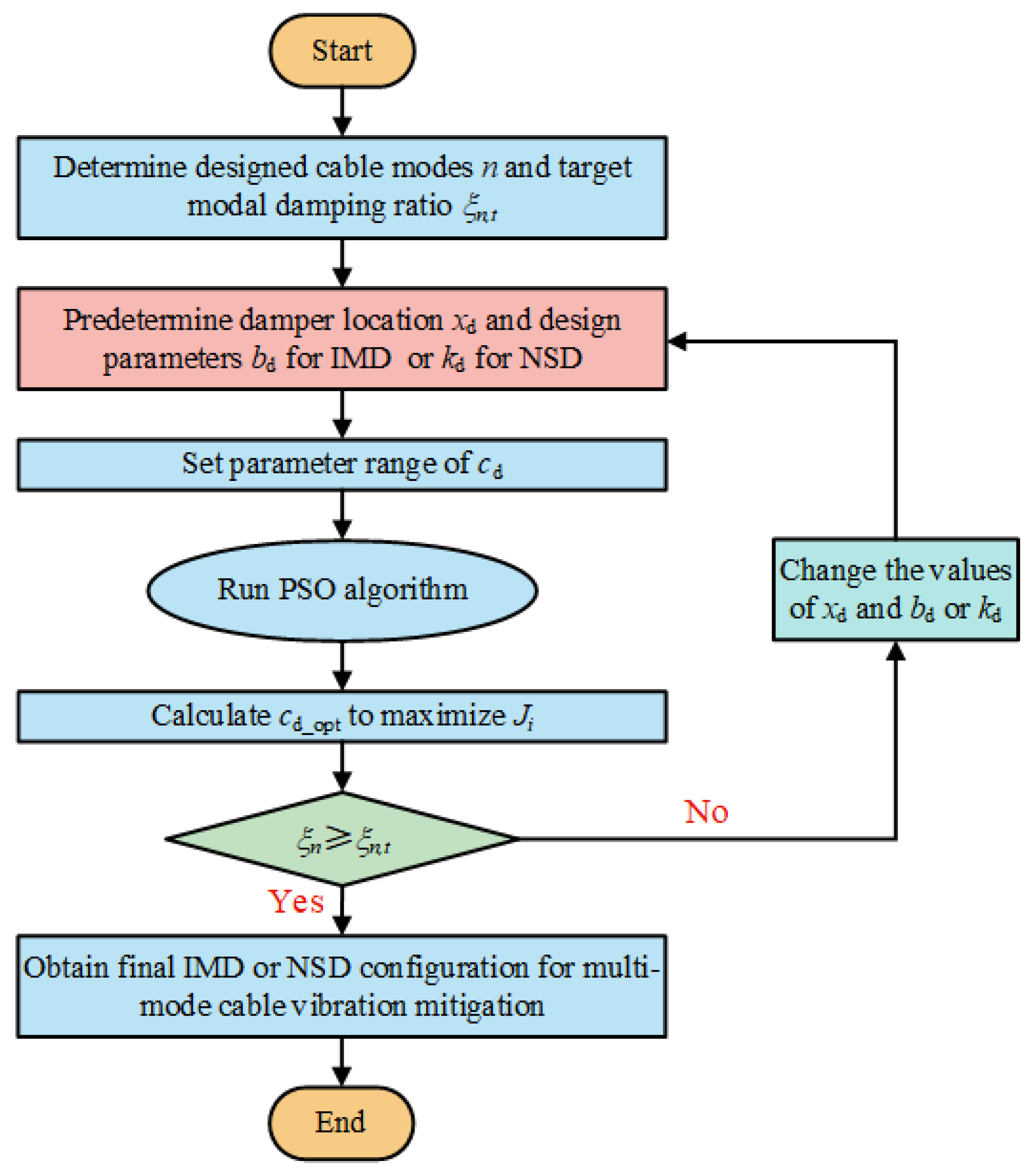
3. Design IMD and NSD for Controlling Multi-Mode Cable Vibrations
3.1. Effectiveness of Multi-Mode Optimization Strategies
3.2. Design Parameters of IMD and NSD
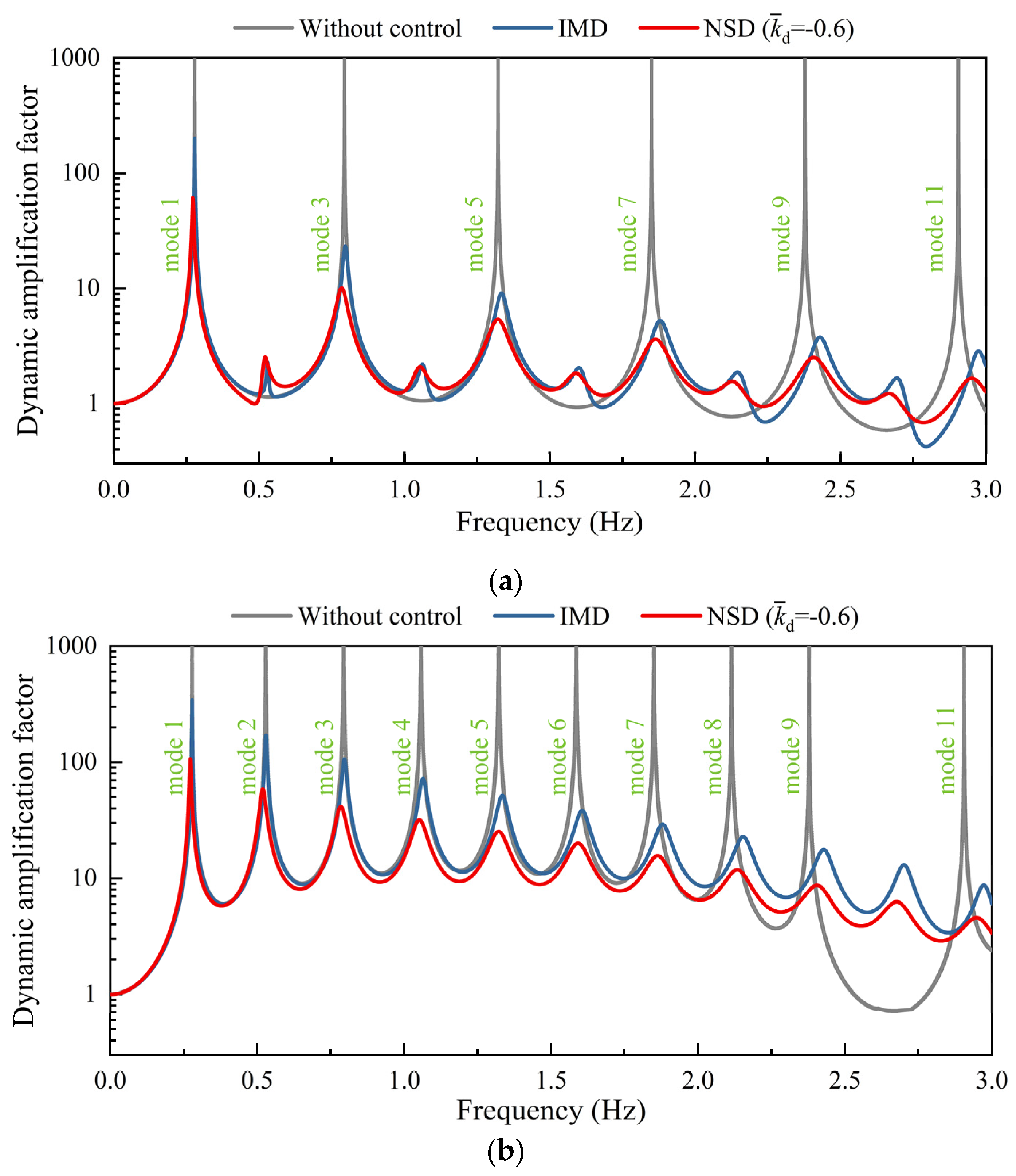
4. Performance Comparison Between IMD and NSD
4.1. Harmonic Excitation
4.2. White Noise Excitation
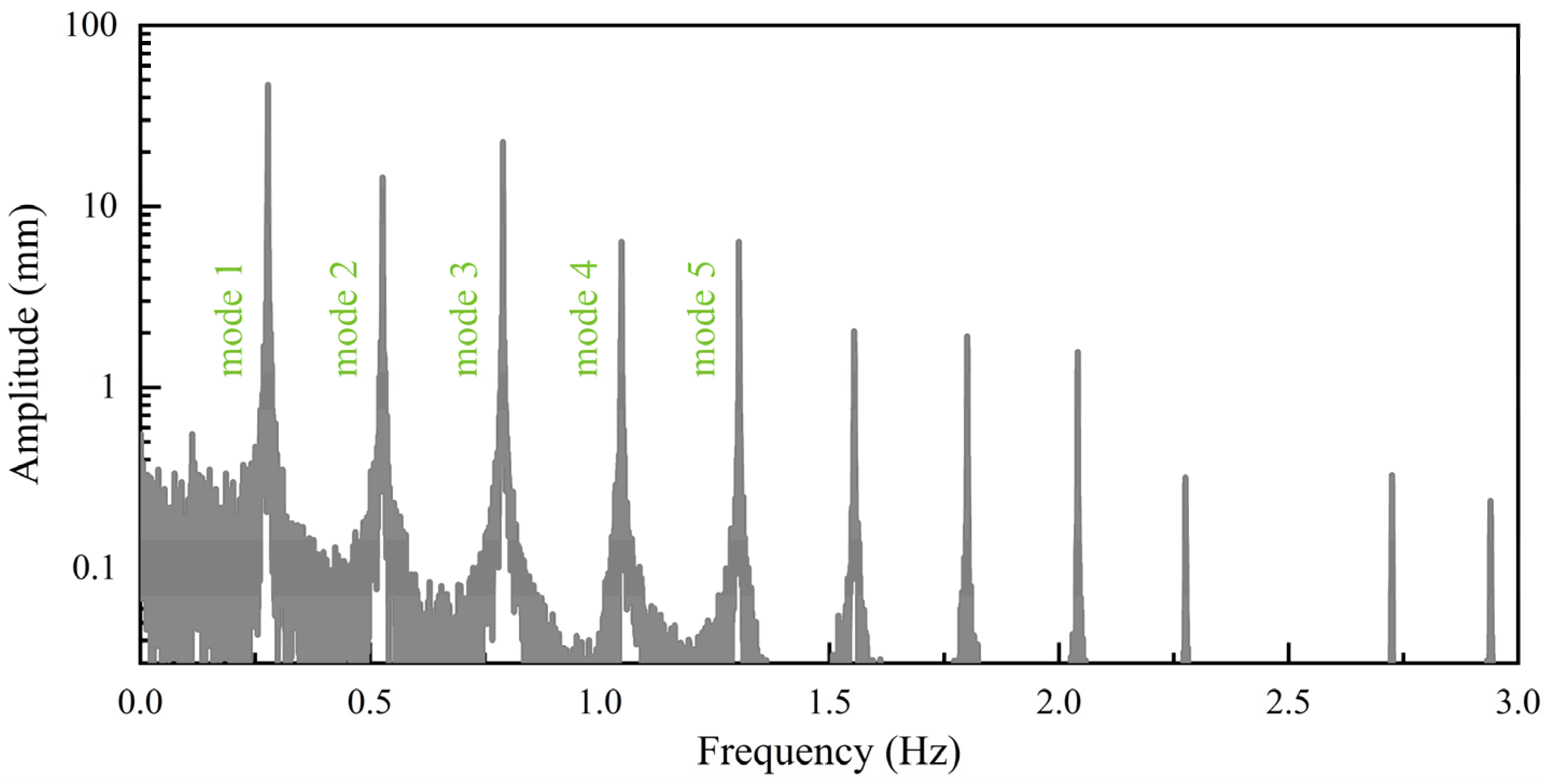
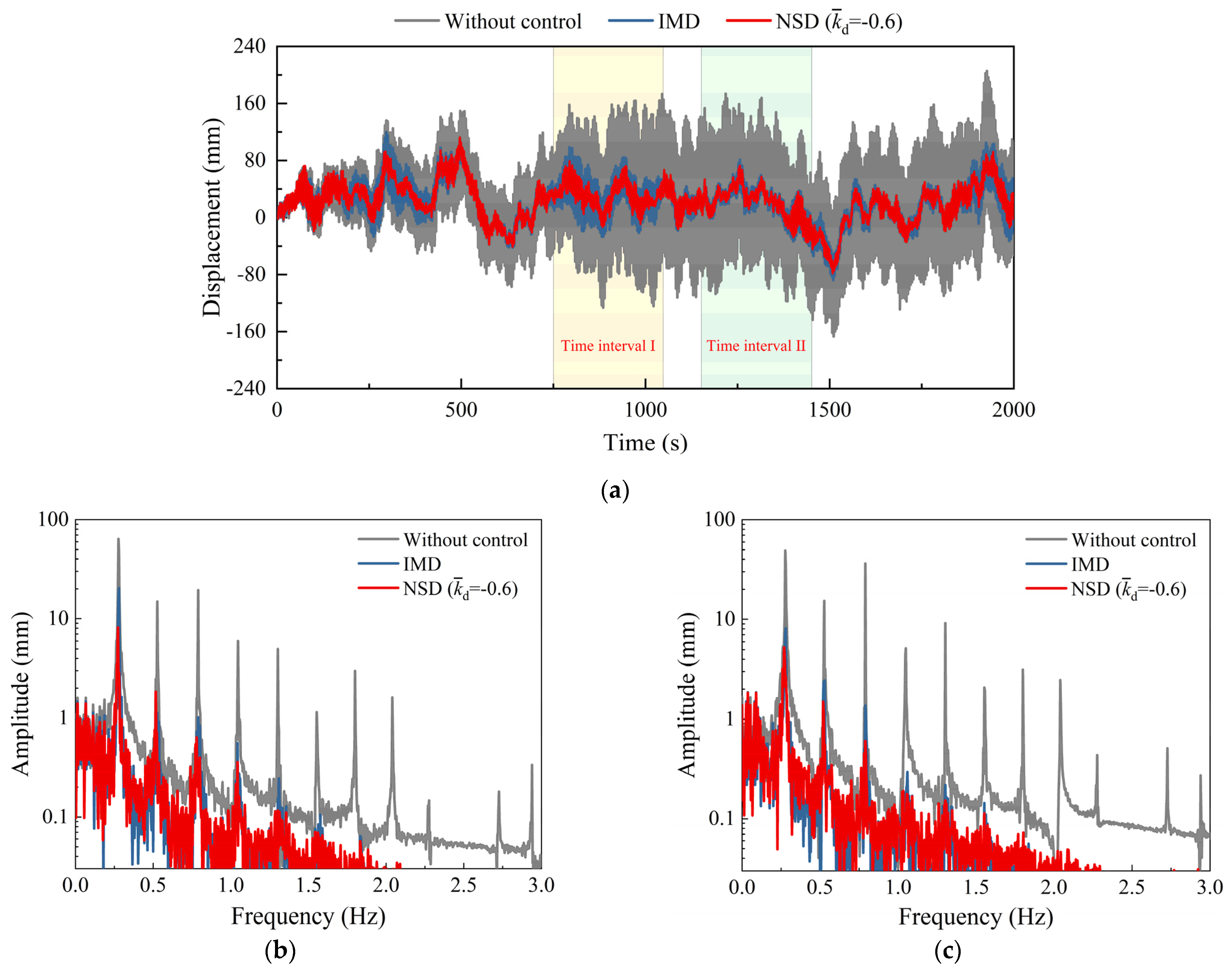
4.3. Wind Excitation
5. Conclusions
- (1)
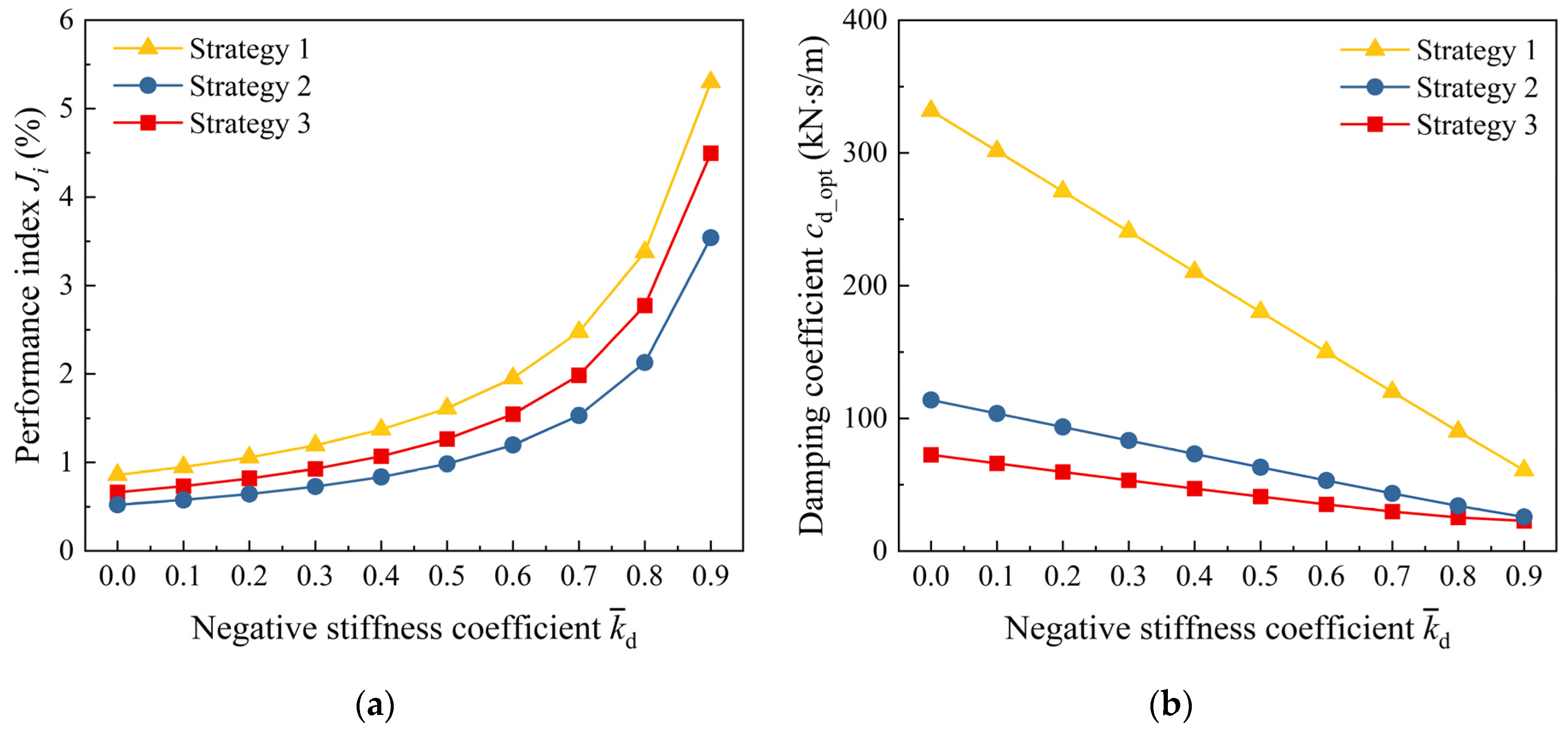
- Strategy 3 is recommended for the IMD or NSD to achieve better control effectiveness in suppressing multi-mode cable vibrations compared to strategies 1 and 2.
- (2)
- The NSD significantly improves the cable damping ratios for multiple vibration modes as its negative stiffness coefficient increases, while the IMD performs well only within a small inertia coefficient.
- (3)
- The NSD requires a smaller damping coefficient than the IMD to achieve superior control performance, and its required damping coefficient decreases as the negative stiffness increases.
- (4)
- The sensitivities of the multi-mode cable damping with respect to the damping coefficients of the IMD and NSD are comparable, with no significant differences observed.
- (5)
- The NSD outperforms the IMD in suppressing multi-mode cable vibrations induced by harmonic, white noise and wind excitations. The dynamic responses of the ultra-long cable equipped with the NSD are significantly reduced compared to those equipped with the IMD under the three types of external excitations.
- (6)
- The negative stiffness of the NSD significantly amplifies the displacement of its damping element compared to the inertia of the IMD, resulting in a considerably greater energy dissipation capacity for the NSD in comparison to the IMD when applied to suppress multi-mode cable vibrations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Wang, X.; Ko, J.; Ni, Y.; Spencer, B.; Yang, G.; Hu, J. MR damping system for mitigating wind-rain induced vibration on Dongting Lake Cable-Stayed Bridge. Wind. Struct. 2004, 7, 293–304. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, P.; Yu, T.; Li, Z. Optimal design of nonlinear negative-stiffness damper with flexible support for mitigating cable vibration. Buildings 2023, 13, 2620. [Google Scholar] [CrossRef]
- Chen, L.; Di, F.; Xu, Y.; Sun, L.; Xu, Y.; Wang, L. Multimode cable vibration control using a viscous-shear damper: Case studies on the Sutong Bridge. Struct. Control Health Monit. 2020, 27, e2536. [Google Scholar] [CrossRef]
- Di, F.; Sun, L.; Chen, L.; Zou, Y.; Qin, L.; Huang, Z. Frequency and damping of hybrid cable networks with cross-ties and external dampers: Full-scale experiments. Mech. Syst. Signal Process. 2023, 197, 110397. [Google Scholar] [CrossRef]
- Calò, M.; Ruggieri, S.; Doglioni, A.; Morga, M.; Nettis, A.; Simeone, V.; Uva, G. Probabilistic-based assessment of subsidence phenomena on the existing built heritage by combining MTInSAR data and UAV photogrammetry. Struct. Infrastruct. Eng. 2024, 2024, 116. [Google Scholar] [CrossRef]
- Li, H.; Zhou, P.; Li, Z. Using a rigid restraint with a built-in tuned mass damper to control the vibration of cables. Buildings 2024, 14, 3785. [Google Scholar] [CrossRef]
- Li, J.; Shen, J.; Zhu, S. Adaptive self-powered active vibration control to cable structures. Mech. Syst. Signal Process. 2023, 188, 110050. [Google Scholar] [CrossRef]
- Zhang, C. The active rotary inertia driver system for flutter vibration control of bridges and various promising applications. Sci. China Technol. Sci. 2023, 66, 390–405. [Google Scholar] [CrossRef]
- Johnson, E.; Christenson, R.; Spencer, B. Semi-active damping of cables with sag. Comput. Civ. Infrastruct. Eng. 2003, 18, 132–146. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H. Semi-active damping with negative stiffness for multi-mode cable vibration mitigation: Approximate collocated control solution. Smart. Mater. Struct. 2015, 24, 115015. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.; Shi, X.; Shen, W. Electromagnetic shunt damper for bridge cable vibration mitigation: Full-scale experimental study. J. Struct. Eng. 2020, 146, 04019175. [Google Scholar] [CrossRef]
- He, D.; Xu, H.; Wang, M.; Wang, T. Transmission and dissipation of vibration in a dynamic vibration absorber-roller system based on particle damping technology. Chin. J. Mech. Eng. 2024, 37, 108. [Google Scholar] [CrossRef]
- Zucca, M.; Longarini, N.; Simoncelli, M.; Aly, A. Tuned mass damper design for slender masonry structures: A framework for linear and nonlinear analysis. Appl. Sci. 2021, 11, 3425. [Google Scholar] [CrossRef]
- Ma, R.; Han, C.; Jiang, S.; Bi, K.; Du, X. Concept, optimization and performance evaluation of a novel particle tuned inertial damper (PTID). Eng. Struct. 2024, 317, 118678. [Google Scholar] [CrossRef]
- Ma, R.; Bi, K.; Zuo, H.; Song, J.; Han, Q. A novel tuned torsional mass damper (TTMD) for seismic protection of structures. Eng. Struct. 2024, 300, 117233. [Google Scholar] [CrossRef]
- Kovacs, I. Zur frage der seilschwingungen und der seildampfung. Die Bautechnik. 1982, 59, 325–332. (In German) [Google Scholar]
- Pacheco, B.; Fujino, Y.; Sulekh, A. Estimation curve for modal damping in stay cables with viscous damper. J. Struct. Eng. 1993, 119, 1961–1979. [Google Scholar] [CrossRef]
- Krenk, S. Vibrations of a taut cable with an external damper. J. Appl. Mech. 2000, 67, 772–776. [Google Scholar] [CrossRef]
- Fournier, J.; Cheng, S. Impact of damper stiffness and damper support stiffness on the efficiency of a linear viscous damper in controlling stay cable vibrations. J. Bridg. Eng. 2014, 19, 04013022. [Google Scholar] [CrossRef]
- Fujino, Y.; Hoang, N. Design formulas for damping of a stay cable with a damper. J. Struct. Eng. 2008, 134, 269–278. [Google Scholar] [CrossRef]
- Zhou, H.; Sun, L.; Xing, F. Damping of full-scale stay cable with viscous damper: Experiment and analysis. Adv. Struct. Eng. 2014, 17, 265–274. [Google Scholar] [CrossRef]
- Main, J.; Jones, N. Free vibrations of taut cable with attached damper. II: Nonlinear damper. J. Struct. Eng. 2002, 128, 1072–1081. [Google Scholar] [CrossRef]
- Krenk, S.; Høgsberg, J. Damping of cables by a transverse force. J. Eng. Mech. 2005, 131, 340–348. [Google Scholar] [CrossRef]
- Chen, L.; Sun, L. Steady-state analysis of cable with nonlinear damper via harmonic balance method for maximizing damping. J. Struct. Eng. 2017, 143, 04016172. [Google Scholar] [CrossRef]
- Zhou, Q.; Nielsen, S.; Qu, W. Semi-active control of three-dimensional vibrations of an inclined sag cable with magnetorheological dampers. J. Sound Vib. 2006, 296, 1–22. [Google Scholar] [CrossRef]
- Xu, Y.; Yu, Z. Vibration of inclined sag cables with oil dampers in cable stayed bridges. J. Bridg. Eng. 1998, 3, 194–203. [Google Scholar] [CrossRef]
- Hoang, N.; Fujino, Y. Analytical study on bending effects in a stay cable with a damper. J. Eng. Mech. 2007, 133, 1241–1246. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, H.; Fan, B.; Chen, Z. Inertial mass damper for vibration control of cable with sag. J. Low Freq. Noise Vib. Act. Control 2020, 39, 749–760. [Google Scholar] [CrossRef]
- Wang, X.; Ni, Y.; Ko, J.; Chen, Z. Optimal design of viscous dampers for multi-mode vibration control of bridge cables. Eng. Struct. 2005, 27, 792–800. [Google Scholar] [CrossRef]
- Weber, F.; Feltrin, G.; Malanka, M.; Fobo, W.; Distl, H. Design of viscous dampers targeting multiple cable modes. Eng. Struct. 2009, 31, 2797–2800. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Z.; Wang, W.; Hua, X.; Wang, Y. Optimal design of two viscous dampers for multi-mode control of a cable covering broad frequency range. Eng. Struct. 2021, 245, 112830. [Google Scholar] [CrossRef]
- Cheng, S.; Darivandi, N.; Ghrib, F. The design of an optimal viscous damper for a bridge stay cable using energy-based approach. J. Sound Vib. 2010, 329, 4689–4704. [Google Scholar] [CrossRef]
- Di, F.; Sun, L.; Chen, L. Cable vibration control with internal and external dampers: Theoretical analysis and field test. Smart Struct. Syst. 2020, 26, 575–589. [Google Scholar] [CrossRef]
- An, M.; Li, S.; Sorokin, V.; Chen, Z.; Flay, R. Experimental study of vortex-induced vibration of stay cables installed with two types of perforated shroud light devices. J. Wind Eng. Ind. Aerodyn. 2024, 253, 105882. [Google Scholar] [CrossRef]
- Li, H.; Liu, M.; Ou, J. Negative stiffness characteristics of active and semi-active control systems for stay cables. Struct. Control Health Monit. 2008, 15, 120–142. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.; Guo, Y.; Zhou, M.; Zhao, Y.; Yang, Y.; Dai, J.; Zhang, J.; Zhu, C.; Ji, B.; et al. A programmable pseudo negative stiffness control device and its role in stay cable vibration control. Mech. Syst. Signal Process. 2022, 173, 109054. [Google Scholar] [CrossRef]
- Li, H.; Bi, K.; Hao, H.; Yu, Y.; Xu, L. Experimental study of a novel quasi-active negative stiffness damper system for achieving optimal active control performance. Eng. Struct. 2024, 299, 117082. [Google Scholar] [CrossRef]
- Ma, R.; Bi, K.; Hao, H. Inerter-based structural vibration control: A state-of-the-art review. Eng. Struct. 2021, 243, 112655. [Google Scholar] [CrossRef]
- Wang, Z.; Song, L.; Cheng, Z.; Yang, H.; Wen, J.; Qi, M. Finite element model for vibration serviceability evaluation of a suspended floor with and without tuned mass dampers. Buildings 2023, 13, 309. [Google Scholar] [CrossRef]
- Li, H.; Bi, K.; Han, Q.; Ma, R. A state-of-the-art review on negative stiffness-based structural vibration control. Eng. Struct. 2025, 323, 119247. [Google Scholar] [CrossRef]
- Gao, H.; Wang, H.; Li, J.; Wang, Z.; Liang, R.; Xu, Z.; Ni, Y. Optimum design of viscous inerter damper targeting multi-mode vibration mitigation of stay cables. Eng. Struct. 2021, 226, 111375. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, Z.; Wang, H.; Yue, F.; Gao, H.; Fan, B. Damping of a stay cable with two eddy-current inertial mass dampers: Theoretical analysis, experimental study, and parameter optimization. Struct. Control Health Monit. 2022, 29, e3085. [Google Scholar] [CrossRef]
- Dong, S.; Duan, Y.; Xu, S.; Yun, C. Vibration mitigation of sagged cables using a viscous inertial mass damper: An experimental investigation. Struct. Control Health Monit. 2023, 2023, 4361740. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Gao, H.; Cheng, Z.; Xu, K.; Zhao, S. Vibration control of a stay cable with a rotary electromagnetic inertial mass damper. Smart Struct. Syst. 2019, 23, 627–639. [Google Scholar] [CrossRef]
- Li, Y.; Shen, W.; Zhu, H. Vibration mitigation of stay cables using electromagnetic inertial mass dampers: Full-scale experiment and analysis. Eng. Struct. 2019, 200, 109693. [Google Scholar] [CrossRef]
- Shen, W.; Hao, J.; Zhu, H. Design approach and practical formulas of electromagnetic inertial mass dampers for cable multimode control. J. Bridg. Eng. 2022, 27, 04022121. [Google Scholar] [CrossRef]
- Zhou, P.; Li, H. Modeling and control performance of a negative stiffness damper for suppressing stay cable vibrations. Struct. Control Health Monit. 2016, 23, 764–782. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Z.; Zou, Y.; Wang, M.; Nagarajaiah, S.; Sun, F.; Sun, L. Practical negative stiffness device with viscoelastic damper in parallel or series configuration for cable damping improvement. J. Sound Vib. 2023, 560, 117757. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.; Spencer, B. Experimental study on passive negative stiffness damper for cable vibration mitigation. J. Eng. Mech. 2017, 143, 04017070. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, Z.; Yin, G.; Shen, W. A magnetic negative stiffness eddy-current inertial mass damper for cable vibration mitigation. Mech. Syst. Signal Process. 2023, 188, 110013. [Google Scholar] [CrossRef]
- Cheng, Z.; Bi, K.; Wang, Z.; Ma, R.; Lin, W. Performance enhanced magnetic negative stiffness eddy-current damper: Numerical simulation and experimental investigation. Mech. Syst. Signal Process. 2025, 223, 111890. [Google Scholar] [CrossRef]
- Chen, L.; Nagarajaiah, S.; Sun, L. A unified analysis of negative stiffness dampers and inerter-based absorbers for multimode cable vibration control. J. Sound Vib. 2021, 494, 115814. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Yang, C.; Liu, Z.; He, J.; Feng, Z. A novel eddy current damper system for multi-mode high-order vibration control of ultra-long stay cables. Eng. Struct. 2022, 262, 114319. [Google Scholar] [CrossRef]
- Mehrabi, A.; Tabatabai, H. Unified finite difference formulation for free vibration of cables. J. Struct. Eng. 1998, 124, 1313–1322. [Google Scholar] [CrossRef]
- Kiani, K.; Efazati, M. Three-dimensional nonlocal-surface energy-based statics, dynamics, and divergence instability of movable cable-like nanostructures with arbitrary translational motion. Arch. Appl. Mech. 2021, 91, 3095–3123. [Google Scholar] [CrossRef]
- Kiani, K.; Efazati, M. Nonlocal vibrations and instability of three-dimensionally accelerated moving nanocables. Phys. Scr. 2020, 95, 105005. [Google Scholar] [CrossRef]
- Luo, J.; Jiang, J. Macdonald JHG. Cable vibration suppression with inerter-based absorbers. J. Eng. Mech. 2019, 145, 04018134. [Google Scholar] [CrossRef]
- Huang, Z.; Hua, X.; Chen, Z.; Niu, H. Performance evaluation of inerter-based damping devices for structural vibration control of stay cables. Smart. Struct. Syst. 2019, 23, 615–626. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, X.; Yao, G.; Sun, L.; Xing, F. Free vibration of two taut cables interconnected by a damper. Struct. Control Health. Monit. 2019, 26, e2423. [Google Scholar] [CrossRef]
- PTI-DC45.1; Recommendations for Stay Cable Design, Testing and Installation. Post-Tensioning Institute: Farmington Hills, MI, USA, 2018.
- Shen, J.; Wu, T.; Zou, J.; Wu, P.; Liao, Y. Development of deep ultraviolet LED packaging. J. Opt. Photon. Res. 2025, 2, 1–10. [Google Scholar] [CrossRef]
- Lee, H.; Yoon, H.; Kim, S. Vibration detection of stay-cable from low-quality CCTV images using deep-learning-based dehazing and semantic segmentation algorithms. Eng. Struct. 2023, 292, 116567. [Google Scholar] [CrossRef]
- Chin, S. Artificial perovskite multiple quantum well optoelectronics. J. Opt. Photon. Res. 2024, 2024, 1–9. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
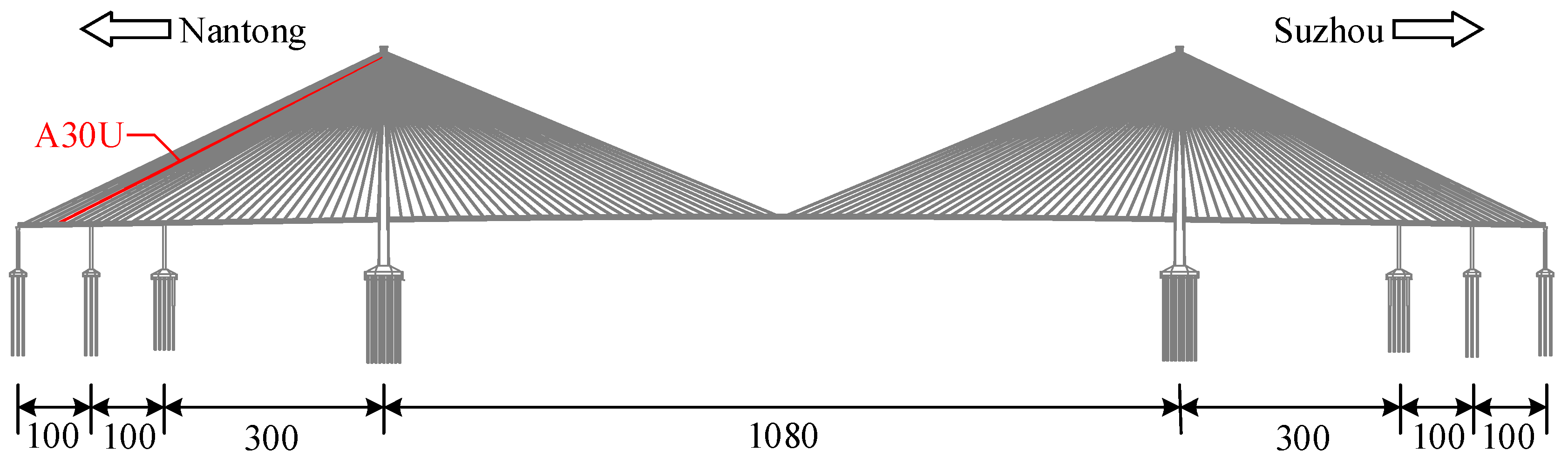
| Cable length () | 493.72 (m) |
| Mass per unit length () | 78.50 (kg/m) |
| Diameter () | 0.142 (m) |
| Tension force () | 5347 (kN) |
| Flexural rigidity () | 3.460 × 105 (N·m2) |
| Inclination angle () | 25.84 (°) |
| Sag parameter () | 1.30 |
| Strategy | Optimal Inertia Coefficient | Optimal Damping Coefficient (kN·s/m) | Average Value of Cable Damping Ratios (%) | Average Value of Cable Damping Ratios (%) |
|---|---|---|---|---|
| 1 | 0.19 | 290.42 | 0.48 | 0.19 |
| 2 | 0.04 | 116.26 | 0.80 | 0.54 |
| 3 | 0.06 | 60.22 | 1.14 | 0.30 |
| Strategy | Negative Stiffness Coefficient | Optimal Damping Coefficient (kN·s/m) | Average Value of Cable Damping Ratios (%) | Average Value of Cable Damping Ratios (%) |
|---|---|---|---|---|
| 1 | −0.4 | 210.45 | 0.67 | 0.29 |
| −0.6 | 150.00 | 0.95 | 0.41 | |
| −0.8 | 90.10 | 1.63 | 0.70 | |
| 2 | −0.4 | 73.23 | 1.20 | 0.84 |
| −0.6 | 53.22 | 1.71 | 1.20 | |
| −0.8 | 34.04 | 2.96 | 2.13 | |
| 3 | −0.4 | 47.13 | 1.36 | 0.57 |
| −0.6 | 35.20 | 1.94 | 0.84 | |
| −0.8 | 25.30 | 3.34 | 1.66 |
| Mode Order | Damper Type | (kN·s/m) | (%) | |||
|---|---|---|---|---|---|---|
| 11 | IMD | 2%l | 0.06 | N/A | 60.22 | 0.767 |
| NSD | N/A | −0.4 | 47.13 | 1.070 | ||
| N/A | −0.6 | 35.20 | 1.545 | |||
| N/A | −0.8 | 25.30 | 2.772 |
| Mode Order | Damper Type | (kN·s/m) | (%) | |||
|---|---|---|---|---|---|---|
| 11 | IMD | 2%l | 0.06 | N/A | 1.2 | 0.753 |
| 1.1 | 0.762 | |||||
| 1.0 | 0.767 | |||||
| 0.9 | 0.761 | |||||
| 0.8 | 0.745 | |||||
| NSD | N/A | −0.6 | 1.2 | 1.496 | ||
| 1.1 | 1.531 | |||||
| 1.0 | 1.545 | |||||
| 0.9 | 1.528 | |||||
| 0.8 | 1.473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Sun, X.; Cheng, Z.; Ma, R. A Comparative Study of Inertial Mass Dampers and Negative Stiffness Dampers for the Multi-Mode Vibration Control of Stay Cables. Buildings 2025, 15, 1230. https://doi.org/10.3390/buildings15081230
Shen Z, Sun X, Cheng Z, Ma R. A Comparative Study of Inertial Mass Dampers and Negative Stiffness Dampers for the Multi-Mode Vibration Control of Stay Cables. Buildings. 2025; 15(8):1230. https://doi.org/10.3390/buildings15081230
Chicago/Turabian StyleShen, Zhaowei, Xiaohong Sun, Zhipeng Cheng, and Ruisheng Ma. 2025. "A Comparative Study of Inertial Mass Dampers and Negative Stiffness Dampers for the Multi-Mode Vibration Control of Stay Cables" Buildings 15, no. 8: 1230. https://doi.org/10.3390/buildings15081230
APA StyleShen, Z., Sun, X., Cheng, Z., & Ma, R. (2025). A Comparative Study of Inertial Mass Dampers and Negative Stiffness Dampers for the Multi-Mode Vibration Control of Stay Cables. Buildings, 15(8), 1230. https://doi.org/10.3390/buildings15081230







