Numerical Modeling of Reinforcement Solutions in Traditional Stone Masonry Using a Particle Model
Abstract
1. Introduction
2. Particle Model (PM) for Ancient Masonry Analysis
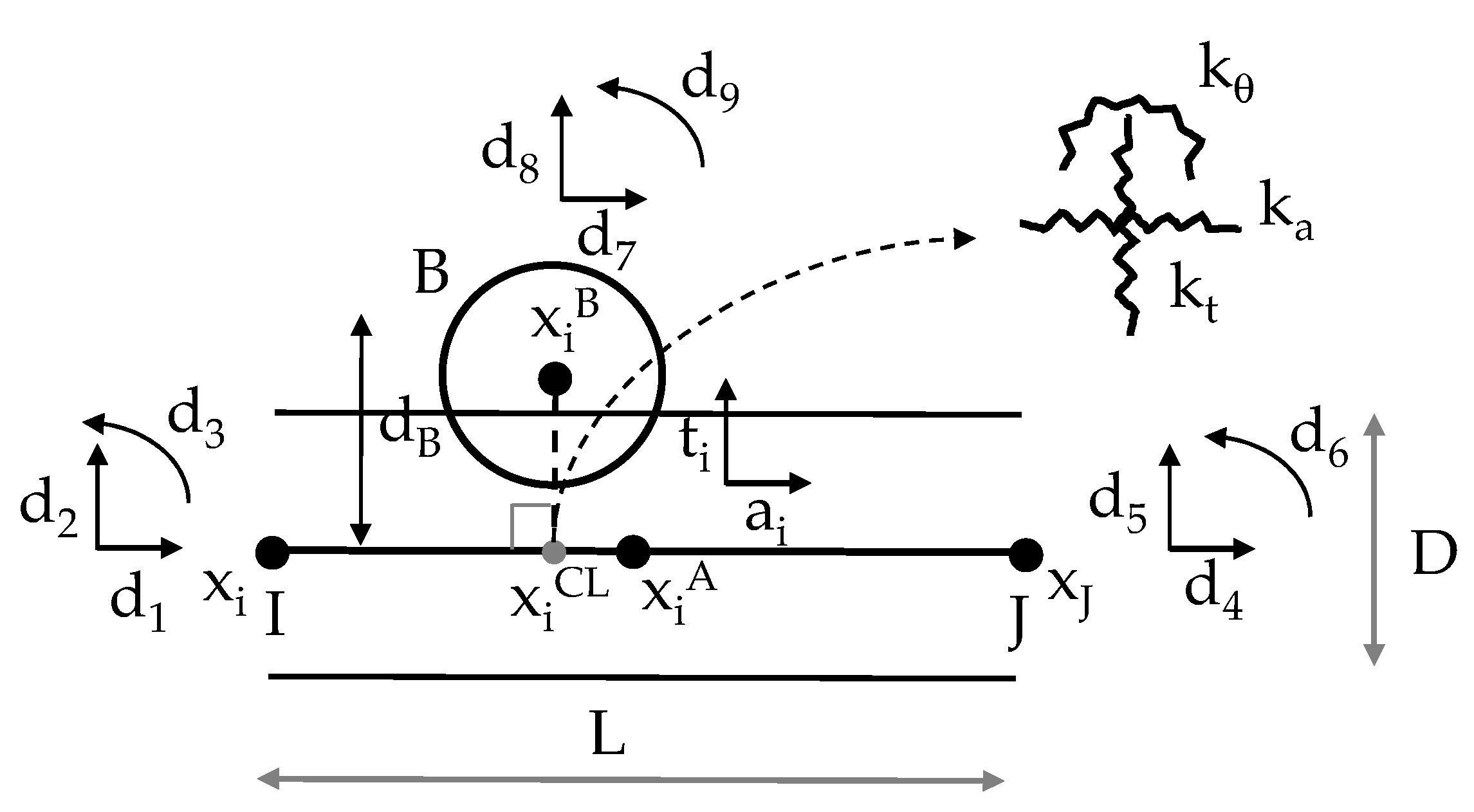
2.1. Fundamentals
- -
- Force–displacement law: the forces acting on each particle are related to the particle’s displacement relative to neighboring particles.
- -
- Laws of Motion (Newton’s Second law): given the forces applied to the centroid of the particle, the new position of the particle is determined by applying Newton’s second law.
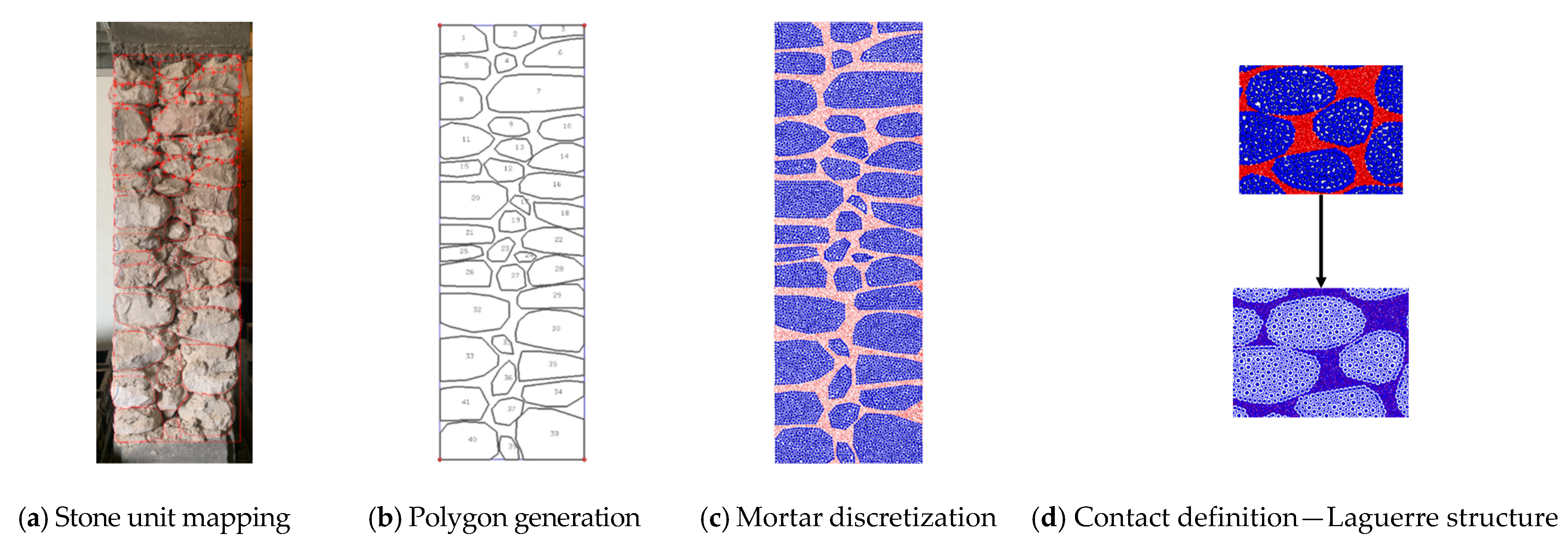
2.2. Model Generation from Images
2.3. Contact Properties Calibration
3. Uniaxial Compression Tests
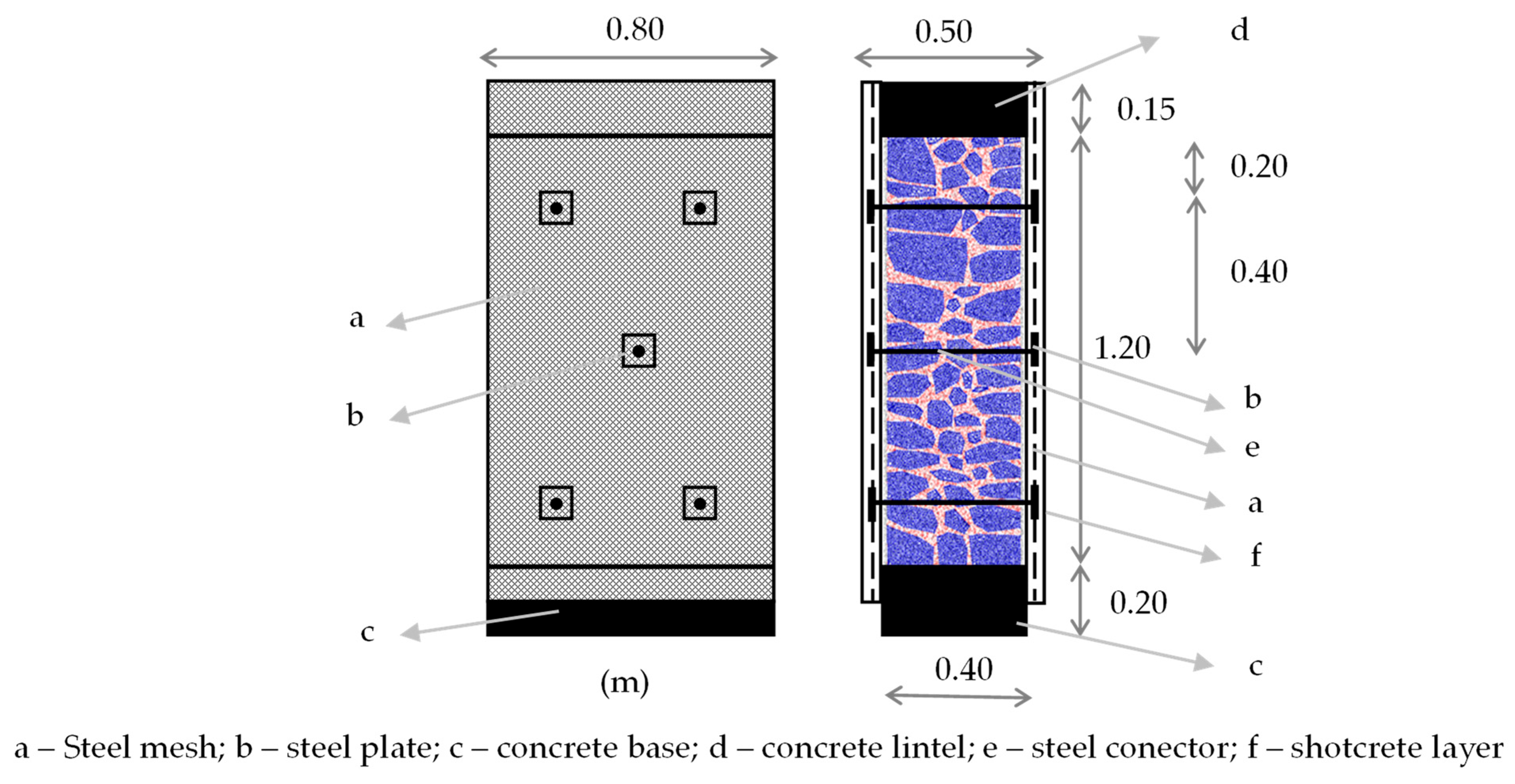
3.1. Experimental Work
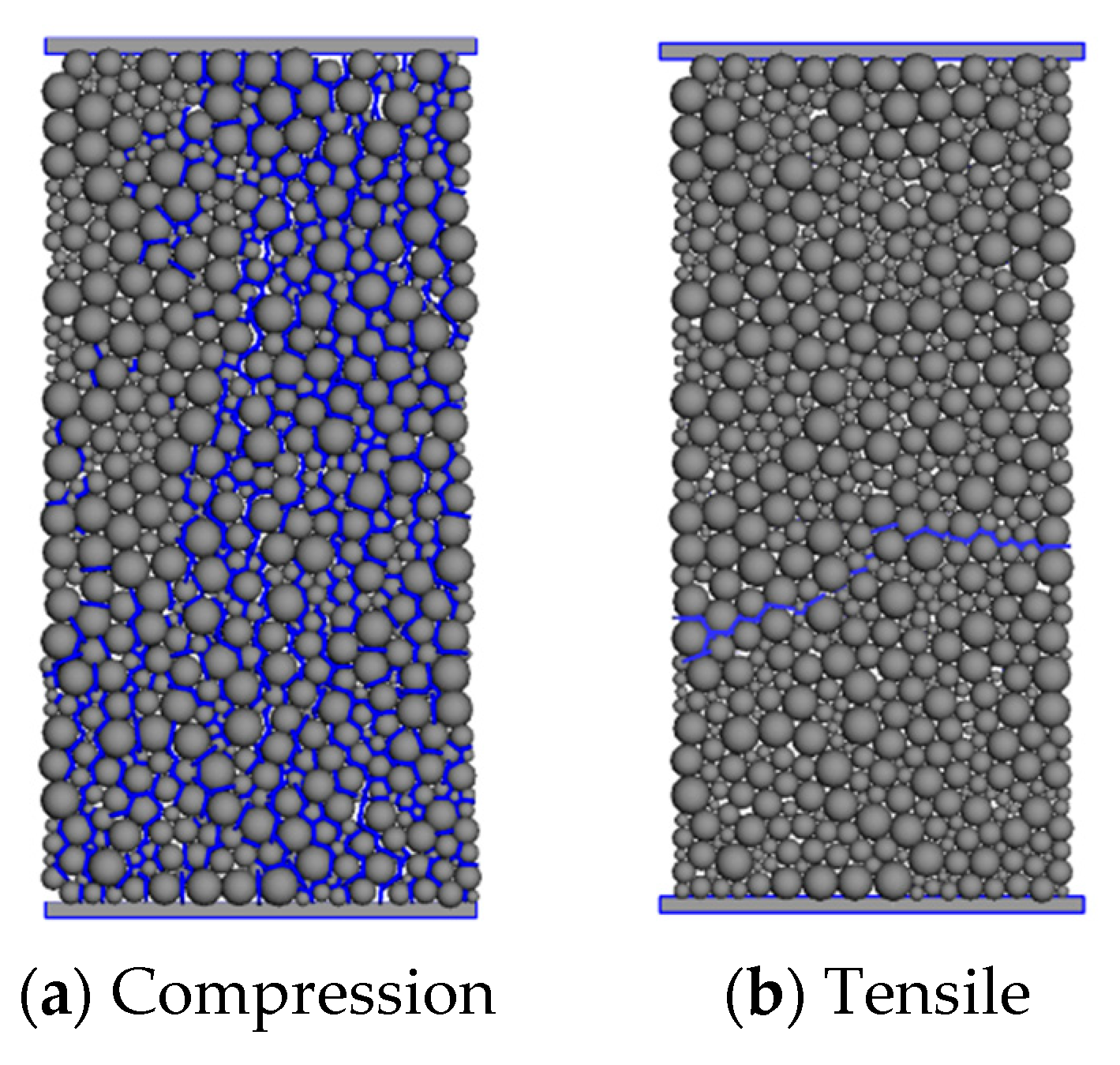
3.2. Computational Models for RPM Predictions
4. Results and Discussion
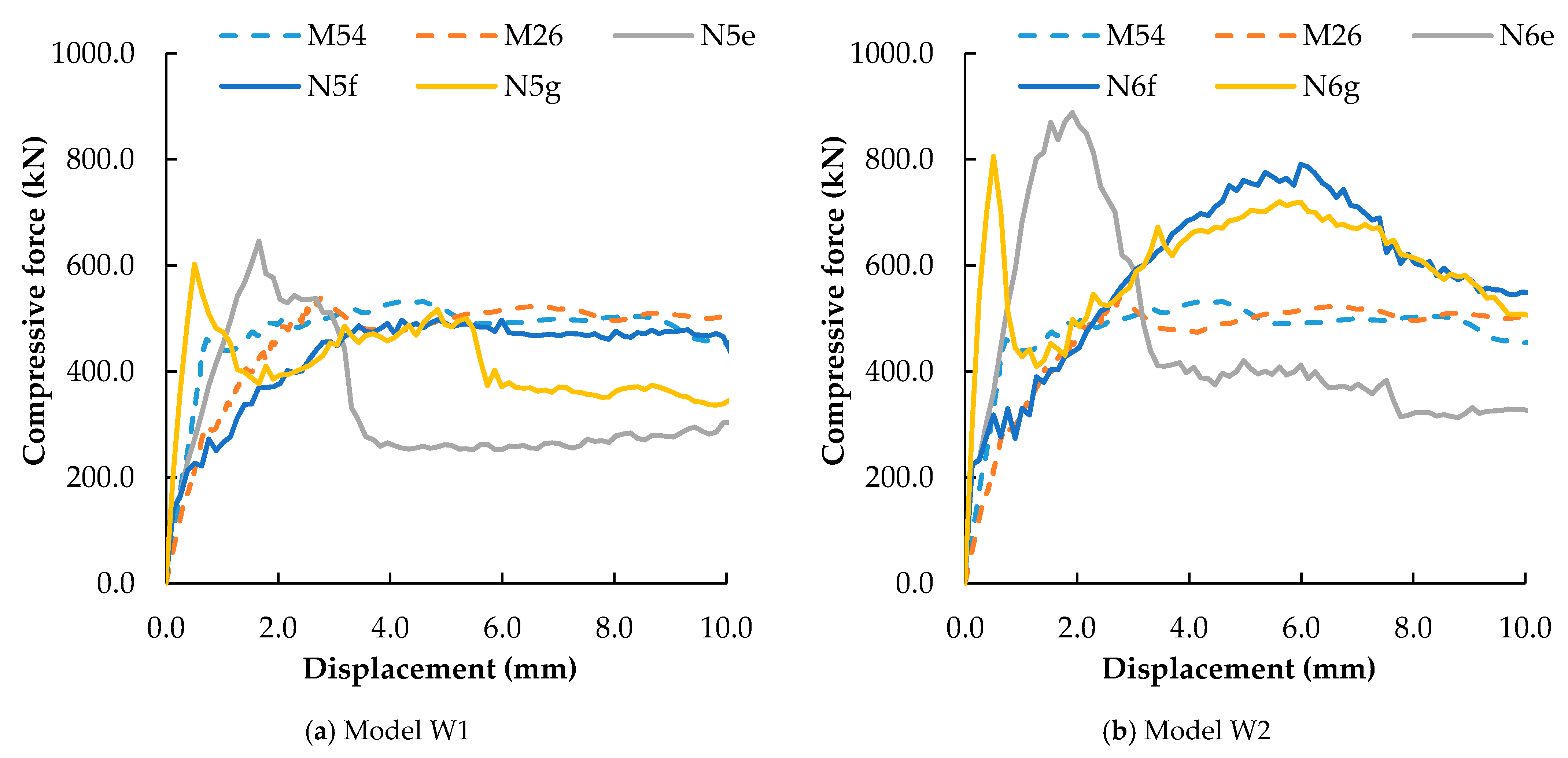
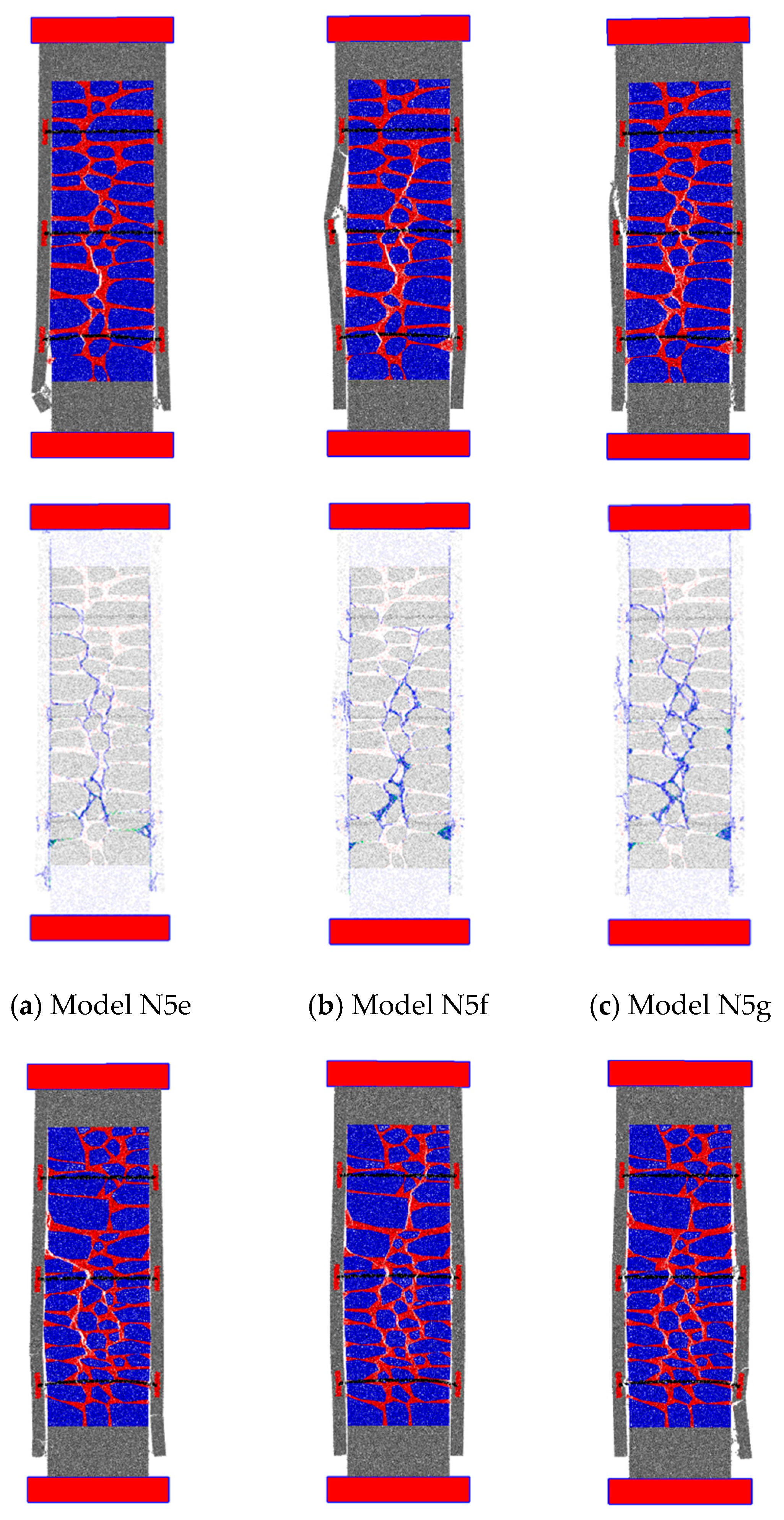
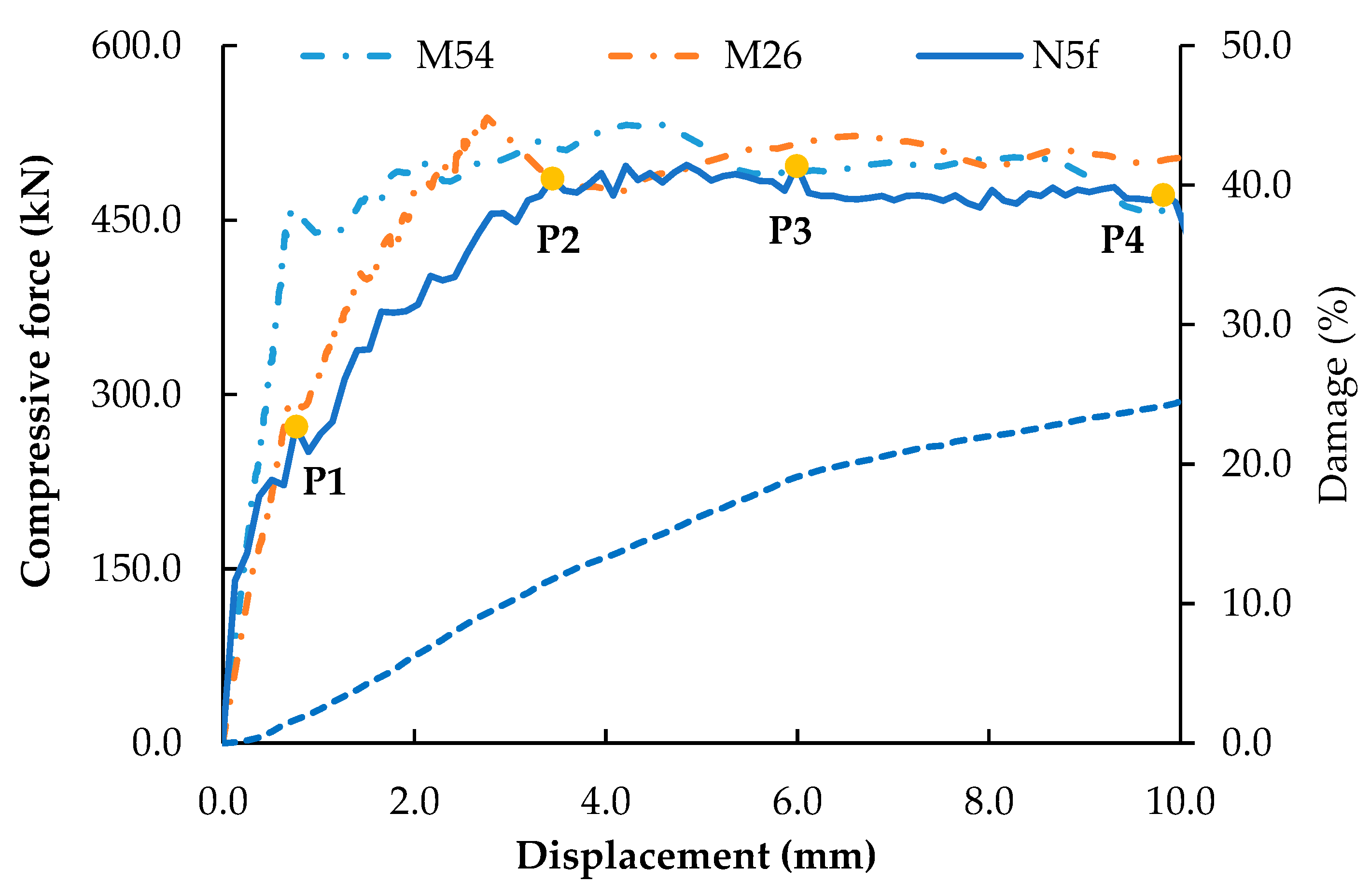
4.1. Calibrated Parameters Macroscopic Predictions
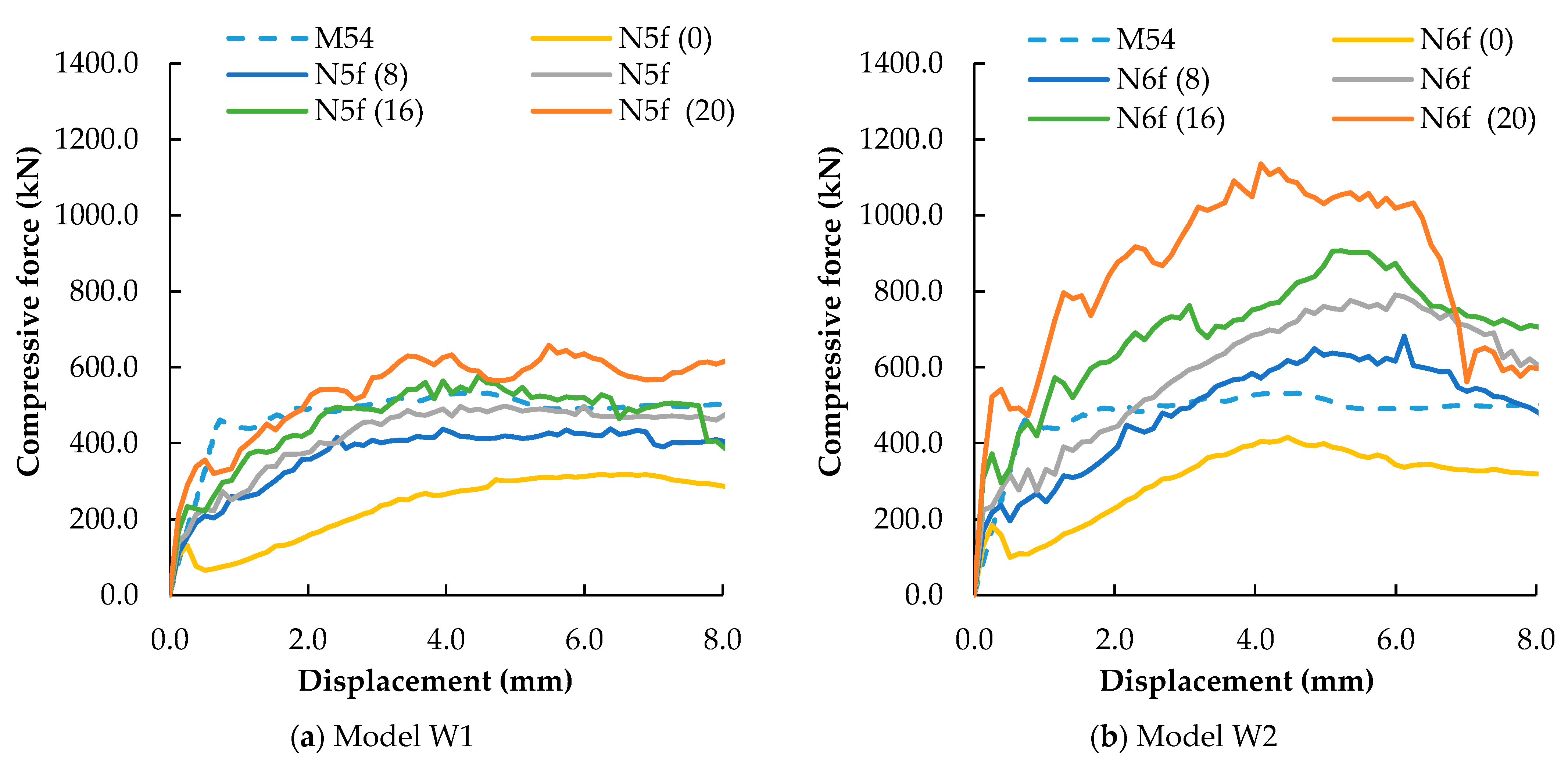
4.2. Overall Effect on the Macroscopic Response–Parametric Studies
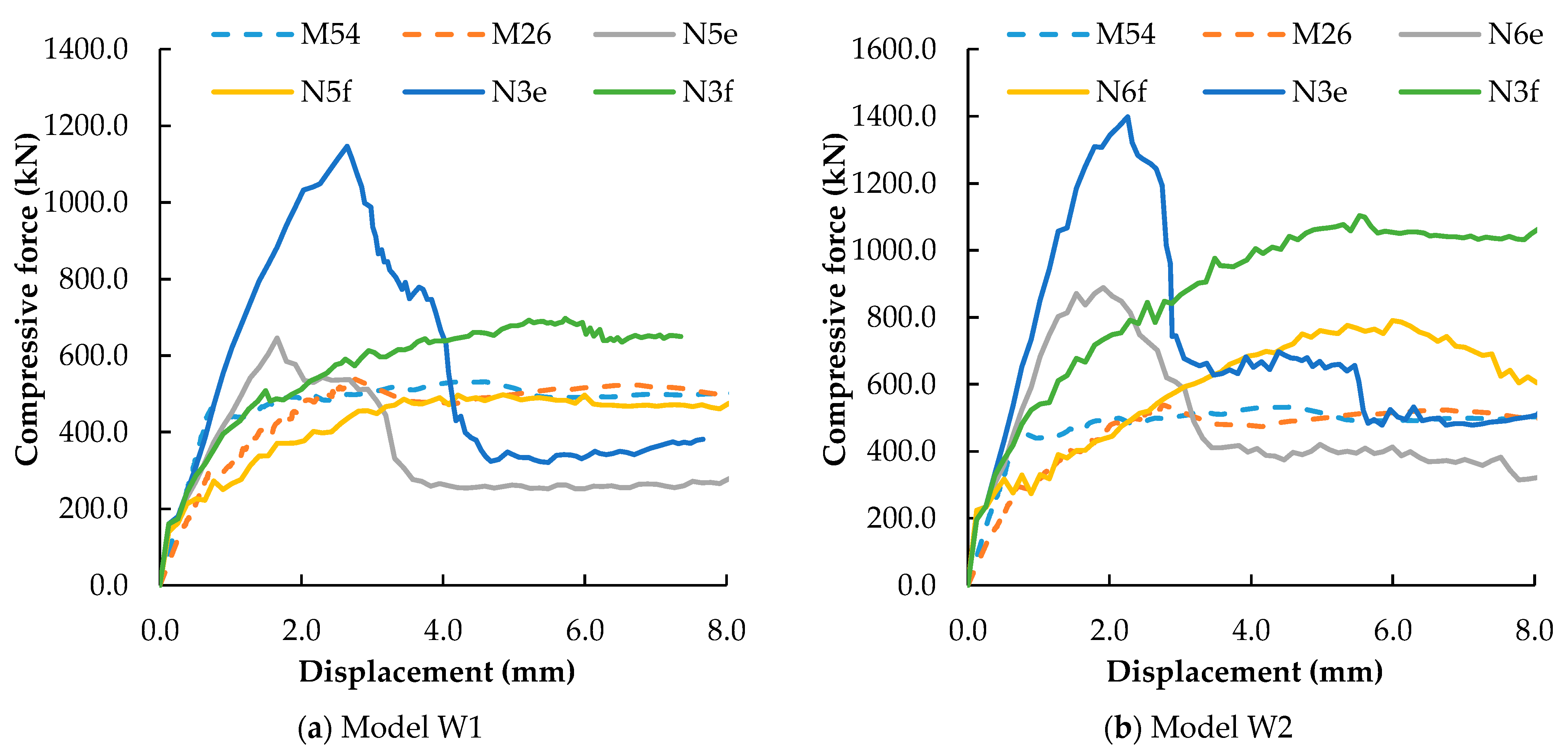
4.2.1. Steel Plate External to Micro-Concrete
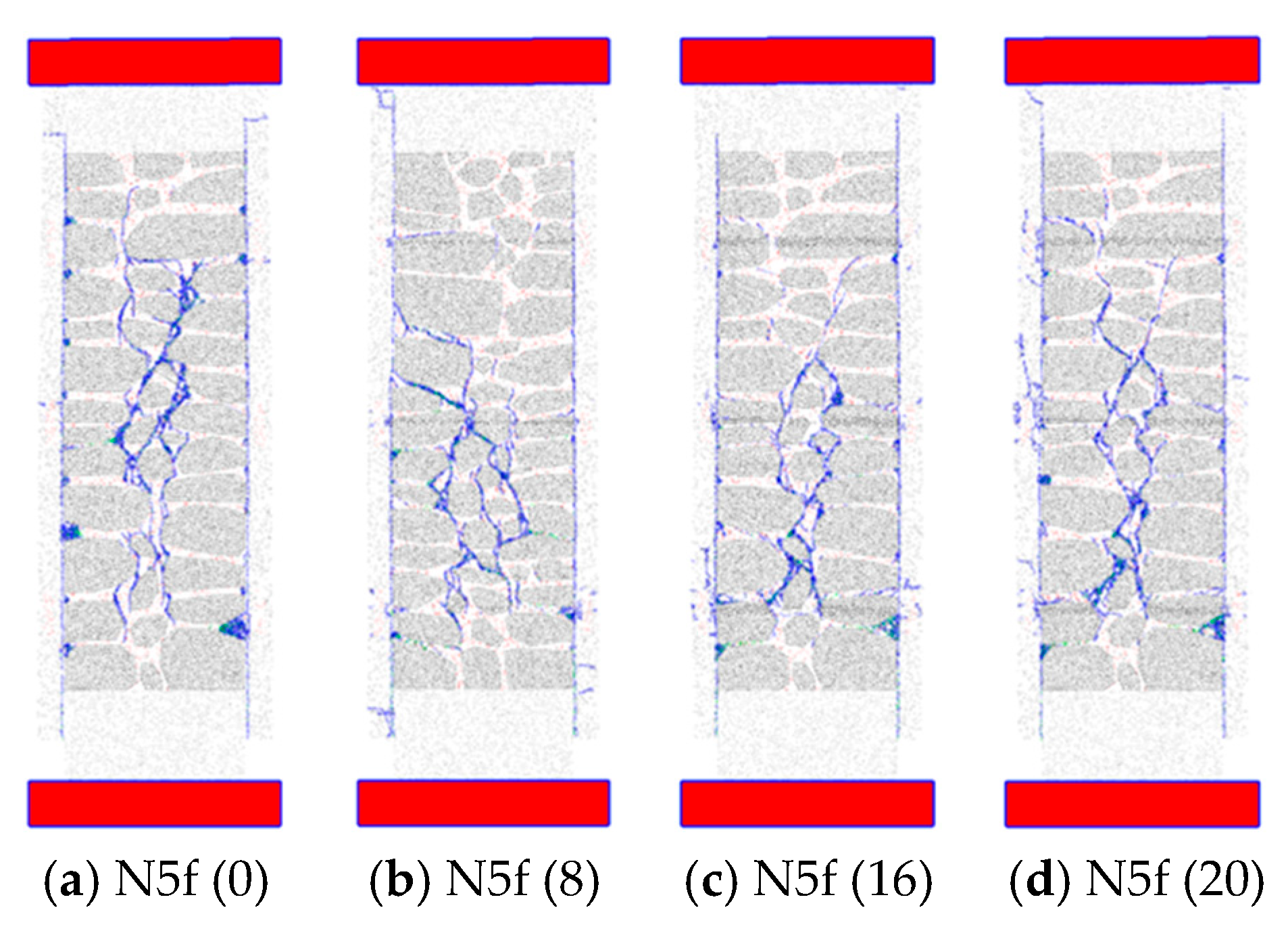
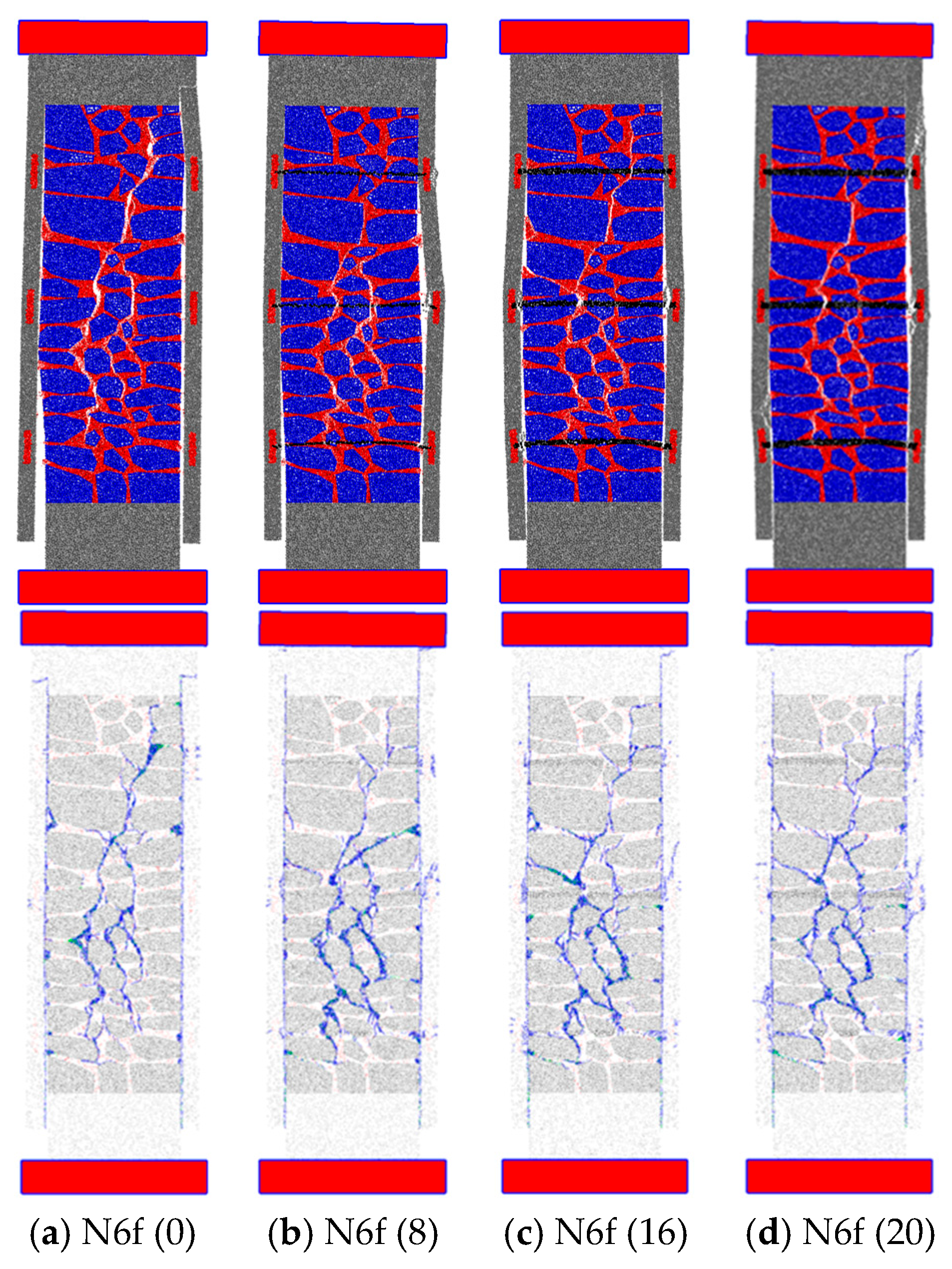
4.2.2. Steel Bar Diameter
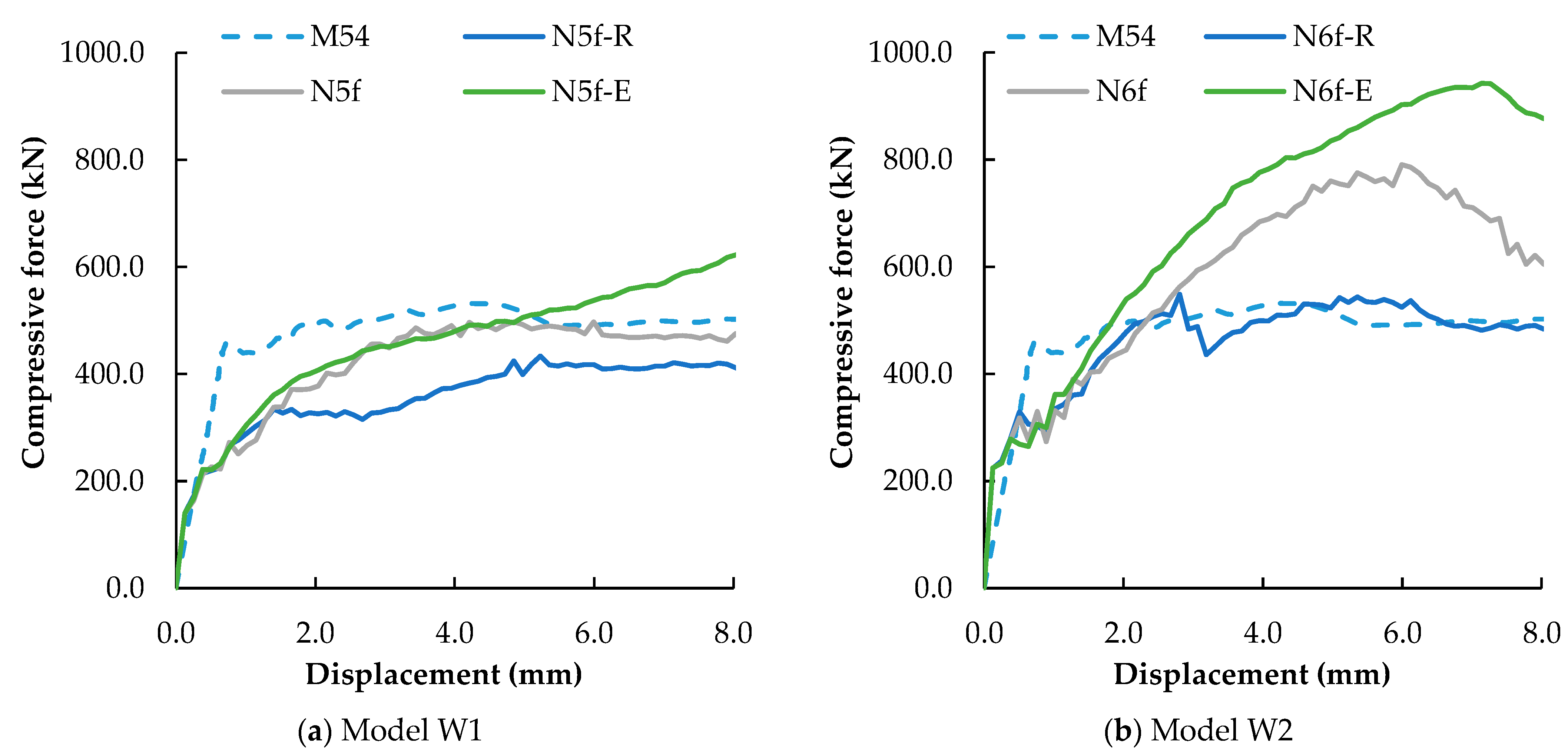
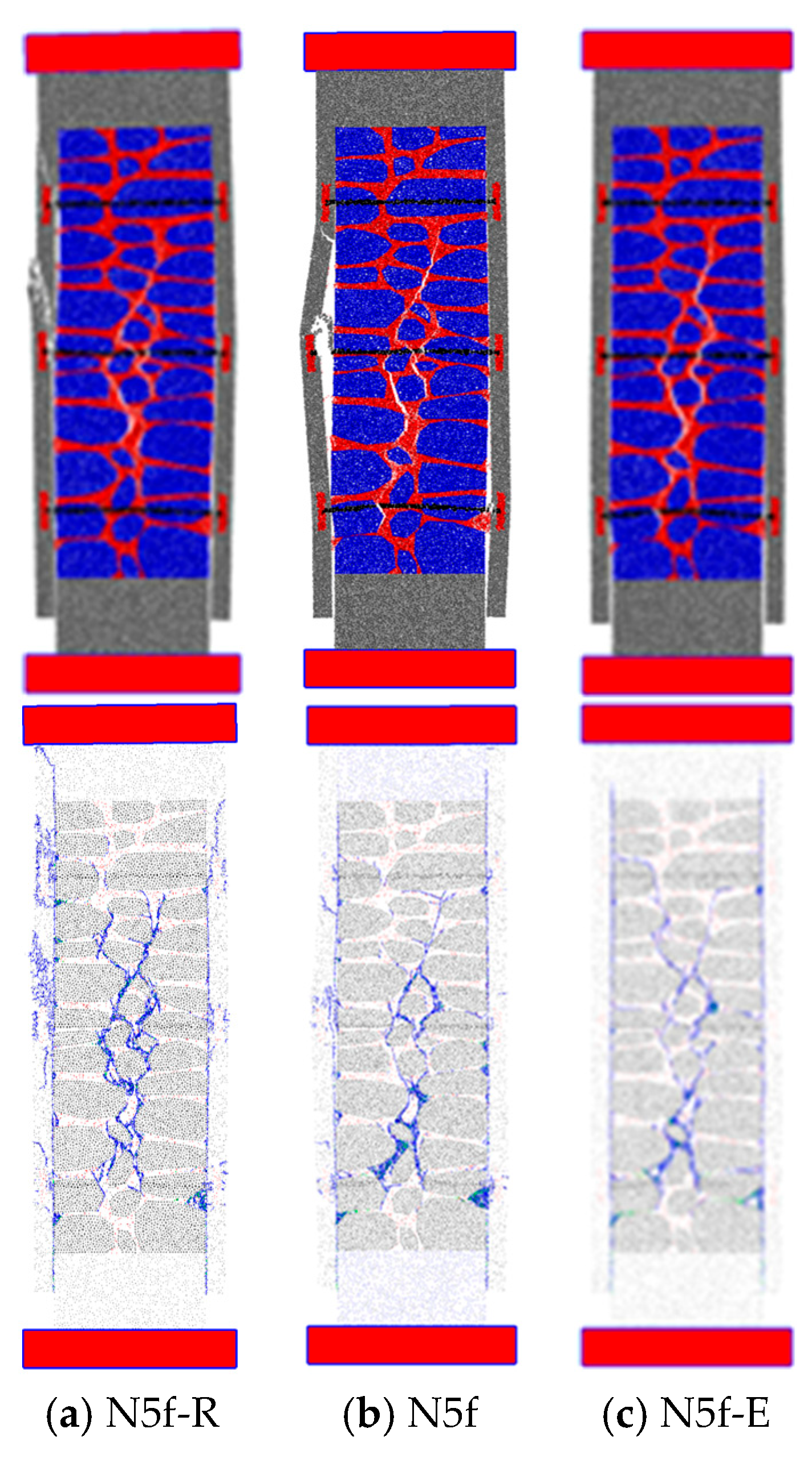
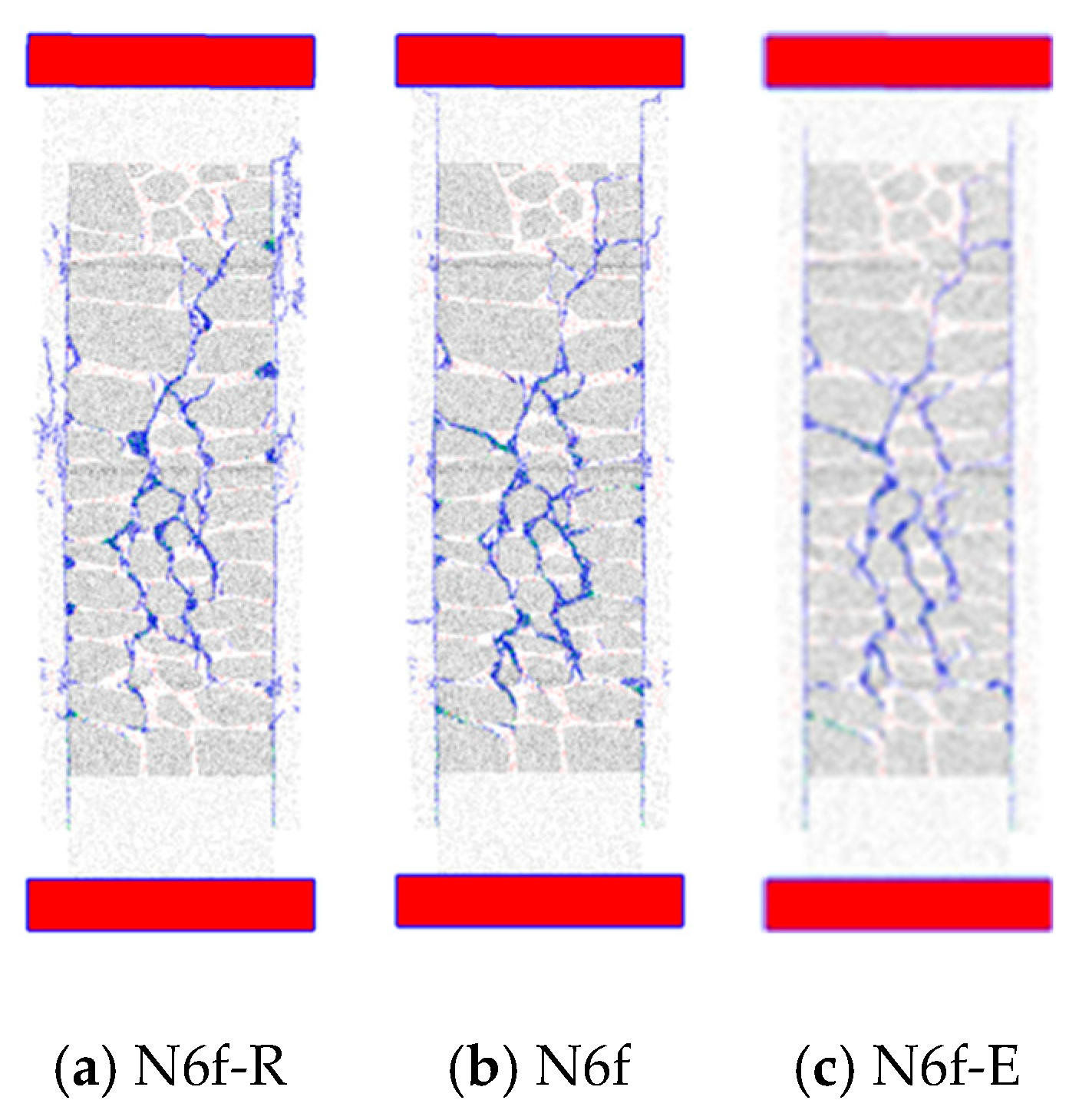
4.2.3. Micro-Concrete Strength Properties
4.3. Modeling Limitations and Future Developments
5. Conclusions
- Micro-concrete strength has a direct influence on both the peak strength and residual strength value. A higher micro-concrete strength yields a higher peak and residual strength.
- The presence of the transverse steel bars is fundamental for lateral confinement to occur, assuring a better transfer of forces from the micro-concrete layer to the masonry walls.
- Despite possible application difficulties (namely, the need to cover metallic elements), the steel plates that are external to the micro-concrete layers contribute to an increase in resistance/strength, as does the presence of transverse steel bars, which are fundamental for lateral confinement to occur, ensuring a more effective transfer of forces from the micro-concrete layer to the masonry wall.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| URM | Unreinforced masonry |
| RM | Reinforced masonry |
| FEM | Finite element method |
| DEM | Discrete element method |
| PM | Particle model |
| RPM | Reinforced particle model |
References
- Roca, P.; Lourenço, P.B.; Gaetani, A. Historic Construction and Conservation: Materials, Systems and Damage; Routledge: New York, NY, USA, 2019. [Google Scholar]
- Malomo, D.; DeJong, M.J.; Penna, A. Influence of bond pattern on the in-plane behavior of URM piers. Int. J. Arch. Herit. 2021, 15, 1492–1511. [Google Scholar] [CrossRef]
- Pulatsu, B.; Gonen, S.; Parisi, F.; Erdogmus, E.; Tuncay, K.; Funari, M.F.; Lourenço, P.B. Probabilistic approach to assess URM walls with openings using discrete rigid block analysis (D-RBA). J. Build. Eng. 2022, 61, 105269. [Google Scholar] [CrossRef]
- Pinho, F.F.S.; Lúcio, V.J.G.; Baião, M.F.C. Rubble stone masonry walls in Portugal strengthened with reinforced micro-concrete layers. Bull. Earthq. Eng. 2012, 10, 161–180. [Google Scholar] [CrossRef]
- Coburn, A.; Spence, R. Earthquake Protection; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Ferretti, F.; Ferracuti, B.; Mazzotti, C.; Savoia, M. Destructive and minor destructive tests on masonry buildings: Experimental results and comparison be-tween shear failure criteria. Constr. Build. Mater. 2019, 199, 12–29. [Google Scholar] [CrossRef]
- İzol, R.; Işık, E.; Avcil, F.; Arslan, M.H.; Arkan, E.; Büyüksaraç, A. Seismic performance of masonry structures after 06 February 2023 earthquakes; site survey and FE modelling approach. Soil Dyn. Earthq. Eng. 2024, 186, 108904. [Google Scholar] [CrossRef]
- Adhikari, R.K.; D’Ayala, D. Nepal earthquake: Seismic performance and post-earthquake reconstruction of stone in mud mortar masonry buildings. Bull. Earthq. Eng. 2020, 18, 3863–3896. [Google Scholar] [CrossRef]
- Brando, G.; Rapone, D.; Spacone, E.; O’Banion, M.S.; Olsen, M.J.; Barbosa, A.R.; Faggella, M.; Gigliotti, R.; Liberatore, D.; Russo, S.; et al. Damage reconnaissance of unreinforced masonry buildings after the 2015 Gorkha, Nepal, earthquake. Earthq. Spectra 2017, 33 (Suppl. 1), 243–273. [Google Scholar] [CrossRef]
- Sorrentino, L.; Cattari, S.; da Porto, F.; Magenes, G.; Penna, A. Seismic behaviour of ordinary masonry buildings during the 2016 central Italy earthquakes. Bull. Earthq. Eng. 2019, 17, 5583–5607. [Google Scholar] [CrossRef]
- Vlachakis, G.; Vlachaki, E.; Lourenço, P.B. Learning from failure: Damage and failure of masonry structures, after the 2017 Lesvos earthquake (Greece). Eng. Fail. Anal. 2020, 11, 104803. [Google Scholar] [CrossRef]
- Bilgin, H.; Leti, M.; Shehu, R.; Özmen, H.B.; Deringol, A.H.; Ormeni, R. Reflections from the 2019 Durrës Earthquakes: An Earthquake Engineering Evaluation for Masonry Typologies. Buildings 2023, 13, 2227. [Google Scholar] [CrossRef]
- Vintzileou, E.; Palieraki, V. Damage to stone masonry buildings in historical centers due to the 2023 earthquake sequence in Turkey. Earthq. Spectra 2024, 40, 2306–2338. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; De Maria, A. The Failure of Masonry Walls by Disaggregation and the Masonry Quality Index. Heritage 2020, 3, 1162–1198. [Google Scholar] [CrossRef]
- Costa, A.; Arêde, A.; Costa, A.; Guedes, J.; Silva, B. Experimental testing, numerical modeling and seismic strengthening of traditional stone masonry: Comprehensive study of a real azorean pier. Bull. Earthq. Eng. 2012, 10, 135–159. [Google Scholar] [CrossRef]
- Gkournelos, P.D.; Triantafillou, T.C.; Bournas, D.A. Seismic upgrading of existing masonry structures: A state-of-the-art review. Soil Dyn. Earthq. Eng. 2022, 161, 107428. [Google Scholar] [CrossRef]
- Keshmiry, A.; Hassani, S.; Dackermann, U.; Li, J. Assessment, repair, and retrofitting of masonry structures: A comprehensive review. Constr. Build. Mater. 2024, 442, 137380. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Silva, R.A.M.; Garbin, E.; Lourénço, P.B. Strengthening of three-leaf stone masonry walls: An experimental research. Mater. Struct. 2012, 45, 1259–1276. [Google Scholar] [CrossRef]
- Porto, F.; Valluzzi, M.R.; Munari, M.; Modena, C.; Arêde, A.; Costa, A.A. Strengthening of Stone and Brick Masonry Buildings. In Strengthening and Retrofitting of Existing Structures; Costa, A., Arêde, A., Varum, H., Eds.; Building Pathology and Rehabilitation; Springer: Singapore, 2018; Volume 9. [Google Scholar] [CrossRef]
- Rezaee, S.R.S.; Soltani, M.; Nikooravesh, M. Cyclic in-plane behavior of un-reinforced and confined masonry walls retrofitted by shotcrete: Experimental investigation. Eng. Struct. 2022, 264, 114432. [Google Scholar] [CrossRef]
- Pinho, F.F.S. Paredes de alvenaria ordinária—Estudo experimental com modelos simples e reforçados, Tese de doutoramento em Engenharia Civil—Ciências da Construção. Ph.D. Thesis, FCT NOVA, Universidade Nova de Lisboa, Lisboa, Portugal, 2007. (In Portuguese). [Google Scholar]
- Pinho, F.F.S.; Lúcio, V.J.G.; Baião, M.F.C. Rubble Stone Masonry Walls Strengthened By Three-dimensional Steel Ties and Textile Reinforced Mortar Render, under Compression and Shear Loads. Int. J. Archit. Herit. 2015, 9, 844–858. [Google Scholar] [CrossRef]
- Penna, A. Seismic assessment of existing and strengthened stone-masonry buildings: Critical issues and possible strategies. Bull. Earthq. Eng. 2015, 13, 1051–1071. [Google Scholar] [CrossRef]
- Pinho, F.F.S.; Lúcio, J.G.V. Rubble stone masonry walls. Material properties, carbonation depth and mechanical characterization. Int. J. Archit. Herit. 2017, 11, 685–702. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computations of historical masonry constructions. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
- D’altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arch. Comput. Methods Eng. 2020, 27, 1153–1185. [Google Scholar] [CrossRef]
- Ibrahim, Y.; Nagy, B.; Benedek, C. Deep Learning-Based Masonry Wall Image Analysis. Remote Sens. 2020, 12, 3918. [Google Scholar] [CrossRef]
- Wang, Q.; Santos, K.R.M.; Beyer, K. Micro Modeling of Irregular Stone Masonry Walls Using Mathematical Programming. In Structural Analysis of Historical Constructions; SAHC 2023. RILEM Bookseries; Endo, Y., Hanazato, T., Eds.; Springer: Cham, Switzerland, 2024; Volume 46. [Google Scholar] [CrossRef]
- Zhang, S.; Mousavi, S.M.T.; Richart, N.; Molinari, J.F.; Beyer, K. Micro-mechanical finite element modeling of diagonal compression test for historical stone masonry structure. Int. J. Solids Struct. 2017, 112, 122–132. [Google Scholar] [CrossRef]
- Zhang, S.; Hofmann, M.; Beyer, K. A 2D typology generator for historical masonry elements. Construct. Build. Mater. 2018, 184, 440–453. [Google Scholar] [CrossRef]
- Roca, P.; Cervera, M.; Gariup, G.; Pela’, L. Structural analysis of masonry historical constructions. Classical and advanced approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar]
- Lourenço, P.B.; Rots, J.G. Multisurface Interface Model for Analysis of Masonry Structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Lemos, J. Discrete element modelling of the seismic behaviour of stone masonry arches. In Computer Methods in Structural Masonry—4 Fourth International Symposium, 1st ed.; Pande, G., Middleton, J., Kralj, B., Eds.; CRC Press: London, UK, 1998; pp. 220–227. ISBN 9780419235408. [Google Scholar]
- Azevedo, N.M.; Lemos, J.V.; Rocha, J.d.A. Discrete Element Particle Modelling of Stone Masonry. In Computational Modeling of Masonry Structures Using the Discrete Element Method; IGI Global: Hershey, PA, USA, 2016; pp. 146–170. [Google Scholar]
- Sarhosis, V.; Lemos, J. A detailed micro-modelling approach for the structural analysis of masonry assemblages. Comput. Struct. 2018, 206, 66–81. [Google Scholar] [CrossRef]
- Cismaşiu, C.; Silva, P.B.S.; Lemos, J.V.; Cismaşiu, I. Seismic Vulnerability Assessment of a Stone Arch Using Discrete Elements. Int. J. Archit. Herit. 2021, 17, 730–744. [Google Scholar] [CrossRef]
- Smoljanović, H.; Živaljić, N.; Željana, N. A combined finite-discrete element analysis of dry stone masonry structures. Eng. Struct. 2013, 52, 89–100. [Google Scholar] [CrossRef]
- Munjiza, A.; Smoljanović, H.; Živaljić, N.; Mihanovic, A.; Divić, V.; Uzelac, I.; Nikolić, Ž.; Balić, I.; Trogrlić, B. Structural applications of the combined finite–discrete element method. Comput. Part. Mech. 2020, 7, 1029–1046. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J.V. A Hybrid Particle/Finite Element Model with Surface Roughness for Stone Masonry Analysis. Appl. Mech. 2022, 3, 608–627. [Google Scholar] [CrossRef]
- Wu, B.; Dai, J.; Jin, H.; Bai, W.; Chen, B. Numerical simulation on the seismic performance of retrofitted masonry walls based on the combined finite-discrete element method. Earthq. Eng. Eng. Vib. 2023, 22, 777–805. [Google Scholar] [CrossRef]
- Chen, X.; Liang, Z.; Chan, A.H. Simulating the damage of rubble stone masonry walls using FDEM with a detailed micro-modelling approach. Comput. Part. Mech. 2024, 11, 2839–2855. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J. Aggregate shape influence in the fracture be-haviour of concrete. Struct. Eng. Mech. 2006, 24, 411–427. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J.V.; Almeida, J. A discrete particle model for reinforced concrete fracture analysis. Struct. Eng. Mech. 2010, 36, 343–361. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. Discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Fernando, F.F.S.; Cismasiu, I.; Souza, M. Prediction of Rubble-Stone Masonry Walls Response under Axial Compression Using 2D Particle Modelling. Buildings 2022, 12, 1283. [Google Scholar] [CrossRef]
- Cismaşiu, I.; Azevedo, N.M.; Fernando, F.F.S. Numerical Evaluation of Transverse Steel Connector Strengthening Effect on the Behavior of Rubble Stone Masonry Walls under Compression Using a Particle Model. Buildings 2023, 13, 987. [Google Scholar] [CrossRef]
- Devanand, K.; Ghiassi, B.; Faramarzi, A.; Mehravar, M. Particle-Based DEM to Assess Masonry Behaviour Under Compression. In 18th International Brick and Block Masonry Conference; Milani, G., Ghiassi, B., Eds.; IB2MaC 2024. Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2025; Volume 613. [Google Scholar] [CrossRef]
- Vasconcelos, G.; Lourenço, P.B. Experimental characterization of stone masonry in shear and compression. Constr. Build. Mater. 2009, 23, 3337–3345. [Google Scholar] [CrossRef]
- Ponte, M.; Penna, A.; Bento, R. In-plane cyclic tests of strengthened rubble stone masonry. Mater. Struct. 2023, 56, 41. [Google Scholar] [CrossRef]
- Saloustros, S.; Settimi, A.; Ascencio, A.C.; Gamerro, J.; Weinand, Y.; Beyer, K. Geometrical digital twins of the as-built microstructure of three-leaf stone masonry walls with laser scanning. Sci. Data 2023, 10, 533. [Google Scholar] [CrossRef]
- Murano, A.; Ortega, J.; Rodrigues, H.; Vasconcelos, G. Updating mechanical properties of two-leaf stone masonry walls through experimental data and Bayesian inference. Constr. Build. Mater. 2021, 298, 123626. [Google Scholar] [CrossRef]
- Croce, P.; Beconcini, M.L.; Formichi, P.; Landi, F.; Puccini, B.; Zotti, V. Bayesian Methodology for Probabilistic Description of Mechanical Parameters of Masonry Walls. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021008. [Google Scholar] [CrossRef]
- Kibriya, G.; Botzheim, J.; Orosz, Á.; Bagi, K. Automatic calibration of a discrete element model of a masonry arch by swarm intelligence methods. Comput. Struct. 2024, 299, 107401. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Lourenço, P.B. Implementation of a constitutive model for the cyclic behaviour of interface elements. Comput. Struct. 2004, 82, 1451–1461. [Google Scholar] [CrossRef]
- Senthivel, R.; Lourenço, P.B. Finite element modelling of deformation characteristics of historical stone masonry shear wall. Eng. Struct. 2009, 31, 1930–1943. [Google Scholar] [CrossRef]
- Riddington, J.R.; Naom, N.F. Finite element prediction of masonry compressive strength. Comput. Struct. 1994, 52, 113–119. [Google Scholar]
- Yan, B.; Regueiro, R.A. Comparison between pure MPI and hybrid MPI-OpenMP parallelism for Discrete Element Method (DEM) of ellipsoidal and poly-ellipsoidal particles. Comput. Part. Mech. 2019, 6, 271–295. [Google Scholar]
- Dong, Y.; Yan, D.; Cui, L. An Efficient Parallel Framework for the Discrete Element Method Using GPU. Appl. Sci. 2022, 12, 3107. [Google Scholar] [CrossRef]








| Material | Experimental Values | Calibrated Values | ||||||
|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (GPa) | (MPa) | (MPa) | (GPa) | |||
| Stone | 47.8 | - | 6.0 | 0.29 | 47.8 | - | 5.9 | 0.30 |
| Mortar | 0.65 | 0.30 | 0.075 | 0.16 | 0.66 | 0.16 | 0.075 | 0.16 |
| Micro-concrete | 37.43 | - | 28.50 | 0.20 | 37.44 | 1.86 | 28.50 | 0.20 |
| Concrete (C25/30) | - | - | 0.075 | 0.16 | - | - | 30.00 | 0.20 |
| Contacts | (GPa) | (MPa) | (MPa) | (N/m) | (N/m) | ||
|---|---|---|---|---|---|---|---|
| s-s | 8.6 | 0.11 | 8.9 | 35.7 | 1.0 | 0.3838 | 56.1403 |
| m-m | 0.09 | 0.43 | 0.22 | 0.22 | 1.0 | 0.0013 | 0.0031 |
| mc-mc | 35.38 | 0.32 | 1.92 | 30.50 | 0.5 | 6.5500 | 46,949.44 |
| c-c | 37.50 | 0.32 | - | - | - | - | - |
| Model | (mm) | Main Characteristic | Designation |
|---|---|---|---|
| W1 | 0.0 | Steel bars are absent | N5f (0) |
| W2 | 0.0 | N6f (0) | |
| W1 | 8.0 | 8 mm diameter steel bars | N5f (8) |
| W2 | 8.0 | N6f (8) | |
| W1 | 12.0 | 12 mm diameter steel bars (reference model) | N5f |
| W2 | 12.0 | N6f | |
| W1 | 16.0 | 16 mm diameter steel bars | N5f (16) |
| W2 | 16.0 | N6f (16) | |
| W1 | 20.0 | 20 mm diameter steel bars | N5f (20) |
| W2 | 20.0 | N6f (20) |
| Model | Main Characteristic | Designation |
|---|---|---|
| W1 | Elastic micro-concrete | N5f-E N6f-E |
| W2 | ||
| W1 | Reference model | N5f N6f |
| W2 | ||
| W1 | Micro-concrete with half of the strength | N5f-R N6f-R |
| W2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azevedo, N.M.; Cismaşiu, I.; Pinho, F.F.S.; Neves, F. Numerical Modeling of Reinforcement Solutions in Traditional Stone Masonry Using a Particle Model. Buildings 2025, 15, 1058. https://doi.org/10.3390/buildings15071058
Azevedo NM, Cismaşiu I, Pinho FFS, Neves F. Numerical Modeling of Reinforcement Solutions in Traditional Stone Masonry Using a Particle Model. Buildings. 2025; 15(7):1058. https://doi.org/10.3390/buildings15071058
Chicago/Turabian StyleAzevedo, Nuno Monteiro, Ildi Cismaşiu, Fernando F. S. Pinho, and Filipe Neves. 2025. "Numerical Modeling of Reinforcement Solutions in Traditional Stone Masonry Using a Particle Model" Buildings 15, no. 7: 1058. https://doi.org/10.3390/buildings15071058
APA StyleAzevedo, N. M., Cismaşiu, I., Pinho, F. F. S., & Neves, F. (2025). Numerical Modeling of Reinforcement Solutions in Traditional Stone Masonry Using a Particle Model. Buildings, 15(7), 1058. https://doi.org/10.3390/buildings15071058









