The Risk Assessment of Bridge Pile Foundation Construction in Karst Regions Based on the Fuzzy Analytic Hierarchy Process

Abstract

The construction of bridge pile foundations in karst regions faces significant risks, including karst collapse and ground subsidence caused by dewatering during excavation. Both karst collapse and shallow soil cavity subsidence are influenced by numerous factors, which significantly complicates the risk assessment of bridge pile foundation construction in these areas. This study proposes a risk assessment method for bridge pile foundation construction in karst regions based on the Fuzzy Analytic Hierarchy Process (FAHP). An evaluation index system for pile foundation construction risks was established through experimental research, expert surveys, and data analysis. Additionally, the concept of fuzzy mathematics was introduced to quantify the weights of the indicators, enabling the comprehensive assessment of multi-source risks. Experimental results from bridges across the project area demonstrate that this method exhibits a certain level of reliability in assessing the risks of bridge pile foundation construction in karst regions, with the evaluation results aligning well with actual conditions.

1. Introduction

Karst is the most distinctive geological process and phenomenon in carbonate rock distribution areas. Influenced by the chemical dissolution and mechanical erosion of water, karst forms grooves, cavities, and fissures in rock masses, which exhibit a highly complex distribution and morphology [1]. These features are often concealed underground, making them difficult to detect. For pile foundation engineering, karst landforms such as caves, fissures, grooves (trenches), underground rivers, and soil caves developed in bedrock pose significant geological hazards [2]. The randomness and unpredictability of these karst landforms can lead to frequent risks during construction, including borehole collapse, slurry leakage, and ground subsidence. These risks not only threaten construction safety but may also cause project delays and cost overruns. The primary risk in bridge pile foundation construction in karst regions is karst collapse. However, due to the influence of numerous interrelated factors, the assessment and prediction of pile foundation construction risks in these areas are highly complex. The risks associated with pile foundation construction in karst regions are multi-source and coupled [3]. In addition to the predominant risk of karst-induced ground collapse, the following risk types are also significant: (1) Hydrogeological Risks: These include the thickness of the overburden, the degree of fissure development in the rock layers, and the intensity of groundwater activity. For example, insufficient stability in the cave roof may lead to pile-bearing capacity failure, loose overburden can cause borehole wall collapse, and fluctuations in groundwater levels may result in sudden drops in slurry levels, exacerbating the risk of borehole collapse [4,5,6]. (2) Technical Risks: These encompass risks related to pile foundation construction techniques, cave treatment technologies, and concrete-pouring processes [7,8]. (3) Environmental and External Risks: These include risks to adjacent structures, ecological impacts, and water source contamination. For instance, vibrations from pile foundation construction may cause cracking in nearby buildings, and the infiltration of chemically treated slurry into karst conduits may pollute groundwater [9,10,11]. (4) Management and Design Risks: These arise from deficiencies in geological surveys and design, as well as lapses in construction management [12,13]. The complexity and interdependence of these factors make risk assessment and management in pile foundation construction in karst regions a challenging yet critical task.

Early research on risk assessment primarily relied on empirical judgment and qualitative analysis. For instance, geological experts assessed risk levels through field surveys and drilling data [1]. However, such approaches struggled to quantify risk probabilities, heavily depended on expert experience, and lacked systematic rigor, making them inadequate for addressing the complexity and uncertainty of karst geology. In recent years, scholars both domestically and internationally have gradually introduced quantitative analysis tools, such as probabilistic statistics, numerical simulation techniques, and the Analytic Hierarchy Process (AHP) [2,9,10,14,15,16,17]. Nevertheless, these methods still fall short in effectively handling the inherent fuzziness and data deficiencies in risk assessment. To address these limitations, the concept of fuzzy mathematics and multi-criteria decision-making methods have been increasingly integrated into the field of risk assessment. For example, Perrin et al. proposed a multi-criteria approach based on weight-of-evidence analysis for predicting karst geological hazards [18]. Zhang et al. [19] developed a system for assessing surface stability in karst regions using an improved fuzzy comprehensive evaluation method, with the results showing good agreement with historical records of ground subsidence. Wei et al. [20] combined the Analytic Hierarchy Process, catastrophe theory, and entropy models to evaluate susceptibility to karst collapse. Lou et al. [21] introduced a high-precision risk assessment method specifically tailored to thermokarst hazards in permafrost regions. Zhang et al. [22] established a risk assessment system for ground subsidence along tunnels in karst areas by refining and extending evaluation methods. Additionally, Lu et al. [23] enhanced the network structure analysis method, addressing the inherent subjectivity in weight allocation.

In summary, although existing studies have established multi-level risk assessment frameworks for construction in karst regions, they often analyze individual risks in isolation and fail to adequately consider the interactions among geological, technical, and managerial factors. Furthermore, most assessments are conducted based on regional engineering projects, and a unified standard system has yet to be established. The establishment of a unified standard system can improve the accuracy and credibility of risk assessment. To address these issues, this paper proposes a risk assessment model for bridge pile foundation construction in karst areas based on the Fuzzy Analytic Hierarchy Process (FAHP). By utilizing fuzzy mathematics to quantify the uncertainty of expert judgment and incorporating a dynamic weight adjustment mechanism, the model enables the collaborative assessment of multi-source risks. This research is expected to provide more accurate risk prediction and decision-making support for bridge engineering in complex geological conditions.

2. Fuzzy Analytic Hierarchy Process (FAHP)

FAHP is an extension of the traditional Analytic Hierarchy Process (AHP) that incorporates fuzzy logic to handle uncertainty and imprecision in decision-making [19]. It combines the principles of AHP with fuzzy set theory to address situations where the criteria or judgments are subjective, vague, or unclear.

2.1. Establishing the Hierarchy

According to the AHP method, based on the specific conditions of bridge pile foundations in karst regions, we selected the primary and secondary factor sets that influenced the risk levels, established a hierarchy that reflected the relationships between these factors, and constructed a hierarchical structure.

2.2. Calculating Triangular Fuzzy Numbers

Triangular fuzzy numbers are used to integrate the experts’ opinions, thereby establishing a more objective fuzzy judgment matrix as much as possible. It is assumed that through expert surveys, the relative importance between the i and j elements at a certain level under a given criterion has been determined by k experts and is represented by $B_{ijk}$.

$$a_{ij}=\left(l_{ij},m_{ij},u_{ij}\right)$$

(1)

$$l_{ij}=\min (B_{ijk})$$

(2)

$$m_{ij}={\left({\displaystyle \prod _{k=1}^n{B}_{ijk}}\right)}^{1/n}$$

(3)

$$u_{ij}=\max \left(B_{ijk}\right)$$

(4)

where k is the number of scoring experts; $B_{ijk}$ is the score of experts k on the relative importance of attributes i and j; $\min \left(B_{ijk}\right)$ is the minimum value of all expert scoring results; $\max \left(B_{ijk}\right)$ is the maximum value of all expert scoring results; and ${\left({\displaystyle \prod _{k=1}^n{B}_{ijk}}\right)}^{1/n}$ is the geometric mean of all expert scoring results.

2.3. Establishing a Fuzzy Judgment Matrix

By combining the actual conditions of bridge pile foundations in karst areas with expert surveys, field tests, mechanical experiments, and other methods, the importance of various factors affecting the risk classification of bridge pile foundations is obtained. Triangular fuzzy numbers are calculated, and a fuzzy judgment matrix can be established.

$$A={\left(a_{ij}\right)}_{n\times n}=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right]$$

(5)

where $a_{ij}=\left[l_{ij},m_{ij},u_{ij}\right]$ denotes the triangular fuzzy number, and $a_{ji}=\left[{\displaystyle \frac{1}{u_{ij}}},{\displaystyle \frac{1}{m_{ij}}},{\displaystyle \frac{1}{l_{ij}}}\right]$, $a_{ij}>0$,$a_{ij}\times a_{ij}\approx 1$ ($i,j=1,2,3,\dots n$). The scale of $a_{ij}$ is judged according to the scale method of 1 to 9. A two-by-two comparison is performed of the importance of factors at the same level, as shown in

Table 1. Scale definitions for 1 to 9.

Scale	Define
1	Indicates that the two are of equal importance compared to each other
3	Indicates the relative importance of the former compared to the latter
5	Indicates that the former is more important than the latter
7	Indicates that the former is quite important compared to the latter
9	Indicates that the former is very important compared to the latter
2, 4, 6, 8	Indicates a compromise between the two scales
Countdown of the above values	Denotes that the latter is more important than the former

.

2.4. Calculating Fuzzy Weights

Based on the obtained judgment matrix, the fuzzy weight values for each influencing factor can be calculated. In the process of calculating the comprehensive evaluation fuzzy weights, the geometric mean fuzzy weight method proposed by J. J. Buckley is used to calculate the fuzzy weights of the factors in the fuzzy pairwise comparison matrix. This method not only considers the consistency index (CI) but also meets the normalization requirements [24]. It also has significant advantages in terms of stability, consistency, multi-level decision-making, mathematical properties, fuzzy handling, and computational simplicity. The consistency test states that the CR of the matrix should be less than 0.1. The calculation process is as follows:

$$CR={\displaystyle \frac{CI}{RI}}$$

(6)

$$CI={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(7)

In this formula, ${\lambda }_{\max }$ represents the maximum eigenvalue of the judgment matrix, and n denotes the order of the matrix. RI is the random consistency index, which can be obtained by referring to a standard table. The standardized table is shown in

Table 2. Standard table of random consistency index (RI) values.

Order of Matrix	1	2	3	4	5	6	7	8	9	10
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

.

We assume that the fuzzy matrix $A=\left[a_{ij}\right]$ has satisfied the consistency requirement of becoming a symmetric matrix and $a_{ij}=\left[l_{ij},m_{ij},u_{ij}\right]$ is a triangular fuzzy number. The first step is to calculate the column geometric mean of each column of matrix A.

$$z_i={\left[a_{i1}\otimes \cdots \otimes a_{in}\right]}^{1/n}$$

(8)

Then, the weight of the ith factor is

$$w_i=z_i\otimes {\left(z_1\oplus \cdots \oplus z_n\right)}^{-1}$$

(9)

where $\oplus$ and $\otimes$ denote the addition and multiplication of fuzzy numbers, respectively, and $W_i$ is a column vector of fuzzy weights for each factor.

After obtaining the fuzzy weights of each factor, the fuzzy values are regularized by geometric averaging to obtain explicit weight values:

$${\tilde{W}}_i=\sqrt[3]{w_{il}\times w_{im}\times w_{iu}}$$

(10)

$$W_i={\tilde{W}}_i/{\displaystyle \sum _{j=1}^n{\tilde{W}}_j}$$

(11)

2.5. Calculating the Construction Safety Risk Value

When establishing a hierarchical structure for safety risk assessment in bridge pile foundation construction in a karst area, it is necessary to formulate the corresponding scoring criteria at the same time. Based on the scoring criteria, a value $r_i$ can be assigned to each influence factor, and after obtaining the fuzzy weight $W_i$ of each evaluation factor, the total value for the construction safety risk assessment can be calculated.

$$R={\displaystyle \sum _{i=1}^n(}{r}_i\times W_i)$$

(12)

2.6. Establishing Grading Standards

After obtaining the total safety risk value for bridge pile foundation construction in karst areas, it is necessary to establish a grading standard for construction risks. This will allow the risk level of the project to be determined based on the value, providing a reference for the next steps in risk management. The risk level reference table is shown in

Table 3. Risk classification reference table for bridge pile foundation construction in a karst area.

Risk Level	Overall Risk Value for Bridge Piling Construction Safety, R
Significant risk (IV)	R > 5.5
Higher risk (III)	4 < R ≤ 5.5
General risk (II)	2.5 < R ≤ 4
Low risk (I)	R ≤ 2.5

The data in the table are empirical values obtained from experiments and are for reference only. Can be adapted to the actual situation.

.

3. Application Case

3.1. Project Overview

The research is based on the Qinghua Expressway project located in Guangdong Province, China. The route generally runs from north to south, starting in Taiping Town, Qingxin District, Qingyuan City, and ending in Tanbu Town, Huadu District, Guangzhou City. The total length of the route is approximately 53.728 km, with 45 mainline bridges spanning a total of 29,774.1 m. Among these, there are 11 extra-large bridges totaling 14,153.6 m, 28 large bridges totaling 15,175.5 m, and 6 medium bridges totaling 445.0 m. The bridge-to-total-length ratio is approximately 55.42%.

The Qinghua Expressway project traverses a variety of geomorphological types, primarily including tectonically denuded hills interspersed with inter-hill valleys, alluvial plains, and local low-relief hills and low-mountainous areas. The project area is influenced by the Qinhuang River, Beijiang River, its tributary the Dayan River, and the Baini River, which have formed extensive alluvial plains. The plain regions are characterized by flat and open terrain, offering relatively convenient transportation conditions. The primary adverse geological conditions in the project area include concealed karst, collapses, and sand liquefaction. According to the geological survey results of the Qinghua Expressway project, karst regions are widely distributed along the route, with a cumulative length of approximately 34.8 km, accounting for 64% of the total route length. The borehole encounter rate of cavities at bridge sites ranges from 34.8% to 100%, while the linear dissolution rate varies between 5.0% and 42.4%. The geologic overview of the study area is shown in Figure 1.

The groundwater in the study area exhibits significant annual variations, with one to two peak water levels occurring between April and September, and a low water level observed in January. Additionally, the water table of the Quaternary unconsolidated porous aquifers is relatively shallow, with the thickness of the Quaternary strata generally ranging from 5 to 60 m. Following heavy rainfall, the water level rises rapidly, typically reaching its peak within about 10 h. The annual fluctuation range of the water level is between 1 and 4 m.

3.2. Evaluation Content

3.2.1. Determination of Evaluation Indicators

The methods for determining evaluation indicators include theoretical analysis, expert interviews, questionnaire surveys, and analysis of practical engineering cases. In this study, the risk assessment indicator system was established by reviewing the distribution characteristics of karst in Guangdong, researching disaster mechanisms, and consulting experts. The assessment indicators and scoring guidelines are shown in

Table 4. Level 1 indicators (criterion-level).

L1 Indicator	Clarification
Pile characteristics (A1)	Pile length, diameter, and quantity directly affect construction difficulty.
Geohydrological conditions (A2)	Directly affects the stability of pile foundations and is a core risk factor in karst areas.
Construction environment (A3)	Constraints on construction space due to terrain, crossings, etc.
Construction technology (A4)	Lack of technical maturity and experience may lead to operational errors.

,

Table 5. Level 2 indicators (alternative-level).

L1	L2 Indicator	Clarification
A1	Foundation pile factor (A11)	Includes type of piles, length of piles, and number of pile foundations.
A2	Geological engineering conditions (A21)	Indicates the geological structure of the work area, adverse geological phenomena, etc.
	Degree of karst development (A22)	Refers to the distribution density, size, and filling of caves.
	Groundwater dynamics (A23)	Depth of burial and seasonal variations in groundwater.
	Cover thickness (A24)	Type of foundation soil layer (e.g., sand, clay) and its thickness.
	Hardness of the top rock layer (A25)	Lithology and hardness of the rock layer on the roof of the cave.
A3	Route crossing (A31)	Refers to local topographical conditions and transportation.
	Nearby facilities(A32)	Foundation form and load distribution of neighboring buildings and their effect on pile foundation construction.
A4	Construction process (A41)	Refers to the method of hole formation, concrete placement process, etc.
	Construction experience (A42)	Successes and failures in construction under similar geologic conditions.

and

Table 6. Scoring criteria for indicators.

Indicators	Rate
	[0,2]	[3,5]	[6,8]	[9,10]
Foundation pile factor (A11)	L < 10 m/D < 1 m	L < 30 m/D < 2 m	L > 30 m/D > 2 m	L > 50 m/D > 5 m
Geological engineering conditions (A21)	Simple geology, no karst	Weak karst geology	Single-story cave	Multilayered cavern
Degree of karst development (A22)	Linear karst ratio: <10%	Linear karst ratio: 10–30%	Linear karst ratio: 3060%	Linear karst ratio: >60%
Groundwater dynamics (A23)	Q < 50 m3/d/fluctuation < 0.5 m/d	Q ≤ 200 m3/d/fluctuation ≤ 2 m/d	Q > 200 m3/d/fluctuation > 2 m/d	-
Cover thickness (A24)	H > 30 m	30 m > H > 10 m	H < 10 m	H < 5 m
Hardness of the top rock layer (A25)	Rc ≤ 30 Mpa	Rc ≤ 60 Mpa	Rc > 60 Mpa	-
Route crossing (A31)	Non-crossing	Country road	Class I roads/class IV waterways	Crossing high-speed rail or highway
Nearby facilities (A32)	No	50 m < Gap	5 m < gap < 50 m	-
Construction process (A41)	Mature	Simple	Conventional	Complex
Construction experience (A42)	Similar projects ≥ 3	Similar projects ≥ 1	Inexperienced	-

.

3.2.2. Calculation of Indicator Weights

The weights of the indicators were determined using the FAHP method, and the calculation process is as follows: Firstly, it is necessary to collect the importance evaluation results of each factor independently provided by five experts in related fields (the criteria for selecting experts here are that at least five professors or experts from different fields should be selected and these experts should include, for example, geological engineers, geotechnical engineers, construction technicians, etc. These experts should have high recognition and a good reputation in the industry, to ensure the comprehensiveness and accuracy of the evaluation). Then, a fuzzy positive reciprocal matrix A is established using fuzzy theory. For the first-level factor set (A₁, A₂, A₃, A₄), matrix A can be decomposed into three matrices.

$$A=\left[\begin{array}{cccc}\left(1,1,1\right)& \left(0.111,0.237,1\right)& \left(0.111,1.236,7\right)& \left(0.111,0.542,7\right)\\ \left(1,4.213,9\right)& \left(1,1,1\right)& \left(3,5.733,9\right)& \left(7,8.207,9\right)\\ \left(0.143,0.809,9\right)& \left(0.111,0.174,0.333\right)& \left(1,1,1\right)& \left(0.111,1.747,7\right)\\ \left(0.143,1.845,9\right)& \left(0.111,0.122,0.143\right)& \left(0.143,0.572,9\right)& \left(1,1,1\right)\end{array}\right],$$

$$l=\left[\begin{array}{cccc}1& 0.111& 0.111& 0.111\\ 1& 1& 3& 7\\ 0.143& 0.111& 1& 0.111\\ 0.143& 0.111& 0.143& 1\end{array}\right], m=\left[\begin{array}{cccc}1& 0.237& 1.236& 0.542\\ 4.213& 1& 5.733& 8.207\\ 0.809& 0.174& 1& 1.747\\ 1.845& 0.122& 0.572& 1\end{array}\right], \mu =\left[\begin{array}{cccc}1& 1& 7& 7\\ 9& 1& 9& 9\\ 9& 0.333& 1& 7\\ 9& 0.143& 9& 1\end{array}\right]$$

We calculate the geometric mean of the columns:

$${\left({\displaystyle \prod _{k=1}^4{l}_{1k}}\right)}^{1/4}={(1,1,0.143,0.143)}^{1/4}=0.192$$

The same reasoning leads to

$${\displaystyle \prod _{k=1}^4{l}_{2k}}=2.141,{\displaystyle \prod _{k=1}^4{l}_{3k}}=0.205,{\displaystyle \prod _{k=1}^4{l}_{4k}}=0.218$$

$${\displaystyle \prod _{k=1}^4{m}_{1k}}=0.631,{\displaystyle \prod _{k=1}^4{m}_{2k}}=3.752,{\displaystyle \prod _{k=1}^4{m}_{3k}}=0.705,{\displaystyle \prod _{k=1}^4{m}_{4k}}=0.599$$

$${\displaystyle \prod _{k=1}^4{u}_{1k}}=2.646,{\displaystyle \prod _{k=1}^4{u}_{2k}}=5.196,{\displaystyle \prod _{k=1}^4{u}_{3k}}=2.140,{\displaystyle \prod _{k=1}^4{u}_{4k}}=1.845$$

The fuzzy weights are then calculated:

$${}^{0}w_1=\left[{\displaystyle \frac{({\displaystyle \prod _{k=1}^6{l}_{1k}{)}^{1/6}}}{{\displaystyle \sum _{j=1}^6{\left({\displaystyle \prod _{k=1}^6{u}_{jk}}\right)}^{1/6}}}},{\displaystyle \frac{({\displaystyle \prod _{k=1}^6{u}_{1k}{)}^{1/6}}}{{\displaystyle \sum _{j=1}^6{\left({\displaystyle \prod _{k=1}^6{l}_{jk}}\right)}^{1/6}}}}\right]=\left[0.016,0.960\right], {}^{1}w_1={\displaystyle \frac{({\displaystyle \prod _{k=1}^6{m}_{1k}{)}^{1/6}}}{{\displaystyle \sum _{j=1}^6{\left({\displaystyle \prod _{k=1}^6{m}_{jk}}\right)}^{1/6}}}}=\left[0.111\right]$$

i.e., $w_1=\left[0.016,0.111,0.960\right]$. Similarly, the fuzzy weights of the remaining factors can be obtained as follows:

$$w=\left[\begin{array}{ccc}0.181& 0.660& 1.885\\ 0.017& 0.124& 0.777\\ 0.019& 0.105& 0.669\end{array}\right]$$

The regularization of the fuzzy weight values using the geometric mean method gives the relative weights of the first-level factors:

(A₁, A₂, A₃, A₄) = (0.159, 0.536, 0.157, 0.148)

The remaining indicators were calculated in the same way as above, and the results are shown in

Table 7. Table of indicator weights.

L1	Weight	L2	Weight	WTL	WTLIRM
Pile characteristics (A1)	0.159	Foundation pile factor (A11)	1.000	0.159	0.170
Geohydrological conditions (A2)	0.536	Geological engineering conditions (A21)	0.181	0.097	0.110
		Degree of karst development (A22)	0.352	0.189	0.190
		Groundwater dynamics (A23)	0.196	0.105	0.130
		Cover thickness (A24)	0.136	0.073	0.050
		Hardness of the top rock layer (A25)	0.135	0.072	0.030
Construction environment (A3)	0.157	Route crossing (A31)	0.517	0.081	0.090
		Nearby facilities (A32)	0.483	0.076	0.070
Construction technology (A4)	0.148	Construction process (A41)	0.904	0.134	0.150
		Construction experience (A42)	0.096	0.014	0.010

It should be noted that the weights in the table are empirical values obtained from this experiment and may have some regional limitations. When applying them to other work areas, it is necessary to recalculate and dynamically adjust the weighting coefficients of the indicators to ensure the accuracy of the evaluation.

. The target level weights (WTL) are equal to the weight of each level 2 indicator multiplied by the weight of the corresponding level 1 indicator.

In addition to consistency checks, the results of the calculations need to ensure that the sum of the weights of the indicators at each level is 1, thus guaranteeing the homogeneity of the system.

3.3. Evaluation Results

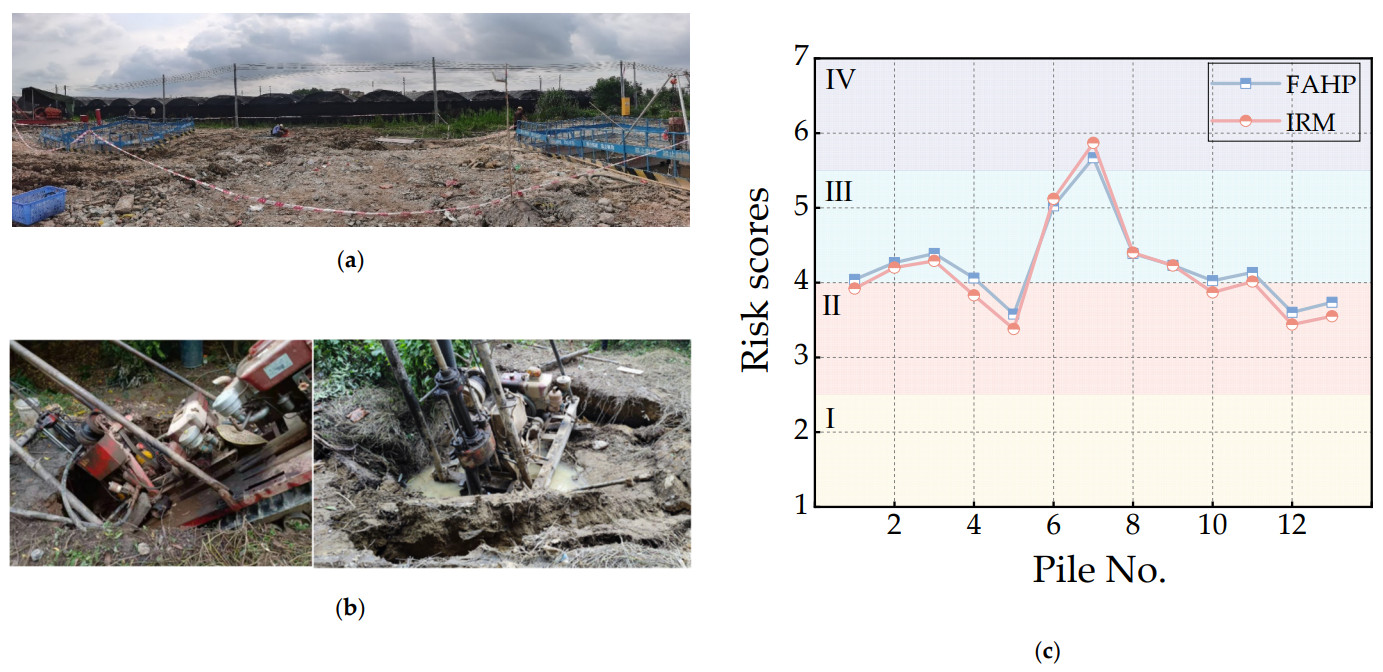
According to the construction ground investigation report of the Qinghua Expressway section, some pile foundations were involved in accidents such as ground collapse and borehole collapse during the investigation and construction stages, as shown in

Table 8. Pile foundation incident record table.

Pile No.	Borehole Number	Accident Type	FAHP Score	IRM Score
1	BNHQZK11	Ground subsidence	4.042	3.920
2	BNHQZK107	Ground subsidence	4.266	4.200
3	BNHQZK106	Ground subsidence	4.388	4.290
4	BNHQZK110	Pile machine tilting	4.061	3.830
5	BNHQZK14	Borehole collapse	3.579	3.380
6	BNHQZK160	Ground subsidence	5.025	5.120
7	BNHQZK170	Ground subsidence	5.670	5.870
8	BNHQZK179	Pile machine tilting	4.389	4.400
9	BNHQZK198	Ground subsidence	4.231	4.230
10	BNHQZK66	Ground subsidence	4.025	3.870
11	HBIQZK15	Pile machine tilting	4.136	4.013
12	HSQZK20	Borehole collapse	3.602	3.440
13	HSQZK29	Borehole collapse	3.737	3.550

. Based on the determined index system, the weight coefficients of each factor were calculated by the FAHP and IRM (refer to Appendix A for the calculation methodology) methods, respectively (e.g., Table 7), and then the risk assessment of accidental pile foundations in Table 8 was carried out. The scoring criteria for the indicators are shown in Table 6 (on a 10-point scale).

The evaluation results are shown in Figure 2c, where the scores for the accident pile foundations are generally consistent between the two methods. Specifically, when the score is greater than 4.4, the IRM yields a higher score than the FAHP method. When the score is lower than 4.4, the FAHP method yields a higher score than the IRM. Based on the weight coefficient values of the two methods presented in Table 7, this outcome arises because the IRM, in comparison to the FAHP method, assigns slightly larger weights to the higher-ranked factors and smaller weight coefficients to the lower-ranked factors. This may be due to the IRM not adequately taking into account the correlation between the indicators and the systematic nature of the indicators. For pile foundations 1, 4, and 10, the evaluation levels differ between the two methods, with the FAHP method assigning a Level III rating and the IRM assigning a Level II rating. Since all evaluated pile foundations are accident pile foundations, a higher risk evaluation score indicates greater reliability for high-risk pile foundations. Therefore, it can be concluded that the FAHP method provides a more accurate assessment in this case, as the evaluation results are more in line with the actual situation and are thus more reasonable.

Finally, the risk of pile foundation construction for four different types of bridge in the Qinghua Expressway section was evaluated using the FAHP method, and the relevant parameters of the bridges are shown in

Table 9. Parameters related to bridges.

Bridge	Length/m	No. Piles	Karst Encounter Rate	Linear Karst Rate	Depth of Groundwater Table/m	Route Crossing
Bai Nihe Bridge	2166.400	169.000	53.670%	3.140–36.860%	1.000–7.300	Crossing S112, Baini River
Hengbei Bridge	975.600	30.000	36.000%	5.200–39.900%	0.800–16.800	Plain
Dayanhe Super Bridge	325.000	41.000	70.500%	31.500%	0.600–3.200	Crossing the Dayan River
Beijiang Super Bridge	1440.000	45.000	71.000%	12.300%	0.900–2.000	Crossing the North River

.

The evaluation results are illustrated in Figure 3. As can be observed from the results, among the four bridges, Class II piles constitute the largest proportion: 40.48% for the Baini River Grand Bridge, 53.33% for the Hengbei Bridge, 60% for the main bridge of the Dayan River Grand Bridge, and 64.44% for the Beijiang Grand Bridge. The proportions of Class I and Class IV piles are relatively smaller. Specifically, Class I piles account for 21.43%, 33.33%, 0%, and 0%, respectively, while Class IV piles account for 6.55%, 0%, 7.32%, and 4.44%, respectively. Notably, besides the Hengbei Bridge, the other three bridges have pile foundations with Class IV construction risks. This is attributed to the relatively stable site conditions and weaker karst development (the linear karst rate is 12.3%) in the bridge area of the Hengbei Bridge. The mean risk scores for four bridges are all in the range of 3–4, and the standard deviation of the scores was around 1.000, The specific values are shown in

Table 10. Bridge scoring result statistics.

Bridge	Bai Nihe	Hengbei	Dayanhe	Beijiang
Average ± standard deviation	3.674 ± 1.134	3.072 ± 0.894	3.984 ± 1.000	3.867 ± 0.825

. This result indicates that the overall construction risk of bridge pile foundations in the area is average to high, with small differences in risk between bridges. Based on the evaluation results and actual construction survey data, the risk level assessments of the four bridges are generally consistent with the actual working conditions. Therefore, the evaluation results can serve as an important reference for subsequent construction activities.

4. Conclusions and Future Prospects

A risk assessment model for bridge pile foundation construction in karst areas based on the Fuzzy Analytic Hierarchy Process (FAHP) is proposed, establishing a comprehensive evaluation index system. This model employs fuzzy mathematical concepts to quantify the subjective experiences inherent in traditional evaluations while incorporating a dynamic weight adjustment mechanism to enable the synergistic assessment of multi-source risks.

The construction risk scores of accident pile foundations were calculated based on the weight coefficients of each factor obtained using the FAHP method and the IRM, respectively. The results indicate that the scores derived from the FAHP method are relatively higher. Higher scores signify greater pile foundation risks, which aligns with the initial assumptions, thereby demonstrating that the weight coefficients calculated by the FAHP method are more reasonable. Finally, the FAHP method was employed to assess the construction risks of pile foundations for four different types of bridges within the working area. The results show that the average risk values of the bridges are all in the range of 3 to 4 points, and the standard deviations are all around 1.000. The evaluation conclusions are largely consistent with actual working conditions.

There are many risk factors affecting the pile foundation construction of bridges in karst regions, and different regions have corresponding local characteristics. This evaluation was conducted based on the area along the Qinghua Expressway in Guangdong Province, where the project is located. The selection of risk factors may have certain limitations. Further research can be conducted in the future to identify more representative risk factors, thereby expanding the scope of application.