A Study on the Calculations of the Bottom Void Range of an Underground Pipe Gallery Structure Under the Action of Ground Fissure Dislocations
Abstract
1. Introduction
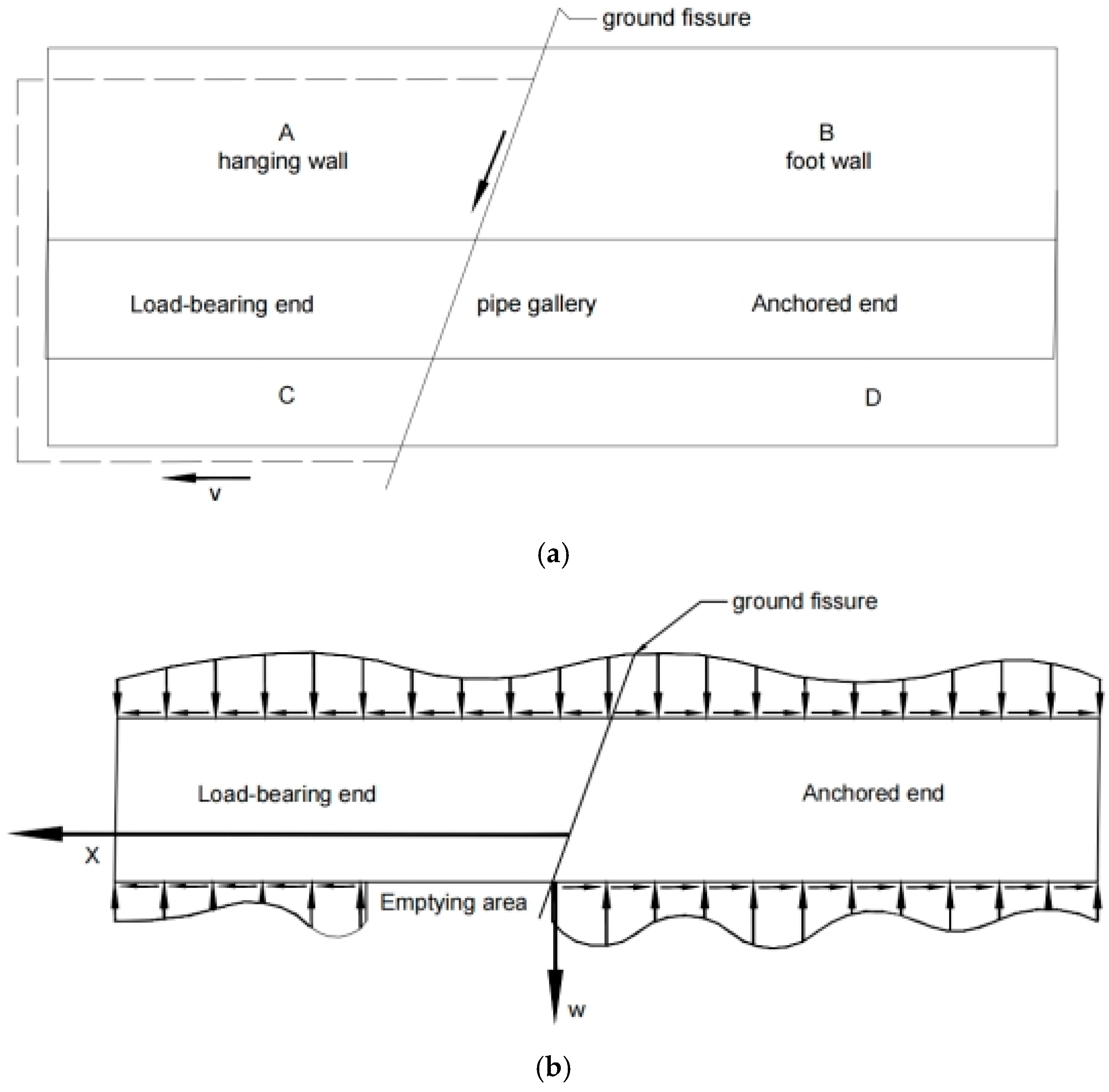
2. Bottom Void Mechanism of Pipe Gallery
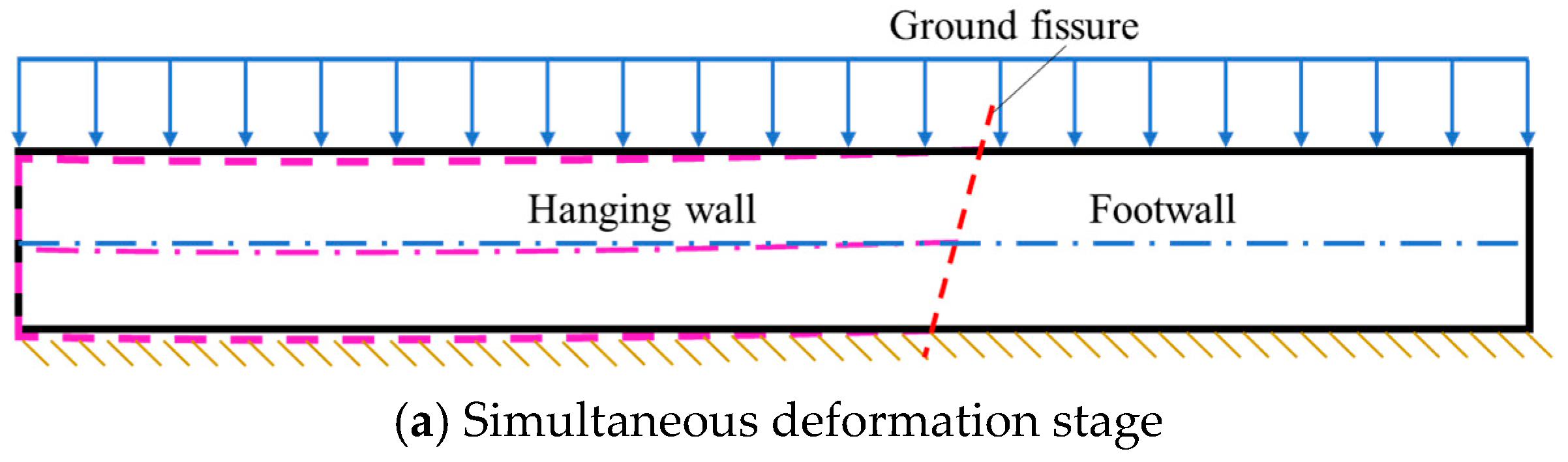
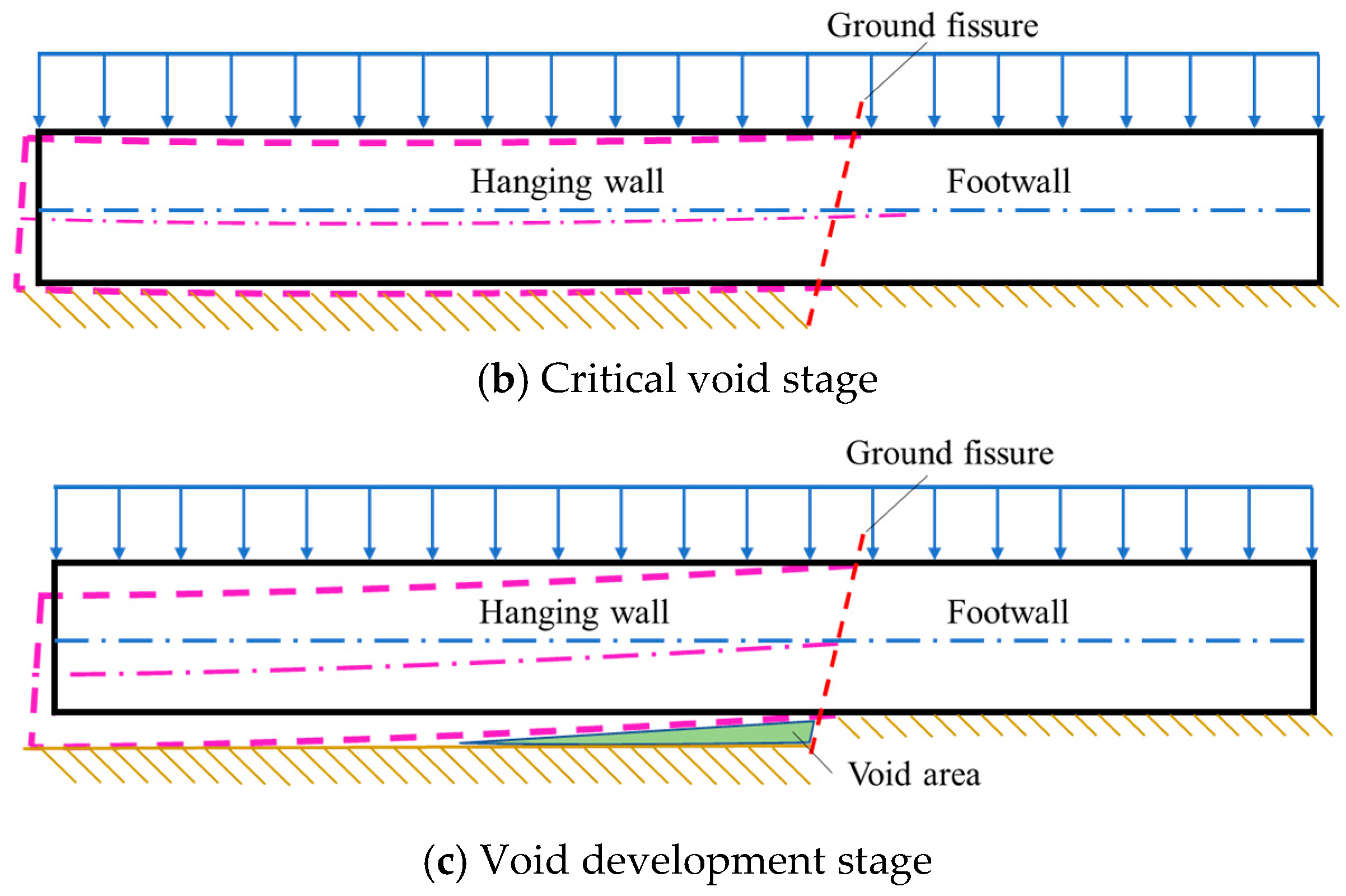
2.1. Mechanism Analysis of Structural De-Voiding in Pipeline Corridors in Region of Ground Cracks
2.2. The Process of Dehollowing at the Bottom of the Pipeline Corridor
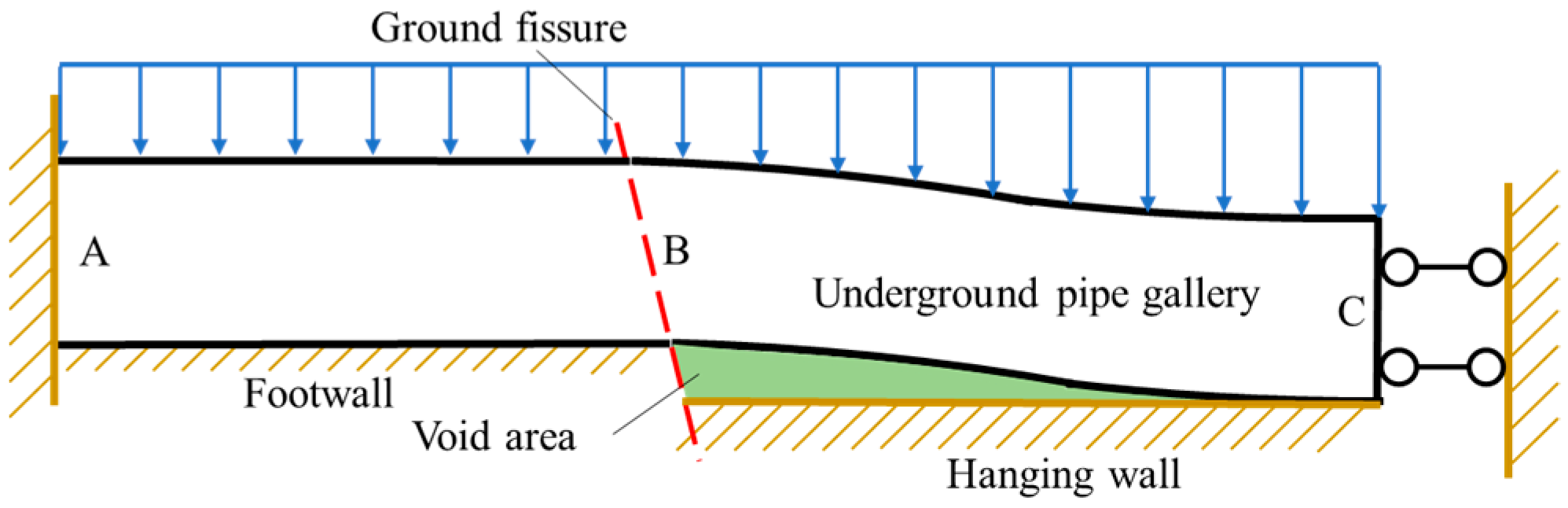
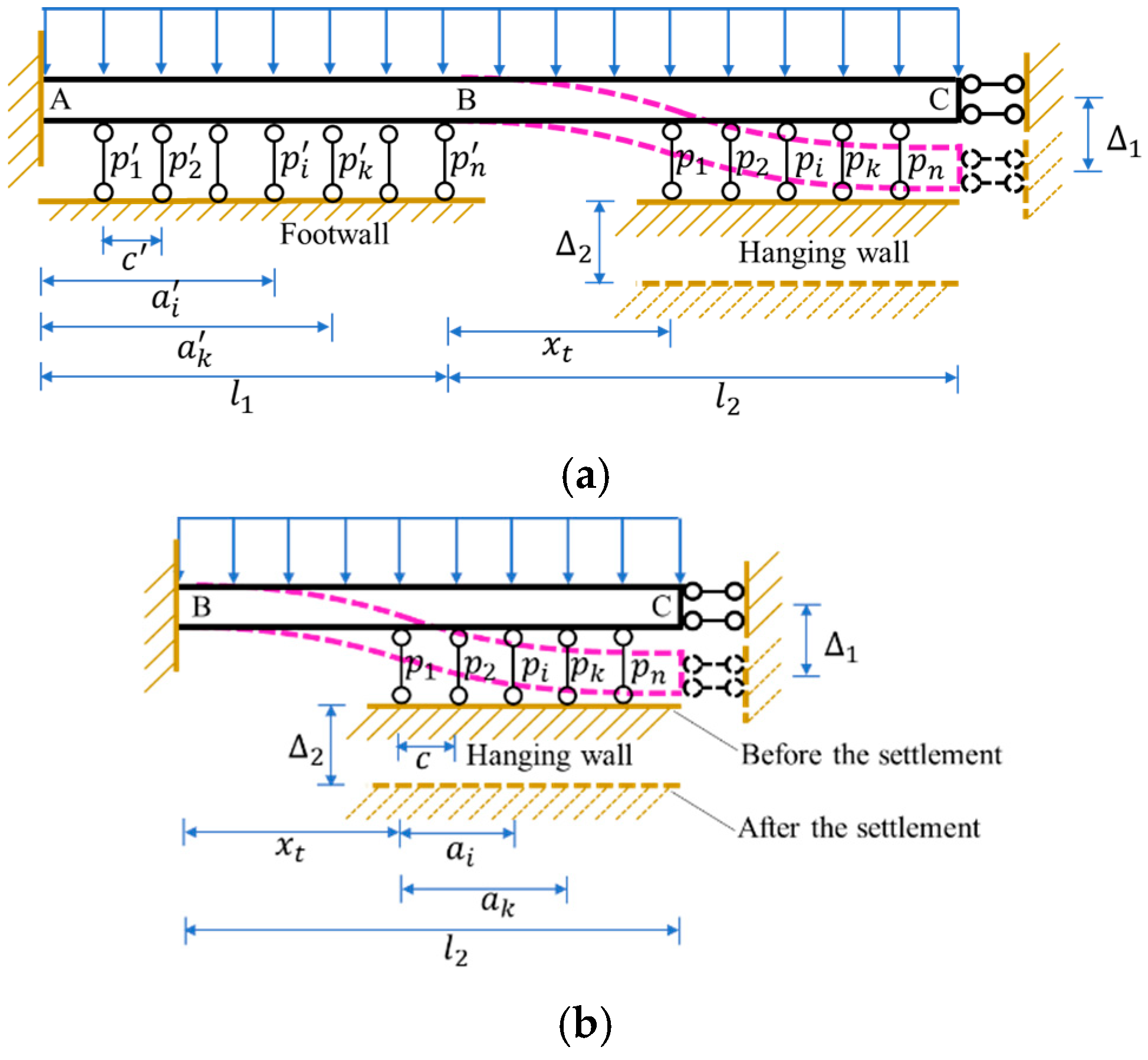
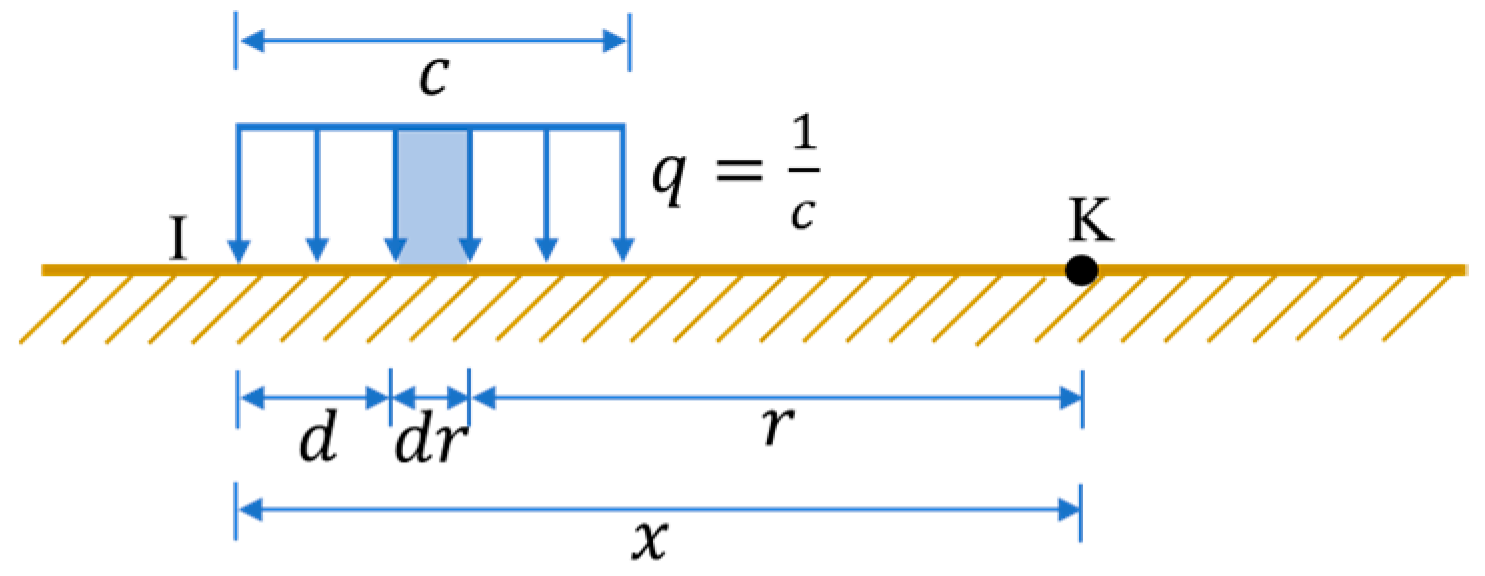
3. Theoretical Calculation of Void Area Range
3.1. Establishing the Calculation Model
3.2. Calculation Method for Pipe Gallery’s Bottom Void Range
4. Model Test for Ground Fissure Dislocation
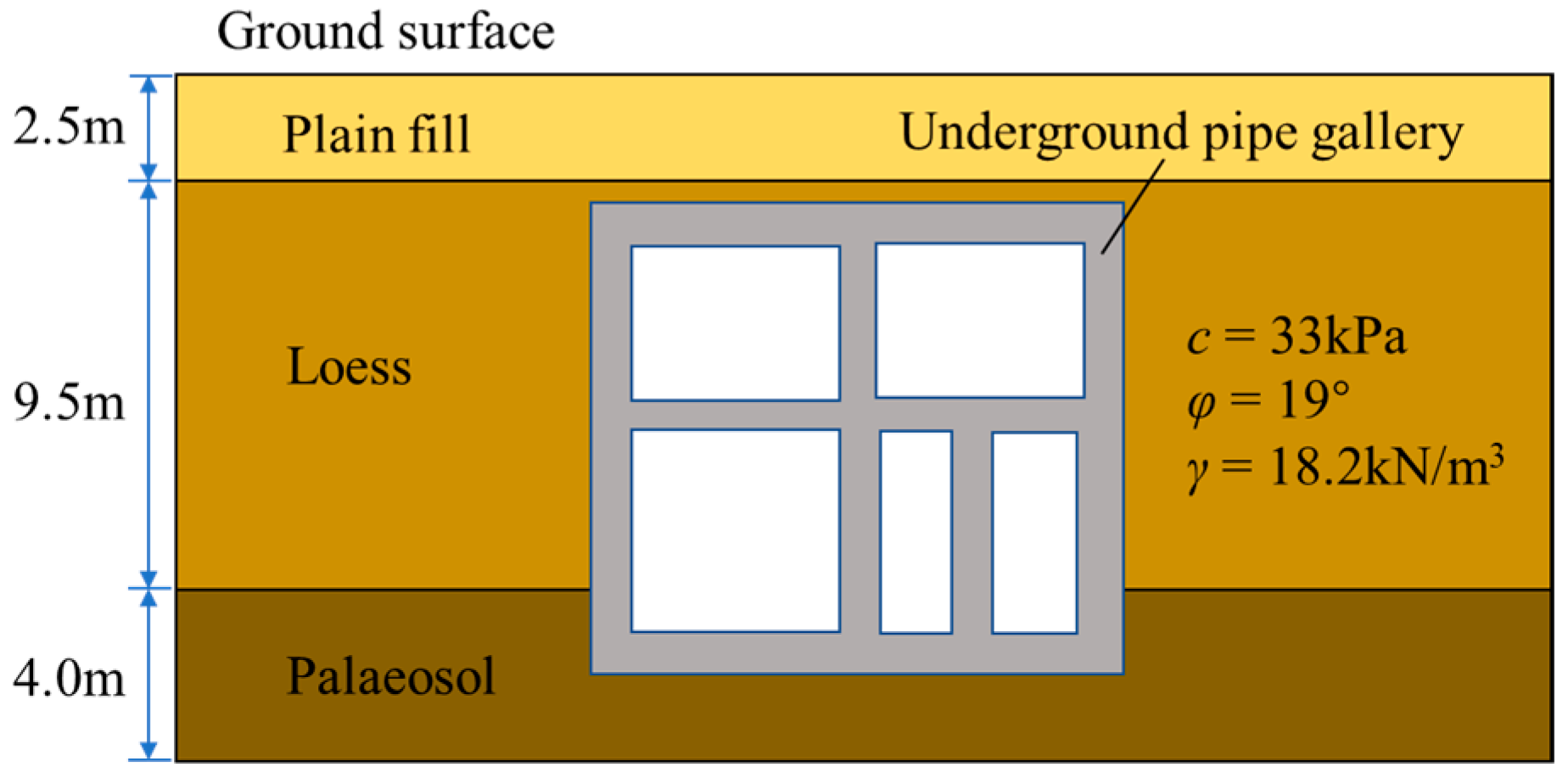
4.1. Test Background
4.2. Similarity Ratio of Model Test
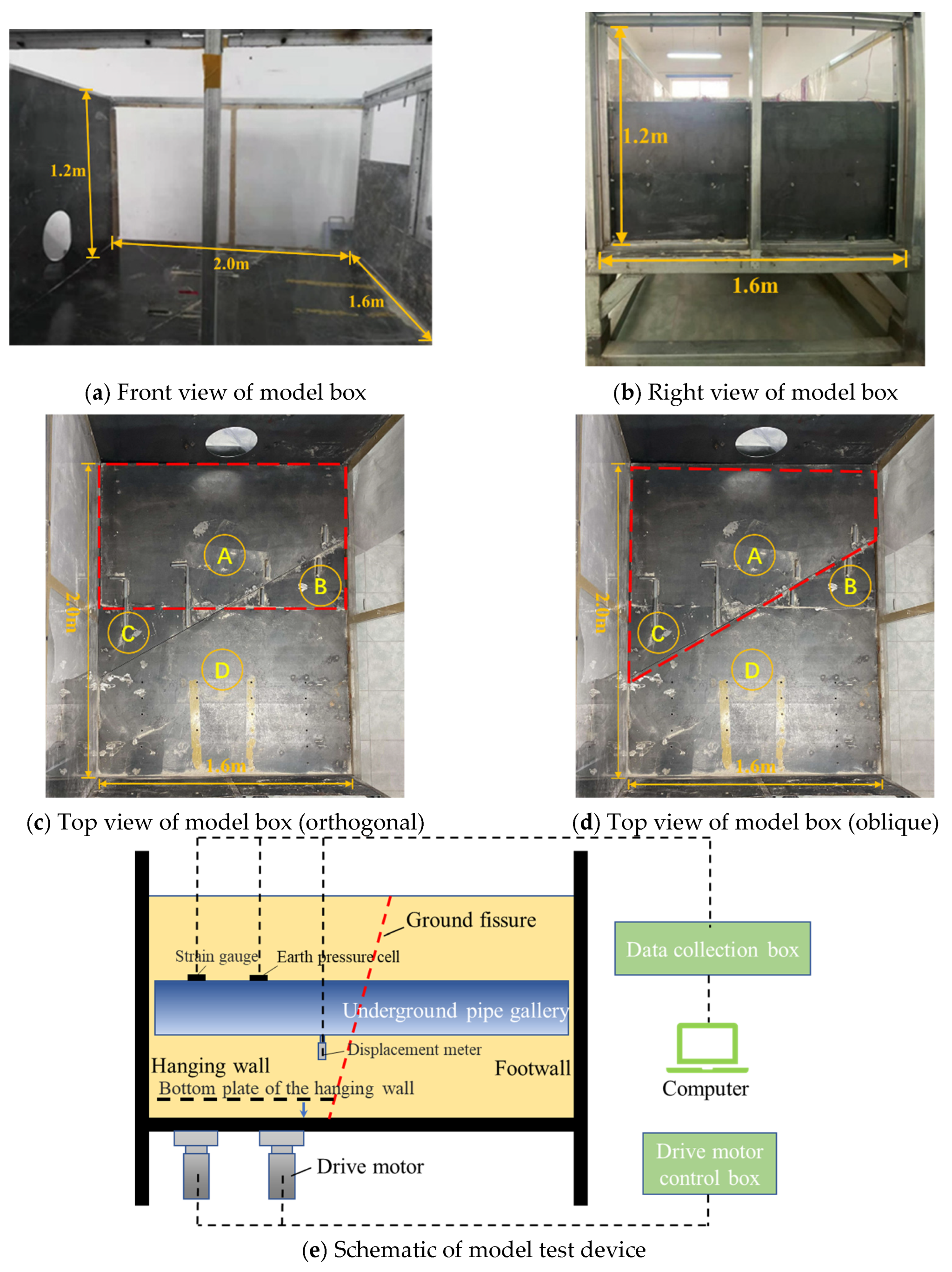
4.3. Sensor Layout and Loading Schemes
4.4. Test Phenomenon
5. Analysis of Test Results
5.1. Structural Strain of Pipe Gallery
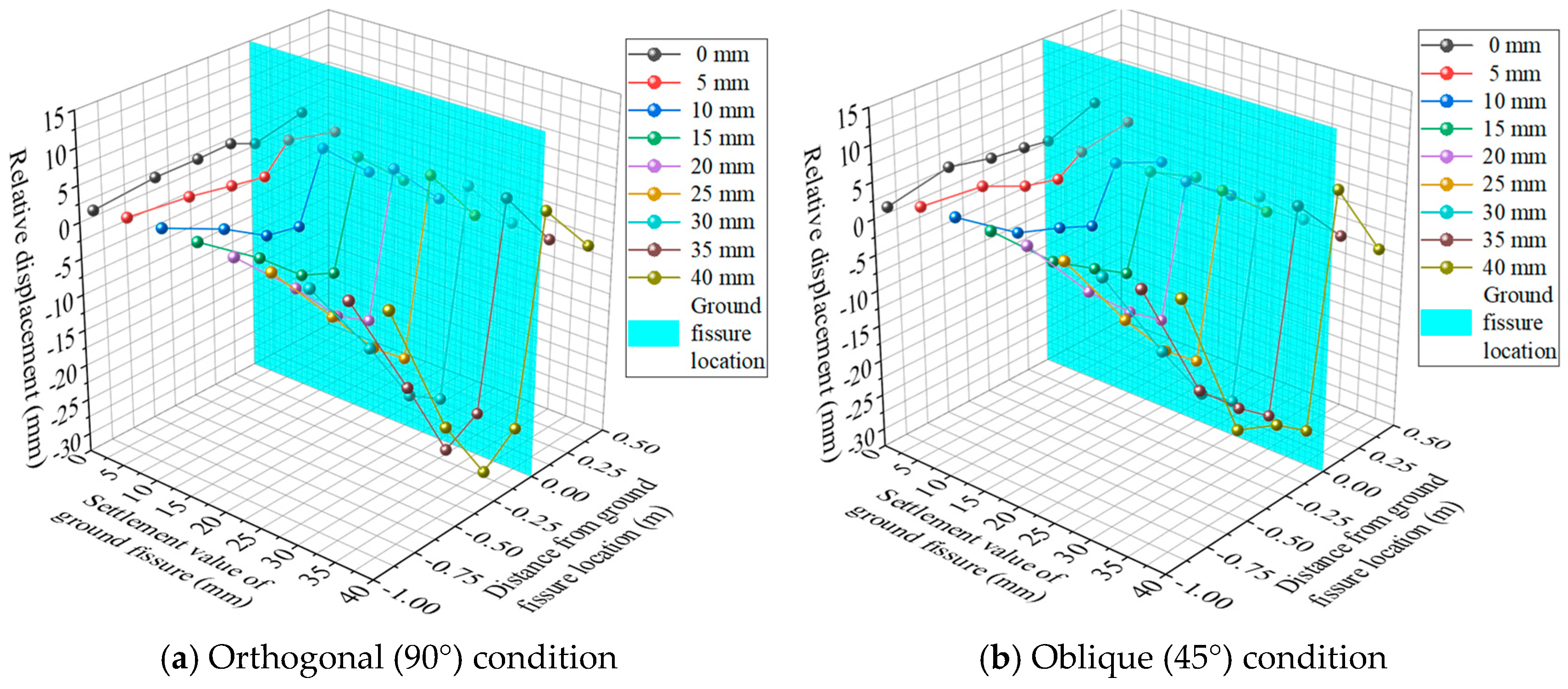
5.2. Displacement Analysis of Pipe Gallery’s Bottom
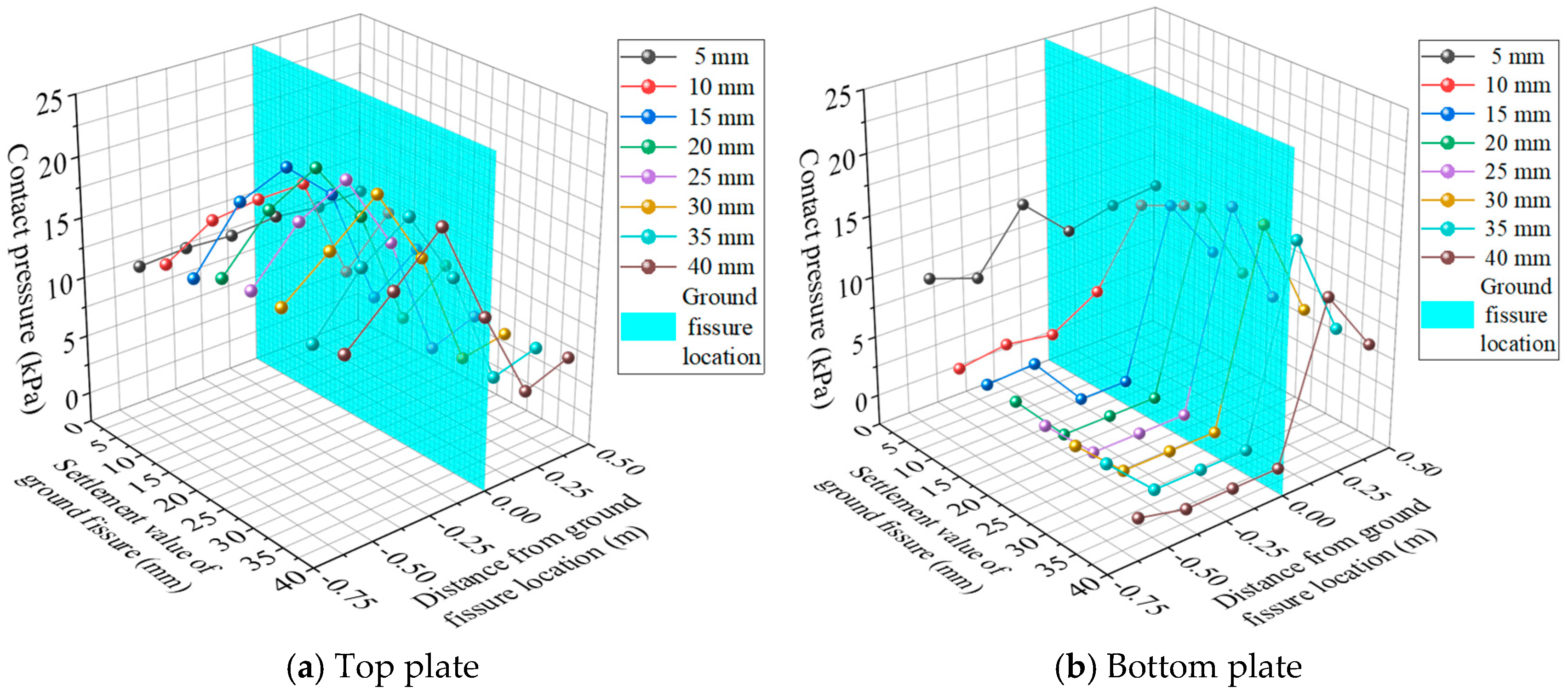
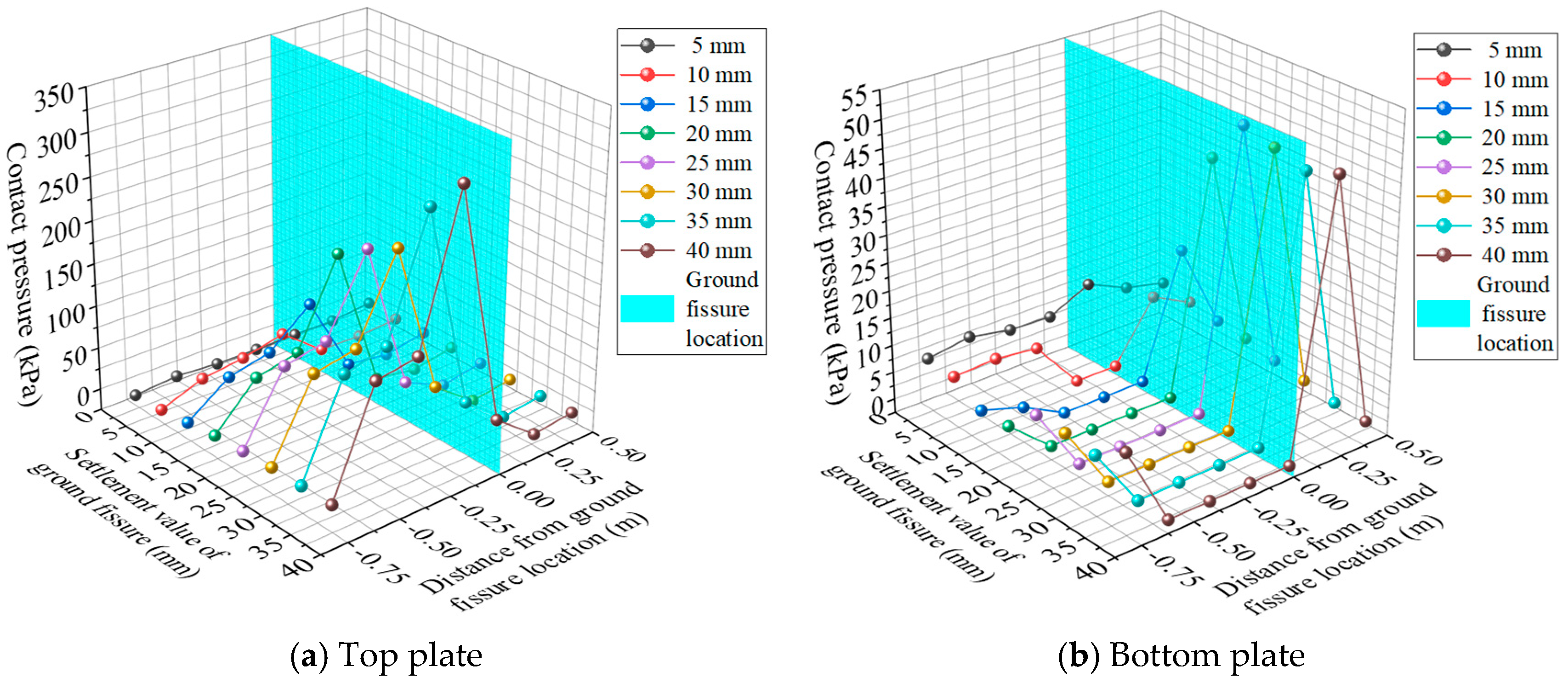
5.3. The Contact Pressure Between the Pipe Gallery Structure and the Surrounding Soil
5.4. A Discussion of the Void Area
5.5. Verification of Calculation Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Canto-Perello, J.; Curiel-Esparza, J.; Calvo, V. Criticality and threat analysis on utility tunnels for planning security policies of utilities in urban underground Space. Expert Syst. Appl. 2013, 40, 4707–4714. [Google Scholar] [CrossRef]
- Canto-Perello, J.; Curiel-Esparza, J.; Calvo, V. Strategic Decision Support System for Utility Tunnel’s Planning Database A ’WOT Method. Tunn. Undergr. Space Technol. 2016, 55, 146–152. [Google Scholar] [CrossRef]
- Qian, Q. Construction of urban underground comprehensive pipe corridor and transformation of urban development mode. Tunn. Constr. 2017, 37, 647–654. [Google Scholar]
- Canto-perello, J.; Curielesparza, J. Assessing governance issues of urban utility tunnels. Tunn. Undergr. Space Technol. 2013, 33, 82–87. [Google Scholar] [CrossRef]
- Huang, Q.; Liang, A.; Men, Y.; Liu, H.; Ma, Y. A full-scale model test on the influence of ground fracture activity on underground water transmission pipeline. Chin. J. Rock Mech. Eng. 2016, 35, 2968–2977. [Google Scholar] [CrossRef]
- Peng, J. Ground Fissure Disaster in Xi’an; Science Press: Beijing, China, 2012. [Google Scholar]
- Peng, J.; Qiao, J.; Leng, Y.; Wang, F.; Xue, S. Distribution and mechanism of the ground fissures in Wei river basin, the origin of the silk road. Environ. Earth Sci. 2016, 75, 718. [Google Scholar] [CrossRef]
- Peng, J.; Sun, X.; Wang, W.; Sun, G. Characteristics of land subsidence, Earth Fissures and Related Disaster Chain Effects with Respect to Urban Hazards in Xi’an, China. Environ. Earth Sci. 2016, 75, 1190. [Google Scholar] [CrossRef]
- Wang, G.; You, G.; Zhu, J.; Yu, J.; Li, W. Earth Fissures in Su–Xi–Chang Region, Jiangsu, China. Surv. Geophys. 2016, 37, 1095–1116. [Google Scholar] [CrossRef]
- Youssef, A.M.; Sabtan, A.A.; Maerz, N.H.; Zabramawi, Y.A. Ground fissure in Wadi Najran. Kingdom of Saudi Arabia. Nat. Hazards 2014, 71, 2013–2027. [Google Scholar] [CrossRef]
- Ha, D.; Abdoun, T.H.; O’Rourke, M.J.; Symans, M.D.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Centrifuge Modeling of Earthquake Effects on Buried High-Density Polyethylene (HDPE) Pipelines Crossing Fault Zones. J. Geotech. Geoenviron. Eng. 2008, 134, 1501–1515. [Google Scholar] [CrossRef]
- Michael, O.; Vikram, G.; Tarek, A. Centrifuge modeling of PGD response of buried pipe. Earthq. Eng. Eng. Vib. 2005, 4, 74–78. [Google Scholar]
- Polynikis, V.; Spyros, A.K.; Panos, D. Finite element analysis of buried steel pipelines under strike-slip fault displacements. Soil Dyn. Earthq. Eng. 2010, 30, 1361–1376. [Google Scholar] [CrossRef]
- Prentice, C.S.; Ponti, D.J. Coseismic deformation of the Wrights tunnel during the 1906 San Francisco earthquake: A key to understanding 1906 fault slip and 1989 surface ruptures in the southern Santa Cruz Mountains. J. Geophys. Res. 1997, 102, 635–648. [Google Scholar] [CrossRef]
- Rojhani, M.; Moradi, M. Centrifuge Modeling of Buried Pipelines Response Due to Normal Faulting. In Proceedings of the 14th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering Geotechnics for transportation and infrastructure, Hong Kong, China, 23–27 May 2011. [Google Scholar]
- Russo, M.; Germani, G.; Amberg, W. Design and construction of large tunnel through active faults a recent application. In Proceedings of the International Conference of Tunnelling & Underground Space Use, Istanbul, Turkey, 16–18 October 2002. [Google Scholar]
- Susumu, Y.; Hiroya, K. Countermeasures of buried steel pipes against surface fault rapture. In Proceedings of the Canada 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 916. [Google Scholar]
- Vazouras, P.; Dakoulas, P.; Karamanos, S.A. Pipe-soil interaction and pipeline performance under strike-slip fault movements. Soil Dyn. Earthq. Eng. 2015, 72, 48–65. [Google Scholar] [CrossRef]
- Zhou, M.; Moore Ian, D.; Lan, H. Experimental Study of Structural Response of Lined-Corrugated HDPE Pipe Subjected to Normal Fault. J. Geotech. Geoenviron. Eng. 2019, 145, 04019117. [Google Scholar] [CrossRef]
- Liu, C.; Qiao, J.; Yan, T.; Lu, Q.; Zhan, J.; Peng, J. Ground fissure water supply pipeline 45° inclined wear full scale model test research. J. Civ. Eng. 2022, 56, 1–12. [Google Scholar] [CrossRef]
- Deng, B.T.; Li, P.; Li, X.; Tian, J.T.; Zhi, B. Mechanical behavior of underground pipe gallery structure considering ground fissure. J. Mt. Sci. 2022, 19, 547–562. [Google Scholar] [CrossRef]
- Deng, B.T.; Li, P.; Li, X.; Tian, J.T.; Zhi, B. Rationality determination method and mechanical behavior of underground utility tunnels in a ground fissure environment. Bull. Eng. Geol. Environ. 2022, 81, 50. [Google Scholar] [CrossRef]
- Gou, Y.; Huang, Q.; Yang, X.; Wang, L.; Shi, W.; Yang, Z. Model test on deformation and failure mechanism of shield tunnel intersecting ground fissure with large angle. J. Civ. Eng. 2022, 55, 117–130. [Google Scholar] [CrossRef]
- Hu, Z.; Peng, J.; Wang, Q.; Zhu, Q.; Zhao, Z. Experimental study on deformation and failure mechanism of shield tunnel with 60° oblique penetrating crack. Chin. J. Rock Mech. Eng. 2010, 29, 176–183. [Google Scholar]
- Li, J.; Shao, S.; Xiong, T. Model test study of tunnel crossing ground crack in oblique direction. Rock Soil Mech. 2010, 31, 115–120+126. [Google Scholar] [CrossRef]
- Li, K.; Men, Y.; Yan, J.; Li, X. Experimental study on interaction mechanism of subway tunnel crossing ground crack in orthogonal way. Chin. J. Rock Mech. Eng. 2011, 30, 556–563. [Google Scholar]
- Liu, N.; Huang, Q.; Ma, Y.; Bulut, R.; Peng, J.; Fan, W.; Men, Y. Experimental study of a segmented metro tunnel in a ground fissure area. Soil Dyn. Earthq. Eng. 2017, 100, 410–416. [Google Scholar] [CrossRef]
- Peng, J.; He, K.; Tong, X.; Huang, Q.; Liu, C. Failure Mechanism of an Underground Metro Tunnel Intersecting Steep Ground Fissure at Low Angle. Int. J. Geomech. 2017, 17, E4016006. [Google Scholar] [CrossRef]
- Xiong, T.; Shao, S.; Wang, T.; Gao, Z. Model test study of orthogonal ground fracture tunnel in Xi’an metro. Rock Soil Mech. 2010, 31, 179–186. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, Q.; Xie, Y.; Qiu, J.; Han, Y.; Teng, H.; Liu, T. Failure analysis and deformation mechanism of segmented utility tunnels crossing ground fissure zones with Different intersection angles. Eng. Fail. Anal. 2022, 139, 106456. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, Q.; Yang, X. Wang P Research on the deformation and force characteristics of underground utility tunnel crossing ground fissure. J. Eng. Geol. 2018, 26, 1203–1210. [Google Scholar] [CrossRef]
- Peng, J.; Huang, Q.; Hu, Z.; Wang, M.; Li, T.; Men, Y.; Fan, W. A proposed solution to the ground fissure encountered in urban metro construction in Xi’an. Tunn. Undergr. Space Technol. 2017, 61, 12–25. [Google Scholar] [CrossRef]
- Yan, Y.; Qiu, J.; Huang, Q.; Wang, Z.; Xie, Y.; Liu, T. Ground fissures geology in Xi’an and failure mitigation measures for utility tunnel system due to geohazard. Arab. J. Geosci. 2021, 14, 1207. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Zhang, Q.; Li, Y.; Guo, X. Development of A New Geomechanical Similar Material. Chin. J. Rock Mech. Eng. 2006, 9, 1842–1847. [Google Scholar]
- Maqsood, Z.; Koseki, J.; Ahsan, M.K.; Shaikh, M.; Kyokawa, H. Experimental study on hardening characteristics and loading rate dependent mechanical behaviour of gypsum mixed sand. Constr. Build. Mater. 2020, 262, 119992. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Y.; Li, L.; Zhang, Q.; Song, S.; Li, J.; Wang, K.; Wang, Q. Development and Application of A New Similar Material For Underground Engineering Fluid-Solid Coupling Model Test. Chin. J. Rock Mech. Eng. 2012, 6, 1128–1137. [Google Scholar]
- Li, S.; Wang, Q.; Li, W.; Li, Z.; Wang, H.; Jiang, B.; Zhang, H. Research on application of flexible uniform pressure loading device to model test. Rock Soil Mech. 2014, 1, 61–66. [Google Scholar] [CrossRef]
- Li, K.; Men, Y.; Liu, Y.; Jiang, R. Model test study on influence of ground fracture profile morphology on metro tunnel deformation. Rock Soil Mech. 2011, 32, 1691–1697. [Google Scholar] [CrossRef]
- Pang, X.; Yan, J. Model test study on oblique crossing of subway tunnel through ground crack. J. Railw. Sci. Eng. 2016, 13, 1354–1359. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, D.; Zhang, Y.; Wang, S.; Li, F. Experimental study on deformation and failure mechanism of underground integrated pipe corridor structure through active ground cracks. Chin. J. Rock Mech. Eng. 2019, 38, 2550–2560. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, Z.; Lu, G.; Wang, R.; Ren, X. Experimental Study on Deformation Mechanism of a Utility Tunnel in a Ground Fissure Area. Adv. Mater. Sci. Eng. 2020, 2020, 6758978. [Google Scholar] [CrossRef]
- Mei, Y.; Zhang, Y.; Yuan, Y.; Ma, H.; Zhang, L.; Zhao, J. Study on mechanical response and warning standard of underground integrated pipe corridor crossing ground cracks. J. Saf. Environ. 2020, 20, 1255–1304. [Google Scholar] [CrossRef]
- Men, Y.; Zhang, J.; Liu, H.; Han, D.; Wang, H. Discussion on calculation model of Xi’an subway tunnel crossing ground fissure zone. J. Earth Sci. Environ. 2011, 33, 95–100. [Google Scholar]
- Qiao, L.; Liu, J.; Li, S.; Wang, C.; Jiang, Y.; Wang, Z. Underground engineering excavation surface characteristics of the effect of space and application. Rock Soil Mech. 2014, 35, 481–487. (In Chinese) [Google Scholar]


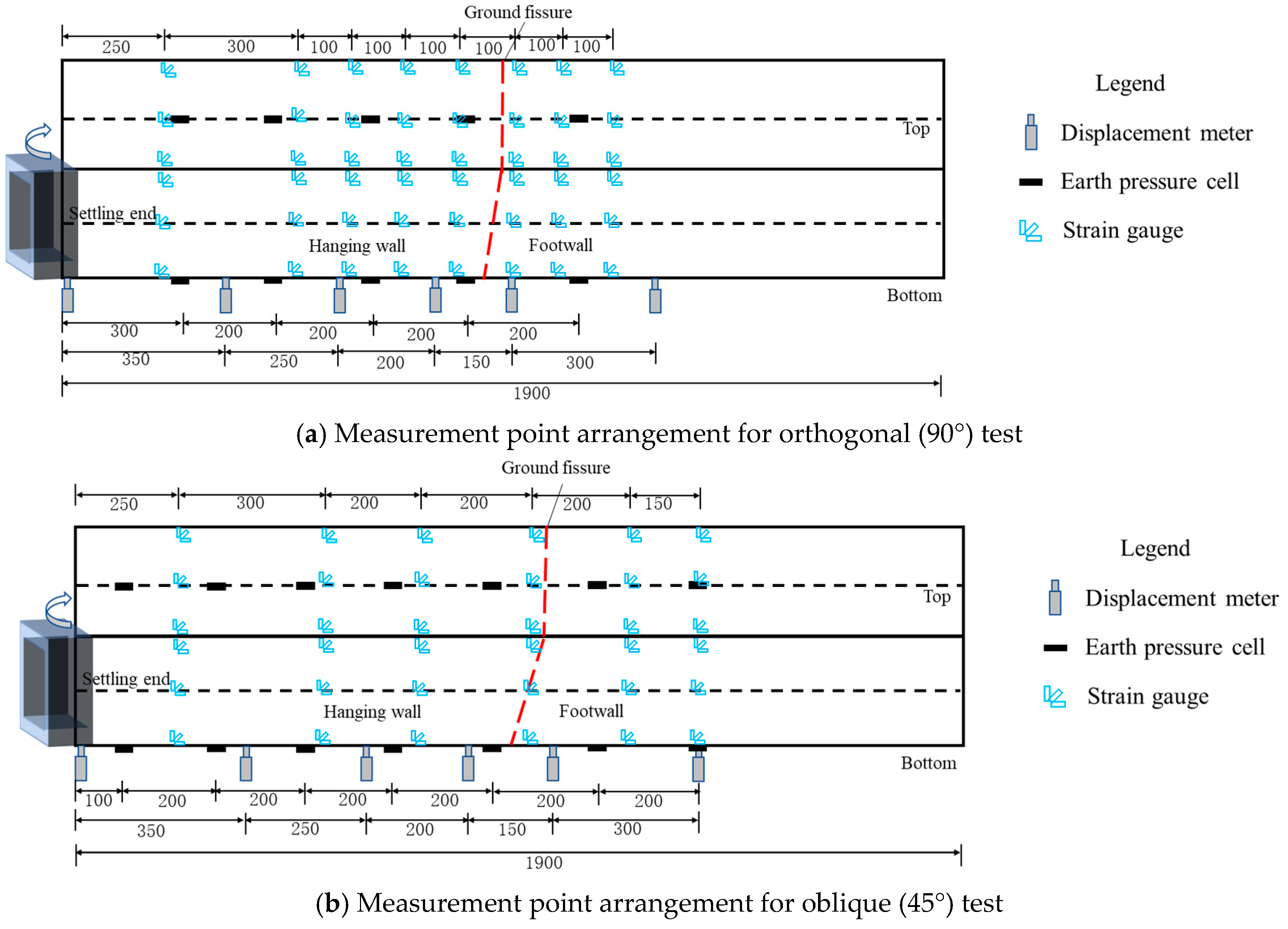
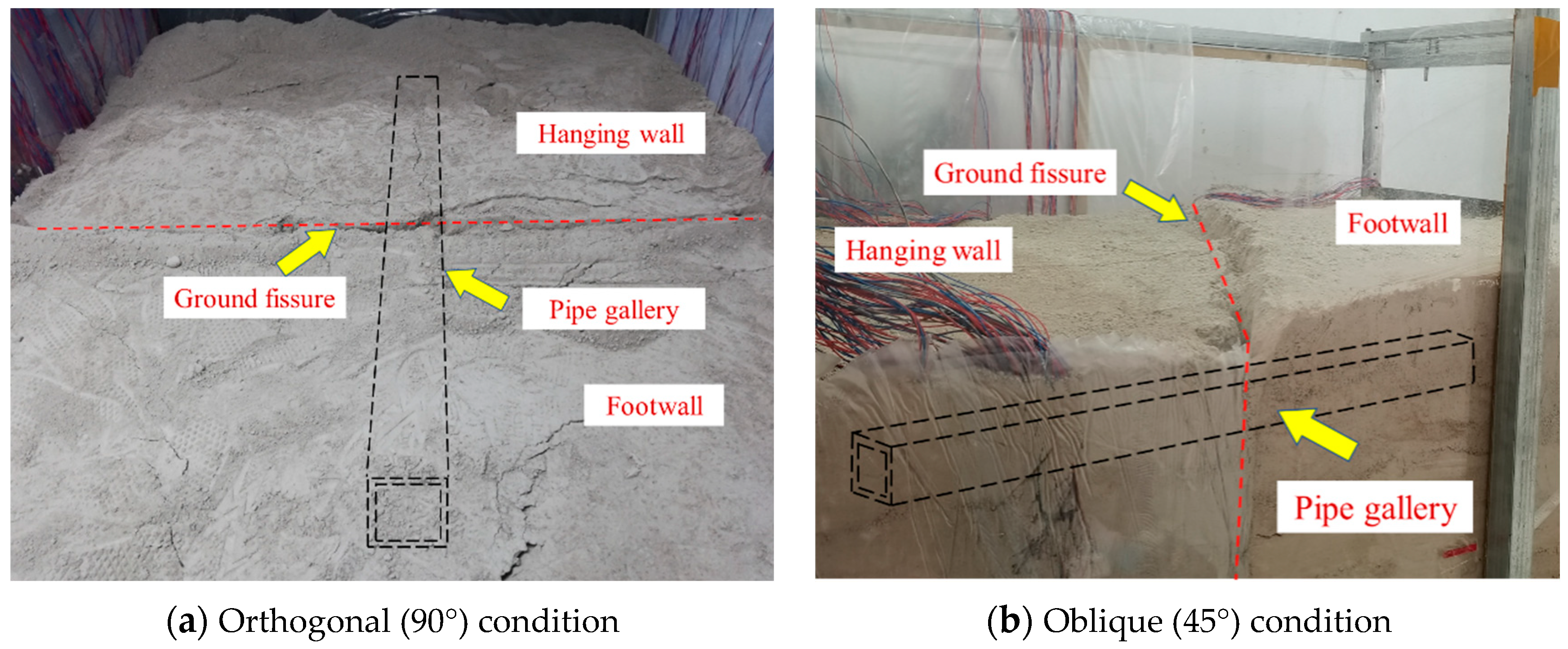

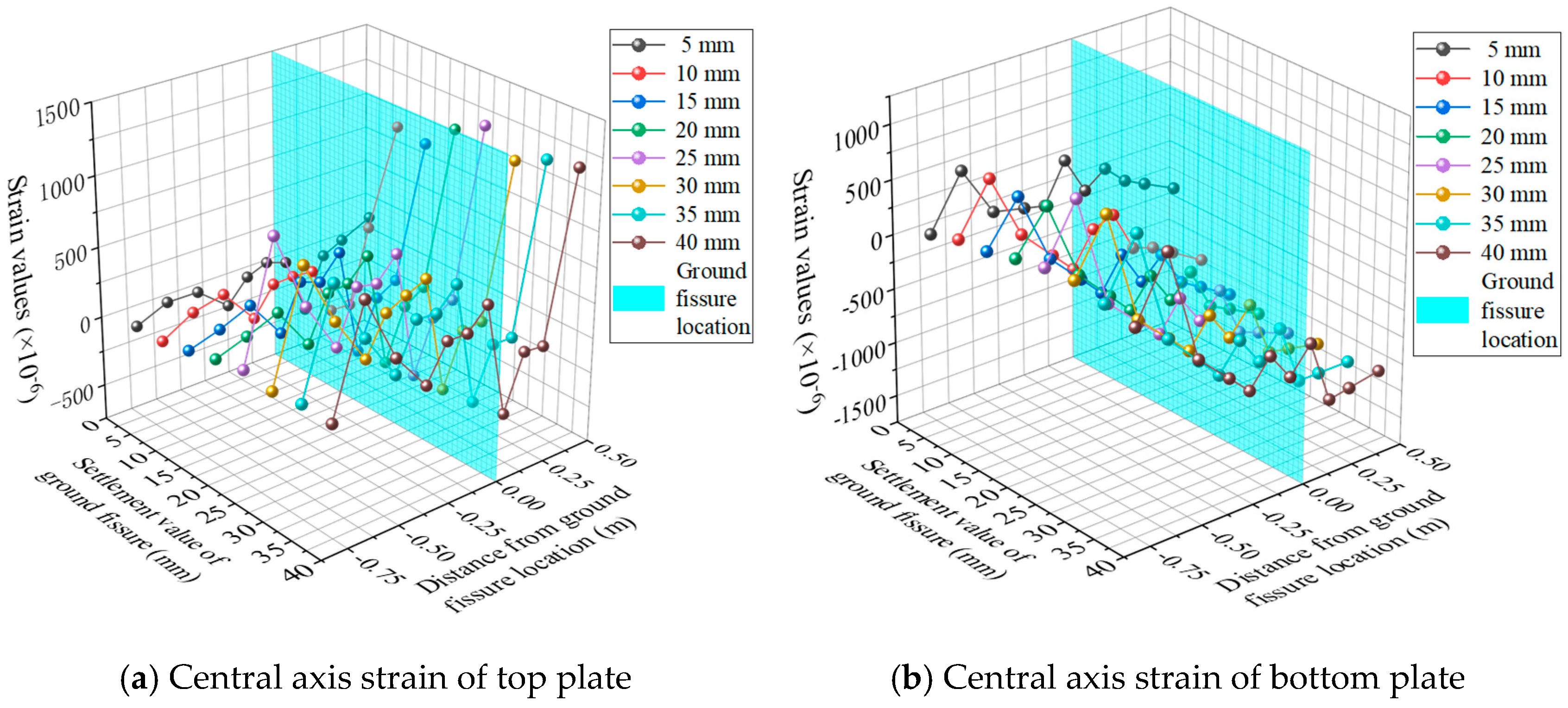

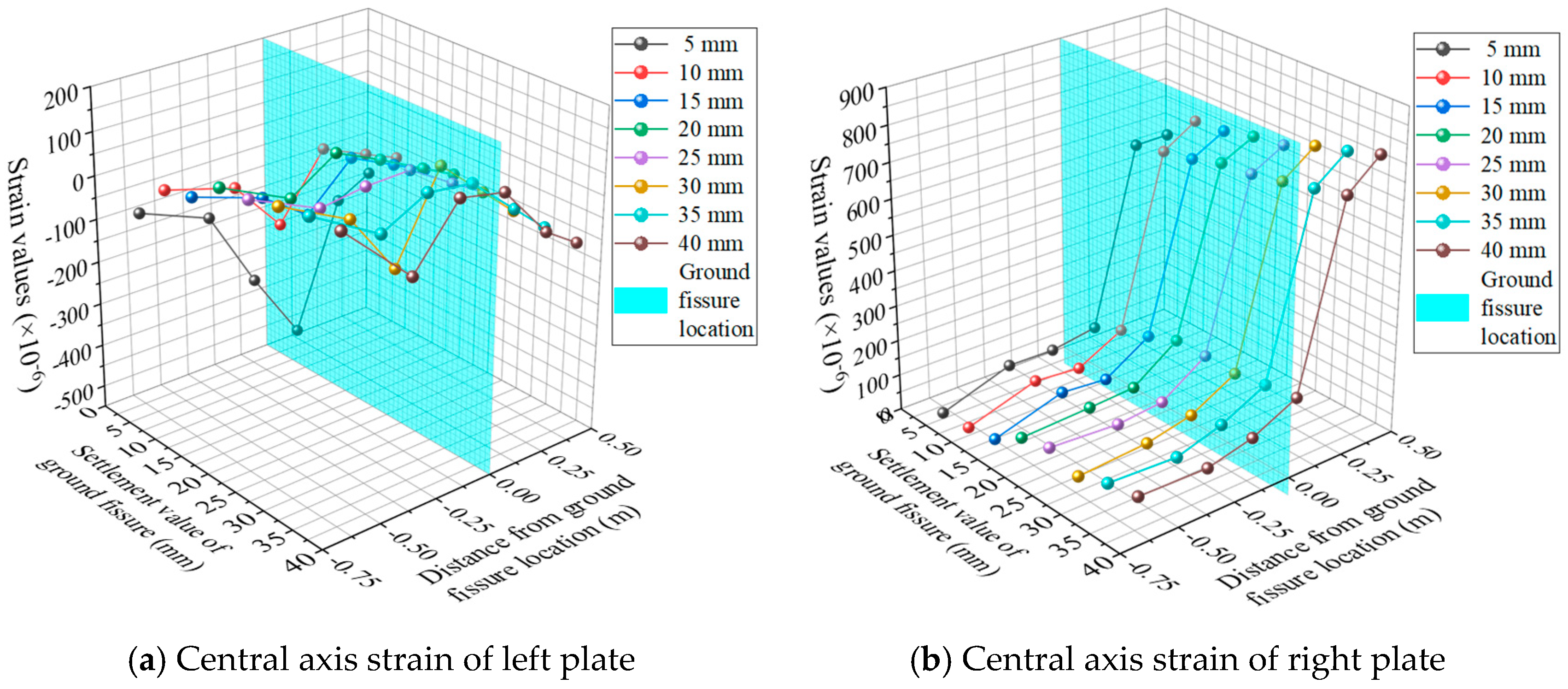
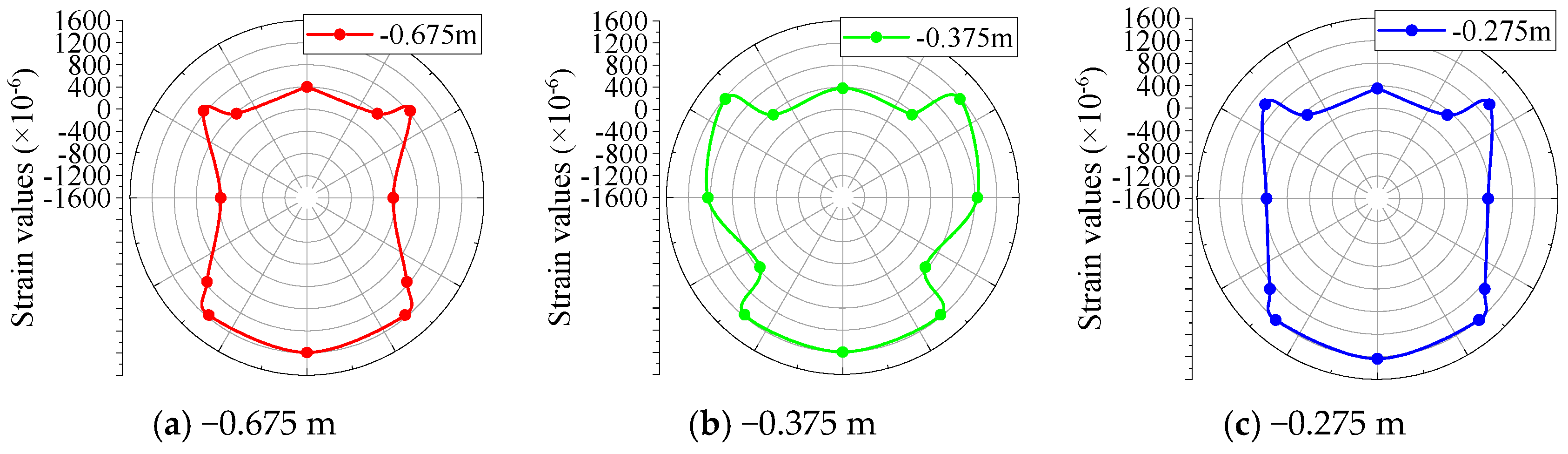
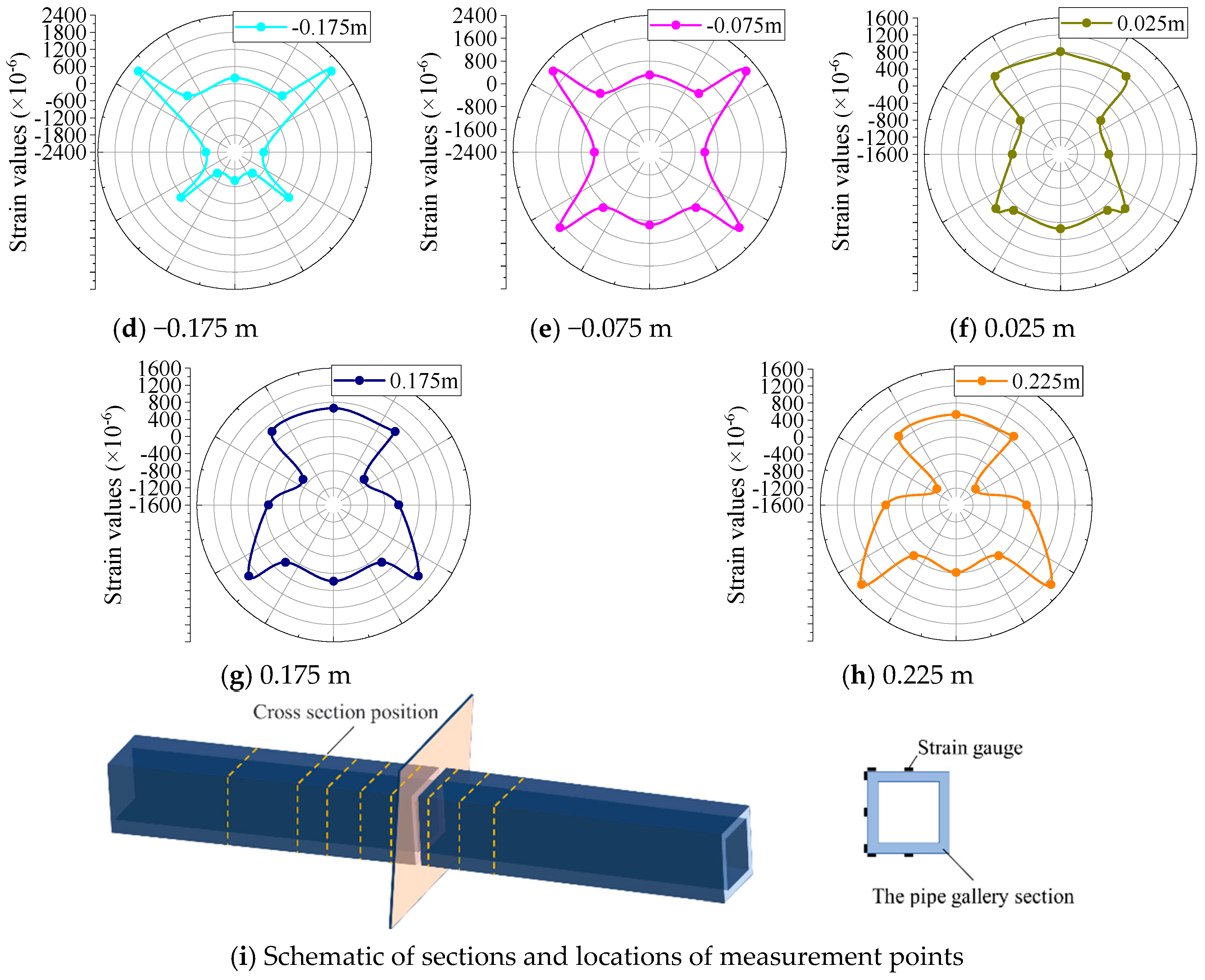
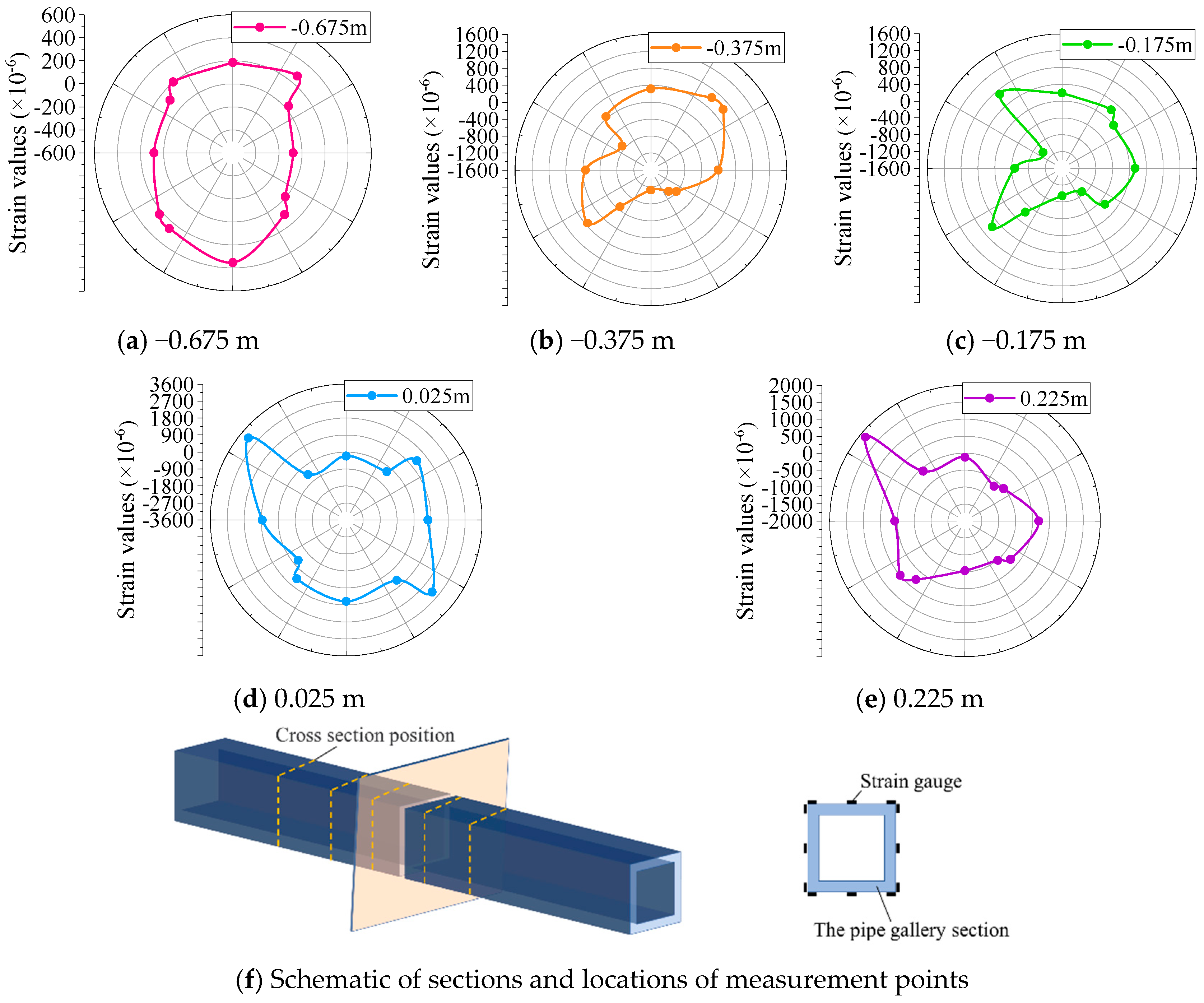
| Type | Physical Parameters | Similar Relationships | Similarity Ratios (Prototype/Model) | |
|---|---|---|---|---|
| Pipe Gallery Structure | Soil | |||
| Geometric features | Length | 20 | — | |
| Moment of inertia | 160,000 | — | ||
| Displacement | 20 | 20 | ||
| Material characteristics | Elasticity modulus | 12 | 15 | |
| Stress | 12 | — | ||
| Strain | 1 | — | ||
| Bulk density | — | 1 | ||
| Moisture content | — | 1 | ||
| Cohesion | — | 20 | ||
| Internal friction angle | — | 1 | ||
| Hanging Wall Dislocations | Void Stages | Bottom Void Range of Pipe Gallery | Damage Range of Pipe Gallery |
|---|---|---|---|
| 5 mm | Simultaneous deformation and critical void stages | There is only a slight void between the pipe gallery and the foundation near the ground fissure. | Tensile failure of the top plate occurs. |
| 10 mm | Void development stage | With an increasing hanging wall dislocation, the bottom void of the pipe gallery structure gradually increased. At the end of the test, the bottom void ranges were 2.875–3 L and 3.125–3.5 L under the in orthogonal and oblique conditions, respectively. | In the orthogonal test, fracturing failure occurred when the hanging wall dislocation was 10 mm. In the test under oblique conditions, compressive failure occurred when the hanging wall dislocation was 15 mm, and then the range gradually expanded, mainly in the footwall’s bottom plate. |
| 15 mm | |||
| 20 mm | |||
| 25 mm | |||
| 30 mm | |||
| 35 mm | |||
| 40 mm |
| (m) | θB | θC | Calculated Value (m) | |
|---|---|---|---|---|
| 0.005 | 0.0049 | 0.3757 | 0.3122 | 0.1230 |
| 0.010 | 0.0097 | 0.3705 | 0.307 | 0.2328 |
| 0.015 | 0.0143 | 0.3656 | 0.3021 | 0.0811 |
| 0.020 | 0.0184 | 0.3611 | 0.2976 | 0.1536 |
| 0.025 | 0.0221 | 0.3571 | 0.2936 | 0.3876 |
| 0.030 | 0.0254 | 0.3536 | 0.2901 | 0.4591 |
| 0.035 | 0.0281 | 0.3506 | 0.2871 | 0.6737 |
| 0.040 | 0.0304 | 0.3481 | 0.2846 | 0.6561 |
| Method | Orthogonal Bottom Void Range | Oblique Bottom Void Range |
|---|---|---|
| Theoretical calculations | 0.6561 | 0.6561 |
| Model tests | 0.6 | 0.7 |
| 9.35% | −4.39% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Han, B.; Zhao, Y.; Deng, B.; Du, K.; Liu, H. A Study on the Calculations of the Bottom Void Range of an Underground Pipe Gallery Structure Under the Action of Ground Fissure Dislocations. Buildings 2025, 15, 920. https://doi.org/10.3390/buildings15060920
Yu X, Han B, Zhao Y, Deng B, Du K, Liu H. A Study on the Calculations of the Bottom Void Range of an Underground Pipe Gallery Structure Under the Action of Ground Fissure Dislocations. Buildings. 2025; 15(6):920. https://doi.org/10.3390/buildings15060920
Chicago/Turabian StyleYu, Xintao, Baoan Han, Yubo Zhao, Botuan Deng, Kang Du, and Haosheng Liu. 2025. "A Study on the Calculations of the Bottom Void Range of an Underground Pipe Gallery Structure Under the Action of Ground Fissure Dislocations" Buildings 15, no. 6: 920. https://doi.org/10.3390/buildings15060920
APA StyleYu, X., Han, B., Zhao, Y., Deng, B., Du, K., & Liu, H. (2025). A Study on the Calculations of the Bottom Void Range of an Underground Pipe Gallery Structure Under the Action of Ground Fissure Dislocations. Buildings, 15(6), 920. https://doi.org/10.3390/buildings15060920





