1. Introduction
The exponential advancement of artificial intelligence and cloud computing has positioned data centers as energy-intensive nodal points in modern building ecosystems. With escalating heat flux resulting from high-power equipment clustering, thermal energy regulation has become a critical determinant of building energy performance. Conventional HVAC systems demonstrate limited capacity to reconcile the conflicting requirements of precision thermal control and energy efficiency optimization in hyperscale data centers. This energy management paradox necessitates the synergistic integration of advanced heat recovery architectures and adaptive cooling technologies within building energy systems.
Effective data center thermal design requires the co-optimization of facility-scale thermodynamic loads and equipment-level heat dissipation strategies. Through the systemic integration of liquid cooling circuits, waste heat redistribution mechanisms, and AI-driven predictive thermal controls, building energy systems can achieve concurrent improvements in the coefficient of performance (COP) and power usage effectiveness (PUE). The convergence of chip-level thermal challenges (driven by increased transistor density and heterogeneous integration) and facility-scale cooling demands underscores the imperative for holistic energy management frameworks.
The advancement of electronic chips toward higher performance, increased centralization, and miniaturization, coupled with the associated rise in heat generation, presents significant challenges for chip thermal management as well as for data center design and thermal control. For high heat flux electronic chips, traditional air natural cooling makes it difficult to meet the heat dissipation demand, and, although the parameter and structure optimization of air-cooled fins can achieve 60 W chip heat dissipation [
1], it is difficult to cope with higher power consumption. In contrast, liquid water, with a specific heat capacity 3500 times higher than that of air and a thermal conductivity 25 times higher [
2], it has become an effective means of heat dissipation for high heat flux chips [
3]. Liquid cooling is divided into two categories: direct contact and indirect contact. Direct contact liquid cooling includes jet cooling [
4], spray cooling [
5], submerged cooling [
6], and submerged jet cooling [
7], etc., but the requirements for the cooling medium are high. Among the indirect contact liquid cooling, cold plate cooling is the most mature and widely used [
8], and it is viewed as a crucial technology for addressing the thermal management challenges of chips with high power consumption [
9].
Numerous studies have verified the effectiveness of liquid-cooled plates in heat dissipation of high heat flow density chips. Zhao J [
10] et al. found that square pin ribs have better thermal performance compared to columnar pin ribs by adding pin ribs and optimizing the shape and angle of the pin ribs in the liquid-cooled plates. Song H [
11] et al. designed and numerically simulated four different runner shapes, and the results showed that the double-layer structure of liquid-cooled plates is better than the other three types in terms of thermal and flow properties, and the best cooling performance is achieved with a 20% ethylene glycol–water solution as the cooling medium. Chiu H C [
12] et al. investigated the effect of the diameter and gap rate of circular ribs on heat transfer and flow properties in liquid-cooled plates and found that the circular ribs significantly reduced the overall thermal resistance of the plates, whereas changes in the gap rate did not have a significant effect on the thermal resistance. As an improvement, Zhao K [
13] et al. added circular ribs versus finned ribs to a conventional refolded liquid-cooled plate, and the results showed that the cold plate with added finned ribs outperformed the circular-ribbed cold plate with respect to overall performance. Unlike the traditional large runner cold plate, the microchannel cold plate has a leap in heat transfer efficiency, and the microchannel cold plate has a significant cooling effect on electronic chips with high heat flux [
14,
15].
Researchers have conducted in-depth studies on the structural parameters of the flow channels of straight microchannel cold plates. Chiu H C [
16] et al. explored the effects of aspect ratio and cross-sectional porosity on the performance of cold plates. The findings indicated that the aspect ratio influences the thermal resistance of the cold plates to some extent. In contrast, the porosity in the range from 53% to 75% does not significantly affect the thermal resistance. Wang H [
17] et al. analyzed the performance of microchannels of different geometrical shapes (rectangular, trapezoidal, and triangular), and it was observed that rectangular microchannels with aspect ratios between 8.904 and 11.442 performed the best, while increasing the number of channels reduced the thermal resistance but was accompanied by a higher pressure drop. Kumavat P S [
18] et al. investigated the effect of sinusoidal waves with different pulsation frequencies in the range of 0.02 Hz to 25 Hz on the flow of the cooling work mass, and the findings revealed that heat transfer is poor at low frequencies, while high frequencies significantly enhance the heat transfer performance. Subsequently, they further analyzed the impact of asymmetric sinusoidal pulsating flow on thermal performance [
19] and found that its fast-fluctuating characteristics enhanced the fluid momentum and improved the heat transfer performance by 11% compared with the steady-state flow.
It has been shown that the addition of perturbation structures in straight microchannels can significantly reduce the thermal resistance of liquid-cooled plates, but it also increases the challenge of flow resistance. Haque I [
20] et al. added rhombic pin ribs to rectangular microchannel cold plates to investigate the influence of various aspect ratios on thermal performance and flow characteristics, and the results show that incorporating rhombic pin ribs can substantially enhance thermal performance, with the largest increase in Nu at an aspect ratio of 1.00. Rehman M M U [
21] et al. performed numerical simulations by adding different-shaped wall ribs (elliptical, trapezoidal, hydrofoil, rectangular) on both sides of a rectangular microchannel and found that hydrofoil-shaped wall ribs had the best overall performance with the least enhancement in entropy generation rate. Chu X [
22] et al. introduced a vortex generator (SMA-VG) based on the automatic deformation of fluid temperature and found that the SMA-VG was better than the non-deformed vortex generator (NDF) and had a better performance than the non-deformed vortex generator (NDF). The deformed vortex generator (NDF-VG) significantly improves the heat transfer performance, and the Nu is increased by 112% and 9% compared to no generator and NDF-VG, respectively, at a heat flux of 100,000 W/m². Xia G D [
23] et al. examined the impacts of inlet/outlet position, head shape, and cross-sectional shape regarding the efficiency of a microchannel cold plate, with the findings indicating that the intermediate inlet/outlet position has the best flow performance, the rectangular head shape has better flow uniformity, and the microchannel cold plate with offset semicircular or triangular concave cavity has better heat transfer than the rectangular microchannel.
Researchers have developed various non-straight microchannel designs to lower thermal resistance and pressure drop. Ahmed F. Al-Neama [
24] et al. evaluated the performance of straight rectangular, single, double, and triple serpentine microchannel cold plates. Their findings revealed that the single serpentine design achieved a 35% increase in Nu and a 19% reduction in total thermal resistance at a volumetric velocity of 0.51 L/min, albeit with a higher pressure drop compared to the straight rectangular design. Toghraie D [
25] et al. examined smooth, sinusoidal, and serrated microchannel cold plates, along with nanofluids, and found that serrated designs provided the best thermal performance. Furthermore, modifying the channel shape had a greater effect on heat transfer than using nanofluids. Wang X Q [
26] et al. analyzed tree-branching microchannels, identifying the bifurcation angle as a critical parameter, with smaller angles significantly reducing temperature and pressure drop. Naqiuddin N H [
27] et al. proposed a segmented microchannel design, optimizing fin and flow parameters using the Taguchi gray method. Their study concluded that a three-segment structure, with a fin width of 1 mm, length of 2 mm, transversal distance of 5 mm, and channel width is 1 mm, minimizes the pressure drop.
Researchers have explored better cold plate performance by innovatively improving traditional microchannel structures. Gilmore N [
28] et al. designed an open manifold microchannel cold plate and compared its performance with that of traditional manifold microchannels, finding that the pressure drop was reduced by 45%~75%, but the change in thermal resistance was not significant, and the improvement in the thermal performance of the chamfering treatment of the tips of the microchannel walls was poor. Tan H [
29] et al. proposed four numerical simulations to show that the spider web structure has the best thermal performance, and experiments further verify that the thermal performance of the optimized spider web microchannel cold plate is much better than that of the straight microchannel cold plate. Zhou J [
30] et al. combined manifold microchannels with topology optimization and designed three kinds of optimized manifold microchannel structures, and the study shows that increasing the density in topology optimization leads to a more pronounced enhancement in heat transfer performance, but the pressure drop increases accordingly. Hung T [
29] et al. proposed four kinds of biomimetic microchannel structures, and numerical simulations show that the topology optimization density and the heat transfer performance improvement are more significant. However, this is accompanied by a corresponding increase in pressure drop. Hung T C [
31] et al. analyzed the thermal performance of a double-layer microchannel cold plate, and numerical simulation results showed that the thermal efficiency of a double-layer microchannel cold plate was enhanced by 6.3% compared to a single layer under the same geometry.
In summary, on the one hand, researchers have enhanced the heat transfer performance by optimizing the geometric parameters of straight microchannel cross-sections or adding perturbation structures [
16,
17,
18,
19,
20,
21,
22,
23], but there are large temperature gradients in the upstream and downstream of the straight microchannels, which may reduce the reliability of the electronic chip [
27]. On the other hand, innovative designs of non-straight microchannel structures have been developed to reduce the temperature gradient and achieve a better balance between heat transfer performance and flow resistance [
24,
25,
26,
27,
28,
29,
30,
31]. Despite the problem of a large temperature gradient in a straight microchannel cold plate, the advantage of a smaller pressure drop relative to other microchannel cold plates is often overlooked. If this problem can be solved effectively, an optimal balance between heat transfer performance and flow resistance may be achieved. To this end, a counter-flow rectangular microchannel cold plate is designed in this paper to study the impact of velocity, rectangular flow, the channel aspect ratio, the form of import and export of the cooling medium on heat transfer, and flow efficiency of the cold plate. By designing orthogonal tests and numerical simulations, the effects of single-factor and multi-factor interactions on the efficiency of the cold plate is analyzed to identify the optimal parameter combinations, and the cold plate of the optimal parameter group is compared with the cold plate of the other parameter groups to verify the superiority of its cold plate performance. Finally, a correlation equation about Nu is established based on the simulation data, and the calculated Nu is fitted to the simulated Nu to determine the accuracy and predictability of the correlation equation.
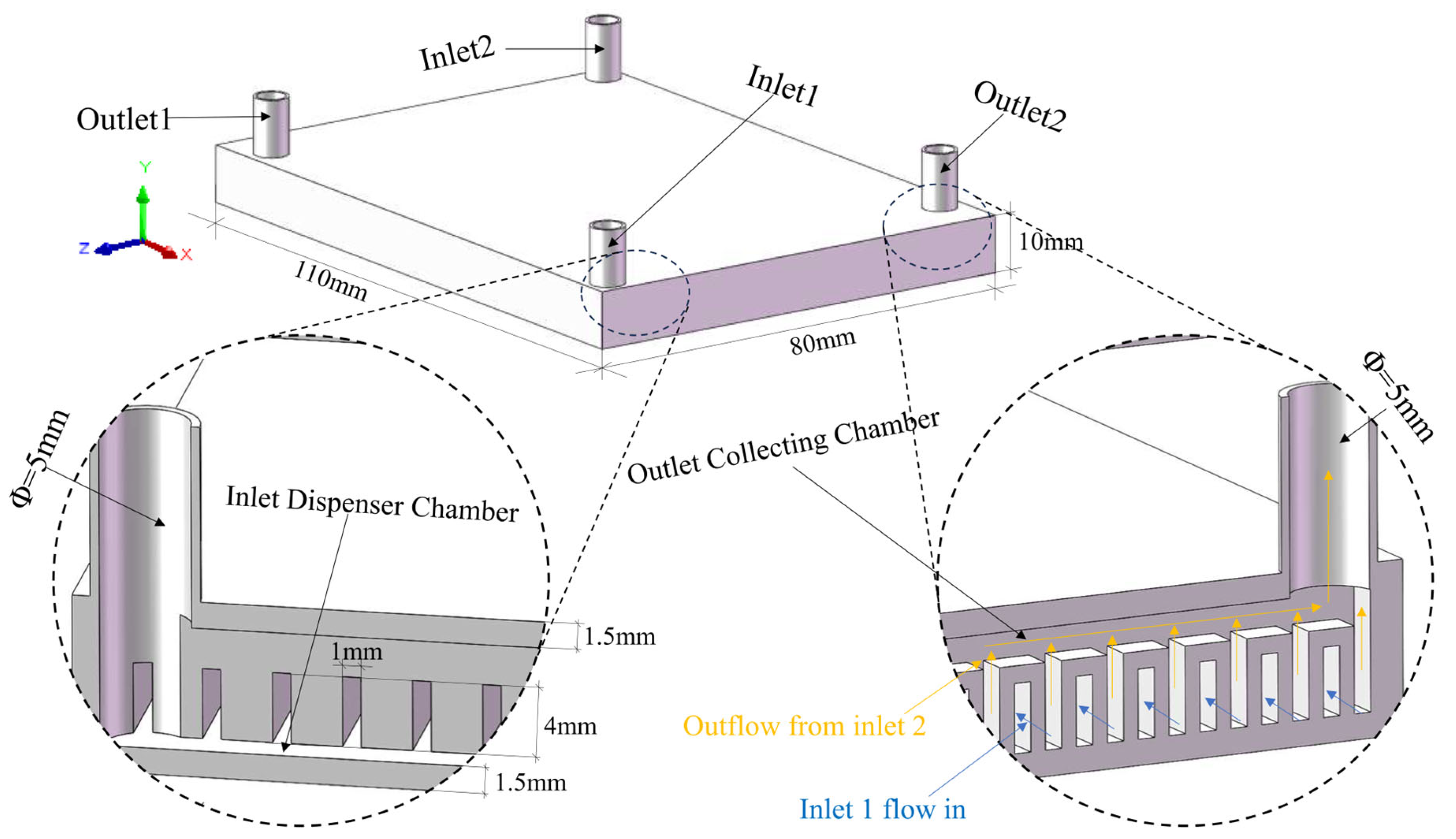
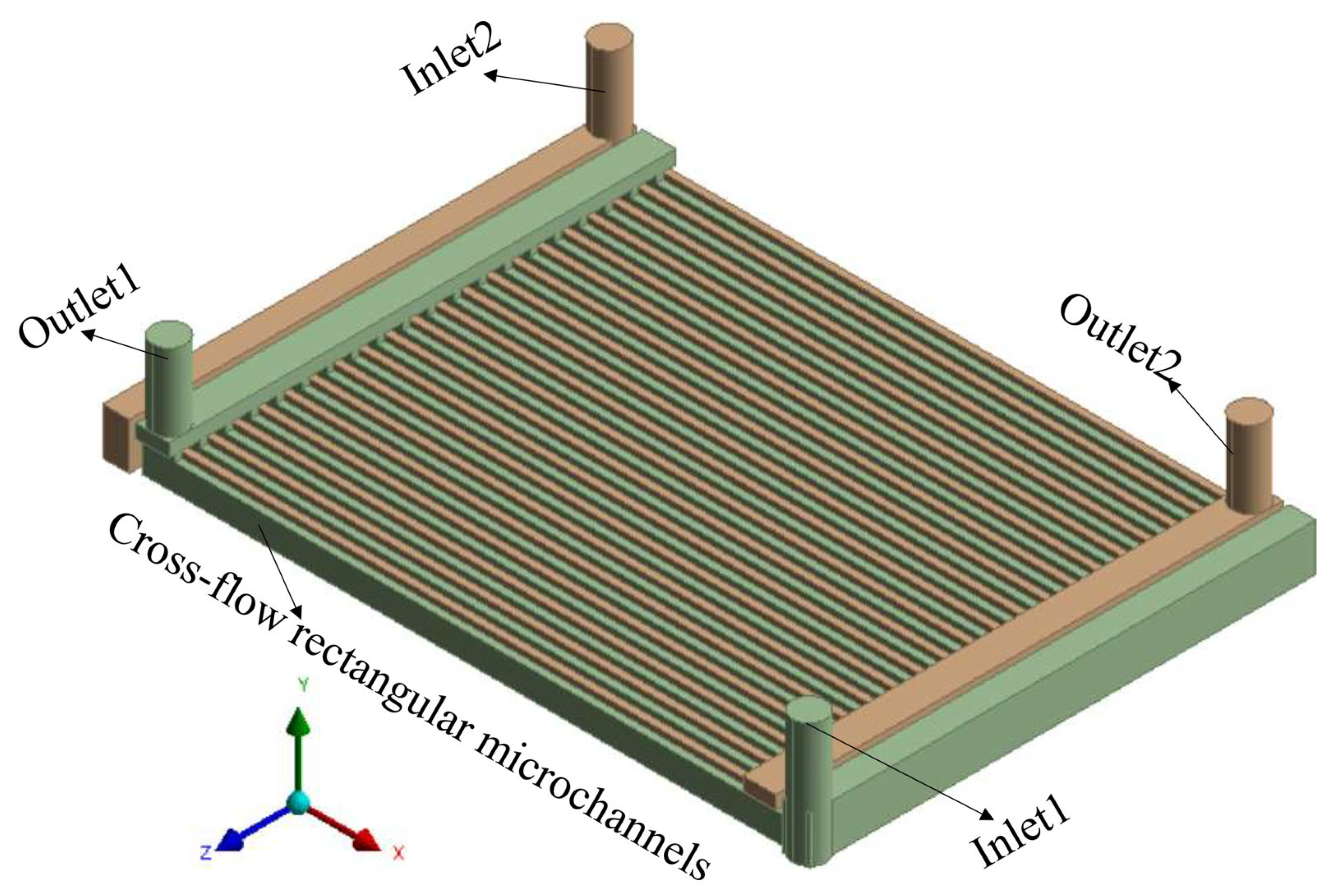
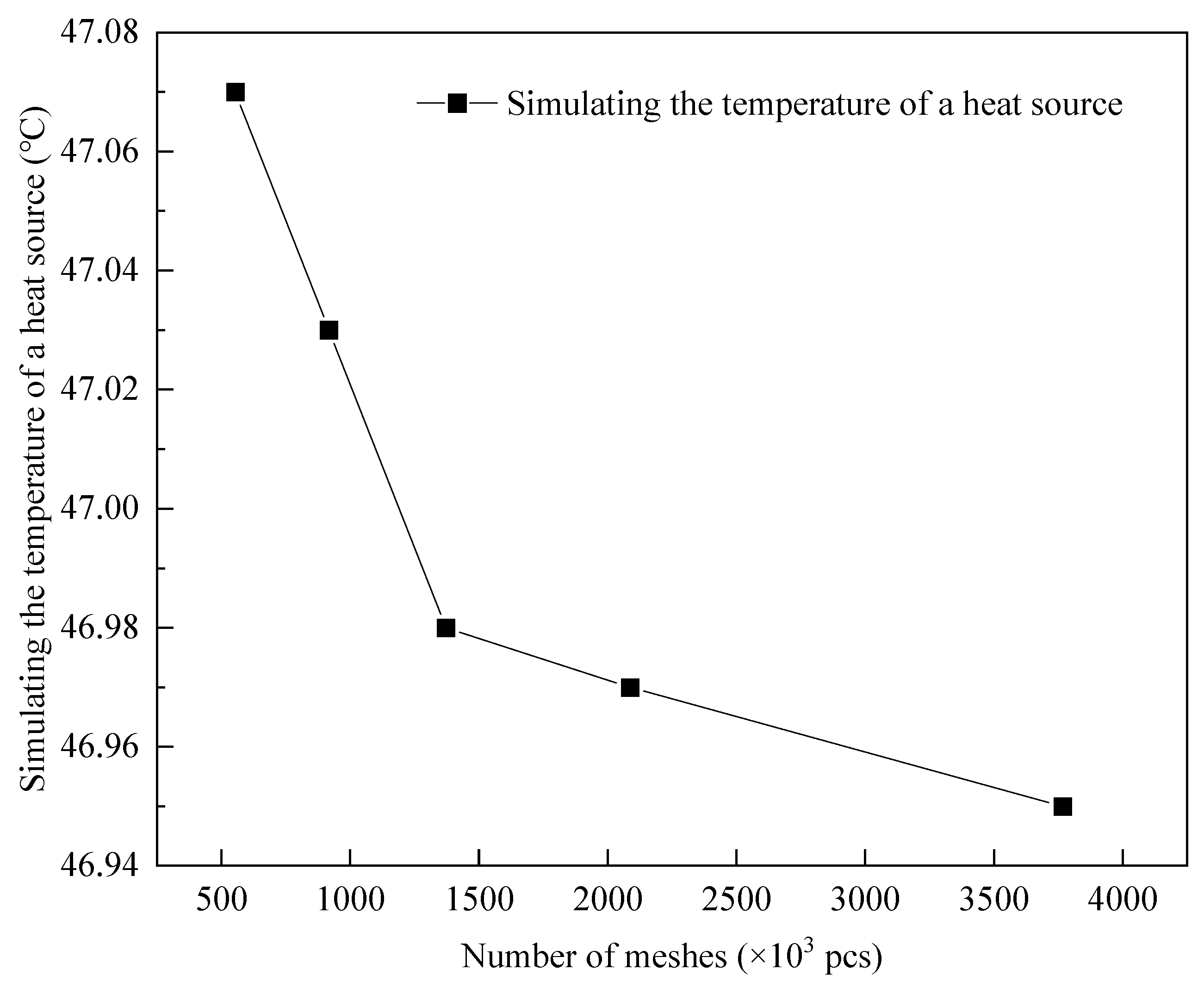
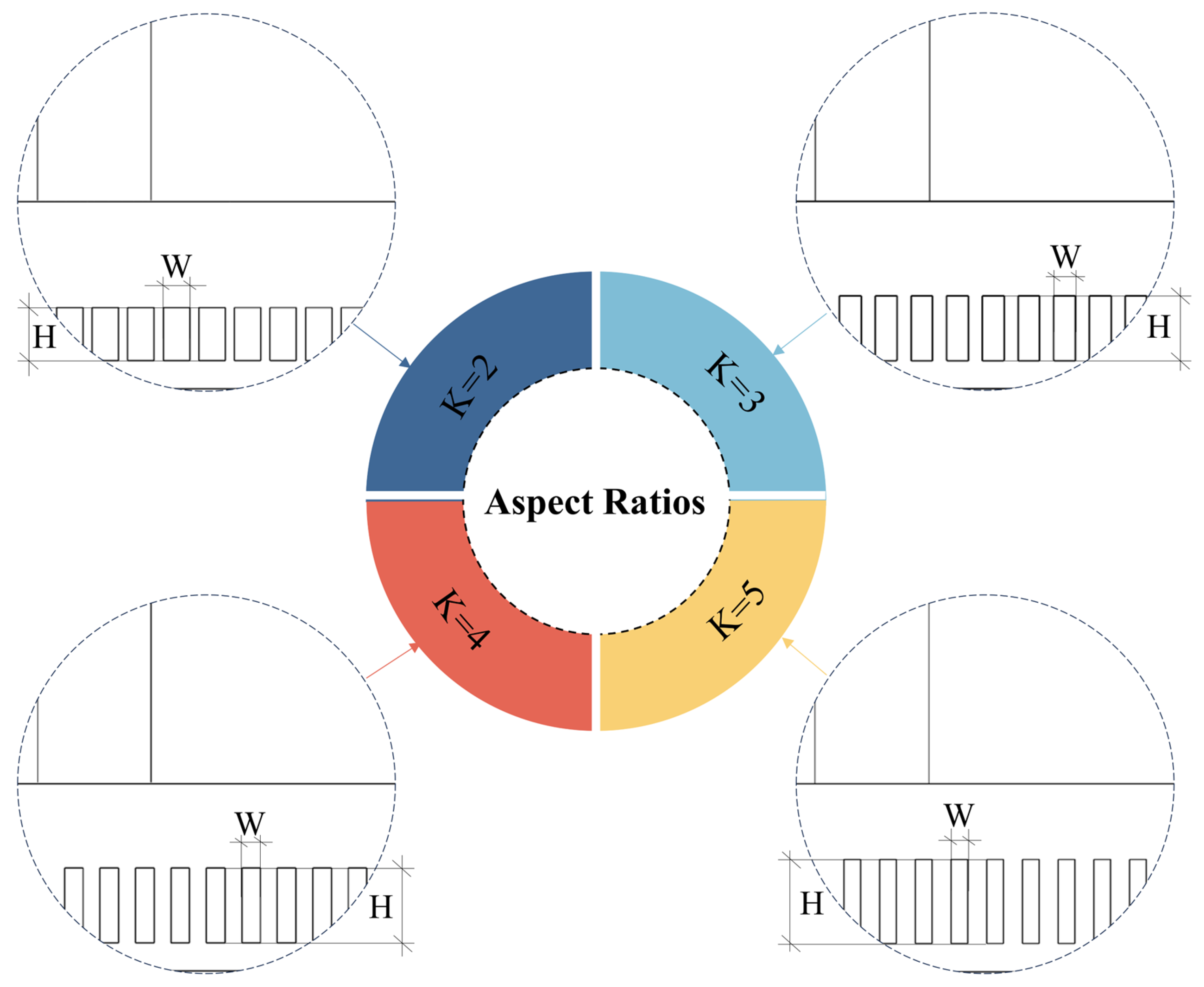
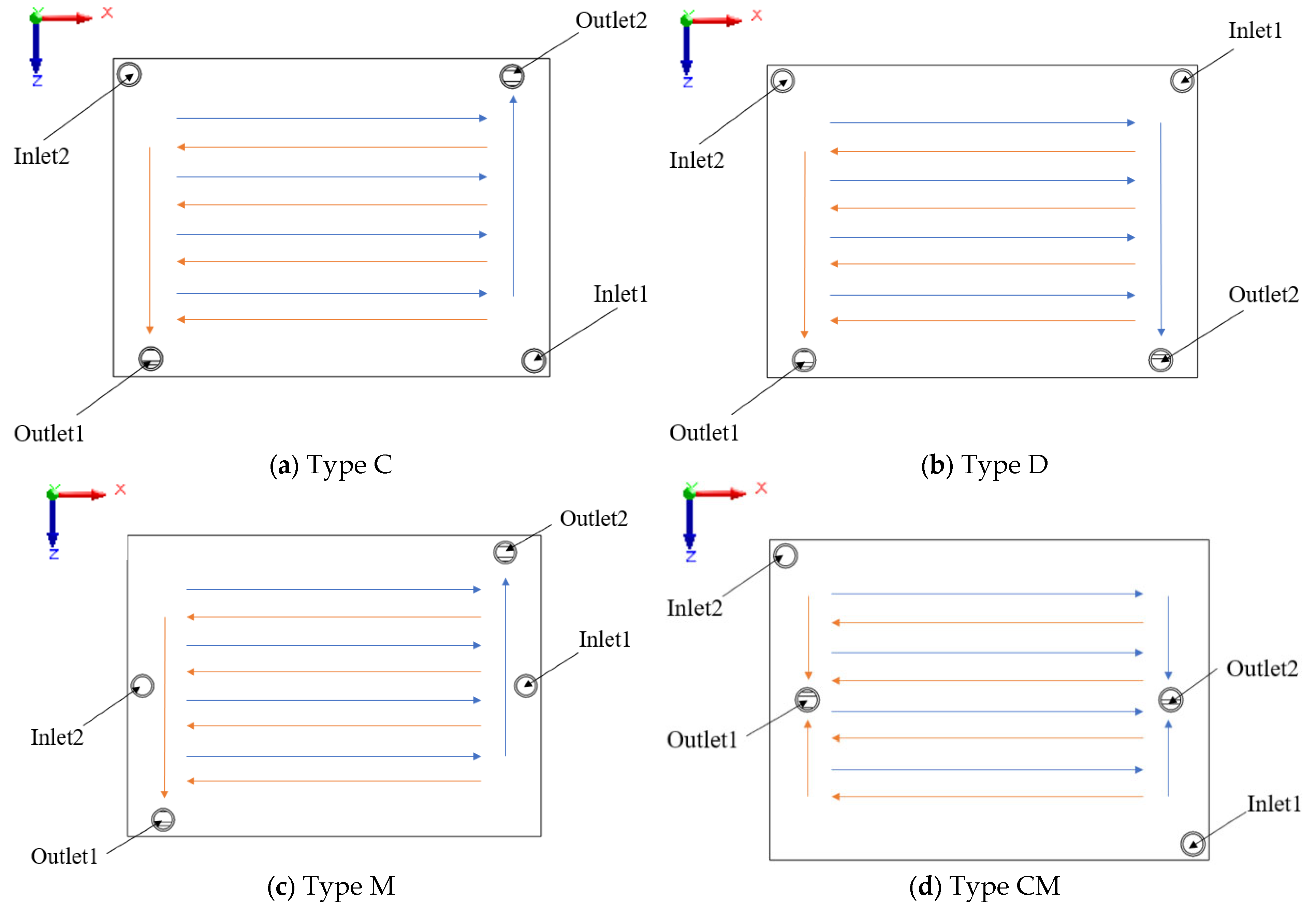
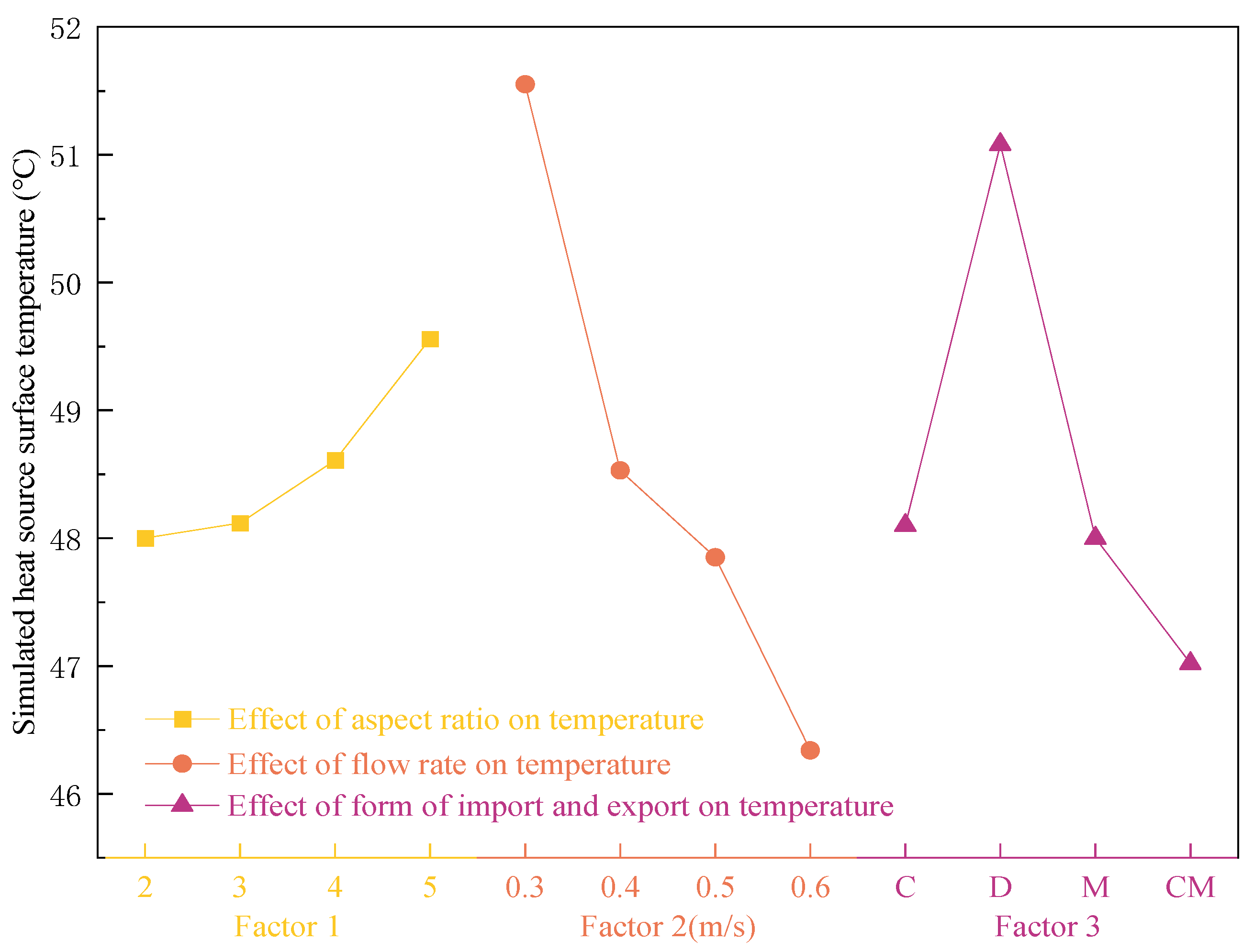
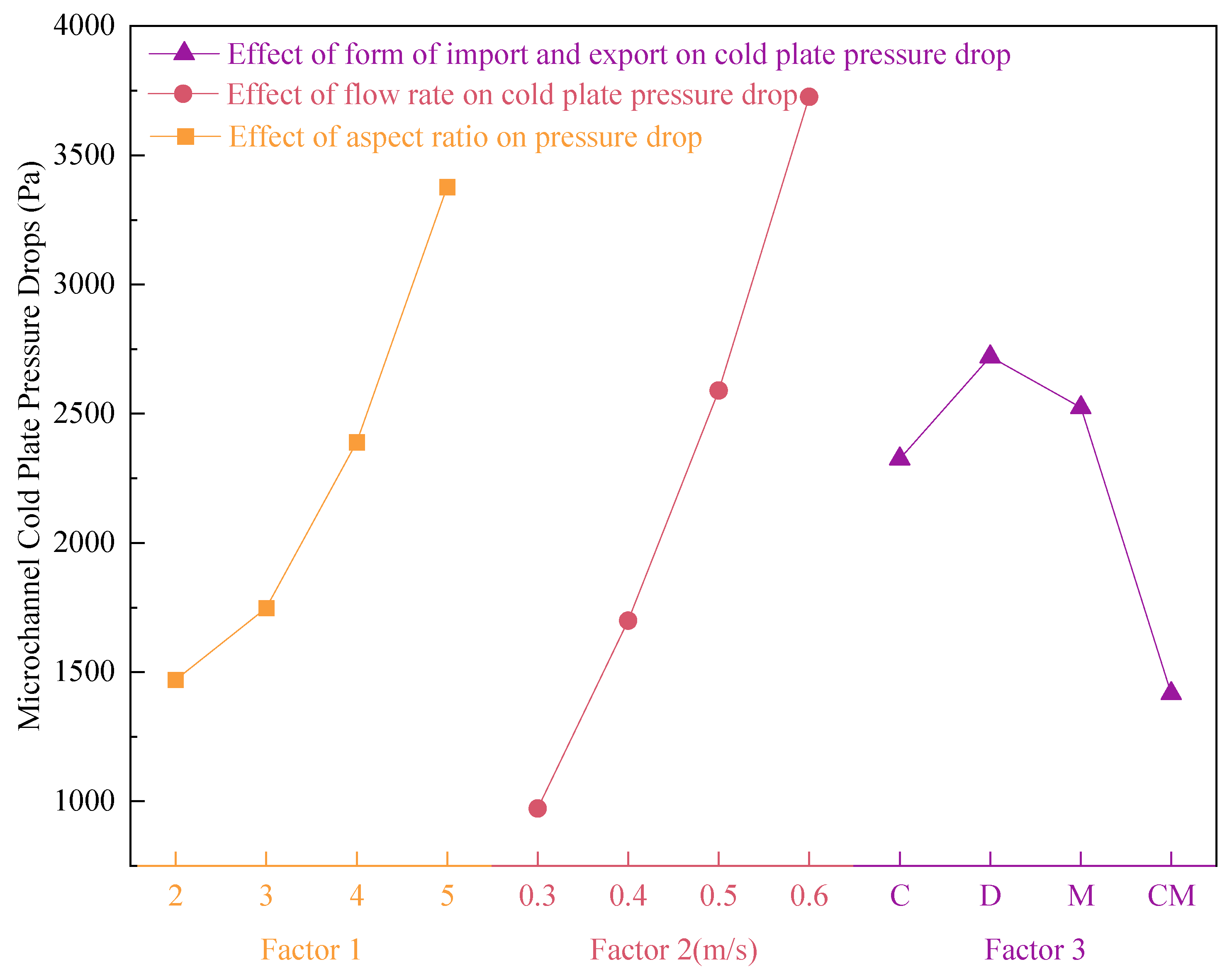
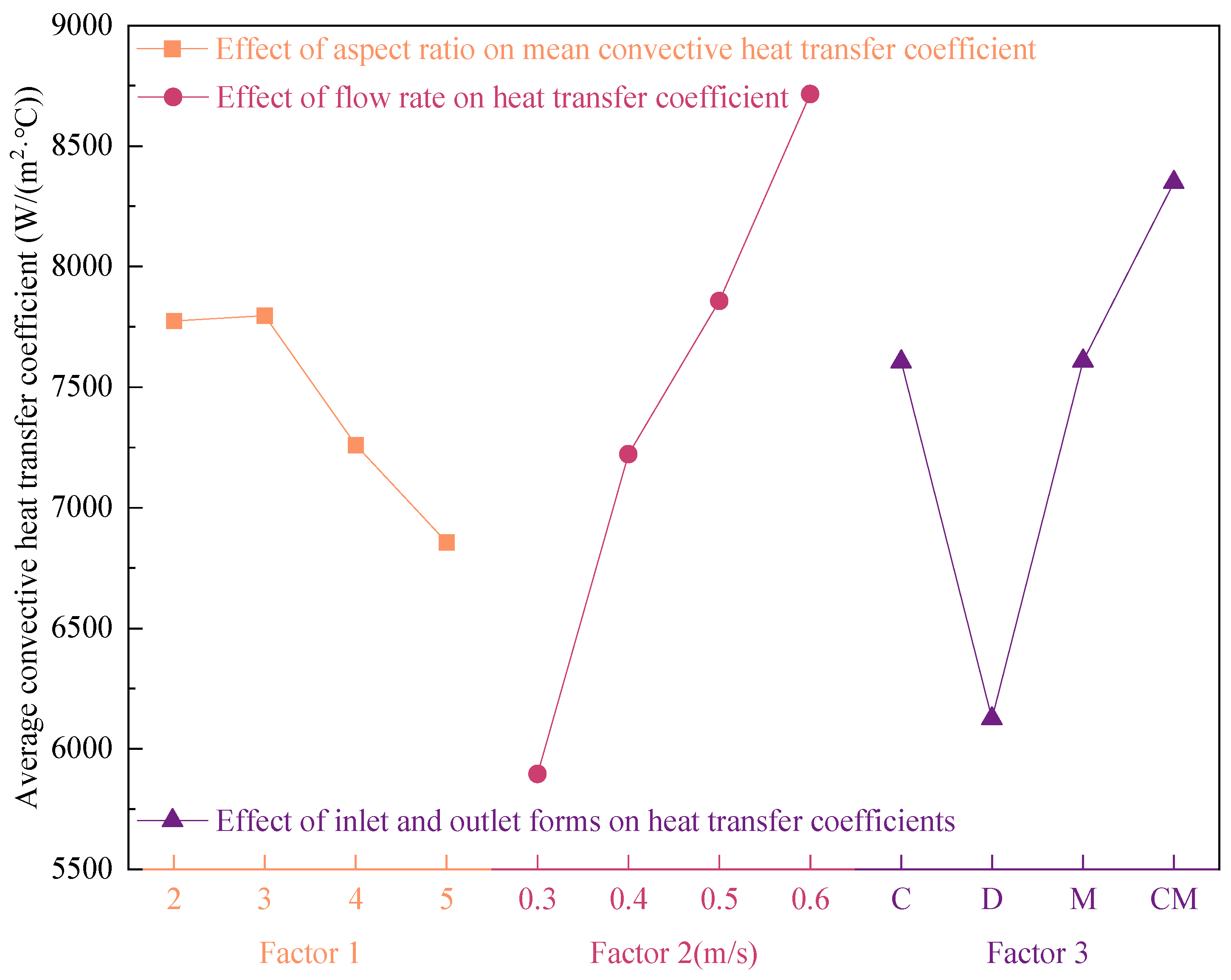
The novelty of this paper lies in the design of a counter-flow rectangular microchannel cold plate for the heat dissipation of high-power electronic chips. This cold plate improves the issue of a significant temperature gradient of a straight microchannel cold plate and realizes a greater uniformity in temperature distribution through the cross-reverse flow of the cooling medium. Through orthogonal tests, the key factors of cooling medium velocity (0.3 m/s, 0.4 m/s, 0.5 m/s, 0.6 m/s), microchannel aspect ratio (2, 3, 4, 5), and inlet/outlet forms (side-in-side-out, side-in-diagonal-out, side-in-in-side-out, side-in-middle-out) are set up to analyze the effects of single factors and interactions on the performance of the plate and to determine the optimal parameter combinations, so that the thermal performance and the flow resistance balance of the plate can be optimized. The best parameter combination is identified to achieve an improved balance between heat transfer efficiency and flow resistance in the cold plate. The designed and optimized cold plate structure in this paper can meet the heat dissipation requirements of CPUs with power consumption of up to 350 W.