Next Article in Journal
Integrating Construction and Operation of Large Interorganizational Projects Based on Resource Orchestration: A Case Study of Shanghai Airports
Next Article in Special Issue
Demand Response Strategy Optimization Method Based on Differentiated Comprehensive Benefit Model of Air-Conditioning Customers
Previous Article in Journal
Development, Performance, and Mechanism of Fluidized Solidified Soil Treated with Multi-Source Industrial Solid Waste Cementitious Materials
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 6
10.3390/buildings15060865
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of Factors Influencing Thermal Comfort at Tram Stations in Guangzhou Based on Machine Learning

by
Xin Chen
1,
Huanchen Zhao
2,
Beini Wang
2 and
Bo Xia
2,*
1
Guangzhou Metro Design & Research Institute Co., Ltd., Guangzhou 510010, China
2
School of Architecture, Chang’an University, Xi’an 710064, China
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(6), 865; https://doi.org/10.3390/buildings15060865
Submission received: 4 February 2025 / Revised: 26 February 2025 / Accepted: 5 March 2025 / Published: 10 March 2025
(This article belongs to the Special Issue Building Energy Performance and Thermal Comfort: Synergies and Challenges)
Browse Figures
Versions Notes

Abstract

As global climate change intensifies, the frequency and severity of extreme weather events continue to rise. However, research on semi-outdoor and transitional spaces remains limited, and transportation stations are typically not fully enclosed. Therefore, it is crucial to gain a deeper understanding of the environmental needs of users in these spaces. This study employs machine learning (ML) algorithms and the SHAP (SHapley Additive exPlanations) methodology to identify and rank the critical factors influencing outdoor thermal comfort at tram stations. We collected microclimatic data from tram stations in Guangzhou, along with passenger comfort feedback, to construct a comprehensive dataset encompassing environmental parameters, individual perceptions, and design characteristics. A variety of ML models, including Extreme Gradient Boosting (XGB), Light Gradient Boosting Machine (LightGBM), Categorical Boosting (CatBoost), Random Forest (RF), and K-Nearest Neighbors (KNNs), were trained and validated, with SHAP analysis facilitating the ranking of significant factors. The results indicate that the LightGBM and CatBoost models performed exceptionally well, identifying key determinants such as relative humidity (RH), outdoor air temperature (Ta), mean radiant temperature (Tmrt), clothing insulation (Clo), gender, age, body mass index (BMI), and the location of the space occupied in the past 20 min prior to waiting (SOP20). Notably, the significance of physical parameters surpassed that of physiological and behavioral factors. This research provides clear strategic guidance for urban planners, public transport managers, and designers to enhance thermal comfort at tram stations while offering a data-driven approach to optimizing outdoor spaces and promoting sustainable urban development.

1. Introduction

The thermal comfort of transportation stations is a critical concern in both academic research and practical applications. These stations comprise multiple temporary spaces, which are generally not fully enclosed, but rather serve as waiting areas for passengers or travelers. The intelligent design and effective management of the thermal environment in these spaces can enhance user comfort and improve energy efficiency. Consequently, a comprehensive understanding of the environmental needs of users in these settings is essential [1,2,3,4,5,6]. Since the 1980s, China has innovated its tram systems, gaining widespread recognition for their environmental sustainability, energy efficiency, and cost-effectiveness. By the end of 2022, a total of 40 tram lines had been established across 24 cities in China, spanning a total length of 588.2 km and featuring 624 stations. In 2022 alone, the network expanded by 74.465 km, reflecting a growth rate of 14.78% [7]. Furthermore, the year 2024 is projected to witness a year-on-year increase in passenger traffic of 4.6%.
The rapid development of tram systems in China, particularly in cities like Guangzhou, characterized by a “hot summer and warm winter” climate, has made the study of thermal comfort at transportation stations increasingly important. Guangzhou’s subtropical climate, with high temperatures and humidity in the summer and mild winters, presents unique challenges for thermal comfort management at its transit stations [8,9,10,11,12,13,14]. As the city’s tram network continues to expand, it is expected to attract more passengers [7,15]. Therefore, investigating thermal comfort in Guangzhou will not only enhance the comfort and energy efficiency of local transit infrastructure but also provide valuable insights for other cities with similar climatic conditions.
Existing studies on thermal comfort primarily focus on indoor and outdoor environments, with comparatively limited research on semi-outdoor and transitional spaces. The tram stations studied in this paper are specifically chosen for this purpose and characteristic. Semi-outdoor spaces combine features of both indoor buildings and outdoor environments, generally exhibiting higher thermal resilience [1,16,17]. Indoor thermal comfort can be regulated through heating, ventilation, and air conditioning systems (HVACs), thereby ensuring a comfortable indoor environment [18]. However, due to the inherent challenges of controlling outdoor conditions, achieving outdoor thermal comfort is considerably more difficult than maintaining its indoor counterpart [19,20].
Previous research has indicated that human thermal comfort is influenced by both physical and personal factors [21]. Physical factors encompass outdoor air temperature (Ta), mean radiant temperature (Tmrt), relative humidity (RH), wind speed (V), and solar radiation (Sr) [19,22,23,24], while personal factors include age, body mass index (BMI), gender, clothing insulation (Clo), and thermal history [23,25,26]. Currently, the primary models employed to assess thermal comfort are the Predicted Mean Vote (PMV), Physiologically Equivalent Temperature (PET), and Universal Thermal Climate Index (UTCI) [27]. The PMV model, due to its simplicity and comprehensive consideration of environmental and individual factors, is widely utilized in indoor thermal comfort studies [28,29]. However, this model is only applicable under steady-state conditions and does not align with actual human thermal perception [30,31]. In contrast, PET and the UTCI are more suitable for outdoor environments [27,32,33,34,35,36], but they face limitations in addressing individual differences, thermal experiences, and other conditions, which affect their predictive accuracy [21]. Machine learning (ML) methods have demonstrated their simplicity, directness, and efficiency in evaluating thermal comfort, effectively supplementing traditional assessment approaches in handling complex individual factors. With advancements in ML technologies and enhanced computational capabilities, an increasing number of researchers are adopting these methods for direct thermal comfort predictions, proving their accuracy to exceed that of conventional physical models [21,37,38,39,40,41,42,43].
Table 1 presents a comprehensive overview of recent studies employing ML techniques to explore both indoor and outdoor thermal comfort, arranged in chronological order. This table details the sources of datasets, influential factors, types of ML algorithms utilized, and the accuracy of the resulting models. As shown in Table 1, the physiological and environmental data utilized in these studies were primarily derived from climate chambers, field surveys, and extensive thermal comfort databases, encompassing various output variables, including Thermal Comfort Vote (TCV), Thermal Sensation Vote (TSV), Thermal Acceptability (TA), thermal preference (TP), and PET, with the accuracy of the majority of models surpassing 65%. The data cover both indoor [43,44,45] and outdoor comfort [20,21,30,37]. Key influencing factors for indoor thermal comfort comprise Clo, age, Ta, indoor air temperature (Ti), metabolic equivalent of task (MET), and Tmrt. Conversely, determinants of outdoor thermal comfort include Ta, Tmrt, RH, and length of stay.
This study identifies key factors influencing thermal comfort through a systematic review of the relevant literature. Previous research indicates that human thermal comfort is influenced by physical factors, including outdoor air temperature, mean radiant temperature, relative humidity, wind speed, and solar radiation, as well as personal factors, such as age, body mass index, gender, clothing insulation, and thermal history [19,22,23,24,25,26]. However, due to the shielding structure of the station, which includes side and top coverage, solar radiation was excluded from this study. The station’s shielding elements, such as walls and shading devices, effectively block direct sunlight, resulting in relatively low solar radiation levels inside the station and minimal impact on thermal comfort. Additionally, variations in station length, width, and area are primarily determined by the station’s design, making the station layout a key factor for analysis in this study.
This study seeks to identify and rank the factors influencing outdoor thermal comfort at tram stations using ML techniques. Initially, microclimatic data from tram stations and passenger comfort feedback were collected to create a comprehensive dataset that encompasses environmental parameters, individual perceptions, and station design characteristics. The analysis considers various influencing factors, including the length of stay in Guangzhou, Clo, age, BMI, RH, V, Ta, Tmrt, the location of the space occupied in the past 20 min prior to waiting (SOP20), gender, and station type. Subsequently, a range of ML models, including XGB, LightGBM, CatBoost, KNN, and RF, were employed to train and validate the data, enabling the identification and ranking of key factors affecting thermal comfort. These findings will aid urban planners, public transport managers, and designers in formulating strategies to optimize the thermal environment design of stations, thereby enhancing passenger experiences and providing data support for sustainable urban development.

2. Methodology

Grounded in Positivism and employing an inductive research type, this study adopts a quantitative case study approach, structured into four key stages: data collection, data preprocessing, the training and optimization of machine learning models, and the selection and interpretation of the optimal model (see Figure 1). Initially, microclimatic data and thermal comfort survey results from tram stations in the Huangpu District of Guangzhou were gathered. Subsequently, the data underwent cleansing and normalization. The processed dataset was employed to train the ML models, all of which underwent parameter optimization using Bayesian Optimization (BO) techniques. By comparing the accuracy of various models, the one exhibiting the highest performance was selected, and the SHapley Additive exPlanations (SHAP) method was applied for a comprehensive performance analysis of this model [30,45,46,47,48].

2.1. Data Collection

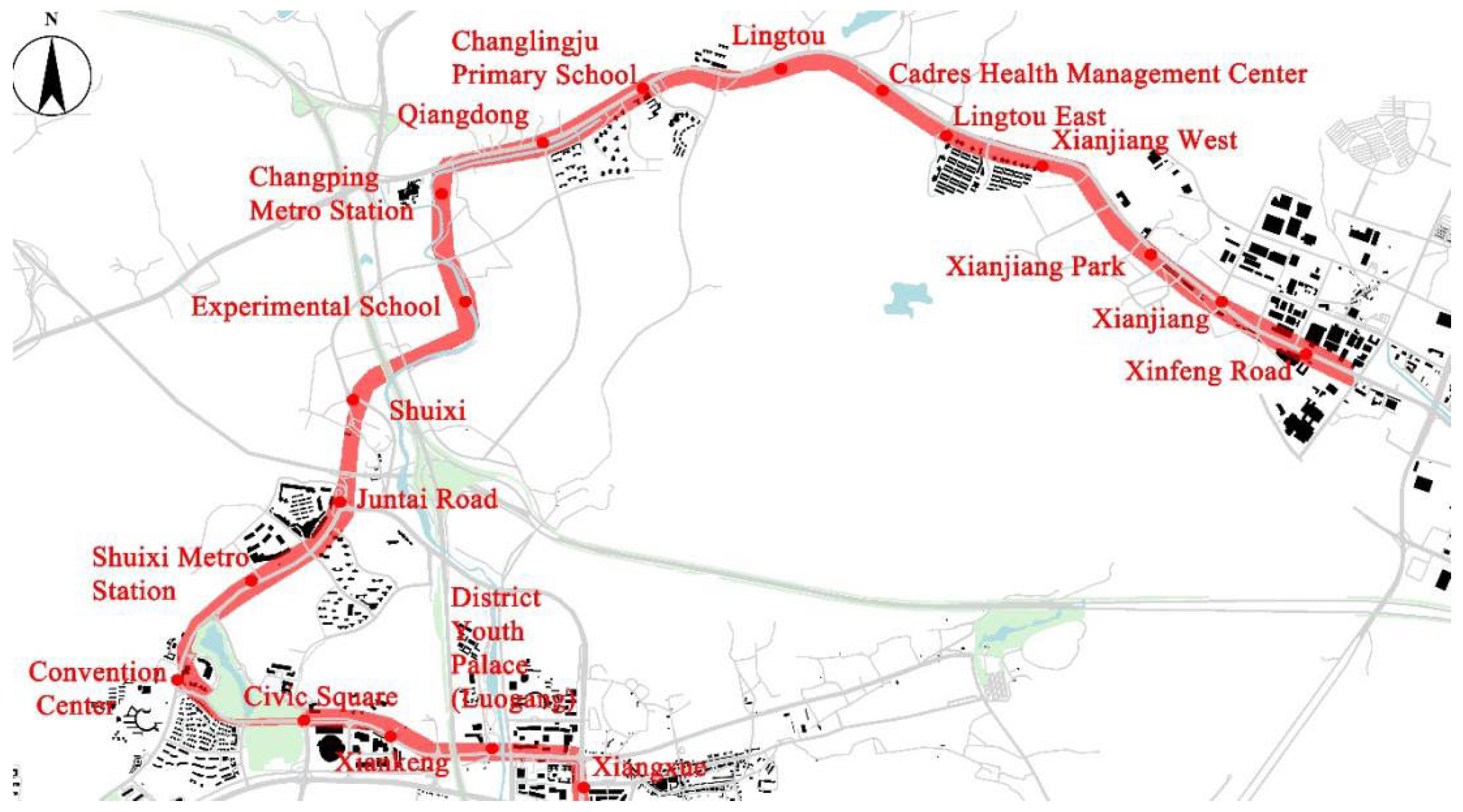
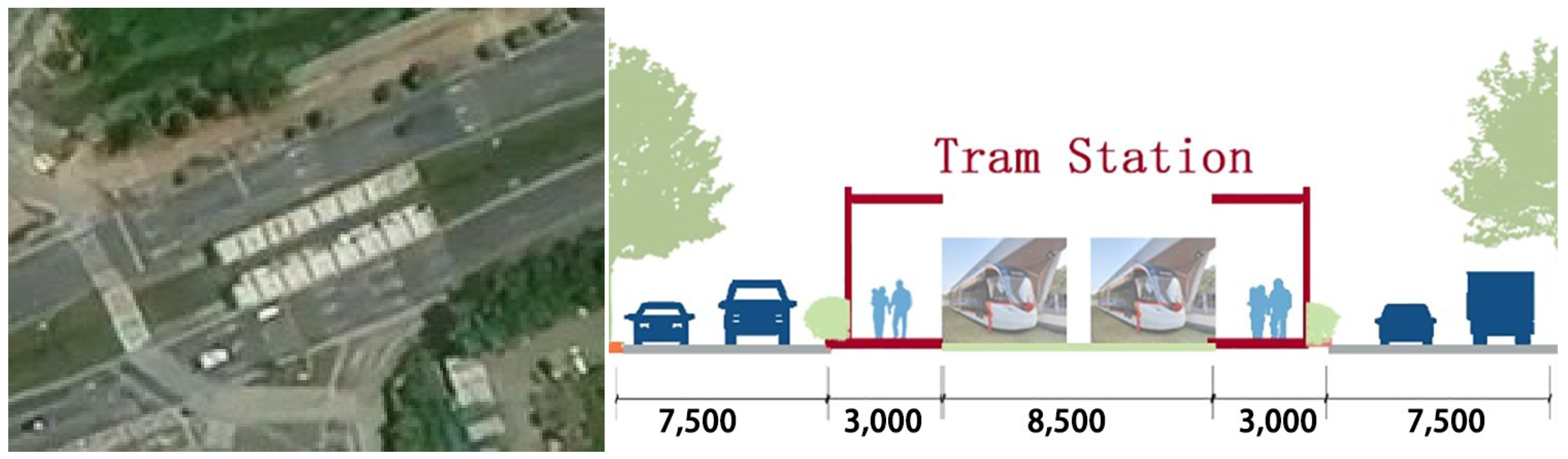
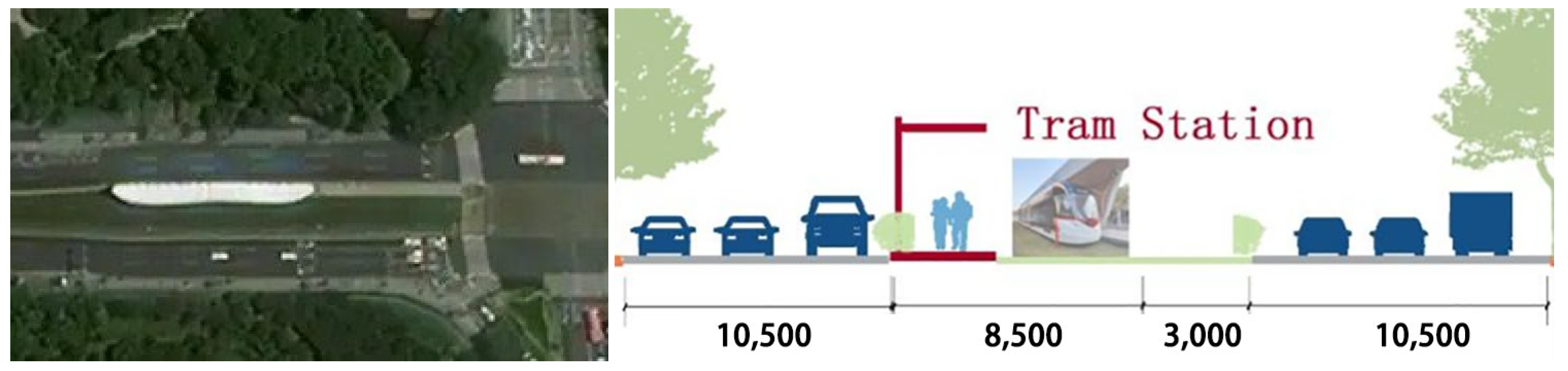
2.1.1. Study Area

Guangzhou, situated in southern Guangdong Province, is centrally located in the Pearl River Delta. It falls within the subtropical monsoon climate zone, exhibiting the typical characteristics of a humid monsoon climate. The summer months are marked by high temperatures and humidity, along with significant rainfall. The hottest month is July, with an average temperature of 30.3 °C [49].
A comprehensive analysis of the surrounding environments of the existing tram stations was conducted and compared with the urban environment of Guangzhou. The results indicated that the environment of Huangpu District tram line 1 closely resembles the broader urban environment of Guangzhou. To enhance the applicability and reliability of the study, the analysis was focused on Huangpu District tram line 1 (see Figure 2).
Additionally, to ensure the representativeness of the study, particular attention was given to the age distribution of participants, aiming for balanced representation across various age groups. This study employs a case study approach to provide an overview of the age distribution of residents in the selected area: Xiankeng includes all age groups; Civic Square is predominantly inhabited by middle-aged and elderly residents; the Convention Center primarily attracts young and middle-aged residents; Juntai Road is mostly populated by young and middle-aged residents; the Experimental School is mainly occupied by adolescent residents; and Xinfeng Road is predominantly inhabited by young and middle-aged residents. These factors informed the selection of six survey points for administering thermal comfort questionnaires and conducting physical environment assessments, as detailed in Table 2.
The survey identified two primary types of platform configurations: ground-level side platforms and ground-level separated platforms (see Figure 3 and Figure 4). Thermal environment measurements were taken at one-meter intervals along each platform, with temperature variations remaining within 0.3 °C. Therefore, the central positions of each platform were selected as the measurement points for the recording of thermal conditions.

2.1.2. Physical Measurements

This study employed both questionnaire surveys and field measurements for data collection. A one-day pilot experiment was conducted prior to the main experiment, from 7:00 a.m. to 10:00 p.m., with testing intervals set at 30, 15, 5, and 3 min. The results indicated that variations in temperature, globe temperature, and humidity were more pronounced during the morning and afternoon, with smaller changes observed during other times. Therefore, the average values of these differences were selected for analysis (see Table 3). Wind speed, due to significant fluctuations, was excluded from the analysis. Furthermore, the temperature and humidity differences within 5 min and 3 min intervals fell within the instrument’s error range (see Table 4). Considering the stability, reliability, and feasibility of the experiment, the 5 min interval was deemed the most appropriate for testing.
This study employed a cross-sectional research design, with the formal experiment conducted from 4 to 15 July 2024, during Guangzhou’s hottest month. Meteorological parameters at each measurement point were recorded at 5 min intervals from 7:00 a.m. to 11:00 p.m. on each experimental day. During the testing period, the weather remained clear, with no precipitation observed. The instruments used in the experiments were positioned at a height of 1.5 m above the ground and comprised a black globe thermometer, a temperature and humidity data logger, and an anemometer. All instruments utilized in this study adhered to ISO 7726 standards [50], thereby ensuring rapid response times and high accuracy. Table 4 summarizes the instruments employed along with their specific parameters. The equipment is sourced from Extech Instruments, Inc., located in Nashua, NH, USA. Table 5 presents the range of variation in the microclimatic parameters in this study.

2.1.3. Questionnaire Surveys

During the on-site experiment, a concurrent questionnaire survey was administered. At the time of distributing the questionnaires, both the location and time of distribution, as well as the specific positions of the participants, were recorded. Afterward, the respondents completed the forms accordingly. A total of 786 participants were involved, with ages ranging from 15 to 68 years, all situated within the station. The questionnaire was distributed using a non-probability sampling method, with efforts made to ensure a balanced gender ratio and age distribution throughout the process. Table 6 provides detailed information about the participants. Before completing the questionnaire or answering any questions, a verbal interview was conducted to ensure that the respondents had been at the station or outdoors for at least 15 min to acclimatize to the outdoor thermal environment. Only those meeting the criteria were provided with the questionnaire. Of the 786 questionnaires distributed, 744 were considered valid.
The questionnaire designed for this study adhered to the ASHRAE 55-2020 standard [51] and was divided into two core sections: basic information and thermal sensation assessment. In the basic information section, participants were required to provide details such as age, gender, height, weight, Clo, length of stay in Guangzhou, length of stay at the station, and the location they occupied in the 20 min prior to waiting for the tram. The thermal sensation section focused on evaluating respondents’ perceptions of thermal comfort across different environments, including TCV, TSV, TA, and Humidity Sensation Vote (HSV) (see Table 7).
Each questionnaire assessment corresponds to the physical environmental conditions recorded within the same 5 min interval, ensuring a direct correlation between participants’ thermal perceptions and the measured climatic data.

2.2. ML Model Establishment and Optimization

2.2.1. Data Preprocess

The primary objective of data preprocessing is to ensure the quality and applicability of the dataset, thereby optimizing the performance and interpretability of ML models. This involves addressing issues such as filling in missing values, reducing redundancy, identifying and managing outliers, and standardizing the data scale. These measures are critical for enhancing the model’s predictive accuracy [53].
We employed label encoding techniques to convert the textual data from the questionnaires into numerical form, thereby simplifying the complexities of data preprocessing and ensuring that the algorithm can effectively process non-numeric information. Specifically, in the questionnaire, gender options were encoded as follows: male as 0 and female as 1; within the SOP20 options, indoor spaces were encoded as 0 and outdoor spaces as 1. This method assigns a unique integer to each textual label, facilitating both the numerical representation of the data and the feasibility of model computations [30].
In the presence of outliers, such as recording errors or incorrectly completed questionnaires, participants whose age is less than their length of stay in Guangzhou, or who select the same answer for all questions, will be considered outliers and manually excluded from the analysis. Furthermore, the Isolation Forest method effectively identifies anomalies by utilizing a tree structure to isolate observations. We removed the questionnaires containing these outliers, resulting in the elimination of 59 invalid entries after the initial cleaning, thus yielding a final dataset of 744 entries [30].
To eliminate differences in feature scales caused by varying units, all numeric data underwent normalization. This process adjusts the data to a uniform scale (the range of 0 to 1), ensuring that each feature is evaluated fairly during model training. Following data preprocessing, the dataset was divided into two parts: a training set (80%) and a test set (20%), with the model trained on the training set and evaluated on the test set [30].
In this study, the thermal comfort feedback provided by respondents, including TCV, TSV, TA, and HSV, served as target variables for training the model. During the summer in Guangzhou, feedback for lower vote levels (ranging from −3 to 0 for TSV) was scarce due to the high-temperature environment. To prevent model overfitting resulting from data imbalance, we removed these data points, simplifying the TSV seven-category problem into a three-category issue [30,54,55]. Similarly, for the five-level TA scale, feedback ranging from 0 to 2 was limited, leading to the exclusion of this subset and the simplification of the problem to a binary classification. For the TCV analysis, feedback for options ranging from −3 to 0 was also limited, resulting in the removal of these data points and simplifying the problem to a three-category classification. Regarding HSV, feedback for options ranging from −3 to 0 was infrequent, prompting the removal of these data points and transforming the seven-category problem into a three-category classification.
Finally, this study’s dataset includes 11 independent variables: length of stay in Guangzhou, Clo, age, BMI, RH, V, Ta, Tmrt, SOP20, gender, and station type. The dependent variables consist of four components: TSV, TCV, TA, and HSV.

2.2.2. Model Construction and Evaluation

In this study, we employed five distinct ML algorithms to construct models: XGB, LightGBM, CatBoost, RF, and KNN. XGB develops a robust learner by incrementally integrating multiple base learners and iteratively optimizing prediction accuracy, thereby effectively rectifying errors in prior thermal sensation models [56]. LightGBM serves as a gradient boosting framework that leverages histogram-based methods to construct decision trees efficiently, which in turn accelerates training times, boosts efficiency, and improves predictive accuracy for extensive thermal sensation datasets [30,57]. Meanwhile, CatBoost is a refined machine learning technique that applies a boosting algorithm specifically designed to handle categorical features effectively, thereby enhancing the predictive accuracy of thermal sensation datasets containing such variables [30,58]. As one of the ensemble learning algorithms, RF constructs multiple decision trees and derives final decisions through a voting mechanism [59]. KNN classifies data by first identifying the k nearest neighbors of the target and then employing majority voting based on the categories of these neighbors, relying on the identification of the k-closest points within the training sample [59]. Advantages of each algorithm are detailed in Table 8. The construction of all models was carried out using the scikit-learn library in Python 3.11. Hyperparameter tuning for all ML models was conducted using BO, with the types of hyperparameters detailed in Table 9 and a total of 500 iterations performed.
In this study, we address the class imbalance caused by the uneven distribution of samples across different categories, where some categories are oversized and others are still undersized. To effectively construct the thermal comfort model and alleviate this imbalance, we utilized a weighted averaging method to evaluate the accuracy of the ML models. The weight assigned to each category was determined by its sample size. We first calculated the macro precision (Macro-P), macro F1 score (Macro-F1), and macro recall (Macro-R) for each category, subsequently multiplying these metrics by their respective weight coefficients; higher scores reflect superior model performance [30]. Furthermore, to enhance the accuracy and reliability of our evaluations, we incorporated five-fold cross-validation, which systematically assesses the model across different data subsets, yielding an average accuracy metric. This approach is vital for validating the model’s stability and reliability [47].

2.2.3. Model Explanation

Traditional methods for ranking influential factors often fall short of clearly representing the extent to which each factor impacts the model. In contrast, SHAP presents an innovative solution by employing Shapley values from game theory to evaluate the contributions of individual features to the model’s predictions. This methodology not only quantifies the influence of each feature on predicted outcomes but also offers a visual representation of these effects [30,46,48,60].
SHAP quantifies the effect of each input feature on a specific sample by calculating the average marginal contribution of that feature across all possible combinations. The importance of features is visually represented, with the x-axis showing the absolute SHAP values and the y-axis ranking features based on their total SHAP values across all samples. Summary plots further illustrate the positive and negative impacts of each feature on the model’s results; positive SHAP values indicate beneficial effects, while negative values denote detrimental impacts. A larger SHAP value for a feature indicates a more significant influence on the model’s output [30,61].

3. Results

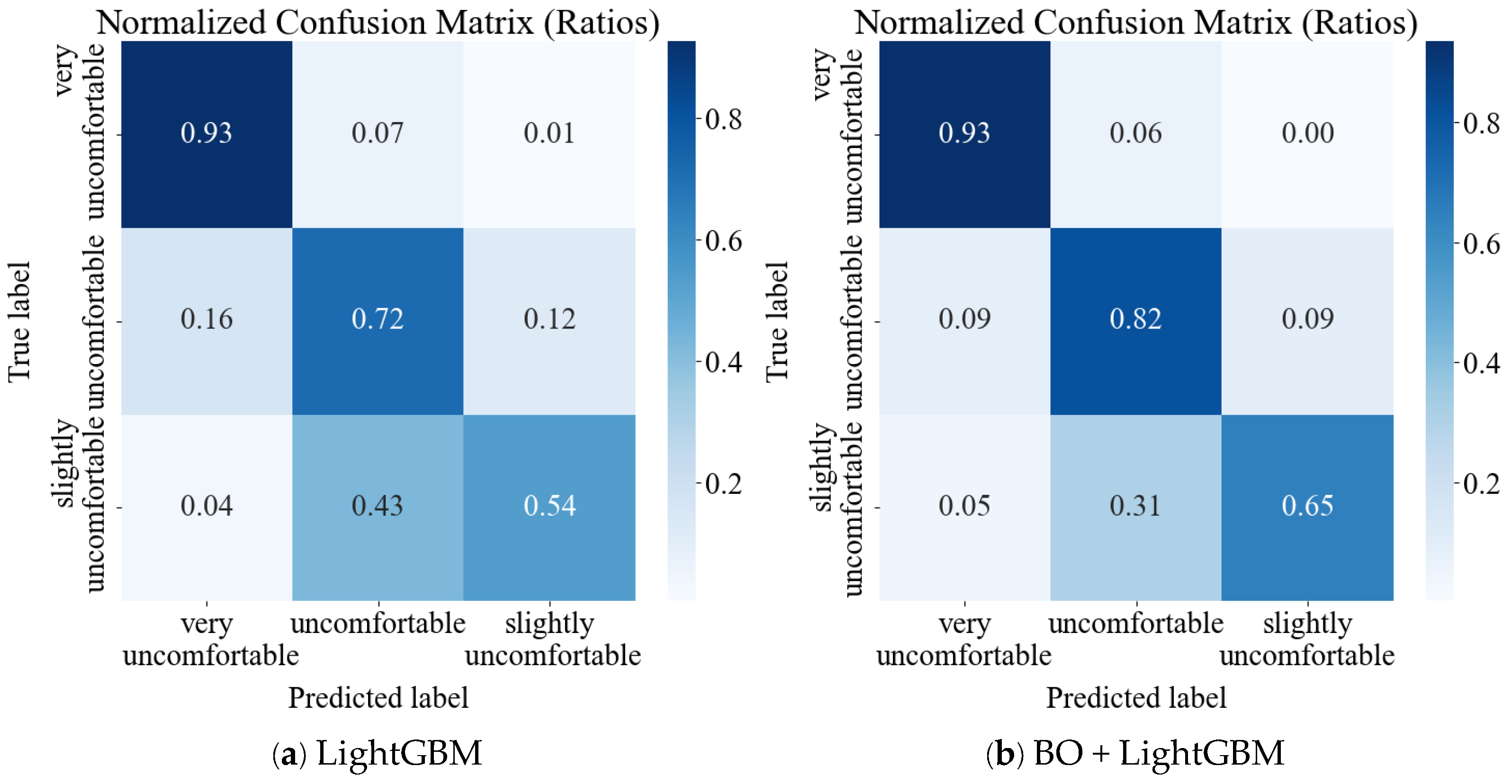
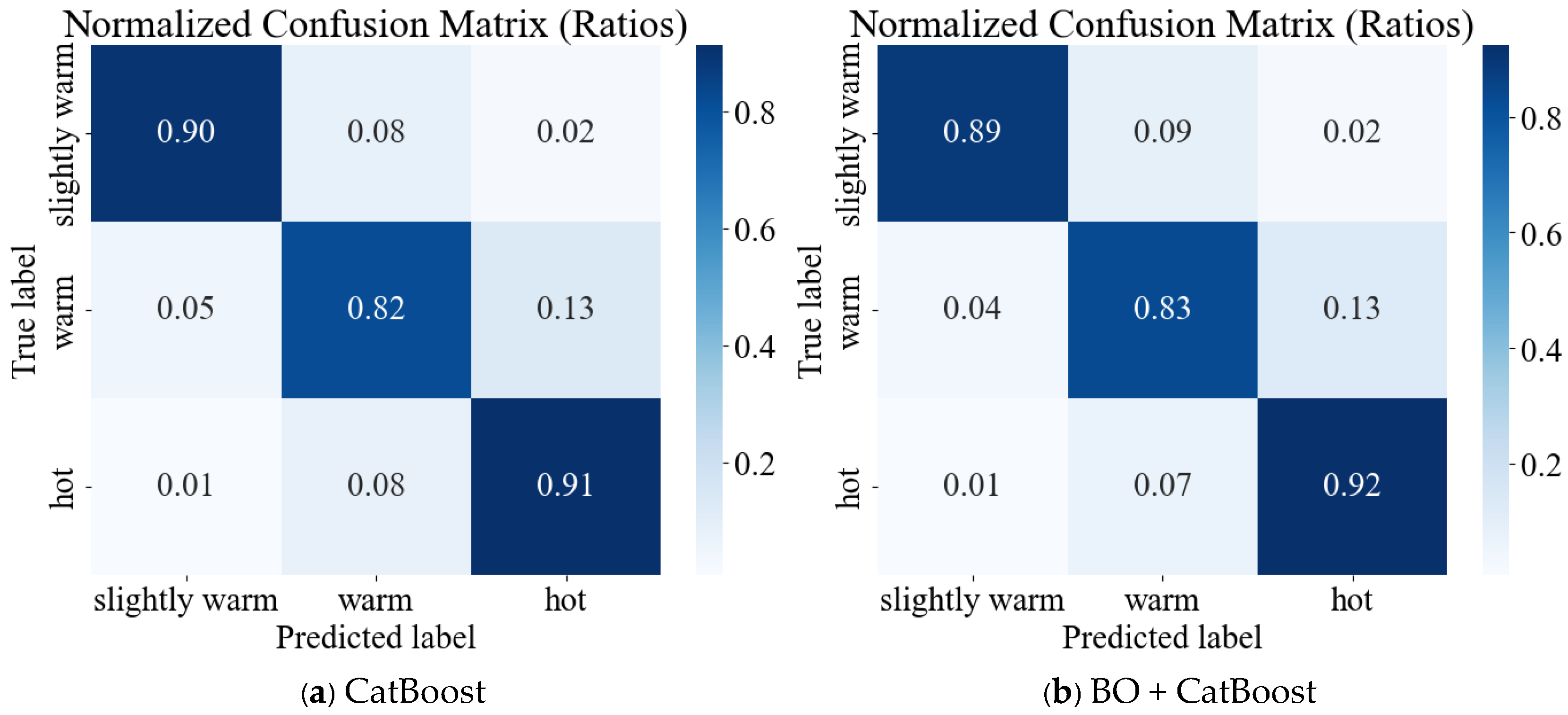
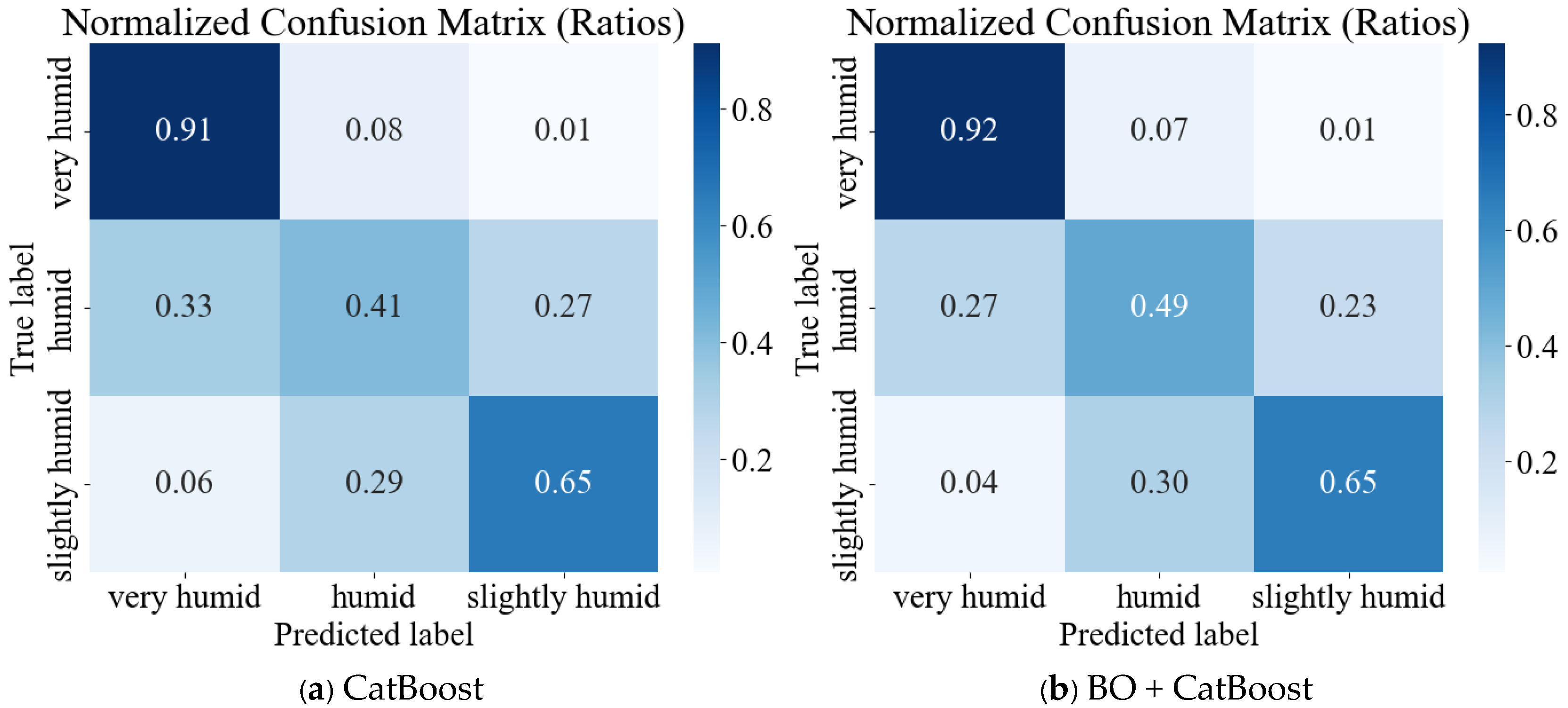
3.1. Model Optimization and Selection

Table 10, Table 11, Table 12 and Table 13 present the performance metrics of various ML algorithms across different datasets. All reported figures are weighted by sample size and include metrics such as Macro-P, Macro-R, and Macro-F1. Overall, significant discrepancies in performance exist among the datasets, as indicated by a one-way ANOVA analysis with a p-value of less than 0.05. Notably, the LightGBM algorithm achieved a Macro-P of 86.07%, a Macro-R of 84.67%, and a Macro-F1 of 84.78%, establishing it as the best-performing model across the entire dataset. This performance surpasses that of the least effective model, KNN, by margins of 9.37%, 7.26%, and 8.41%, respectively, with particular excellence demonstrated on the TA dataset.
Table 10 evaluates the efficacy of various ML algorithms in predicting TCV, with LightGBM emerging as the top performer, attaining Macro-P, Macro-R, and Macro-F1 scores exceeding 84%. In comparison to the underperforming KNN model, LightGBM’s Macro-P, Macro-R, and Macro-F1 exceed those of KNN by 11.66%, 11.32%, and 12.27%, respectively. Table 11 assesses the algorithms’ performance in predicting TSV, where CatBoost stands out, achieving Macro-P, Macro-R, and Macro-F1 scores all exceeding 80%. Relative to the KNN model, CatBoost’s scores are superior by 10.72%, 9.54%, and 8.51%, respectively. Table 12 examines the algorithms’ efficacy in predicting TA, revealing no significant differences among the models’ Macro-P, Macro-R, and Macro-F1 scores. Nonetheless, LightGBM again demonstrates exceptional performance, with all three metrics surpassing 94%. Table 13 focuses on the performance of different algorithms in predicting HSV, where CatBoost excels, achieving Macro-P, Macro-R, and Macro-F1 scores exceeding 76%. Compared to the KNN model, CatBoost’s scores are higher by 13.13%, 7.32%, and 11.43%, respectively.
In summary, LightGBM exhibits high predictive accuracy in TCV and TA, while the CatBoost model demonstrates superior accuracy in TSV and HSV, outperforming other algorithms. However, among all datasets, the performance differences between LightGBM and CatBoost are minimal, revealing remarkably similar results.

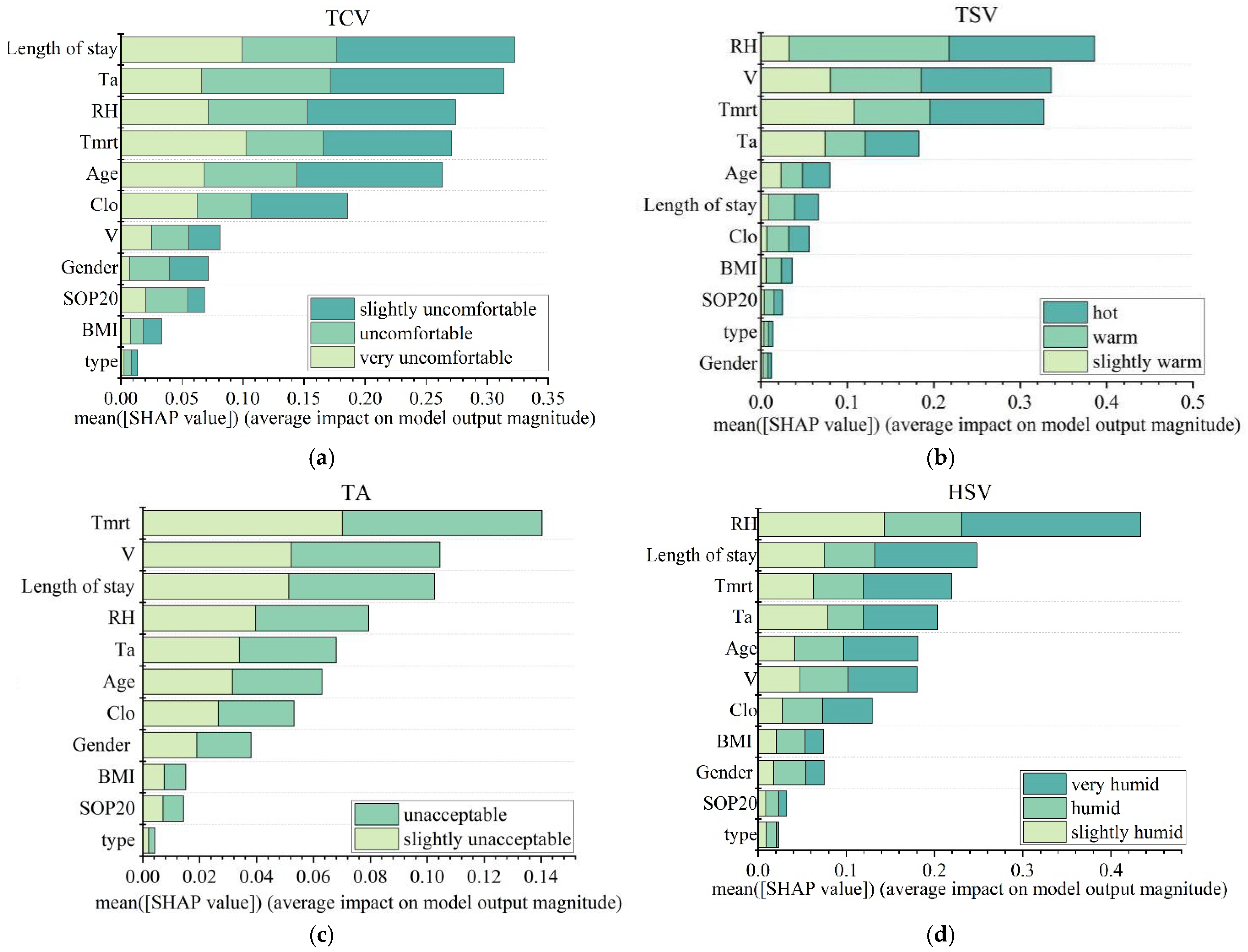
3.2. SHAP Analysis of Feature Impacts

3.2.1. Importance Ranking of Features

As shown in Figure 5, this study utilizes SHAP values to assess and rank the importance of various features. The horizontal axis displays the absolute mean SHAP values across all samples, reflecting each influencing factor’s contribution to the model; higher values indicate a more significant impact on the model. Different colors represent the distinct categories of TCV, TSV, TA, and HSV [30].
Figure 5a displays the ranking of features influencing the TCV prediction model. Significant factors such as length of stay, Ta, RH, Tmrt, age, and Clo exert considerable effects on the model, while other features have a comparatively minor impact. Although the general ranking of feature importance remains consistent across different TCV ratings, Tmrt emerges as the most influential factor in the “very uncomfortable” category, while Ta emerges as the most influential factor in the “uncomfortable” category.
Figure 5b presents the ranking of features affecting the TSV prediction model. The results indicate that RH, V, Tmrt, and Ta significantly influence the model, whereas other factors exhibit lesser impacts. Consistently, the ranking of feature importance holds across various TSV voting categories, with V and Tmrt being the most influential in the “slightly warm” category.
Figure 5c shows the ranking of features influencing the TA prediction model. The final results reveal that Tmrt, V, length of stay, RH, Ta, age, Clo, and gender are the most significant features, while other factors have minimal effects. The ranking of feature importance remains stable across all voting categories.
Figure 5d illustrates the ranking of features impacting the HSV prediction model. The findings indicate that RH, length of stay, Tmrt, Ta, age, V, and Clo exert substantial influence on the model, while other features have minor impacts. The ranking of feature importance remains largely consistent across different HSV voting categories; however, in the “slightly humid” category, Ta’s influence surpasses that of length of stay and Tmrt.
The analysis of the four thermal comfort prediction models (TCV, TSV, TA, and HSV) using SHAP values reveals the key factors influencing thermal comfort. In general, physical parameters such as Tmrt, Ta, RH, and V, as well as physiological factors like length of stay, age, and Clo, are significant contributors across all models. Other influencing factors have a relatively minor impact on the models.

3.2.2. Impact of Features: Positive or Negative

To effectively employ SHAP analysis for assessing the impact of various features on TCV, TSV, TA, and HSV, we convert these target labels into binary classifications. Specifically, we set the median values of TCV, TSV, TA, and HSV as thresholds, designating values above the median as 1 (representing higher values) and those below as 0 (indicating lower values). As illustrated in the color bar of Figure 6, blue signifies smaller feature values, while red denotes larger feature values. Positive SHAP values indicate a beneficial impact of a feature on the model, whereas negative values reflect a detrimental effect [30].
Figure 6a illustrates the positive and negative effects of various features on the TCV prediction model. Notably, increased length of stay, age, and V significantly enhance TCV, suggesting that as these values rise, individuals’ comfort voting levels also increase. Conversely, Tmrt, RH, Ta, Clo, and BMI exert significant negative effects on TCV, indicating that higher values correspond to lower comfort voting levels. Gender differences are pronounced, with females reporting a higher proportion of discomfort (refer to Section 2.2.1). The SOP20 is associated with greater discomfort indoors compared to outdoors. The variable type does not exhibit a clear positive or negative impact on the TCV model.
Figure 6b depicts the effects of features on the TSV prediction model. Increased RH, Tmrt, Ta, and Clo significantly enhance TSV, indicating that higher values lead to elevated thermal sensation voting levels. Conversely, V and age negatively affect TSV, suggesting that as these values increase, comfort voting levels decrease. Gender differences are less pronounced, and length of stay, SOP20, BMI, and type do not demonstrate a clear positive or negative influence on the TSV model.
Figure 6c reveals the impacts of features on the TA prediction model. Increased length of stay, age, and V positively influence TA, indicating that higher values correspond to greater levels of acceptance regarding the environment. Conversely, Tmrt, RH, Ta, and Clo exert significant negative effects on TA, suggesting that higher values correlate with lower acceptance levels. Gender differences are evident, with females reporting a higher proportion of unacceptability, and SOP20 indicating poorer environmental acceptance indoors compared to outdoors. BMI and type do not clarify a positive or negative influence on the TA model.
Figure 6d presents the impacts of features on the HSV prediction model. Increased RH, Tmrt, Ta, Clo, and BMI significantly enhance HSV, suggesting that higher values lead to elevated humid sensory discomfort voting levels. In contrast, length of stay, age, and V negatively impact HSV, indicating that higher values correspond to lower levels of humid sensory discomfort voting. Gender differences are not pronounced, and SOP20 and type do not elucidate a clear positive or negative influence on the HSV model.
Although the influencing factors differ across models, physical parameters (such as RH, Tmrt, Ta, and V) and physiological factors (such as length of stay, age, and Clo) generally have a significant impact on thermal comfort, thermal sensation, environmental acceptance, and humidity discomfort. Gender differences are more pronounced in certain models, while the impact of station type and SOP20 is relatively minor.

4. Discussion

4.1. Comparison in TSV, TA, TCV, and HSV

To evaluate outdoor environments, this study employs the TCV, TSV, TA, and HSV metrics (see Table 7), utilizing five ML methodologies for model construction and assessment (refer to Table 10, Table 11, Table 12 and Table 13). Among these, the TA model demonstrates the highest accuracy, achieving 94.22%. This notable performance can be attributed to the transformation of TA into a binary classification problem following a reduction in categories, while the accuracies of the other models stabilized around 75%, reflecting their inherent multiclass nature [47,62].
Furthermore, this research analyzes the ranking of significant feature values and visualizes the positive and negative impacts of these influencing factors on the four models (TCV, TSV, TA, and HSV) using SHAP values (see Figure 5 and Figure 6). By comparing the rankings of key features across multiple models, it becomes evident that in the high-temperature and high-humidity environment of Guangzhou during summer, physical parameters such as Ta, RH, and Tmrt exert considerable influence on all models. This prominence arises from the fact that Ta and RH are fundamental quantities for assessing thermal comfort, directly affecting the body’s heat dissipation and sweat evaporation, while Tmrt plays a critical role in radiative heat exchange, which is particularly significant for human perception [20,21,30]. In contrast, parameters such as age, Clo, gender, BMI, and SOP20 hold secondary significance, suggesting that spending 20 min in an indoor environment prior to waiting outdoors results in reduced tolerance to external thermal conditions. Compared to physical parameters, individual and behavioral factors like age, Clo, gender, BMI, and SOP20 exhibit relatively minor effects on the models. Although these parameters influence thermal perceptions and adaptability, their impact is indirect, primarily affecting physiological and psychological states. For instance, age, gender, and BMI may influence metabolic rates and blood circulation, thereby affecting thermal perception and regulatory abilities [63,64]. Clo directly impacts the heat exchange between the body and the environment [65,66,67,68]. Conversely, the type of station has the least impact on the models, potentially due to similarities in design and material usage across most stations, such as extensive glass structures and shading facilities, which yield relatively consistent thermal characteristics and minimal variation in their effects on thermal comfort. This uniformity among stations results in negligible differences in the influence of type on thermal comfort models.
Beyond these factors, variations in the significance of other influencing factors across different models are pronounced. Length of stay carries considerable weight in the TCV, TA, and HSV models but plays a minor role in the TSV model. This discrepancy arises primarily from the differing evaluative focuses of each model. TCV and TA typically consider individual adaptation and behavioral responses within the environment; therefore, an increase in the duration of stay in Guangzhou often correlates with enhanced thermal comfort, as individuals have more time to adjust their perceptions. Conversely, the TSV model emphasizes immediate responses to overall thermal sensations, rendering it less sensitive to variations in length of stay [28,69,70,71,72]. In the HSV model, length of stay consistently holds significant weight, primarily due to discomfort associated with high humidity. Throughout the testing period, the proportion of comfortable humidity was only 3.2%. The influence of V varies across TCV, TSV, TA, and HSV, potentially due to the low and irregular fluctuations of V observed throughout the day [73].

4.2. Model BO Optimization

As outlined in Section 2.2, BO was utilized to enhance the predictive performance of five ML models during training. Table 10, Table 11, Table 12 and Table 13 present a comparative analysis of the TCV, TSV, TA, and HSV predictive models before and after the application of BO. The results demonstrate that the BO algorithm significantly improved the prediction accuracy for TCV, TSV, TA, and HSV, with average improvements of 2.43% for Macro-P, 2.62% for Macro-R, and 2.28% for Macro-F1.
In Table 10, the LightGBM classifier with BO emerged as the optimal model for the TCV dataset, exhibiting the most substantial improvement among the evaluated models. Compared to the best model prior to optimization, Macro-P increased by 6.27%, Macro-R by 5.78%, and Macro-F1 by 6.12%. Other models demonstrated varying degrees of improvement, ranging from 0.38% to 4.78%. For TSV prediction, Table 11 indicates that the CatBoost classifier with BO was the optimal model, surpassing the pre-optimization best model with increases of 0.91% for Macro-P, 0.85% for Macro-R, and 0.60% for Macro-F1. Other models also exhibited improvements ranging from 0.56% to 4.73%, with the KNN model achieving the highest increase—Macro-P improved by 4.73%, Macro-R by 4.33%, and Macro-F1 by 1.85%. In Table 12, the LightGBM classifier with BO was again the optimal model for TA prediction, demonstrating enhancements over the pre-optimization best model, with Macro-P increasing by 2.48%, Macro-R by 1.96%, and Macro-F1 by 2.28%. Other models exhibited improvements ranging from 0.12% to 7.98%, with RF showing the greatest improvement and XGB the least. Table 13 indicates that the CatBoost classifier with BO was the optimal model for HSV prediction, with Macro-P improving by 3.25%, Macro-R by 2.97%, and Macro-F1 by 3.18% compared to the pre-optimization best model. Other models also showed improvements ranging from 0.02% to 4.16%, with XGB achieving the highest increase—Macro-P improved by 3.71%, Macro-R by 4.07%, and Macro-F1 by 3.90%, while RF exhibited the smallest improvement.
A comparative analysis of the model performance matrices before and after BO (see Figure 7, Figure 8, Figure 9 and Figure 10) resulted in notable performance enhancements across most categories. The optimization process notably reduced the misclassification rate; for instance, the accuracy of predicting the “uncomfortable” state in the TCV model improved from 0.72 to 0.82, indicating greater reliability of the model post-optimization. Conversely, the accuracy for the “slightly warm” state in the TSV model decreased by 0.01, suggesting that the optimization process involved trade-offs among different categories, improving the predictive performance of some while sacrificing accuracy in others. Nevertheless, the overall accuracy of the models improved, underscoring the effectiveness of BO in fine-tuning model parameters [30].
In summary, all models demonstrated improved performance following BO; however, certain models exhibited only marginal enhancements on the dataset. This limited improvement may be primarily attributed to the similarity between the optimized hyperparameters and their default values [74,75].

4.3. Comparison with Other Studies

Given that the subject of this study is semi-outdoor space, this paper reviews relevant studies on the impact of semi-open spaces (shaded areas) on thermal comfort, including subjective questionnaires, TCV, TSV, TA, and TP, and compares these findings with the results of the present study.

4.3.1. Selection of Influencing Factors

Ruiqi Guo’s study [30] explored 10 factors in shaded and non-shaded areas within parks in Xi’an, China, including length of stay of park, emotion, Clo, age, BMI, RH, V, Ta, Tmrt, and SVF. In Tianyu Xi’s research [21], factors influencing thermal comfort in outdoor spaces (tree-shaded roads) on university campuses in Shenyang during spring were investigated. These factors included individual factors (residence time, distance between hometown and residence, Clo, age, height, and weight) and environmental factors (RH, V, Ta, and Tg), all of which had varying impacts on thermal comfort evaluation.
This study examined 11 factors, including length of stay in Guangzhou, Clo, age, BMI, RH, V, Ta, Tmrt, SOP20, gender, and type. The SOP20 in this study corresponds to the length of stay in the park in Ruiqi Guo’s study, as both represent the respondent’s stay duration in a specific space. Additionally, length of stay in Guangzhou in this study parallels residence time in Tianyu Xi’s research. This factor is closely related to the respondent’s activity patterns and adaptability in Guangzhou, particularly under the high-temperature and humid climate conditions prevalent in summer, thus serving a similar role and significance.
SVF was not included in this study, as its variation across different stations was minimal, making it less relevant for analysis (see Figure 11). Similarly, although emotion (Em) was identified as a significant factor in Ruiqi Guo’s study, it was excluded from this analysis. Tianyu Xi’s study also highlighted distance between hometown and residence as an important factor, but this was not addressed in this study. Future research may consider including these factors to further enhance the understanding of thermal comfort.

4.3.2. Research Metrics and Ranking of Influencing Factors

Ruiqi Guo’s study [30] explored three objectives: TSV, TCV, and TA. In contrast, Tianyu Xi’s study [21] focused solely on TCV. While this study shares similar objectives with Ruiqi Guo’s, it introduces an additional objective, HSV, due to the high humidity characteristics of Guangzhou.
In Ruiqi Guo’s study [30], the main factors influencing the TSV model were Tmrt, Ta, RH, SVF, Clo, and V. In this study, the factors with the greatest impact on the TSV model were RH, V, Tmrt, Ta, and length of stay in Guangzhou. For the TA model, Ruiqi Guo identified Ta, emotion, RH, age, Tmrt, and length of stay in the park as the most influential factors. In this study’s TA model, the key factors were Clo, RH, gender, Tmrt, Ta, and length of stay in Guangzhou.
In the TCV model, Ruiqi Guo’s study [30] found that the major factors were Tmrt, Ta, emotion, RH, V, and Clo. Tianyu Xi’s study [21] highlighted RH, residence time, distance between hometown and residence, Clo, V, and age as significant factors. In this study’s TCV model, length of stay in Guangzhou, age, Tmrt, Ta, RH, and Clo were the primary influencing factors. These differences are primarily due to climate variations [21,30].

4.4. Limitations and Future Research

(1)
Limitations of Data Collection: This study combines survey responses and physical measurements; however, the survey results may be influenced by participants’ subjective factors, potentially introducing bias. Future research could incorporate more objective measurement tools, such as thermal comfort sensors or physiological data (e.g., skin temperature and heart rate), to complement subjective data. Additionally, optimizing the survey design to reduce subjective bias would improve the reliability of the results.
(2)
Limitations of Time Span: The study’s time frame is relatively short, covering only July 2024, which may not fully capture the long-term effects of climate change on thermal comfort. Future research should extend the time span to include multiple seasons or years and consider factors such as air pollution and seasonal variations, providing a more comprehensive analysis of thermal comfort and a deeper understanding of the long-term effects of climate change.
(3)
Limitations of Model Selection: This study utilizes supervised learning models for analysis, but the performance of these models may be limited by the algorithms themselves and may vary across different scenarios. Future research could explore additional machine learning algorithms, such as deep learning or ensemble learning, and conduct cross-validation and repeated experiments to improve model stability and generalization. Moreover, incorporating more complex models or deep learning techniques could enhance prediction accuracy and interpretability [76,77,78].
(4)
Limitations of Data Coverage: This study primarily focuses on data from the Guangzhou tram stations. Future research should expand to include more cities and regions to enhance the generalizability and applicability of the findings. Cross-regional studies will provide a more comprehensive evaluation of thermal comfort across different urban climates.
(5)
Exploring Additional Influencing Factors: While this study considers various environmental and individual factors affecting outdoor thermal comfort, future research should explore other potential influences, such as cultural differences and individual health conditions. These factors could significantly affect perceptions of thermal comfort. A deeper investigation into these elements would contribute to refining thermal comfort assessment methods [79,80].

5. Conclusions

This research conducted a systematic evaluation of the effects of different factors on outdoor thermal comfort at tram stations, employing machine learning algorithms and SHAP analysis techniques. The factors considered include length of stay in Guangzhou, Clo, age, BMI, RH, V, Ta, Tmrt, SOP20, gender, and type. The primary findings are as follows:
(1)
Among the ML models utilized in this study, LightGBM and CatBoost demonstrated particularly notable performance. LightGBM exhibited high predictive accuracy for TCV and TA, while CatBoost excelled in predicting TSV and HSV.
(2)
SHAP analysis revealed that the key factors influencing outdoor thermal comfort at tram stations primarily include RH, Ta, Tmrt, and Clo, alongside gender, age, BMI, and SOP20. Notably, the significance of physical parameters surpassed that of physiological and behavioral parameters.
(3)
In terms of predictive accuracy in machine learning models, the accuracy of binary classification models is significantly higher than that of multi-class classification models.
This study quantitatively analyzes the factors influencing outdoor thermal comfort by combining physical tests with subjective surveys, providing a basis for optimizing outdoor thermal comfort. Future research should expand the sample size and integrate objective sensors and physiological data to enhance the accuracy and representativeness of the results. Additionally, the research period should be extended to account for long-term climate changes and incorporate factors such as air pollution. Moreover, utilizing a broader range of machine learning algorithms could improve model accuracy. Future studies should also explore the application of artificial intelligence and big data analytics to investigate thermal comfort across different climates, optimizing comfort prediction and regulation.

Author Contributions

X.C.: software, methodology, investigation, formal analysis, data curation, and writing—original draft preparation. H.Z.: investigation and conceptualization. B.W.: investigation and supervision. B.X.: validation and supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the General Program of the National Natural Science Foundation of China “Construction and Application of Climate Parameter Models for High-Density Urban Buildings”, grant number [52278087]. And The APC was funded by company Guangzhou Metro Design & Research Institute Co., Ltd.

Data Availability Statement

The original contributions presented in this study are included in the article. Furtsher inquiries can be directed to the corresponding author.

Conflicts of Interest

Author Xin Chen was employed by the company Guangzhou Metro Design & Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The sponsors had no role in the design, execution, interpretation, or writing of the study.

References

  1. Cardoso, V.E.; Ramos, N.M.; Almeida, R.M.; Barreira, E.; Martins, J.P.; Simões, M.L.; Sanhudo, L. A discussion about thermal comfort evaluation in a bus terminal. Energy Build. 2018, 168, 86–96. [Google Scholar] [CrossRef]
  2. Kotopouleas, A.; Nikolopoulou, M. Thermal comfort conditions in airport terminals: Indoor or transition spaces? Build. Environ. 2016, 99, 184–199. [Google Scholar] [CrossRef]
  3. Katavoutas, G.; Assimakopoulos, M.N.; Asimakopoulos, D.N. On the determination of the thermal comfort conditions of a metropolitan city underground railway. Sci. Total Environ. 2016, 566, 877–887. [Google Scholar] [CrossRef] [PubMed]
  4. Liu, G.; Cen, C.; Zhang, Q.; Liu, K.; Dang, R. Field study on thermal comfort of passenger at high-speed railway station in transition season. Build. Environ. 2016, 108, 220–229. [Google Scholar] [CrossRef]
  5. Han, J.; Kwon, S.-B.; Chun, C. Indoor environment and passengers’ comfort in subway stations in Seoul. Build. Environ. 2016, 104, 221–231. [Google Scholar] [CrossRef]
  6. Deb, C.; Ramachandraiah, A. Evaluation of thermal comfort in a rail terminal location in India. Build. Environ. 2010, 45, 2571–2580. [Google Scholar] [CrossRef]
  7. Shanghai Tram Engineering Technology Center. The length of tram operating lines in China steadily increased in 2022. Urban Rail Transit Res. 2023, 26, 246. [Google Scholar]
  8. Sadakorn, W.; Tetiranont, S.; Prasittisopin, L.; Kaewunruen, S. Assessing thermal comfort in hot and humid (tropical) climates: Urban outdoor and semi-outdoor conditions in waiting areas of railway stations. Build. Environ. 2025, 267, 112240. [Google Scholar] [CrossRef]
  9. Feng, T.; Peng, R. Outdoor thermal comfort and the cooling effect in different layouts of shaded spaces: A study of Guangzhou, China. Energy Build. 2025, 331, 115403. [Google Scholar] [CrossRef]
  10. Chen, W.-A.; Fang, P.-L.; Hwang, R.-L. Calibrating the UTCI scale for hot and humid climates through comprehensive year-round field surveys to improve the adaptability. Urban Clim. 2025, 59, 102267. [Google Scholar] [CrossRef]
  11. Jiang, J.; Li, Z.; Bedra, K.B.; Xie, L.; An, Y.; Zhong, Q. Assessing outdoor thermal comfort variations between residents and tourists in a hot-humid traditional village setting. Build. Environ. 2025, 269, 112398. [Google Scholar] [CrossRef]
  12. Guo, T.; Lin, Z.; Zhao, Y.; Fang, Z.; Fan, Y.; Zhang, X.; Yang, J.; Li, Y. Investigation and optimization of outdoor thermal comfort in elementary school campuses: Example from a humid-hot area in China. Build. Environ. 2024, 248, 111055. [Google Scholar] [CrossRef]
  13. Lam, C.K.C.; Cui, S.; Liu, J.; Kong, X.; Ou, C.; Hang, J. Influence of acclimatization and short-term thermal history on outdoor thermal comfort in subtropical South China. Energy Build. 2021, 231, 110541. [Google Scholar] [CrossRef]
  14. Villadiego, K.; Velay-Dabat, M.A. Outdoor thermal comfort in a hot and humid climate of Colombia: A field study in Barranquilla. Build. Environ. 2014, 75, 142–152. [Google Scholar] [CrossRef]
  15. Editorial Department of “Tunnel Construction (Chinese and English)”. Annual Data Statistics of Urban Rail Transit in China 2019. Tunn. Constr. 2020, 40, 762–767. [Google Scholar]
  16. Chun, C.; Kwok, A.; Tamura, A. Thermal comfort in transitional spaces—Basic concepts: Literature review and trial measurement. Build. Environ. 2004, 39, 1187–1192. [Google Scholar] [CrossRef]
  17. Hwang, R.-L.; Lin, T.-P. Thermal comfort requirements for occupants of semi-outdoor and outdoor environments in hot-humid regions. Archit. Sci. Rev. 2007, 50, 357–364. [Google Scholar] [CrossRef]
  18. Zhou, X.; Xu, L.; Zhang, J.; Niu, B.; Luo, M.; Zhou, G.; Zhang, X. Data-driven thermal comfort model via support vector machine algorithms: Insights from ASHRAE RP-884 database. Energy Build. 2020, 211, 109795. [Google Scholar] [CrossRef]
  19. Lin, T.P.; de Dear, R.; Hwang, R.L. Effect of thermal adaptation on seasonal outdoor thermal comfort. Int. J. Climatol. 2011, 31, 302–312. [Google Scholar] [CrossRef]
  20. Jeong, J.; Jeong, J.; Lee, M.; Lee, J.; Chang, S. Data-driven approach to develop prediction model for outdoor thermal comfort using optimized tree-type algorithms. Build. Environ. 2022, 226, 109663. [Google Scholar] [CrossRef]
  21. Xi, T.; Wang, M.; Cao, E.; Li, J.; Wang, Y.; Sa’ad, S.U. Preliminary Research on Outdoor Thermal Comfort Evaluation in Severe Cold Regions by Machine Learning. Buildings 2024, 14, 284. [Google Scholar] [CrossRef]
  22. Kuang, W. Seasonal Variation in Air Temperature and Relative Humidity on Building Areas and in Green Spaces in Beijing, China. Chin. Geogr. Sci. 2020, 30, 75–88. [Google Scholar] [CrossRef]
  23. Lam, C.K.C.; Gao, Y.; Yang, H.; Chen, T.; Zhang, Y.; Ou, C.; Hang, J. Interactive effect between long-term and short-term thermal history on outdoor thermal comfort: Comparison between Guangzhou, Zhuhai and Melbourne. Sci. Total Environ. 2021, 760, 144141. [Google Scholar] [CrossRef] [PubMed]
  24. Ji, Y.; Song, J.; Shen, P. A review of studies and modelling of solar radiation on human thermal comfort in outdoor environment. Build. Environ. 2022, 214, 108891. [Google Scholar] [CrossRef]
  25. Zafarmandi, S.; Matzarakis, A.; Norford, L. Effects of clothing’s thermal insulation on outdoor thermal comfort and thermal sensation: A case study in Tehran, Iran. Sustain. Cities Soc. 2024, 100, 104988. [Google Scholar] [CrossRef]
  26. Xu, T.; Yao, R.; Du, C.; Li, B. Outdoor thermal perception and heatwave adaptation effects in summer—A case study of a humid subtropical city in China. Urban Clim. 2023, 52, 101724. [Google Scholar] [CrossRef]
  27. Lai, D.; Lian, Z.; Liu, W.; Guo, C.; Liu, W.; Liu, K.; Chen, Q. A comprehensive review of thermal comfort studies in urban open spaces. Sci. Total Environ. 2020, 742, 140092. [Google Scholar] [CrossRef]
  28. Fanger, P.O. Thermal comfort. In Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
  29. Cheung, T.; Schiavon, S.; Parkinson, T.; Li, P.; Brager, G. Analysis of the accuracy on PMV—PPD model using the ASHRAE Global Thermal Comfort Database II. Build. Environ. 2019, 153, 205–217. [Google Scholar] [CrossRef]
  30. Guo, R.; Yang, B.; Guo, Y.; Li, H.; Li, Z.; Zhou, B.; Hong, B.; Wang, F. Machine learning-based prediction of outdoor thermal comfort: Combining Bayesian optimization and the SHAP model. Build. Environ. 2024, 254, 111301. [Google Scholar] [CrossRef]
  31. Potchter, O.; Cohen, P.; Lin, T.-P.; Matzarakis, A. Outdoor human thermal perception in various climates: A comprehensive review of approaches, methods and quantification. Sci. Total Environ. 2018, 631–632, 390–406. [Google Scholar] [CrossRef]
  32. Staiger, H.; Laschewski, G.; Matzarakis, A. Selection of Appropriate Thermal Indices for Applications in Human Biometeorological Studies. Atmosphere 2019, 10, 18. [Google Scholar] [CrossRef]
  33. Blazejczyk, K.; Epstein, Y.; Jendritzky, G.; Staiger, H.; Tinz, B. Comparison of UTCI to selected thermal indices. Int. J. Biometeorol. 2012, 56, 515–535. [Google Scholar] [CrossRef] [PubMed]
  34. Fang, Z.; Feng, X.; Liu, J.; Lin, Z.; Mak, C.M.; Niu, J.; Tse, K.-T.; Xu, X. Investigation into the differences among several outdoor thermal comfort indices against field survey in subtropics. Sustain. Cities Soc. 2019, 44, 676–690. [Google Scholar] [CrossRef]
  35. Huang, B.; Hong, B.; Tian, Y.; Yuan, T.; Su, M. Outdoor thermal benchmarks and thermal safety for children: A study in China’s cold region. Sci. Total Environ. 2021, 787, 147603. [Google Scholar] [CrossRef]
  36. Jendritzky, G.; de Dear, R.; Havenith, G. UTCI—Why another thermal index? Int. J. Biometeorol. 2012, 56, 421–428. [Google Scholar] [CrossRef]
  37. Chan, S.Y.; Chau, C.K. Development of artificial neural network models for predicting thermal comfort evaluation in urban parks in summer and winter. Build. Environ. 2019, 164, 106364. [Google Scholar] [CrossRef]
  38. Feng, X.; Zheng, Z.; Yang, Y.; Fang, Z. Quantitative seasonal outdoor thermal sensitivity in Guangzhou, China. Urban Clim. 2021, 39, 100938. [Google Scholar] [CrossRef]
  39. Lee, S.; Bilionis, I.; Karava, P.; Tzempelikos, A. A Bayesian approach for probabilistic classification and inference of occupant thermal preferences in office buildings. Build. Environ 2017, 118, 323–343. [Google Scholar] [CrossRef]
  40. Wu, Y.; Liu, H.; Li, B.; Kosonen, R.; Wei, S.; Jokisalo, J.; Cheng, Y. Individual thermal comfort prediction using classification tree model based on physiological parameters and thermal history in winter. Build. Simul. 2021, 14, 1651–1665. [Google Scholar] [CrossRef]
  41. Zhang, J.; Zhang, F.; Gou, Z.; Liu, J. Assessment of macroclimate and microclimate effects on outdoor thermal comfort via artificial neural network models. Urban Clim. 2022, 42, 101134. [Google Scholar] [CrossRef]
  42. Vučković, D.; Jovic, S.; Bozovic, R.; Dżamić, V.; Kićović, D. Potential of neuro-fuzzy methodology for forecasting of outdoor thermal comfort index at urban open spaces. Urban Clim. 2019, 28, 100467. [Google Scholar] [CrossRef]
  43. Jiang, L.; Yao, R. Modelling personal thermal sensations using C-Support Vector Classification (C-SVC) algorithm. Build. Environ. 2016, 99, 98–106. [Google Scholar] [CrossRef]
  44. Farhan, A.A.; Pattipati, K.; Wang, B.; Luh, P. Predicting individual thermal comfort using machine learning algorithms. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 708–713. [Google Scholar]
  45. Kim, J.; Zhou, Y.; Schiavon, S.; Raftery, P.; Brager, G. Personal comfort models: Predicting individuals’ thermal preference using occupant heating and cooling behavior and machine learning. Build. Environ. 2018, 129, 96–106. [Google Scholar] [CrossRef]
  46. Zheng, G.; Zhang, Y.; Yue, X.; Li, K. Interpretable prediction of thermal sensation for elderly people based on data sampling, machine learning and SHapley Additive exPlanations (SHAP). Build. Environ. 2023, 242, 110602. [Google Scholar] [CrossRef]
  47. Yang, B.; Li, X.; Liu, Y.; Chen, L.; Guo, R.; Wang, F.; Yan, K. Comparison of models for predicting winter individual thermal comfort based on machine learning algorithms. Build. Environ. 2022, 215, 108970. [Google Scholar] [CrossRef]
  48. Molnar, C. Interpretable Machine Learning; Lulu: Morrisville, NC, USA, 2020. [Google Scholar]
  49. Chen, G.; Chen, Y.; Tan, X.; Zhao, L.; Cai, Y.; Li, L. Assessing the urban heat island effect of different local climate zones in Guangzhou, China. Build. Environ. 2023, 244, 110770. [Google Scholar] [CrossRef]
  50. ISO 7726:2002; Ergonomía de Los Ambientes Térmicos. Instrumentos de Medida de las Magnitudes Físicas. ISO: Geneva, Switzerland, 2002.
  51. ASHRAE 55-2020; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air Conditioning Engineers: Atlanta, GA, USA, 2020.
  52. An, N.; Yao, J.; Zhou, Y. Study on Outdoor Thermal Comfort in Summer on Campus in Shanghai: A Case Study of Tongji University. Build. Sci. 2022, 38, 250–260. [Google Scholar] [CrossRef]
  53. Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
  54. Yao, F.; Fang, H.; Han, J.; Zhang, Y. Study on the outdoor thermal comfort evaluation of the elderly in the Tibetan plateau. Sustain. Cities Soc. 2022, 77, 103582. [Google Scholar] [CrossRef]
  55. Nuttall, F.Q. Body mass index: Obesity, BMI, and health: A critical review. Nutr. Today 2015, 50, 117–128. [Google Scholar] [CrossRef]
  56. Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
  57. Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
  58. Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6639–6649. [Google Scholar] [CrossRef]
  59. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  60. Lan, H.; Hou, H.; Gou, Z. A machine learning led investigation to understand individual difference and the human-environment interactive effect on classroom thermal comfort. Build. Environ. 2023, 236, 110259. [Google Scholar] [CrossRef]
  61. Lundberg, S.M.; Erion, G.G.; Lee, S.-I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
  62. Hosenie, Z.; Lyon, R.J.; Stappers, B.W.; Mootoovaloo, A. Comparing Multiclass, Binary, and Hierarchical Machine Learning Classification schemes for variable stars. Mon. Not. R. Astron. Soc. 2019, 488, 4858–4872. [Google Scholar] [CrossRef]
  63. Watanabe, S.; Horikoshi, T.; Ishii, J.; Tomita, A. The measurement of the solar absorptance of the clothed human body—The case of Japanese, college-aged male subjects. Build. Environ. 2013, 59, 492–500. [Google Scholar] [CrossRef]
  64. Saito, M.; Ishii, A.; Oi, H. Prediction of clothing insulation in a outdoor environment, based on questionnaires. In Environmental Ergonomics; Elsevier Ergonomics Book Series; Elsevier: Amsterdam, The Netherlands, 2005; Volume 3, pp. 355–360. [Google Scholar]
  65. Li, J.; Sun, R.; Chen, L. Identifying sensitive population associated with summer extreme heat in Beijing. Sustain. Cities Soc. 2022, 83, 103925. [Google Scholar] [CrossRef]
  66. Zhen, M.; Dong, Q.; Chen, P.; Ding, W.; Zhou, D.; Feng, W. Urban outdoor thermal comfort in western China. J. Asian Archit. Build. Eng. 2020, 20, 222–236. [Google Scholar] [CrossRef]
  67. Salata, F.; Golasi, I.; Ciancio, V.; Rosso, F. Dressed for the season: Clothing and outdoor thermal comfort in the Mediterranean population. Build. Environ. 2018, 146, 50–63. [Google Scholar] [CrossRef]
  68. Amindeldar, S.; Heidari, S.; Khalili, M. The effect of personal and microclimatic variables on outdoor thermal comfort: A field study in Tehran in cold season. Sustain. Cities Soc. 2017, 32, 153–159. [Google Scholar] [CrossRef]
  69. De Dear, R.; Brager, G.S. Developing an Adaptive Model of Thermal Comfort and Preference. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1998. [Google Scholar]
  70. Humphreys, M.A.; Nicol, J.F. The validity of ISO-PMV for predicting comfort votes in every-day thermal environments. Energy Build. 2002, 34, 667–684. [Google Scholar] [CrossRef]
  71. Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments: Part I: Local sensation of individual body parts. Build. Environ. 2010, 45, 380–388. [Google Scholar] [CrossRef]
  72. ISO 7730:2005.; Ergonomics of the Thermal Environment–Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. ISO: Geneva, Switzerland, 2005.
  73. Deng, Y.; Gan, D.; Tang, N.; Cai, Z.; Li, X.; Chen, S.; Li, X. Research on outdoor thermal comfort and activities in residential areas in subtropical China. Atmosphere 2022, 13, 1357. [Google Scholar] [CrossRef]
  74. Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
  75. Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
  76. Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
  77. Mohammed, A.; Kora, R. A comprehensive review on ensemble deep learning: Opportunities and challenges. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
  78. Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
  79. Kenawy, I.; Elkadi, H. Effects of cultural diversity and climatic background on outdoor thermal perception in Melbourne city, Australia. Build. Environ. 2021, 195, 107746. [Google Scholar] [CrossRef]
  80. Aljawabra, F.; Nikolopoulou, M. Influence of hot arid climate on the use of outdoor urban spaces and thermal comfort: Do cultural and social backgrounds matter? Intell. Build. Int. 2010, 2, 198–217. [Google Scholar] [CrossRef]
Buildings 15 00865 g001
Figure 1. Research framework.
Figure 1. Research framework.
Buildings 15 00865 g001
Buildings 15 00865 g002
Figure 2. Map of tram line 1 in Huangpu District, Guangzhou, and measurement point layout map.
Figure 2. Map of tram line 1 in Huangpu District, Guangzhou, and measurement point layout map.
Buildings 15 00865 g002
Buildings 15 00865 g003
Figure 3. Ground-level side platforms.
Figure 3. Ground-level side platforms.
Buildings 15 00865 g003
Buildings 15 00865 g004
Figure 4. Ground-level separated platforms.
Figure 4. Ground-level separated platforms.
Buildings 15 00865 g004
Buildings 15 00865 g005
Figure 5. Importance ranking of features of optimal prediction models: (a) TCV; (b) TSV; (c) TA; (d) HSV.
Figure 5. Importance ranking of features of optimal prediction models: (a) TCV; (b) TSV; (c) TA; (d) HSV.
Buildings 15 00865 g005
Buildings 15 00865 g006
Figure 6. The characteristics of TCV, TSV, TA, and HSV prediction models have positive and negative effects: (a) TCV; (b) TSV; (c) TA; (d) HSV.
Figure 6. The characteristics of TCV, TSV, TA, and HSV prediction models have positive and negative effects: (a) TCV; (b) TSV; (c) TA; (d) HSV.
Buildings 15 00865 g006
Buildings 15 00865 g007
Figure 7. Normalized Confusion Matrix for TCV predictions from the ML model.
Figure 7. Normalized Confusion Matrix for TCV predictions from the ML model.
Buildings 15 00865 g007
Buildings 15 00865 g008
Figure 8. Normalized Confusion Matrix for TSV predictions from the ML model.
Figure 8. Normalized Confusion Matrix for TSV predictions from the ML model.
Buildings 15 00865 g008
Buildings 15 00865 g009
Figure 9. Normalized Confusion Matrix for TA predictions from the ML model.
Figure 9. Normalized Confusion Matrix for TA predictions from the ML model.
Buildings 15 00865 g009
Buildings 15 00865 g010
Figure 10. Normalized Confusion Matrix for HSV predictions from the ML model.
Figure 10. Normalized Confusion Matrix for HSV predictions from the ML model.
Buildings 15 00865 g010
Buildings 15 00865 g011
Figure 11. The SVF diagrams of different stations.
Figure 11. The SVF diagrams of different stations.
Buildings 15 00865 g011
Table 1. Summary of ML applications in predicting human thermal sensation in summer (bold entries indicate the best-performing ML types and top-ranked input factors).
Table 1. Summary of ML applications in predicting human thermal sensation in summer (bold entries indicate the best-performing ML types and top-ranked input factors).
LiteraturePredictive IndexData SourceInfluencing Factors (Input Features)Algorithms and Results
2015 [44]TSVHVAC artificial climate chamberClo, air turbulence, Ti, age, Ta, MET, TmrtSVM (76.7%)
2016 [44]TSVHVAC artificial climate chamber, ChongqingTa, Tmrt, V, RH, MET, CloC-SVC (89%)
2017 [45]TPoffice, Northern CaliforniaDevice usage, Ti, Ta, HVAC system data, CloCT, GPC, GBM, SVM, regLR, RF (Median AUC = 0.71)
2019 [37]TCVPark, Hong Kong, Chinaage, education level, income level, occupation, gender, health status, thermal sensitivity, Ta, Tg, V, RH, Sr, thermal sensation, humidity sensation, purpose of visit, Clo, perceived number of water space in the park, metabolic rate, perceived density of trees in the parkANN (Summer average R value 0.821)
2022 [20]PETConstruction Site, KoreaTa, RH, V, Tmrt, PET, Sr, seasonDT, RF, XGB, AdaBoost, Bayesian Ridge (Different models perform differently on different datasets; DT consistently lowest, all greater than or equal to 80%)
2024 [21]TCVShenyang University Outdoor Space, Chinalength of stay, distance between hometown and residence, Clo, age, height, weight, RH, V, Ta, Tgextreme gradient lifting (93.13%)
gradient lifting
RF
neural network
2024 [30]TCV,
TSV,
TA		Xi’an Park around City, Chinalength of stay of park, emotion, Clo, age, BMI, RH, V, Ta, Tmrt, SVFKNN, MLR, OPM, DT, RF, SVM, XGB, LightGBM, CatBoost (65.49%)
Note: Tg = globe temperature; SVF = sky view factor; MLR = multinomial logistic regression; OPM = ordered probit model; SVM = support vector machine; CT = classification tree; GPC = Gaussian Process Classification; regLR = Regularized Logistic Regression; C-SVC = C-Support Vector Classification; XGB = Extreme Gradient Boosting; LightGBM = Light Gradient Boosting Machine; CatBoost = Categorical Boosting; RF = Random Forest; KNN = K-Nearest Neighbors; ANN = artificial neural network models; GBM = Gradient Boosting Method.
Table 2. Measurement point statistics.
Table 2. Measurement point statistics.
Measurement Point NamePlatform TypePlatform Image
Xiankengground-level side platformsBuildings 15 00865 i001
Civic Squareground-level separated platformsBuildings 15 00865 i002
Convention Centerground-level separated platformsBuildings 15 00865 i003
Juntai Roadground-level side platformsBuildings 15 00865 i004
Lingtouground-level side platformsBuildings 15 00865 i005
Xinfeng Roadground-level side platformsBuildings 15 00865 i006
Table 3. Average difference statistics.
Table 3. Average difference statistics.
Time IntervalTemperatureGlobe TemperatureHumidity
30 min0.8 °C0.9 °C8%
15 min0.6 °C0.5 °C4%
5 min0.3 °C0.2 °C2%
3 min0.2 °C0.2 °C2%
Table 4. Instruments and accuracy.
Table 4. Instruments and accuracy.
ParametersInstrumentsAccuracy
Black globe temperatureTR-102 black globe temperature meter (Extech Instruments, Inc., Hudson, NH, USA)±0.2 °C
Air temperature
Relative humidity		TR-72Ui temperature and humidity meter (Extech Instruments, Inc.)±0.3 °C
±5%
Air velocityHD 2303.0 omni-directional anemometer (Extech Instruments, Inc.)±0.02 m/s (0–0.99 m/s)
±0.1 m/s (1–5 m/s)
Table 5. Summary of microclimate parameters in the study site.
Table 5. Summary of microclimate parameters in the study site.
VariableMinMaxMeanStd
Ta (°C)29.2038.7934.132.65
Tmrt (°C)28.4539.0533.902.87
RH (%)42.5069.0557.527.03
V (m/s)0.021.900.720.47
Table 6. Volunteers attributes.
Table 6. Volunteers attributes.
GenderNumberAge (Years)Height (cm)Weight (kg)
Male35441.5 ± 27.50165 ± 9.565 ± 12.9
Female43239.5 ± 23.50158 ± 8.558 ± 9.3
Table 7. Questionnaire scoring table.
Table 7. Questionnaire scoring table.
Scale PointsReference Standard
TSV7 points−3: very cold; −2: cold; −1: cool; 0: neutral;
1: warm; 2: hot; 3: very hot		ASHRAE 55-2020
TA5 points−2: very unacceptable; −1: unacceptable; 0: neutral; 1: acceptable; 2: very acceptable
TCV7 points−3: very uncomfortable; −2: uncomfortable; −1: slightly uncomfortable; 0: neutral; 1: slightly comfortable; 2: comfortable; 3: very comfortable
HSV7 points−3: very dry; −2: dry; −1: slightly dry; 0: neutral; 1: slightly humid; 2: humid; 3: very humidASHRAE standard 55-2020 in conjunction with [52]
Table 8. Advantages of each algorithm.
Table 8. Advantages of each algorithm.
ModelKey AdvantageApplicable Scenarios
XGBEfficiency (optimized algorithms, parallel processing) and high accuracy (gradient boosting, regularization)Complex predictive tasks requiring high precision and flexibility
LightGBMSpeed (histogram-based algorithm) and memory efficiency (reduces computation time and memory usage)Large-scale data scenarios, memory-constrained environments
RFResistance to overfitting (through Bagging and random feature selection) and robustness (handles noise and missing data)Suitable for various types of data, especially noisy or missing data
CatBoostHandling categorical features and training speed (ordered target encoding, symmetric tree structure)Complex data processing, especially for data with categorical features
KNNSimplicity and intuitiveness, easy to understand and implementSmall datasets and beginner-level tasks, problems with well-distributed feature spaces
Table 9. Types of hyperparameters for ML.
Table 9. Types of hyperparameters for ML.
Types of MLHyperparameter Types
XGBlearning Rate; max_depth;n_estimators; booster; min_child_weight; subsample; colsample_bytree; colsample_bylevel; reg_lambda; reg_alpha; gamma
LightGBMn_estimators; learning_rate; max_depth; min_samples_split; min_samples_leaf; max_features; subsample
CatBoostIterations; depth; learning_rate; l2_leaf_reg; border_count
RFmax_depth; min_samples_leaf; min_samples_split; n_estimators; bootstrap; oob_score; class_weight; max_samples; max features
KNNn_neighbors; weights; p; algorithm; leaf_size; metric
Table 10. Comparative analysis of performance for five ML models (distinguished by BO) in predicting TCV on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
Table 10. Comparative analysis of performance for five ML models (distinguished by BO) in predicting TCV on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
AlgorithmMacro-PMacro-RMacro-F1Macro-PMacro-RMacro-F1
DefaultModel + BO
XGB80.6680.8480.3783.3783.8483.27
LightGBM78.9579.6778.7885.2285.4584.90
CatBoost83.0683.5682.9784.8385.0784.55
RF78.9979.7478.8779.4180.1279.28
KNN69.5069.9967.8573.5674.1372.63
Table 11. Comparative analysis of performance for five ML models (distinguished by BO) in predicting TSV on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
Table 11. Comparative analysis of performance for five ML models (distinguished by BO) in predicting TSV on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
AlgorithmMacro-PMacro-RMacro-F1Macro-PMacro-RMacro-F1
DefaultModel + BO
XGB87.8380.6583.3588.6581.1982.99
LightGBM88.0076.6880.2288.5681.3583.31
CatBoost87.7880.7683.3388.6981.6183.93
RF86.3979.3881.5387.7580.7082.88
KNN73.2467.7473.5777.9772.0775.42
Table 12. Comparative analysis of performance for five ML models (distinguished by BO) in predicting TA on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
Table 12. Comparative analysis of performance for five ML models (distinguished by BO) in predicting TA on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
AlgorithmMacro-PMacro-RMacro-F1Macro-PMacro-RMacro-F1
DefaultModel + BO
XGB92.6793.2592.8393.1893.6792.95
LightGBM91.7492.3091.9294.2294.2694.20
CatBoost92.2693.0292.4293.6694.1593.80
RF89.5890.9889.9192.8298.9692.88
KNN89.3290.8989.0391.7892.4691.61
Table 13. Comparative analysis of performance for five ML models (distinguished by BO) in predicting HSV on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
Table 13. Comparative analysis of performance for five ML models (distinguished by BO) in predicting HSV on test set (Macro-P, Macro-R, and Macro-F1 are all calculated as weighted averages).
AlgorithmMacro-PMacro-RMacro-F1Macro-PMacro-RMacro-F1
DefaultModel + BO
XGB70.7772.5971.4974.4876.6675.39
LightGBM72.1174.6373.1176.2777.6276.69
CatBoost73.3875.3474.0676.6378.3177.24
RF69.9273.8471.2370.1773.8771.25
KNN59.9468.1162.4663.5070.9965.81
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, X.; Zhao, H.; Wang, B.; Xia, B. Study of Factors Influencing Thermal Comfort at Tram Stations in Guangzhou Based on Machine Learning. Buildings 2025, 15, 865. https://doi.org/10.3390/buildings15060865

AMA Style

Chen X, Zhao H, Wang B, Xia B. Study of Factors Influencing Thermal Comfort at Tram Stations in Guangzhou Based on Machine Learning. Buildings. 2025; 15(6):865. https://doi.org/10.3390/buildings15060865

Chicago/Turabian Style

Chen, Xin, Huanchen Zhao, Beini Wang, and Bo Xia. 2025. "Study of Factors Influencing Thermal Comfort at Tram Stations in Guangzhou Based on Machine Learning" Buildings 15, no. 6: 865. https://doi.org/10.3390/buildings15060865

APA Style

Chen, X., Zhao, H., Wang, B., & Xia, B. (2025). Study of Factors Influencing Thermal Comfort at Tram Stations in Guangzhou Based on Machine Learning. Buildings, 15(6), 865. https://doi.org/10.3390/buildings15060865

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop