Experimental Study on Cyclic Loading and Unloading of Remodeled Loess Using True Triaxial Testing
Abstract
1. Introduction
2. Test Materials, Apparatus and Methods
2.1. Soil Samples
2.2. True Triaxial Apparatus
2.3. Test Plan
3. Results and Discussion
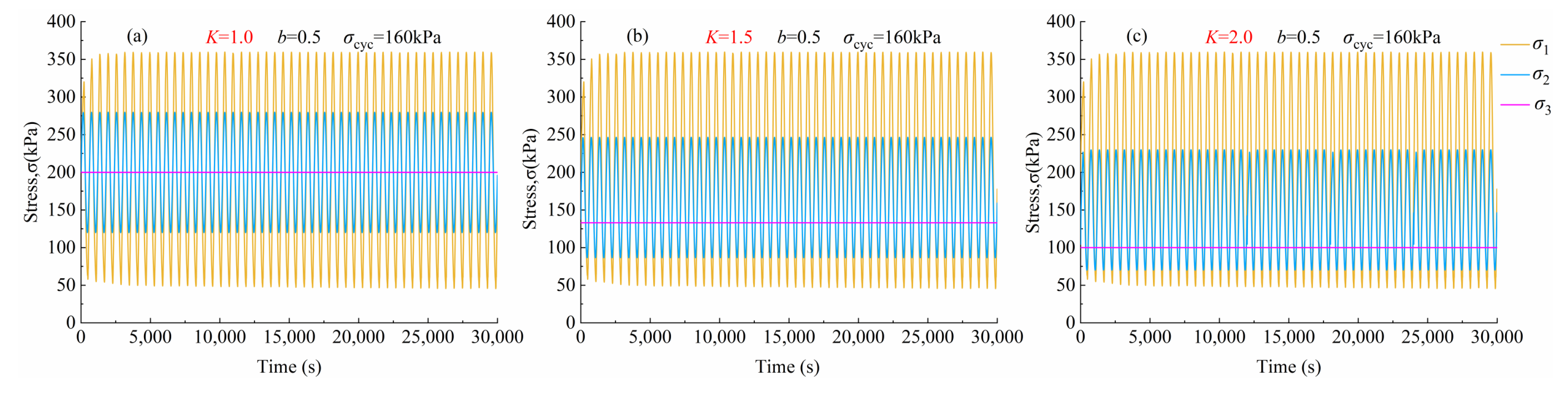
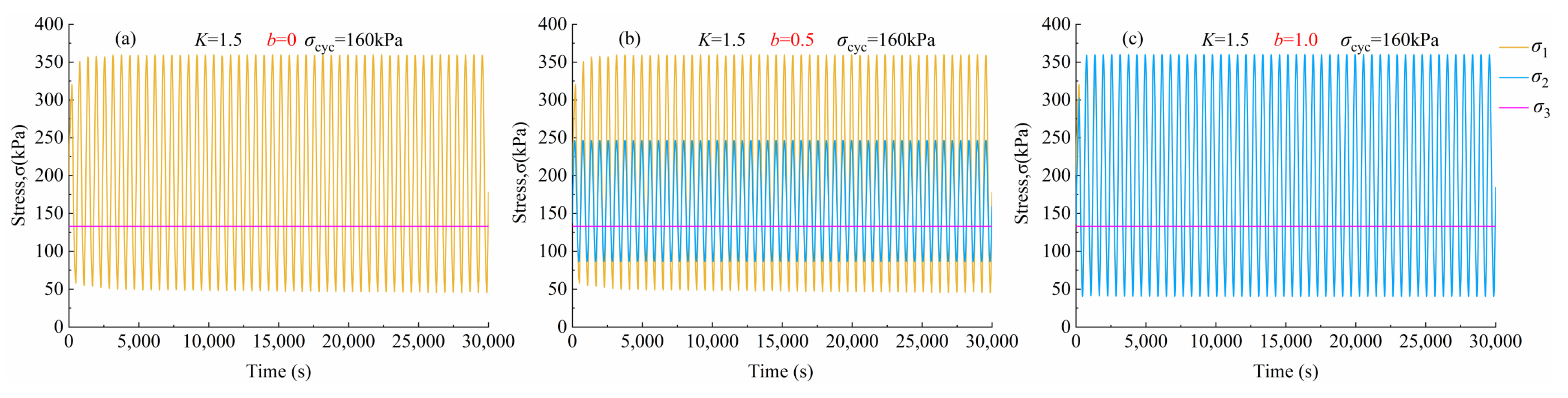
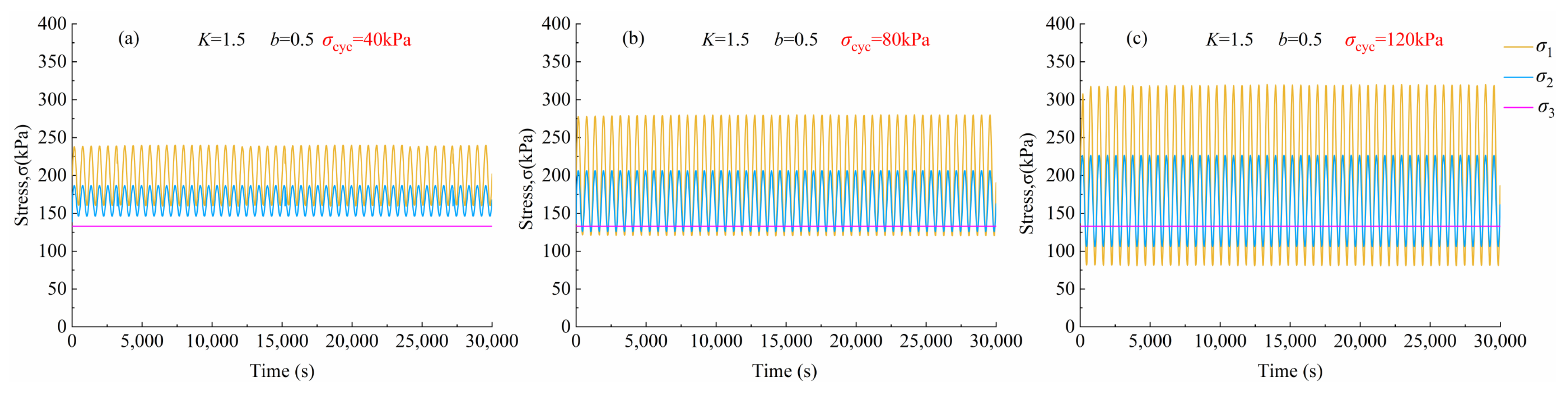
3.1. Stress Time History Curve
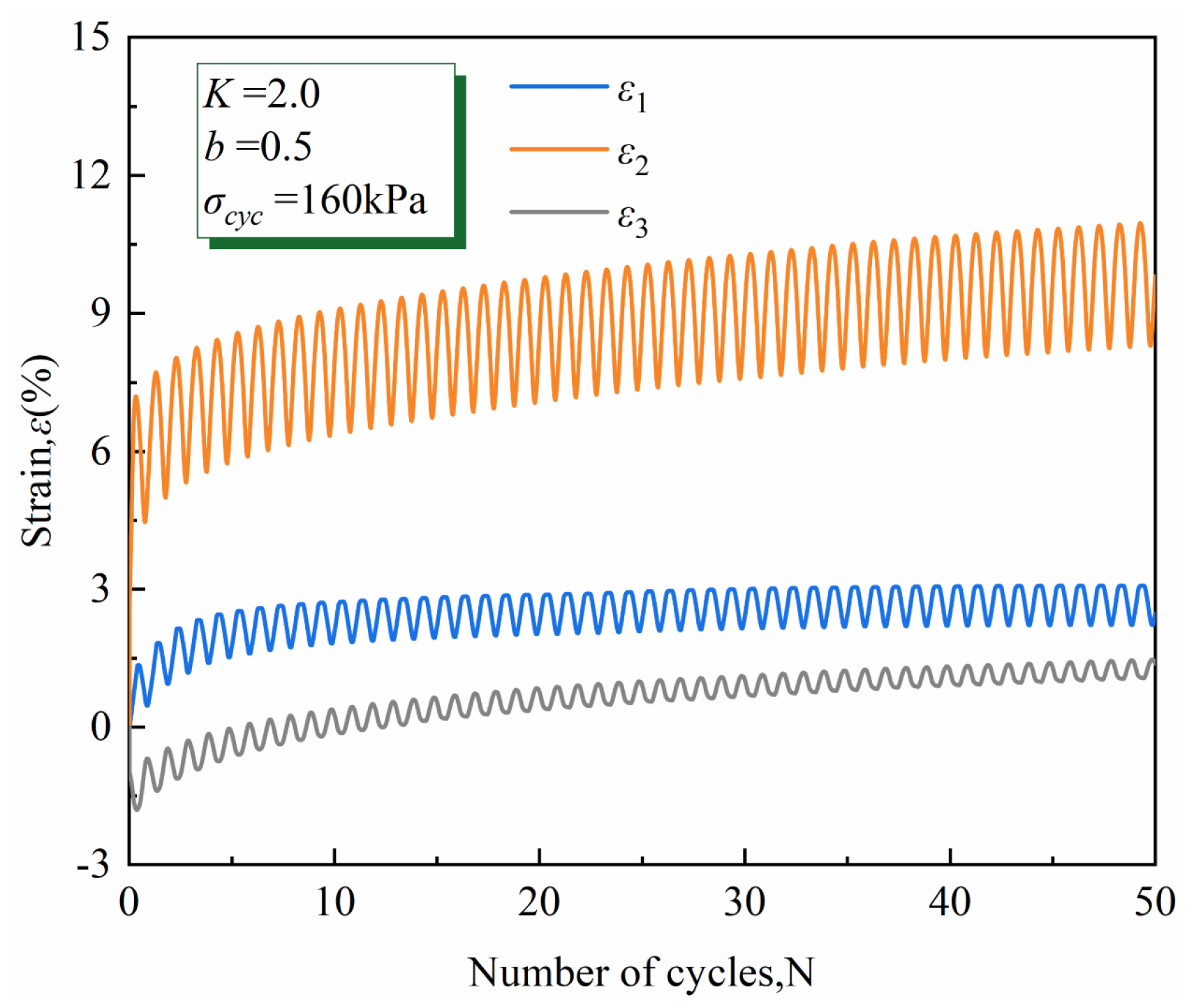
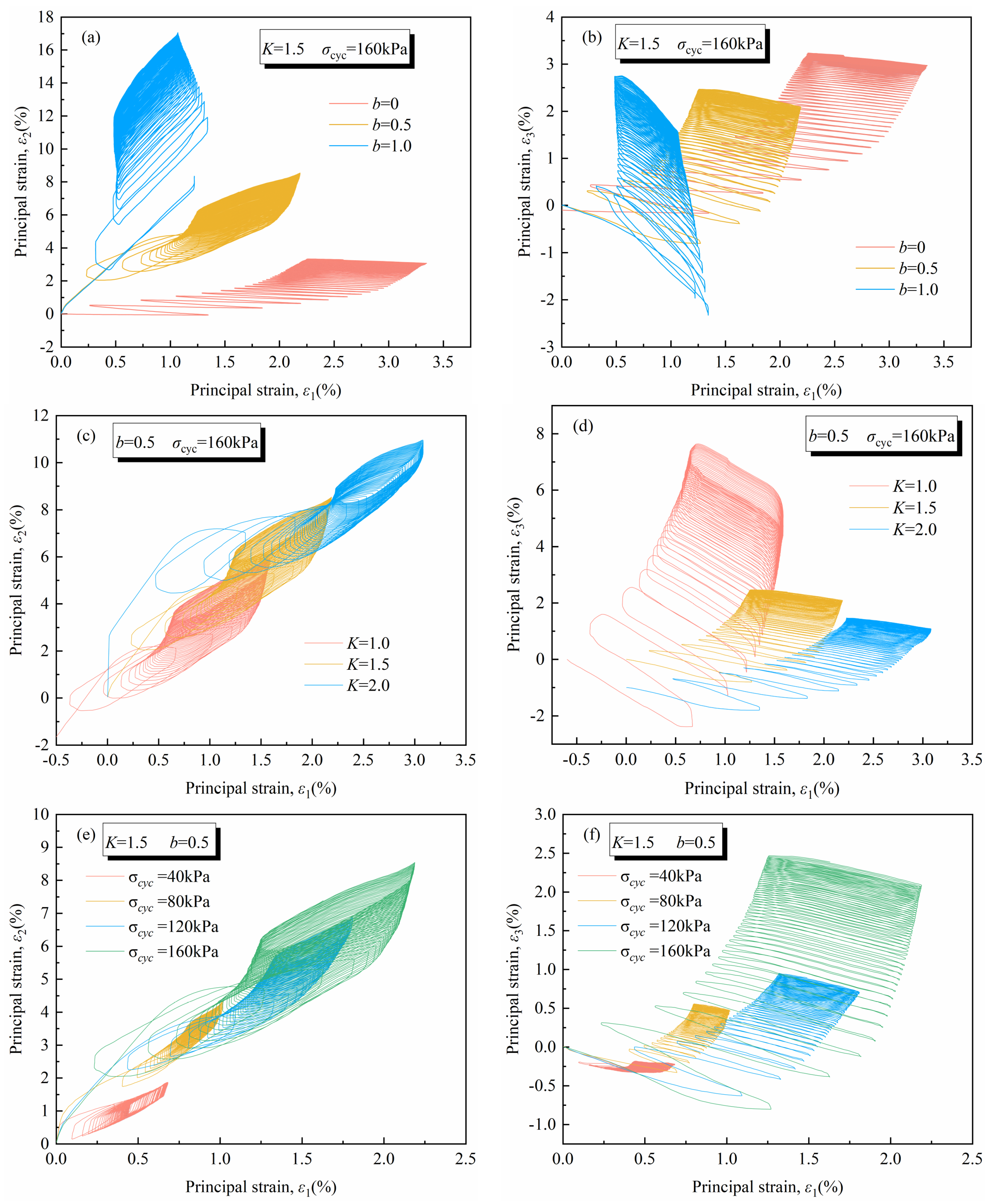
3.2. Principal Strain
3.2.1. Typical Principal Strain Components
3.2.2. Relationship Between Lateral Strain and Axial Strain
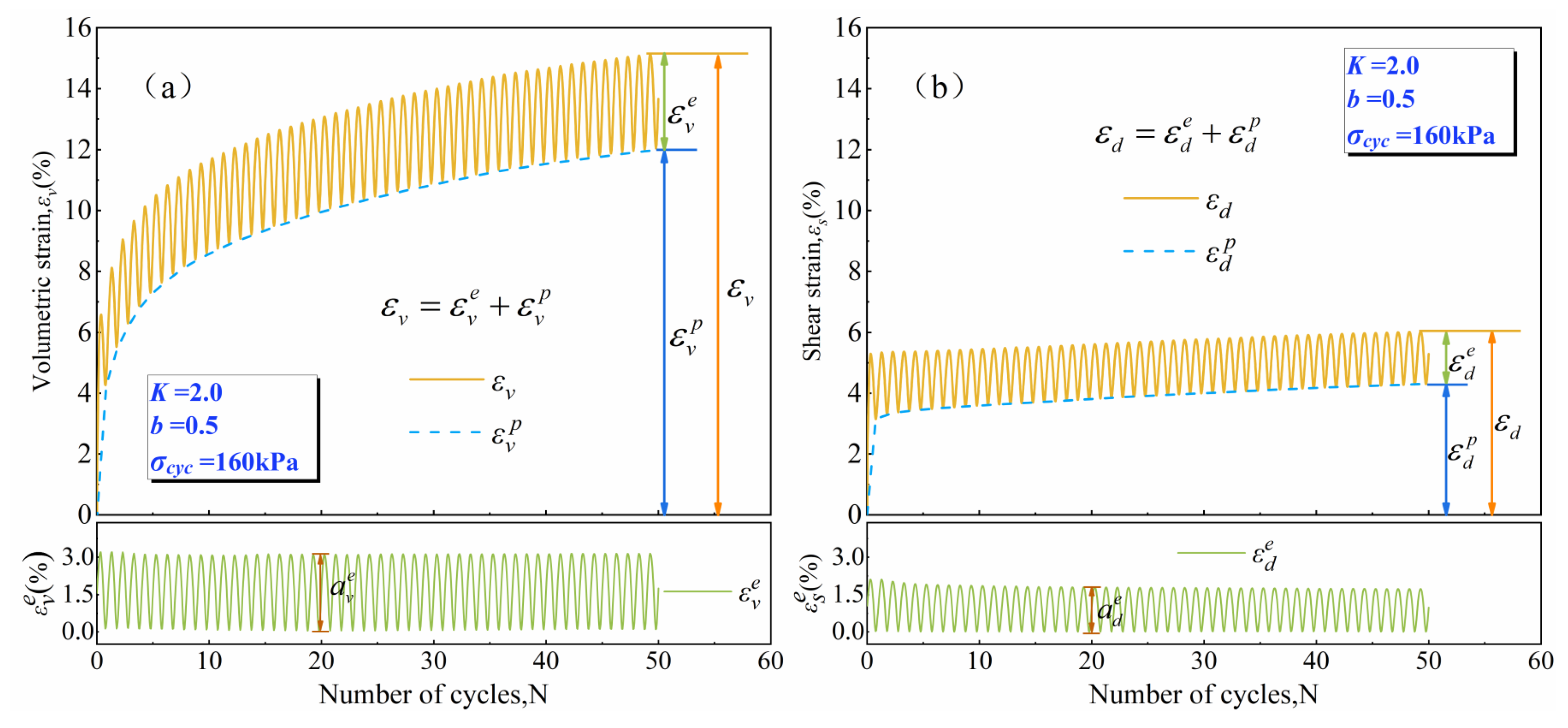
3.3. Volumetric Strain and Shear Strain
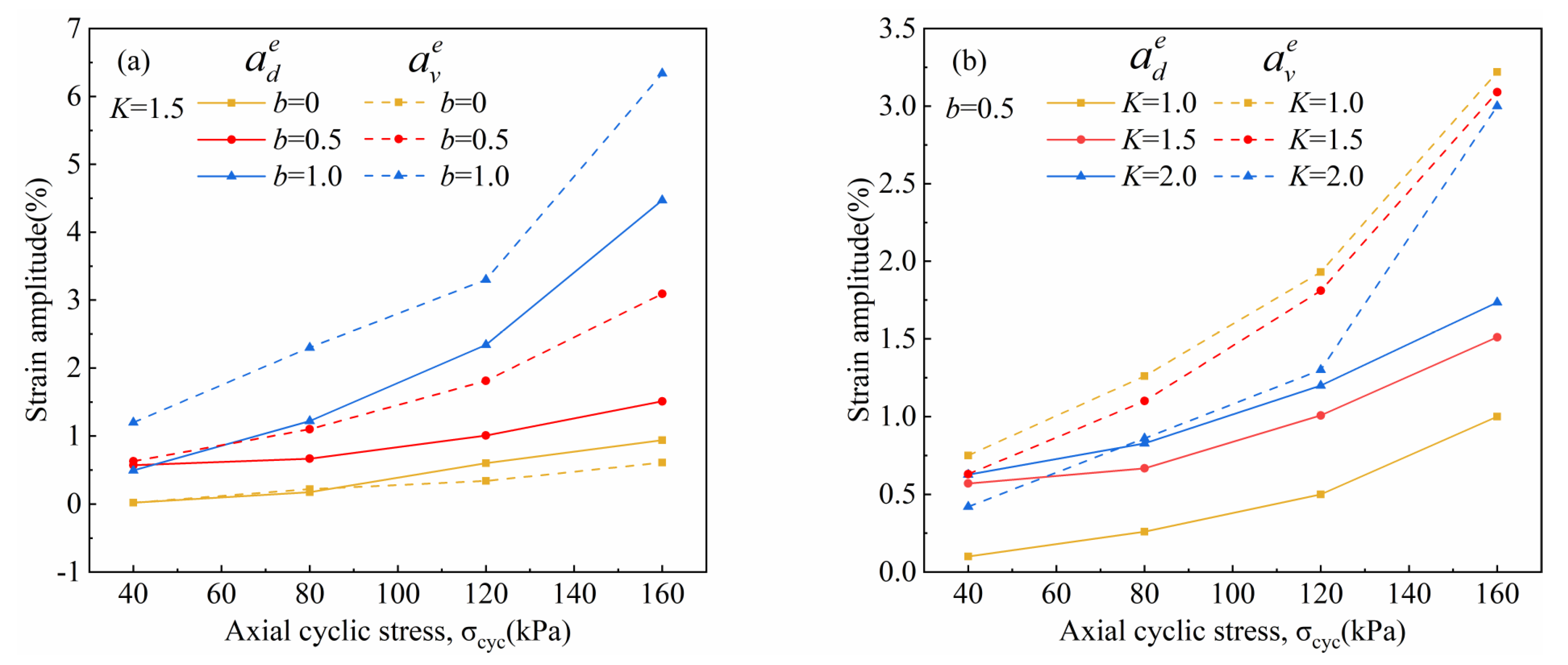
3.3.1. Elastic Volumetric Strain and Elastic Shear Strain
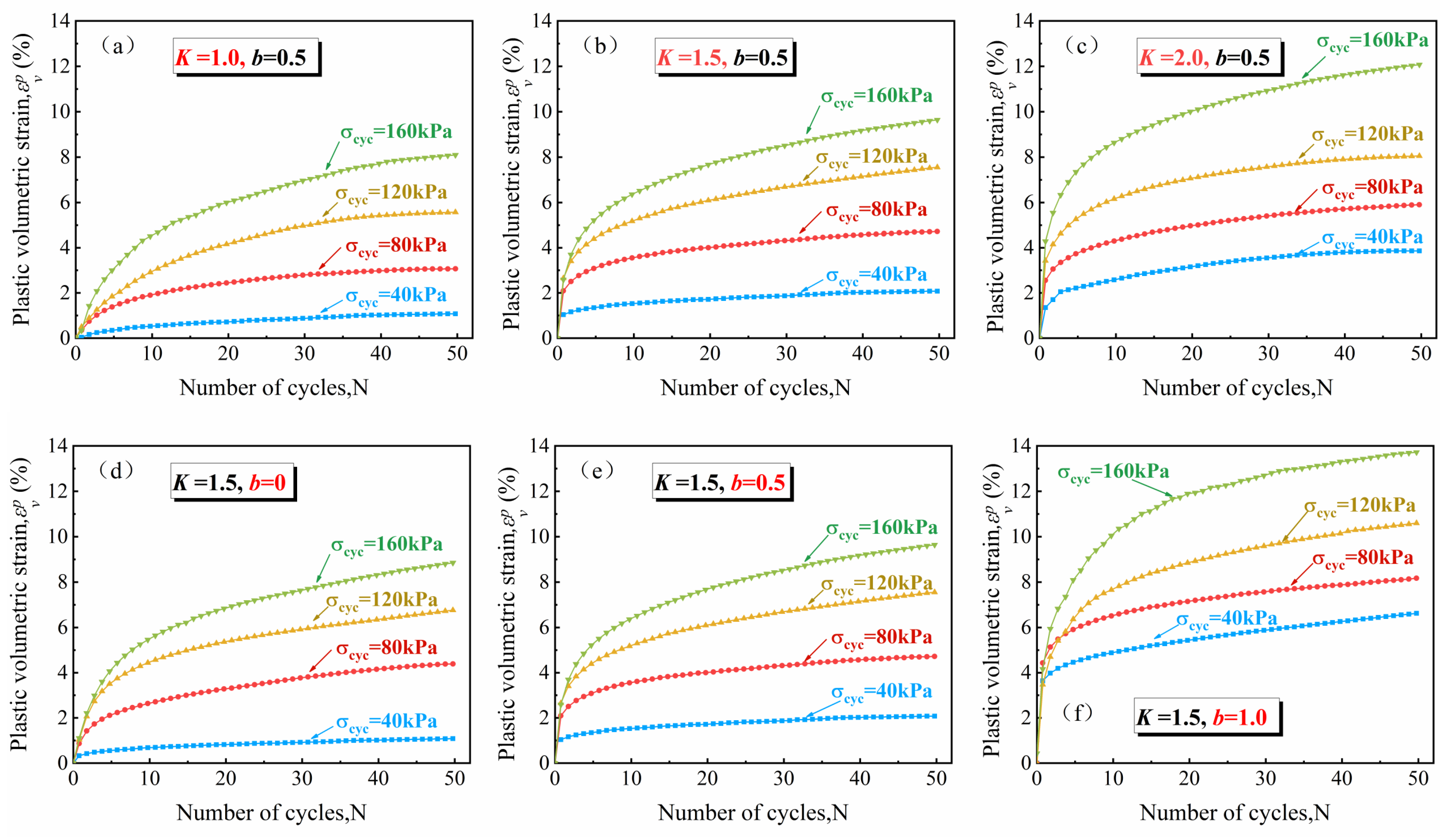
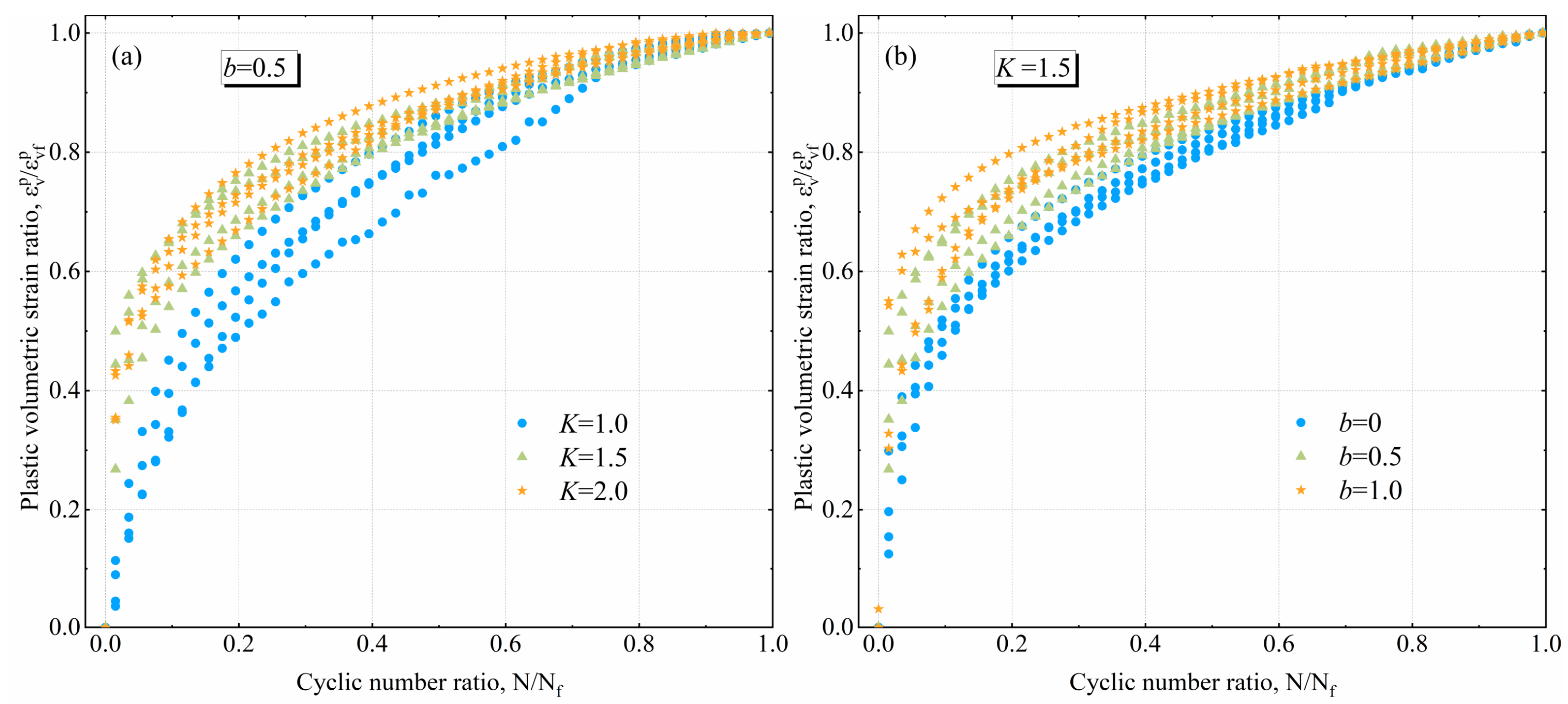
3.3.2. Plastic Accumulated Volumetric Strain
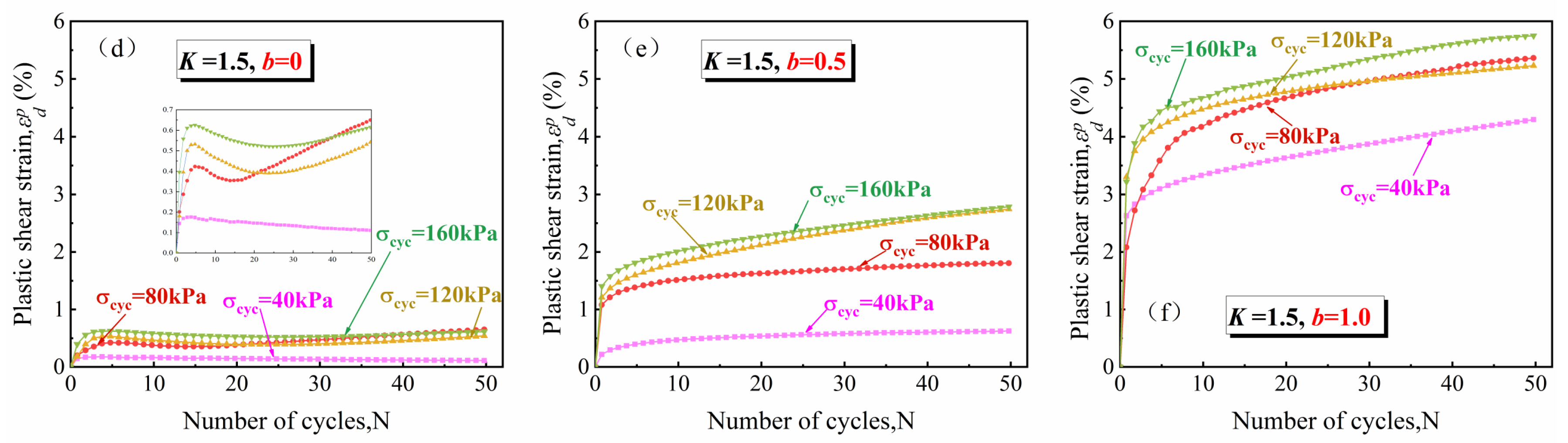
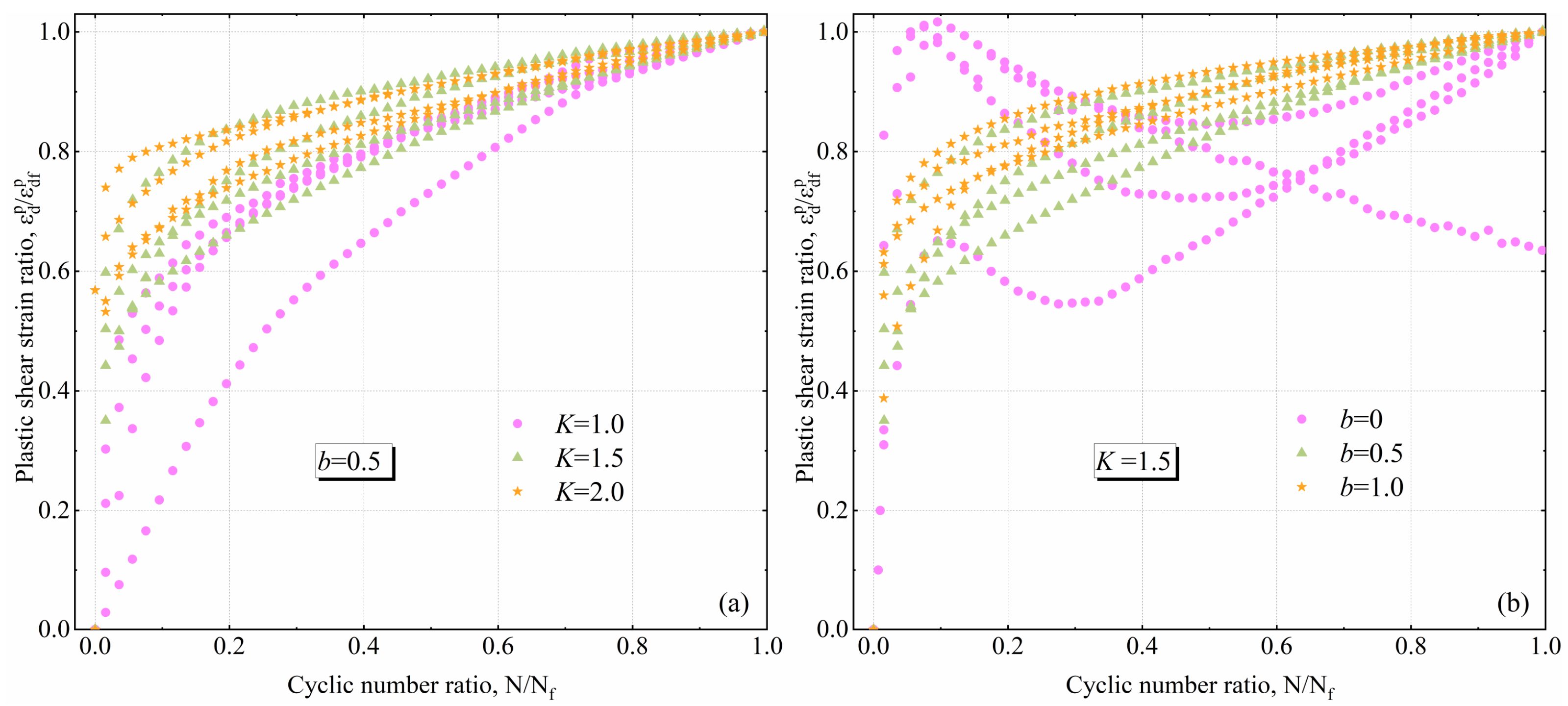
3.3.3. Plastic Accumulated Shear Strain
4. Conclusions
- (1)
- Principal strain develops in two stages: a rapid initial increase followed by a slower increase until stabilization. is the compressive deformation. isotropic consolidation () begins with expansion deformation and slowly transitions to compressive deformation with cyclic shear, while anisotropic consolidation ( and ) is always compressive deformation. is initially expansion deformation and then slowly transitions to compressive deformation.
- (2)
- The magnitudes of the elastic volumetric strain and elastic shear strain depend on the magnitude of the spherical or shear stress and are largely unaffected by their loading history.
- (3)
- All forms of plastic volume strain show volume shrinkage, which increases with increases in and . After normalization, the consolidation mode has a greater effect on the plastic volume strain ratio. The distribution range of the points of each anisotropic consolidation is smaller, and the points of isotropic consolidation and its dispersion are larger. The intermediate principal stress coefficient has a lesser effect on the plastic volume strain ratio, and the degree of normalization of the measurement points is higher.
- (4)
- All types of plastic shear strain exhibit shear shrinkage. They increase significantly with an increase in the intermediate principal stress coefficient, and there is no obvious relationship between the magnitude of the plastic shear strain and the anisotropic consolidation ratio. After normalization, the fall points of the plastic shear strain ratios for different anisotropic consolidation ratios and intermediate principal stress coefficients are scattered, and both and have a significant effect on the plastic shear strain ratios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| anisotropic consolidation ratio | |
| intermediate principal stress coefficient | |
| specific gravity | |
| natural moisture content | |
| natural dry density | |
| limits liquid limit | |
| plastic limit | |
| plasticity limit | |
| axial stress | |
| intermediate principal stress | |
| minor principal stress | |
| axial consolidation stress | |
| initial confining pressure | |
| axial stress amplitude | |
| cyclic time | |
| loading time | |
| axial strain | |
| intermediate principal strain | |
| minor principal strain | |
| volumetric strain | |
| shear strain | |
| plastic volumetric strain | |
| maximum of the volumetric shear strain | |
| elastic volumetric strain | |
| amplitude of elastic volumetric strain | |
| plastic shear strain | |
| elastic shear strain | |
| maximum of the plastic shear strain | |
| amplitude of elastic shear strain | |
| spherical stress | |
| deviatoric stress |
References
- Wu, H.; Shao, S.; Shao, S.; Wang, Z.; Yan, G. Cyclic loading deformation response and microstructure evolution of undisturbed loess subjected to pre-humidification process. Eng. Geol. 2024, 337, 107573. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, S.; Zhang, X.; Jiang, P. Dynamic Response Law of Loess Slope with Different Shapes. Adv. Mater. Sci. Eng. 2019, 2019, 4853102. [Google Scholar] [CrossRef]
- Cheng, Y.; Huo, A.; Zhao, Z.; Peng, J. Analysis of loess fracture on slope stability based on centrifugal model tests. Bull. Eng. Geol. Environ. 2021, 80, 3647–3657. [Google Scholar] [CrossRef]
- Umar, M.; Chiaro, G.; Kiyota, T.; Ullah, N. Deformation and cyclic resistance of sand in large-strain undrained torsional shear tests with initial static shear stress. Soils Found. 2021, 61, 765–781. [Google Scholar] [CrossRef]
- Thevakumar, K.; Indraratna, B.; Ferreira, F.B.; Carter, J.; Rujikiatkamjorn, C. The influence of cyclic loading on the response of soft subgrade soil in relation to heavy haul railways. Transp. Geotech. 2021, 29, 100571. [Google Scholar] [CrossRef]
- Zhu, W.; Ye, G.; Gu, L.; Zhang, F. Modeling of monotonic and cyclic behaviors of sand under small and normal confining stresses. Soil Dyn. Earthq. Eng. 2022, 156, 107209. [Google Scholar] [CrossRef]
- Dörner, J.; Horn, R.; Uteau, D.; Rostek, J.; Zúñiga, F.; Peth, S.; Dec, D.; Fleige, H. Studying the soil pore physical resistance and resilience of a shallow volcanic ash soil subjected to pure cyclic loading. Soil Tillage Res. 2020, 204, 104709. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Wu, S.; Tang, H.; Xin, P.; Liang, C. Dynamics stress–strain behavior of Tianshui soils. Landslides 2016, 14, 323–335. [Google Scholar] [CrossRef]
- Vargas, R.R.; Ueda, K.; Uemura, K. Influence of the relative density and K0 effects in the cyclic response of Ottawa F-65 sand—Cyclic Torsional Hollow-Cylinder shear tests for LEAP-ASIA-2019. Soil Dyn. Earthq. Eng. 2020, 133, 106111. [Google Scholar] [CrossRef]
- Yang, J.; Cui, Z.-D.; Xi, B.; Song, W. Experimental study on cyclic triaxial behaviors of saturated soft soil considering time intermittent and variable confining pressure. Soil Dyn. Earthq. Eng. 2024, 179, 108508. [Google Scholar] [CrossRef]
- Truong, M.H.; Indraratna, B.; Nguyen, T.T.; Carter, J.; Rujikiatkamjorn, C. Analysis of undrained cyclic response of saturated soils. Comput. Geotech. 2021, 134, 104095. [Google Scholar] [CrossRef]
- Ueno, K.; Kuroda, S.; Hori, T.; Tatsuoka, F. Elastic shear modulus variations during undrained cyclic loading and subsequent reconsolidation of saturated sandy soil. Soil Dyn. Earthq. Eng. 2018, 116, 476–489. [Google Scholar] [CrossRef]
- Kumar, A.; Azizi, A.; Toll, D.G. Application of Suction Monitoring for Cyclic Triaxial Testing of Compacted Soils. J. Geotech. Geoenviron. Eng. 2022, 148, 04022009. [Google Scholar] [CrossRef]
- Lei, H.; Li, B.; Lu, H.; Ren, Q. Dynamic Deformation Behavior and Cyclic Degradation of Ultrasoft Soil under Cyclic Loading. J. Mater. Civ. Eng. 2016, 28, 04016135. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, Z.; Kong, L.; Zhang, X.; Yin, S. Undrained dynamic behaviour of peaty organic soil under long-term cyclic loading, Part I: Experimental investigation. Soil Dyn. Earthq. Eng. 2018, 107, 279–291. [Google Scholar] [CrossRef]
- Liu, X.; Qin, Z.; Yang, J. Undrained cyclic behaviour of loess with initial shear stress: A focus on failure mode. Soil Dyn. Earthq. Eng. 2023, 171, 107971. [Google Scholar] [CrossRef]
- Liu, X.; Huang, G.; Qin, Z.; Miao, X. Shear behaviour of loess under varied drainage conditions subjected to monotonic and cyclic loads. Soil Dyn. Earthq. Eng. 2024, 177, 108397. [Google Scholar] [CrossRef]
- Shafiee, A.; Fathipour, H.; Payan, M.; Jalili, J.; Chenari, R.J. Modulus reduction and damping characteristics of geotextile-reinforced sands. Soil Dyn. Earthq. Eng. 2024, 181, 108641. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Hu, X.; Guo, L.; Cai, Y. Effects of principal stress rotation and cyclic confining pressure on behavior of soft clay with different frequencies. Soil Dyn. Earthq. Eng. 2018, 118, 75–85. [Google Scholar] [CrossRef]
- Chiaro, G.; Kiyota, T.; Koseki, J. Strain localization characteristics of loose saturated Toyoura sand in undrained cyclic torsional shear tests with initial static shear. Soils Found. 2013, 53, 23–34. [Google Scholar] [CrossRef]
- Wang, Y.; Wan, Y.; Liu, M.; Guo, C.; Zeng, C.; Wu, D. Undrained multi-dimensional deformation behavior and degradation of natural soft marine clay from HCA experiments. Soils Found. 2020, 60, 103–114. [Google Scholar] [CrossRef]
- Yang, L.; Shao, S.; Wang, F.; Wang, L. Experimental Study on the Axial Deformation Characteristics of Compacted Lanzhou Loess under Traffic Loads. Sustainability 2023, 15, 10939. [Google Scholar] [CrossRef]
- Zheng, D.; Tang, L.; Wang, Y.; Sun, Y. Dynamic stress accumulation effects on soil strength under cyclic loading. Soils Found. 2022, 62, 101164. [Google Scholar] [CrossRef]
- Cui, K.; Zhang, D.; Li, P.; Li, Q.; Zhang, H.; Qing, Y. Influence of the initial static stress state on the accumulation behaviour of a coarse-grained soil under long-term cyclic loading. Soil Dyn. Earthq. Eng. 2023, 172, 108042. [Google Scholar] [CrossRef]
- Pan, K.; Yuan, Z.; Zhao, C.; Tong, J.; Yang, Z. Undrained shear and stiffness degradation of intact marine clay under monotonic and cyclic loading. Eng. Geol. 2022, 297, 106502. [Google Scholar] [CrossRef]
- Wang, H.; Sun, P.; Liu, E.; Li, R. Dynamic properties of Tianshui saturated remolded loess: A laboratory study. Eng. Geol. 2020, 272, 105570. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. Chinese Standard: Beijing, China, 2019.
- Zheng, F.; Shao, S.; Wang, Y.; Shao, S. A New Suction-Controlled True Triaxial Apparatus for Unsaturated Soil Testing. Geotech. Test. J. 2021, 44, 833–850. [Google Scholar] [CrossRef]
- Li, G. Advanced Soil Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Zhang, J.M. Reversible and irreversible dilatancy of sand. Chin. J. Geotech. Eng. 2020, 22, 15–20. (In Chinese) [Google Scholar]

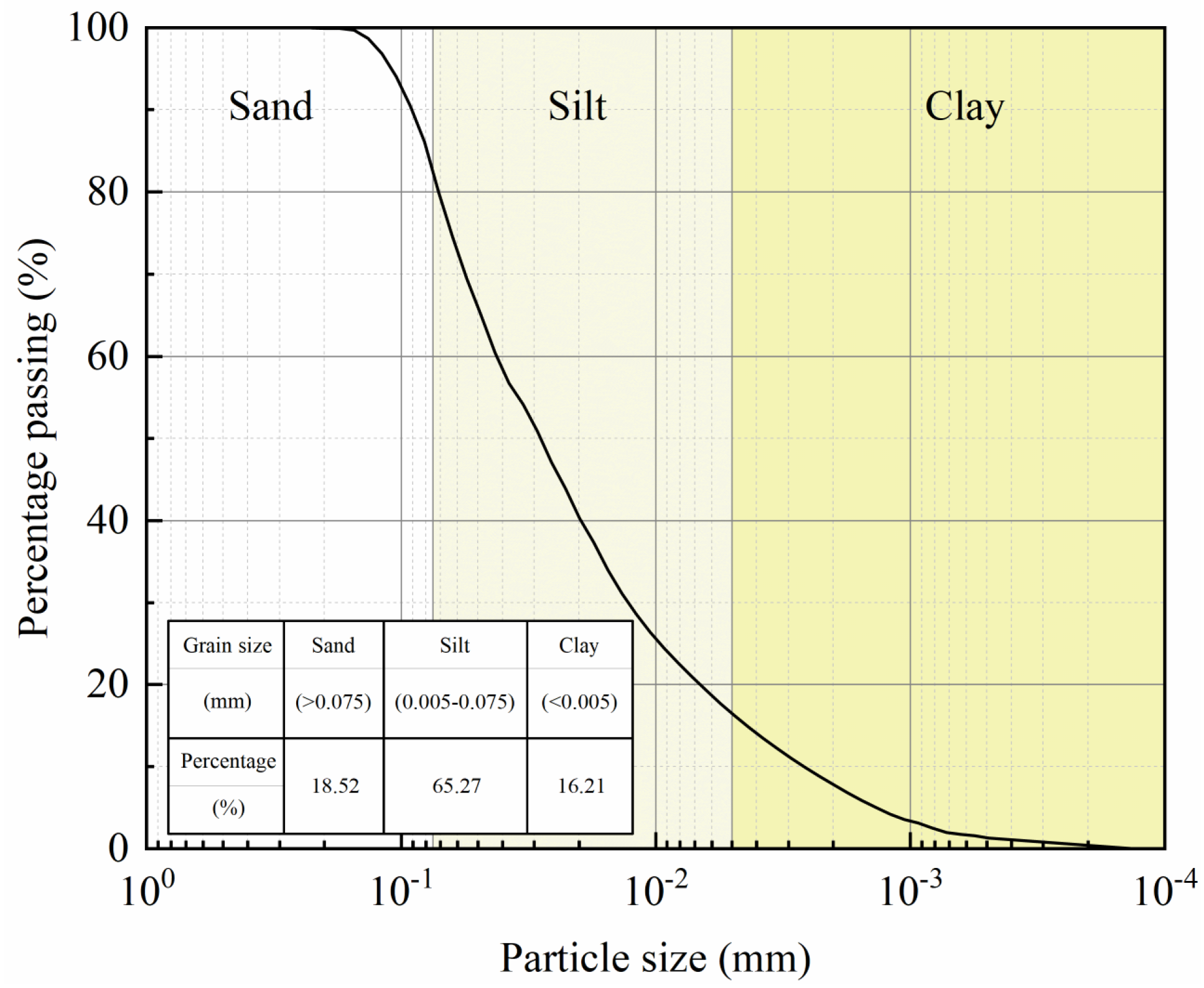
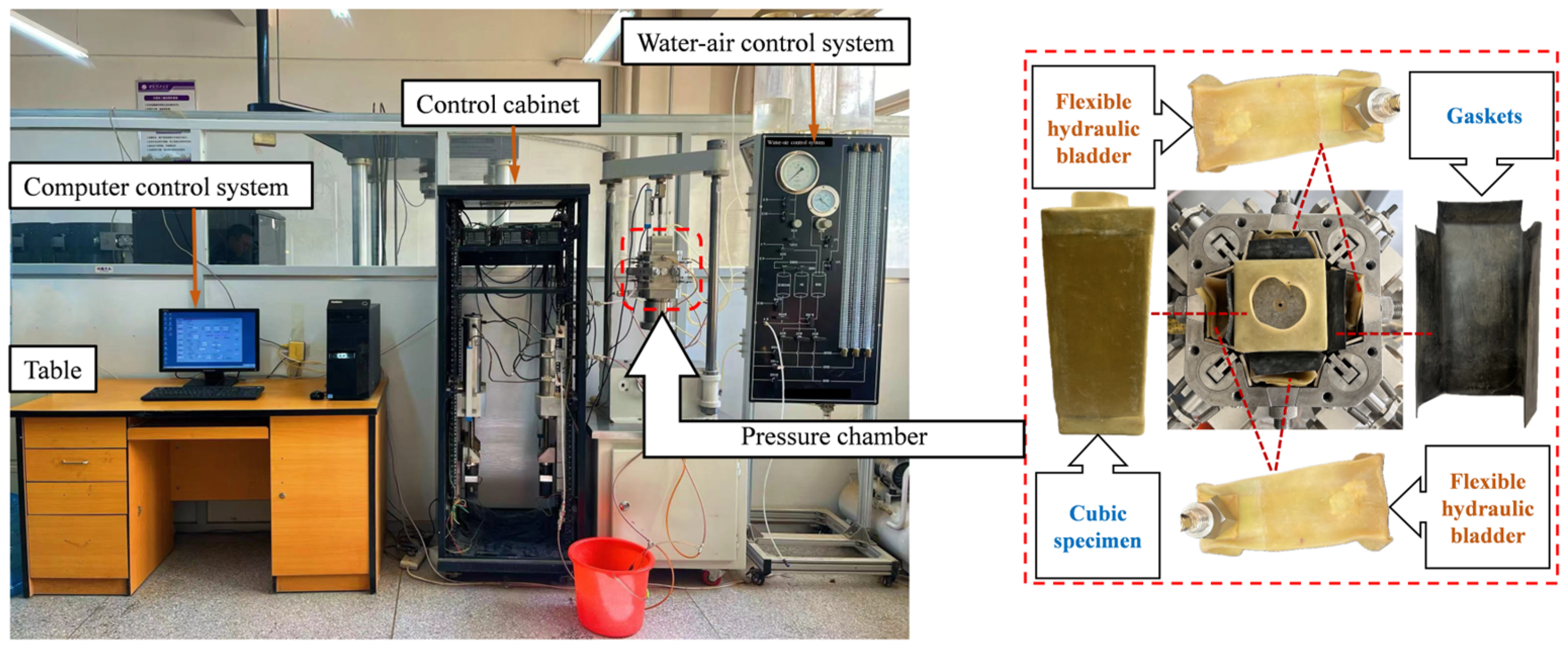
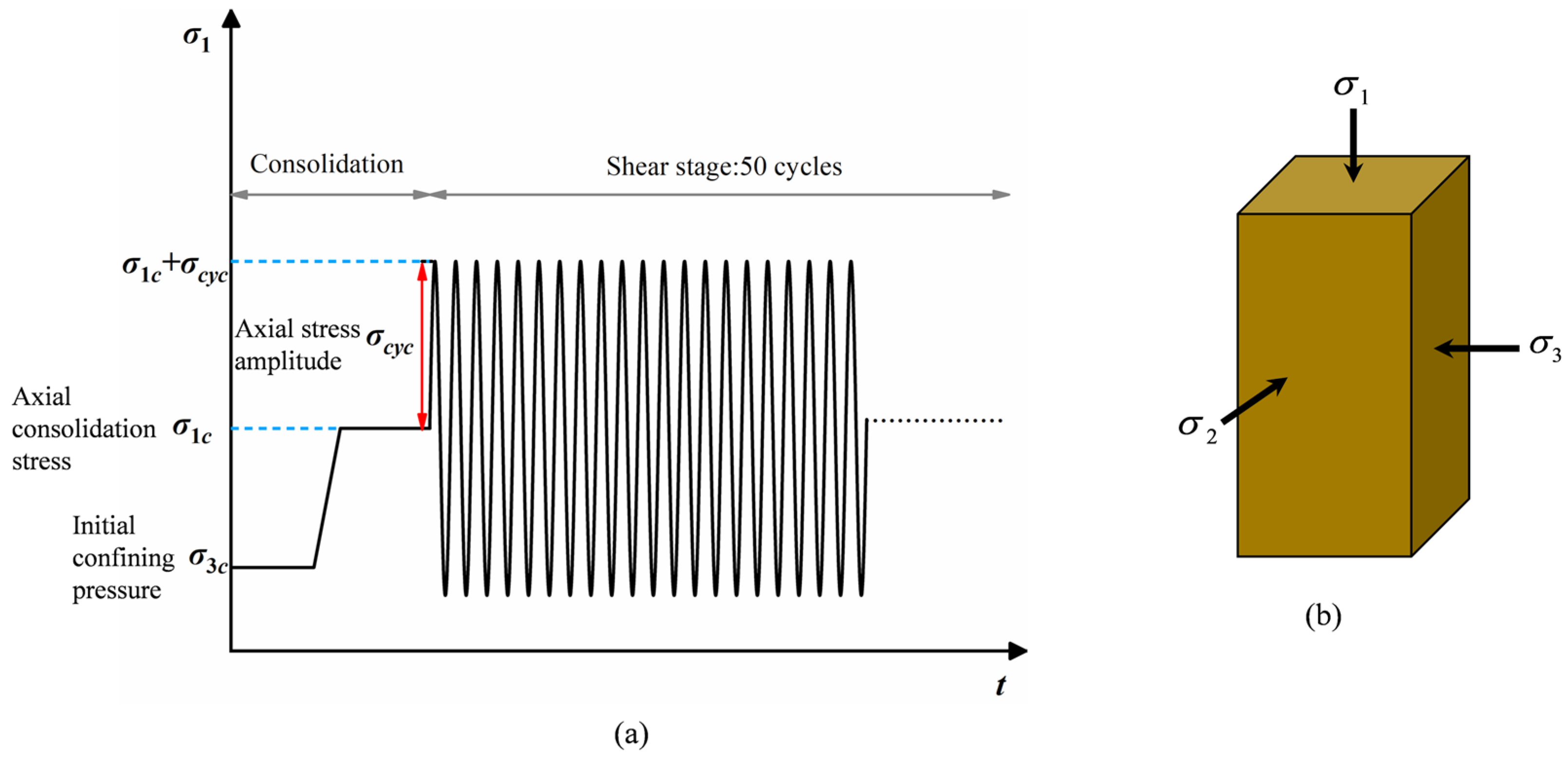
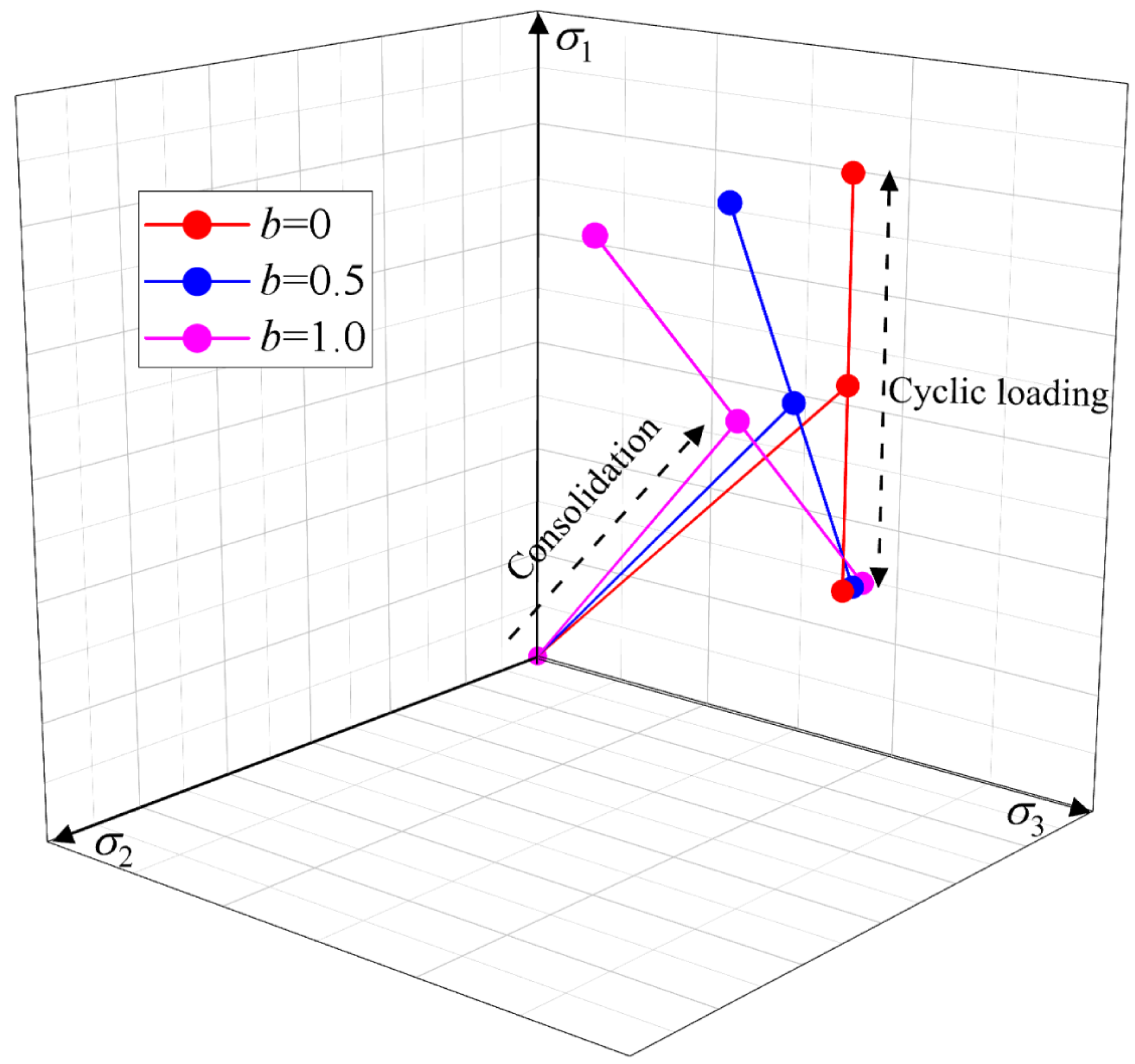

| Property | Value |
|---|---|
| Specific gravity, Gs | 2.70 |
| Natural moisture content, w/% | 21 |
| Natural dry density, ρd/g·cm−3 | 1.23 |
| Liquid limit, wl/% | 35.49 |
| Plastic limit, wp/% | 23.08 |
| Plasticity limit, Ip | 12.41 |
| Main minerals | |
| Quartz (%) | 36.2 |
| Mica (%) | 21.6 |
| Feldspar (%) | 14.3 |
| Calcite (%) | 18.2 |
| Dolomite (%) | 1.9 |
| Illite (%) | 7.8 |
| Test Series | /kPa | /kPa | /kPa | ||
|---|---|---|---|---|---|
| A01 | 200 | 200 | 1.0 | 0.5 | 40, 80, 120, 160 |
| B01 | 200 | 133 | 1.5 | 0 | 40, 80, 120, 160 |
| B02 | 200 | 133 | 1.5 | 0.5 | 40, 80, 120, 160 |
| B03 | 200 | 133 | 1.5 | 1 | 40, 80, 120, 160 |
| C01 | 200 | 100 | 2.0 | 0.5 | 40, 80, 120, 160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Shao, S.; Shao, S. Experimental Study on Cyclic Loading and Unloading of Remodeled Loess Using True Triaxial Testing. Buildings 2025, 15, 602. https://doi.org/10.3390/buildings15040602
Guo D, Shao S, Shao S. Experimental Study on Cyclic Loading and Unloading of Remodeled Loess Using True Triaxial Testing. Buildings. 2025; 15(4):602. https://doi.org/10.3390/buildings15040602
Chicago/Turabian StyleGuo, Dan, Shuai Shao, and Shengjun Shao. 2025. "Experimental Study on Cyclic Loading and Unloading of Remodeled Loess Using True Triaxial Testing" Buildings 15, no. 4: 602. https://doi.org/10.3390/buildings15040602
APA StyleGuo, D., Shao, S., & Shao, S. (2025). Experimental Study on Cyclic Loading and Unloading of Remodeled Loess Using True Triaxial Testing. Buildings, 15(4), 602. https://doi.org/10.3390/buildings15040602





