Abstract
The construction method of first splicing the low brackets and then lifting steel arch bridges has become increasingly popular, and its construction control has become a key issue. According to the unstressed state control theory, both the horizontal displacement and rotation angle at the lifted arch segment ends should be approximately 0 during the lifting process. An analytical solution for the position of the lifting points and the tension force in temporary horizontal rods is proposed. The analytical method is verified through a detailed comparison of the analytical results with the finite element model results and the on-site monitoring results. The results show that, for steel arch bridges whose main arch axis is the n-order parabola, the reasonable range of the parameter k is 0.8~0.9 and the specific value is related to the parameter n. The tension force in temporary horizontal rods can be quickly determined. The results meet the requirements of the unstressed state control theory, and the internal forces at the vault and lifting points can be maintained within a reasonable range. This research could be used to effectively control the deformation and stress distributions in the main arch of Shunjiang Bridge during the overall lifting process. The methods proposed provide effective guidance for using the overall lifting method for steel arch bridges.
1. Introduction
Steel arch bridges have remarkable performance advantages, such as a light weight, high strength, variable shape, and convenient construction [1]. Thus, this kind of arch bridge has been widely applied in bridge engineering, especially in large-scale municipal bridge projects. In the construction of large-scale steel arch bridges, the main arch is mostly prefabricated in segments and assembled on site. The stress distribution characteristics of the segmental prefabricated main arch are significantly different from those of the integrated main arch before closure. Also, temporary facilities or structures, such as framing and cables, are necessary to improve the safety of the main arch’s construction. The construction control of the main arch is a key factor during construction [2,3]. Instead of the full-framing method, the swivel method and the cable-hoisting method are commonly used for concrete arch bridges and concrete-filled steel tubular arch bridges [4,5,6], while the cable-stayed cantilever method and free cantilever method are traditionally used for steel arch bridges. In recent years, the overall lifting method, in which a large, prefabricated steel arch segment is lifted into the designated position using large-scale equipment, has been commonly used [7]. This method was initially applied in the construction of large special steel structures [8] and was further adopted in bridge construction after its successful application in many airports and large ports [9].
In the overall lifting method used in the construction of steel arch bridges, a low support system is first used to assemble each large segment, and then the large segment that will be positioned in the middle is lifted. This method not only has the advantages of framing construction methods, such as a simple operation and high safety level, but also has a short construction period, reduces the required aerial work, and has high stability [10,11]. For example, the Huaihe Bridge of the Shanghang high-speed railway employed the overall lifting construction method for large-section steel pipe arch ribs, which shortened the construction period by nearly one month and reduced the material usage significantly [12].
A schematic diagram of the overall lifting construction method is shown in Figure 1. Firstly, an arc-shaped low support system is erected on a trestle under the longitudinal projection of the designed arch axis, and then the arch elements are vertically assembled to form three segments, namely the two side arch segments and the middle arch segment. Next, two temporary towers are erected to lift the middle arch segment into the designated position. Finally, the three arch segments are drawn together either via welding with a closure section or by directly and accurately trimming a small number of arch plates without a closure section. To control the stability and deformation of the large-segment steel arch during the overall lifting process, especially when using the method without a closure section, temporary auxiliary measures must be implemented. Tensioning temporary horizontal tie rods at the lifting points is a common method, as shown in Figure 1.
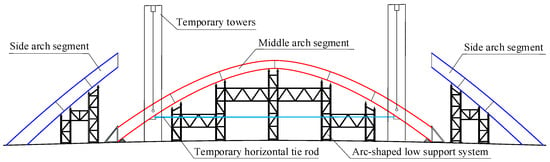
Figure 1.
A schematic diagram of the overall lifting construction method for large-segment steel arch ribs.
Due to the strong reliance on lifting facilities [13,14], the theoretical research on and engineering applications of the overall lifting construction method for steel arch bridges are less developed than those of other types of construction methods. Regarding the insufficient theoretical research, numerical analysis is an effective method for studying large steel structures [15]. Most existing studies on the overall lifting method have used practical engineering projects as the research background and used the finite element method for qualitative analysis. For example, Yu Wang et al. [16] studied the overall lifting construction method used for a large cross-sea bridge and developed a monitoring scheme focusing on the control of the arch–rib alignment, the stress, and the temperature, which are key aspects of overall lifting construction control. Focusing on the determination of the lifting point position through a floating crane, Xinge Miao et al. [17] proposed a method that combines mechanical calculation formulas with finite element modeling. The objective of finding a reasonable lifting point position was put forward to ensure a balanced bending moment distribution along the arch rib. Importantly, the bending moments at the vault and lifting point should be equal. Hui Xiang et al. [18] conducted a detailed construction-phase analysis using finite element software, focusing on the overall lifting construction method used for the Xinjiang Jiangxi Branch Bridge of the Changjing–Huang Railway. The specific construction control measures were provided to ensure strict control of the stress and deformation of arch ribs and brackets during construction.
With the development and application of the overall lifting construction method for steel arch bridges, construction control has become an urgent issue. However, the above-mentioned studies based on the finite element method only obtained qualitative conclusions. Studies focused on key technical parameters, such as the optimal lifting point position and the temporary horizontal tension force, are insufficient and cannot provide immediate and accurate references for bridge construction. This study focuses on the key technical parameters for the overall lifting construction method when applied to large-segment steel arch ribs. Based on the unstressed state control theory, a method to determine the optimal lifting point position was proposed and an analytical formula to determine the tension force of the temporary horizontal tie rod was derived. The research findings were applied to the construction of a steel box tied-arch bridge, guiding the overall lifting construction process of large-segment steel arch ribs. This paper will provide a convenient reference for steel arch bridge projects that adopt the overall lifting construction method.
2. Review of Unstressed State Control Theory
The unstressed state control method [19,20] was first proposed by Qin Shunquan, the chief engineer of the China Railway Bridge Bureau, and is a theoretical control method proposed for the phased construction of bridges. This method has been widely used in the construction control of large-scale bridge projects, making significant contributions to high-quality bridge construction [21,22,23]. This method points out that the following mechanical equilibrium formula should be satisfied during the phased construction of bridges:
where [K] is the stiffness matrix composed of the boundary conditions of the structural system; {δ} is the node displacement vector of the structure; {P} is the external load vector; and {} is the additional generalized load vector, caused by variations in the stress-free states of the elements in the finished bridge state influenced by different construction methods and processes.
Formula (1) indicates that the final internal force and displacement of the bridge using the phased construction method are uniquely solved by four conditions: (1) the position and magnitude of the external loads; (2) the geometric dimensions, positions, and stiffnesses of the structural elements; (3) the boundary conditions of the structure; and (4) the unstressed length and unstressed curvature of each element. According to the unstressed state control theory, once the four specific conditions are met, the internal force and displacement in the finished bridge state are uniquely determined for any bridge structure constructed in stages and are independent of the construction process. That is, the final bridge state achieved through the phrased construction can be theoretically identical to the state achieved through the single-stage construction. Among these conditions, the first three are relatively easy to control, whereas the unstressed length and curvature of the elements change during the phased construction. This is the key and most challenging point in construction control. Linking the intermediate and finished bridge states through the unstressed length and curvature of the elements to control the construction processes is the core concept of the stress-free state control theory.
According to the concept of the unstressed state control theory, to ensure that the main arch of the steel arch bridge can achieve the design target state upon the completion of the phased construction process, the unstressed length and curvature should closely match the design targets. After the middle section of the steel arch is lifted, it should accurately connect with the two side arch segments. To achieve this, the horizontal displacement and rotation angle at both ends of the middle arch segment need to be controlled so that they remain around zero before closure, and the middle arch segment can be seamlessly welded with the side arch segments on the support brackets. However, owing to the fact that the lifted segment is large and the loading conditions are complex, significant deformations may occur during lifting. Furthermore, the structural system is unstable before closure, making it prone to being in an unfavorable stress state. Therefore, it is essential to adopt specific construction measures to control horizontal displacement and rotation angle at the ends of the lifted segment and ensure that the arch is in a favorable internal force state. Here, selecting appropriate lifting points and tensioning temporary horizontal tie rods between them is a low-cost and effective method.
On the basis of the principles of the unstressed state control method, the following sections provide an innovative analytical control method for the determinations of the appropriate positions of the lifting points and the optimal temporary horizontal tension force.
3. Analytical Control Method for the Overall Lifting Method
3.1. Analytical Formula of Temporary Horizontal Tension
In the analytical method, only the self-weight is considered. Other load types, such as the wind load and temperature action, are not considered. The deformation diagram of the lifted steel arch segment during the lifting process is shown in Figure 2. The basic parameters of the lifted steel arch are defined as follows: the longitudinal length of the whole lifted arch segment is l; the sagittal height of the lifted arch segment is f; the axis shape of the arch is assumed to be the n-order parabola; to simplify the tension force calculation of the temporary horizontal tie rod, the section of the steel arch is assumed to be uniform and the cross-sectional area and the moment of inertia are A and I, respectively; the elastic modulus of the arch rib material is E; the ratio of the longitudinal distance between the two lifting points to longitudinal length of the whole lifted arch segment l is k (0 < k ≤ 1); and the temporary horizontal tension force after the elastic deformation of the horizontal tie rod is P.
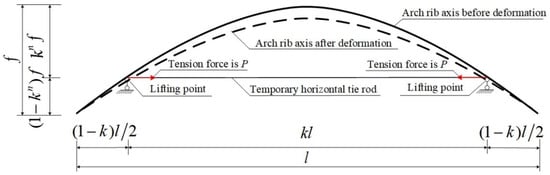
Figure 2.
Deformation diagram of the lifted steel arch segment during the lifting process.
Here, since the external forces and bounding conditions acting on the arch rib are symmetrical, only half of the structure was analyzed. The force analysis diagram of the half structure for the overall lifting method of the lifted steel arch segment is shown in Figure 3. In the follow-up analysis, the longitudinal bridge direction is defined as the x-axis direction and the vertical bridge direction is defined as the y-axis direction. The vault is defined as the origin of the coordinates. The function of the arch axis curve is defined as y(x). The weight of the uniform-section steel arch per unit length along the x-axis is marked as q. For the steel arch bridge, the structural self-weight is low and the rise–span ratio of the lifted arch segment f/l is usually small, while the weight of the steel arch per unit length in the longitudinal direction q1(x) is approximately equal to q, as shown below.
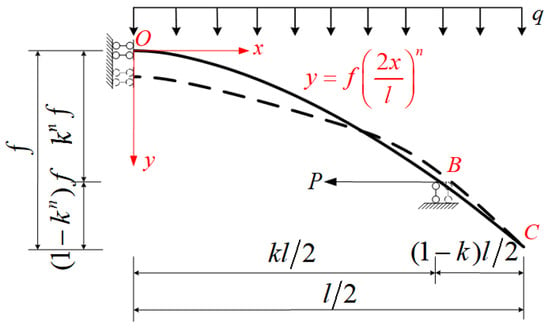
Figure 3.
Force analysis diagram of the half structure for the overall lifting method.
Because the lifted steel arch segment is subject to small deformations and remains in the linear and elastic state during construction, according to the linear elastic theory [24], the deformation occurring during the overall lifting of the steel arch is primarily due to the internal bending moments and axial forces, whereas the deformation from shear forces can be ignored. The following conventions for internal forces are established: the bending moment is defined as positive when the lower edge of the steel arch is in tension and negative when the upper edge is in tension. Similarly, the axial force is considered positive when the section is under tension and negative when the section is under compression. By using the unit load method derived from the principle of virtual work [25], the displacement at point C at the end of the lifted steel arch segment can be calculated as follows:
In Formula (3), since the rise–span ratio of the lifted arch segment f/l is usually small, ds can be approximated as dx. M(x) and N(x) are the bending moment and axial force of the arch rib along the longitudinal bridge direction, respectively, which can be calculated as follows:
In Formula (3), and are the bending moment and axial force under the virtual unit load at point C, respectively. The horizontal unit force to the left is assumed to act at point C, and the bending moment and axial force of the arch rib are obtained as follows:
A clockwise unit moment is assumed to act at point C, and the bending moment and axial force of the arch rib are obtained as follows:
By substituting Formulas (4) and (5) into Formula (3) and letting ΔCx = 0, the following equation can be obtained:
In Formula (6), X(n,k) and φ(n,k,A,I,f,l) are the dimensionless coefficients of the arch rib parameters, and the analytical formula is derived as follows:
In the above formula, X(n,k) is related to the bending moment and φ(n,k,A,I,f,l) is related to the axial force. The axial force of the steel arch in the overall lifting process mainly comes from the force of temporary horizontal tension rods and is small compared with the stress state of the completed bridge; thus, the horizontal displacement of the arch rib is generally very small. Thus, the order of magnitude of φ(n,k,A,I,f,l) is generally less than 10−2. Therefore, Formula (6) can be further simplified by ignoring the influence of the axial force of the steel arch in the lifting process:
By substituting Formulas (4) and (6) into Formula (3) and letting ΔCθ = 0, the following equation can be obtained:
In Formula (11), θ(n,k) is the dimensionless coefficient only about n and k, and the analytical formula is as follows:
3.2. Coefficient Analysis
Equations (10) and (11) indicate that if the axial force in the overall lifting process of the steel arch is ignored, the reasonable tension force of the temporary horizontal tie rods required to ensure that the horizontal displacement and rotation angle at the end of the lifted arch segment are approximately equal to 0 depends only on the values of the coefficients X(n,k) and θ(n,k). As shown in Figure 4, the variation trends of X(n,k) and θ(n,k) with the parameter k are the same. Both coefficients are positively correlated with parameter k, and their growth rates decrease as k increases. It can be discovered from Figure 4 that the X(n,k)–k curves with different parameter n values converge together within a certain range of k, as well as the θ(n,k)–k curves.
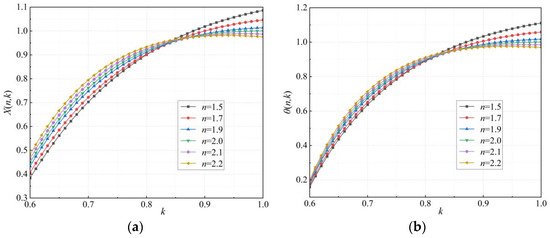
Figure 4.
Relationships between the coefficients and the parameter k. (a) X(n,k); (b) θ(n,k).
According to the unstressed state control method, the horizontal displacement and the rotation angle at the end of the lifted arch segment should be controlled to be close to 0 at the same time during actual construction, while the force of the temporary horizontal tie rod is unique. Thus, a reasonable lifting point position, which corresponds to a reasonable parameter k, should be determined to solve this contradiction. According to Equations (10) and (11), the ratio of the tension forces when the horizontal displacement and the rotation angle are 0 is equal to the ratio of X(n,k) to θ(n,k). Figure 5 shows the relationship between the ratio of X(n,k) to θ(n,k) and the parameter k. It can be found from the figure that when the value of k is in the range of 0.8~0.9, the value of X(n,k)/θ(n,k) can be controlled within the range 0.99~1.01. This means that the deviation of the tension forces when the horizontal displacement and the rotation angle are 0 is within 1%, which fully meets the requirements in engineering use. Furthermore, the specific value of k gradually increases as the parameter n increases.
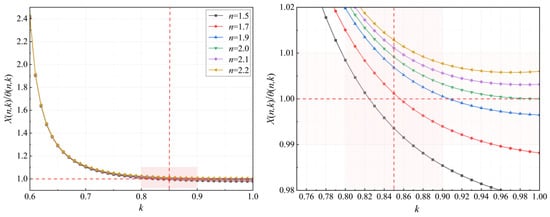
Figure 5.
Relationships between the ratio of X(n,k) to θ(n,k) and the parameter k.
3.3. Internal Force Analysis of Key Sections of Steel Arch Segment
During the lifting process, the vault section and the sections at lifting points are the key sections [18]. According to Formulas (3) and (6), the internal forces at the vault section can be obtained as follows:
The internal force of the section at the lifting point is as follows:
According to Formulas (13) and (14), the bending moments and axial forces of the key sections of the steel arch are plotted in Figure 6 and Figure 7, respectively. In Figure 7, for the convenience of comparison, the rise–span ratio of the lifted arch segment is taken as 1:4. Figure 6a shows that the absolute value of the bending moment of the vault section decreases at first and then increases as the parameter k increases for different n parameter values. It reaches the minimum value when k is approximately 0.85. Figure 6b shows that the absolute value of the bending moment at the lifting point decreases as the parameter k increases and is independent of the parameter n. Furthermore, the rate of decrease begins to reduce when k is approximately 0.85. Relevant studies [17,18] have pointed out that, when the peak values of positive and negative bending moments of arch ribs are closed, it is easier to control the internal force level of arch ribs within a reasonable range. Figure 6c indicates that when k is in the range of 0.8~0.9, the bending moments of the vault and the lifting point are approximately equal and the internal force of the bending moment of the arch rib during lifting is in a reasonable state.
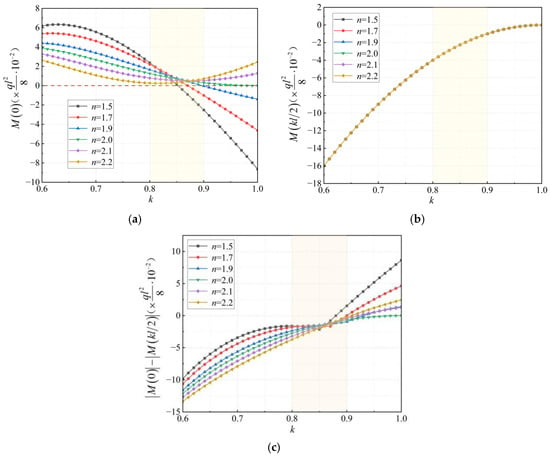
Figure 6.
Relationships between bending moments of key sections and the parameter k. (a) Vault section; (b) lifting point; (c) difference between the absolute values.
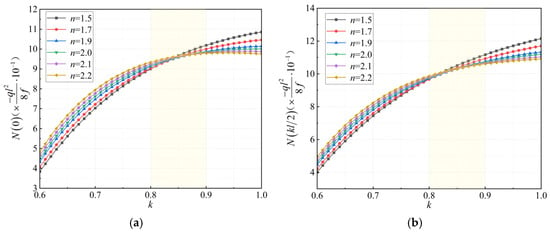
Figure 7.
Relationships between axial forces of key sections and the parameter k. (a) Vault section; (b) lifting point (take f/l = 1:4).
It can be seen from Figure 7 that the cross-sectional axial forces at the vault and the lifting point gradually increase as the parameter k increases, and the rate of increase rate begins to decrease when k is approximately 0.85. For different parameter n values, the cross-sectional axial forces at the vault and the lifting point are similar when k is approximately 0.85.
In summary, when the value of k is in the range of 0.8~0.9, the bending moment and axial force of the key section of the steel arch are within a reasonable range, and the peak value of the bending moment of the key section of the arch rib is relatively low. This means that the recommended range of k obtained by controlling the deviation of X(n,k) and θ(n,k) at the end of the lifted arch segment based on the unstressed state control method meets the internal force requirements in key sections of the steel arch.
3.4. Selection of Lifting Point and Calculation of Temporary Horizontal Tension
It can be seen from Section 3.2 and Section 3.3 that, when X(n,k)/θ(n,k) = 1 and the internal forces in the key sections are taken as the optimization objectives, the recommended range of k is 0.8~0.9. According to Figure 5, the specific value of k is related to the arch rib parameter n. Assuming that the value of k is determined as k0 through Figure 5, the temporary tension force in the horizontal tie rod P0 can be calculated as follows:
Notably, if the influence of the axial force generated by the horizontal tension cables during the lifting process is considered, the value of needs to be reduced. According to Equations (7) and (9), the temporary tension force in the horizontal tie rod considering the influence of the axial force is as follows:
If the actual influence of the axial force on the arch rib is considered, the vertical coordinate in Figure 5 should actually be X/[(1 + φ)·θ], and the reasonable value of k should be smaller. Therefore, it is recommended that the value of should be determined through Figure 5 by taking the upper limit value of X/θ, which is 1.01 in this paper. If so, is recommended to be approximately 0.815 when n = 1.5, while it is recommended to be approximately 0.890 when n = 2.0.
To facilitate the use of the proposed analytical construction control method in practical projects, the recommended lifting point position and the tension force of the temporary horizontal tie rod for different values of the parameter n are calculated and summarized in Table 1.

Table 1.
Quick calculation table of arch rib lifting point selection and temporary horizontal tension.
3.5. Example Verification
To verify the accuracy of the proposed construction control method, a certain steel arch segment to be lifted was considered as an example and finite element analysis was conducted. The structural and material parameters were as follows: n = 2, l = 103.2 m, f = 22.6 m, E = 2.06 × 105 MPa, I = 0.8545 m4, A = 0.4331 m2, and q = 34.0 kN/m.
From Table 1, the suggested value of is 0.890. The calculated result of is 1963.0 kN, while the calculated value of is 1946.0 kN. The relative deviation of from is 0.9%. It is verified that the actual axial force has little influence on the reasonable value of the temporary horizontal tension force.
Based on the recommended values of and , the beam element model of the lifted steel arch segment established through the finite element software Midas Civil 2021 is shown in Figure 8. The deformation of the steel arch before and after the tie rod is tightened is shown in Figure 9 and Figure 10, respectively. The results show that the horizontal displacement and rotation angle at the end of the lifted arch segment are close to 0 when is 0.890 and the temporary horizontal tension is 1946.0 kN. This indicates that the derived formula can provide a reasonable and accurate solution to meet the requirements of the unstressed state control method under the given conditions.
Figure 8.
Finite element model of the steel arch example.
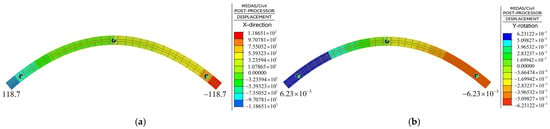
Figure 9.
Deformation of the arch rib before the tie rod is tightened. (a) Horizontal displacement (unit: mm); (b) rotation angle (unit: rad).
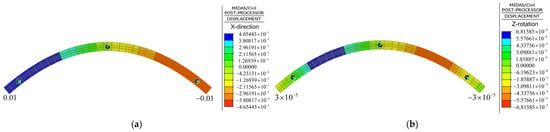
Figure 10.
Deformation of the arch rib after the tie rod is tightened. (a) Horizontal displacement (unit: mm); (b) rotation angle (unit: rad).
4. Application of Proposed Construction Control Method
The proposed construction control method was applied in the engineering project of Shunjiang Bridge. This application case is introduced as follows.
4.1. Design Overview
Shunjiang Bridge is located in Shangyu District of Shaoxing City, which is in Zhejiang Province of China. It is a bottom-supported box-section steel arch bridge with a standard span of 176 m. The completed state of the bridge is shown in Figure 11a. The calculated span of Shunjiang Bridge is 170 m, while the arch height is 50 m. The theoretical rise–span ratio of the main arch is 0.294. The longitudinal projection lines of the main arches are a 1.5-order parabola followed by a 1.7-order parabola, as shown in Figure 11b. The transverse projection lines of the main arches are the oblique straight lines, as shown in Figure 11c. The cross-section of the main arch is octagonal. The cross-sectional sizes of the arch springing and the vault are 4.5 m × 2.2 and 2.5 m × 2.2 m with linear transition. The arch vault section and the arch springing section are shown in Figure 11d,e. The standard cross-sectional width in the middle span of the bridge is 22.5 m. There are 26 pairs of suspenders along the whole bridge, which employ parallel steel wire stay cables with a standard strength of 1670 MPa. The maximum length of these suspenders is 47 m. The spacing between the upper lifting points of the suspenders is 4 m, and the spacing between the lower lifting points of the suspender is 6 m. The suspenders are attached to the beam via an anchor pipe and are connected to the arch through lifting lugs. A cantilever sidewalk is set on one side of the main girder to help pedestrians on the east bank levee and the west bank beach to cross the bridge. The cantilever and the main arch form a loop on the facade to enhance the overall look of the main bridge.
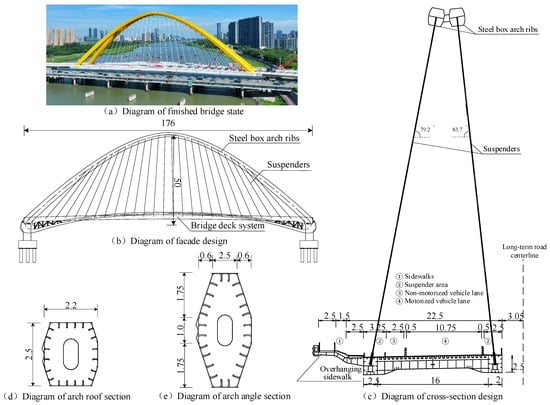
Figure 11.
Design drawing of Shunjiang Bridge (unit: m). (a) Completed bridge state; (b) facade design; (c) cross-sectional design; (d) arch vault section; (e) arch springing section.
4.2. Construction Method Overview
Shunjiang Bridge was constructed with the sequence of “beam first and arch second”. All the segmented steel components were fabricated in a centralized manner in a factory and transported to the site for lifting and assembly. Once the main girder installation was completed, arch rib welding and overall lifting construction were carried out, which was the critical construction phase. The arch ribs were divided into three longitudinal sections. The main arch segments at both ends were hoisted and welded into place by gantry cranes, which were temporarily supported and fixed through steel pipe tire frames. All of the segments were assembled vertically on the tire frame through a gantry crane. The middle main arch segment, which is made of Q345 steel, has a longitudinal length of 103.7 m and a dead weight of 858.3 t. Two portal lifting frames were employed to elevate the assembled middle main arch segment to the designated installation position. When they were welded to the adjacent arch segments, the structural conversion of the steel arch was completed. The construction site for the overall lifting construction of Shunjiang Bridge is illustrated in Figure 12, and the relevant design parameters are detailed in Table 2.
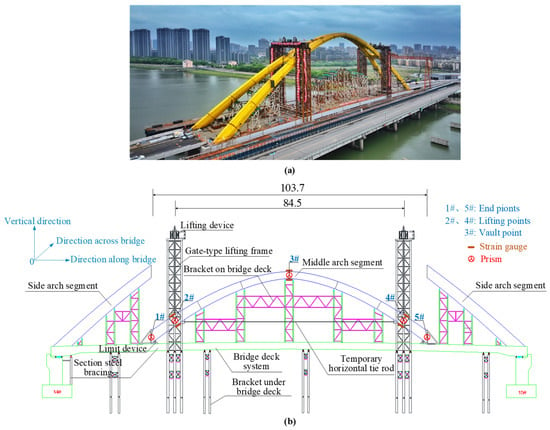
Figure 12.
Drawing of the overall lifting construction of Shunjiang Bridge. (a) Construction state; (b) overall lifting construction (unit: m).

Table 2.
Design parameters of the lifted main arch segment.
The overall lifting arch segment of Shunjiang Bridge is a 1.5-order parabola arch rib. According to Table 1, the recommended value of is 0.815. Then, the reasonable lifting point spacing k0l is calculated as 84.5 m, and the equivalent uniform load is determined as q = 31.7 kN/m. According to the data in Table 1, the recommended temporary horizontal tension is 1734.2 kN, and each main arch is tensioned with one horizontal tie rod. Since the arch rib of Shunjiang Bridge is a type of oblique arch rib with non-uniform cross-sections, and the two steel arch ribs are slightly asymmetrical in the transverse direction, the reasonable tension force of the temporary horizontal tie rod calculated above needs to be further iteratively optimized through finite element analysis.
4.3. Finite Element Analysis Model
MIDAS Civil 2021 software was used to establish the beam element analysis model of the lifted middle main arch segment by setting a reasonable lifting point position and inputting the initial force of the temporary horizontal tie rod, as shown in Figure 13a. The whole lifting section model was constructed by the beam element B31 and the truss element T3D2. The model contained 214 beam elements, 2 truss elements, and 224 nodes. Here, the value of was set as 0.815 through the proposed analytical method. Based on the recommended temporary horizontal tension , the iterative optimization with the goal of controlling the horizontal deformation and rotation angle of the arch end so that they remained around 0 at the same time was performed. The optimized inner arch cable force was 1575.0 kN, and the optimized outer arch cable force was 1915.0 kN, and these values were used in actual construction. The vertical lifting cable force of 2171 kN was one quarter of the weight of the lifted middle main arch segment. In addition, to analyze the local mechanical performance around the arch lifting point, the local shell element model of the segment near the arch lifting point was established in ABAQUS 6.14 software, as shown in Figure 13b. The local model was constructed by the shell element S4R. The mesh size was not unique and was more refined in the lift anchor components. The local model contained 62,464 elements and 61,535 nodes. In this model, the simply supported coupling points were set at the end of the lifted arch segment. The horizontal tension force and vertical lifting force were applied at the lifting points, respectively. The internal forces transmitted on the ends of the middle main arch segment were added into the model.
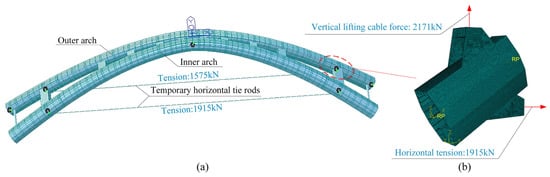
Figure 13.
Calculation model of the lifted middle main arch segment. (a) Beam element model of the lifted middle main arch segment; (b) local shell element model of the segment near the arch lifting point.
4.4. Finite Element Analysis Results
4.4.1. Calculation Results of Beam Element Model
After setting the reasonable lifting point position through the proposed analytical method and the tension force of the temporary horizontal tie rod through the finite element analysis, the deformation of the middle main arch segment of Shunjiang Bridge in overall lifting construction is shown in Figure 14. It can be seen from Figure 14 that both the horizontal displacement and the rotation angle at the end of the lifted arch segment are close to 0 simultaneously.
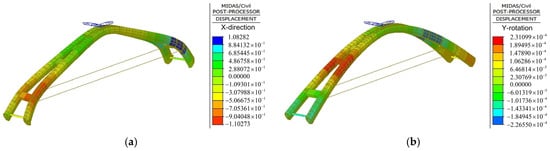
Figure 14.
Deformation of middle arch segment in overall lifting construction. (a) Horizontal displacement (unit: mm); (b) rotation angle (unit: rad).
The stress distribution of the middle arch segment during the overall lifting process of Shunjiang Bridge is depicted in Figure 15. The normal stress at the upper edge of the middle main arch segment ranges from −11.8 to 9.4 MPa, whereas the stress at the lower edge ranges from −19.7 to 0 MPa. The maximum absolute values of the stresses at the vault section are −5.3 MPa and −7.9 MPa for the upper and lower edges, respectively. At the lifting point, the maximum stresses for the upper and lower edges of the arch rib are 9.4 MPa and −19.7 MPa, respectively. The stress in the key sections is relatively low, which indicates that the lifted arch segment is in a secure state with a significant safety margin.
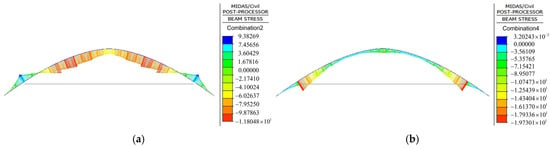
Figure 15.
Stress distribution of middle arch segment in overall lifting construction (unit: MPa). (a) Upper edge; (b) lower edge.
4.4.2. Calculation Results of Local Shell Element Model
Owing to the constructional complexity near the lifting point, the overall calculation results cannot accurately reflect the stress distribution and stability performance of steel plates in local areas. Further analysis based on the local shell element model is necessary.
Figure 16a shows the von Mises stress distribution for the established segment near the lifting point of the steel arch. The maximum von Mises stress in the main arch near the lifting point is 51.9 MPa, as shown in Figure 16b. The maximum stress in the temporary tension and lift anchor components is 138.9 MPa, as shown in Figure 16c. Both values are less than the design strength of Q345 steel, which is 270 MPa, thus meeting the specification requirements. The maximum von Mises stress at the lifting point occurs on the steel member at the anchor point of the arch rib. The first-order instability mode for the established segment near the lifting point is depicted in Figure 17. It can be seen that the critical load coefficient is 21.5, which exceeds the limiting value of 4.0 in the design code [26], thus meeting the specification requirements. The most instability-susceptible area is located at the diaphragm near the lifting point of the main arch.
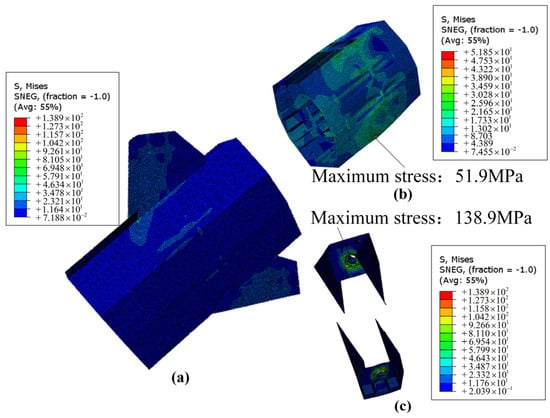
Figure 16.
Von Mises stress nephogram of the established arch segment near the lifting point (unit: MPa). (a) Whole established arch segment; (b) main body of the steel arch segment; (c) temporary tension and lift anchor components.
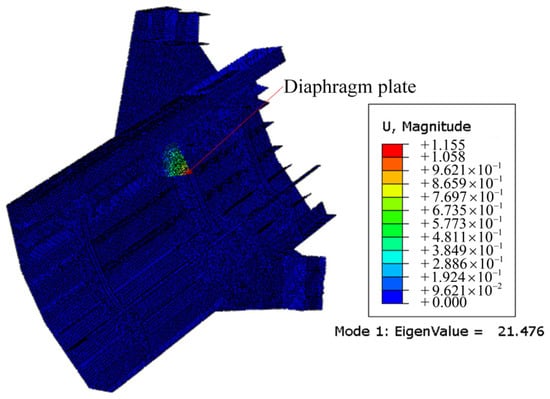
Figure 17.
First-order buckling mode of the established segment near the lifting point.
4.5. On-Site Monitoring Results
During the actual lifting process for the middle arch segment, the inclinometers were positioned at the wind support near the lifting point and the inclination angle of the arch segment was monitored throughout the whole lifting process. Figure 18 shows the measured inclination angle of the arch rib lifting section in both the longitudinal and transverse directions during the lifting process. Table 3 presents the changes in the coordinates of the measuring points at the end of the lifted arch segment. The locations of the monitoring points in Table 3 are marked in Figure 12.
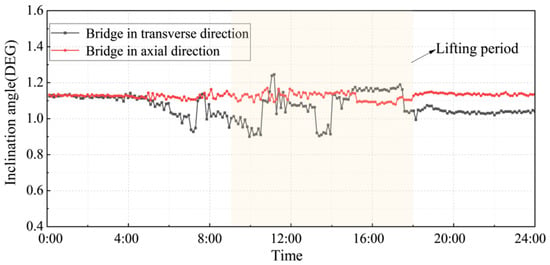
Figure 18.
Measurement results of the inclination angle in the lifting section.

Table 3.
Coordinate measurement results at the end of the lifted arch segment.
The measurements indicated that the inclination angle of the lifted arch segment remained stable throughout the lifting process, the posture of the arch rib in the overall lifting section was in a controllable state. The maximum offset between mileage and each measuring point was 10.17 mm and reached 15.06 mm after accounting for the lifting height, indicating that the lifted middle arch segment was essentially in place.
Based on the finite element analysis results, the key stress measuring points, which included the vault section and the lifting points of the lifted arch segment, were selected for real-time monitoring. A wireless automatic comprehensive testing system was employed for stress monitoring. The sampling frequency was every 10 min.
Figure 19 displays the stress changes of the measuring points on the day when the middle arch segment was lifted. The lifting period of the middle arch segment was from 12:00 to 16:00. The real-time stress monitoring data from key sections of the arch demonstrated that the stress variation in the lifting sections was small throughout the lifting process, and the variation was similar to the theoretical calculation results of the beam element model. Numerical analysis and on-site monitoring results show that the stress of key sections of the steel arch rib was in the range of −25 MPa to 10 MPa, which also verifies the accuracy of the finite element model. This confirmed that the arch lifting section remained essentially stable during the overall lifting process.
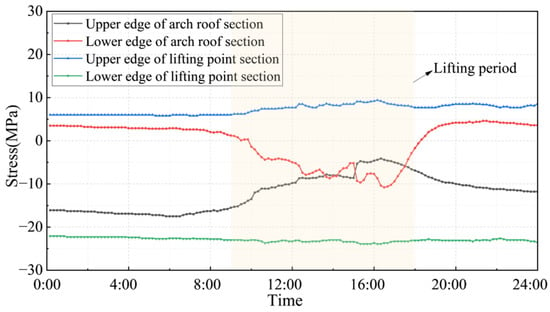
Figure 19.
Stress monitoring results in the arch lifting process.
Overall, the on-site monitoring results indicate that the deformation and stress distributions of the main arch during the overall lifting process can be effectively controlled when employing the proposed construction control method. As a result, the middle arch segment of Shunjiang Bridge was successfully lifted, and joint formation was completed in one day.
5. Conclusions and Discussion
5.1. Conclusions
The overall lifting construction method for large-segment steel arch bridges is commonly used. The lifting point positions and the temporary horizontal tension force are key technical parameters for this construction method. On the basis of the unstressed state control theory, this study proposed the analytical control method to ensure that both the horizontal displacement and rotation angle at the lifted arch segment ends are approximately 0 during the lifting process. This method provides an analytical solution for the positioning of lifting points and determination of tension force in temporary horizontal rods. Furthermore, the application case of the proposed construction control method in Shunjiang Bridge was deeply analyzed. The following conclusions have been drawn in this study:
- (1)
- In the proposed overall lifting construction control method, the position of the lifting point significantly impacts the deformation and internal forces of the steel arch. According to the proposed analytical control method, for steel arch bridges whose main arch axis is an n-order parabola, the reasonable range of the parameter k is 0.8~0.9 under the action of uniformly distributed dead loads. The specific value is related to the parameter n.
- (2)
- Once the reasonable lifting points are determined, the tension force in the temporary horizontal rods can be quickly determined by using the theoretical formula provided in this study. By using the recommended lifting point positions and temporary horizontal tension force, the horizontal displacement and rotation angle at the end of the lifted arch segment can be controlled at around 0 simultaneously, and the bending moments at the vault and lifting points can be maintained within relatively low ranges and at similar values. The axial force of the arch rib is also within a reasonable range.
- (3)
- In the whole lifting process of the middle arch segment of Shunjiang Bridge, the lifting point parameter k was set as 0.815 based on the proposed analytical control method, and the tension force of the temporary horizontal tie rod was further determined through the finite element analysis. On-site monitoring indicates that the deformation and stress distributions of the main arch during the overall lifting process are effectively controlled. The methods proposed in this paper provide direct and effective guidance for steel arch bridge construction using the overall lifting construction method.
5.2. Discussion
In this paper, to simplify the tension force calculation of the temporary horizontal tie rod, only the uniformly distributed dead load is considered in the analytical process. However, arch ribs often have non-uniform cross sections in practical engineering, and they also bear temperature and wind loads, causing the real-world situation to be much more complicated. Therefore, there is some deviation between the simplified conditions presented in this paper and the practical construction site. It is necessary to use the finite element method for some theoretical corrections and dynamic adjustments in the application of this technique. In the future, more complex load conditions will be considered, such as the influence of non-uniform loads and temperature fields.
Author Contributions
Conceptualization, methodology, and writing—original draft, Z.L.; software and formal analysis, X.D.; visualization, data curation, and supervision, H.C.; resources and investigation, L.C.; writing—review and editing and project administration, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the research project of Hangzhou Urban and Rural Construction Committee (No. 2023071).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Hairong Chen and Liangjun Chi were employed by the company Shaoxing Shangyu Urban Construction Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| l | Horizontal projection length of the axis of the whole lifting arch rib segment |
| f | Sagittal height of the axis of the whole lifting arch rib segment |
| n | Sub-parabolic axis shape parameter of the arch rib |
| A | Cross-sectional area of the whole lifting arch rib segment |
| E | Elastic modulus of the arch rib material |
| I | Moment of inertia of the arch rib section around the transverse bridge direction |
| k | Ratio of the horizontal distance between the two lifting points to the horizontal projected length of the arch rib |
| q | Arch rib bears a uniformly distributed vertical load |
| P | Temporary horizontal tension |
| M | Bending moment |
| N | Axial force |
References
- Xie, K.; Wang, H.; Guo, X.; Zhou, J. Study on the safety of the concrete pouring process for the main truss arch structure in a long-span concrete-filled steel tube arch bridge. Mech. Adv. Mater. Struct. 2019, 6, 731–740. [Google Scholar] [CrossRef]
- Chen, B.C.; Liu, J.P. Review of construction and technology development of arch bridges in the world. J. Traffic Transp. Eng. 2020, 20, 27–41. (In Chinese) [Google Scholar]
- Qi, L.; Zhao, Y.Y. Stress optimization analysis of long-span concrete-flled steel tube arch bridge based on midas full-bridge fnite element analysis model. Proc. Indian Natl. Sci. Acad. 2023, 89, 267–278. [Google Scholar] [CrossRef]
- Zheng, J.L.; Wang, J.J. Concrete-flled steel tube arch bridges in China. Engineering 2018, 4, 143–155. [Google Scholar] [CrossRef]
- Sun, J.; Li, J.; Jiang, Y.; Ma, X.; Tan, Z.; Zhufu, G. Key construction technology and monitoring of long-span steel box tied arch bridge. Int. J. Steel Struct. 2023, 23, 191–207. [Google Scholar] [CrossRef]
- Feng, Y.; Qi, J.; Wang, J.; Zhang, W.; Zhang, Q. Rotation construction of heavy swivel arch bridge for high-speed railway. Structures 2020, 26, 755–764. [Google Scholar] [CrossRef]
- Shi, Y.C. Theoretical Analysis and Model Test Study on Integral Lifting of Six Thousands Tons’ Steel Box Arch Bridge. Master’s Dissertation, Southwest Jiaotong University, Chengdu, China, 2018. [Google Scholar]
- Ruan, R.; Lai, M.; Jiang, C.; Wang, J.; Lin, Y. Integral Lifting of Steel Structure Corridor between Two Super High-Rise Buildings under Wind Load. Buildings 2023, 13, 2441. [Google Scholar] [CrossRef]
- Li, G.; Mo, T.; Xu, N.; Zhang, W.; Lu, H.; Deng, D. Improvement of overall lifting construction technology of large span steel structure hangar. In Proceedings of the 2nd International Conference on Internet of Things and Smart City, Xiamen, China, 18–20 February 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12249, pp. 923–928. [Google Scholar] [CrossRef]
- Zhou, G.J. Construction technology of main bridge superstructure of Cuijiaying Hanjiang river bridge on Han-Shi High-speed railway. World Bridges 2021, 49, 10314. (In Chinese) [Google Scholar]
- Wang, J.F.; Xiang, H.W.; Zhang, J.T.; Wu, T.M.; Xu, R.Q. Geometric state transfer method for construction control of a large-segment steel box girder with hoisting installation. J. Zhejiang Univ.-Sci. A 2020, 21, 382–391. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, W. Lift planning and optimization in construction: A thirty-year review. Autom. Constr. 2020, 118, 103271. [Google Scholar] [CrossRef]
- Song, W.H. Study on Mechanical Performance and Key Issues of Long-span Steel Box Arch Bridge During Integral Lifting and Incremental Launching Construction. Master’s Dissertation, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Zheng, J. Recent Construction Technology Innovations and Practices for Large-Span Arch Bridges in China. Engineering 2024, 41, 110–129. [Google Scholar] [CrossRef]
- Nassiraei, H. Probabilistic Analysis of Strength in Retrofitted X-Joints under Tensile Loading and Fire Conditions. Buildings 2024, 14, 2105. [Google Scholar] [CrossRef]
- Wen, F.; Liang, X.; Chen, C.; Xu, L.; Feng, Q. Construction Control and Monitoring Platform of a Large-Segment Steel Box Girder with Hoisting Installation. Appl. Sci. 2023, 13, 9573. [Google Scholar] [CrossRef]
- Miao, X.; Yuan, A.; Wang, X.; Chen, Q. Arch First and Beam Later Technology: An Accelerated and Safe Construction for Tied Arch Bridges. Struct. Eng. Int. 2024, 1–9. [Google Scholar] [CrossRef]
- Xiang, H.; Xia, D.; Wang, S.; Zhang, Z.; Luo, S.; Chen, W. Stress and deformation analysis of the steel pipe arch integral lifting construction process of a continuous beam arch bridge. Sci. Rep. 2024, 14, 10314. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.Q. Theory and Practice of Stress-Free-State Control Method; People’s Communications Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Qin, S.Q. Stress-free-state control method for bridges constructed in stages bridge construction. Bridge Constr. 2008, 1, 8–14. (In Chinese) [Google Scholar]
- Qin, S.; Wei, K.; Qin, J.; Yuan, R.; Xu, L.; Dan, Q. Stress-free-state based structural analysis and construction control theory for staged construction bridges. Adv. Bridge Eng. 2020, 1, 1. [Google Scholar] [CrossRef]
- Du, M.; Tang, H.; Xue, X.; Wang, H.; Wu, G.; Gao, Q. Intelligent control method of large-span arch bridge based on stress-free state. In Proceedings of the International Conference on Mathematics and Machine Learning, Nanjing, China, 24–26 November 2023; pp. 287–291. [Google Scholar] [CrossRef]
- Wei, S.Y.; Gong, W.F.; Wu, X.G.; Zhang, Z.H. Nonlinear Stress-Free-State Forward Analysis Method of Long-Span Cable-Stayed Bridges Constructed in Stages. Buildings 2023, 13, 1735. [Google Scholar] [CrossRef]
- Xanthakos, P.P. Theory and Design of Bridges; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Strydom, J.H.; Elvin, A. Optimizing the design of steel bridges using the principle of virtual work. In Insights and Innovations in Structural Engineering, Mechanics and Computation; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- JTG D64-2015; Industry Standards of the People’s Republic of China. Code for Design of Highway steel Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).