Bending Performance of Steel-Reinforced Concrete Beams Strengthened with Highly Ductile Cementitious Composites in the Compression Zone
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
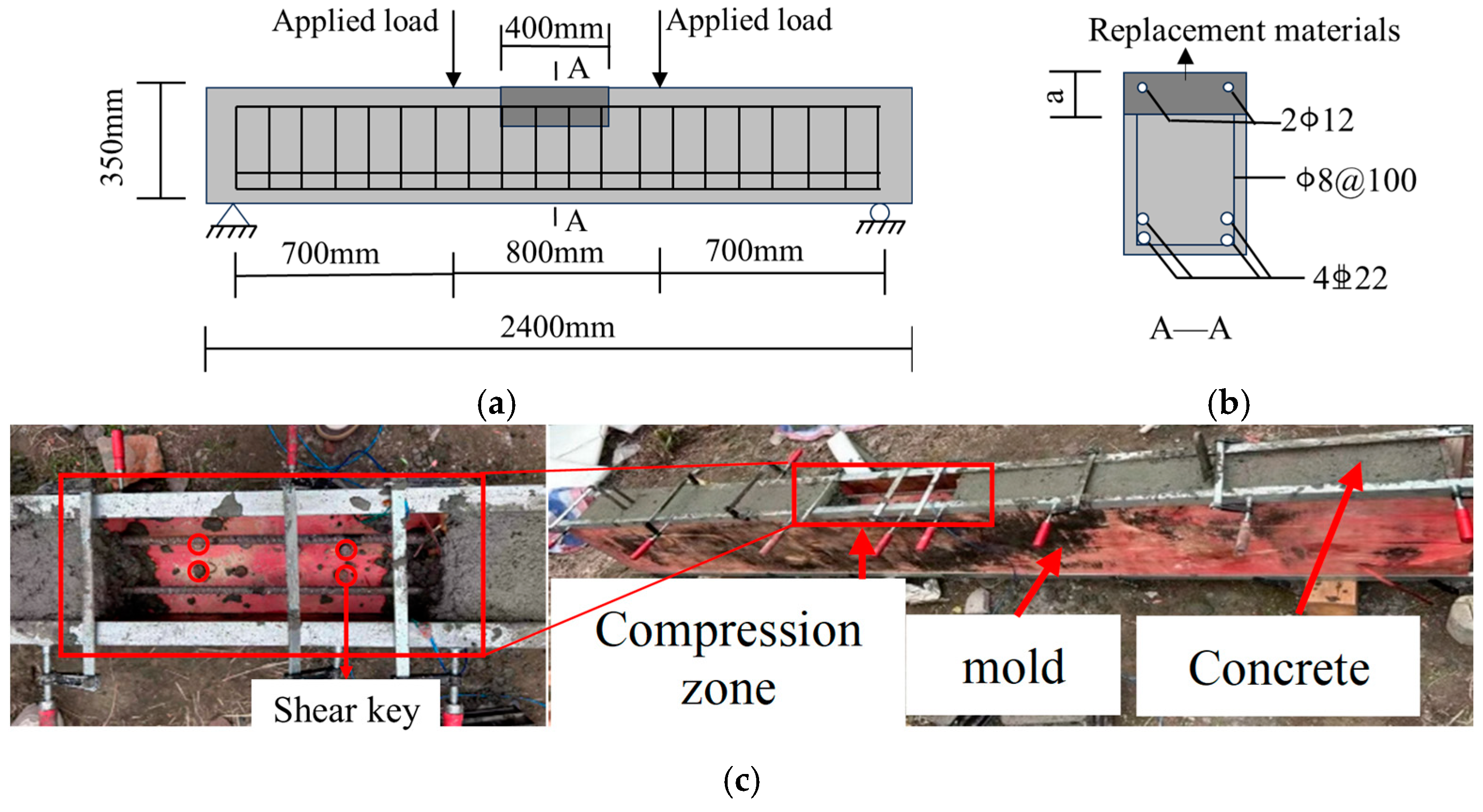
2.2. Preparation of Steel-Reinforced Concrete Beams
2.3. Four-Point Bending Test
3. Results and Discussion
3.1. Failure Mode
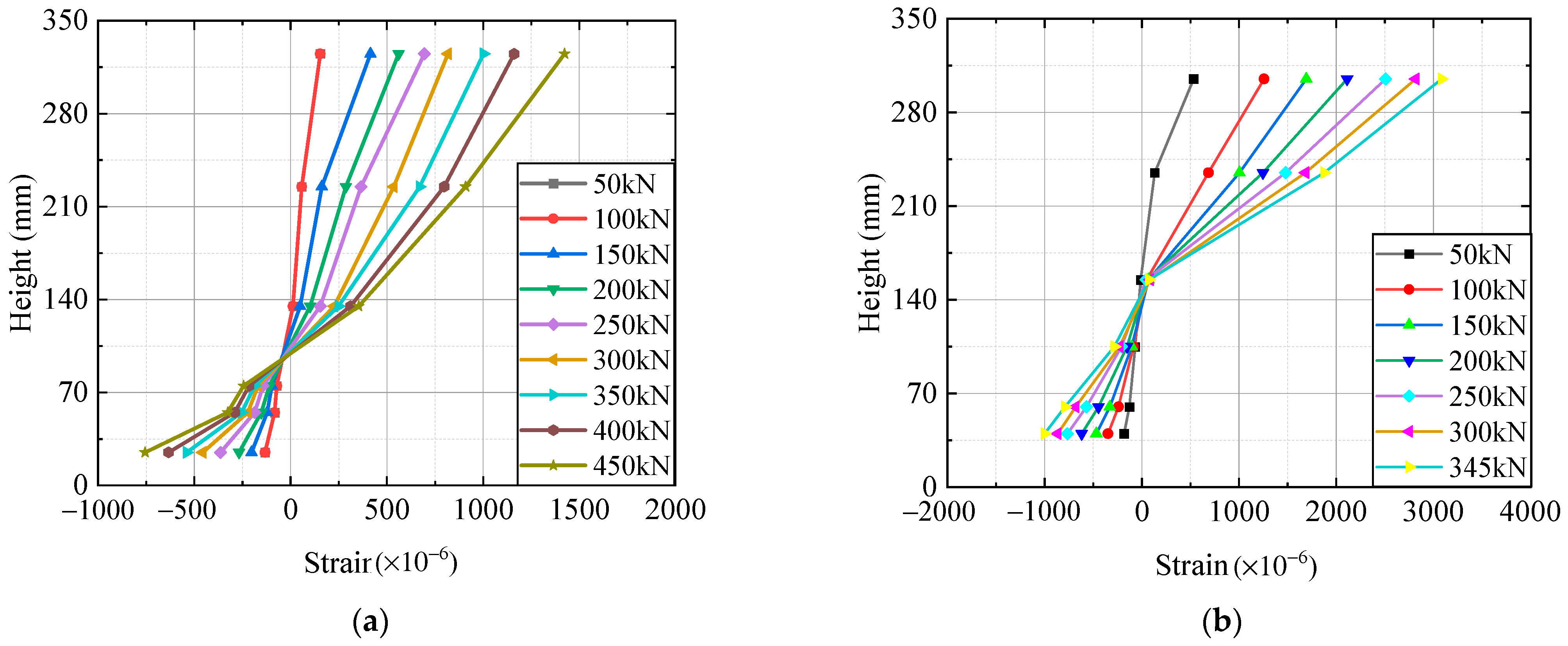
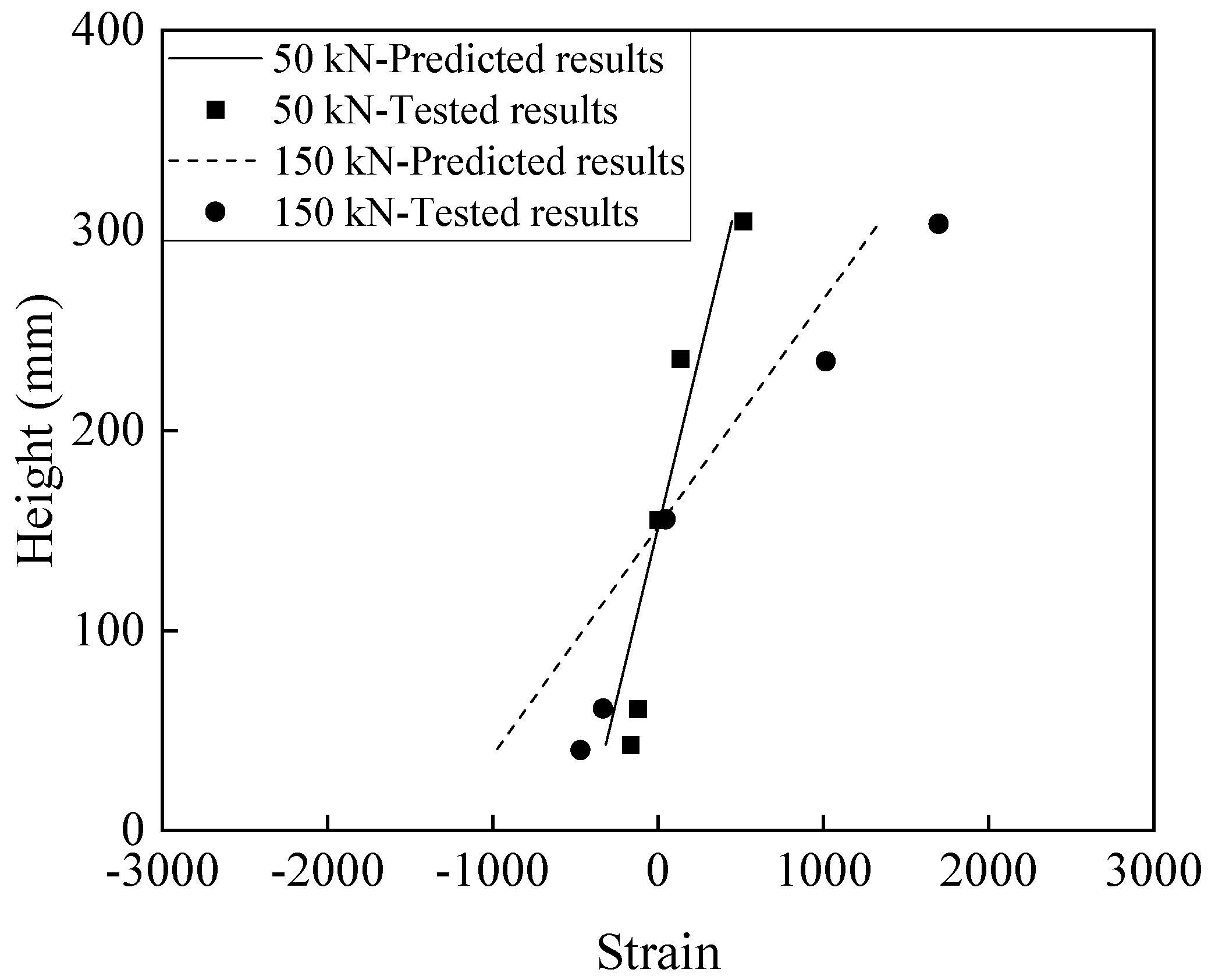
3.2. Cross-Section Strain Distribution
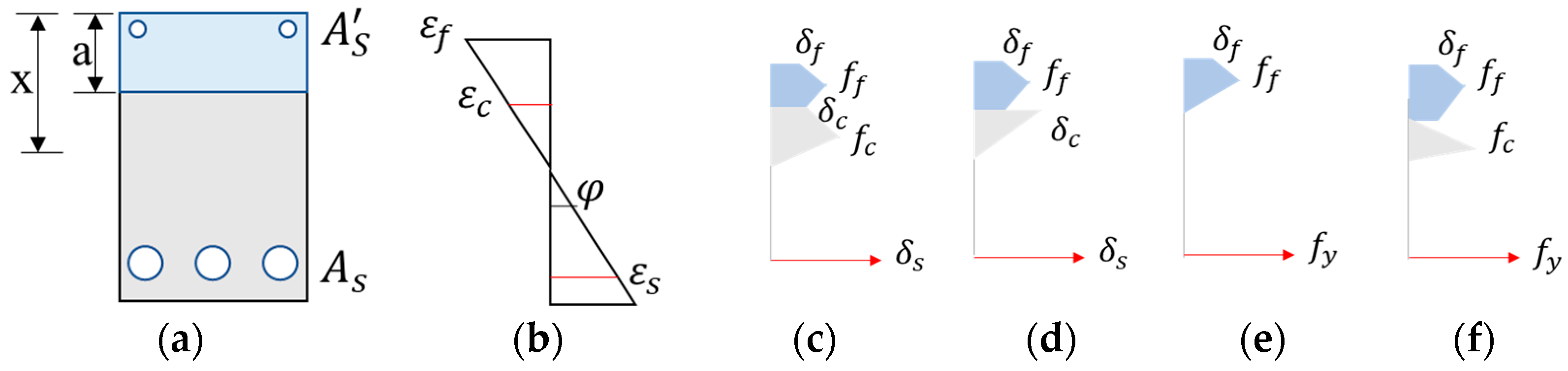
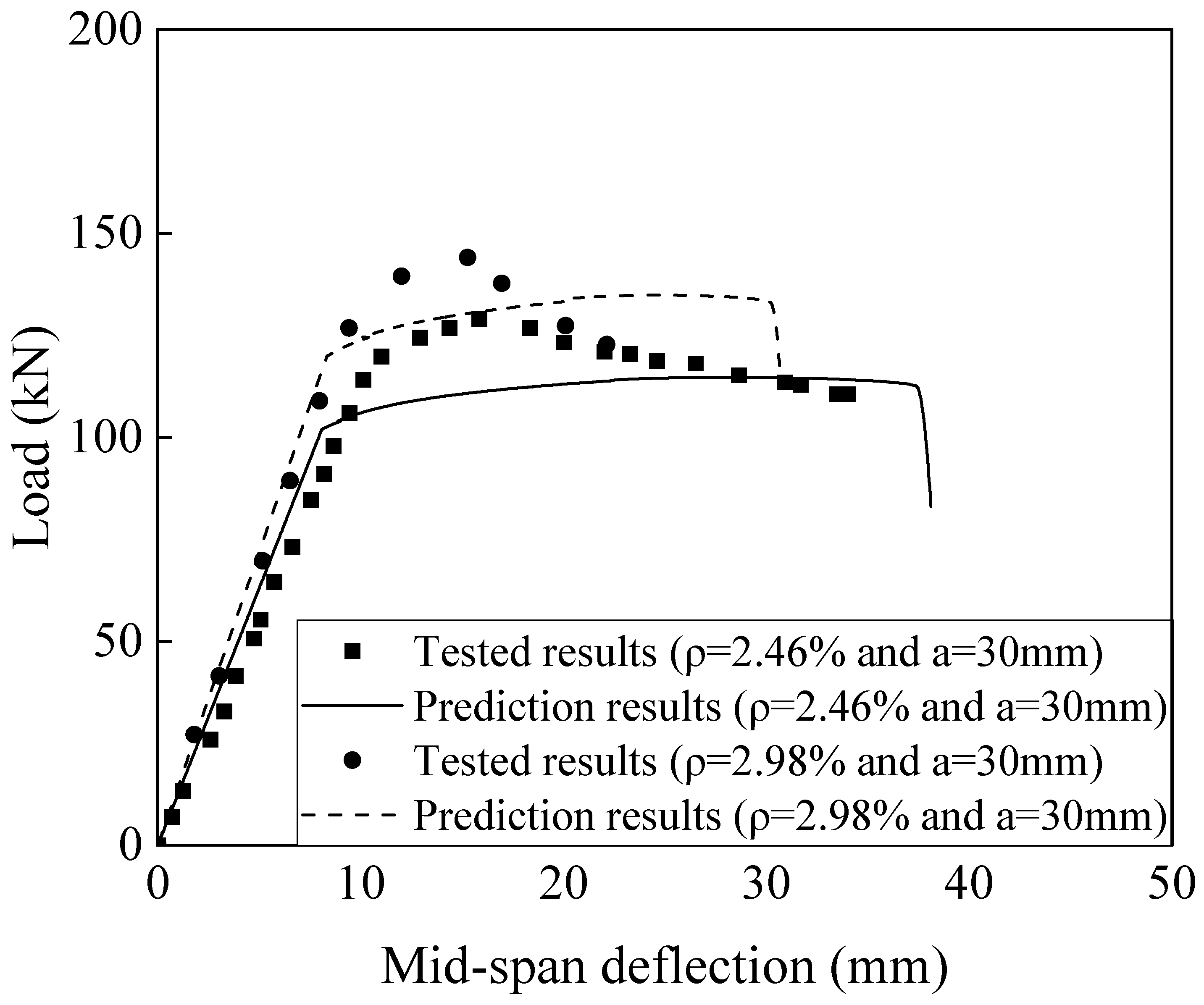
3.3. Theoretical Analysis
3.4. Parametric Analysis
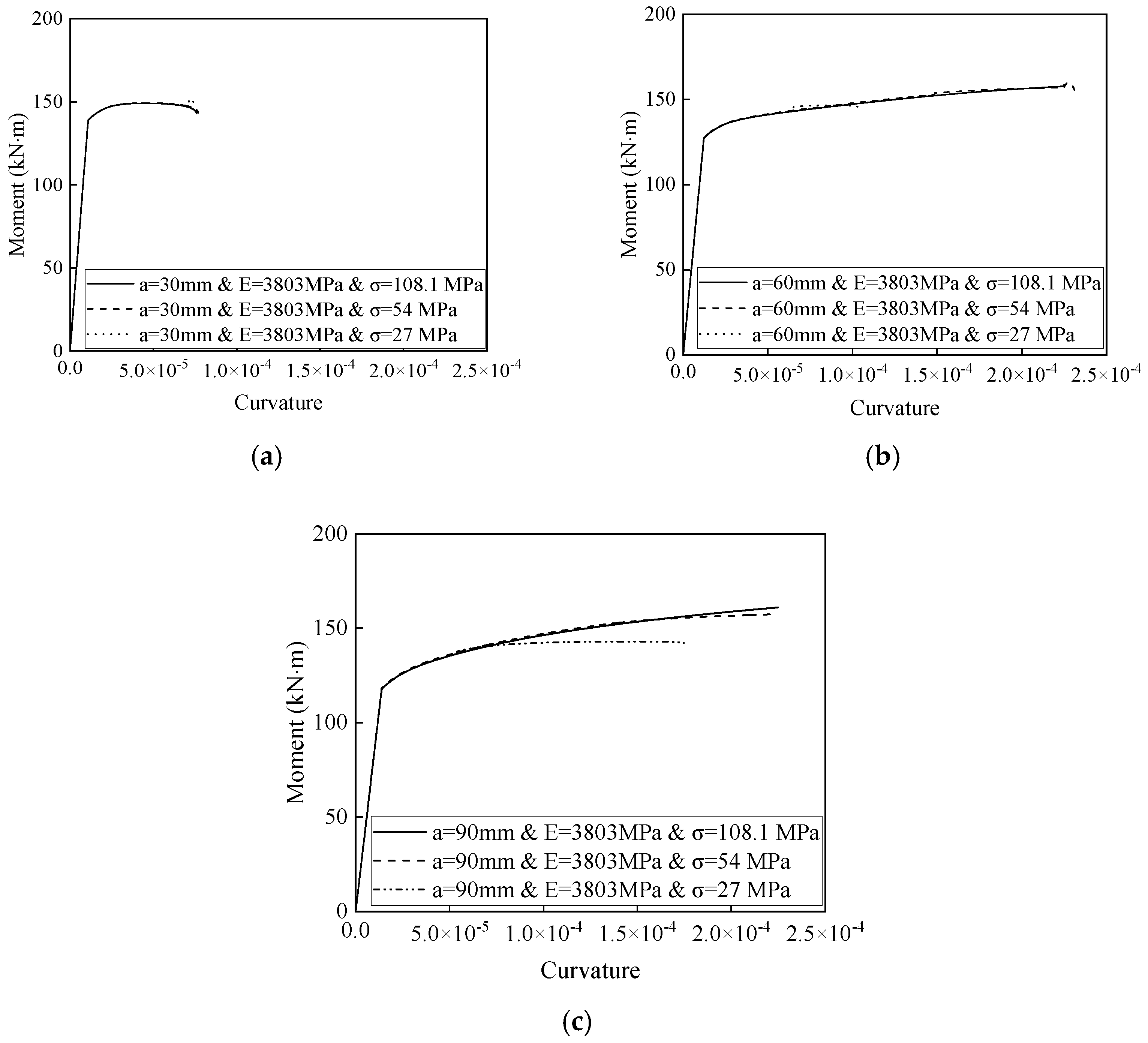
3.4.1. Effects of the Compressive Strength of Materials in the Compressed Zone on the Moment–Curvature Curves
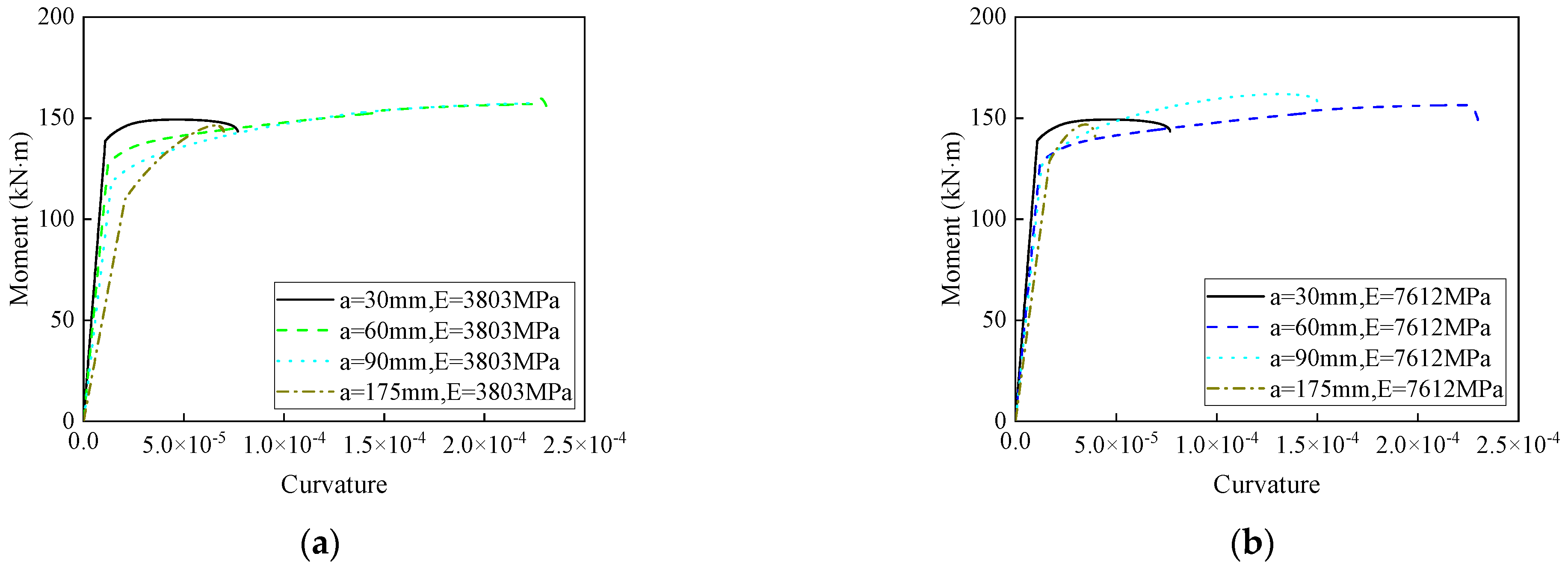
3.4.2. Effects of the Height of the Replacement Material in the Compressed Zone on the Moment–Curvature Curves
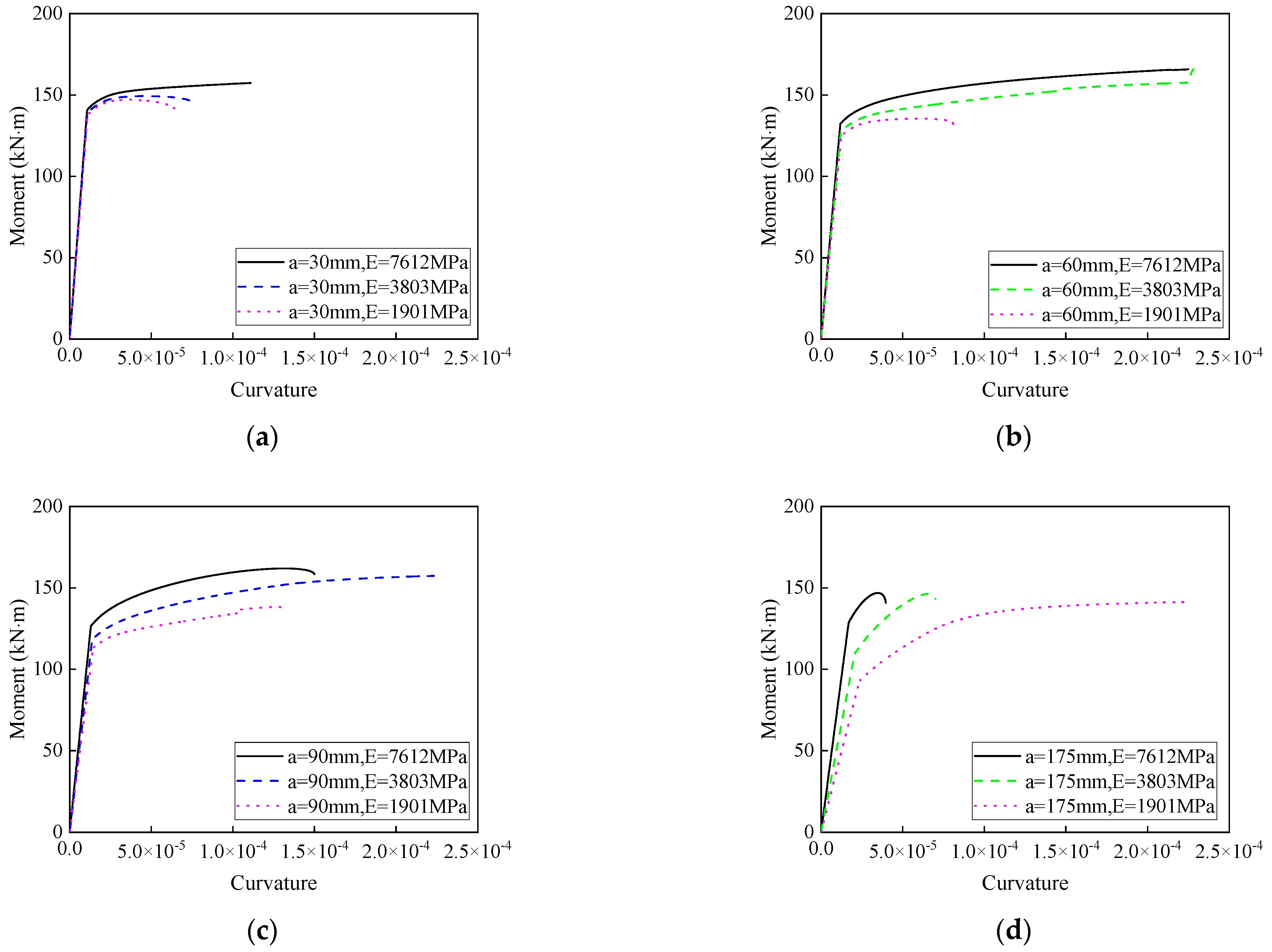
3.4.3. Effects of the Elastic Modulus of the Materials in the Compressed Zone on the Moment–Curvature Curves
4. Conclusions
- Replacing concrete with SIFCON retains the linear strain distribution across the beam height, aligning with the plane section assumption. It was proven that the bending performance can be calculated using the strip method.
- The proposed theoretical formulas effectively predict the mechanical performance of beams strengthened with highly ductile cementitious composites. The parametric analysis indicates that the curvature is more sensitive to the material height, modulus, and strength than the maximum moment.
- The compressive strength of the materials in the compression zone does not affect the initial stiffness of the moment–curvature curves. Increased material height and strength lead to higher maximum moments and ultimate curvatures.
- Increasing the material’s elastic modulus raises the maximum curvature. At a height of 60 mm, the curvature improves by up to 177%.
- As the compression zone height increases, the maximum curvature rises. For a material modulus of 3803 MPa, the curvature increases by up to 192%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, M.; Xu, W.; Wang, J.; Chen, Y.; Du, X.; Fang, R.; Huang, X.; Sun, H. Plastic hinge regions of prefabricated concrete columns with grouted sleeves and simplified calculation method for plastic hinge length. Structures 2022, 43, 710–725. [Google Scholar] [CrossRef]
- Duhaim, H.M.; Mashrei, M.A. The effect of using steel fibers reinforced concrete layer in compression zone on the flexural behavior of over-reinforced concrete beams. Struct. Concr. 2024, 25, 456–472. [Google Scholar] [CrossRef]
- Lu, Z.; Su, L.; Xian, G.; Lu, B.; Xie, J. Durability study of concrete-covered basalt fiber-reinforced polymer (BFRP) bars in marine environment. Compos. Struct. 2020, 234, 111650. [Google Scholar] [CrossRef]
- Xian, G.; Zhou, P.; Li, C.; Dong, S.; Du, H.; Tian, J.; Guo, R.; Peng, Z.; Zhang, Z.; He, T. Mechanical properties evaluation of glass fiber reinforced thermoplastic composite plate under combined bending loading and water immersion. Constr. Build. Mater. 2024, 440, 137470. [Google Scholar] [CrossRef]
- Wu, G.; Wang, X.; Wu, Z.; Dong, Z.; Zhang, G. Durability of basalt fibers and composites in corrosive environments. J. Compos. Mater. 2015, 49, 873–887. [Google Scholar] [CrossRef]
- Wu, Y.F. Ductility demand of compression yielding fiberreinforced polymer-reinforced concrete beams. ACI Struct. J. 2008, 105, 104. [Google Scholar]
- Wang, B.; Cui, C.; Xu, C.; Meng, K.; Li, J.; Xu, L. A novel analytical solution for horizontal vibration of partially embedded offshore piles considering the distribution effect of wave loads. Ocean Eng. 2024, 307, 118179. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Zhou, Y.-W.; He, X.-Q. Performance-based optimal design of compression-yielding FRP-reinforced concrete beams. Compos. Struct. 2010, 93, 113–123. [Google Scholar] [CrossRef]
- Shi, J.; Qin, T.; Zhou, J.; Zhao, H.; Wang, H.; Fu, J.; Jin, L. Interlaminar shear behavior of basalt fiber-reinforced polymer tendons subjected to a combined effect of prestress, grout and seawater. Constr. Build. Mater. 2025, 462, 139982. [Google Scholar] [CrossRef]
- Shoji, D.; He, Z.; Zhang, D.; Li, V.C. The greening of engineered cementitious composites (ECC): A review. Constr. Build. Mater. 2022, 327, 126701. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Asgarkhani, N.; Yoo, D.-Y. Machine-learning methods for estimating compressive strength of high-performance alkali-activated concrete. Eng. Appl. Artif. Intell. 2024, 136, 109053. [Google Scholar] [CrossRef]
- Xue, J.; Mao, S.; Cacciola, P.; Contento, A.; Lampropoulos, A.; Nicolaides, D.; Petrou, M.F.; Yang, Z.; Briseghella, B. Experimental evaluation of the effectiveness of fiber orientation methods on the mechanical performance of UHPFRC. Constr. Build. Mater. 2024, 448, 138184. [Google Scholar] [CrossRef]
- Curosu, I.; Mechtcherine, V.; Forni, D.; Cadoni, E. Performance of various strain-hardening cement-based composites (SHCC) subject to uniaxial impact tensile loading. Cem. Concr. Res. 2017, 102, 16–28. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Liu, X.; Zhang, Y.; Wang, C. Reusing waste glass fines to substitute cement and sand for recycled ultra-high performance strain-hardening cementitious composites (UHP-SHCC). Constr. Build. Mater. 2024, 455, 139186. [Google Scholar] [CrossRef]
- Kobayashi, K.; Le Ahn, D.; Rokugo, K. Effects of crack properties and water-cement ratio on the chloride proofing performance of cracked SHCC suffering from chloride attack. Cem. Concr. Compos. 2016, 69, 18–27. [Google Scholar] [CrossRef]
- Ali, M.H.; Atiş, C.D.; Al-Kamaki, Y.S.S. Mechanical properties and efficiency of SIFCON samples at elevated temperature cured with standard and accelerated method. Case Stud. Constr. Mater. 2022, 17, e01281. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Lv, J.; Liu, Y.; Li, H.; Mu, F. Uniaxial compression performance of SIFCON with the arc-shaped steel fibers. J. Build. Eng. 2025, 100, 111678. [Google Scholar] [CrossRef]
- Ding, Y.; Yu J-t Yu, K.-Q.; Xu, S.-l. Basic mechanical properties of ultra-high ductility cementitious composites: From 40 MPa to 120 MPa. Compos. Struct. 2018, 185, 634–645. [Google Scholar] [CrossRef]
- Yu, K.-Q.; Yu, J.-T.; Dai, J.-G.; Lu, Z.-D.; Shah, S.P. Development of ultra-high performance engineered cementitious composites using polyethylene (PE) fibers. Constr. Build. Mater. 2019, 216, 698. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wang, D. Uniaxial compression behavior of ultra-high performance concrete with hybrid steel fiber. J. Mater. Civ. Eng. 2016, 28, 06016017. [Google Scholar] [CrossRef]
- Feng, L.; Wu, Y.-F.; Guo, B.-C.; Huang, X.-X. Reducing target reliability index of concrete bridge beams through compression yielding. Eng. Struct. 2024, 316, 118506. [Google Scholar] [CrossRef]
- Ziara, M.M.; Haldane, D.; Kuttab, A.S. Flexural behavior of beams with confinement. ACI Struct. J. 1995, 92, 103–114. [Google Scholar]
- Yuan, F.; Pan, J.; Leung, C.K.Y. Flexural behaviors of ECC and concrete/ECC composite beams reinforced with basalt fiber-reinforced polymer. J. Compos. Constr. 2013, 17, 591–602. [Google Scholar] [CrossRef]
- Atta, A.M.; Khalil, A.E.-H. Improving the failure mode of over-reinforced concrete beams using strain-hardening cementitious composites. J. Perform. Constr. Facil. 2016, 30, 04016003. [Google Scholar] [CrossRef]
- Shen, X.; Li, B.; Shi, W.; Chen, Y.-T. Numerical study on flexural behaviour of FRP reinforced concrete beams with compression yielding blocks. Case Stud. Constr. Mater. 2022, 17, e01169. [Google Scholar] [CrossRef]
- Deng, M.; Zhang, M.; Zhu, Z.; Ma, F. Deformation capacity of over-reinforced concrete beams strengthened with highly ductile fiber-reinforced concrete. Structures 2021, 29, 1861–1873. [Google Scholar] [CrossRef]
- Balaji, S.; Thirugnanam, G. Behaviour of reinforced concrete beams with SIFCON at various locations in the beam. KSCE J. Civ. Eng. 2018, 22, 161–166. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Pan, Y.; Ng, P.L.; Leung, C.K.Y.; Zhao, X. Compressive properties of a novel slurry-infiltrated fiber concrete reinforced with arc-shaped steel fibers. J. Zhejiang Univ.-Sci. A 2023, 24, 543–556. [Google Scholar] [CrossRef]
- GB/T 50010-2010; Code for Design of Concrete Structures. China Standard Publishing House: Beijing, China, 2010.
- GB/T 28900-2022; Test Methods of Steel for Reinforcement of Concrete. State Administration for Market Regulation: Beijing, China, 2022.
- Su, M.; Gong, S.; Liu, Y.; Peng, H. Flexural behavior of RC beams strengthened with fully or partially prestressed near-surface mounted FRP strips: An experimental investigation. Eng. Struct. 2022, 262, 114345. [Google Scholar] [CrossRef]


| Grade | Water (kg/m3) | Cement (kg/m3) | Coarse Aggregate (kg/m3) | Fine Aggregate (kg/m3) | 28-Day Compressive Strength (MPa) |
|---|---|---|---|---|---|
| C50 | 205 | 488 | 1195 | 562 | 54.7 |
| Grade | Water | Cement | Fly Ash | Silica Fume | Fine Sand | Superplasticizer | Steel Fibers (%) |
|---|---|---|---|---|---|---|---|
| C40 | 274 | 593 | 274 | 46 | 913 | 4.9 | 6.8 |
| Type | Length (mm) | Diameter (mm) | Aspect Ratio | Tensile Strength (MPa) | Density (kg/m3) |
|---|---|---|---|---|---|
| Hooked-end steel fibers | 30.0 | 0.50 | 60 | 1100 | 7800 |
| Type | Diameter (mm) | Elastic Modulus (GPa) | Yielding Strength (MPa) | Ultimate Strength (MPa) | Elongation at Break (%) |
|---|---|---|---|---|---|
| HRB300 | 10 | 210 | 430 | 518 | 16 |
| HRB400 | 22 | 200 | 456 | 588 | 24 |
| Specimens | Compression Zone Height (mm) | SIFCON Compressive Strength (MPa) | Ratio of Reinforcement (%) |
|---|---|---|---|
| SB-50-30 | 30 | 50 | 3.37 |
| SB-50-60 | 60 | 50 | 3.37 |
| Height (mm) | Compressive Strength (MPa) | Maximum Bending Moment (kN·m) | Ultimate Curvature (×10−4) |
|---|---|---|---|
| 30 | 108 | 149.2 | 0.76 |
| 54 | 149.3 | 0.77 | |
| 27 | 151.2 | 0.75 | |
| 60 | 108 | 175.7 | 2.3 |
| 54 | 159.9 | 2.3 | |
| 27 | 146.6 | 1.1 | |
| 90 | 108 | 161.1 | 2.3 |
| 54 | 157.4 | 2.3 | |
| 27 | 143.0 | 1.8 |
| Elastic Modulus (MPa) | Height (mm) | Maximum Bending Moment (kN·m) | Ultimate Curvature (×10−4) |
|---|---|---|---|
| 3803 | 30 | 149.2 | 0.8 |
| 60 | 159.9 | 2.3 | |
| 90 | 157.4 | 2.2 | |
| 175 | 146.4 | 0.7 | |
| 7612 | 30 | 149.2 | 0.8 |
| 60 | 156.6 | 2.3 | |
| 90 | 161.9 | 1.5 | |
| 175 | 146.9 | 0.5 |
| Height (mm) | Elastic Modulus (MPa) | Maximum Bending Moment (kN·m) | Ultimate Curvature (×10−4) |
|---|---|---|---|
| 30 | 7612 | 157.4 | 1.1 |
| 3803 | 149.3 | 0.8 | |
| 1901 | 147.1 | 0.7 | |
| 60 | 7612 | 165.8 | 0.2 |
| 3803 | 167.3 | 0.2 | |
| 1901 | 135.5 | 0.8 | |
| 90 | 7612 | 161.9 | 1.5 |
| 3803 | 157.4 | 2.2 | |
| 1901 | 138.3 | 1.3 | |
| 175 | 7612 | 146.9 | 0.4 |
| 3803 | 146.4 | 0.7 | |
| 1901 | 141.8 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Wang, J.; Chang, B.; Ma, Z.; Li, C. Bending Performance of Steel-Reinforced Concrete Beams Strengthened with Highly Ductile Cementitious Composites in the Compression Zone. Buildings 2025, 15, 510. https://doi.org/10.3390/buildings15040510
Pan Y, Wang J, Chang B, Ma Z, Li C. Bending Performance of Steel-Reinforced Concrete Beams Strengthened with Highly Ductile Cementitious Composites in the Compression Zone. Buildings. 2025; 15(4):510. https://doi.org/10.3390/buildings15040510
Chicago/Turabian StylePan, Yunfeng, Junmin Wang, Bing Chang, Zhi Ma, and Chenggao Li. 2025. "Bending Performance of Steel-Reinforced Concrete Beams Strengthened with Highly Ductile Cementitious Composites in the Compression Zone" Buildings 15, no. 4: 510. https://doi.org/10.3390/buildings15040510
APA StylePan, Y., Wang, J., Chang, B., Ma, Z., & Li, C. (2025). Bending Performance of Steel-Reinforced Concrete Beams Strengthened with Highly Ductile Cementitious Composites in the Compression Zone. Buildings, 15(4), 510. https://doi.org/10.3390/buildings15040510






