Investigation on Buckling Behaviour of Scaffold Independent Supporting System Considering Semi-Rigid Nodes
Abstract
1. Introduction
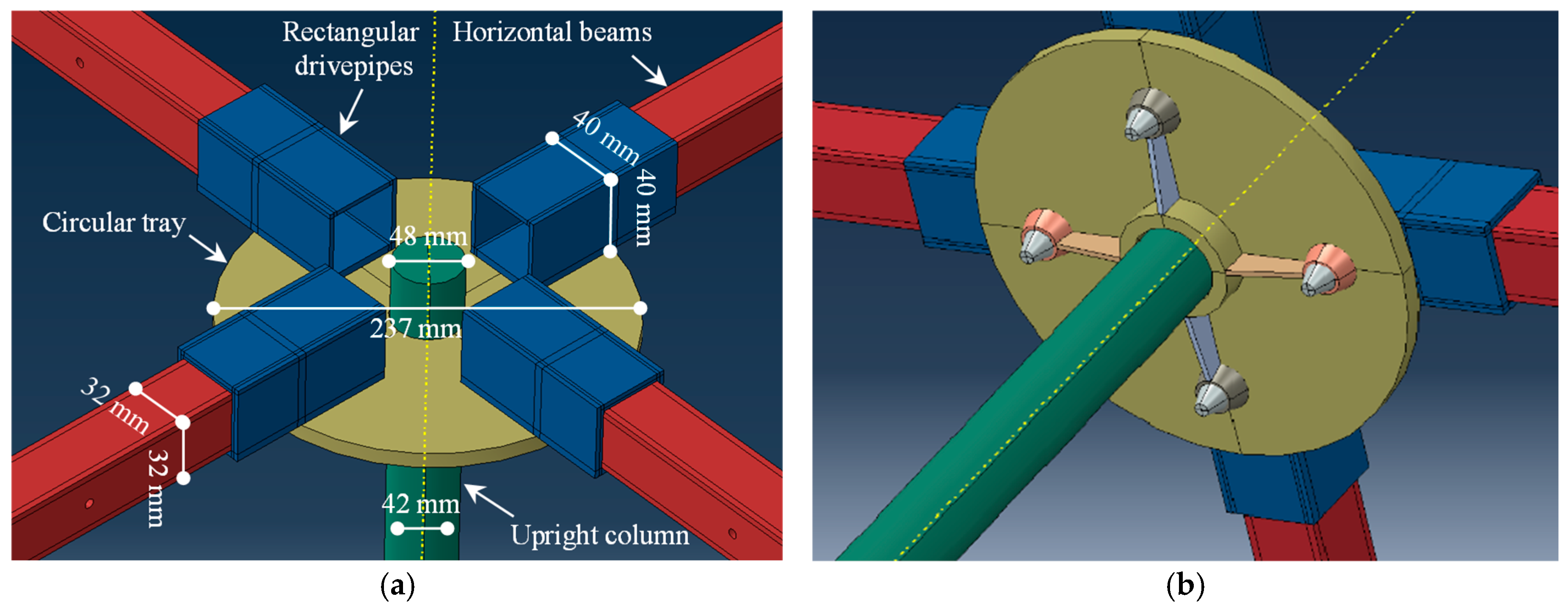
2. Description of the Scaffold Independent Supporting System
3. Analysis on the Rigidness of the Beam–Column Node
3.1. Three-Dimensional Finite Element Modeling of the Beam–Column Node
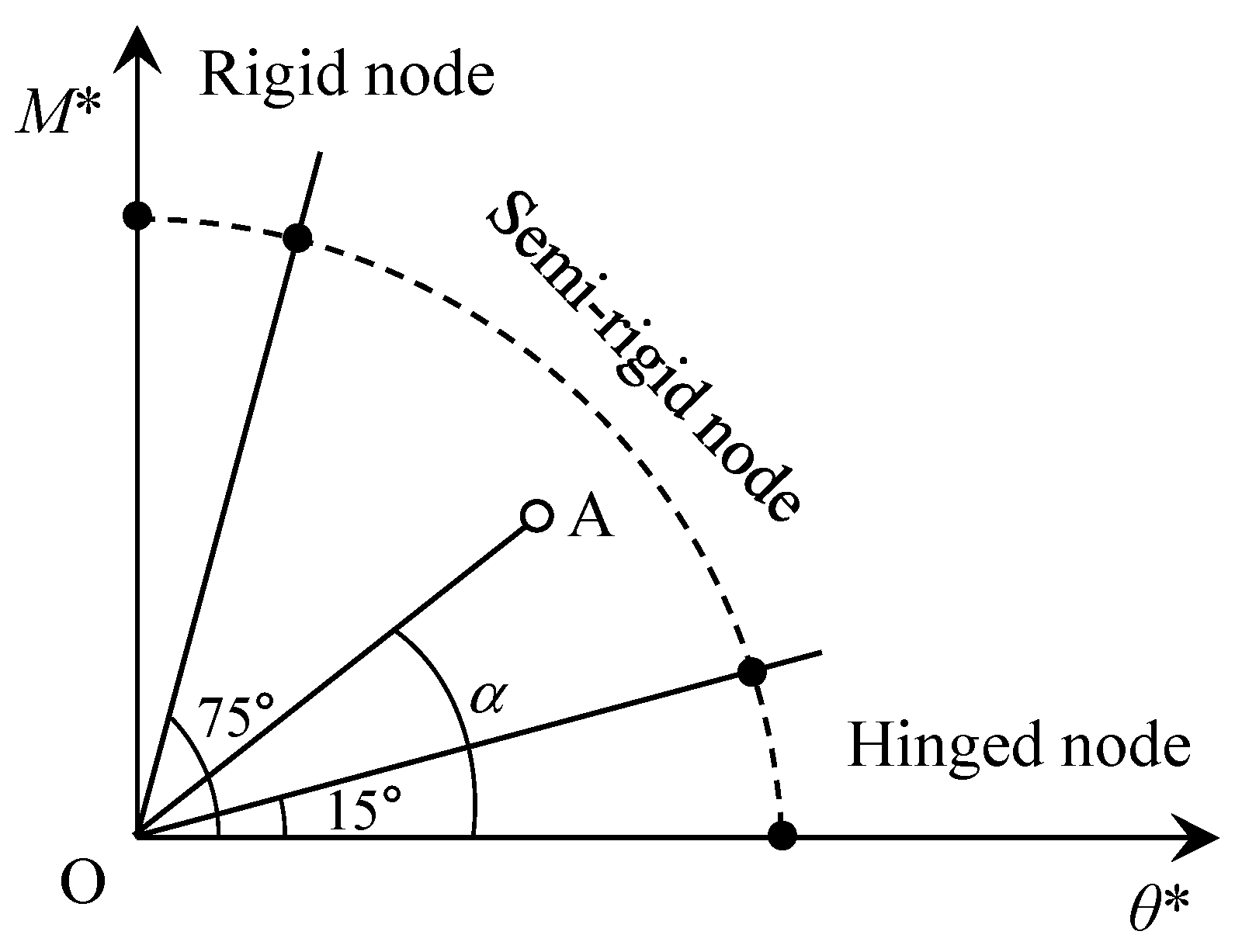
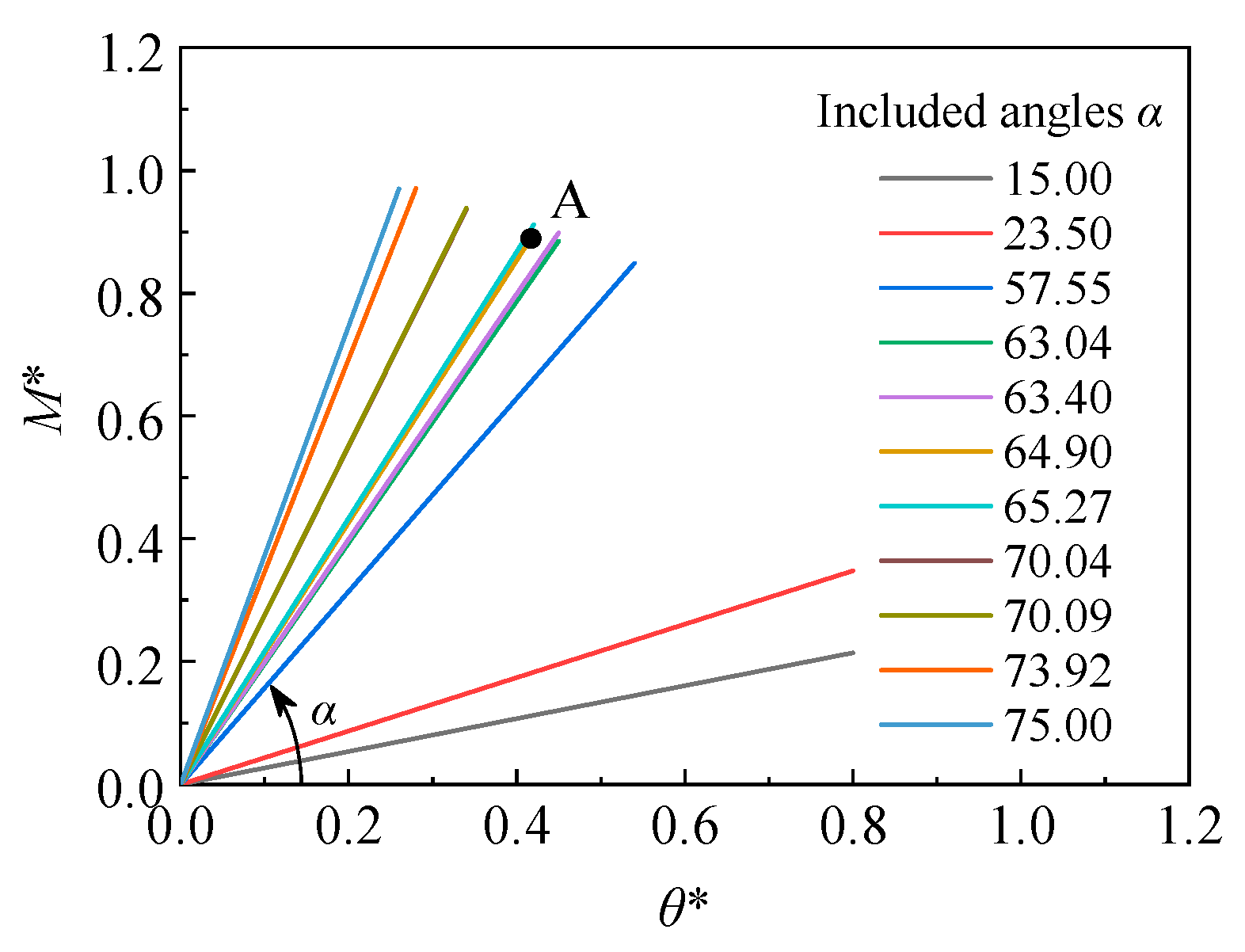
3.2. Assessing the Rigidness of the Beam–Column Node
4. Numerical Simulation of the Buckling Behaviour of the Scaffold Independent Supporting System
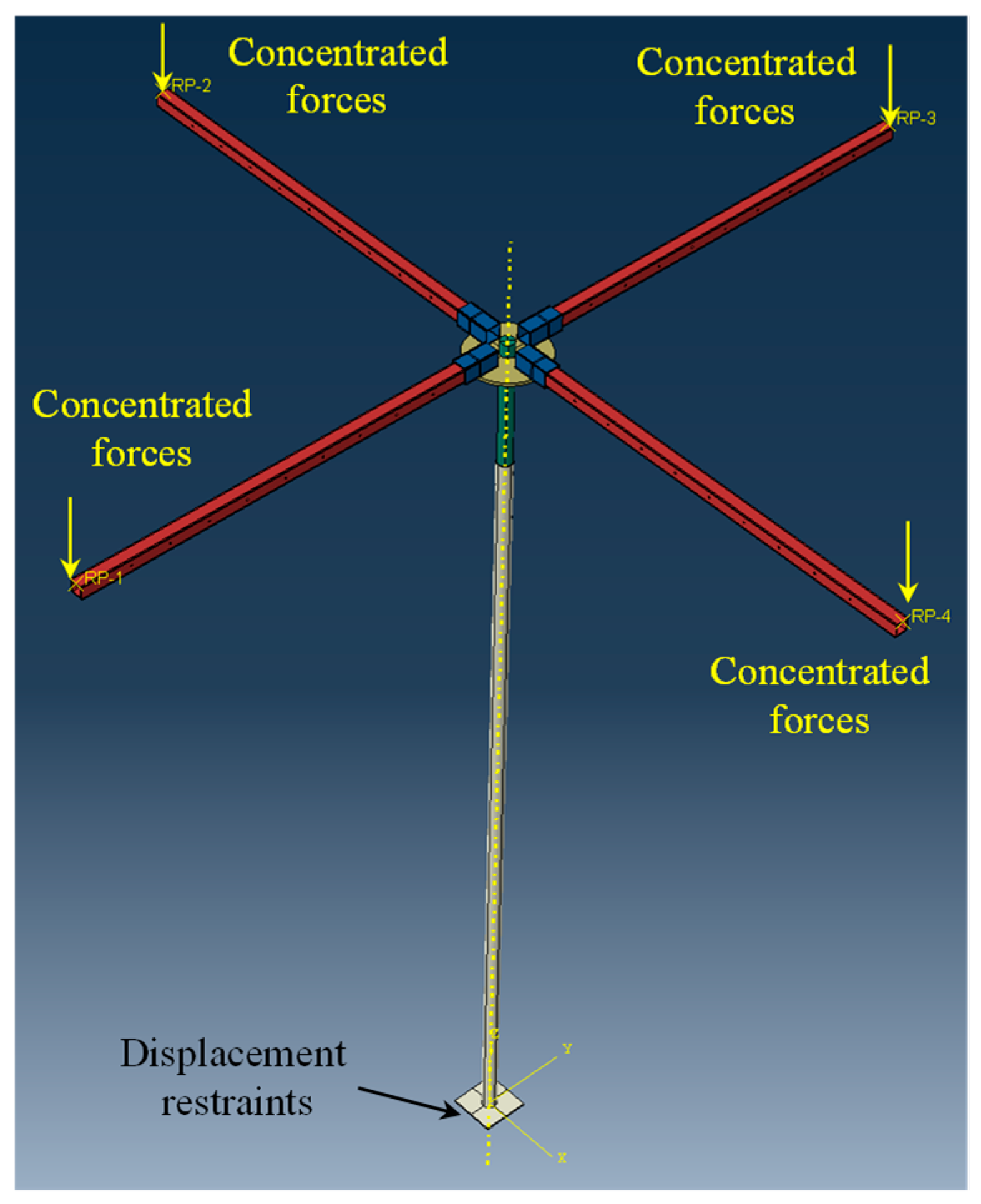
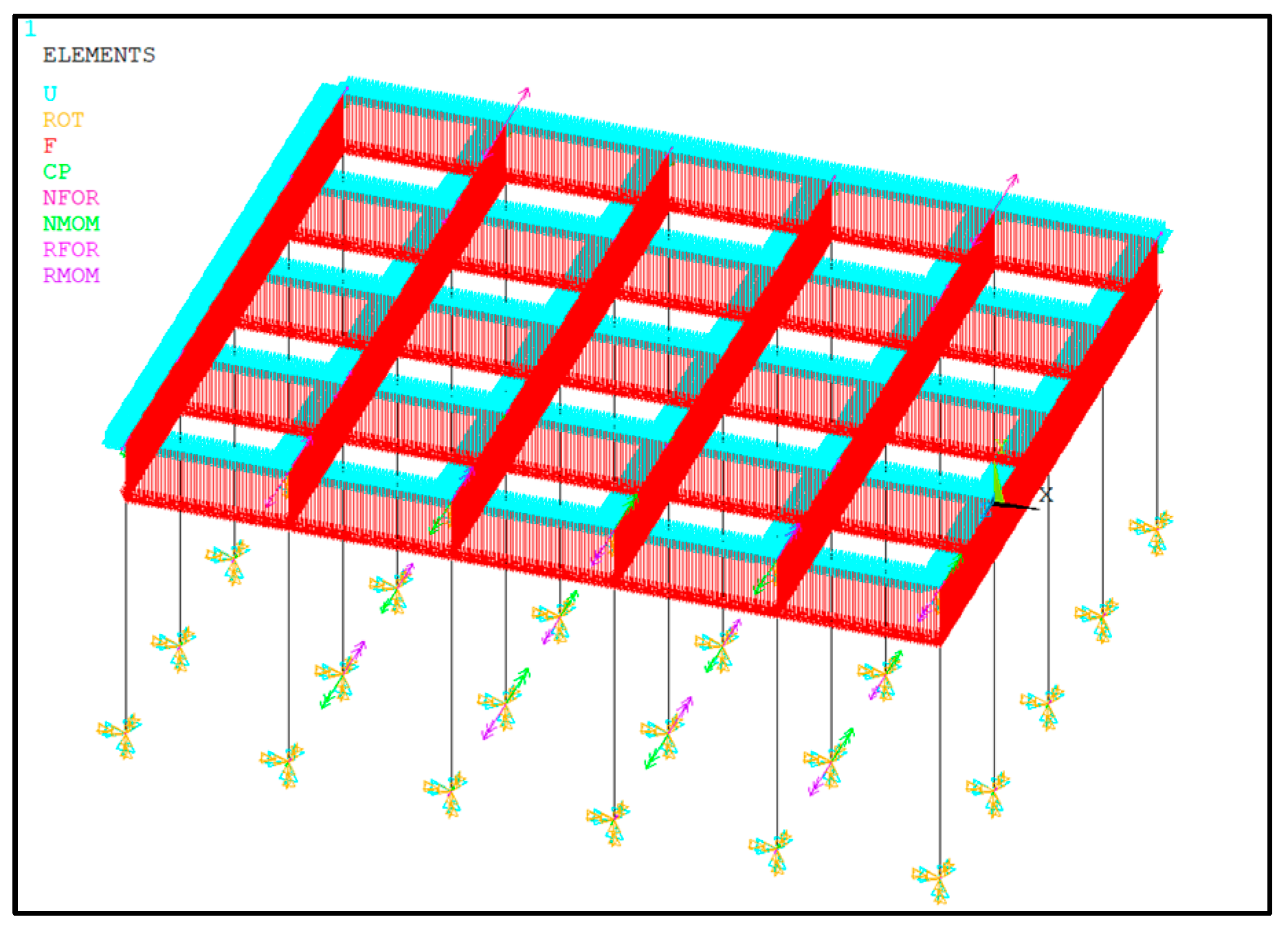
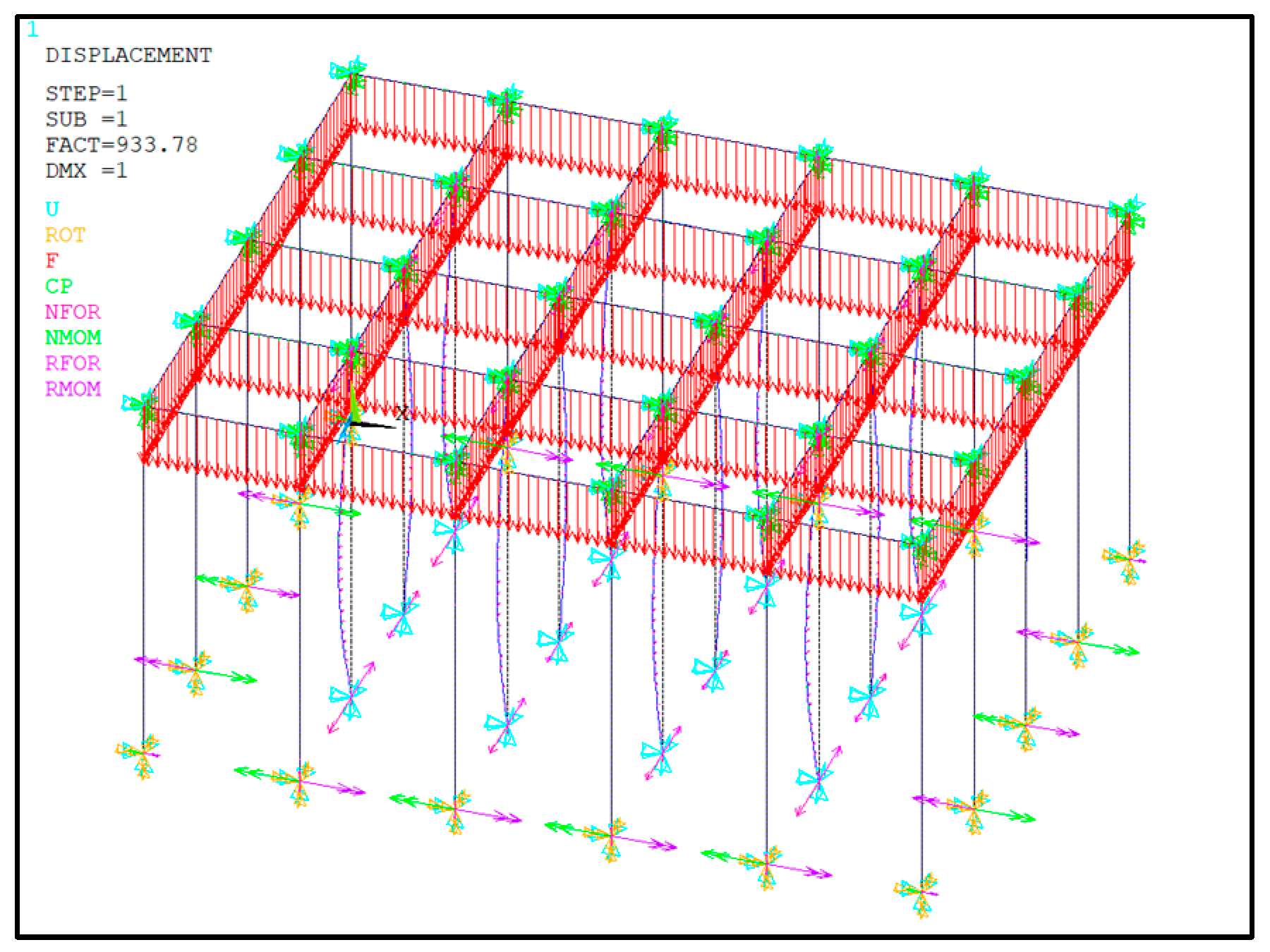
4.1. Numerical Simulation Method of the Buckling Behaviours
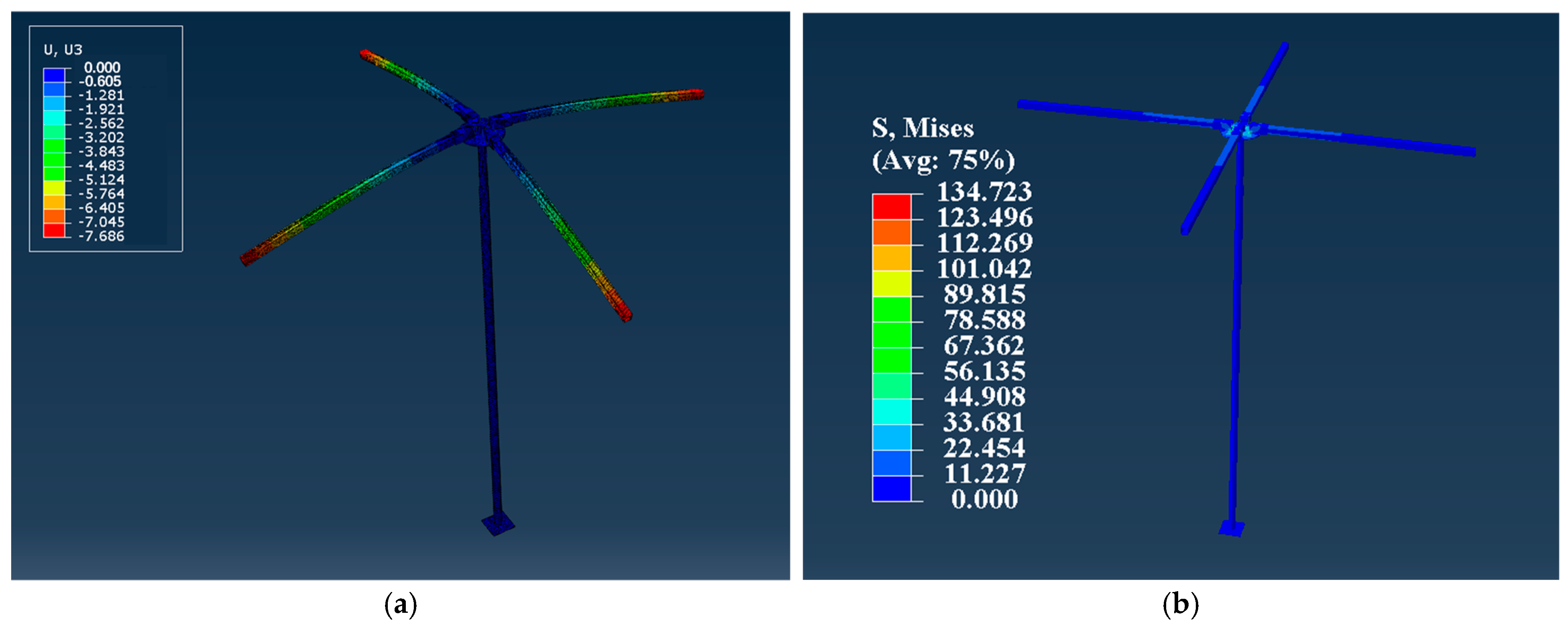
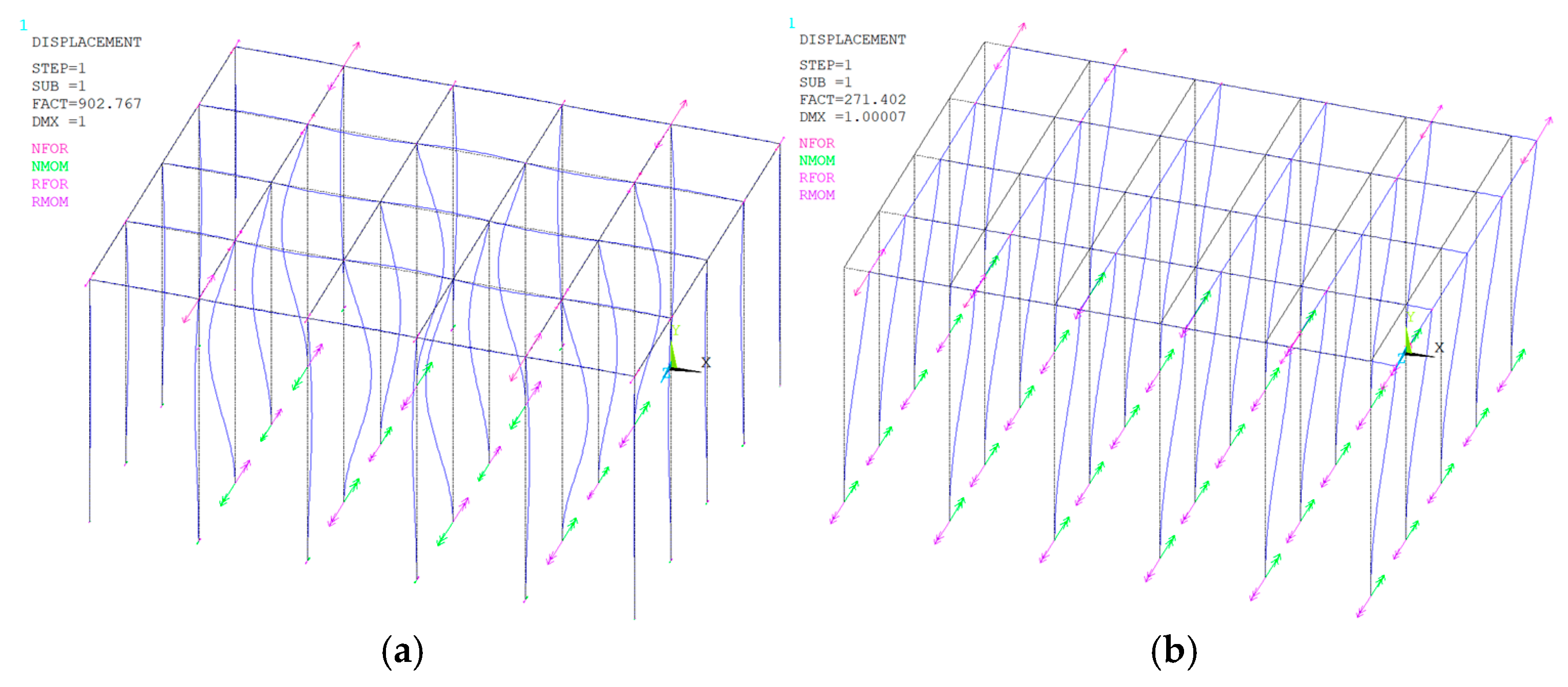
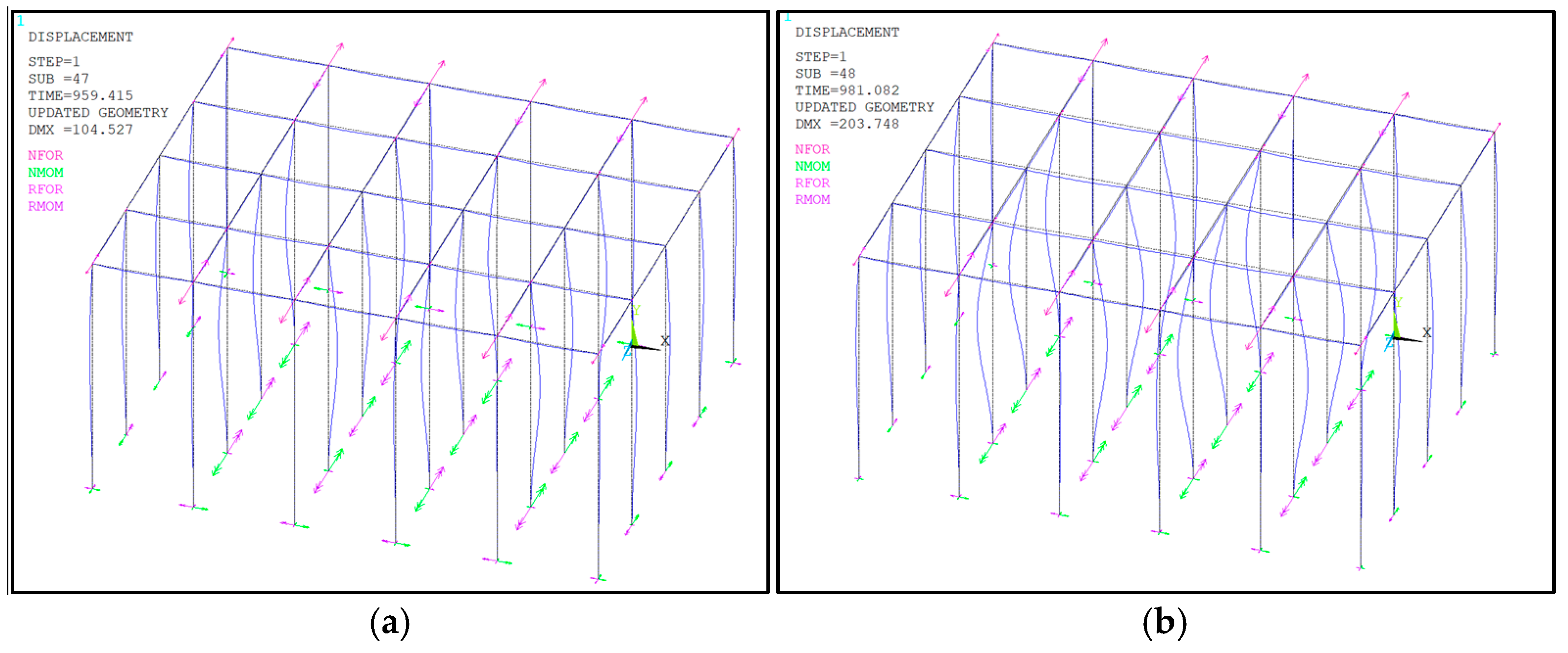
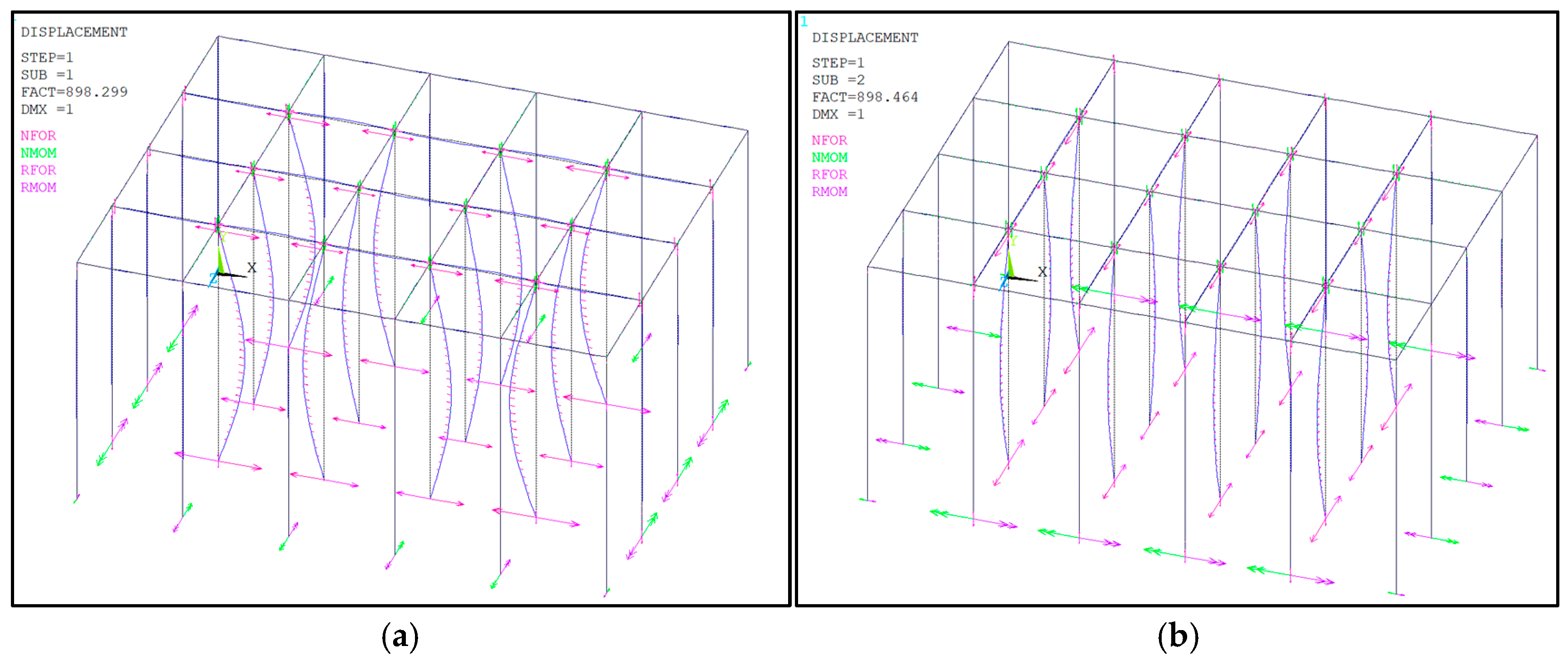
4.2. Buckling Behaviour of the Scaffold Independent Supporting System Under the Rigid Connections at All the Bottom Nodes
4.3. Buckling Behaviour of the Scaffold Independent Supporting System Under the Rigid Connections at the Bottom Side Nodes and the Hinged Connections at the Bottom Internal Nodes
5. Conclusions
- (1)
- A scaffold independent supporting system without horizontal and diagonal braces was proposed in this study. The scaffold independent supporting system consisted of horizontal beams located in the concrete formwork and upright columns, and at the beam–column nodes. The tops of the upright columns were connected by the horizontal beams to form a highly interconnected structure. There existed a lot of free space within the scaffold independent supporting system, which made it possible to conduct other operational work during the curing of concrete.
- (2)
- Finite element simulation was performed to calculate the mechanical responses at the beam-–column nodes in the scaffold independent supporting system. By establishing the refined finite element model, the mechanical response of the beam–column nodes was calculated, and the rotation stiffness of the beam–column nodes was determined as 37.18 kN·m/rad. According to the existing sorting method, the beam–column nodes in the scaffold independent supporting system were determined as semi-rigid nodes.
- (3)
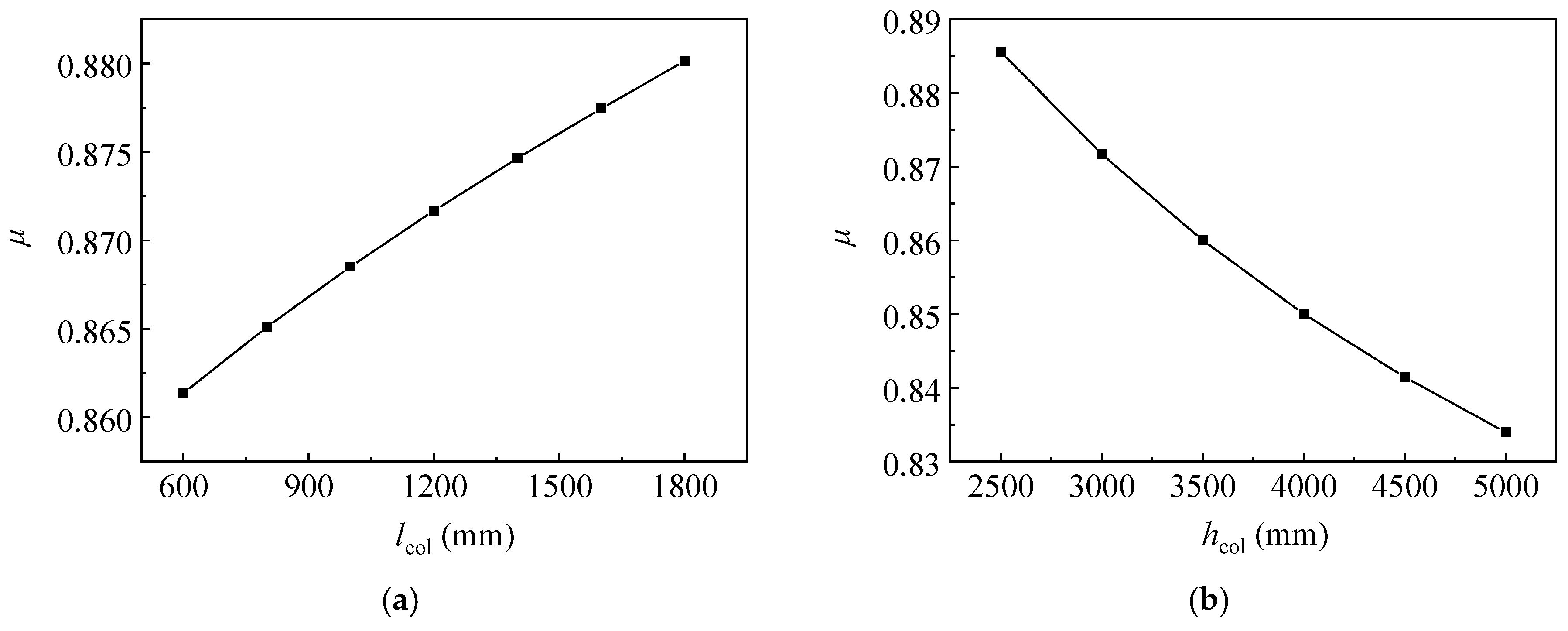
- A numerical simulation method was proposed and verified in this study to analyse the buckling behaviour of the scaffold independent supporting system, in which the semi-rigid connection was characterized by setting the spring elements at the beam–column nodes. The linear and nonlinear buckling analyses were performed to calculate the buckling behaviour of scaffold independent supporting system. It was found that the effective length factor increased with the increase in the column space, but decreased with the increase in the column height. In addition, the buckling loads under the linear and nonlinear buckling analyses had no significant differences, indicating the initial imperfections had no significant effects on the buckling behaviour.
- (4)
- It is worthwhile to point out that only the initial end displacement with the magnitude of 1/100 of the column length was considered in the nonlinear buckling analysis. The decrement ratios of the buckling loads induced by other factors, e.g., the initial crack, local node failure and installation error, should be explored further. In addition, only the numerical simulation was conducted to analyse the buckling behaviour of the scaffold independent supporting system, and the rationality of the numerical simulation was verified by the analytical expressions. The experimental investigation into the mechanical response at the semi-rigid nodes under fatigue loading will be conducted later, and extensive exploration of the buckling behaviour of the scaffold independent supporting system will be reported later.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pieńko, M.; Błazik-Borowa, E. Numerical analysis of load-bearing capacity of modular scaffolding nodes. Eng. Struct. 2013, 48, 1–9. [Google Scholar] [CrossRef]
- Dong, J.; Liu, H. Effective length correction factor of disc-buckle type scaffolding by considering joint bending stiffness and geometrical size. PLoS ONE 2022, 17, 0276340. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Jia, L.; Wen, S. Experimental and theoretical studies on the stability of steel tube-coupler scaffolds with different connection joints. Eng. Struct. 2016, 106, 80–95. [Google Scholar] [CrossRef]
- Zhang, H.; Chandrangsu, T.; Rasmussen, K. Probabilistic study of the strength of steel scaffold systems. Struct. Saf. 2010, 32, 393–401. [Google Scholar] [CrossRef]
- Peng, J.; Yen, T.; Kuo, C.; Chan, S. Analytical and experimental bearing capacities of system scaffolds. J. Zhejiang Univ.-Sci. A Appl. Phys. Eng. 2009, 10, 82–92. [Google Scholar] [CrossRef]
- Liu, H.; Meng, Y.; Jia, L. Structural behavior of steel tube and coupler scaffolds with stability strengthening details. Int. J. Steel Struct. 2018, 18, 79–95. [Google Scholar] [CrossRef]
- Peng, J.; Wu, C. Experimental and numerical studies of practical system scaffolds. J. Constr. Steel Res. 2013, 91, 64–75. [Google Scholar] [CrossRef]
- Zhang, H.; Rasmussen, K.; Ellingwood, B.R. Reliability assessment of steel scaffold shoring structures for concrete formwork. Eng. Struct. 2012, 36, 81–89. [Google Scholar] [CrossRef]
- Xie, X.; Chen, G.; Yin, L. Multi-parameter simulation method of semi-rigid node of steel tubular scaffold with couplers. J. Civ. Environ. Eng. 2019, 41, 92–103. [Google Scholar]
- Prabhakaran, U.; Beale, R. Analysis of scaffolds with connections containing looseness. Comput. Struct. 2011, 89, 1944–1955. [Google Scholar] [CrossRef]
- Zheng, Y.; Guo, Z. Investigation of joint behavior of disk-lock and cuplok steel tubular scaffold. J. Constr. Steel Res. 2021, 177, 106415. [Google Scholar] [CrossRef]
- Liu, C.; He, L.; Wu, Z. Experimental and numerical study on lateral stability of temporary structures. Arch. Civ. Mech. Eng. 2018, 18, 1478–1490. [Google Scholar] [CrossRef]
- Chandrangsu, T.; Rasmussen, K. Investigation of geometric imperfections and joint stiffness of support scaffold systems. J. Constr. Steel Res. 2011, 67, 576–584. [Google Scholar] [CrossRef]
- Ihaddoudène, A.; Saidani, M.; Chemrouk, M. Mechanical model for the analysis of steel frames with semi rigid joints. J. Constr. Steel Res. 2009, 65, 631–640. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, H.; Liang, B. Novel numerical method for the analysis of semi-rigid jointed lattice shell structures considering plasticity. Adv. Eng. Softw. 2017, 114, 208–214. [Google Scholar] [CrossRef]
- Bjorhovde, R.; Colson, A. Classification system for beam-to-column connections. J. Struct. Eng. 1990, 116, 3059–3076. [Google Scholar] [CrossRef]
- Jones, S.; Kirby, P.; Nethercort, D. The analysis of frames with semi-rigid connections—A state-of-the-art report. J. Constr. Steel Res. 1983, 3, 2–13. [Google Scholar] [CrossRef]
- Chan, S.; Huang, H.; Fang, L. Advanced analysis of imperfect portal frames with semirigid base connections. J. Eng. Mech. 2005, 131, 633–640. [Google Scholar] [CrossRef]
- Özel, H. Modeling of the Nonlinear Behavior of Semi-Rigid Connections in Steel Framed Structures and Its Influence on Three Dimensional Analysis of Structural Systems. Ph.D. Thesis, Middle East Technical University, Ankara, Türkiye, 2019. [Google Scholar]
- Dong, J.; Liu, H. Buckling behavior of a wheel coupler high-formwork support system based on semi-rigid connection joints. Adv. Steel Constr. 2022, 18, 425–435. [Google Scholar]
- Zhang, L.; Liu, J.; Tang, Q.; Liu, Z. A numerical study on rotational stiffness characteristics of the disk lock joint. J. Constr. Steel Res. 2023, 207, 107968. [Google Scholar] [CrossRef]
- Chenaghlou, M.; Nooshin, H.; Harding, J. Proposed mathematical model for semi-rigid joint behaviour (M-θ) in space structures. Int. J. Space Struct. 2014, 29, 71–80. [Google Scholar] [CrossRef]
- Li, P.; Chen, G.; Qiu, J.; Qian, J.; Ding, D.; Jian, B.; Zhang, X.; Xiong, G. Experimental and numerical investigation into the load-carrying capacity of aluminium alloy H-sectional stocky columns under axial compression. J. Build. Eng. 2024, 87, 108777. [Google Scholar] [CrossRef]
- Chen, G.; Li, P.; Bao, H.; Huang, Y.; Liu, C.; Zhang, T.; Xiong, G. Design method for axially compressed H-sectional aluminium alloy slender column based on CSM. Thin-Walled Struct. 2024, 205, 112417. [Google Scholar] [CrossRef]
- Li, P.; Chu, S.; Qin, S.; Ding, H.; Luo, N.; Yu, Y.; Zhang, T.; Xiong, G. Optimisation of prestressed stayed steel columns based on strengthen elitist genetic algorithm. J. Constr. Steel Res. 2025, 227, 109324. [Google Scholar] [CrossRef]
- Ji, M. Study on the Node Performance of Disc-Type Steel Pipe Support and the Stable Bearing Capacity of the Support. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2024. [Google Scholar]
- Wang, N. Study on the Mechanical Properties of Semi-Rigid Nodes of Disc-Type Steel Pipe Scaffolding. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2023. [Google Scholar]
- Xiao, H. Study on Node Stiffness and Support Stability of Disc-Type Steel Pipe Support. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2022. [Google Scholar]
- Liu, H. Study on Mechanical Properties and Stability of a New Disc-Type Lattice Support. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2023. [Google Scholar]
- JGJ/T 300-2013; Technical Code for Temporary Support Structures in Construction. China Architecture and Building Press: Beijing, China, 2013.
- Chen, S.; Hao, J. Fundamentals of Steel Structures, 5th ed.; China Architecture and Building Press: Beijing, China, 2023. [Google Scholar]




| Steel Frame Forms | Node Types | Plin (kN) | unum | uth | R.E. (%) |
|---|---|---|---|---|---|
| Non-sway | Rigid | 73.476 | 0.576 | 0.580 | 0.69 |
| Semi-rigid | 62.520 | 0.624 | 0.644 | 3.11 | |
| Hinged | 48.594 | 0.708 | 0.700 | 1.14 | |
| Sway | Rigid | 21.632 | 1.061 | 1.078 | 1.58 |
| Semi-rigid | 15.517 | 1.253 | 1.240 | 1.05 | |
| Hinged | 5.938 | 2.025 | 2.000 | 1.25 |
| hcol (mm) | lcol (mm) | Plin (kN) | μ | Pnon (kN) | Rde (%) |
|---|---|---|---|---|---|
| 2500 | 1200 | 89.168 | 0.633 | 87.178 | 2.23 |
| 3000 | 1200 | 63.789 | 0.624 | 62.363 | 2.24 |
| 3500 | 1200 | 48.075 | 0.616 | 47.002 | 2.23 |
| 4000 | 1200 | 37.635 | 0.609 | 36.796 | 2.23 |
| 4500 | 1200 | 30.324 | 0.603 | 29.647 | 2.23 |
| 5000 | 1200 | 24.993 | 0.598 | 24.435 | 2.23 |
| 3000 | 600 | 65.271 | 0.617 | 63.816 | 2.23 |
| 3000 | 800 | 64.727 | 0.619 | 63.280 | 2.23 |
| 3000 | 1000 | 64.238 | 0.622 | 62.804 | 2.23 |
| 3000 | 1200 | 63.789 | 0.624 | 62.363 | 2.24 |
| 3000 | 1400 | 63.370 | 0.626 | 61.954 | 2.23 |
| 3000 | 1600 | 62.974 | 0.628 | 61.569 | 2.23 |
| 3000 | 1800 | 62.597 | 0.630 | 61.201 | 2.23 |
| hcol (mm) | lcol (mm) | Plin (kN) | μ | Pnon (kN) | Rde (%) |
|---|---|---|---|---|---|
| 2500 | 1200 | 45.596 | 0.886 | 44.846 | 1.65 |
| 3000 | 1200 | 32.682 | 0.872 | 32.145 | 1.64 |
| 3500 | 1200 | 24.668 | 0.860 | 24.263 | 1.64 |
| 4000 | 1200 | 19.332 | 0.850 | 19.014 | 1.64 |
| 4500 | 1200 | 15.587 | 0.842 | 15.331 | 1.64 |
| 5000 | 1200 | 12.853 | 0.834 | 12.642 | 1.64 |
| 3000 | 600 | 33.470 | 0.861 | 32.931 | 1.61 |
| 3000 | 800 | 33.181 | 0.865 | 32.647 | 1.61 |
| 3000 | 1000 | 32.921 | 0.869 | 32.380 | 1.64 |
| 3000 | 1200 | 32.682 | 0.872 | 32.145 | 1.64 |
| 3000 | 1400 | 32.461 | 0.875 | 31.927 | 1.64 |
| 3000 | 1600 | 32.253 | 0.878 | 31.723 | 1.64 |
| 3000 | 1800 | 32.058 | 0.880 | 31.531 | 1.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Tao, Q.; Liu, Z.; Tan, Q.; Wang, Y.; Dong, W.; Zhang, B. Investigation on Buckling Behaviour of Scaffold Independent Supporting System Considering Semi-Rigid Nodes. Buildings 2025, 15, 443. https://doi.org/10.3390/buildings15030443
Li R, Tao Q, Liu Z, Tan Q, Wang Y, Dong W, Zhang B. Investigation on Buckling Behaviour of Scaffold Independent Supporting System Considering Semi-Rigid Nodes. Buildings. 2025; 15(3):443. https://doi.org/10.3390/buildings15030443
Chicago/Turabian StyleLi, Rui, Qian Tao, Zhihua Liu, Qihou Tan, Yiming Wang, Wei Dong, and Binsheng Zhang. 2025. "Investigation on Buckling Behaviour of Scaffold Independent Supporting System Considering Semi-Rigid Nodes" Buildings 15, no. 3: 443. https://doi.org/10.3390/buildings15030443
APA StyleLi, R., Tao, Q., Liu, Z., Tan, Q., Wang, Y., Dong, W., & Zhang, B. (2025). Investigation on Buckling Behaviour of Scaffold Independent Supporting System Considering Semi-Rigid Nodes. Buildings, 15(3), 443. https://doi.org/10.3390/buildings15030443





_Dong.png)


