Dynamic Response of an Over-Track Building to Metro Train Loads: A Scale Model Test

Abstract

Vibration control for over-track structures is a key challenge in urban rail transit. To systematically investigate the determining effects of building height and train speed on dynamic response, this study developed a novel moving excitation system. Unlike conventional fixed-point or shaking table methods, this system faithfully reproduces the spatio-temporal “scanning effect” of train loads. In conjunction with a 1:20 modular scaled physical model, a systematic experimental investigation was conducted on structures of different heights (2, 5, 8, 11, and 15 stories) under various train speeds (60, 80, and 100 km/h), with an experimental uncertainty controlled within ±6%. The results revealed two distinct patterns: low-rise rigid structures (≤5 stories) exhibited a monotonic amplification of vibration (top-floor response amplified by 13–28%), whereas mid-to-high-rise flexible structures (≥8 stories) displayed an “attenuation-followed-by-amplification” pattern, with mid-height vibration levels reduced by over 50%. This transition is attributed to a shift in structural dynamics, as the fundamental frequency decreases from approximately 230 Hz (2-story) to approximately 100 Hz (15-story). Furthermore, linear regression analysis (R² > 0.93) confirmed that while train speed linearly scales the response amplitude, the distribution pattern is strictly dictated by the structure’s intrinsic low-order modes. These findings provide a quantified theoretical basis for vibration mitigation in over-track developments.

1. Introduction

With the acceleration of global urbanization, urban rail transit systems, particularly metros, have become a cornerstone of infrastructure for alleviating traffic pressure and optimizing urban layouts. However, the rapid expansion of metro networks has also introduced severe environmental vibration problems [1]. Vibrations generated during train operations propagate through the track structure and soil medium to surrounding buildings. These vibrations not only affect residential comfort but also potentially threaten precision instruments and the structural integrity of historical buildings [2,3,4]. Owing to limited land resources and increasing metro traffic volumes, the construction of above-ground structures in close proximity to underground tunnels has become a common strategy to address land scarcity in major cities. In this configuration, the pile foundations of the superstructure are closely coupled with, or even directly situated on, the tunnel structure, forming a complex “tunnel-soil-over-track structure” coupled vibration system [5,6]. The propagation paths and response mechanisms of vibration waves within this system are exceedingly complex [7,8]. Therefore, a thorough understanding of the dynamic response characteristics of this coupled system under train loads is of paramount engineering significance. Currently, a common engineering approach to mitigate such vibrations is to install base isolation systems between the track and the structure or utilize vibration-reducing tracks [1,9]. However, the effective design of these mitigation measures relies heavily on a clear understanding of the vibration propagation laws. Consequently, clarifying the influence patterns of the two core controlling factors—the structure’s intrinsic dynamic properties and the external excitation characteristics—is urgent for optimizing building design and formulating effective vibration mitigation strategies.

The dynamic response and vibration propagation mechanisms of over-track structures within the “tunnel-soil-over-track structure” coupled system have been the subject of extensive research. Scholars globally have employed various methods, including field measurements [10,11,12,13,14,15,16], numerical simulations [17,18,19,20], and physical model tests [8,9,20]. While field measurements yield real-world vibration data that serves as a direct reference for specific projects, they are hindered by high costs and the difficulty of performing systematic parametric analyses. Numerical simulations, prized for their flexibility and efficiency, are widely used to model complex soil–structure interactions and assess the impact of different parameters on the system’s dynamic response. Nevertheless, the reliability of such models heavily relies on the accuracy of the model parameters and constitutive laws, and therefore must be validated by experimental data.

Physical model testing, especially using scaled-down models, has emerged as a potent approach for investigating this problem. This is due to its ability to faithfully replicate the primary dynamic characteristics of the prototype structure while permitting systematic control over key parameters. However, existing physical model tests predominantly rely on fixed-point excitation due to the complexity of simulating moving loads in a laboratory setting. For instance, Yang et al. [21] and Yang et al. [22] employed electromagnetic shakers fixed at the tunnel invert to investigate long-term settlement and cross-sectional shape effects, respectively. Even in advanced geotechnical centrifuge modeling, Zhou et al. [23] utilized a fixed pre-stressed actuator to apply train loads. While these methods are effective for analyzing localized dynamic responses, they inherently fail to reproduce the spatial “scanning effect” and the transient wave propagation characteristics induced by the moving nature of train loads. This limitation was explicitly acknowledged by Guo et al. [24] in their study on road-metro tunnels. They adopted fixed-point excitation solely due to “test operability” constraints and emphasized that moving train loads should be prioritized in future research. Consequently, neglecting the moving nature of the load can lead to significant discrepancies in vibration prediction. As demonstrated by Sheng et al. [25], the dynamic component induced by wheel–rail interaction can exceed the quasi-static response by over 20 dB. Furthermore, beyond the limitations of excitation simulation, the specific coupling between the tunnel and the over-track structure is often oversimplified in the current literature. Previous studies have frequently treated the superstructure as a lumped mass or focused on a single height configuration. However, recent investigations have quantified the critical sensitivity of vibration response to structural configuration. Seyedi [2] reported that over-track buildings can experience vertical accelerations 87% to 135% higher than adjacent near-track buildings due to direct coupling mechanisms. Similarly, field measurements by Tao et al. [26] revealed that vibration levels at the foundation of a low-rise transfer-structure building were over 20 dB higher than those of a high-rise shear-wall building within the same depot. These quantitative discrepancies underscore that the vibration response is heavily dependent on the building height and structural system. Consequently, a generalized conclusion cannot be drawn from a single building type, highlighting the critical need for a systematic parametric study on the “height-dependent” evolution of dynamic properties. Consequently, due to the lack of systematic parametric analysis using realistic moving loads, the interplay between core controlling factors remains ambiguous. Specifically, the mechanisms by which train speed and building height individually and collectively govern the vibration response have not been clearly decoupled. It remains unclear whether variations in train speed fundamentally alter the vibration distribution pattern along the building height or merely scale the response amplitude. Furthermore, it is not well understood how this interaction evolves as the structure transitions from a low-rise to a high-rise configuration.

To overcome these limitations, this study utilizes a custom-designed moving excitation system and a modular physical model based on a retrofitting project in Guangzhou, China. This research is driven by two specific objectives designed to clarify the system’s dynamic mechanisms. First, it investigates the evolution of vibration propagation patterns as the structure transitions from a low-rise rigid type to a high-rise flexible type. Second, it determines whether the effects of train speed and building height can be decoupled, examining if speed acts solely as an amplitude scaling factor rather than altering the spatial distribution. By systematically conducting tests under multiple scenarios, this study accomplishes these objectives and provides empirical support for vibration assessment.

2. Scaled Model Test

To systematically investigate the dynamic response of the over-track structure within the “tunnel-soil-over-track structure” coupled system under metro train loads, a series of sophisticated scaled model tests were designed and conducted in this study. The experiments strictly adhered to similitude theory, enabling the construction of a physical model that faithfully reproduces the primary dynamic characteristics of the prototype. Furthermore, a custom-developed movable excitation system was utilized to acquire more realistic experimental data.

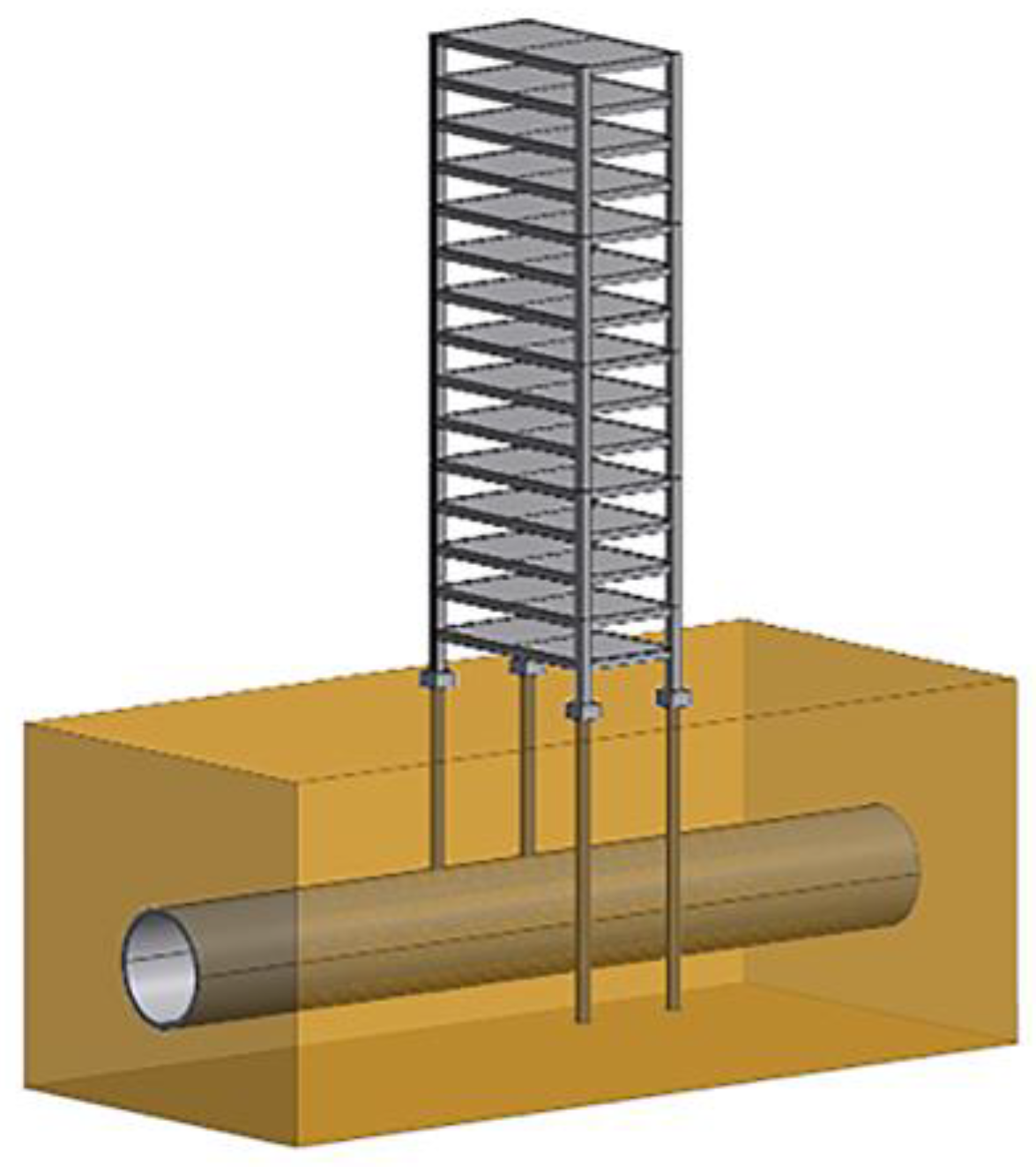
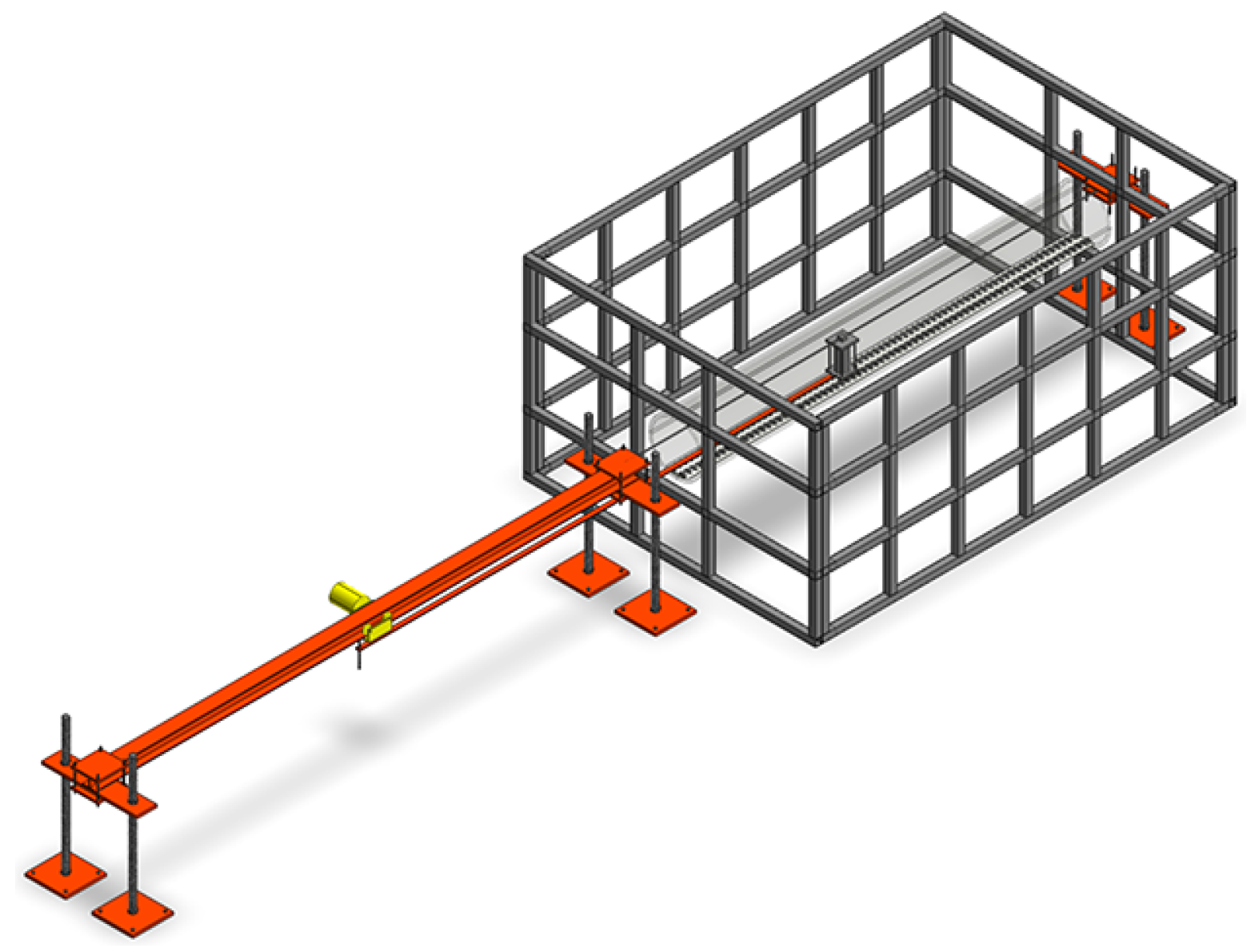
2.1. Model Design and Similitude Relationships

(1)

Prototype Project

The prototype for this experimental study, illustrated in Figure 1, is based on a metro over-track development project in Guangzhou, China. This project serves as a classic case study for investigating near-field vibration propagation. The key parameters of the system are as follows:

Superstructure: The over-track building is a 15-story reinforced concrete (RC) frame structure with a total height of 42 m. The main structure is constructed with C50 grade concrete and is supported by a bored pile foundation. The piles have a diameter of 1 m and a length of 20 m.

Underground Tunnel: The tunnel is constructed using the shield method and has an outer diameter of 8.5 m. The overburden depth above the tunnel crown is 10 m.

Soil Conditions: The site is predominantly underlain by silty clay, whose dynamic characteristics are a crucial factor governing the propagation of vibration waves.

Coupling Features: The core feature of this system is the extremely close proximity and coupling between the tunnel and the foundation piles of the superstructure, with a minimum clearance of only 2.75 m. These near-field coupling conditions offer a representative case study for investigating the complex dynamics of soil-structure interaction.

(2)

Similitude Design

To ensure that the scaled model could accurately replicate the dynamic response of the prototype structure, the physical model was designed in strict accordance with the Buckingham π theorem. Taking into account the constraints imposed by the model container and the laboratory space, the geometric similarity ratio was established as D_l = 20. Plexiglass was selected as the model material. This choice is substantiated by previous studies, such as Wang et al. [27], where organic glass was successfully employed to investigate the elastic dynamic response of tunnel-soil-structure systems due to its excellent homogeneity and stable linear elastic behavior. In this study, the vibration induced by metro trains is characterized as a low-amplitude dynamic response [28]. Consequently, the induced dynamic stresses in the structure are far below the material’s yield strength, justifying the assumption that the model operates strictly within the linear elastic range. Since the prototype has an elastic modulus of 34.5 GPa and the plexiglass has a theoretical modulus of 1.725 GPa, the elastic modulus similarity ratio was set to D_E = 20. To satisfy the dynamic similarity equation D_E/(D_ρ D_l D_a) = 1, consistent with the scaling strategy in the recent literature [26], and given that the density similarity ratio was set to D_ρ = 1 by incorporating additional mass, the acceleration similarity ratio was derived as follows: D_a = D_E/(D_ρ D_l) = 1. This derivation ensures that both gravitational effects and dynamic inertia forces are correctly scaled. The similitude relationships for the remaining physical quantities are presented in

Table 1. Similarity ratios of the model.

Type	Physical Quantity	Relationship	Similarity Ratio
Geometry	Length $l$	$D_l$	20
	Displacement $u$	$D_u=D_l$	20
	Area $A$	$D_A=D_l^2$	400
Material Property	Stress $\sigma$	$D_{\sigma }=D_E$	20
	Strain $\epsilon$	$D_{\epsilon }=1$	1
	Elastic Modulus $E$	$D_E$	20
	Density $\rho$	$D_{\rho }$	1
Load Property	Concentrated Load $F$	$D_F=D_E{D}_l^2$	8000
	Surface Load $P$	$D_P=D_E$	20
Dynamic Property	Time $t$	$D_t=D_l{D}_{\rho }^{1/2}{D}_E^{-1/2}$	4.472
	Frequency $f$	$D_f=D_l^{-1}{D}_{\rho }^{-1/2}{D}_E^{1/2}$	0.224
	Velocity $v$	$D_v=D_{\rho }^{-1/2}{D}_E^{1/2}$	4.472
	Acceleration $a$	$D_a=1$	1

.

(3)

Model Fabrication

To accurately simulate the dynamic characteristics of the prototype structure, each subsystem of the model was meticulously fabricated in accordance with the established similitude relationships.

Superstructure Model: Plexiglass was selected as the material for the structural components. To investigate the influence of the number of stories, a modular design was adopted. This approach allowed for the flexible assembly of the superstructure into five different configurations—2, 5, 8, 11, and 15 stories—by combining various modules, as illustrated in Figure 2. On each floor, precisely weighed sandbags were distributed to serve as additional mass, thereby fulfilling the requirement of the density similarity ratio.

Tunnel Model: The tunnel lining segments were fabricated from cast gypsum with an embedded steel wire mesh (as shown in Figure 3) to achieve a stiffness equivalent to that of reinforced concrete. The sleepers were represented by small iron blocks, and the rails by steel rods with an approximate diameter of 12 mm. The geometric dimensions were scaled according to the length similarity ratio and were further verified based on the principle of equivalent bending stiffness. The main physical parameters of the tunnel model are detailed in

Table 2. Main Physical Parameters of the Tunnel Model.

Structure	Type	ρ (kg/m3)	E (GPa)
Tunnel lining	Prototype	2400	34.5
	Theoretical model	2400	1.725
	Actual model	2320	1.7
Track bed	Prototype	2400	30
	Theoretical model	2400	1.5
	Actual model	2320	1.7

.

Model Soil: The model soil was prepared by mixing silty clay, barite powder, and fine sand in a mass ratio of 12:10:3, as depicted in Figure 4. A series of geotechnical tests, including triaxial shear tests, was conducted to ensure that the key dynamic parameters of the model soil—such as density, elastic modulus, and shear wave velocity—were in close agreement with the theoretical values derived from the prototype soil through the similitude relationships. The physical parameters of the soil are listed in

Table 3. Main physical parameters of the soil.

Category	ρ (kg/m3)	E (MPa)	VS (m/s)	$\nu$
Prototype soil	1730	40	170.3	0.3
Theoretical model soil	1730	2.0	38.1	0.3
Actual model soil	1705	2.1	40.4	0.32

.

Model Container: The experiment was conducted within a rigid steel container measuring 3.0 m × 2.1 m × 1.5 m, as shown in Figure 5a. To mitigate the influence of boundary reflections on the test results, the inner walls of the container were lined with a 10 cm thick layer of foam sponge. This foam layer functioned as an energy-absorbing boundary, effectively minimizing wave reflection interference, as depicted in Figure 5b.

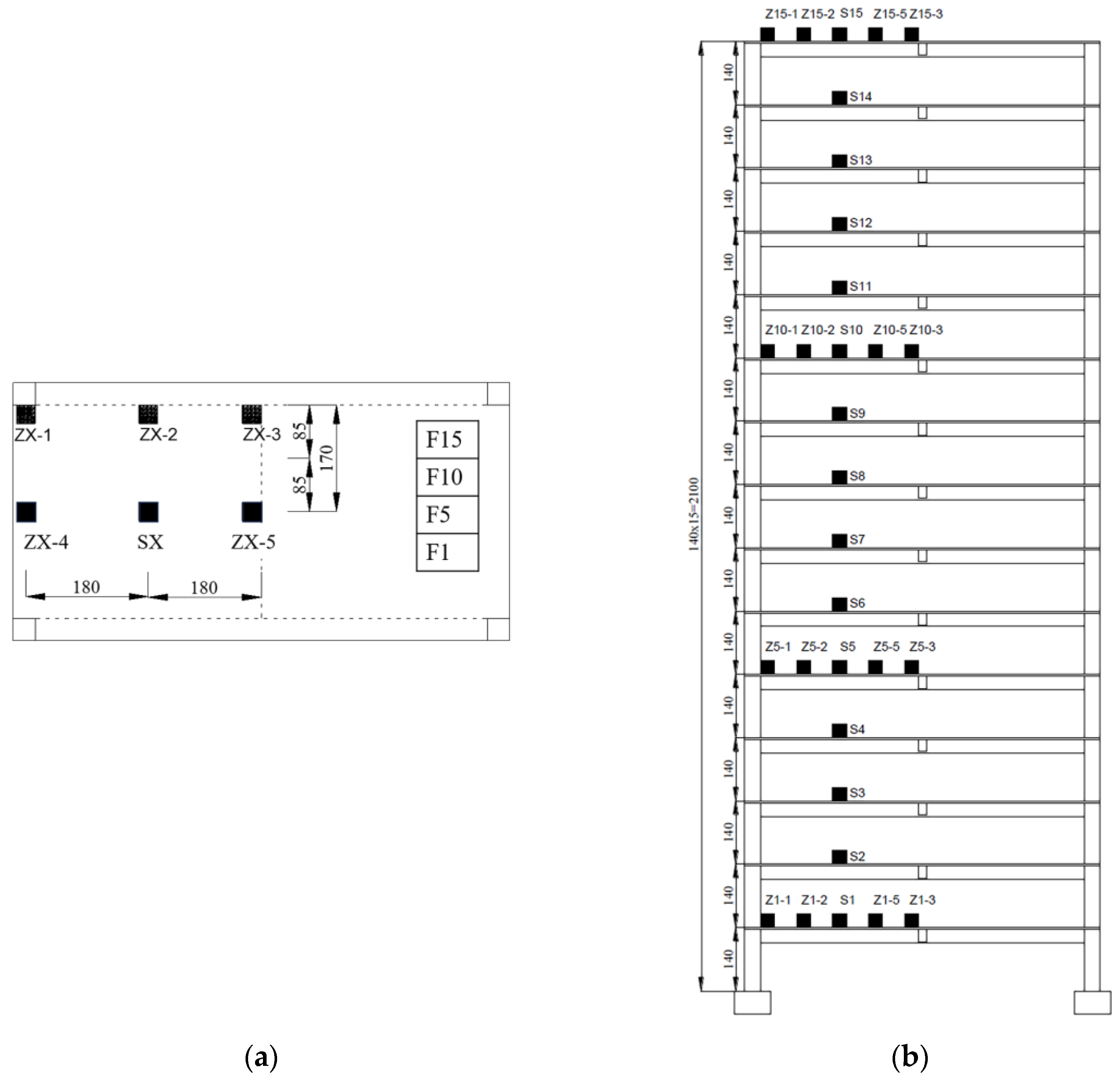
2.2. Dynamic Loading and Data Acquisition

To overcome the limitations of traditional fixed-point excitation and to realistically simulate moving train loads, a custom-designed moving excitation system was developed for this study, as illustrated in Figure 6.

The system is primarily composed of three main components:

Reaction Frame and Guide Rail System: A height-adjustable reaction frame was rigidly attached to one end of the model container. An I-beam guide rail was mounted on this frame, extending precisely along the tunnel’s longitudinal axis. This rail provides a stable and accurate trajectory for the moving excitation cart.

Traction System: The traction system consists of an electric hoist and a connecting rod. By precisely controlling the speed of the hoist, this system ensures stable control over the cart’s velocity, enabling the simulation of different train speeds, namely 60, 80, and 100 km/h.

Moving Excitation Cart: The cart serves as the actuator for applying the dynamic load. As shown in Figure 7 and Figure 8, this compact unit is equipped with an electromagnetic shaker (DH40100; Jiangsu Donghua Testing Technology Co., Ltd., Jingjiang, China) (rated force: 100 N; operating frequency range: 5–2000 Hz) firmly mounted on its body. The cart features U-shaped pulleys as wheels to ensure stable movement along the I-beam guide rail. To prevent derailing or excessive oscillation during transit, a limit slider is installed at the top center of the cart. The dynamic force generated by the shaker is transmitted vertically through an actuator rod to a simulated track beneath the cart, and ultimately to the tunnel structure.

The operational workflow of the system proceeds as follows: initially, the desired load function is configured in a signal generator (DG1022Z; RIGOL Technologies Co., Ltd., Suzhou, China). The traction system is then engaged, setting the cart in motion at a predetermined speed. Concurrently, the signal from the generator is fed through a power amplifier (DH5874; Jiangsu Donghua Testing Technology Co., Ltd., Jingjiang, China), which in turn drives the electromagnetic shaker. By seamlessly integrating the load’s temporal dynamics (dynamic variation over time) with its spatial translation (movement through space), this system faithfully reproduces the characteristics of the vibration source as it occurs in a real-world train-rail interaction scenario.

Loading Protocol: To ensure the authenticity of the applied loads, the moving load time-history function was derived from the internationally recognized excitation force formula (Equation (1)). This model, originally proposed by the UK’s Derby Railway Technical Centre [29,30], has been extensively validated and utilized in investigating train-induced vibrations under various complex conditions, such as thawing soil environments [31] and grade-separated tunnel interactions [32].

The load F(t) is expressed as

$$F(t)=k_1{k}_2(P_0+P_1\sin {\omega }_{1}t+P_2\sin {\omega }_{2}t+P_3\sin {\omega }_{3}t)$$

(1)

where k₁ is the load superposition coefficient between wheels and k₂ is the load dispersion coefficient between the wheel and rails. P₀ represents the static wheel load. The dynamic components Pi are calculated as P_i = M₀α_iω_i², where M₀ is the metro mass and α_i is the versine (amplitude) of the irregularity. The angular frequency ω_i is defined by ω_i = 2πv/L_i, where v is the train speed and L_i is the typical wavelength of the irregularity.

This model simplifies the broad, continuous spectrum of track irregularities into three dominant harmonic components (P₁, P₂, P₃). These components are not arbitrary; they represent distinct physical mechanisms of track geometry defects. Considering the actual operating speed of the prototype (Guangzhou Metro), its typical irregular vibration wavelengths (L_i) and corresponding versines (a_i) were selected as:

1.

Long-wave (L₁ = 10 m, a₁ = 3.5 mm): Represents low-frequency irregularities affecting driving stability.

2.

Medium-wave (L₂ = 1 m, a₂ = 0.3 mm): Represents medium-frequency dynamic additional loads from static geometry irregularity.

3.

Short-wave (L₃ = 0.5 m, a₁ = 0.07 mm): Represents high-frequency rail surface corrugation and dynamic wheel–rail interaction. To evaluate the validity of the experimental simulation, the load’s temporal and spatial characteristics were rigorously considered. Temporally, the system effectively reproduces the frequency content of the vibration source. By incorporating the specific irregularity parameters (L₁, L₂, L₃) derived from the Guangzhou Metro, the excitation covers the critical frequency bands for ride comfort and wheel–rail interaction. Spatially, while the single moving cart represents a simplification of a multi-axle train, it captures the fundamental moving nature of the load. This setup successfully simulates the essential “scanning effect” and transient wave propagation phenomena, which are the primary spatial factors influencing vibration transmission in this study, distinguishing it from traditional fixed-point excitation methods.

The experiments simulated several train speeds (60, 80, and 100 km/h) to cover a range of typical operating conditions from low to high speeds. Based on Equation (1), the load time history was calculated, as exemplified by the 60 km/h case shown in Figure 9. For the sake of brevity, only a 0.1 s segment of the total 10 s time history is presented. Furthermore, a sinusoidal sweep excitation from 0 to 1000 Hz was applied as a fixed-point load at the mid-span of the tunnel to comprehensively characterize the structural dynamic properties. Although this bandwidth covers the full prototype spectrum (approximately 224 Hz), the subsequent analysis is truncated to the 0–300 Hz range. This strategy, adopted in similar scale model studies [23,24], ensures that the identified natural frequencies are within the valid similarity window, thereby eliminating potential high-frequency artifacts.

To ensure the reliability of the test data, specific measures were implemented to minimize experimental uncertainties. Regarding load amplitude control, the non-linearity of the electromagnetic shaker was compensated by a closed-loop control system comprising a signal generator and a power amplifier. A dynamic force sensor was used to calibrate the input signal prior to testing, ensuring the output force amplitude remained consistent with the theoretical Derby formula, with a control error estimated to be within ±5%. Furthermore, positioning and movement errors were effectively mitigated by the previously described rigid guidance system. The mechanical constraints provided by the U-groove wheels and the limit slider ensured strict alignment along the I-beam guide rail, thereby preventing lateral deviation and derailing. Additionally, the electric hoist traction system maintained a stable moving speed, minimizing velocity-induced uncertainties during data acquisition.

Sensor Layout: To accurately capture the dynamic response of the superstructure, a specific sensor arrangement was designed. Figure 10 illustrates the layout for Case V (the 15-story building), which was identically replicated for all other building configurations. The monitoring scheme involved placing sensors at the mid-span of each floor slab to track the propagation of vibrations along the building’s height. Additionally, on representative floors (the 1st, 5th, 10th, and 15th), a denser array of sensors was deployed at critical locations—including the column bases, and the mid-spans of the main and secondary beams—to acquire more detailed local response data.

Uncertainty Analysis: Due to the scale and complexity of the physical model test, extensive statistical repetition for every case was constrained. To ensure the robustness of the conclusions, an instrumental uncertainty analysis was conducted. The piezoelectric accelerometers (ACC1837; Megsig Sensing Technology Co., Ltd., Shenzhen, China) have a documented linearity error of ≤1%. Furthermore, considering the electro-mechanical coupling of the moving excitation system and minor variability in wheel–rail contact, the control accuracy of the loading amplitude is conservatively estimated at ±5%. Therefore, a total combined experimental uncertainty of ±6% is adopted to represent the reliability margin of the data. This margin of error is represented by error bars in the quantitative analysis of train speed effects.

2.3. Test Cases

To conduct an in-depth investigation into the propagation characteristics of train-induced vibrations under various conditions, this study considered the influence of two primary factors: the number of stories in the superstructure and the type of excitation force. The experimental program was structured around five main test cases, defined by the number of stories in the superstructure. Two distinct types of excitation forces were applied to simulate different vibration source effects during metro operations: swept-sine excitation and simulated train loads. The swept-sine excitation was employed to analyze the system’s dynamic response characteristics over a broad frequency range, whereas the train loads were used to replicate the actual vibration conditions during a train passage. For the fixed-point excitation mode, a frequency sweep from 0 to 1000 Hz was used. For the moving load mode, excitation forces corresponding to three train speeds—60, 80, and 100 km/h—were applied. A comprehensive summary of the test cases is provided in

Table 4. Test Conditions.

Floor Level	Train Speed (km/h)	Frequency Range (Hz)
2nd floor (Case I)	60/80/100	0–1000
5th floor (Case II)	60/80/100	0–1000
8th floor (Case III)	60/80/100	0–1000
11th floor (Case IV)	60/80/100	0–1000
15th floor (Case V)	60/80/100	0–1000

.

3. Results and Discussion

This chapter presents a systematic analysis of the dynamic response of the superstructure within the “tunnel-soil-over-track structure” coupled system when subjected to moving metro train loads. The investigation focuses on elucidating the distinct mechanisms through which building height and train speed—the two principal factors—govern the structural vibration response. By integrating analyses in both the time and frequency domains, this section clarifies the interplay between the structure’s intrinsic dynamic characteristics and the external excitation, with a particular emphasis on decoupling their effects. The findings establish a theoretical framework for the development of vibration control strategies for similar engineering projects.

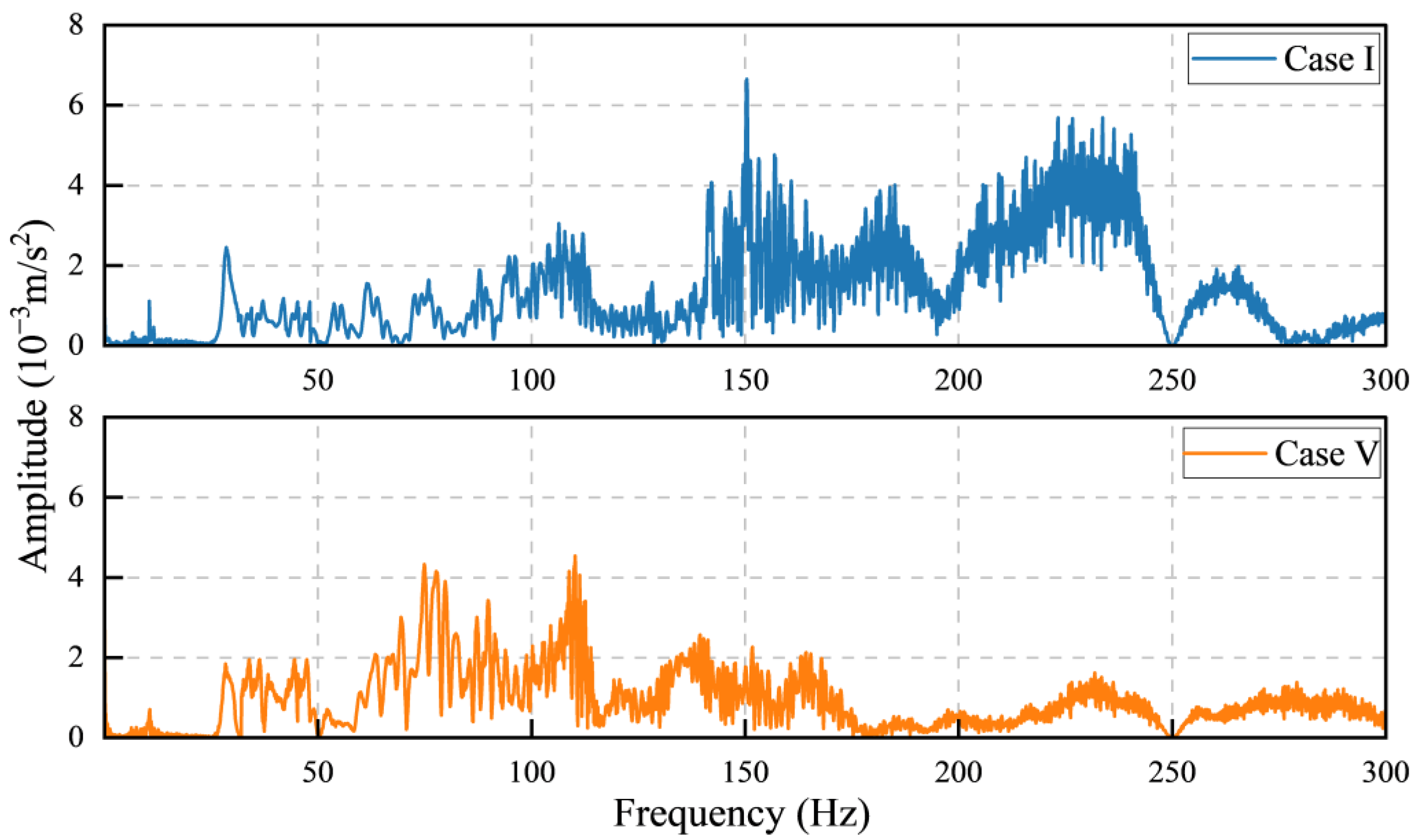
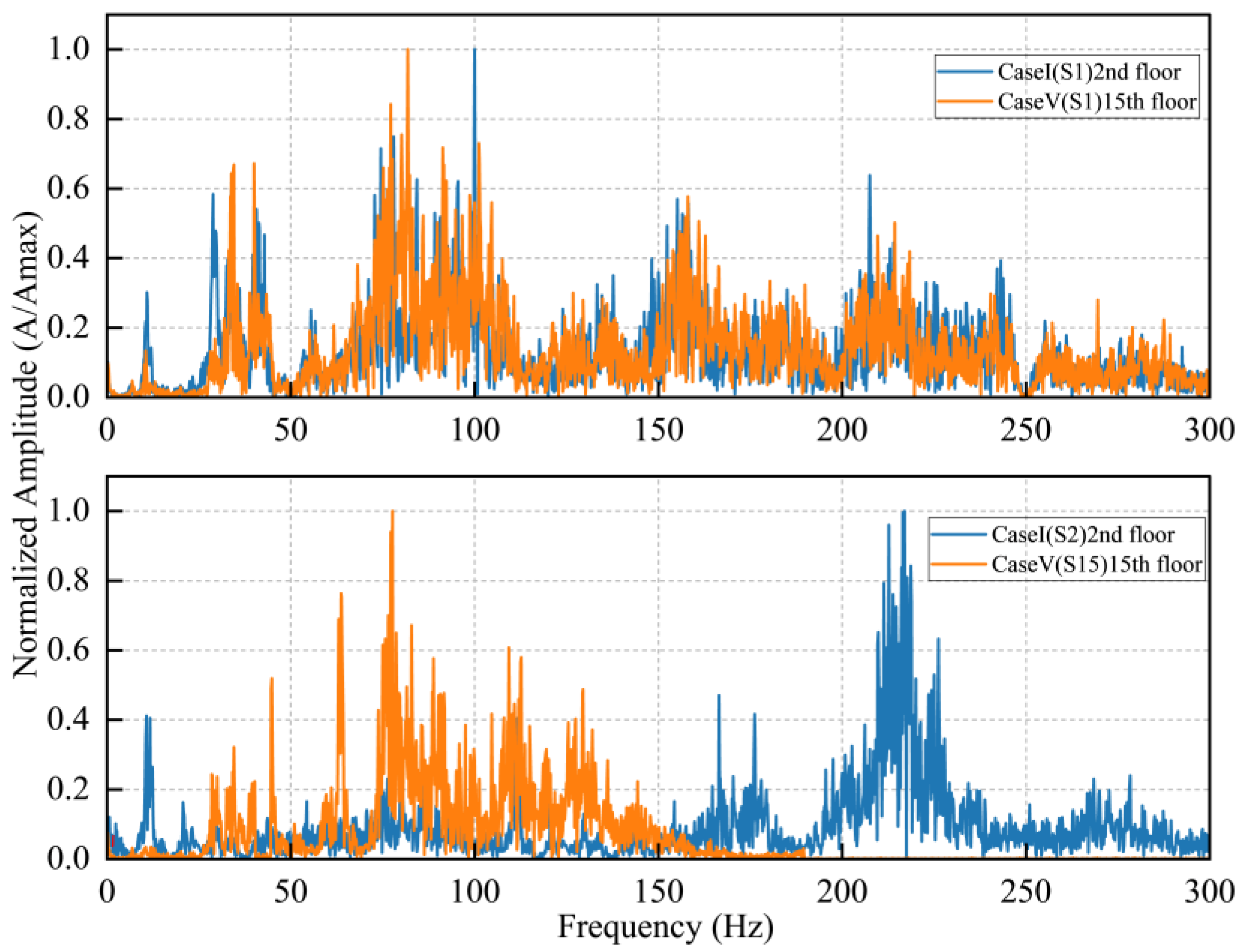
3.1. Effect of Building Height on Vibration Response Distribution

To elucidate how building height fundamentally alters the propagation and distribution of vibrations within the structure, this section presents a comparative analysis of the response patterns along the height for the five different structural configurations. The analysis focuses on a representative medium-speed case, corresponding to a prototype train speed of 80 km/h.

The distribution of Peak Ground Acceleration (PGA) across the building’s height, as shown in Figure 11, clearly identifies two distinct vibration propagation and amplification patterns, which are determined by the structural type: (1) Monotonic Amplification in Low-Rise Structures (Cases I and II): For the low-rise buildings, the PGA exhibits a monotonic amplification trend from the base to the roof. In Case I and Case II, the PGA at the top floor was approximately 13% and 28% greater than at the base, respectively. This suggests that energy dissipation is minimal over the short propagation path, while the free-surface reflection effect at the top of the structure becomes dominant, leading to a significant enhancement of the vibration. (2) Attenuation-Followed-by-Amplification in Mid- to High-Rise Structures (Cases III, IV, and V): Beginning with the structure in Case III, the response pattern undergoes a qualitative transformation. The response curve clearly illustrates a characteristic “attenuation-followed-by-amplification” profile. The PGA significantly attenuates from the base (S1) towards the middle floors (near S5) and then experiences a sharp rebound and amplification in the section from S5 to the roof. As the number of stories increases, this pattern becomes progressively more pronounced, exhibiting two key evolutionary trends:

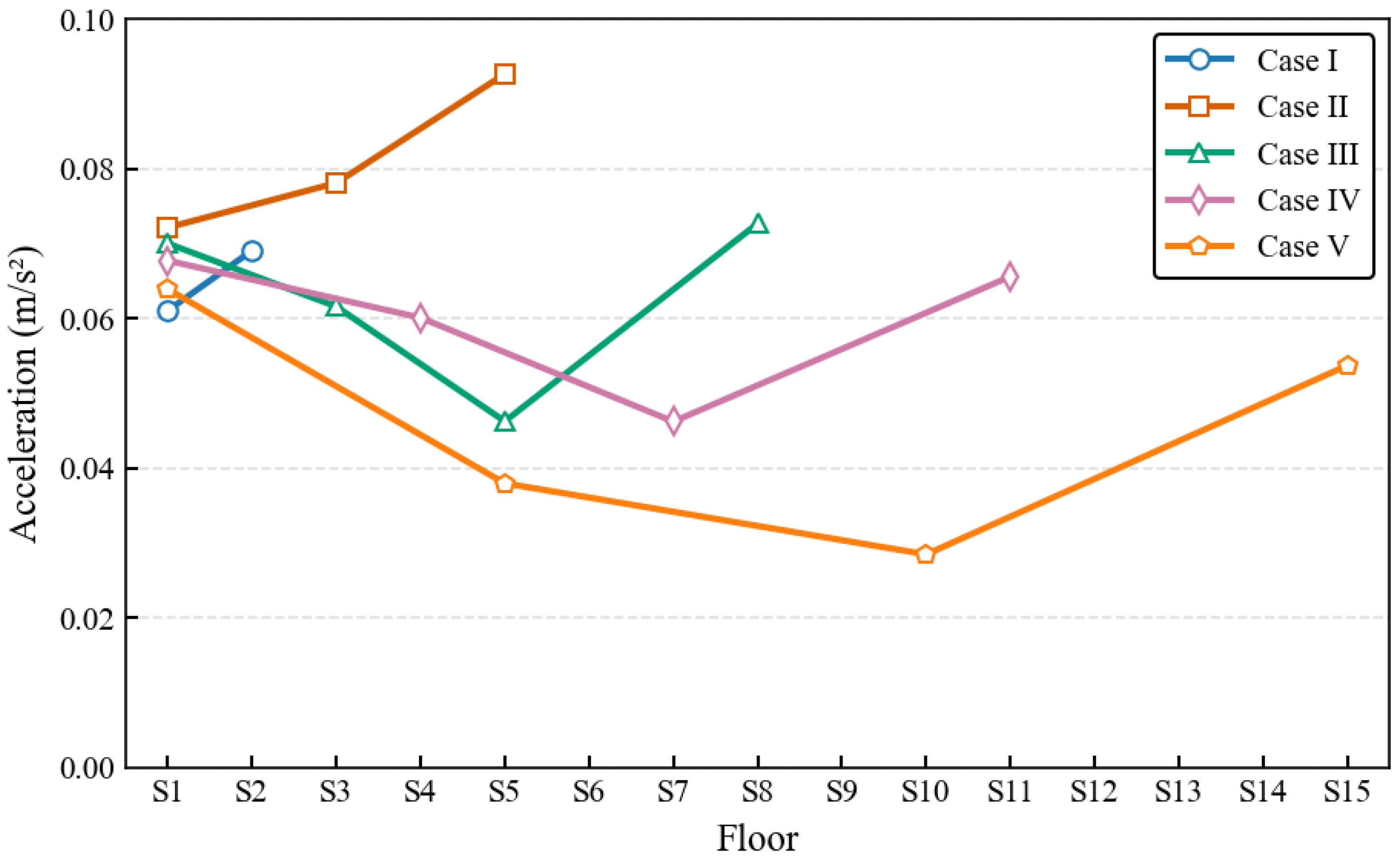
(a)

Deeper and Wider Attenuation Zone: As the number of stories increases, the attenuation zone in the middle portion of the structure becomes more pronounced. In the 15-story structure (Case V), the PGA at the S10 measurement point was approximately 0.029 m/s², which is less than half of the PGA at the base (S1), recorded at about 0.063 m/s².

(b)

Upward Shift in the Attenuation Minimum: The location of the minimum response point shifts upward with increasing building height. It migrates from the S5 floor in Case III, to the S7 floor in Case IV, and ultimately reaches the S10 floor in Case V. This phenomenon is closely correlated with the shape of the structure’s dominant mode, as the point of maximum attenuation generally corresponds to a modal node or a region of minimal modal contribution.

Figure 11. Peak acceleration distribution over the floors for structures of varying heights at 80 km/h.

Figure 11. Peak acceleration distribution over the floors for structures of varying heights at 80 km/h.

The root cause of this qualitative transformation in the propagation pattern lies in the fundamental evolution of the structure’s global dynamic characteristics, which is driven by the increase in building height. To validate this mechanism, the intrinsic dynamic properties of each structural system were precisely identified through wide-band (0–1000 Hz) frequency sweep tests. As shown in Figure 12, the results indicate that as the building height increases from 2 to 15 stories, the fundamental frequency of the structure undergoes a sharp decrease from approximately 230 Hz to about 100 Hz. This shift signifies that the system has transitioned from a “high-frequency, rigid” type to a “low-frequency, flexible” type.

To further investigate the underlying physical mechanisms, a direct comparison was made between the acceleration response spectra at the base and top floors of the two extreme configurations: the 2-story (Case I) and the 15-story (Case V) structures. To specifically focus on the “spectral reconfiguration” mechanism and eliminate the influence of absolute amplitude differences, the response spectra in Figure 13 were normalized by their respective peak amplitudes. As shown in Figure 13, at the base of the structures (measurement point S1), the normalized spectra for both cases are broadly similar in shape, exhibiting broadband characteristics across the 0–300 Hz range. This consistency accurately reflects the broadband nature of the wheel–rail interaction input and confirms the comparability of the vibration input across different test cases. In stark contrast, a dramatic “spectral reconfiguration” occurs at the top of the structures. The response of the top floor in Case I (S2) retains its broadband characteristics, with energy distributed over a wide frequency range. However, the response of the top floor in Case V (S15) transforms entirely into a distinct narrowband profile. Frequency components above 150 Hz are almost completely suppressed, while vibrational energy becomes highly concentrated around 100 Hz. Crucially, this dominant spectral peak aligns precisely with the fundamental frequency approximately 100 Hz independently identified via the swept-sine modal analysis (as shown in Figure 12). This empirical alignment transforms the understanding of the “attenuation-followed-by-amplification” pattern from theoretical speculation to validated fact. It confirms that the flexible high-rise structure acts as a narrowband filter: on one hand, the effective attenuation of high-frequency components is caused by inherent energy dissipation and longer propagation paths; on the other hand, a strong resonant response is triggered when excitation components match the structure’s natural frequency. This interplay—filtering high frequencies while resonating at the fundamental frequency—is definitively identified as the physical mechanism driving the characteristic response of high-rise over-track buildings.

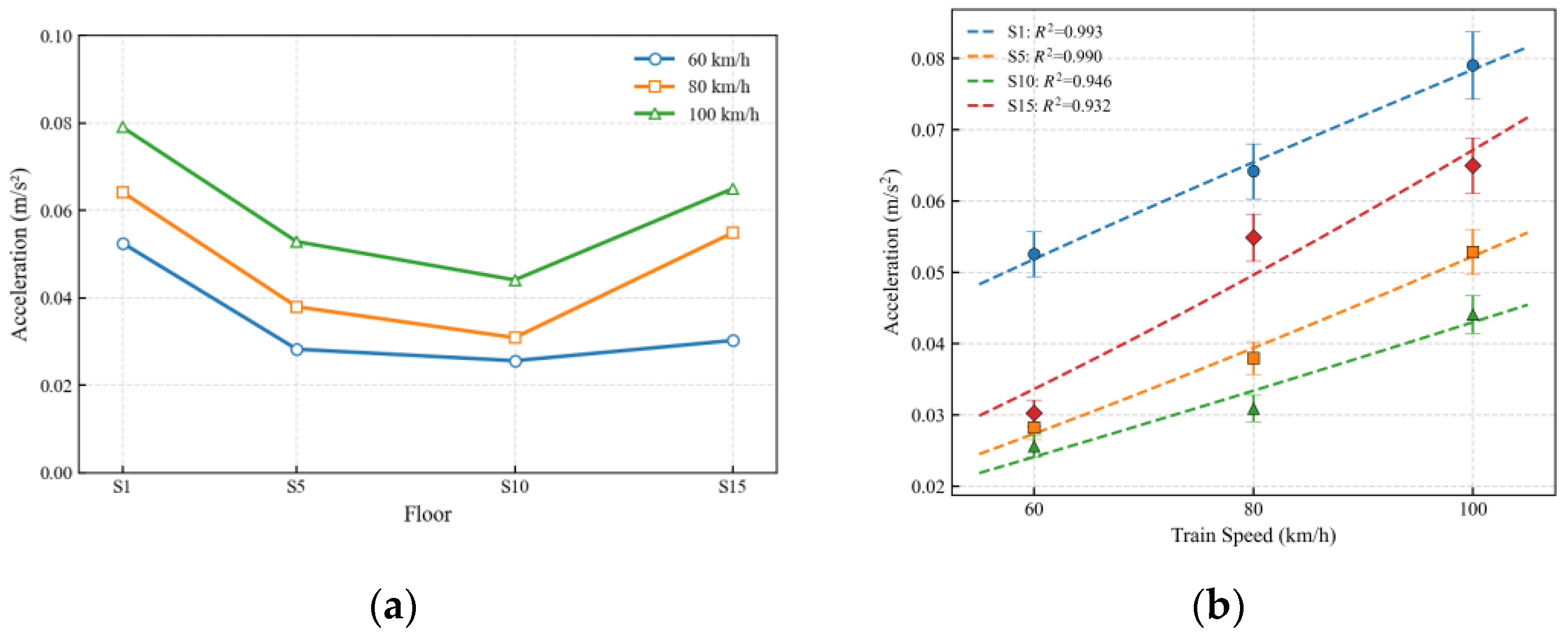
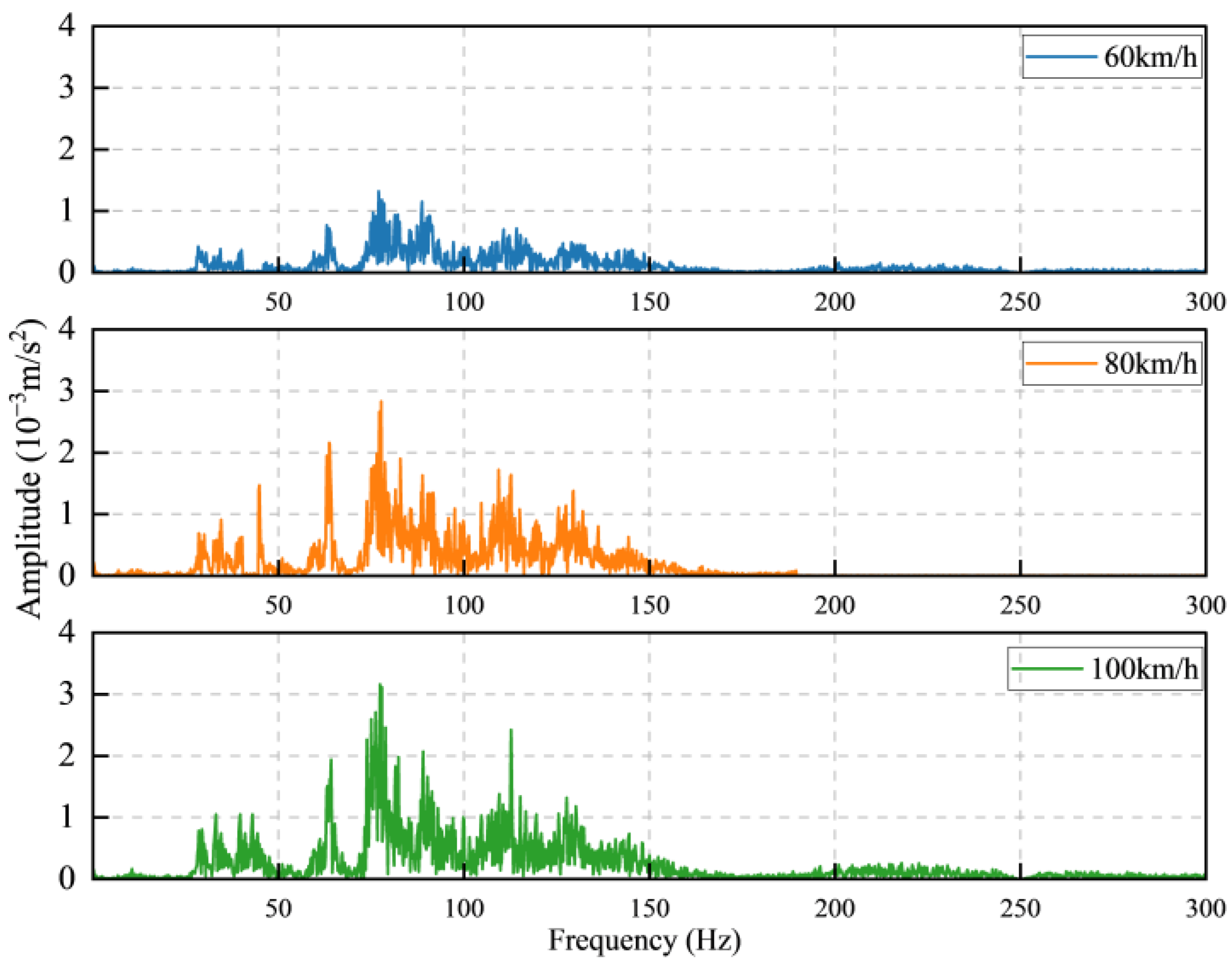
3.2. Effect of Train Speed on Vibration Response

To assess the influence of train speed on the magnitude of the vibration response, this section focuses on the 15-story structure (Case V) as a representative case. A systematic analysis is presented, examining the changes in its dynamic response under three different train speeds: 60, 80, and 100 km/h.

As illustrated in Figure 14, the analysis reveals two distinct and unequivocal patterns regarding the interplay between excitation and structural response: (1) Response Magnitude is Governed by Speed: The train’s operating speed is the decisive factor controlling the magnitude of the vibration response. To quantify this relationship, a linear regression analysis was performed on the peak floor accelerations, as shown in Figure 14b. The results demonstrate a strong linear correlation, with coefficients of determination (R²) ranging from 0.932 to 0.993 across all monitored floors. This quantitatively confirms that the vibration excitation intensity scales linearly with train speed. Specifically, as the speed increases from 60 km/h to 100 km/h, the PGA at the base (S1) grows by approximately 54%, while at the top floor (S15), the increase exceeds 100%. Furthermore, the reliability of these trends is supported by the uncertainty analysis; the error bars (±6%) in Figure 14b indicate that the observed variations significantly exceed the range of systematic measurement uncertainty. (2) Response Pattern is Dictated by the Structure: Although the absolute amplitude varies with speed, the spatial distribution along the building’s height demonstrates remarkable consistency, as depicted in Figure 14a. Under all three speed conditions, the PGA curves exhibit the identical “attenuation-amplification” profile. This observation clearly indicates that the vibration distribution pattern is an intrinsic response characteristic of this high-rise structure, determined by its own modal properties and independent of the external excitation intensity

Frequency-domain analysis, as shown in Figure 15, further substantiates this understanding. A vertical comparison of the response spectra for the top floor (S15) reveals that the overall amplitude of the spectrum increases significantly with train speed. This directly confirms that higher speeds lead to a greater energy input from the vibration source. However, despite the variation in the absolute energy levels with speed, the dominant vibrational energy consistently remains concentrated within the 50–150 Hz frequency band. Furthermore, the principal peaks in the spectra consistently appear in the vicinity of the structure’s fundamental frequency (approximately 80–100 Hz).

This key finding indicates that for high-rise flexible structures, the dynamic response is predominantly controlled by the structure’s own low-order modes. Within the range of speeds tested, a change in velocity acts more as a scaling factor for the excitation intensity; it proportionally adjusts the response amplitude—which is determined by the structure’s inherent modal properties—rather than altering the frequency content of the response. This dependency also underscores the critical importance of considering the line’s maximum design speed as the most unfavorable condition for assessment in any vibration environmental analysis of metro over-track structures.

4. Conclusions

Through a series of scaled model tests, this study has systematically elucidated the decisive roles of building height and train speed in governing the vibration response of metro over-track structures. The main conclusions are as follows:

(1)

Evolution of Structural Dynamics: Building height acts as a primary parameter influencing the dynamic behavior of over-track structures. As the height increases, the structure transitions from a “high-frequency, rigid” system to a “low-frequency, flexible” system. This shift is characterized by a notable decrease in the fundamental frequency (from approximately 230 Hz to 100 Hz in this study), which fundamentally alters the vibration transmission mechanism.

(2)

Height-Dependent Propagation Patterns: The variation in dynamic properties leads to two distinct vibration propagation patterns. Low-rise structures (≤5 stories) exhibit a “monotonic amplification” trend. In contrast, high-rise flexible structures (≥8 stories) display an “attenuation-followed-by-amplification” profile. This phenomenon indicates that the filtering effect of the structure becomes more dominant as the number of stories increases.

(3)

Distinct Roles of Speed and Structure: The effects of train speed and structural modes on the vibration response operate through distinct mechanisms. Train speed primarily scales the overall response amplitude, showing a strong linear correlation (R² > 0.93). Meanwhile, the spatial distribution of vibration along the building’s height is governed primarily by the structure’s intrinsic modal properties, remaining consistent across different speeds.

Limitations: It should be noted that these findings are based on a 1:20 scaled model test. While the similitude laws were strictly followed, scale effects regarding soil nonlinearity and complex damping mechanisms may still exist. Additionally, the study simplified the train load using a single-cart excitation system driven by a superposition of three discrete harmonic components. While this approach effectively captures the fundamental moving load effect and critical characteristic wavelengths, it represents a simplification of the actual broadband continuous spectrum inherent in real rail profiles. Future research should integrate these experimental results with full-scale field measurements to validate these findings against broadband random excitations.