Time-Based Fire Resistance Performance of Axially Loaded, Circular, Long CFST Columns: Developing Analytical Design Models Using ANN and GEP Techniques

Abstract

Concrete-filled steel tube (CFST) columns are composite structural elements preferred in various engineering structures due to their superior properties compared to those of traditional structural elements. However, fire resistance analyses are complex due to CFST columns consisting of two components with different thermal and mechanical properties. Significant challenges arise because current design codes and guidelines do not provide clear guidance for determining the time-dependent fire performance of these composite elements. This study aimed to address the existing design gap by investigating the fire behavior of circular long CFST columns under axial compressive load and developing robust, accurate, and reliable design models to predict their fire performance. To this end, an up-to-date database consisting of 62 data-points obtained from experimental studies involving variable material properties, dimensions, and load ratios was created. Analytical design models were meticulously developed using two advanced soft computing techniques: artificial neural networks (ANNs) and genetic expression programming (GEP). The model inputs were determined as six main independent parameters: steel tube diameter (D), wall thickness (t_s), concrete compressive strength (f_c), steel yield strength (f_sy), the slenderness ratio (L/D), and the load ratio (μ). The performance of the developed models was comprehensively compared with experimental data and existing design models. While existing design formulas could not predict time-based fire performance, the developed models demonstrated superior prediction accuracy. The GEP-based model performed well with an R-squared value of 0.937, while the ANN-based model achieved the highest prediction performance with an R-squared value of 0.972. Furthermore, the ANN model demonstrated its excellent prediction capability with a minimal mean absolute percentage error (MAPE = 4.41). Based on the nRMSE classification, the GEP-based model proved to be in the good performance category with an nRMSE value of 0.15, whereas the ANN model was in the excellent performance category with a value of 0.10. Fitness function (f) and performance index (PI) values were used to assess the models’ accuracy; the ANN (f = 1.13; PI = 0.05) and GEP (f = 1.19; PI = 0.08) models demonstrated statistical reliability by offering values appropriate for the expected targets (f ≈ 1; PI ≈ 0). Consequently, it was concluded that these statistically convincing and reliable design models can be used to consistently and accurately predict the time-dependent fire resistance of axially loaded, circular, long CFST columns when adequate design formulas are not available in existing codes.

1. Introduction

Concrete-filled steel tube (CFST) columns are composite structural elements consisting of a steel tube filled with concrete [1]. The two components of these composite columns ideally complement each other. The fundamental purpose of using concrete and steel together is to utilize the compressive strength of concrete and the tensile strength of steel, thereby creating a structural element capable of withstanding both compressive and tensile loads. While steel offers high stiffness, ductility, and strength performance, concrete provides high compressive strength, homogeneous filling, and an economical design [2,3,4,5]. The confinement effect delays the local buckling of steel and reduces strength issues after local buckling. On the other hand, the confinement effect of steel increases the strength of concrete and thus the strength and ductility of the column [6]. Additionally, the steel tube provides fire protection to the concrete fill inside and relatively delays the temperature increase within the concrete. For these reasons, CFST columns have higher fire resistance compared to concrete and steel equivalents [7].

High strength, rigidity, high ductility, and high fire resistance are the main reasons why CFST columns are preferred in various high-performance engineering structures such as offshore structures, bridges, towers, tunnels, underground train platforms, stadiums, and high-rise buildings [8,9]. However, because CFST columns consist of two materials with different thermal and mechanical properties, fire resistance analysis is a complex process. Significant challenges arise because current design codes and guidelines do not provide clear guidance for determining the time-dependent fire performance of these structural elements.

Various experimental and numerical studies exist in the literature regarding material and dimensional properties that affect the fire resistance of CFST columns (such as cross-sectional area, steel tube thickness, concrete compressive strength, steel yield strength, and load level) [2,7,9,10,11,12]. Knowing the effects of these parameters and their degrees of influence is necessary to develop design models that predict fire resistance. Various mathematical expressions have been developed in the literature to estimate the fire resistance of concrete-filled steel tube (CFST) columns [13,14,15,16,17,18]. Existing design formulas are generally used to predict the residual axial load-carrying capacity of a CFST column. These numerical models do not have the ability to predict the time-dependent fire performance of a CFST column. Although the formula used in the Japanese code [19] includes a time parameter, it has been concluded that it does not provide reliable results at low axial load-carrying capacities. Consequently, the time-dependent fire resistance performance of axially loaded CFST circular long columns cannot be predicted from existing design formulas (except for the simplified equation in Kodur [20]). Since structural elements such as circular long CFST columns form the load-bearing system of modern buildings and information on fire resistance is still insufficient, developing high-accuracy design models is of vital importance.

The primary objective of this study was to develop high-performance analytical design models to easily and reliably calculate the fire performance of axially loaded, circular, long CFST columns. To this end, software-based numerical design models were meticulously developed using advanced soft computing techniques based on artificial intelligence principles, namely genetic expression programming (GEP) and artificial neural networks (ANNs), drawing on experimental studies in the literature. These developed design models benefit from advanced soft computing techniques that provide high accuracy and reliability [21,22]. The prediction performance of these proposed models was statistically validated by comparing them with experimental results and existing models [20]. It was found that these newly developed models (ANN R² = 0.972 and GEP R² = 0.937) show superior prediction accuracy compared to the existing Kodur model (R² = 0.549).

2. Fire Performance of CFST Columns and Literature Review

Fire resistance analysis of CFST columns is a complex process because they are composed of two materials with different thermal and mechanical properties.

2.1. Behavior of CFST Columns Under Fire

In the literature, the deformation of CFST columns during fire is explained in four stages.

−

First stage: Steel expands faster than concrete because it is a material with a higher thermal expansion coefficient and heats up more quickly. Therefore, the longitudinally expanding steel tube carries most of the load. Subsequently, a gap forms between the transversely expanding steel and the concrete, and heat transfer to the concrete slows down.

−

Second stage: Steel rapidly shortens due to the load it bears and the increase in temperature, which causes its yield strength to decrease, and at a certain point, it can no longer bear the load. The rapid shortening and shrinkage of steel within approximately 20–30 min causes the load to be transferred to the concrete core.

−

Third stage: Due to the low thermal conductivity of concrete, the temperature increase in the element begins to slow down. In this stage, the concrete core begins to carry more load. The concrete core continues to carry the load until the deterioration of the concrete reaches a certain level.

−

Fourth and final stage: As the temperature increase continues, the concrete loses its strength, and the column can no longer carry the load. This moment when the concrete breaks or buckles is referred to as the fire resistance of the column [3,7,9].

2.2. Fire Test Method

In the literature, CFST columns have been tested under standard fire exposure conditions. Gas furnaces are generally used in these studies. First, the end plates of the columns are properly placed in the furnace for protection and fixed. Then, thermocouples are placed to enable temperature measurements at specific points. A load is applied to the columns before they are exposed to fire, and this load is kept constant throughout the test. To simulate fire conditions, the temperature change inside the furnace follows the temperature–time curve shown in Figure 1, as per ISO 834-1 [23]. The time and temperature at which the column breaks or buckles as a result of the temperature increase determine the fire resistance of the element [24,25].

2.3. Effect of Parameters on Fire Resistance

Various experimental and numerical studies on the fire resistance of CFST columns exist in the literature. In these studies, the fire resistance of circular long CFST columns has been tested, the effect of various parameters on fire resistance has been investigated, and fire resistance design models for such elements have been developed to estimate their fire resistance. In a previous study [26], the authors performed a detailed examination of the parameters affecting the fire resistance of CFST columns and determined the most effective parameters in light of the studies in the literature.

• Effect of cross-section area: Yin et al. [2] examined the effect of cross-section area on fire resistance in their study comparing the fire resistance of square and circular CFST columns. In general, it has been reported that fire resistance decreases as the cross-sectional area decreases. Similarly, in Lie and Chabot’s study [10], one of the parameters used in investigating the fire resistance of plain square- and circular-section CFST columns was the cross-sectional area. The study reported that increasing cross-sectional dimensions resulted in higher fire resistance. Han et al. [27] investigated the behavior of axially loaded square- and circular-section CFST columns under standard fire test conditions. Their study reported that section size had a significant effect on fire resistance and that fire resistance increased significantly with increasing section size. As the section size increased from 300 mm to 1200 mm, the fire resistance increased from 83 min to 188 min for the circular section. This was attributed to faster heat transfer and quicker deterioration in columns with smaller cross-sectional areas.
• Effect of steel tube wall thickness (t_s): Lie and Chabot [10] conducted experimental studies to determine the fire resistance of square and circular CFST columns. One of the parameters in this study was the steel tube wall thickness. It was reported that increasing the steel tube thickness from 4.78 mm to 6.35 mm for columns tested under the same load increased the fire resistance from 76 min to 81 min. However, two different sample tests yielded opposite results, reporting that increasing the steel tube thickness decreased the fire resistance. Within the scope of this study, it was stated that the thickness of the steel tube had very little effect on fire resistance.
• Effect of concrete compressive strength (f_c): The literature presents varying results regarding concrete compressive strength. Mao et al. [11] investigated the effect of concrete strength on the fire resistance of CFST columns. The study was conducted on steel-reinforced CFST columns and reported that increasing concrete strength from 30 MPa to 60 MPa resulted in an 11% decrease in fire resistance. They attributed this result to the gradual decrease in concrete strength with increasing temperature and the greater loss in strength at high temperatures. In their experimental studies, Wang and Young [12] reached a conclusion contrary to the findings of Mao et al. [11]. It was reported that in CFST columns with the same material and dimensional properties, increasing the concrete strength from 30 MPa to 50 MPa increased fire resistance from 151 min to 227 min. Han et al. [27] investigated the effect of concrete strength on the fire resistance of CFST columns. They concluded that when columns have relatively small cross-sectional dimensions, concrete strength has a moderate effect on fire resistance, while in columns with larger cross-sectional dimensions, fire resistance generally increases significantly with increasing concrete strength.
• Effect of steel yield strength (f_sy): Wang and Young [12] also examined the effect of steel strength in the same study. They reported a fire resistance of 151 min when the steel strength was 275 MPa, 73 min when it was 460 MPa, and 46 min when it was 690 MPa. Xiong and Liew [28] conducted experimental and analytical studies on the fire resistance of CFST columns. They reported that fire resistance decreased by up to 21% with increasing steel strength.
• Effect of load ratio (μ): Lie and Chabot [10] conducted an experimental study examining the effect of load level on the fire resistance of square and circular CFST columns. As a result of the study, it was reported that fire resistance decreased as the load level increased. It was reported that increasing the load level of a sample from 74% to 141% reduced the fire resistance from 133 min to 70 min. Wang and Young [12] reported that the fire resistance of columns decreased as the load level increased. They reported that the fire resistance of two columns of the same dimensions and materials decreased from 151 min to 54 min when the load level was increased from 0.3 to 0.5. The studies concluded that the load level has a significant effect on the fire resistance of columns, and this effect is observed relatively more in columns with larger diameters.

3. Previous Approaches

Various mathematical expressions have been developed in the literature to estimate the fire resistance of concrete-filled steel tube (CFST) columns [13,19,20,29,30]. Some of these numerical models include the simplified calculation model in EN 1994-1-2 [13], the simplified design equation proposed by Kodur [20], the design equation used in the Japanese code [19], China’s technical code for CFST structures [29], and China’s code for the fire safety of steel structures in buildings [30].

The simplified calculation model of EN 1994-1-2 [13], China’s technical code for CFST structures [29], and China’s fire safety code for steel structures in buildings [30] are used to estimate the residual axial load-carrying capacity of a CFST column. None of these numerical models have the ability to predict the time-dependent fire performance of a CFST column. The result of the design equation used in the Japanese code [19] is also the remaining axial load-carrying capacity, like that of the other three formulas mentioned, but this formula includes a time parameter to obtain the result. In this study, an attempt was made to calculate the fire resistance duration using this formula. In the formula, time is set as an unknown parameter in the equation, and the axial load-carrying capacity is placed on the right side of the equation as a known parameter. However, as a result of this process, it was concluded that the formula does not provide reliable results, especially when the axial load-carrying capacity is very low. Therefore, this model from the Japanese code was not used for comparison with the models created within the scope of this study.

As a result, the time-dependent fire performance of axially loaded, circular, long CFST columns cannot be predicted using the existing design formulas mentioned above. Among the current approaches, it can only be predicted using the simplified design equation proposed by Kodur [20]. Due to this critical gap, Kodur’s model was considered the main reference in the validation and comparison of the analytical design model developed in this study. While calculating the time-dependent fire resistance for the 62 data-points used in the study, the model’s formula was also used for data-points outside the limits of Kodur’s formula.

4. Description of the Dataset

In this study, a database consisting of the results of experimental studies testing the fire resistance of axially loaded, circular, long CFST columns in the literature was used to develop design models using soft computing techniques (example geometric details and loading configuration are shown in Figure 2). The compiled dataset integrates results from various experimental programs; thus, the potential influence of differences in testing conditions must be addressed to justify data homogeneity. All referenced studies adhered to standardized fire testing protocols concerning furnace type, end plate placement, thermocouple configuration, and loading setup, with only negligible experimental variations. A key difference lies in the temperature–time curves used: four of the six references utilized the ISO 834-1 Standard Fire Curve [27,31,32,33], while two studies [10,34] followed the ASTM-E119 procedure. We justify the use of this combined data based on the findings of Harmathy et al. [35], which demonstrated that for typical fire tests of shorter duration (relevant to the failure times observed in the dataset), the difference in severity between the ASTM and ISO 834-1 curves is slight and becomes negligible in longer tests. Therefore, considering the consistency in other critical experimental parameters, the dataset is considered sufficiently homogeneous for the development of robust predictive models.

The data repository created for model development contains a total of 62 data-points, obtained from six different experimental studies in the literature summarized in

Table 1. A summary of the dataset gathered from the experimental studies. #: number of data.

Sources	#	D (mm)	ts (mm)	fc (MPa)	fsy (MPa)	L/D	µ	R (min)
Lie and Chabot [10]	37	141.3–406.4	4.78–12.70	23.5–90.5	300.0–350.0	9.4–27.0	0.09–0.45	46–292
Kodur and Lie [34]	5	323.9–406.4	6.35	41.2–43.2	300.0	9.4–11.8	0.35–0.67	66–224
Romero et al. [32]	5	159.0	6.00	28.6–71.1	337.8–341.4	20.0	0.20–0.60	11–14
Han et al. [27]	2	300.0	5.00	53.2	451.0	12.0	0.30–0.45	67–132
Tao et al. [33]	2	195.6–196.2	2.95	40.3	292.9	9.5–9.6	0.31–0.48	122–197
Li et al. [31]	11	230.6–314.5	4.81–7.81	30.0–50.0	235.0–420.0	12.1–16.5	0.30–0.40	33–80

[10,27,31,32,33,34]. For developing an acceptable model, Frank and Todeschini [36] suggested a minimum ratio of three between the number of datasets and the number of input variables. To guarantee the robustness of the model, a ratio of five or more is recommended [37,38,39,40,41,42,43]. In the present investigation, this ratio was 62/6 = 10.33, which substantially exceeds the recommended criterion. Furthermore, there are studies in the literature with data/parameter ratios much lower than or almost equal to that in the current study. For example, one of the studies was quite similar to the current study, with 64 samples and 6 features, and was carried out by Moradi et al. [4].

The following independent (input) parameters were used in the derivation of the design models: circular steel tube diameter (D), steel tube wall thickness (t_s), 28-day concrete cylinder strength (f_c), steel tube yield strength (f_sy), the slenderness ratio (L/D), and the load ratio (μ). The time-dependent fire performance (t) of axially loaded, circular, long CFST columns was identified as the dependent (output) parameter.

In the present study, it is acknowledged that certain input parameters such as D, t_s, and L/D are geometrically interrelated and may potentially lead to multicollinearity. While this situation can lead to instability in the coefficients in traditional linear regression models, the non-linear machine learning techniques preferred in this study, ANNs and GEP, exhibit higher robustness against such dependencies [21,44,45]. These models enable the combined use of geometrically related engineering parameters because they can successfully capture complex and non-linear relationships. ANNs, in particular, effectively incorporate these dependencies into the model by transforming the input space in a non-linear manner through hidden layers.

The concrete compressive strength (f_c) values tested in the studies were converted to standard cylindrical specimens using coefficients provided by the researchers to ensure uniformity in the model development, as these values were measured using specimens of different sizes and shapes [46,47]. For the developed models, the units of the parameters are defined as MPa for material strength, mm for the diameter and thickness of the steel tube, and dimensionless for the slenderness and load ratios.

To visualize the distributions of the variables, the density histograms and normal distributions of the input and output parameters are shown in Figure 3. The statistical variability of the circular long CFST columns under investigation is characterized by the histograms of seven fundamental parameters and the normal distribution curves (red curves) fitted to them. When examining material and geometric properties, steel tube diameter (D) and yield strength (f_sy) exhibited relatively symmetric distributions centered around approximately 250 mm and 350 MPa, respectively. In contrast, variables such as steel tube thickness (t_s) (center ≈ 8 mm) and 28-day concrete compressive strength (f_c) (center ≈ 30−40 MPa) were observed to have a structure closer to the theoretical normal distribution but slightly skewed. Among the element-level behavior parameters, the slenderness ratio (L/D) showed a pronounced right skewness with the highest frequency in the 5–10 range, indicating that most elements had low slenderness. The load ratio (μ) presented a distribution that could be considered symmetric, concentrated in the 0.3–0.4 range, while the fire resistance duration (t) variability was characterized by a positively skewed distribution, with the majority clustered in the 100–150 min band. These distributions successfully modeled the input uncertainties of the elements for reliability analyses.

The correlation matrix presented in Figure 4 clearly shows the linear relationship between parameters of the models, fire resistance duration (t), and each of the six input parameters. According to the analysis results, steel tube diameter (D) (+0.547) and slenderness ratio (L/D) (−0.523) are the dominant variables with the strongest correlation with the output parameter. As the diameter (D) increases, the fire resistance time increases at a moderate–strong level; conversely, as the slenderness ratio (L/D) increases, the resistance time decreases at a moderate–strong level and to a significant extent. The negative relationship determined as −0.385 with steel tube yield strength (f_sy) indicates that an increase in strength has a weak to moderate negative effect on fire resistance duration (t). When the other input variables are examined, steel tube thickness (t_s) exhibits a weak positive correlation (+0.224), and the load ratio (μ) (−0.106) and especially concrete compressive strength (f_c) (−0.028) show an almost negligible weak linear relationship with fire resistance duration (t). These findings indicate that the effects of the diameter and slenderness ratio variables are much more pronounced and significant compared to the others in the analytical modeling process.

5. Overview of Soft Computing Techniques

Soft computing is defined as the sum of various methods that utilize uncertainty, imprecision, and partial accuracy tolerance to provide traceability, robustness, better alignment with reality, and lower solution costs [21,22]. This approach models the cognitive approach of human reasoning and intelligence and typically involves iterative development or learning based on empirical data [48]. Fuzzy computing deals with approximate models and provides solutions to complex real-life problems such as engineering problems, communication, financial forecasting, signal processing, design, and manufacturing [49,50]. Genetic expression programming (GEP) and artificial neural networks (ANNs) are the two most popular soft computing techniques used to derive such analytical models.

5.1. Genetic Expression Programming (GEP)

To solve specific problems, scientists have sought solutions inspired by nature and based on Darwin’s ideas of evolution, conducting research to create self-learning artificial systems. Holland [51] designed genetic algorithms (GAs) by applying an oversimplified version of evolutionary theory to computer systems. A decade later, Cramer [52] proposed genetic programming (GP), which was further developed by Koza [53].

Gene expression programming (GEP), introduced by Ferreira [54], can be considered an advanced form of GAs and GP. Like GP and GAs, GEP uses populations of individuals, selects them based on fitness, and provides diversity using a set of genetic operators. The fundamental difference between the three algorithms stems from the nature of the individuals. While individuals in GAs are fixed-length linear strings, individuals in GP are non-linear entities of various sizes and shapes [54]. In GEP, individuals are encoded using fixed-length linear strings and then represented by non-linear entities of different dimensions [54,55].

In GEP, the process begins by generating a random initial population. The fitness of all chromosomes in the population is evaluated. Those that meet the desired requirements are selected using various operators. This process is repeated until a certain number of generations are obtained or a correct solution is found [54,55]. A flowchart indicating the process following a gene expression algorithm provided by Koza [53] is shown in Figure 5.

5.2. Artificial Neural Networks (ANNs)

Artificial neural networks (ANNs) are computational programs inspired by the human brain’s operating system. In this technological system, which mimics the human brain, neural networks gather and generalize information to solve problems they encounter for the first time. In biological systems, the learning process occurs through synaptic connections between neurons. The learning process in ANNs is based on the backpropagation principle and consists of three stages: the first stage is the forward propagation of the input learning model; the second stage is the calculation and backward propagation of the relevant errors; and the final stage is the adjustment of the weights [56]. Various optimization methods can be used to execute this learning process. The weights of the previous layers are updated through backpropagation of the error between the output and target values, as shown in Figure 6 [57,58].

6. Development of GEP and ANN Models

The developed design models aim to estimate the fire resistance duration of circular long CFST columns subjected to axial load. In developing these models, the diameter of the steel tube (D), the wall thickness of the steel tube (t_s), the 28-day cylinder strength of the concrete (f_c), the yield strength of the steel tube (f_sy), the slenderness ratio (L/D), and the load ratio (μ) were determined as input (independent) parameters. The output (dependent) parameter is the time-dependent fire performance of circular long CFST columns subjected to axial load.

GeneXproTools.5.0 [59] and MatlabV.R2018 [60] software were used to develop these design models.

6.1. GEP Model

The GEP model presented in this study was obtained with a generation with 300 chromosomes, 15 head sizes, and 12 genes.

Model parameters and operations: The mathematical operation selected to connect genes was ‘addition’. Various mathematical operations were assigned in the generation to increase the accuracy of the model: addition (+), subtraction (−), multiplication (*), division (/), square root (Sqrt), natural logarithm (ln), square of x (X2), cube root (3Rt), and tangent (tan). A constant per gene was not considered during the creation of the design model. The mutation, inversion, recombination, and transposition rates used in the development of the model are listed in

Table 2. GEP parameters used in the development of the design model [22].

P1: Function set	+, −, *, /, Sqrt, ln, X2, 3Rt, tan
P2: Number of generations	998,975
P3: Chromosomes	300
P4: Head size	15
P5: Number of genes	12
P6: Linking function	Addition
P7: Mutation rate	0.00138
P8: Inversion rate	0.00546
P9: One-point recombination rate	0.00277
P10: Two-point recombination rate	0.00277
P11: Gene recombination rate	0.00277
P12: Gene transposition rate	0.00277
P13: Constants per gene	-

(e.g., mutation rate of 0.00138, number of genes of 12).

GEP Formula: The expression trees of the model developed using GEP (presented in Figure 7) and its formulaic expression are presented in Equation (1). Equation (1) is the final, composite GEP formula, which is the sum of the twelve sub-expression trees. Equations (1a) to (1l) are the step-by-step mathematical representations derived from Figure 7a to Figure 7l, respectively. These equations are essential for readers who wish to manually verify or implement the GEP model using the full analytical expression.

$$t_{\mathrm{G}\mathrm{E}\mathrm{P}}=t_1+t_2+t_3+t_4+t_5+t_6+t_7+t_8+t_9+t_{10}+t_{11}+t_{12}$$

(1)

$$t_1=\tan \left(f_{sy}\right)+\tan \left({\displaystyle \frac{{\left(f_{sy}\times L/D-\mu \right)}^2}{D-f_{sy}+f_c}}+{\displaystyle \frac{f_c}{L/D}}\right)$$

(1a)

$$t_2=\sqrt[3]{\left(L/D-2f_c+f_{sy}+{\displaystyle \frac{\mu \times L/D}{\tan \left(L/D\right)}}\right)\times {\displaystyle \frac{2D\sqrt{f_c}}{L/D}}}$$

(1b)

$$t_3=\sqrt[9]{\left(\tan \left(f_c\right)+t_s^2-{\displaystyle \frac{D}{t_s}}\right)\times D^3\times \tan \left(t_s-f_c\right)\times L/D}$$

(1c)

$$t_4=\tan \left(f_{sy}+L/D+f_C\times \ln \left(t_s\right)\right)$$

(1d)

$$t_5=\sqrt{\left(f_c+{\displaystyle \frac{D}{t_s}}\right)\times \left(\sqrt{D}+\tan \left(D\right)\right)-\tan \left(D\right)\times t_s^2-\left(\mu -L/D\right)\times t_s}$$

(1e)

$$t_6=\sqrt[3]{2\times \tan \left(\sqrt[3]{{(L/D)}^4}\right)\times \tan \left(\sqrt[3]{{(L/D)}^2}\right)\times L/D-D}$$

(1f)

$$t_7={\displaystyle \frac{\ln \left({\left(f_{sy}\times \left(f_{sy}-D\right)\right)}^2+f_c^4\times f_{sy}\right)}{\ln \left(\sqrt{t_s}\right)}}$$

(1g)

$$t_8=\tan \left({\displaystyle \frac{\mu }{\tan \left(\frac{f_{sy}}{\frac{\left(f_{sy}-D\right)\times t_s\times f_c}{\mu +L/D}-f_c+D\times f_c}\right)}}\right)$$

(1h)

$$t_9=\sqrt[3]{\left(\sqrt{f_c}\times \left(t_s+f_{sy}-t_s\times f_c\right)+\mu -f_c-D\right)\times \tan \left(f_{sy}+\mu \right)\times \mu }$$

(1i)

$$t_{10}=\sqrt[3]{D^2-f_c\times L/D-\tan \left(f_{sy}\right)\times 2f_{sy}+\mu -2f_{sy}-f_{sy}\times f_c}$$

(1j)

$$t_{11}=\sqrt[3]{f_c\times \left(t_s\times \left(t_s+f_{sy}-f_{sy}\times L/D\times \mu \right)+\left(D-2\right)\times L/D+f_{sy}\right)}$$

(1k)

$$t_{12}=\tan \left(\sqrt{D\times \left(\left(1+\mu \right)\times L/D+f_c\right)}\right)$$

(1l)

Symbol Notation: The symbols d0, d1, d2, d3, d4, and d5 in the expression trees represent the following input parameters:

−

d0: Diameter of the circular steel tube (D);

−

d1: Wall thickness of the steel tube (t_s);

−

d2: Twenty-eight-day concrete cylinder strength (f_c);

−

d3: Yield strength of the steel tube (f_sy);

−

d4: Slenderness ratio (L/D);

−

d5: Load ratio (μ).

During model creation, the software may sometimes omit certain input parameters in order to train the optimal model with the best fit; however, in this study, it can be clearly observed that all input parameters are used repeatedly. In addition, the complex structure of the GEP model stems from the need to capture the non-linear and multi-dimensional relationships between input parameters with high accuracy. While this complexity reduces interpretability to a certain extent compared to traditional equations, the high prediction performance achieved and the ability to present results in an explicit form demonstrate that the model retains its value for practical engineering applications.

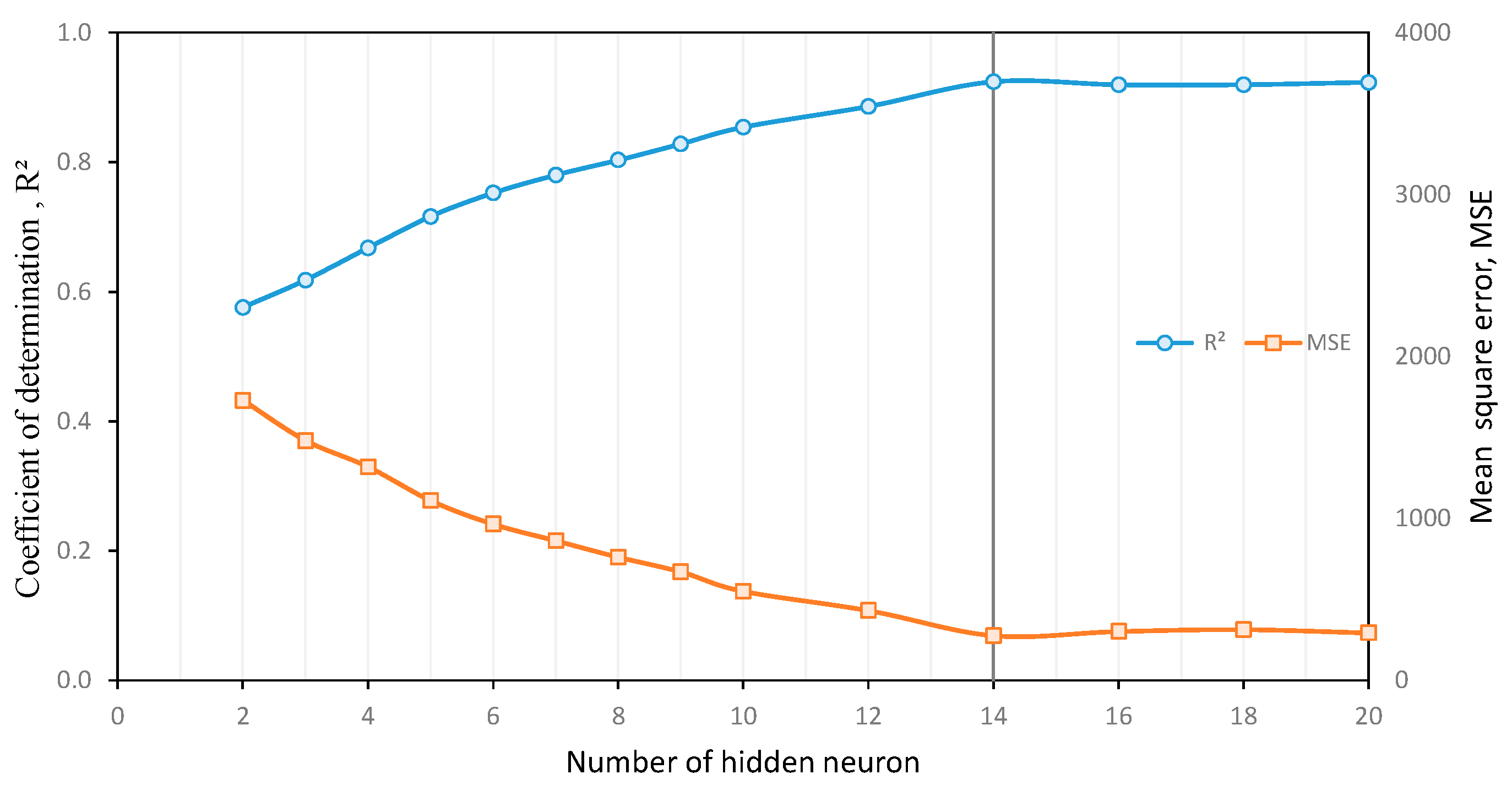
6.2. ANN Model

When creating the ANN model, bias values that have no relationship or interaction with the actual input values were used to better fit the output data. The activation data was shifted to the left and right to better fit the output data.

Normalization: Since the fuzzy–neural controller manages all operations based on normalized values, the output values are also in normalized form. The actual input values are normalized using Equation (2). The coefficients a and b are calculated using Equations (2a) and (2b). The goal is to obtain maximum and minimum values of +1 and −1, respectively, using these normalization coefficients. The minimum–maximum values in the database and the normalization coefficients are shown in

Table 3. Normalization coefficients for the database.

Input and Output Variables	Normalization Parameters
	βmax	βmin	a	b
D (mm)	406.4	141.3	0.007544	−2.06601
ts (mm)	12.7	2.95	0.205128	−1.60513
fc (MPa)	90.5	23.5	0.029851	−1.70149
fsy (MPa)	451	235	0.009259	−3.17593
L/D	27	9.4	0.113636	−2.06818
µ	0.67	0.09	3.448276	−1.31034
t (min)	292	11	0.007117	−1.07829

.

$${\beta }_{norm}=a\beta +b$$

(2)

$$a={\displaystyle \frac{2}{{\beta }_{max}-{\beta }_{min}}}$$

(2a)

$$b=-{\displaystyle \frac{{\beta }_{max}+{\beta }_{min}}{{\beta }_{max}-{\beta }_{min}}}$$

(2b)

Learning algorithms and architecture: The Levenberg–Marquardt regularization backpropagation algorithm was preferred in model derivation to achieve better generalization results. The model was derived using a single-layer neural network consisting of three layers: input, hidden, and output. The number of nodes in the input layer was specified as six, as there were six input parameters. The number of nodes in the output layer was set to one, as the fire resistance duration of circular long CFST columns was the single output parameter. Trial and error was applied to determine the appropriate number of nodes for the hidden layer. As shown in Figure 8, showing the average R² and MSE values corresponding to the number of neurons in the hidden layer, improvement was observed up to a node count of 14; no significant improvement in the model’s prediction performance was achieved when selecting a node count higher than 14. Based on this observation, the number of nodes in the hidden layer was selected as 14. Hyperbolic tangent transfer functions were defined in the hidden layer and linear transfer functions in the output layer. The schematic representation of this neural network, created according to the criteria mentioned, is presented in Figure 9.

ANN formula: The expression of the simplified ANN design model is given in Equation (3), while its structural representation is given in Equation (4). Equation (4) shows the Bias_{output layer} value as −0.88562. Equation (5) presents the matrix that can be used to calculate the functions from t₁ to t₁₄ in normalized form. The hyperbolic tangent activation function is obtained using Equation (6).

$$t_{ANN}=\sum _{j=1}^n{W}_k{f(U}_k)+{Bias}_{output layer}$$

(3)

$$\begin{array}{cc}\hfill t_{ANN}=-0.61422& \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_1\right)-2.0038\tanh \left(t_2\right)+0.61434\tanh \left(t_3\right)+1.5169\tanh \left(t_4\right)-2.0028\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_5\right)\hfill \\ \hfill & -1.4074\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_6\right)-1.6519\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_7\right)-1.8728\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_8\right)-1.0833\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_9\right)\hfill \\ \hfill & -1.7094\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_{10}\right)+1.2352\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_{11}\right)+0.172\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_{12}\right)-2.0114\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_{13}\right)\hfill \\ \hfill & +1.4323\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(t_{14}\right)-0.88562\hfill \end{array}$$

(4)

$$\left[\begin{array}{ccc}0.15137& 1.8484& -0.20257\\ -2.6671& 0.77012& -0.92724\\ \begin{array}{c}-1.5826\\ -0.30966\\ \begin{array}{c}0.28927\\ 0.32064\\ \begin{array}{c}0.9522\\ -3.0535\\ \begin{array}{c}-1.2385\\ -1.7721\\ \begin{array}{c}-1.4933\\ -1.609\\ \begin{array}{c}2.9038\\ -1.2663\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}-0.0033986\\ 0.7034\\ \begin{array}{c}-2.4093\\ -3.0434\\ \begin{array}{c}0.856\\ 0.64893\\ \begin{array}{c}0.81613\\ 3.3639\\ \begin{array}{c}-0.073577\\ 0.40477\\ \begin{array}{c}0.1047\\ 0.10891\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}-0.86054\\ 1.7967\\ \begin{array}{c}1.4273\\ 1.5038\\ \begin{array}{c}-2.2753\\ 1.6889\\ \begin{array}{c}-2.6525\\ -0.12434\\ \begin{array}{c}1.0759\\ 0.76739\\ \begin{array}{c}-0.95076\\ -1.9804\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array} \begin{array}{ccc}0.084887& -2.5866& -0.71378\\ 2.0349& 0.34084& 5.793\\ \begin{array}{c}-0.14422\\ -1.15\\ \begin{array}{c}0.36594\\ 3.2107\\ \begin{array}{c}-0.32085\\ -2.3425\\ \begin{array}{c}-0.34209\\ 2.3629\\ \begin{array}{c}2.4223\\ 0.05804\\ \begin{array}{c}-0.30116\\ 0.44688\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}-1.0944\\ -0.98321\\ \begin{array}{c}-0.28529\\ -0.57974\\ \begin{array}{c}2.126\\ -1.2741\\ \begin{array}{c}3.4326\\ -0.015379\\ \begin{array}{c}-0.27775\\ 2.7292\\ \begin{array}{c}0.16171\\ 1.5778\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}-0.21906\\ 3.5522\\ \begin{array}{c}-1.4177\\ 2.0869\\ \begin{array}{c}-5.0477\\ -0.16844\\ \begin{array}{c}2.8859\\ 1.766\\ \begin{array}{c}-1.8841\\ 2.0466\\ \begin{array}{c}1.413\\ -0.50587\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}D\\ t_s\\ \begin{array}{c}{f}_c\\ f_{sy}\\ \begin{array}{c}L/D\\ \mu \end{array}\end{array}\end{array}\right]+\left[\begin{array}{c}-0.11037\\ 4.6321\\ \begin{array}{c}1.1119\\ 3.7169\\ \begin{array}{c}-0.64188\\ 0.64726\\ \begin{array}{c}-0.58825\\ 0.16229\\ \begin{array}{c}0.32649\\ 0.97631\\ \begin{array}{c}-0.95535\\ -3.853\\ \begin{array}{c}0.15672\\ 1.4241\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array} \right]=\left[\begin{array}{c}{t}_1\\ t_2\\ \begin{array}{c}{t}_3\\ t_4\\ \begin{array}{c}{t}_5\\ t_6\\ \begin{array}{c}{t}_7\\ t_8\\ \begin{array}{c}{t}_9\\ t_{10}\\ \begin{array}{c}{t}_{11}\\ t_{12}\\ \begin{array}{c}{t}_{13}\\ t_{14}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array} \right]$$

(5)

$$\tanh \left(x\right)={\displaystyle \frac{2}{1-e^{-2x}}}-1$$

(6)

The need for denormalization: It is important to denormalize the fire resistance duration value calculated using Equation (4) using the normalization coefficients in Table 3 by Equation (7):

$${\beta }_{denormalized}={\displaystyle \frac{{\beta }_{norm}-b}{a}}$$

(7)

7. Results and Discussion

In this study, a dataset was used that was compiled from experimental data in the literature and met the proposed criteria in terms of the data/input variable ratio. However, increasing the size of the dataset is always desirable to further improve the performance and generalization ability of machine learning models. In this context, synthetic data generation approaches stand out in the literature as a solution to limited experimental datasets. For example, the study by Kazemi et al. [61] enriched the dataset with synthetic data using artificial intelligence-based tools and improved model robustness with this method. Validating a design model and evaluating its prediction performance is an important step. Within the scope of this study, the prediction performance of developed design models aimed at predicting the time-dependent fire performance of circular long CFST columns subjected to axial load was compared.

7.1. Independent Validation with Synthetic Data

Due to the methodological preference of maximizing the training power of the limited experimental dataset (62 data-points), the generalization and robustness capabilities of the developed ANN and GEP models were externally validated using an independent synthetic dataset. This approach aimed to demonstrate that the models did not merely memorize training data (overfitting) but also learned the fundamental physical relationships underlying the dataset.

Five different synthetic data generation algorithms (Gaussian Noise, interpolation, Jittering, MixUp, and SMOTE-Regression) were used to create the synthetic dataset, and these algorithms were combined with four different basic modeling approaches: Gradient Boosting, Random Forest, Ridge, and Lasso. Three different standard deviation (std) values of 5%, 7%, and 10% were applied for each model–algorithm combination, producing a total of 60 different synthetic datasets (5 algorithms × 4 models × 3 std). All synthetic datasets produced were evaluated in terms of their Cross-Validation Root Mean Square Error (CV RMSE) value, and it was determined that synthetic datasets obtained from the combination of the interpolation algorithm with Gradient Boosting and Random Forest models yielded the lowest CV RMSE values. Although the CV RMSE values of these two models were quite close to each other, the final independent validation set consisting of 62 data-points was taken from this combination due to the slightly superior performance of the Gradient Boosting model in synthetic data generation.

The selected synthetic dataset preserves the statistical properties of the original experimental data. The ranges of the synthetic input and output parameters are as follows:

-

Circular steel tube diameter (D): Between 141.3 mm and 390.5 mm (ave: 272.4 mm).

-

Steel tube wall thickness (t_s): Between 2.95 mm and 10.55 mm (ave: 6.35 mm).

-

Twenty-eight-day concrete cylinder strength (f_c): Between 23.5 MPa and 48.4 MPa (ave: 34.6 MPa).

-

Steel tube yield strength (f_sy): Between 267.7 MPa and 451.0 MPa (ave: 338.5 MPa).

-

Slenderness ratio (L/D): Between 9.6 and 27.0 (ave: 14.9).

-

Load ratio (μ): Between 0.12 and 0.59 (ave: 0.30).

-

Time-dependent fire performance (t): Between 39.3 min and 230.7 min (ave: 103 min).

The prediction performance of the GEP and ANN models developed using the independent synthetic dataset obtained using the method detailed above is presented in Figure 10. This figure clearly shows the strong correlation between the fire resistance duration (t) predicted by the models and the t values in the synthetic dataset. The fact that both the GEP and ANN models grouped the data-points close to an ideal prediction line (the 45° line) confirms that the models successfully captured the overall distribution of the synthetic dataset.

The performance metrics, mean square error (MSE), and mean absolute error (MAE) calculated using Equations (8) and (9), obtained using the independent synthetic dataset, were as follows:

$$MSE={\displaystyle \frac{1}{n}}{\left(\sqrt{\sum _{i=1}^n{{(m}_i-p_i)}^2} \right)}^2$$

(8)

$$MAE={\displaystyle \frac{1}{n}} \sum _{i=1}^n\left|{\displaystyle \frac{m_i-p_i}{m_i}}\right|$$

(9)

-

GEP Model: MSE value of 496 min² and MAE value 18.3 min.

-

ANN Model: MSE value of 569 min² and MAE value of 17.8 min.

The evaluation of MSE and MAE values in terms of the model’s generalization ability shows that both models exhibited very high accuracy. In this context, the ANN model demonstrated slightly superior performance in terms of average error with an MAE value (17.8 min), which means that the model’s predictions had a lower absolute error value. On the other hand, the GEP model demonstrated greater robustness against large errors with its MSE value (496 min²), as MSE penalizes large errors more heavily. Both models, trained on the original limited experimental dataset, were able to make predictions on the synthetic dataset with similar and low error rates. This definitively confirms that the models do not overfit but rather effectively learn the fundamental physical behavior and engineering relationships represented by datasets. This independent validation demonstrates that the models possess strong generalization capabilities and can provide reliable predictions for future unseen data.

7.2. Graphical and R² Assessment

The relationships between the predicted and experimental time-dependent fire resistances of Kodur’s model and the GEP and ANN design models are presented in Figure 11a, 11b, and 11c, respectively. The coefficient of determination (R²) values, some of the basic criteria used to measure the accuracy of the models, were calculated using Equation (10) and are listed in

Table 4. Statistical parameters of Kodur’s equation and developed GEP and ANN design models.

Design Models	Statistical Parameters
	MAPE	nRMSE	f	PI	R2
Kodur	41.81	0.52	2.35	0.30	0.549
GEP	12.96	0.15	1.22	0.08	0.937
ANN	4.41	0.10	1.13	0.05	0.972

MAPE: mean absolute percent error; nRMSE: normalized root mean square error; f: fitness function; PI: performance index; R-squared: coefficient of determination.

. The R² value is an important parameter because it measures the ratio of the variance of predicted results, directly reflecting the prediction performance of a model. An R² value close to 1 (perfect prediction) is a desirable goal in the development of such design models.

$$R^2={\left({\displaystyle \frac{\sum \left(m_i-m\right)\left(p_i-p\right)}{\sqrt{\sum \sum {\left(m_i-m\right)}^2\sum {\left(p_i-p\right)}^2}}} \right)}^2$$

(10)

Model Comparison

When comparing machine learning models with empirical formulas in the literature (e.g., the Kodur formula), it is critically important to consider the experimental constraints under which the formulas were calibrated. The geometric constraints of the formula are as follows:

Column diameter (D): 140 mm ≤ D ≤ 410 mm

Column length (L): 2 m ≤ L ≤ 4 m

D/t_s ratio: D/t_s ≤ 67

All column diameters in our dataset fall within the range recommended by Kodur. Similarly, the D/t_s ratio of all data-points also meets the 67 constraint. In terms of column lengths, 60 out of 62 data-points fall within the recommended 2–4 m range; the remaining 2 data-points (1864 mm and 1878 mm) were not excluded from the assessment as they are very close to the 2 m limit. As a result of this assessment, it was confirmed that the vast majority of the data in the dataset compiled within the scope of this study meet the geometric and structural constraints.

However, the upper limit for the fire resistance duration (t) in the Kodur formula is set at 120 min. Nineteen experimental data-points in our dataset exceed this upper limit, with t > 120 min. The reason for using all 62 data-points in the comparison is that, when these 19 data-points are excluded, the prediction performance of the Kodur formula (R² ≈ 0.03) drops to a meaningless level. This situation clearly demonstrates how weak the generalization ability of empirical formulas is for data outside their calibration range. Therefore, to demonstrate the prediction ability of the ANN and GEP models that overcome the limitations of empirical formulas, a comparison using the entire dataset was methodologically preferred.

To demonstrate the superiority of the proposed computational models, Figure 11 presents the prediction performance (blue line) of the empirical Kodur model and GEP and ANN models against experimental time-dependent fire resistance results (orange line). The Kodur model information shown in Figure 11a indicates that the predicted values fell significantly below the experimental data. This systematic deviation (bias) shows that, although the model generally erred on the safe side, it captured the dynamic behavior of the data and the true peak value with a high margin of error.

In contrast, the developed GEP model (Figure 11b) showed a much closer fit to the experimental data compared to the Kodur model. The model’s successful prediction of high and low time-dependent fire resistance points to the superiority of machine learning-based solutions over traditional empirical approaches. The ANN model presented in Figure 11c showed the highest prediction performance among all approaches examined. The ANN prediction line almost perfectly matches the experimental data, capturing all critical points of the time series (start, peak value, and decay rate) with an error margin close to zero. This visual evidence confirms that artificial neural networks provide the highest accuracy in modeling complex physical behavior, thereby strengthening the scientific validity and practical applicability of the solution. A study [62] to predict the compressive strength capacity of brick columns under various confinement materials obtained results consistent with the current study, and this study indicated that the ANN predictions were in good agreement with the experimental data, while the GEP model showed acceptable prediction performance but performed more sparsely than the ANN model. In another study [22] on the development of prediction models using ANNs and GEP for elliptical CFST columns, it was reported that a design model developed by ANN method yielded a statistically better prediction performance compared to that developed by the GEP method. It was also emphasized that while the distribution of the data obtained from the ANN model was in the form of a straight line, the GEP model showed an acceptable accuracy in prediction performance but was distributed over a wider region.

The R² values used to quantitatively compare the prediction accuracy of the models clearly demonstrate the superiority of the developed computational solutions over traditional approaches. The performance of the empirical model proposed by Kodur is presented in Figure 11a and Table 4, and the R² value was calculated as 0.549. This low R² value statistically proves that the model could explain only approximately 55% of the total variability in the experimental data and that the prediction error was high. This confirms the systematic deviation of the prediction curve observed in the graph from the experimental data. The developed computational models, however, provided a significant leap in performance. The GEP model (Figure 11b and Table 4) increased the R² value to 0.937, explaining more than 93% of the data and radically increasing reliability compared to traditional empirical formulas. However, the ANN model (Figure 11c and Table 4) achieved the highest predictive power. With an R² value of 0.972, the ANN model demonstrated the highest performance among all approaches examined. These results statistically confirm that the ANN model modeled the experimental time series with the highest accuracy using the highest R² value, thereby adding the most accurate and reliable prediction to the knowledge base in this field. It should be emphasized that these models (GEP and ANN) were specifically developed to predict the fire resistance duration of circular long CFST columns subjected to axial load.

7.3. Assessment of Statistical Parameters

Evaluating a model’s prediction performance based solely on the R² value and graphical comparison is insufficient. Therefore, advanced statistical evaluations were used to determine the acceptability of the model performance.

The statistical parameters used, for which results are presented in Table 4 (calculated using Equations (11)–(14)), were the following:

$$\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n} \mathrm{a}\mathrm{b}\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{e} \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e} \mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r} (\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}) ={\displaystyle \frac{1}{n}} \sum _{i=1}^n\left|{\displaystyle \frac{m_i-p_i}{m_i}}\right|x100$$

(11)

$$\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d} \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t} \mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n} \mathrm{s}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{e} \mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r} (\mathrm{n}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}) ={\displaystyle \frac{\frac{\sqrt{{\sum }_{i=1}^n{{(m}_i-p_i)}^2}}{n} }{\overline{m}}}$$

(12)

$$\mathrm{F}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{f}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} (\mathrm{f}) =nRMSE+{\displaystyle \frac{1}{R^2}}$$

(13)

$$\mathrm{P}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e} \mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x} (\mathrm{P}\mathrm{I}) ={\displaystyle \frac{nRMSE}{R+1}}$$

(14)

Error criteria (MAPE and nRMSE): MAPE and nRMSE define the error that occurs during estimation; in such problems, the goal is to have low MAPE values and nRMSE values close to zero. Regarding nRMSE classification, between 0 and 0.1 means excellent performance and between 0.1 and 0.2 means good performance. It can be said that the most reliable prediction performance was obtained from the ANN design model since it had the lowest MAPE value, 4.41. The Kodur model was insufficient in explaining data variation with the highest errors (nRMSE: 0.198; MAPE: 13.90%), while the GEP model (nRMSE: 0.089; MAPE: 6.42%) provided a significant improvement by reducing errors by more than half. Although the MAPE value of the GEP model, 12.96, was relatively high, its prediction capability cannot be ignored. The nRMSE values of the GEP (0.15) and ANN (0.10) models indicate that their prediction performance fell into the good category. When compared in terms of nRMSE values, the prediction capability of the ANN design model was much better than the other two models. Chen et al. [63] developed three models for predicting axial compressive strength, two of which were GEP- and ANN-based, and compared their models with existing design codes using various statistical metrics, similarly to the comparisons made above. The researchers noted that these two models were more accurate in predicting experimental results than the other models and design codes compared, as they achieved lower MAPE and RMSE values. Similarly to the model in the current study, when comparing the GEP and ANN models, the ANN model demonstrated better prediction capability based on statistical evaluations.

Suitability and performance index (f and PI): The target is for the f value to be close to 1 and the PI value to be close to 0. The f value of the ANN design model was obtained as 1.13 and the PI value as 0.05. The f value of the GEP design model was obtained as 1.19 and the PI value as 0.08. The f value of the current model proposed by Kodur was calculated as 2.35 and the PI value as 0.30. In a study on the evaluation of ANNs and GEP as predictive tools, Gandomi and Roke [37] compared the performance of these modeling techniques using several statistical metrics. One of the metrics used in this study was PI, and they stated that the model predicted true values well when a PI value close to zero was obtained. They obtained PI values of the GEP and ANN models as 0.073 and 0.056, respectively, and stated that both models had good predictive abilities since the PI value was less than 0.2. In the current study, the PI values of 0.08 and 0.05 indicate that the ANN and GEP models met the target criteria. In addition, as in the study carried out by Gandomi and Roke [37], the model developed by the ANN method yielded a lower PI value compared to the GEP method’s model.

Similarly, İpek et al. [55] compared the prediction performance of GEP and ANN models on the basis of the identical statistical metrics. These metrics were MAPE, nRMSE, f, and PI, the same metrics as those in the current study. They concluded that existing design models may have good predictive performance, but this statistical comparison concluded that the prediction capability of ANN- and GEP-based design models is much better. Their results also revealed that the ANN-based design model exhibited a higher prediction performance than the GEP-based one.

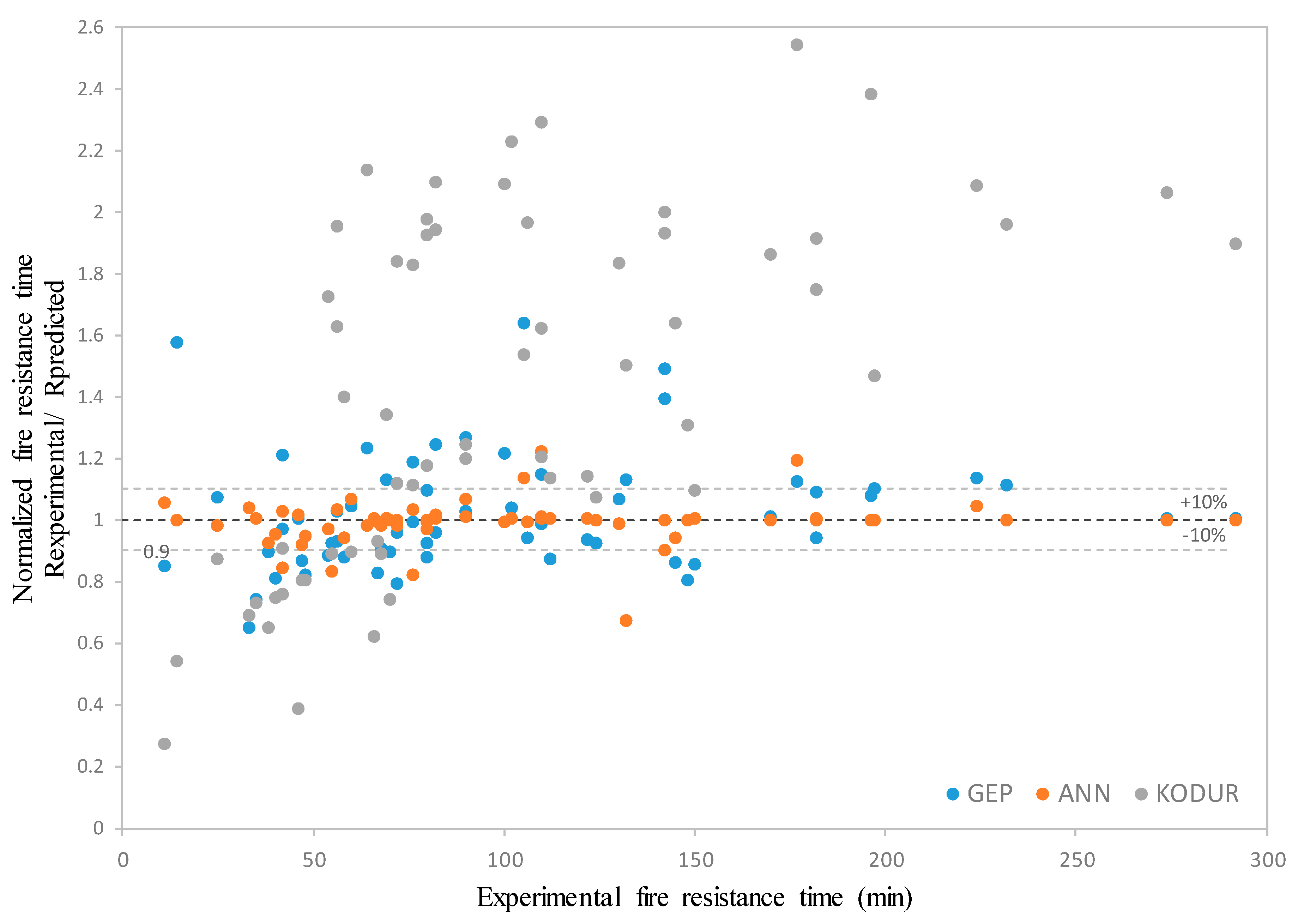
7.4. Comparison of Normalized Results

All three models were also evaluated and compared in terms of normalized time-dependent fire resistance values. Figure 12 is a graph showing the error distribution of the proposed prediction model across the entire dataset. The vertical axis of the graph represents the experimental/predicted ratio (R_exp/R_pred), while the horizontal axis represents experimental fire resistance time. This ratio measures how close the predicted result is to the experimental result. For an ideal model, this ratio is expected to be 1.0. The straight line at the center of the graph (the 1.0 line) represents the ideal situation where the predicted results are exactly equal to the experimental results. This graph is a critical tool that validates previous statistical findings across the entire dataset.

The Kodur model, represented by gray dots, shows the predictions that are furthest from the ideal line of 1.0 and spread over the widest area among the three models examined. This wide deviation directly supports the model’s low R² value (0.549) and high error rates (MAPE: 13.90%) visually. The tendency for the vast majority of Kodur points to lie above the 1.0 line indicates that the model systematically underestimated (on the safe side) the experimental values. In contrast, the GEP model, shown by blue dots, clusters in a much narrower band around the 1.0 line, ideal according to Kodur. This visually reinforces the significant improvement achieved in the model’s performance (GEP R²: 0.937). The ANN model, represented by the orange points, shows the highest performance. All points belonging to the ANN model exhibit the closest and tightest clustering to the ideal 1.0 line compared to the other two approaches. This visual analysis clearly demonstrates that the ANN model had the lowest error (nRMSE: 0.071), offered the highest consistency, and produced accurate predictions without systematic deviation across the entire data range, thereby confirming the model’s superiority across the entire dataset. Evaluation of the estimation capability of the models developed by the ANN and GEP methods based on the normalized values was carried out using the literature. Among these evaluations, one revealed that the ANN method generally led to a significantly narrow range for the normalized values compared to the GEP method [55]. In other words, the normalized peak strength values of the GEP-based design were found to be within a wide range, whereas those of the ANN-based design model were found to be within an extremely narrow range, independent of the experimental peak strength. When comparing the normalized values of the GEP and ANN models, the current study produced results that were compatible with the results of this investigation.

7.5. Sensitivity Analysis Based on Input Parameters

Following the development and comparison of the models, an analysis was also conducted on how their prediction capabilities changed according to the input parameters (D, t_s, f_c, f_sy, L/D, μ). These changes are presented in Figure 13a–f. The graphs show the normalized strength values (Y-axis) predicted by the GEP (blue dots) and ANN (orange dots) models in response to changes in the input parameters (X-axis). These graphs visualize the sensitivity and fitness of the models to one of their key input parameters.

Upon examining Figure 13a, it is seen that the blue points belonging to the GEP model follow the general trend of normalized strength values as the steel tube diameter increases, but they exhibit a distribution with significant dispersion and noise. This dispersion indicates that the GEP model’s predictions are less consistent even for the same diameter values and that the model captures the physical relationship between diameter and strength with less accuracy than the ANN model. In contrast, the orange points predicted by the ANN model are clustered in a much smoother and more distinct, narrow band along the X-axis. This tight clustering demonstrates that the ANN model modeled the complex non-linear relationship between steel tube diameter and normalized strength much more successfully and consistently than the GEP. The high consistency of the ANN model provides strong visual validation, supporting the high R² value (0.972) that indicates the overall success of the model.

In regard to Figure 13b, it can be stated that the blue points belonging to the GEP model show noticeable dispersion and noise, despite capturing the trend that normalized strength values should generally increase with the increase in steel tube thickness. This situation indicates that the GEP model’s predictions were less consistent with thickness changes, as they were with tube diameter, and that the model could model this fundamental physical relationship with less accuracy compared with the ANN model. In contrast, the orange points belonging to the ANN model cluster around a much tighter and more pronounced trend along the X-axis. The fact that the distribution range of the orange points is significantly narrower than that of the blue points proves that the ANN model captured the complex relationship between steel tube thickness and normalized strength much more successfully and consistently than the GEP model.

Regarding the examination of Figure 13c, it can be concluded that although the blue points belonging to the GEP model follow the general upward trend in normalized strength values along with the increase in concrete strength, they exhibit significant dispersion. In particular, the lateral dispersion of the points increases in the high-compressive-strength ranges, indicating that the GEP model’s predictions are less consistent and more sensitive to noise with respect to this important input variable. The most important finding observed is that the orange points belonging to the ANN model follow the tightest and smoothest trend along the X-axis, corresponding to the increase in concrete strength. The distribution range of the orange points is significantly narrower than that in all other sensitivity analyses, as determined by GEP. This demonstrates that the ANN model possesses the highest consistency and accuracy in modeling even complex and non-linear variables such as concrete compressive strength.

The examination of Figure 13d revealed that the blue points belonging to the GEP model capture the general trend in the predicted values along with the increase in steel yield strength. However, they exhibit significant dispersion and noise, particularly in regions where yield strength is high. This situation indicates that the GEP model’s predictions are less consistent against the complex non-linear effect of this variable. The most prominent result observed is that the orange points belonging to the ANN model follow the tightest and smoothest trend corresponding to the change in steel yield strength along the X-axis. The distribution range of the orange points is significantly narrower than that of the blue points belonging to the GEP, proving that the ANN model has the ability to model complex material properties such as steel tube yield strength with the highest consistency and accuracy compared to the GEP.

With respect to scattering in Figure 13e, it can be stated that the blue points belonging to the GEP model capture the expected general trend in the estimated strength values along with the increase in the brittleness ratio. However, they exhibit significant dispersion across the entire range of ductility ratios, particularly at critical medium and high ductility ratios. This dispersion indicates that the GEP model’s predictions are less consistent with the complex buckling behavior of this variable and that the model can model this structural parameter with less accuracy than the ANN model. The ANN model, represented by orange dots, clusters around a much tighter and smoother trend across the entire range of the slenderness ratio, unlike the GEP. This superior consistency in the distribution of orange dots proves that the ANN model has the ability to model the effect of the slenderness ratio on the carrying capacity with minimal error and maximum reliability.

According to Figure 13f, it can be concluded that the blue points belonging to the GEP model exhibit a distinct dispersion across the entire load ratio range. Particularly at points where the load ratio is critical (typically at medium and high load ratios), the deviation of the points from the ideal trend line increases. This indicates that the GEP model’s predictions are less consistent with the complex behavior of this variable and that the model can model this operational parameter with less precision than the ANN model. The ANN model, represented by orange dots, follows a much tighter and smoother trend compared to the blue dots belonging to GEP. The distribution range of the orange dots is significantly narrower than that of the blue dots belonging to the GEP, proving that the ANN model has the ability to model operational and potentially noisy variables such as the load ratio with the highest consistency and accuracy compared to the GEP.

8. Conclusions

In this study, the ANN and GEP models developed to address the problem of predicting the time-dependent fire resistance of circular long CFST columns were compared with a traditional empirical approach (Kodur’s) and their performance was comprehensively analyzed. The main findings are summarized below:

• The prediction performance of the developed GEP and ANN design models was compared with that of the existing Kodur model (R² = 0.549), and it was found that the new models demonstrated significantly superior prediction accuracy.
• As a result of the statistical evaluations performed, it was determined that the ANN-based design model had the highest prediction performance. The ANN model stood out with a coefficient of determination (R²) value of 0.972 and the lowest MAPE = 4.41.
• According to the nRMSE classification, the ANN model fell into the excellent performance category with a value of 0.10 (between 0 and 0.1), while the GEP-based model was observed to fall into the good performance category with an R² value of 0.937 and an nRMSE value of 0.15.
• The reliability and generalization ability of the models were examined in terms of fitness function (f) and performance index (PI) values; the ANN (f = 1.13; PI = 0.05) and GEP (f = 1.19; PI = 0.08) models proved to be statistically convincing and reliable by providing values suitable for the expected targets (f ≈ 1; PI ≈ 0).
• The study revealed that existing design formulas can generally only estimate residual axial load-carrying capacity and cannot predict time-dependent fire performance. However, it was concluded that by developing GEP and ANN models using a wide range of data, the fire resistance duration can be reliably estimated even in situations where the Kodur model has limitations.

Limitation of the Developed Models

The ANN and GEP models developed demonstrate high accuracy and generalization capability; however, for the models to be used reliably in practical engineering applications, the scope and limitations of the dataset used to train them must be clearly stated. As with all empirical or data-driven models, predictions made outside the interpolation range (extrapolation) carry the risk of yielding meaningless results. Therefore, the reliability of the models is limited to the input parameter ranges given in

Table 5. Reliable application ranges and data density constraints of developed ANN and GEP models.

Parameter	Description	Unit	Reliable Application Range (Minimum–Maximum)	Data Density/Preferred Range
D	Circular steel tube diameter	mm	141.3–406.4	The entire dataset
ts	Steel tube wall thickness	mm	2.95–12.7	The range of 4.00–8.50 mm has significantly denser data
fc	28-day concrete cylinder strength	MPa	23.5–90.5	The range of 23.5–55.0 MPa has significantly denser data
fsy	Steel tube yield strength	MPa	235–451	The range of 278–356 MPa has significantly denser data
L/D	Slenderness ratio	-	9.4–27	The entire dataset
μ	Load ratio	-	0.09–0.67	The range of 0.09–0.48 has significantly denser data

The ranges indicated above represent the safe application limits of the models. Furthermore, even within this range, it is recommended that the model be used cautiously in areas with low data density. Future studies should expand the dataset to include data outside these ranges in order to increase the scope of application of the models. This warning addresses the criticism that the model should be used for design purposes only and with caution.

covered by the 62-data-point set used.