Study on Wind Load Distribution and Aerodynamic Characteristics of a Yawed Cylinder

Abstract

The flow mechanism around a yawed cylinder is highly complex. While previous research has confirmed the limitation of the Independence Principle at high yaw angles, the specific flow phenomena beyond 20° yaw remain poorly understood, particularly concerning the spanwise development of the critical regime and the mechanism behind asymmetric surface pressure. Most studies have focused on spatially averaged forces or specific angles, lacking a systematic investigation of the inherent flow characteristics in the intermediate region of finite-length cylinders. To bridge this gap, the present study conducts a detailed wind tunnel test on a yawed cylinder across a wide range of yaw angles (0–60°). By analyzing the pressure distribution and aerodynamic forces in the mid-span region, this study yields the following core findings of universal significance: (1) As the yaw angle increases, the critical flow regime in the intermediate section occurs prematurely. This leads to a decrease in the Reynolds number at which the critical region begins, resulting in the formation of separation bubbles and consequent localized negative-pressure zones on either the upper or lower windward surface of the cylinder. (2) When the yaw angle β ≤ 17.4°, the mean drag and lift in the middle region resemble those of a straight cylinder. However, as the yaw angle increases further, the drag coefficient decreases beyond a certain critical Reynolds number, which itself decreases with increasing yaw angle. (3) At β = 0°, the circumferential mean pressure distribution is symmetric about the cross-sectional axis and remains largely uniform along the span. High yaw angles disrupt this symmetry and uniformity, leading to complex three-dimensional flow structures. These findings have critical implications for the design of structures like inclined bridge towers and cables under oblique winds.

1. Introduction

Super-high-rise buildings often adopt the circular cross-sectional form of a cylinder, which is a common structure in engineering. Force characteristics are some of the key factors to be considered in the design of wind resistance in structures. In practical applications, in addition to the cross-sectional form of high-rise buildings, cylinders are also widely used in aerospace, bridge engineering, power transmission lines, water conservancy projects, mechanical engineering, coastal engineering, nuclear engineering, etc. Great achievements have been made in research on air flow around straight cylinders. When the incoming flow is perpendicular to the cylinder, there are many parameters that affect its flow regime and aerodynamic characteristics, mainly including incoming flow conditions [1,2], surface roughness [3,4], Reynolds number [5,6,7,8,9,10] and slenderness ratio [11,12]. However, in practical engineering applications, not all the axes of the cylinders are perpendicular to the direction of the incoming flow; instead, most have a certain angle, such as in the flow of air over stay cables, transmission lines and bridge towers under the action of oblique wind, oblique ocean currents passing through seabed pipelines seabed, etc. [13]. All of these can be simulated by fluid flowing around a yawed cylinder.

Unlike a cylinder perpendicular to the oncoming flow, the flow mechanism around a yawed cylinder is more complex, especially as the flow regime around finite-length yawed cylinders at high yaw angles remains unclear.

Early researchers studying yawed cylinders decomposed the oncoming flow velocity into a component perpendicular to the cylinder axis (U cos β) and a component parallel to the axis (U sin β). They then used the perpendicular component (U cos β) as the effective flow velocity for studying the yawed cylinder. Sears [14], considering the small viscosity coefficient in the laminar boundary layer, simplified the Navier–Stokes equations for a finite yawed cylinder and theoretically established the role of the perpendicular component. Hoerner [15] proposed that the perpendicular and parallel velocity components act independently, leading to the concept known as the “Independence Principle”.

Wind tunnel tests on finite-length cylinders by King et al. [16] confirmed that the Independence Principle can estimate aerodynamic forces at small yaw angles. This is because the parallel velocity component is small at low yaw angles, having minimal impact on the flow regime. However, the Independence Principle breaks down as the yaw angle increases. Due to the significant magnitude, the axial flow component significantly influences boundary layer separation and vortex formation. Measuring pressure time histories at three different positions on a finite yawed cylinder and performing spectral analysis, Hogan et al. [17] indicated that vortex shedding near the upstream end becomes disordered at high yaw angles (≥30°) and that the Independence Principle is no longer applicable.

Shirakashi et al. [18] investigated vortex shedding around yawed cylinders through wind tunnel tests, revealing that the larger the yaw angle is, the less regular and lower-frequency the vortex shedding is. Vakil [19] conducted numerical simulations on yawed cylinders with varying aspect ratios and yaw angles at low Reynolds numbers, demonstrating that the drag coefficient peaks at a yaw angle of 40°. Gu Ming et al. [20], through an investigation on inclined stay-cable models, documented that both mean and fluctuating wind pressure coefficients vary with yaw angle: as the yaw angle increases, both the stagnation and separation points shift. They emphasized that variations in yaw angle are the primary factor for flow behavior differences between yawed and straight cylinders.

In recent years, numerical simulation has become an important tool for studying this issue. For instance, Wang et al. [21] employed large eddy simulation to investigate flow field structures at high Reynolds numbers, while Zhang et al. [22] combined numerical and experimental methods to reveal the coupling effect of yaw angle and surface roughness. In terms of experimental research, Sun and Gu [23] and Zhou et al. [24] systematically analyzed the surface pressure and aerodynamic characteristics of static yawed cylinders through wind tunnel pressure measurements, and Wei et al. [25] further extended the study to dynamic yaw processes. With the advancement of research methods, emerging technologies such as deep learning have been applied to the rapid prediction of aerodynamic forces [26]. Additionally, related research has expanded to non-circular cross-sections [27,28] and wind engineering applications [29,30,31,32].

However, existing research still lacks a systematic understanding of the evolution of flow patterns in the intermediate region under large yaw angles (>20°), as well as the critical Reynolds number effects and their quantitative relationship with the yaw angle. Most studies have focused on spatially averaged aerodynamic forces or specific angles, failing to clearly reveal the inherent flow characteristics of the intermediate region of finite-length cylinders.

To address these gaps, the present study conducts a detailed wind tunnel test on a yawed cylinder across a wide range of yaw angles (0–60°). By analyzing pressure distributions and aerodynamic forces in the mid-span region, this work aims to (1) systematically document the breakdown of the Independence Principle and identify the critical angle for significant aerodynamic deviation; (2) quantify the effect of yaw angle on the critical Reynolds number and reveal the phenomenon of premature critical transition; and (3) provide a physical explanation for the observed flow phenomena by linking them to yaw-angle-induced boundary layer transition and separation bubble formation. The findings offer new insights for the modeling and design of yawed cylindrical structures under oblique winds.

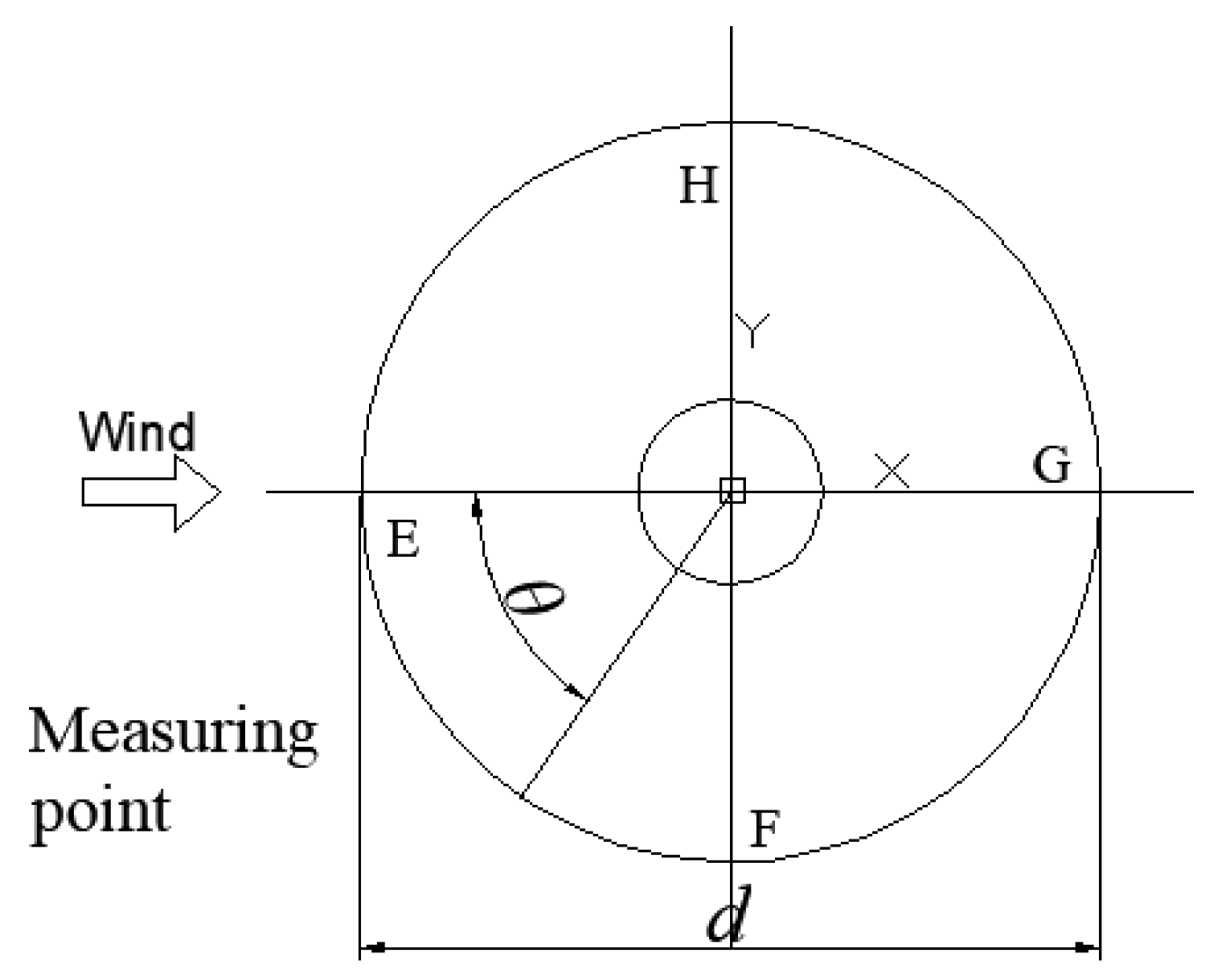
2. Test Overview

2.1. Test Model and Working Condition

The tests were conducted in the low-speed test section of the Wind Tunnel Laboratory at Shijiazhuang Railway University. The test section’s dimensions are 24 m (length) × 4.38 m (width) × 3 m (height), with a maximum wind speed of approximately 30 m/s [33]. The tests were conducted with a turbulence intensity of ≤0.4% and a blockage ratio of 4.0%. The tests were conducted at wind speeds ranging from 5 m/s to 18 m/s. The pressure test was conducted using an ESP-64Hd Pressure Scanning Valve Tester (USA).

As illustrated in Figure 1, the model was constructed of acrylic with a diameter of d = 180 mm. A 40 mm diameter steel tube installed along its central axis enhances structural stiffness. Upstream endplate: 2.4 m (length) × 1.2 m (width). Downstream endplate: 3.6 m (length) × 1.2 m (width). Vertical separation between endplates: 2.9 m. Both endplates contain 0.35 m diameter openings for mounting to the steel frame via steel tubes. Model length varied with the yaw angle β: β = 0°: model length = 3.0 m; β = 60°: model length = 6.0 m.

The cylinder diameter of D = 180 mm was selected to achieve the target Reynolds number range for studying subcritical and critical flow transitions within the wind tunnel’s operational envelope while maintaining a low blockage ratio (<5%). This diameter also provided sufficient surface area for instrumentation and ensured structural integrity.

Figure 2 shows the measurement configuration diagram. Four circumferential measurement arrays (A, B, C, D) were installed along the spanwise direction to capture the flow development and identify the intermediate region. Their distances from the spanwise center were set as follows: A: 1300 mm; B: 650 mm; C: 0 mm (centerline); D: 780 mm. This arrangement was designed to provide sufficient resolution for analyzing spanwise variations and symmetry, based on the model geometry and established practices for studying finite-length cylinders [11,12]. Each array comprised 44 pressure taps positioned at circumferential angles θ.

Figure 3 shows a schematic of the model’s cross-section. There were four axial measurement rows (E, F, G, H) along the span at corresponding circumferential angles of θ = 0°, 90°, 180° and 270°. Each row contained 56 measurement points. Row E was oriented directly into the oncoming flow, with an axial spacing between adjacent points of 100 mm.

The upstream endplate was sealed to prevent partial airflow from circumventing the upstream end of the cylinder. Concurrently, considering the significant axial flow component (U sin β) at large yaw angles—which could lead to flow accumulation near the downstream endplate region—and accounting for the influence of axial flow on the leeward side of the yawed cylinder, the downstream endplate remained unsealed. The configuration of the endplate installation is illustrated in Figure 1.

At small yaw angles, the wind pressure near the downstream endplate is influenced by the endplate configuration. At larger yaw angles, the horseshoe vortex induced by the axial flow alters the spanwise distribution of circumferential pressure. To investigate the aerodynamic forces and flow characteristics in the mid-span region of the yawed cylinder, the study focuses on cross-section C (mid-span) at β = 0°, 17.4°, 30° and 38.6°, and cross-section B at β = 0°, 17.4°, 30° and 38.6°.

2.2. Test Parameters

In this study, the pressure coefficient is defined based on the component of the incoming flow perpendicular to the cylinder axis [34]. The formula is as follows:

$$C_{pn}(t)={\displaystyle \frac{P_{\theta }(t)-P_0}{0.5\rho {(U\cos \beta )}^2}}$$

(1)

In the equation, C_pn(t) represents the time history of the pressure coefficient at the measurement point, θ denotes the circumferential angle, P_θ(t) is the time-dependent wind pressure measured at the point, P₀ refers to the static pressure, ρ is the air density, β is the yaw angle and U represents the wind velocity at the measurement point.

The arithmetic mean of the pressure coefficient time history C_pn(t) is defined as the mean pressure coefficient, denoted as C_pn.

The time histories of the lift coefficient and drag coefficient for the circular cross-section in this experiment are given by, respectively,

$$C_{Dn}(t)={\displaystyle \sum _1^{44}\pi C_{Pni}(t)\cos {\theta }_i}/44$$

(2)

$$C_{Ln}(t)={\displaystyle \sum _1^{44}\pi C_{Pni}(t)\sin {\theta }_i}/44$$

(3)

In the equation, i denotes the index of the measurement point, C_pni(t) represents the instantaneous pressure coefficient at the i-th measurement point, θ_i is the wind angle (or circumferential angle) corresponding to the i-th measurement point, C_Ln(t) denotes the lift coefficient at time t and C_Dn(t) denotes the drag coefficient at time t.

The Reynolds number during the experiment can be calculated using Formula (4).

$$Re={\displaystyle \frac{UD}{\frac{\mu }{\rho }}}={\displaystyle \frac{UD}{\nu }}$$

(4)

In the equation, U is the free-stream velocity of the incoming flow, D is the diameter of the cylinder (this article is for d), μ is the dynamic viscosity coefficient, ρ is the air density and ν is the kinematic viscosity of air with a general value of 1.5 × 10⁻⁵.

2.3. Symmetry of the Oncoming Flow

A symmetry check of the model was conducted to verify that it had been correctly fabricated and installed. Selecting the mean wind pressure at any wind speed for the four measurement rings (A, B, C, D) at β = 0°, analysis of the mean pressure coefficients revealed that the values at the lower surface measurement points essentially coincided with those at the upper surface points. This indicates good uniformity and symmetry of the flow field, confirms the satisfactory symmetry of the model and verifies the accurate calculation of the wind pressure coefficients corresponding to the surface measurement points.

3. Analysis of Experimental Results

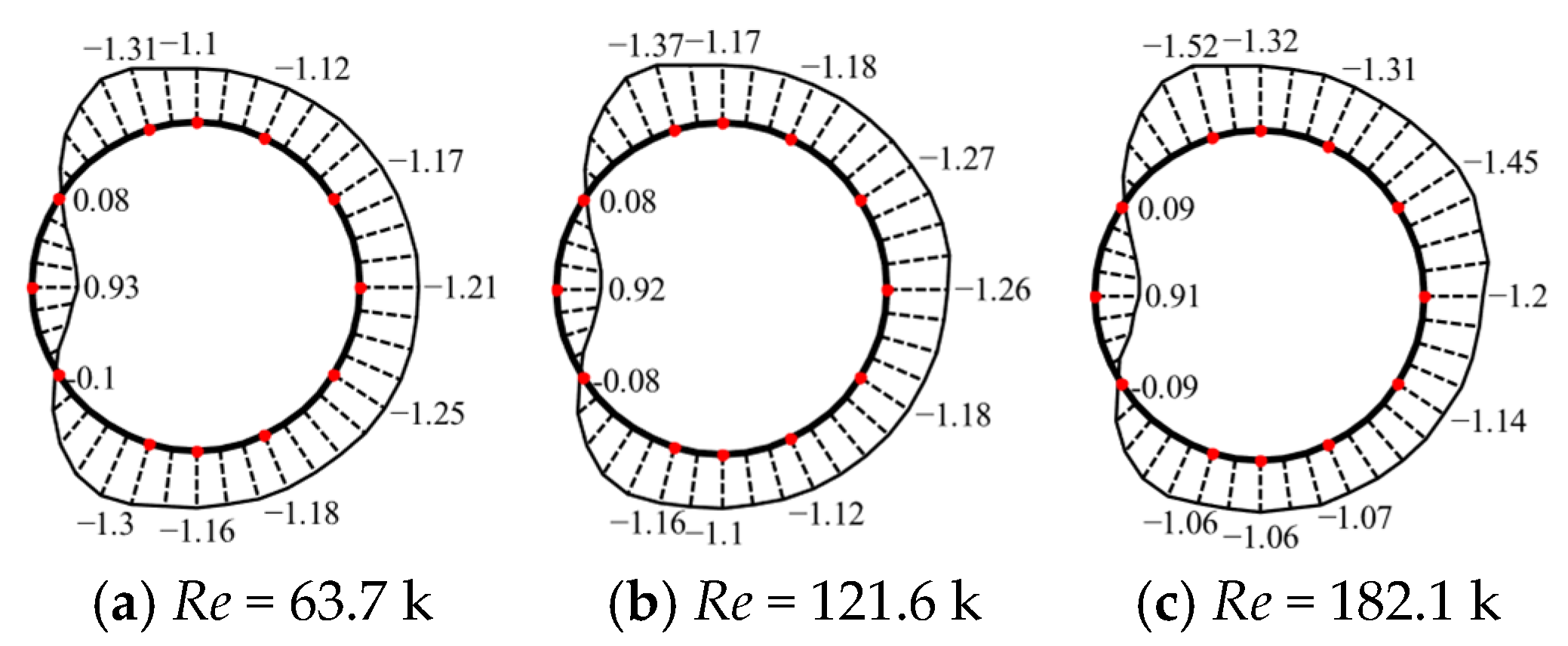
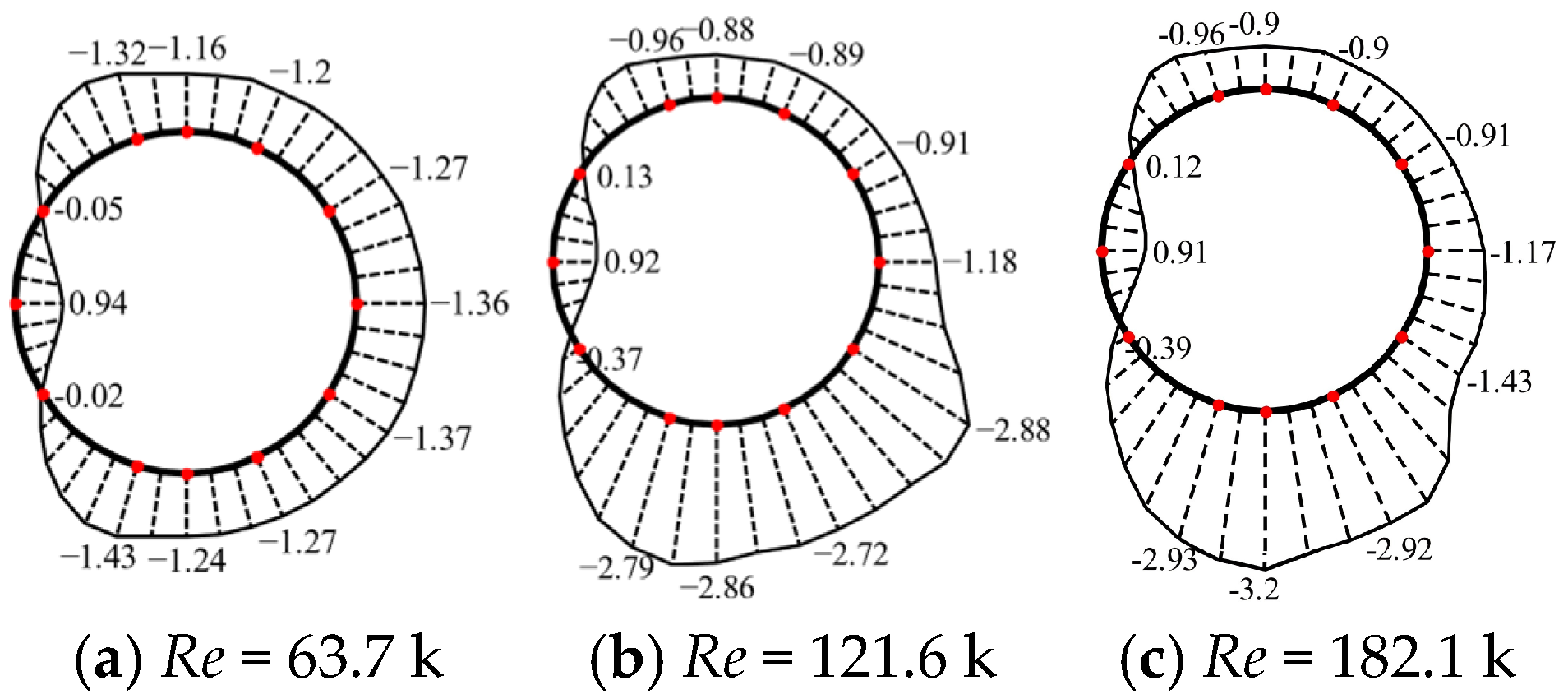
3.1. Mean Pressure Distribution

The mean pressure distributions of Ring C at yaw angles of β = 0°, 17.4°, 30° and 38.6° were obtained through pressure measurement tests, as shown in Figure 4, Figure 5, Figure 6 and Figure 7.

As shown in Figure 4, at β = 0°, the circumferential distribution of the mean pressure under the three Reynolds numbers exhibits minimal variation with Reynolds number in the subcritical regime for a straight cylinder.

In Figure 5 β = 17.4°, (1) the pressure at each circumferential position is higher than the corresponding value at β = 0° for the same Reynolds number; (2) the pressure on both the upper and lower windward surfaces gradually increases (reduced suction) with increasing Reynolds numbers; (3) at Re = 182.1 k, the leeward pressure shows higher values compared to the other two Reynolds numbers.

In Figure 6, at β = 30°, an apparent asymmetry in pressure distribution develops. Notably, at Re = 182.1 k, a localized suction plateau emerges on the lower windward surface, with the maximum suction difference between the upper and lower surfaces reaching 0.9. The presence of this plateau, which is a classic signature of flow separation followed by reattachment [7], strongly indicates the formation of a separation bubble on the lower surface.

In Figure 7, at β = 38.6°, the pressure distribution remains symmetric at Re = 63.7 k. As the Reynolds number increases, the upper windward surface pressure gradually decreases (increased suction) while the lower windward surface pressure increases (reduced suction), gradually forming a maximum-suction zone on the upper windward surface. This phenomenon, characterized by the formation of a concentrated suction zone, is attributed to the early arrival of the critical regime at the mid-span section due to the increased yaw angle. The observed narrowing of the wake pressure plateau (i.e., the base pressure becoming less negative) and the separation points’ rearward shift collectively serve as key indicators for identifying the onset of the critical flow regime. This is consistent with the experimental observations of Gu and Du [20].

Figure 4 demonstrates the stability of the subcritical regime for a straight cylinder (β = 0°), as the pressure distribution shows minimal variation from (a) to (c). Conversely, Figure 5 reveals a dramatic change with Reynolds number at β = 38.6°: the symmetric distribution at low Re (Figure 8a) evolves into a highly asymmetric one with a strong suction peak on the surface at high Re (Figure 8b [35]), indicative of the critical regime [8].

The mean pressure distributions of Ring B at yaw angles of β = 0°, 17.4°, 30° and 38.6° were obtained through pressure measurement tests, as shown in Figure 9, Figure 10, Figure 11 and Figure 12.

As shown in Figure 9, when β = 0°, the pressure distribution is similar to that of Ring C and shows minimal variation with Reynolds number.

In Figure 10, at β = 17.4°, the pressure on the lower surface in the wake region is slightly lower than that on the upper surface, resulting in an asymmetric pressure distribution.

In Figure 11, at β = 30°, the pressure distribution is generally symmetric, with slightly higher pressure on the upper surface compared to the lower. As the Reynolds number increases to Re = 121.6 k, a region of strong suction emerges on the lower surface, which may be related to the formation of a separation bubble [13].

In Figure 12, at β = 38.6° and lower Reynolds numbers, the boundary layer remains laminar, and transition occurs in the shear layer. As the Reynolds number increases, the transition point moves toward the cylinder, and when transition occurs in the vortex formation region, it affects vortex shedding. With a substantial increase in Reynolds number, boundary layer transition also occurs, leading to flow reattachment on the cylinder surface. Specifically, at Re = 63.7 k, transition occurs in the shear layer, while at Re = 121.6 k and Re = 182.1 k, transition occurs in the boundary layer. As shown in Figure 8, the formation of a separation bubble significantly reduces the suction pressure between the separation and reattachment points.

3.2. Occurrence of Vortex-Induced Vibrations

Figure 13 shows the fluctuating pressure distributions at Rings B and C at β = 0° under three Reynolds numbers.

It can be observed that the fluctuating pressure characteristics of Rings B and C are generally similar, with minimal variation as the Reynolds number increases.

The fluctuating pressure at the stagnation point shows some differences between Re = 63.7 k and the higher Reynolds numbers (Re = 121.6 k and 182.1 k). This discrepancy may be attributed to flow instability at lower Reynolds numbers.

At circumferential positions θ = 74° and 286°, where flow separation occurs [36], the fluctuating pressure reaches relatively high values. Two distinct peaks appear at θ = 155° and 205°, associated with boundary layer reattachment at these locations.

As the Reynolds number increases, the positions where the extreme values occur in Rings B and C are the same, indicating that the locations of the separation points and boundary layer reattachment points on the straight cylinder are essentially unaffected by the Reynolds number.

Figure 14 presents the fluctuating pressure distributions of Rings B and C at β = 17.4° under three Reynolds numbers.

For Ring C, the fluctuating pressure peaks at θ = 74° and 286°, indicating that the flow separation positions remain essentially unchanged with increasing yaw angles. The peak values at θ = 74° and 286° are smaller than the corresponding values at β = 0°, suggesting reduced likelihood of flow reattachment as the yaw angle increases.

For Ring B, flow separation occurs at the same circumferential positions (θ = 74° and 286°) as observed for Ring C.

Figure 15 shows the fluctuating pressure distributions of Rings B and C at β = 30° under three Reynolds numbers.

In Ring C, the number of extreme values in the fluctuating pressure reduces from four to three. The separation points remain unchanged at θ = 74° and 286°, while a distinct peak appears at θ = 155°. This prominent peak at 155° is a key indicator of a fundamental change in the flow regime. In the subcritical regime of a straight cylinder, the shear layer separating from the shoulder (around 74°/286°) typically reattaches intermittently, creating fluctuating pressure peaks in the rear separation bubble. However, at this high yaw angle (β = 30°), the strong peak at 155° suggests that the primary source of flow unsteadiness has shifted (see Figure 8). It is likely that the separated shear layer is no longer reattaching, instead undergoing an instability and rolling up into a vortex much closer to the point of separation. This signifies a suppression of the large-scale vortex shedding in the near-wake and the formation of a different, more unstable separation region on the cylinder’s leeward side, a phenomenon discussed in reference [37].

In Ring B, the fluctuating pressure also shows a significant peak at θ = 155°. Particularly at Re = 121.6 k and 182.1 k, this peak becomes exceptionally prominent, indicating that the likelihood of boundary layer separation decreases at higher Reynolds numbers. The enhanced peak suggests a more intense and localized fluctuating pressure load at this circumferential position, which has important implications for the structural response and fatigue analysis of yawed cylindrical structures.

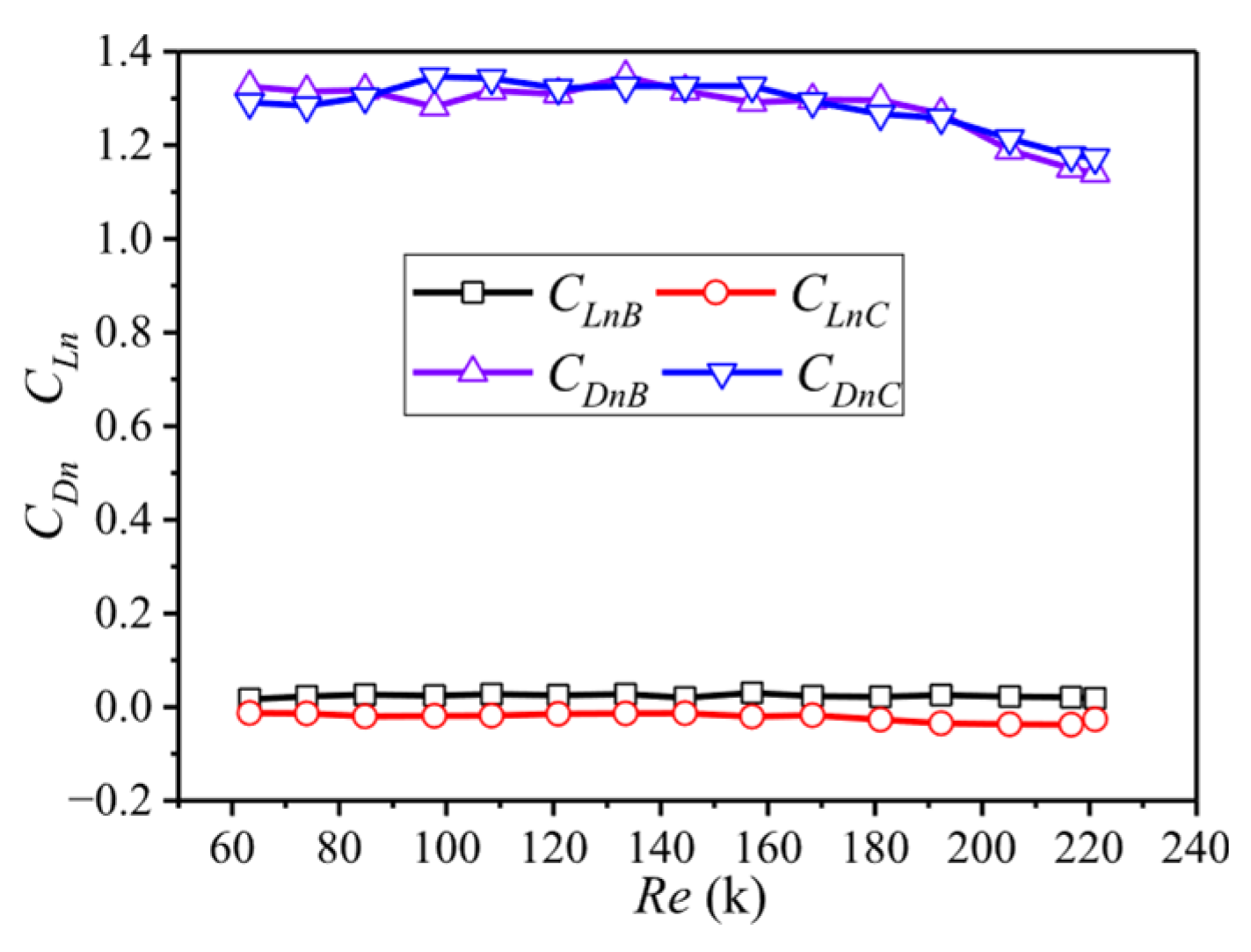
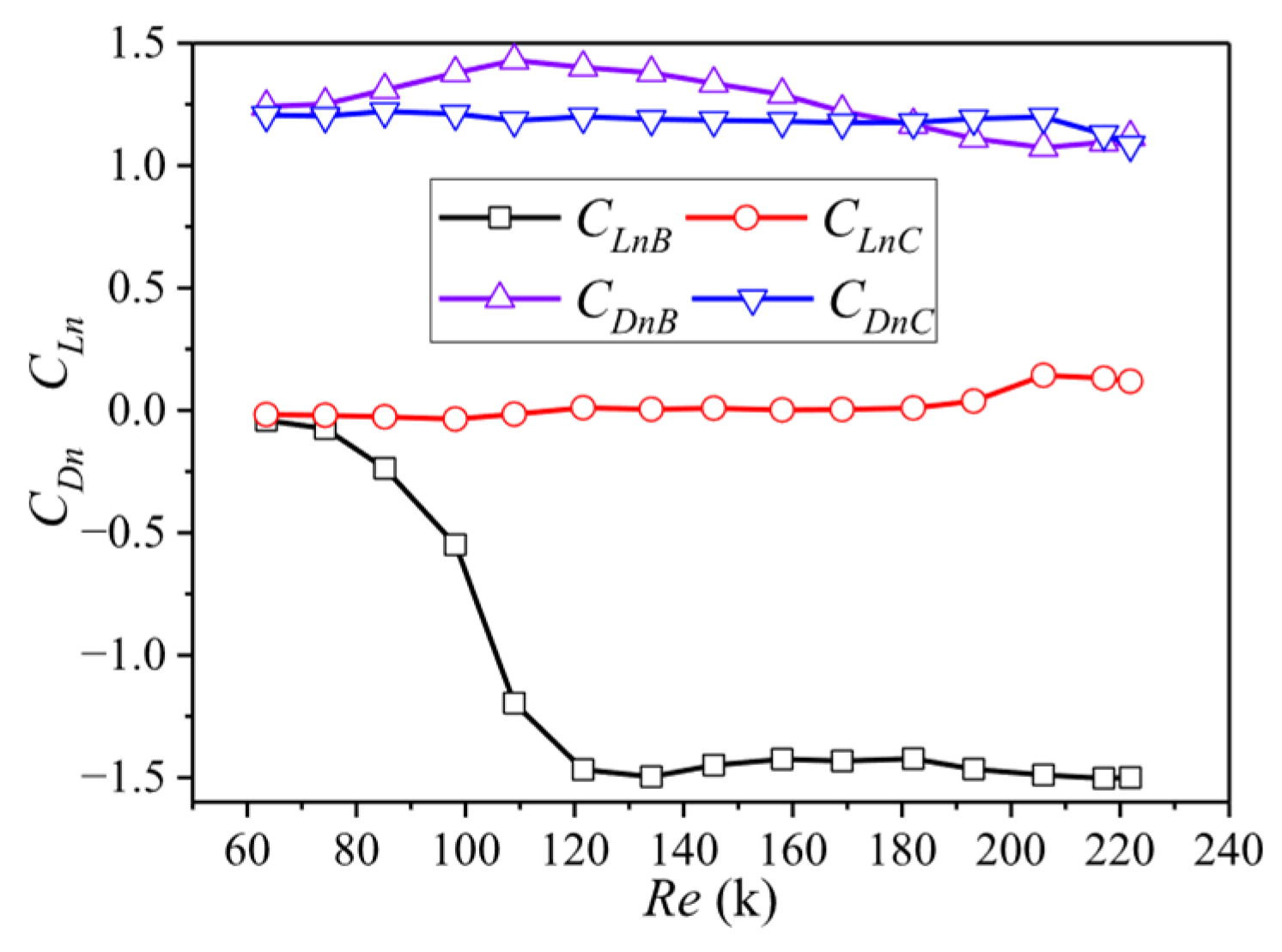
3.3. Mean Aerodynamic Forces

Figure 16 shows the variation in the mean lift and drag coefficients for Rings B and C with Reynolds number at β = 0°.

It can be observed that the mean lift and drag coefficients for both Rings B and C essentially coincide, indicating that the mean aerodynamic forces along the span of the straight cylinder remain nearly constant.

When Re < 160 k, the mean drag coefficient shows minimal variation with Reynolds number (approximately 1.3), which falls within the range recommended by the Engineering Sciences Data Unit (ESDU). The mean drag coefficient exhibits a distinct transition, as when Re > 160 k, it shows a sustained decreasing trend. This sharp reduction in mean drag coefficient with increasing Reynolds numbers is a definitive marker for the onset of the critical regime for circular cylinders [13], and the coincidence of the drag curves for Rings B and C confirms a uniform spanwise transition at β = 0°. At Re = 220 k, the mean drag coefficient is approximately 1.15. The mean lift coefficient remains essentially constant (approximately zero) with increasing Reynolds numbers, primarily because the mean pressure distribution on the cylinder surface remains symmetric in the subcritical regime.

In summary, at a yaw angle of β = 0°, the mean aerodynamic coefficients show no variation along the span, and the lift coefficient remains unchanged with Reynolds number in the subcritical regime (approximately zero). Beyond a certain critical Reynolds number of approximately 160 k, the drag coefficient begins to decrease with increasing Reynolds numbers.

Figure 17 shows the variations in the mean drag and lift coefficients with Reynolds number for Rings B and C at β = 17.4°.

Under these conditions, Ring C’s drag coefficient closely matches that observed at β = 0°. For Re < 134 k, it remains essentially constant with changing Reynolds numbers, but at Re > 134 k, the drag coefficient shows a decreasing trend as the Reynolds number increases, while the lift coefficient remains approximately zero.

For Ring B, both the lift and drag coefficients follow trends similar to Ring C when Re < 205 k. However, when Re > 205 k, Ring B exhibits a sharp decrease in lift coefficient and an increase in drag. This abrupt change in both force coefficients, deviating from the trend of Ring C, is identified as a premature entry into the critical regime at this specific spanwise location. The method of identification here relies on the divergence of aerodynamic behavior between different spanwise sections, highlighting the non-uniformity of the critical transition under increasing yaw angle. Furthermore, the identified threshold for the breakdown of the Independence Principle beyond 17.4° is in strong qualitative agreement with the experimental conclusions of King [16].

Figure 18 shows the variation in the mean drag and lift coefficients with Reynolds number for Rings B and C at β = 30°.

Ring C’s lift and drag coefficient trends are similar to those observed at β = 17.4°. However, Ring B exhibits significant changes in lift coefficient: When 74 k < Re < 120 k, the lift coefficient gradually decreases with increasing Reynolds numbers. When 120 k < Re < 220 k, the lift coefficient remains approximately constant at −1.5. The development of a significant mean lift force at high yaw angles is consistent with the findings of Gu & Du [20] on inclined cables. The mean drag coefficient measured in this study at β = 30° (approximately 1.1–1.2 prior to the critical drop) aligns quantitatively with the value of 1.15 reported by Vakil & Green [19] from numerical simulations at a comparable yaw angle and Reynolds number.

The significant changes in lift and drag coefficients, particularly for Ring B, are primarily associated with the formation of a separation bubble, as inferred from the pressure distributions in Section 3.1. The development of a sustained, non-zero mean lift coefficient provides direct quantitative evidence of the pressure asymmetry caused by the bubble.

In summary, at β = 0, the critical Reynolds number, characterized by the onset of a sustained drag reduction, is approximately 160 k. As the yaw angle increases, this critical transition occurs at progressively lower Reynolds numbers. For instance, at β = 17.4°, the critical Reynolds number for the onset of drag reduction is approximately 134 k. At β = 30°, the critical Reynolds number for a significant drop in drag and the emergence of substantial mean lift falls to approximately 120 k. These values demonstrate a clear trend: an increase in yaw angle actively promotes an earlier onset of the critical regime. This study quantifies the critical Reynolds numbers governing the aerodynamic transition for a yawed cylinder, providing key parameters for practical applications.

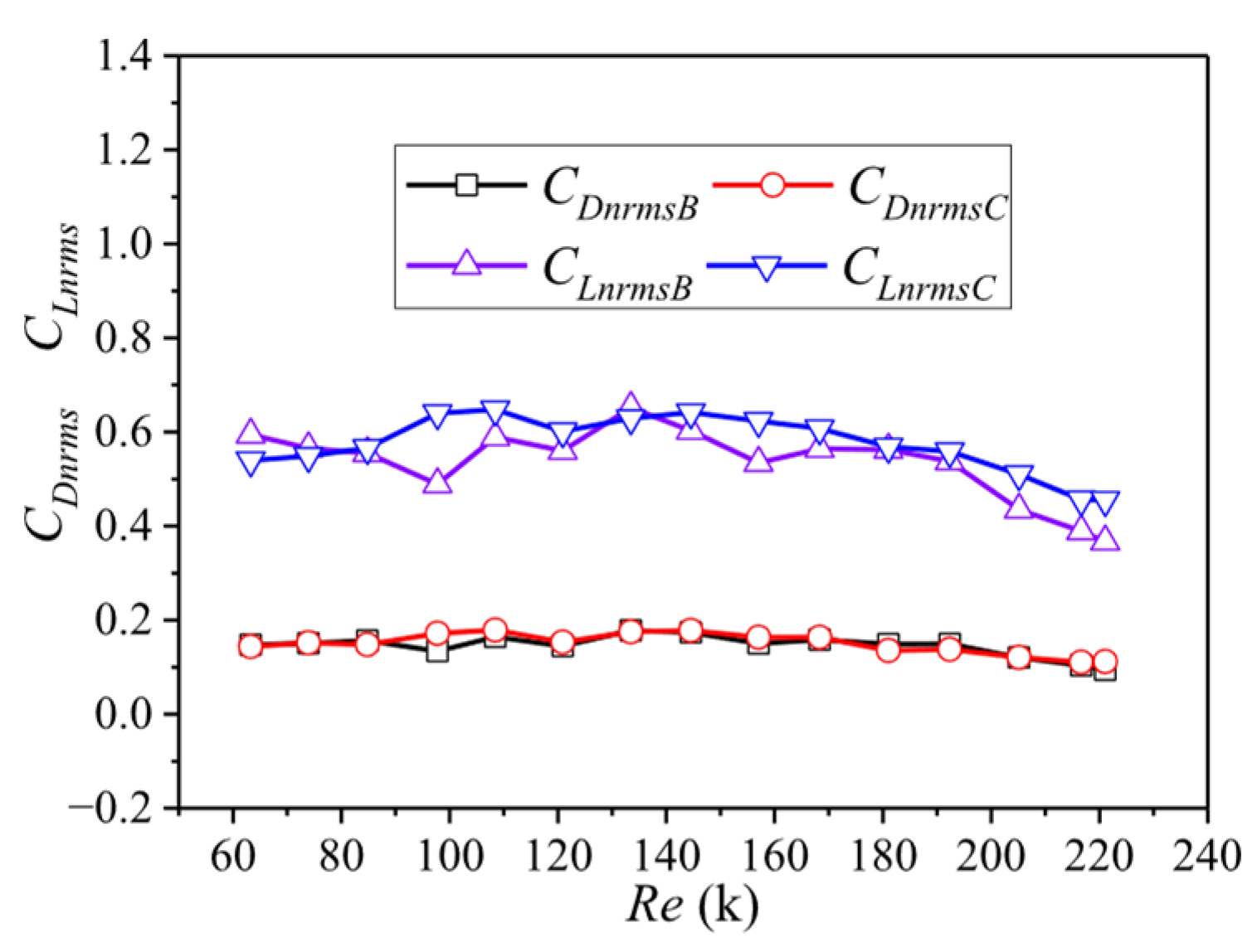
3.4. Fluctuating Aerodynamic Forces

Figure 19 shows the variations in fluctuating lift and drag coefficients with Reynolds number for Rings B and C at β = 0°.

The close agreement between the fluctuating lift and drag coefficients of Rings B and C indicates that the variation amplitude of aerodynamic forces along the span is essentially similar and uniformly distributed.

The fluctuating drag coefficient remains approximately 0.15, but shows a decreasing trend when Re > 194 k. At Re = 221 k, the fluctuating drag coefficient reaches about 0.1, indicating enhanced drag coefficient stability at higher Reynolds numbers.

In the range of 64 k < Re < 134 k, the fluctuating lift coefficients of both Rings B and C oscillate around 0.6, with an overall increasing trend. At Re = 134 k, the fluctuating lift coefficient reaches approximately 0.65, suggesting growing instability in mean lift coefficient fluctuations with increasing Reynolds numbers within this range.

When Re > 134 k, both Rings B and C exhibit decreasing trends in fluctuating lift coefficients with Reynolds number. At Re = 222 k, the fluctuating lift coefficient is about 0.37 for Ring B and 0.45 for Ring C. The more pronounced decrease observed in Ring B indicates that the mean lift coefficient becomes more stable with increasing Reynolds numbers beyond Re = 134 k.

Figure 20 shows the fluctuating lift and drag coefficients for Rings B and C at β = 17.4°.

When Re < 205 k, the fluctuating drag coefficients of Rings B and C essentially coincide (approximately 0.12). However, when Re > 205 k, the fluctuating drag coefficient of Ring B increases with Reynolds number, reaching approximately 0.165 at Re = 221 k, while that of Ring C remains around 0.09.

Significant differences are observed in fluctuating lift coefficients between the two rings. When Re < 205 k, Ring C’s fluctuating lift coefficient exceeds that of Ring B, though both exhibit similar trends—initially increasing then decreasing. Specifically, at Re = 97 k, the fluctuating lift coefficient is approximately 0.58 for Ring C and 0.44 for Ring B. A notable change occurs at Re = 205 k: the fluctuating lift coefficient of Ring B increases abruptly, while that of Ring C shows minimal variation. These shifts in fluctuating aerodynamic coefficients at Re = 205 k correspond to the previously mentioned drag coefficient changes and suggest an alteration in the flow regime at this critical Reynolds number.

Figure 21 shows the variations in fluctuating lift and drag coefficients with Reynolds number for Rings B and C at β = 30°.

Significant differences are observed in the fluctuating aerodynamic forces between the two rings, with the fluctuating drag coefficient of Ring B consistently exceeding the corresponding value of Ring C.

At Re = 97 k, both Rings B and C exhibit significant variations in their fluctuating lift coefficients. At this Reynolds number, Ring B reaches its maximum fluctuating lift coefficient value of 0.6.

As the Reynolds number increases, both rings’ fluctuating lift coefficients gradually stabilize, and at Re = 222 k, they converge to approximately 0.23.

In summary, this study quantifies fluctuating lift (CL) and drag (CD) coefficients for yawed cylinders, which are critical for predicting vortex-induced vibration and buffeting. Our key findings reveal that at β = 30°, the maximum fluctuating lift coefficient for Ring B reaches 0.6 at Re = 97 k, while the fluctuating drag coefficient peaks at 0.18 under the same condition. The data reveals strong excitation potential and significant spanwise load variations—for instance, at β = 17.4 and Re = 205 k, the fluctuating lift coefficient of Ring B abruptly increases by 85% compared to Ring C, highlighting the non-uniform distribution of dynamic loads along the span. These quantified fluctuating force characteristics provide a vital benchmark for validating high-fidelity CFD models and improving design codes against dynamic wind loads, particularly for stay cables and inclined structural elements subjected to oblique winds.

4. Conclusions

This study aimed to investigate the evolution of aerodynamic characteristics and the underlying flow mechanisms of a finite-length yawed circular cylinder at high yaw angles (0–60°). By combining wind tunnel pressure measurements and analysis of the intermediate flow field region, the following main findings are obtained:

(1)

The flow regime around the yawed cylinder undergoes a fundamental transition as the yaw angle increases. While it remains similar to that of a straight cylinder at small angles (β ≤ 17.4°), a critical change occurs at higher angles. The enhanced axial flow component (U sin β) destabilizes the boundary layer, leading to a premature onset of the critical regime. This is evidenced by a systematic reduction in the critical Reynolds number with increasing yaw angle—from approximately 160,000 at β = 0° to about 120 k at β = 30°.

(2)

This early transition directly dictates the evolution of aerodynamic forces. It triggers the formation of asymmetric separation bubbles on the windward surface, which generates significant mean lift forces (e.g., C_L ≈ −1.5) and causes a distinct, premature reduction in the mean drag coefficient beyond the identified critical Reynolds number.

(3)

Aerodynamic effects are not uniform along the cylinder span. The mid-span “intermediate region” (i.e., Ring C) exhibits behavior distinct from sections more influenced by end-effects (i.e., Ring B), with the latter often entering the critical regime earlier. This highlights the necessity of considering three-dimensional flow effects in design.

The quantified critical Reynolds numbers and force coefficients provided in this study deliver crucial reference data for engineering applications. They enable more accurate prediction of wind loads—including dynamic effects driven by fluctuating forces—on real-world structures such as inclined bridge towers, stay cables and offshore piles subjected to oblique winds, thereby contributing to enhanced design safety and reliability.

It should be noted that this study has certain limitations; for instance, flow field visualization measurements were not conducted to directly observe the separation bubble structures, and the Reynolds number range was confined to the subcritical regime. Based on these limitations, future research should focus on the quantitative observation of separation bubbles using techniques like CFD and extend the investigation of aerodynamic characteristics into the critical and supercritical Reynolds number regimes.