Evaluation and Calibration of Analytical Models for Predicting Splitting in Precast Concrete Tunnel Segments During TBM Thrust
Abstract
1. Introduction
2. Background
2.1. Analytical Models Available in the Literature
2.2. Experimental Campaigns Available in the Literature
3. Materials and Methods
3.1. Selected Experimental Campaigns
3.2. Selected Analytical Models
3.3. Statistical Analysis
4. Results and Discussion
4.1. Applicability of the Models Considering the fMC
4.2. Applicability of the Models Considering Experimental fct Values
5. Conclusions
- -
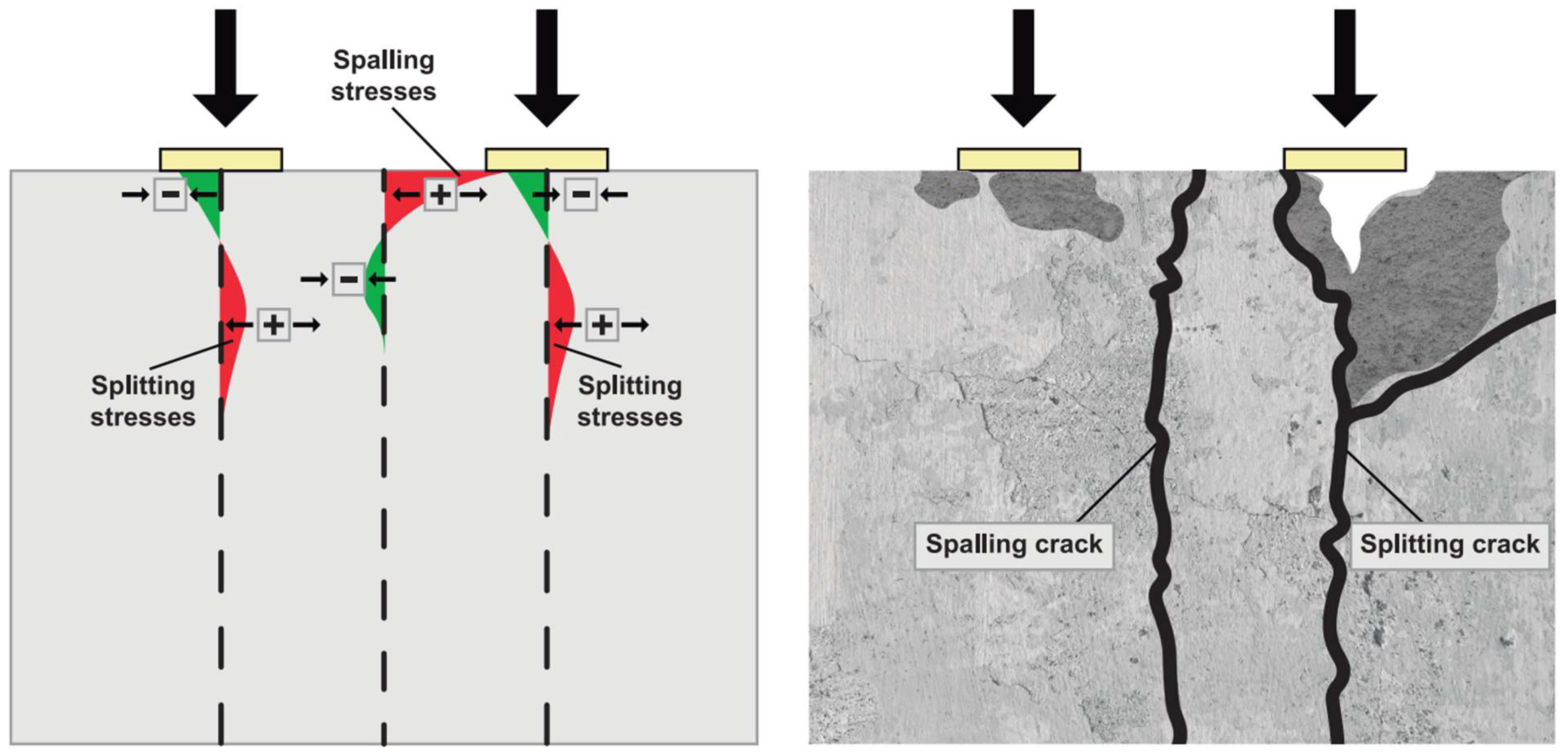
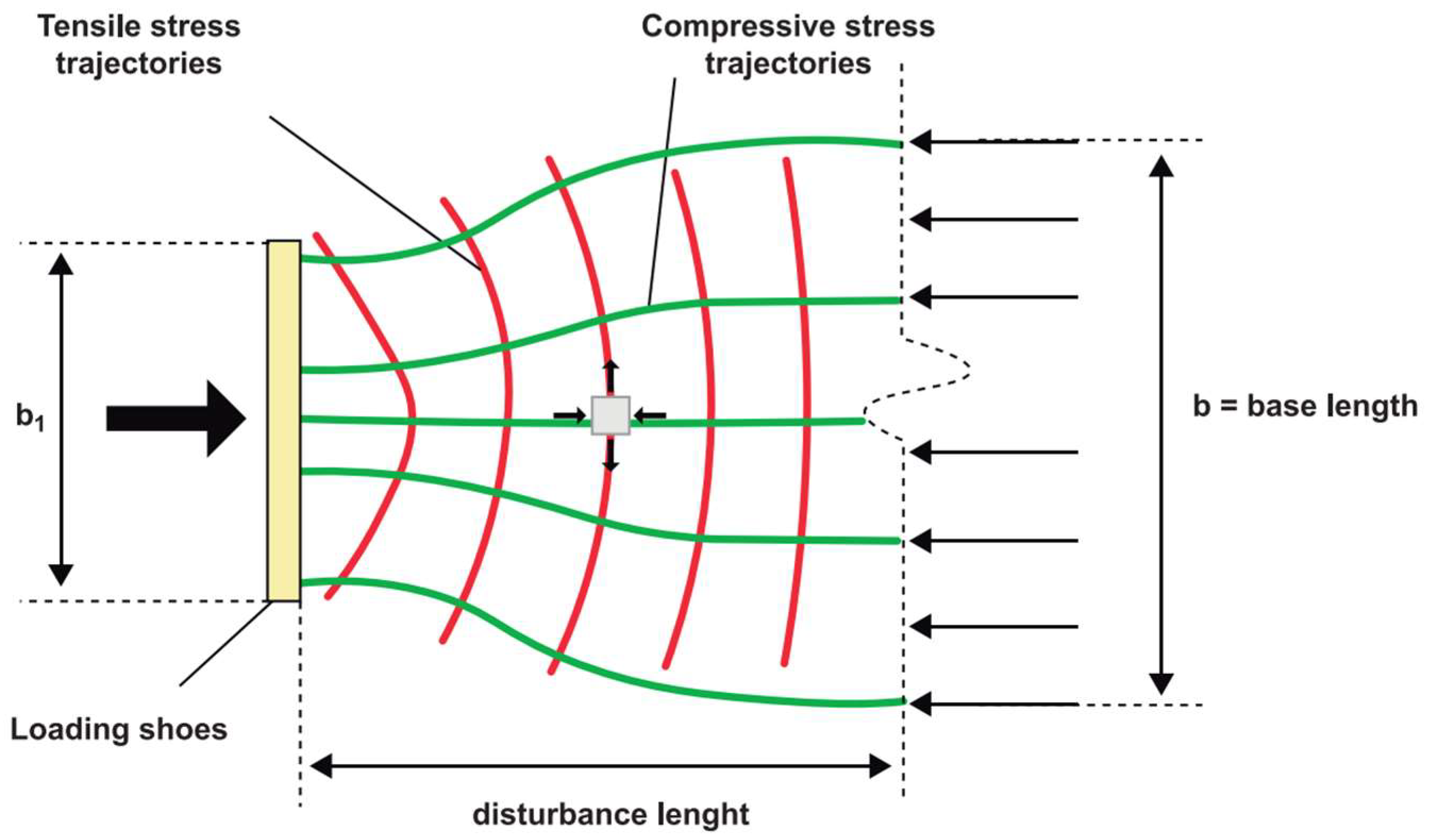
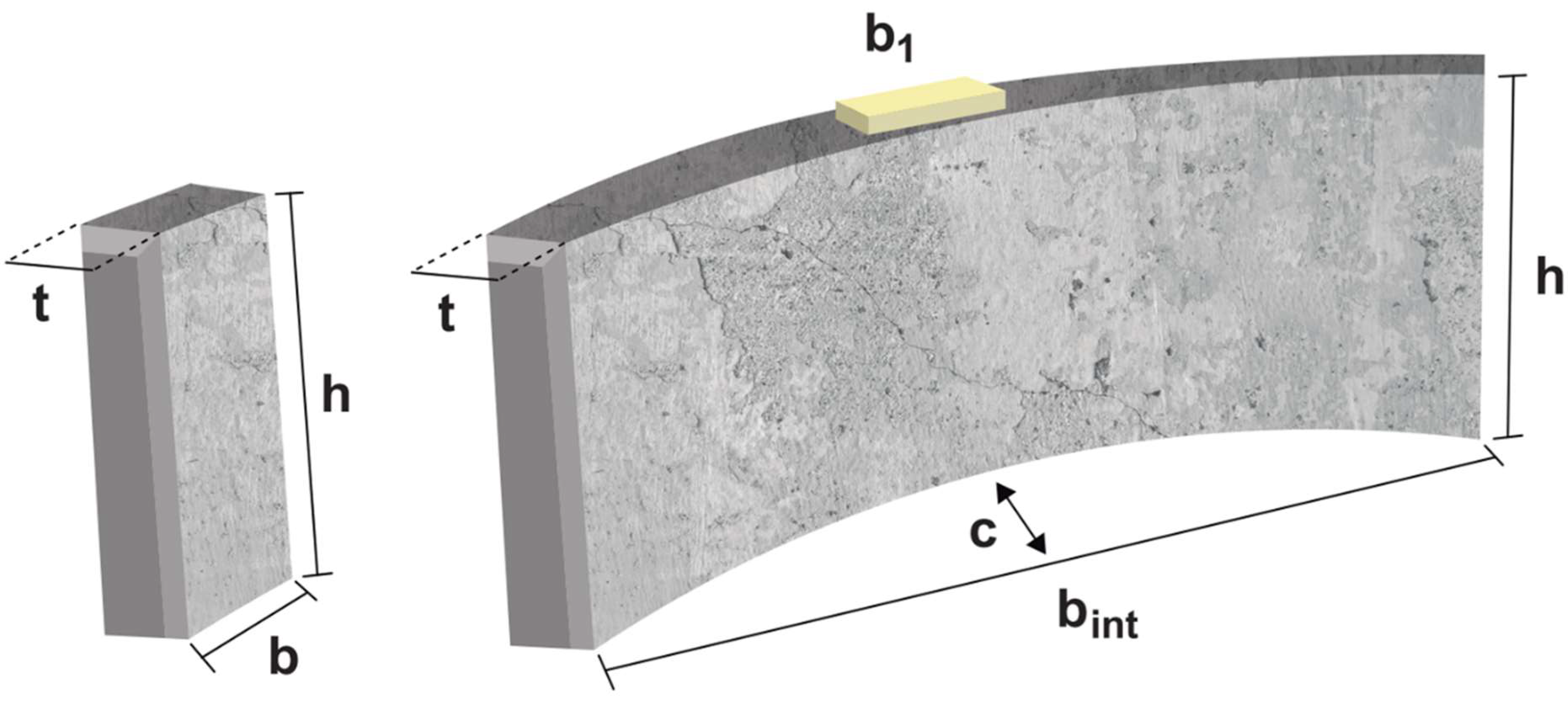
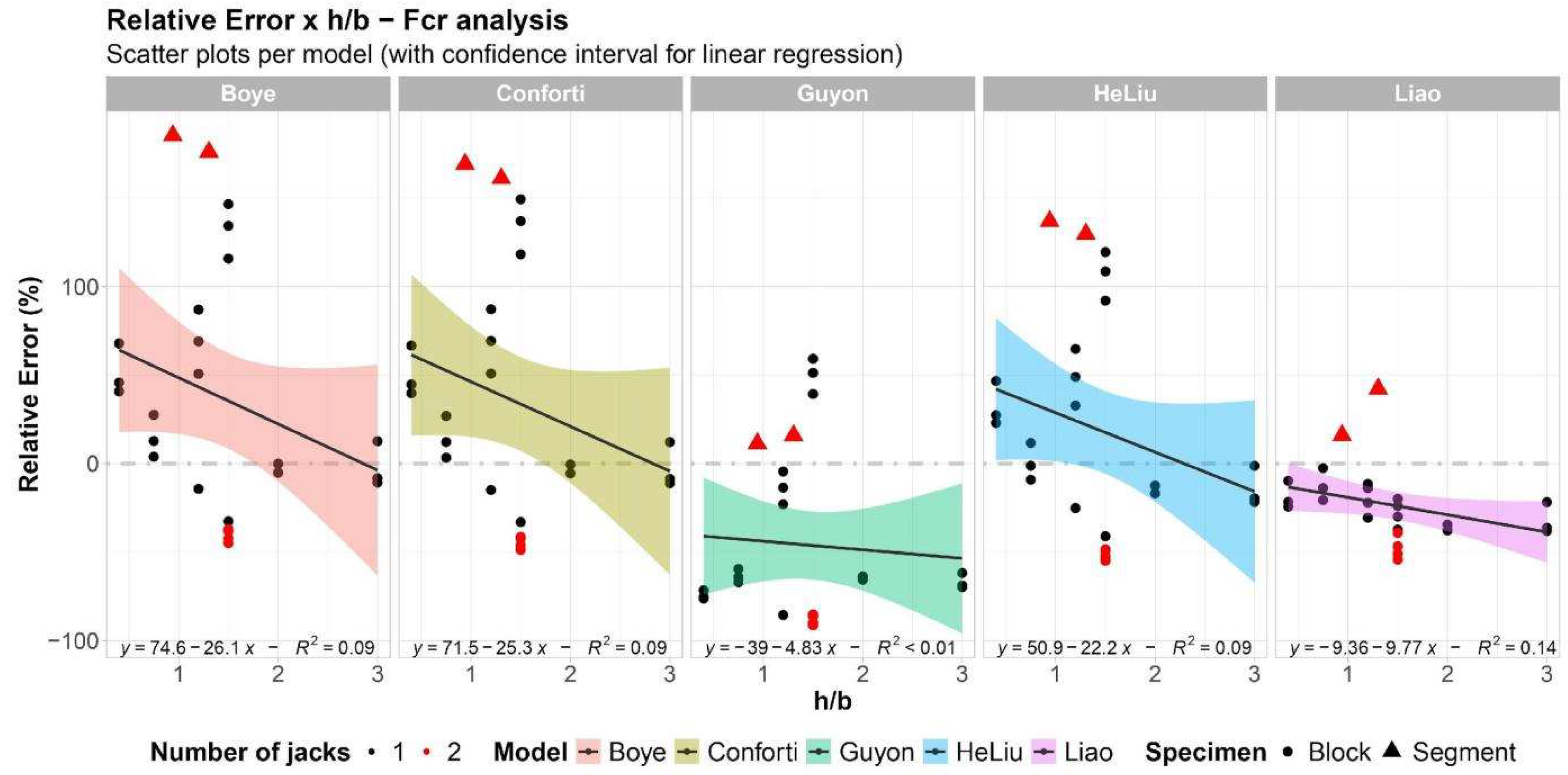
- The splitting load under double jack configuration predicted by the analytical models tends to be generally underestimated for concrete blocks and overestimated for real scale segments. This means that the capacity of the models to predict splitting is influenced by the geometry, size, and scale of the specimens, as well as the test configuration (single or double jacks).
- -
- Given the limited number of studies in literature employing concrete blocks and segments under double jack configuration, the quantitative comparison between groups (one and more one jack) is inconclusive. In this sense, the data was assumed to be from the same statistical population for all subsequent conclusions.
- -
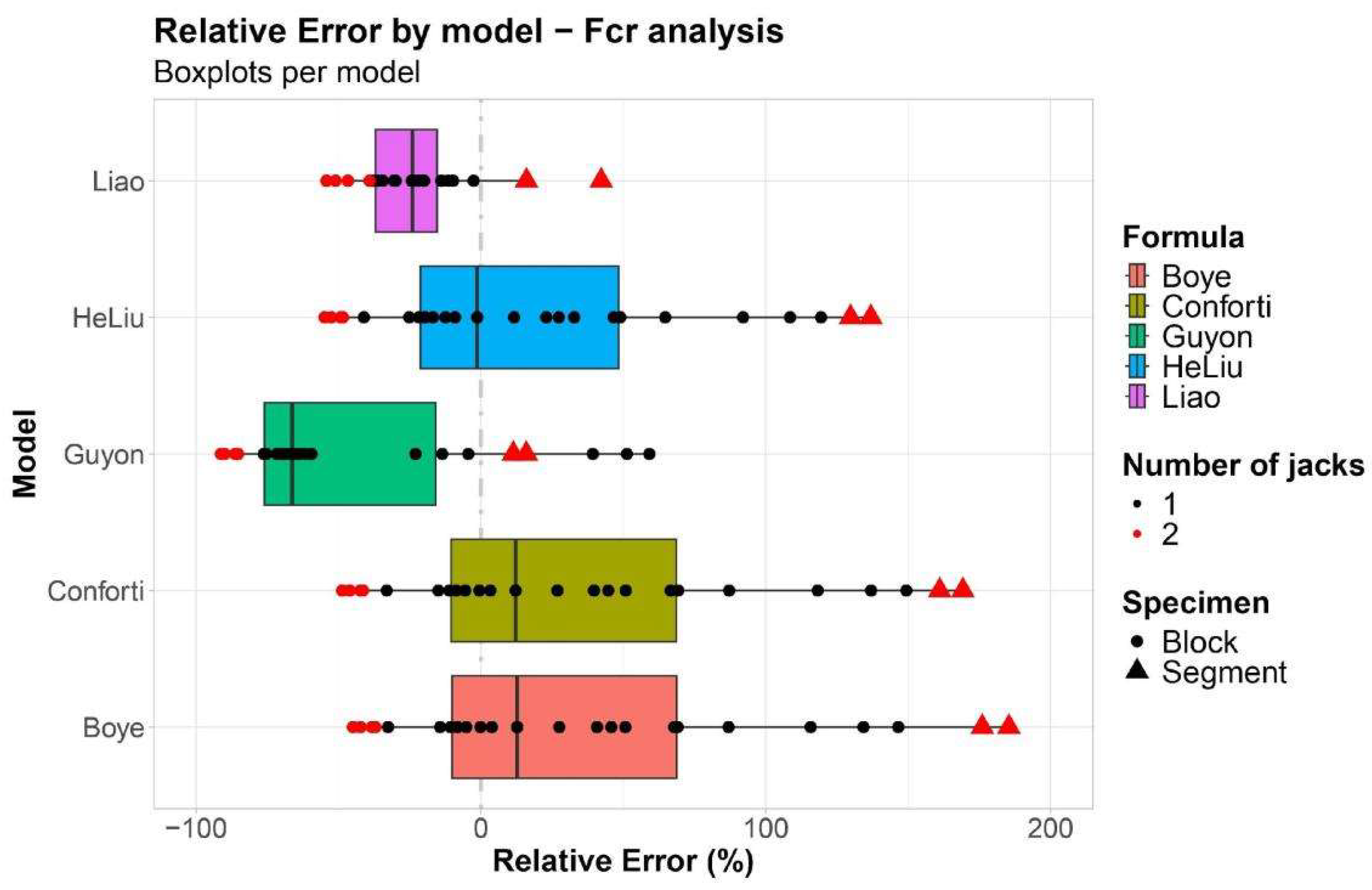
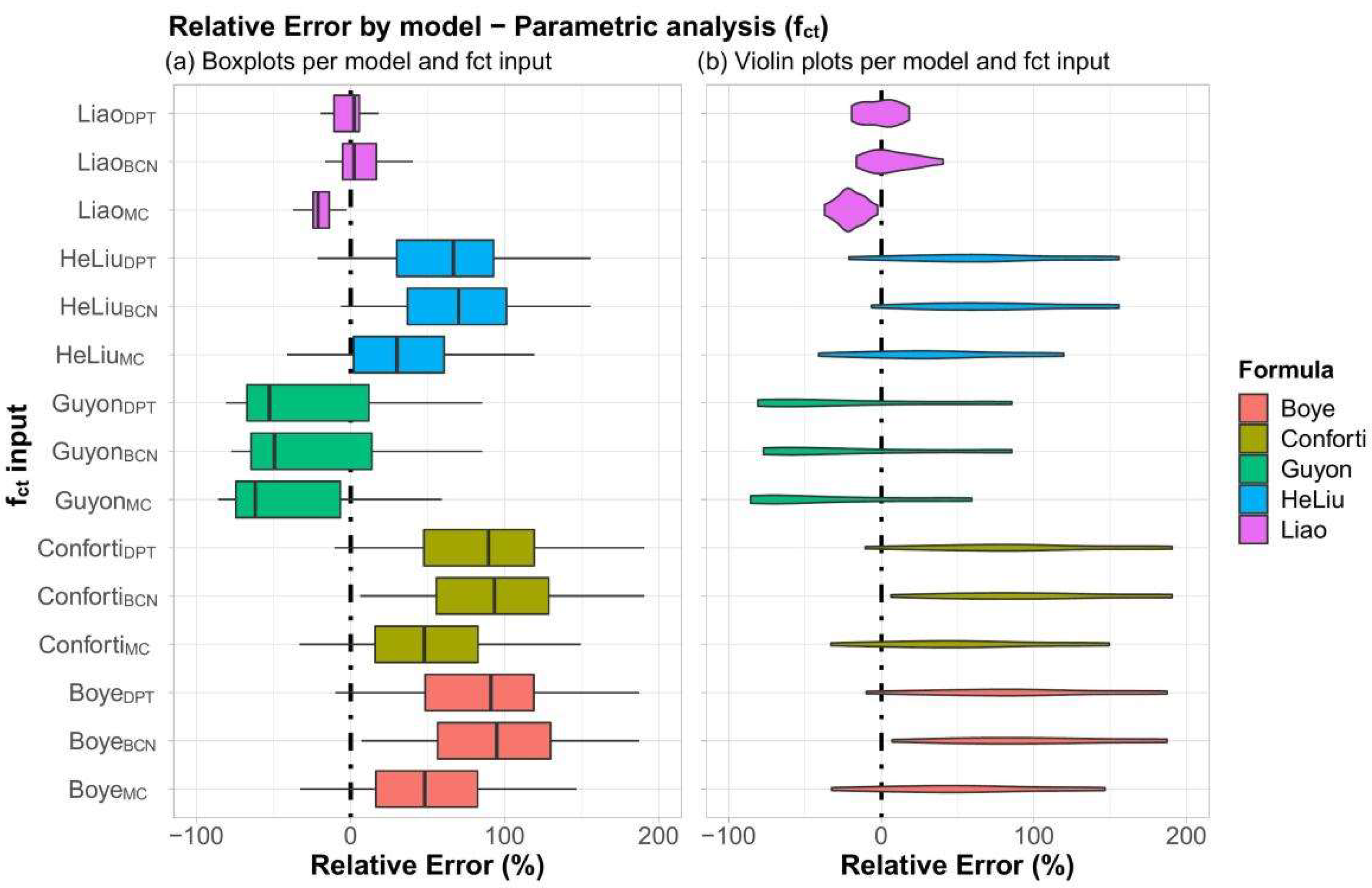
- The models presented distinct behaviors: Guyon [17] and Liao et al. [20] models presented central tendency results that underestimate the splitting load, which is in favor of safety for design purposes. Alternatively, He and Liu [19] model showed a tendency centered in zero with a right-skewed distribution (more dispersion for positive relative errors). Conforti et al. [18] and Boye et al. [21] presented positive central tendencies with similar relative error distributions, meaning that these models are against safety when designing segments for splitting.
- -
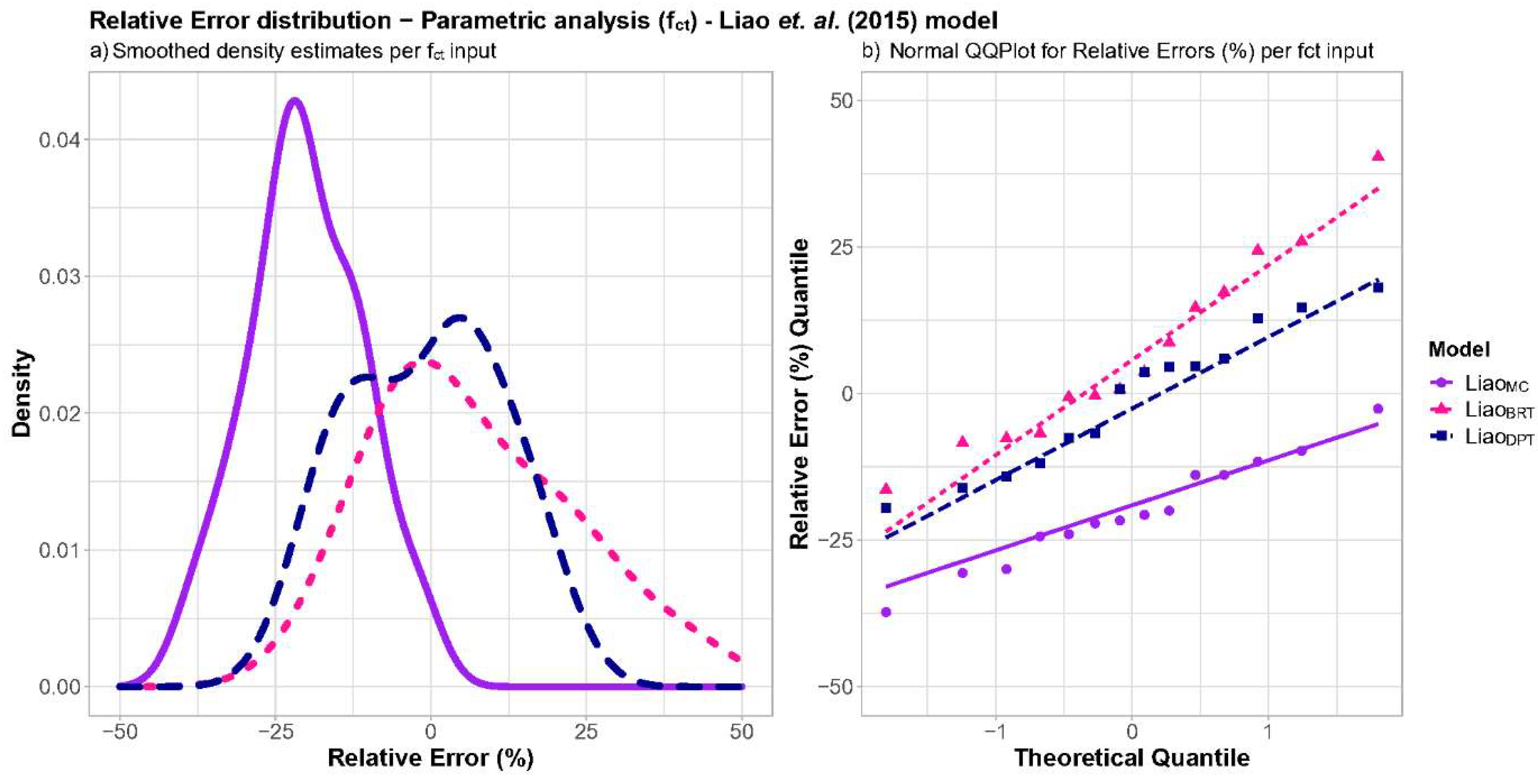
- The model proposed by Liao et al. [20] was the most accurate model evaluated in this study, with the least dispersive response. Additionally, the Liao et al. [20] model showed great adherence to a normal distribution with a relative error centered at approximately −25% and minimal influence of geometrical parameters, such as specimens’ width ratio (b1/b) and aspect ratio (h/b). Guyon [17] showed the best responses for real scale segments with two jacks based on the magnitude of the relative error and the adherence in the regression model based on the width ratio (b1/b).
- -
- The influence of the tensile strength parameter used as input for the analytical models was evaluated. Three different approaches were evaluated: fib Model Code 2010 [39] approach (fMC), the DPT (fDPT), and the Brazilian test (fBRT). It was shown that Liao et al. [20] and Guyon [17] presented better predictions when used associated with experimental tensile inputs (fBRT and fDPT). Moreover, using fMC led the results toward a safer scenario for the models proposed by He and Liu [19], Conforti et al. [18], and Boye et al. [21].
- -
- Based on the results of this study, improved analytical models for Liao et al. [20] and Guyon [17] are suggested from the applicability analysis. The improvement in the Liao et al. [20] model was based on a correction for bias, while the model of Guyon [17] was improved regarding its relation to the width ratio (b1/b).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Josa, I.; Aguado, A. Infrastructure, Innovation and Industry as Solutions for Breaking Inequality Vicious Cycles. IOP Conf. Ser. Earth Environ. Sci. 2019, 297, 012016. [Google Scholar] [CrossRef]
- Klenert, D.; Mattauch, L.; Edenhofer, O.; Lessmann, K. Infrastructure and Inequality: Insights from Incorporating Key Economic Facts about Household Heterogeneity. Macroecon. Dyn. 2018, 22, 864–895. [Google Scholar] [CrossRef]
- Bäppler, K. New Developments in TBM Tunnelling for Changing Grounds. Tunn. Undergr. Space Technol. 2016, 57, 18–26. [Google Scholar] [CrossRef]
- Lance, G.A. The Risk to Third Parties from Bored Tunnelling in Soft Ground; Health and Safety Executive: Merseyside, UK, 2006. [Google Scholar]
- Sugimoto, M. Causes of Shield Segment Damages during Construction. In Proceedings of the International Symposium on Underground Excavation and Tunnelling, Bangkok, Thailand, 2–4 February 2006; pp. 67–74. [Google Scholar]
- Cavalaro, S.H.P.; Blom, C.B.M.; Walraven, J.C.; Aguado, A. Structural Analysis of Contact Deficiencies in Segmented Lining. Tunn. Undergr. Space Technol. 2011, 26, 734–749. [Google Scholar] [CrossRef]
- Conforti, A.; Tiberti, G.; Plizzari, G.A. Combined Effect of High Concentrated Loads Exerted by TBM Hydraulic Jacks. Mag. Concr. Res. 2016, 68, 1122–1132. [Google Scholar] [CrossRef]
- Lanes, R.M.; Greco, M.; Guerra, M.B.B.F. Strut-and-Tie Models for Linear and Nonlinear Behavior of Concrete Based on Topological Evolutionary Structure Optimization (ESO). Rev. IBRACON Estrut. Mater. 2019, 12, 87–100. [Google Scholar] [CrossRef]
- Groeneweg, T.W. Shield Driven Tunnels in Ultra High Strength Concrete, Reduction of the Lining Thickness. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Silveira, M.V.G.; Bitencourt, L.A.G.; Das, S. A Performance-Based Optimization Framework Applied to a Classical STM-Designed Deep Beam. Structures 2022, 41, 488–500. [Google Scholar] [CrossRef]
- Silveira, M.V.G.; Paini, B.; Bitencourt, L.A.G., Jr.; Das, S. Design and Experimental Investigation of Deep Beams Based on the Generative Tie Method. Eng. Struct. 2022, 255, 113913. [Google Scholar] [CrossRef]
- Hsu, T.T.C. Unified Theory of Reinforced Concrete; Taylor & Francis: London, UK, 1993. [Google Scholar]
- Zaborac, J.; Choi, J.; Bayrak, O. Assessment of Deep Beams with Inadequate Web Reinforcement Using Strut-and-Tie Models. Eng. Struct. 2020, 218, 110832. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, M.S. Investigation and Improvement of Bursting Force Equations in Posttensioned Anchorage Zone. Adv. Mater. Sci. Eng. 2019, 2019, 9807975. [Google Scholar] [CrossRef]
- Morsh, E. Uber Die Berchnung Der Gelenkquader. In Beton und Eisen; Verlag von W. Ernst and Sohn: Berlin, Germany, 1924. [Google Scholar]
- Leonhardt, F.; Monnig, E. Part I. Fundamentals in the Design of Reinforced Concrete Construction. In Lectures on Structural Engineering; Springer: Berlin/Heidelberg, Germany, 1973; pp. 45–50. [Google Scholar]
- Guyon, Y. Prestressed Concrete; UC Berkeley Transportation Library: Berkeley, CA, USA, 1953. [Google Scholar]
- Conforti, A.; Tiberti, G.; Plizzari, G.A. Splitting and Crushing Failure in FRC Elements Subjected to a High Concentrated Load. Compos. B Eng. 2016, 105, 82–92. [Google Scholar] [CrossRef]
- He, Z.; Liu, Z. Investigation of Bursting Forces in Anchorage Zones: Compression-Dispersion Models and Unified Design Equation. J. Bridge Eng. 2011, 16, 820–827. [Google Scholar] [CrossRef]
- Liao, L.; de la Fuente, A.; Cavalaro, S.; Aguado, A.; Carbonari, G. Experimental and Analytical Study of Concrete Blocks Subjected to Concentrated Loads with an Application to TBM-Constructed Tunnels. Tunn. Undergr. Space Technol. 2015, 49, 295–306. [Google Scholar] [CrossRef]
- Boye, B.A.; Abbey, S.J.; Ngambi, S.; Fonte, J. Development of Improved Models for Estimation of Bursting Stresses in Elements under High-Concentrated Load. Lat. Am. J. Solids Struct. 2019, 16, 156. [Google Scholar] [CrossRef]
- Schnütgen, B.; Erdem, E. Sub-Task 4.4–Splitting of SFRC Induced by Local Forces; Ruhr-University: Bochum, Germany, 2001. [Google Scholar]
- Tiberti, G.; Conforti, A.; Plizzari, G.A. Precast Segments under TBM Hydraulic Jacks: Experimental Investigation on the Local Splitting Behavior. Tunn. Undergr. Space Technol. 2015, 50, 438–450. [Google Scholar] [CrossRef]
- Trabucchi, I.; Tiberti, G.; Conforti, A.; Medeghini, F.; Plizzari, G.A. Experimental Study on Steel Fiber Reinforced Concrete and Reinforced Concrete Elements under Concentrated Loads. Constr. Build. Mater. 2021, 307, 124834. [Google Scholar] [CrossRef]
- Caratelli, A.; Meda, A.; Rinaldi, Z. Design According to MC2010 of a Fibre-Reinforced Concrete Tunnel in Monte Lirio, Panama. Struct. Concr. 2012, 13, 166–173. [Google Scholar] [CrossRef]
- Iyengar, K.S.R. Two-Dimensional Theories of Anchorage Zone Stresses in Post-Tensioned Prestressed Beams. J. Proc. 1962, 59, 1443–1466. [Google Scholar]
- Serafini, R.; Santos, F.P.; Agra, R.R.; De la Fuente, A.; Figueiredo, A.D. de Effect of Specimen Shape on the Compressive Parameters of Steel Fiber Reinforced Concrete after Temperature Exposure. J. Urban Technol. Sustain. 2018, 1, 10–20. [Google Scholar] [CrossRef]
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites, 2nd ed.; Bentur, A., Mindess, S., Eds.; Taylor & Francis: New York, NY, USA, 2007. [Google Scholar]
- Gettu, R.; Barragán, B.; García, T.; Fernández, C.; Oliver, R. Steel Fiber Reinforced Concrete for the Barcelona Metro Line 9 Tunnel Lining. In Proceedings of the 6th International RILEM Symposium on Fibre Reinforced Concretes, Varenna, Italy, 20–22 September 2004; pp. 141–156. [Google Scholar]
- Breitenbücher, R.; Meschke, G.; Song, F.; Hofman, M.; Zhan, Y. Experimental and Numerical Study on the Load-Bearing Behaviour of Steel Fibre Reinforced Concrete for Precast Tunnel Lining Segments under Concentrated Loads. In Proceedings of the FRC 2014 Joint ACI-fib International Workshop, Montreal, QC, Canada, 24–25 July 2014; pp. 417–429. [Google Scholar]
- Sorelli, L.; Toutlemonde, F. On the Design of Steel Fiber Reinforced Concrete Tunnel Lining Segments. In Proceedings of the 11th International Conference on Fracture, Turin, Italy, 20–26 March 2005; pp. 5702–5707. [Google Scholar]
- Poh, J.; Tan, K.H.; Peterson, G.L.; Wen, D. Structural Testing of Steel Fibre Reinforced Concrete (SFRC) Tunnel Lining Segments in Singapore. In Proceedings of the World Tunnel Congress 2009, Budapest, Hungary, 23–28 May 2009; pp. 1–17. [Google Scholar]
- Hilar, M.; Vitek, J.L.; Pukl, R. Laboratory Testing and Numerical Modelling of SFRC Tunnel Segments. In Proceedings of the Eastern European Tunnelling Congress, Budapest, Hungary, 18–21 September 2012. [Google Scholar]
- Meda, A.; Rinaldi, Z.; Caratelli, A.; Cignitti, F. Experimental Investigation on Precast Tunnel Segments under TBM Thrust Action. Eng Struct 2016, 119, 174–185. [Google Scholar] [CrossRef]
- Spagnuolo, S. Influence of Non-Uniform Support on FRC and Hybrid Precast Tunnel Segments with Glass Fiber Reinforced Polymer Bars under TBM Thrust. In Proceedings of the First fib Italy YMG Symposium on Concrete and Concrete Structures, Parma, Italy, 15 October 2019. [Google Scholar]
- Beňo, J.; Hilar, M. Steel Fibre Reinforced Concrete for Tunnel Lining–Verification by Extensive Laboratory Testing and Numerical Modelling. Acta Polytech. 2013. [Google Scholar] [CrossRef] [PubMed]
- Abbas, S.; Soliman, A.; Nehdi, M. Structural Behaviour of Ultra-High Performance Fibre Reinforced Concrete Tunnel Lining Segments. In Proceedings of the FRC 2014 Joint ACI-fib International Workshop. Fibre Reinforced Concrete Applications, Montreal, QC, Canada, 24–25 July 2014; pp. 532–543. [Google Scholar]
- Conforti, A.; Trabucchi, I.; Tiberti, G.; Plizzari, G.A.; Caratelli, A.; Meda, A. Precast Tunnel Segments for Metro Tunnel Lining: A Hybrid Reinforcement Solution Using Macro-Synthetic Fibers. Eng. Struct. 2019, 199, 109628. [Google Scholar] [CrossRef]
- Federation Internationale du Beton. FIB Model Code for Concrete Structures 2010; Ernst & Sohn: Berlin, Germany, 2013; 434p, ISBN 978-3-433-03061-5. [Google Scholar]
- Bussab, W.; Morettin, P.A. Estatística Básica; Saraivauni, Ed.; Saraivauni: São Paulo, Brazil, 2017; ISBN 9788547220228. [Google Scholar]
- Devore, J.L. Probability and Statistics for Engineering and the Sciences, 9th ed.; Cengage Learning: Boston, MA, USA, 2021; ISBN 978-1-305-25180-9. [Google Scholar]
- Silveira, M.V.G.; Bitencourt, L.A.G.; Das, S. Experimental and Numerical Investigation of Large-Scale Reinforced Concrete Deep Beams Designed with the Generative Tie Method. Structures 2023, 58, 105555. [Google Scholar] [CrossRef]


| Model | Fpred | Context | Assumptions | Formulation |
|---|---|---|---|---|
| [15] | Prestressed concrete | Semi-infinite strut and tie | Strut and tie | |
| [17] | Prestressed concrete | Semi-infinite strip | Elastic solution with corrections | |
| [16] | Prestressed concrete | Semi-infinite strut and tie | Elastic solution | |
| [19] | Prestressed concrete | Semi-infinite strip | Compression-dispersion model | |
| [20] | TBM tunnels | Short blocks | Strut-and-tie model | |
| TBM tunnels | Long blocks | Strut-and-tie model | ||
| [18] | TBM tunnels | Semi-infinite strip | Exact elastic solution | |
| [21] | TBM tunnels | Semi-infinite strip | Linear regression based on numerical model improvements |
| Authors | Specimen | Type | b1 (mm) | b (mm) | t (mm) | fc (MPa) | ft (MPa) | Fexp (kN) |
|---|---|---|---|---|---|---|---|---|
| [22] | Block | SFRC | 350 | 150 | 350 | 58.2 | fMC = 4.08 | 2000 |
| SFRC | 350 | 150 | 350 | 50.2 | fMC = 3.64 | 1875 | ||
| [23] | Block | PC | 100 | 250 | 250 | 57.2 | fMC = 4.03 | 1044 |
| PFRC | 100 | 250 | 250 | 48.5 | fMC = 3.54 | 917 | ||
| [20] | Block | PC | 150 | 200 | 150 | 40.0 | fMC = 3.25 fBRT = 4.33 fDPT = 4.33 | 407 |
| PC | 150 | 200 | 150 | 50.0 | fMC = 3.81 fBRT = 4.09 fDPT = 4.40 | 417 | ||
| SFRC | 150 | 200 | 150 | 40.0 | fMC = 2.99 fBRT = 3.99 fDPT = 4.74 | 406 | ||
| SFRC | 150 | 200 | 150 | 50.0 | fMC = 3.73 fBRT = 4.32 fDPT = 4.49 | 429 | ||
| PC | 150 | 250 | 150 | 40.0 | fMC = 3.25 fBRT = 4.33 fDPT = 4.33 | 410 | ||
| PC | 150 | 250 | 150 | 50.0 | fMC = 3.81 fBRT = 4.09 fDPT = 4.40 | 434 | ||
| SFRC | 150 | 250 | 150 | 40.0 | fMC = 2.98 fBRT = 3.99 fDPT = 4.74 | 374 | ||
| SFRC | 150 | 250 | 150 | 50.0 | fMC = 3.73 fBRT = 4.32 fDPT = 4.49 | 527 | ||
| PC | 150 | 400 | 150 | 40.0 | fMC = 3.25 fBRT = 4.33 fDPT = 4.33 | 633 | ||
| SFRC | 150 | 400 | 150 | 40.0 | fMC = 2.98 fBRT = 3.99 fDPT = 4.74 | 631 | ||
| SFRC | 150 | 400 | 150 | 50.0 | fMC = 3.73 fBRT = 4.32 fDPT = 4.49 | 641 | ||
| PC | 150 | 750 | 150 | 40.0 | fMC = 3.25 fBRT = 4.33 fDPT = 4.33 | 744 | ||
| SFRC | 150 | 750 | 150 | 40.0 | fMC = 2.98 fBRT = 3.99 fDPT = 4.74 | 660 | ||
| SFRC | 150 | 750 | 150 | 50.0 | fMC = 3.73 fBRT = 4.32 fDPT = 4.49 | 715 | ||
| [7] | Block | SFRC | 100 | 250 | 250 | 39.1 | fMC = 2.97 | 790 |
| [18] | PC | 100 | 1000 | 150 | 57.2 | fMC = 4.03 | 1465 | |
| PFRC | 100 | 1000 | 150 | 48.5 | fMC = 3.54 | 1470 | ||
| PC | 150 | 1000 | 150 | 57.2 | fMC = 4.03 | 1700 | ||
| PFRC | 150 | 1000 | 150 | 48.5 | fMC = 3.54 | 1598 | ||
| [24] | Block | SFRC | 100 | 250 | 250 | 38.4 | fMC = 3.54 | 747 |
| [25] | Segment | SFRC | 480 | 1840 | 500 | 43.0 | fMC = 3.21 | 2688 |
| [38] | Segment | RC-PFRC | 734 | 3020 | 300 | 43.0 | fMC = 3.21 | 2389 |
| Model | Fpred | Context | Assumptions | Formulation |
|---|---|---|---|---|
| [17] | Prestressed concrete | Semi-infinite strip | Elastic solution with corrections | |
| [18] | TBM tunnels | Semi-infinite strip | Exact elastic solution | |
| [19] | Prestressed concrete | Semi-infinite strip | Compression-dispersion model | |
| [20] | TBM tunnels | Short blocks | Strut-and-tie model | |
| [20] | TBM tunnels | Long blocks | Strut-and-tie model | |
| [21] | TBM tunnels | Semi-infinite strip | Linear regression based on numerical model improvements |
| Model | Improved Fpred | Improvement |
|---|---|---|
| [17] | Equation with parametric correction obtained in the linear regression between relative error and b1/b | |
| [20] for short blocks | Correction for bias, assuming a normal distribution of the relative errors centered at −25% | |
| [20] for long blocks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marum, T.H.; Serafini, R.; Nunhez, R.; Agra, R.R.; de Figueiredo, A.D.; Bitencourt, L.A.G., Jr. Evaluation and Calibration of Analytical Models for Predicting Splitting in Precast Concrete Tunnel Segments During TBM Thrust. Buildings 2025, 15, 4302. https://doi.org/10.3390/buildings15234302
Marum TH, Serafini R, Nunhez R, Agra RR, de Figueiredo AD, Bitencourt LAG Jr. Evaluation and Calibration of Analytical Models for Predicting Splitting in Precast Concrete Tunnel Segments During TBM Thrust. Buildings. 2025; 15(23):4302. https://doi.org/10.3390/buildings15234302
Chicago/Turabian StyleMarum, Tiago Haddad, Ramoel Serafini, Ricardo Nunhez, Ronney Rodrigues Agra, Antonio Domingues de Figueiredo, and Luís Antonio Guimarães Bitencourt, Jr. 2025. "Evaluation and Calibration of Analytical Models for Predicting Splitting in Precast Concrete Tunnel Segments During TBM Thrust" Buildings 15, no. 23: 4302. https://doi.org/10.3390/buildings15234302
APA StyleMarum, T. H., Serafini, R., Nunhez, R., Agra, R. R., de Figueiredo, A. D., & Bitencourt, L. A. G., Jr. (2025). Evaluation and Calibration of Analytical Models for Predicting Splitting in Precast Concrete Tunnel Segments During TBM Thrust. Buildings, 15(23), 4302. https://doi.org/10.3390/buildings15234302






