Monitoring Method for the Self-Bearing Process During the Construction of Long-Span Steel Roof Structures with Ring Beams
Abstract
1. Introduction
2. Stiffness Monitoring Method Based on Structural Internal Force and Displacement Data
2.1. Method for Determining Local Stiffness
2.2. Method for Determining Overall Stiffness
3. Monitoring and Optimisation Feedback for the Structure’s Self-Bearing Process
Method for Monitoring Stiffness Variation During the Structure’s Self-Bearing Process
4. Stiffness Monitoring and Self-Bearing Optimisation of the Long-Span Steel Roof of Shenzhen Stadium
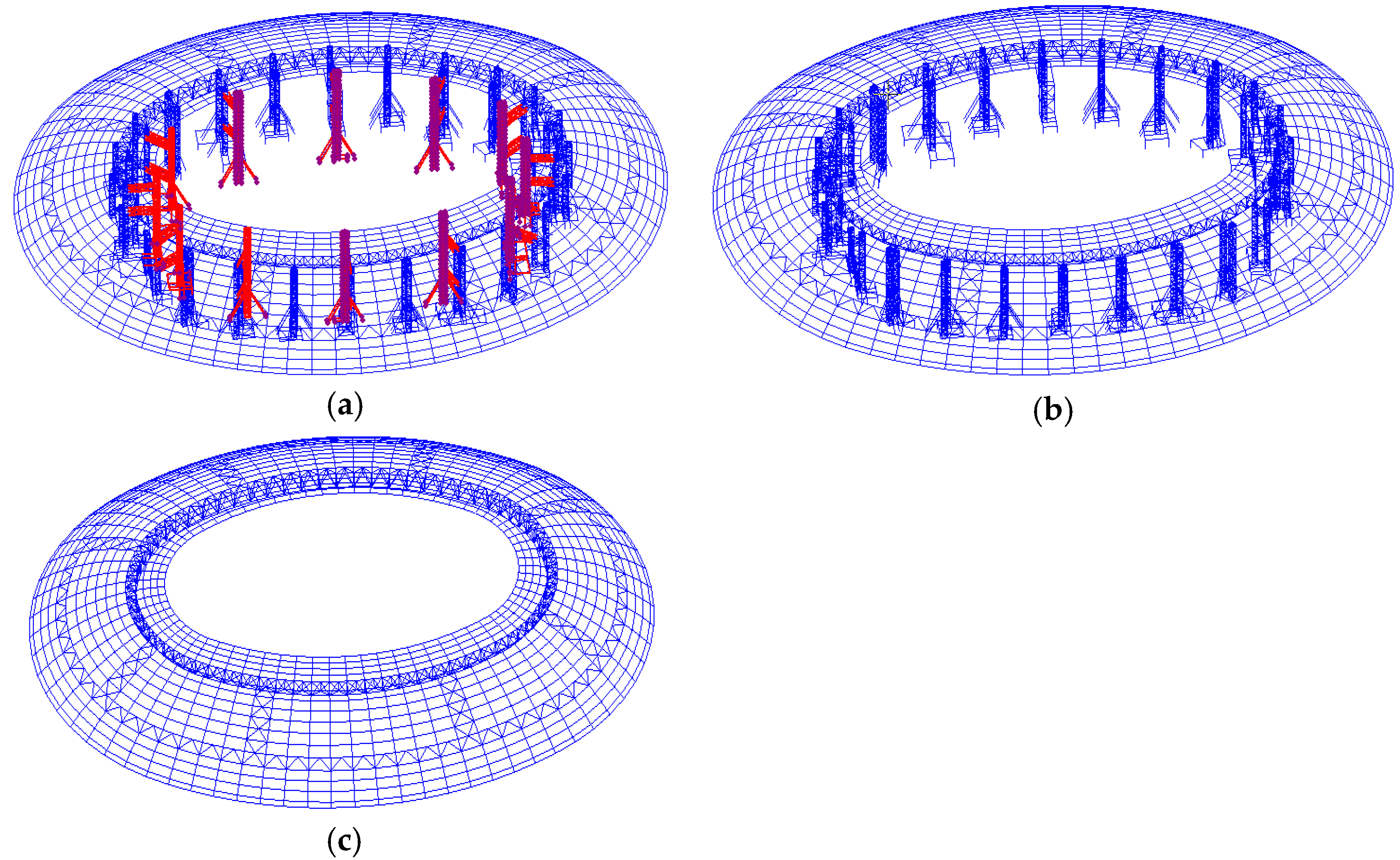
4.1. Project Overview
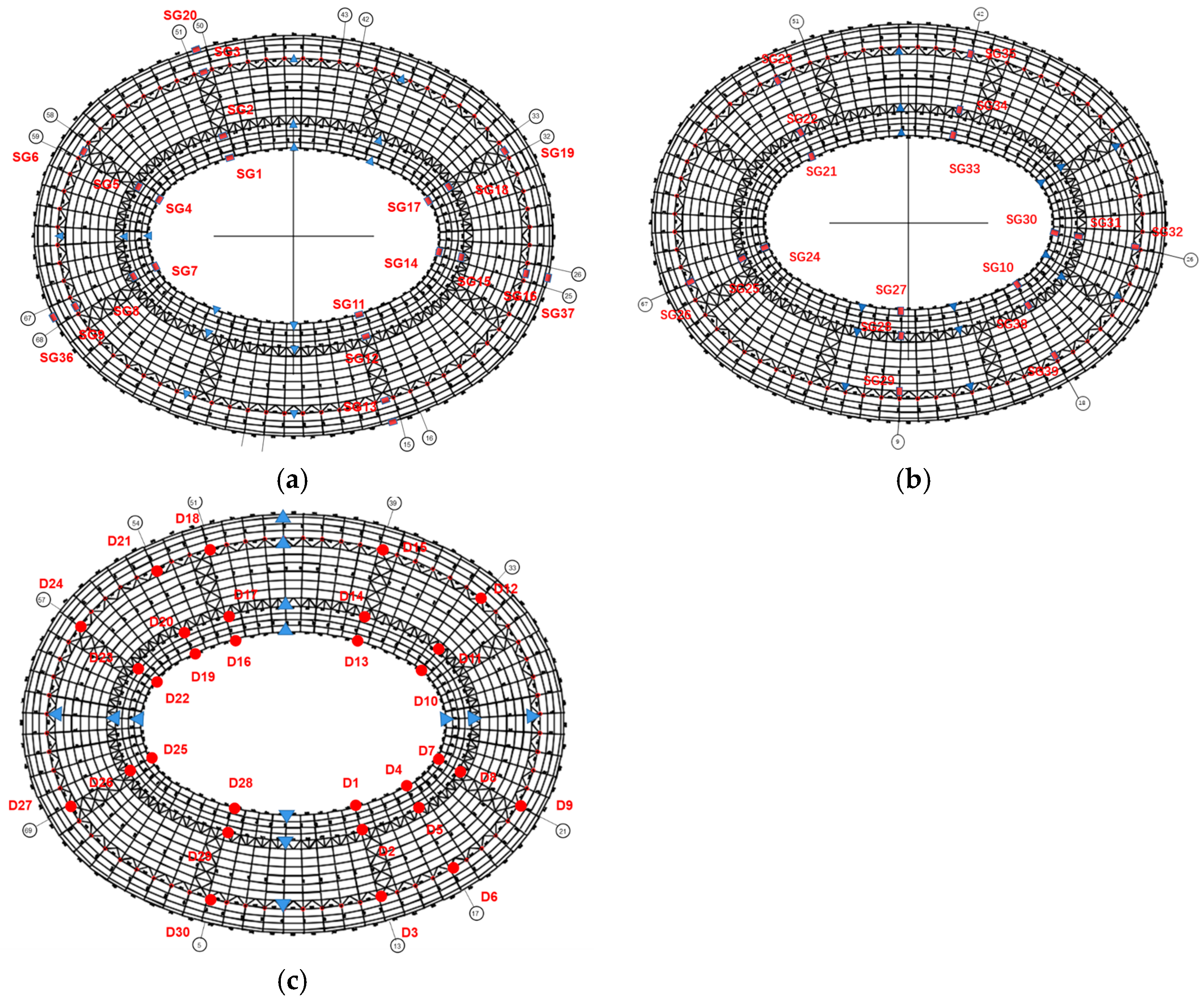
4.2. Determination of Monitoring Points and Establishment of a Monitoring System
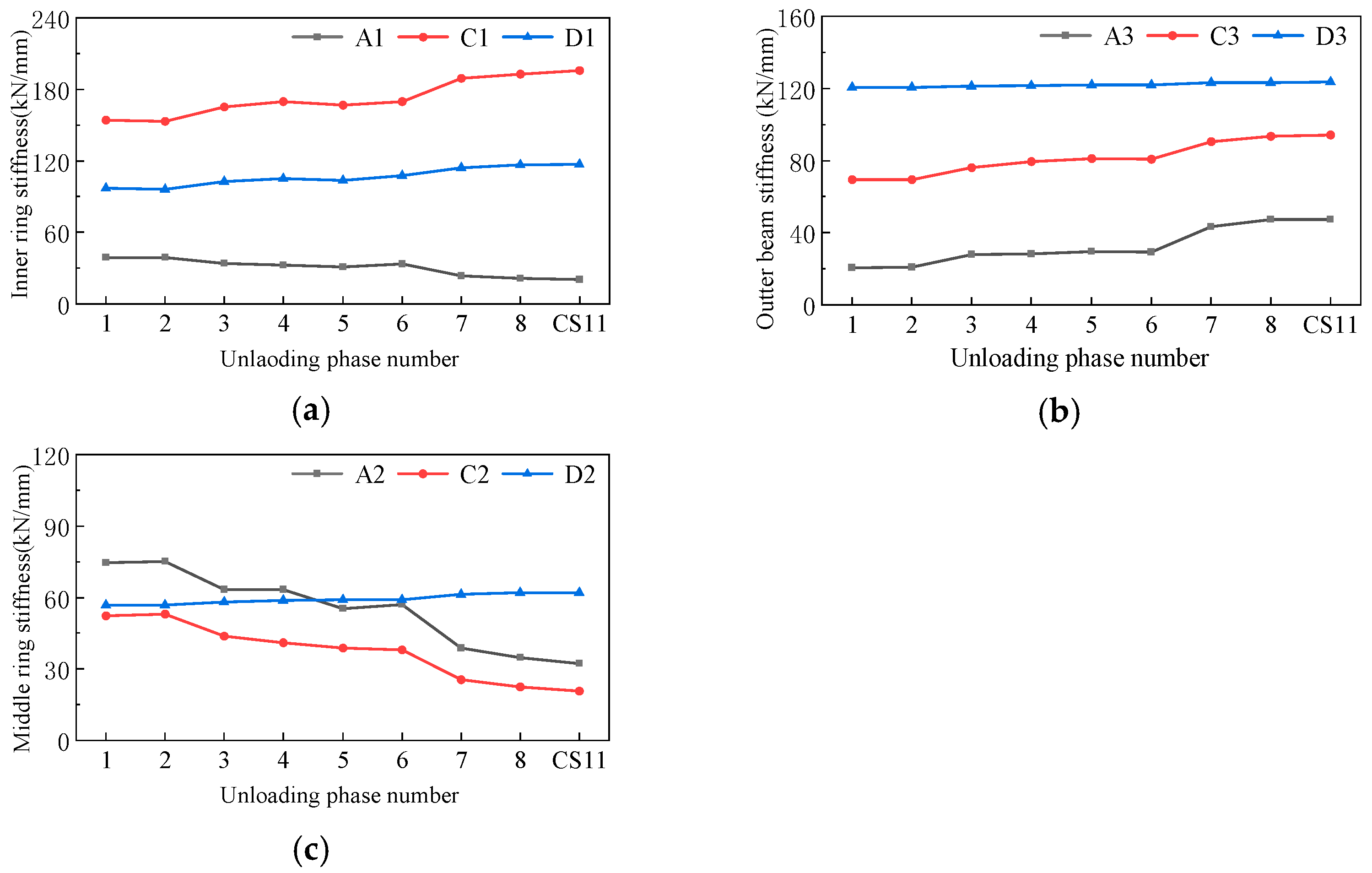
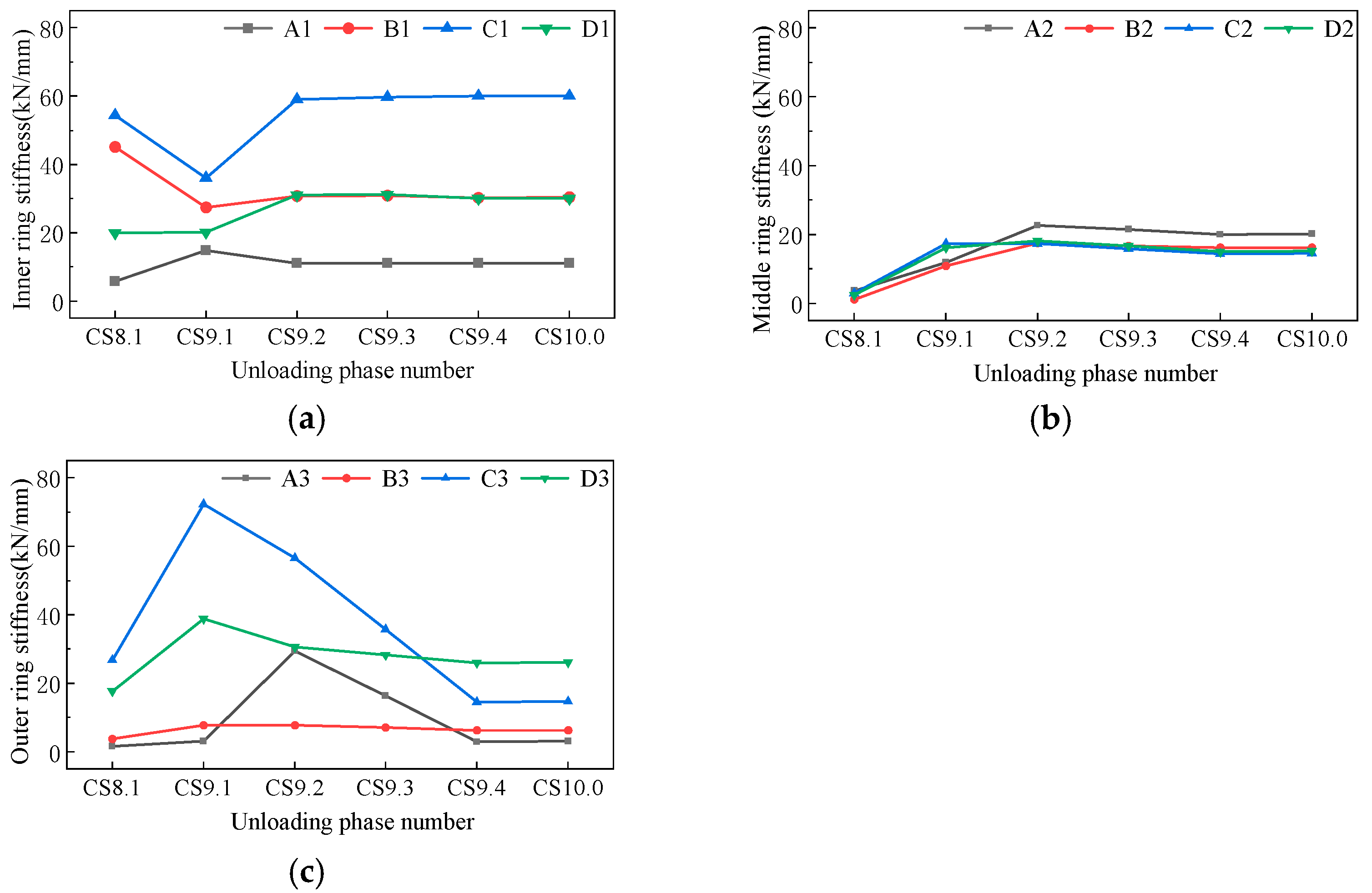
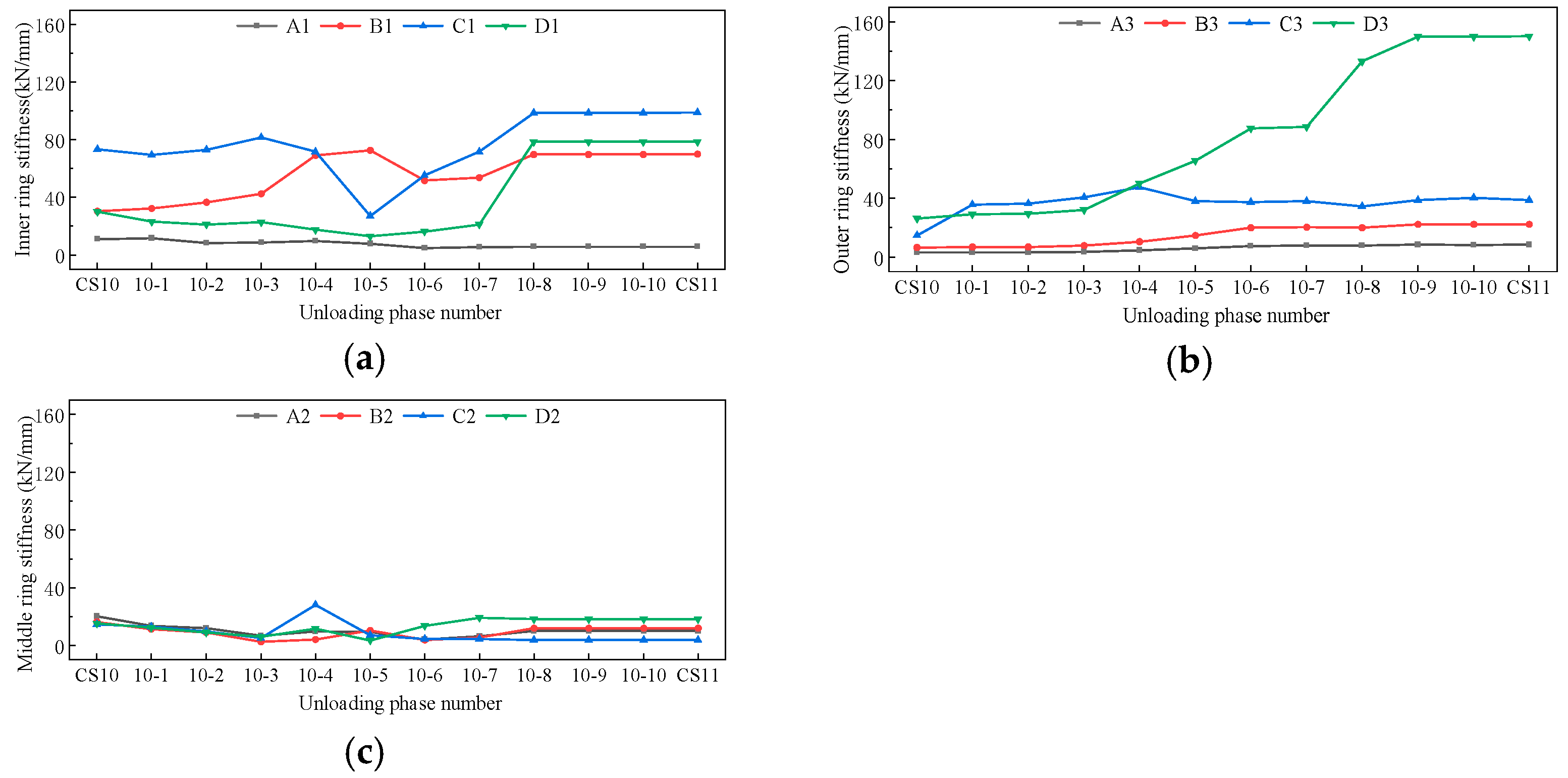
4.3. Stiffness Monitoring
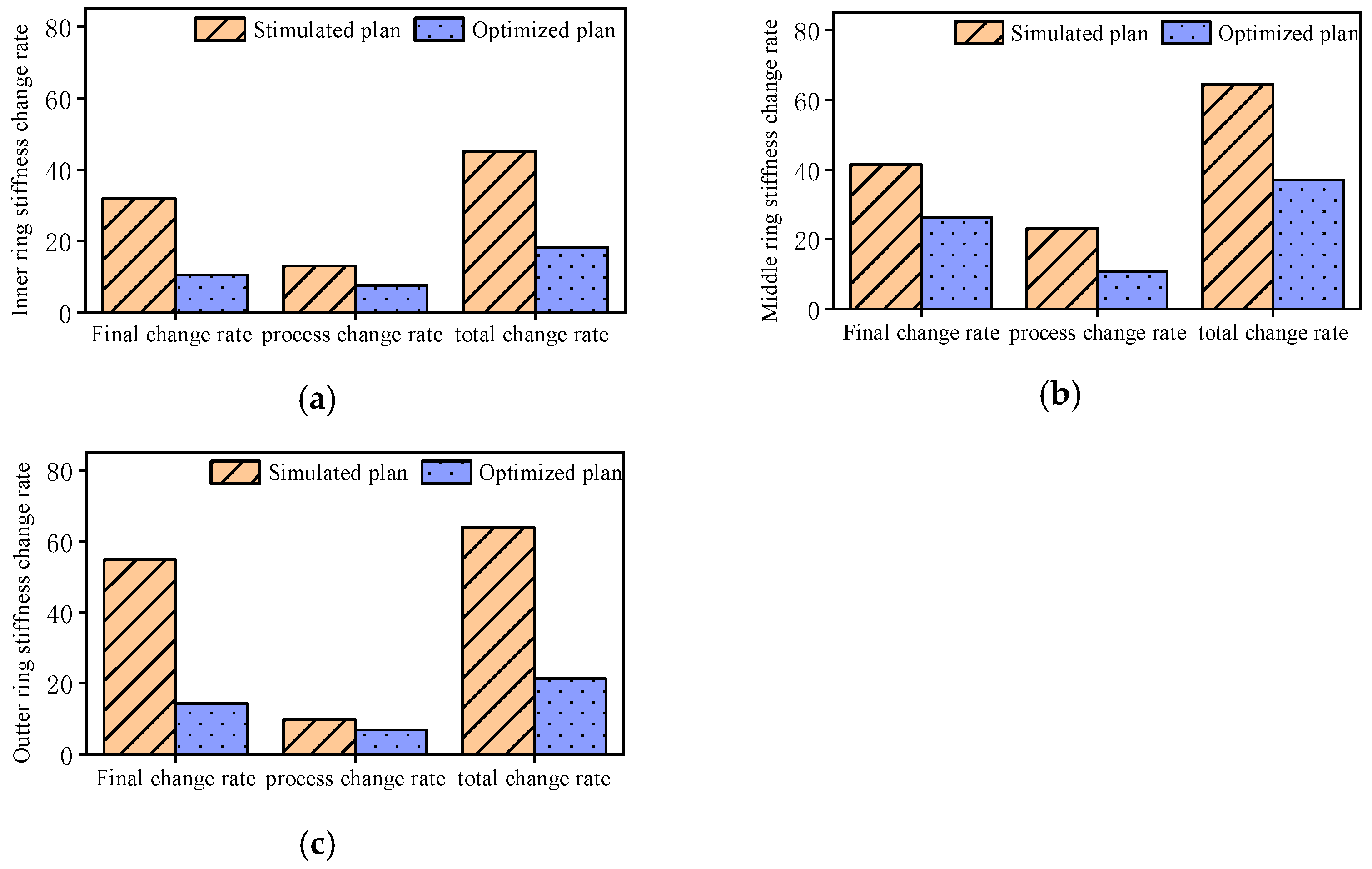
4.4. Self-Bearing Optimisation
- A method is introduced to derive axial force vector sums at symmetric points of the ring beam based on on-site stress and displacement data. By installing strain gauges and displacement monitoring prisms on the steel roof structure, mechanical parameters such as stress and displacement at critical locations can be continuously monitored and fed back during construction, thereby ensuring structural safety.
- The stiffness variation rate indicator introduced in this study provides a basis for optimising the unloading process in practical engineering applications. Increasing the single-cut unloading height of the falsework reduces the spatial stiffness variation rate of the unloading ring beam and mitigates the effects of internal force redistribution on the steel roof structure during unloading, thereby refining the construction process.
5. Conclusions
- The study established layout principles for stress and displacement monitoring points in steel roof structures with ring beams as the core load-bearing element. Building on the definition of ring beam stiffness, a theoretical method for determining global stiffness was derived. Additionally, a comprehensive stiffness monitoring approach based on monitored internal force and displacement data were proposed.
- The concept of non-dimensionalisation was employed to convert absolute stiffness changes between adjacent construction stages into stiffness change rates, thereby more clearly capturing the trend in stiffness evolution during the self-bearing process. Two unloading schemes were formulated, each associated with a corresponding finite element model. This indicator of stiffness change rate was then applied to complete the optimisation feedback for the structural self-bearing process.
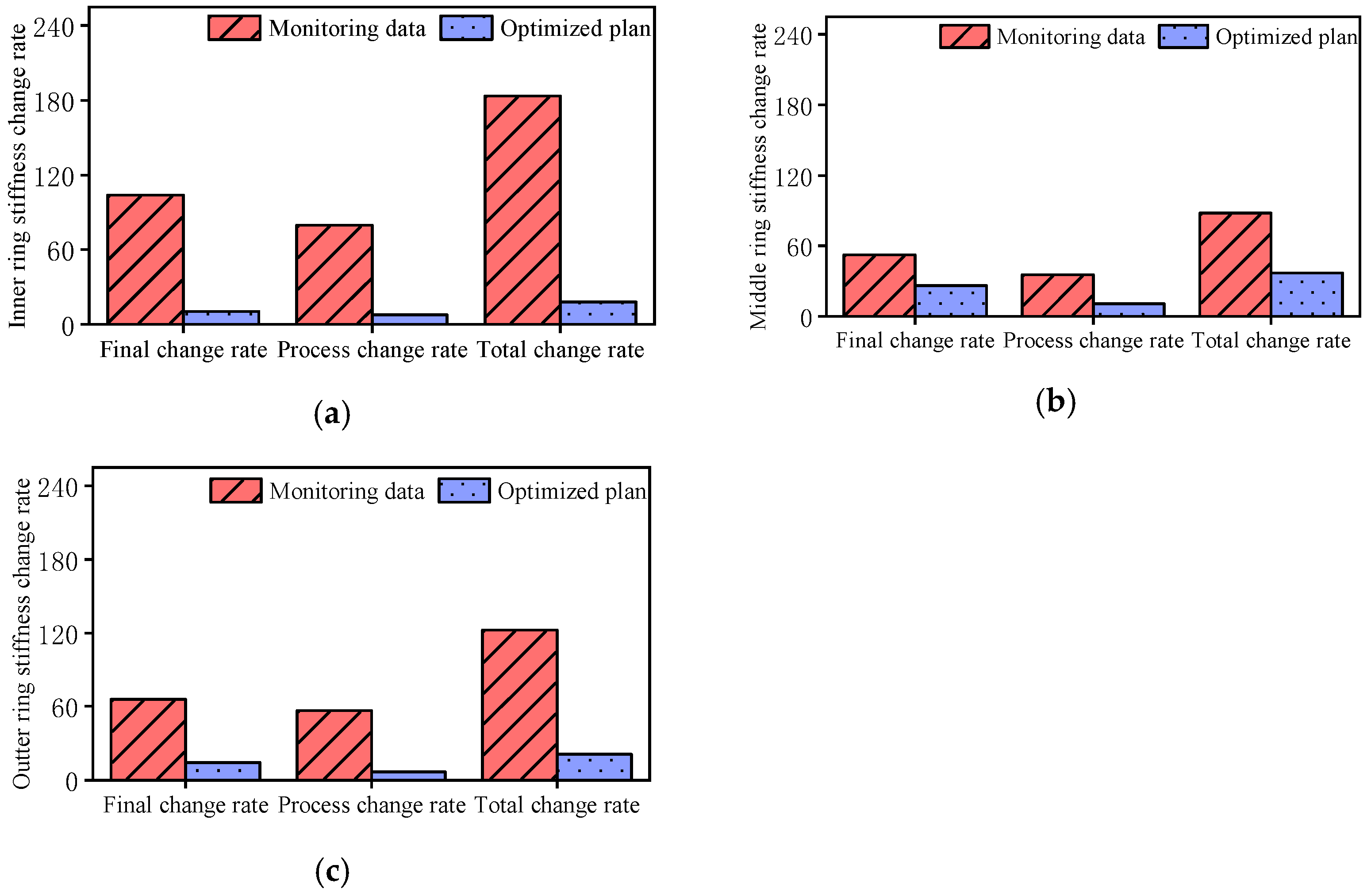
- A monitoring system was deployed at Shenzhen Stadium to track stress, displacement and stiffness-related mechanical indicators. Comparison with the optimised scheme from the finite element model revealed that the implemented unloading plan had potential for further improvement in self-bearing performance, offering valuable guidance for similar future projects.
- When verifying the mechanism of spatial stiffness formation in the ring beams, the construction simulation of the Shenzhen Stadium considered only the structural self-weight load. In practice, monitoring data from the stadium clearly show that temperature effects significantly influence the internal force distribution of the steel structure. Future work could further examine the influence of temperature effects on the spatial stiffness of the ring beams.
- The optimisation scheme proposed in this study focuses solely on the unloading stage. However, due to the path-dependent and time-dependent effects of the construction process, the assembly and closure sequence of the ring beams considerably affect the spatial stiffness and self-bearing state before unloading. Subsequent research could refine the finite element model to consider various ring beam closure scenarios, analyse the self-bearing state of the steel roof under these conditions and explore the influence of closure sequences on self-bearing behaviour.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ngamkhanong, C.; Kaewunruen, S.; Costa, B.J.A. State-of-the-Art Review of Railway Track Resilience Monitoring. Infrastructures 2018, 3, 3. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sresakoolchai, J.; Zhou, Z. Sustainability-Based Lifecycle Management for Bridge Infrastructure Using 6D BIM. Sustainability 2020, 12, 2436. [Google Scholar] [CrossRef]
- Chucheepsakul, S.; Phungpaigram, B. Elliptic Integral Solutions of Variable-Arc-Length Elastica under an Inclined Follower Force. ZAMM—J. Appl. Math. Mech. Z. Angew. Math. Mech. 2004, 84, 29–38. [Google Scholar] [CrossRef]
- Sibanda, K.; Kaewunruen, S. Life Cycle Assessment of Retrofit Strategies Applied to Concrete Infrastructure at Railway Stations Exposed to Future Extreme Events. In Proceedings of the RILEM Spring Convention and Sustainable Materials, Systems and Structures Conference: RILEM RMSS 2019, Rovinj, Croatia, 20–22 March 2019; RILEM Publications SARL: Paris, France, 2019; pp. 168–175. [Google Scholar]
- Ngamkhanong, C.; Kaewunruen, S.; Baniotopoulos, C. Nonlinear Buckling Instabilities of Interspersed Railway Tracks. Comput. Struct. 2021, 249, 106516. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ngamkhanong, C.; Baniotopoulos, C. Resilience and Robustness of Long-Span and Tall Structures under Extreme Actions. Front. Built Environ. 2020, 6, 67. [Google Scholar]
- Ben, N.; Chen, Z. Simulation Analysis of the Steel Roof of the Tianjin Grand Theatre in the Unloading Process. In Proceedings of the 2013 Fourth International Conference on Digital Manufacturing & Automation, Qingdao, China, 29–30 June 2013; pp. 1203–1206. [Google Scholar]
- Zhou, G.; Zhang, J.; Liu, J.; You, G.; Wang, Y. Construction Simulation Analysis of Steel Structure for Hangzhou Olympic Sports Center Main Stadium. Constr. Technol. 2014, 43, 1–5. [Google Scholar]
- Liu, H.; Zhou, R.; Sheng, X.; Xu, J.; Xu, F.; Wang, Y. Nonlinear-Response Study on the Two Beams Coupled by the Multiple Nonlinear Elements with the Cubic Stiffness. Nonlinear Dyn. 2024, 112, 19735–19757. [Google Scholar] [CrossRef]
- Xu, C.; Ye, L.; Pan, S.; Luo, W. Integrated Time-Dependent Analysis of a Hydraulic Structure on Soft Foundations during Construction. Water 2024, 16, 1375. [Google Scholar] [CrossRef]
- Dai, P.; Tang, J. Research on Construction Monitoring Techniques for Cable Replacement of the Cable-Stayed Bridge. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3202–3208. [Google Scholar]
- Huang, W.; Jin, T.; Zhu, Z.; Cai, X.; Cai, T.; Huang, Y.; Zhou, M.; Liu, Q.; Shen, Y. Monitoring and Analysis of Construction Process for Reconstruction of Existing Cantilever Roof Structure in a Stadium. Spat. Struct. 2023, 29, 62–68. (In Chinese) [Google Scholar]
- Wu, J. Full Process Analysis and Application of Steel Structure Jacking and Unloading in a Stadium. Prog. Steel Build. Struct. 2021, 23, 119–128. (In Chinese) [Google Scholar]
- Prem, K. A Review of Developments in Steel: Implications for Long-Span Structures. Trans. Indian Inst. Met. 2021, 74, 1055–1064. [Google Scholar] [CrossRef]
- Wang, H.; Yang, F.; Shen, B.; Ma, K.J.; Zheng, T.H.; Fan, Y.H. Construction Process Analysis for a Multi-Story Building Structure with Floors Slab of Long-Span. Civ. Eng. J. 2019, 28, 404–419. [Google Scholar] [CrossRef]
- Chen, K.; Yuan, G.; Wang, L.; Zhang, W.; Wang, X. Research on Construction Monitoring of Large-Span Steel Pipe Truss Structure. Open J. Civ. Eng. 2019, 09, 255–267. [Google Scholar] [CrossRef]
- Furukawa, S.; Iwami, R.; Kimura, Y. Development of an Environmentally Friendly Steel Structural Framework: Evaluation of Bending Stiffness and Yield Bending Moment of Cross-Laminated Timber Slab–H-Shaped Steel Composite Beams for Component Reuse. Sustainability 2025, 17, 2073. [Google Scholar] [CrossRef]
- Shao, J.H.; Duan, M.J.; Yang, W.; Li, Y.Z. Research on the Critical Technique of Synchronous Rotation Construction with Large Angle for T-shape Curve Rigid Frame Bridge. Sci. Rep. 2022, 12, 1530–1545. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.H.; Wang, Z.H.; Tao, G.Y. Research on the Unloading Process of Long-Span Steel Roof and the Design of Temporary Bracing Structure. Adv. Mater. Res. 2011, 163, 251–258. [Google Scholar] [CrossRef]
- Shi, N.Q.; Shi, Z.J.; Tong, C.C.; Jin, X.G. Construction Mechanics of Ultra Deep Ventilation Shaft in Subway Station Under Complex Engineering Environment. In Proceedings of the 2019 International Conference on Energy, Environmental and Civil Engineering (EECE 2019), Wuhan, China, 23–24 June 2019; pp. 264–270. [Google Scholar]
- Yang, W.; Hong, G.; Wang, M.; Yang, G.; Zhang, G.; Wang, S.; Duan, Y.; Ge, J.; Zhou, W. Simulation Analysis of the Entire Construction Process of a Multi-Story Large Cantilever Steel Structure. J. Build. Struct. 2012, 33, 87–94. [Google Scholar]
- Ren, L.; Yuan, C.L.; Li, H.N.; Yi, T.H. Structural Health Monitoring System Developed for Dalian Stadium. Int. J. Struct. Stab. Dyn. 2016, 16, 1640018. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Wang, M.; Cao, W.; Yan, Q. Research on Unloading Technology for the Long-Span Open Single-Layer Arch-Shell Steel Roof of Beijing Workers’ Stadium. Build. Struct. 2023, 53, 26–30. [Google Scholar]
- Zhou, G.P.; Li, A.Q.; Li, N.; Li, J.H. Design and Analysis of the Health Monitoring System for the Steel Arch of the Main Stadium Roof in Nanjing Olympic Sports Center. Appl. Mech. Mater. 2016, 858, 3–9. [Google Scholar] [CrossRef]
- Zhao, F.W.; Fei, G. Application and Research of Steel Structure Construction Monitoring of Costa Rica State Stadium Canopy with Measurement Robot. Energy Procedia 2011, 13, 2794–2801. [Google Scholar] [CrossRef]
- Huang, T.R.; Wu, J.J.; Deng, X.Y.; Bai, G.B.; Zhu, Z.Y.; Zhang, J. Research and Application of Monitoring Technology for De-Propping Stress and Deformation of Lusail Stadium Steel Structure. Spat. Struct. 2024, 30, 47–54. [Google Scholar]
- Zhao, H.; Zhang, X.; Ding, Y.; Guo, T.; Li, A.; Soh, C.K. Probabilistic Mixture Model Driven Interpretable Modeling, Clustering, and Predicting for Physical System Data. Eng. Appl. Artif. Intell. 2025, 160, 112069. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Yuan, C.; Xiong, H.; Xiang, Y.; Xia, H.; Mao, R.; Teng, J.; Hu, W. Monitoring Method for the Self-Bearing Process During the Construction of Long-Span Steel Roof Structures with Ring Beams. Buildings 2025, 15, 4293. https://doi.org/10.3390/buildings15234293
Lu W, Yuan C, Xiong H, Xiang Y, Xia H, Mao R, Teng J, Hu W. Monitoring Method for the Self-Bearing Process During the Construction of Long-Span Steel Roof Structures with Ring Beams. Buildings. 2025; 15(23):4293. https://doi.org/10.3390/buildings15234293
Chicago/Turabian StyleLu, Wei, Cheng Yuan, Hang Xiong, Yiyang Xiang, Huasheng Xia, Rongying Mao, Jun Teng, and Weihua Hu. 2025. "Monitoring Method for the Self-Bearing Process During the Construction of Long-Span Steel Roof Structures with Ring Beams" Buildings 15, no. 23: 4293. https://doi.org/10.3390/buildings15234293
APA StyleLu, W., Yuan, C., Xiong, H., Xiang, Y., Xia, H., Mao, R., Teng, J., & Hu, W. (2025). Monitoring Method for the Self-Bearing Process During the Construction of Long-Span Steel Roof Structures with Ring Beams. Buildings, 15(23), 4293. https://doi.org/10.3390/buildings15234293






