Effects of Joint Configurations on Shear Behavior of Prefabricated Segmental Cap Beams
Abstract
1. Introduction
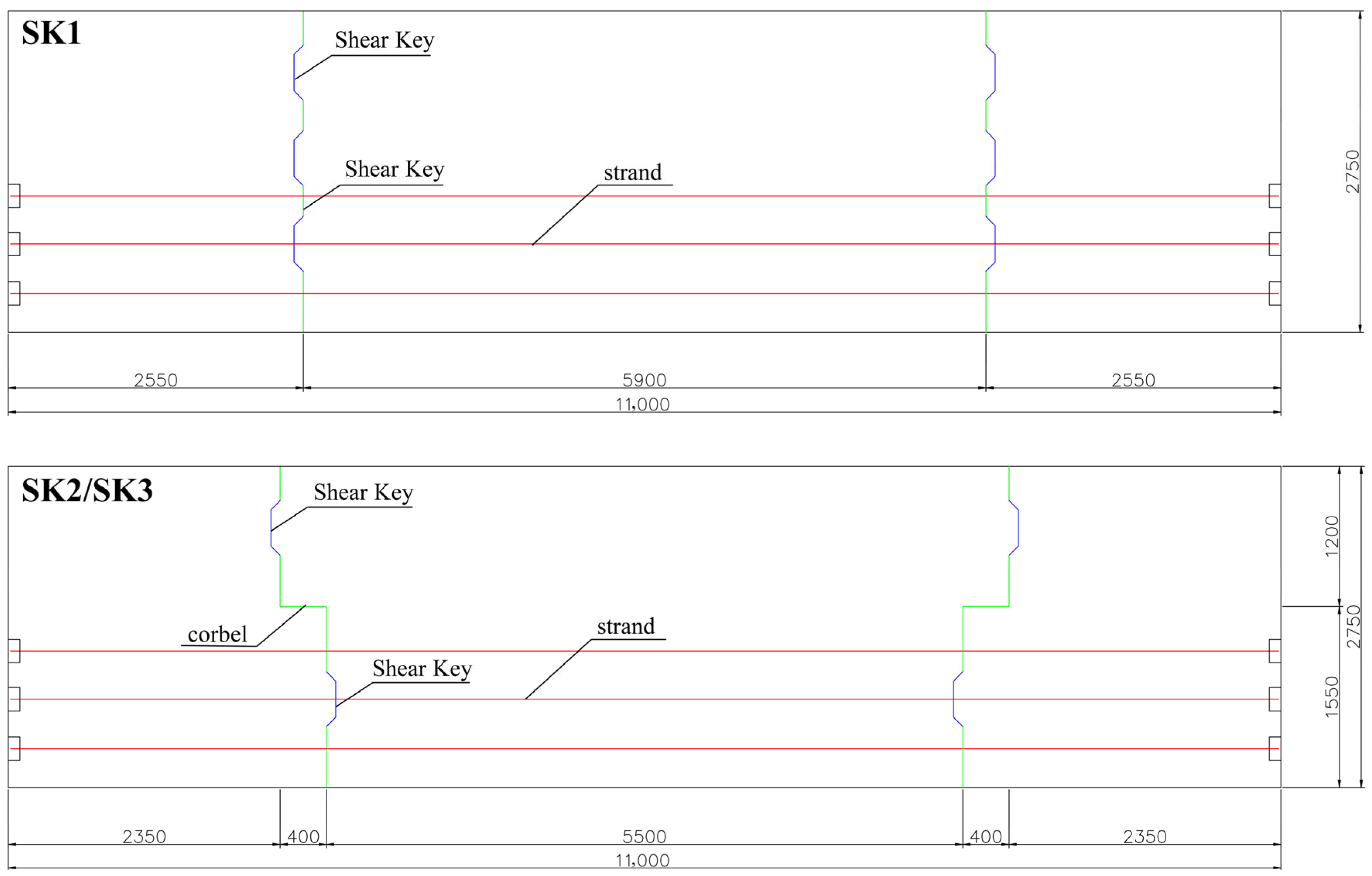
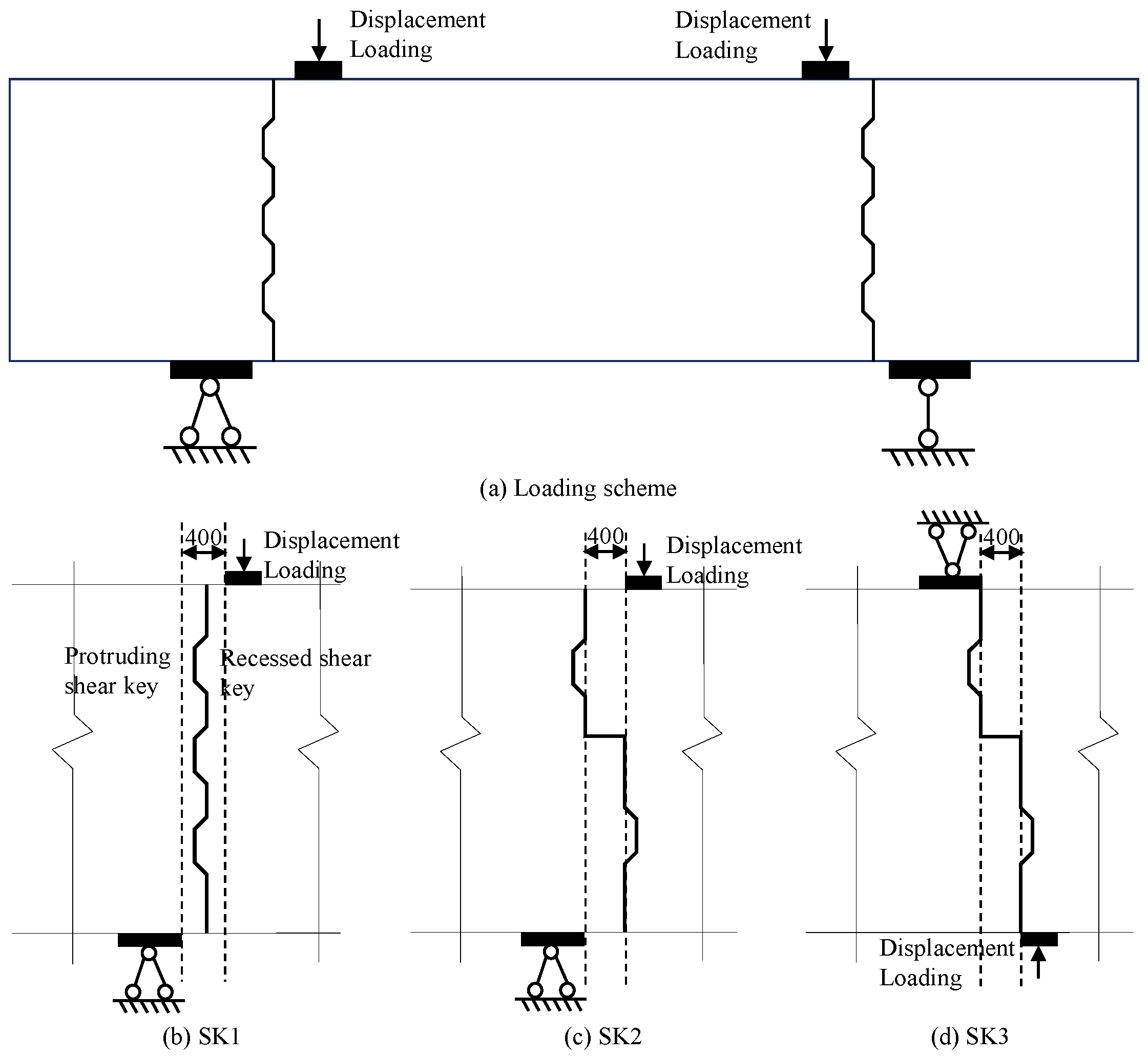
2. Component Design
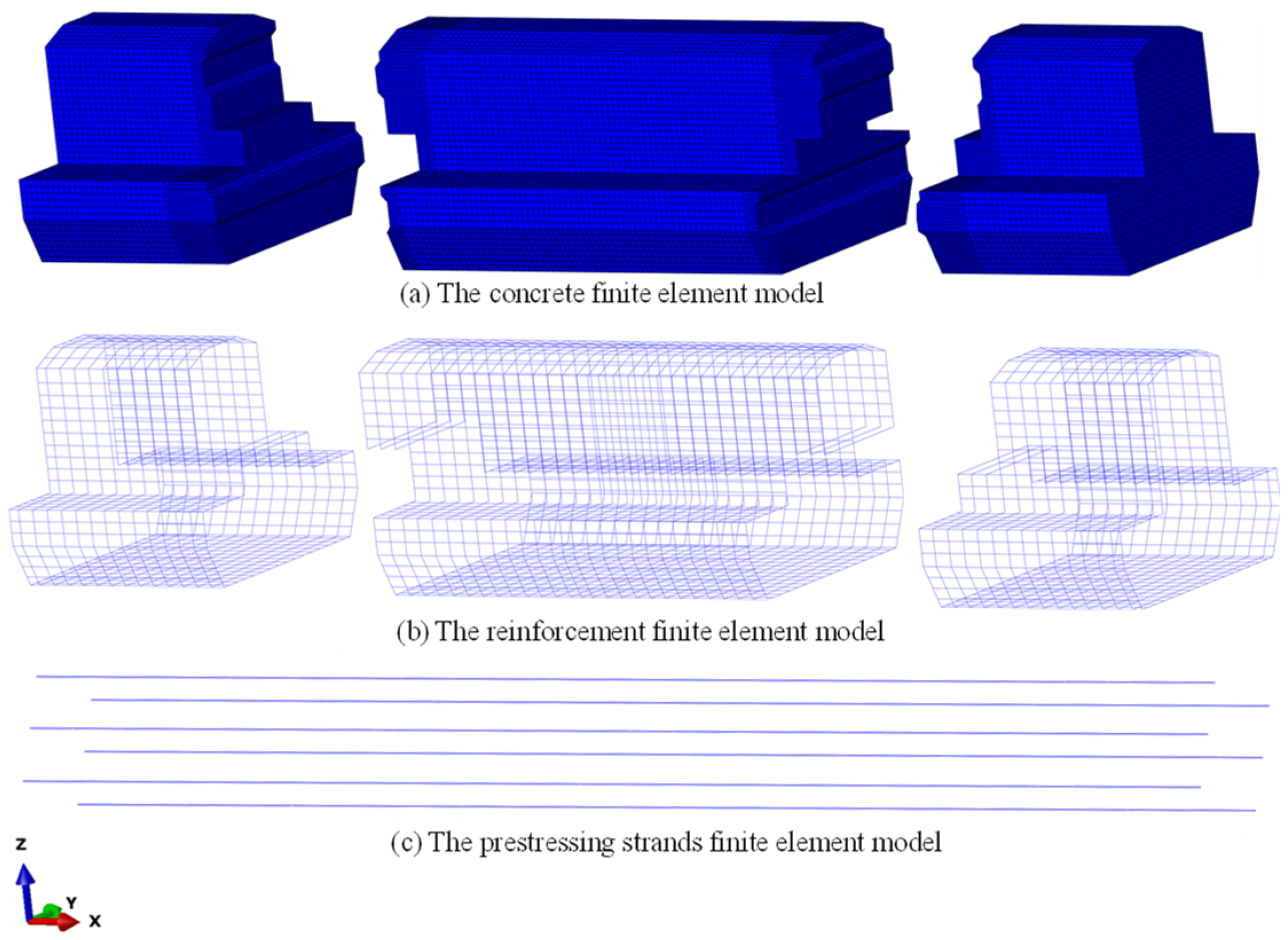
3. Numerical Model
4. Comparative Analysis
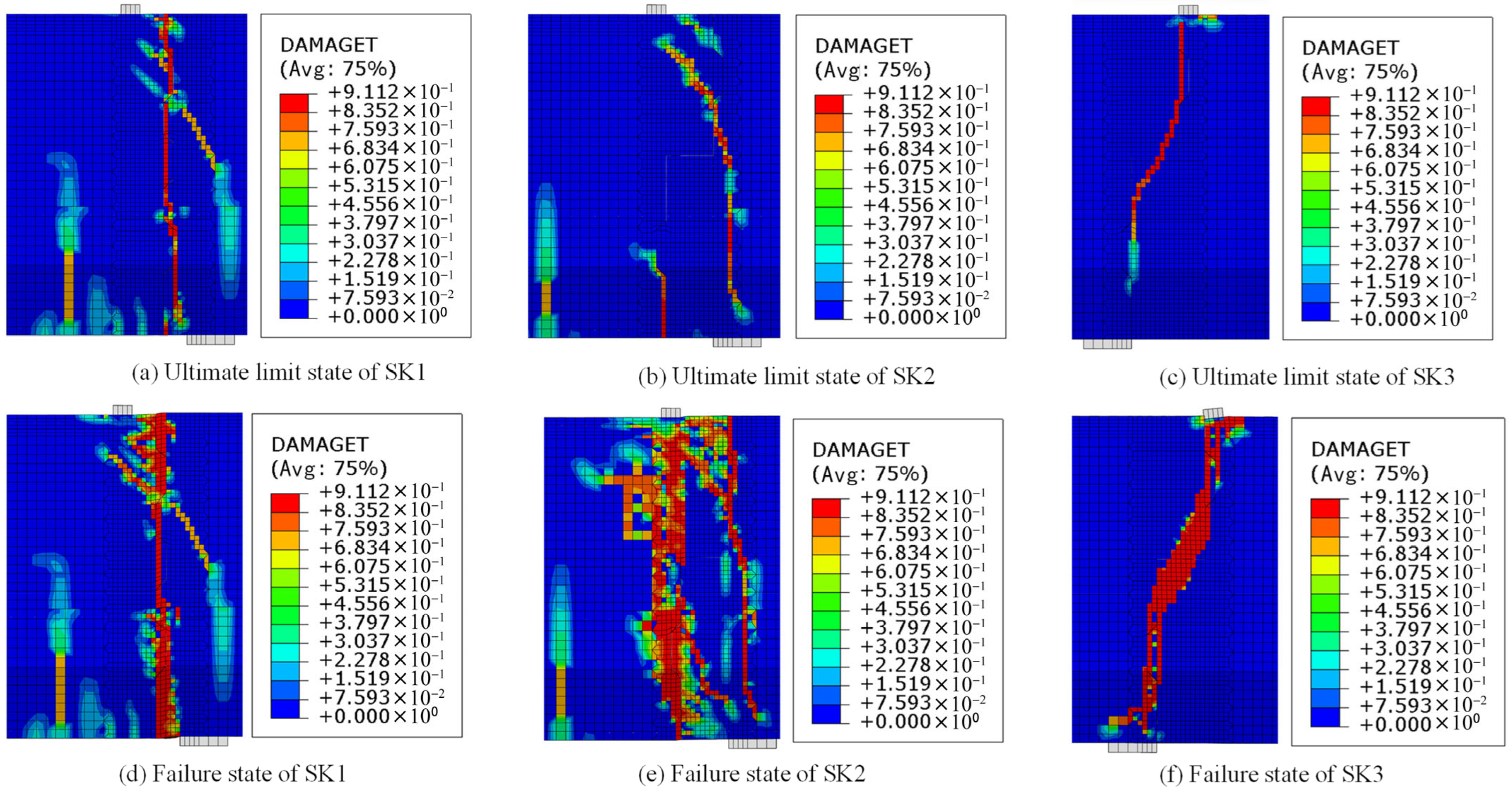
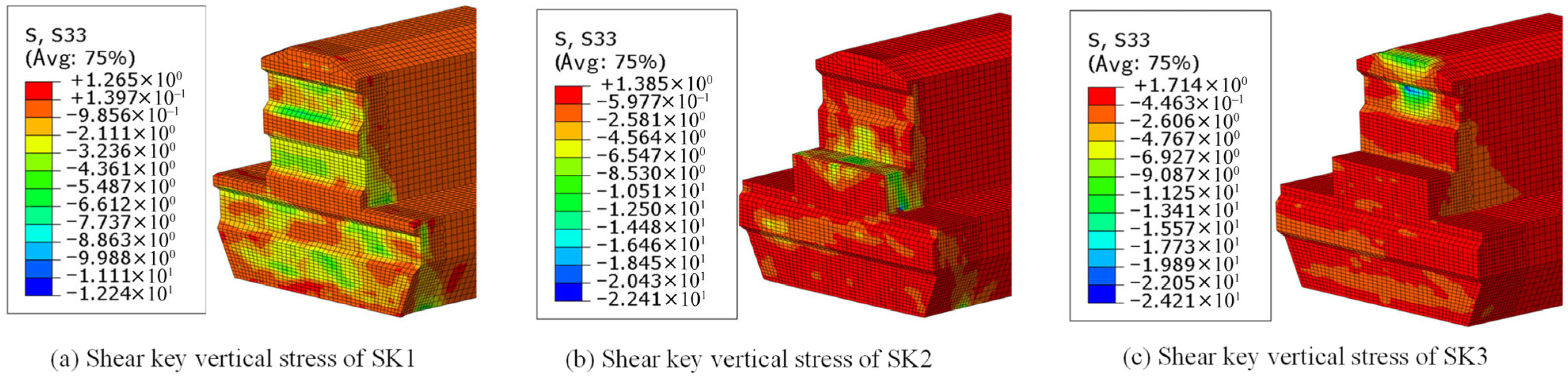
4.1. Crack Propagation and Failure Modes
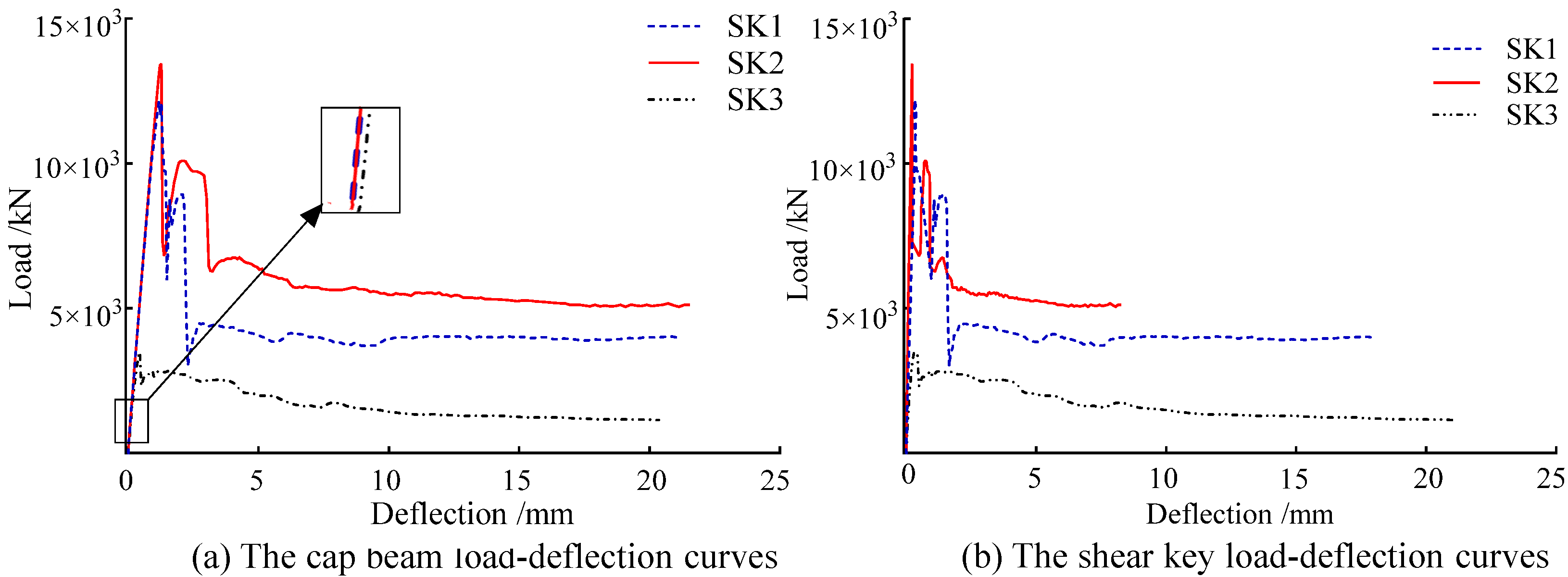
4.2. Load–Deflection Curves Comparison
- Under small displacement loading with intact shear keys, all models exhibited elastic behavior. The bearing capacity increased proportionally with the loading-point displacement, indicating a linear response, with identical initial stiffness observed for all models.
- Upon entering the crack development stage, initial diagonal cracks propagated into the surrounding regions in all models. The slope of the load–deflection curves gradually decreased, indicating pronounced nonlinear behavior. During most of this stage, the tangent stiffness of SK1, SK2, and SK3 remained nearly identical. However, in the later stages, due to the sequential failure of shear keys, the reduction in bearing capacity for SK1 and SK2 occurred in distinct stages. In contrast, the shear keys of the SK3 model failed completely at an early stage, leading to a rapid reduction in bearing capacity, followed by gradual stiffness degradation as cracks continued to develop.
- In the failure stage, the slope of the load–deflection curves approached zero. As the loading-point displacement increased, the load stabilized, and all models ultimately failed as a result of shear key fracture. In comparison with the SK3 model, both SK1 and SK2 exhibited markedly higher ultimate bearing and deformation capacities, with SK2 demonstrating the highest values for both parameters. The shear performance results of the three cap beam models are summarized in Table 3.
4.3. Internal Force Analysis
5. Conclusions
- The load–deflection response of the SK2 model is broadly consistent with SK1, with failure progression characterized by vertical cracking at the lower supports, inclined crack initiation at the key roots, and eventual shear key fracture. By contrast, the SK3 model exhibits diagonal cracking at the key roots that rapidly develop into penetrating main cracks, indicative of concentrated diagonal tension failure. Comparative analysis shows that SK2 attains a higher ultimate capacity with more complex failure surfaces, whereas the altered load path in SK3 results in more brittle behavior and markedly reduced residual capacity.
- All three models exhibit a three-phase load–displacement response comprising elastic, cracking, and failure stages. Despite identical initial stiffness, SK1 and SK2 undergo gradual capacity reduction during cracking, whereas SK3 experiences rapid stiffness loss due to premature key failure. SK1 and SK2 achieve higher ultimate capacities with sequential key fracture and superior residual deformation, while SK3’s diagonal cracking induces abrupt capacity loss and the poorest residual performance. Among them, SK2 demonstrates the most favorable shear behavior, combining enhanced ultimate capacity with greater deformation capability, thereby highlighting the decisive role of joint configuration in governing ductility and load efficiency.
- SK2 exhibits the highest initial stiffness with minimal key displacement at ultimate load (1.10 mm), whereas SK3 presents the lowest stiffness due to insufficient corbel engagement. Despite lower residual capacity, SK1 achieves markedly greater displacement (17.98 mm), indicating superior deformation capacity. Thus, while the shear key–corbel configuration in SK2 enhances overall shear resistance, it compromises deformability, rendering the conventional SK1 design more suitable where large deformation capacity is required.
- SK1 transfers loads via diagonal compression within shear keys, inducing 45° inclined cracks. SK2 primarily mobilizes the corbel for load transfer with supplementary key contribution, whereas SK3’s reversed loading shifts resistance to the upper keys with negligible corbel engagement, consistent with its inferior shear performance. Thus, while SK1 and SK3 rely predominantly on key mechanisms, SK2 achieves optimized load distribution through key–corbel synergy, confirming the corbel’s role as the primary shear-resisting component.
- In future research, we will design multiple sets of experiments to provide recommendations for the optimal configuration of shear keys and corbels, dimensional suggestions, and reinforcement details for cap beam components of various spans and under different load requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, M.A. Accelerated Bridge Construction: Best Practices and Techniques; Butterworth-Heinemann: Oxford, UK, 2015; ISBN -13 978-0124072251. [Google Scholar]
- Xiang, Y.Q.; Zhu, S.; Zhao, Y. Research and development on accelerated bridge construction technology. China J. Highw. Transp. 2018, 31, 1–27. [Google Scholar] [CrossRef]
- Huo, L.F.; Fang, C.P.; Yao, X.F.; Liu, H.; Liu, S. Research on bending resistance of prefabricated and assembled cap beams with large cantilever prestressed segments. Concrete 2024, 10, 137–142. [Google Scholar] [CrossRef]
- Ye, M.; Li, L.; Hu, F.; Shao, X.; Tang, J. Flexural Behavior of a Fully Prefabricated Lightweight UHPC Bent Cap. J. Bridge Eng. 2020, 25, 04020085. [Google Scholar] [CrossRef]
- Ye, M.; Li, L.; Hu, F.; Wang, L.; Shao, X. UHPC-Based Precast Large-Cantilevered Thin-Walled Bent Caps: Design and Experiments. Eng. Struct. 2022, 272, 114909. [Google Scholar] [CrossRef]
- Li, C.; Zhuo, W.; Lin, K.; Sun, Y.; Chen, M. Experimental Study on Flexural Behavior of Segmental Precast Large-Cantilevered Prestressed Concrete Cap Beam. Structures 2023, 57, 105166. [Google Scholar] [CrossRef]
- Chung, C.H.; Lee, J.H.; Kwon, S.H. Proposal of a New Partially Precast Pier Cap System and Experimental Verification of Its Structural Performance. KSCE J. Civ. Eng. 2018, 22, 2362–2370. [Google Scholar] [CrossRef]
- Ge, J.P.; Mei, D.L.; Yan, X.F.; Wang, Z. Comparison and analysis of construction methods for precast pier caps. J. Technol. 2018, 18, 56–62. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Hao, Y. Flexural Behaviour of Precast Segmental Concrete Beams Internally Prestressed with Unbonded CFRP Tendons under Four-Point Loading. Eng. Struct. 2018, 168, 371–383. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Yuan, C. Performance of Precast Segmental Concrete Beams Posttensioned with Carbon Fiber-Reinforced Polymer (CFRP) Tendons. Compos. Struct. 2019, 208, 56–69. [Google Scholar] [CrossRef]
- Jiang, H.B.; Li, H.Y.; Xiao, J.; Chen, Y.; Fang, Z. Shear behavior of precast concrete segmental simply supported beam with external strands and dry joints. China J. Highw. Transp. 2018, 31, 188–195. [Google Scholar] [CrossRef]
- Li, G.; Wang, J.; Shen, Y.; Li, L.; Chen, M. Experimental Study on the Combined Shear and Bending Behaviour of Corbel Joints in Precast Concrete Segmental Inverted-T Caps. Structures 2020, 28, 2367–2378. [Google Scholar] [CrossRef]
- Shen, C.; Zhang, D.; Liu, W.; Fu, K.; Wang, F.; Wu, X.; Wang, D. Shear Capacity Model of Prefabricated Shear-Keyed Tooth Joints Under Confining Stress. Buildings 2024, 14, 4042. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Li, H. Behavior of Precast Segmental Concrete Beams Prestressed with External Steel and CFRP Tendons. J. Compos. Constr. 2020, 24, 04020053. [Google Scholar] [CrossRef]
- Li, C.C.; Zhuo, W.D.; Sun, Z.X.; Xiao, Z.; Chen, G.; Huang, X. Static behavior of segmental precast assembled cap beam with corbel joints. J. Harbin Eng. Univ. 2023, 44, 1328–1335. [Google Scholar] [CrossRef]
- Yan, X.F.; Ge, J.P.; Wang, Z.Q.; Gao, F.; Han, S.; Zhang, C.; Zhang, T. Research on flexural performance of prefabricated segmental prestressed concrete bent caps with large cantilevers. China Munic. Eng. 2019, 4, 72–76+118–119. [Google Scholar] [CrossRef]
- Huang, B.C.; Huang, Y.C.; Zhang, S. Research on the effect of shear keys on the mechanical properties of precast segmental cap beams. J. China Foreign Highw. 2020, 44, 192–197. [Google Scholar] [CrossRef]
- Huang, W.X.; Tang, W.H.; Xiao, T.L.; Zhe, H.; Huang, Z. Experimental and finite element analysis on shear performance of new keyed epoxy joint. J. Yangtze Univ. 2025, 1–10. [Google Scholar] [CrossRef]
- Chen, C.; He, W.Z.; Gao, Y.X. Optimal Design and Performance Analyses of RPC Bracket Joint. Bull. Sci. Technol. 2017, 33, 216–219. [Google Scholar] [CrossRef]
- Li, C.C.; Qin, Z.Q.; Chen, J.D.; Zhuo, W.D. Tests and Parametric Analysis of Shear Bearing Capacity of Epoxy Joints in Concrete Cap Beam. J. Tianjin Univ. 2025, 58, 368–378. [Google Scholar] [CrossRef]
- Wu, C.X.; Gao, P.Y.; Zhang, G.M.; Zhang, C. Structural behavior analysis of precast concrete cap beams. J. China Foreign Highw. 2023, 43, 208–217. [Google Scholar] [CrossRef]
- Liang, X.; Sritharan, S. Use of Unstressed Strands for Connections of Precast Concrete Members. PCI J. 2021, 66, 49–66. [Google Scholar] [CrossRef]
- Lu, W.; Li, F.; Zhu, L.; Wen, C.; Peng, W. Experimental Study on the Shear Behavior of Precast Concrete Segmental Simply Supported Beam with Internal Tendons and Glue Joints. Case Stud. Constr. Mater. 2022, 17, e01545. [Google Scholar] [CrossRef]
- Chen, P.; Cao, P.; Shi, F.; Chen, L.; Pei, X.; Tan, Z. Bolted Connections in Prefabricated Cantilevered Cap Beam-Column Structures: A Comprehensive Experimental and Numerical Study. Eng. Struct. 2024, 310, 118124. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Ludwig, W. Abaqus CFD User’s Guide; Version 6.13.1; Dassault Systèmes Simulia Corp: Waltham, MA, USA, 2013; pp. 691–693. [Google Scholar]
- Jiang, H.; Chen, L.; Ma, Z.J.; Feng, W. Shear Behavior of Dry Joints with Castellated Keys in Precast Concrete Segmental Bridges. J. Bridge Eng. 2015, 20. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Z.; Guo, J.; Wang, J. Shear Strength of Dry Joints in Precast UHPC Segmental Bridges: Experimental and Theoretical Research. J. Bridge Eng. 2019, 24, 1–18. [Google Scholar] [CrossRef]



| Dilation Angle ψ | Eccentricity e | Ultimate Compressive Strength Ratio | Constant Stress Ratio Kc | Viscosity Parameter ν | |||
| 30 | 0.1 | 1.16 | 0.667 | 0.0005 | |||
| Compressive behavior | Tensile behavior | ||||||
| Damaged factor | Cracking strain | Damaged factor | Inelastic strain | ||||
| 0.00000 | 0.00000 | 0.00000 | 0.00000 | ||||
| 0.16698 | 0.00043 | 0.07146 | 0.00001 | ||||
| 0.20465 | 0.00060 | 0.09322 | 0.00002 | ||||
| 0.24221 | 0.00078 | 0.12822 | 0.00003 | ||||
| 0.27889 | 0.00097 | 0.27544 | 0.00007 | ||||
| 0.37235 | 0.00148 | 0.41286 | 0.00012 | ||||
| 0.47408 | 0.00206 | 0.51288 | 0.00016 | ||||
| 0.55951 | 0.00262 | 0.58506 | 0.00019 | ||||
| 0.62612 | 0.00314 | 0.63864 | 0.00022 | ||||
| 0.67751 | 0.00364 | 0.77793 | 0.00037 | ||||
| 0.81381 | 0.00588 | 0.83735 | 0.00050 | ||||
| 0.87048 | 0.00798 | 0.87051 | 0.00063 | ||||
| 0.90095 | 0.01005 | 0.90672 | 0.00089 | ||||
| 0.93276 | 0.01415 | 0.92632 | 0.00115 | ||||
| 0.94914 | 0.01822 | 0.94339 | 0.00153 | ||||
| 0.96276 | 0.02433 | 0.95627 | 0.00204 | ||||
| 0.97257 | 0.03246 | 0.96411 | 0.00256 | ||||
| Type | Yield Strength /MPa | Ultimate Strength /MPa | Elastic Modulus /GPa |
|---|---|---|---|
| Strands ϕS | 1560 | 1860 | 195 |
HRB400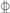 12 12 | 400 | 540 | 200 |
HRB400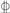 16 16 | 400 | 540 | 200 |
HRB400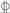 28 28 | 400 | 540 | 200 |
| Cap Beams | Ultimate Bearing Capacity /kN | Residual Bearing Capacity /kN | Ultimate Deflection /mm | Shear key Deflection at Ultimate Load /mm | Shear Key Ultimate Deflection /mm |
|---|---|---|---|---|---|
| SK1 | 12,155 | 4000 | 2.29 | 1.65 | 17.98 |
| SK2 | 13,400 | 5100 | 3.24 | 1.10 | 8.38 |
| SK3 | 3480 | 1140 | 0.52 | 0.51 | 21.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, H.; Zhang, Q.; Zhang, Y.; Li, X.; Yu, D. Effects of Joint Configurations on Shear Behavior of Prefabricated Segmental Cap Beams. Buildings 2025, 15, 4286. https://doi.org/10.3390/buildings15234286
Gan H, Zhang Q, Zhang Y, Li X, Yu D. Effects of Joint Configurations on Shear Behavior of Prefabricated Segmental Cap Beams. Buildings. 2025; 15(23):4286. https://doi.org/10.3390/buildings15234286
Chicago/Turabian StyleGan, Hong, Qing Zhang, Yaqiang Zhang, Xingze Li, and Dinghao Yu. 2025. "Effects of Joint Configurations on Shear Behavior of Prefabricated Segmental Cap Beams" Buildings 15, no. 23: 4286. https://doi.org/10.3390/buildings15234286
APA StyleGan, H., Zhang, Q., Zhang, Y., Li, X., & Yu, D. (2025). Effects of Joint Configurations on Shear Behavior of Prefabricated Segmental Cap Beams. Buildings, 15(23), 4286. https://doi.org/10.3390/buildings15234286






