Selection of the Optimal Intensity Measure for Unreinforced Masonry Buildings Using Vulnerability-Based Metrics
Abstract
1. Introduction
2. Materials and Methods
2.1. Description and Modelling of the Selected Unreinforced Masonry Building
2.1.1. Description and Attributes of the Selected Building
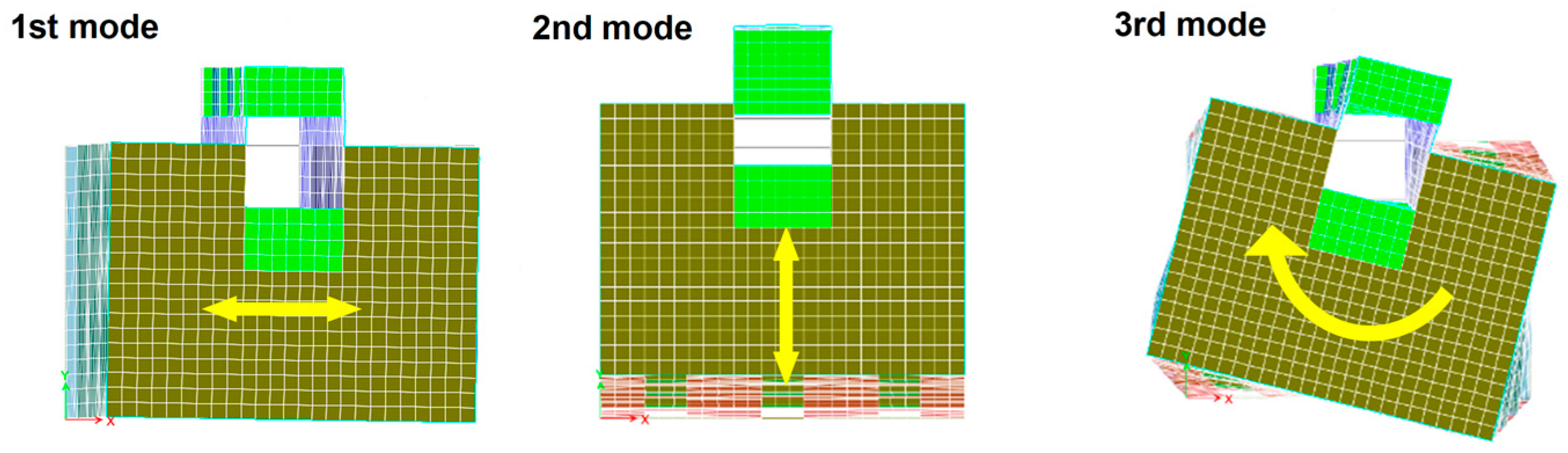
2.1.2. Nonlinear Finite Element Model of the Selected Building
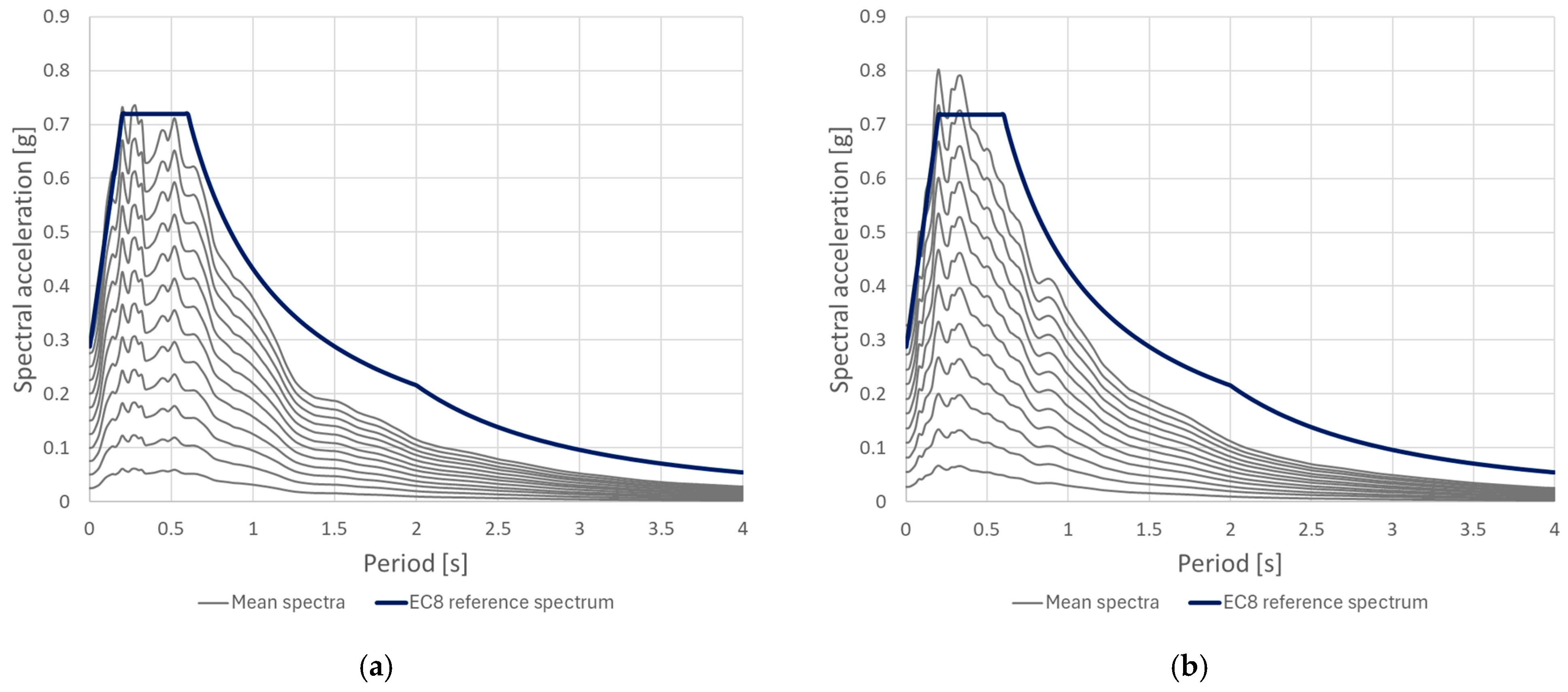
2.2. Selection and Scaling of Ground Motions for IDA Analyses
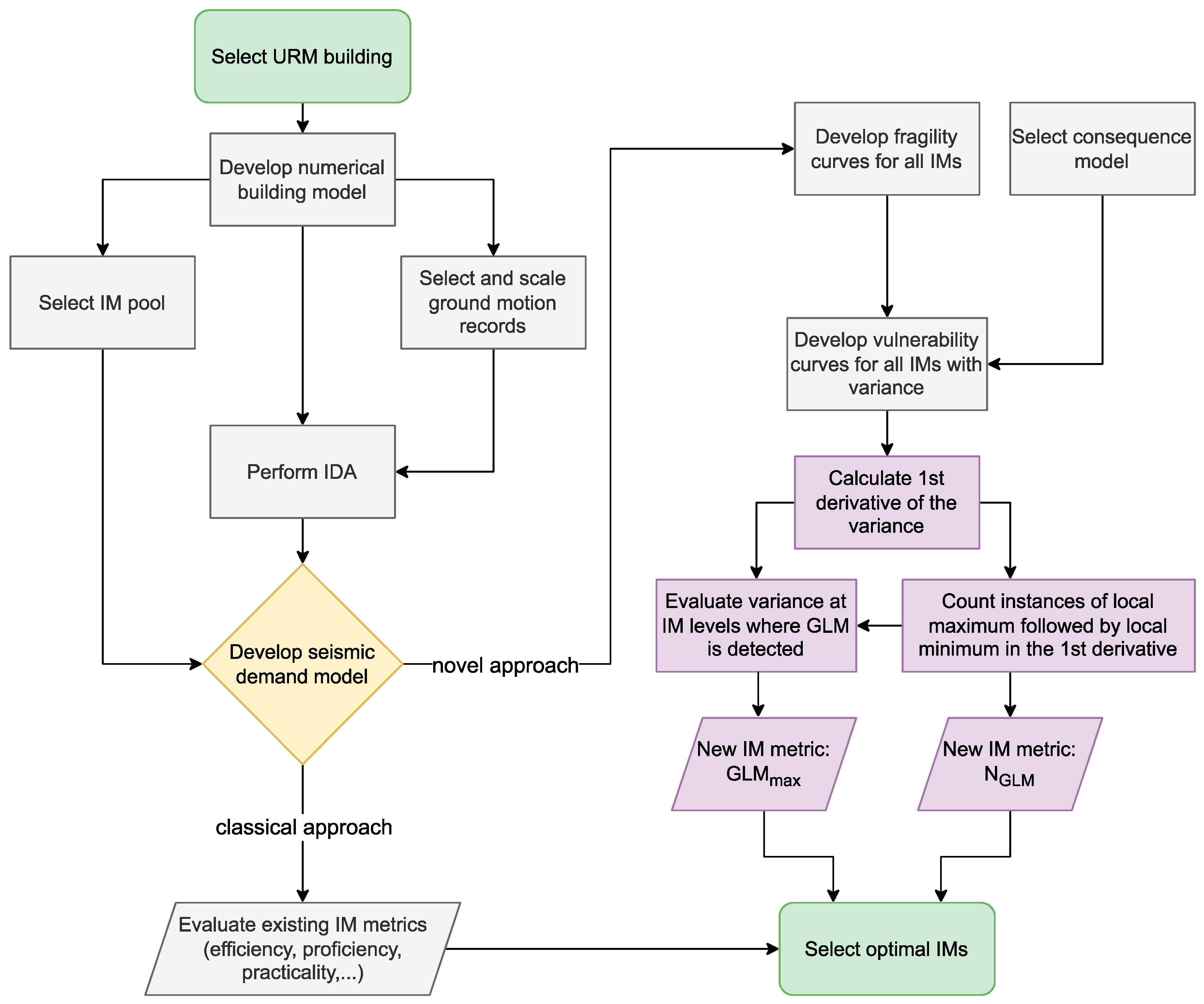
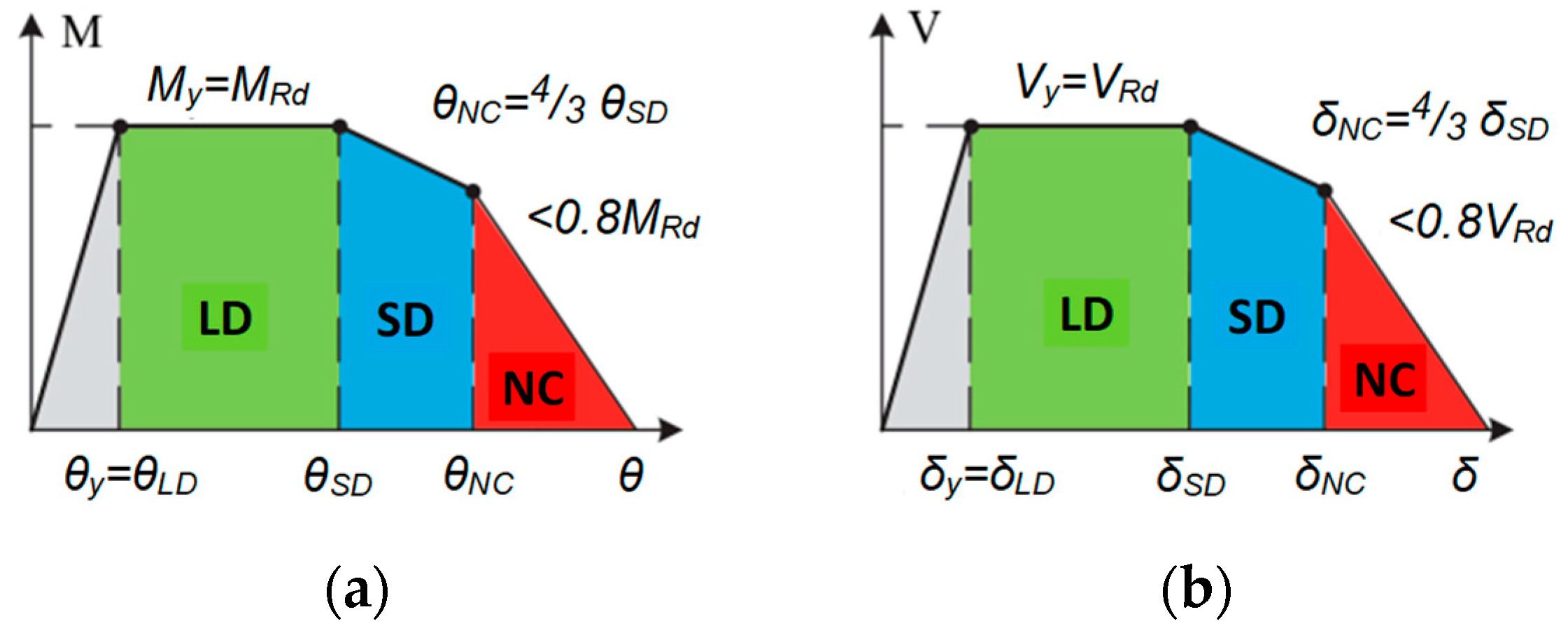
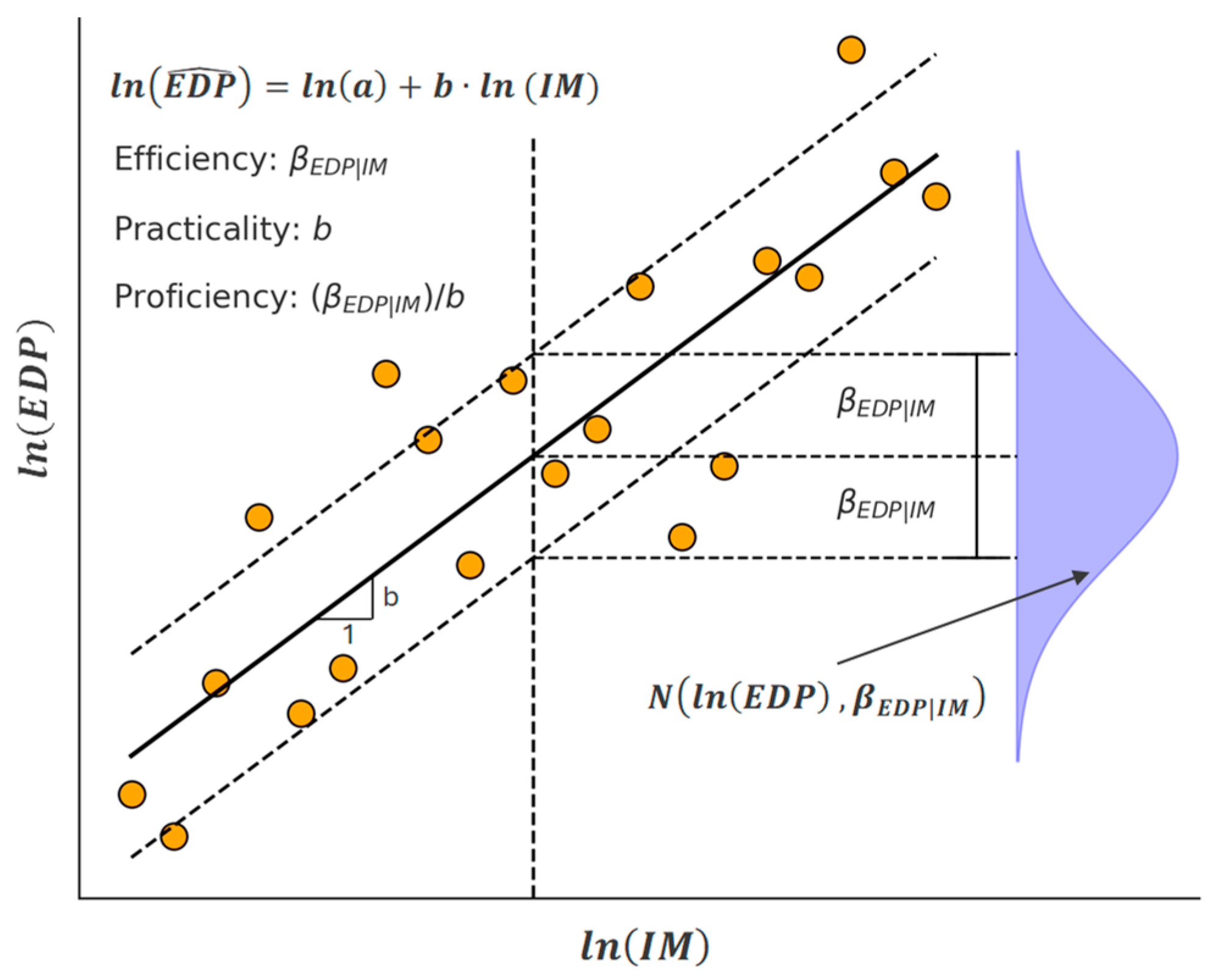
2.3. Optimal Intensity Measure Metrics and Seismic Demand Model
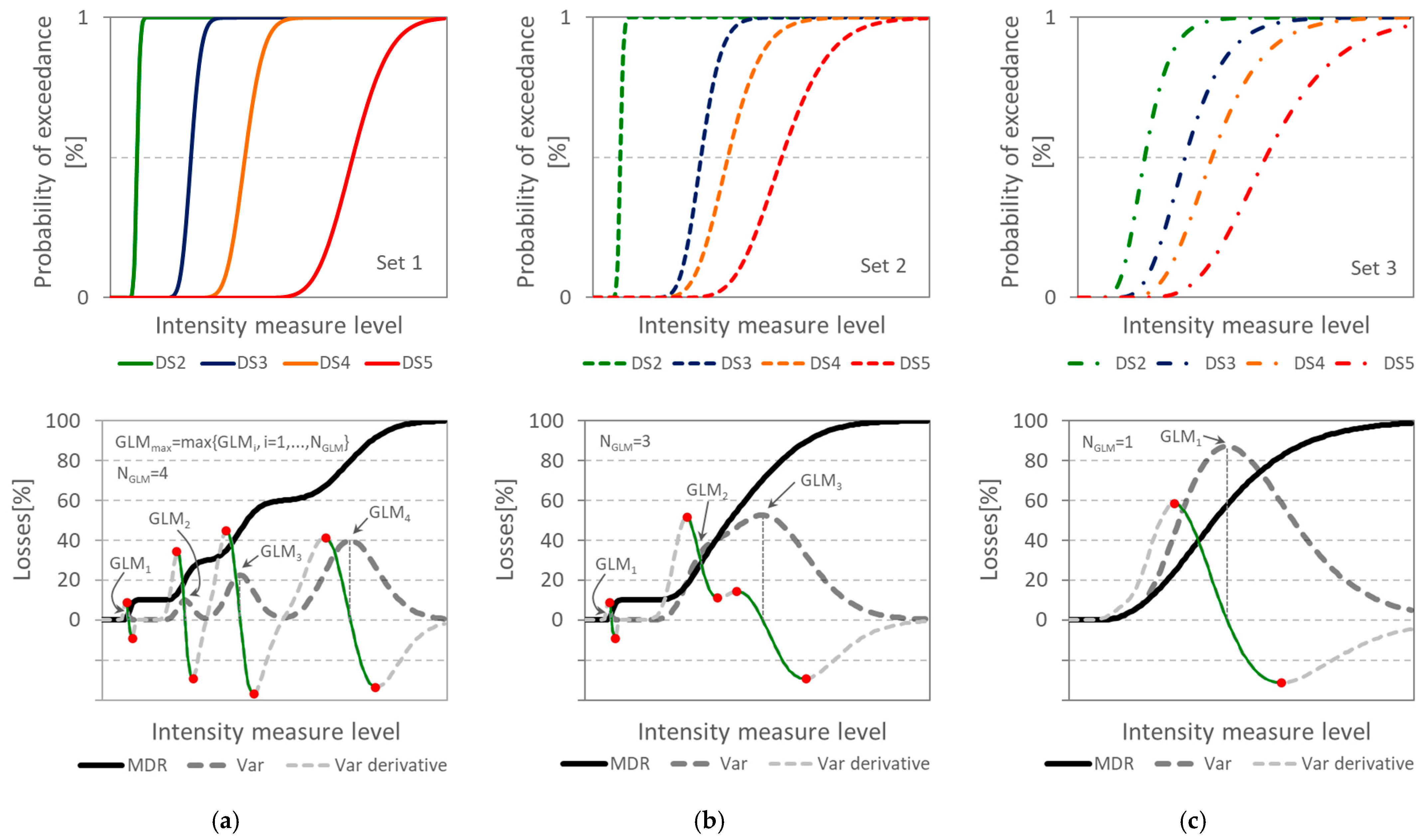
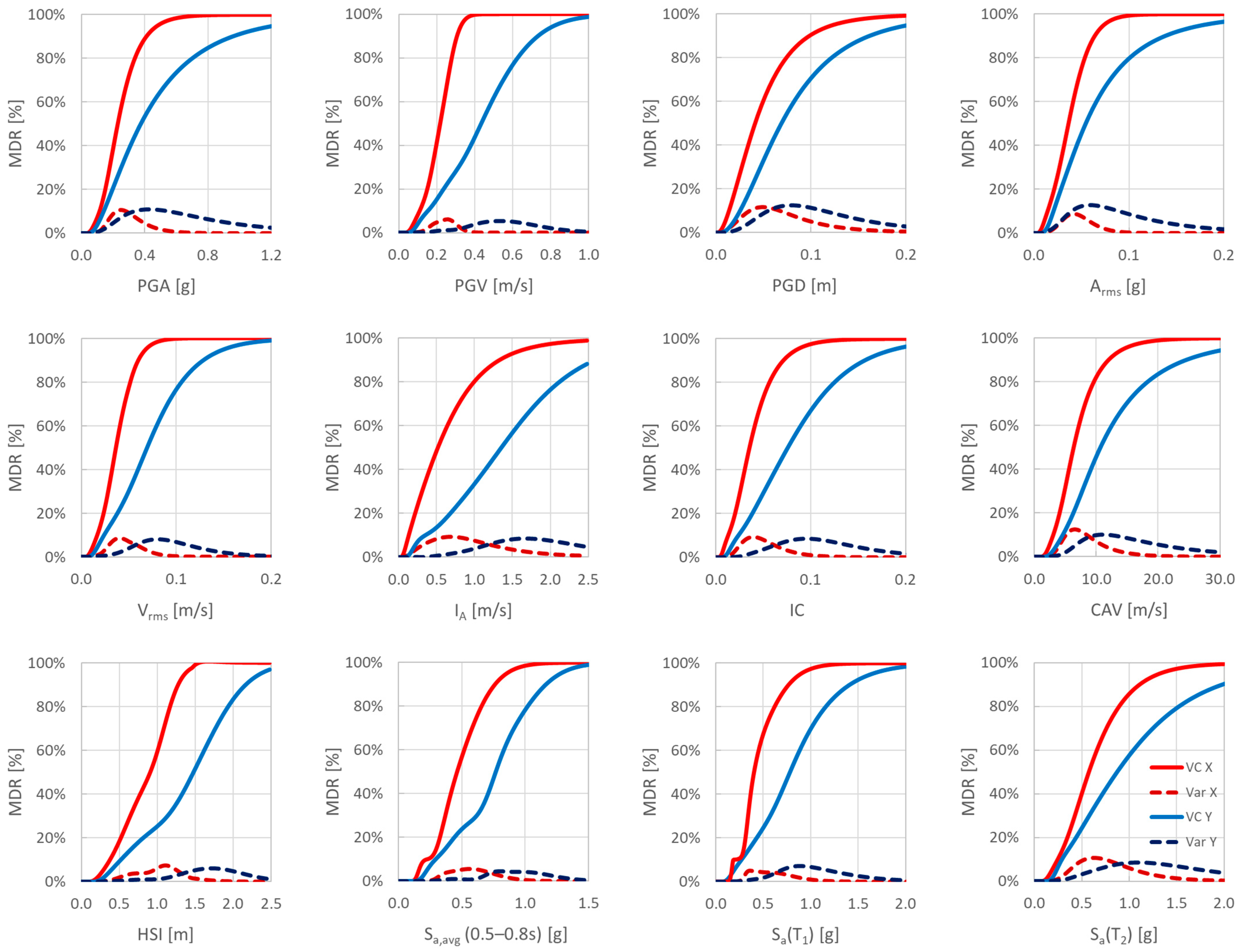
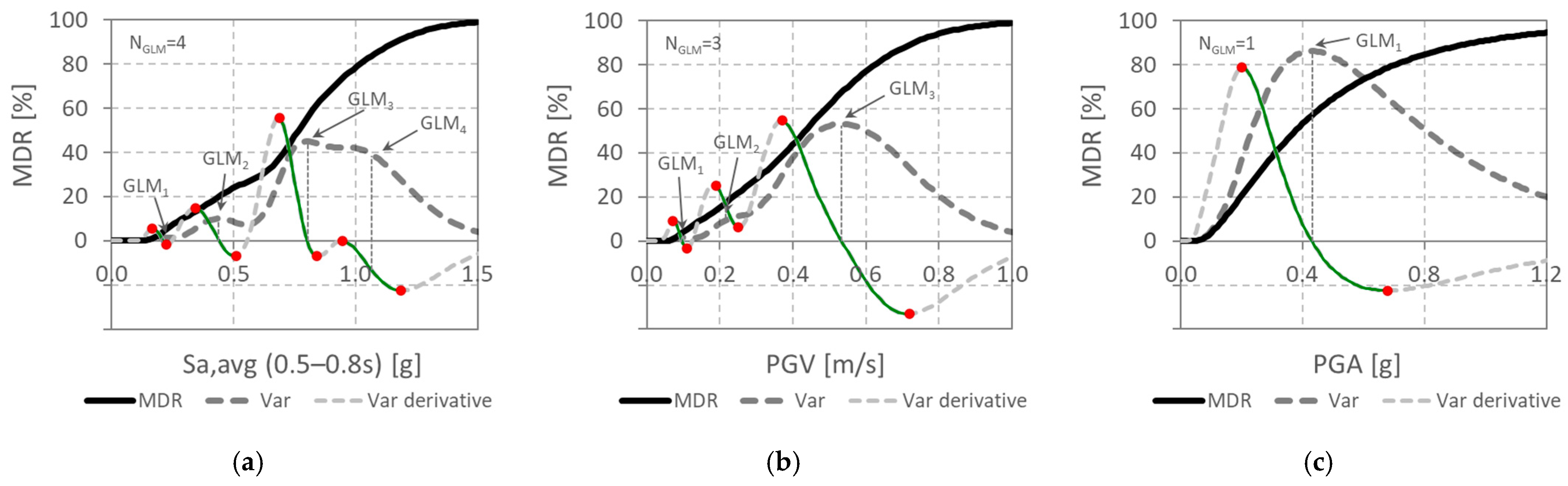
2.4. New Metrics for Optimal IMs Based on Vulnerability Curve Variance
3. Results
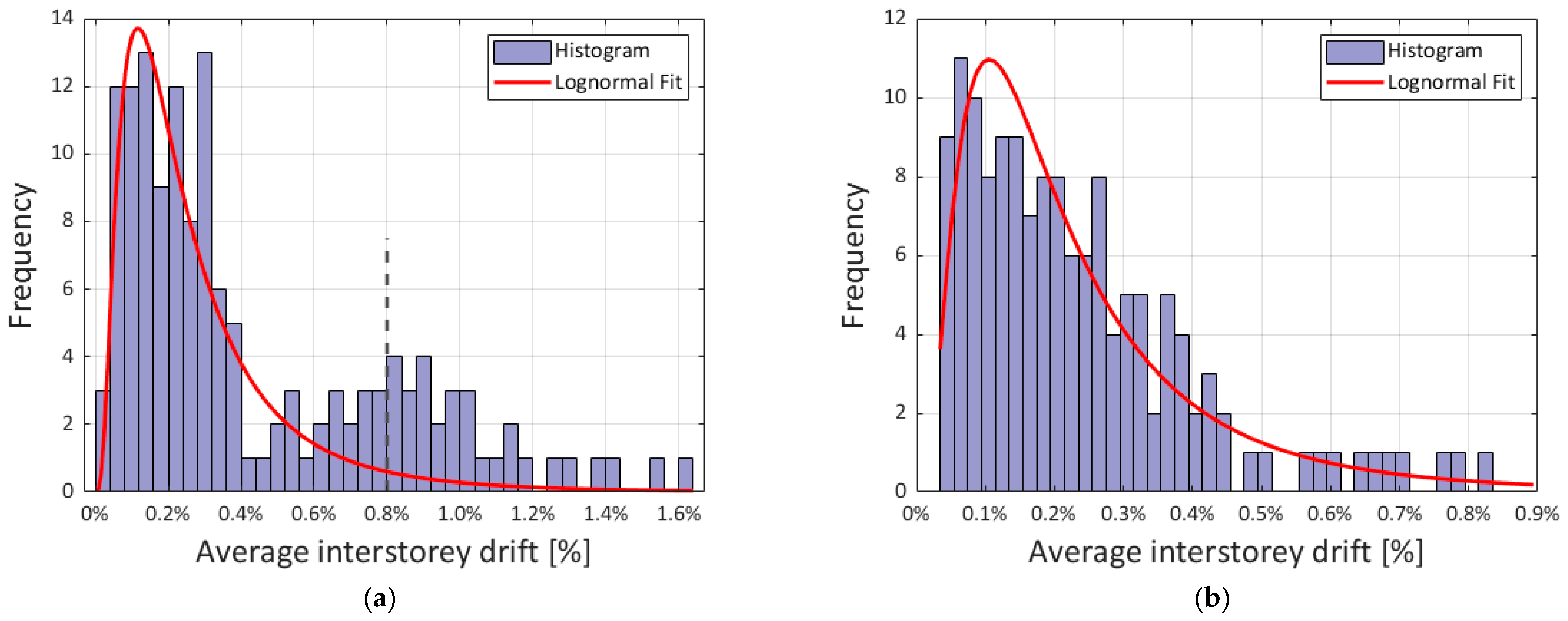
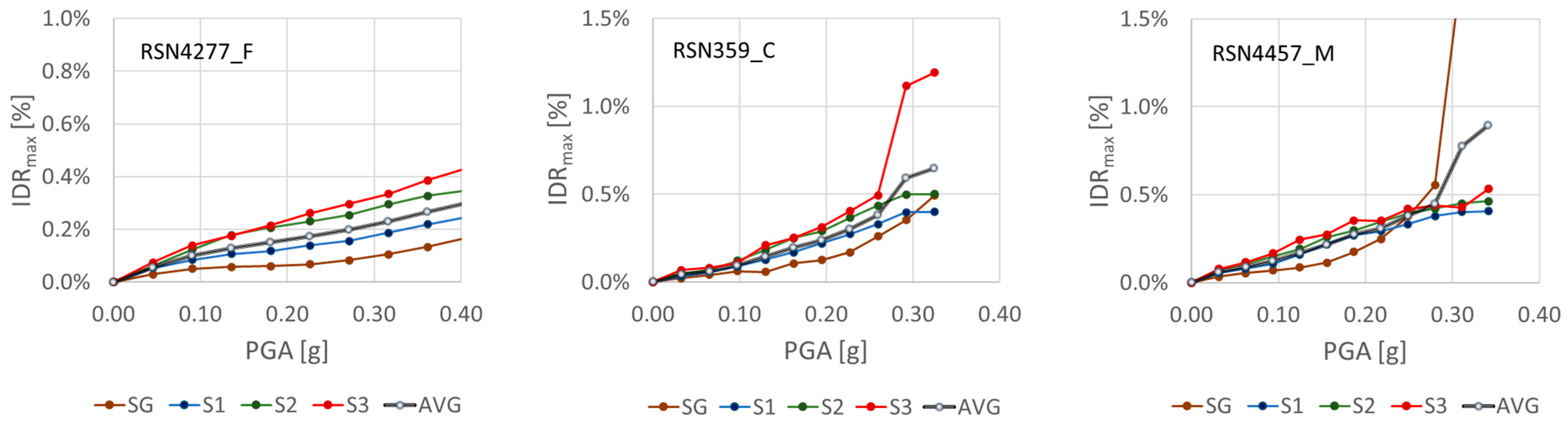
3.1. Distribution of Structural Responses
3.1.1. Behaviour of Individual Storeys
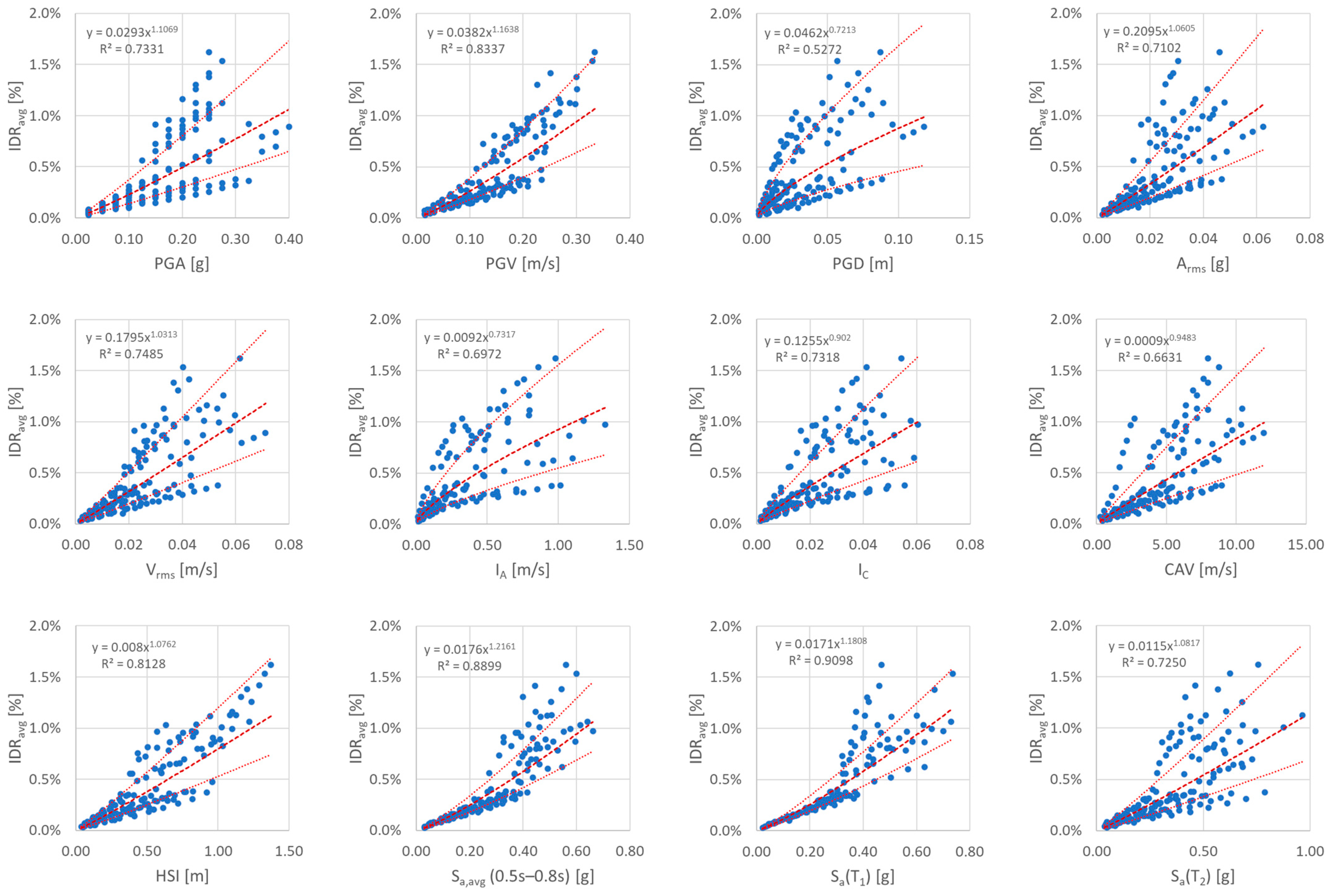
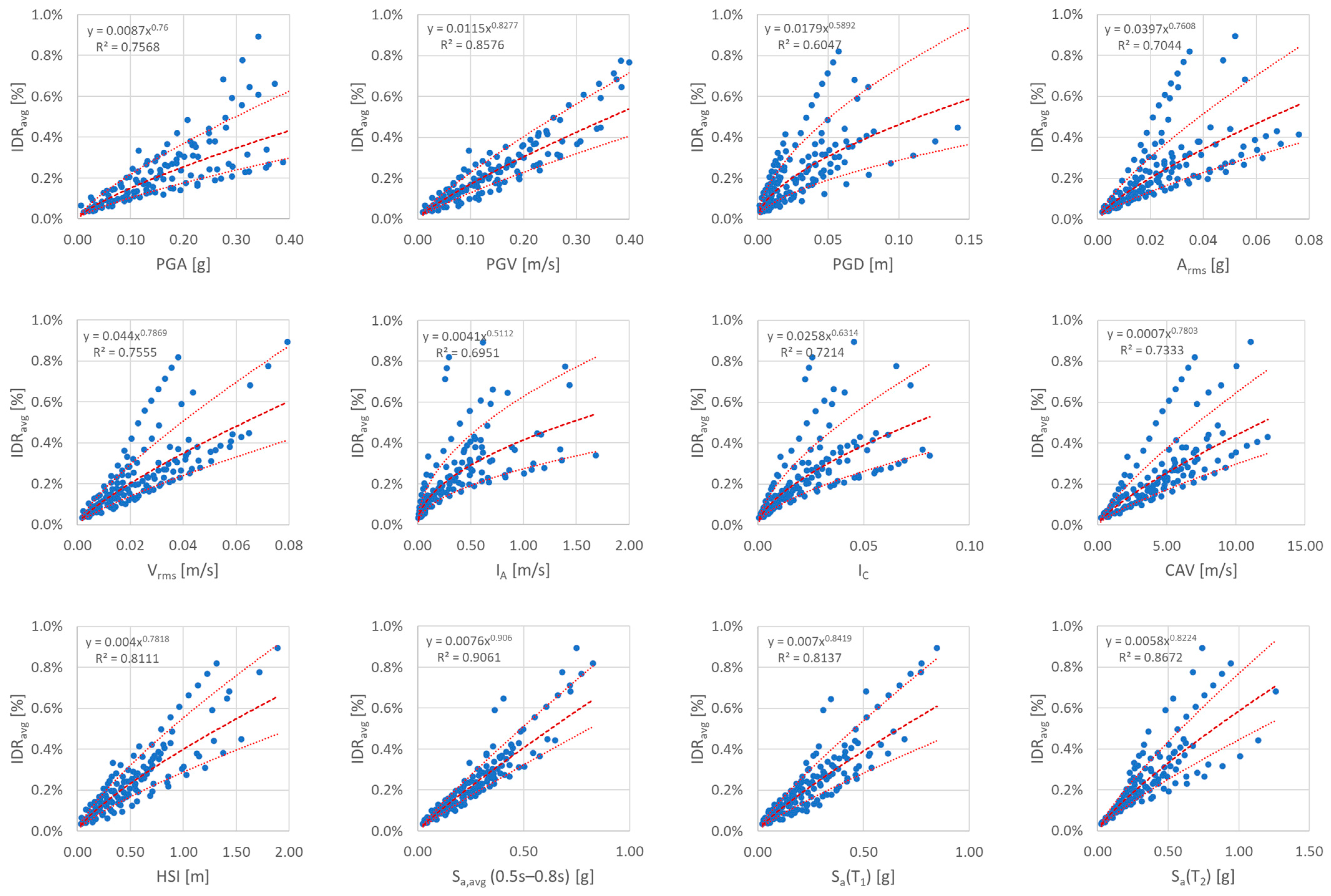
3.2. Seismic Demand Model and IM Metrics Results
| EDP: IDRavg | Direction X | Direction Y | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity Measure | Equation | a | b | R2 | σ | C.O.V. | a | b | R2 | σ | C.O.V. |
| PGA [g] | 0.0293 | 1.1069 | 0.7331 | 0.2129 | 0.0841 | 0.0087 | 0.7600 | 0.7568 | 0.1608 | 0.0588 | |
| PGV [m/s] | 0.0382 | 1.1638 | 0.8337 | 0.1680 | 0.0663 | 0.0115 | 0.8277 | 0.8576 | 0.1230 | 0.0450 | |
| PGD [m] | 0.0462 | 0.7213 | 0.5272 | 0.2834 | 0.1119 | 0.0179 | 0.5892 | 0.6047 | 0.2049 | 0.0749 | |
| Arms [g] | 0.2095 | 1.0605 | 0.7102 | 0.2218 | 0.0876 | 0.0397 | 0.7608 | 0.7044 | 0.1772 | 0.0648 | |
| Vrms [m/s] | 0.1795 | 1.0313 | 0.7485 | 0.2067 | 0.0816 | 0.0440 | 0.7869 | 0.7555 | 0.1612 | 0.0589 | |
| IA [m/s] [67] | 0.0092 | 0.7317 | 0.6972 | 0.2268 | 0.0895 | 0.0041 | 0.5112 | 0.6951 | 0.1800 | 0.0658 | |
| IC [56] | 0.1255 | 0.9020 | 0.7318 | 0.2134 | 0.0843 | 0.0258 | 0.6314 | 0.7214 | 0.1720 | 0.0629 | |
| CAV [m/s] [68] | 0.0009 | 0.9483 | 0.6631 | 0.2392 | 0.0944 | 0.0007 | 0.7803 | 0.7333 | 0.1683 | 0.0615 | |
| HSI [m] [69] | 0.0080 | 1.0762 | 0.8128 | 0.1783 | 0.0704 | 0.0040 | 0.7818 | 0.8111 | 0.1417 | 0.0518 | |
| Sa,avg (0.5–0.8 s) [g] [70] | 0.0176 | 1.2161 | 0.8899 | 0.1367 | 0.0540 | 0.0076 | 0.9060 | 0.9061 | 0.0999 | 0.0365 | |
| Sa(T1) [g] | 0.0171 | 1.1808 | 0.9098 | 0.1238 | 0.0489 | 0.0070 | 0.8419 | 0.8137 | 0.1407 | 0.0514 | |
| Sa(T2) [g] | 0.0115 | 1.0817 | 0.7250 | 0.2161 | 0.0853 | 0.0058 | 0.8224 | 0.8672 | 0.1188 | 0.0434 | |
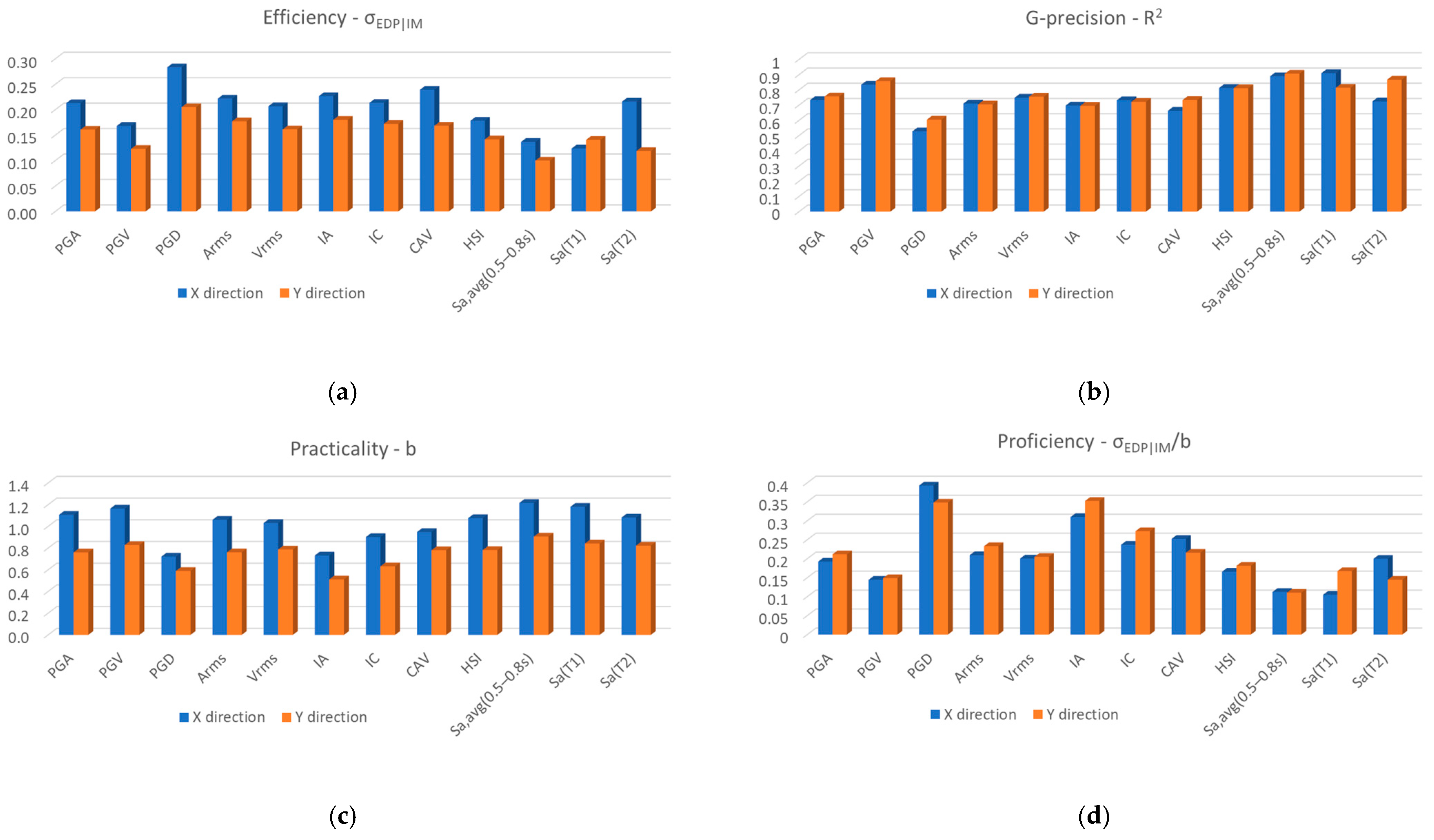
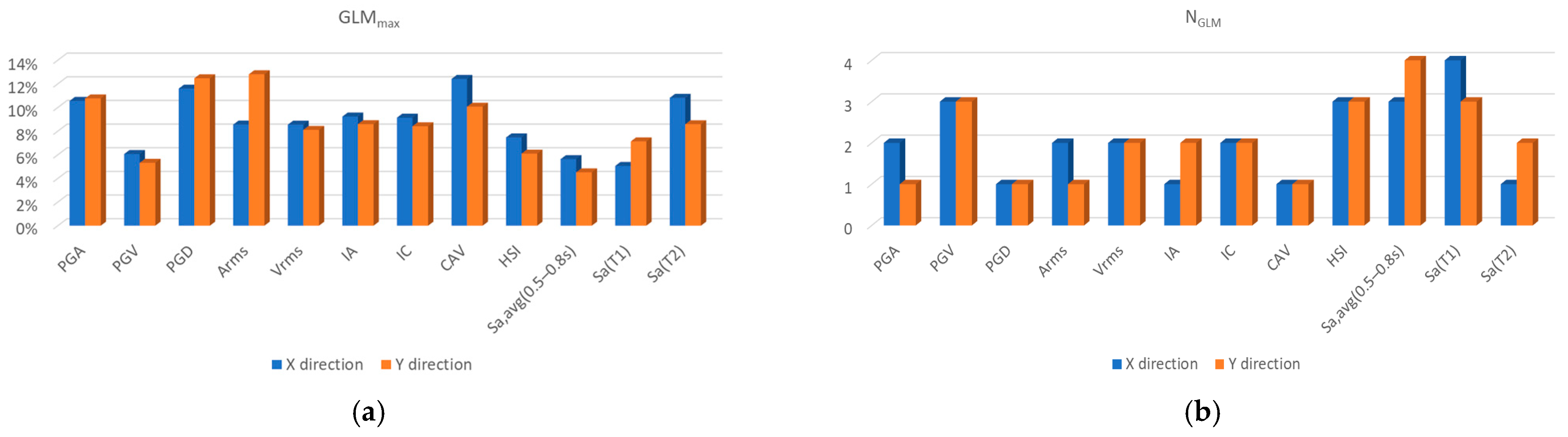
3.3. Evaluation of IMs According to New Criteria Based on Vulnerability Curve Variance
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atalić, J.; Novak, M.Š.; Uroš, M. Seismic Risk for Croatia: Overview of Research Activities and Present Assessments with Guidelines for the Future. Gradjevinar 2019, 71, 923–947. [Google Scholar]
- Baker, J.; Bradley, B.; Stafford, P. Seismic Hazard and Risk Analysis; Cambridge University Press: Cambridge, UK, 2021; ISBN 9781108348157. [Google Scholar]
- Aquib, T.A.; Sivasubramonian, J.; Mai, P.M. Analysis of Ground Motion Intensity Measures and Selection Techniques for Estimating Building Response. Appl. Sci. 2022, 12, 12089. [Google Scholar] [CrossRef]
- Lin, J.; Smerzini, C. Validated Physics-Based Numerical Simulations of Earthquake Ground Motion in the Thessaloniki Area. In Proceedings of the 3rd European Conference on Earthquake Engineering and Seismology, Bucharest, Romania, 4–9 September 2022. [Google Scholar]
- Smerzini, C.; Vanini, M.; Paolucci, R.; Renault, P.; Traversa, P. Regional Physics-Based Simulation of Ground Motion within the Rhȏne Valley, France, during the MW 4.9 2019 Le Teil Earthquake. Bull. Earthq. Eng. 2023, 21, 1747–1774. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 1st ed.; Hall, W.J., Ed.; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Lachanas, C.G.; Vamvatsikos, D.; Dimitrakopoulos, E.G. Intensity Measures as Interfacing Variables versus Response Proxies: The Case of Rigid Rocking Blocks. Earthq. Eng. Struct. Dyn. 2023, 52, 1722–1739. [Google Scholar] [CrossRef]
- Giannouli, V.D.; Athanatopoulou, A.M.; Manoukas, G.E.; Athanatopoulou, A.M. Earthquake Intensity Measures and Structural Damage Indices: A Review since 2015. In Proceedings of the 18th World Conference on Earthquake Engineering (WCEE2024), Milan, Italy, 30 June–5 July 2024. [Google Scholar]
- Zhen, W.; Qiu, Y.; Zhang, Y.; Li, W. Ground-Motion Intensity Measures for the Seismic Response of the Roof-Isolated Large-Span Structure. Buildings 2024, 14, 411. [Google Scholar] [CrossRef]
- Kostinakis, K.; Fontara, I.K.; Athanatopoulou, A.M. Scalar Structure-Specific Ground Motion Intensity Measures for Assessing the Seismic Performance of Structures: A Review. J. Earthq. Eng. 2018, 22, 630–665. [Google Scholar] [CrossRef]
- Yang, D.; Pan, J.; Li, G. Non-Structure-Specific Intensity Measure Parameters and Characteristic Period of near-Fault Ground Motions. Earthq. Eng. Struct. Dyn. 2009, 38, 1257–1280. [Google Scholar] [CrossRef]
- Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D.; Spillatura, A. Conditional Spectrum-Based Ground Motion Record Selection Using Average Spectral Acceleration. Earthq. Eng. Struct. Dyn. 2017, 46, 1667–1685. [Google Scholar] [CrossRef]
- Baker, J.W. Conditional Mean Spectrum: Tool for Ground-Motion Selection. J. Struct. Eng. 2011, 137, 322–331. [Google Scholar] [CrossRef]
- Kohrangi, M.; Vamvatsikos, D.; Bazzurro, P. Site Dependence and Record Selection Schemes for Building Fragility and Regional Loss Assessment. Earthq. Eng. Struct. Dyn. 2017, 46, 1625–1643. [Google Scholar] [CrossRef]
- Giovenale, P.; Cornell, C.A.; Esteva, L. Comparing the Adequacy of Alternative Ground Motion Intensity Measures for the Estimation of Structural Responses. Earthq. Eng. Struct. Dyn. 2004, 33, 951–979. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, C.A. Structure-Specific Scalar Intensity Measures for near-Source and Ordinary Earthquake Ground Motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef]
- Kazantzi, A.K.; Vamvatsikos, D. Intensity Measure Selection for Vulnerability Studies of Building Classes. Earthq. Eng. Struct. Dyn. 2015, 44, 2677–2694. [Google Scholar] [CrossRef]
- Padgett, J.E.; Nielson, B.G.; DesRoches, R. Selection of Optimal Intensity Measures in Probabilistic Seismic Demand Models of Highway Bridge Portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Developing Efficient Scalar and Vector Intensity Measures for IDA Capacity Estimation by Incorporating Elastic Spectral Shape Information. Earthq. Eng. Struct. Dyn. 2005, 34, 1573–1600. [Google Scholar] [CrossRef]
- Zavala, N.; Bojórquez, E.; Barraza, M.; Bojórquez, J.; Villela, A.; Campos, J.; Torres, J.; Sánchez, R.; Carvajal, J. Vector-Valued Intensity Measures Based on Spectral Shape to Predict Seismic Fragility Surfaces in Reinforced Concrete Buildings. Buildings 2023, 13, 137. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Hurtado, J.E.; Pujades, L.G. New Insights into the Relationship between Seismic Intensity Measures and Nonlinear Structural Response. Bull. Earthq. Eng. 2022, 20, 2329–2365. [Google Scholar] [CrossRef]
- Deierlein, G.G.; Krawinkler, H.; Cornell, C.A.; Blume, J.A. A Framework for Performance-Based Earthquake Engineering. In Proceedings of the 2003 Pacific Conference on Earthquake Engineering, Christchurch, New Zealand, 13–15 February 2003. [Google Scholar]
- Lagomarsino, S.; Cattari, S. Fragility Functions of Masonry Buildings. In SYNER-G: Typology Definition and Fragility Functions for Physical Elements at Seismic Risk: Buildings, Lifelines, Transportation Networks and Critical Facilities; Pitilakis, K., Crowley, H., Kaynia, A.M., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 111–156. ISBN 978-94-007-7872-6. [Google Scholar]
- Tothong, P.; Luco, N. Probabilistic Seismic Demand Analysis Using Advanced Ground Motion Intensity Measures. Earthq. Eng. Struct. Dyn. 2007, 36, 1837–1860. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Probabilistic Seismic Demand Model and Optimal Intensity Measure for Concrete Dams. Struct. Saf. 2016, 59, 67–85. [Google Scholar] [CrossRef]
- Jalayer, F.; Cornell, C.A. Alternative Non-Linear Demand Estimation Methods for Probability-Based Seismic Assessments. Earthq. Eng. Struct. Dyn. 2009, 38, 951–972. [Google Scholar] [CrossRef]
- Khosravikia, F.; Clayton, P. Updated Evaluation Metrics for Optimal Intensity Measure Selection in Probabilistic Seismic Demand Models. Eng. Struct. 2020, 202, 109899. [Google Scholar] [CrossRef]
- Šavor Novak, M.; Uroš, M.; Demšić, M.; Jevtić Rundek, R.; Pilipović, A.; Atalić, J. Detailed Structural Typology of Existing Substandard Masonry and Reinforced Concrete Buildings in the City of Zagreb, Croatia. Buildings 2024, 14, 3644. [Google Scholar] [CrossRef]
- Pilipović, A.; Rundek, R.J.; Uroš, M.; Novak, M.Š.; Demšić, M.; Prevolnik, S. New Vulnerability Model of an Unreinforced Masonry Building in the Urban Area of Zagreb. In Proceedings of the 18th World Conference on Earthquake Engineering, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
- Uroš, M.; Šavor Novak, M.; Atalić, J.; Baniček, M. Procjena Potresnog Rizika Za Grad Zagreb; University of Zagreb: Zagreb, Croatia, 2023. (In Croatian) [Google Scholar]
- Serdar, N.; Pejović, J. National Seismic Risk Assessment for Montenegro. J. Appl. Eng. Sci. 2024, 22, 291–296. [Google Scholar] [CrossRef]
- Yön, B. Identification of Failure Mechanisms in Existing Unreinforced Masonry Buildings in Rural Areas after April 4, 2019 Earthquake in Turkey. J. Build. Eng. 2021, 43, 102586. [Google Scholar] [CrossRef]
- Pilipović, A.; Uroš, M.; Demšić, M. Identification of Critical Elements of Unreinforced Masonry Buildings for Selection of Optimal Retrofit Solutions. In Proceedings of the 14th International Conference on Structural Analysis of Historical Constructions, Lausanne, Switzerland, 15–17 September 2025; EPFL: Lausanne, Switzerland, 2025. [Google Scholar]
- Žagar, T.; Uroš, M.; Atalić, J. Exposure of standardised buildings in Zagreb built in the second half of the 20th century. In Proceedings of the 7th Doctoral Symposium in Civil Engineering, Stuttgart, Germany, 11–13 September 2021; Štirmer, N., Ed.; University of Zagreb Faculty of Civil Engineering: Zagreb, Croatia, 2021; pp. 135–150. [Google Scholar]
- Pilipović, A.; Uroš, M. Selection of Optimal Intensity Measure for a Typical Masonry Building in the Urban Area of Zagreb. In Proceedings of the 8th Doctoral Symposium in Civil Engineering, Zagreb, Croatia, 5–6 September 2022; Štirmer, N., Ed.; University of Zagreb: Zagre, Croatia, 2022; pp. 111–124. [Google Scholar]
- Atalić, J.; Uroš, M.; Šavor Novak, M.; Demšić, M.; Nastev, M. The Mw5.4 Zagreb (Croatia) Earthquake of March 22, 2020: Impacts and Response. Bull. Earthq. Eng. 2021, 19, 3461–3489. [Google Scholar] [CrossRef] [PubMed]
- Uroš, M.; Demšić, M.; Šavor Novak, M.; Atalić, J.; Baniček, M.; Jevtić Rundek, R.; Duvnjak, I.; Košćak, J.; Pilipović, A.; Prevolnik, S. Damage Evaluation and Seismic Assessment of a Typical Historical Unreinforced Masonry Building in the Zagreb 2020 Earthquake: A Case Study—Part I. Buildings 2024, 14, 474. [Google Scholar] [CrossRef]
- Novak, M.Š.; Uroš, M.; Atalić, J.; Herak, M.; Demšić, M.; Baniček, M.; Lazarević, D.; Bijelić, N.; Crnogorac, M.; Todorić, M. Zagreb Earthquake of 22 March 2020—Preliminary Report on Seismologic Aspects and Damage to Buildings. Gradjevinar 2020, 72, 843–867. [Google Scholar] [CrossRef]
- Angiolilli, M.; Brunelli, A.; Cattari, S. Fragility Curves of Masonry Buildings in Aggregate Accounting for Local Mechanisms and Site Effects. Bull. Earthq. Eng. 2023, 21, 2877–2919. [Google Scholar] [CrossRef]
- Angiolilli, M.; Lagomarsino, S.; Cattari, S.; Degli Abbati, S. Seismic Fragility Assessment of Existing Masonry Buildings in Aggregate. Eng. Struct. 2021, 247, 113218. [Google Scholar] [CrossRef]
- Demšić, M.; Pinasco, S.; Pilipović, A.; Cattari, S.; Lagomarsino, S.; Novak, M.Š.; Uroš, M. Development of Fragility Curves of Masonry Buildings Build in a Regular Row Aggregate. In Proceedings of the 18th World Conference on Earthquake Engineering, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
- Pinasco, S.; Demšić, M.; Pilipović, A.; Novak, M.Š.; Uroš, M.; Lagomarsino, S.; Cattari, S. Seismic Fragility Assessment of Existing Masonry Buildings in Aggregate Located in Zagreb. Bull. Earthq. Eng. 2025, 23, 2715–2741. [Google Scholar] [CrossRef]
- Atalić, J.; Todorić, M.; Uroš, M.; Novak, M.Š.; Crnogorac, M.; Lakušić, S. Potresno Inženjerstvo: Obnova Zidanih Zgrada; University of Zagreb: Zagreb, Croatia, 2021; ISBN 9789538168437. (In Croatian) [Google Scholar]
- Computers & Structures, Inc. ETABS: Integrated Building Design Software; Computers & Structures, Inc.: Walnut Creek, CA, USA, 2018. [Google Scholar]
- EN 1998-1:2004; CEN Eurocode 8: Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings, European Standard; Comité Européen de Normalisation: Brussels, Belgium, 2004.
- Vamvatsikos, D.; Allin Cornell, C. Incremental Dynamic Analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI Program: An Equivalent Frame Model for the Nonlinear Seismic Analysis of Masonry Buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- Herak, D.; Herak, M.; Tomljenović, B. Seismicity and Earthquake Focal Mechanisms in North-Western Croatia. Tectonophysics 2009, 465, 212–220. [Google Scholar] [CrossRef]
- Ancheta, T.D.; Bozorgnia, Y.; Darragh, R.; Silva, W.J.; Chiou, B.; Stewart, J.P.; Boore, D.M.; Graves, R.; Abrahamson, N.A.; Campbell, K.W.; et al. PEER NGA-West2 Database: A Database of Ground Motions Recorded in Shallow Crustal Earthquakes in Active Tectonic Regions. In Proceedings of the 15th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Herak, M.; Herak, D.; Orlić, N. Properties of the Zagreb 22 March 2020 Earthquake Sequence—Analyses of the Full Year of Aftershock Recording. Geofizika 2021, 38, 93–116. [Google Scholar] [CrossRef]
- Herak, M.; Herak, D. Properties of the Petrinja (Croatia) Earthquake Sequence of 2020–2021—Results of Seismological Research for the First Six Months of Activity. Tectonophysics 2023, 858, 229885. [Google Scholar] [CrossRef]
- Seismosoft SeismoSignal—A Computer Program for Signal Processing of Time-Histories. Available online: https://seismosoft.com/ (accessed on 16 November 2025).
- Yan, Y.; Xia, Y.; Yang, J.; Sun, L. Optimal Selection of Scalar and Vector-Valued Seismic Intensity Measures Based on Gaussian Process Regression. Soil Dyn. Earthq. Eng. 2022, 152, 106961. [Google Scholar] [CrossRef]
- Jafari, A.; Rajabi, E.; Ghodrati Amiri, G. Investigating the Reliability of Ground Motion Intensity Measures. Adv. Civ. Eng. 2024, 2024, 2542967. [Google Scholar] [CrossRef]
- Bakalis, K.; Vamvatsikos, D. Seismic Fragility Functions via Nonlinear Response History Analysis. J. Struct. Eng. 2018, 144, 04018181. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.; Wen, Y.K. Seismic damage analysis of reinforced goncrete buildings. J. Struct. Eng. 1985, 111, 740–757. [Google Scholar] [CrossRef]
- Rudman, A.; Tubaldi, E.; Douglas, J.; Scozzese, F. The Impact of the Choice of Intensity Measure and Seismic Demand Model on Seismic Risk Estimates with Respect to an Unconditional Benchmark. Earthq. Eng. Struct. Dyn. 2024, 53, 4183–4202. [Google Scholar] [CrossRef]
- Hamburger, R.O.; Rojahn, C.; Heintz, J.A.; Mahoney, M.G. FEMA P58: Next-Generation Building Seismic Performance Assessment Methodology. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Pejovic, J.; Jankovic, S. Seismic Fragility Assessment for Reinforced Concrete High-Rise Buildings in Southern Euro-Mediterranean Zone. Bull. Earthq. Eng. 2016, 14, 185–212. [Google Scholar] [CrossRef]
- Grünthal, G. European Seismological Commission. Working Group “Macroseismic Scales”. In European Macroseismic Scale 1998: EMS-98; European Seismological Commission, Subcommission on Engineering Seismology, Working Group Macroseismic scales: Istanbul, Turkey, 1998; ISBN 2879770084. [Google Scholar]
- Iervolino, I. Assessing Uncertainty in Estimation of Seismic Response for PBEE. Earthq. Eng. Struct. Dyn. 2017, 46, 1711–1723. [Google Scholar] [CrossRef]
- Whittaker, A.; Deierlein, G.G.; Hooper, J.; Merovich, A. Engineering Demand Parameters for Structural Framing Systems; Federal Energency Management Agency: Washington, DC, USA, 2004. [Google Scholar]
- Inarritu, P.G.d.Q.; Kohrangi, M.; Bazzurro, P. Damage Assessment of Unreinforced Masonry Buildings Incorporating Damage Accumulation. Earthq. Eng. Struct. Dyn. 2024, 53, 2122–2140. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A Test of Goodness of Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Pinasco, S.; Demšić, M.; Šavor Novak, M.; Uroš, M.; Cattari, S.; Lagomarsino, S. Numerical Investigation of the Seismic Response of an Unreinforced Masonryresidential Building Hit by Zagreb Earthquake in 2020. In Proceedings of the 2nd Croatian Conference on Earthquake Engineering, Zagreb, Croatia, 22–24 March 2023; pp. 638–648. [Google Scholar]
- Bradley, B.A. A Generalized Conditional Intensity Measure Approach and Holistic Ground-Motion Selection. Earthq. Eng. Struct. Dyn. 2010, 39, 1321–1342. [Google Scholar] [CrossRef]
- Arias, A. A Measure of Earthquake Intensity. In Seismic Design for Nuclear Power Plants; Hansen, R., Ed.; MIT Press: Cambridge, UK, 1970; pp. 438–483. [Google Scholar]
- Reed, J.W.; Kassawara, R.P. A Criterion for Determining Exceedance of the Operating Basis Earthquake. Nucl. Eng. Des. 1990, 123, 387–396. [Google Scholar] [CrossRef]
- Housner, G. Measures of Severity of Earthquake Ground Shaking. In Proceedings of the US National Conference on Earthquake Engineering, Ann Arbor, MI, USA, 18–20 June 1975; EERI: Ann Arbor, Michigan, 1975. [Google Scholar]
- Eads, L.; Miranda, E.; Lignos, D.G. Average Spectral Acceleration as an Intensity Measure for Collapse Risk Assessment. Earthq. Eng. Struct. Dyn. 2015, 44, 2057–2073. [Google Scholar] [CrossRef]
- Caicedo, D.; Lourenço, P.B.; Bernardo, V.; Karimzadeh, S. Optimal Intensity Measures for Probabilistic Seismic Demand Models of Historical Masonry Buildings Considering In-Plane and out-of-Plane Response. In Proceedings of the Atas do 13 Congresso Nacional de Sismologia e Engenharia Sismica, Guimaraes, Portugal, 17–19 April 2024; Oliviera, D.V., Lourenco, P.B., Guerreiro, L., Silva, R.A., Eds.; University of Minho: Guimanaraes, Portugal, 2024. [Google Scholar]
- Makris, N.; Black, C.J. Evaluation of Peak Ground Velocity as a “Good” Intensity Measure for Near-Source Ground Motions. J. Eng. Mech. 2004, 130, 1032–1044. [Google Scholar] [CrossRef]
- Rajabi, R.; Barghi, M.; Rajabi, R. Investigation of Park-Ang Damage Index Model for Flexural Behavior of Reinforced Concrete Columns. Struct. Des. Tall Spec. Build. 2013, 22, 1350–1358. [Google Scholar] [CrossRef]
- Garcia De Quevedo Inarritu, P.; Bazzurro, P.; Lagomarsino, S.; Cattari, S. Validation of an Energy and Drift Based EDP for Cumulative Damage on URM Buildings. In Proceedings of the 18th World Conference on Earthquake Engineering, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
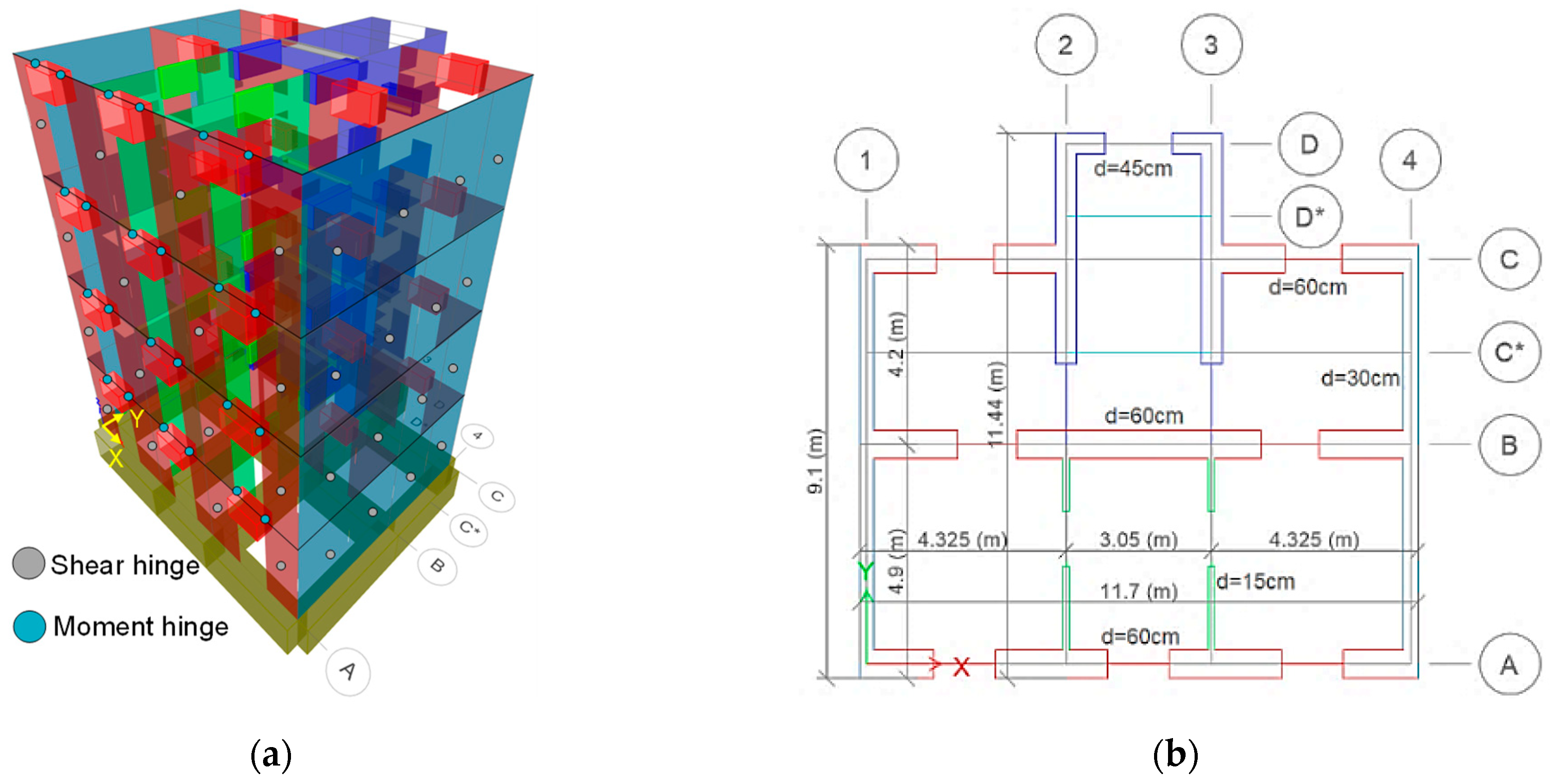
| Volumetric weight | γ [kN/m3] | 18 |
| Modulus of elasticity | EM [N/mm2] | 1500 |
| Shear modulus | GM [N/mm2] | 500 |
| Masonry compression strength | fm [N/mm2] | 3.400 |
| Initial shear strength of masonry | fv0 [N/mm2] | 0.160 |
| Diagonal tensile strength of masonry | ft [N/mm2] | 0.114 |
| Friction coefficient | μ | 0.400 |
| Brick compression strength | fb [N/mm2] | 10.00 |
| ID | Station | Magnitude Mw | Distance to Source Rrup [km] | Shear Wave Velocity Vs,30 [m/s] | PGA [g] | PGV [m/s] | Sa,avg [g] | Scale Factor (Min) | Scale Factor (Max) |
|---|---|---|---|---|---|---|---|---|---|
| RSN70_SFE | San Fernando | 6.61 | 27.4 | 425.34 | 0.151 | 0.182 | 0.287 | 0.165 | 1.816 |
| RSN130_F | Friuli 02–Buia | 5.91 | 11.03 | 310.68 | 0.110 | 0.108 | 0.242 | 0.227 | 2.267 |
| RSN359_C | Coalinga–01 | 6.36 | 26.38 | 381.27 | 0.179 | 0.180 | 0.293 | 0.140 | 1.400 |
| RSN949_N | Northridge–01–Arleta | 6.69 | 8.66 | 297.71 | 0.345 | 0.411 | 0.578 | 0.072 | 0.724 |
| RSN953_N | Northridge–01–Beverly Hills | 6.69 | 17.15 | 355.81 | 0.443 | 0.593 | 0.893 | 0.056 | 0.564 |
| RSN957_N | Northridge–01–Burbank | 6.69 | 16.88 | 581.93 | 0.112 | 0.107 | 0.240 | 0.224 | 2.240 |
| RSN4276_F | Friuli Aftershock–Buia | 5.5 | 12.39 | 310.68 | 0.231 | 0.217 | 0.536 | 0.108 | 1.083 |
| RSN4277_F | Friuli Aftershock–Forgaria Cornino | 5.5 | 16.52 | 412.37 | 0.129 | 0.088 | 0.222 | 0.193 | 2.124 |
| RSN4455_M | Montenegro–Herceg Novi | 7.1 | 25.55 | 585.04 | 0.218 | 0.140 | 0.470 | 0.114 | 1.145 |
| RSN4456_M | Montenegro–Petrovac | 7.1 | 8.01 | 543.26 | 0.463 | 0.387 | 0.951 | 0.054 | 0.539 |
| RSN4457_M | Montenegro–Ulcinj | 7.1 | 4.35 | 410.35 | 0.183 | 0.192 | 0.363 | 0.136 | 1.500 |
| UHS ZG_22_03 | Zagreb UHS 22.3.2020. | 5.3 | 8 | <380.00 | 0.179 | 0.115 | 0.242 | 0.140 | 2.095 |
| UHS_Petrinja | Petrinja UHS December 2020. | 6.4 | 47 | <380.00 | 0.098 | 0.063 | 0.154 | 0.256 | 4.098 |
| IM | GLM X Direction | GLMmax | GLM Y Direction | GLMmax | NGLM X | NGLM Y | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PGA | 0.15% | 10.55% | 10.55% | 10.76% | 10.76% | 2 | 1 | |||||
| PGV | 0.15% | 4.34% | 6.06% | 6.06% | 0.15% | 0.98% | 5.31% | 5.31% | 3 | 3 | ||
| PGD | 11.59% | 11.59% | 12.46% | 12.46% | 1 | 1 | ||||||
| Arms | 0.26% | 8.56% | 8.56% | 12.81% | 12.81% | 2 | 1 | |||||
| Vrms | 8.55% | 5.90% | 8.55% | 0.23% | 8.10% | 8.10% | 2 | 2 | ||||
| IA | 9.23% | 9.23% | 0.15% | 8.58% | 8.58% | 1 | 2 | |||||
| IC | 0.17% | 9.14% | 9.14% | 0.16% | 8.41% | 8.41% | 2 | 2 | ||||
| CAV | 12.41% | 12.41% | 10.06% | 10.06% | 1 | 1 | ||||||
| HSI | 0.16% | 3.61% | 7.46% | 7.46% | 0.17% | 0.92% | 6.09% | 6.09% | 3 | 3 | ||
| Sa,avg | 0.11% | 3.62% | 5.63% | 5.63% | 0.15% | 1.00% | 4.51% | 4.01% | 4.51% | 3 | 4 | |
| Sa(T1) | 0.15% | 5.06% | 4.68% | 4.04% | 5.06% | 0.16% | 0.87% | 7.13% | 7.13% | 4 | 3 | |
| Sa(T2) | 10.81% | 10.81% | 0.27% | 8.58% | 8.58% | 1 | 2 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilipović, A.; Uroš, M.; Šavor Novak, M. Selection of the Optimal Intensity Measure for Unreinforced Masonry Buildings Using Vulnerability-Based Metrics. Buildings 2025, 15, 4261. https://doi.org/10.3390/buildings15234261
Pilipović A, Uroš M, Šavor Novak M. Selection of the Optimal Intensity Measure for Unreinforced Masonry Buildings Using Vulnerability-Based Metrics. Buildings. 2025; 15(23):4261. https://doi.org/10.3390/buildings15234261
Chicago/Turabian StylePilipović, Ante, Mario Uroš, and Marta Šavor Novak. 2025. "Selection of the Optimal Intensity Measure for Unreinforced Masonry Buildings Using Vulnerability-Based Metrics" Buildings 15, no. 23: 4261. https://doi.org/10.3390/buildings15234261
APA StylePilipović, A., Uroš, M., & Šavor Novak, M. (2025). Selection of the Optimal Intensity Measure for Unreinforced Masonry Buildings Using Vulnerability-Based Metrics. Buildings, 15(23), 4261. https://doi.org/10.3390/buildings15234261






