Causal Discovery and Validation in Summer Weather Data with a Conceptual Extension to Cooling Energy Use
Abstract
1. Introduction
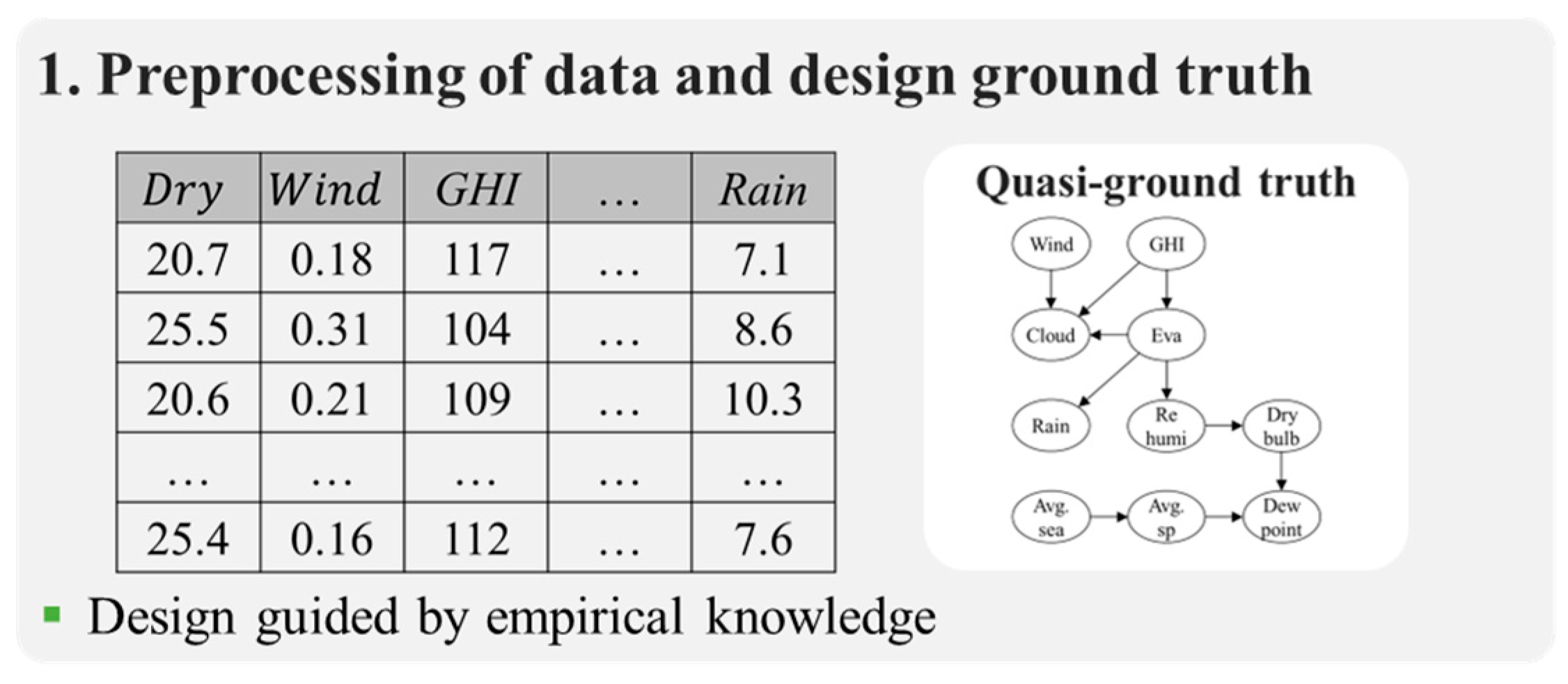
- Preprocessing of weather data and specification of a researcher-defined (hypothesized) causal structure.
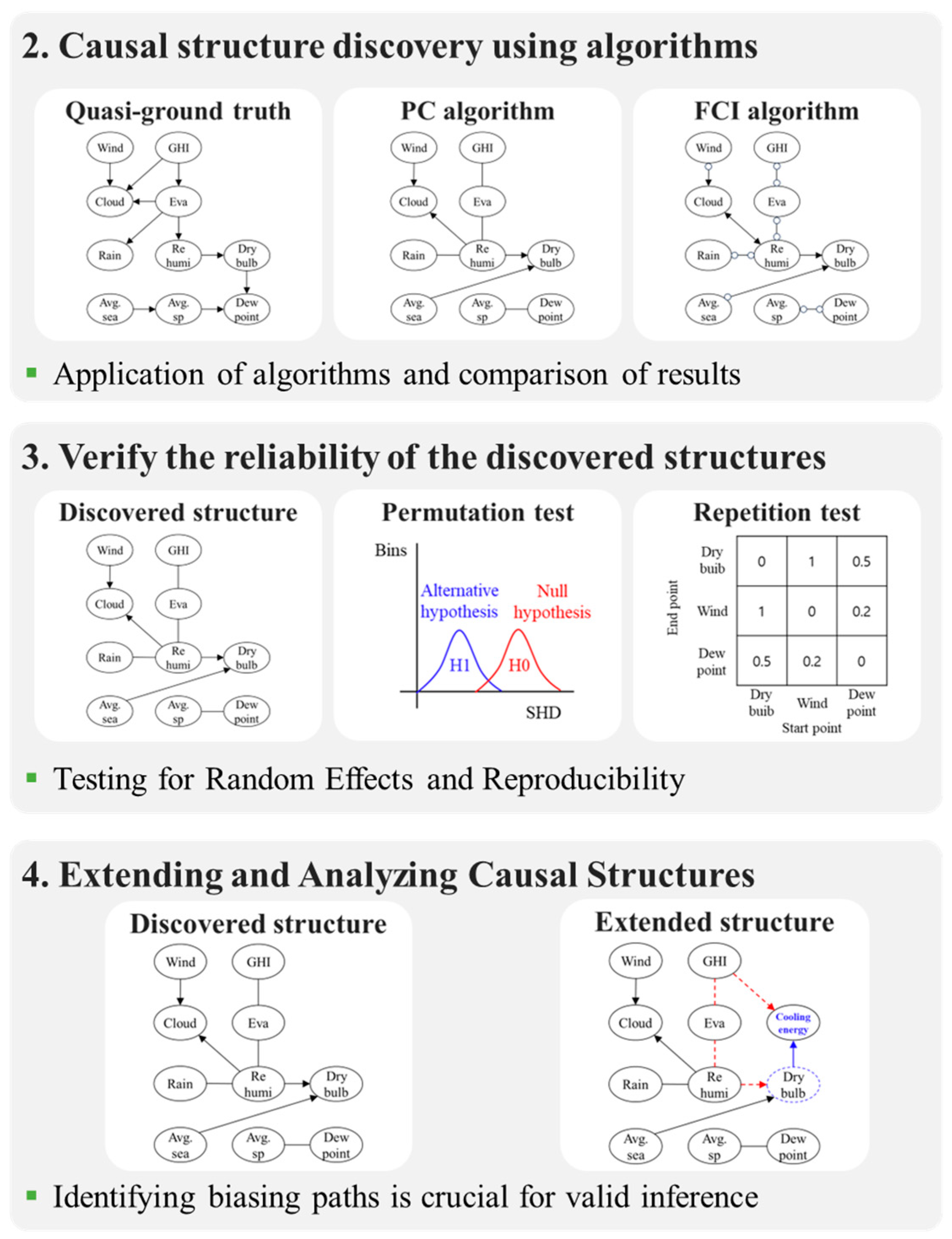
- Causal structure discovery using the PC and FCI algorithms.
- Application of the permutation test and the repetition test, followed by comparative analysis of the results.
- Extension of the discovered causal structure to incorporate a cooling energy variable and analysis of biasing paths.
2. Method
2.1. Causal Discovery Algorithm
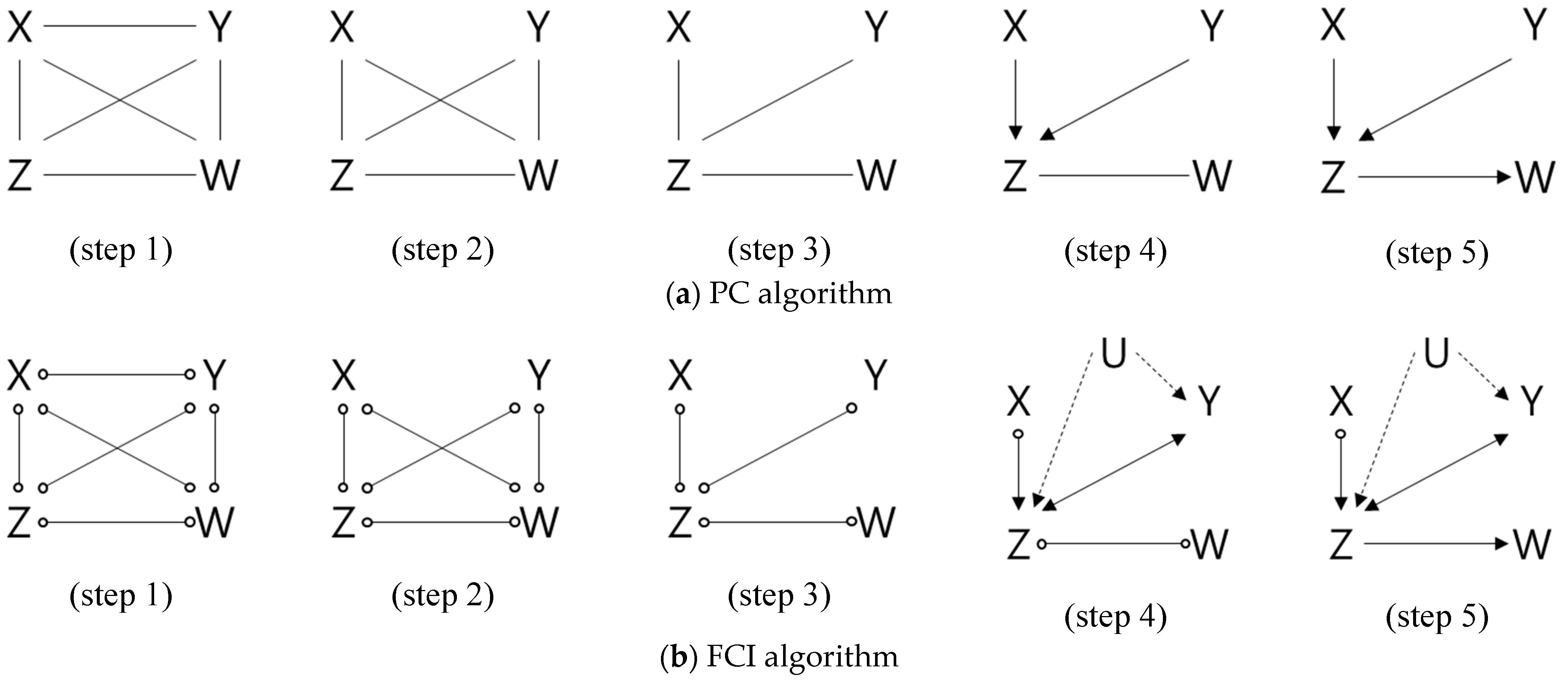
- Step 1. Construct the initial graph by drawing undirected edges between all variables.
- Step 2. Test marginal (unconditional) independence for every pair of variables and remove the corresponding edge if independence holds.
- -
- Example: if X⊥Y, remove X−Y (e.g., chi-square test, G-test, or correlation-based test).
- Step 3. For every pair (X, Y), perform conditional independence tests given a conditioning set Z.
- -
- Example: if X⊥Y∣Z holds, remove the edge X−Y. Repeat this procedure while increasing the size of the conditioning set.
- Step 4. For any triple X−Z−Y that is connected, if X and Y are not independent given Z (X not⊥Y∣Z), orient it as a collider: X→Z←Y.
- Step 5. Determine the remaining edge orientations using orientation propagation (e.g., Meek’s rules), ensuring acyclicity, preserving non-colliders, and enforcing additional orientation constraints [13].
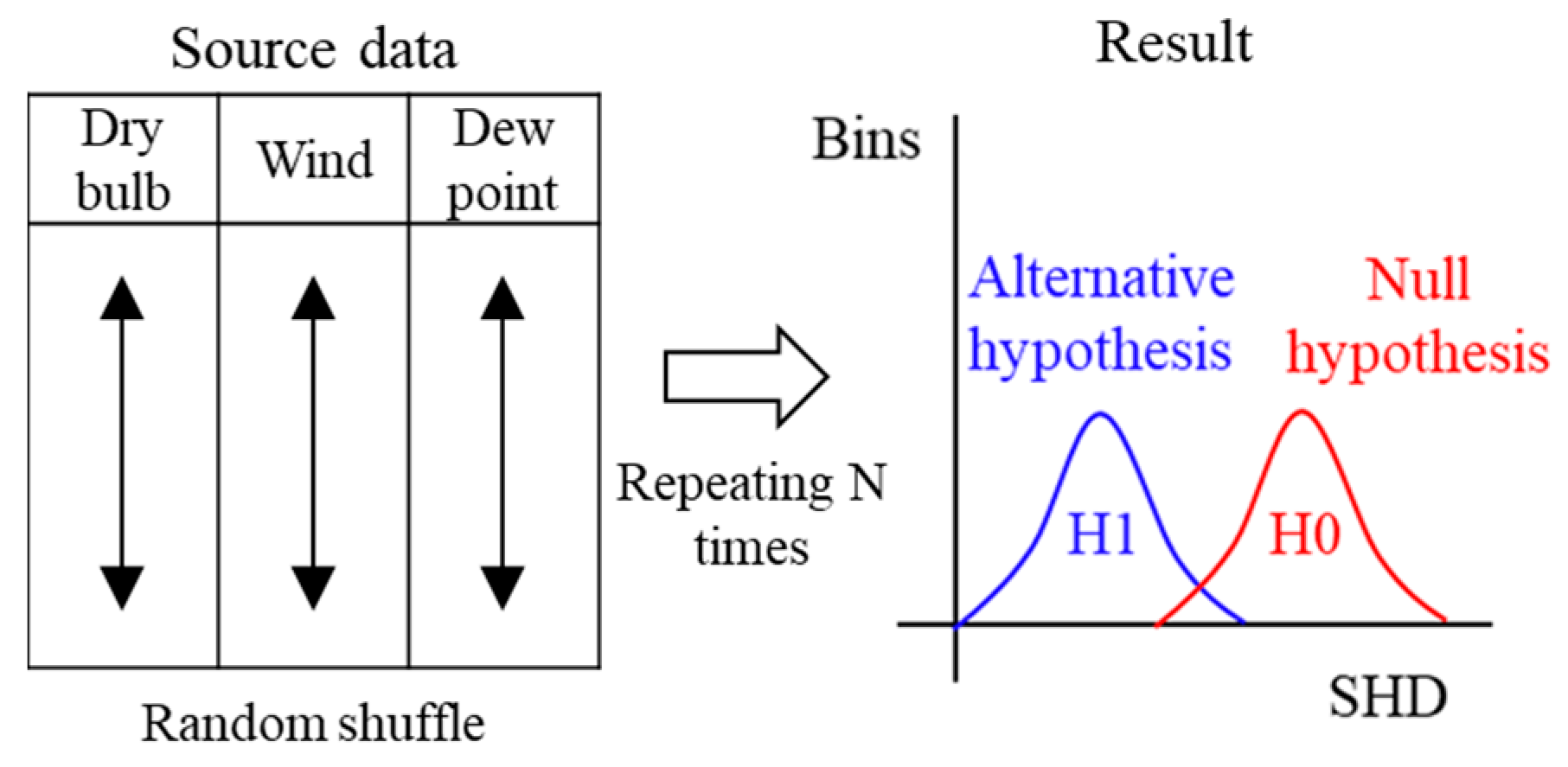
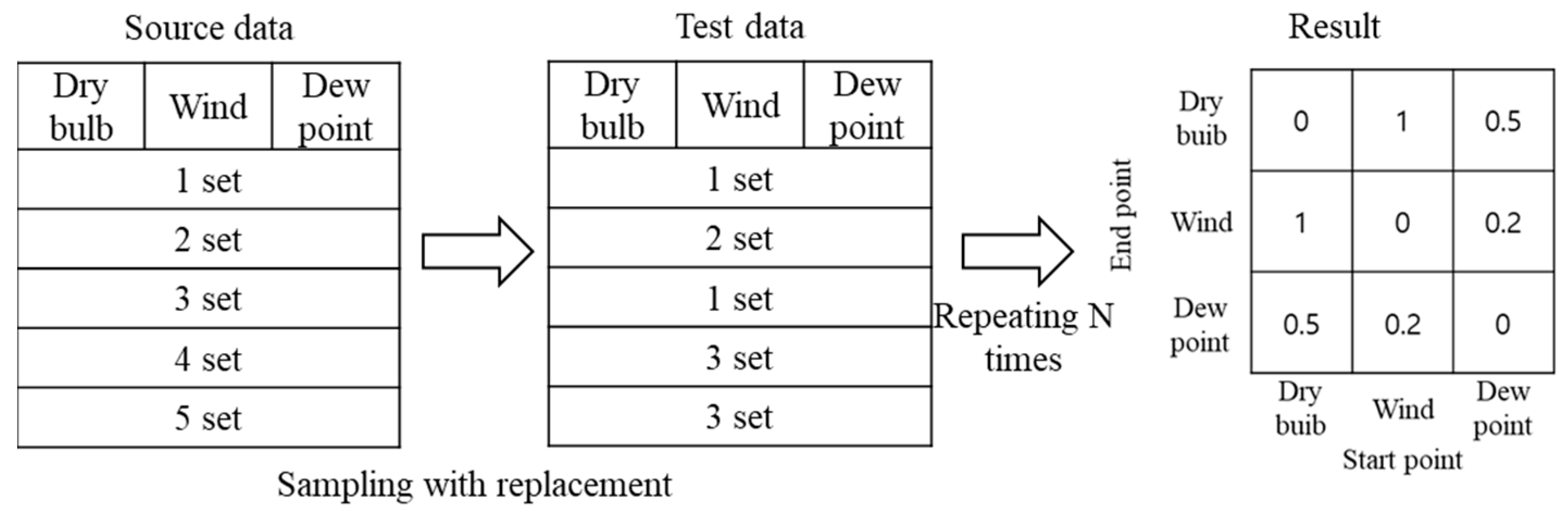
2.2. Permutation and Repetition Tests for Validating Discovered Causal Structure
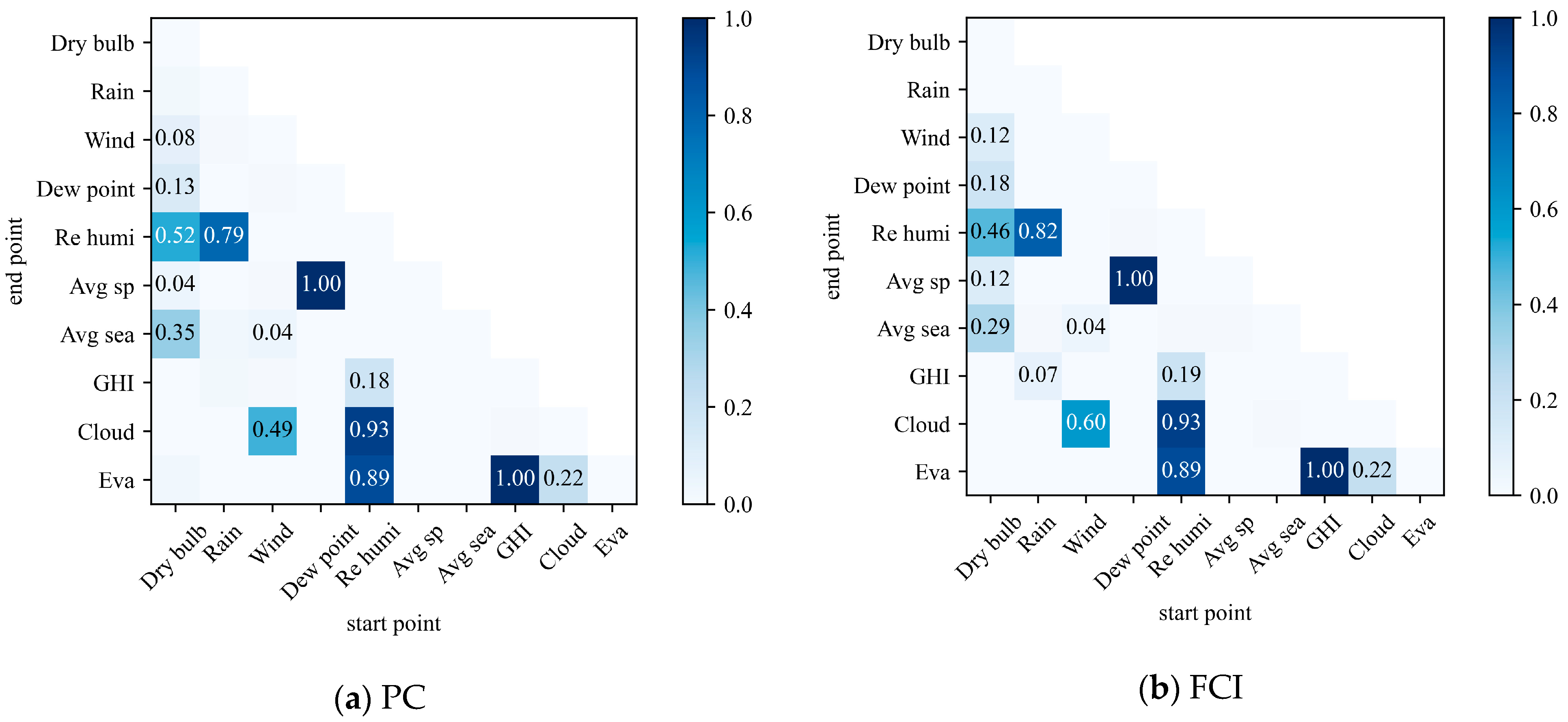
2.3. Analysis of Causal Path
3. Case Study
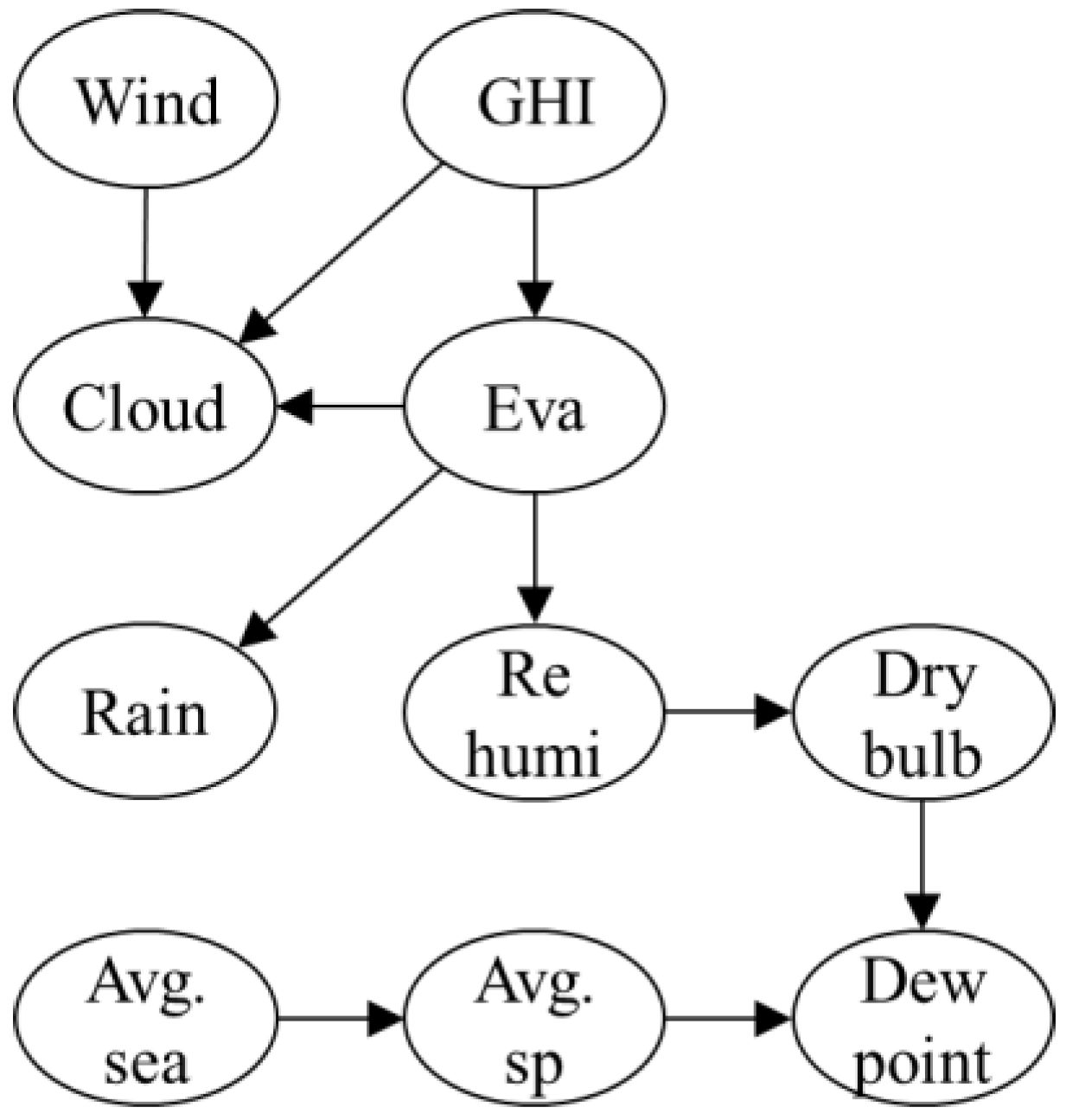
3.1. Weather Data and Quasi-Ground Truth
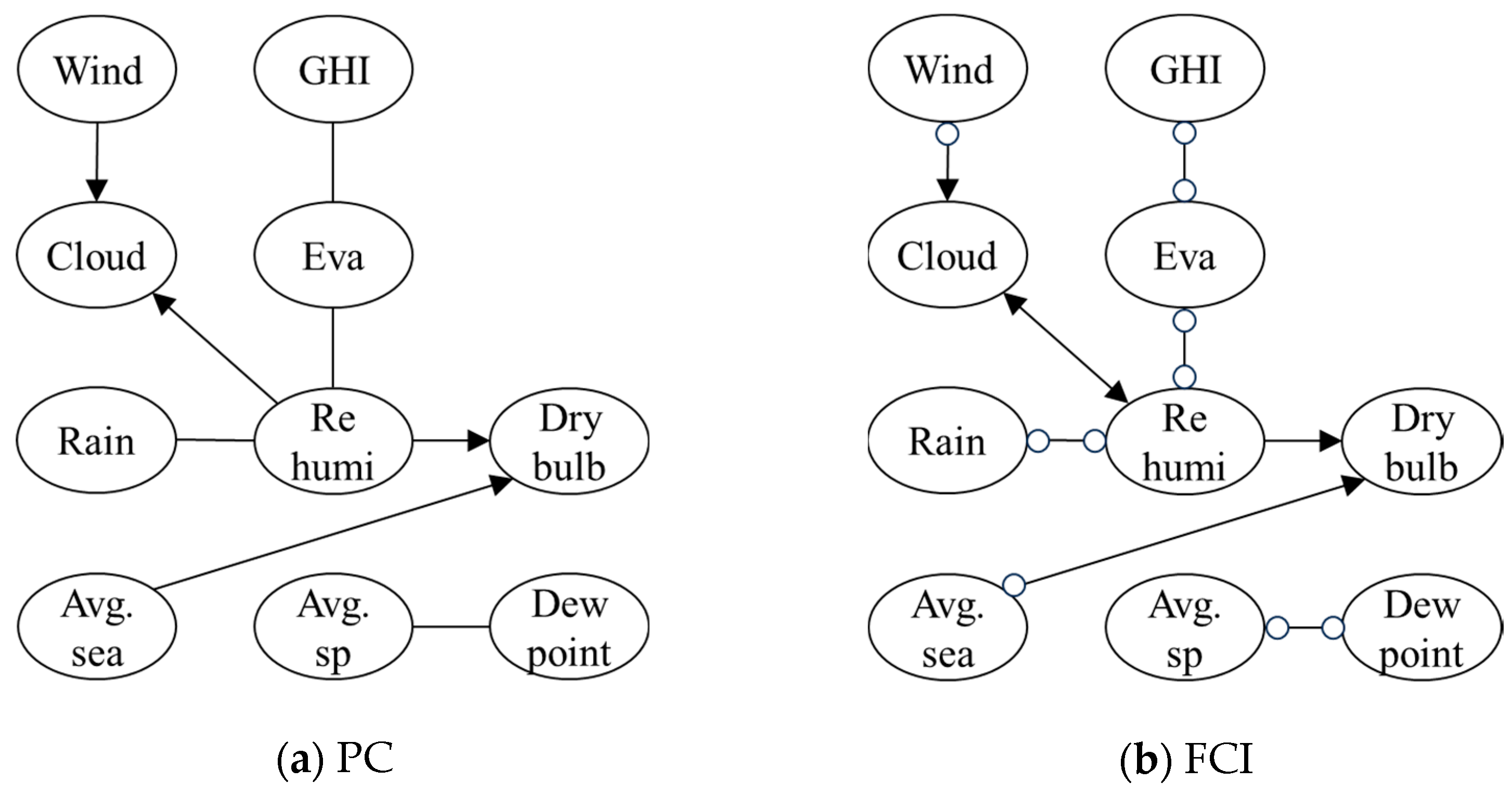
3.2. Comparison of Causal Structures
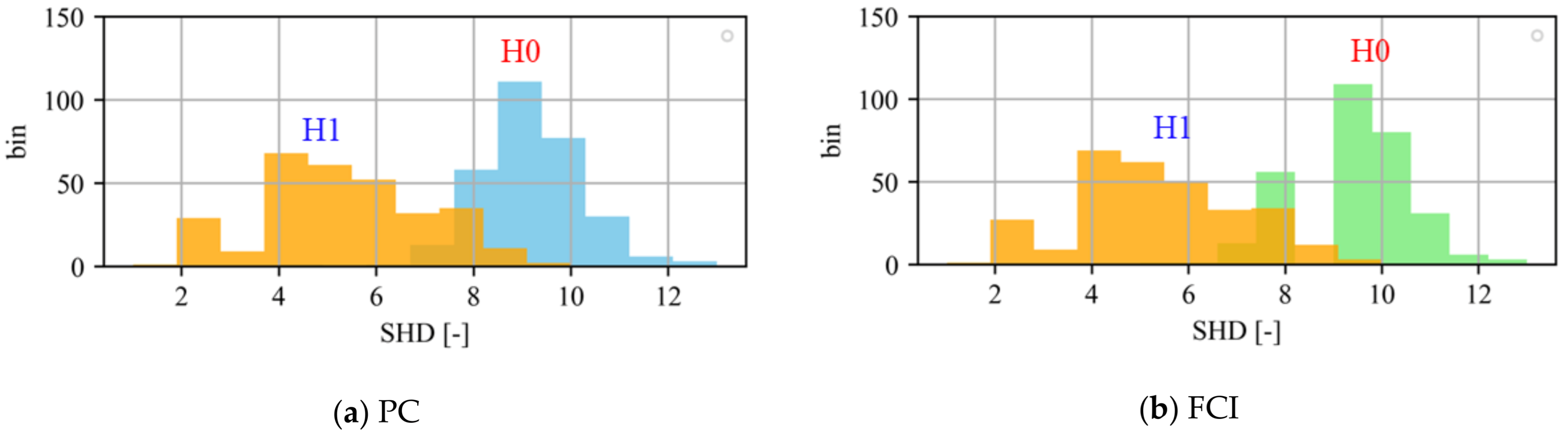
3.3. Reliability of the Discovered Structures
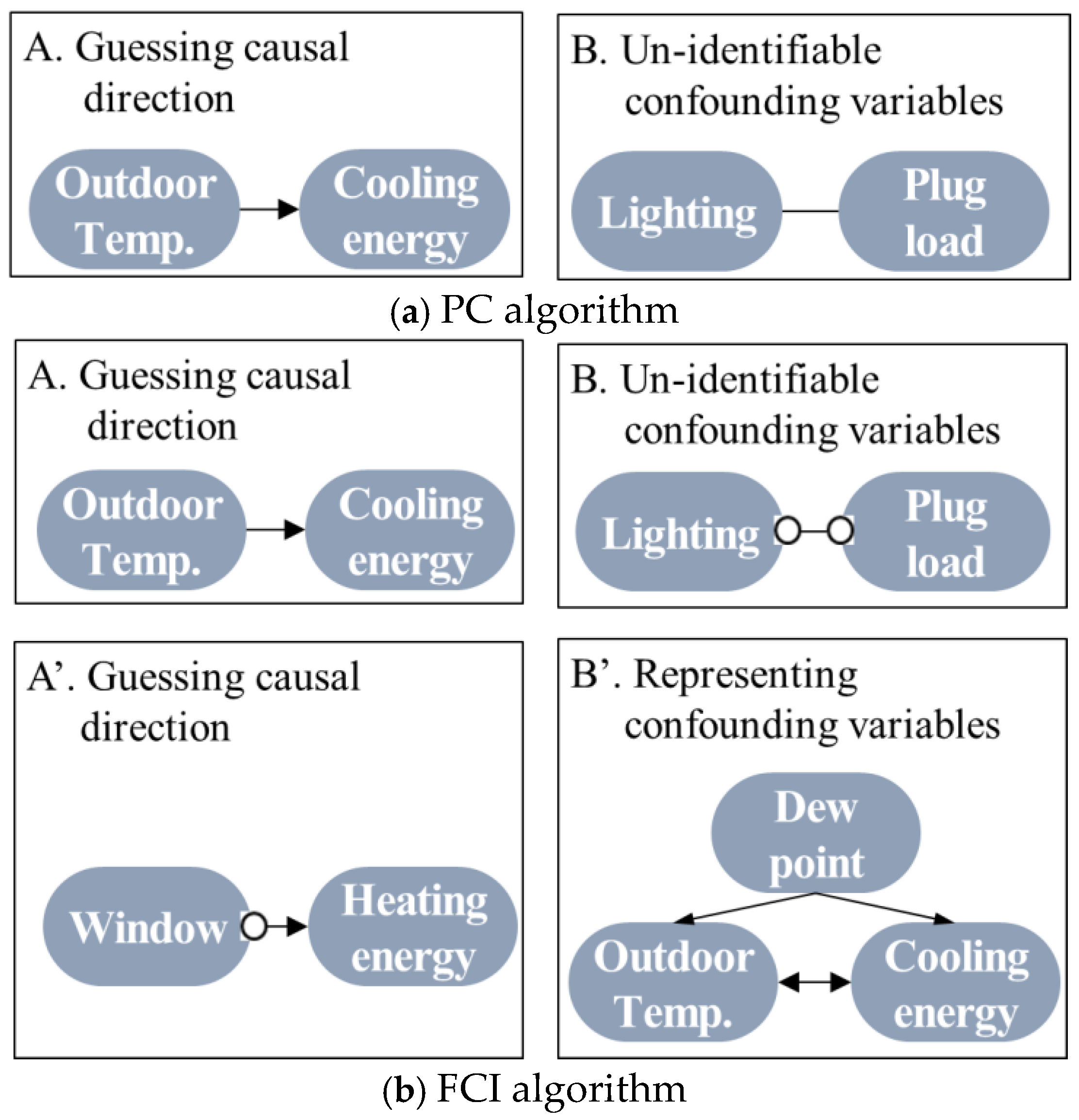
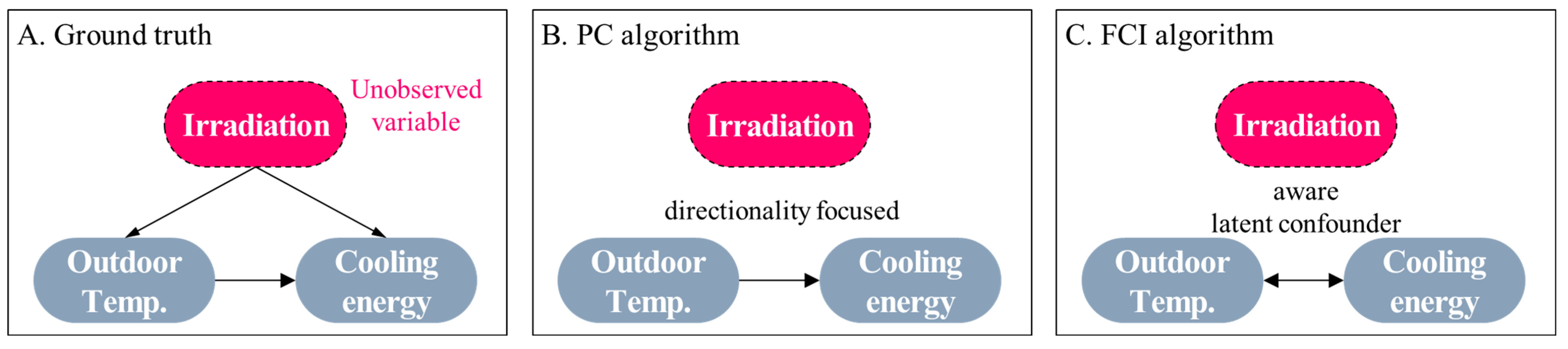
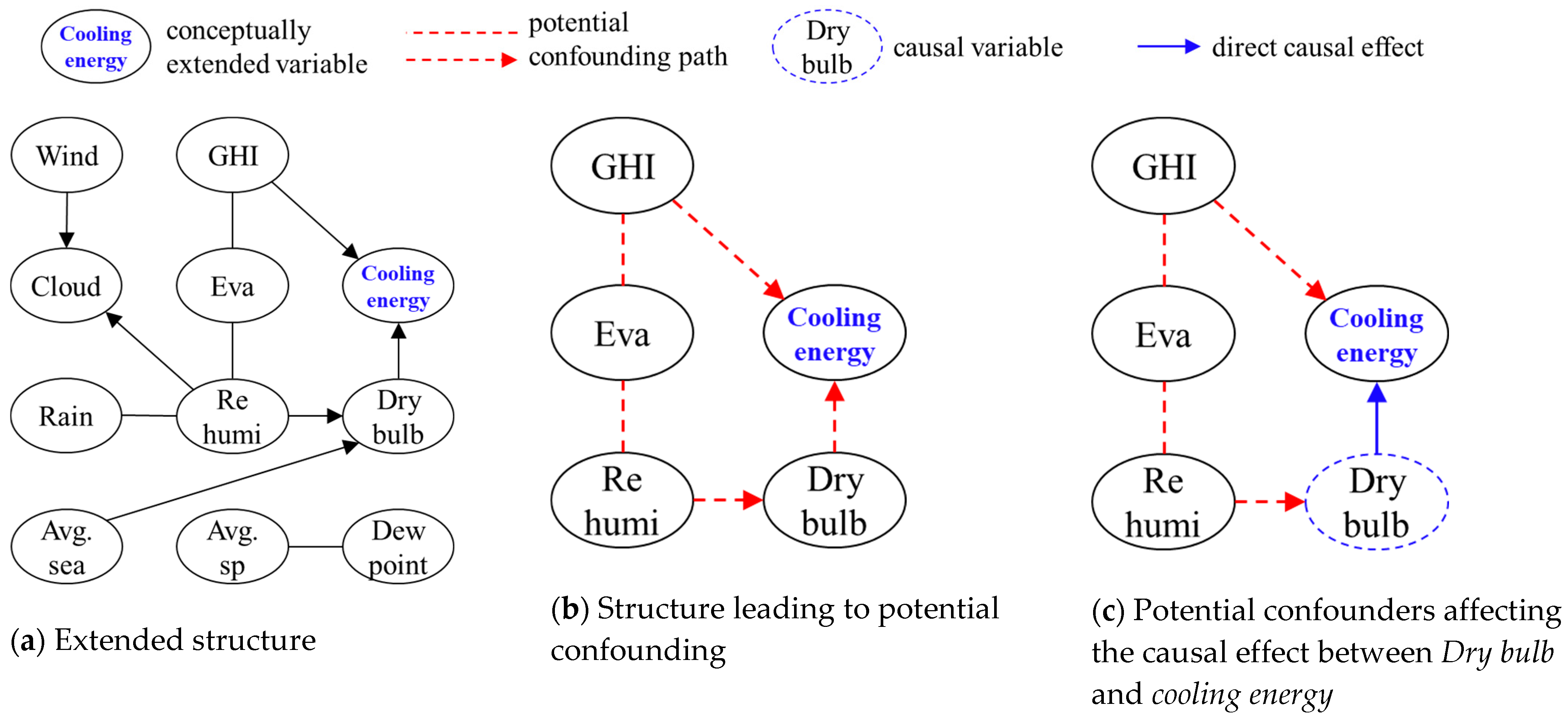
3.4. Extending the Causal Structure and Identifying Back-Door Paths
4. Discussion
- Algorithmic assumptions. Constraint-based methods such as the PC and FCI algorithms are suitable for identifying causal relations under assumptions of linearity and Gaussianity. However, with nonlinear or non-Gaussian data, weakened conditional-independence tests can distort causal identification, indicating the need for data preprocessing or complementary algorithmic approaches. Moreover, because the PC algorithm operates under the no-hidden-confounders (causal sufficiency) assumption, accurate identification can be difficult when such confounding factors are present.
- Data scope and generalizability. This study used two months of summer weather data collected from the Seoul area, which limits both the temporal and spatial generalizability of the findings. While the dataset reflects typical urban climatic characteristics of central South Korea, it may not fully represent broader regional or seasonal variability. Future work should therefore extend the causal discovery analysis to multiple regions with diverse climatic conditions—such as coastal and southern zones—and to multi-year and interseasonal datasets to enhance the robustness and general applicability of the identified causal relationships.
- A conceptually extended causal structure. Rather than providing a quantitative validation using actual cooling energy data, this study presents only a conceptual demonstration of how the causal framework may be extended to include a cooling energy variable. In future work, we plan to explore causal structures using datasets that incorporate actual building energy use and to examine the biasing paths that may arise in such expanded structures.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ko, Y.-D.; Park, C.-S. Parameter Estimation of Unknown Properties Using Transfer Learning from Virtual to Existing Buildings. J. Build. Perform. Simul. 2021, 14, 503–514. [Google Scholar] [CrossRef]
- Kim, D.W.; Kim, Y.M.; Lee, S.E. Development of an Energy Benchmarking Database Based on Cost-Effective Energy Performance Indicators: Case Study on Public Buildings in South Korea. Energy Build. 2019, 191, 104–116. [Google Scholar] [CrossRef]
- Chen, X.; Abualdenien, J.; Singh, M.M.; Borrmann, A.; Geyer, P. Introducing Causal Inference in the Energy-Efficient Building Design Process. Energy Build. 2022, 277, 112583. [Google Scholar] [CrossRef]
- Bareinboim, E.; Correa, J.D.; Ibeling, D.; Icard, T. On Pearl’s Hierarchy and the Foundations of Causal Inference. In Probabilistic and Causal Inference: The Works of Judea Pearl; Association for Computing Machinery: New York, NY, USA, 2022; Volume 36, pp. 507–556. ISBN 978-1-4503-9586-1. [Google Scholar]
- Zhou, A.; Wang, S.; Chen, B. Impact of New Energy Demonstration City Policy on Energy Efficiency: Evidence from China. J. Clean. Prod. 2023, 422, 138560. [Google Scholar] [CrossRef]
- Sun, R.; Schiavon, S.; Brager, G.; Arens, E.; Zhang, H.; Parkinson, T.; Zhang, C. Causal Thinking: Uncovering Hidden Assumptions and Interpretations of Statistical Analysis in Building Science. Build. Environ. 2024, 259, 111530. [Google Scholar] [CrossRef]
- Mun, J.; Park, C.S. Beyond Correlation: A Causality-Driven Model for Indoor Temperature Control. Energy Build. 2025, 338, 115739. [Google Scholar] [CrossRef]
- Nogueira, A.R.; Pugnana, A.; Ruggieri, S.; Pedreschi, D.; Gama, J. Methods and Tools for Causal Discovery and Causal Inference. WIREs Data Min. Knowl. Discov. 2022, 12, e1449. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R.; Kauffman, S.; Aimale, V.; Wimberly, F. Constructing Bayesian Network Models of Gene Expression Networks from Microarray Data. J. Contrib. Carnegie Mellon Univ. 2000. [Google Scholar] [CrossRef]
- Eberhardt, F. Introduction to the Foundations of Causal Discovery. Int. J. Data Sci. Anal. 2017, 3, 81–91. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Spirtes, P.L.; Meek, C.; Richardson, T.S. Causal Inference in the Presence of Latent Variables and Selection Bias. arXiv 2013. [Google Scholar] [CrossRef]
- Meek, C. Causal Inference and Causal Explanation with Background Knowledge. arXiv 2013. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, B.; Chen, W.; Ramsey, J.; Gong, M.; Cai, R.; Shimizu, S.; Spirtes, P.; Zhang, K. Causal-Learn: Causal Discovery in Python. arXiv 2023. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 66–70. ISBN 978-1-4612-4380-9. [Google Scholar]
- Assaad, C.K.; Devijver, E.; Gaussier, E. Survey and Evaluation of Causal Discovery Methods for Time Series. J. Artif. Intell. Res. 2022, 73, 767–819. [Google Scholar] [CrossRef]
- Choi, K.; Park, J.; Kim, D.-W.; Joe, J. Development of a Regression Model for Evaluating Energy Consumption Performance of Daycare Centers Using Open Public Data. J. Korean Sol. Energy Soc. 2024, 44, 35–48. [Google Scholar] [CrossRef]
- Kim, H.-J.; Joo, H.-B.; Kim, D.-W.; Heo, Y.-S. Examining the Influencing Factors of Base and Heating Energy Use Intensities for the Energy Benchmarking of School Buildings. J. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2024, 18, 491–501. [Google Scholar] [CrossRef]
- Kim, J.-H.; Seonin, K.; Park, Y.-J.; Kim, D.-W.; Euijong, K. Correlation Analysis Between Non-Energy Public Data of Residential Buildings and Annual Energy Consumption by Usage. Korea J. Air-Cond. Refrig. Eng. 2024, 36, 606–618. [Google Scholar] [CrossRef]
- Kim Gi, H.; Shin Ry, H.; Kim Woo, D. DataNet Project: A Framework for Linking Multi-Faceted Building Energy Datasets for Effective Performance Analysis. In Proceedings of the ASim Conference 2024: 5th Asia Conference of IBPSA, Osaka, Japan, 8–10 December 2024; Volume 5, pp. 483–490. [Google Scholar]
- Shin, H.-R.; Kim, H.-G.; Kim, D.-W. DataNet: A Framework for Linking Nationwide Building Energy Datasets to Support Effective Performance Analysis. J. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2024, 18, 564–575. [Google Scholar] [CrossRef]

| Reference | Method | Domain | Summary |
|---|---|---|---|
| [3] | Causal inference | Building energy design | This study introduces causal inference into energy-efficient building design to identify cause–effect links between design parameters and performance outcomes. It further demonstrates that causal reasoning improves the quality design decision-making. |
| [4] | Causal inference and discovery | General causal theory | It explains Judea Pearl’s three-level hierarchy (association, intervention, counterfactual) and formalizes the mathematical foundations of causal inference. It also highlights conceptual distinction between correlation and causation. |
| [5] | Causal inference | Energy policy | This study applies causal inference to evaluate the policy’s impact on energy efficiency. The analysis shows that the policy increased energy efficiency in demonstration cities by approximately 4.8% relative to non-demonstration cities. |
| [6] | Causal inference | Building science | It emphasizes that reversing the causal direction between variables leads to different interpretations. Using two regression approaches in thermal comfort research, it shows that causal reasoning—unlike mere correlation—reveals distinct comfort zones with actionable implications for energy efficiency. |
| [7] | Causal inference | HVAC control | This work introduces a causality-driven modeling framework for building cooling control using double machine learning (DML). The causality-driven DML model outperformed the ANN (MSE = 0.19 °C), revealed true causal effects, and produced physically consistent predictions across varied control conditions. |
| [8] | Causal inference and discovery | Data science | This review surveys algorithms, assumptions, and applications of causal inference and discovery. It also identifies practical challenges and emerging trends in applying these methods to real-world data. |
| [9] | Causal discovery | Bioinformatics | It constructs Bayesian network models from gene expression data using the PC algorithm, illustrating large-scale causal discovery from purely observational data in early work. |
| [10] | Causal discovery | Data science | This work outlines the foundational assumptions required for causal discovery and reviews several prominent approaches used in practice. |
| Algorithm | Test | Metric | Value | Interpretation |
|---|---|---|---|---|
| PC | Permutation | p-value | 0.01 | The discovered structure is non-random |
| Repetition | Edge recurrence rate | >0.4 | Stable structure across runs | |
| FCI | Permutation | p-value | 0.01 | The discovered structure is non-random |
| Repetition | Edge recurrence rate | >0.3 | Stable structure across runs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, H.-G.; Kim, H.-G.; Kim, D.-W. Causal Discovery and Validation in Summer Weather Data with a Conceptual Extension to Cooling Energy Use. Buildings 2025, 15, 4248. https://doi.org/10.3390/buildings15234248
Chu H-G, Kim H-G, Kim D-W. Causal Discovery and Validation in Summer Weather Data with a Conceptual Extension to Cooling Energy Use. Buildings. 2025; 15(23):4248. https://doi.org/10.3390/buildings15234248
Chicago/Turabian StyleChu, Han-Gyeong, Hye-Gi Kim, and Deuk-Woo Kim. 2025. "Causal Discovery and Validation in Summer Weather Data with a Conceptual Extension to Cooling Energy Use" Buildings 15, no. 23: 4248. https://doi.org/10.3390/buildings15234248
APA StyleChu, H.-G., Kim, H.-G., & Kim, D.-W. (2025). Causal Discovery and Validation in Summer Weather Data with a Conceptual Extension to Cooling Energy Use. Buildings, 15(23), 4248. https://doi.org/10.3390/buildings15234248






