Blast Performance of UHMWPE Cavity Protection Structure for Reinforced Concrete Walls

Abstract

Escalating global explosive threats pose persistent challenges to building security. To address this issue, a novel Ultra-High-Molecular-Weight Polyethylene (UHMWPE) cavity protection structure is proposed to enhance the blast resistance of reinforced concrete (RC) walls. In this study, numerical simulation was conducted to investigate the blast resistance and protective mechanisms of the UHMWPE cavity protection structure. The results reveal that the protection mechanism involves two synergistic processes: dissipating energy through plastic deformation of the high-toughness panel and attenuating the shock wave via cavity wave modulation. This configuration achieves a peak overpressure attenuation exceeding 88% within the cavity zone, thereby effectively mitigating blast effects. Compared to an unprotected wall, the UHMWPE cavity protection system achieves a peak overpressure attenuation rate exceeding 86.3% on the blast-facing surface and decreases the peak displacement at the wall center by 60%, effectively suppressing localized damage. Parametric research further indicates that adding stiffeners to the cavities and making the panels thicker can greatly increase the ability to dissipate energy and overall stability of the UHMWPE cavity protection panel. The findings of this study offer valuable guidance for the design of high-performance blast-resistant structures.

1. Introduction

Reinforced concrete (RC) walls, as key load-bearing and protective components in buildings, are highly susceptible to brittle failure under explosive loads, including cracking, spalling, and overall instability [1,2,3]. These failures pose a serious threat to both structural integrity and personnel safety. With the increasing risk of explosions in modern urban and industrial environments [4], improving the blast resistance of RC walls has become a core research direction in the field of protective engineering and structural safety in response to major challenges [5,6].

Current research on improving the blast resistance of RC walls primarily follows two technical approaches: material enhancement and structural innovation. In terms of material strengthening, the traditional strategies for improving the blast resistance of RC walls usually mainly include increasing the thickness of the components, using higher grades of concrete, and increasing the reinforcement ratio [7,8,9]. Lin et al. [10] conducted numerical simulations to study the effects of panel thickness and reinforcement ratio on the explosive performance of reinforced concrete panels. Yao Shujian et al. [11] analyzed the blast resistance and damage characteristics of reinforced concrete slabs under different reinforcement ratios through explosion tests and numerical simulations. These methods can improve the load-bearing capacity and ductility of structures to a certain extent. However, they often lead to increased self-weight and higher construction costs. Furthermore, under the action of strong explosive loads, the structure may still suffer brittle failure. To transcend these constraints, investigators have turned their attention to High-Performance Fiber-Reinforced Polymer (HPFRP) [12]. Materials such as steel fiber [13,14], glass fiber [15], and carbon fiber cloth (CFRP) [16] exhibit outstanding performance in improving structural ductility, inhibiting crack propagation, and enhancing energy absorption capacity. With respect to the blast resistance of fiber-reinforced concrete slabs, numerous scholars have conducted extensive theoretical studies, experimental validations, and numerical simulations [17,18]. Ngo Tuan et al. [19] focused on the blast resistance of ultrahigh-strength concrete (UHSC) slabs, and the experimental results showed that 100 mm-thick UHSC slabs exhibited significant blast resistance. Mao Lei et al. [20] carried out a numerical study on the behavior of UHPFRC under blast loading and analyzed the effects of reinforcement bars and steel fibers on enhancing its blast resistance. The above-mentioned fiber materials are effective in improving the ductility and blast resistance of structures. Nevertheless, issues such as high cost, complex construction techniques, and non-uniform fiber distribution have partially constrained their practical engineering application and broader utilization [21,22]. Moreover, these studies primarily focus on optimizing material properties while giving insufficient consideration to the modulation of blast wave propagation, thereby limiting their overall protective effectiveness.

Regarding structural innovations, researchers have developed various novel protective systems, such as steel–concrete–steel walls (SCS) [23], reinforced concrete sandwiched panels [24], reinforced concrete panel using foam cladding [25], and fence-type blast wall [26,27,28]. These structures typically induce the reflection and prolongation of shock waves through cavities or interlayers to achieve energy dissipation. Although these studies have, to some extent, improved the blast resistance of RC walls, issues such as excessive self-weight, limited energy-dissipation capacity, and inadequate applicability persist.

In summary, existing research shows limitations in both material and structural dimensions: conventional materials and structures struggle to balance lightweight design with efficient energy dissipation, whereas new material systems lack innovative structural configurations that can fully unlock their potential. Therefore, exploring novel protection systems that combine lightweight design, high strength, and efficient energy-dissipation capacity has become an urgent research need. UHMWPE fiber materials have garnered widespread attention in protective engineering owing to their high specific strength, high toughness, and excellent impact resistance [29,30,31,32]. Under blast loading, UHMWPE composite materials can markedly attenuate shock-wave transmission, delay crack propagation, and significantly enhance structural toughness and energy-dissipation capacity [33,34]. Meanwhile, cavity protection structures achieve multi-stage attenuation through the dispersion and reflection of shock waves, effectively mitigating blast-energy-induced damage to the primary structure [35]. Nevertheless, the coupling mechanism between the exceptional toughness of UHMWPE and cavity wave modulation has not yet been thoroughly investigated in current research.

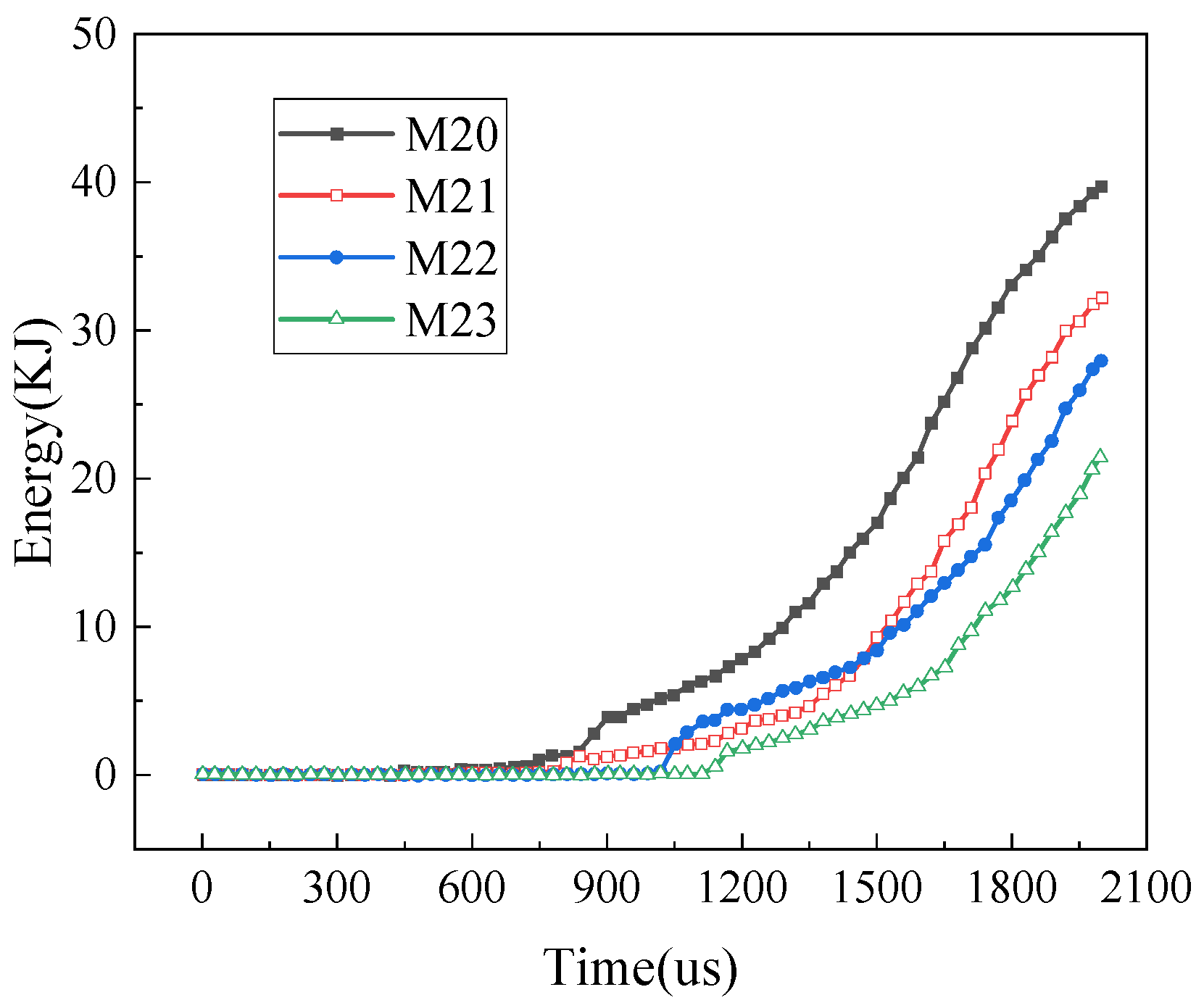
Building on the preceding context, this study integrates the synergistic integration of the dynamic energy dissipation characteristics of UHMWPE material with the wave modulation mechanism of cavity structures, thereby proposing a novel UHMWPE cavity protective panel. The dynamic response and blast resistance of the structure under near-field blast loading are investigated via numerical simulations using the LS-DYNA finite-element program. This study focuses on blast-wave decay characteristics, wall damage patterns, and energy-dissipation behavior, and performs parametric analyses to refine critical design variables, including the thicknesses of the front and rear panels, cavity geometry, and rib configuration. This study aims to provide a novel solution to overcome the bottleneck of existing protective technologies and to offer a solid theoretical basis and engineering reference for the high-performance protection design of RC walls. In subsequent work, the dynamic response of the UHMWPE cavity-based protective panel under combined loading from blast overpressure and fragment impact will be investigated.

2. UHMWPE Cavity Protection Structure and Finite-Element Model

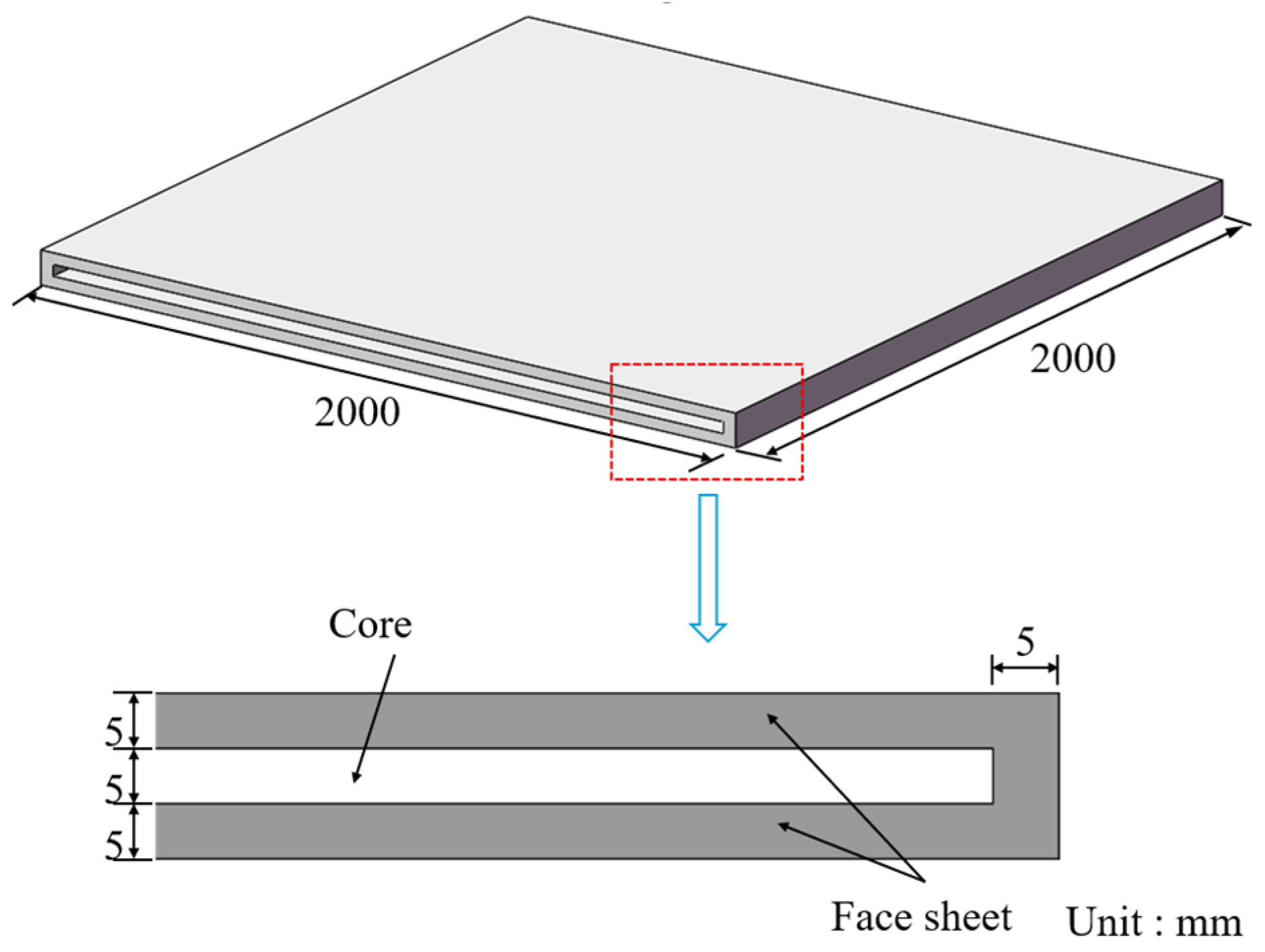
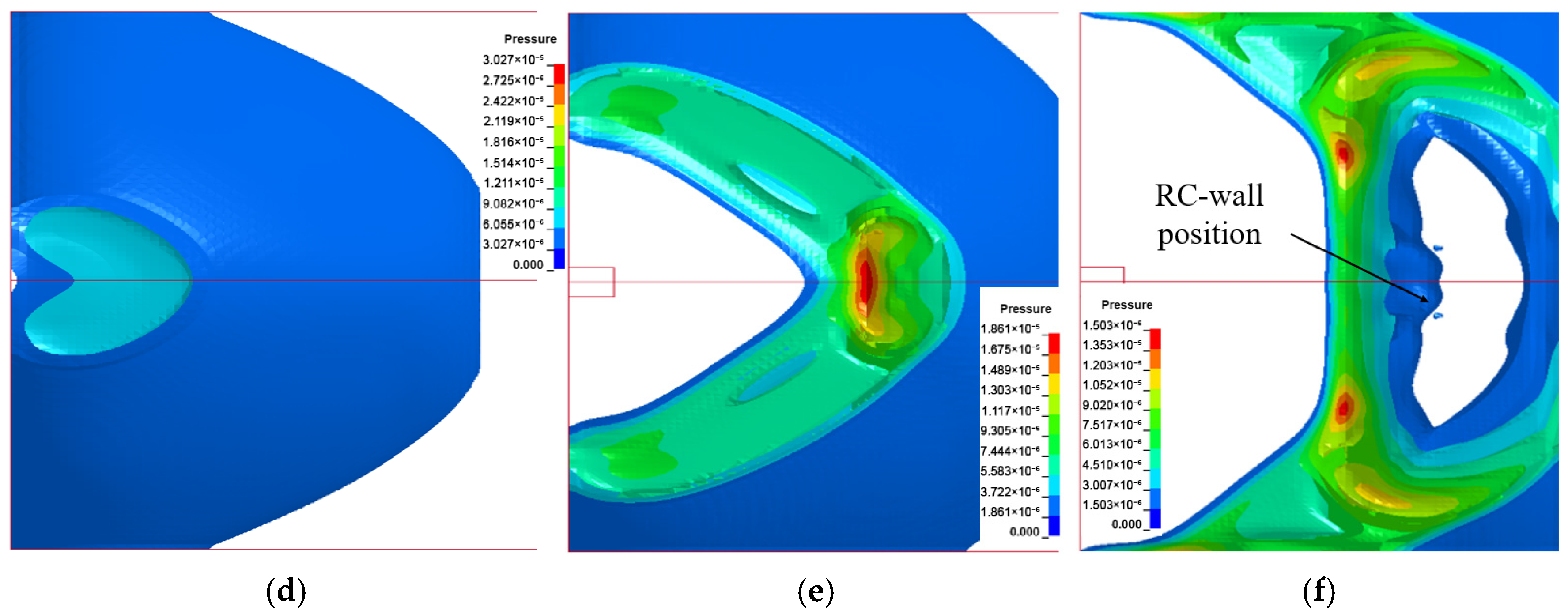
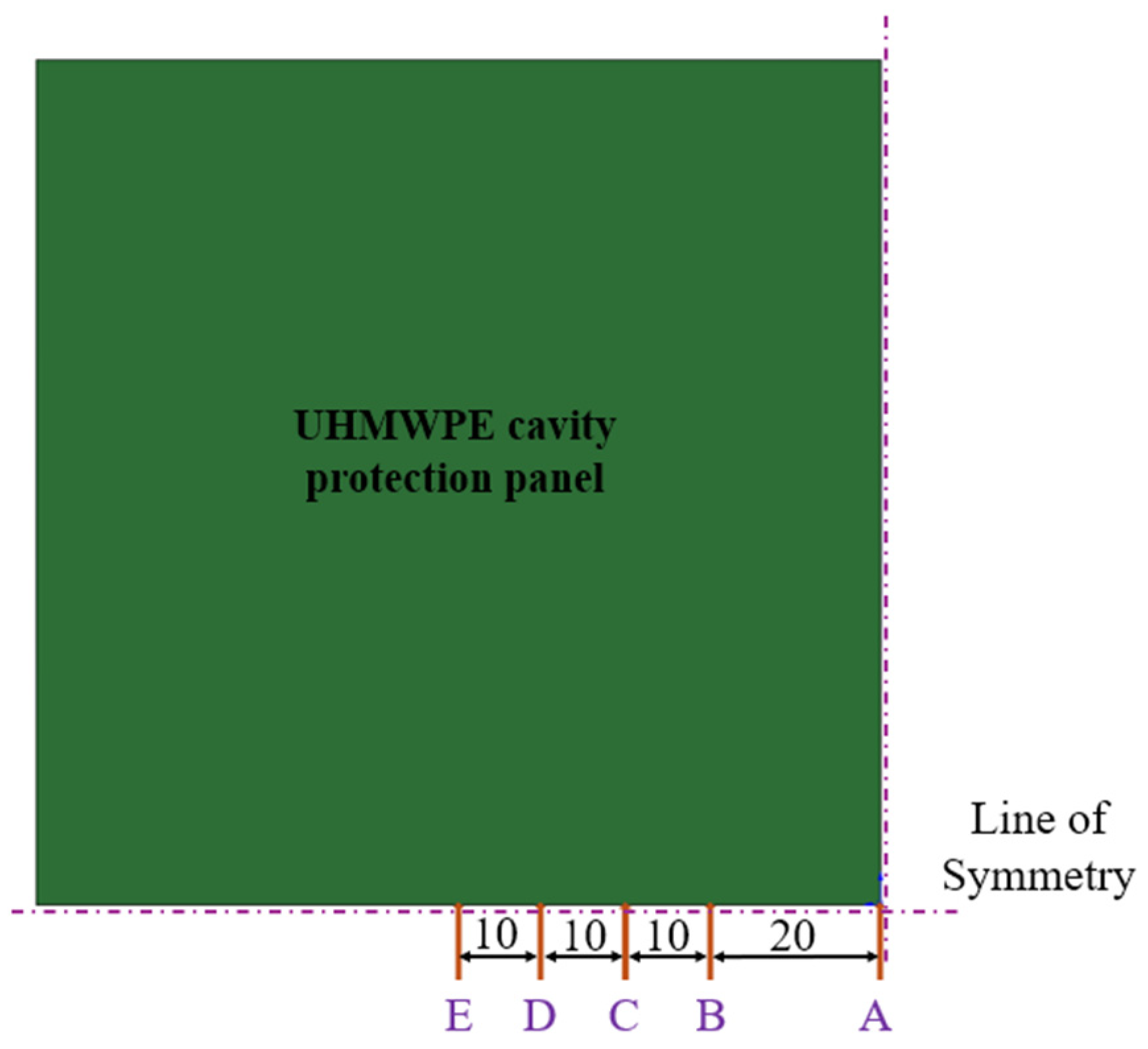
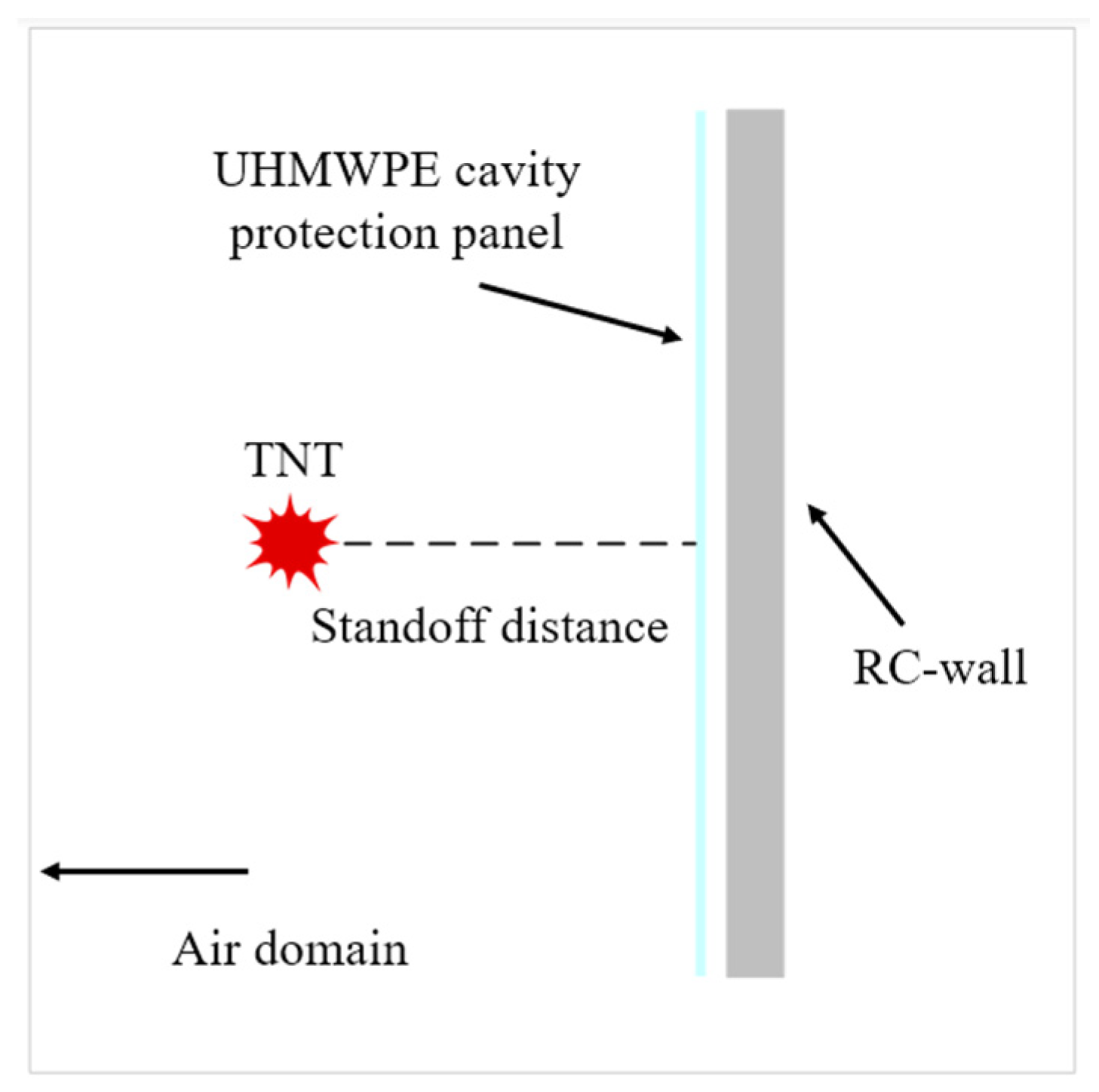
The UHMWPE fiber panel was designed as a double-layer thin plate structure with a cavity. This cavity effectively attenuated the overpressure and suppressed the development of the shockwave under the action of the explosion shockwaves. The configuration and dimensions of the protection panel are illustrated in Figure 1. The UHMWPE protection panel measures 2000 mm × 2000 mm × 15 mm in overall size, with both the front and back face layers having a thickness of 5 mm. The internal cavity region has a thickness of 5 mm, resulting in a rectangular frame-like cross-sectional geometry. This study investigates the influence of external protective structures on the blast resistance performance of reinforced concrete walls. The wall specimen measures 2000 mm × 2000 mm × 240 mm. The specimen were reinforced with steel bars with a yield strength of 235 MPa and a diameter of 10 mm. Each reinforcing bar had a length of 1800 mm and was spaced at 300 mm intervals. A clear cover thickness of 35 mm is maintained for the reinforcement. To elucidate the blast mitigation mechanism of the cavity protection panel, the standoff distance between the panel and the reinforced concrete wall was set to 100 mm. Furthermore, the entire model was enclosed within an air domain. To reduce computational cost and avoid simulating nonessential air elements, the dimensions of this air domain were adjusted accordingly based on the equivalent explosive mass and the standoff distance. A schematic diagram of the blast-resistant wall with the cavity protection panel is shown in Figure 2.

2.1. Finite-Element Modeling and Validation

Numerical modeling based on LS-DYNA is an effective way to obtain a more accurate description of the stress distribution and propagation law of waves. In this study, a three-dimensional finite-element model was established using LS-DYNA R11.1 explicit dynamic analysis software to simulate the dynamic response of the cavity protection structure and reinforced concrete wall under explosive loading. The SOLID164 element is an eight-node explicit solid element suitable for simulating complex nonlinear dynamic behaviors, including large deformations, high strain rates, and material failure under blast and impact loading. Based on these properties, the UHMWPE cavity protection slab and RC wall adopted SOLID164 elements in the simulation. 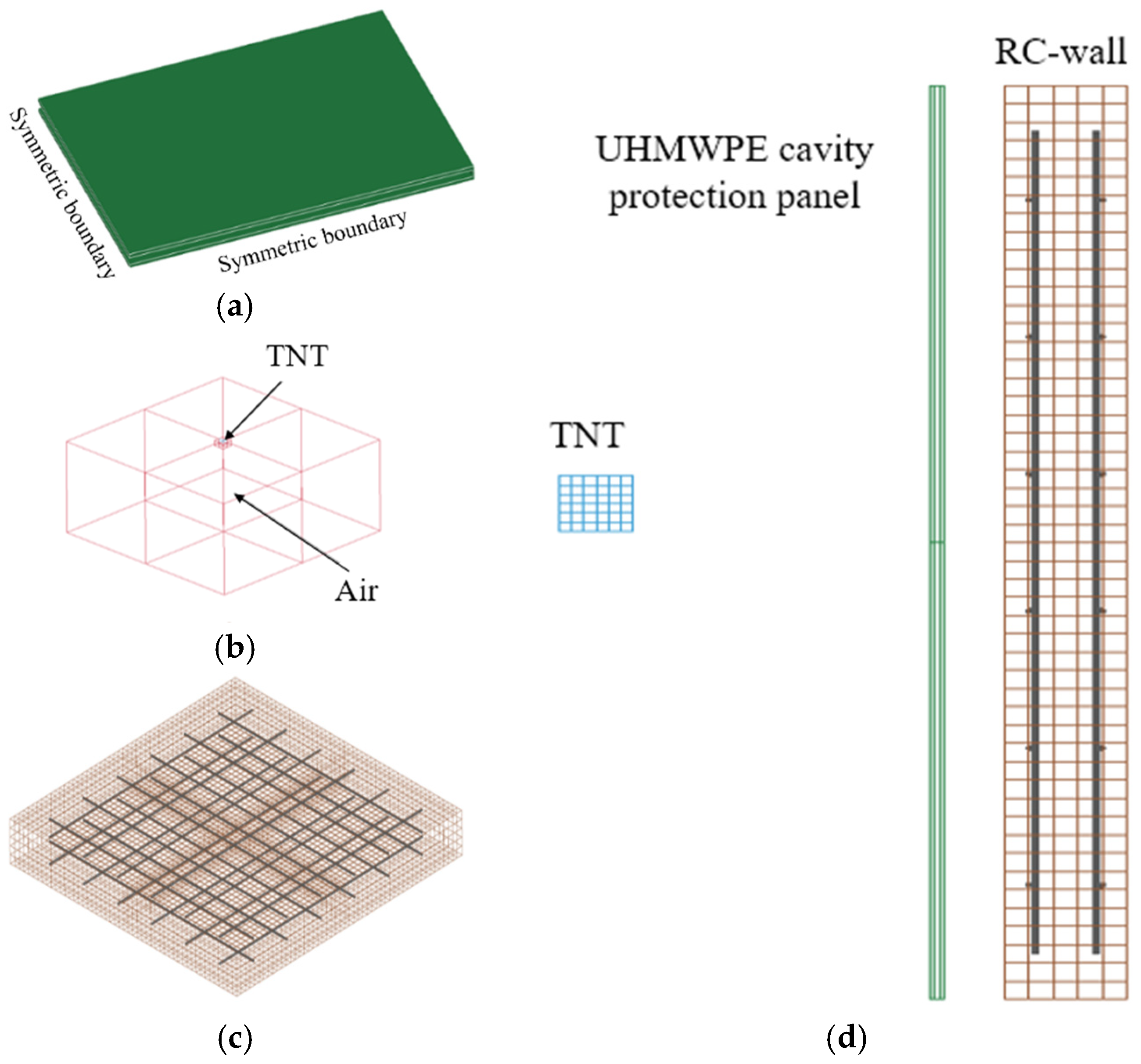TNT is controlled by volume, with a density of 1.73 g/cm³. Taking 1730 g of TNT equivalent as an example, its corresponding dimensions are a 100 mm × 100 mm × 100 mm cube. To emulate an unbounded domain, non-reflecting (NR) boundary conditions were imposed on the air domain on all sides except the bottom surface and the symmetry boundaries. The entire model was enclosed by an air domain, and TNT was positioned a certain distance in front of the cavity protection structure. To reduce the consumption of computational resources, the air domain size is adjusted based on the TNT equivalent and the standoff distance to eliminate ineffective air elements. As shown in Figure 3, a 1/4 model has been built, setting symmetric boundaries along the xz plane and yz plane.

In the simulation, the ALE algorithm was used for air and TNT, and the LAGRANGE algorithm was used for UHMWPE cavity protection panel and the RC wall. Fluid–structure interaction is built between ALE materials and LAGRANGE materials, to realize pressure propagation in the medium, where the energy is transferred from the explosive to the air through the co-node method. Air and TNT are modeled by ALE elements, which can effectively simulate the propagation of the shockwave. The protective plate and the reinforced concrete wall are simulated using Lagrangian elements, which accurately reflect the dynamic response of the structure. In the LS-DYNA, the card of “CONSTRAINED_LAGRANGE_IN_SOLID” provides a coupling mechanism to model the fluid–structure interaction. Fluid–structure interaction calculation adopts the method of the penalty function. The penalty-function method permits the flow field to move around the structure and prevents fluid–structure interpenetration by applying an interfacial penalty force.

An eroding contact algorithm was applied between the protective plate and the concrete wall to simulate potential material failure and penetration. Furthermore, the simulation controls the sand clock and adjusts other necessary parameters to ensure accuracy. The time step factor is set to 0.4, based on the characteristics of the explosion shock problem, to maintain the stability of the computation process.

2.2. Material Model

2.2.1. Material Model of Concrete

In the study of concrete explosion and other high-strain-rate problems, commonly used models include the JHC model [36], RHT model, BRITTLE model [37], and KC model [38], among others. In this study, MAT_JOHNSON_HOLMQUIST_CONCRETE (MAT 111) in LS-DYNA is selected to model the concrete material. The model is widely applied in the study of concrete’s resistance to explosive impact due to its excellent response to large deformations and high strain rates, making it particularly suitable for fluid–structure coupling problems [39]. The equivalent stress of this model, after considering the strain rate, can be expressed as:

$${\sigma }^{\ast }=\left[A\left(1-D\right)+B{P}^{\ast N}\right]\left(1+C\ln {\epsilon }^{\ast }\right)$$

(1)

where ${\sigma }^{\ast }$ is the ratio of the actual equivalent stress to the static yield strength; $P^{\ast }$ is the dimensionless pressure; ${\epsilon }^{\ast }$ is the dimensionless strain rate; A, B, C, and N are material constants; and D (0 ≤ D ≤ 1) is the damage factor, which is obtained by accumulating the equivalent plastic strain and plastic volumetric strain. The parameters of the concrete are presented in

Table 1. Concrete model parameters of C40 (JHC).

ρ (kg/m3)	G (GPa)	A	B	C	N	FC (MPa)
2400	13.5	0.79	1.86	0.006	0.84	30
T (MPa)	EPS0	EFMIN	SFMAX	PC (MPa)	UC	UL
2.0	1 × 10−6	0.01	7	1.3	0.001	0.16
PL (MPa)	D1	D2	K1	K2	K3
800	0.04	1.0	0.85	−1.71	2.08

.

2.2.2. Material Model of Rebar

The MAT_PLASTIC_KINEMATIC model is used for the reinforcement bar. This model is suitable for describing isotropic hardening and rate-dependent kinematic hardening under strain rate effects. The strain rate is typically described using the Cowper–Symonds model. A strain rate-dependent function is added to influence the yield strength. The stress–strain relationship is:

$${\sigma }_y=\left[1+{\left({\displaystyle \frac{\stackrel{·}{\epsilon }}{C}}\right)}^{{\displaystyle \frac{1}{P}}}\right]{\sigma }_0$$

(2)

where P and C are the parameters related to the strain rate. The parameters of the rebar are presented in

Table 2. Rebar material parameters.

ρ (kg/m3)	E (GPa)	PR	SIGY (MPa)	ETAN (MPa)	BETA	SRC	SRP	FS	VP
7.8	212	0.3	235	80,000	0	40	5	0.18	0

.

2.2.3. Material Model of UHMWPE

MAT_COMPOSITE_DAMAGE (MAT 22) in LS-DYNA is applied for the UHMWPE cavity protection panel. This model captures the overall mechanical properties of the fiber material by considering the Young’s modulus of both the fiber and matrix materials in different directions, which makes it suitable for describing the failure characteristics of various types of fiber composite laminates under high-speed impact and high strain rate conditions. The parameters of UHMWPE are presented in

Table 3. Material parameters of UHMWPE.

ρ (kg/m3)	EA (GPa)	EB (GPa)	EC (GPa)	PRBA	PRCA	PRCB
1006	40.6	40.6	2.6	0.008	0.044	0.044
GAB (GPa)	GBC (GPa)	GCA (GPa)	KFAIL (GPa)	AOPT	MACF	SC (GPa)
1.75	1.6	1.6	2.2	0	3	0.5
XT (GPa)	YT (GPa)	YC (GPa)	ALPH	SN (GPa)	SYZ (GPa)	SZX (GPa)
3.6	3.6	3.0	0.5	0.9	0.9	0.9

.

2.2.4. Material Model for Air and Explosive

In this study, air is considered an ideal gas. Material model MAT 9 (MAT NULL) is adopted to model the air, with EOS_LINEAR_POLYNOMIAL state equation. The linear polynomial equation of state is:

$$P=C_0+C_1\mu +C_2{\mu }^2+C_3{\mu }_3+\left(C_4+C_5\mu +C_6{\mu }^2\right)E$$

(3)

$$\mu ={\displaystyle \frac{1}{V}}-1$$

(4)

where $P$ is the pressure, $E$ is the internal energy per unit volume, $V$ is the relative volume, and the initial value is $V_0=1.0$. For the ideal gas, the coefficients are set as $C_0=C_1=C_2=C_3=C_6=0, C_4=C_5=0.4$, and the air parameters are shown in

Table 4. Air state equation parameters.

ρ (kg/m3)	C0 (GPa)	C1	C2	C3
1.225	−0.0001	0	0	0
C4	C5	C6	V	E0(KJ/m3)
0.4	0.4	0	1	253

.

The explosive material is modeled using MAT_HIGH_EXPLOSIVE_BURN, along with the JWL equation of state. The JWL equation of state is:

$$P=A\left(1-{\displaystyle \frac{\omega }{R_{1}V}}\right)e^{-R_{1}V}+B\left(1-{\displaystyle \frac{\omega }{R_{2}V}}\right)e^{-R_{2}V}+{\displaystyle \frac{\omega E}{V}}$$

(5)

where $P$ is the detonation pressure; V is the relative volume; E is the internal energy per unit volume; and $\omega$, $A$, $B$, $R_1$, and $R_2$ are the material-related parameters, with their specific meanings and values given in

Table 5. Explosive material parameter meanings and values.

ρ (kg/m3)	D (m/s)	P (Pa)	A (Pa)	B (Pa)
1730	7900	37	374	3.23
R1	R2	$\mathit{\omega }$	E0 (J/m3)	V0
4.19	0.95	0.3	1	9

.

2.3. Numerical Methods and Material Model Verification

In this paper, a step-by-step validation method is used to verify the accuracy of the numerical simulation system. Due to the relatively limited research on UHMWPE protection structures for RC walls under explosive loading, this paper sequentially validated the explosion simulation method, concrete constitutive model, and UHMWPE material model. Initially, the accuracy of the explosion simulation method and the concrete constitutive model is validated based on the concrete explosion tests in reference [40]. Then, the applicability of the material model of UHMWPE under high-strain-rate impact conditions is verified using the fragment penetration tests of UHMWPE fiber laminates from reference [41]. This validation strategy provided a reliable foundation for the subsequent simulation studies of UHMWPE protection structures for RC walls under explosive loading.

2.3.1. Numerical Methods and Concrete Model Validation

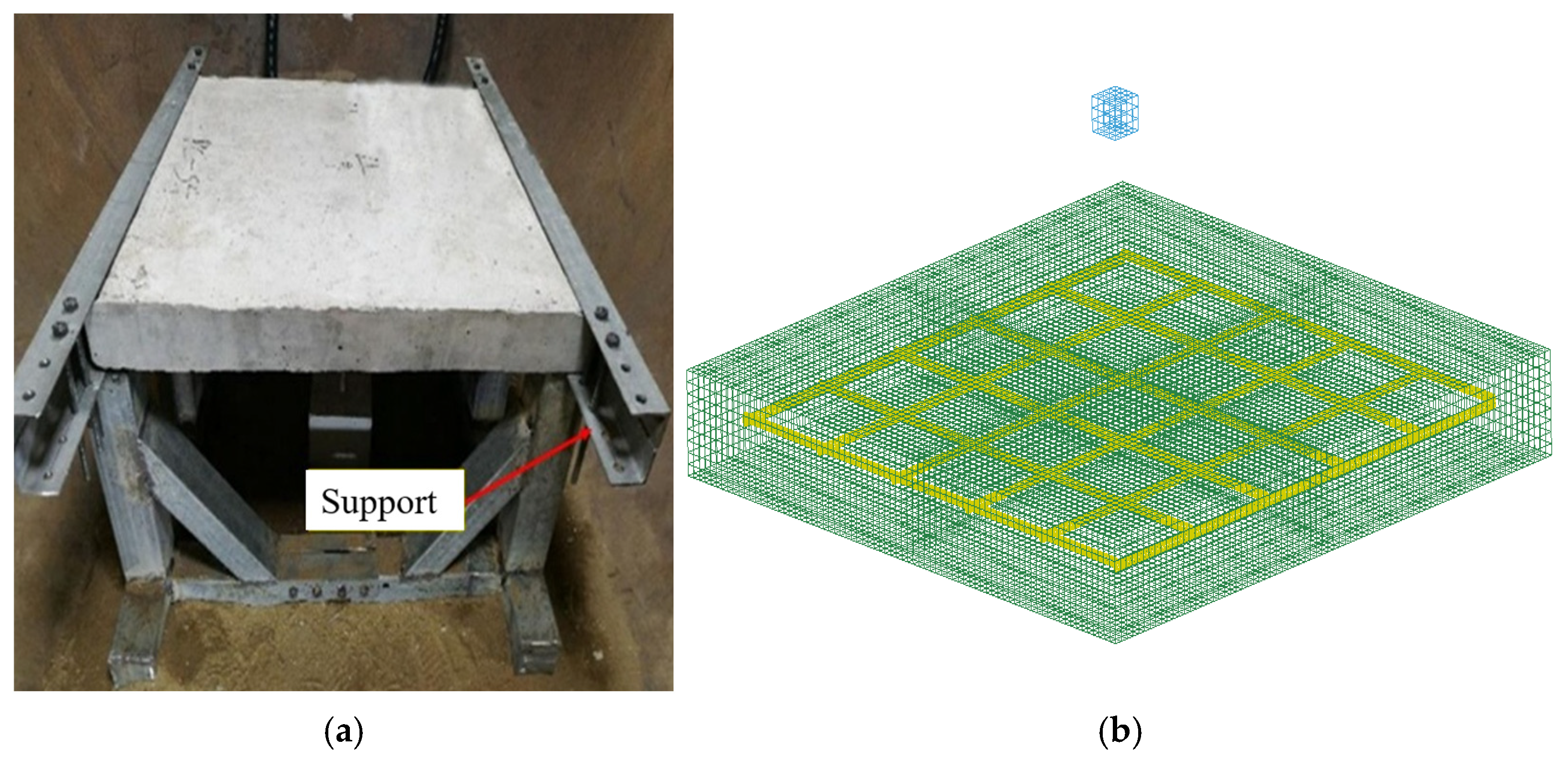
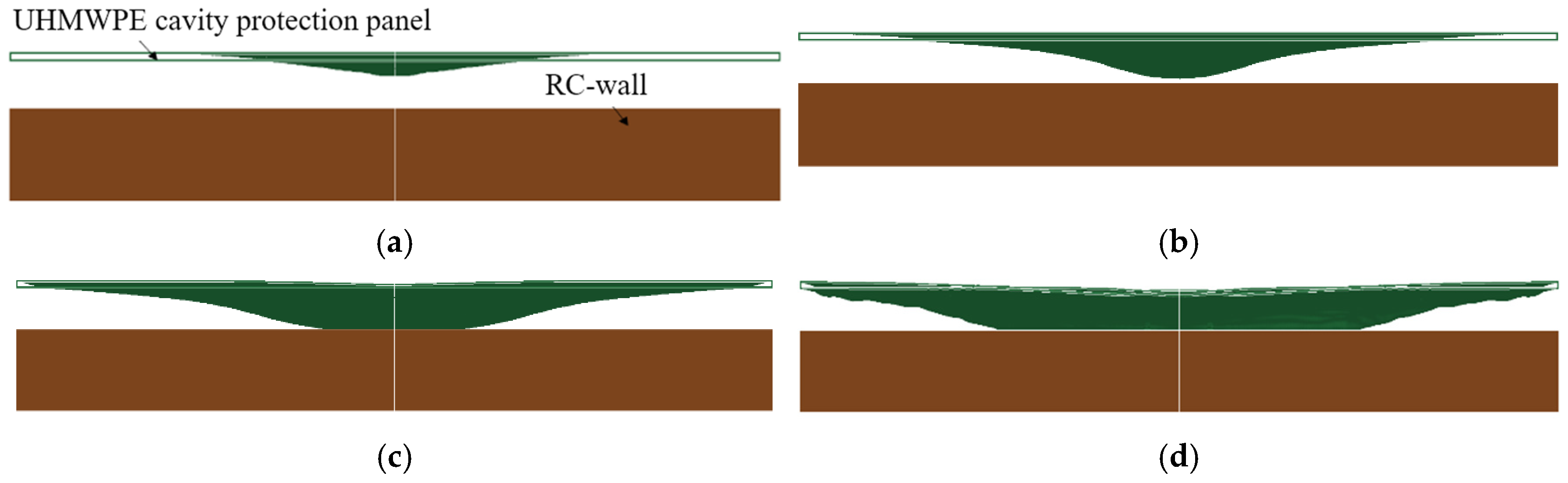
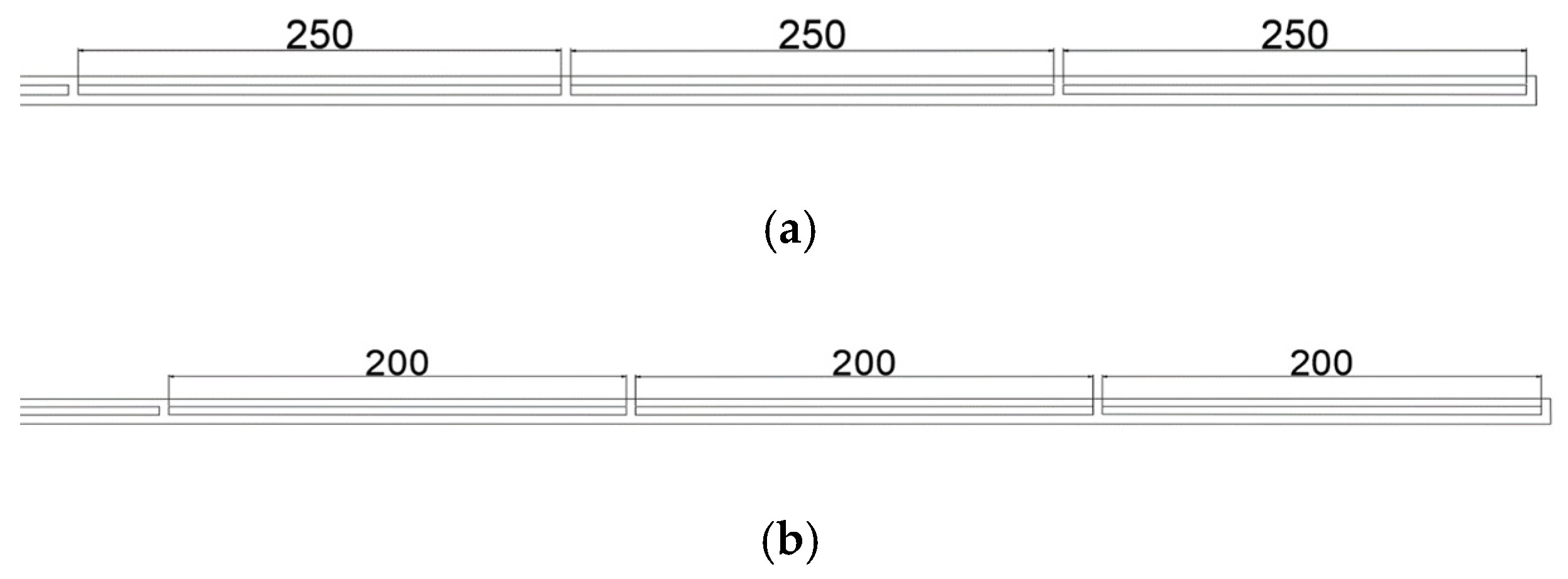
The finite-element model (FEM) and simulation method were validated for accuracy and reliability through the explosion test of the RC panel [40], as illustrated in Figure 4. The RC panel in the experiment has geometric dimensions of 750 mm × 850 mm × 90 mm (length × width × thickness). 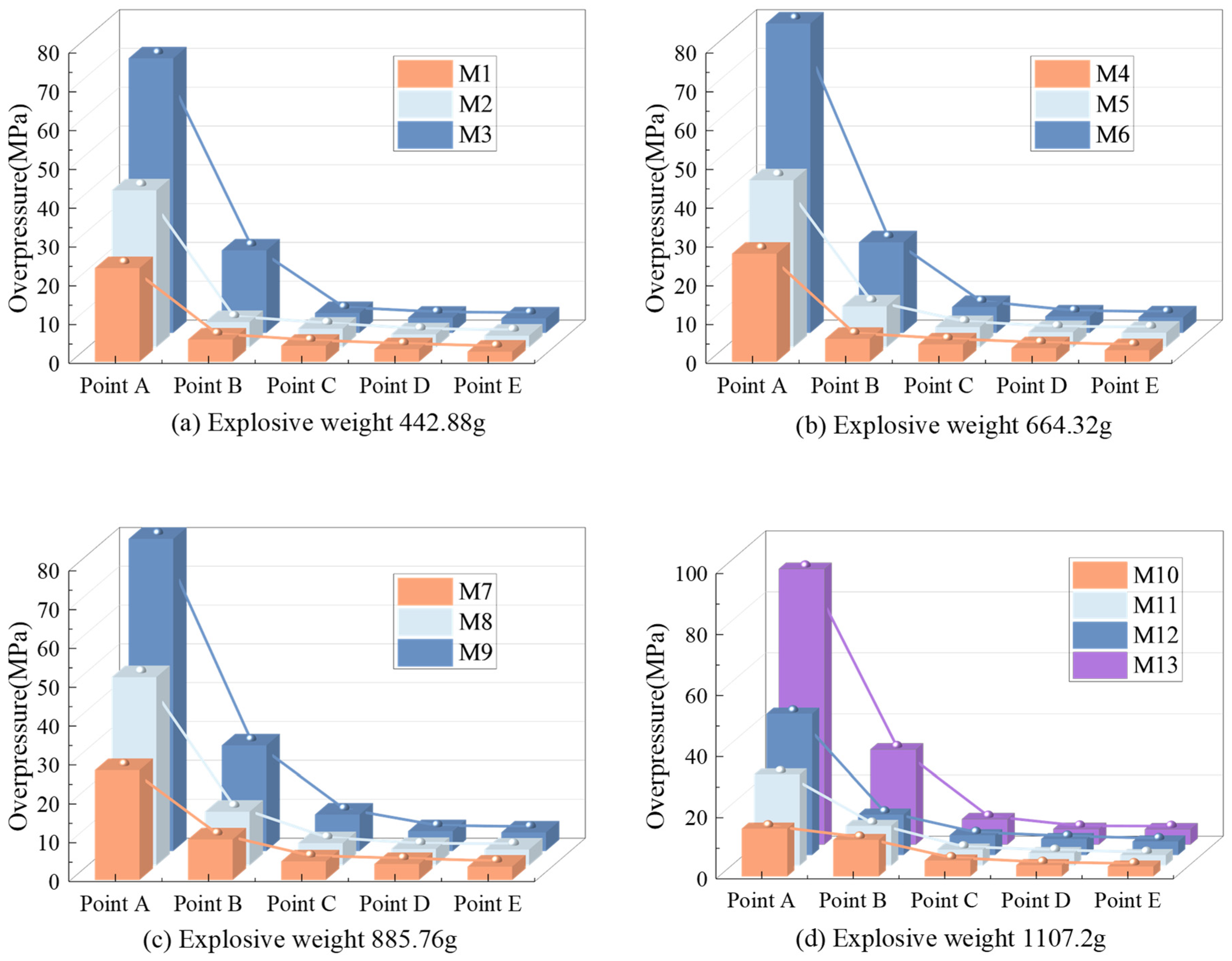Steel braces are used to support the RC panel, with the two opposite edges of the RC specimen fixed by supports and the other two edges left free, as shown in Figure 3. The reinforcement bars in the RC panel have a diameter of 8 mm, with a spacing of 130 mm between each bar. In addition, the specimens are placed in a sealed explosion chamber for testing, with the explosive suspended directly above the center of the panel. Each specimen undergoes 10 explosion tests. In this paper, three typical tests are selected for analysis, and the explosive charge and detonation point distances of TNT are shown in

Table 6. Experimental conditions.

Test	Explosive Charge (g)	Standoff Distance (mm)	Central Deflection (mm)
			Experiment Results	Numerical Results	Absolute Error
B2	20	200	2.62	2.9	0.28
B4	40	200	3.78	2.95	0.79
B8	30	100	2.78	5.1	1.32

. The yield strength and elastic modulus of the reinforcement are 235 MPa and 200 GPa, respectively. The compressive strength and elastic modulus of the concrete are 30 MPa, 4.3 MPa, and 30 GPa, respectively. A finite-element model consistent with the experimental conditions is established based on the simulation methods and modeling strategies discussed earlier, as shown in Figure 4b.

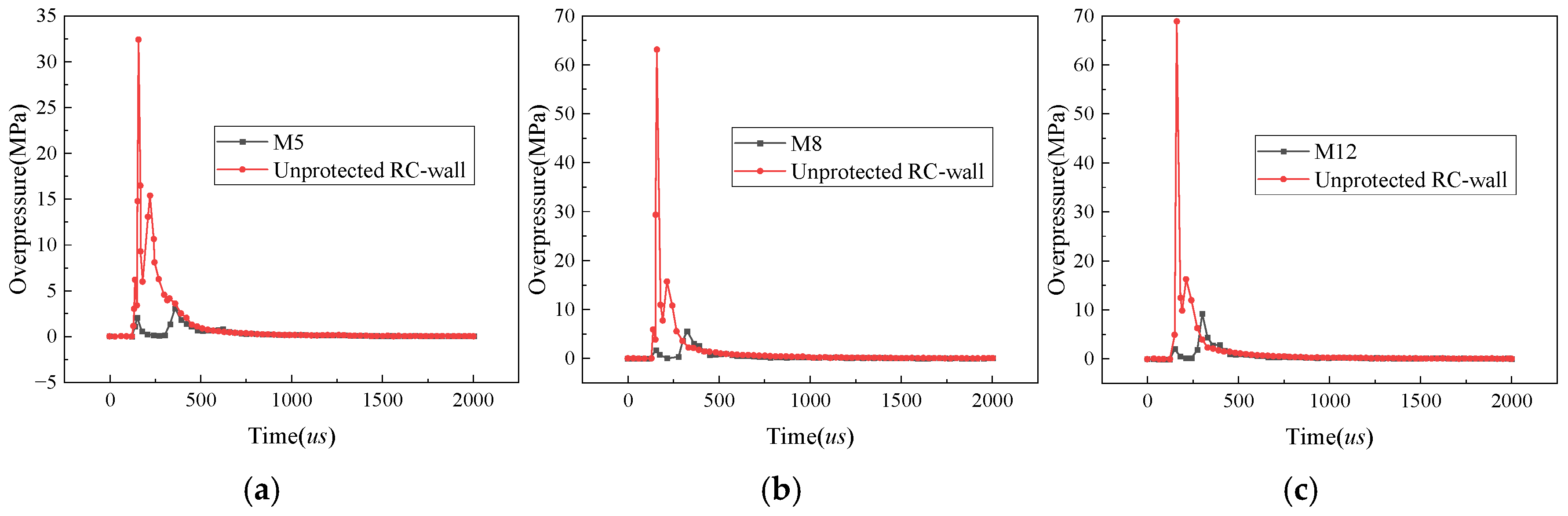
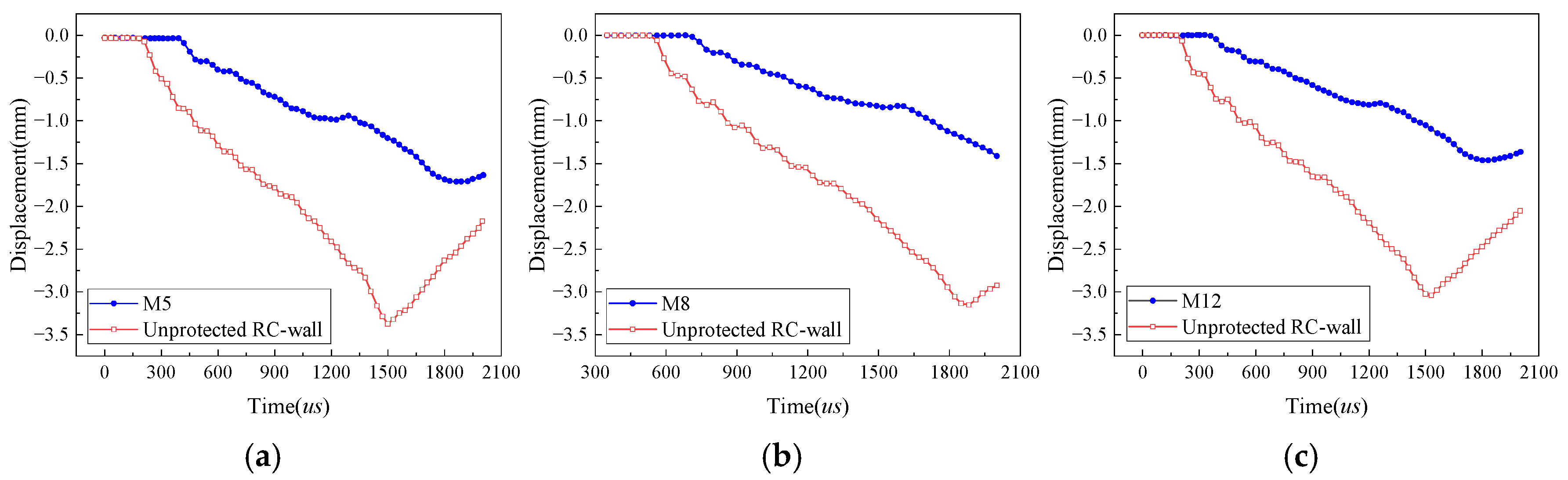
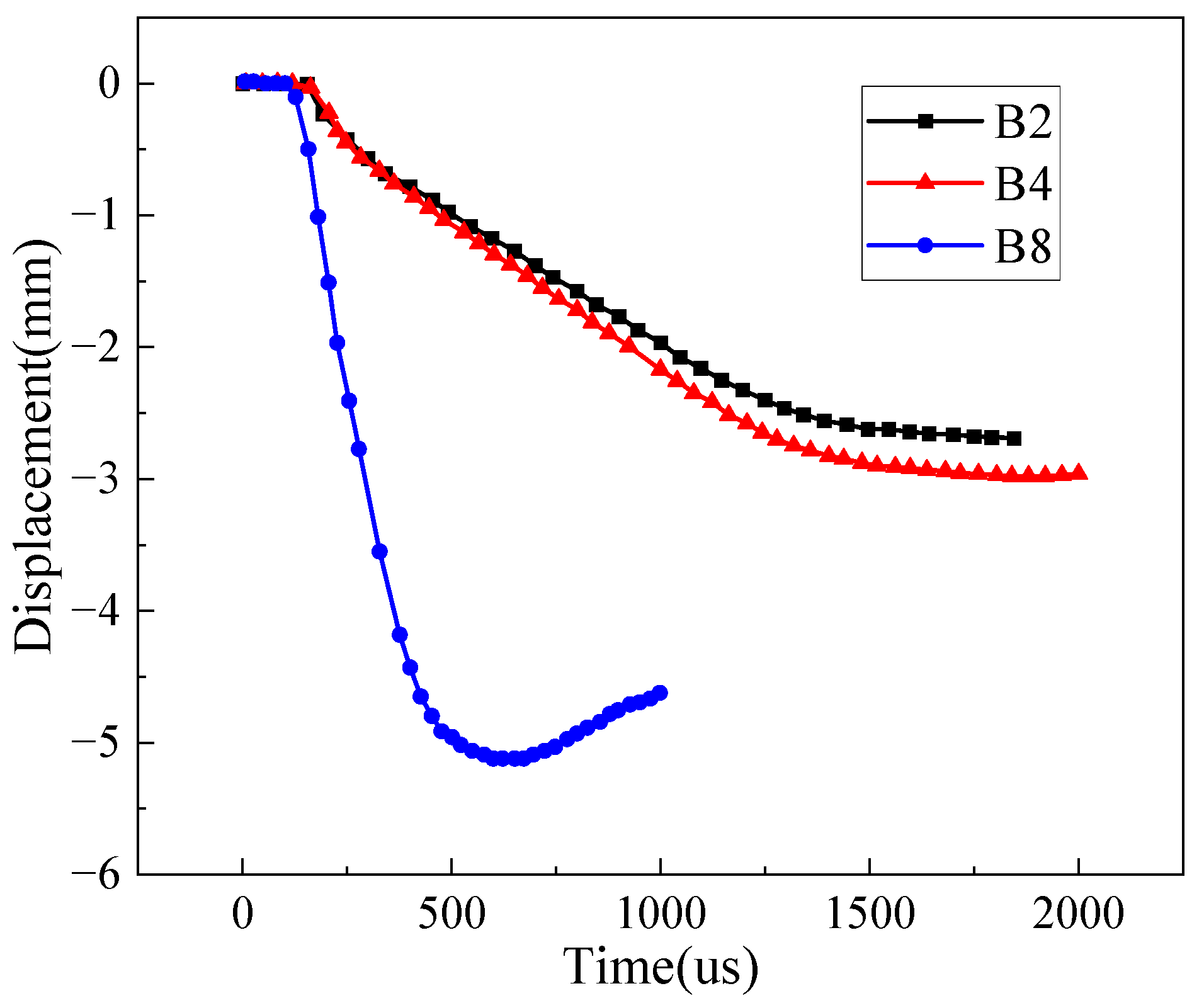
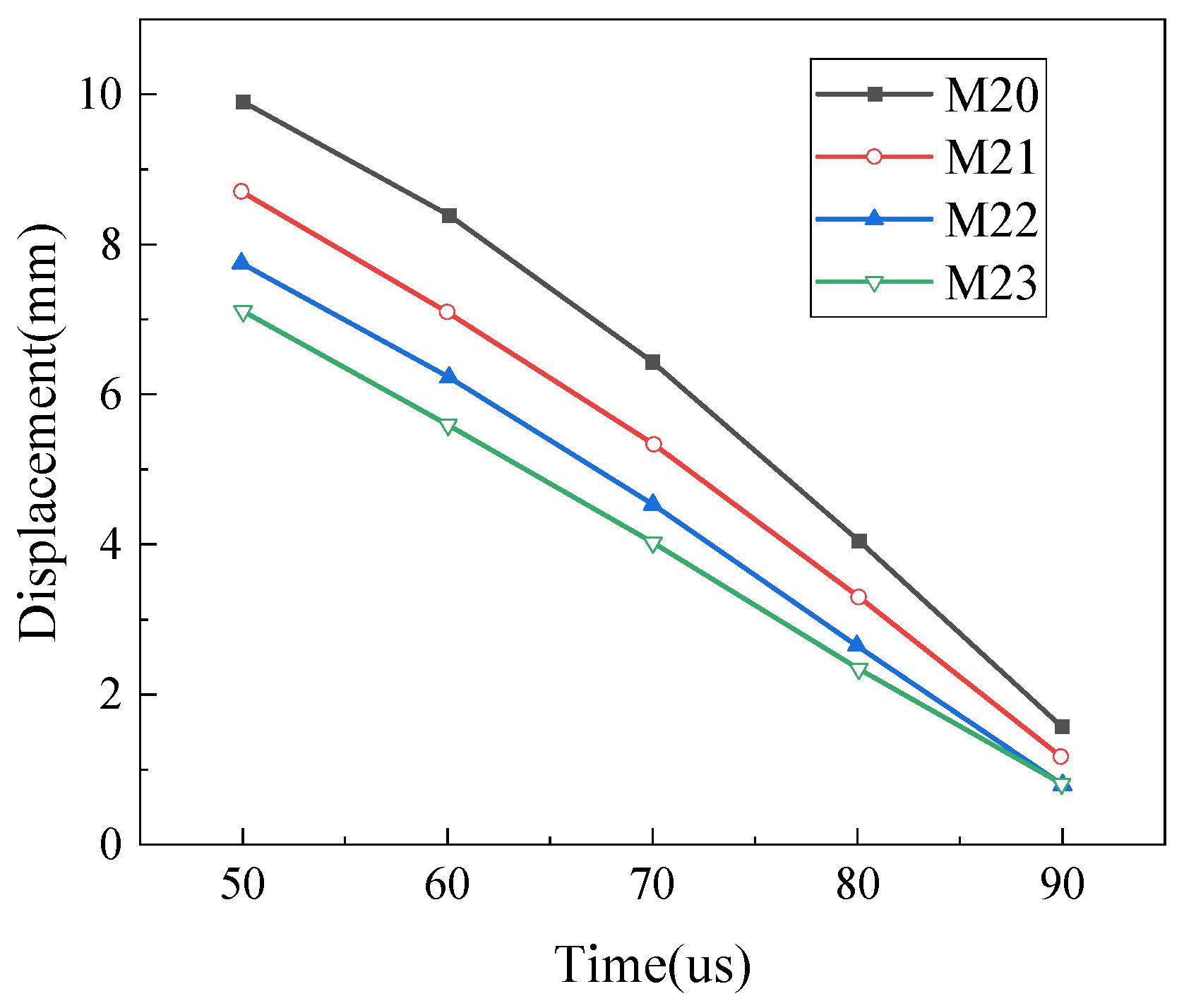
In this paper, the dynamic response of the RC panel under three typical operating conditions was numerically simulated and compared with experimental results, and the accuracy and reliability of the model were evaluated. Figure 5 presents the displacement–time history curve at the center of the panel for different conditions. The simulated and experimental values of the maximum displacement under each condition are listed in Table 6. The comparison results indicate that the absolute errors between the simulated and experimental values of the maximum displacement for each condition are kept within a small range, with the maximum error being 1.32 mm, demonstrating good computational precision. Notably, despite the relatively small explosive charge used in the experiment, which caused the displacement response at the center of the panel to be generally lower, the simulation results still demonstrate good consistency with the measured data. This phenomenon suggests that the adopted JHC constitutive model is capable of effectively representing the dynamic response characteristics of concrete under explosive loading. The good agreement between the finite-element simulation results and experimental data also demonstrates the high accuracy and reliability of the finite-element analysis method established in this paper for simulating the explosive response of concrete structures.

2.3.2. UHMWPE Model Validation

This paper conducted numerical simulations of the UHMWPE fiber laminate fragment penetration tests, validating the accuracy of the constitutive model for UHMWPE under high-strain-rate conditions. Multiple ballistic impacts on the UHMWPE fiber laminates are performed using cubic tool steel projectiles (with a side length of 7.5 mm and a weight of 3.3 g) in the experiment. In the simulation, MAT_PLASTIC_KINEMATIC (Mat 3) is selected as the projectile material, and the specific parameters are provided in

Table 7. Bullet material parameters.

$\mathit{\rho }$ (kg/m3)	E (GPa)	$\mathit{\gamma }$	$\mathit{\sigma }$0 (MPa)	$\mathbf{E}\mathit{\tau }$ (MPa)	${\mathit{\epsilon }}_{\mathrm{f}}$ (%)
7800	200	0.3	1900	15,000	2.15

. The specimen consists of a layered protection panel made from ultra-high-molecular-weight polyethylene (UHMWPE) fiber nonwoven fabric, with a single-layer thickness of 0.16 mm, a total thickness of 4.8 mm, comprising 30 layers, and fixed boundary conditions around the edges. In the simulation, the projectile and the target plate were discretized using SOLID164 solid elements, and automatic surface-to-surface contact was defined between them. To improve computational efficiency, a 1/4 finite-element model is established, and symmetric boundary conditions are applied.

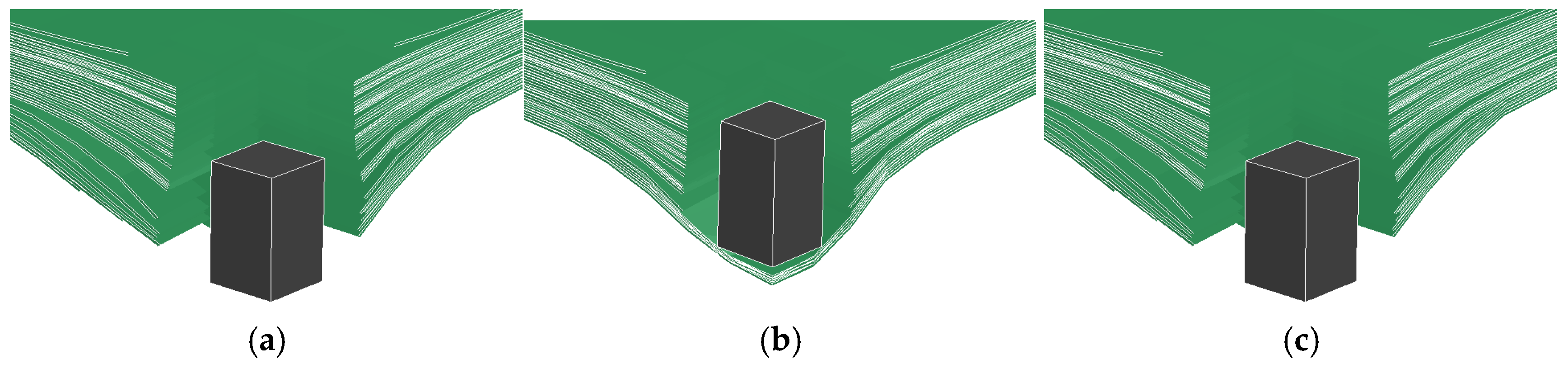
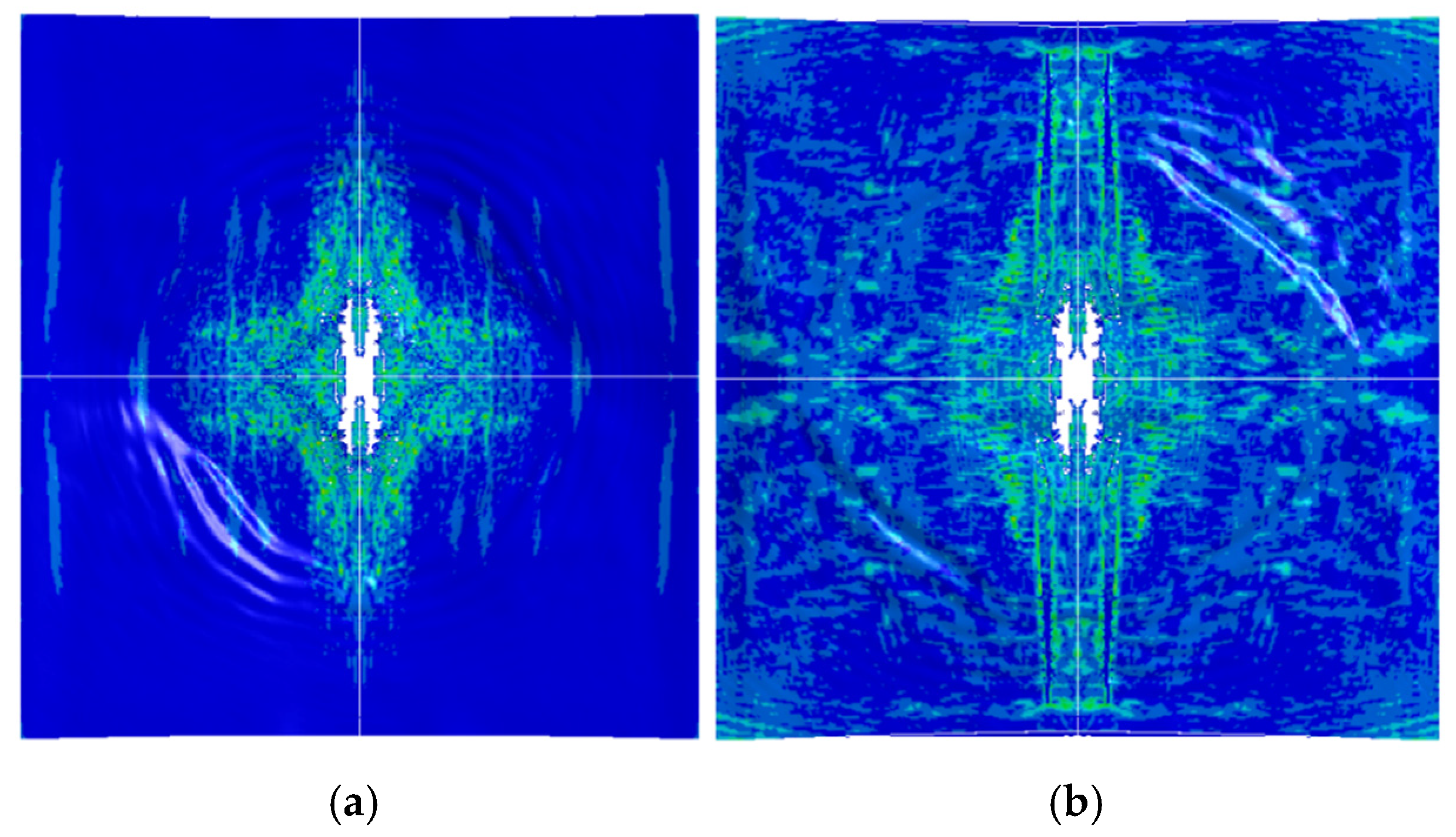
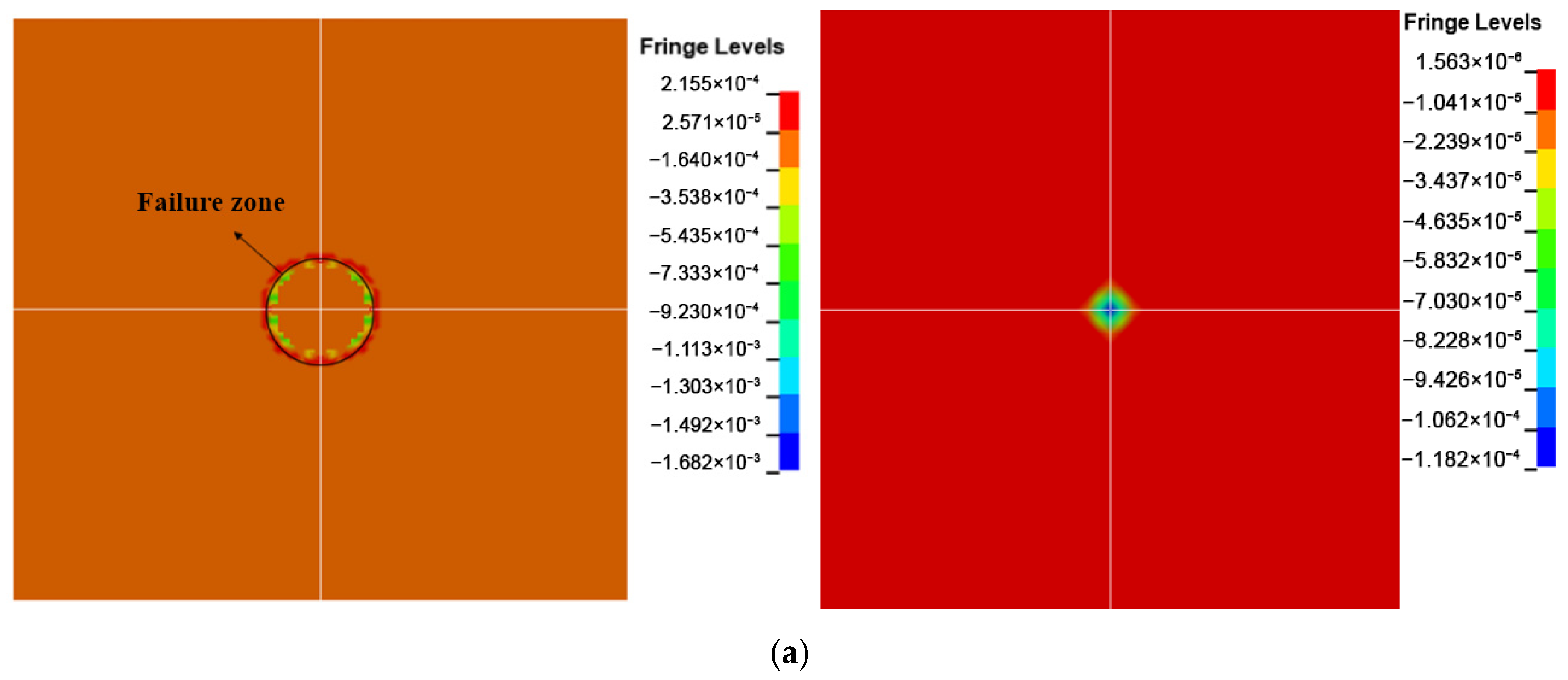
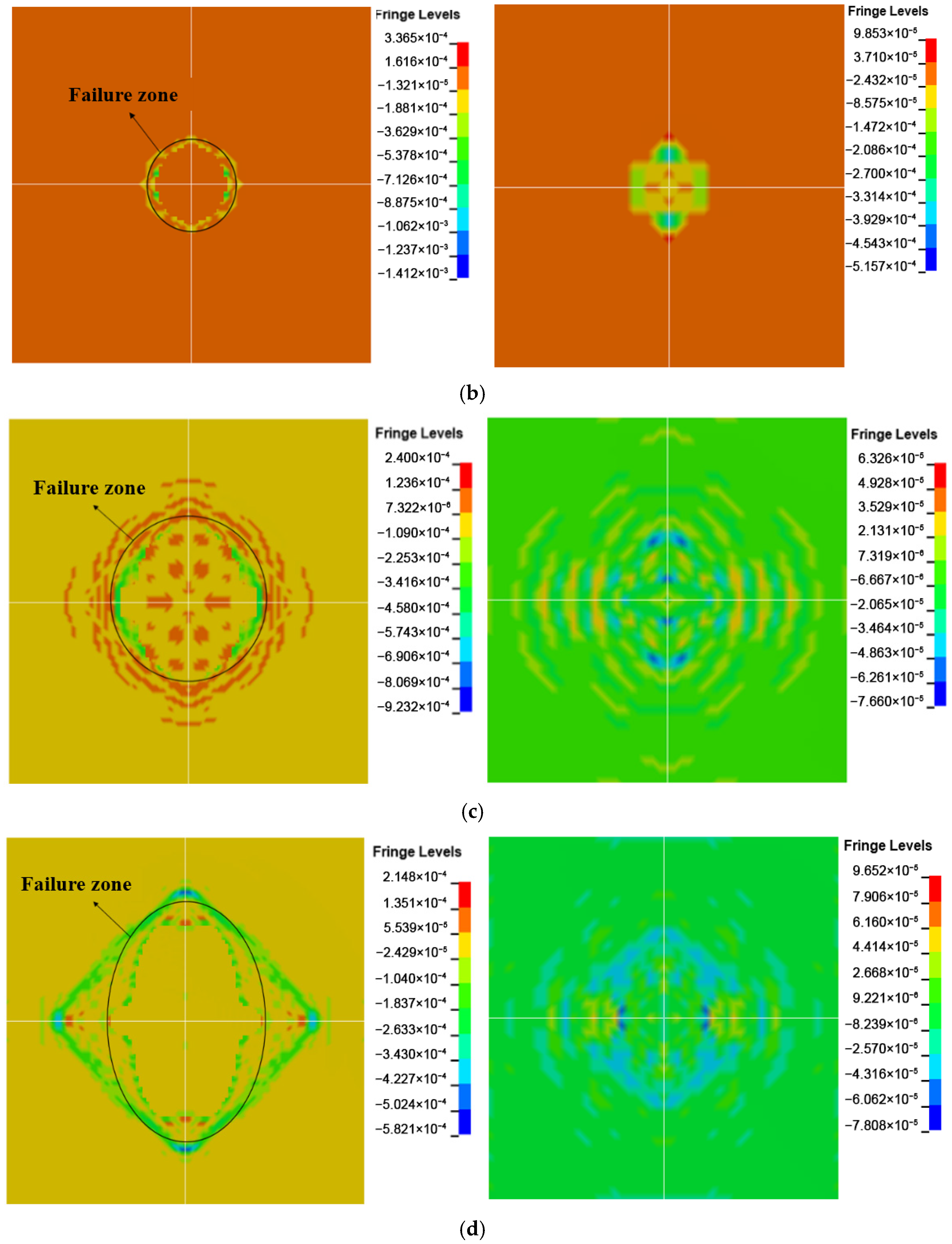
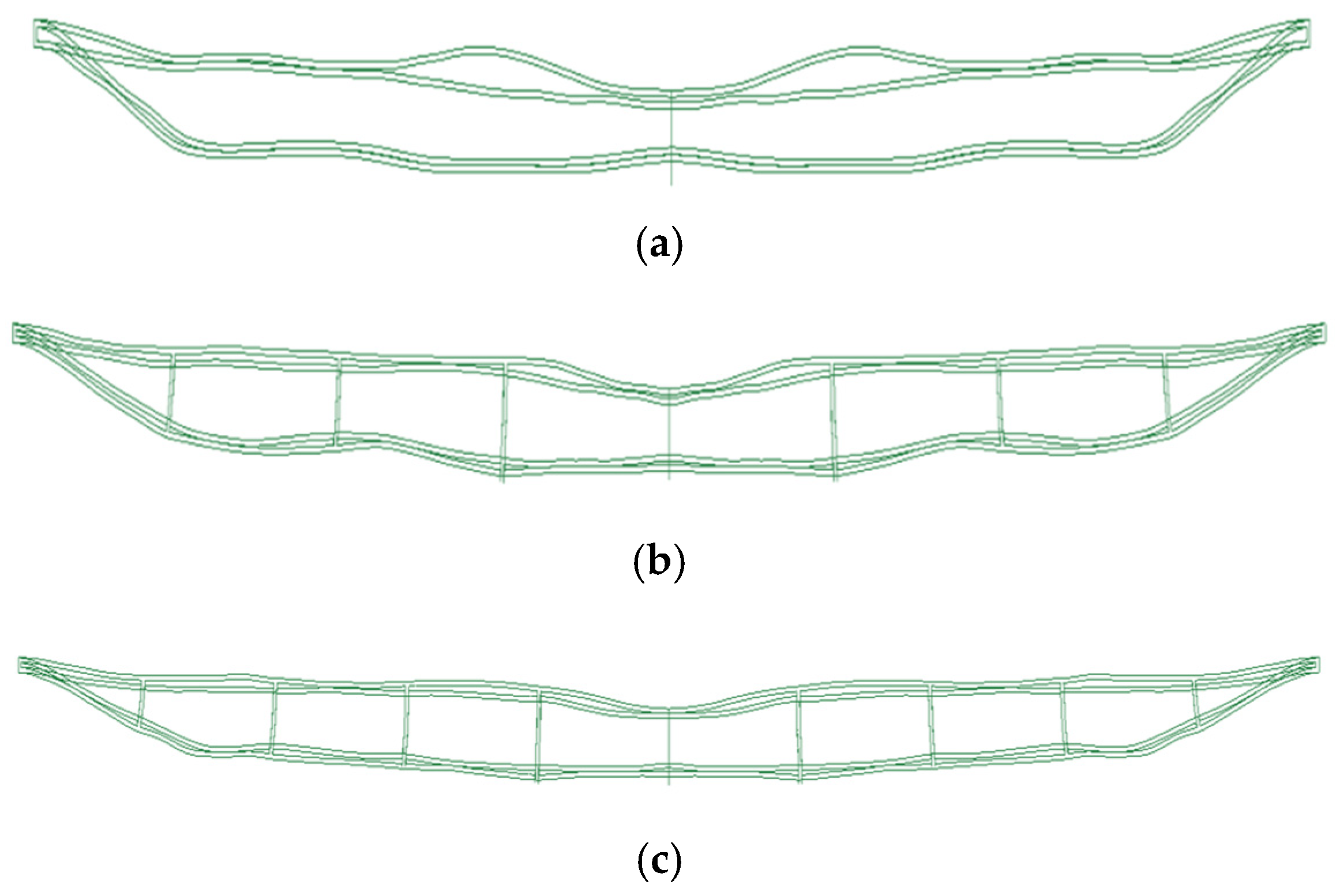
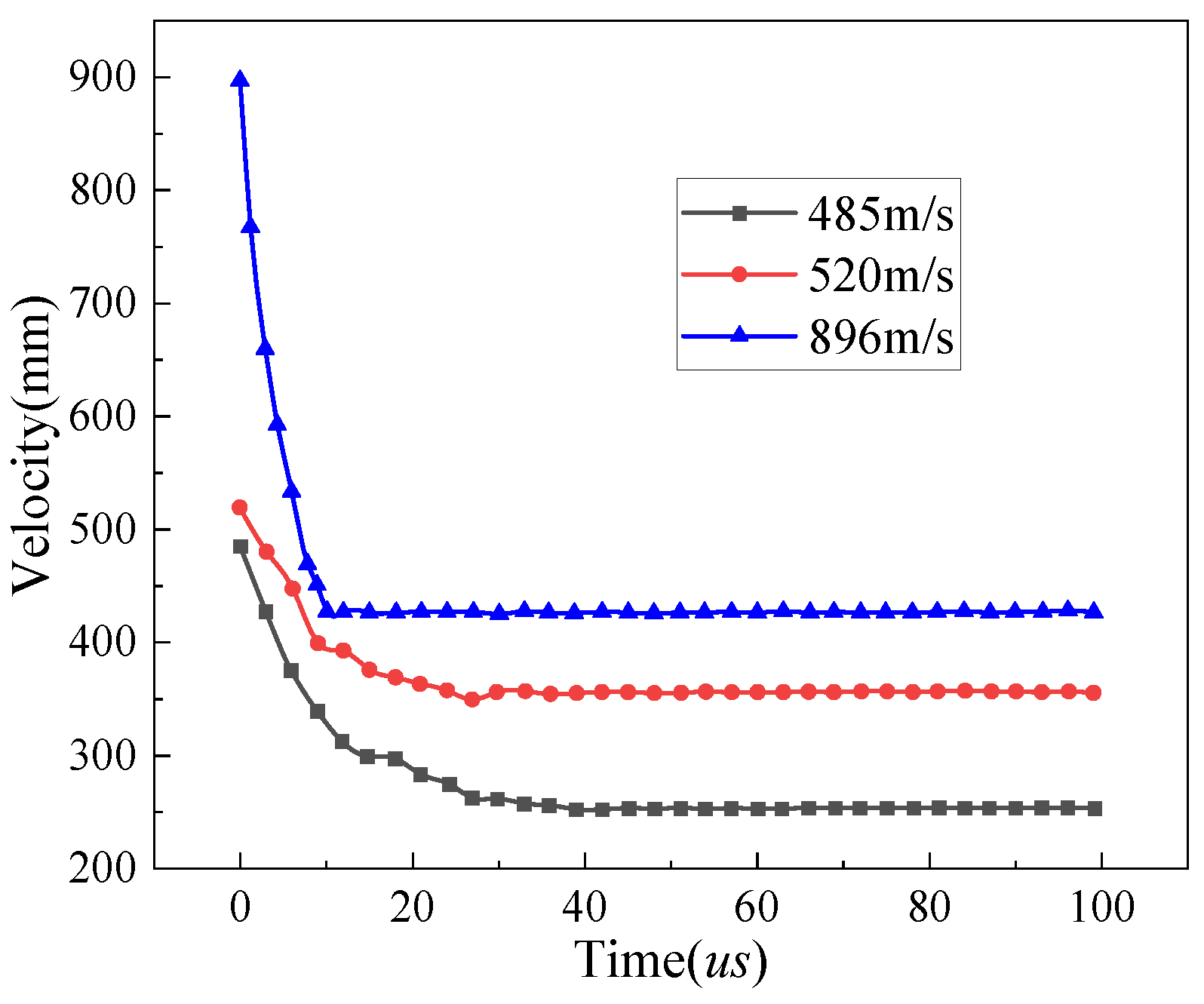
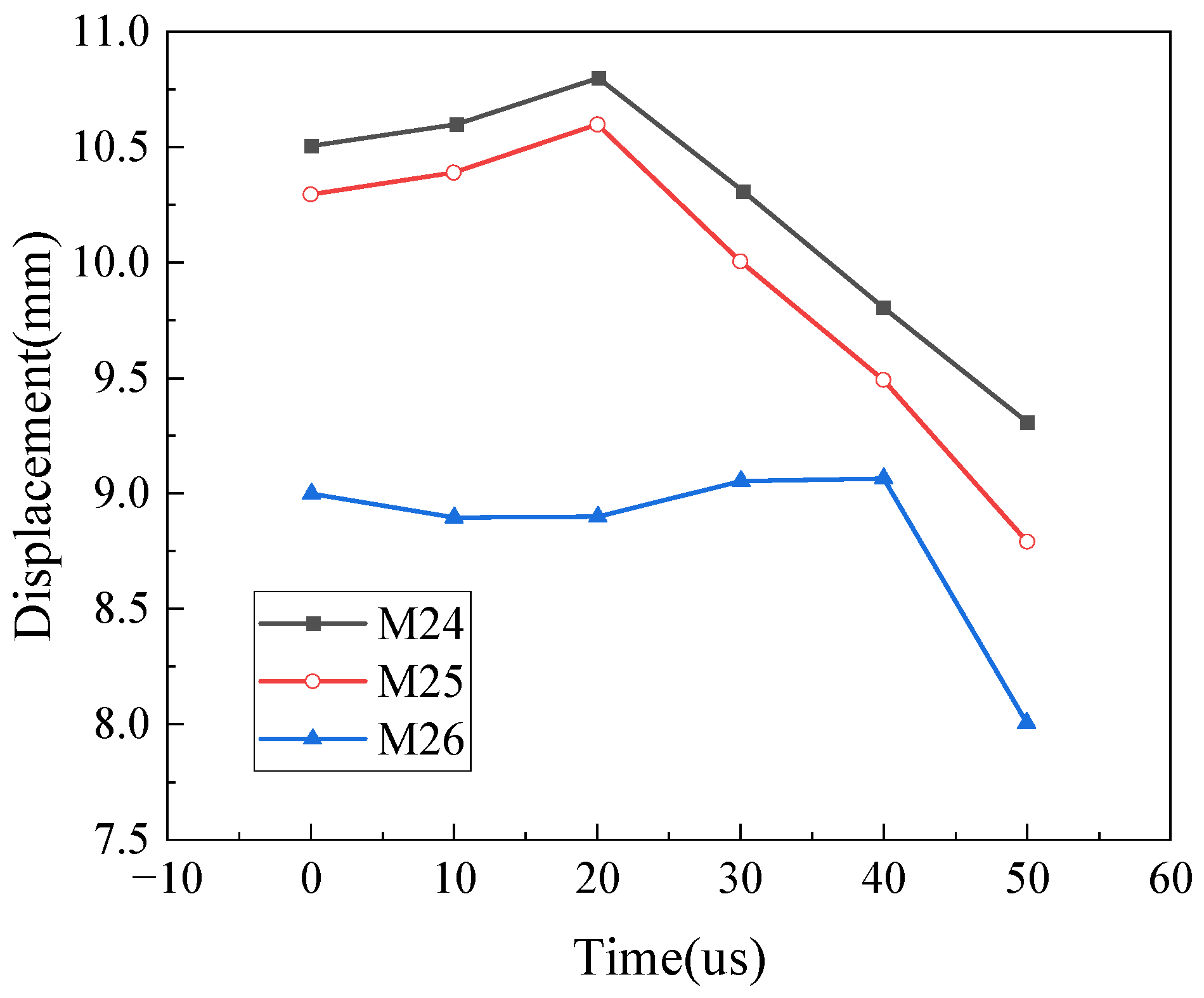
Figure 6 illustrates the damage patterns of the target plate at different times under an initial velocity of 520 m/s, providing a clear view of the penetration process and the dynamic response of the laminate. Figure 7 shows the velocity–time history curves of the projectile under different initial velocity conditions, and the comparison of the exit velocity with experimental data is provided in

Table 8. Comparison of experimental and simulation results.

Total Layer of the Panel	30
Impact Number	First Impact	Second Impact	Third Impact
Penetration layers	30	30	30
Incident velocity (m/s)	896.27	520.62	485.86
Experimental value of exit velocity (m/s)	475.55	334.38	233.13
Numerical simulation value of exit velocity (m/s)	426.63	355.77	252.98
relative error (%)	10.3	6.4	8.5

. The results show that the experimental values of the projectile’s residual velocity match well with the simulated values, with a maximum relative error of 10.3%. It is shown that the MAT_COMPOSITE_DAMAGE model effectively captures the dynamic response behavior of the UHMWPE protection plate under high-strain-rate impacts, offering strong engineering prediction accuracy.

3. Numerical Simulation Results and Discussion

In this study, validated numerical methods and models were utilized to investigate the dynamic response of the UHMWPE cavity protection panel under blast loading and its protective performance for concrete walls.

3.1. Dynamic Response of UHMWPE Cavity Protection Panel

The explosive charge quantity is a critical factor in determining the degree of structural damage. To thoroughly analyze the dynamic response of the UHMWPE cavity protection panel, this study carried out multiple explosive scenarios, including five different explosive charges (442.88 g, 664.32 g, 885.76 g, 1107.2 g, and 1328.6 g) and a standoff distance ranging from 300 mm to 600 mm. The detailed parameters for all conditions are provided in

Table 9. Relevant working conditions of safety protection distance analysis.

Test	Explosive Charge (g)	Standoff Distance (mm)
M1	442.88	500
M2	442.88	400
M3	442.88	300
M4	664.32	500
M5	664.32	400
M6	664.32	300
M7	885.76	500
M8	885.76	400
M9	885.76	300
M10	1107.2	600
M11	1107.2	500
M12	1107.2	400
M13	1107.2	300
M14	1328.6	500
M15	1328.6	400

. The dimension parameters of the UHMWPE protection panel and the RC slab are consistent with those described in Section 2, and their finite-element model structure is shown in Figure 3.

Figure 8 shows the typical shock wave propagation process under explosive condition M10 (with an explosive charge of 1107.2 g and a standoff distance of 600 mm). The red outer frame in the figure indicates the air domain range, and the frame at the center on the left marks the position of the explosive charge. Upon detonation, a spherical shock wave centered at the initiation point begins to spread outwards in all directions and propagates through the air medium. Because the explosion process occurs in a very short time, the overpressure spherical wave quickly decays and fades away after reaching a certain distance. When the shock wave impacts the surface of the wall, part of the wave is reflected, while the remaining part propagates along the wall surface and creates a vortex phenomenon at the edges. Ultimately, the wave propagates to the non-reflective boundary at the rear of the air domain and dissipates completely. The transient overpressure distribution throughout the air domain is shown in Figure 9.

Figure 10 illustrates the dynamic failure process of the cavity protection panel under explosive condition M4 (with an explosive charge of 664.32 g and a standoff distance of 500 mm). It can be observed that the blast wave first impacts the blast-facing layer of the UHMWPE cavity protection panel. This causes significant bending deformation in this layer, followed by contact between the deformed blast-facing layer and the back blast-side layer. During this process, the central regions of both panels undergo bulging deformation toward the direction of the wall. Under progressive loading, the central region of the blast-facing layer reaches the ultimate load-bearing capacity, undergoes shear failure, and exhibits localized tearing, as shown in Figure 11a. Subsequently, the back-facing layer of the cavity panel continues to deform and contacts the rear wall. Influenced by the shock wave propagation within the confined cavity volume, the contact area progressively expands; however, the overpressure transmitted to the back blast-side layer becomes significantly attenuated. Under the continued overpressure, the core region of the back blast-side layer ultimately reaches the limit state, undergoing shear failure and developing a tearing rupture as captured in Figure 11b. As the shock wave propagates further through the cavity structure, the progressive failure of the composite panel continues to develop. Then a gradually expanding cross-shaped tear is formed in the central region. Additionally, intense vibrations occur in the regions near the edges of both the blast-facing and back-facing surfaces, with more pronounced wave-like bulging observed on the back-facing surface (as shown in Figure 12). This phenomenon is intrinsically governed by two interplaying mechanisms within the cavity: multiple shock wave reflections and abrupt wave impedance discontinuities. Superimposed reflections induce oscillatory interactions, generating high-eigenmode dynamic vibrations within the access portal zones. Simultaneously, drastic impedance transitions drive mechanical energy redistribution, channeling substantial energy flux toward the blast-rear surfaces and initiating distinct early-phase bulge deformation.

Figure 13 shows different locations on the slab for pressure prediction. Figure 14 presents the overpressure distribution within the cavity domain under different explosive conditions. The peak overpressure undergoes rapid decay with increasing stand-off distance from the blast-facing surface center. At a stand-off distance of 500 mm (point E), the peak overpressure in all blast scenarios had universally dropped below the 10 MPa threshold, signifying substantially diminished shock wave energy.

Table 10. Average attenuation rate of overpressure in cavity under different equivalents.

Explosive weight (g)	442.88	664.32	885.76	1107.2	1328.6
Average reduction rate (%)	92	91.6	90	88	89

shows the average attenuation rate of overpressure in the cavity under different equivalents. Notably, the pressure attenuation ratios within the cavity domain consistently surpassed 88% across all blast conditions with varying TNT equivalence magnitudes. This represents a marked improvement over the 40.99% attenuation reported for fence walls in Ref. [27]. This significant performance enhancement is primarily attributed to the unique protective mechanism of the UHMWPE cavity panel. The cavity configuration promotes repeated shock-wave reflections and reverberation within a confined volume, where impedance discontinuities induce significant energy dissipation. Subsequently, the UHMWPE panel actively absorbs the residual shock energy, which has been preliminarily attenuated by the cavity, through extensive plastic deformation. Overall, by effectively modulating shock wave propagation and energy transfer, the UHMWPE cavity panel achieves a significant reduction in peak pressure and a prolongation of pressure propagation, thereby demonstrating outstanding pressure relief and cushioning performance.

3.2. Protective Performance Analysis of UHMWPE Cavity Protection Panels

To investigate the effectiveness of the UHMWPE cavity protection panels on reducing the blast loads, numerical simulations are also carried out with the same blast scenarios with a RC wall of the same dimensions and without UHMWPE cavity protection panels. The dynamic damage process of the blast-facing surface under explosive condition M12 (with an explosive equivalent of 664.32 g and a standoff distance of 400 mm) is compared in Figure 15. Numerical results indicate that under unprotected scenarios, the shockwave arrived at the blast-incident surface around 200 μs, with the central zone reaching ultimate strain and undergoing material failure. With sustained blast loading, the damaged zone continuously expanded, and the final failure area accounted for about 25% of the total blast-facing surface. In contrast, under the condition with the UHMWPE cavity protection panel, the wall exhibits distinctly different response characteristics at the same time. A significant reduction in the peak stress of the blast-facing surface is observed, along with a noticeable slowdown in the expansion of the high-stress region. Under the mid-to-late stage of loading, the stress distribution becomes more uniform, and no local element failures similar to those in the unprotected case occur. The results demonstrate the effectiveness of the UHMWPE cavity protection panel in mitigating shock wave effects and delaying wall failure.

Figure 16 delineates the overpressure time–history profiles on blast-facing air elements at a standoff distance of 400 mm under three explosive charges (664.32 g, 885.76 g, and 1107.2 g TNT-equivalent). Peak overpressure comparisons for additional charge mass configurations are consolidated in

Table 11. Attenuation rate of overpressure on the front surface of the wall.

Test	M2	M5	M8	M12	M15
Peak overpressure without protection (MPa)	28.6	32.4	63.2	68.8	70.6
Peak overpressure under protection (MPa)	3.00	4.28	5.65	8.97	9.69
Reduction rate (%)	90.0	86.8	91.1	87.0	86.3

. As shown in Figure 16, the peak overpressure on the blast-facing surface of the wall is significantly reduced under the effect of the UHMWPE cavity protection panel. In addition, the UHMWPE cavity protection panel contributes to postponing the arrival of the peak overpressure to a certain degree. At a standoff distance of 400 mm, with the increase in charge weight, the unprotected wall exhibits sharp peaks followed by rapid decay under blast loading, showing typical brittle impact characteristics. As shown in Table 11, after installing the UHMWPE cavity protection panel, the peak overpressure on the blast-facing surface is significantly reduced to about 3–10 MPa, with an attenuation generally exceeding 85% and reaching up to 91.1%, while the arrival time of the peak is also delayed. The overpressure attenuation achieved in this study is markedly superior to the 57% reduction in fence blast walls [26]. The results indicate that the protection panel can effectively attenuate the shock wave intensity and provide a cushioning effect, thereby significantly enhancing the blast resistance of the wall.

In addition, the displacement response of the wall is markedly mitigated once the protection structure is applied. Figure 17 shows the displacement–time history curves of the central point behind the wall under different charge conditions. The results demonstrate a remarkable reduction in displacement: from 3.0 mm for the unprotected wall to merely 1.2 mm after installing the protective panel, representing a 60% decrease. Concurrently, the flattened slope of the displacement-time curve reveals a significantly slower development rate. This further confirms the effectiveness of the UHMWPE protection panel in buffering impact loads and dissipating explosive energy.

4. Blast Performance Optimization of UHMWPE Cavity Protection Panels

4.1. Effect of Thickness Optimization

To investigate the effect of UHMWPE protection panel thickness on the blast-resistant performance of the structure, numerical simulations were conducted on four protection panels with thicknesses of 6–9 mm and an air cavity thickness of 10 mm; the specific conditions are listed in

Table 12. Working condition of UHMWPE cavity Protection Panel.

Test	Explosive Charge (g)	Standoff Distance (mm)	Dimensions of Shield and Cavity
M20	885.76	500	Thickness of face plate: 6 mm; Thickness of cavity: 10 mm
M21	885.76	500	Thickness of face plate: 7 mm; Thickness of cavity: 10 mm
M22	885.76	500	Thickness of face plate: 8 mm; Thickness of cavity: 10 mm
M23	885.76	500	Thickness of face plate: 9 mm; Thickness of cavity: 10 mm

. During the explosion, the explosive releases a large amount of thermal energy and generates a strong shock wave, and the energy exchange induced by shock wave propagation causes changes in the internal energy of the surrounding structures. Therefore, the variation in wall internal energy can serve as an indicator to assess the energy absorption capability of the protection structure. The internal energy variation curves of the wall under various conditions are shown in Figure 18. From the figure, it is evident that the M20 condition exhibits the highest internal energy curve, demonstrating that the wall absorbs the maximum internal energy in this scenario. Compared with the M20 condition, the wall under other conditions absorbed 19.1% (M21), 29.6% (M22), and 46.1% (M23) less internal energy, respectively. With the increase in thickness of the UHMWPE protection panel layers, the panel’s energy absorption ability improves markedly, effectively reducing the damage inflicted by the shock wave on the wall behind.

Deformation displacements at different positions of the protection plate are shown in Figure 19. The deformation in all working conditions shows a typical pattern, with the central area exhibiting larger deformation and the edges showing smaller deformation. Compared to the M20 condition, the maximum and minimum displacements of the protection panel in the M23 condition were reduced by 28% and 50%, respectively. Meanwhile, no tearing phenomenon was observed at the constrained boundary of the protection panel during the simulation process, further indicating that the structure possesses good toughness properties. The UHMWPE fiber matrix demonstrates excellent anti-damage capability when subjected to large deformation impacts, indicating that such fiber-reinforced composite cavity protection panels not only possess outstanding blast resistance but also have the potential to serve as lightweight and efficient protection materials.

4.2. Effect of Stiffener Optimization

It can be concluded from the previous analysis of the cavity panel’s protective performance that the UHMWPE cavity structure exhibits excellent shock wave attenuation properties, providing effective protection for the wall. Meanwhile, appropriately increasing the panel thickness can significantly enhance its energy absorption capacity. However, under the action of explosive loads, the protection panel exhibited significant overall deformation, with a noticeable expansion of the tear at the center region. To improve the above response characteristics, this paper introduces a rib structure into the cavity panel for reinforcement optimization and conducts a comparative analysis based on a small equivalent explosive load scenario. The partial structure of the optimized protection panel is illustrated in Figure 20, with the corresponding operational parameters provided in

Table 13. Structural optimization conditions.

Test	Stiffener	Standoff Distance (mm)	Explosive Charge (g)
M24	NONE	600	220
M25	Spacing of 250 mm	600	220
M26	Spacing of 200 mm	600	220

.

Figure 21 shows the deformation profiles of the protection panel in three different cases. It can be observed that, from the cavity panel (M24) to the 250 mm stiffened panel (M25) and the 200 mm stiffened panel (M26), the overall deflection of the protection panels decreases sequentially, and their contours gradually become flatter. The unstiffened cavity panel exhibited pronounced local bulging or indentation in the central region, whereas this deformation was effectively restrained after stiffeners were added. With the stiffener spacing reduced to 200 mm, the central region was nearly flattened. In addition, the structural deformation mode changed from a single-span concentrated form to a multi-span dispersed form, with the deformation distributed more evenly. The stiffeners and panels acted together, enhancing the equivalent flexural stiffness of the structure and reducing its effective span length. The grid effect effectively suppressed local buckling and the propagation of out-of-plane waves, with the effect being particularly significant in the central region. Figure 22 reveals that incorporating stiffening ribs can effectively reduce the maximum displacement at the center and lead to a more uniform deformation distribution. Hence, the addition of stiffening ribs within the cavity protection panel structure provides an effective optimization strategy to control deformation and improve energy absorption performance.

5. Conclusions

This study proposes a cavity-protection panel fabricated from UHMWPE for application to RC walls. The LS-DYNA finite-element program, combined with a validated numerical simulation method, was employed to examine the protective behavior of UHMWPE cavity protection panels on reinforced concrete walls subjected to blast loading, and an optimization analysis of the UHMWPE cavity protection panel was subsequently conducted. The principal findings are summarized as follows:

(1)

The protective mechanism of the UHMWPE cavity protection panel is governed by the synergistic interaction between cavity-induced wave modulation and controlled plastic dissipation in the material. By inducing multiple reflections and scattering of stress waves at interfacial impedance discontinuities, the cavity geometry disperses and attenuates blast-wave energy during multipath propagation, yielding an average overpressure attenuation exceeding 88%. Subsequently, the shock wave energy is further dissipated through extensive plastic deformation and localized tearing of the UHMWPE panel. Moreover, the pronounced vibrational response at the periphery of both the blast-facing and rear surfaces further promotes impact-energy dissipation.

(2)

The UHMWPE cavity protective panel can significantly improve the blast resistance of RC walls. Under the protection of the UHMWPE cavity panel, the RC wall achieves a peak overpressure attenuation rate of 86.3% to 91.1% on the blast-facing surface, approximately 60% reduction in peak displacement at the center point, along with effective suppression of the initiation and propagation of localized damage.

(3)

Structural optimization analysis reveals that increasing the thickness of the front and back layers of the protective panel effectively suppresses global deformation and significantly enhances the energy dissipation capacity of the structure. The incorporation of evenly spaced ribs within the cavity effectively restrains the local buckling of the protection panel and the transmission of out-of-plane waves, while improving the global energy dissipation behavior of the protection system. Adjusting panel thickness and incorporating rib design are effective structural optimization approaches to enhance the energy absorption performance of UHMWPE cavity protection panels.