Seismic Performance Analysis of Hybrid Damped Structures in High-Intensity Seismic Regions

Abstract

This study was conducted based on hybrid damping control theory, and an equivalent damping ratio calculation method was proposed. Additionally, a response calculation method for the elastoplastic stage of the hybrid control system was developed. Furthermore, a cooperative working mechanism between viscous dampers and metal composite dampers was introduced. A time–history analysis was employed to verify the system’s effectiveness in optimizing the multi-dimensional seismic performance of frame structures. Using actual engineering as the research background, an elastoplastic analysis of the hybrid control system was conducted. The analysis results show that the first three natural periods of vibration were shortened by 6.1% (in the X direction), 5.9% (in the Y direction), and 21.0% (torsion), effectively enhancing the overall stiffness of the structure. Under seismic action, the inter-story displacement decreased by 37.1% to 0.166 m in the X direction and by 48.3% to 0.080 m in the Y direction; the base shear forces were reduced by 58.8% (in the X direction) and 41.7% (in the Y direction). Regarding damage control, the number of plastic hinges was significantly reduced, and they appeared only on the most unfavorable floors; the axial compressive stress peaks in the frame columns were strictly controlled below 0.65 fc, and the inter-story displacement angles (<1/50) met the standards of GB50011-2010 for key protection structures. The hybrid system demonstrated multi-dimensional synergistic effects, whereby the viscous dampers primarily controlled the acceleration responses in the X direction, while the metal composite dampers dominated energy dissipation in Y displacement. The difference in seismic reduction efficiency between the two main axes was less than 11%, and a 21% improvement in the torsional period was achieved simultaneously.

1. Introduction

For decades, seismic engineering focused on enhancing the seismic performance of building structures, particularly those in high-intensity seismic zones and those that are strategically important. Traditional seismic design methods have become inadequate to meet modern engineering demands, while hybrid control technology has emerged as a research focus in structural vibration control due to its superior energy dissipation capacity and adaptability. Since the 20th century, frequent destructive earthquakes worldwide have provided valuable empirical data for seismic research. The 2008 Wenchuan earthquake (M8.0) caused widespread building collapse. Post-earthquake investigations revealed that reinforced concrete frames designed with the conventional “strong column–weak beam” principle, although avoiding complete collapse, predominantly exhibited “column hinge mechanisms” instead of the intended “beam hinge mechanisms”, resulting in difficult post-earthquake repairs [1]. The 2011 Tohoku earthquake (M9.0) further prompted a critical reassessment of structural performance beyond design basis seismic motions. Notably, some buildings employing passive control technology demonstrated remarkable vibration mitigation under long-period ground motions. These seismic events catalyzed a paradigm shift in earthquake-resistant design philosophy from “collapse prevention” to “functional recovery”. China’s Code for Seismic Design of Buildings (GB50011-2010) [2] explicitly mandates that critical facilities (e.g., hospitals and emergency command centers) maintain either “immediate occupancy” or “rapid repairability” performance levels under rare earthquakes. However, conventional ductility design or localized strengthening measures alone have proven insufficient to achieve these objectives [3,4]. Consequently, structural vibration control technologies, particularly hybrid control strategies, have become promising solutions.

The “hybrid mass damping system” proposed by researchers has been successfully implemented in practical engineering applications, achieving over 40% reduction in structural acceleration responses under both strong winds and seismic excitations [5]. Scholars developed a “force–displacement hybrid control method” specifically for large-stiffness multi-degree-of-freedom structures. Through the synchronized operation of shaking tables and hydraulic actuators, they resolved the long-standing challenge of stiffness simulation inaccuracy in conventional pseudo-dynamic testing. This methodology was validated through reinforced concrete core tube experiments, demonstrating less than 5% error and establishing a novel analytical approach for evaluating complex hybrid systems [6]. Researchers also engineered various damping devices [7,8] and optimized dynamic damping systems, significantly enhancing control precision and robustness [9,10]. These systems underwent rigorous performance testing and validation in real-world applications. Through equivalent linearization methods, optimal high damping ratios were achieved [11,12], effectively decoupling the system’s internal mass from damping layer interactions [13]. The rotational damping system implemented in structural designs demonstrated superior performance metrics (including 99.5% energy efficiency and dynamic behavior indicators, such as the peak rate and energy loss ratio) compared to those of existing technologies [14]. Smart damping devices [15] successfully realized solid-state reverse conversion characteristics and time–frequency balance. The FCM (friction control mechanism) exhibited exceptional performance in mitigating static jitter, periodic disturbances, and self-centering intensity attenuation, accomplishing high-strength objectives with compact dimensions [16,17]. These advancements collectively propelled the engineering application of hybrid control technologies. The hybrid passive control method of the Combined Viscous-Stiffness Damper System (CVSDS) explored time-frequency characteristics in the frequency domain through wavelet transform (WT) to achieve optimal vibration damping effects [18,19]. Based on the principle of multi-body kinematics and through the simplified elastoplastic analysis method, the implementation strategy for earthquake repair was redefined [20,21,22].

In summary, researchers have conducted both experimental and theoretical investigations on the vibration control of non-proportionally damped structures. However, relatively limited studies have been devoted to hybrid control strategies for strategically important structures in high-intensity seismic zones with cold climates. In this study, comparative analyses between uncontrolled structures and non-proportionally damped structures are conducted. A computational method for equivalent damping ratios is proposed, and the modal characteristics, structural responses, and damage patterns of both uncontrolled and energy-dissipated structures are investigated under rare earthquake events. The findings provide valuable references for structural control applications in high-intensity seismic regions.

2. Coupled Analysis of Equivalent Damping and Dynamic Response for Time-Varying Hybrid Control Systems

Prior to the establishment of the theoretical framework for the hybrid control system incorporating viscous and magnetorheological (MR) dampers, it was considered essential that an intrinsic connection be established between the mathematical treatment methods and practical engineering problems. In this study, the governing equations for structures, which accounted for large deformation effects in the elastoplastic stage, were systematically derived. Furthermore, the control differential equations for the structural system were constructed. This provided a quantitative analysis tool for the collaborative working mechanism of the hybrid control system. Consequently, a solid theoretical foundation was laid for the optimal configuration of intelligent dampers and the design of control strategies, thereby ensuring the safety and reliability of complex engineering structures under extreme loads.

For an N-degree-of-freedom shear-type structural system, the equations of motion are established as follows:

$$M\stackrel{..}{x}(t)+C\stackrel{.}{x}(t)+Kx(t)=-ML{\ddot{x}}_g(t)+U(t)$$

(1)

The nonlinear damping force is expanded to the third order:

$$F_{FD}^{\alpha }=c_1^{\alpha }\Delta {\dot{x}}^{\alpha }+c_2^{\alpha }\left|\Delta {\dot{x}}^{\alpha }\right|\Delta {\dot{x}}^{\alpha }+c_3^{\alpha }{(\Delta {\dot{x}}^{\alpha })}^3$$

(2)

The state space enhanced representation is introduced:

$$\left\{\begin{array}{l}{F}_{MRD}^{\beta }=c_0^{\beta }\Delta {\dot{x}}^{\beta }+k_0^{\beta }\Delta x^{\beta }+{\alpha }^{\beta }{z}^{\beta }+f^{\beta }(\Delta {\dot{x}}^{\beta })\hfill \\ {\dot{z}}^{\beta }=A^{\beta }\Delta {\dot{x}}^{\beta }-{\gamma }^{\beta }\left|\Delta {\dot{x}}^{\beta }\right|z^{\beta }-{\beta }^{\beta }\Delta {\dot{x}}^{\beta }\left|z^{\beta }\right|\hfill \end{array}\right.$$

(3)

The Hamiltonian function is constructed:

$$\mathcal{H}={\displaystyle \frac{1}{2}}{p}^T{M}^{-1}p+{\displaystyle \frac{1}{2}}{x}^{T}Kx$$

(4)

The total energy change rate of the system is

$$\stackrel{.}{\mathcal{H}}=-{\stackrel{.}{x}}^{T}C\stackrel{.}{x}+{\displaystyle \sum _{\alpha }{F}_{FD}^{\alpha }}\Delta {\dot{x}}^{\alpha }+{\displaystyle \sum _{\beta }{F}_{MRD}^{\beta }}\Delta {\dot{x}}^{\beta }-{\stackrel{.}{x}}^{T}ML{\ddot{x}}_g$$

(5)

The frequency response operator is

$$H(\omega )={\left[-{\omega }^{2}M+i\omega \tilde{C}(\omega )+K\right]}^{-1}$$

(6)

The equivalent damping matrix is

$$\tilde{C}(\omega )=C+B_{FD}\left[\begin{array}{c}{c}_1^{\alpha }+(3c_3^{\alpha }-i{c}_2^{\alpha }){\omega }^2\end{array}\right]B_{FD}^T+B_{MR}\left[\begin{array}{c}{c}_0^{\beta }+{\displaystyle \frac{i{\alpha }^{\beta }}{i\omega +{\gamma }^{\beta }}}\end{array}\right]B_{MR}^T$$

(7)

The actual part is

$$\mathrm{Re}[\tilde{C}(\omega )]=C+B_{FD}\left[\begin{array}{c}{c}_1^{\alpha }+3c_3^{\alpha }{\omega }^2\end{array}\right]B_{FD}^T+B_{MR}\left[\begin{array}{c}{c}_0^{\beta }+{\displaystyle \frac{{\alpha }^{\beta }{\gamma }^{\beta }}{{\omega }^2+{({\gamma }^{\beta })}^2}}\end{array}\right]B_{MR}^T$$

(8)

The imaginary part is

$$\mathrm{Im}[\tilde{C}(\omega )]=B_{FD}\left[\begin{array}{c}-c_2^{\alpha }{\omega }^2\end{array}\right]B_{FD}^T+B_{MR}\left[\begin{array}{c}{\displaystyle \frac{{\alpha }^{\beta }\omega }{{\omega }^2+{({\gamma }^{\beta })}^2}}\end{array}\right]B_{MR}^T$$

(9)

where

$$\left\{\begin{array}{ll}C\hfill & :\mathrm{Inherent} \mathrm{structural} \mathrm{damping} \mathrm{matrix}\hfill \\ B_{FD}\hfill & :\mathrm{Location} \mathrm{matrix} \mathrm{for} \mathrm{viscous} \mathrm{dampers}\in {ℝ}^{n\times m}\hfill \\ c_1^{\alpha }\hfill & =c^{\alpha }{v}_0^{\alpha -1}\hspace{1em}(1\mathrm{st}\text{-}\mathrm{order} \mathrm{velocity} \mathrm{coefficient})\hfill \\ c_2^{\alpha }\hfill & =(\alpha -1)c^{\alpha }{v}_0^{\alpha -2}\hspace{1em}(\mathrm{Nonlinear} \mathrm{correction} \mathrm{term})\hfill \\ c_3^{\alpha }\hfill & ={\displaystyle \frac{(\alpha -1)(\alpha -2)}{6}}{c}^{\alpha }{v}_0^{\alpha -3}\hspace{1em}(\mathrm{Higher}\text{-}\mathrm{order} \mathrm{correction})\hfill \\ B_{MR}\hfill & :\mathrm{Location} \mathrm{matrix} \mathrm{for} \mathrm{MR} \mathrm{dampers}\in {ℝ}^{n\times p}\hfill \\ {\displaystyle \frac{i{\alpha }^{\beta }}{i\omega +{\gamma }^{\beta }}}\hfill & :\mathrm{Frequency}\text{-}\mathrm{dependent} \mathrm{hysteretic} \mathrm{damping}\hfill \end{array}\right.$$

(10)

$$\left[M+{\displaystyle \frac{\Delta t}{2}}C+{\displaystyle \frac{\Delta t^2}{6}}K\right]{\stackrel{..}{x}}_{k+1}=R_k-F_{NL}({\stackrel{.}{x}}_{k+1/2})$$

(11)

Response of the hybrid control system in the elastoplastic stage

The deformation gradient tensor is

$$F={\displaystyle \frac{\partial x}{\partial X}}=I+{\nabla }_{0}u$$

(12)

The Green–Lagrange strain tensor is

$$E={\displaystyle \frac{1}{2}}\left(F^{\mathrm{T}}F-I\right)={\nabla }_{0}u+{({\nabla }_{0}u)}^{\mathrm{T}}+{\displaystyle \frac{1}{2}}{({\nabla }_{0}u)}^{\mathrm{T}}{\nabla }_{0}u$$

(13)

The component form of the Green–Lagrange strain tensor is

$$E_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i}{\partial X_j}}+{\displaystyle \frac{\partial u_j}{\partial X_i}}+{\displaystyle \sum _{k=1}^3\frac{\partial u_k}{\partial X_i}}{\displaystyle \frac{\partial u_k}{\partial X_j}}\right)$$

(14)

The nonlinear damping force of viscous dampers is

$$F_{FD}=c_{FD}\cdot \mathrm{sign}(\Delta v)\cdot |\Delta v{|}^{\alpha }$$

(15)

The Jacobian matrix is

$${\displaystyle \frac{\partial F_{FD}}{\partial v}}=\alpha c_{FD}|\Delta v{|}^{\alpha -1}I$$

(16)

The Buc–Wen model of the damper is

$$\left\{\begin{array}{l}{F}_{MRD}=c_{MR}\Delta v+k_{MR}\Delta u+\alpha z\hfill \\ \dot{z}=-\gamma |\Delta v|z|z{|}^{n-1}-\beta \Delta v|z{|}^n+A\Delta v\hfill \end{array}\right.$$

(17)

$$\stackrel{°}{\sigma }=\stackrel{.}{\sigma }-\sigma \Omega +\Omega \sigma ,\hspace{1em}\Omega ={\displaystyle \frac{1}{2}}\left(L-L^T\right)$$

(18)

The elastoplastic tangential modulus is

$${ℂ}^{ep}={ℂ}^e-{\displaystyle \frac{\left({ℂ}^e:\frac{\partial f}{\partial \sigma }\right)\otimes \left(\frac{\partial f}{\partial \sigma }:{ℂ}^e\right)}{H+\frac{\partial f}{\partial \sigma }:{ℂ}^e:\frac{\partial f}{\partial \sigma }}}$$

(19)

where ${ℂ}^{ep}$ represents the elastic stiffness tensor (fourth order), which describes the stress–strain relationship of the material during the elastic stage. $f$ represents the yield function, which is used to determine whether the material has undergone plastic deformation. ${\displaystyle \frac{\partial f}{\partial \sigma }}$ is the yield function corresponding to the gradient of the stress tensor, representing the direction of plastic flow (and also the direction of plastic strain increment in the associated flow rule). $H$ represents the plastic modulus, which describes the hardening/softening behavior.

It is supposed that the material obeys the von Mises yield criterion, as follows:

$$f=\sqrt{{\displaystyle \frac{3}{2}}s:s}-{\sigma }_y=0$$

(20)

where

$$s=\sigma -{\displaystyle \frac{1}{3}}\mathrm{tr}(\sigma )I$$

(21)

Using equal-parameter elements, the interpolation of the displacement field and velocity field is

$$u={\displaystyle \sum _{I=1}^N{N}_I}{u}_I,\hspace{1em}v={\displaystyle \sum _{I=1}^N{N}_I}{v}_I$$

(22)

Within the time step t (n + 1), the K-th iteration is

$$\left[\begin{array}{cc}M& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}\Delta a\\ \Delta \lambda \end{array}\right]+\left[\begin{array}{cc}{K}_T& C_d\\ {\displaystyle \frac{\partial g}{\partial u}}& {\displaystyle \frac{\partial g}{\partial \lambda }}\end{array}\right]\left[\begin{array}{c}\Delta u\\ \Delta \lambda \end{array}\right]=\left[\begin{array}{c}{R}_{ext}-F_{int}-F_d\\ -g\end{array}\right]$$

(23)

where

$$K_T={\displaystyle {\int }_V{B}^T}{ℂ}^{ep}B\mathrm{d}V+{\displaystyle {\int }_V{G}^T}\sigma G\mathrm{d}V+{\displaystyle {\int }_V(B^T\sigma )}\cdot {\displaystyle \frac{\partial B}{\partial u}}\mathrm{d}V$$

(24)

$${\sigma }_{n+1}^{trial}={\sigma }_n+{ℂ}^e:\Delta ϵ$$

(25)

$$f^{trial}=\sqrt{{\displaystyle \frac{3}{2}}{s}^{trial}:s^{trial}}-{\sigma }_y$$

(26)

If

$$f^{trial}\le 0\hspace{1em}{\sigma }_{n+1}={\sigma }^{\mathit{trial}}$$

(27)

otherwise,

$$\Delta \gamma ={\displaystyle \frac{f^{trial}}{3G+H}}\hspace{1em}{\sigma }_{n+1}={\sigma }^{\mathit{trial}}-2G\Delta \gamma$$

(28)

3. Case Analysis

3.1. Project Overview

The site had a seismic fortification intensity of level 8 (0.2 g), with the second seismic grouping of a Category II site and a fundamental period (Tg) of 0.40 s. The seismic design classification was considered a key protection category (Category B). Seismic effects were evaluated based on level 8 (0.2 g), while seismic measures were designed considering level 9. The structural system was a cast-in-place reinforced concrete frame structure with viscous dampers (Figure 1), 32 viscous dampers were installed in the X-axis direction, and 42 metal dampers were installed in the Y-axis direction. The types and parameters of the dampers are shown in

Table 1. Velocity damper parameters.

Damper Design Damping Force (kN)		Design Displacement (mm)		Damping Factor (kN) (s/mm)α	Damping Index
Lower limit	Upper limit	Lower limit	Upper limit
800	1100	25	55	450	0.20

and

Table 2. Metallic damper parameters.

Damper Design Damping Force (kN)	Design Displacement (mm)	Strain Energy (kN·m)
600	30	9

, respectively. The damping ratios of the uncontrolled and damped structures were 5% and 10.50%, respectively. with the frame seismic fortification grade being level 1 and the shear wall seismic fortification grade also being level 1. The structure length was 231.00 m, the width was 109.80 m, the floor height was 5.7/4.5 m, and the overall building height was 19.20 m, as shown in Figure 2. The damper parameters were detailed in Table 1 and Table 2. The above-ground structure had 4 floors (excluding the rooftop equipment room). The concrete materials used were C50, C45, C40, C35, and C30, and the reinforcement steel was HRB400. The frame beam cross-sectional dimensions were 450 mm × 900 mm, 400 mm × 800 mm, and 200 mm × 400 mm. The frame column cross-sectional dimensions were 650 mm × 900 mm, 600 mm × 800 mm, and 400 mm × 400 mm. The slab thicknesses were 120 mm and 100 mm. In the finite element model, geometric nonlinearity and material nonlinearity were considered. Plastic hinge models were used for the frame beams and columns, and a fiber section model was adopted for the shear walls.

In the analysis, a dynamic elastoplastic analysis was conducted using the Perform-3D V10.0 finite element software, with the dampers using connection elements. In the Perform-3D software, dampers are typically simulated using two-node connection elements (Two-Node Link Element) or zero-length elements (Zero-Length Element), the specific choice depending on the connection method and mechanical characteristics requirements of the dampers. In the elastoplastic time-history analysis, the dampers can work collaboratively with the structural framework through these elements to achieve energy dissipation and damping effects.

3.2. Seismic Waves

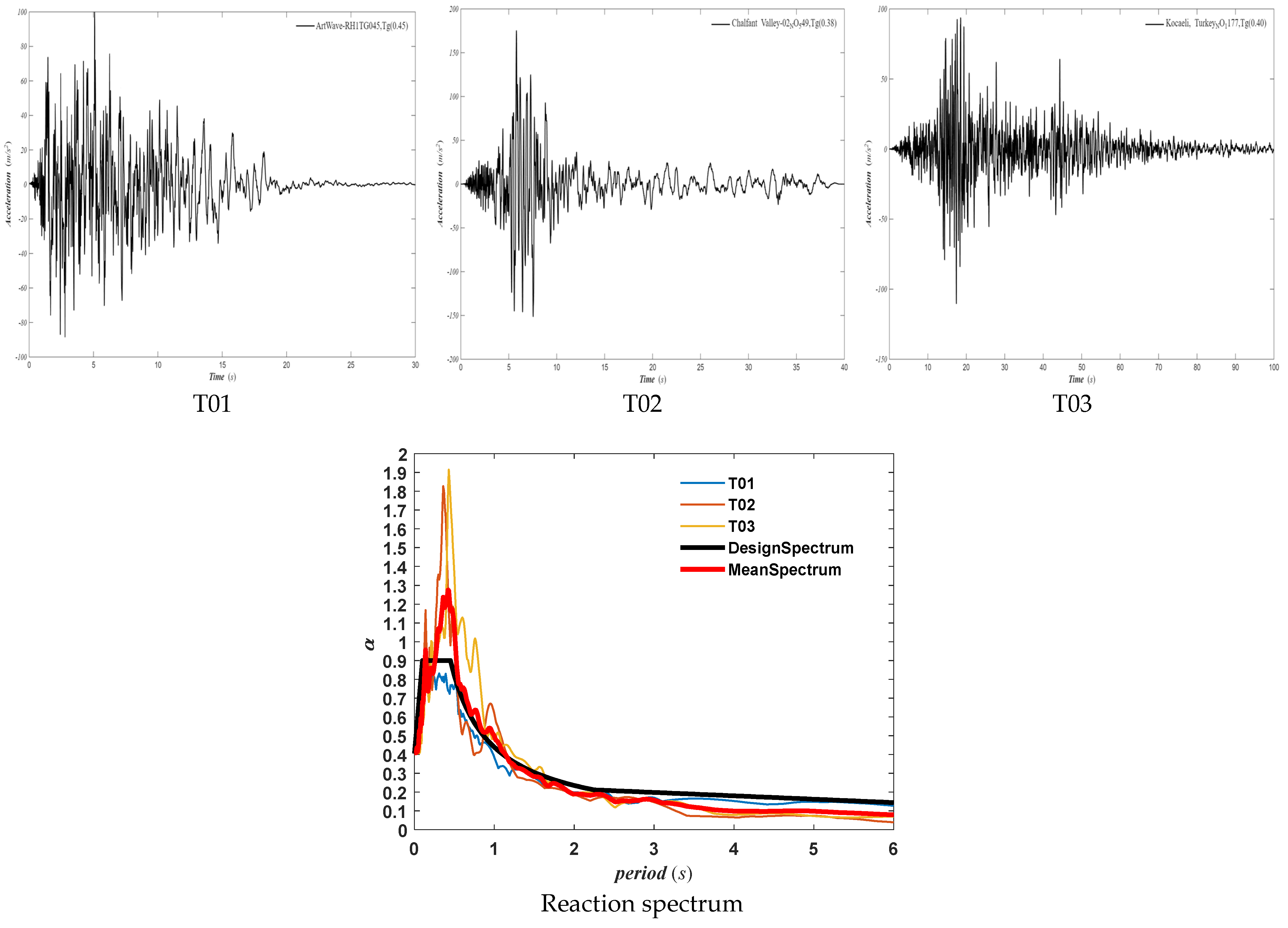
Referring to the seismic design code [2,23], three seismic waves (Figure 3) were selected for a dynamic elastoplastic analysis of the unreinforced and damped structures. The peak acceleration was 400 cm/s², and the seismic input motions were scaled according to the ratio coefficient of X:Y:Z = 1:0.85:0.65.

3.3. Structural Modal Analysis

According to a modal analysis of the uncontrolled structure and damped structure, as shown in Figure 4, the natural periods of the uncontrolled structure are 1.093 s, 1.027 s and 0.8626 s, the natural periods of the damped structure are 1.061 s, 1.010 s and 0.65 s. the mode shapes for the uncontrolled structure and damped structure were identified as translational modes in the X and Y directions and torsional modes. The structural vibration patterns were similar, with the ratios of the torsional mode to the translational mode are 0.79 and 0.61, respectively (

Table 3. Comparison of structural natural oscillation periods.

	Uncontrolled Structure	Damped Structure
T1	1.093	1.061
T2	1.027	1.010
T3	0.8626	0.65

), which met the requirements of the relevant codes.

3.4. Comparison of Overall Structural Indicators

Through a dynamic elasto-plastic analysis, the overall performance indicators of the uncontrolled structure and the damped structure were compared. The effectiveness of the energy dissipation technology was thus quantitatively and intuitively verified. Furthermore, the working mechanism, whereby the structural response was reduced and the primary structural system was protected through the dissipation of energy, was profoundly revealed.

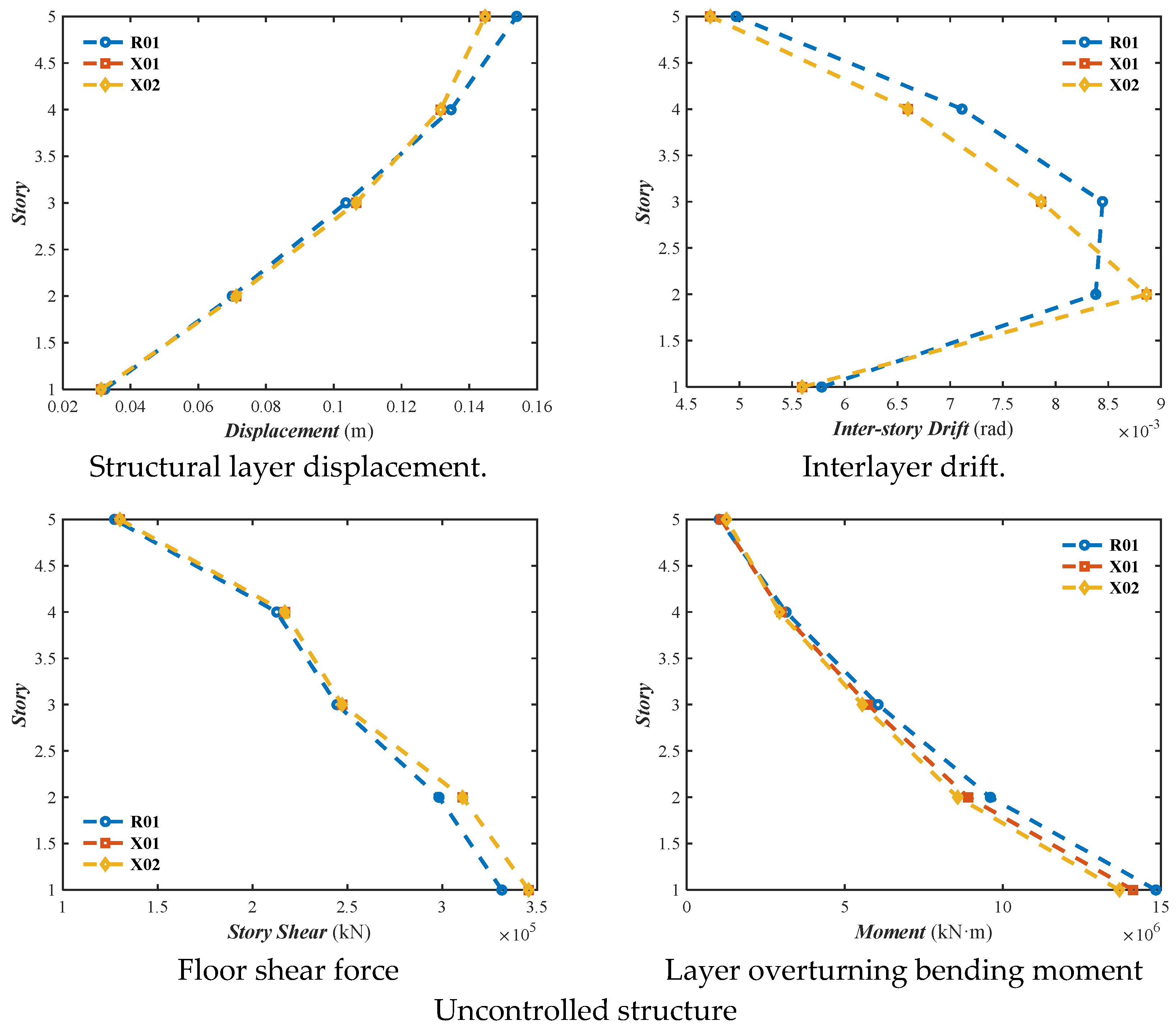
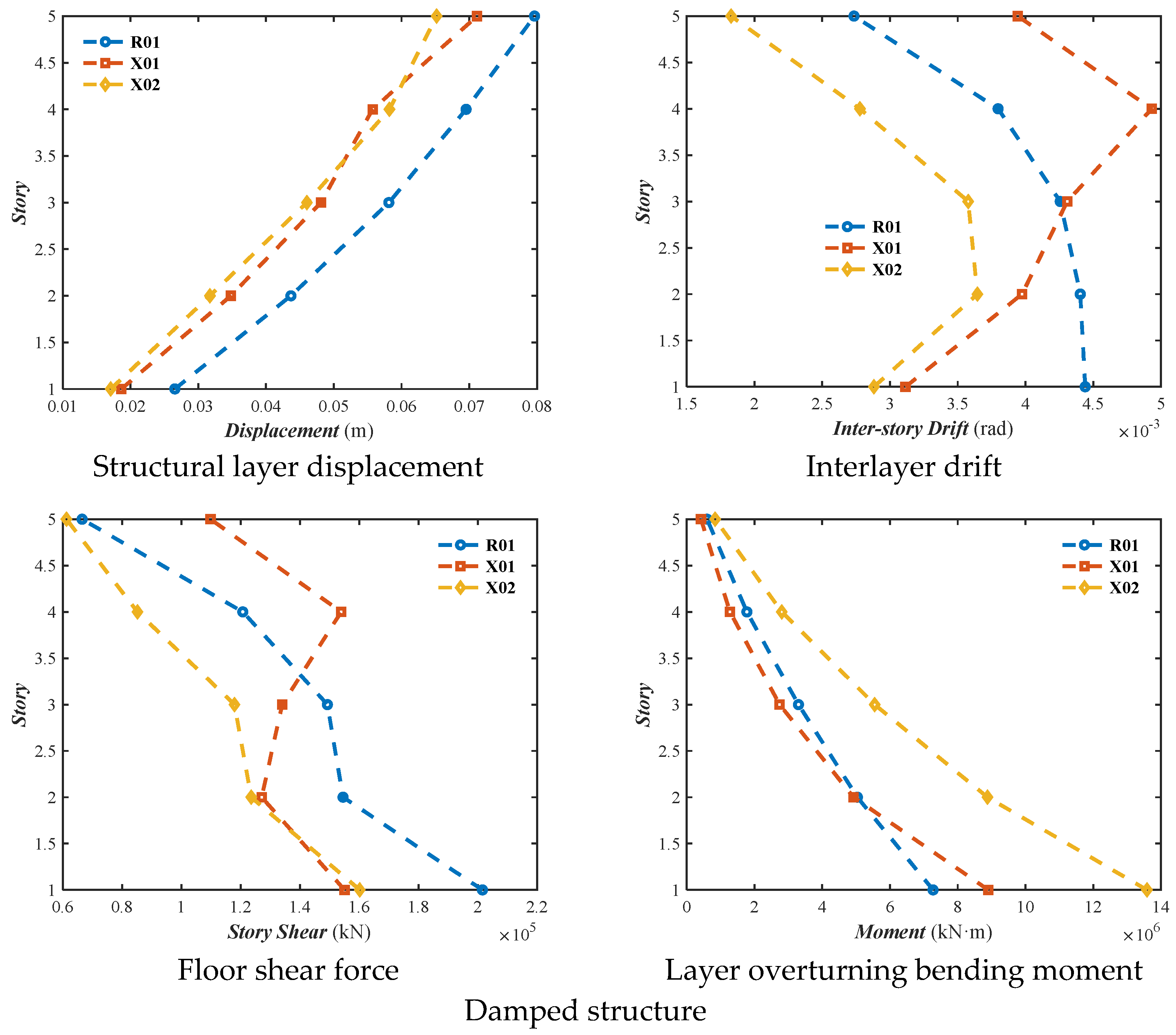
In the analysis result legend, R01, X01, and X02, respectively, represented the dynamic elastoplastic response results of the structure under the excitation of artificial wave 01, natural wave 01, and natural wave 02.

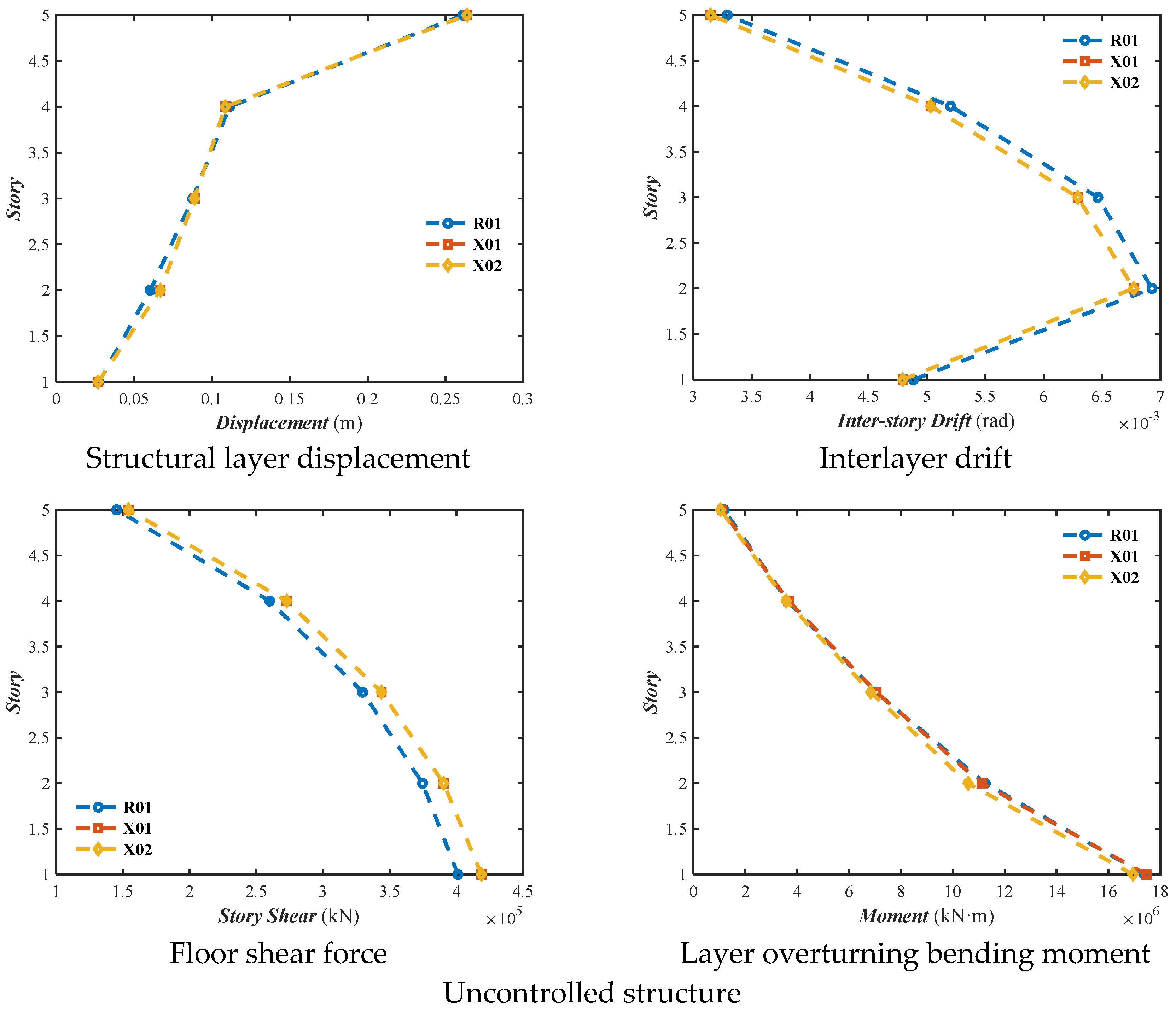
According to a comparative analysis of the overall indicators for the unreinforced and damped structures, as shown in Figure 5, the displacement of the unreinforced structure in the X direction was 0.2639 m, the displacement angle was 0.0069 radians, the inter-story shear force was 418,684.5625 kN, and the inter-story bending moment was 17,468,468 kN·m. The damped structure’s displacement was 0.1660 m, the displacement angle was 0.0042 radians, the inter-story shear force was 172,598.9219 kN, and the inter-story bending moment was 12,516,883 kN·m. The displacement angles calculated for all three seismic motions were less than 1/50, satisfying the code requirements. The inter-story displacement reduction reached 37.09%, the shear force reduction was 58.78%, the bending moment reduction was 28.35%, and the displacement angle reduction was 39.16%. These results indicate that the hybrid control technology in the X direction significantly improved the structural dynamic response.

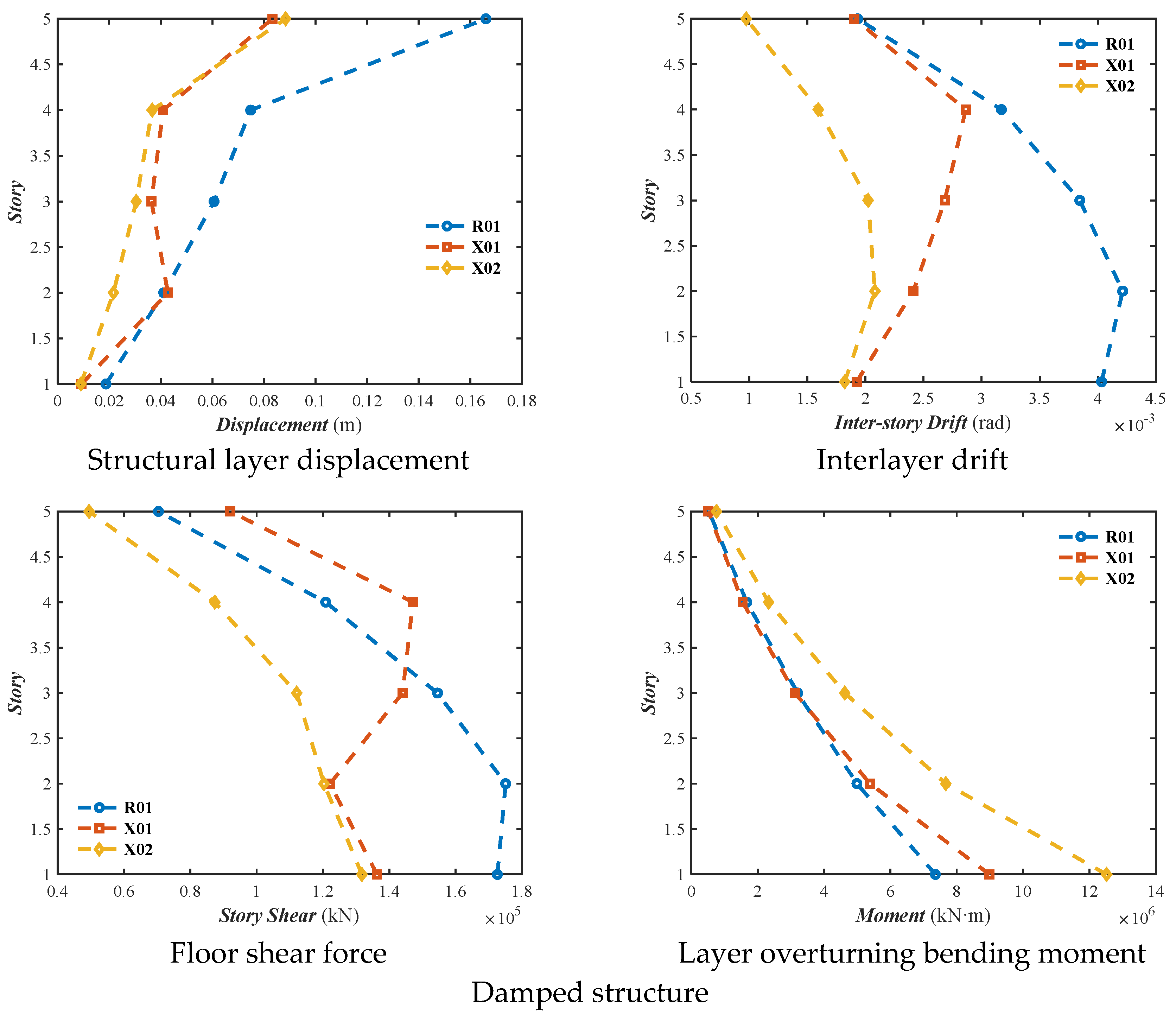
According to a comparative analysis of the overall indicators for the unreinforced and damped structures, as shown in Figure 6, the Y-direction displacement of the unreinforced structure was 0.1540 m, the displacement angle was 0.0089 radians, the inter-story shear force was 345,588.5625 kN, and the inter-story bending moment was 14,838,435 kN·m. The damped structure’s displacement was 0.0796 m, the displacement angle was 0.0049 radians, the shear force was 201,595.2969 kN, and the bending moment was 13,584,687 kN·m. The inter-story displacement reduction reached 48.29%, the shear force reduction was 41.67%, the bending moment reduction was 8.45%, and the displacement angle reduction was 44.35%. The overall indicator comparison showed low data dispersion, and the displacement angles calculated for all three seismic motions were less than 1/50, satisfying the code requirements. These results indicate that the hybrid control technology in the Y direction significantly improved the structural dynamic response.

3.5. Structural Analysis Results

Seismic waves were applied to the structure in three directions, with X and Y as the primary directions, scaled according to a ratio of 1:0.85:0.65. A structural dynamic elastoplastic analysis was conducted under rare earthquake conditions.

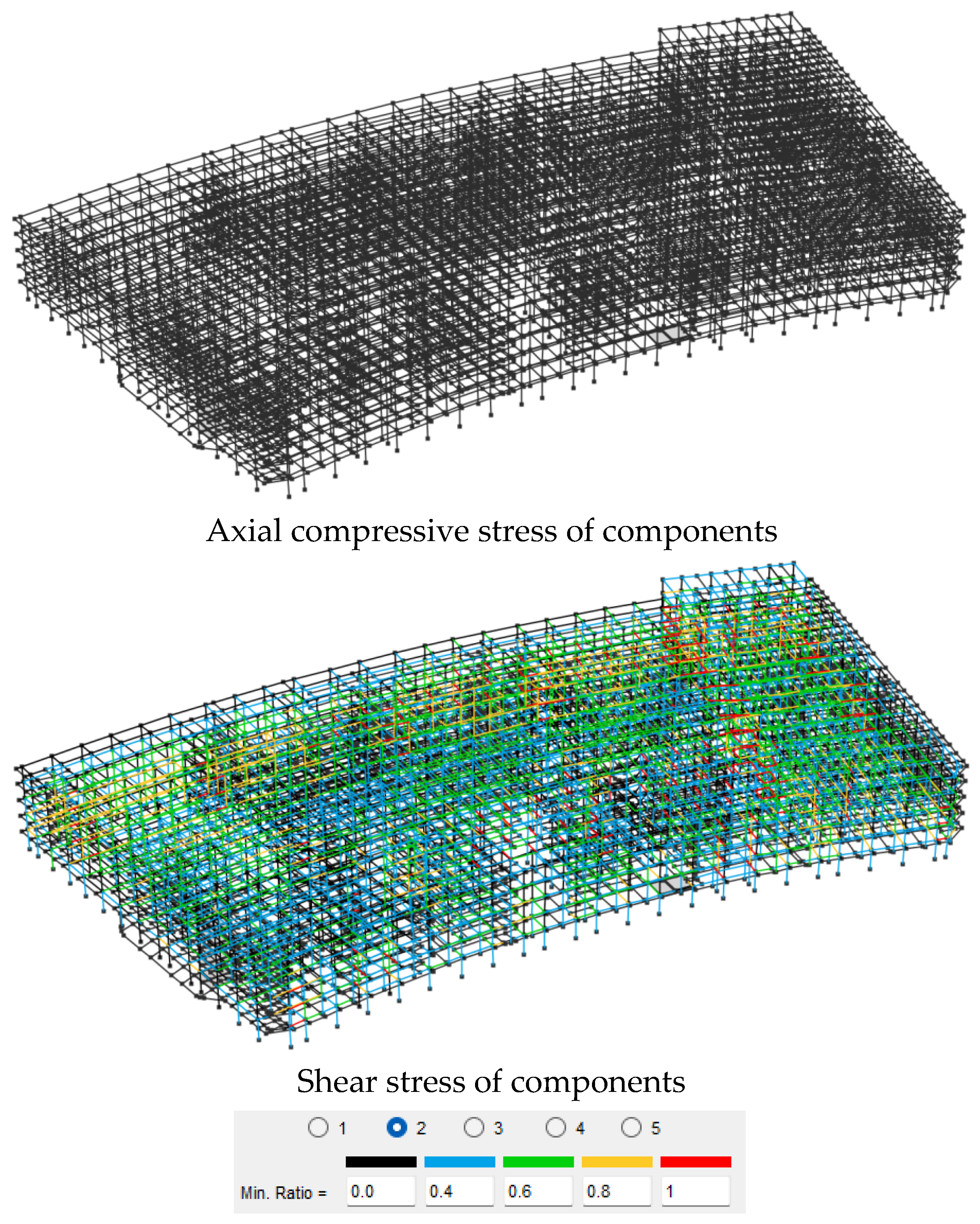
3.5.1. Damage Distribution of Seismic Excitation Structures in the X Direction

According to a comparative analysis of the damage indicator distributions for the unreinforced and damped structures, as shown in Figure 7 and Figure 8, the plastic hinge distribution in the frames of the uncontrolled structure was concentrated in the central regions, with higher damage levels in the upper-floor frame beams. The axial compressive strain of the members did not exceed the ultimate compressive strain, while the shear stress levels were relatively high, mainly concentrated in the upper regions. Compared to the unreinforced structure, the damped structure exhibited an overall improvement in damage levels, with lower degrees of plastic hinge damage in the frames, as well as reduced axial compressive strains and shear stress levels in the members.

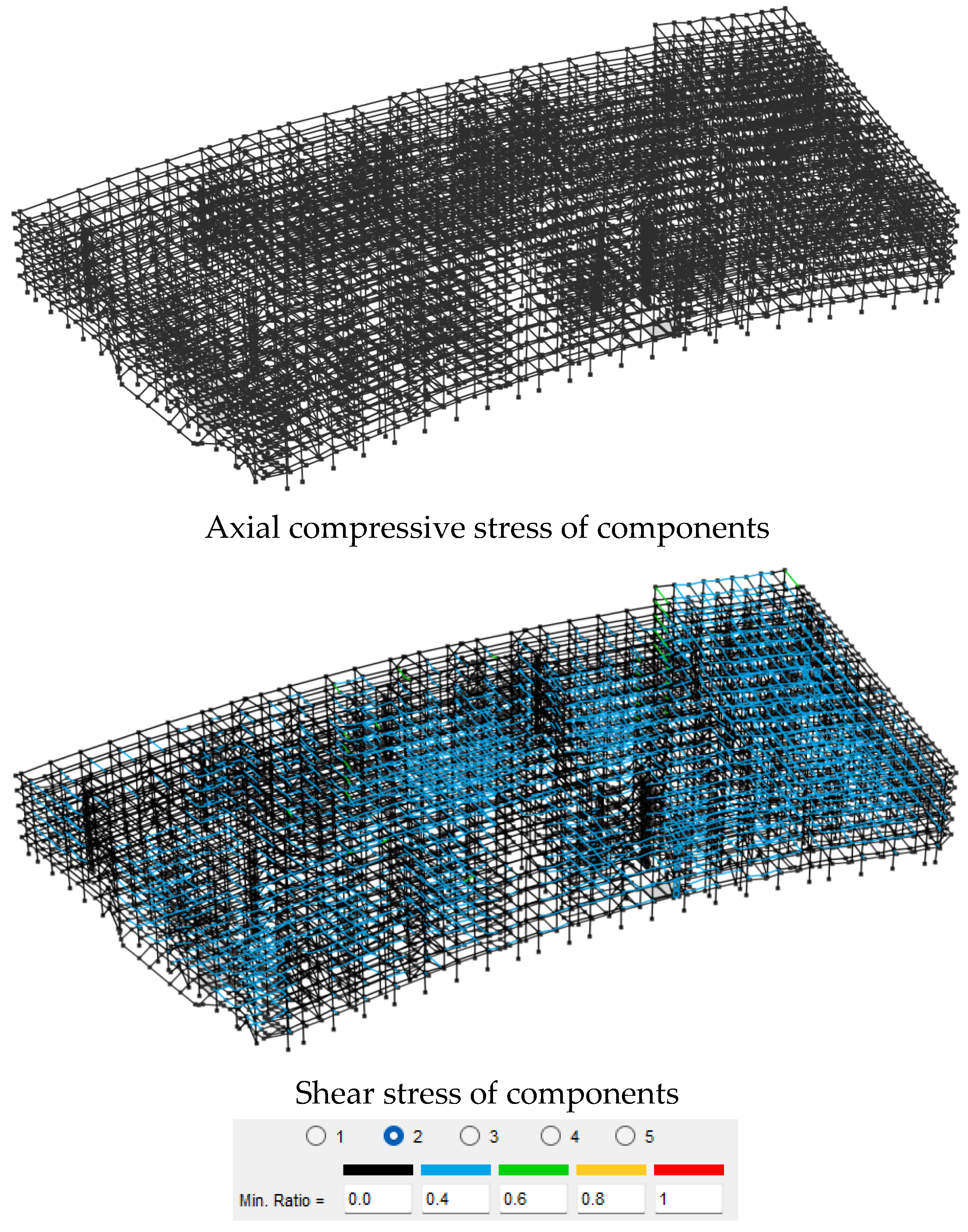
3.5.2. Damage Distribution of Seismic Excitation Structures in the Y Direction

According to a comparative analysis of the damage indicator distributions for the unreinforced and damped structures, as shown in Figure 9 and Figure 10, the plastic hinge distribution in the unreinforced structure’s frames was concentrated in the left regions, with higher damage levels in the upper-floor frame beams. The axial compressive strain of the members did not exceed the ultimate compressive strain, while the shear stress levels in the middle regions were relatively high. Compared to the unreinforced structure, the damped structure showed an overall improvement in damage levels, with lower degrees of plastic hinge damage in the frames, as well as reduced axial compressive strains and shear stress levels, indicating that the plastic hinges in the frames were in a minor damage state. This improvement was attributed to the hybrid control system’s dissipation of seismic energy through the dampers, which reduced the internal forces within the main structure and optimized the stiffness distribution, thus shifting plastic hinges toward low-damage areas. Additionally, the velocity-dependent dampers effectively suppressed inter-story shear transfer, thereby decreasing axial strains and shear stresses.

4. Conclusions

The hybrid damping system significantly improved the dynamic response characteristics of the structure. By adopting a combined control scheme of “viscous dampers + metal composite dampers,” the first three natural periods of vibration were shortened by 6.1% (X-direction translation), 5.9% (Y-direction translation), and 21.0% (torsion), indicating that this system effectively enhanced the overall stiffness of the structure. Under seismic action in the X direction, the damped structure reduced inter-story displacements by 37.1% (from 0.264 m to 0.166 m) and improved inter-story displacement angles by 39.2% (from 1/144 to 1/237). The effects in the Y direction were even more pronounced, with a 48.3% reduction in inter-story displacement (from 0.154 m to 0.080 m) and a 44.4% decrease in inter-story displacement angles (from 1/113 to 1/203). The damping measures also had notable effects on base shear forces and bending moments, with the X-direction base shear decreasing by 58.8% and the Y-direction base shear decreasing by 41.7%.

The structure’s damage control achieved the targeted performance goals. A plastic hinge distribution analysis revealed that the damping measures significantly optimized the damage pattern. Compared to the dense plastic hinges at the beam ends observed in the unreinforced structure on the upper and middle floors, the damped structure only exhibited minor plastic hinges on the most unfavorable floors. Notably, the damping scheme maintained the axial compressive stress peaks in the frame columns within 0.65 fc, effectively avoiding crushing failure risks. A time–history analysis with three seismic waves demonstrated that the maximum inter-story drift angles were strictly controlled within the 1/50 limit, fulfilling the seismic design requirements for key protection buildings, as per GB50011-2010.

The hybrid damping system showed multi-dimensional seismic resilience advantages. The results indicate that the viscous dampers primarily reduced the vibration responses in the X direction, with their velocity-dependent characteristics effectively suppressing structural accelerations. Meanwhile, the metal composite dampers reduced displacements along the Y direction through yielding energy dissipation. This complementary effect maintained the difference in damping efficiency between the two main axes within 11%, significantly addressing the weak-axis problem that is common in conventional frame structures. Furthermore, reasonable damper placement decreased the torsional period of the structure by 21%, demonstrating that the hybrid system effectively balanced translational and torsional control needs.

The engineering application demonstrated great practical value and optimization potential. This project confirmed the technical feasibility of the “viscous damper + MR damper” hybrid scheme, which offers advantages such as cost-effectiveness, easy construction, and simple maintenance.