Experimental Characterization of the Seismic Response of Industrial Steel Piping Systems
Abstract
1. Introduction
2. Experimental Campaign
2.1. Cyclic Tension Test
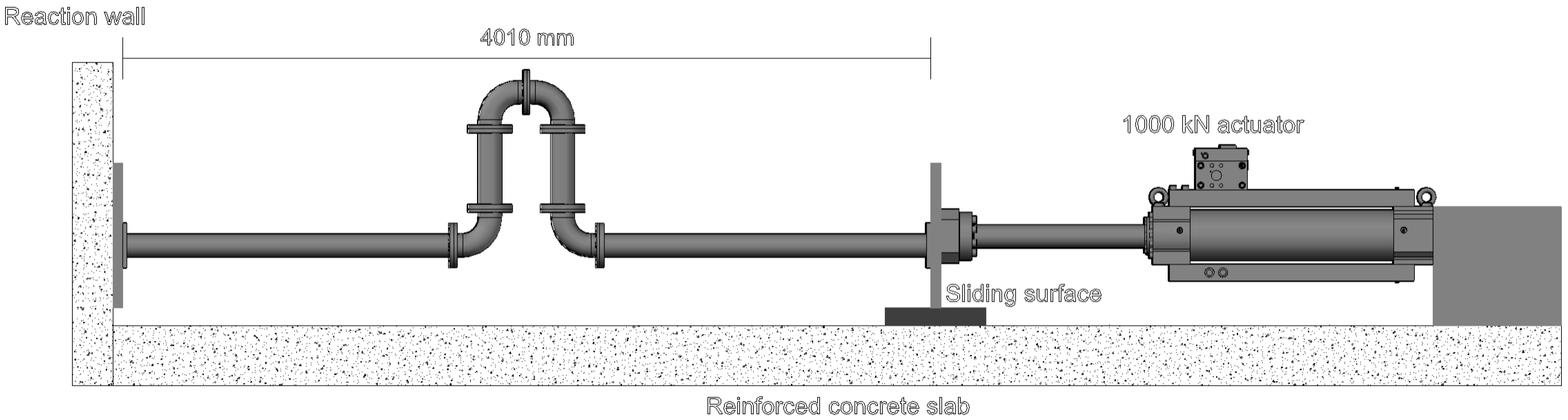
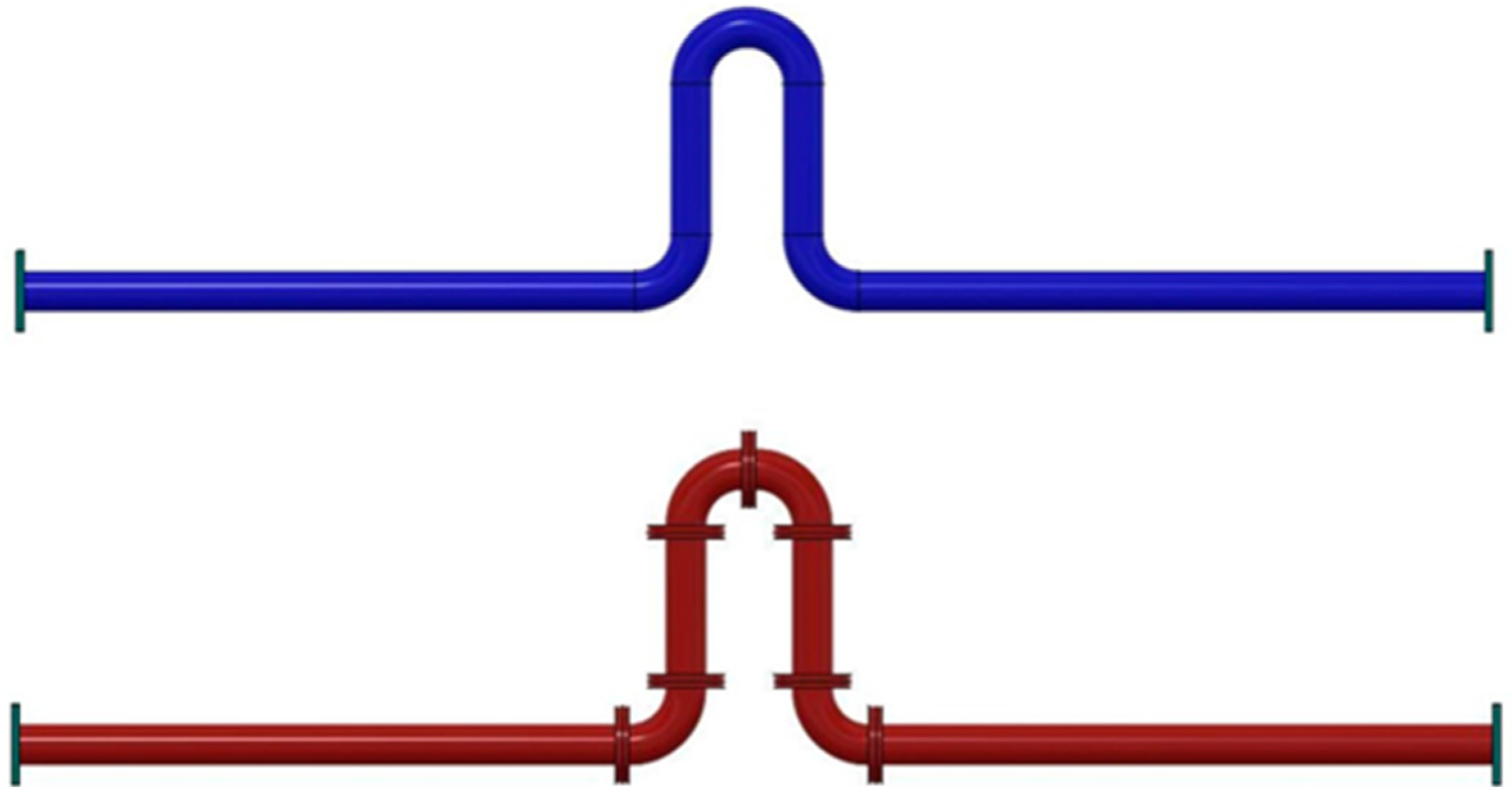
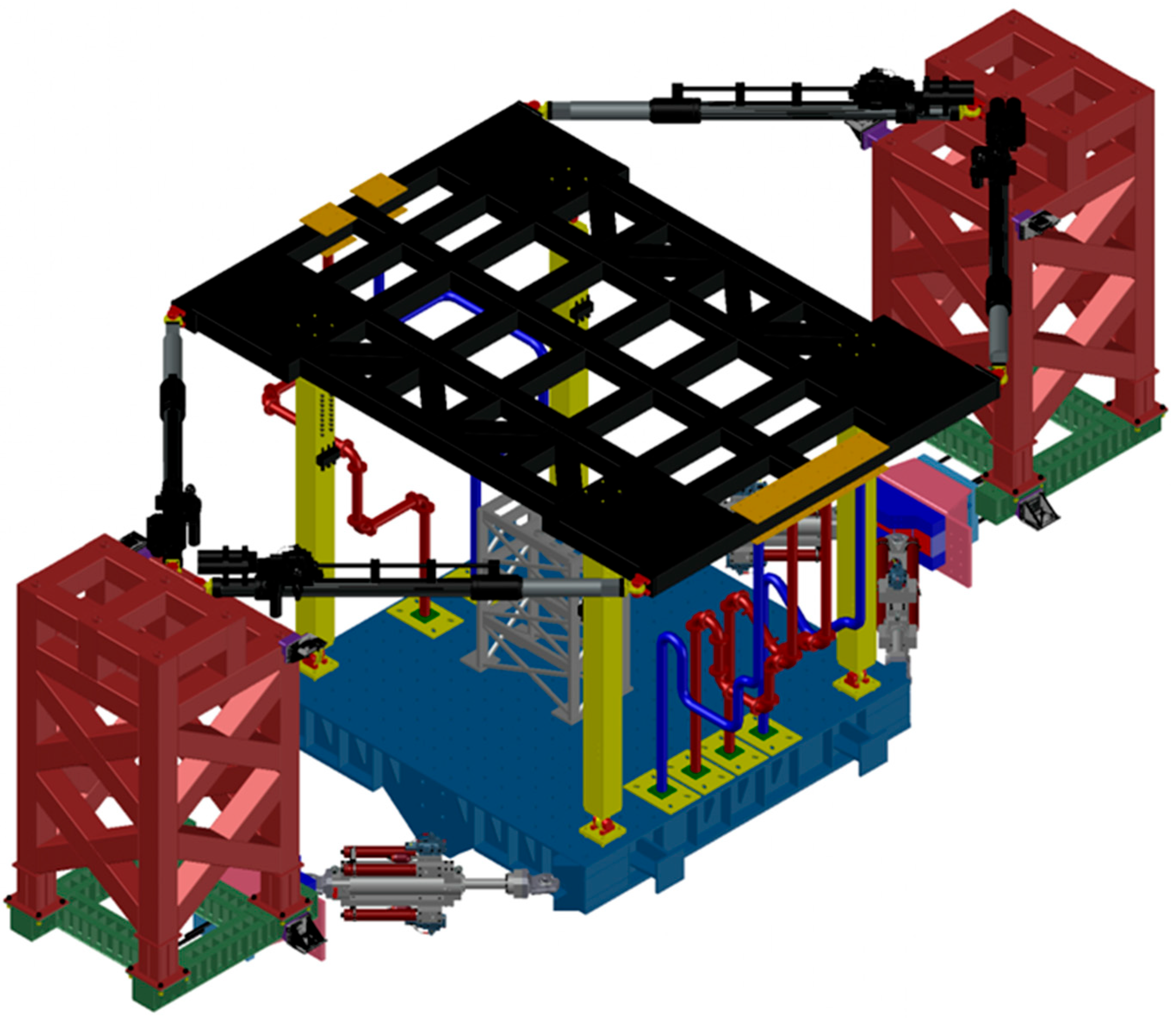
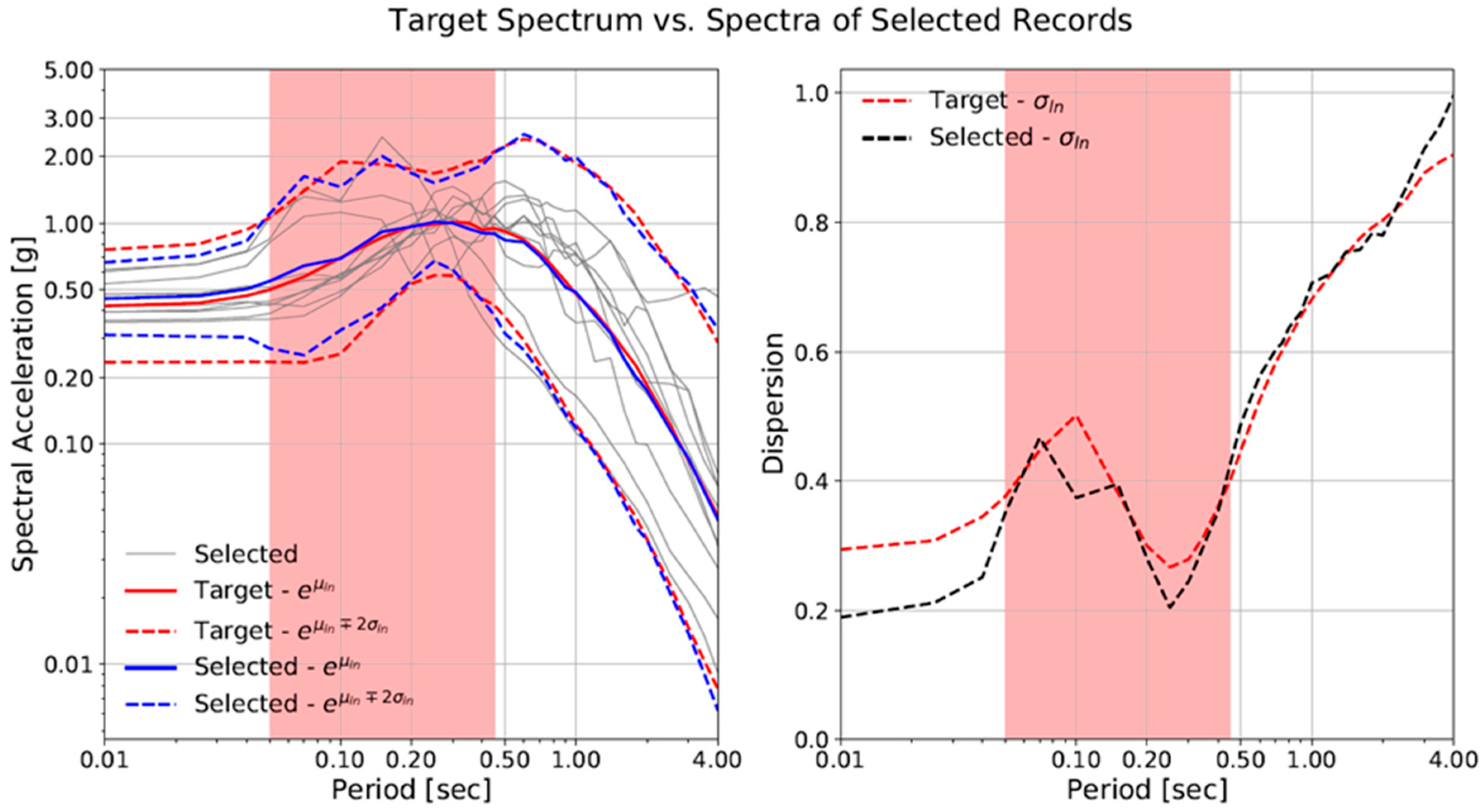
2.2. Shake Table Test
3. Experimental Results
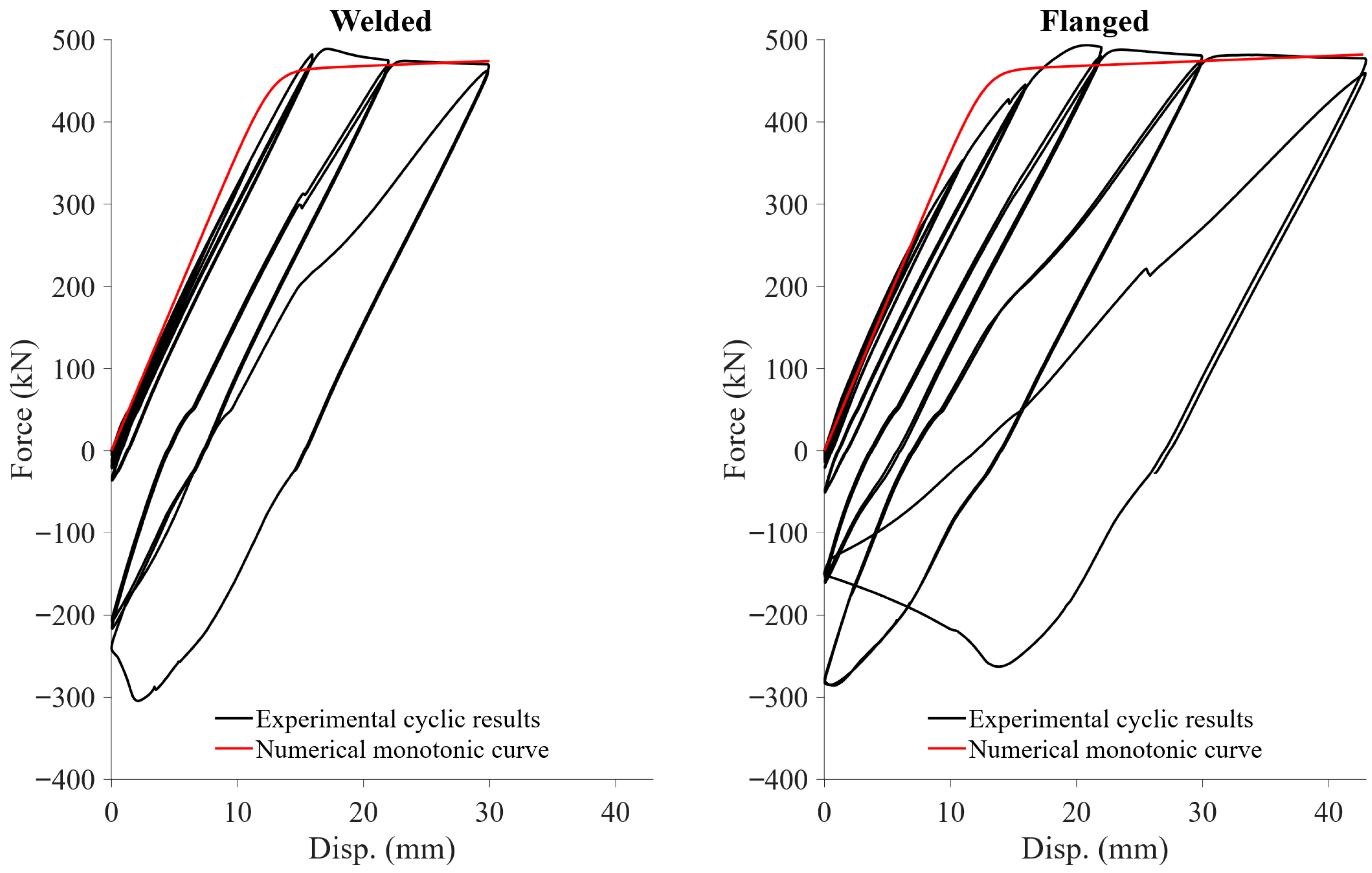
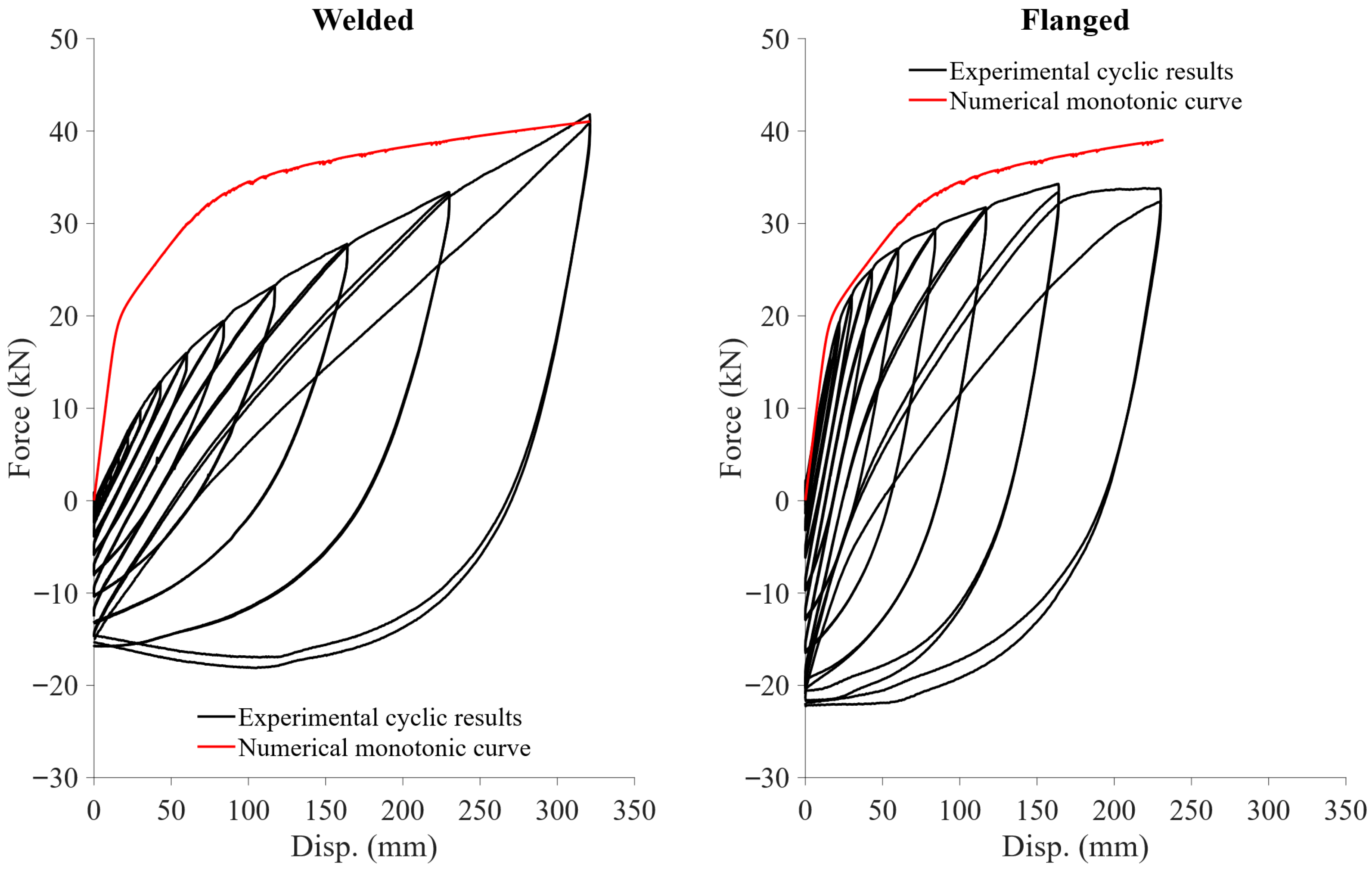
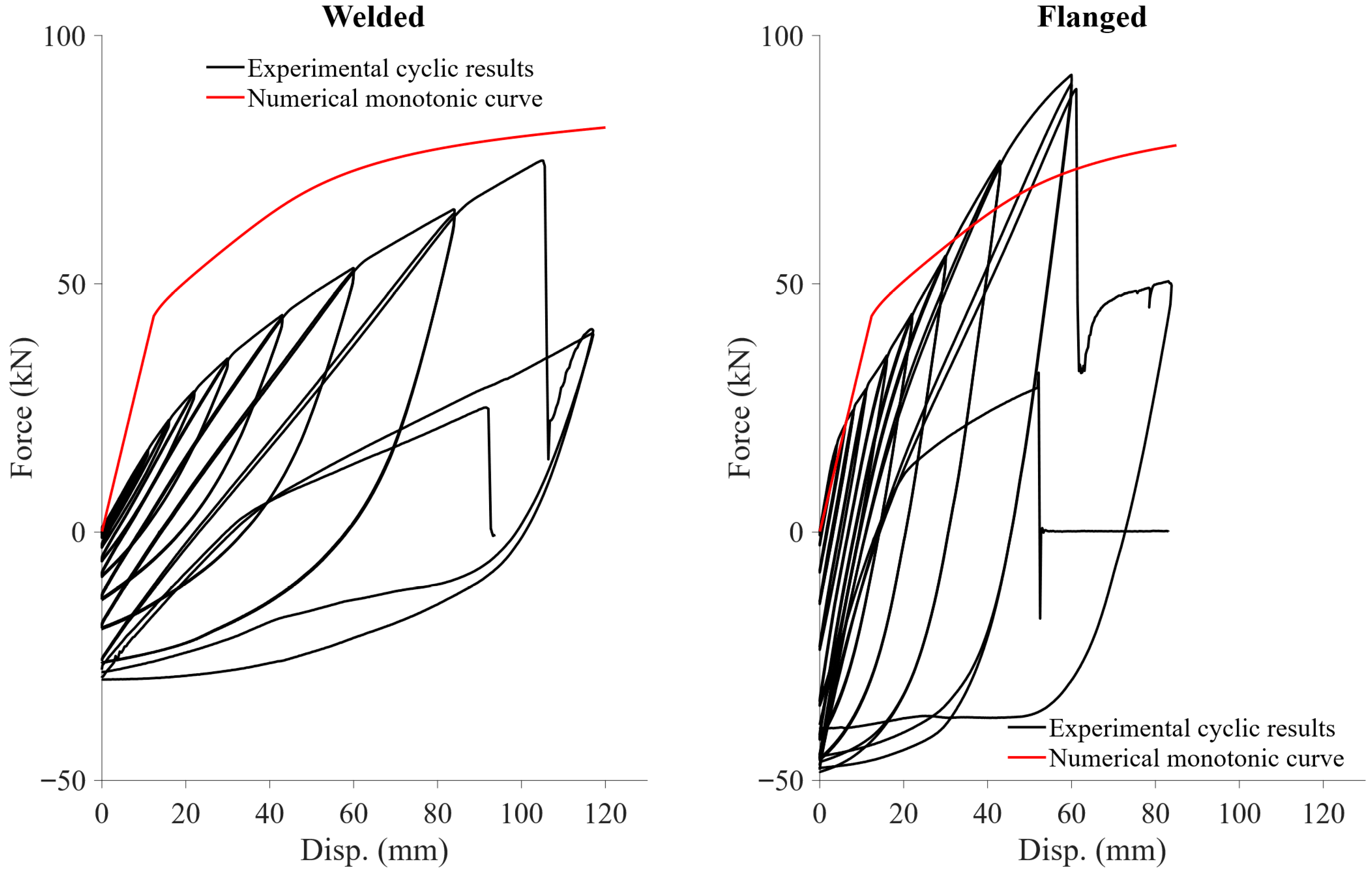
3.1. Cyclic Axial Tension Test Results
3.2. Shake Table Test Results
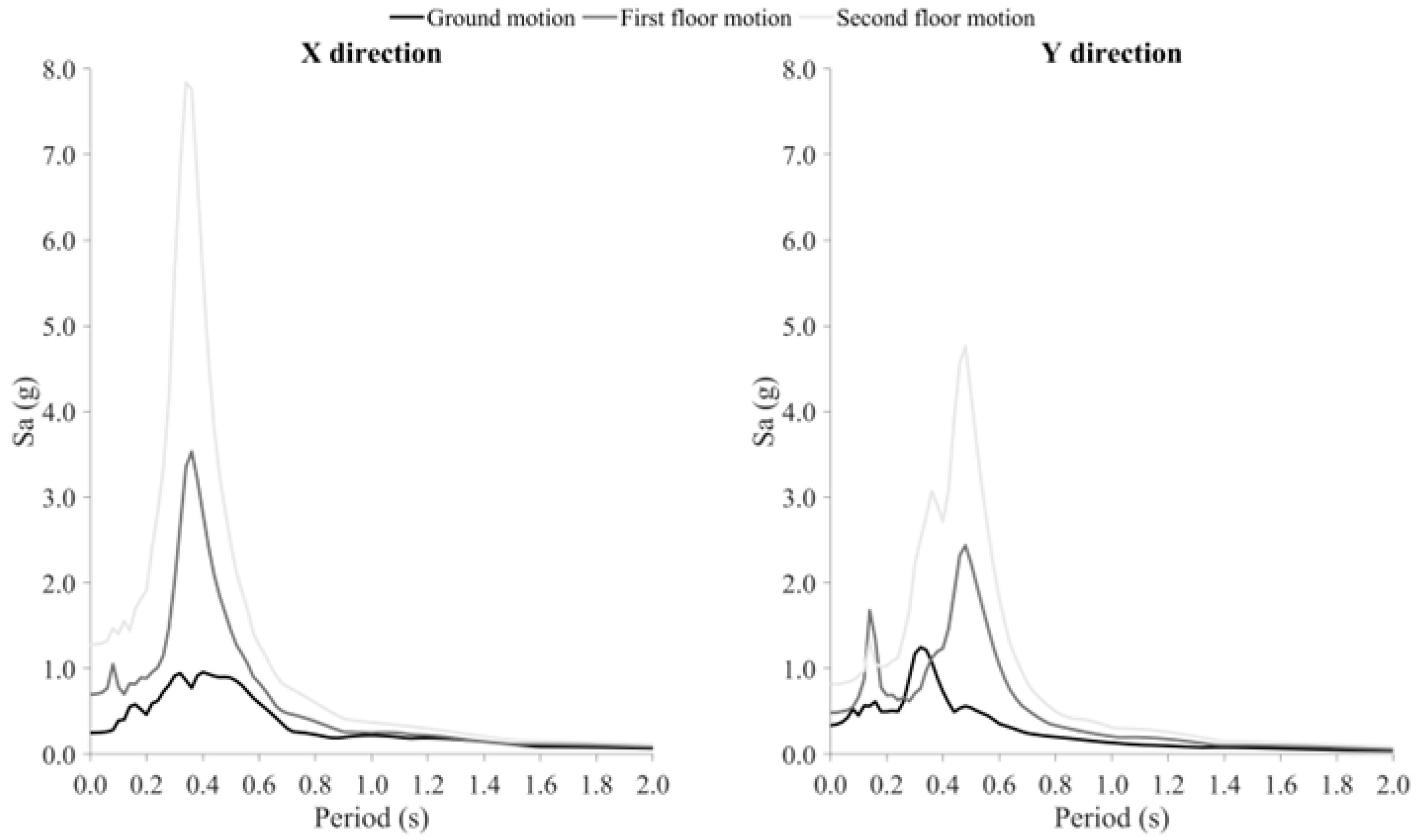
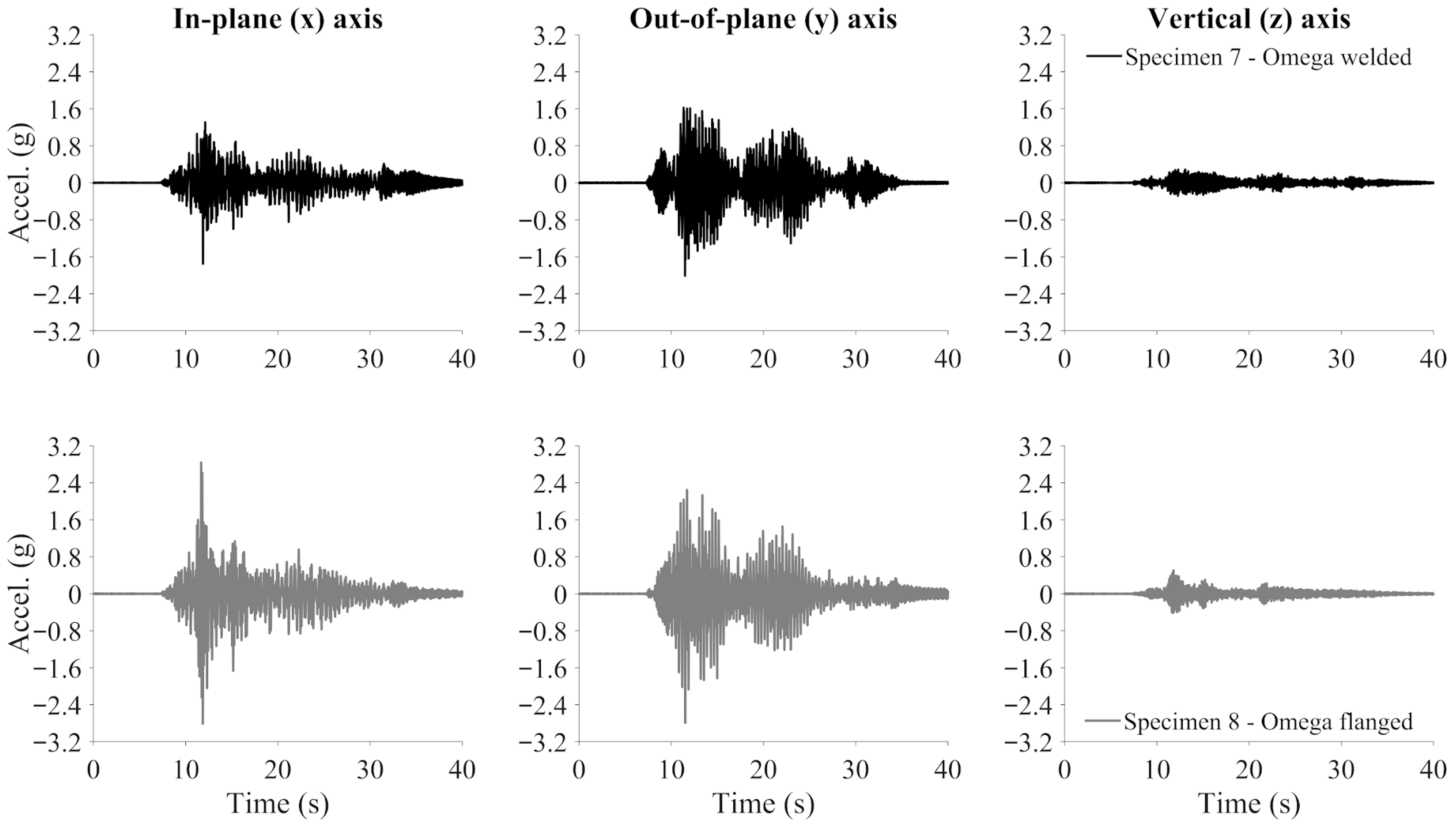
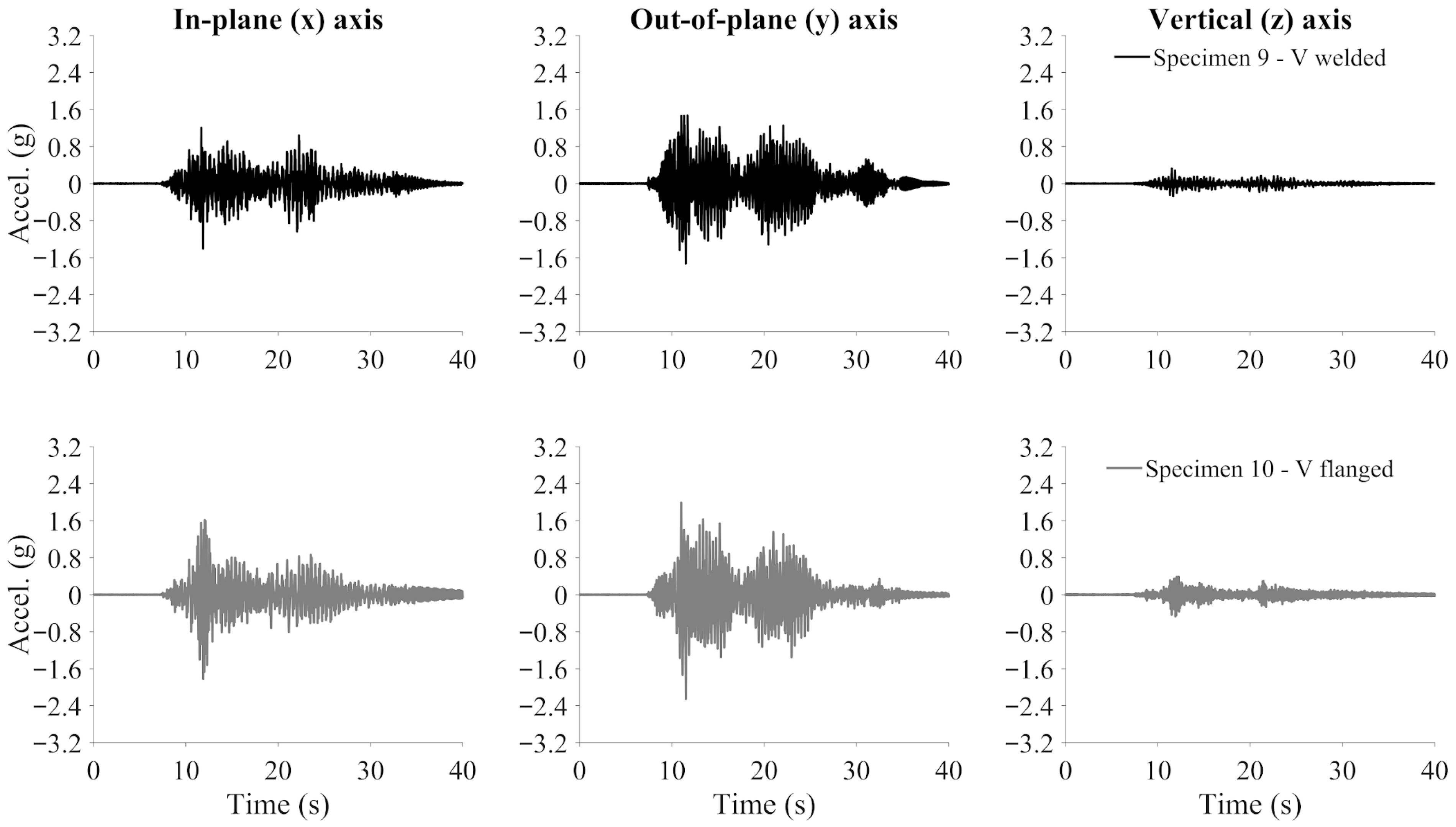
3.2.1. Acceleration Response
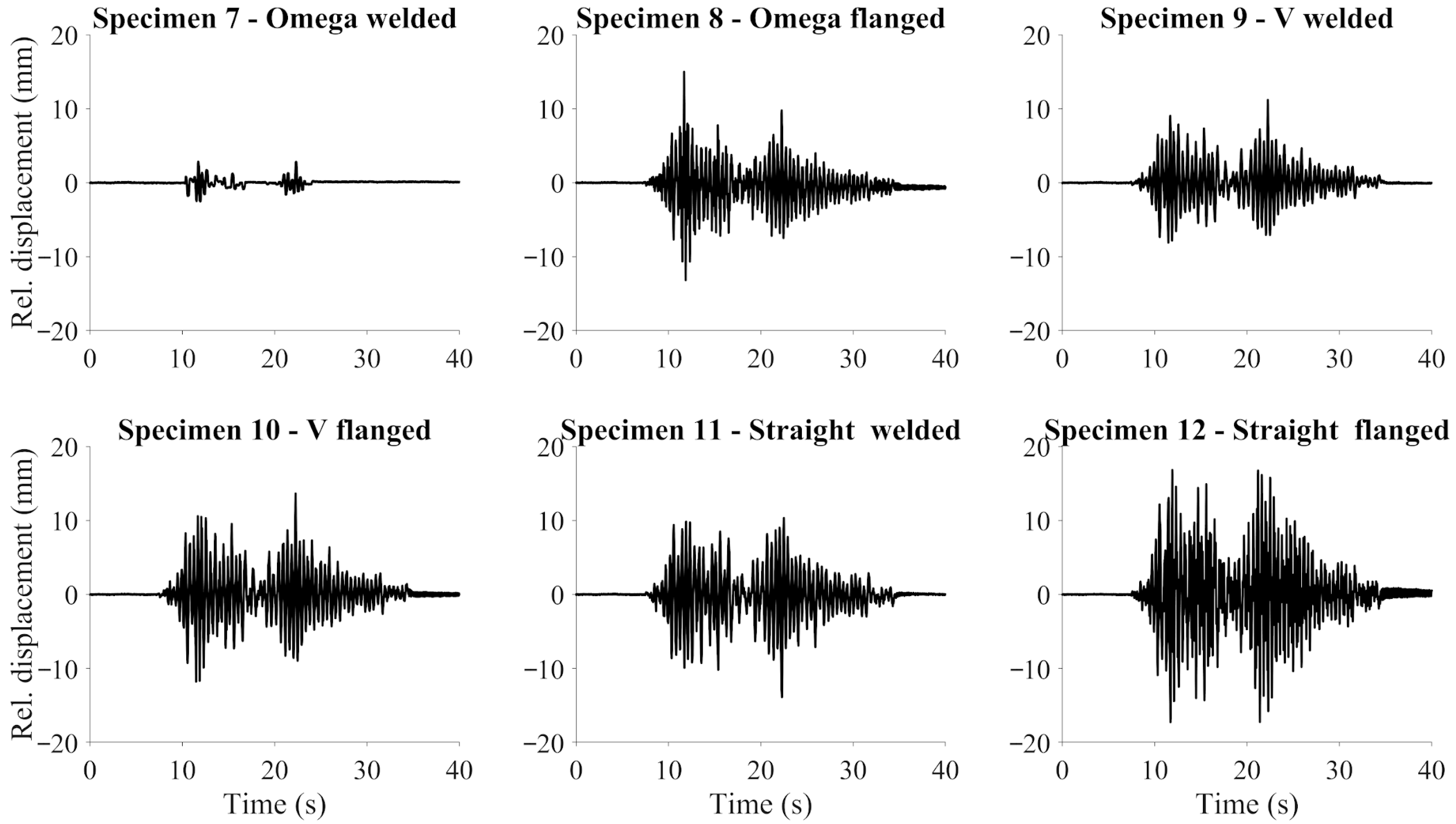
3.2.2. Displacement Response
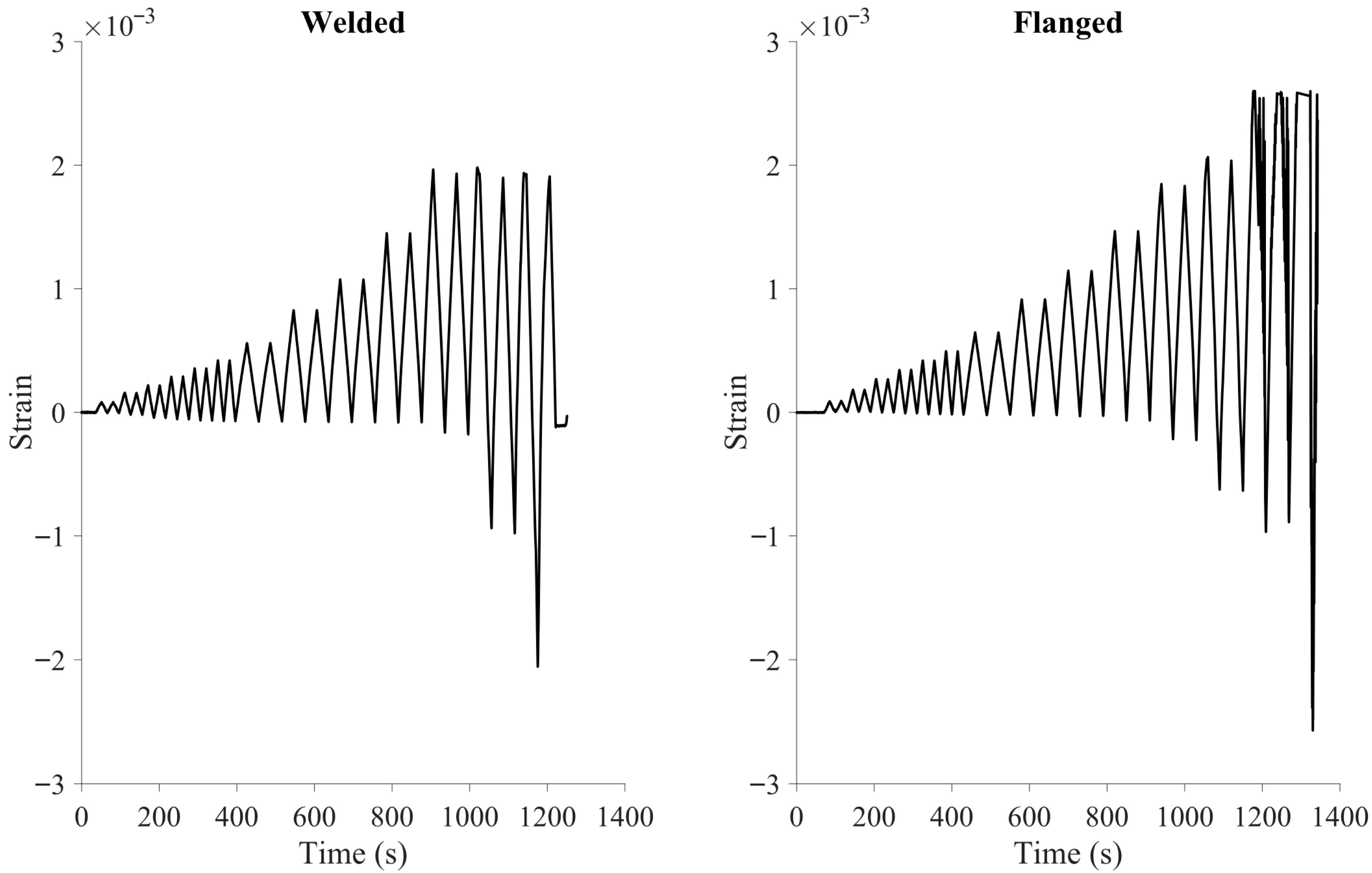
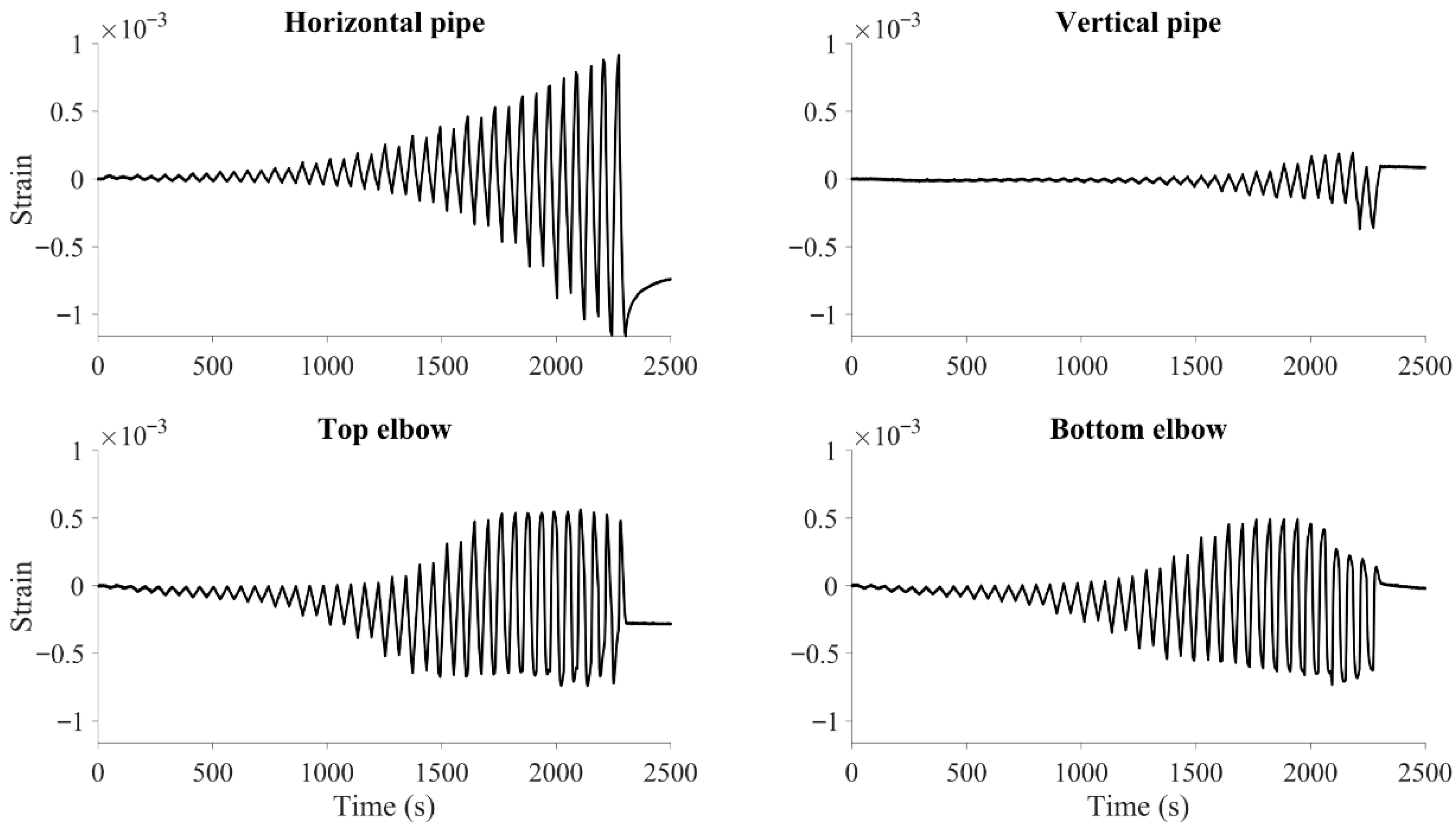
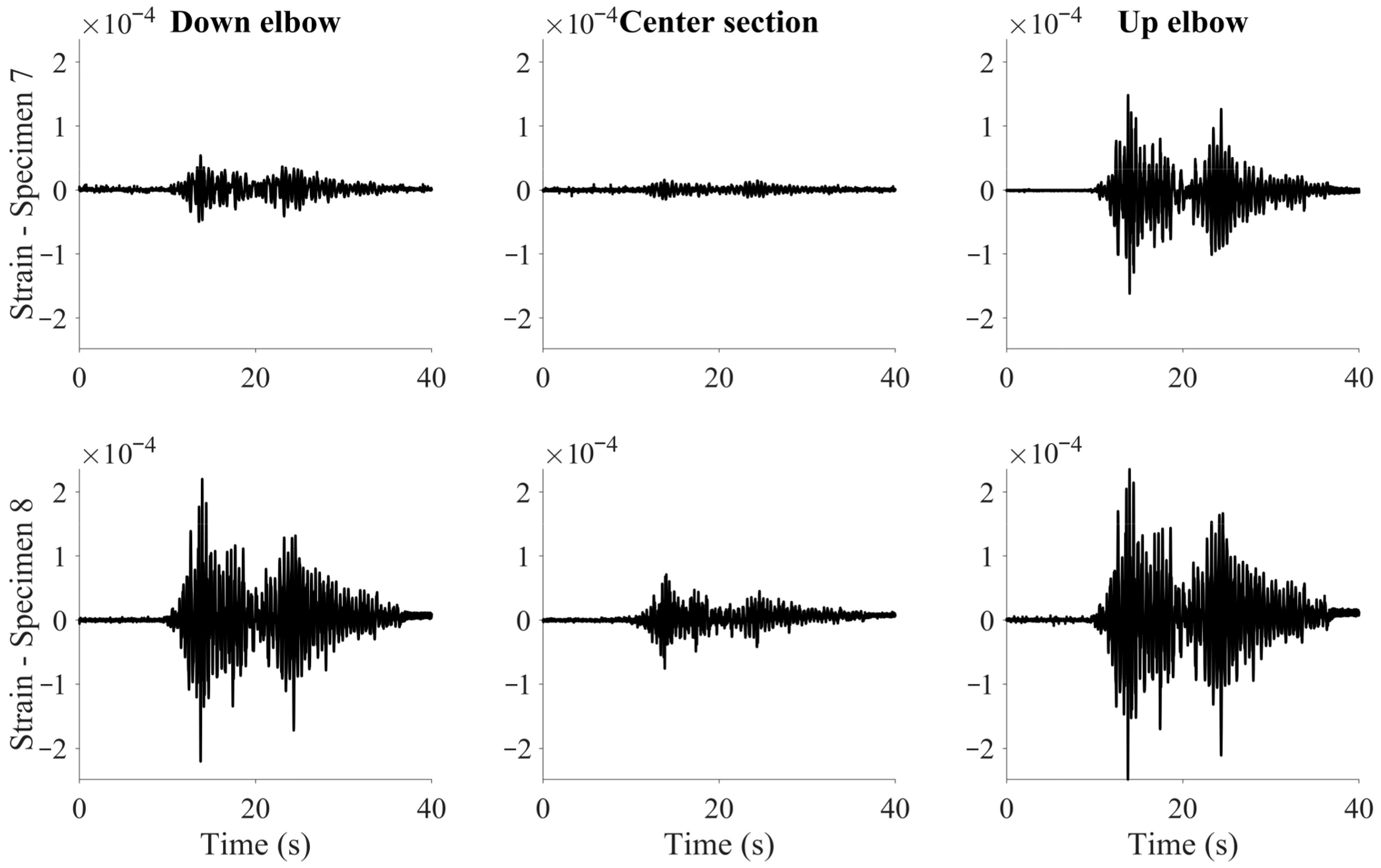
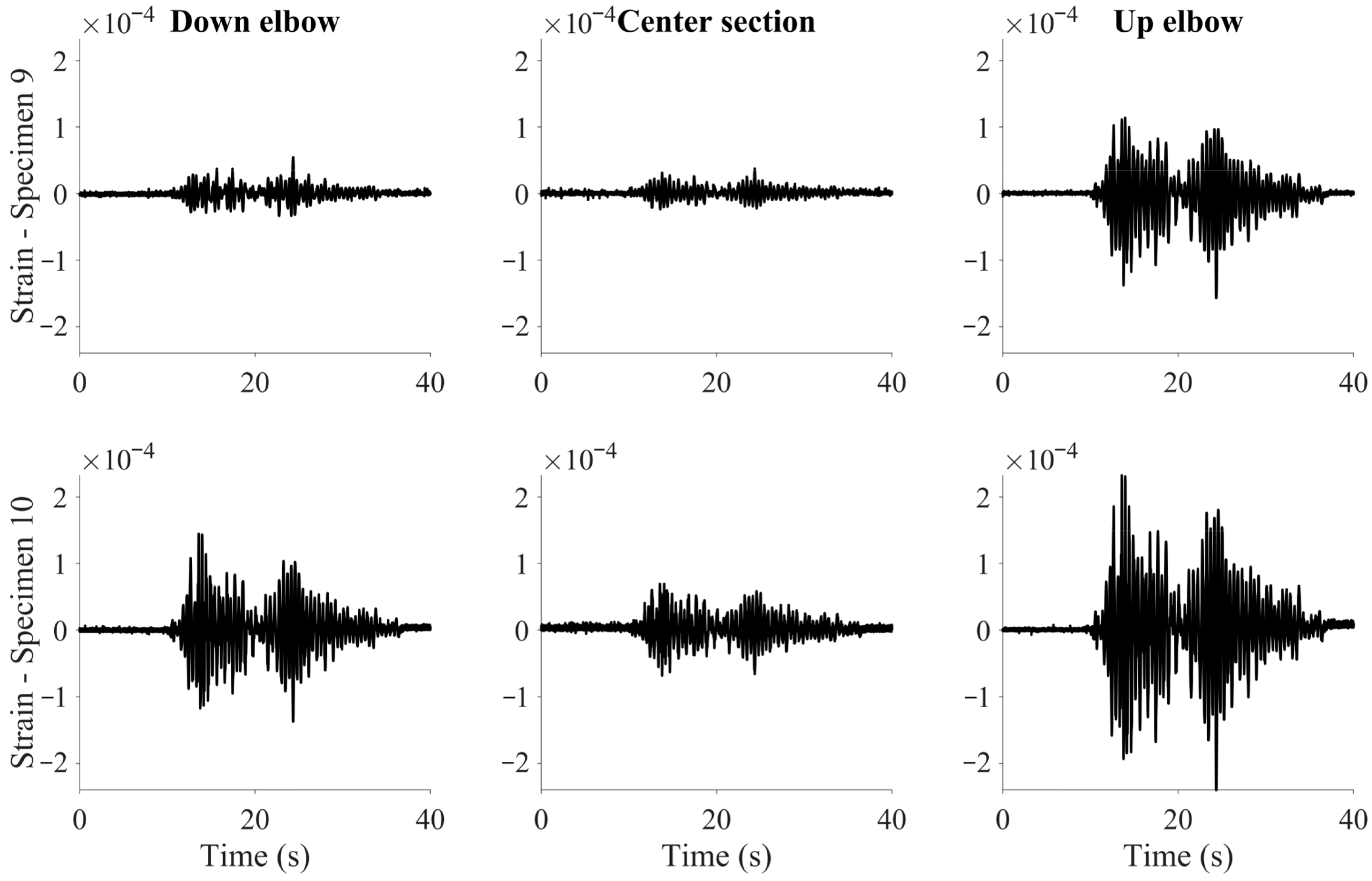
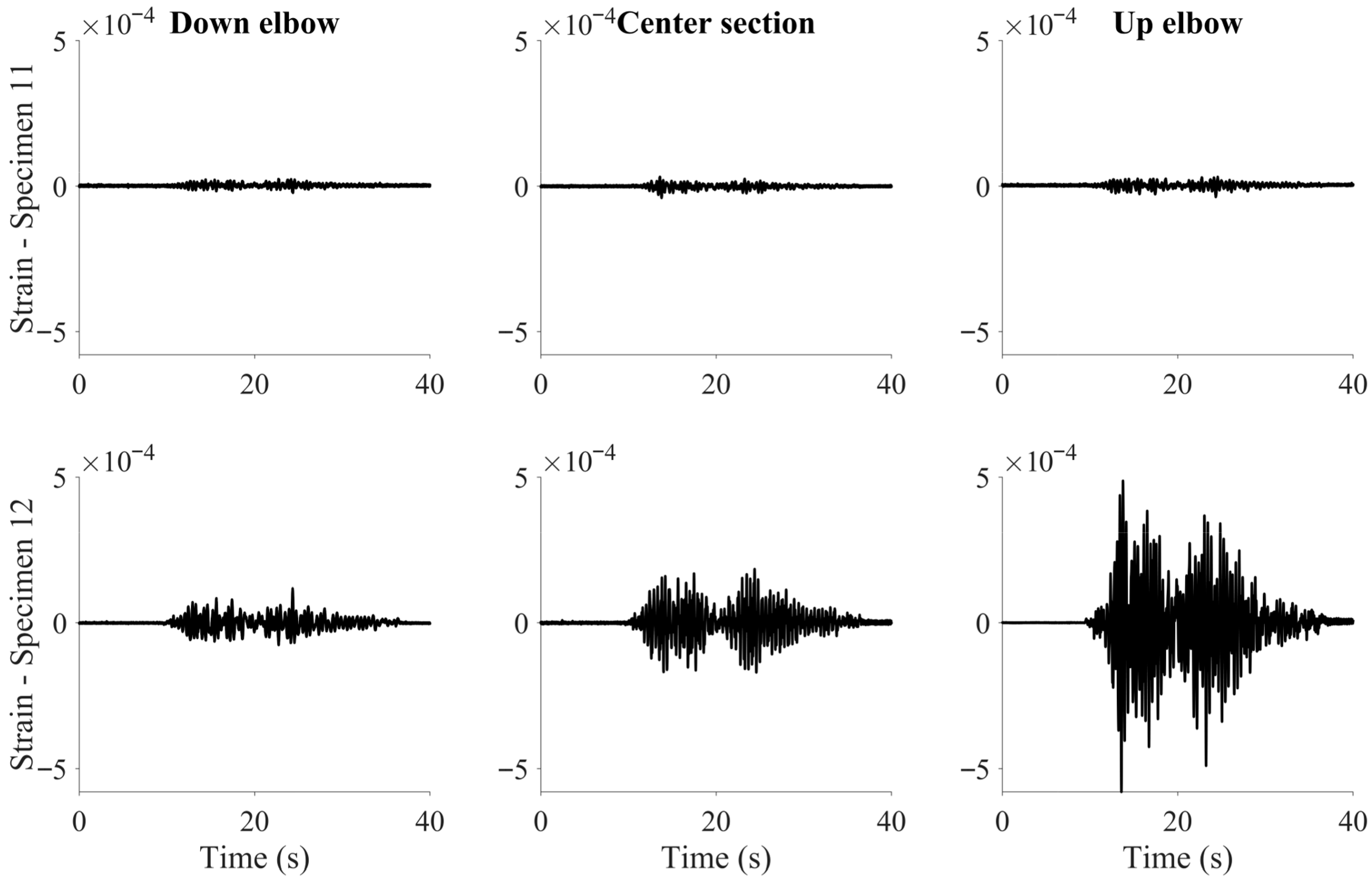
3.2.3. Strain Measurements
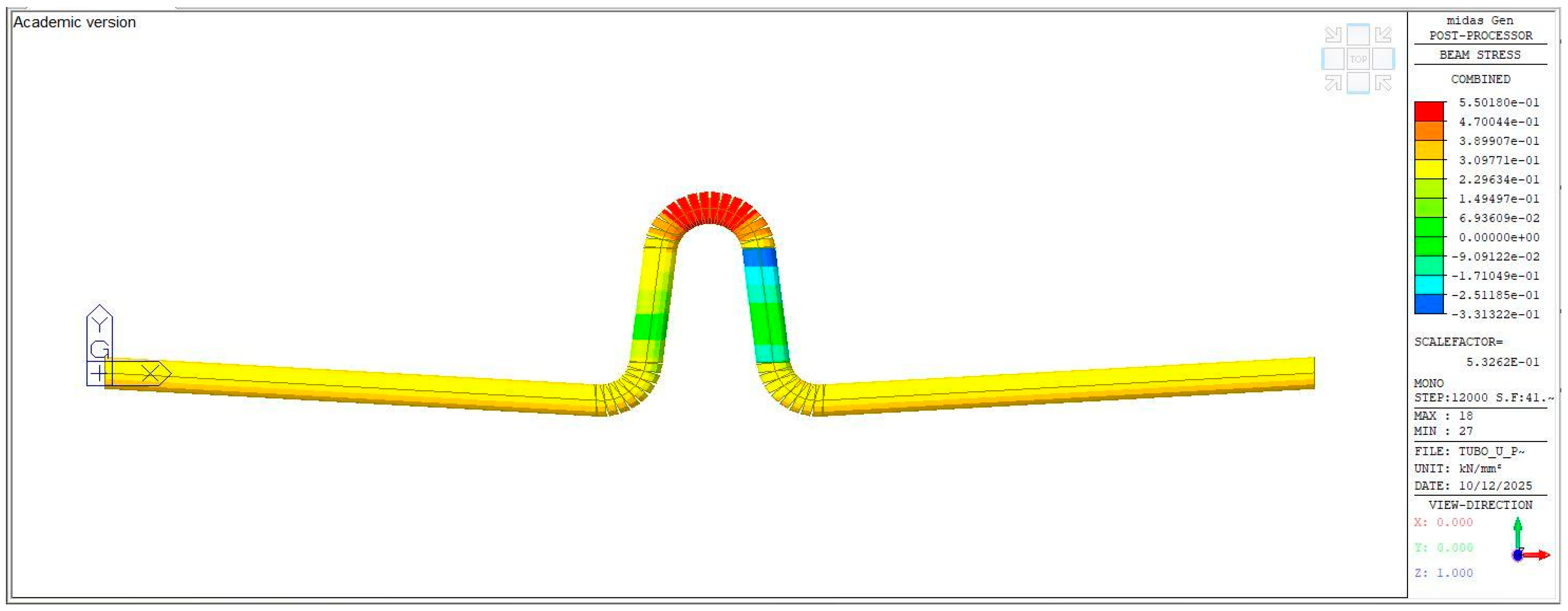
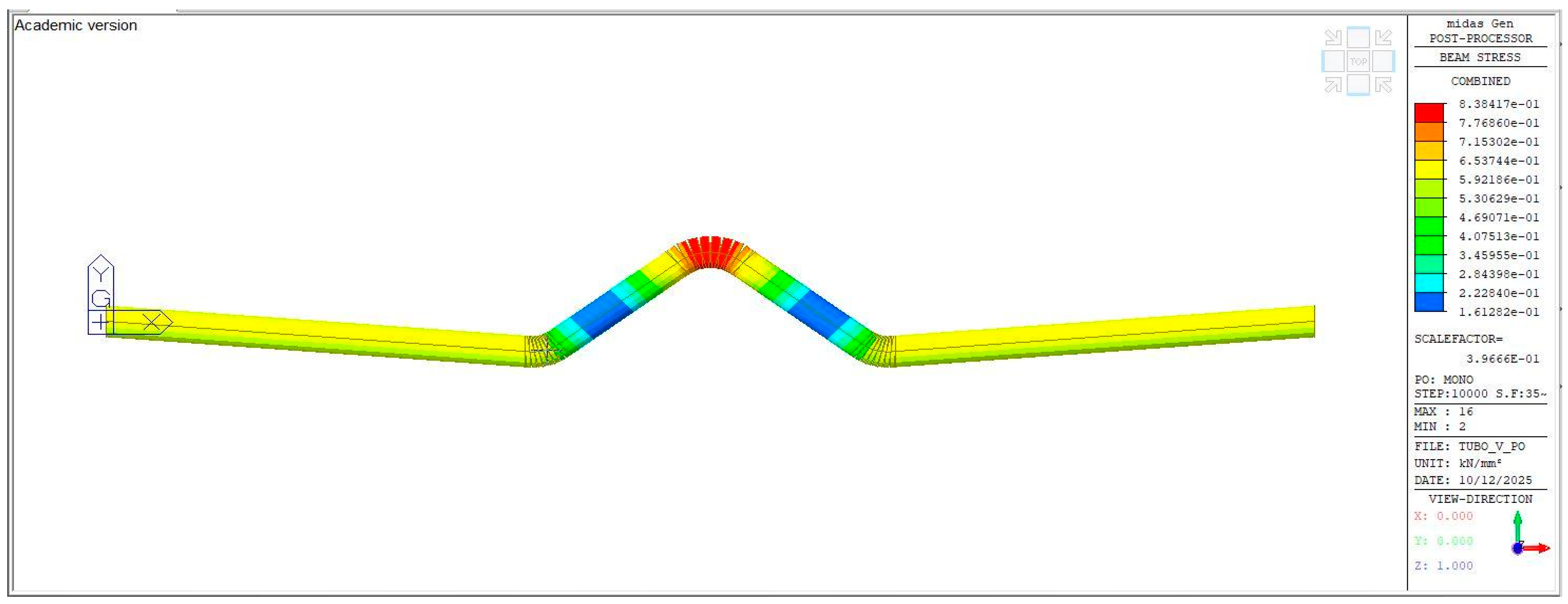
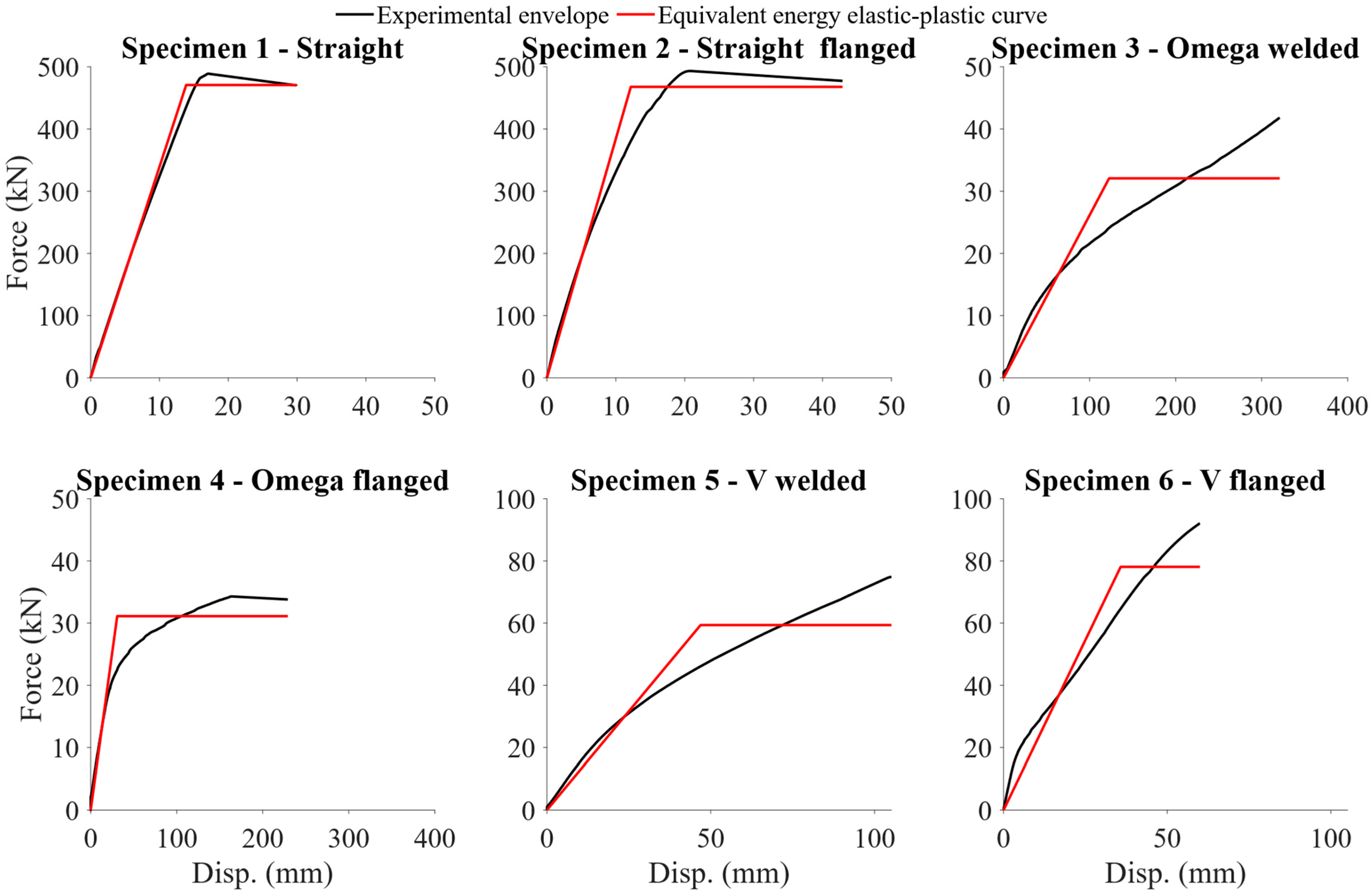
4. Characterization of Structural Properties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Campedel, M. Analysis of Major Industrial Accidents Triggered by Natural Events Reported in the Principal Available Chemical Accident Databases; OPOCE: Luxembourg, 2008; Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC42281 (accessed on 2 November 2025).
- Van Loenhout, J.; Below, R. Human Cost of Disasters: An Overview of the Last 20 Years 2000–2019; Centre of Research on the Epidemiology of Disasters–United Nations Office for Disaster Risk Reduction: Brussels, Belgium, 2021. [Google Scholar]
- Bevere, L.; Ewald, M.; Wunderlich, S. A Decade of Major Earthquakes: Lessons for Business; Swiss Re Institute: Zurich, Switzerland, 2019. [Google Scholar]
- Miglietta, C.; Perrone, D.; Gabbianelli, G.; Micelli, F.; Ciucci, M. Release of Hazardous Substance Due to Seismic Loads: Influence of Pipe to Tank Connection in Fragility Estimation. Chem. Eng. Trans. 2024, 111, 127–132. [Google Scholar] [CrossRef]
- Nascimbene, R. Vulnerability of Industrial Plant Equipment to Natural Hazards. In Management Strategies and Resilience Against NaTech Events; Cozzani, V., Paolacci, F., Eds.; CISM International Centre for Mechanical Sciences: Udine, Italy; Springer: Berlin/Heidelberg, Germany, 2025; Volume 616. [Google Scholar] [CrossRef]
- Vathi, M.; Karamanos, S.A.; Kapogiannis, I.A.; Spiliopoulos, K.V. Performance criteria for liquid storage tanks and piping systems subjected to seismic loading. J. Press. Vessel. Technol. 2017, 139, 051801. [Google Scholar] [CrossRef]
- Perrone, D.; Brunesi, E.; Filiatrault, A.; Peloso, S.; Nascimbene, R.; Beiter, C.; Piccinin, R. Seismic numerical modelling of suspended piping trapeze restraint installations based on component testing. Bull. Earthq. Eng. 2020, 18, 3247–3283. [Google Scholar] [CrossRef]
- Gabbianelli, G.; Rapone, A.; Milanesi, R.R.; Nascimbene, R. Impact of Far- and Near-Field Records on the Seismic Fragility of Steel Storage Tanks. Appl. Mech. 2025, 6, 24. [Google Scholar] [CrossRef]
- Melissianos, V.E.; Karaferis, N.D.; Bakalis, K.; Kazantzi, A.K.; Vamvatsikos, D. Operational status effect on the seismic risk assessment of oil refineries. Int. J. Disaster Risk Reduct. 2024, 113, 104842. [Google Scholar] [CrossRef]
- Grajales-Ortiz, C.; Melissianos, V.E.; Bakalis, K.; Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D. Seismic Damage Assessment of a Crude Oil Hydrodesulphurisation Unit. Part I: Exposure and Modelling. Int. J. Disaster Risk Reduct. 2025, 124, 105519. [Google Scholar] [CrossRef]
- Melissianos, V.E.; Karaferis, N.D.; Bakalis, K.; Kazantzi, A.K.; Vamvatsikos, D. Hazard, exposure, fragility, and damage state homogenization of a virtual oil refinery testbed for seismic risk assessment. Earthq. Spectra 2025, 41, 547–578. [Google Scholar] [CrossRef]
- FEMA E-74; Reducing the Risk of Nonstructural Earthquake Damage—A Practical Guide. National Earthquake Hazard Reduction Program (NEHRP): Gaithersburg, MD, USA, 2012.
- Jain, S.K.; Lettis, W.R.; Murty, C.V.R.; Bardet, J.P. Bhuj, India Earthquake Reconnaissance Report. 2001. Available online: https://sudhirjain.info/INL_005.pdf (accessed on 2 November 2025).
- Karagiannakis, G.; Di Sarno, L.; Necci, A.; Krausmann, E. Seismic risk assessment of supporting structures and process piping for accident prevention in chemical facilities. Int. J. Disaster Risk Reduct. 2022, 69, 102748. [Google Scholar] [CrossRef]
- Kamel Abbasnia, S.; Shariati, M. Experimental and numerical investigation of ratcheting behavior in seamless carbon steel 90° elbow pipe with small dimensions under constant internal pressure and in-plane cyclic bending. Int. J. Press. Vessel. Pip. 2023, 204, 104974. [Google Scholar] [CrossRef]
- Pournara, A.E.; Karamanos, S.A. Mechanical Behavior of Steel Pipes With Local Wall Distortions Under Cyclic Loading, in: Volume 3: Design and Analysis. In Proceedings of the ASME 2012 Pressure Vessels and Piping Conference, American Society of Mechanical Engineers, Toronto, ON, Canada, 15–19 July 2012; pp. 507–513. [Google Scholar] [CrossRef]
- Wang, T.; Shang, Q.; Chen, X.; Li, J. Experiments and Fragility Analyses of Piping Systems Connected by Grooved Fit Joints With Large Deformability. Front. Built Environ. 2019, 5, 49. [Google Scholar] [CrossRef]
- Bursi, O.S.; Reza, M.S.; Abbiati, G.; Paolacci, F. Performance-based earthquake evaluation of a full-scale petrochemical piping system. J. Loss Prev. Process Ind. 2015, 33, 10–22. [Google Scholar] [CrossRef]
- Karamanos, S.A.; Giakoumatos, E.; Gresnigt, A.M. Nonlinear Response and Failure of Steel Elbows Under In-Plane Bending and Pressure. J. Press. Vessel Technol. 2003, 125, 393–402. [Google Scholar] [CrossRef]
- EN 13480-3; Metallic Industrial Piping e Part 3: Design and Calculation. British Standards Institution: London, UK, 2002.
- Nakamura, I.; Shibutani, T.; Kuriyama, Y.; Kasai, N. Shaking Table Test on a Piping System Model for Developing High-Quality Simulation Model. In Volume 7: Seismic Engineering; ASME Nondestructive Evaluation, Diagnosis and Prognosis (NDPD) Division; The American Society of Mechanical Engineers: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Naeim, B.; Javadzade Khiavi, A.; Khajavi, E.; Taghavi Khanghah, A.R.; Asgari, A.; Taghipour, R.; Bagheri, M. Machine Learning Approaches for Fatigue Life Prediction of Steel and Feature Importance Analyses. Infrastructures 2025, 10, 295. [Google Scholar] [CrossRef]
- FEMA. Interim Testing Protocols for Determining the Seismic Performance Characteristics of Structural and Nonstructural Components; FEMA 461; Federal Emergency Management Agency: Washington, DC, USA, 2007. [Google Scholar]
- Filiatrault, A.; Perrone, D.; Brunesi, E.; Beiter, C.; Piccinin, R. Effect of cyclic loading protocols on the experimental seismic performance evaluation of suspended piping restraint installations. Int. J. Press. Vessel. Pip. 2018, 166, 61–71. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of Analysis of Cyclically Loaded RC Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements Under Normal Force and Bending; Preliminary Report IABSE; IABSE: Zurich, Switzerland, 1973; Volume 13. [Google Scholar]
- European Committee for Standardization. Eurocode 3, Design of Steel Structures; Tech. Rep.; European Committee for Standardization: Brussels, Belgium, 2011. [Google Scholar]
- European Committee for Standardization. Eurocode 8, Design of Structures for Earthquake Resistance: Part 1: General Rules, Seismic actions and Rules for Buildings; Tech. Rep.; European Committee for Standardization: Brussels, Belgium, 2011. [Google Scholar]




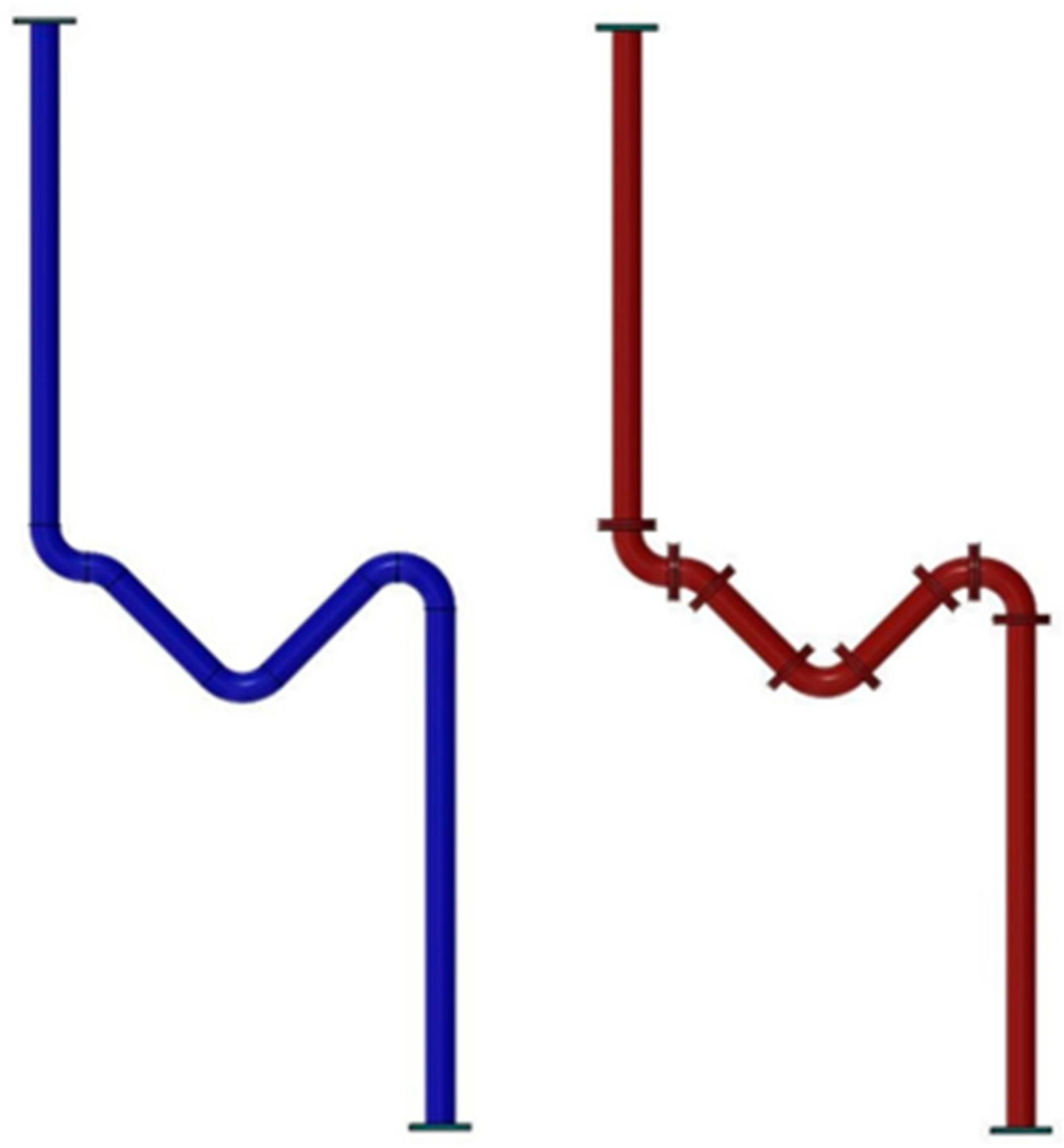
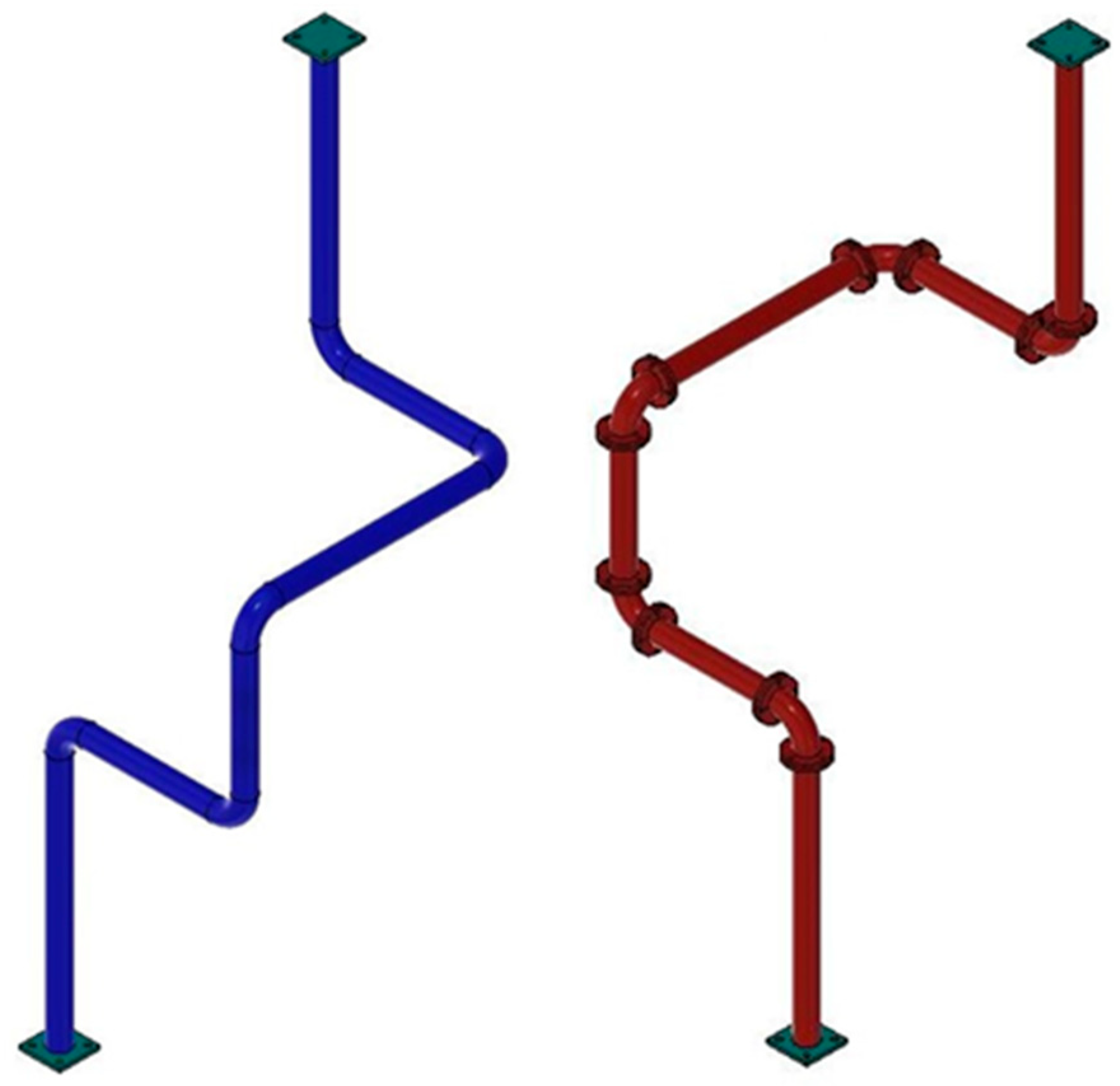










| Pipe | Outer Diameter | Thickness | Area | Moment of Inertia | Radius of Gyration | Yield Strength | Outer Diameter | Thickness | Area |
|---|---|---|---|---|---|---|---|---|---|
| mm | mm | cm2 | cm4 | mm | MPa | mm | mm | cm2 | |
| CHS 114.3 × 3.6 | 114.3 | 3.6 | 15.52 | 191.98 | 39.2 | 235 | 114.3 | 3.6 | 15.52 |
| Pipe | Specimen | Periods (s) at 10% Intensity | Periods (s) at 140% Intensity |
|---|---|---|---|
| Welded Omega loop | 0.0666 | 0.0680 | |
| 7 | 0.0350 | 0.0353 | |
| 0.0236 | 0.0237 | ||
| Flanged Omega loop | 0.1079 | 0.1129 | |
| 8 | 0.0620 | 0.0629 | |
| 0.0236 | 0.0236 | ||
| 0.0557 | 0.0565 | ||
| Welded V loop | 9 | 0.0295 | 0.0299 |
| 0.0236 | 0.0235 | ||
| 0.0978 | 0.0992 | ||
| Flanged V loop | 10 | 0.0494 | 0.0498 |
| 0.0206 | 0.0208 | ||
| 0.0830 | 0.0835 | ||
| Welded straight loop | 11 | 0.0594 | 0.0596 |
| 0.0341 | 0.0346 | ||
| Flanged straight loop | 0.1276 | 0.1285 | |
| 12 | 0.0830 | 0.0835 | |
| 0.0594 | 0.0596 |
| Pipe | Specimen | Peak Absolute Acceleration (g) | ||
|---|---|---|---|---|
| In-Plane (x) Axis | Out-of-Plane (y) Axis | Vertical (z) Axis | ||
| Welded Omega loop | 7 | 1.75 | 2.01 | 0.29 |
| Flanged Omega loop | 8 | 2.84 | 2.79 | 0.50 |
| Welded V loop | 9 | 1.41 | 1.72 | 0.33 |
| Flanged V loop | 10 | 1.82 | 2.25 | 0.47 |
| Welded straight loop | 11 | 2.00 | 1.50 | 1.02 |
| Flanged straight loop | 12 | 3.09 | 2.40 | 1.41 |
| Pipe | Specimen | Peak Relative in-Plane Displacement (mm) | |||
|---|---|---|---|---|---|
| 10% Intensity | 50% Intensity | 100% Intensity | 140% Intensity | ||
| Welded Omega loop | 7 | 0.13 | 0.60 | 2.85 | 5.93 |
| Flanged Omega loop | 8 | 1.74 | 6.91 | 14.99 | 22.44 |
| Welded V loop | 9 | 0.99 | 5.22 | 11.20 | 16.14 |
| Flanged V loop | 10 | 1.46 | 7.10 | 13.66 | 19.97 |
| Welded straight loop | 11 | 1.75 | 7.04 | 13.90 | 19.10 |
| Flanged straight loop | 12 | 3.42 | 8.84 | 17.29 | 25.01 |
| Property | Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | Specimen 6 |
|---|---|---|---|---|---|---|
| Straight | Straight Flanged | Omega Welded | Omega Flanged | V Welded | V Flanged | |
| Elastic stiffness (kN/mm) | 33.93 | 38.42 | 0.26 | 1.01 | 1.27 | 2.18 |
| Yield force (kN) | 470.79 | 467.83 | 32.08 | 31.12 | 59.37 | 78.11 |
| Yield displacement (mm) | 13.88 | 12.18 | 122.66 | 30.82 | 46.92 | 35.79 |
| Ultimate force (kN) | 488.93 | 493.32 | 41.81 | 34.28 | 74.81 | 92.08 |
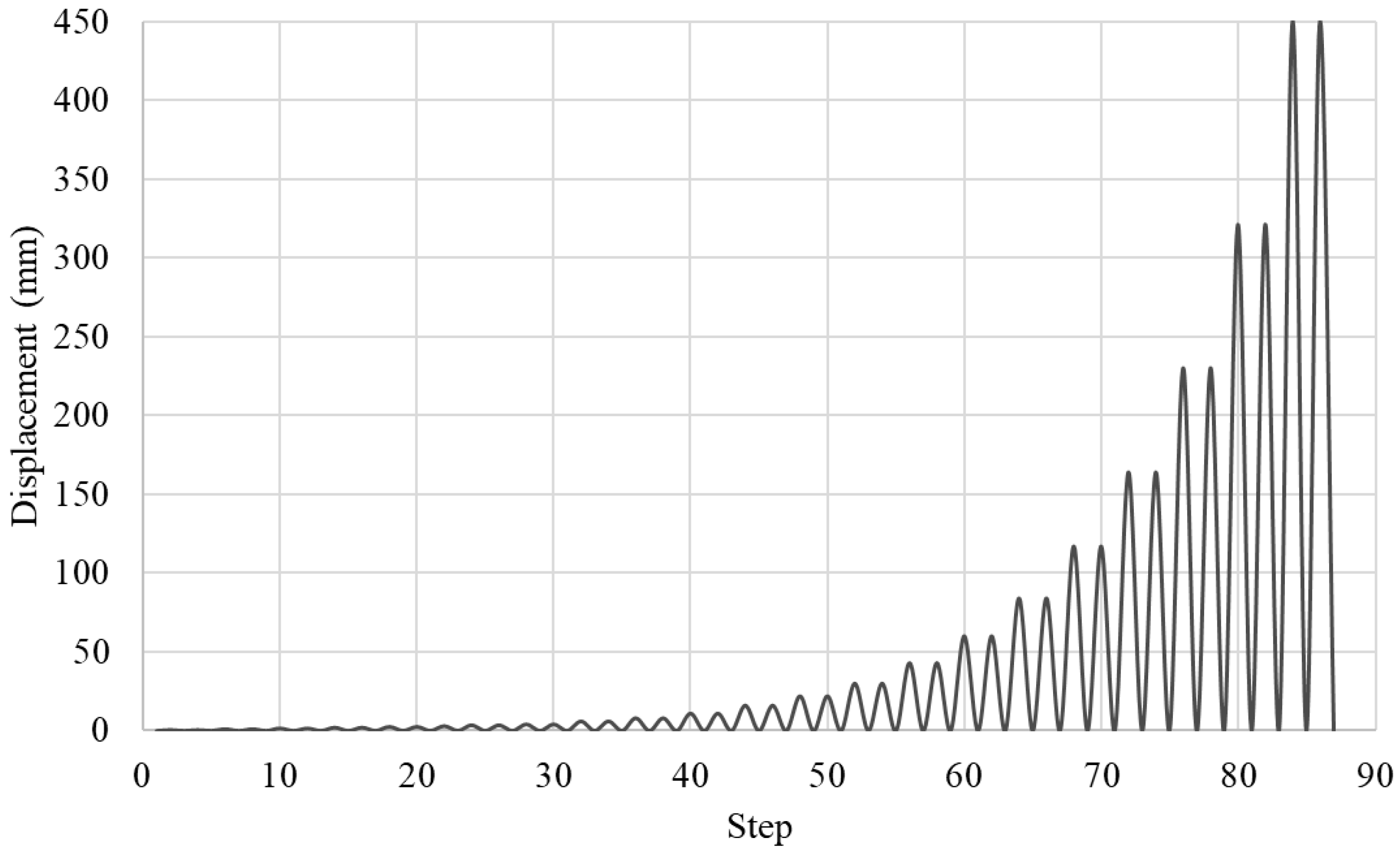
| Ultimate displacement (mm) | 29.94 | 42.97 | 321.22 | 230.16 | 105.16 | 60.04 |
| Axial ductility | 2.16 | 3.53 | 2.62 | 7.47 | 2.24 | 1.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalarca, B.; Gabbianelli, G.; Brunesi, E.; Perrone, D.; Ciucci, M. Experimental Characterization of the Seismic Response of Industrial Steel Piping Systems. Buildings 2025, 15, 4197. https://doi.org/10.3390/buildings15224197
Chalarca B, Gabbianelli G, Brunesi E, Perrone D, Ciucci M. Experimental Characterization of the Seismic Response of Industrial Steel Piping Systems. Buildings. 2025; 15(22):4197. https://doi.org/10.3390/buildings15224197
Chicago/Turabian StyleChalarca, Bryan, Giammaria Gabbianelli, Emanuele Brunesi, Daniele Perrone, and Mariano Ciucci. 2025. "Experimental Characterization of the Seismic Response of Industrial Steel Piping Systems" Buildings 15, no. 22: 4197. https://doi.org/10.3390/buildings15224197
APA StyleChalarca, B., Gabbianelli, G., Brunesi, E., Perrone, D., & Ciucci, M. (2025). Experimental Characterization of the Seismic Response of Industrial Steel Piping Systems. Buildings, 15(22), 4197. https://doi.org/10.3390/buildings15224197









