Harnessing Machine Learning for Multiclass Seismic Risk Assessment in Reinforced Concrete Structures

Abstract

The objective of this study is to develop an artificial intelligence algorithm that can predict both the risk level and damage level of reinforced concrete structures through classification and proportioning. This algorithm identifies buildings that require preventive measures before an earthquake and buildings that require immediate repair or demolition after an earthquake. A key aspect of the approach is calculating each building’s risk level as the ratio of its risky story to the total number of stories. That calculation provides a normalized figure, enabling comparison between buildings of varying sizes and complexities in an equitable way. The dataset of this study includes 100 buildings affected by previous earthquakes in Türkiye and 782 buildings with detailed seismic analysis. Thirteen different building parameters, structural, seismic, and geometric, have been considered within the scope of this study. Rapid visual screening (RVS) methods were applied for structural integrity analysis, and machine learning models were used for improvement in accuracy and efficiency. In the comparison of the model sets, the approach achieved the highest accuracy of 77% with an ensemble of four models. The results demonstrate the value of blending AI with traditional methodologies for risk analysis. It shows a viable and scalable mechanism for prioritization of retrofit and inspections and helps engineers and policymakers enhance disaster preparedness. By identifying structures at high risk, this work contributes towards overall aims for earthquake resilience in buildings. This study introduces a Pearson-correlation-based feature analysis and a Random Oversampling strategy to enhance model balance. The ensemble model achieved 83% external accuracy and outperformed the traditional RVS method (68%), reducing computation time from minutes to seconds.

1. Introduction

Developing countries suffer most in urban planning and construction standards with a combination of factors such as a lack of technical expertise, indeterminate regulatory frameworks, poor financial capacities, and unregulated, uncontrolled urbanization fueled by growing populations. This chaotic and unregulated development growth is inherently unsustainable, even in economically developed urban areas, because it tends to encourage the widespread use of inferior building materials and shoddy workmanship. Those vulnerabilities in buildings produce catastrophic consequences during earthquakes, in which structure collapses can result in widespread loss of property, financial loss, and loss of life in a most unfortunate scenario. Strong ground motions can produce strong dynamic forces, imposing high deformative forces on buildings, culminating in partial to complete collapses in a range of forms of damage. Considering such weaknesses, it is important for developing nations to have overall strategies for enhancing existing stocks of buildings and efficient re-urbanization processes. Most such strategies involve a planned demolition of high-risk buildings in urban transformation activities. However, in a search for efficient seismic hazard mitigation, new approaches deviating from traditional ones must be embraced.

The literature describes a range of methodologies for seismic risk estimation for individual buildings. Conventional techniques involve sophisticated analysis with explicit requirements for detail in terms of both materials and geometry, for instance, in documents such as FEMA 356 [1], Eurocode 2 [2], Turkish Earthquake Code (TEC) [3], Guidelines for the Assessment of Buildings under High Risk (GABHR) 2013 [4], and GABHR 2019 [5]. Conventional techniques demand a lot of time and expert studies, and, for a high level of evaluations in a widespread manner, in environments with a scarcity of resources, such techniques become unfeasible. To counter such limitations, rapid visual screening (RVS) methodologies have been proposed [6,7,8,9,10,11,12,13,14], most of which have been developed for reinforced concrete (RC) structures. Large-scale seismic vulnerability can be evaluated using empirical, analytical, or rapid visual screening (RVS) methodologies. Among these, RVS-based approaches provide a balance between field practicality and statistical robustness [15].

The RVS approach was introduced in Law No. 6306, “Law on the Transformation of Areas Under Disaster Risk,” by Ministry of Environment and Urbanization of Türkiye [4] enacted following the 1999 Golcuk and 2011 Van earthquakes in Türkiye. The Legislation aims to reduce seismic risk and enhance urban safety by systematic identification, assessment, and restoration of vulnerable structures. In its operations, RVS involves exterior observation and gathering information about load-bearing system type, number of stories, building age, and presence of any discrepancies and visible structural defects. All such information is processed through a rating system that clusters buildings in terms of seismic hazard and can be used for prioritization for efficient use of resources and time.

The RVS technique possesses a range of significant advantages. It can enable quick identification of high-risk structures, and hence, it is ideal for inspecting large inventories of buildings, for instance, high-rise buildings, in a relatively short span of time. It is a viable alternative for preliminary seismic risk assessments because it is both a time-saving assessment and less costly in terms of engineering studies.

Additionally, compliance with post-2000 codes can be facilitated through RVS, retrofitting resistivity of older buildings. In its use, its application is obstructed through its susceptibility to assessments’ subjectivity and variation in its output. Public awareness and acceptance of its output form critical factors in successful urban transformation programs’ realization.

In order to improve the extensibility and accuracy of RVS, integration with advanced technology in terms of machine learning (ML) and RVS is becoming more a reality. In this article, a filtering mechanism with increased accuracy using ML algorithms for estimating seismic vulnerability of buildings, prioritization of buildings for urban transformation, and deciding demolition and retrofit requirements is proposed. In developing an ML model for predicting vulnerability of RC structures, computationally complex algorithms have been adopted for supporting urban planning and disaster risk management decision-making in this article.

The foundation for RVS can be seen in early Japanese studies with the 1973 Nemuro and 1978 Miyagi earthquakes. Umemura and Okada developed a technique for seismic performance evaluation of in-service structures, and in 1980, a refinement of such a technique included rapid seismic performance evaluation for low- and mid-rise buildings in terms of guides for such structures [8]. Globally, significant studies include FEMA 154 [16] and FEMA 155 [12], developed under the Applied Technology Council (ATC) and approved under FEMA, and updated at times to include new development in seismic risk evaluation.

In Türkiye, a significant study in formulating methodologies for RVS is Sucuoglu, Yazgan [17], who proposed a low-rise RC building screening criterion with information taken from the 1999 Duzce earthquake. In this method, several factors were considered as evaluation criteria, including the seismicity of the building, the seismicity of the location, the number of stories, the presence of soft story, the presence or absence of overhang, and the visible quality of the building. Based on these criteria, a scoring system was proposed. Following the 2001 Bhuj earthquake in India, a criterion for similar purpose was proposed by Jain, Mitra [18], with factors such as presence of a basement, height in terms of number of floors, and presence of a structural irregularity. Yadollahi, Adnan [19] and Aldemir, Guvenir [20] have proposed such methodologies in follow-up studies, with improvements in predictive efficiency and generalizability to a range of building types. Similarly, Coskun, Aldemir [14] sought to determine the riskiness of reinforced concrete buildings through the utilization of rapid screening methods. In the 2024 publication of Bahsi, Coskun [21], the regulatory parameters of the ‘Guide for the Assessment of Buildings at High Risk’ were analyzed.

The aim of this study is to obtain more accurate and realistic assessments by incorporating artificial intelligence technology into rapid scanning methods. When conducting a literature review on the application of artificial intelligence in civil engineering, a study conducted by Adeli and Yeh [22] in 1989 was encountered. This study aimed to predict load capacities using artificial neural networks.

In later studies, artificial intelligence applications in areas such as damage detection, risk analysis, and structural integrity control began to attract attention. In their 1992 study, Kudva, Munir [23] developed an artificial neural network model for the purpose of determining the locations of possible damage in rigid floor slabs. The objective of the study was to ascertain the locations of the holes to be drilled in the plates and the optimal hole diameters through the utilization of the model. Elkordy, Chang [24] sought to ascertain the extent of damage to buildings in earthquakes through the utilization of an artificial neural network. To this end, the researchers initially trained an artificial neural network with artificially created sample building models. These were subsequently manufactured in small scale and subjected to a series of shaking table tests. The performance of the artificial neural network model was then tested by comparing the damage conditions of the physical models with the results obtained from the artificial neural network.

In their 2001 publication, Sohn and Farrar [25] determined buildings’ undamaged and damaged state time-dependent natural acceleration values for acceleration in terms of its impact on foundation accelerations in terms of vibration to evaluate its impact in structures. In creating an autoregressive moving average (ARMA) model, using collected data, they moved subsequently. In 2013, Caglar and Garip [26] developed an artificial neural network model for its use in estimating buildings’ level of damage. In creating such a model, relevant rapid screening study parameters, in terms of the literature, were taken and utilized as input parameters for creating such a model. In checking such a model’s performance in buildings subjected to damage during the Bingöl earthquake in 2003, collected data were utilized for testing its performance.

A review of existing literature identifies early studies in researching earthquakes, and then, in investigating structural elements, damage, in having utilized artificial neural networks for such studies in a predominant manner. In contrast, emerging trends have involved alternative approaches in machine learning, a notch higher in terms of artificial neural networks, in a quest to address complex problems in civil engineering. Dong and Shan [27] in 2013 explored spatial damage assessment by leveraging pre- and post-disaster imagery alongside image processing techniques. In a similar manner, in 2015, Geiß, Pelizari [28] applied machine learning algorithms, including random forest and support vector machines, to identify specific structural systems of buildings using imagery captured by drones. In 2022, in an evaluation of masonry structures’ vulnerability to collapsing, or extreme damaging, under seismic forces, Coskun and Aldemir [29] adopted machine learning approaches to evaluate the risk of collapse or severe damage in masonry structures under seismic conditions. Liu, Zhang [30] utilized support vector machine algorithms to integrate geographic information system (GIS) data for assessing the efficacy of seismic urban vulnerability evaluation methods for both masonry and reinforced concrete buildings. Cinar, Aldemir [31] developed an artificial neural network-based approach in an estimation of buildings’ fundamental period of vibration for undamaged and damaged buildings. Most recently, Coskun, Aktepe [32] utilized ensemble learning approaches to estimate the risk classification of masonry buildings. In another recent study on this subject by Ruggeria et al. [15], the regional seismic vulnerability and direct economic loss functions for existing reinforced concrete (RC) buildings were derived using a multidimensional discrete sampling approach. In this process, the Gibbs Sampling algorithm and the Kullback–Leibler divergence sampling process were utilized with the specific aim of resolving the issues of multi-modality and multidimensionality encountered in the input data.

These studies in concert illustrate increased application of machine learning techniques in earthquake engineering, namely for application in such domains as estimation of damage, analysis of risk, and system identification of structures. Traditional engineering practice is being facilitated through integration with high-tech computational tools, generating ever-improved efficiency and accuracy and enhancing disaster management and urban planning.

2. Details on the RC Building Database

A comprehensive RC building database was developed to facilitate robust risk assessment methodologies for earthquake-prone structures. The primary objective is prioritizing buildings requiring preventive measures pre-earthquake and identifying structures needing urgent retrofitting or demolition post-earthquake. The dataset includes a total of 882 buildings, consisting of 782 buildings analyzed according to the GABHR (2019) [5] and 100 buildings affected by various earthquakes in Türkiye.

Specifically, the database includes buildings affected by the 2019 Istanbul-Silivri, 2020 Elazıg-Sivrice, and 2020 Samos-Izmir earthquakes with varying damage levels—ranging from no damage to severe damage. The damage levels were categorized in accordance with the Circular on Damage Assessment [33] and Law No. 7269 on Measures to Be Taken Due to Disasters Affecting Public Life and Assistance to Be Provided [34]. Furthermore, the studies conducted by Bal et al. [35] in 2008, Silva et al. in 2015 [36], and Kohrangi et al. [37] were examined, and the building parameters mentioned in this study, which were deemed suitable for use in earthquake loss prediction models, were also utilized.

Buildings from various geographical regions with distinct seismic characteristics are included, enabling comprehensive assessment. The inclusion of pre- and post-earthquake data supports a total analysis of structural vulnerabilities. This comprehensive dataset supports developing machine learning models automating the building assessment process. A novel aspect is using a filtering method ensuring fair comparisons across buildings of different sizes and complexities, representing a pioneering effort in earthquake risk assessment research.

2.1. Features

The RC building database constructed for this study contains in-depth structural and seismic information important for seismic hazard analysis. The database includes 13 basic factors derived from general standards and previous research and supplemented with specific parameters specifically adapted for this study:

• Soil Class (SC): Determined based on the average shear wave velocity (VS30) of the uppermost 30 m of soil. It is classified into categories ZA, ZB, ZC, ZD, ZE, and ZF according to predefined VS30 thresholds. (

  Table 1. Local soil classes according to TEC-2018 [3].

  Local Soil Class	Soil Type	Vs30 [m/s]
  ZA	Solid, hard rocks	>1500
  ZB	Less weathered, moderately strong rocks	760–1500
  ZC	Very tight layers of sand, gravel, and hard clay or weathered, very cracked weak rocks	360–760
  ZD	Medium-firm layers of sand, gravel, or very solid clay	180–360
  ZE	Profiles containing loose sand, gravel, or soft-solid clay layers or more than 3 m soft clay layer	<180
  ZF	Soils requiring site-specific research and evaluation: (1) Soils with potential for collapse under earthquake influence (liquefiable soils, sensitive clays) (2) Clays with a total thickness of more than 3 m of peat and/or high organic content (3) High plasticity soils (PI > 50) with a total thickness of more than 8 m (4) Very thick (>35 m) soft or medium solid clays

  Notes: ZF soils require site-specific research and evaluation. These include (1) soils with potential for collapse under earthquake influence (liquefiable or sensitive clays); (2) clays with a total thickness of more than 3 m of peat and/or high organic content; (3) high plasticity soils (PI > 50) with a total thickness exceeding 8 m; and (4) very thick (>35 m) soft or medium solid clays.

  )
• Seismic Zone (SZ): Derived using the short-period spectral acceleration coefficient (Ss) and the local soil effect factor (Fs) provided in the TEC [3].
• Number of Floors (N): Total number of floors, including basements.
• Structural System Type (SS): Categorized based on vertical supporting structures. Frame or frame with shear walls.
• Vertical Irregularity (VI): Deviations in vertical load paths due to discontinuities in columns or shear walls.
• Neighboring Structure Status (NS): Relationship of a building to adjacent structures.
• Position of Neighboring Slabs (SIoc): Structural relationship of floor slabs in adjacent buildings.
• Slope of the Soil (SSlop): The building is constructed on a slope exceeding 20% incline or not.
• Short Column Effect (Scol): The presence of partially unbraced columns due to architectural or structural design considerations.
• Plan Irregularities (PI): Existing of geometric asymmetry or irregular structural element arrangements that could induce torsional effects.
• Existing of Soft/Weak Story (SoftS): Differences in stiffness between floors.
• Building Age (BA): The elapsed time since the building’s completion.
• Risk Level (RL): Under the 2019 Turkish GAHBR [5], reinforced concrete (RC) buildings are classified as risky if they fail to meet specific structural performance criteria. These criteria are designed to assess a building’s ability to withstand seismic forces and ensure public safety. A building is considered at risk if any of its critical components exceed the regulatory thresholds.
• Damage Level (DL): Damage levels, as defined by Turkish regulations such as the Damage Assessment Circular [33] and the 7269 Law on Measures and Aids in the Event of Disasters Affecting Public Life [34].

In the development of the methodology, the parameters and their corresponding input formats are presented in Table 1 and

Table 2. Summary of selected features and their definitions.

Abbreviation	Variable Name	Data Type	Ranges
SC	Soil class	Categorical/Nominal	1–2–3–4–5–6
SZ	Seismic zone	Numerical	Real numbers in the range (0, ∞)
N	Number of floors	Categorical/Nominal	1–12
SS	Structural system	Categorical	0: RC Frame + Shear Wall|1: RC Frame
VI	Vertical irregularity	Categorical	0: None|1: Exist
OH	Overhang	Categorical	0: None|1: Exist
Sloc	Position of Neighboring Slabs	Categorical	1: Leveled|2: Non-leveled
Sslop	Slope of the soil	Categorical	1: Flat|2: Sloped
NS	Neighboring Structure Status	Categorical	1: Separate|2: Adjacent 3: Adjacent to the corner
Scol	Short column	Categorical	0: None|1: Exist
PI	Plan Irregularities	Categorical	0: None|1: Exist
SoftS	Soft Story	Categorical	0: None|1: Exist
BA	Building Age	Numerical	4–113 years
RL	Risk Level	Numerical	Real numbers in the range (0, 1)
DL	Damage Level	Categorical	No Damage: 1|Slight Damage: 2|Moderate Damage: 3|Severe Damage: 4

.

2.2. Exploratory Data Analysis

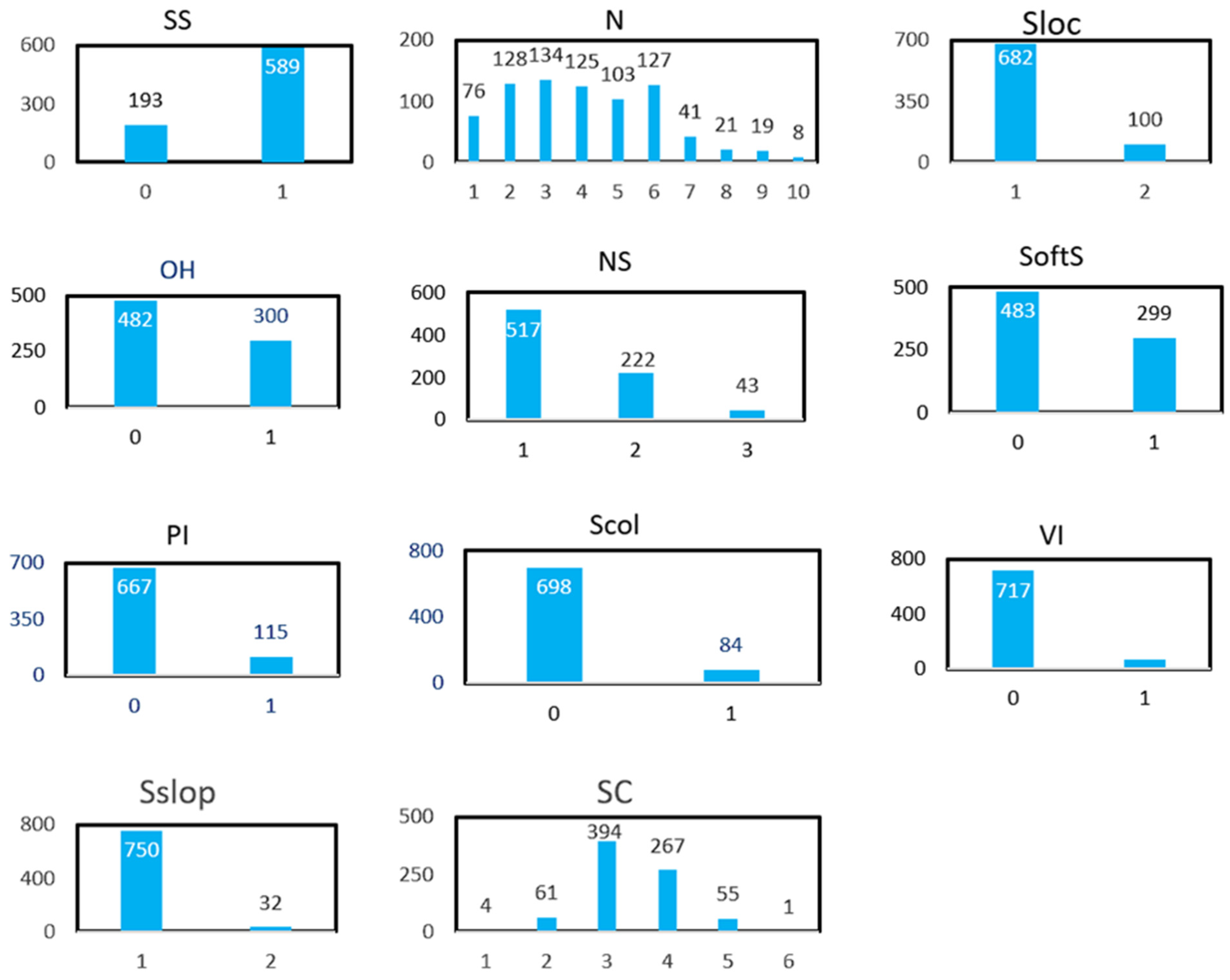
Exploratory data analysis (EDA) was conducted in an attempt to comprehend distribution, relationships, and trends in the training dataset for both numerical and categorical variables. Bar charts were generated to explore the frequency distributions of the categorical variables, and significant trends in structural characteristics were noticed. Distribution of stories (N) revealed that buildings with three and six stories were most dominant, with taller buildings being less dominant. Distribution of neighboring structure status (NS) revealed that most of the buildings were standalone buildings. This category indicates that the seismic response is less likely to be disturbed by the interaction of adjacent buildings.

Overhang (OH) feature was present in almost half the buildings with overhang, a feature that could potentially be a cause for concern in the event of seismic activity. There existed a soft story (SoftS) in a significant portion of buildings, indicative of a potential vulnerability. Analysis of structural system (SS) revealed that most of the buildings shared a specific design, and there was limited variation in the dataset. All the other categorical features such as plan irregularities (PI), short columns (Scol), position of slabs (Sloc), slope of soil (Sslop), and vertical irregularities (VI) exhibited similar trends, with most of the buildings not possessing these potentially risky features (Figure 1).

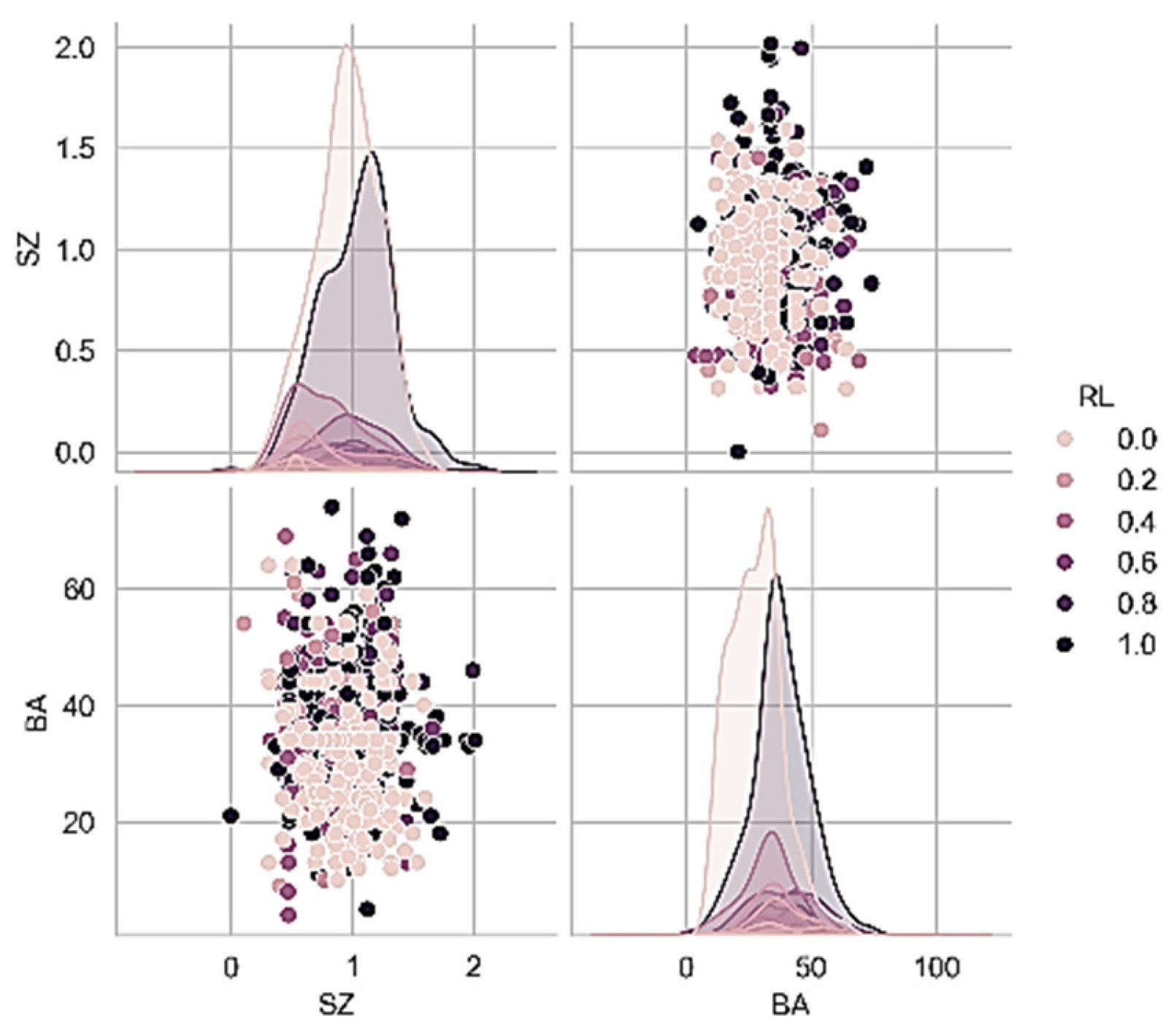
Numerical variables, such as seismic zone (SZ), age of buildings (BA), and level of risk (RL), were analyzed via pair plots, shown in Figure 2. Analysis revealed older buildings have a higher level of risk, and age and vulnerability have a positive correlation. In addition, seismic zone categories played a significant role in characterizing the level of risk, with buildings in areas with a high level of seismic activity having a high level of vulnerability. Building concentration in certain age groups added to emerging trends indicative of continuous degradation in structures.

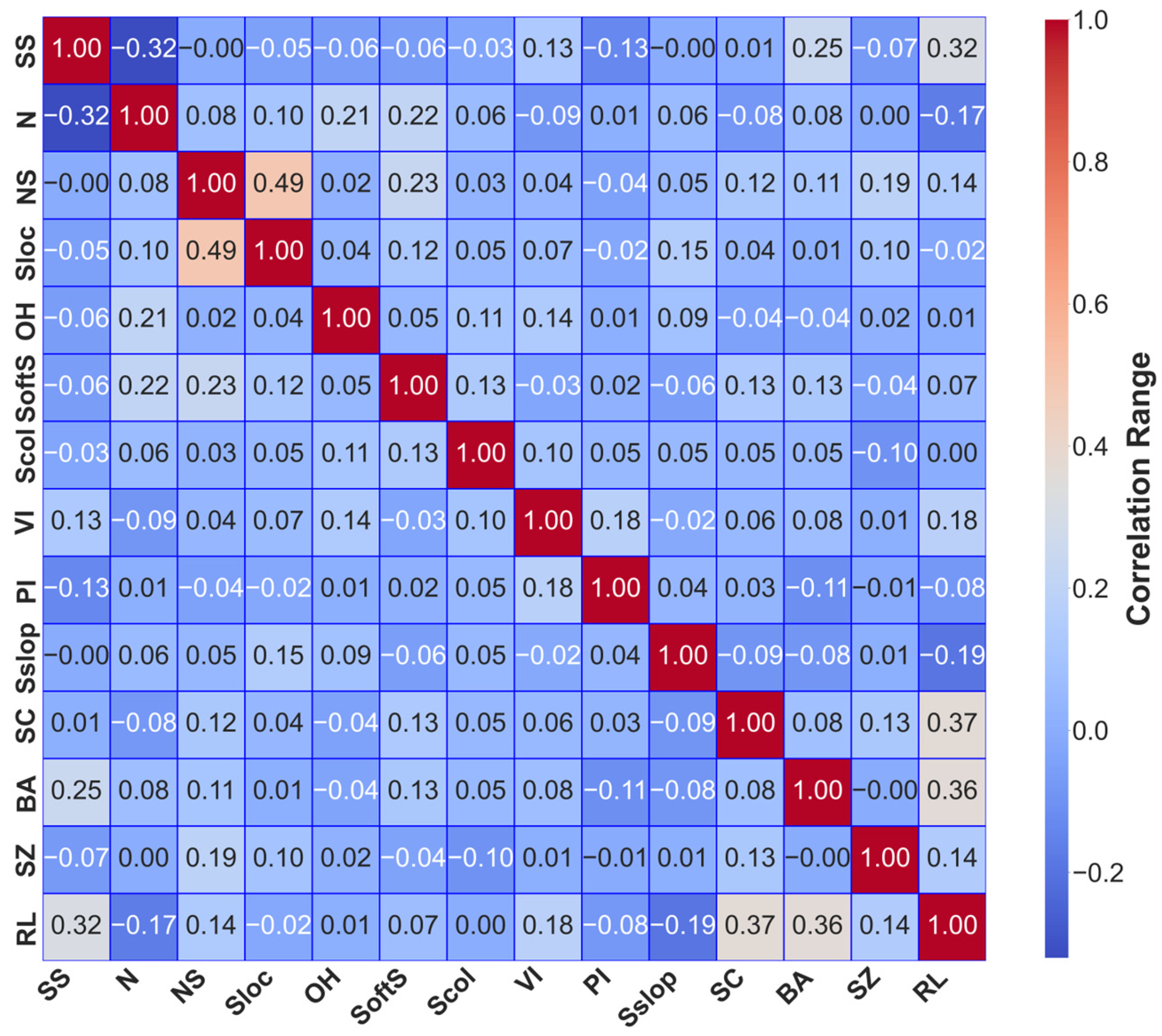
A correlation heatmap was used to explore the relationships between numerical variables, revealing a moderate positive correlation (0.36) between building age and risk level, suggesting that older structures are generally at greater risk (Figure 3). There existed a less strong relation between seismic zone and level of risk, and for that reason, factors apart from location in a region have a high contribution towards structure risk.

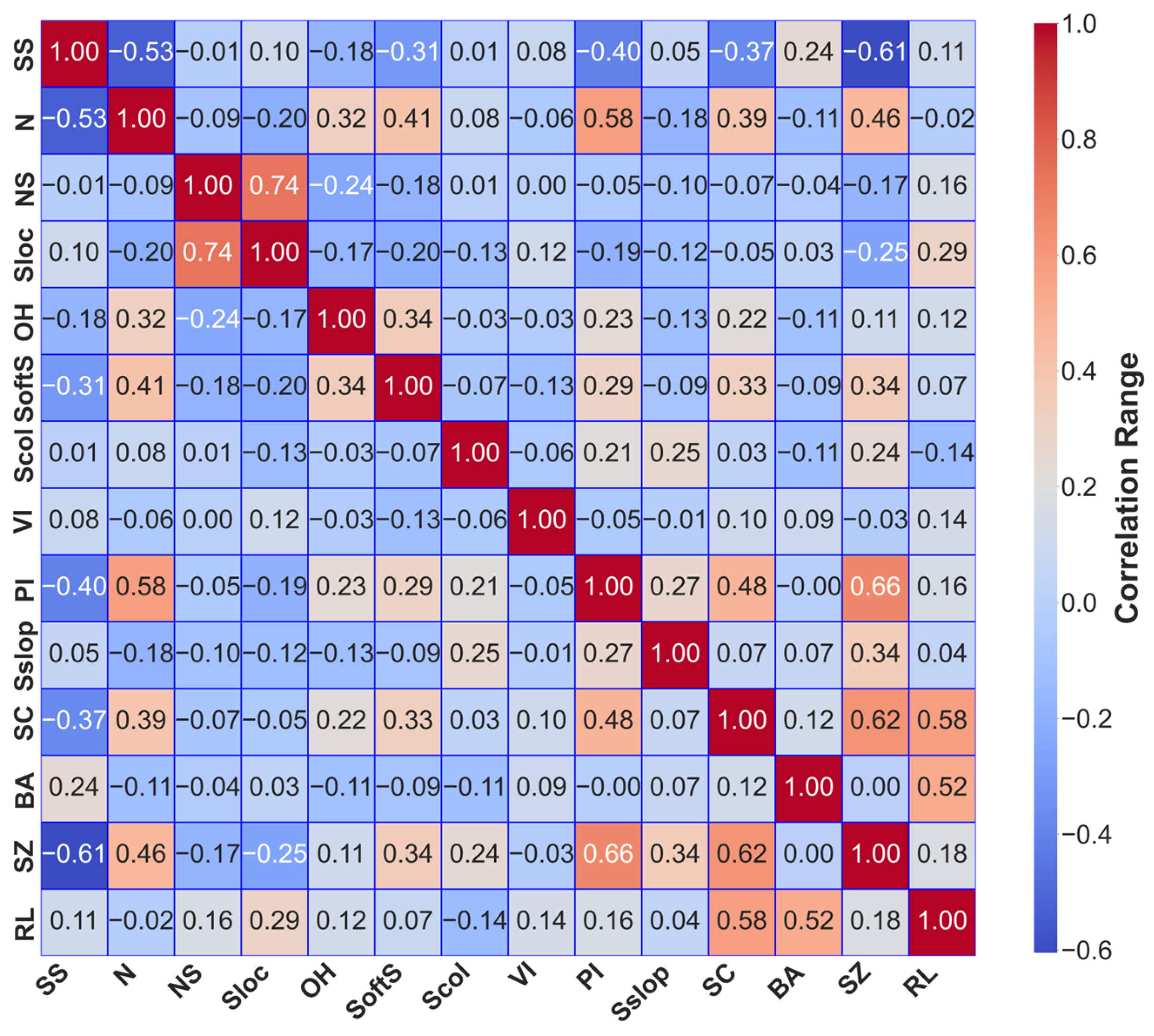
The correlation heatmap provides a general view of the intercorrelations between the various features in training data. The values for correlation range between 1 and −1, with positive values representing a direct relationship between variables and negative values representing an inverse one. Inspection reveals most feature correlations to be moderate to weak, with a number of interesting associations providing useful information about the structural risk estimation model.

At 0.37, the heatmap shows a modest association between risk level (RL) and building age (BA). Therefore, older buildings represent more risk, since aging buildings sometimes suffer with architectural defects and material deterioration. Comparably, the little positive connection between seismic zone (SZ) and risk level (RL) (0.36) suggests that structures in seismically high-risk areas are more prone to damage. Conversely, the correlations between RL and other structural attributes, including soft story presence (SoftS), plan irregularities (PI), and short columns (Scol), are comparatively weak. This suggests that risk levels are not significantly affected by individual structural characteristics alone but rather emerge from complex interactions among various factors. This study shows a modest association (0.49) between neighboring structure status (NS) and slab position (Sloc), suggesting that nearby buildings could influence slab placement choices and thus affect structural stability during seismic events.

The Pearson correlation coefficient was employed to quantify linear relationships among numerically encoded features, as it is most suitable for continuous and ordinal categorical variables. Correlations above |r| = 0.8 were examined for redundancy; none exceeded this threshold. A weak negative correlation between the number of floors (N) and the structural system type (SS) indicates that taller buildings may have implemented particular design modifications to efficiently handle structural load distribution. Low correlations between categorical variables, including overhang (OH), vertical irregularity (VI), and soil slope (Sslop), are suggestive of a complex way in which these variables contribute to risk assessment that might not be entirely reflected by linear correlation analysis alone.

The results of the correlation analysis show that most structural parameters have poor individual connections. This highlights the necessity for sophisticated modeling methods that can effectively capture non-linear interactions to enhance predictive accuracy. The weak correlations among independent variables indicate minimal multicollinearity, which is advantageous for machine learning models by reducing redundancy and improving interpretability.

The correlation analysis emphasizes the complex nature of building risk assessment, as it is known that reinforced concrete buildings are subject to structural, environmental and design factors. The insights establish a basis for feature selection and engineering strategies aimed at developing robust predictive models for structural risk evaluation.

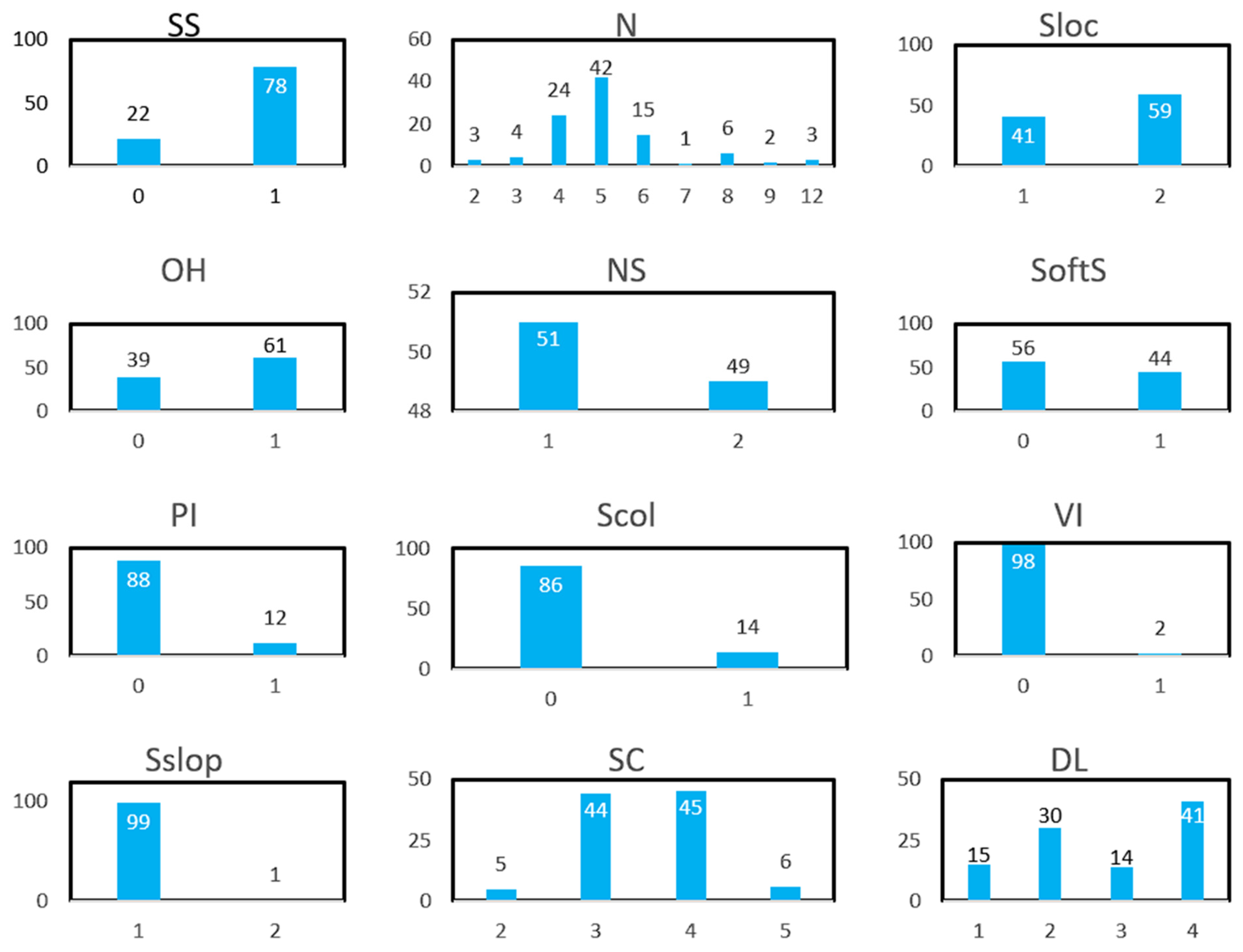
Analyzing the external data reveals significant new insights into the distribution and interconnections of the specified features (Figure 4). Bar graphs illustrate the frequency distribution of categorical variables, thus highlighting patterns and inconsistencies within the dataset.

The NS feature demonstrates a nearly equitable distribution, with 49 in one group and 51 in the other. The PI characteristic indicates a significant discrepancy: 12 cases in one group and 88 cases in the other. This indicates potential biases that may necessitate alternative models or compensatory measures. The SS variable exhibits considerable distortion, with 78 data points categorized in a single group.

From the external dataset point of view, some features—like VI—have great skews; 98 events fall into one category and just 2 into the other. This distribution implies the requirement of careful management to avoid biassed training and evaluation procedures. Moreover, given 99 observations in one class, the Sslop variable in the external data is quite dominant and emphasizes the need of strong evaluation measures considering class imbalance. All things considered, external information is a mix of balanced and unbalanced feature sets that must go through computed preprocessing in a quest to maximize model performance. In contrast, observations regarding frequency distribution speak towards a demand for potential data augmentation and resampling techniques, but correlation analysis reveals a demand for selecting non-redundant features in a quest to maintain predictive model integrity. All such observations serve as a basis for developing a strong model of analysis that effectively addresses certain characteristics in external information.

The correlation heatmap analysis (Figure 5) illustrates significant interdependencies among components. The correlation between NS and Sloc is noteworthy; a coefficient of 0.74 indicates a substantial positive relationship. This indicates that additional dimension reduction or feature engineering may be necessary, as these two attributes could contain redundant information. Moreover, in predictive modeling, a moderate positive correlation of 0.66 between Sslop and BA indicates a substantial interaction between these variables. In contrast, the SS characteristic exhibits negative correlations with several variables, particularly SZ (−0.61), potentially indicating opposing inclinations that could influence categorization tasks. Conversely, several have a reverse, not positive, correlation, such as between SS and N, with a strong reverse correlation of −0.53, with one feature tending to rise when the other will drop, and a possible contrasting underlaying controlling factor for these traits. SS and SZ demonstrate a significant reverse correlation with a score of −0.61.

Several feature pairings, such as PI and SC (0.48) and BA and SZ (0.62), exhibit modest correlations that may elucidate overall model complexity. These interactions emphasize the necessity of conducting multicollinearity tests to ensure that the inclusion of correlated variables does not adversely impact model stability and interpretability.

The comparative analysis of feature correlation matrices for training and external datasets reveals important information about feature relation variance and stability. Several feature relations have been observed to dominate both datasets, such as strong relations between Sloc and NS (0.49 in training and 0.74 in external), indicative of strong relations at a deeper level, but important discrepancies have been observed in many cases. Additionally, a strong negativity between N and SS in the external dataset (−0.53) stands in contrast with its relatively lesser negativity in training (−0.32), indicative of a probable variation in data distribution and behavior in terms of sampling.

Similarly, a relation between SS and SZ shifts from a negligible value in training (−0.07) to a strong negativity in the external dataset (−0.61), indicative of a probable structural variation in feature relations. In addition, new relations, such as an increased relation between BA and Sslop (rising from 0.10 to 0.66), reveal the impact of external factors in changing relations in a manner not captured in training datasets.

These inconsistencies help to highlight the need to make models more robust. This is achievable via methods like feature engineering, feature normalization, and feature scaling, and by increasing adaptability during training. Resolving such inconsistencies beforehand minimizes biases and allows the model to generalize more effectively. Eliminating such inconsistencies reinforces a model’s prediction performance and accuracy, especially when working with diverse datasets and real-world situations.

3. Building Risk and Damage Assessment

Building risk and damage assessment is an important tool for estimating the vulnerability of buildings to natural hazards, specifically seismic events. It involves a systematic analysis of probable risks, guided by a variety of factors concerning structures and environments, and grading of severity of damage incurred in buildings. The Turkish Regulation on the Determination of Risky Structures, GAHBR, is a complete guideline for estimating seismic vulnerability in buildings. Under the regulation, buildings with ten floors and below fall under low-rise RC structures. Seismic hazard in such buildings is analyzed in terms of a series of factors discussed in the regulation, with a view to defining weaknesses in structures and prioritizing countermeasures for them. In this study, prioritization of earthquake risk in low-rise RC buildings is the key objective. For such a purpose, data have been drawn exclusively from such buildings to maintain uniformity and pertinency in analysis.

The research utilizes two databases in formulating and testing the proposed risk evaluation technique. In training algorithms, use is made of the Risky Building Database (RBD), consisting of buildings rated as risky or not regarding compliance with the GAHBR regulation. Actual cases in real life in which risk rating is calculated through traditional methodologies can be learned through structures in this database, rated regarding compliance with regulating requirements. For model testing and evaluation, use is then made of the Damage Assessment Database (DAD), consisting of buildings having experienced earthquakes in the past, and through this database, predictive performance of a model can be evaluated in terms of actual earthquake-related damage.

This study aimed to prioritize the earthquake hazard of low-rise buildings, and the databases created in this context were determined from such buildings. In the training of the algorithm, buildings that were determined to be risky and non-risky according to the GAHBR regulation used the RBD. In the testing of this trained model, buildings damaged in earthquakes used the DAD.

3.1. Machine Learning Framework for Seismic Risk Prediction

The GAHBR [5] gives a framework for the seismic vulnerability assessment of buildings. According to this regulation, RC buildings up to ten floors are considered low-rise buildings. The regulation introduces clear criteria for assessing earthquake risk, prioritizing the identification of structural deficiencies and necessary mitigation measures. The aim of this study is to assess earthquake risk in RC buildings, with the condition that all data to be analyzed are only from these types of buildings in order to maintain consistency and relevance. To this purpose, the research utilizes two primary databases for training and validation of the risk assessment methodology. The main dataset (n = 782) was collected from nationwide RVS surveys, while an external validation dataset (n = 100) comprising post-earthquake-inspected RC buildings. The latter dataset reflects field-observed damage levels in high-seismic regions, which explains minor shifts in correlation strength across variables.

The RBD used to train the algorithm consists of buildings labeled as risky or non-risky according to the GAHBR regulation. Since this database is formulated based on pre-established regulatory actions, it enables the model to learn from actual instances where the risk categorization has been officially determined. For validation and testing, the research uses the DAD that consists of buildings damaged in past seismic activities. This allows the model’s predictions of actual earthquake damage to be tested, and hence, the robustness of its predictive ability can be determined.

Seismic risk analysis in GAHBR involves in-depth analysis of low-rise RC buildings’ behavior under seismic forces in detail. As per the code, one must assess displacements and capacities in terms of moment for vertical structures such as columns and shear walls in an attempt to evaluate such structures’ capacity for seismic forces. The seismic demand for such structures is calculated and contrasted with capacities in terms of moment for such structures. The demand-to-capacity ratio is used as the most important measure of structural fragility. If this ratio exceeds the threshold values specified for the different structural elements, the building is defined as at risk. The procedure is a quantitative and standardized method of identifying buildings that are potentially structurally deficient.

Furthermore, GAHBR requires the computation of axial compressive stresses in columns and shear walls for the determination of general structural stability. These are computed from the vertical loads on the structure, and the code stipulates that the average axial compressive strength at each floor level shall not exceed 65% of the current compressive strength of the concrete. If any vertical structural element surpasses this, the building in general is deemed to be hazardous. This stringent requirement underscores the overriding importance of load bearing capacity for the structural integrity of buildings, citing how even a single overstressed element can compromise the safety of the entire structure.

The second essential component of the GAHBR risk assessment procedure is the calculation of the story shear force ratio, which is an indicator of the seismic force distribution in the structure. This is calculated as the division of the summation of the shear forces on elements that have reached their risk level by the total shear force on the floor. When this ratio is greater than the limit established in the regulation—between 0 and 0.35 depending on the axial compressive strength levels—the building is considered to be at risk. This ensures that the analysis considers both the localized and overall seismic impact, providing a more comprehensive assessment of the building’s structural performance.

Overall, the GAHBR procedure offers a complete and systematic approach to seismic risk assessment of low-rise RC buildings. By incorporating element-level capacity checks, floor-level axial load determination, and shear force ratio calculations, the code ensures a complete and standardized assessment process. This study seeks to contribute to earthquake vulnerability reduction by developing insights from regulatory compliance assessments and real damage observations and thereby inform risk prioritization and decision-making in seismic resilience planning.

A schematic overview of the proposed methodology is illustrated in Figure 6, highlighting the data acquisition (RVS forms), preprocessing, oversampling, model training, and ensemble evaluation stages.

3.2. Machine Learning Framework for Damage Assessment

Post-earthquake damage assessment is a critical activity in rehabilitation and response to disasters, and it oversees defining integrity of buildings and usability in case of a quake. The evaluation entails checking for the intensity of damage generated in buildings during strong motions, with buildings placed in a variety of categories in relation to specific requirements. In Türkiye, post-earthquake damage assessments are conducted based on the Law No. 7269 on Measures to Be Taken Due to Disasters Affecting Public Life and Assistance to Be Provided [34] and the guidelines specified in the Damage Assessment Circular issued by the government. These regulations define the procedures and principles for evaluating and classifying building damages, ensuring a standardized approach across affected regions.

In terms of the Circular on Damage Assessment [33], buildings fall into four general categories: undamaged, slightly damaged, moderately damaged, and heavily damaged. All these categories will serve to inform future actions, including rehabilitation, retrofit, and demolition, in a manner that will preserve occupant security and a resilient environment in buildings.

The damage evaluation of buildings is conducted through careful field observations conducted by seasoned technical professionals, who assess both structural and non-structural elements in a systematic manner. Buildings in the undamaged category have no sign of damage sustained during the earthquake. In such a case, both the structural frame and non-structural parts have no impairments in terms of load-bearing and non-bearing parts, respectively. It is worth noting that any defects and damage present in a building even before the earthquake have not been considered in such an evaluation. Undamaged buildings can be considered safe for immediate occupancy with no intervention, and no repair work is needed to make them operational again.

Slight damage is incurred by buildings that have developed slight cracks in the paint, plaster, or walls and falling wall plasters caused by the earthquake. These are cosmetic damages that do not affect the structural strength or load-bearing capacity of the building. Filling up cracks and painting are minor repairs that are adequate to restore these buildings to their pre-earthquake condition. There are no safety concerns regarding their continued use.

Conversely, moderately damaged buildings show significant but not irreparable structural damage. Examples include cracks in vertical load-bearing elements (i.e., columns, shear walls,) and beams that could jeopardize the stability of a building if no intervention is performed. Despite this, a moderately damaged building is not considered uninhabitable, provided proper strengthening and retrofit interventions are performed. Buildings in this group can suffer secondary, non-structural damage, i.e., partition walls, and ceilings, and require additional work for rehabilitation. The most important criterion for such a rating is the fact that it is feasible to regain the bearing capacity and general usability of a building through retrofitting. Conversely, severely damaged buildings have extensive structural damage that threatens safety and stability to a great extent. In these buildings, structures experience extensive shear failures, extensive diagonal cracks in supporting members, partial or complete collapse of supporting structures, or large deformations, such as tilting and sliding. In these structures, irreparable damage is assumed, and retrofitting cannot restore the integrity of structures. In these buildings, a great degree of hazard to public safety is presented, and demolition is thus recommended to prevent future hazard. This classification system offers a clear, sequential system of damage appraisal, allowing for effective decision-making regarding usability, rebuild ability, or demolition of compromised buildings in post-disaster scenarios.

The Circular’s damage classification system is a general framework for post-earthquake damage assessment, enabling effective decision-making for subsequent interventions. Through the correct definition of damage severity, response teams are able to allocate resources efficiently, prioritize rehabilitation and reconstruction, and reduce secondary risks from aftershocks and further degradation of structures. The damage assessment exercise assists in long-term disaster readiness by obtaining information for refining construction practices, revising codes, and developing seismic resilience strategies.

Consequently, distinguishing between undamaged, slightly damaged, moderately damaged, and severely damaged classes for earthquake-prone building damage provides a logical approach for analyzing and addressing post-disaster structural vulnerabilities. Such logical analysis is necessary to ensure public safety, inform reconstruction efforts, and promote overall community resilience.

3.3. Classification

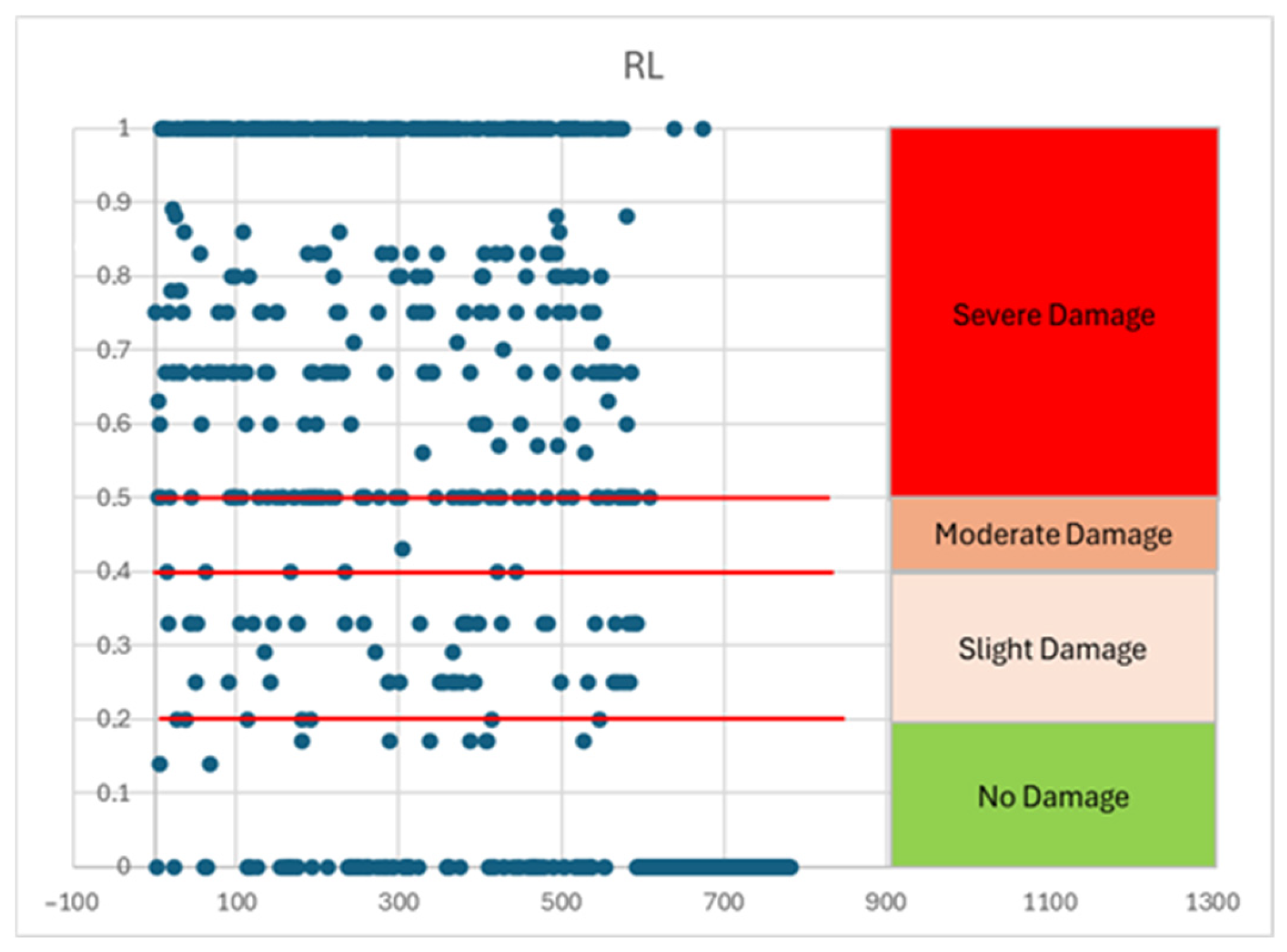
Figure 7 shows the distribution of risk levels (RLs) and their corresponding predicted damage levels (PDLs) for buildings in the training data, according to four separate damage severity classifications: No Damage (PDL 1), Slight Damage (PDL 2), Moderate Damage (PDL 3), and Severe Damage (PDL 4).

PDL category 1 (No Damage, RL ≤ 0.2), shown in green, consists of buildings that will not suffer any significant structural damage and have negligible or no apparent damage.

PDL category 2 (Slight Damage, 0.2 < RL ≤ 0.4), shown in light orange, consists of buildings with minor degradation of structures, most often superficial or easily repaired.

PDL category 3 (Moderate Damage, 0.4 < RL ≤ 0.5), shown in dark orange, consists of buildings with deeper structural weaknesses that require additional examination and potential retrofitting.

PDL category 4 (Severe Damage, RL > 0.5), shown in red, corresponds to buildings with high structural vulnerabilities and a high probability of failure or collapse during an earthquake (as in

Table 3. Predicted damage levels with corresponding risk level range and damage classification.

Predicted Damage Level (PDL)	Risk Level (RL) Range	Damage Classification
1	RL ≤ 0.2	No Damage
2	0.2 < RL ≤ 0.4	Slight Damage
3	0.4 < RL ≤ 0.5	Moderate Damage
4	RL > 0.5	Severe Damage

).

This classification scheme is important for enhancing computerized damage estimation methodologies and bridging the gap between quantitative hazard values and real-life damage interpretations. By defining threshold values for RL in predictive modeling, the scheme enables data-driven decision-making in urban planning, disaster management, and post-disaster rehabilitation processes.

This classification scheme is important for enhancing computerized damage estimation methodologies, bridging gaps between quantitative hazard values and real-life damage interpretations. By having thresholds for RL in predictive modeling, the scheme enables data-driven decision in urban planning, disaster management, and post-disaster rehabilitation processes.

Classification of severity in a systemic format maximizes efficiency and accuracy in vulnerability assessments of buildings and enables effective counterstrategies for disaster and planning for resilience of seismic zones.

4. New Risk Estimation Method

In this study, a method has been developed using artificial intelligence algorithms to identify buildings that require precautions before an earthquake and buildings that require urgent repair or demolition after an earthquake. The risk level of each building in the dataset was calculated as the ratio of the number of risky levels to the total number of levels in the building. This measurement provided a normalized value for a level of risk that could allow buildings with a variable level count to rank consistently with one another in a fair manner. With such a formula, both overall and comparative level of risk in a structure have been taken into consideration in a fair manner regardless of a building’s size in a risk evaluation.

4.1. Machine Learning Algorithms

All analyses were conducted using Python 3.11.7, together with NumPy 1.26.4, pandas 2.1.4, Matplotlib 3.10.0, Seaborn 0.13.2, scikit-learn 1.2.2, XGBoost 2.0.3, LightGBM 4.4.0, CatBoost 1.2.5, imbalanced-learn 0.11.0, and openpyxl 3.0.10.

In the development of the technique, a range of regression algorithms, under three general categories, were systematically considered: tree algorithms, linear algorithms, and other algorithms. Linear algorithms including Linear Regression [38], Ridge [39], Lasso [40], and ElasticNet [41] have been considered for use for their simplicity and interpretability, and for countering overfitting through regularization. Tree algorithms including Random Forest [42], Gradient Boosting [43], XGBoost [44], LightGBM [45], and CatBoost [46] have been considered for use for being powerful and for discovering complex patterns. Other algorithms including Support Vector Regressor [47], Huber Regressor [48], and Extra Trees Regressor [49] have been considered for use for specific strengths in specific types of datasets.

In this regard, 12 algorithms including Linear Regression [38], Ridge Regression [39], Lasso Regression [40], Elastic Net Regression [41], Huber Regression [48], Gradient Boosting Regression [43], Extremely Randomized Trees Regressor [49], Support Vector Regressor [47], Random Forest Regressor [42], Extreme Gradient Boost Regression [43], Light Gradient Boosting Machine Regressor [45], Cat Boost Regressor [46], and Ensemble Learning have been considered to be used. To present a quick rundown of algorithms considered for use, Linear Regression is one of the most basic and most general-purpose algorithms for regression. It formulates a relation between a target variable and one or several feature variables with a model in a linear form. It is powerful in its simplicity, interpretability, and computational efficiency but suffers from an assumption of a linear relation between variables, possibly not applicable in real-life scenarios, and vulnerability to outliers and multicollinearity. Linear Regression is considered for use as a general-purpose problem for a baseline.

To mitigate the influence of correlated variables, regularized regressors (Ridge and ElasticNet) were integrated within the ensemble. These algorithms penalize redundant parameters and improve generalization. Ridge Regression is a regularization of Linear Regression with an L2 penalty (magnitude of coefficients squared added to loss function) added to it. Ridge shrinks coefficients and is best at handling multicollinearity but, unlike Lasso Regression, does not perform feature selection, and all features will, therefore, make it into the model. It is a beneficial alternative when multicollinearity in the data can arise. Lasso Regression adds an L1 penalty (absolute value of coefficients) to the loss function, and it induces sparsity through shrinking a subset of coefficients towards zero. Lasso can use feature selection in that it can drop less important features. Lasso, nevertheless, does not work well with high-correlated features, because it will select one feature out of a group of high-correlated ones. Lasso performs best when feature selection is important.

Elastic Net is a combination of Lasso’s L1 penalty and Ridge’s L2 penalty and brings both its strengths together in harmony. Elastic Net is particularly beneficial in scenarios with both feature selection and multicollinearity requirements in datasets. Elastic Net, however, comes with two hyperparameters (L1 and L2 penalty weights) that must be tuned and, for that reason, can become a bit tedious to implement. Elastic Net is a general-purpose tool for application in scenarios with both regularization and feature selection requirements for a problem in a regression scenario.

Huber Regression is a robust algorithm for Huber loss function regression, less sensitive to outliers compared to a traditional squared loss function. Huber Regression incorporates both L1 and L2 regularization and is a robust alternative for datasets with outliers. Huber Regression is computationally expensive compared to Linear Regression but can function effectively when a dataset holds outliers that can destroy model performance.

Gradient Boosting is an algorithm for creating trees in an iterative manner, with one tree working to correct its predecessor’s errors. It is famous for its high predictive accuracy and its ability to model non-linear relations. However, it can become computationally expensive and overfitted when not optimized in a proper manner. Gradient Boosting is a powerful tool for use in regression when high accuracy is a necessity.

Extremely Randomized Trees Regression (Extra Trees) is a tree algorithm for an ensemble that involves increased randomness in tree development through random selection of splits. Extra Trees have less overfitting in comparison with Random Forests, and training is faster. Nevertheless, it can introduce increased bias with increased randomness added in. Extra Trees is an ideal alternative when computational efficiency and reduced overfitting become most important.

Support Vector Regression (SVR) is a form of support vector machine (SVM) in a regression model. It utilizes an application of a kernel function for mapping a non-linear relation and works effectively in high-dimensional spaces but can become computationally expensive, especially with larger datasets, and requires proper hyperparameter tuning.

Random Forest Regression (RF) is an ensemble method that builds multiple decision trees and averages their predictions. It is robust to overfit and manages non-linear relationships well. However, it is less interpretable than single decision trees and can be computationally expensive for large datasets. Random Forest is a versatile and reliable choice for general-purpose regression tasks.

Extreme Gradient Boost (XGBoost) is an optimized performance and efficiency boosted gradient algorithm. XGBoost is a high-performance, high-accuracy model with capabilities for dealing with missing values and regularization for overfit protection. XGBoost is a model that must be carefully tuned and overfits when not tuned in a proper manner. XGBoost is applied in high-performance critical regressions in general use.

Light Gradient Boosting Machine Regressor (LightGBM) is a high-speed and efficient gradient boosting platform optimized for use with big datasets. It is efficient compared to XGBoost but may be overfitted in smaller datasets. CatBoost is a gradient boosting algorithm that can work with categorical features naturally. CatBoost is overfit robust, and less preprocessing for categorical values is needed, but it can be slow in training when compared to LightGBM. CatBoost is specifically beneficial for datasets with categorical values.

Ensemble Learning is a powerful tool when one wishes to merge a variety of models in an effort to generate a performance boost. It pools a variety of model predictions (e.g., averaging, stacking, or boosting) to boost overall performance. It will have a higher level of accuracy over individual models and less overfit and variance. However, it will have a computationally high price and less interpretability.

In determining which algorithms to use, 12 preferred algorithms out of many algorithms for machine learning and regression models have been chosen, with consideration for the algorithmic factors.

4.2. Proposed Risk Estimation Approach

Assessing the structural risk of buildings is a critical task in disaster management and urban planning, especially in regions prone to natural disasters such as earthquakes. The ability to predict risk levels of buildings can help decision makers prioritize inspections, remediation efforts, and evacuation plans, ultimately improving public safety. Traditional risk evaluation processes have long involved expert analysis and manual audits, both of which can be a significant use of time and resources. With new technologies in machine learning, it can be made an automated process where fast and effective predictions can be made through the analysis of data.

This study proposes a novel predictive model for predicting vulnerability levels of buildings using a machine learning pipeline. With a rich source of structural and environmental information, this study aims to overcome a variety of predictive modeling issues including data imbalance, feature scaling, and model generalizability. A unique aspect of this work is the introduction of a risk level calculation based on the ratio of risky levels to the total number of levels in a building. To the best of the authors’ knowledge, this methodology represents a first in the study area, offering a new perspective on assessing structural vulnerabilities.

This study addresses a range of machine learning algorithms, including tree-based, linear, and ensemble methodologies, in a quest to develop a best practice for predicting risk. With methodologies including hyperparameter search, oversampling for balancing, and ensemble learning, the pipeline is designed to produce robust and interpretable predictions. Performance is evaluated with a set of metrics that provide a comprehensive analysis of model accuracy and generalization. In a quest to contribute towards an emerging field of data-driven disaster management, a scalable and efficient tool for estimating structural risk is developed in this work.

The dataset for the work exhibited unbalanced distribution regarding classes of risk level (RL), and unbalanced distributions tend to produce biased prediction because most classes are preferred for prediction by models. To mitigate, oversampling of underpopulated classes was conducted. Underpopulated classes (the minority classes) were identified, and samples for them were increased with a function for oversampling until a desired level was attained. Overbalanced samples and samples for the majority class were then blended to create a balanced dataset, offering fairness and efficient learning for all classes.

Feature scaling was another critical preprocessing step. Since machine learning models, particularly those relying on distance calculations, are sensitive to feature magnitudes, the standard scaler was employed. This method standardized numerical features by centering them to have a mean of zero and scaling them to have a standard deviation of one. This enabled equitable contribution of all the features and sped up model training and hyperparameter search. For hyperparameter search-supported models, grid search enabled the identification of the best settings, with the use of cross-validation for dependable performance estimation. To enhance predictive accuracy, top-performing models based on R² values were combined into an ensemble using a voting regressor. The ensemble generalizes by averaging the prediction of top-selected models, leveraging individual model strengths and yielding a superior generalization.

4.3. Performance Evaluation

The performance of the model was evaluated with a range of metrics, including the coefficient of determination (R²), mean squared error (MSE), and mean absolute error (MAE). R² measured proportion of variance in the model, and MSE and MAE measured prediction errors, with MSE assigning larger errors a larger weight in its calculation. Individual models performed less, with smaller values for R² and larger values for both error metrics, compared to an ensemble model, with its high predictive performance in estimating building risk level. With balancing, feature scaling, hyperparameter search, and ensemble learning techniques, the modeling pipeline generates reliable and interpretable predictions and can act as a useful tool for use cases in disaster management and urban security.

For a thorough evaluation of model generalizability, an external testing dataset with the same structural characteristics and risk level (RL) categories as the training data was used. The values for the dataset in terms of RL values were partitioned into four discrete damage levels (PDLs) for several categories of structural vulnerability. Preprocessing for the external dataset used feature scaling with the previously trained standard scaler. All model predictions were generated and then grouped into PDLs according to their respective RL values. The ensemble model, consisting of a combination of the best four single models, was also utilized for predicting RL values and PDL labels for the external data for comparative analysis between models.

To further assess model accuracy, performance metrics including R², MSE, and MAE were computed for all models on the external test data. Additionally, confusion matrices were generated to compare predicted versus actual PDL classifications, providing a detailed evaluation of each model’s effectiveness in correctly identifying damage levels. The results demonstrated that the models, particularly the ensemble model, maintained high accuracy and reliability across all damage categories, affirming their robustness and applicability to real-world scenarios. These findings underscore the efficacy of machine learning in automating structural risk assessment, offering a scalable and data-driven approach for post-earthquake damage evaluation and resilience planning.

5. Results and Discussion

5.1. Result of Training

The training focused on developing machine learning algorithms for accurately predicting severity level of earthquake-prone building damage. A total of 782 buildings in the dataset were boosted to 884 samples through oversampling for increased representativeness in terms of severity level of damage, and 20% of a testing set in a validation testing environment was drawn for estimating generalization performance before external testing. Performance measures in terms of R² (coefficient of determination), mean squared error (MSE), and mean absolute error (MAE) were used in model performance evaluation.

Results validate that tree-based ensemble approaches accurately captured intricate relations in the dataset and showed excellent predictive performance. The Extra Trees Regressor had a perfect MSE of 0.000 and a minimal MAE of 0.002, resulting in a high training R² value of 0.998, hence demonstrating exceptional proficiency in learning intrinsic trends within the training data. The performance of algorithms in predicting earthquakes is for the ensemble model, R² = 0.947; Random Forest Regressor, R² = 0.9931; and XGB Regressor, R² = 0.917. Tree-based methodologies in such a case confirm that boosting techniques, including CatBoost Regressor (R² = 0.828) and Gradient Boosting Regressor (R² = 0.811), have high predictive accuracy (

Table 4. Evaluation of the training database.

Model	Train R2	Train MSE	Train MAE
Extra Trees Regressor	0.998	0.000	0.002
Ensemble	0.947	0.009	0.069
Random Forest Regressor	0.931	0.011	0.076
XGB Regressor	0.917	0.013	0.083
Cat Boost Regressor	0.828	0.028	0.125
Gradient Boosting Regressor	0.811	0.031	0.133
LGBM Regressor	0.740	0.042	0.157
SVR	0.643	0.058	0.168
Linear Regression	0.360	0.104	0.262
Ridge	0.360	0.104	0.263
Elastic Net	0.360	0.104	0.264
Huber Regressor	0.353	0.105	0.259
Lasso	0.352	0.105	0.269

).

The validation tests showed high performance of machine learning algorithms, with the best performance for the ensemble model with a test R² value of 0.575, with high generalizability to new samples. There was high performance for boosting algorithms, with CatBoost Regressor (test R² value of 0.545), XGBoost Regressor (test R² value of 0.529), and Gradient Boosting Regressor (test R² value of 0.522), with high consistency of performance between training and testing sets. All these prove the high performance and generalizability of ensemble and boosting algorithms in capturing complex relationships in training samples and having high predictive performance in new samples, proving them ideal for application in earthquake damage prediction (

Table 5. Evaluation of the validation test data.

Model	Test R2	Test MSE	Test MAE
Ensemble	0.575	0.069	0.193
Cat Boost Regressor	0.545	0.074	0.205
Extra Trees Regressor	0.542	0.075	0.190
XGB Regressor	0.529	0.077	0.199
Random Forest Regressor	0.524	0.077	0.201
Gradient Boosting Regressor	0.522	0.078	0.217
LGBM Regressor	0.490	0.083	0.223
SVR	0.373	0.102	0.246
Lasso	0.282	0.117	0.289
Elastic Net	0.281	0.117	0.286
Ridge	0.279	0.117	0.285
Linear Regression	0.278	0.117	0.285
Huber Regressor	0.256	0.121	0.282

).

Linear regression-based algorithms such as Linear Regression, Ridge Regression, and ElasticNet generated consistent and interpretable values with a variety of test R² values between 0.278 and 0.281. In such a case, these algorithms have no ability to detect complex nonlinear relations in the data but can serve as useful baselines, offering general trends and interpretability in scenarios when simplicity trumps complexity.

As a result, the ensemble and retrofit models achieved high accuracy and stable performance in earthquake damage classification, and consequently, they represent useful tools for structural risk assessment. Optimization of oversampling methods and integration of the models with real-time data streams should be prioritized in future research to enhance their practical applicability in disaster response.

5.2. Result of Test

The external test phase was conducted with a view to assess the generalizability of trained models. For internal assessment, R² was used, but for the external dataset, accuracy was preferred since it was graded based on the level of damage to buildings and thus a better metric for assessment in a classification framework. To further extend the robustness of the evaluation, experiments with three, four, five, and twelve models, with and without oversampling, have been conducted.

The results validate the effectiveness of ensemble prediction in predicting earthquakes’ impact on buildings, with an optimized four-model selection being most accurate, 77%, as seen in

Table 6. Accuracy results for the different models.

Model	3 Models	4 Models	4 Models No Oversample	5 Models	12 Models	12 Models No Oversample
Linear Regression	0.44	0.44	0.47	0.44	0.44	0.47
Ridge	0.43	0.43	0.47	0.43	0.43	0.47
Lasso	0.5	0.5	0.54	0.5	0.5	0.54
ElasticNet	0.45	0.45	0.46	0.45	0.45	0.46
Huber Regressor	0.39	0.39	0.45	0.39	0.39	0.45
Gradient Boosting Regressor	0.64	0.64	0.52	0.64	0.64	0.52
Extra Trees Regressor	0.55	0.55	0.58	0.55	0.55	0.58
SVR	0.46	0.46	0.63	0.46	0.46	0.63
Random Forest Regressor	0.45	0.45	0.63	0.45	0.45	0.63
XGB Regressor	0.65	0.65	0.52	0.65	0.65	0.52
LGBM Regressor	0.44	0.44	0.56	0.44	0.44	0.56
CatBoost Regressor	0.61	0.61	0.45	0.61	0.61	0.45
Ensemble	0.75	0.77	0.64	0.74	0.52	0.63

. This confirms that a well-chosen combination of models maximizes predictive performance, balancing diversity and generalizability. The five-model combination performed well, with 74% accuracy, confirming the value in employing an ensemble model. However, when 12 models were included, performance decreased (to 52%), and it appears that having a lot of additional models does not necessarily maximize accuracy and can introduce redundancy and conflicting predictions.

The selected model consistently included XGB Regressor, Gradient Boosting Regressor, Extra Trees Regressor, and CatBoost Regressor, which meant high individual accuracy in classification. All these models consistently rank well across numerous settings and confirmed their robust performance in predicting earthquake damage. Tree-based models such as Extra Trees Regressor and Random Forest Regressor performed well with accuracy values of 0.58 and 0.63, respectively, when trained without oversampling. This demonstrates that tree-based methodologies can effectively detect structural risk tendencies even without oversampling. Oversampling maintained high accuracy for models such as XGB Regressor and Gradient Boosting Regressor, while reducing the performance of models such as Random Forest Regressor and SVR. Both models achieved high accuracy (0.63) when trained on datasets without oversampling. To cope with oversampling, the resampling method in sklearn.utils was applied to balance underrepresented risk classes. Synthetic methods (SMOTE, ADASYN) were not used due to the dominance of categorical features and the risk of unrealistic feature combinations.

Furthermore, the experiments verify that a considerable performance improvement is achieved through ensemble learning, but only to a state of optimality. With three models, performance was high (75%), and with a fourth model, accuracy rose to 77%. After that, it generated a loss in performance, corroborating the fact that a perfect balance between model diversity and model complexity is critical for achieving a high level of classification accuracy. In total, experiments confirm that ensemble methods, and more precisely those with boosting and tree-based methods, are the most reliable way for earthquake damage classification. Moreover, research determines model selection optimization, preprocessing method refinement, and model number balancing within an ensemble for optimal performance.

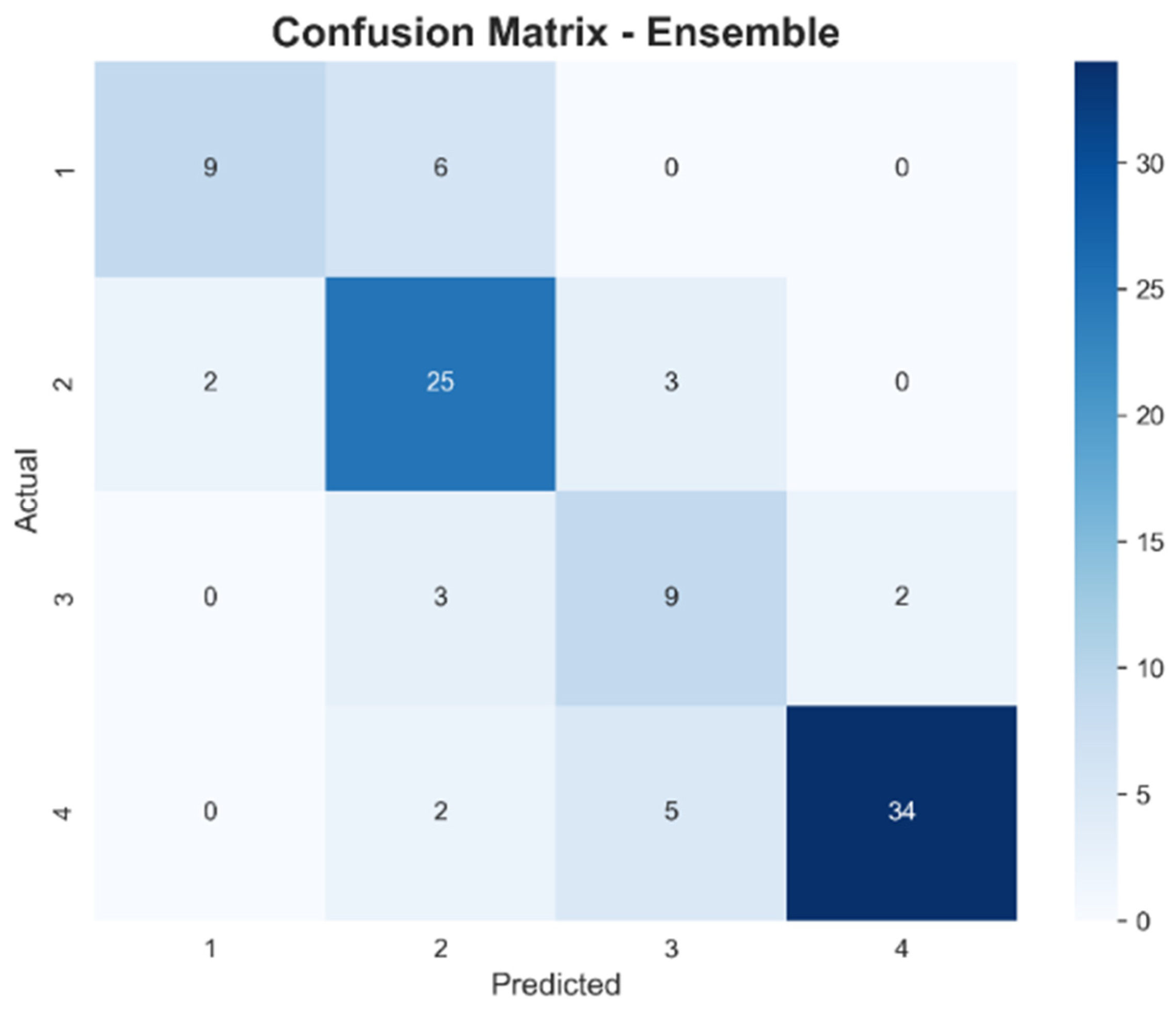
The ensemble model’s predictive performance in earthquake-prone building damage is revealed in the confusion matrix in Figure 8. Good predictive power is observed for severe and slight damage classes, with misclassifications observed, particularly between neighboring classes. The confusion matrix for the ensemble model portrays a deep examination of its performance in all four categories of damage, its weaknesses, and its strengths. Class 4 (severe damage) exhibited its best accuracy, with 34 out of 41 cases predicted accurately. This attests to its high confidence in accurately predicting buildings with widespread structural damage. There were five cases predicted as Class 3 (moderate damage), a sign of underprediction in cases with severity at a boundary between a moderate and a severe one.

In the case of Class 2 (slightly damaged buildings), the model performed well, and 25 out of 30 cases were predicted correctly. Two cases, nevertheless, were predicted under Class 1 (undamaged buildings) and three cases under Class 3 (moderate damage). This observation confirms that even when the model can detect slightly damaged, minor similarities between slight and moderate damage, and between non-damaged and slightly damaged, this sometimes leads to mistakes.

For Class 1 (undamaged buildings), the model correctly predicted nine out of fifteen examples, wrongly predicting six samples in Class 2 (minutely damaged). This is a general tendency for the model to confound a portion of undamaged buildings with slight, cosmetic damage, most likely due to feature representations for these classes having a high level of overlap. Class 3 (moderate damage) proved to be the most challenging category for the model, with only nine out of nineteen instances correctly classified. Five samples were misclassified as Class 4 (severe damage), and three samples were misclassified as Class 2 (slight damage).

This suggests that moderate damage shares feature with both the severe and slight damage categories and is therefore inherently more difficult to classify accurately. The complexity of moderate damage, which lies in the middle of the damage spectrum, likely contributes to this higher rate of misclassification.

Overall, the model possesses a high potential for prediction of severe and slight damage, both of which are significant for prioritization of post-earthquake rehabilitation and safety actions. Misclassifications between adjacent categories predominate, and these naturally follow from sequential development of types of damage. To make model performance improvements, future studies can include improvement in feature engineering, differentiation between closely spaced classes, and selection of optimized classification thresholds. All these can contribute effectively towards model accuracy and dependability in real field observations in earthquakes.

5.3. Discussion on Results

The results of the current study disclose that ensemble learning methods possess accurate predictability for the extent of earthquake-prone building damage. Through meticulous consideration of an array of ensemble configurations, it is observed that four carefully tuned base models provide an optimum accuracy of 77%. This result demonstrates that strategic model selection can significantly enhance predictive performance while preserving the model’s ability to generalize to unseen data. A five-model ensemble also performed well, achieving an accuracy of 74%, further validating the robustness of ensemble-based methodologies. However, when the model group size increased to 12, accuracy dropped to 52%. That drop reveals that a larger model group does not necessarily mean better performance and can even introduce redundancy and conflicting forecasts. All these observations speak to balancing diversity and model complexity in order to achieve optimal performance.

This study also revealed that XGBoost, Gradient Boosting, and CatBoost Regressors, all boosting algorithms, consistently outperformed in terms of accuracy in classification. All three algorithms exhibit high success in identifying complex structures in terms of damage and therefore exhibit high suitability for predicting earthquakes’ damage. Tree algorithms, such as Extra Trees Regressor and Random Forest Regressor, exhibit strong generalizability, and when trained with non-oversampled datasets, both achieved accuracy values of 0.58 and 0.63, respectively.

All such models have been proven to effectively differentiate between types of damage and therefore in supporting utility in rapid visual screening and in terms of structural risk evaluation.

The other important observation in the research is on oversampling for model performance improvement. For some of the architectures, oversampling methods were beneficial, most significantly for boosting algorithms, but with mixed effect for various architectures. Random Forest Regressor and Support Vector Regressor (SVR), for example, performed extremely well with non-oversampled datasets, with accuracy increasing from 0.46 to 0.63. The implication of these observations is that oversampling can successfully neutralize imbalanced datasets but, in its implementation, must be carefully optimized not to introduce artificial noise that will compromise generalizability in real-world environments. Optimizing balancing methods to specific architectures is thus paramount in the pursuit of predictive accuracy maximization.

The confusion matrix analysis of the ensemble model also certifies its strong predictive performance, particularly in accurately classifying severely and moderately damaged buildings. The model accurately identified 34 instances of Class 4 (severe damage) and 25 instances of Class 2 (slight damage), attesting to its reliability in detecting buildings with high risk. Misclassifications were observed, however, particularly between adjacent damage levels such as Classes 1 and 2 (undamaged and slightly damaged) and Classes 3 and 4 (moderate and severe damage). These suggest that while the model identifies overall damage patterns effectively, further feature differentiation refinement is necessary to improve accuracy, particularly in borderline cases where structural features overlap.

Overall, this work re-emphasizes careful ensemble construction, algorithm selection, and balancing techniques in developing effective and reliable earthquake damage prediction. The studies have revealed that the proposed ML-RVS model enables proactive risk prediction by inputting the RVS parameters and seismic zone coefficients of the examined buildings. Thus, the model can predict potential risk levels before an event occurs and support the determination of pre-earthquake planning and reinforcement priorities. Post-event data can further improve the model and enable adaptive learning for regional scenario simulations.

6. Conclusions

This study reveals the effectiveness of rapid visual screening via machine learning in estimating the level of structural risk in buildings, offering an efficient and scalable tool for earthquake damage classification. With an optimized selection of four to five models and through application of ensemble and boosting models, the proposed model achieved a high accuracy of 77%. This reveals the effectiveness of ensemble learning in estimating the level of structural risk and its use in supporting decision-making in post-disaster settings. Methods for preprocessing, such as oversampling, played a significant role in balancing the dataset and improving the generalizability of the models for a range of types of building damage.

Boosting algorithms, including XGBoost, Gradient Boost, and CatBoost Regressors, and tree algorithms, including Extra Trees and Random Forest Regressors, performed uniformly well in earthquake damage classification in this work. All these algorithms could model complex structures in terms of risk effectively, and hence, they are best for rapid and reliable estimation of building damage. Yet another novel contribution of this work is using derived risk categories as a target variable and thus enabling algorithms to model effectively the proportion of risky buildings, a critical requirement in structural risk analysis. Thus, new algorithms can predict both the risk level and damage level of reinforced concrete structures either by using classification or proportioning.

The methodology proposed in this work can have important applications in disaster risk mitigation projects. It is a useful tool for urban planning, disaster preparedness, and post-earthquake damage estimation for earthquake-prone buildings. The developed model, trained on RVS-based data and validated with real post-earthquake buildings, demonstrates high potential for the nationwide implementation of data-driven risk screening. While the findings are positive, future room for improvement can be discerned. Expanding the dataset to include a wider variety of building and structure types will make the model even more specific and relevant in a variety of urban environments. Including new, advanced techniques such as real-time structural monitoring and remote sensing for data collection will make analysis even more in-depth and penetrating. All these enhancements improve the model, which is even more effective at predicting structural vulnerability risk with even greater accuracy. The proposed AI-based framework demonstrates strong potential for integration into national-level risk screening systems (e.g., KAYES, ARAAD). It enables automatic prioritization of RC buildings for detailed assessment.

Future work will focus on enhancing generalization using regionally diverse datasets, drone-based visual parameters, and transfer learning to further improve scalability and accuracy. Also, future research can explore feature engineering and mixed-model techniques, including deep learning integration. In its development, it can become a robust and effective tool for estimating structural risk. It can not only contribute to creating earthquake-resilient urban environments but also contribute to retrofitting security and supporting data-driven decision-making in disaster response and rehabilitation operations. With continued refinement and improvement, the model in this work can make a meaningful contribution towards lessening earthquakes’ impact in urban communities.