A Novel Active Learning Method Combining Adaptive Support Vector Regression and Monte Carlo Simulation for Structural Reliability Assessment
Abstract
1. Introduction
2. The Proposed Method: ASVR-MCS
2.1. Support Vector Regression
2.2. Active Learning Reliability Method: ASVR-MCS
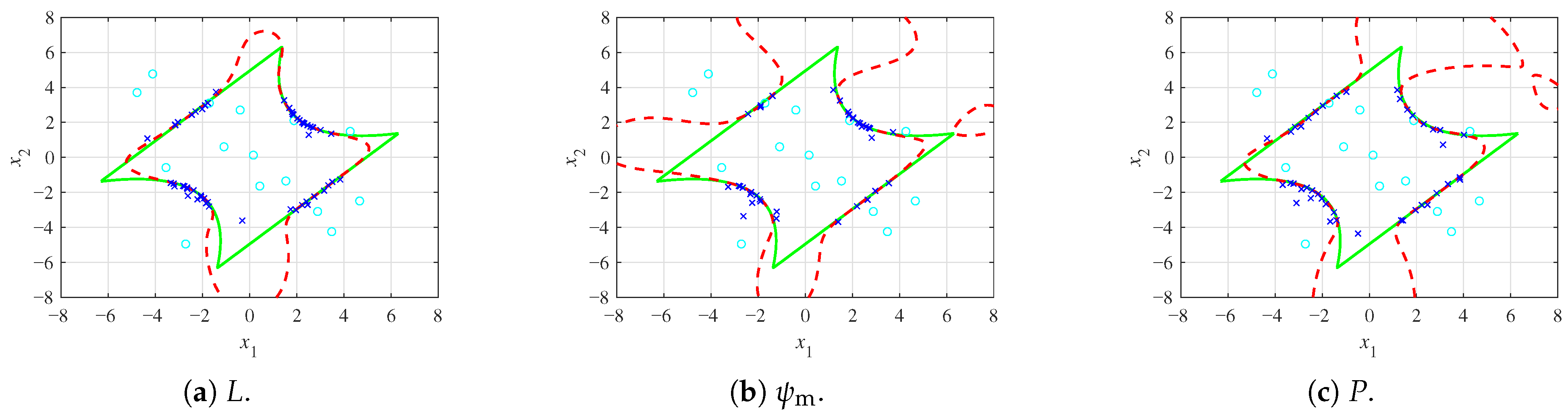
2.2.1. Learning Function
- I.
- The modified classical learning function
- II.
- The mixed learning function
- III.
- The proposed weighting penalty learning function
2.2.2. Stop Criteria
2.2.3. Implementation of the Proposed Method
3. Numerical Examples
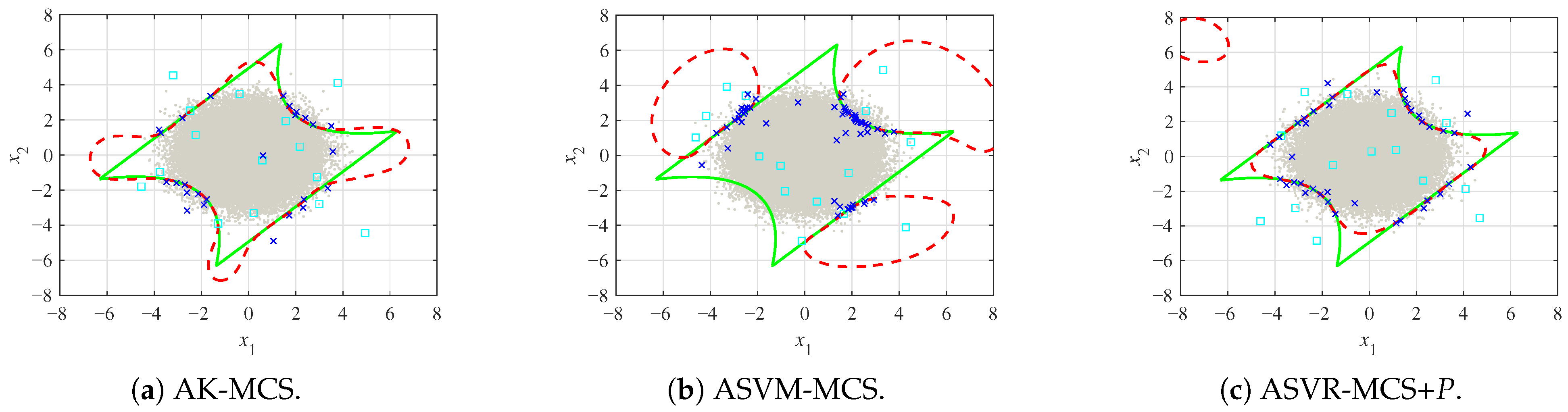
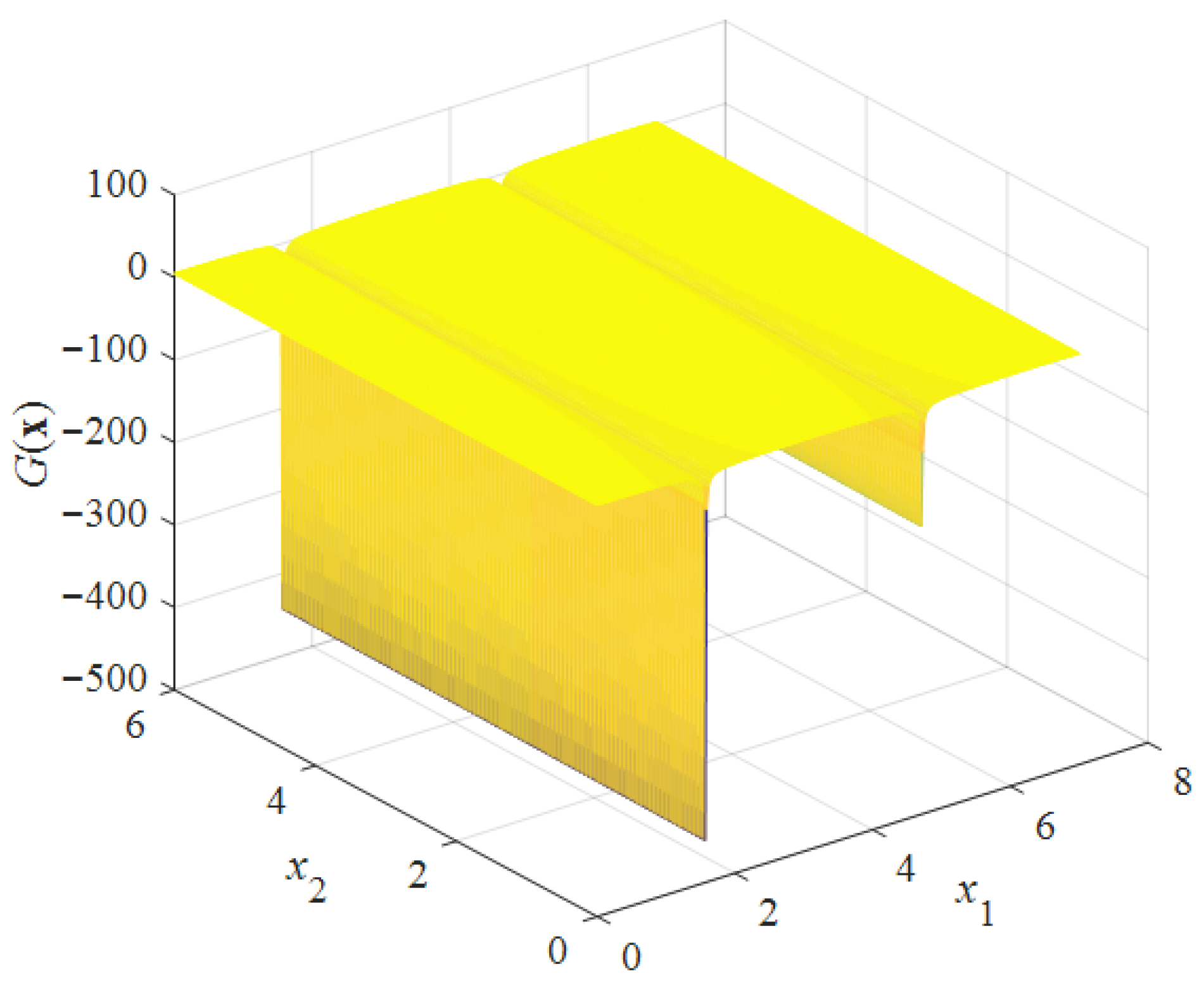
3.1. Example One
3.2. Example Two
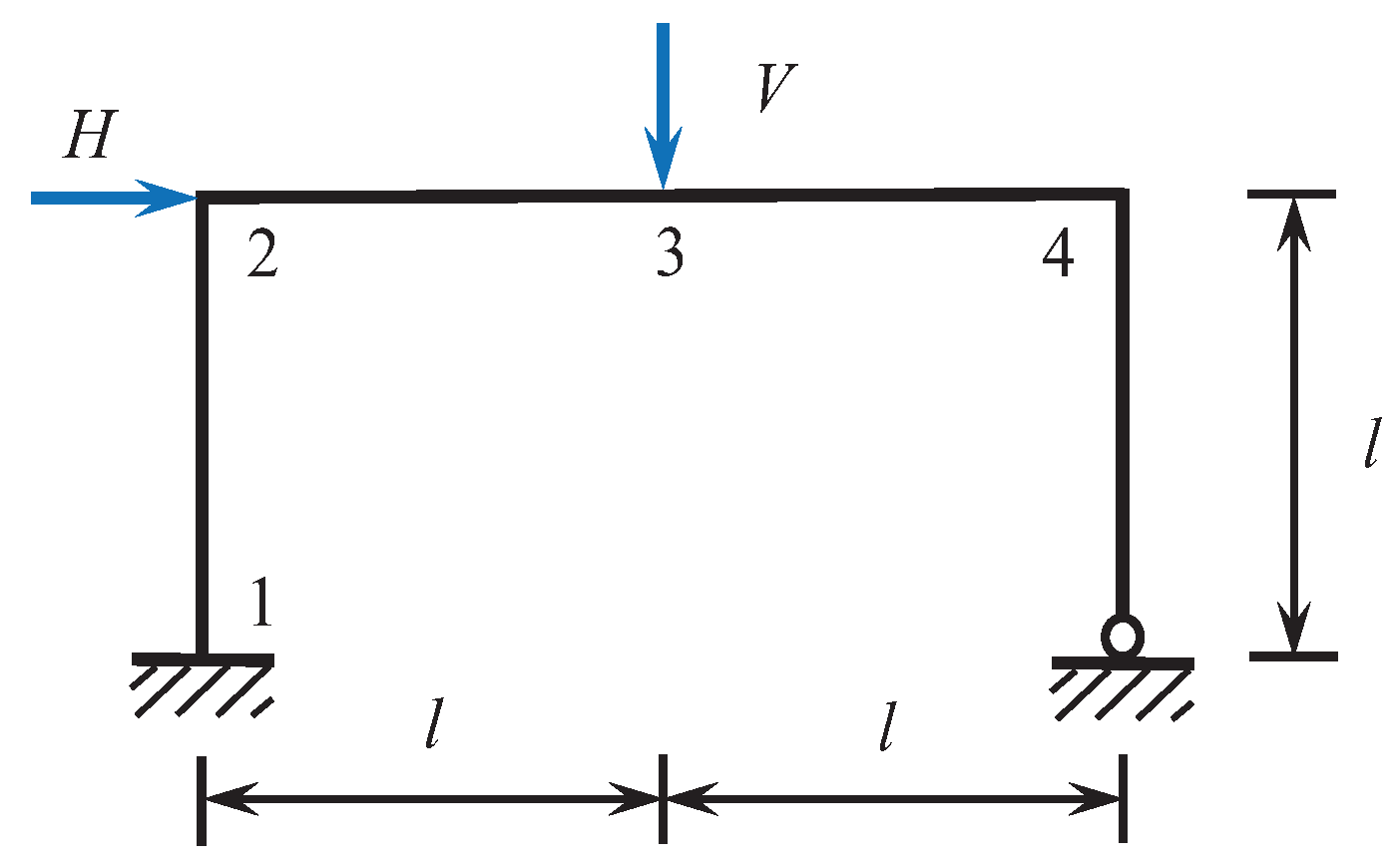
3.3. Example Three
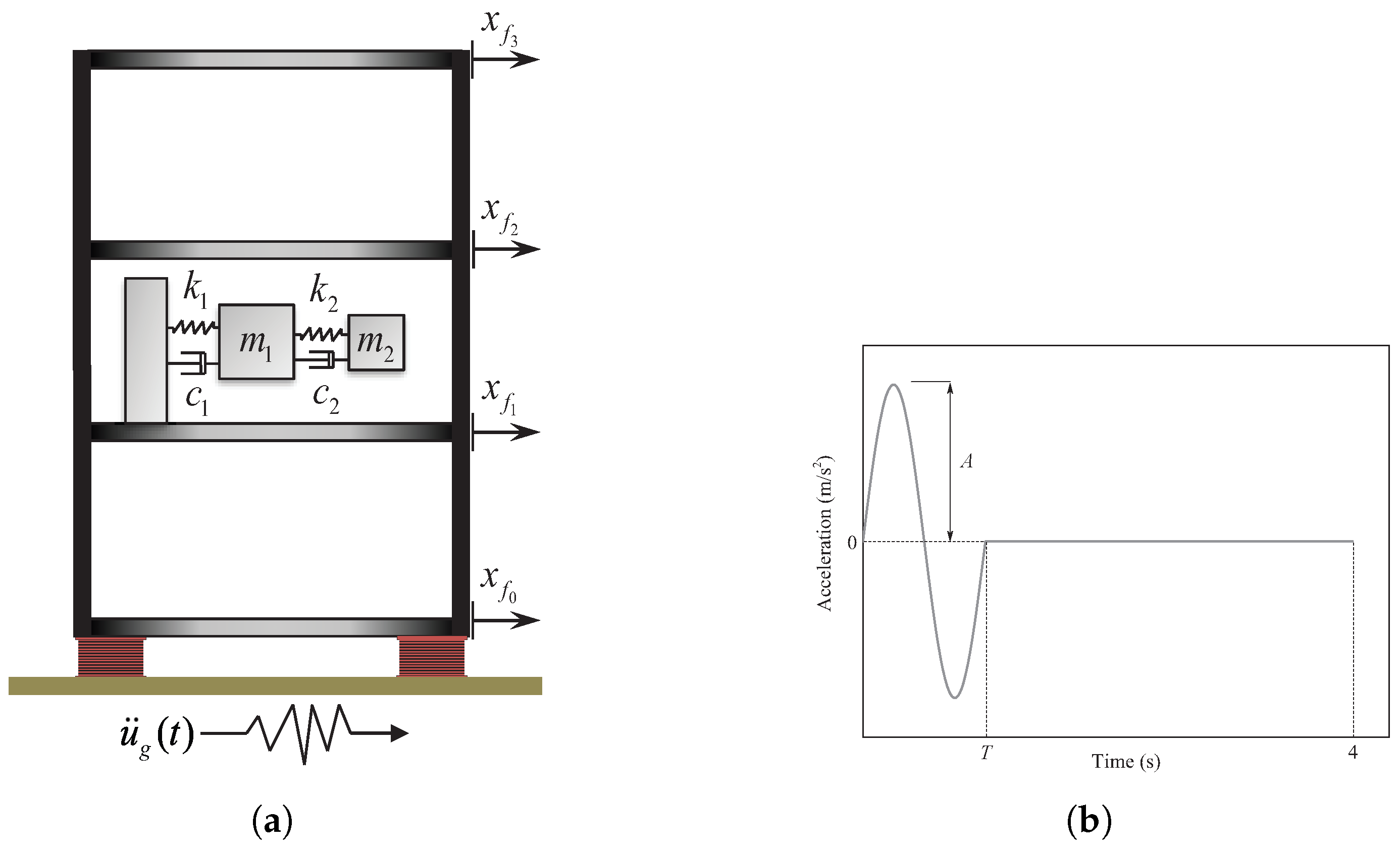
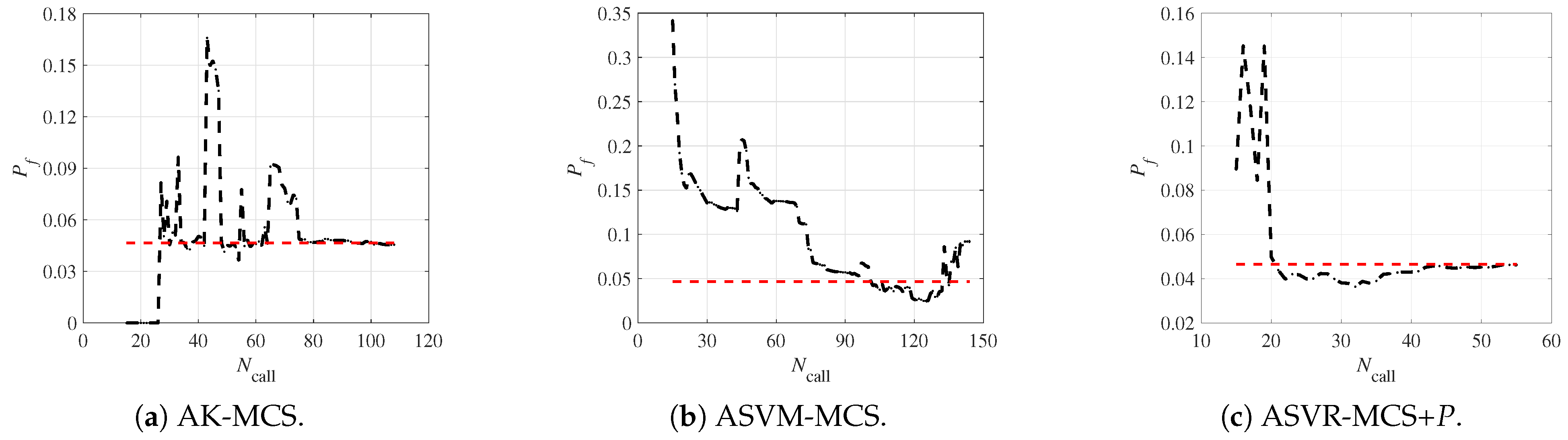
3.4. Example Four
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, Z.; Dai, H.; Beer, M. Efficient structural reliability analysis via a weak-intrusive stochastic finite element method. Probabilistic Eng. Mech. 2023, 71, 103414. [Google Scholar] [CrossRef]
- Wang, B.; Ma, S.; Li, Y.P.; Wang, N.; Ren, Q.X. Axial compression mechanical properties of UHTCC-hollow steel tube square composited short columns. J. Constr. Steel Res. 2025, 228, 109424. [Google Scholar] [CrossRef]
- Proppe, C. Estimation of failure probabilities by local approximation of the limit state function. Struct. Saf. 2008, 30, 277–290. [Google Scholar] [CrossRef]
- Zhang, R.; Dai, H. Stochastic analysis of structures under limited observations using kernel density estimation and arbitrary polynomial chaos expansion. Comput. Methods Appl. Mech. Eng. 2023, 403, 115689. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, R.; Beer, M. A new method for stochastic analysis of structures under limited observations. Mech. Syst. Signal Process. 2023, 185, 109730. [Google Scholar] [CrossRef]
- Fauriat, W.; Gayton, N. AK-SYS: An adaptation of the AK-MCS method for system reliability. Reliab. Eng. Syst. Saf. 2014, 123, 137–144. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, R.; Beer, M. A new perspective on the simulation of cross-correlated random fields. Struct. Saf. 2022, 96, 102201. [Google Scholar] [CrossRef]
- Zhang, R.; Dai, H. A non-Gaussian stochastic model from limited observations using polynomial chaos and fractional moments. Reliab. Eng. Syst. Saf. 2022, 221, 108323. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y.J.; Ren, Q.X.; Feng, H.Y.; Bi, R.; Zhao, X. Axial compression properties of reinforced concrete columns strengthened with textile-reinforced ultra-high toughness cementitious composite in chloride environment. J. Build. Eng. 2025, 111, 113116. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, H.; Dai, H.; Shen, L. A deep learning-aided seismic fragility analysis method for bridges. Structures 2022, 40, 1056–1064. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, R.; Zhang, H. A new fractional moment equation method for the response prediction of nonlinear stochastic systems. Nonlinear Dyn. 2019, 97, 2219–2230. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Zhang, R.; Dai, H. An optimal transport method for the PC representation of non-Gaussian fields. Mech. Syst. Signal Process. 2025, 224, 112172. [Google Scholar] [CrossRef]
- Cadini, F.; Santos, F.; Zio, E. An improved adaptive kriging-based importance technique for sampling multiple failure regions of low probability. Reliab. Eng. Syst. Saf. 2014, 131, 109–117. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M.; Relun, N. A combined Importance Sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models. Reliab. Eng. Syst. Saf. 2013, 111, 232–240. [Google Scholar] [CrossRef]
- Bichon, B.J.; Eldred, M.S.; Swiler, L.P.; Mahadevan, S.; McFarland, J.M. Efficient Global Reliability Analysis for Nonlinear Implicit Performance Functions. AIAA J. 2008, 46, 2459–2468. [Google Scholar] [CrossRef]
- Papadopoulos, V.; Giovanis, D.G.; Lagaros, N.D.; Papadrakakis, M. Accelerated subset simulation with neural networks for reliability analysis. Comput. Methods Appl. Mech. Eng. 2012, 223–224, 70–80. [Google Scholar] [CrossRef]
- Xiao, N.C.; Zuo, M.J.; Zhou, C. A new adaptive sequential sampling method to construct surrogate models for efficient reliability analysis. Reliab. Eng. Syst. Saf. 2018, 169, 330–338. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. An efficient reliability method combining adaptive Support Vector Machine and Monte Carlo Simulation. Struct. Saf. 2017, 67, 85–95. [Google Scholar] [CrossRef]
- Bourinet, J.M.; Deheeger, F.; Lemaire, M. Assessing small failure probabilities by combined subset simulation and Support Vector Machines. Struct. Saf. 2011, 33, 343–353. [Google Scholar] [CrossRef]
- Basudhar, A.; Missoum, S. Adaptive explicit decision functions for probabilistic design and optimization using support vector machines. Comput. Struct. 2008, 86, 1904–1917. [Google Scholar] [CrossRef]
- Basudhar, A.; Missoum, S. An improved adaptive sampling scheme for the construction of explicit boundaries. Struct. Multidiscip. Optim. 2010, 42, 517–529. [Google Scholar] [CrossRef]
- Hurtado, J.E. Filtered importance sampling with support vector margin: A powerful method for structural reliability analysis. Struct. Saf. 2007, 29, 2–15. [Google Scholar] [CrossRef]
- Gaspar, B.; Teixeira, A.; Soares, C.G. Assessment of the efficiency of Kriging surrogate models for structural reliability analysis. Probabilistic Eng. Mech. 2014, 37, 24–34. [Google Scholar] [CrossRef]
- Bourinet, J.M. Rare-event probability estimation with adaptive support vector regression surrogates. Reliab. Eng. Syst. Saf. 2016, 150, 210–221. [Google Scholar] [CrossRef]
- Roy, A.; Chakraborty, S. Support vector regression based metamodel by sequential adaptive sampling for reliability analysis of structures. Reliab. Eng. Syst. Saf. 2020, 200, 106948. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, J.; Li, R.; Tong, C. LIF: A new Kriging based learning function and its application to structural reliability analysis. Reliab. Eng. Syst. Saf. 2017, 157, 152–165. [Google Scholar] [CrossRef]
- Huang, X.; Chen, J.; Zhu, H. Assessing small failure probabilities by AK–SS: An active learning method combining Kriging and Subset Simulation. Struct. Saf. 2016, 59, 86–95. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Y.; Chen, B.; Zhao, Y. An active learning Kriging model combined with directional importance sampling method for efficient reliability analysis. Probabilistic Eng. Mech. 2020, 60, 103054. [Google Scholar] [CrossRef]
- Ling, C.; Lu, Z.; Cheng, K.; Sun, B. An efficient method for estimating global reliability sensitivity indices. Probabilistic Eng. Mech. 2019, 56, 35–49. [Google Scholar] [CrossRef]
- Qian, J.; Yi, J.; Cheng, Y.; Liu, J.; Zhou, Q. A sequential constraints updating approach for Kriging surrogate model-assisted engineering optimization design problem. Eng. Comput. 2019, 36, 993–1009. [Google Scholar] [CrossRef]
- Wang, Z.; Broccardo, M. A novel active learning-based Gaussian process metamodelling strategy for estimating the full probability distribution in forward UQ analysis. Struct. Saf. 2020, 84, 101937. [Google Scholar] [CrossRef]
- Ren, C.; Aoues, Y.; Lemosse, D.; Souza De Cursi, E. Ensemble of surrogates combining Kriging and Artificial Neural Networks for reliability analysis with local goodness measurement. Struct. Saf. 2022, 96, 102186. [Google Scholar] [CrossRef]
- Moustapha, M.; Marelli, S.; Sudret, B. Active learning for structural reliability: Survey, general framework and benchmark. Struct. Saf. 2022, 96, 102174. [Google Scholar] [CrossRef]
- Zhang, R.; Dai, H. Independent component analysis-based arbitrary polynomial chaos method for stochastic analysis of structures under limited observations. Mech. Syst. Signal Process. 2022, 173, 109026. [Google Scholar] [CrossRef]
- Shi, L.; Sun, B.; Ibrahim, D.S. An active learning reliability method with multiple kernel functions based on radial basis function. Struct. Multidiscip. Optim. 2019, 60, 211–229. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Xu, G.; Li, Y.; Kareem, A. Efficient structural reliability analysis based on adaptive Bayesian support vector regression. Comput. Methods Appl. Mech. Eng. 2021, 387, 114172. [Google Scholar] [CrossRef]
- Zhou, T.; Peng, Y. An active-learning reliability method based on support vector regression and cross validation. Comput. Struct. 2023, 276, 106943. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Dai, H.; Li, D.; Beer, M. Adaptive Kriging-assisted multi-fidelity subset simulation for reliability analysis. Comput. Methods Appl. Mech. Eng. 2025, 436, 117705. [Google Scholar] [CrossRef]
- Thapa, A.; Roy, A.; Chakraborty, S. Reliability analyses of underground tunnels by an adaptive support vector regression model. Comput. Geotech. 2024, 172, 106418. [Google Scholar] [CrossRef]
- Asgarkhani, N.; Kazemi, F.; Jankowski, R. Machine-learning based tool for seismic response assessment of steel structures including masonry infill walls and soil-foundation-structure interaction. Comput. Struct. 2025, 317, 107918. [Google Scholar] [CrossRef]
- Baidya, S.; Roy, B.K. Seismic reliability analysis of base isolated building supplemented with shape memory alloy rubber bearing using support vector regression metamodel. Structures 2024, 65, 106773. [Google Scholar] [CrossRef]
- Moustapha, M.; Lataniotis, C.; Wiederkehr, P.; Wicaksono, D.; Marelli, S.; Sudret, B. UQLib User Manual; Technical Report; Chair of Risk, Safety & Uncertainty Quantification, ETH Zurich: Zürich, Switzerland, 2019; Report # UQLab-V1.2-201. [Google Scholar]
- Xue, G.; Lyu, X. An Adaptive Clustering-Based Active Learning Kriging Method Combining with Importance Sampling for Structural Reliability Analysis with Multiple Failure Regions. IEEE Access 2025, 13, 150308–150320. [Google Scholar] [CrossRef]
- Su, M.; Xue, G.; Wang, D.; Zhang, Y.; Zhu, Y. A novel active learning reliability method combining adaptive Kriging and spherical decomposition-MCS (AK-SDMCS) for small failure probabilities. Struct. Multidiscip. Optim. 2020, 62, 3165–3187. [Google Scholar] [CrossRef]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2004. [Google Scholar]
- Katsuki, S.; Frangopol, D.M. Hyperspace Division Method for Structural Reliability. J. Eng. Mech. 1994, 120, 2405–2427. [Google Scholar] [CrossRef]
- Melchers, R.E. Radial Importance Sampling for Structural Reliability. J. Eng. Mech. 1990, 116, 189–203. [Google Scholar] [CrossRef]
- Cui, F.; Ghosn, M. Implementation of machine learning techniques into the Subset Simulation method. Struct. Saf. 2019, 79, 12–25. [Google Scholar] [CrossRef]
- Dai, H.; Cao, Z. A Wavelet Support Vector Machine-Based Neural Network Metamodel for Structural Reliability Assessment. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 344–357. [Google Scholar] [CrossRef]
- Gavin, H.P.; Yau, S.C. High-order limit state functions in the response surface method for structural reliability analysis. Struct. Saf. 2008, 30, 162–179. [Google Scholar] [CrossRef]

| Method | MCS | AK-MCS | ASVM-MCS | Proposed Method: ASVR-MCS | ||
|---|---|---|---|---|---|---|
| 41.9 | 93.9 | 46.1 | 48.8 | 54.3 | ||
| - | 4.87% | 15.76% | 7.66% | 8.62% | 5.7% | |
| - | −1.9% | −12.3% | −5.6% | −6.9% | −3.2% | |
| Method | MCS | AK-MCS | ASVM-MCS | Proposed Method: ASVR-MCS | ||
|---|---|---|---|---|---|---|
| 81.5 | 136.5 | 132.7 | 115.8 | 188 | ||
| - | 22.44% | 2.95% | 14.66% | 10.92% | 6.56% | |
| - | 19.4% | 1.2% | 6.9% | 0.6% | −3.3% | |
| Variable | H | V | ||||
|---|---|---|---|---|---|---|
| Mean | 1 | 1 | 1 | 1 | 1.05 | 1.5 |
| Standard deviation | 0.15 | 0.15 | 0.15 | 0.15 | 0.1785 | 0.75 |
| Method | MCS | AK-MCS | ASVM-MCS | Proposed Method: ASVR-MCS | ||
|---|---|---|---|---|---|---|
| 138.6 | 154.8 | 96.7 | 100.8 | 89.9 | ||
| - | 27.76% | 5.02% | 4.9% | 4.5% | 3.55% | |
| - | −6.4% | −2.1% | 0.6% | −1.2% | −2.2% | |
| Variable | Mean | Standard Deviation | Units |
|---|---|---|---|
| kg | |||
| N/m | |||
| N/(m/s) | |||
| N | |||
| m | |||
| T | 1 | s | |
| A | 1 |
| Method | MCS | AK-MCS | ASVM-MCS | Proposed Method: ASVR-MCS | ||
|---|---|---|---|---|---|---|
| 106.6 | 105.1 | 52.2 | 51.2 | 56.9 | ||
| - | 3.51% | 166.23% | 2.54% | 1.63% | 2.46% | |
| - | −0.5% | 88.7% | −0.8% | −0.2% | −0.8% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, G.; Su, M.; Li, J. A Novel Active Learning Method Combining Adaptive Support Vector Regression and Monte Carlo Simulation for Structural Reliability Assessment. Buildings 2025, 15, 4183. https://doi.org/10.3390/buildings15224183
Xue G, Su M, Li J. A Novel Active Learning Method Combining Adaptive Support Vector Regression and Monte Carlo Simulation for Structural Reliability Assessment. Buildings. 2025; 15(22):4183. https://doi.org/10.3390/buildings15224183
Chicago/Turabian StyleXue, Guofeng, Maijia Su, and Junhui Li. 2025. "A Novel Active Learning Method Combining Adaptive Support Vector Regression and Monte Carlo Simulation for Structural Reliability Assessment" Buildings 15, no. 22: 4183. https://doi.org/10.3390/buildings15224183
APA StyleXue, G., Su, M., & Li, J. (2025). A Novel Active Learning Method Combining Adaptive Support Vector Regression and Monte Carlo Simulation for Structural Reliability Assessment. Buildings, 15(22), 4183. https://doi.org/10.3390/buildings15224183






