Numerical and Experimental Investigation on Time-Dependent Crack Extension in Concrete Under Sustained Loads
Abstract
1. Introduction
2. Numerical Modeling
2.1. Based Criterion
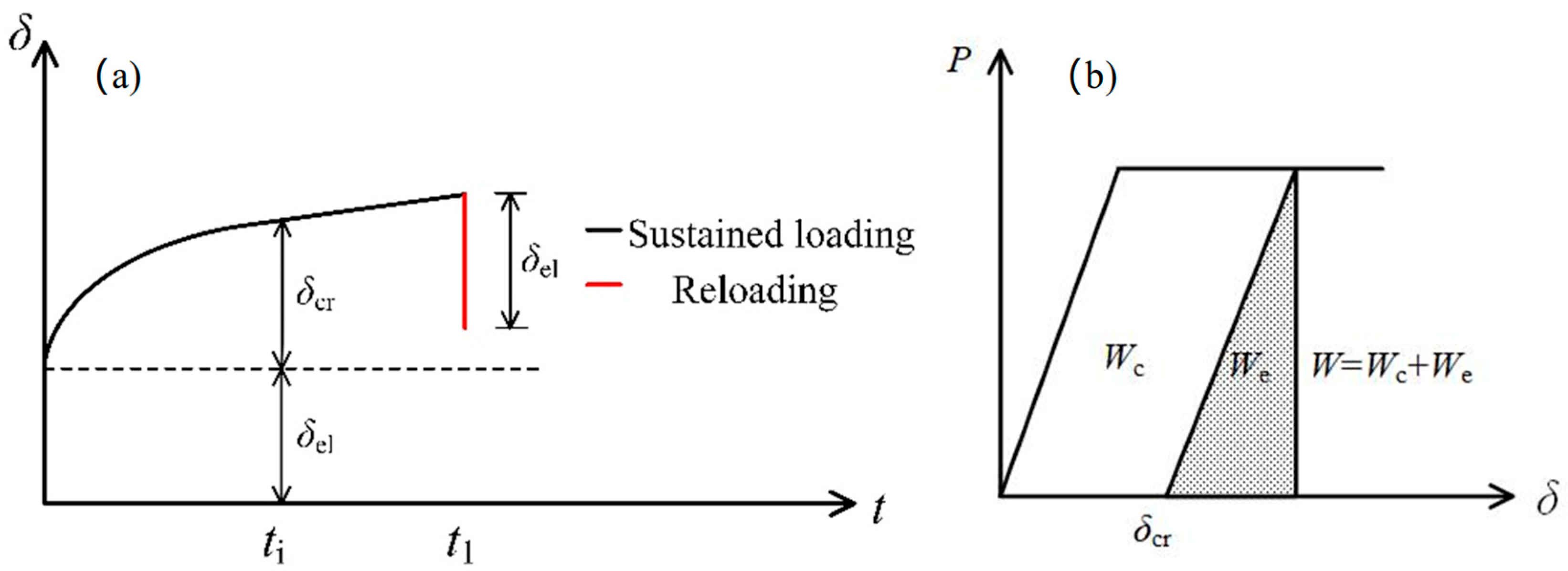
2.2. Derivation of Time-Dependent Tension-Softening Constitutive Law [16]
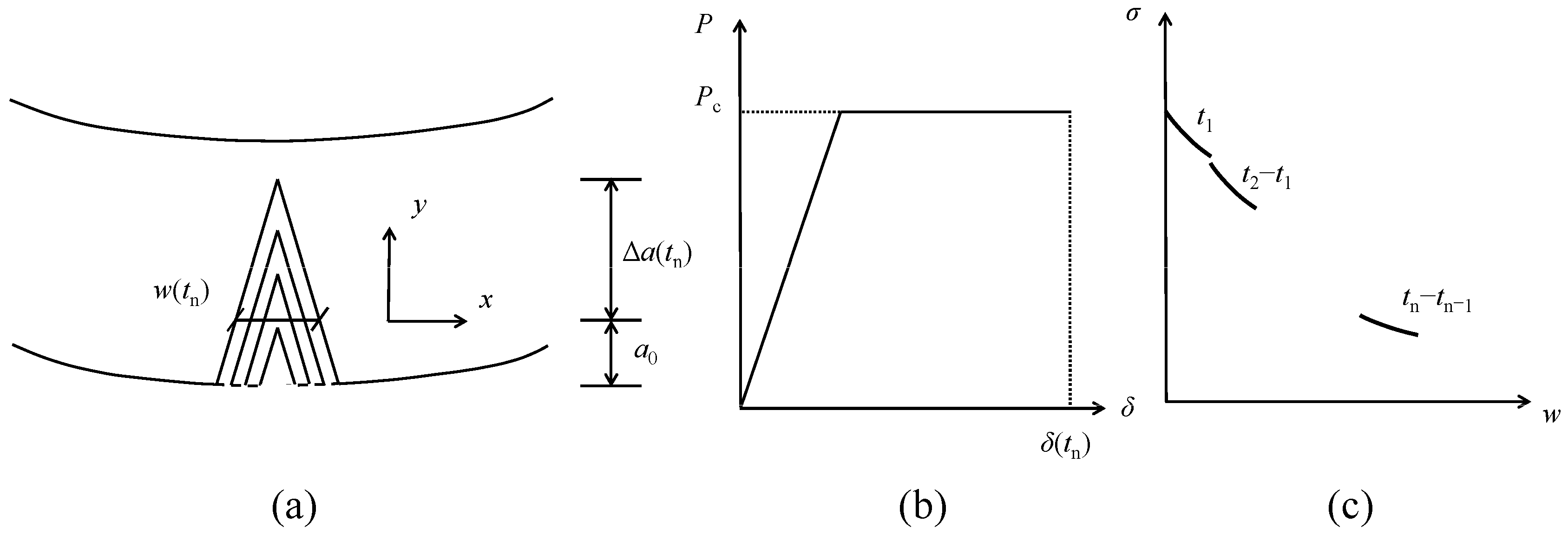
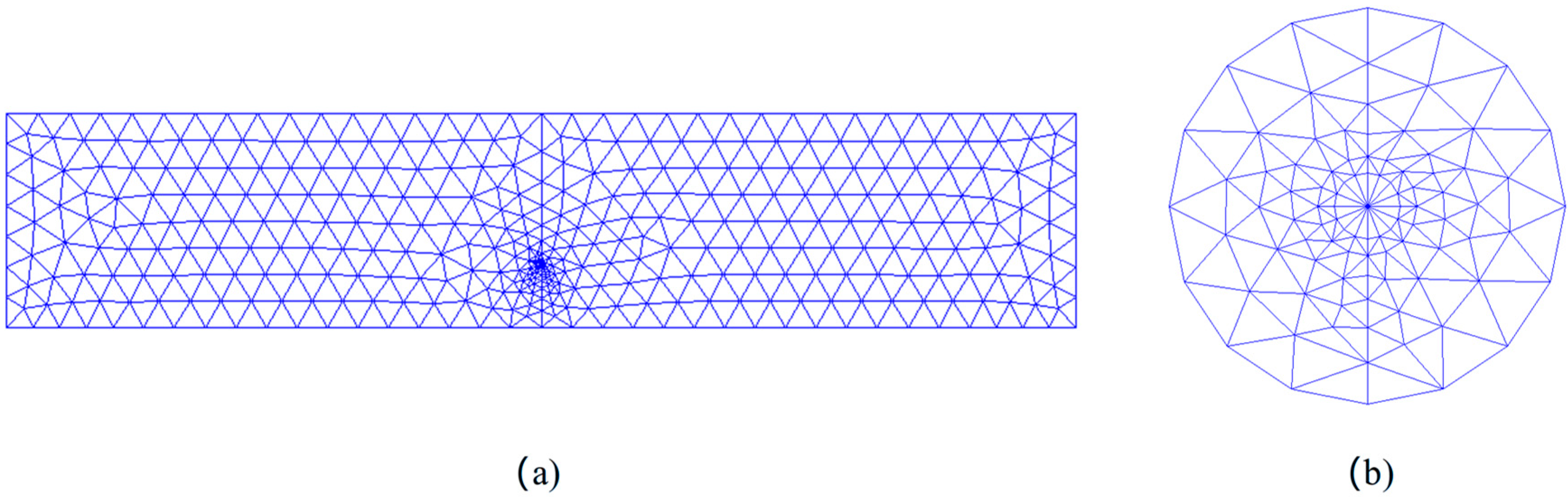
2.3. Finite Element Modeling
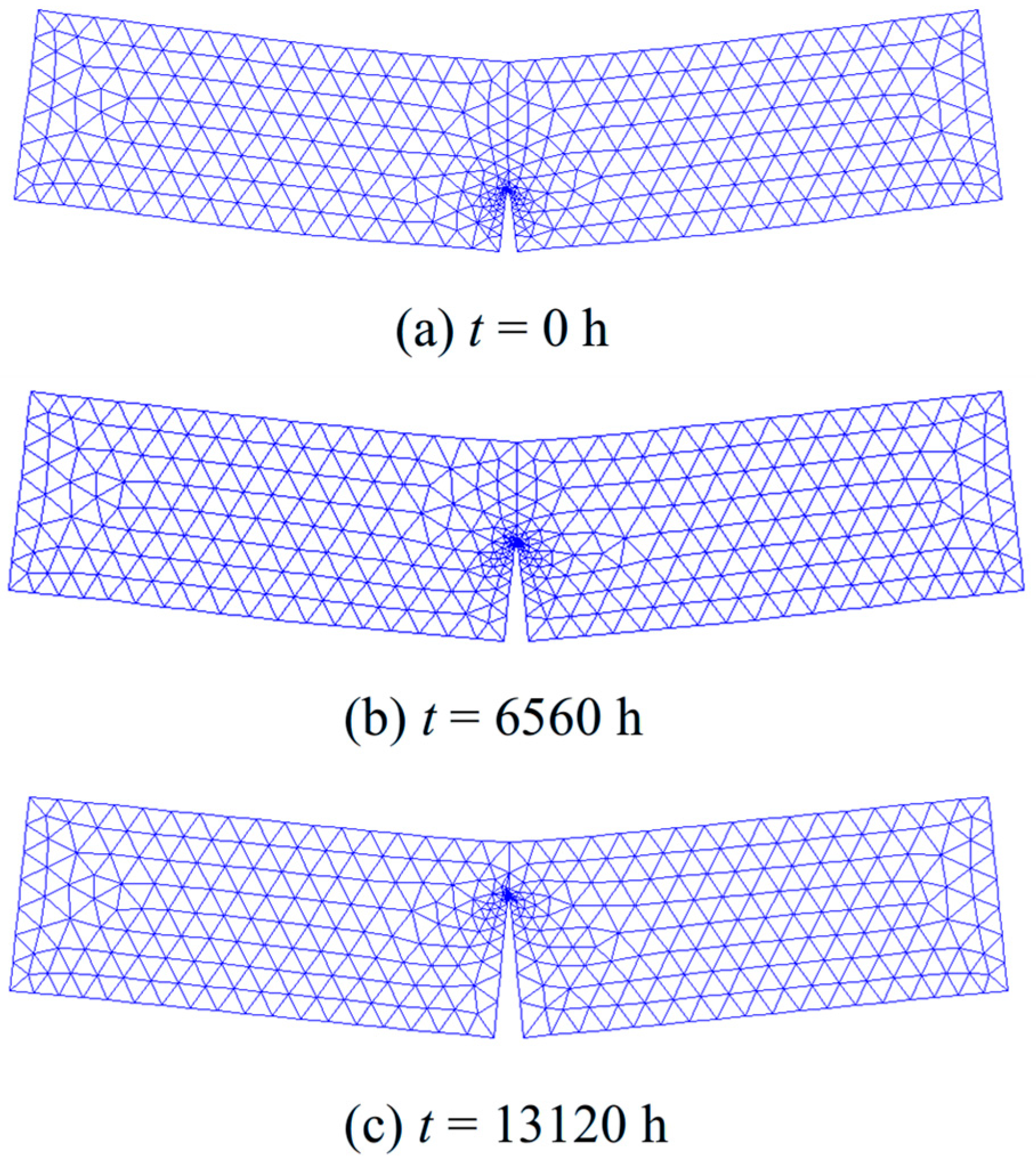
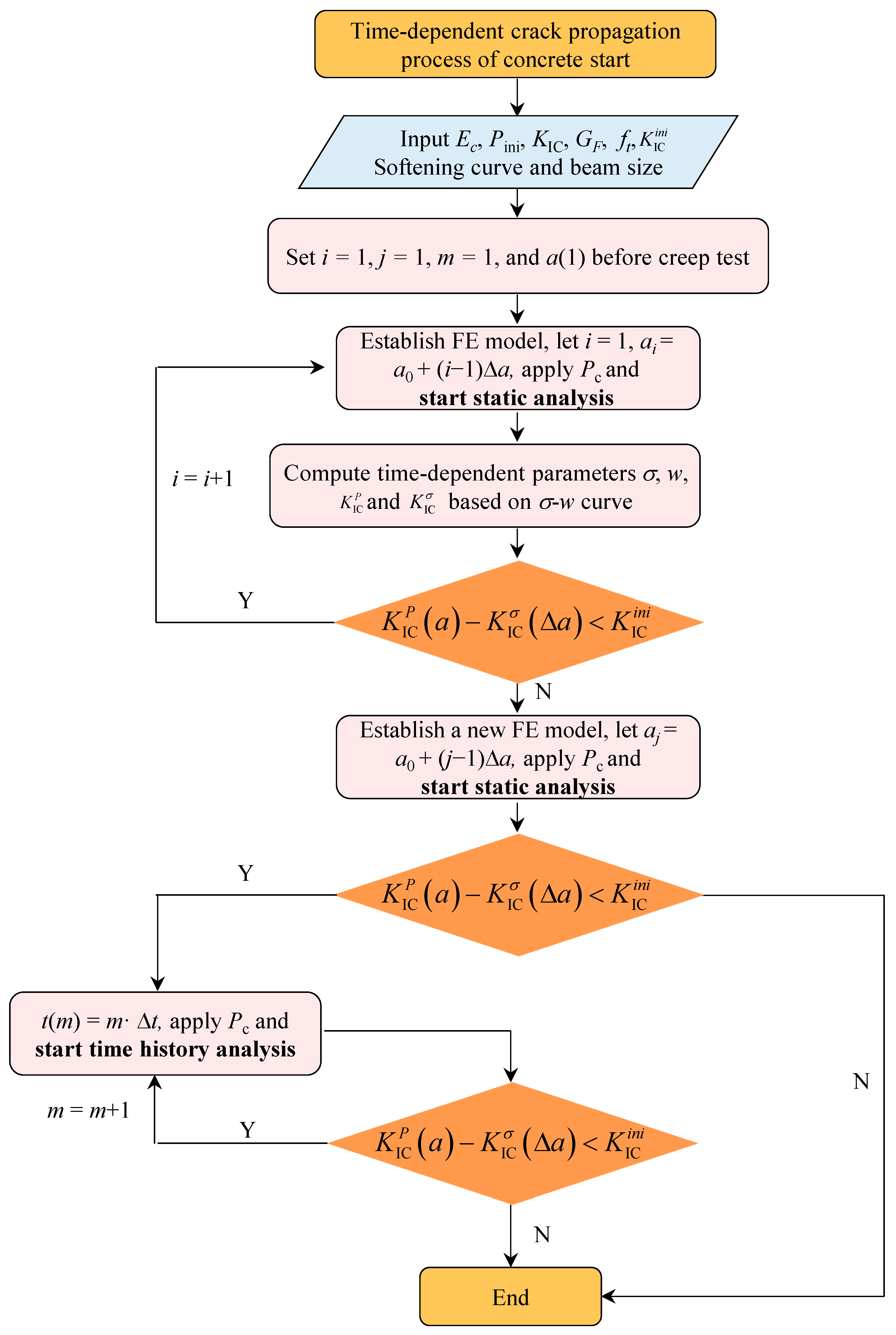
2.4. Calculation of Time-Dependent Crack Extension Process
- Model Initialization. Input the geometrical dimensions and material and fracture properties of 3-p-b beams for creep fracture tests. The parameters are initialized with i = 1 and j = 1, where i and j represent quasi-static and sustained load steps for crack extension, respectively.
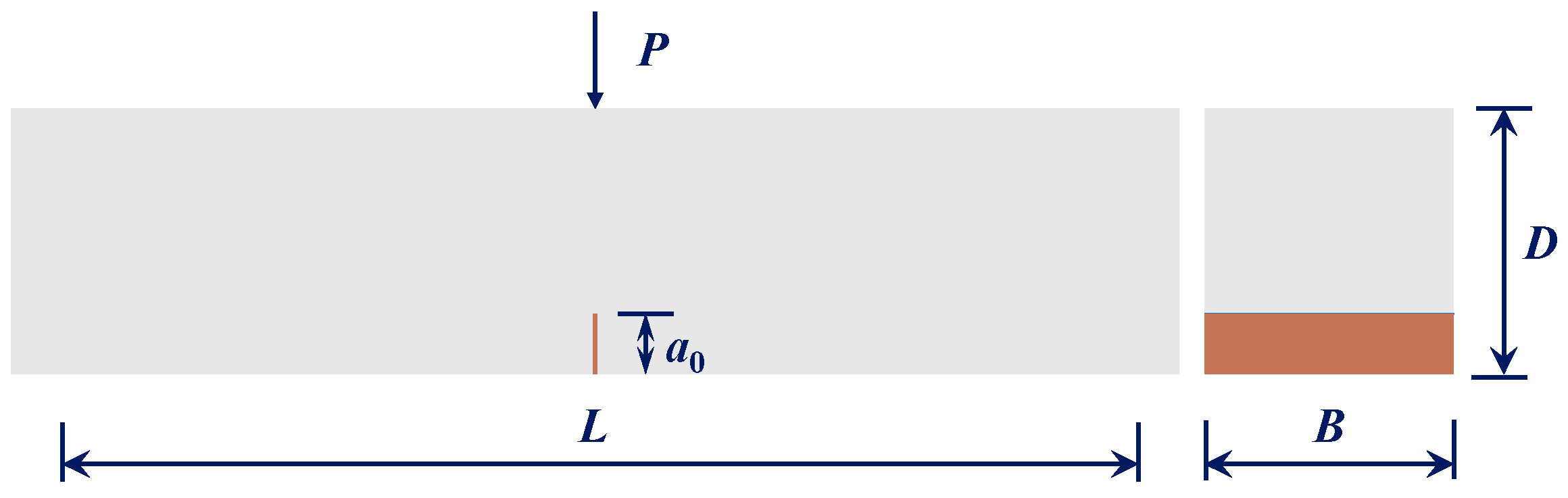
- Quasi-static loading analysis. First, define the crack length a(i) = a0 + (i − 1)Δd, where a0 stands for the initial crack length and Δd refers to the increment crack length for each quasi-static loading step. After the FE model is built, the quasi-static loading analysis starts. Second, apply P = Pc and σw, with which the SIFs and can be computed. Finally, determine the difference between and . If , increment i by I = i + 1 and repeat the aforementioned steps. Else, set a1 = a(i) and proceed to step (iii).
- Sustained loading analysis. First, similar to the quasi-static loading analysis, set a(j) = a1 + (j − 1)Δd. Rebuild the model with Pc. To capture the viscoelastic behavior of concrete, define the material properties using the Prony series derived from the Kelvin chain model. Subsequently, perform the static analysis [see step (ii)]. If , then proceed to step (iv). Otherwise, terminate the program.
- Time history analysis. Define the time at step m as t(m) = mΔt, where m = time step index and Δt = time increment. Apply σw(t) and conduct the time history analysis. Extract and then calculate . If , set m = m + 1 and repeat the analysis; If , then set j = j + 1 and return to step (iii) and proceed steps (iii) and (iv).
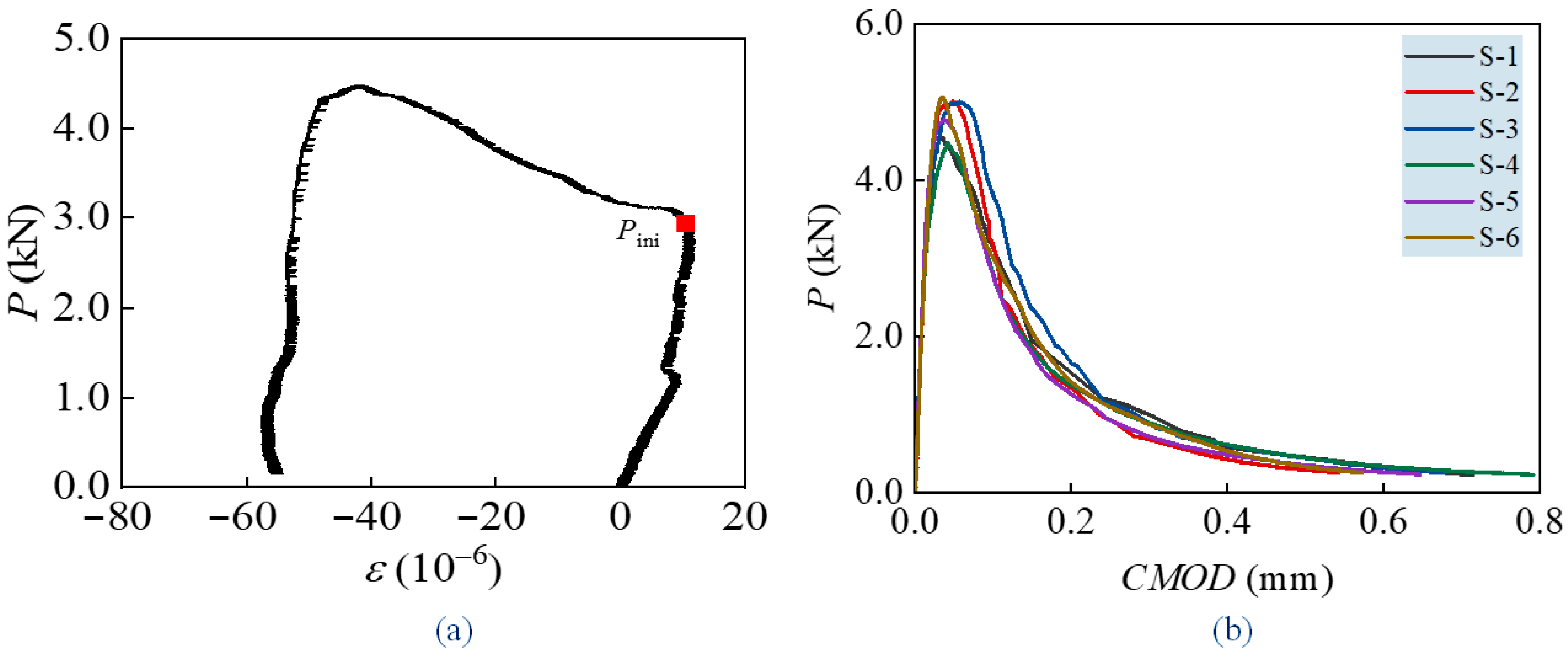
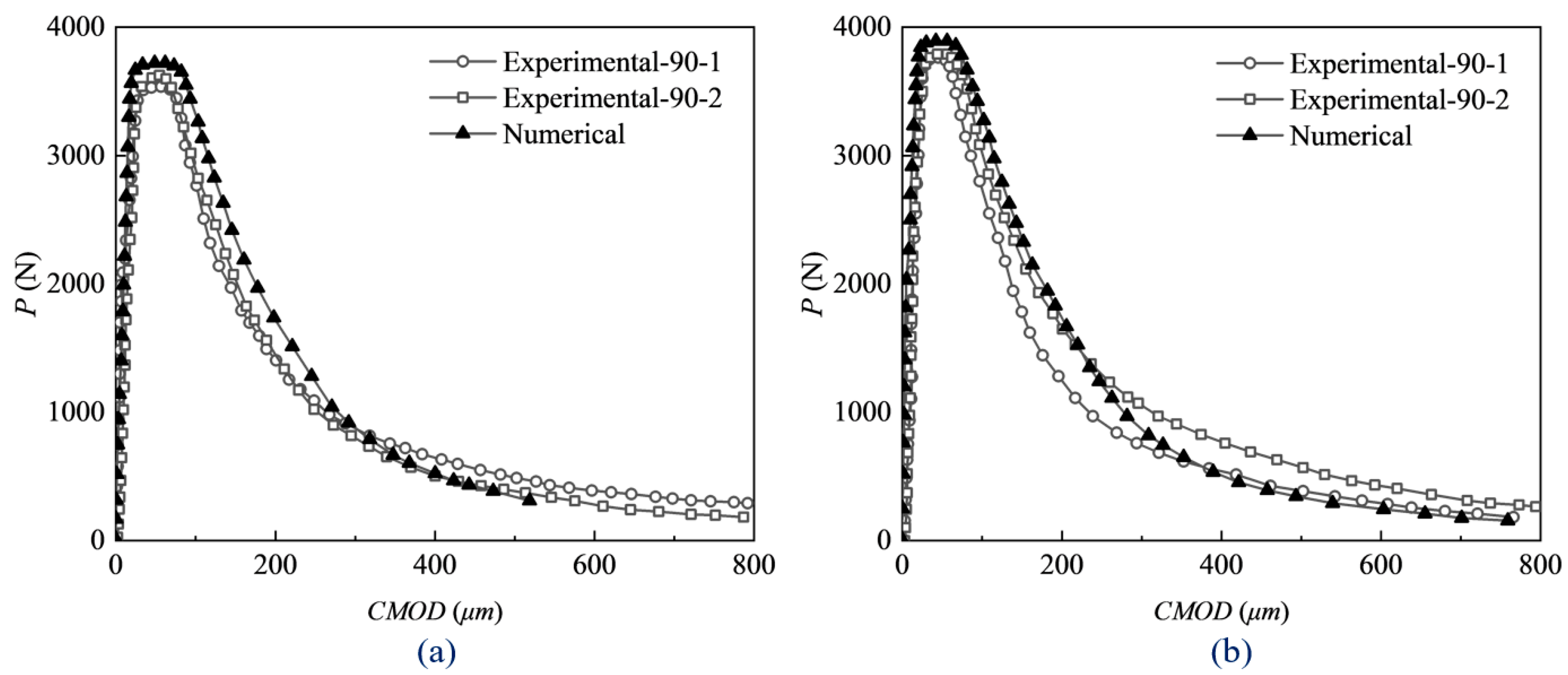
3. Experimental Verification and Discussion
4. Conclusions
- (1)
- Based on the energy equilibrium between external work and dissipation from elastic deformation, creep, and crack growth, a tension-softening constitutive model that quantifies the relation among sw, t, and COD is developed and implemented in the numerical model.
- (2)
- Calibration of creep parameters in the proposed tension-softening model, combined with the fracture properties of concrete, facilitates prediction of time-dependent crack evolution and failure time under sustained loads. This approach integrates viscoelastic behavior with linear elastic fracture mechanics (LEFM) and enables long-term structural assessments.
- (3)
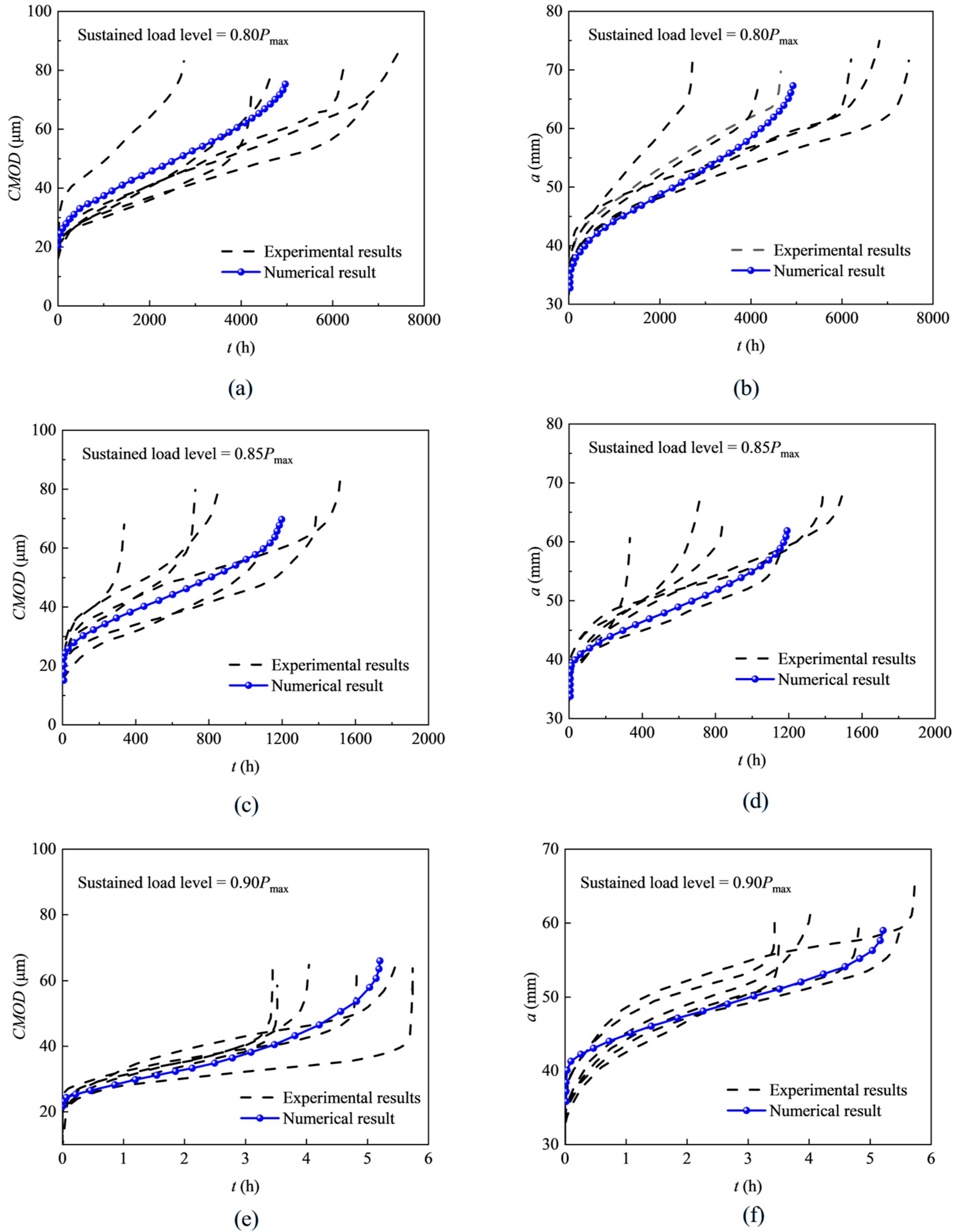
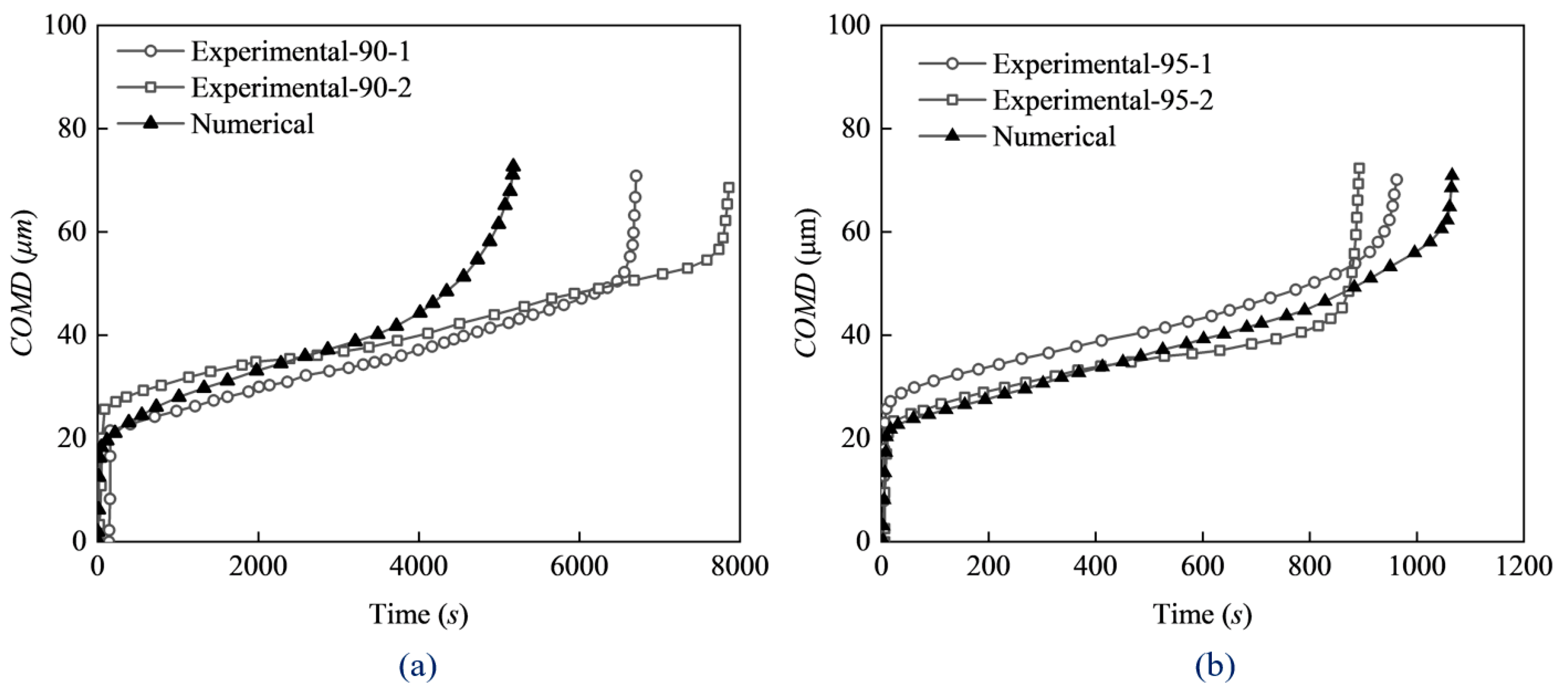
- Through comparisons with two sets of experimental data given in the literature, it is demonstrated that the predicted CMOD versus time and crack length versus time curves match well with the test results. This confirms the predictive capability of the -based criterion in describing crack extension in concrete exposed to sustained loads.
- (4)
- The numerical results indicated that increasing the load level from 0.80 to 0.90 resulted in moderate decreases in CMODf and af by 13.33% and 11.94%, respectively, while the creep fracture lifetime (tf) reduced significantly from 4960 h to 5.21 h.
- (5)
- The -based numerical framework integrates t and COD as primary state variables, employing the generalized Kelvin chain model to describe the viscoelastic behavior of concrete. Therefore, it has potential applications for creep analysis of RC structures where the reinforcement bridging effect can be idealized as equivalent external forces.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiménez, S.; Cornejo, A.; Barbu, L.G.; Barbat, A.H.; Oller, S. Failure pressure analysis of a nuclear reactor prestressed concrete containment building. Eng. Struct. 2021, 236, 112052. [Google Scholar] [CrossRef]
- Meng, T.; Jason, L.; Heitz, T.; Richard, B. Numerical methodology on prestressed reinforced concrete containment building: Creep, aging and leakage. Application to VERCORS mock-up. Eng. Struct. 2023, 280, 115625. [Google Scholar] [CrossRef]
- Li, X.; Gong, J. Effects of steel liner corrosion on the leak-tightness of prestressed concrete containment structure under severe accident loads. Ann. Nucl. Energy 2023, 180, 109487. [Google Scholar] [CrossRef]
- Saliba, J.; Loukili, A.; Grondin, F.; Regoin, J.P. Experimental study of creep-damage coupling in concrete by acoustic emission technique. Mater. Struct. 2012, 45, 1389–1401. [Google Scholar] [CrossRef]
- Omar, M.; Loukili, A.; Pijaudier-Cabot, G.; Le Pape, Y. Creep-Damage Coupled Effects: Experimental Investigation on Bending Beams with Various Sizes. J. Mater. Civ. Eng. 2009, 21, 65–72. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, X.; Zhang, B.S.; Wu, Q. Influence of sustained loading on fracture properties of concrete. Eng. Fract. Mech. 2018, 200, 134–145. [Google Scholar] [CrossRef]
- Dong, W.; Rong, H.; Wu, Q.; Li, J. Investigations on the FPZ evolution of concrete after sustained loading by means of the DIC technique. Constr. Build. Mater. 2018, 188, 49–57. [Google Scholar] [CrossRef]
- Yang, M.; Rong, H.; Dong, W.; Yuan, W.; Zhang, B.; Yu, L. Energy criterion for predicting crack initiation in mixed mode I-II fracture of concrete under long-term loading. Constr. Build. Mater. 2025, 489, 142210. [Google Scholar] [CrossRef]
- Rong, H.; Dong, W.; Zhang, X.; Zhang, B.S. Size effect on fracture properties of concrete after sustained loading. Mater. Struct. 2019, 52, 16. [Google Scholar] [CrossRef]
- Dong, W.; Li, J.; Zhang, X.; Zhang, B.S. Evolutions of SIFs of concrete under sustained loading by considering the effects of stress relaxations. J. Mater. Civ. Eng. ASCE 2019, 31, 4019287. [Google Scholar] [CrossRef]
- Dong, W.; Yuan, W.; Zhang, B.; Zhong, H. Energy-based fracture criterion of rock-concrete interface considering viscoelastic characteristics. J. Eng. Mech. 2022, 148, 04021155. [Google Scholar] [CrossRef]
- Yuan, W.; Dong, W.; Zhang, B.; Huo, J. Viscoelasticity-induced fracture behavior of rock-concrete interface after sustaining creep process. Cem. Concr. Compos. 2023, 136, 104901. [Google Scholar] [CrossRef]
- Yuan, W.; Dong, W.; Wang, S.; Yu, L. Time-Dependent Fracture Analysis of Rock-Concrete Interface Under Compression-Shear State: Modeling and Numerical Implementation. Rock Mech. Rock Eng. 2025, 1–20. [Google Scholar] [CrossRef]
- Yuan, W.; Dong, W.; Li, P.; Wang, S.; Wang, L.; Liu, C. Crack propagation process and lifetime prediction method of concrete-rock interface under constant loading. Int. J. Rock Mech. Min. Sci. 2024, 181, 105839. [Google Scholar] [CrossRef]
- Hillerborg, A. Theoretical analysis of the double torsion test. Cem. Concr. Res. 1983, 13, 69–80. [Google Scholar] [CrossRef]
- Han, X.; Wu, Z.; Gao, H.; Zheng, J.; Yu, R.C. Tension-softening constitutive model of concrete under sustained loading. Constr. Build. Mater. 2024, 421, 135623. [Google Scholar] [CrossRef]
- Han, X.Y.; Wu, Z.M.; Jia, M.D.; Zheng, J.J.; Yu, R.C. A new method for determining the tension-softening curve of concrete. Theor. Appl. Fract. Mech. 2023, 126, 103992. [Google Scholar] [CrossRef]
- Flores, R.D.; Hellmich, C.; Pichler, B. Nonlinear creep of concrete: Stress-activated stick–slip transition of viscous interfaces and microcracking-induced damage. Cement Concrete Res. 2025, 191, 107809. [Google Scholar] [CrossRef]
- Santhikumar, S.; Karihaloo, B.L. Time-dependent tension softening. Mech. Cohesive-Frict. Mater. Int. J. Exp. Model. Comput. Mater. Struct. 1996, 1, 295–304. [Google Scholar] [CrossRef]
- Zhou, F.P. Time-Dependent Crack Growth and Fracture in Concrete; IAEA: Vienna, Austria, 1992. [Google Scholar]
- Li, J.; Dong, W.; Zhang, B.; Zhou, X. Prediction on crack propagation of concrete due to time-dependent creep under high sustained loading. J. Mater. Civ. Eng. 2022, 34, 04021451. [Google Scholar] [CrossRef]
- Yuan, W.; Dong, W.; Zhang, B.; Zhong, H. Time-dependent fracture behavior of rock-Concrete interface coupling viscoelasticity and cohesive stress relaxation. J. Eng. Mech. 2023, 149, 04022100. [Google Scholar] [CrossRef]
- Bažant, Z.P. Size effect on structural strength: A review. Arch. Appl. Mech. 1999, 69, 703–725. [Google Scholar] [CrossRef]
- Carpinteri, A.; Massabó, R. Reversal in failure scaling transition of fibrous composites. J. Eng. Mech. 1997, 123, 107–114. [Google Scholar] [CrossRef]
- Ooi, E.T.; Yang, Z.J. Modelling crack propagation in reinforced concrete using a hybrid finite element-scaled boundary finite element method. Eng. Fract. Mech. 2011, 78, 252–273. [Google Scholar] [CrossRef]
- Yang, Z.J.; Deeks, A.J. Fully-automatic modelling of cohesive crack growth using a finite element-scaled boundary finite element coupled method. Eng. Fract. Mech. 2007, 74, 2547–2573. [Google Scholar] [CrossRef]
- Ooi, E.T.; Yang, Z.J. A hybrid finite element-scaled boundary finite element method for crack propagation modelling. Comput. Methods Appl. Mech. Eng. 2010, 199, 1178–1192. [Google Scholar] [CrossRef]
- Song, C.; Ooi, E.T.; Natarajan, S. A review of the scaled boundary finite element method for two-dimensional linear elastic fracture mechanics. Eng. Fract. Mech. 2018, 187, 45–73. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.; Zhou, X. Calculating crack extension resistance of concrete based on a new crack propagation criterion. Constr. Build. Mater. 2013, 38, 879–889. [Google Scholar] [CrossRef]
- Wu, Z.M.; Wu, X.; Zheng, J.J.; Dong, W.; Wu, Y.-F. An analytical method for determining the crack extension resistance curve of concrete. Mag. Concr. Res. 2014, 66, 719–728. [Google Scholar] [CrossRef]
- Dong, W.; Zhou, X.; Wu, Z. On fracture process zone and crack extension resistance of concrete based on initial fracture toughness. Constr. Build. Mater. 2013, 49, 352–363. [Google Scholar] [CrossRef]
- Yin, T.; Li, X.; Xia, K.; Huang, S. Effect of thermal treatment on the dynamic fracture toughness of Laurentian granite. Rock Mech. Rock Eng. 2012, 45, 1087–1094. [Google Scholar] [CrossRef]
- Yin, T.; Li, X.; Cao, W.; Xia, K. Effects of thermal treatment on tensile strength of Laurentian granite using Brazilian test. Rock Mech. Rock Eng. 2015, 48, 2213–2223. [Google Scholar] [CrossRef]
- Yin, T.; Zhang, S.; Li, X.; Bai, L. A numerical estimate method of dynamic fracture initiation toughness of rock under high temperature. Eng. Fract. Mech. 2018, 204, 87–102. [Google Scholar] [CrossRef]
- Dong, W.; Yang, D.; Zhang, B.; Wu, Z. Rock-concrete interfacial crack propagation under mixed mode I-II fracture. J. Eng. Mech. 2018, 144, 04018039. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.; Tang, X.; Zhou, X. A comparative study on stress intensity factor-based criteria for the prediction of mixed mode I-II crack propagation in concrete. Eng. Fract. Mech. 2018, 197, 217–235. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.; Zhou, X.; Wang, C. A comparative study on two stress intensity factor-based criteria for prediction of mode-I crack propagation in concrete. Eng. Fract. Mech. 2016, 158, 39–58. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zeng, M.H.; Liu, H.B.; Yang, J.Q.; Li, X.X.; Hu, X.Z. A comparative study of nil-SIF-based and initial fracture toughness-based criteria for prediction of mode-I crack propagation in concrete at low temperatures. Eng. Fract. Mech. 2025, 317, 110909. [Google Scholar] [CrossRef]
- Xu, S.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part I: Experimental investigation of crack propagation. Int. J. Fract. 1999, 98, 111–149. [Google Scholar] [CrossRef]
- Xu, S.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams. Int. J. Fract. 1999, 98, 151–177. [Google Scholar] [CrossRef]
- GB 175-2020; Common Portland Cement. China Building Industry Press: Beijing, China, 2020.
- GB 50010-2010; Code for Design of Concrete Structures. China Building Industry Press: Beijing, China, 2010.
- Hu, X.; Wittmann, F. Size effect on toughness induced by crack close to free surface. Eng. Fract. Mech. 2000, 65, 209–221. [Google Scholar] [CrossRef]
- Duan, K.; Hu, X.Z.; Wittmann, F.H. Size effect on fracture resistance and fracture energy of concrete. Mater. Struct. 2003, 36, 74–80. [Google Scholar] [CrossRef]
- Duan, K.; Hu, X.; Wittmann, F.H. Boundary effect on concrete fracture and non-constant fracture energy distribution. Eng. Fract. Mech. 2003, 70, 2257–2268. [Google Scholar] [CrossRef]
- Hu, X.; Duan, K. Mechanism behind the size effect phenomenon. J. Eng. Mech. 2010, 136, 60–68. [Google Scholar] [CrossRef]
- Hu, X.; Duan, K. Size effect and quasi-brittle fracture: The role of FPZ. Int. J. Fract. 2008, 154, 3–14. [Google Scholar] [CrossRef]
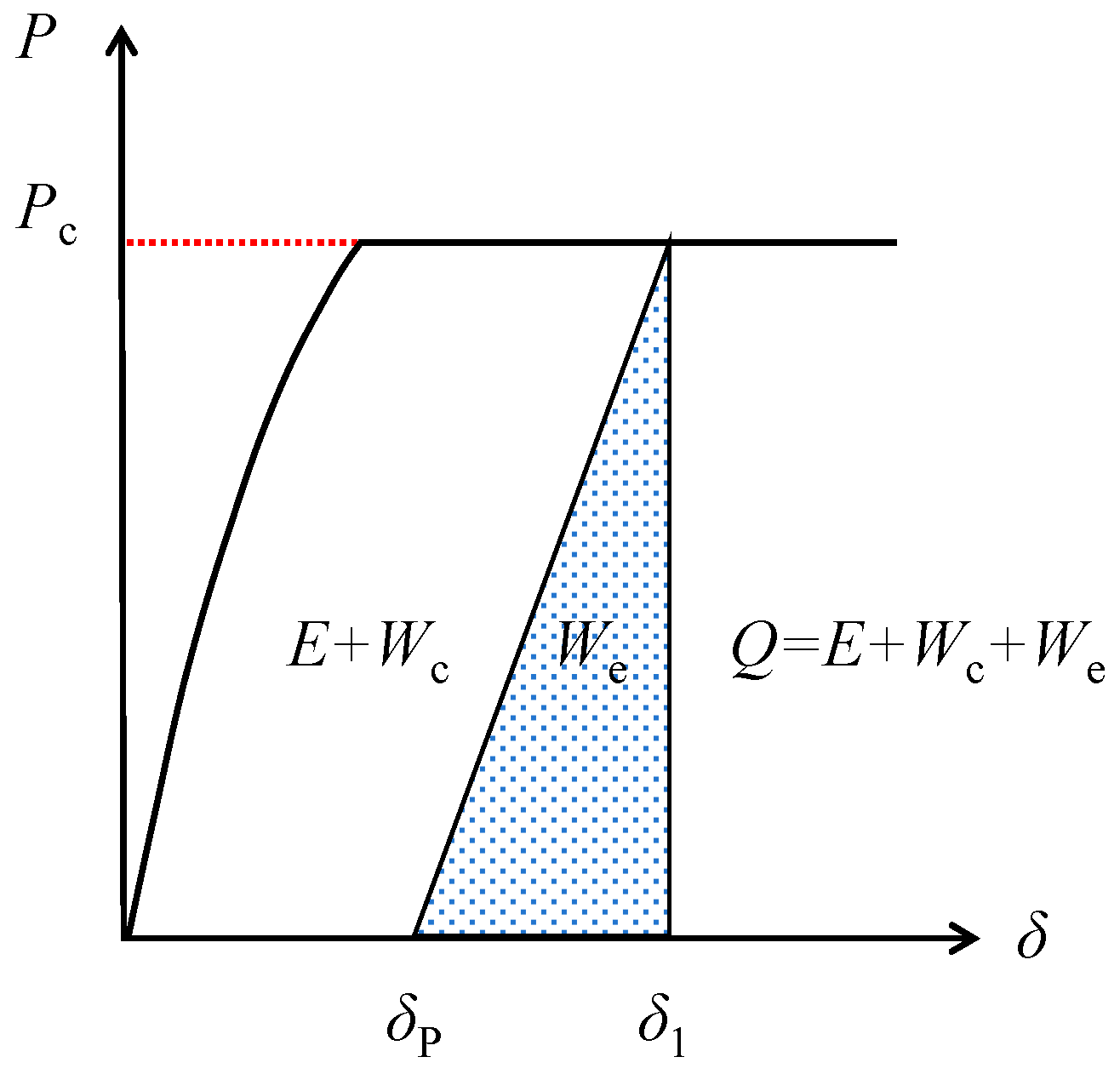


| Specimen No. | Pc (kN) | Δa1 (mm) | Δd (mm) | Δt (h) |
|---|---|---|---|---|
| S-0.90-1 | 4.33 | 6 | 1 | 0.01 |
| Composition | CaO | SiO2 | Al2O3 | Fe2O3 | MgO | SO3 |
| Content (%) | 59.30 | 21.91 | 6.27 | 3.78 | 1.64 | 2.41 |
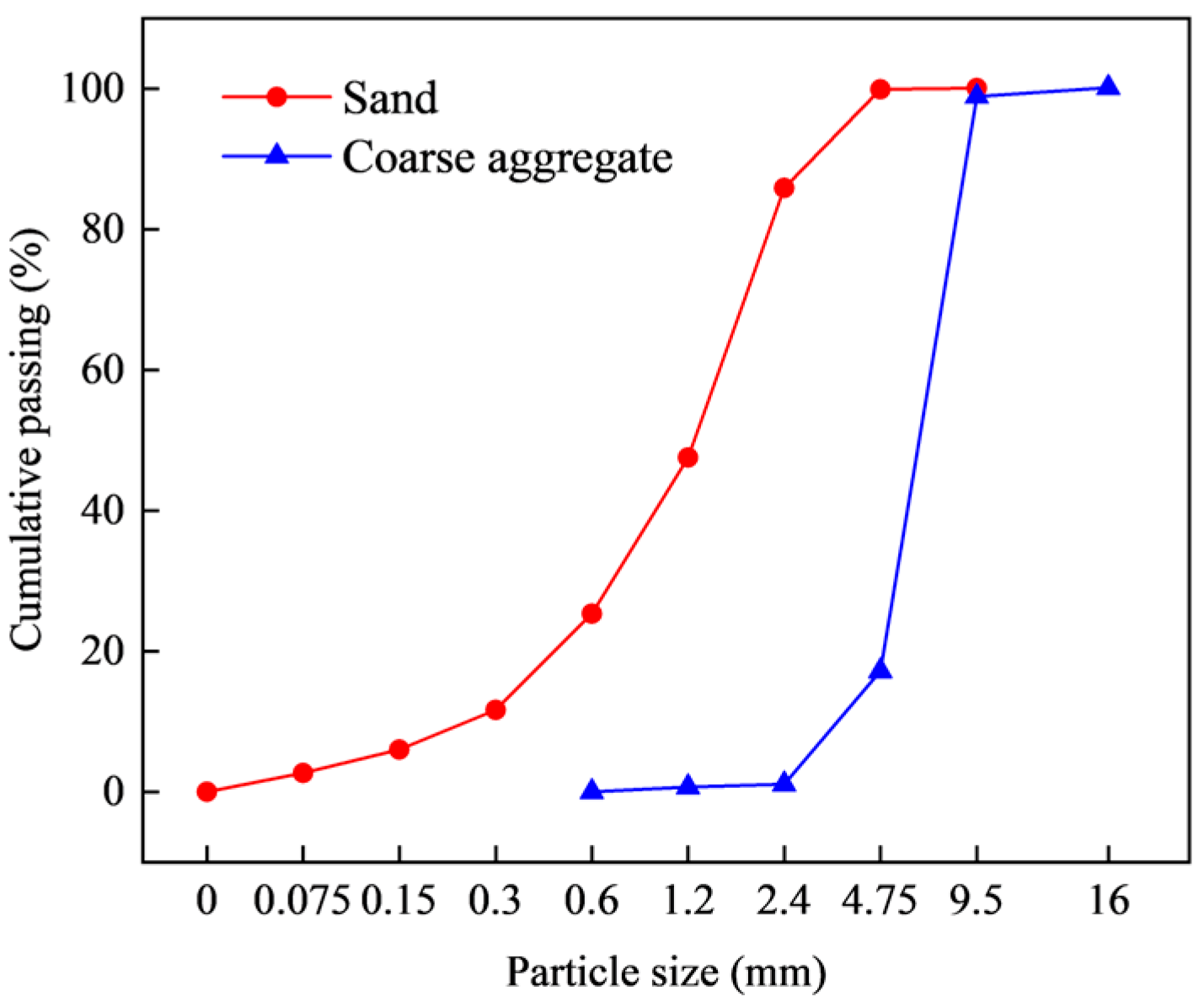
| Cement (kg/m3) | Water (kg/m3) | Fine Aggregate (kg/m3) | Coarse Aggregate (kg/m3) |
| 325 | 195 | 696 | 1184 |
| fcu (MPa) | ft (MPa) | ν | Ec (GPa) |
|---|---|---|---|
| 49.70 ± 1.32 | 3.82 ± 0.34 | 0.20 ± 0.00 | 34.41 ± 2.67 |
| Pini (kN) | Pmax (kN) | Pini/Pmax | Fracture Energy GF (N/mm) | Initial Fracture Toughness (MPa·m1/2) | Unstable Fracture Toughness (MPa·m1/2) |
|---|---|---|---|---|---|
| 3.07 ± 0.25 | 4.81 ± 0.47 | 0.638 ± 0.48 | 112.71 ± 13.47 | 0.5907 ± 0.25 | 1.89 ± 0.17 |
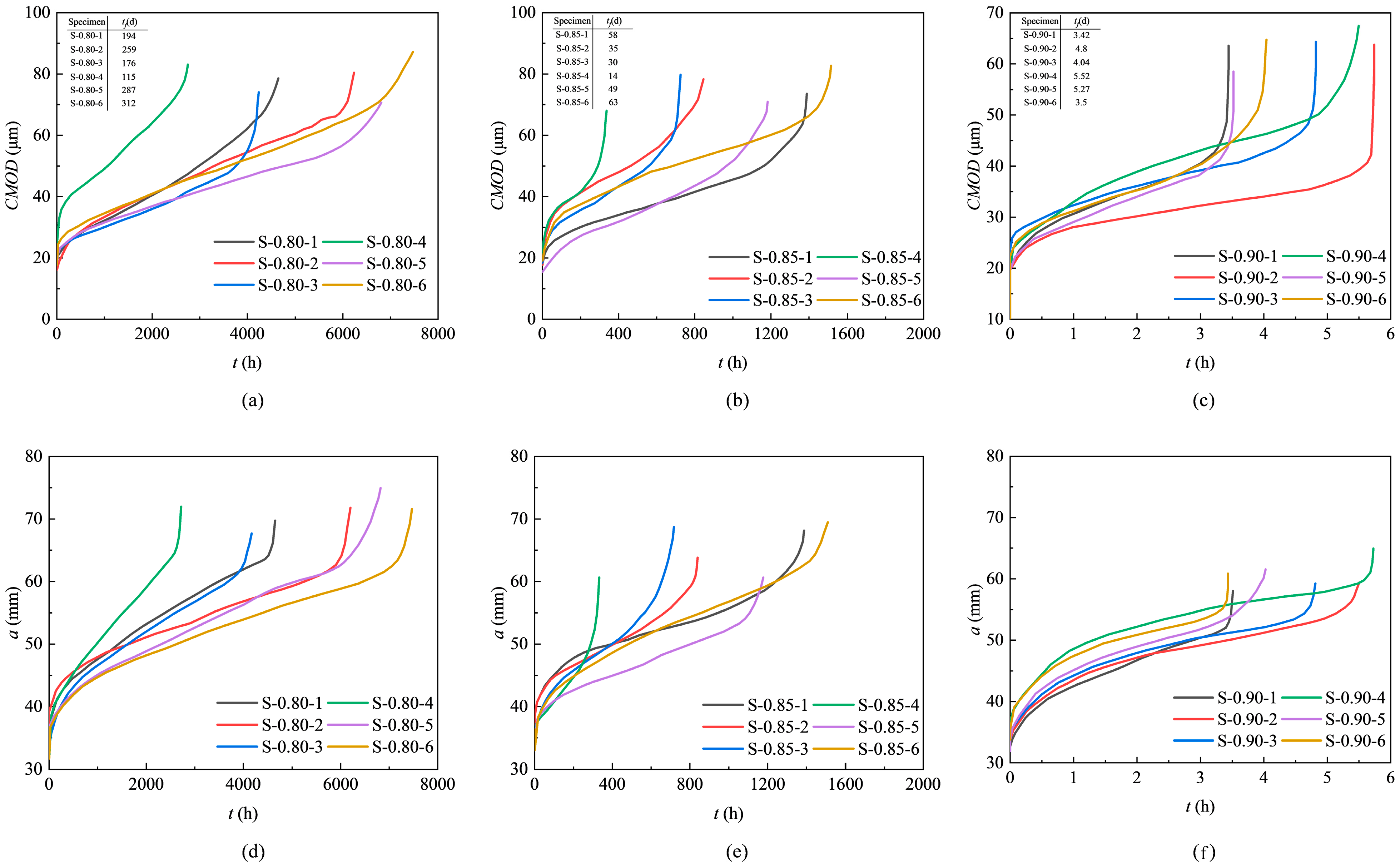
| Specimen No. | Pc (kN) | tf (h) | CMODf (μm) | af (mm) |
|---|---|---|---|---|
| S-0.80-1 | 3.85 | 4652.72 (194 d) | 78 | 69.58 |
| S-0.80-2 | 6216.00 (259 d) | 80 | 71.69 | |
| S-0.80-3 | 4223.82 (176 d) | 74 | 68.33 | |
| S-0.80-4 | 2759.37 (115 d) | 83 | 72.60 | |
| S-0.80-5 | 6885.68 (287 d) | 73 | 75.93 | |
| S-0.80-6 | 7493.84 (312 d) | 88 | 72.21 | |
| Average | 3.85 | 5371.91 ± 1641.51 (224 d) | 79 ± 5.15 | 71.72 ± 2.41 |
| S-0.85-1 | 4.09 | 1390.49 (58 d) | 73 | 67.94 |
| S-0.85-2 | 847.21 (35 d) | 78 | 63.72 | |
| S-0.85-3 | 726.54 (30 d) | 79 | 68.68 | |
| S-0.85-4 | 338.72 (14 d) | 68 | 60.87 | |
| S-0.85-5 | 1181.17 (49 d) | 71 | 60.94 | |
| S-0.85-6 | 1518.17 (63 d) | 82 | 69.44 | |
| Average | 4.09 | 1000.38 ± 406.04 (42 d) | 75 ± 4.88 | 65.27 ± 3.57 |
| S-0.90-1 | 4.33 | 3.42 | 64 | 61.13 |
| S-0.90-2 | 4.80 | 68 | 59.83 | |
| S-0.90-3 | 4.04 | 65 | 61.59 | |
| S-0.90-4 | 5.52 | 73 | 59.90 | |
| S-0.90-5 | 5.72 | 69 | 65.34 | |
| S-0.90-6 | 3.50 | 60 | 58.99 | |
| Average | 4.33 | 4.50 ± 0.91 | 67 ± 4.11 | 61.13 ± 2.07 |
| Specimen No. | tf num (h) | tf exp (h) | CMODf num (μm) | CMODf exp (μm) | af num (mm) | af exp (mm) |
|---|---|---|---|---|---|---|
| S-0.80 | 4960 | 5372 | 75 | 79 | 67 | 72 |
| S-0.85 | 1194 | 1000 | 69 | 75 | 62 | 65 |
| S-0.90 | 5.21 | 4.50 | 65 | 67 | 59 | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Dong, J.; Wu, L.; Li, Z.; Chang, Z.; Yu, Z.; Jiang, B. Numerical and Experimental Investigation on Time-Dependent Crack Extension in Concrete Under Sustained Loads. Buildings 2025, 15, 4180. https://doi.org/10.3390/buildings15224180
Yao Z, Dong J, Wu L, Li Z, Chang Z, Yu Z, Jiang B. Numerical and Experimental Investigation on Time-Dependent Crack Extension in Concrete Under Sustained Loads. Buildings. 2025; 15(22):4180. https://doi.org/10.3390/buildings15224180
Chicago/Turabian StyleYao, Zheng, Jiacheng Dong, Linmei Wu, Zetong Li, Ziheng Chang, Zhuohui Yu, and Binze Jiang. 2025. "Numerical and Experimental Investigation on Time-Dependent Crack Extension in Concrete Under Sustained Loads" Buildings 15, no. 22: 4180. https://doi.org/10.3390/buildings15224180
APA StyleYao, Z., Dong, J., Wu, L., Li, Z., Chang, Z., Yu, Z., & Jiang, B. (2025). Numerical and Experimental Investigation on Time-Dependent Crack Extension in Concrete Under Sustained Loads. Buildings, 15(22), 4180. https://doi.org/10.3390/buildings15224180







