Study on Cumulative Deformation of Silt Soil Under Traffic Loading Based on PSO-BP Neural Network
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
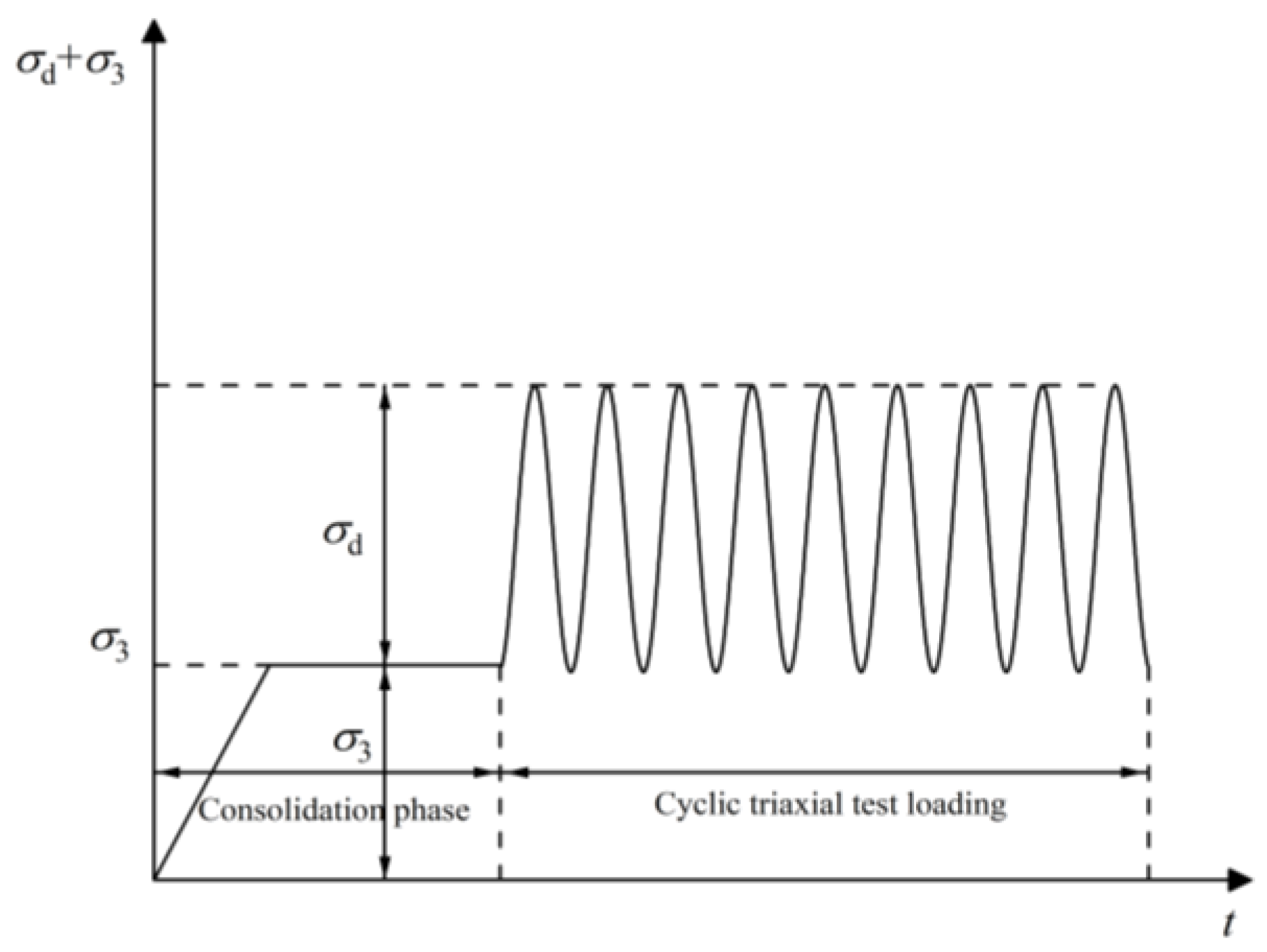
2.2. Testing Methodology
3. Results
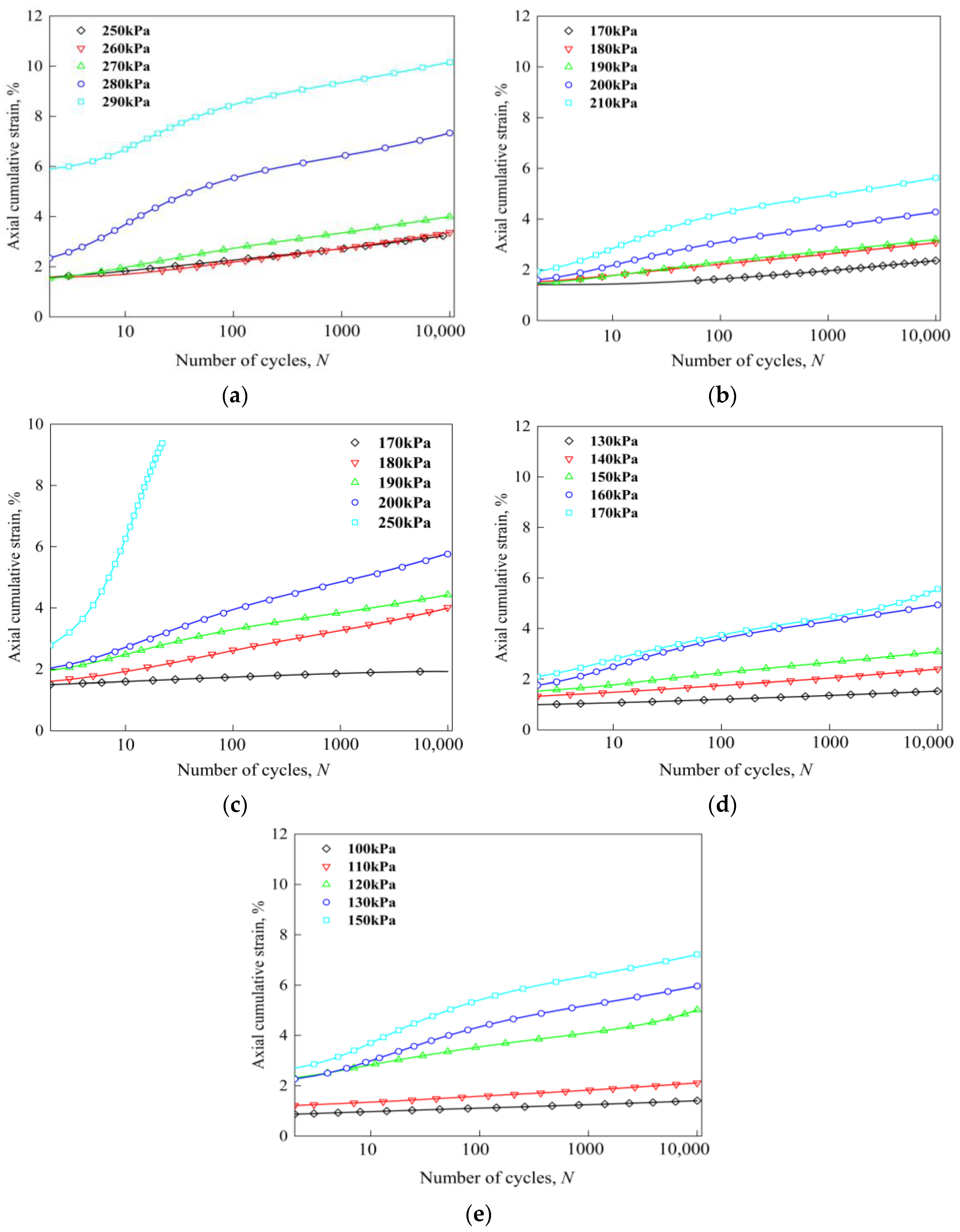
3.1. Axial Cumulative Plastic Strain Analysis
Effect of Confining Pressure on Cumulative Plastic Strain
3.2. Effect of Dynamic Stress on Cumulative Plastic Strain
3.3. Effect of Moisture Contents on Cumulative Plastic Strain
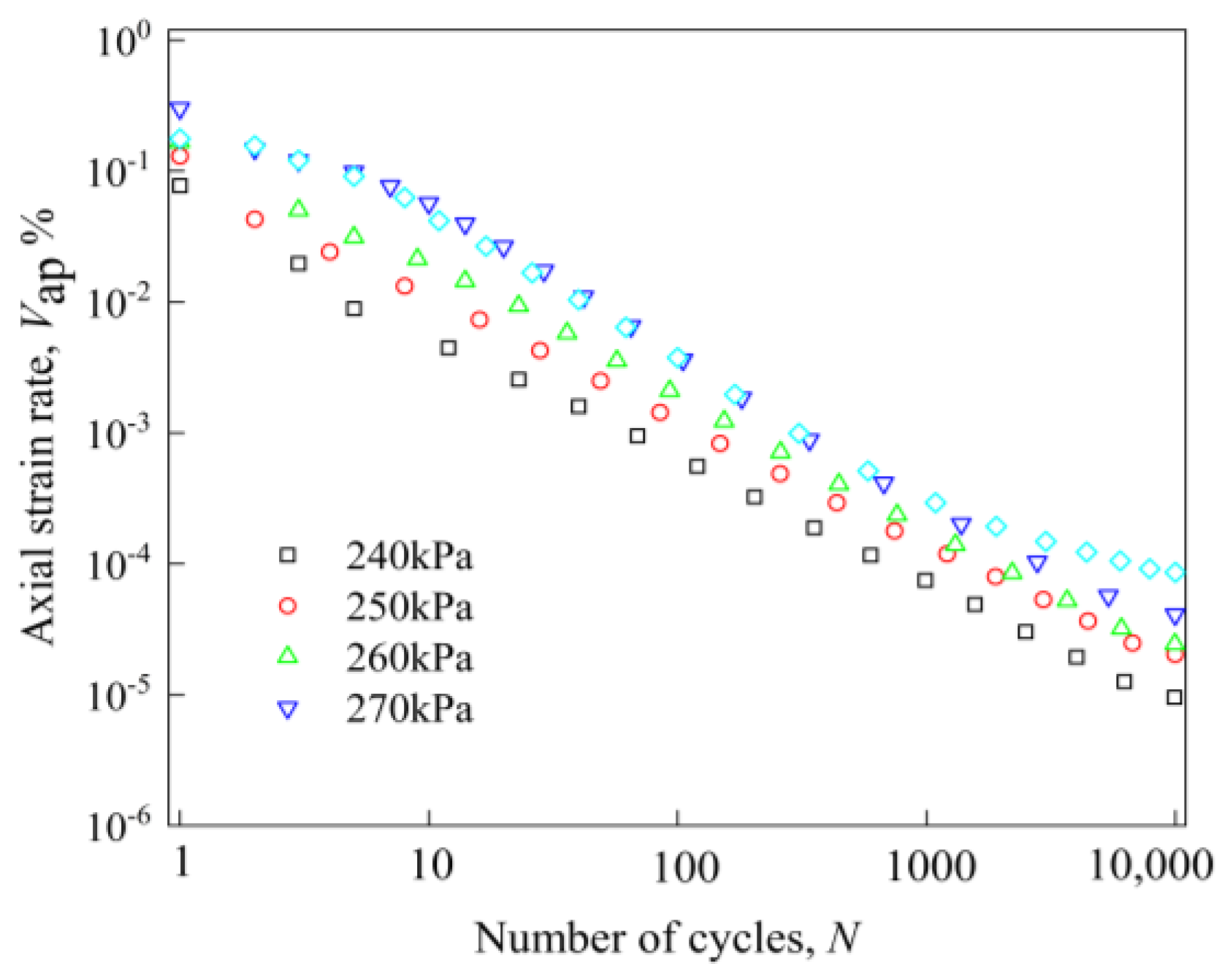
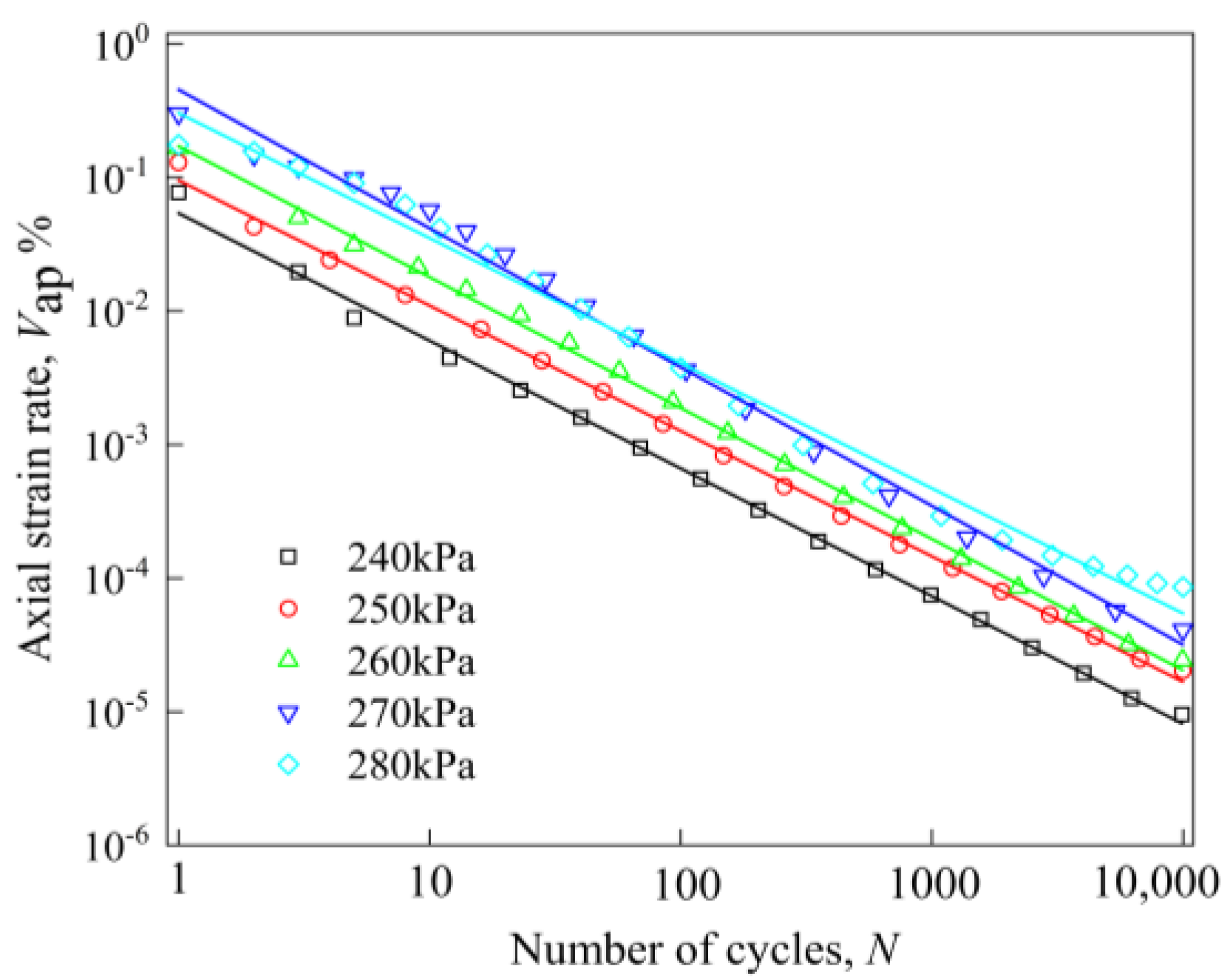
3.4. Change Rule of Axial Strain Rate Under Different Factors
4. Discussion
4.1. Plastic Strain Prediction Model
Monismith Model
4.2. PSO-BP Neural Network Prediction Model
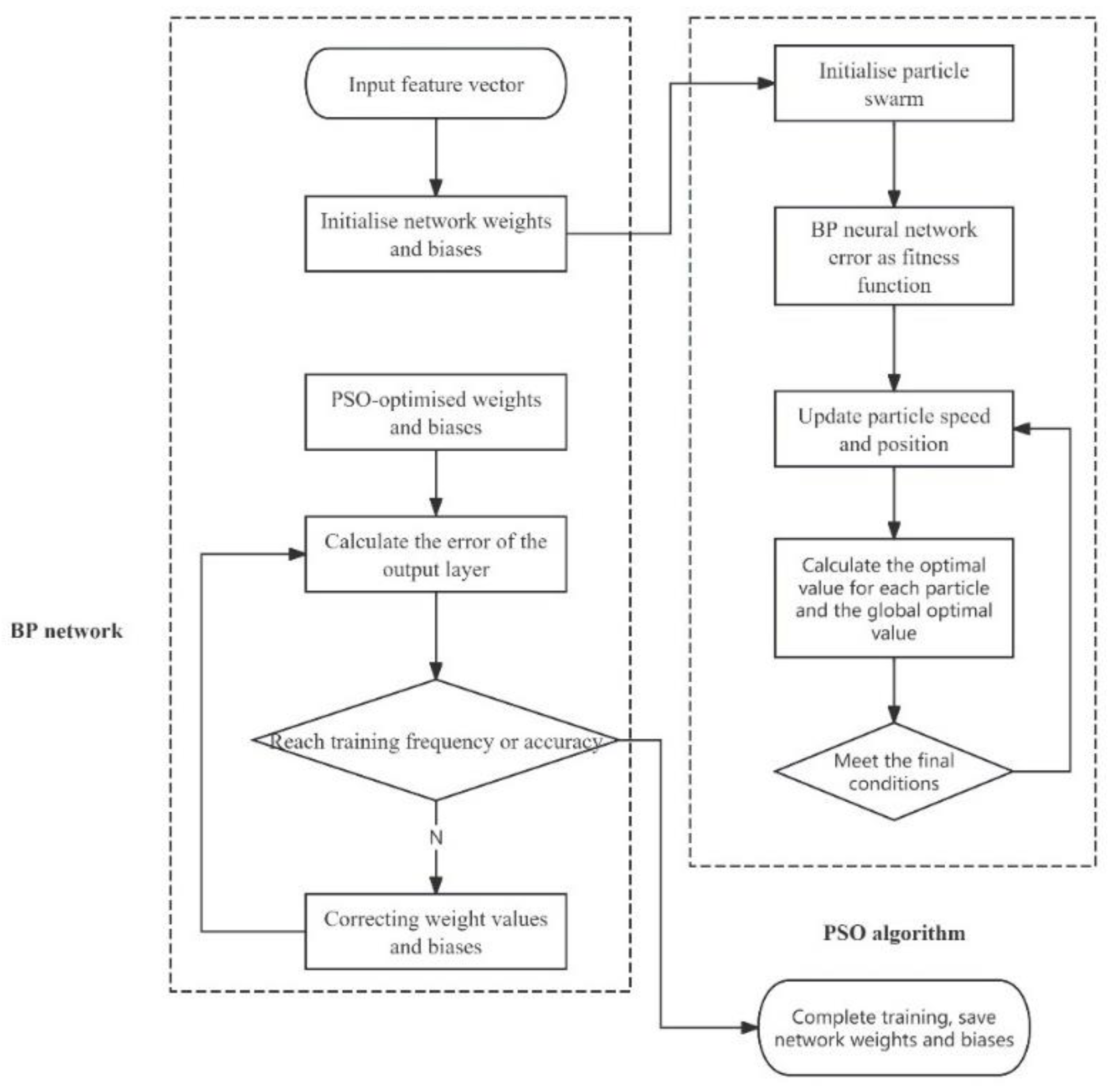
4.2.1. PSO-BP
4.2.2. k-Fold Cross-Validation
4.2.3. Cumulative Plastic Strain Database
4.2.4. Gray Correlation of Cumulative Deformation Influence Factors
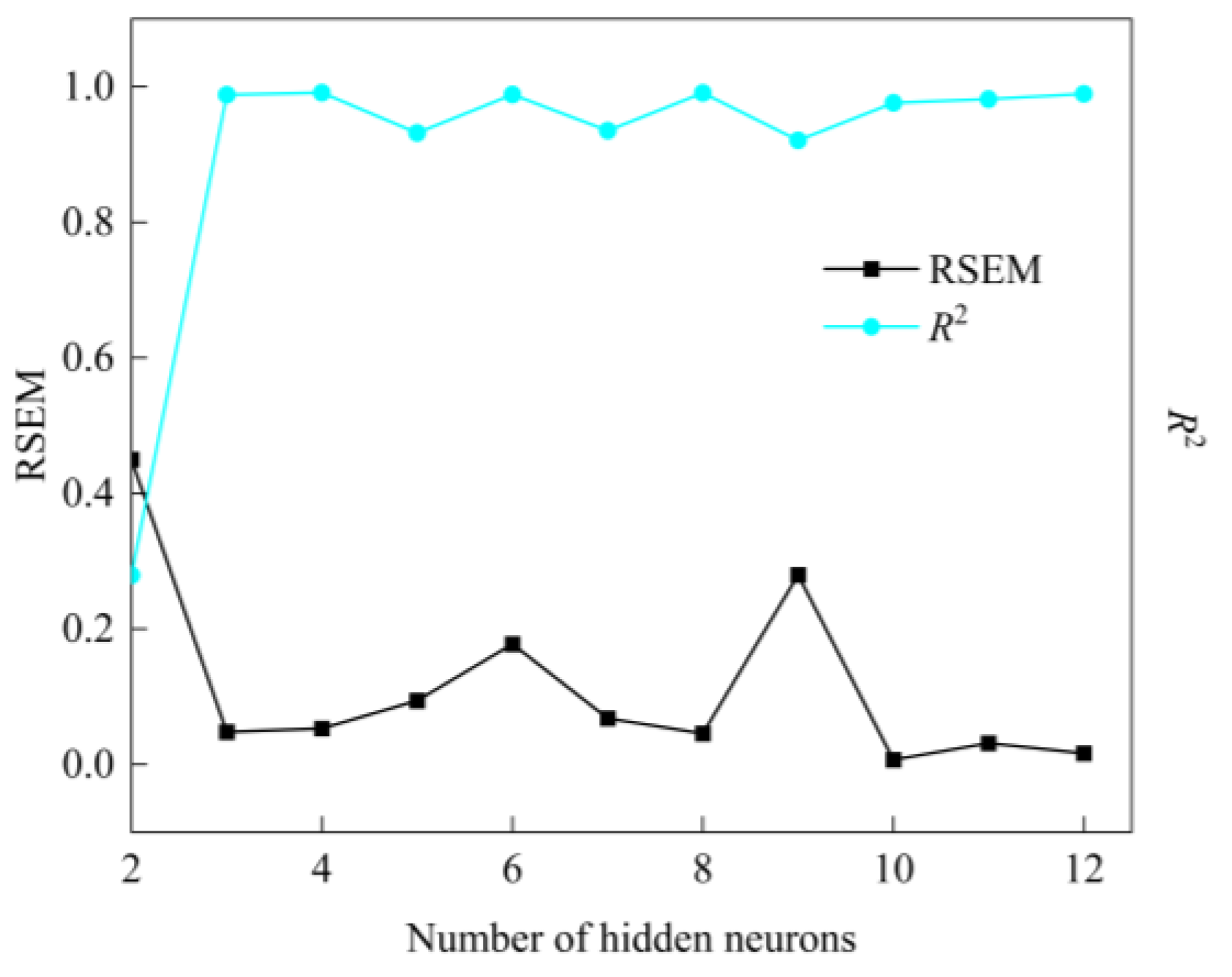
4.2.5. Parameter Optimization of the PSO-BP Model
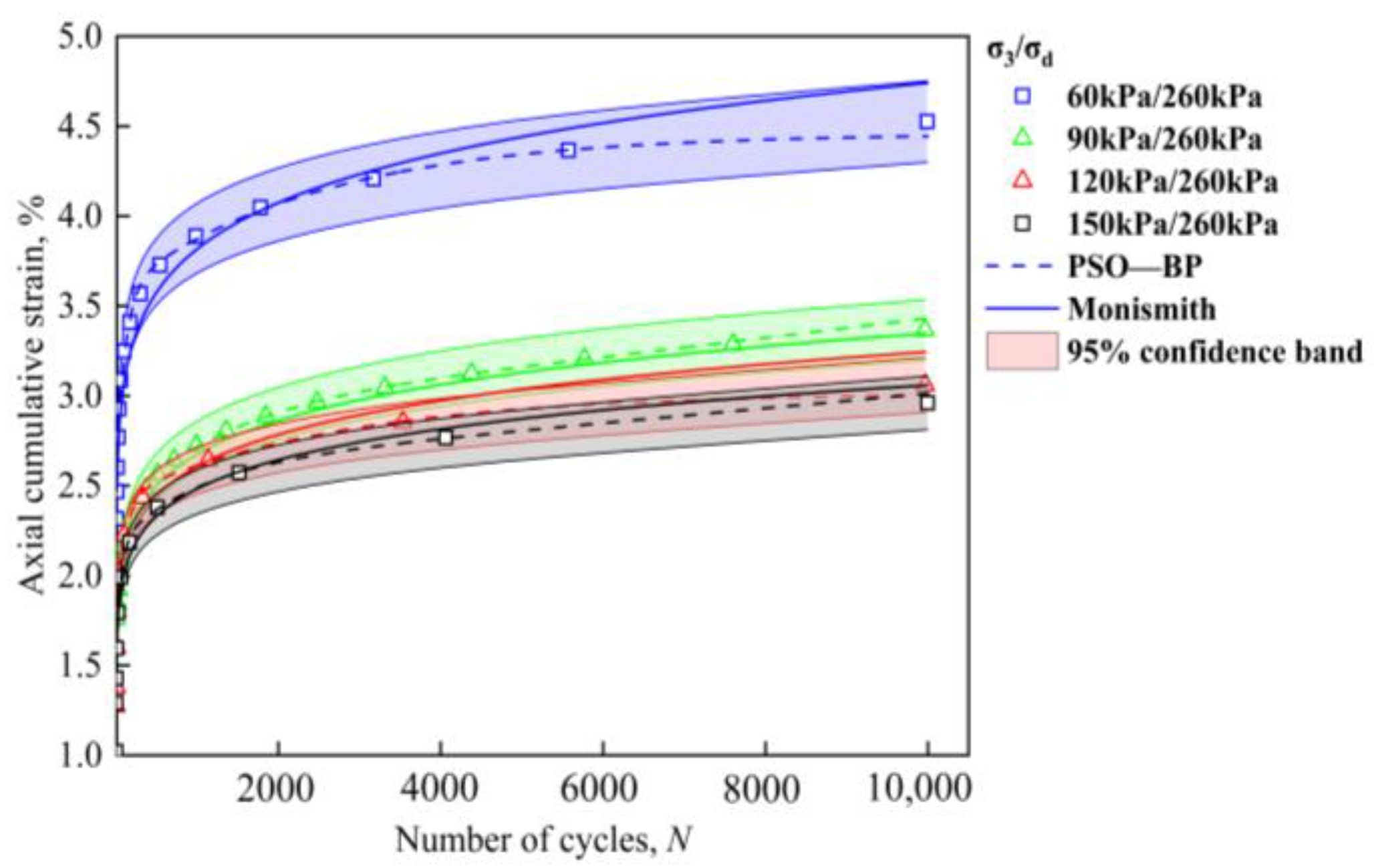
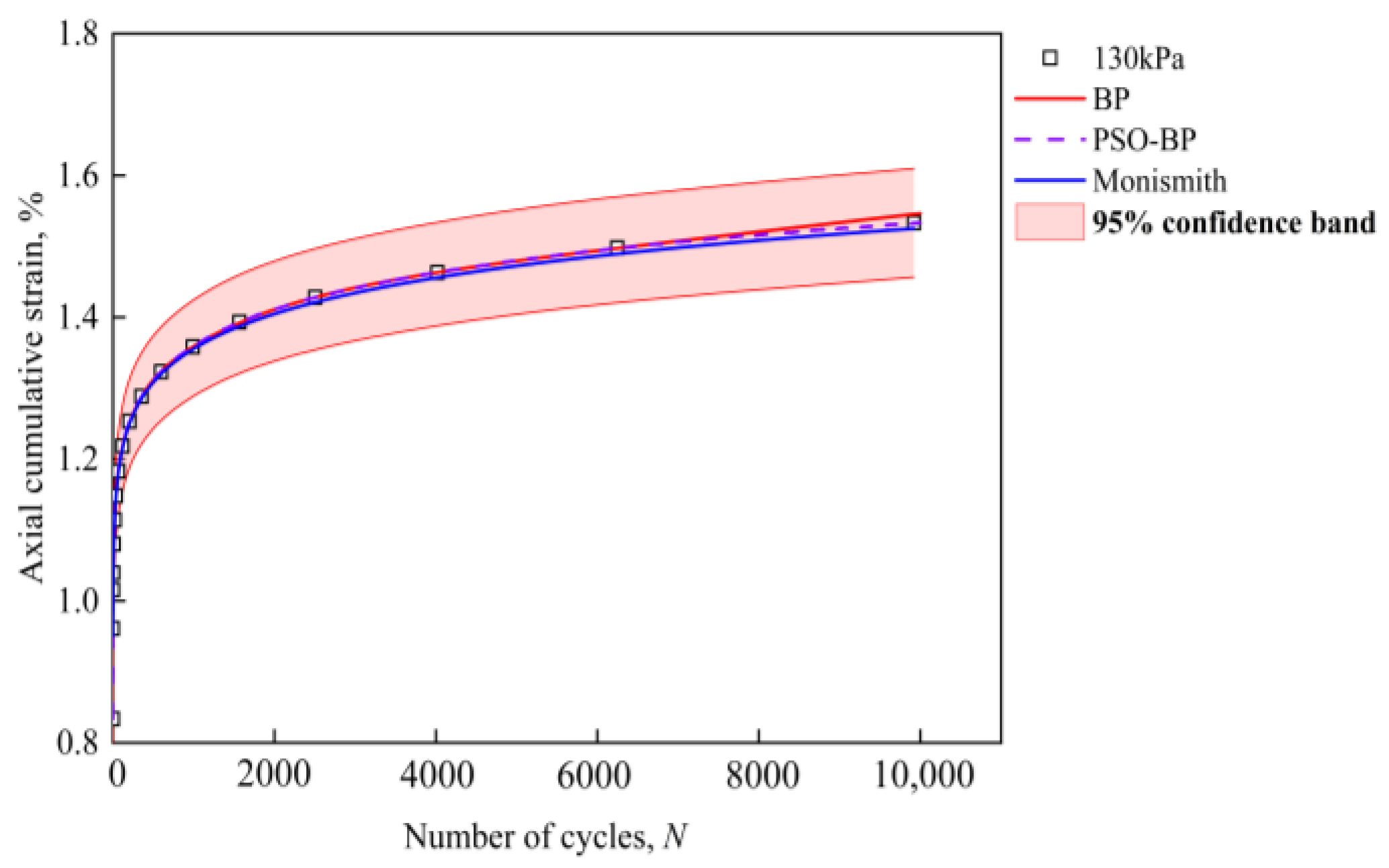
4.3. Analysis of Model Prediction Results
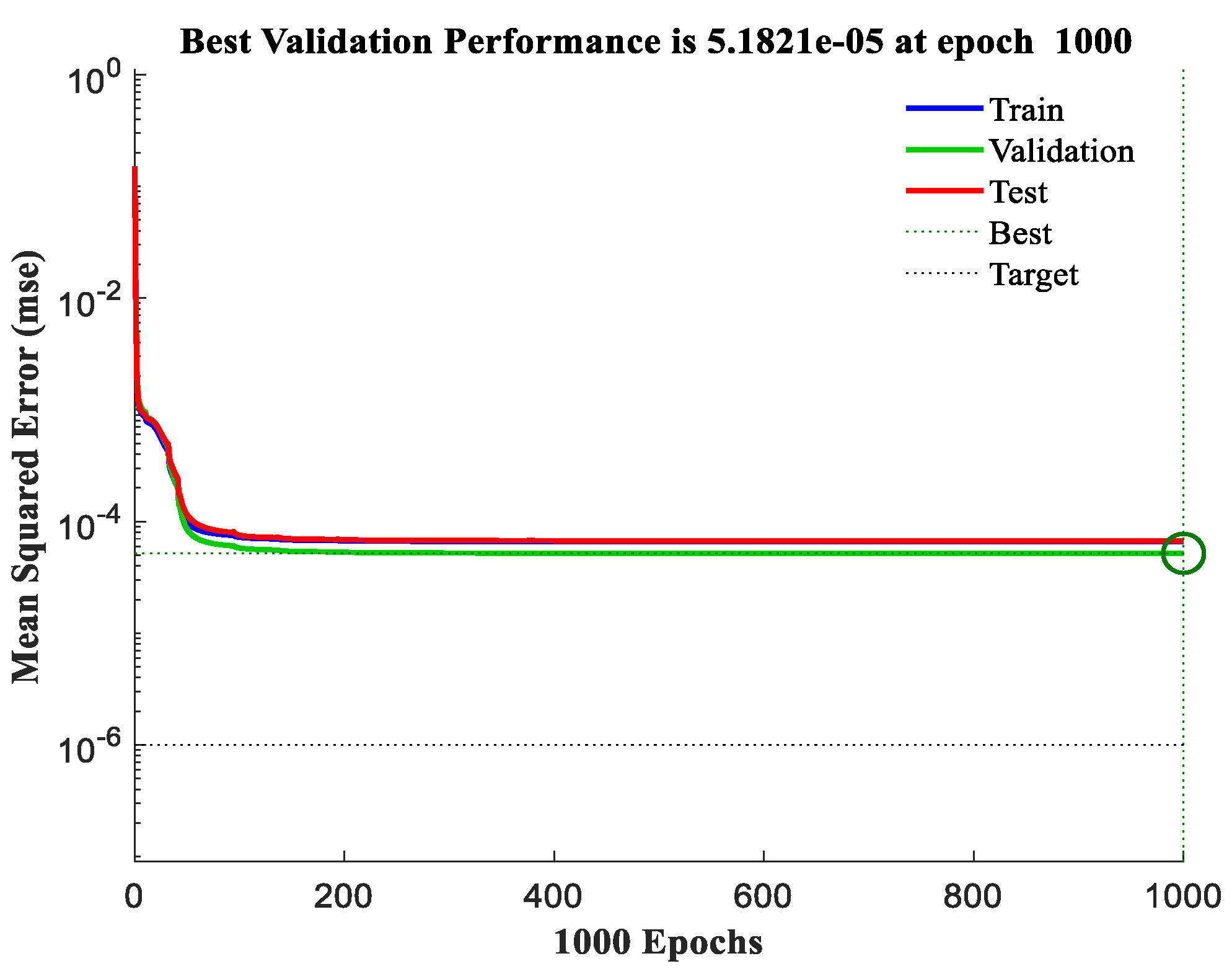
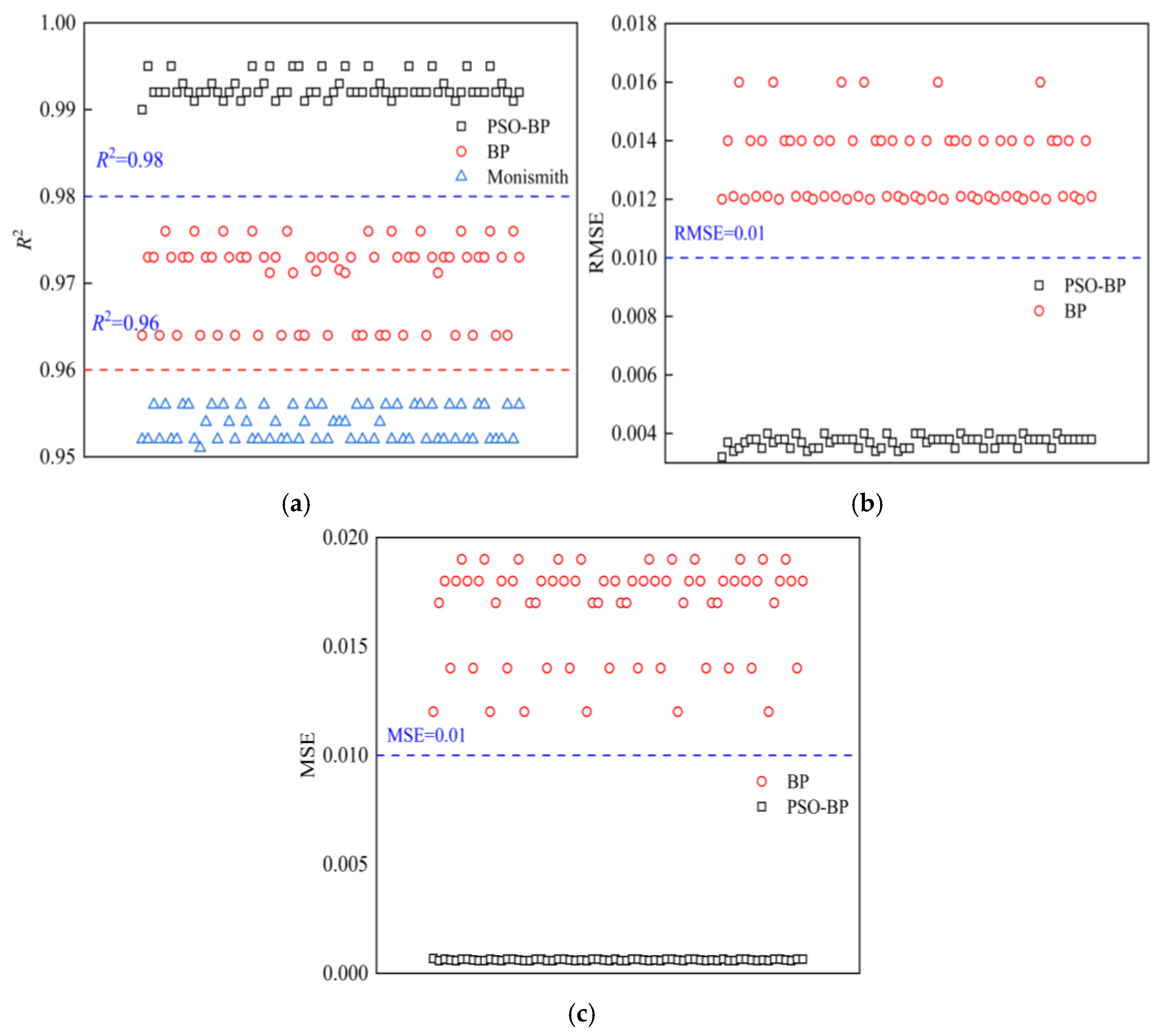
4.3.1. Comparison of BP and PSO-BP Prediction Performance
4.3.2. PSO-BP Prediction Results
4.3.3. Analysis of Model Predictions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, X.W.; Xu, Q.; Teng, J.; Zhao, N.; Lv, L. A novel model for the cumulative plastic strain of soft marine clay under long-term low cyclic loads. Ocean. Eng. 2018, 149, 194–204. [Google Scholar] [CrossRef]
- Ren, X.W.; Xu, Q.; Xu, C.B.; Teng, J.D.; Lv, S.H. Undrained pore pressure behavior of soft marine clay under long-term low cyclic loads. Ocean. Eng. 2018, 150, 60–68. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, R.; Zheng, J.; Sun, H.; Gao, Y. Evolution of axial cumulative strain and micro-pore structure characteristics of solidified mud under cyclic loading. Transp. Geotech. 2025, 50, 101454. [Google Scholar] [CrossRef]
- Ural, N.; Gunduz, Z. Behavior of Nonplastic Silty Soils under Cyclic Loading. Sci. World J. 2014, 2014, 635763. [Google Scholar] [CrossRef]
- Sun, L. Undrained Deformation Characteristics of Soft Marine Clay Subjected to One-Way Cyclic Loading with Variable Confining Pressure. Adv. Mater. Sci. Eng. 2022, 2022, 9630795. [Google Scholar] [CrossRef]
- Sun, L. Undrained behavior of marine clay under one-way cyclic loading with variable confining pressure. Sci. Rep. 2024, 14, 13572. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.B.; Feng, W.Q.; Yin, J.H.; Chen, J.M.; Borana, L.; Chen, R.P. New model for predicting permanent strain of granular materials in embankment subjected to low cyclic loadings. J. Geotech. Geoenviron. Eng. 2020, 146, 04020084. [Google Scholar] [CrossRef]
- Lei, H.; Xu, Y.; Jiang, M.; Jiang, Y. Deformation and fabric of soft marine clay at various cyclic load stages. Ocean. Eng. 2020, 195, 106757. [Google Scholar] [CrossRef]
- Chu, F.; Shao, S.J.; Chen, C.L. Experimental study of dynamic deformation and dynamic strength properties of saturated silty sand. Chin. J. Rock Mech. Eng. 2014, 33, 3299–3305. [Google Scholar]
- Lai, X.; Jian, W.; Xu, X.; Tang, W. Experimental study on dynamic characteristics of muddy soil in Fuzhou. J. Eng. Geol. 2016, 24, 1302–1308. [Google Scholar]
- Li, X.L.; Chen, S.J.; Liu, S.M.; Li, Z.H. AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform. J. Cent. South Univ. 2021, 28, 1843–1856. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Fu, J.; Zhu, N.; Chen, D.; Wang, Y.; Ding, S. Experimental study on compressive behavior and failure characteristics of imitation steel fiber concrete under uniaxial load imitation steel fiber concrete under uniaxial load. Constr. Build. Mater. 2023, 399, 132599. [Google Scholar] [CrossRef]
- Huang, X.; Tong, H.; Li, S. Dynamic Triaxial Test Investigation of Silty Sand Anti-liquefaction Performance. Sci. Technol. Eng. 2018, 18, 252–256. [Google Scholar]
- Cerni, G.; Cardone, F.; Virgili, A.; Camilli, S. Characterisation of permanent deformation behaviour of unbound granular materials under repeated triaxial loading. Constr. Build. Mater. 2012, 28, 79–87. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, Z.; Kong, L.; Zhang, X.; Yin, S. Undrained dynamic behaviour of peaty organic soil under long-term cyclic loading, Part I: Experimental investigation. Soil Dyn. Earthq. Eng. 2018, 107, 279–291. [Google Scholar] [CrossRef]
- Chen, W.B.; Feng, W.Q.; Yin, J.H.; Borana, L.; Chen, R.P. Characterization of permanent axial strain of granular materials subjected to cyclic loading based on shakedown theory. Constr. Build. Mater. 2019, 198, 751–761. [Google Scholar] [CrossRef]
- Guo, L.; Wang, J.; Cai, Y.; Liu, H.; Gao, Y.; Sun, H. Undrained deformation behavior of saturated soft clay under long-term cyclic loading. Soil Dyn. Earthq. Eng. 2013, 50, 28–37. [Google Scholar] [CrossRef]
- Tang, L.; Yan, M.H.; Ling, X.Z.; Tian, S. Dynamic behaviours of railway’s base course materials subjected to long-term low-level cyclic loading: Experimental study and empirical model. Géotechnique 2017, 67, 537–545. [Google Scholar] [CrossRef]
- Wang, J.; Ling, X.; Li, Q.; Zhang, F.; Li, Y. Accumulated permanent strain and critical dynamic stress of frozen silty clay under cyclic loading. Cold Reg. Sci. Technol. 2018, 153, 130–143. [Google Scholar] [CrossRef]
- Monismith, C.L.; Ogawa, N.; Freeme, C.R. Permanent deformation characteristics of subgrade soils due to repeated loading. In Proceedings of the 54th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 1975; pp. 1–17. [Google Scholar]
- Rahman, M.S.; Erlingsson, S. Predicting permanent deformation behaviour of unbound granular materials. Int. J. Pavement Eng. 2014, 16, 587–601. [Google Scholar] [CrossRef]
- He, Z.; Wang, P.; Liu, Y. Cumulative deformation prediction and microstructure change of coarse-grained soil under cyclic loading. Soil Dyn. Earthq. Eng. 2023, 173, 108136. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Y.; Aminu, U.F.; He, Q.; Li, Y.; Li, W. Prediction of resilient modulus and critical dynamic stress of recycled aggregates: Experimental study and machine learning methods. Transp. Geotech. 2024, 49, 101363. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, S.; Meng, S.; Wang, M.; Bai, H. Accumulative plastic strain of freezing–thawing subgrade clay under cyclic loading and its particle swarm optimisation–back-propagation-based prediction model. Cold Reg. Sci. Technol. 2023, 214, 103946. [Google Scholar] [CrossRef]
- Mei, H.; Leng, W.; Liu, W.; Nie, R.; Xu, X. Experimental study on accumulated plastic strain of coarse grained soil filling in subgrade bed under persistent dynamic loading. J. China Railw. Soc. 2017, 39, 119–126. [Google Scholar]
- Ramezan, C.; Warner, T.A.; Maxwell, A.E. Evaluation of sampling and cross-validation tuning strategies for regional-scale machine learning classification. Remote Sens. 2019, 11, 185. [Google Scholar] [CrossRef]
- JTG 3430-2020; Geotechnical Test Procedure for Roads. People’s Communications Press: Beijing, China, 2020.
- Chen, K.; Liu, X.; Jiang, G.; Yuan, S.; Ma, J.; Chen, Y. Effect of water content on dynamic properties of red mudstone fill material. Rock Soil Mech. 2024, 45, 3705–3716. [Google Scholar]
- Ai, X. Research on Cumulative Deformation Behaviour of Loess Improved by Nano-SiO2 Based on Stability Theory. Ph.D. Thesis, Sichuan Agricultural University, Chengdu, China, 2023. [Google Scholar]
- Liu, S. Experimental Study on Deformation Characteristics and Shear Characteristics of Loess Under Wet Load. Master’s Thesis, Changan University, Xi’an, China, 2023. [Google Scholar]
- Liu, S.; Cai, H.; Cao, Y.; Yang, Y. Advance in grey incidence analysis modelling. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AL, USA, 9–12 October 2011; pp. 1886–1890. [Google Scholar]
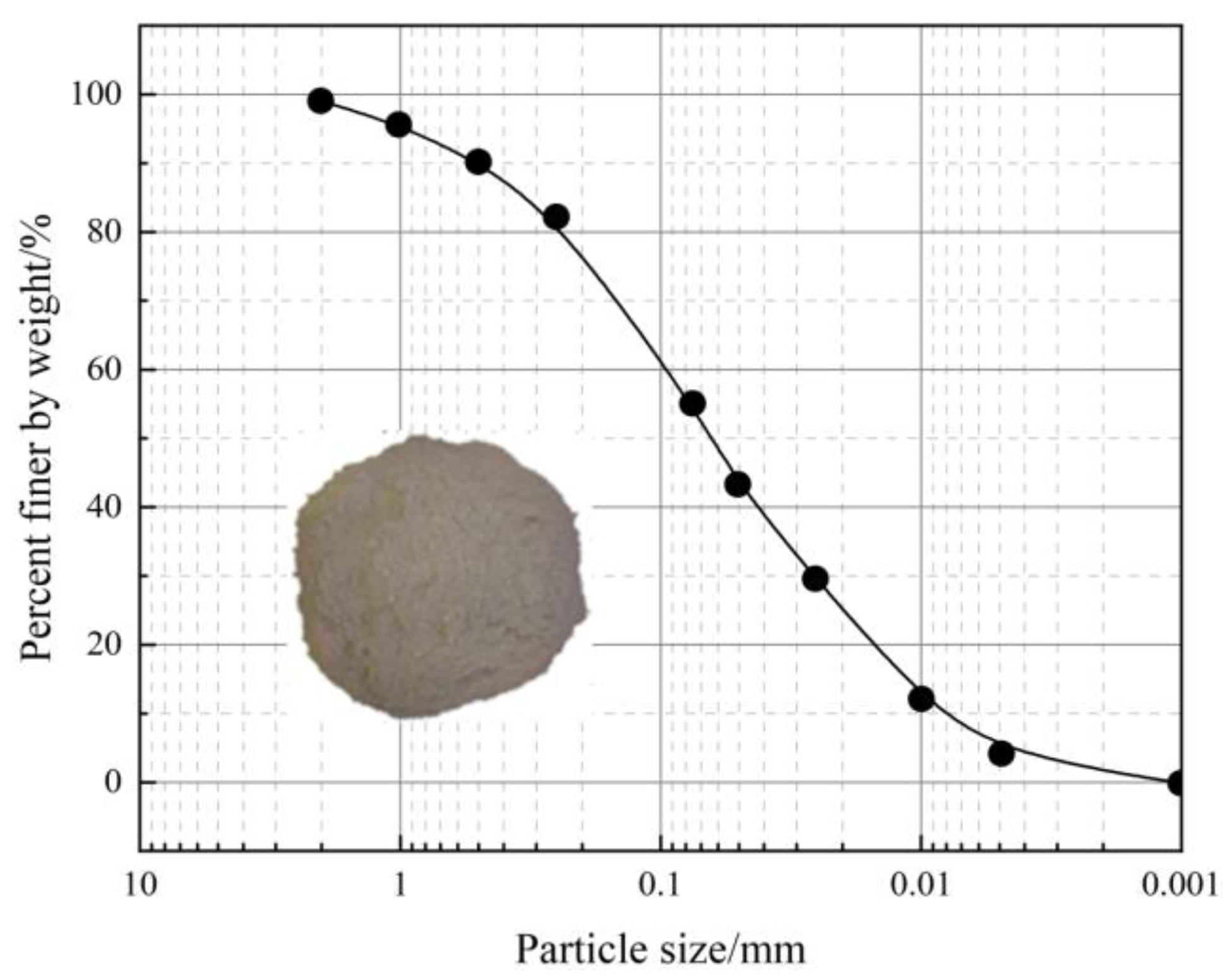










| Natural Moisture Contents (%) | Optimum Moisture Contents (%) | Maximum Dry Density (g/cm3) | Plastic Limit (%) | Liquid Limit (%) |
|---|---|---|---|---|
| 20.3 | 17.4 | 1.74 | 18.79 | 33.51 |
| Moisture Contents/% | Confining Pressure/kPa | Dynamic Stress/kPa |
|---|---|---|
| 17.4 | 60 | 240 → 250 → 260 → 270 → 280 |
| 17.4 | 90, 120, 150 | 250 → 260 → 270 → 280 → 290 |
| 18.4 | 90 | 170 → 180 → 190 → 200 → 210 |
| 19.4 | 90 | 170 → 180 → 190 → 200 → 250 |
| 20.4 | 90 | 130 → 140 → 150 → 160 → 170 |
| 21.4 | 90 | 100 → 110 → 120 → 130 → 150 |
| Moisture Content/% | Dynamic Stress/kPa | f | g |
|---|---|---|---|
| 17.4 | 250 | −0.953 | −0.993 |
| 17.4 | 260 | −0.986 | −0.625 |
| 17.4 | 270 | −1.016 | −0.462 |
| 17.4 | 280 | −0.995 | −0.423 |
| 20.4 | 130 | −0.937 | −0.517 |
| 20.4 | 140 | −1.039 | −0.341 |
| 20.4 | 150 | −0.981 | −0.764 |
| 20.4 | 160 | −0.939 | −1.020 |
| 20.4 | 170 | −0.956 | −1.266 |
| Moisture Content /% | Dynamic Stress /kPa | Confining Pressure /kPa | a | b | R2 |
|---|---|---|---|---|---|
| 17.4 | 250 | 60 | 2.3223 | 0.0806 | 0.9881 |
| 17.4 | 250 | 90 | 1.5194 | 0.0839 | 0.8986 |
| 17.4 | 250 | 120 | 1.3544 | 0.087 | 0.9917 |
| 17.4 | 250 | 150 | 1.3994 | 0.0885 | 0.8779 |
| 18.4 | 180 | 90 | 1.5007 | 0.0798 | 0.9935 |
| 19.4 | 180 | 90 | 1.5902 | 0.1029 | 0.9925 |
| 20.4 | 140 | 90 | 1.2742 | 0.0684 | 0.8998 |
| 21.4 | 110 | 90 | 1.1696 | 0.0645 | 0.9996 |
| Dataset | Coefficient of Determination | Mean Absolute Error | Root Mean Square Error |
|---|---|---|---|
| R2 | MAE | RMSE | |
| Training Set | 0.992 | 0.012 | 0.0031 |
| Test Set | 0.993 | 0.014 | 0.0020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Tong, F.; Luo, J.; Wang, L.; Zhu, W.; Xu, H.; Wang, Y.; Yang, Y.; Han, S. Study on Cumulative Deformation of Silt Soil Under Traffic Loading Based on PSO-BP Neural Network. Buildings 2025, 15, 4126. https://doi.org/10.3390/buildings15224126
Zhao Y, Tong F, Luo J, Wang L, Zhu W, Xu H, Wang Y, Yang Y, Han S. Study on Cumulative Deformation of Silt Soil Under Traffic Loading Based on PSO-BP Neural Network. Buildings. 2025; 15(22):4126. https://doi.org/10.3390/buildings15224126
Chicago/Turabian StyleZhao, Yingying, Fei Tong, Jun Luo, Lianfa Wang, Wenbo Zhu, Haoqing Xu, Yongbo Wang, Yaping Yang, and Sanping Han. 2025. "Study on Cumulative Deformation of Silt Soil Under Traffic Loading Based on PSO-BP Neural Network" Buildings 15, no. 22: 4126. https://doi.org/10.3390/buildings15224126
APA StyleZhao, Y., Tong, F., Luo, J., Wang, L., Zhu, W., Xu, H., Wang, Y., Yang, Y., & Han, S. (2025). Study on Cumulative Deformation of Silt Soil Under Traffic Loading Based on PSO-BP Neural Network. Buildings, 15(22), 4126. https://doi.org/10.3390/buildings15224126





