From Fracture Connectivity to Intelligent Prediction: A Hybrid GA-DBN-SE Framework for Cement Intake Forecasting
Abstract
1. Introduction
- (1)
- Establishing the primary data layer. Initially, the location (lo0), number (n0), length (l0), aperture (a0), inclination (i0), and dip angle (d0) of the fractures in the study area were obtained based on examination of the exposed surface. Subsequently, grouting construction parameters such as the grouting pressure (P), permeability (Lu), water–cement ratio (W/C, by mass), and initial injection rate (Q) were documented using a recorder.
- (2)
- Establishing the methodological layer. This component primarily encompasses deriving 3D fracture connectivity metrics and formulating cement intake forecasting techniques. Drawing from the successful application of three-dimensional fracture network models by scholars in the field, this study employs the discrete fracture network (DFN) methodology to construct a 3D fracture model. Utilizing digital drilling and depth-first search (DFS) algorithms, the fractures connected to each grouting hole segment were sequentially identified. Their connectivity was characterized by calculating the number and cumulative volume of the fractures linked to each segment. A hybrid deep learning framework for cement intake was then proposed, integrating a Deep Belief Network (DBN), squeeze-and-excitation (SE) attention, and genetic algorithm (GA)-driven hyperparameter optimization.
- (3)
- Establishing the application layer. The efficacy of the developed methodology was demonstrated through its application to a curtain grouting project at a hydropower station in southwestern China. This application serves to validate the superiority of the proposed approach in real-world scenarios.
2. Methodology
2.1. Modeling of 3D Fracture Connectivity
2.1.1. Three-Dimensional Fracture Model
2.1.2. Depth-First Search Algorithm (DFS)
2.1.3. 3D Fracture Connectivity
- (1)
- Establishing a coupled 3D model.
- (2)
- Obtaining fractures that can connect with a grouting hole.
- It is assumed that a 3D fracture network model can be expressed in set form by Equation (1):
- It is assumed that a 3D model of grouting holes can be expressed as a set according to Equation (3):
- (3)
- Calculating the connectivity parameters.
- (4)
- Connectivity-Aware Feature Extraction Framework.
2.2. GA-DBN with Squeeze-and-Excitation Attention (GA-DBN-SE)
2.2.1. Deep Belief Network
2.2.2. Channel-Wise Squeeze-and-Excitation Attention
2.2.3. GA for Hyperparameter Optimization
2.3. Prediction Workflow for Cement Intake
- (1)
- Data preparation and partitioning. The dataset comprises grouting construction parameters and fracture connectivity descriptors. The grouting parameters were acquired as follows: permeability was determined from pre-grouting water pressure tests conducted at each grouting stage under untreated conditions and reported in Lugeon units, in accordance with project specifications. P was continuously monitored at the collar of the return line using a calibrated pressure gauge and recorded in real time by the automated grouting recording system. W/C was obtained from the batching module as the stage-specific mix design logged by the grouting control system. Q was calculated based on the discharge volume data recorded during the first sampling interval following packer emplacement and the initiation of grout injection. Fracture connectivity descriptors were derived through a systematic analysis of exposed fracture traces. Statistical analysis of these traces informed the construction of a three-dimensional DFN model. Fracture connectivity metrics were then extracted using digital borehole logs and a DFS-based connectivity algorithm. The dataset was randomly split into training/validation/test sets in an 80/10/10 ratio; feature standardization (z-scoring) was performed using statistics from the training set and consistently applied to the validation and test partitions.
- (2)
- Definition of preset parameters and the GA search space. The experimental framework defines a total of eleven control parameters that govern the training and scheduling configuration of the SE attention-based DBN. Among these, six hyperparameters are optimized using a GA, while the remaining five are preset. The GA search space is defined as follows: number of neurons in hidden layers (n1, n2) [96, 896] to allow sufficient capacity for 10-input features without overfitting small datasets; epochs [200, 440] based on the convergence observed in preliminary trials; learning rate [0.0002, 0.004] to ensure stable training on noisy grouting data while avoiding local minima; batch size [32, 256] for gradient stability in training; and a binary flag indicating whether an additional learning rate scheduling step is applied (∈{0, 1}). All specified ranges and encoding constraints are strictly enforced during GA initialization and mutation operations. The five preset constants comprise the following: the Huber loss parameter is 0.6; dropout rates for both hidden layers are set to 0.10; the gradient clipping threshold is 1.0; and the warm-up period is 8 epochs.
- (3)
- GA-based optimization of an SE attention-augmented DBN. The predictor is a two-layer DBN-style MLP with tanh activations; the second hidden layer is equipped with SE attention and layer normalization, followed by a residual gating and a linear readout. A multi-subpopulation GA is used (five subpopulations with 20 individuals each and 30 generations under the strong-preset regime), with binary tournament selection, one-point crossover (rate 0.6), and adaptive mutation (initialized at 0.06). Fitness is the validation mean absolute percentage error (MAPE, Equation (8)) in the target’s original scale after inverse RankGauss. To stabilize evaluation, 5-fold CV is used inside the GA’s inner loop; early stopping guards the inner trainer.
- (4)
- Prediction and aggregation using the top-ranked models. After GA completes, the top-K candidates are re-evaluated and retained. Their test-set predictions are aggregated by an error-aware weighted average with weights proportional to the inverse validation error.
2.4. Performance Metrics
3. Case Study
3.1. Project Overview
3.2. Data Set
3.2.1. Construction Parameters
3.2.2. Three-Dimensional Fracture Connectivity Parameters
3.3. Cement Intake Prediction
4. Discussion
4.1. The Advantages of Incorporating 3D Fracture Connectivity
4.2. The Advantages of the Proposed Method
4.2.1. Ablation Study Results
4.2.2. Results Compared to Baseline Methods
5. Conclusions
- (1)
- Three-dimensional connectivity matters. By integrating a DFN with a DFS traversal, we quantified the reachable fracture subnetwork around each hole segment and proposed six descriptors (N, I, D, V, r, w). These features capture the extent, scale, and topology of conductive pathways beyond direct intersections and can be computed efficiently from digital drilling data.
- (2)
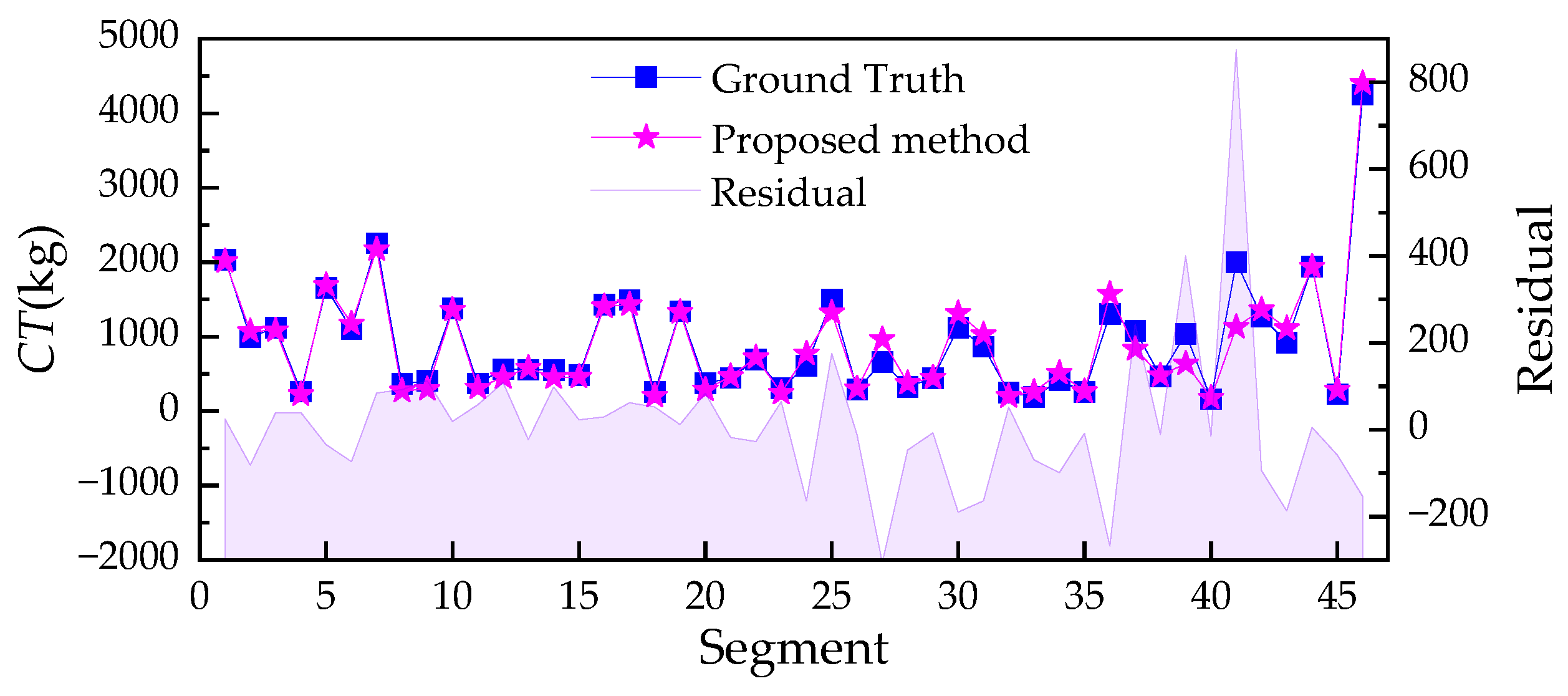
- Connectivity-aware learning improves prediction. On a real curtain-grouting project, explicitly modeling fracture connectivity substantially enhanced agreement with field measurements: the correlation coefficient increased to R = 0.972, while MAE, MAPE, and RMSE were reduced by 27.1%, 12.2%, and 32.8%, respectively, compared to a model that ignored connectivity.
- (3)
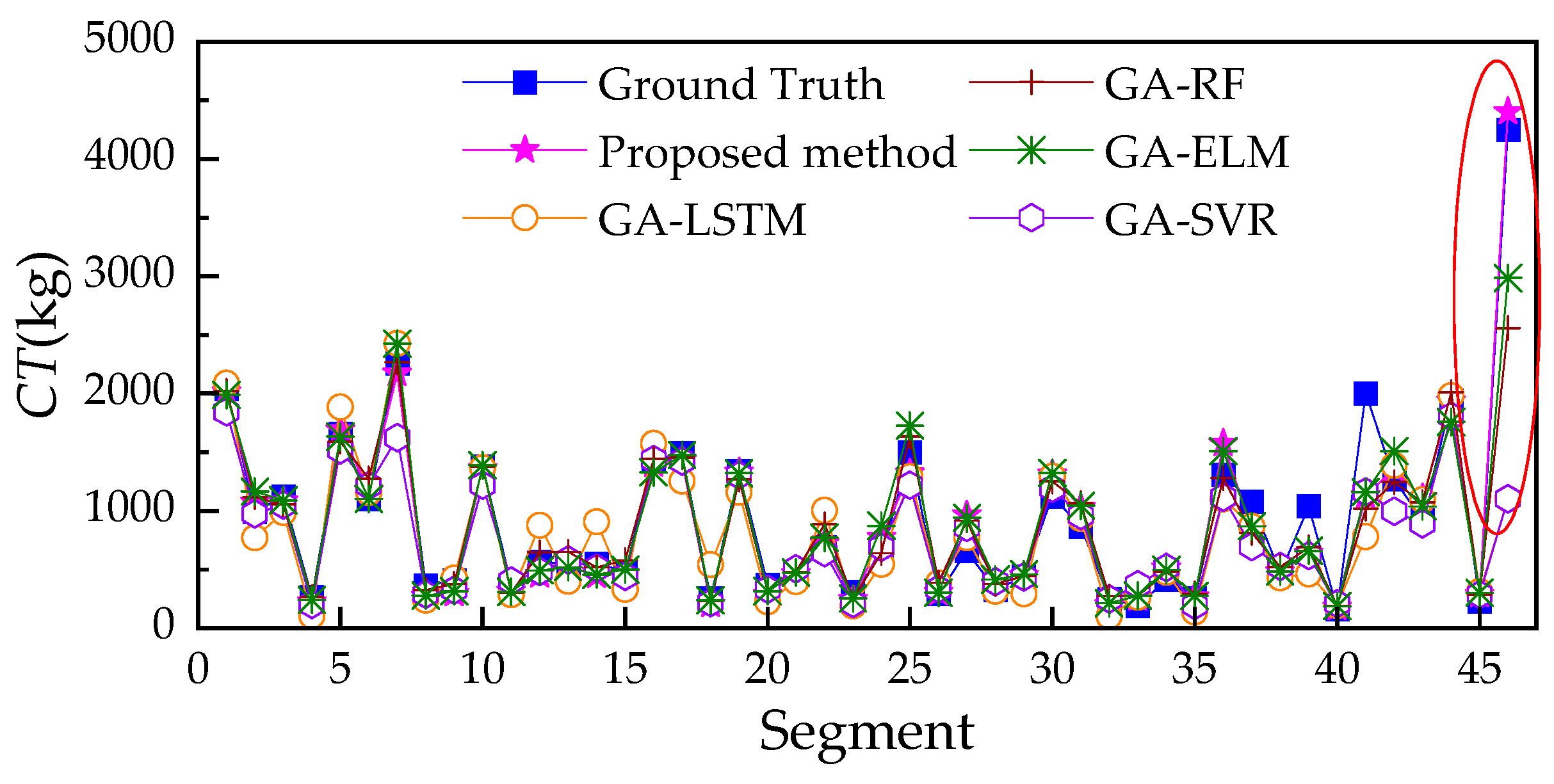
- Practicality. Ablation studies confirmed the value of each component in our integrated model: RBM pretraining improved generalization, SE attention enhanced feature selection, and ensemble learning stabilized predictions. Compared to four optimized baseline models (SVR, RF, ELM, and LSTM), the proposed integrated hybrid model—a GA-optimized DBN with SE attention—achieved improvements of 3–34% in R and reductions of 22–55% in MAE, 31–66% in RMSE, and 2–48% in MAPE on the held-out test set.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, J.; Wang, Q.; Meng, Z.; Song, H.; Chen, B.; Shen, H. Numerical Study of the Internal Fluid Dynamics of Draft Tube in Seawater Pumped Storage Hydropower Plant. Sustainability 2023, 15, 8327. [Google Scholar] [CrossRef]
- Liu, Z.X.; Song, W.S.; Cui, B.; Wang, X.L.; Yu, H.L. A Comprehensive Evaluation Model for Curtain Grouting Efficiency Assessment Based on Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D Numbers. Energies 2019, 12, 3674. [Google Scholar] [CrossRef]
- Öge, İ.F. Prediction of Cementitious Grout Take for a Mine Shaft Permeation by Adaptive Neuro-Fuzzy Inference System and Multiple Regression. Eng. Geol. 2017, 228, 238–248. [Google Scholar] [CrossRef]
- Sohrabi-Bidar, A.; Rastegar-Nia, A.; Zolfaghari, A. Estimation of the Grout Take Using Empirical Relationships (Case Study: Bakhtiari Dam Site). Bull. Eng. Geol. Environ. 2016, 75, 425–438. [Google Scholar] [CrossRef]
- Dou, J.X.; Zhang, G.J.; Zhou, M.X.; Wang, Z.L.; Gyatso, N.; Jiang, M.Q.; Safari, P.; Liu, J.Q. Curtain Grouting Experiment in a Dam Foundation: Case Study with the Main Focus on the Lugeon and Grout Take Tests. Bull. Eng. Geol. Environ. 2020, 79, 4527–4547. [Google Scholar] [CrossRef]
- Li, X.L.; Hao, M.M.; Zhong, Y.H.; Zhang, B.; Wang, F.M.; Wang, L.B. A Quasi-3D Numerical Model for Grout Injection in a Parallel Fracture Based on Finite Volume Method. Complexity 2019, 2019, 4139616. [Google Scholar] [CrossRef]
- Cui, W.; Wang, L.X.; Jiang, Z.A.; Wang, C.; Wang, X.H.; Zhang, S.R. Numerical Simulation of Grouting Process in Rock Mass with Rough Fracture Network Based on Corrected Cubic Law. Rock Soil Mech. 2021, 42, 2250–2258. [Google Scholar] [CrossRef]
- Xuan, D.Y.; Xu, J.L.; Wang, B.L.; Teng, H. Investigation of Fill Distribution in Post-Injected Longwall Overburden with Implications for Grout Take Estimation. Eng. Geol. 2016, 206, 71–82. [Google Scholar] [CrossRef]
- Ajalloeian, R.; Moein, F. Evaluation of Damsites Groutability Using Secondary Permeability Index, Rock Classification (Case Studies). Am. J. Appl. Sci. 2009, 6, 1235–1241. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, X.; Deng, S.; Chen, W.; Shi, Z.; Xue, L.; Lv, M. Grouting Process Simulation Based on 3D Fracture Network Considering Fluid–Structure Interaction. Appl. Sci. 2019, 9, 667. [Google Scholar] [CrossRef]
- Yang, C.P. Estimating Cement Take and Grout Efficiency on Foundation Improvement for Li-Yu-Tan Dam. Eng. Geol. 2004, 75, 1–14. [Google Scholar] [CrossRef]
- Li, X.C.; Zhong, D.H.; Ren, B.Y.; Fan, G.C.; Cui, B. Prediction of Curtain Grouting Efficiency Based on ANFIS. Bull. Eng. Geol. Environ. 2019, 78, 281–309. [Google Scholar] [CrossRef]
- Rahimi, E.; Teshnizi, E.S.; Rastegarnia, A.; Al-Shariati, E.M. Cement Take Estimation Using Neural Networks and Statistical Analysis in Bakhtiari and Karun 4 Dam Sites, in South West of Iran. Bull. Eng. Geol. Environ. 2019, 78, 2817–2834. [Google Scholar] [CrossRef]
- Niu, J.D.; Wang, B.; Chen, G.J.; Chen, K. Predicting the Unit Grouting Quantity in Karst Curtain Grouting by the Water Permeability of Rock Strata. Appl. Sci. 2019, 9, 4814. [Google Scholar] [CrossRef]
- Niu, J.D.; Wang, B.; Wang, H.F.; Deng, Z.W.; Liu, J.X.; Li, Z.W.; Chen, G.J.; Zhang, B.T. An Intelligent Prediction Method of the Karst Curtain Grouting Volume Based on Support Vector Machine. Geofluids 2020, 2020, 8892106. [Google Scholar] [CrossRef]
- Deng, S.H.; Wang, X.L.; Zhu, Y.S.; Lv, F.; Wang, J.J. Hybrid Grey Wolf Optimization Algorithm-Based Support Vector Machine for Groutability Prediction of Fractured Rock Mass. J. Comput. Civ. Eng. 2019, 33, 04018081. [Google Scholar] [CrossRef]
- Zhong, D.H.; Liu, Z.X.; Su, Z.; Li, K.; Li, X.C. Predicting and Controlling the Cement Intake during Curtain Grouting of Dam Foundations. Eur. J. Environ. Civ. Eng. 2022, 26, 4237–4262. [Google Scholar] [CrossRef]
- Fan, G.C.; Zhong, D.H.; Yan, F.G.; Yue, P. A Hybrid Fuzzy Evaluation Method for Curtain Grouting Efficiency Assessment Based on an AHP Method Extended by D Numbers. Expert Syst. Appl. 2016, 44, 289–303. [Google Scholar] [CrossRef]
- Carter, T.G.; Dershowitz, W.; Shuttle, D.; Jefferies, M. Improved Methods of Design for Grouting Fractured Rock. In Grouting and Deep Mixing 2012; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2012; pp. 1472–1483. [Google Scholar]
- Shuttle, D.A.; Dershowitz, W.; Glynn, E.; Burch, S.; Novak, T. Discrete Fracture Network Analysis of Foundation Grouting. In Pacific Rocks 2000: Rock Around the Rim, Proceedings of the 4th North American Rock Mechanics Symposium, NARMS 2000, Seattle, WA, USA, 31 July–3 August 2000; Balkema: Rotterdam, The Netherlands, 2000; pp. 1369–1376. [Google Scholar]
- Xu, C.; Dowd, P.A.; Mardia, K.V.; Fowell, R.J. A Connectivity Index for Discrete Fracture Networks. Math. Geol. 2006, 38, 611–634. [Google Scholar] [CrossRef]
- Gothäll, R.; Stille, H. Fracture–Fracture Interaction during Grouting. Tunn. Undergr. Space Technol. 2010, 25, 199–204. [Google Scholar] [CrossRef]
- Alghalandis, Y.F.; Xu, C.; Dowd, P.A. Connectivity Index and Connectivity Field towards Fluid Flow in Fracture-Based Geothermal Reservoirs. In Proceedings of the Stanford Geothermal Workshop, Stanford, CA, USA, 11–13 February 2013. [Google Scholar]
- Alghalandis, Y.F.; Dowd, P.A.; Xu, C. Connectivity Field: A Measure for Characterising Fracture Networks. Math. Geosci. 2015, 47, 63–83. [Google Scholar] [CrossRef]
- Deng, S.H.; Wang, X.L.; Yu, J.; Zhang, Y.C.; Liu, Z.; Zhu, Y.S. Simulation of Grouting Process in Rock Masses under a Dam Foundation Characterized by a 3D Fracture Network. Rock Mech. Rock Eng. 2018, 51, 1801–1822. [Google Scholar] [CrossRef]
- Zhu, W.W.; Khirevich, S.; Patzek, T.W. Impact of Fracture Geometry and Topology on the Connectivity and Flow Properties of Stochastic Fracture Networks. Water Resour. Res. 2021, 57, e2020WR028652. [Google Scholar] [CrossRef]
- Cao, M.; Sharma, M.M. Factors Controlling the Flow and Connectivity in Fracture Networks in Naturally Fractured Geothermal Formations. SPE Drill. Complet. 2023, 38, 131–145. [Google Scholar] [CrossRef]
- Sun, M.D.; Duan, X.G.; Liu, Q.; Blach, T.P.; Ostadhassan, M.; Liu, B.; Ji, Y.P.; Hu, Q.H.; Pan, Z.J. The Importance of Pore–Fracture Connectivity in Overmature Marine Shale for Methane Occurrence and Transportation. Mar. Pet. Geol. 2023, 157, 106495. [Google Scholar] [CrossRef]
- Baecher, G.; Lanney, N.; Einstein, H. Statistical Description of Rock Properties and Sampling. In ARMA U.S. Rock Mechanics/Geomechanics Symposium, Proceedings of the 18th U.S. Symposium on Rock Mechanics (USRMS), Golden, CO, USA, 22–24 June 1977; Paper No. ARMA-77-0400; ARMA: Denver, CO, USA, 1977. [Google Scholar]
- Villas, M.V.; Ferreira, A.; Leroy, P.; Miranda, C.; Bockman, C. Estruturas de Dados: Conceitos e Técnicas de Implementação; Campus: Rio de Janeiro, Brazil, 1993. [Google Scholar]
- Boaventura Netto, P.O.; Jurkiewicz, S. Grafos: Introdução e Prática; Blucher: São Paulo, Brazil, 2009. [Google Scholar]
- Rodrigues, G.P.W.; Costa, L.H.M.; Farias, G.M.; de Castro, M.A.H. A Depth-First Search Algorithm for Optimizing the Gravity Pipe Networks Layout. Water Resour. Manag. 2019, 33, 4583–4598. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Guan, S.; Wang, X.; Hua, L.; Li, L. Quantitative Ultrasonic Testing for Near-Surface Defects of Large Ring Forgings Using Feature Extraction and GA-SVM. Appl. Acoust. 2021, 173, 107714. [Google Scholar] [CrossRef]
- Wang, M.; Yu, J.; Zhou, M.; Quan, W.; Cheng, R. Joint Forecasting Model for the Hourly Cooling Load and Fluctuation Range of a Large Public Building Based on GA-SVM and IG-SVM. Sustainability 2023, 15, 16833. [Google Scholar] [CrossRef]
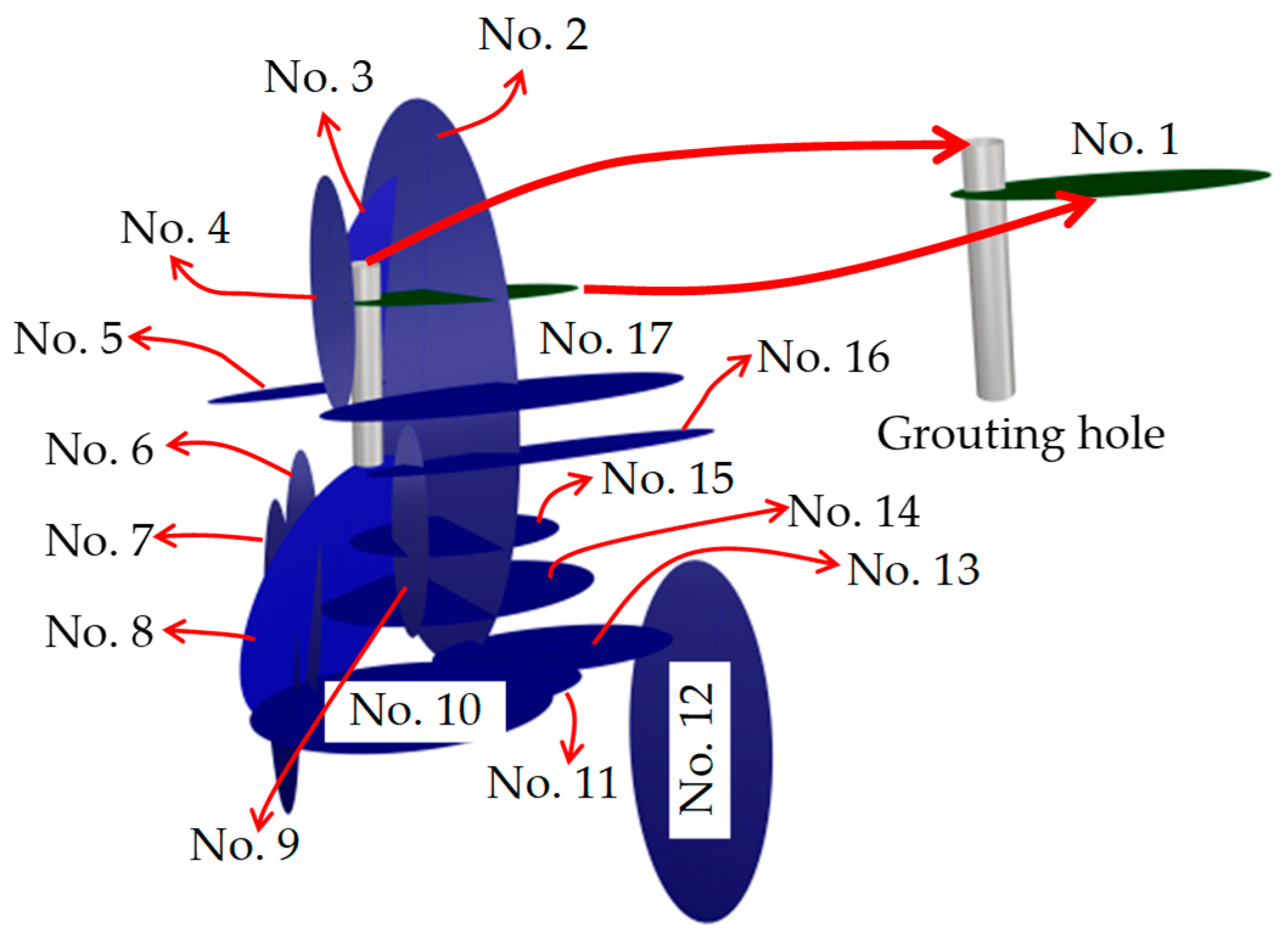





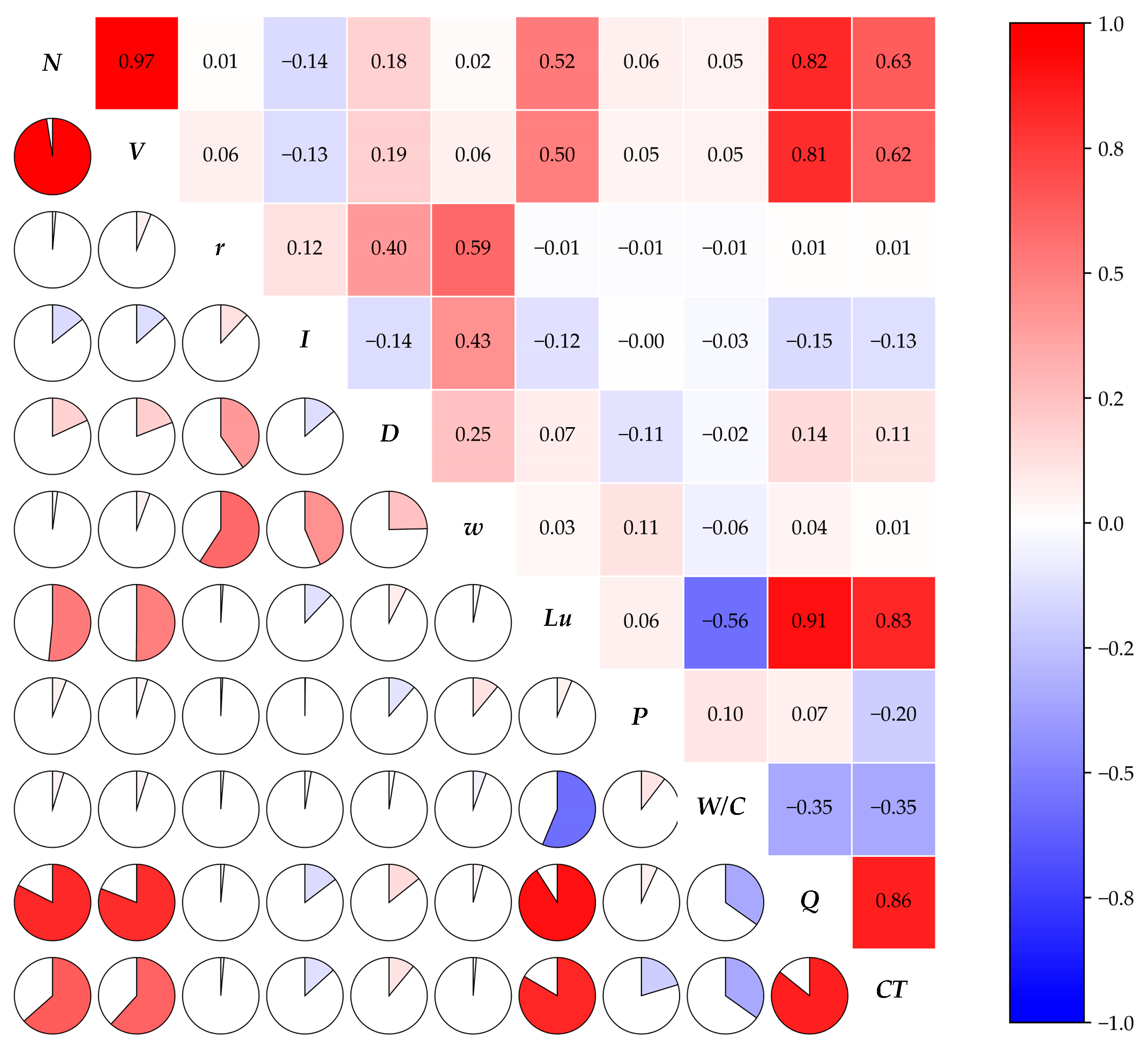


| Parameters | Unit | Mean | Minimum | Maximum |
|---|---|---|---|---|
| P | MPa | 2.97 | 0.06 | 8.70 |
| Lu | Lu | 22.28 | 1.43 | 81.04 |
| W/C | — | 2.65 | 1.00 | 3.00 |
| Q | L/min | 31.73 | 1.70 | 151.05 |
| Groups | Bulk Density | Fracture Number | Parameters | Mean | Minimum | Maximum | Distribution Type |
|---|---|---|---|---|---|---|---|
| 1 | 0.118138687 | 2812 | Coordinate X/m | 17.129 | 0.010 | 33.989 | Uniform |
| Coordinate Y/m | 4.993 | 0.002 | 9.995 | Uniform | |||
| Coordinate Z/m | 35.280 | 0.000 | 69.996 | Uniform | |||
| Radius/m | 1.430 | 1.006 | 1.977 | Negative exponential | |||
| Inclination/degree | 319.189 | 314.402 | 324.394 | Fisher | |||
| Dip-angle/degree | 14.769 | 10.002 | 19.995 | Fisher | |||
| Width/mm | 0.901 | 0.800 | 1.000 | Negative exponential | |||
| 2 | 0.017095641 | 407 | Coordinate X/m | 17.499 | 0.102 | 33.997 | Uniform |
| Coordinate Y/m | 5.055 | 0.003 | 9.982 | Uniform | |||
| Coordinate Z/m | 34.110 | 0.070 | 69.962 | Uniform | |||
| Radius/m | 1.700 | 0.863 | 3.040 | Negative exponential | |||
| Inclination/degree | 353.530 | 347.557 | 357.482 | Fisher | |||
| Dip-angle/degree | 78.154 | 72.506 | 82.492 | Fisher | |||
| Width/mm | 0.896 | 0.800 | 1.000 | Negative exponential | |||
| 3 | 0.041976587 | 999 | Coordinate X/m | 17.035 | 0.021 | 33.909 | Uniform |
| Coordinate Y/m | 4.884 | 0.006 | 9.990 | Uniform | |||
| Coordinate Z/m | 34.316 | 0.062 | 69.964 | Uniform | |||
| Radius/m | 1.785 | 0.899 | 3.077 | Negative exponential | |||
| Inclination/degree | 40.311 | 34.403 | 44.385 | Fisher | |||
| Dip-angle/degree | 85.811 | 80.014 | 90.000 | Fisher | |||
| Width/mm | 0.902 | 0.800 | 1.000 | Negative exponential | |||
| 4 | 0.037525989 | 893 | Coordinate X/m | 16.658 | 0.046 | 33.981 | Uniform |
| Coordinate Y/m | 4.912 | 0.002 | 10.000 | Uniform | |||
| Coordinate Z/m | 34.187 | 0.209 | 69.906 | Uniform | |||
| Radius/m | 1.729 | 1.111 | 2.466 | Negative exponential | |||
| Inclination/degree | 159.161 | 154.417 | 164.384 | Fisher | |||
| Dip-angle/degree | 14.451 | 10.008 | 19.974 | Fisher | |||
| Width/mm | 0.901 | 0.800 | 1.000 | Negative exponential |
| Groups | Parameters | Field Data | Simulated Data | Relative Error (%) |
|---|---|---|---|---|
| 1 | Radius/m | 1.270 | 1.430 | 12.598 |
| Inclination/degree | 319.400 | 319.189 | −0.066 | |
| Dip-angle/degree | 15.000 | 14.769 | −1.540 | |
| Width/mm | 0.850 | 0.901 | 6.000 | |
| 2 | Radius/m | 1.748 | 1.700 | −2.746 |
| Inclination/degree | 352.400 | 353.530 | 0.321 | |
| Dip-angle/degree | 77.500 | 78.154 | 0.844 | |
| Width/mm | 0.900 | 0.896 | −0.444 | |
| 3 | Radius/m | 1.993 | 1.785 | −10.437 |
| Inclination/degree | 39.400 | 40.311 | 2.312 | |
| Dip-angle/degree | 85.000 | 85.811 | 0.954 | |
| Width/mm | 1.000 | 0.902 | −9.800 | |
| 4 | Radius/m | 2.008 | 1.729 | −13.894 |
| Inclination/degree | 159.400 | 159.161 | −0.150 | |
| Dip-angle/degree | 15.000 | 14.451 | −3.660 | |
| Width/mm | 0.850 | 0.901 | 6.000 |
| Methods | R | MAE | MAPE (%) | RMSE |
|---|---|---|---|---|
| Proposed w/o RBM pretraining | 0.968 | 117.525 | 14.975 | 198.679 |
| Proposed w/o SE attention | 0.965 | 133.577 | 16.192 | 206.527 |
| Proposed Top-1 (no ensemble) | 0.970 | 121.129 | 14.837 | 194.353 |
| Proposed method | 0.972 | 105.709 | 14.227 | 177.663 |
| Methods | R | MAE | MAPE (%) | RMSE |
|---|---|---|---|---|
| LSTM | 0.725 | 235.94 | 27.573 | 528.544 |
| SVR | 0.777 | 193.612 | 18.109 | 506.571 |
| RF | 0.923 | 135.025 | 14.575 | 308.191 |
| ELM | 0.944 | 138.404 | 15.421 | 258.364 |
| Proposed method | 0.972 | 105.709 | 14.227 | 177.663 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Lu, X.; Yuan, M.; Zhang, C.; Chen, J. From Fracture Connectivity to Intelligent Prediction: A Hybrid GA-DBN-SE Framework for Cement Intake Forecasting. Buildings 2025, 15, 4122. https://doi.org/10.3390/buildings15224122
Liu Z, Lu X, Yuan M, Zhang C, Chen J. From Fracture Connectivity to Intelligent Prediction: A Hybrid GA-DBN-SE Framework for Cement Intake Forecasting. Buildings. 2025; 15(22):4122. https://doi.org/10.3390/buildings15224122
Chicago/Turabian StyleLiu, Zongxian, Xiang Lu, Mengjie Yuan, Chaofeng Zhang, and Jiankang Chen. 2025. "From Fracture Connectivity to Intelligent Prediction: A Hybrid GA-DBN-SE Framework for Cement Intake Forecasting" Buildings 15, no. 22: 4122. https://doi.org/10.3390/buildings15224122
APA StyleLiu, Z., Lu, X., Yuan, M., Zhang, C., & Chen, J. (2025). From Fracture Connectivity to Intelligent Prediction: A Hybrid GA-DBN-SE Framework for Cement Intake Forecasting. Buildings, 15(22), 4122. https://doi.org/10.3390/buildings15224122






