Dynamic Response and Performance Degradation of a Deployable Antenna Under Sea-Based Excitation
Abstract
1. Introduction
2. High-Fidelity Finite Element Modeling
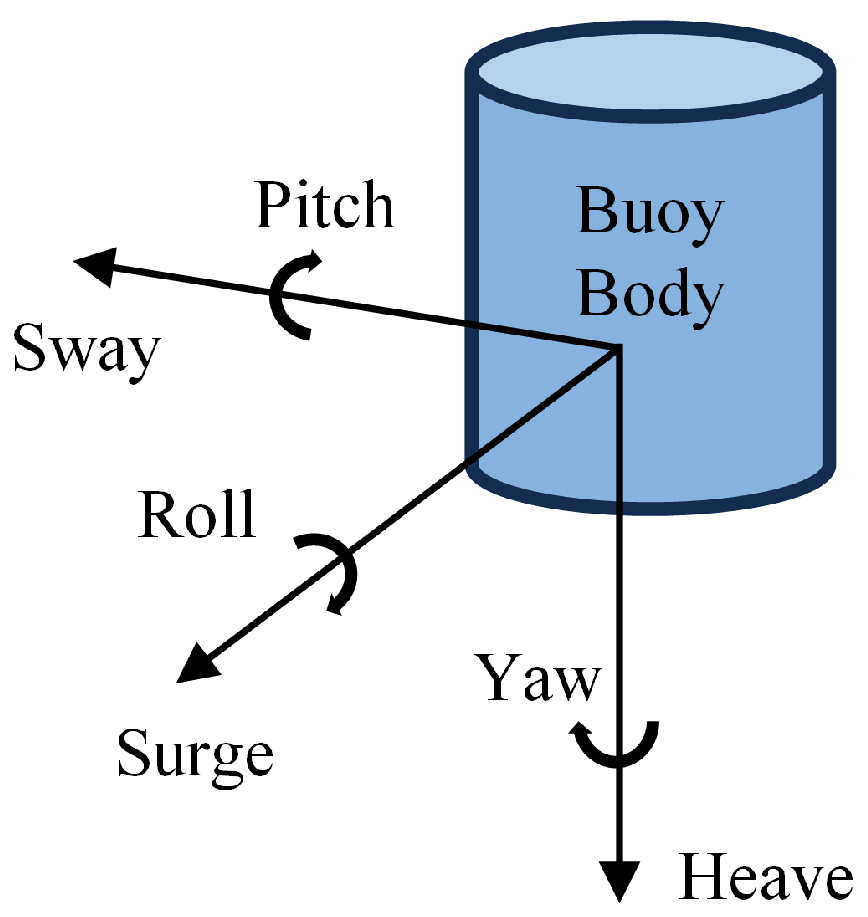
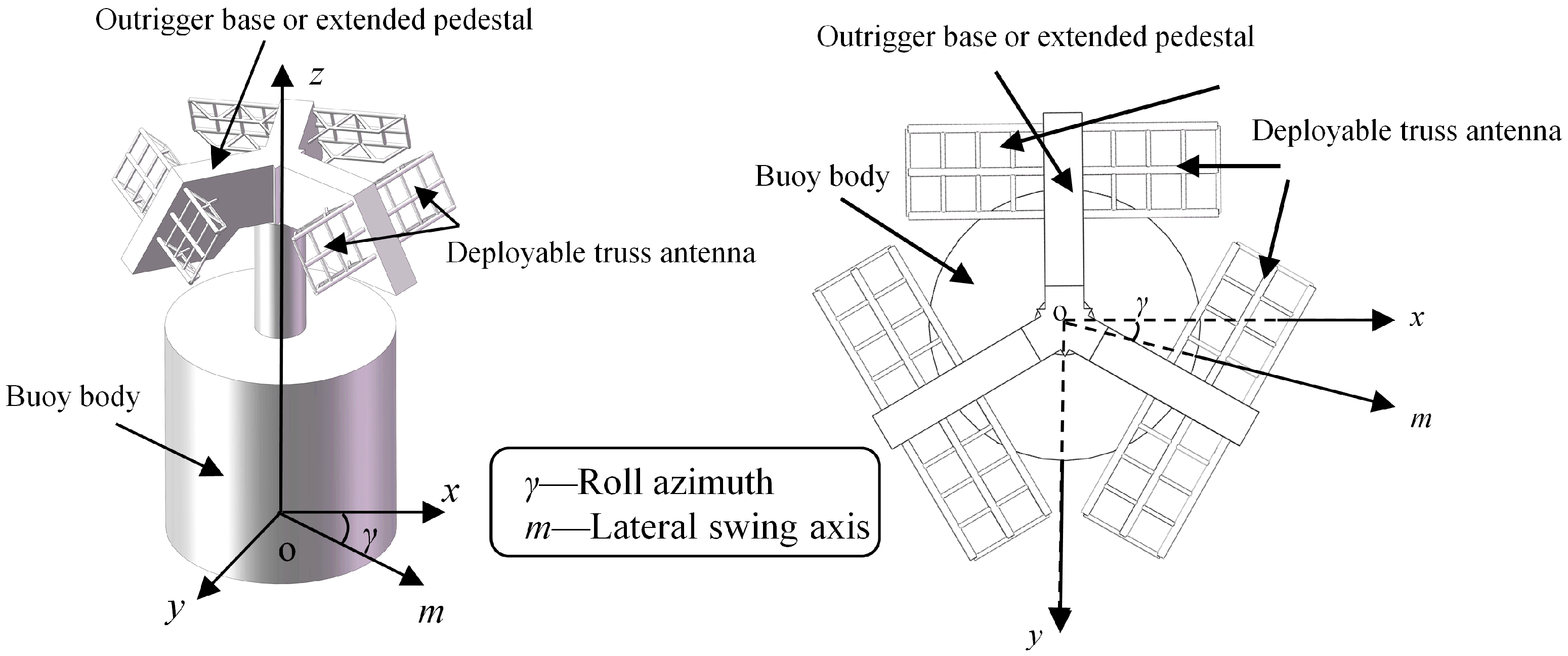
2.1. Physical System Description
2.2. Finite Element Modeling
2.3. Performance Evaluation Metric
3. Baseline Performance Assessment Under Static Loading
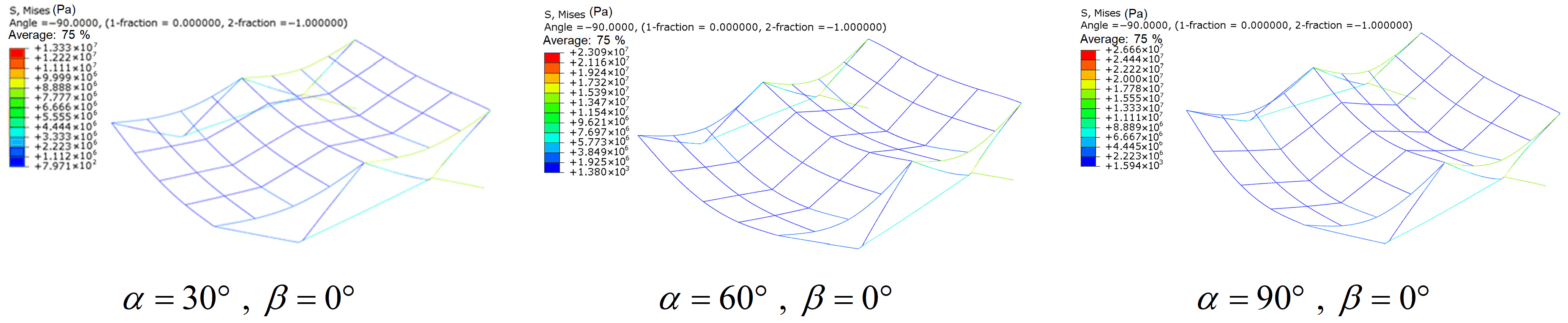
3.1. Structural Performance Under Gravity Loading
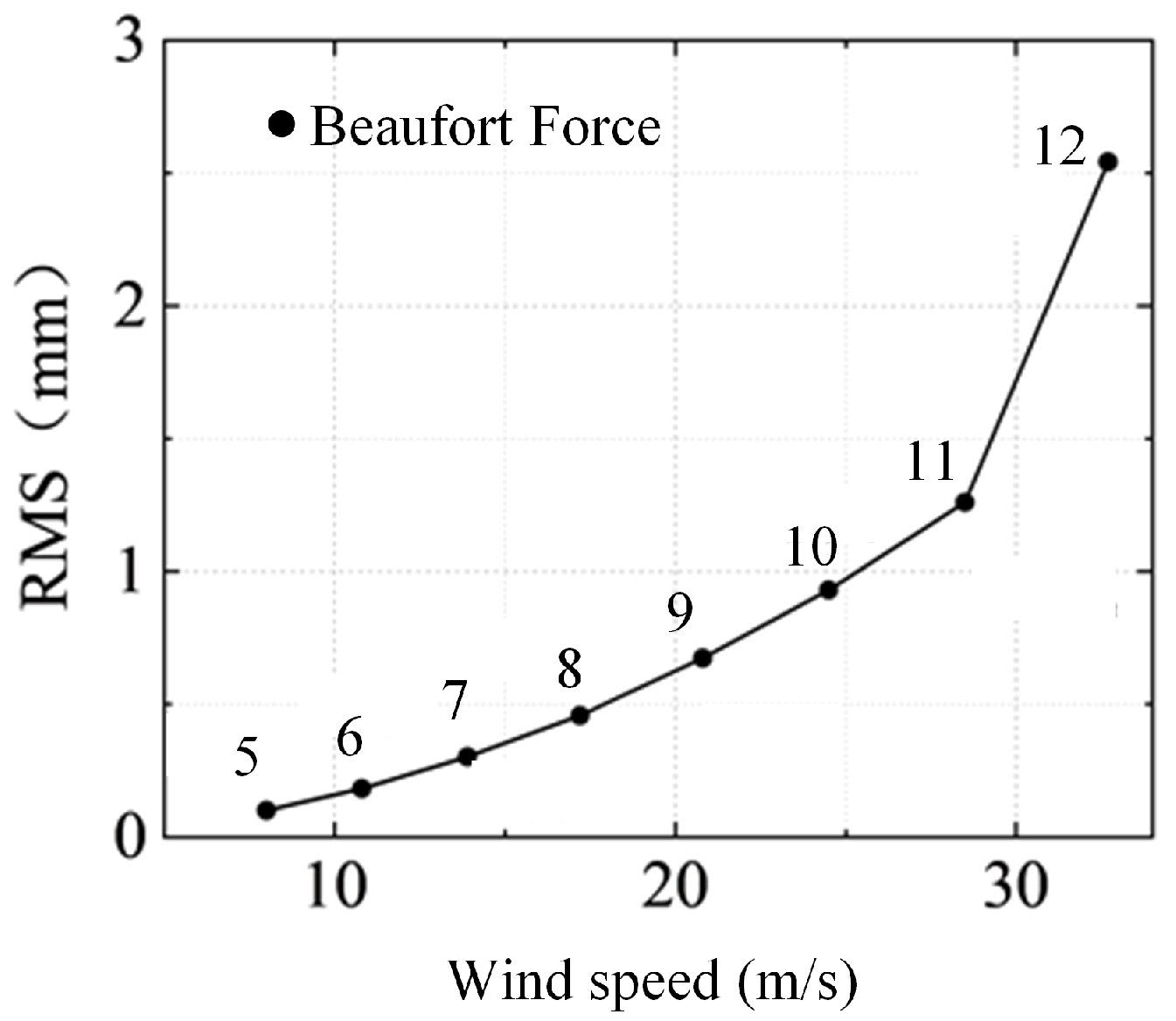
3.2. Impact of Offshore Wind Loading on the Structure
3.3. Combined Impact of Wind Loading and Gravity
4. Dynamic Response to Buoy Motion
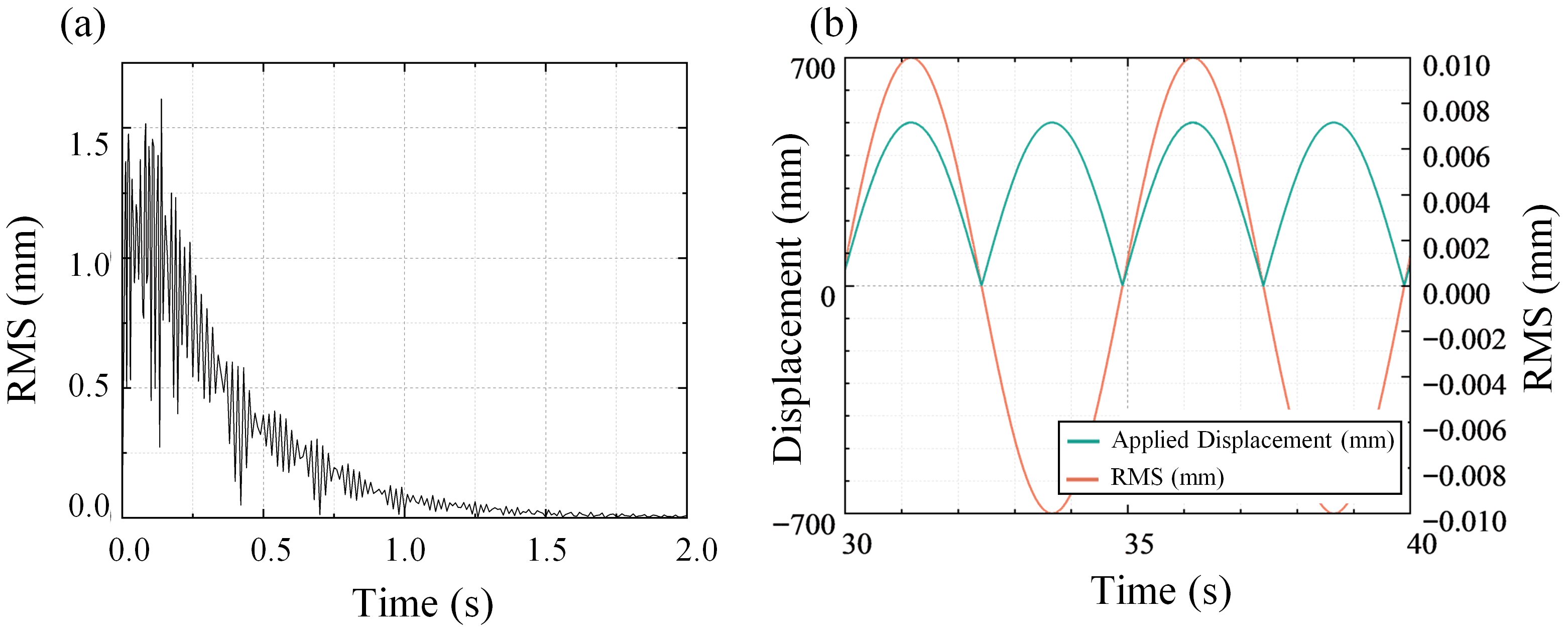
4.1. Response to Heave Motion
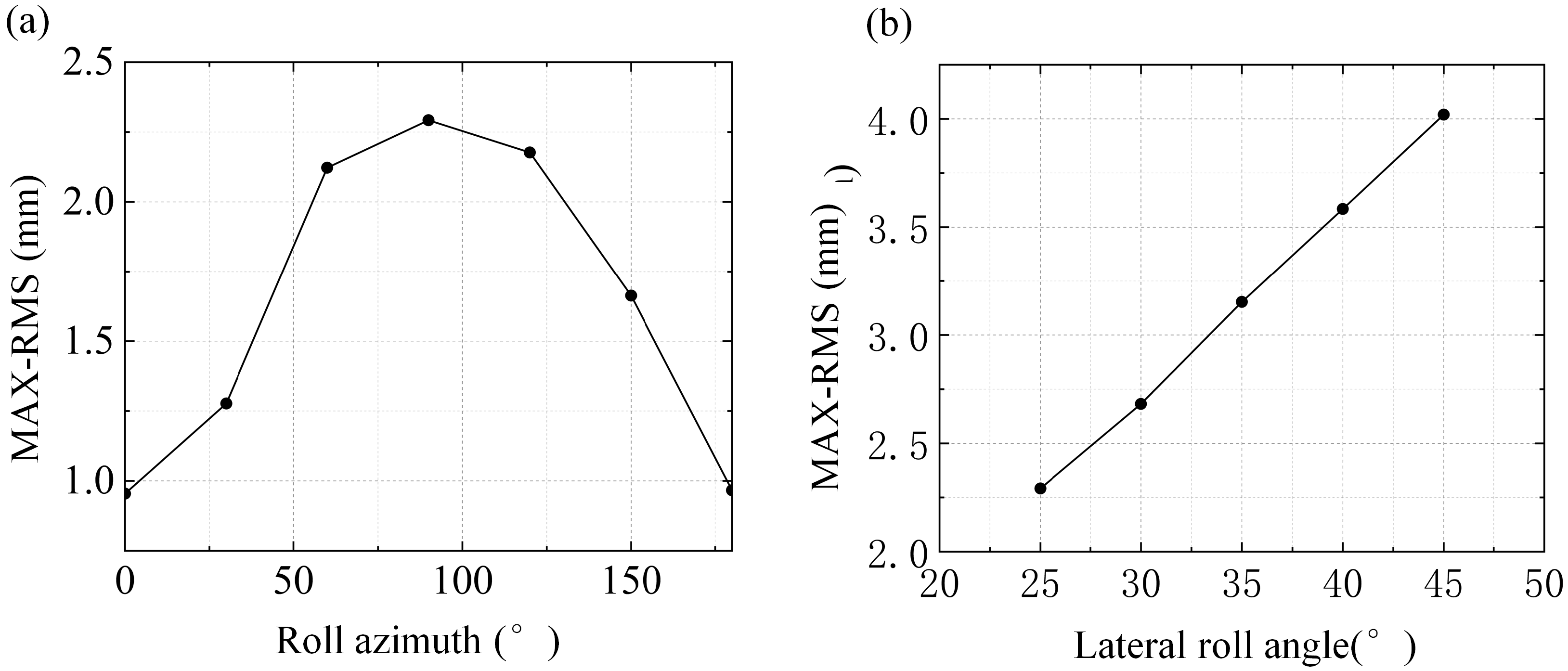
4.2. Effect of Roll Motion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.-Q.; Qiu, H.; Li, X.; Yang, S.-L. Review of Large Spacecraft Deployable Membrane Antenna Structures. Chin. J. Mech. Eng. 2017, 30, 1447–1459. [Google Scholar] [CrossRef]
- Ranjbaran, P.; Yousefi, H.; Gharehpetian, G.; Astaraei, F.R. A review on floating photovoltaic (FPV) power generation units. Renew. Sustain. Energy Rev. 2019, 110, 332–347. [Google Scholar] [CrossRef]
- Nielsen, F.G.; Hanson, T.D.; Skaare, B. Integrated dynamic analysis of floating offshore wind turbines. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; pp. 671–679. [Google Scholar] [CrossRef]
- Wang, B.; Gao, X.; Li, Y.; Liu, L.; Li, H. Dynamic response analysis of a semi-submersible floating wind turbine based on different coupling methods. Ocean Eng. 2024, 297, 116948. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Y.; Liu, H.; Zhou, S.; Ni, Y.; Cai, C.; Zhou, T.; Li, Q. Review of Study on the Coupled Dynamic Performance of Floating Offshore Wind Turbines. Energies 2022, 15, 3970. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind. Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Ishihara, T.; Liu, Y. Dynamic Response Analysis of a Semi-Submersible Floating Wind Turbine in Combined Wave and Current Conditions Using Advanced Hydrodynamic Models. Energies 2020, 13, 5820. [Google Scholar] [CrossRef]
- Yue, M.; Liu, Q.; Li, C.; Ding, Q.; Cheng, S.; Zhu, H. Effects of heave plate on dynamic response of floating wind turbine Spar platform under the coupling effect of wind and wave. Ocean Eng. 2020, 201, 107103. [Google Scholar] [CrossRef]
- Duan, B. Large Spaceborne Deployable Antennas (LSDAs)—A Comprehensive Summary. Chin. J. Electron. 2020, 29, 1–15. [Google Scholar] [CrossRef]
- Rahmat-Samii, Y.; Haupt, R. Reflector Antenna Developments: A Perspective on the Past, Present and Future. IEEE Antennas Propag. Mag. 2015, 57, 85–95. [Google Scholar] [CrossRef]
- Yadav, A.; Singh, S.K.; Das, S.; Kumar, S.; Kumar, A. Shape memory polymer and composites for space applications: A review. Polym. Compos. 2025, 46, 11647–11683. [Google Scholar] [CrossRef]
- Gralewski, M.R.; Adams, L.; Hedgepeth, J.M. Deployable Extendable Support Structure for the RADARSAT Synthetic Aperture Radar Antenna; International Astronautical Federation Congress: Washington, DC, USA, 1992; Available online: https://ui.adsabs.harvard.edu/abs/1992wadc.iafcU....G (accessed on 19 October 2025).
- Chiu, S. Moving target parameter estimation for RADARSAT-2 Moving Object Detection EXperiment (MODEX). Int. J. Remote Sens. 2010, 31, 4007–4032. [Google Scholar] [CrossRef]
- Barbier, C.; Derauw, D.; Orban, A.; Davidson, M.W.J. Study of a passive companion microsatellite to the SAOCOM-1B satellite of Argentina, for bistatic and interferometric SAR applications. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XVIII, Amsterdam, The Netherlands, 22–25 September 2014; Meynart, R., Neeck, S.P., Shimoda, H., Eds.; SPIE: Philadelphia, PA, USA, 2014; p. 92410K. [Google Scholar] [CrossRef]
- Montenbruck, O.; Allende-Alba, G.; Rosello, J.; Tossaint, M.; Zangerl, F. Precise Orbit and Baseline Determination for the SAOCOM-CS Bistatic Radar Mission. Navigation 2018, 65, 15–24. [Google Scholar] [CrossRef]
- Salas, W.A.; Ducey, M.J.; Rignot, E.; Skole, D. Assessment of JERS-1 SAR for monitoring secondary vegetation in Amazonia: I. Spatial and temporal variability in backscatter across a chrono-sequence of secondary vegetation stands in Rondonia. Int. J. Remote Sens. 2002, 23, 1357–1379. [Google Scholar] [CrossRef]
- Buckreuss, S.; Balzer, W.; Muhlbauer, P.; Werninghaus, R.; Pitz, W. The terraSAR-X satellite project. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 3096–3098. [Google Scholar] [CrossRef]
- Li, T. Deployment analysis and control of deployable space antenna. Aerosp. Sci. Technol. 2012, 18, 42–47. [Google Scholar] [CrossRef]
- Yang, S.; Zhao, Q.; Jiang, D.; Guo, J.; Zhang, J.; Hong, J. A laser target digital photogrammetry system for on-orbit surface error measurement of large spaceborne antennas. Measurement 2026, 257, 118526. [Google Scholar] [CrossRef]
- Cozijn, H.; Uittenbogaard, R.; Brake, E.T. Heave, roll and pitch damping of a deepwater CALM buoy with a skirt. In Proceedings of the International Society of Offshore and Polar Engineering Conference, Seoul, Republic of Korea, 19–24 June 2005. [Google Scholar]
- Bunnik, T.H.J.; De Boer, G.; Cozijn, J.L.; Van Der Cammen, J.; Van Haaften, E.; Brake, E.T. Coupled Mooring Analysis and Large Scale Model Tests on a Deepwater Calm Buoy in Mild Wave Conditions. In Proceedings of the ASME 2002 21st International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, 23–28 June 2002; pp. 65–76. [Google Scholar] [CrossRef]
- Cozijn, J.L.; Bunnik, T.H.J. Coupled Mooring Analysis for a Deep Water CALM Buoy. In Proceedings of the ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004; pp. 663–673. [Google Scholar] [CrossRef]
- Ryu, S.; Duggal, A.S.; Heyl, C.N.; Liu, Y. Coupled analysis of deepwater oil offloading buoy and experimental verification. In Proceedings of the Fifteenth International Offshore and Polar Engineering Conference, Seoul, Republic of Korea, 19–24 June 2005. [Google Scholar]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Optimization of Mooring Systems for Floating Offshore Wind Turbines. Coast. Eng. J. 2015, 57, 1550021-1–1550021-19. [Google Scholar] [CrossRef]
- Xu, S.; Ji, C.-Y.; Soares, C.G. Experimental and numerical investigation a semi-submersible moored by hybrid mooring systems. Ocean Eng. 2018, 163, 641–678. [Google Scholar] [CrossRef]
- Li, Y.; Yin, W.; Leng, S.; Meng, Y.; Zhang, Y. Dynamic Analysis of a Spar-Type Floating Offshore Wind Turbine Under Extreme Operation Gust. Sustainability 2025, 17, 5655. [Google Scholar] [CrossRef]
- Nallayarasu, S.; Kumar, N.S. Experimental and numerical investigation on hydrodynamic response of buoy form spar under regular waves. Ships Offshore Struct. 2017, 12, 19–31. [Google Scholar] [CrossRef]
- Penalba, M.; Ringwood, J.V. A Review of Wave-to-Wire Models for Wave Energy Converters. Energies 2016, 9, 506. [Google Scholar] [CrossRef]
- Shim, S. Coupled Dynamic Analysis of Floating Offshore Wind Farms. Available online: https://hdl.handle.net/1969.1/ETD-TAMU-2564 (accessed on 19 October 2025).
- Salic, T.; Charpentier, J.F.; Benbouzid, M.; Le Boulluec, M. Control Strategies for Floating Offshore Wind Turbine: Challenges and Trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef]
- Lu, S.; Qi, X.; Hu, Y.; Li, B.; Zhang, J. Deployment Dynamics of Large Space Antenna and Supporting Arms. IEEE Access 2019, 7, 69922–69935. [Google Scholar] [CrossRef]
- Li, M.; Cui, Q.; Wu, M.; Zhou, X.; Shi, F.; Meng, G. Flatness-oriented parameters allocation of multi-panel deployable antenna based on monte-carlo simulation. In Proceedings of the 2019 9th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 11–14 June 2019; pp. 497–502. [Google Scholar] [CrossRef]
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- GB/T 28591-2012; Wind Scale. Standards Press of China: Beijing, China, 2012.
- Rules for the Division of Navigation Areas; China Maritime Safety Administration: Beijing, China, 2021.
- Rules for Classification of Mobile Offshore Units; China Classification Society (CCS): Beijing, China, 2020.
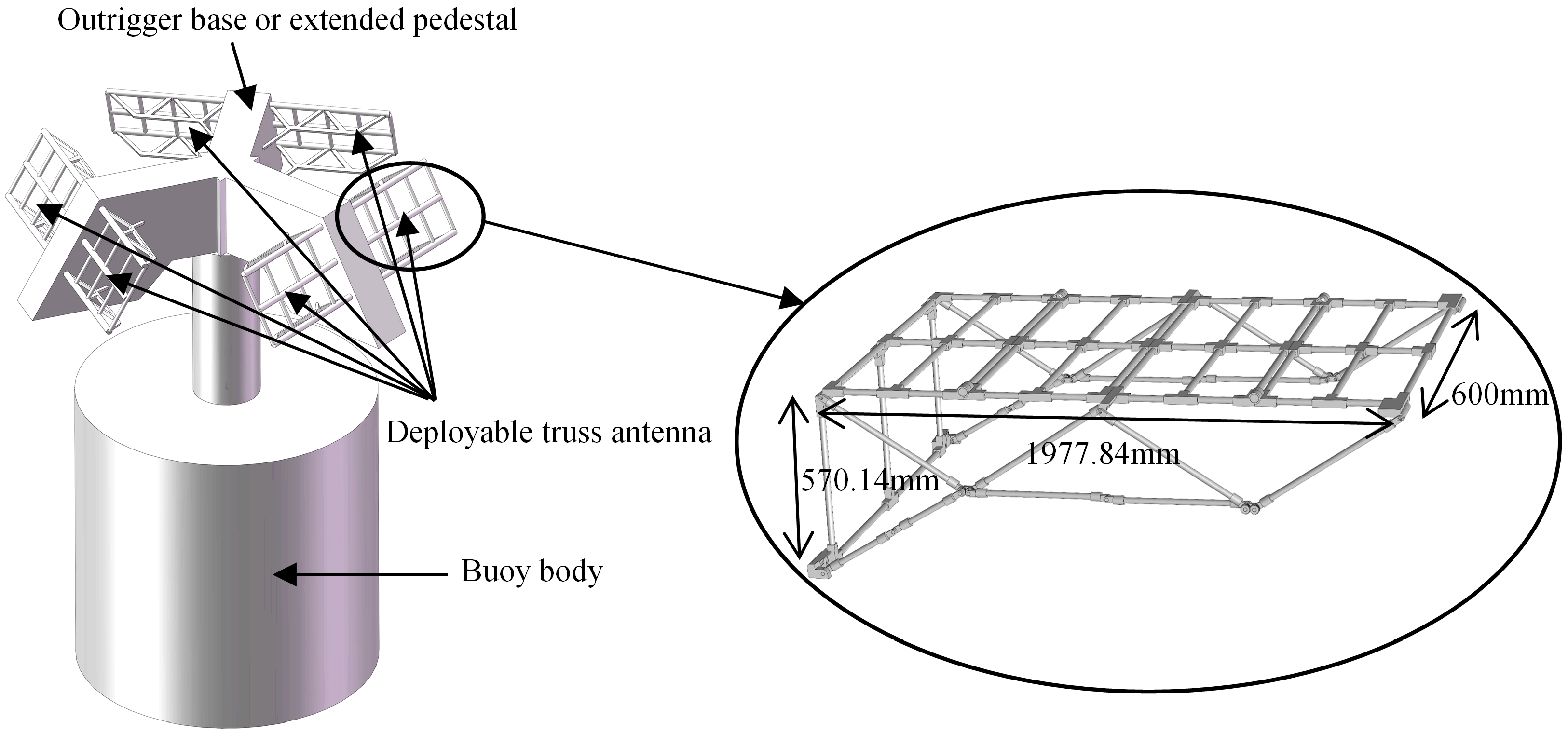


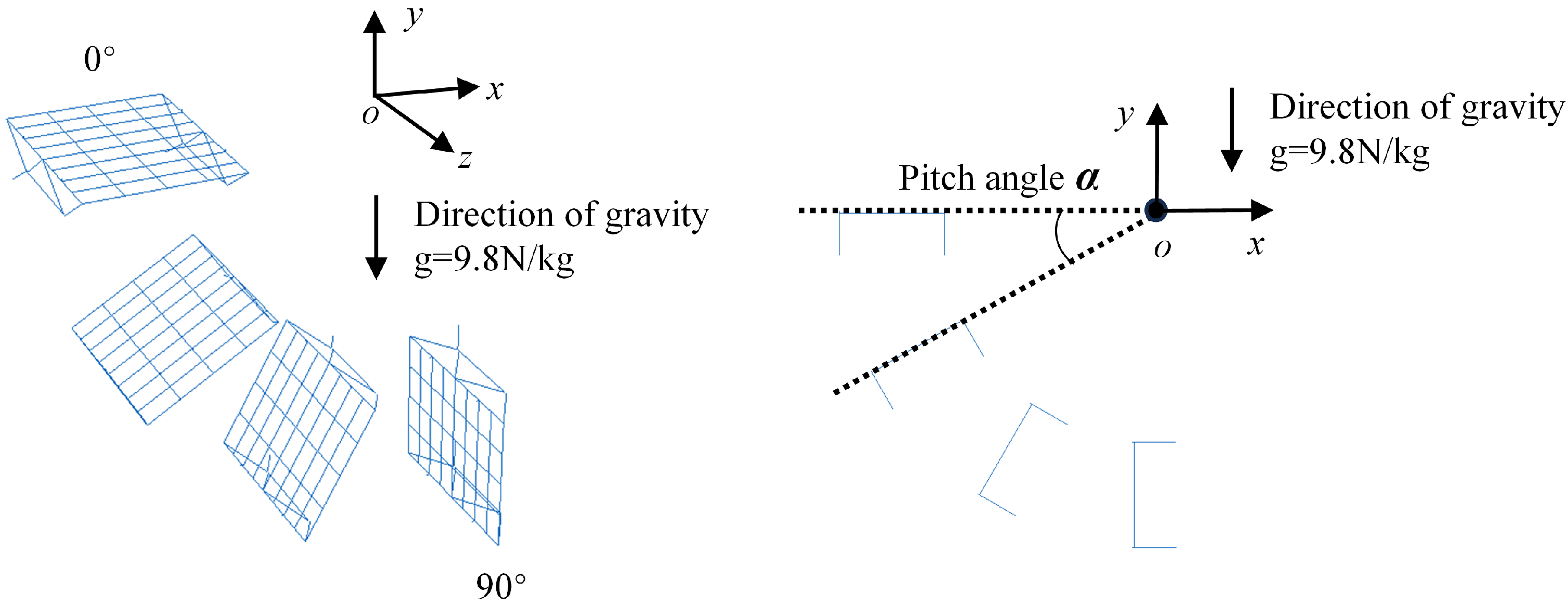








| Component ID | l1 | l2 | l3 | l4 | l5 | l6 | l7 |
| Length (mm) | 284.4 | 268.42 | 494.46 | 570.14 | 30 | 570.14 | 494.46 |
| Component ID | l8 | l9 | l10 | l11 | l12 | l13 | l14 |
| Length (mm) | 570.14 | 478.75 | 478.75 | 494.46 | 30 | 570.14 | 494.46 |
| Case | Elevation Angle α (°) | Surface Precision RMS (mm) | Max. Displacement Umax (mm) | Max. Stress σmax (MPa) |
|---|---|---|---|---|
| I | 30 | 1.27 | 5.05 | 13.33 |
| II | 60 | 2.19 | 8.74 | 23.09 |
| III | 90 | 2.54 | 10.10 | 26.67 |
| Case | Elevation Angle α (°) | Surface Precision RMS (mm) | Max. Displacement Umax (mm) | Max. Stress σmax (MPa) |
|---|---|---|---|---|
| I | 30 | 1.30 | 5.30 | 71.52 |
| II | 60 | 2.17 | 6.94 | 46.90 |
| III | 90 | 2.44 | 7.55 | 20.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Zhong, Q.; Lin, Z.; Feng, J.; Cai, J. Dynamic Response and Performance Degradation of a Deployable Antenna Under Sea-Based Excitation. Buildings 2025, 15, 4108. https://doi.org/10.3390/buildings15224108
Gu Y, Zhong Q, Lin Z, Feng J, Cai J. Dynamic Response and Performance Degradation of a Deployable Antenna Under Sea-Based Excitation. Buildings. 2025; 15(22):4108. https://doi.org/10.3390/buildings15224108
Chicago/Turabian StyleGu, Yeqing, Qiuyue Zhong, Zeyu Lin, Jian Feng, and Jianguo Cai. 2025. "Dynamic Response and Performance Degradation of a Deployable Antenna Under Sea-Based Excitation" Buildings 15, no. 22: 4108. https://doi.org/10.3390/buildings15224108
APA StyleGu, Y., Zhong, Q., Lin, Z., Feng, J., & Cai, J. (2025). Dynamic Response and Performance Degradation of a Deployable Antenna Under Sea-Based Excitation. Buildings, 15(22), 4108. https://doi.org/10.3390/buildings15224108






