Study on Shear Capacity of Horizontal Joints in Prefabricated Shear Walls

Abstract

This study investigates the shear behavior of horizontal joints in prefabricated monolithic short-limb shear walls under static and low-cycle reversed cyclic loading, supported by finite-element simulations. Four specimens were tested to evaluate the influence of the bundled shear reinforcement ratio, initial reinforcement stress level, and loading protocol on shear capacity. The results show that increasing the bundled shear reinforcement ratio significantly enhanced both the yield and peak loads, with increases observed in the yield, peak, and failure loads. Conversely, a higher initial stress level in the reinforcement weakened the shear-friction mechanism, leading to a reduction in the load-carrying capacity. Compared to monotonic loading, low-cycle reversed cyclic loading accelerated crack propagation and cumulative damage, leading to a significant reduction in load-carrying and deformation capacities. Finite-element simulations, using the Concrete Damaged Plasticity (CDP) model, were in good agreement with experimental results, although the simulations slightly overestimated the ultimate capacity, confirming the model’s validity. Parametric analysis indicated that increasing axial tension progressively reduced the yield and peak loads, with the reduction in peak load being more pronounced, while the cracking load remained unchanged. These findings provide a theoretical foundation for the shear design and seismic performance evaluation of horizontal joints in prefabricated shear walls, offering valuable insights for future design improvements and modeling strategies.

1. Introduction

With the rapid adoption of prefabricated reinforced concrete (PRC) structures in China’s construction industry, their application in residential buildings, public facilities, and certain infrastructure projects has steadily increased year by year [1,2,3,4]. Prefabricated structures offer distinct advantages—including shorter construction periods, higher resource utilization efficiency, and lower environmental impact—that align with the objectives of green and low-carbon development [5,6]. However, due to the presence of assembly interfaces—such as horizontal and vertical joints—the structural integrity and seismic performance of prefabricated shear walls, compared with those of monolithic cast-in-place concrete walls, remain key concerns among researchers and engineers [7]. Post-earthquake investigations have consistently identified horizontal joints as the critical weak link in prefabricated shear walls. Under extreme loading conditions such as earthquakes, these joints are highly susceptible to cracking, slippage, and through-interface failure. Such degradation significantly reduces the overall load-carrying and deformation capacities of the structure. Therefore, a comprehensive investigation and clarification of the shear transfer mechanism of horizontal joints under different loading conditions are of great theoretical and practical significance for enhancing the seismic safety of prefabricated structures.

Extensive research has examined the mechanical behavior and failure mechanisms of connections in PRC structures, focusing on reinforcement anchorage performance, grouting material properties, and connection detailing [8,9,10]. Feng et al. [11] improved the cluster connection method by developing a vertical-steel-bar-concentrated restraint overlap connection, resulting in a more rational stress distribution. This modification addressed several limitations in the original cluster connection design. Zhang [12] advanced the understanding of shear resistance in cluster-connected shear walls by deriving a simplified formula for calculating their shear capacity based on the tension–compression rod model, which was validated through laboratory tests. Liu [13] investigated the seismic performance of cluster-connected precast shear walls, finding that while removing corrugated pipes did not enhance bearing capacity, it improved energy dissipation and ductility. Liu also noted that additional reinforcement at the height of the reserved holes reduced crack width without changing the ultimate crack mode. Their failure modes involve not only concrete crushing and crack propagation but also shear sliding, reinforcement pullout, and interface separation [14]. Although previous research has established a fundamental understanding of the shear transfer mechanisms in horizontal joints, a comprehensive explanation of their mechanical response under complex loading conditions is still lacking [15].

Building on this foundation, recent studies have further explored the numerical modeling and simulation of concrete and connection systems, providing valuable insights into their mechanical behavior and validation methods. Eller et al. [16] simulated using the finite element software Concrete Canvas and found that the impact of sharp stones on Concrete Canvas material must be considered. Ibrahim et al. [17] simulated Steel–Polypropylene Hybrid Fiber Reinforced Concrete Deep Beams and discovered that Abaqus can effectively simulate the failure patterns of beams under different fiber combinations. Grubits et al. [18] employed bidirectional evolutionary structural optimization and finite element modeling to comprehensively investigate the plastic limit behavior of I-beams under various loading conditions. These studies validate the effectiveness of simulation software in modeling the failure of concrete components.

The shear capacity of prefabricated shear wall joints is governed by several factors, including the bond strength between grout and concrete, the area and initial stress level of bundled shear reinforcement, and the loading protocol. Under seismic loading, low-cycle reversed cyclic actions cause repeated crack opening and closing, resulting in cumulative damage and stiffness degradation, which significantly reduce the load-carrying and deformation capacities of the joint [19,20]. However, most existing studies have been restricted to monotonic loading, lacking systematic investigation into degradation mechanisms under cyclic loading. Additionally, the limited number of test specimens and narrow parameter ranges adopted in previous experiments have hindered a comprehensive understanding of the influencing factors governing joint shear capacity [21,22,23]. Moreover, numerical models are often overly simplified, neglecting sliding at the steel–concrete interface and cyclic degradation of reinforcement, resulting in discrepancies between simulated and experimental responses [24,25,26].

Therefore, this study focuses on prefabricated monolithic short-limb shear walls and performs both monotonic and low-cycle reversed cyclic loading tests to systematically investigate the influence of the bundled shear reinforcement ratio, initial reinforcement stress level, and loading protocol on the shear capacity and deformation performance of horizontal joints. Concurrently, a finite-element model was established in Abaqus based on the Concrete Damaged Plasticity (CDP) model to clarify the evolution of shear behavior in horizontal joints under different axial load levels. The findings enhance the theoretical understanding of the shear transfer mechanism in prefabricated shear walls and offer a scientific foundation for optimizing the design and seismic performance evaluation of horizontal joints in engineering practice.

2. Test Plan Design

2.1. Test Materials

To accurately determine the mechanical properties of the concrete and grout, companion specimens were prepared during casting. Concrete specimens were tested in accordance with 《GB/T 50081–2019 Standard for Test Methods of Mechanical Properties of Ordinary Concrete》 [27]. The specimens were divided into three batches, each consisting of three standard cubes measuring 150 mm × 150 mm × 150 mm. The average cube compressive strength was 37.9 MPa. JGM^®-II high-strength non-shrink grout was employed, and all specimens were grouted using material from the same production batch. To ensure data accuracy, three prism grout specimens (40 mm × 40 mm × 160 mm) were prepared, with an average compressive strength of 64.8 MPa. Tensile tests on reinforcing steel were performed in accordance with 《GB/T 228.1–2010 Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature》 [28]. Two grades of reinforcing bars—HPB300 and HRB400—were used. Their average yield strengths were 385 MPa and 432 MPa, and their ultimate tensile strengths were 615 MPa and 618 MPa, respectively.

2.2. Specimen Design

As shown in

Table 1. Test Specimen Details.

Specimen Number	Bundled Reinforcing Bars	Loading Method	Stress Level of Bundled Reinforcing Bars
YZA-1	8C14	Reversed cyclic	50 MPa
YZB-1	12C12	Reversed cyclic	50 MPa
YZB-2	12C12	Monotonic	100 MPa
YZB-3	12C12	Reversed cyclic	100 MPa

, four short-limb shear wall specimens with horizontal joints were designed, designated YZA-1, YZB-1, YZB-2, and YZB-3. All specimens were prefabricated and post-assembled. As illustrated in Figure 1, Type A adopted bundled shear reinforcement (8C14) evenly distributed among four preformed ducts, symmetrically arranged about the wall’s centerline. Type B used bundled shear reinforcement (12C12) in the same configuration. To study the influence of the loading protocol on horizontal joints shear capacity, both monotonic and low-cycle reversed cyclic loading were implemented. Considering actuator limits and to avoid premature tensile failure, initial reinforcement stress levels were set to 50 MPa and 100 MPa.

For all precast specimens, horizontal distribution reinforcement was spaced at 100 mm intervals, and closed stirrups with welded laps were used. All horizontal and vertical distribution reinforcement employed HRB400 deformed bars (C8 mm). Boundary (edge-confined) reinforcement used HRB335 deformed bars (C10 mm), while helical stirrups used HPB300 plain bars (C6 mm).

2.3. Strain Gauge Placement

Given the critical role of strain in the shear reinforcement within horizontal joints, strain gauges were installed to monitor bar deformation. Specifically, gauges were attached to the bars at the joint interface and within ±2d (where d denotes the bar diameter) above and below the interface. Real-time strain data were collected using a static strain data-acquisition system. For each bundled shear reinforcement in both Type A and Type B specimens, five gauge locations were distributed vertically from below to above the joint interface, as shown in Figure 2.

2.4. Loading Scheme

The testing program adopted two loading protocols: monotonic and low-cycle reversed cyclic loading. Static monotonic loading evaluated shear capacity under one-way shear action, while quasi-static cyclic loading simulated seismic conditions. This configuration enabled evaluation of how the loading protocol affects joint shear performance. As shown in Figure 3, the experiments were conducted using a 2000-ton reaction frame at Southeast University. The system consisted of:

(i)

a vertical loading assembly (20-ton lug-type hydraulic jack, distribution beam, and loading beam);

(ii)

a horizontal loading system (100-ton MTS actuator, loading fixture, and tie bars);

(iii)

an anchorage/support structure connecting the foundation beam to the reaction frame with out-of-plane bracing.

Each specimen was subjected to combined vertical tension and horizontal shear. A specially designed distribution–loading beam arrangement ensured stable force transmission and prevented unintended lateral translation or torsion.

Before formal loading, each specimen underwent preloading to confirm proper equipment operation. After unloading to zero, all bolts were re-torqued. As shown in Figure 4, horizontal loading was applied under constant axial tension through two control modes: (a) monotonic and (b) low-cycle reversed cyclic loading. Axial tension was applied via a lug-type jack and increased in 10 MPa increments until the reinforcement stress reached the target level, which was then held constant. Monotonic loading was force-controlled up to yielding, followed by displacement control in 3 mm increments. For low-cycle reversed cyclic loading, one cycle was applied per force step in the pre-yield phase, and two cycles per 3 mm displacement step after yielding. Loading was terminated when failure occurred or when the horizontal load dropped below 85% of the peak value. Given the specimens’ brittle behavior, the control mode transitioned to displacement control at later stages to prevent abrupt displacement jumps.

3. Test Results and Analysis

3.1. Test Phenomena

As shown in Figure 5, all four prefabricated shear wall specimens exhibited similar mechanical responses and failure characteristics, classified as a typical brittle shear–compression failure mode. During the early loading stage, initial cracks appeared along the grouted horizontal joint interface and gradually propagated through it. As loading increased, inclined cracks developed in the lower wall region and extended in both length and width. At mid to late stages, concrete spalling and outward bulging occurred in the grout layer, followed by local concrete crushing and progressive debonding between the grout layer and the upper wall. In the final failure stage, triangular spalling blocks and crushed grout regions formed in the lower joint area, accompanied by fragmentation of the concrete surrounding the bundled shear reinforcement and a sharp reduction in shear load-carrying capacity. The overall behavior was characterized by a combination of concrete crushing and shear sliding along the interface, representing a distinctly brittle shear–compression failure.

In summary, all specimens followed a consistent failure evolution sequence: joint cracking, inclined crack propagation, concrete spalling, grout-layer crushing, and strength degradation. This confirms that the grouted horizontal joint interface is the critical weak zone of the assembly, and that the shear resistance and confinement performance of the grout layer play a decisive role in determining both ultimate load capacity and global failure mode.

3.2. Load–Displacement Curves

Two loading protocols were employed: monotonic and reversed cyclic. For cyclic tests, compression was defined as positive and tension as negative. One complete cycle comprised positive loading, unloading to zero, negative loading, and unloading again to zero. Figure 6 shows the horizontal load–displacement curves for the four horizontal joint specimens. Specimens YZA-1, YZB-1, and YZB-3 were tested under reversed cyclic loading, while YZB-2 was subjected to monotonic loading.

A comparison of hysteresis loops for YZA-1, YZB-1, and YZB-3 reveals that during the force-control phase, both load and displacement amplitudes were small, producing nearly linear hysteresis loops with limited energy dissipation capacity. When the horizontal load reached ±50 kN, cracks propagated across the joint interface, and displacement increased slightly (about 0.5–1 mm). As the load increased further, displacement amplitudes grew substantially, local crushing appeared in the grout layer, and the hysteresis loops exhibited a pinched, inverted S-shape, accompanied by reduced ductility and diminished energy dissipation.

During the displacement-control phase, the loops evolved from a pinched (inverted S-shaped) profile to a Z-shaped loop, reflecting increasing interface slip–dominated behavior. The yield plateau was indistinct; once the peak load was reached, displacement increased rapidly while load declined sharply—evidence of brittle failure and loss of joint shear resistance. Peak loads were asymmetric between loading directions, decreasing slightly after the initial peak. This asymmetry is attributed to aggregate interlock degradation and the nonuniform spatial distribution of cracks, leading to localized crushing and reduced shear transfer.

Comparison between YZA-1 and YZB-1 shows that while their early-phase hysteresis curves were similar, YZB-1 achieved a slightly higher peak load due to its larger bundled shear-reinforcement area (≈1.1 × that of YZA-1). During the post-peak stage, YZB-1 exhibited greater strength retention and slower degradation. For YZA-1, sharp load loss occurred near 340 kN at a displacement of ≈10 mm, corresponding to severe joint damage; residual resistance was mainly provided by the dowel action of the bundled reinforcement.

Comparison between YZB-1 and YZB-3 shows similar curve shapes, but at identical displacements, YZB-3 carried lower loads. The reduction is attributed to its higher initial reinforcement stress (100 MPa vs. 50 MPa), which weakens the shear–friction mechanism, lowering interface clamping force and thus shear capacity.

Under monotonic loading (YZB-2), initial cracking occurred at ≈50 kN, followed by a post-cracking hardening branch around 580 kN. As shear load continued to increase, stress in the bundled bars rose until tensile rupture occurred, causing localized spalling in the lower wall and final specimen failure.

3.3. Backbone Curve

The backbone curve represents the locus of peak horizontal load at each displacement amplitude during low-cycle reversed cyclic loading tests. Analysis of the backbone curve allows identification of the loading stages and associated response characteristics of horizontal joints in prefabricated shear walls. A typical backbone curve consists of three stages: elastic, plastic (yielding or hardening), and degradation/failure phases. Prior to yielding, the load–displacement response is approximately linear-elastic. Near the yield point, the backbone curve develops a distinct knee and enters the plastic stage, during which the tangent stiffness degrades and the rate of load increase diminishes. After reaching the peak load, the specimen exhibits post-peak softening with declining load-carrying capacity, marking the initiation of degradation and failure.

Figure 7 presents the backbone curves for all tested specimens. Under reversed cyclic loading, the backbone curve consists of elastic, plastic, and degradation/failure stages, with the plastic range typically short. During the early elastic stage, at a shear load of approximately 50 kN, first cracking initiates at the joint interface and propagates rapidly, resulting in a displacement jump and a knee in the backbone curve. Thereafter, the pre-yield load–displacement branch is approximately linear-elastic. In the plastic stage, the plastic range is short—or nearly absent—for most specimens. At displacements of approximately 12–13 mm, the load dropped rapidly, marking the initiation of the degradation and failure stage. Overall, the specimens exhibited typical brittle post-peak behavior with limited ductility. By contrast, under monotonic loading, the specimens displayed distinct elastic, plastic, and degradation/failure stages; the plastic stage was prolonged, showing additional load increase after yielding, which is indicative of ductile response characteristics.

Further analysis of the backbone curves for specimens YZA-1 and YZB-1 shows that they are nearly identical over the 0–300 kN load range, with only negligible differences. However, for equal displacement amplitudes, YZB-1 exhibits a steeper load increase and reaches its peak at a larger displacement (i.e., the peak load is delayed). This behavior is attributed to YZB-1’s larger bundled shear-reinforcement area (approximately 1.1 times that of YZA-1), which increases the joint-interface stiffness and delays the onset of peak load.

A comparison between the backbone curves of YZB-1 and YZB-3 shows that, although both curves are similar over the 0–300 kN range, YZB-3 attains a lower peak load at a smaller displacement (i.e., an earlier peak). This occurs because, as the initial stress in the bundled shear reinforcement increases (from 50 MPa in YZB-1 to 100 MPa in YZB-3), the shear–friction mechanism at the joint is weakened, effectively reducing the normal stress across the interface. Consequently, the load-carrying capacity decreases and interface separation between the joint grout and the upper wall is accelerated.

Finally, a comparison between the backbone curves of YZB-2 and YZB-3 shows that, under reversed cyclic loading, the initial stiffness was slightly lower than under monotonic loading. At around 500 kN, the displacement increased while the tangent stiffness dropped sharply as the response transitioned into the degradation and failure stage. Reversed cyclic loading significantly reduced the joint’s shear capacity. The displacement at peak load was smaller under cyclic loading, indicating reduced ductility and weakened shear resistance. These results demonstrate that cyclic loading markedly degrades structural performance, particularly the load-carrying and deformation capacities of prefabricated shear wall horizontal joints.

3.4. Load-Carrying Capacity Analysis

According to 《JGJ/T 101–2015 Technical Specification for Seismic Test of Buildings》 [29], the cracking, yield, and failure loads of the shear-wall horizontal-joint specimens were defined as follows:

The cracking load was defined as the load corresponding to the first appearance of a distinct through-joint shear crack at the interface. The yield load was determined using three methods—the Energy Method, the Modified Energy Method, and the R. Park Method [30,31,32]. The arithmetic mean of the three yield estimates was adopted as the yield load for each specimen. The average provides a balanced estimate, minimizing the potential bias or discrepancy from any individual method. The scatter between the methods was relatively small, with variations typically within ±10% for most specimens. The failure load was taken as the load at which the measured load dropped to 85% of the peak value. Load-carrying capacity indicators for each specimen are summarized in

Table 2. Load-Carrying Capacity Index Table.

Specimen Number	Cracking Load Fcr/kN			Yield Load Fy/kN			Peak Load Fp/kN			Failure Load Fm/kN
	Forward	Reverse	Average	Forward	Reverse	Average	Forward	Reverse	Average	Forward	Reverse	Average
YZA-1	50	50	50	498	512	505	497	490	494	422	417	419
YZB-1	50	50	50	552	476	514	566	542	554	481	461	471
YZB-2	50	50	50	673		673	838		838	712		712
YZB-3	50	50	50	422	337	380	451	386	418	383	328	356

and Figure 8.

Overall, because of the coarse force increments used during the force-control phase, all specimens registered a cracking load of approximately 50 kN. The pairwise rank ordering of yield loads was: YZB-1 > YZA-1, YZB-1 > YZB-3, and YZB-2 > YZB-1. The same ordering held for both the peak load and the failure load (85% of peak): YZB-1 > YZA-1, YZB-1 > YZB-3, and YZB-2 > YZB-1. Because specimen YZB-2 was tested under monotonic loading, its monotonic characteristic load values were used for comparison as both the forward-direction value and the average value.

Relative to YZA-1, YZB-1 had a 10.06% larger bundled shear-reinforcement area, resulting in increases of 23.49%, 13.88%, and 12.41% in the yield, peak, and failure loads, respectively. As the bundled shear-reinforcement area increased, all characteristic load-carrying capacity indices improved to varying degrees, except for the cracking load. Among these indices, the yield load showed the greatest increase, followed by the peak load, whereas the failure load exhibited the smallest increase.

Specimens YZB-1 and YZB-3 featured identical bundled shear-reinforcement configurations; the initial stress levels in the reinforcement were 50 MPa and 100 MPa, respectively. Relative to YZB-1, YZB-3 exhibited reductions of 26.09%, 24.49%, and 24.48% in the yield, peak, and failure loads, respectively. Thus, as the initial stress level in the bundled shear reinforcement increased, all characteristic load measures (yield, peak, and failure) decreased to varying degrees, whereas the cracking load remained essentially unchanged; the reduction ratios were comparable across the three load indicators.

Specimens YZB-1 and YZB-2 had identical bundled shear-reinforcement configurations and initial stress levels; the only variable was the loading protocol—reversed cyclic for YZB-1 and monotonic for YZB-2. Relative to YZB-1, YZB-2 showed 31.04%, 51.29%, and 51.29% increases in the yield, peak, and failure loads, respectively. Thus, monotonic loading increased all load-carrying capacity measures relative to reversed cyclic loading, while the cracking load remained essentially unchanged. The percentage increase in yield load was smaller than that in the peak and failure loads, indicating greater post-yield sensitivity to the loading protocol.

4. Finite-Element Analysis

A finite-element model (FEM) was developed in Abaqus 2018 to evaluate the shear capacity of horizontal joints in prefabricated monolithic short-limb shear walls with bundled bar connections. The concrete constitutive behavior was modeled using the CDP model to simulate damage evolution and the load–displacement response under monotonic uniaxial loading. The simulation results were compared with the experimental data, with specimen YZB-2 serving as a representative case.

4.1. Finite-Element Model Setup

For the concrete, 8-node linear hexahedral reduced-integration elements (C3D8R) were adopted to balance accuracy and computational cost, with a global element size of 50 mm. Given that the reinforcing steel primarily resists tension, two-node 3D truss elements (T3D2) were used to model the wall and foundation reinforcement. To represent the dowel (pin-type) action of the bundled shear reinforcement across the horizontal joints, quadratic beam elements (B32) were employed. To satisfy the element-length requirement, the along-bar element length for the bundled reinforcement was set to 140 mm. The finite-element model is shown in Figure 9.

In Abaqus, two main concrete constitutive models are available: the CDP model and the smeared cracking model [33]. The smeared cracking model represents directional stiffness degradation within an isotropic elastic medium and is mainly applied to monotonic analyses of reinforced and plain concrete. The CDP model combines isotropic damaged elasticity with isotropic tensile and compressive plasticity to capture the inelastic response of concrete. It is suitable for uniaxial, cyclic, and dynamic loading of concrete structures and generally exhibits favorable numerical convergence. Accordingly, this study adopts the CDP model to describe the concrete constitutive behavior.

The stress–strain relationships for uniaxial tension and compression, incorporating damage factors, are expressed as follows:

$$\sigma =(1-d)\overline{\sigma }$$

(1)

$$\overline{\sigma }=D_0^{el}(\epsilon -{\tilde{\epsilon }}^{pl})$$

(2)

$$\sigma =(1-d)D_0^{el}(\epsilon -{\tilde{\epsilon }}^{pl})$$

(3)

where d is the damage factor, $\overline{\sigma }$ is the effective stress, ${\tilde{\epsilon }}^{pl}$ is the plastic strain of concrete, and $D_0^{el}$ is the initial stiffness of the material. The finite-element parameters for concrete are listed in

Table 3. Concrete Finite-Element Parameters.

Density	Poisson’s Ratio	Eccentricity	Expansion Angle	fb0/fc0	Kc	μ
2500	0.2	0.1	38	1.16	2/3	0.005

. The stress–strain relationship curves for concrete under uniaxial compression and tension are shown in Figure 10.

The constitutive behavior of reinforcing bars was defined by a bilinear elastic–plastic model [34]. Specifically, after yielding, the stress–strain relationship was simplified to a gently sloping straight line to ensure convergence during computation. The model is illustrated in Figure 11, and the relationship is defined as:

$${\sigma }_s=\left\{\begin{array}{cc}{E}_s{\epsilon }_s& {\epsilon }_s<{\epsilon }_y\\ {E^{\prime }}_s({\epsilon }_s-{\epsilon }_y)+f_y& {\epsilon }_y<{\epsilon }_s<{\epsilon }_{sm}\end{array}\right.$$

(4)

where f_y is the yield strength of the reinforcing bar, ε_y is the yield strain of the reinforcing bar, E_s is the initial elastic modulus of the reinforcing bar, and E^′_s = 0.01E_s.

The steel–concrete interface was modeled using the Embedded Region constraint in the Interaction module of Abaqus, ensuring kinematic compatibility between the reinforcing bars and the surrounding concrete. Contact between the wall and foundation beam was defined as surface-to-surface contact, with hard contact in the normal direction and a Coulomb friction coefficient (μ) of 0.6 in the tangential direction. The interfaces between the grout and the corrugated duct, and between the duct and the wall concrete, were modeled using tie constraints, consistent with the absence of interface failure observed in the experiments. The full monotonic loading sequence of the horizontal joint specimen was simulated in three analysis steps: (i) apply self-weight and boundary conditions; (ii) apply axial tension; and (iii) impose lateral displacement.

4.2. Comparison of Failure Patterns in Finite-Element Models

Equivalent Plastic Strain (PEEQ) is commonly used in Abaqus to evaluate the damage evolution and localized failure of concrete. As shown in Figure 12, inelastic deformation was concentrated at the joint, and as relative slip across the joint shear plane increased, PEEQ values rose monotonically. Failure was primarily governed by grout layer crushing at the joint interface, corresponding to the region of maximum PEEQ. This observation aligns with the experimental results reported in Section 2.1.

Figure 13 and Figure 14 illustrate the evolution of tensile and compressive damage in specimen YZB-2. As the horizontal shear demand increased, tensile damage localized in the wall region below the joint and intensified progressively. Compressive damage initiated at the joint and propagated downward as the load increased. The simulation results were in close agreement with the crack propagation patterns observed in the experiments.

4.3. Comparison of Load–Displacement Curves

As shown in Figure 15, the load–displacement (L–D) curve measured for specimen YZB-2 closely matched that predicted by Abaqus, exhibiting distinct elastic and yielding stages. The main discrepancy appeared after cracking: the experiment showed approximately 5 mm of relative slip across the joint, whereas the FEM did not reproduce interfacial cracking or slip, since bond–slip behavior was not explicitly modeled.

The specimen’s yield load was defined as the average value obtained from the Energy Method, Modified Energy Method, and R. Park Method. Experimentally, the yield and ultimate loads were 673 kN and 838 kN, respectively, while Abaqus predicted 721 kN and 984 kN. Thus, the Abaqus simulation slightly overestimated the load-carrying capacity, likely due to simplifications such as neglecting second-order (P–Δ) effects and bond–slip at the steel–concrete interface.

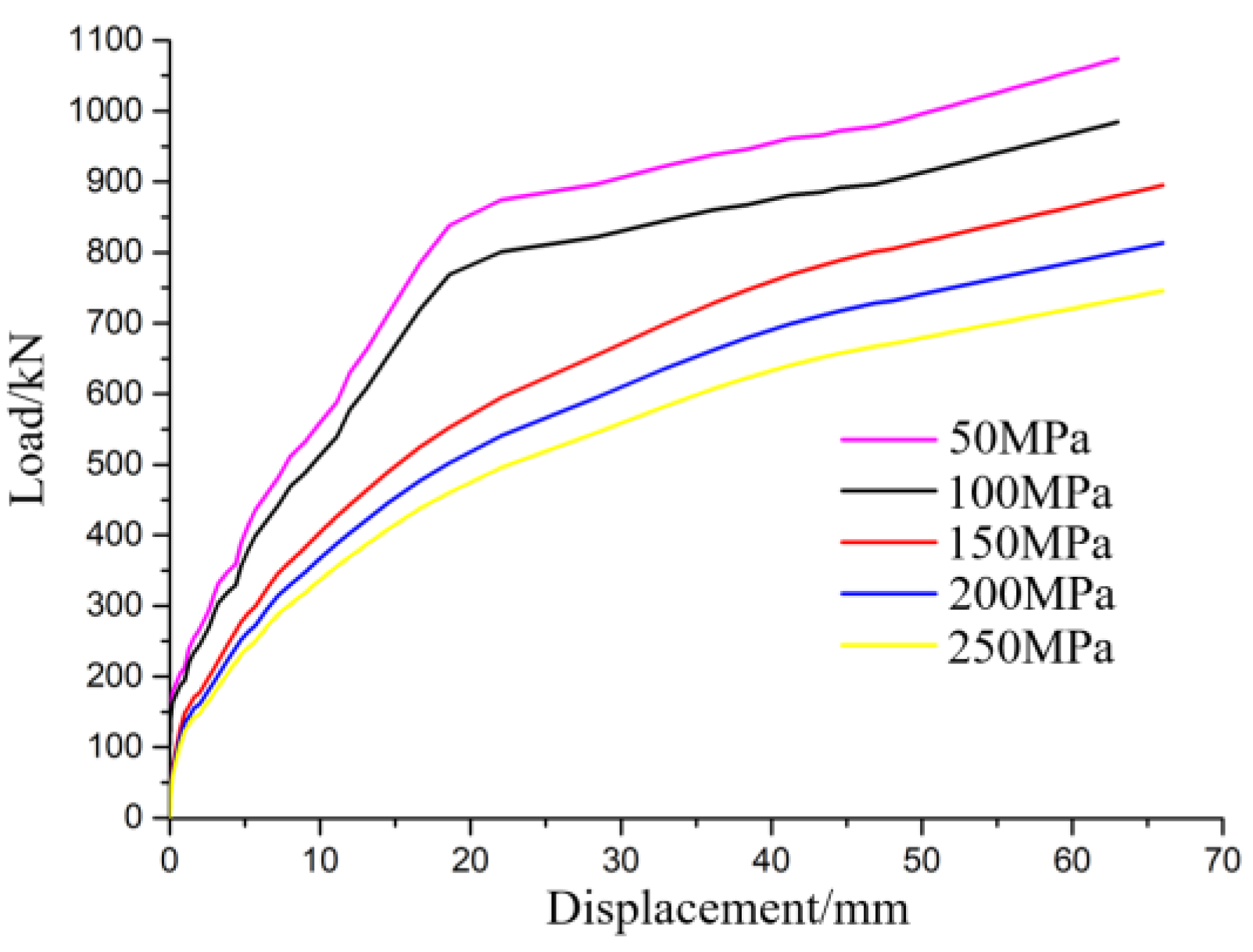
4.4. Parameter Analysis

According to 《JGJ1—2014 Technical Specification for Precast Concrete Structures》 [35], the design shear capacity of horizontal joints in prefabricated shear walls shall be calculated using the following expression:

$$V_{uE}=0.6f_y{A}_{sd}+0.8N$$

(5)

where N represents the design axial force perpendicular to the bond plane corresponding to the shear design value V_uE, taken as positive for compression and negative for tension. A_sd denotes the area of shear reinforcement passing through the bond plane.

To clarify the influence of axial tension, a series of parametric FEM simulations were conducted for Type B specimens with initial bundled-bar stress levels of 50, 100, 150, 200, and 250 MPa. The results are summarized in Figure 16 and

Table 4. Load-bearing Capacity of Type B Specimens at Different Axial Force Design Values.

Bundled Reinforcing Bar Stress/MPa	Axial Tensile Force/kN	Yield Load Fy/kN	Peak Load Fp/kN
50	97.8	787.2	1074.0
100	165.6	721.6	984.5
150	233.4	656.0	895.0
200	301.2	596.4	813.6
250	369.0	546.7	745.8

Note: Tensile force is recorded as negative according to JGJ1; the table shows its amplitude.

. The yield load was defined as the average of the three methods, and both yield and peak loads were recorded. As axial tension normal to the shear plane increased, both yield and peak loads decreased, with the peak load reducing more markedly. With increasing axial tension, the backbone (L–D) curve became flatter, and yielding characteristics were attenuated. Mechanistically, axial tension tends to open the joint interface, thereby reducing shear–friction resistance; once the interface approaches full opening, further increases in axial tension produce only marginal additional separation and limited further capacity loss.

5. Conclusions

Based on the experimental findings and finite-element simulation results, the following conclusions can be drawn:

(1)

All specimens exhibited brittle shear–compression failure characterized by grout layer crushing, through-joint cracking, and triangular block separation in the lower wall region. Increasing the bundled shear reinforcement ratio effectively enhanced the yield and peak loads, whereas a higher initial stress level in the reinforcement weakened the shear–friction mechanism, reducing the overall shear capacity.

(2)

Compared with monotonic loading, low-cycle reversed cyclic loading accelerated crack propagation and damage accumulation, resulting in faster stiffness degradation and reduced load-carrying capacity and ductility. Increasing axial tension further decreased both the yield and peak loads, with the reduction in peak load being more pronounced due to the progressive opening of the joint interface.

(3)

The finite-element simulations using the CDP model closely matched the experimental results, accurately reproducing the cracking and crushing behavior of concrete. The findings provide a theoretical foundation and practical reference for improving the shear design and seismic performance evaluation of horizontal joints in prefabricated shear walls.

While the current study uses monotonic loading for initial validation of the bundled reinforcement configuration, we acknowledge that cyclic degradation is an important factor in real-world seismic conditions. Future research will extend this work by incorporating cyclic loading and more complex modeling, including cohesive elements, to investigate the impact of bond degradation and slip behavior at the steel–concrete and grout–concrete interfaces.