Predicting the Tensile Performance of 3D-Printed PE Fibre-Reinforced ECC Based on Micromechanics Model

Abstract

To elucidate the influence of the extrusion-based 3D printing of concrete on the tensile performance of polyethylene fibre-based engineered cementitious composites (PE-ECC), quantitative analyses of reinforcing filament alignment and pore morphology were carried out using backscattered electron (BSE) imaging and X-ray computed tomography (X-CT). A micromechanics analytical model based on microstructural characteristics was further employed to predict the tensile response of additively manufactured PE-ECC. Due to the extrusion process, fibres in 3D-printed PE-ECC were predominantly oriented along the printing path, resulting in a smaller average inclination angle compared with the randomly distributed fibres in cast specimens. Internal pores exhibited elongated flattened ellipsoidal shapes, with more pronounced anisotropy in axial lengths across the three principal directions. Taking the major semi-axis of the equivalent ellipsoidal voids as a representative pore parameter, the analytical model accurately reproduced the cracking strength, stress-strain evolution, and crack pattern of the printed PE-ECC. This extrusion process enhanced multiple cracking capacity and strain-hardening performance by improving fibre orientation, strengthening interfacial bonding, and altering matrix fracture toughness. The integration of micromechanical modelling with experimentally measured microstructural parameters effectively revealed the intrinsic mechanisms underlying the enhanced tensile behaviour of 3D-printed PE-ECC and provides theoretical support for the optimized design of fibre-reinforced cementitious composites in 3D printing.

1. Introduction

As an emerging smart construction technology, 3D printing concrete (3DPC) has been rapidly developing and gradually advancing into practical engineering applications due to its advantages of highly efficient automated fabrication, free-form construction of complex geometries, and high material utilization [1]. Beyond addressing these issues, 3DPC also holds great potential for transforming conventional structural design and construction practices. Through precise control of material deposition and layer geometry, 3DPC enables the design of lightweight and topology-optimized structures with enhanced mechanical efficiency. In addition, the improved printing process control contributes to superior durability and quality consistency, paving the way for large-scale adoption in prefabricated construction and infrastructure rehabilitation. However, during the layer-by-layer deposition process, conventional 3DPC elements inevitably develop weak interlayer interfaces, pore defects, and anisotropic microstructural features arising from the combined effects of printing path, extrusion rate, interlayer time interval, deposition direction, and inherent variations in material rheology. Moreover, the inherent brittleness and crack-prone nature of printable mortars can significantly compromise their mechanical performance and service durability [2,3].

Engineered cementitious composites (ECC) and ultra-high-performance concrete (UHPC) are complementary members of the high-performance cementitious family: ECC is characterized by high tensile ductility (2–8%) and fine crack control (crack widths ≤ ~100 μm) [4,5,6], while UHPC is distinguished by its ultra-high compressive strength (typically ≥150 MPa) [7,8,9,10]. These materials represent different performance orientations: ductility and crack resistance for ECC, and strength for UHPC. ECC follows micromechanics-based pseudo-strain-hardening criteria, using compliant polymer fibres and tailored matrices to achieve distributed cracking and high ductility, which offer an effective solution to the challenges of insufficient toughness and reinforcement difficulties in 3DPC structures [11]. Among fibre-reinforced ECC systems, polyethylene (PE)-fibre ECC (PE-ECC) exhibits outstanding tensile capacity, chemical durability, and interfacial bridging performance. These attributes enable a wider attainable strength spectrum (approximately 40–120 MPa), improved compatibility with extrusion-based 3D printing, and a higher achievable tensile ductility (>4%) compared with conventional polyvinyl-alcohol (PVA) fibre ECC used in 3D-printed concrete [12,13]. Furthermore, the wide strength adaptability of PE-ECC helps mitigate the structural risks associated with interlayer interface weakening during 3D printing. Consequently, 3D-printed PE-ECC has emerged as a research hotspot in recent years.

Current research on 3D-printed engineered cementitious composites (3DP-ECC) has primarily focused on workability, printing processes, and macroscopic mechanical properties. For example, Teng et al. [14] developed a low-carbon ECC suitable for 3DPC by incorporating diatomite as a natural supplementary cementitious material, and found that a 10% replacement significantly improved tensile, compressive, and flexural strengths while enhancing the hydration process. Du and Qian [15] investigated the fracture behaviour of 3DP-ECC under different printing patterns (parallel vs. cross printing) and loading directions (X and Y directions), revealing the pronounced effects of interfacial mismatches on fracture mechanisms, toughness, and energy dissipation. Ye et al. [16] fabricated 3D-printed ECC hollow panels (honeycomb and rectangular hollow sections) to explore the application and performance of self-reinforced lightweight structures in beam–slab systems. Ivaniuk et al. [17] applied printable ECC to the automated construction of spherical shell frame modules, and found that the edge ECC exhibited pronounced strain-hardening behaviour under tensile testing; the uniaxial tensile strength of single-edge specimens was sufficient to carry high loads, and the bond between connectors and ECC interfaces was reliable. Overall, existing studies on 3DP-ECC have mainly emphasized process parameter optimization and macroscopic mechanical performance, whereas systematic investigations into meso-scale mechanisms, such as fibre orientation evolution, anisotropic pore morphology, and interfacial bonding behaviour induced by the printing process, remain lacking.

In terms of modelling, various meso- or multi-scale predictive models for cast ECC have been developed to accurately describe fibre-bridging constitutive behaviour and crack evolution, achieving substantial progress in elucidating strain-hardening mechanisms [18,19]. However, these models are generally built on idealized assumptions of randomly oriented fibres and uniformly distributed pores, and thus cannot directly capture the microstructural heterogeneities introduced by the 3DPC process. Such microstructural features have a decisive influence on the macroscopic tensile properties and cracking patterns of 3DP-ECC. Accordingly, it becomes crucial to develop meso-scale analytical frameworks that couple experimental evidence of fibre alignment and pore morphology, enabling a more realistic interpretation of how the extrusion-based printing process governs mechanical behaviour. In this work, the measured anisotropic fibre orientation and pore geometry induced during 3D printing are directly incorporated into the modelling framework to capture their influence on the material’s tensile response. This integration enables quantitative prediction of tensile behaviour reflecting the unique microstructural heterogeneities of 3D-printed PE-ECC. This approach not only facilitates understanding of the intrinsic mechanisms underlying ductility enhancement in 3DP-ECC but also provides a theoretical basis and predictive tool for optimizing material design and printing process parameters.

Based on the above background, the main objectives of this study are as follows: (1) to systematically and quantitatively characterize the fibre orientation and pore features of cast and 3D-printed engineered cementitious composites using backscattered electrons (BSE) imaging and X-ray computed tomography (X-CT); (2) to incorporate the equivalent elliptical semi-major axis as a pore descriptor into a meso-scale mechanical analysis framework, thereby refining the conventional cracking strength prediction method; and (3) to establish a meso-scale predictive model integrating the experimentally measured microstructural parameters and to validate its accuracy in predicting stress–strain responses, cracking strength, and crack distribution.

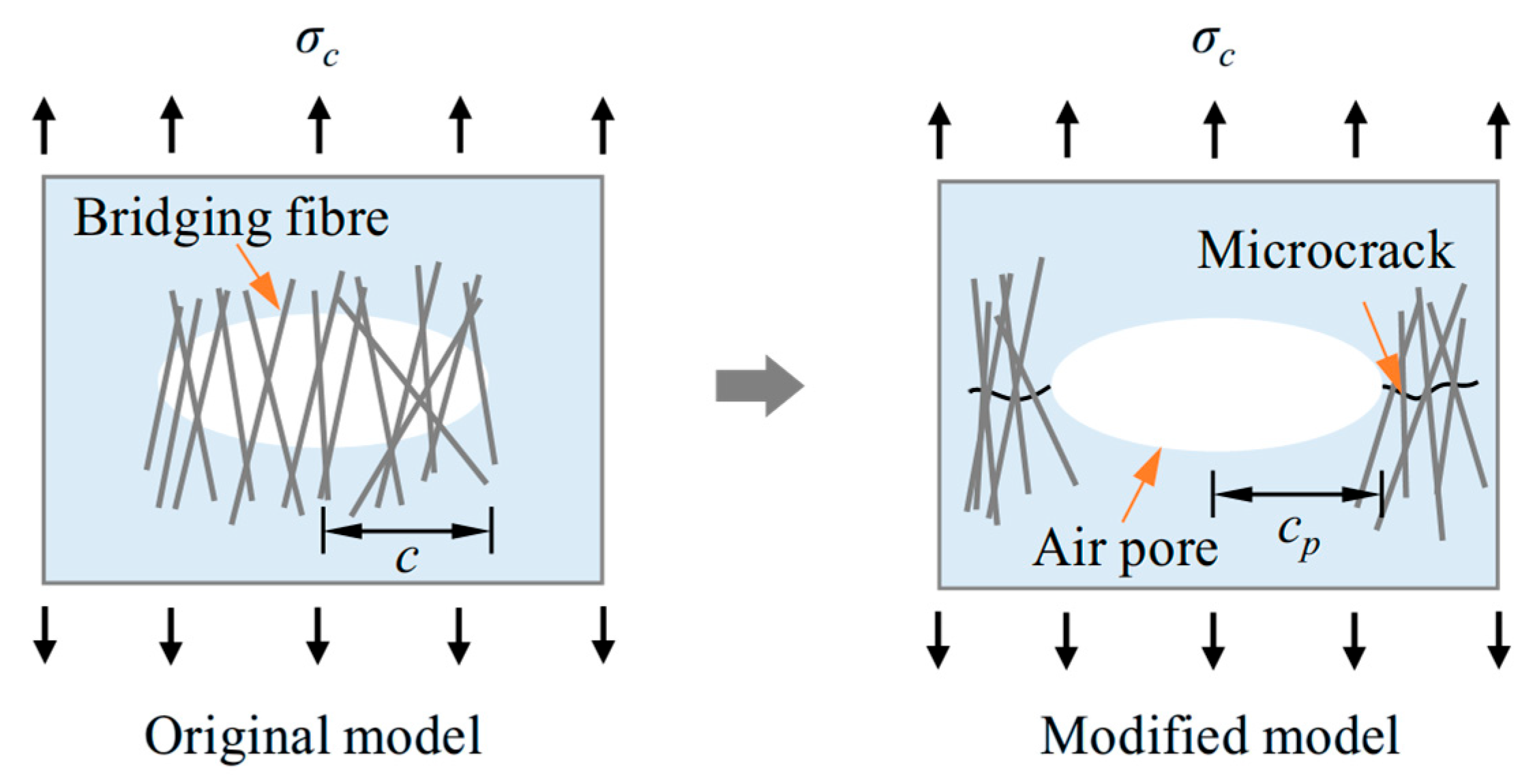
2. Theoretical Basis of the Multiple-Cracking Model

2.1. Cracking Strength

The cracking strength of ECC refers to the critical tensile stress required for the formation of the first through-crack, which is governed by the combined effects of the matrix fracture toughness and the fibre-bridging mechanism. Microcracks typically initiate from pores within the matrix or defects at the aggregate–matrix interface, and then propagate under external loading. Once the crack front reaches the fibres, the fibre bridging force begins to counteract crack propagation [20,21,22].

To describe this process, Li and Leung [23] proposed a fracture mechanics-based analytical framework. The stress intensity factor at the crack tip (K_tip) can be expressed as the superposition of the contribution from the external tensile load (K_L) and that from fibre bridging (K_B). The crack opening displacement $\delta \left(x\right)$ is further related to the elastic modulus of the material and the fracture toughness at the crack tip. Based on this framework, an analytical expression for the cracking strength (${\sigma }_c$) can be derived (Equation (1)).

$${\sigma }_c=g{V}_f\tau \left(l_f/d_f\right)\left[{\displaystyle \frac{\sqrt{\pi }}{2}}{\displaystyle \frac{\overline{K}}{\overline{C}}}+\left({\displaystyle \frac{4}{3}}\sqrt{\overline{C}}-{\displaystyle \frac{1}{2}}\overline{C}\right)\right]/2$$

(1)

where the parameter $g=2(1+e^{{\displaystyle \frac{\pi f}{2}}})/\left(4+f^2\right)$ is identified as the snubbing factor, where f is the empirical snubbing coefficient. $\overline{K}$ represents the ratio between the energy absorbed at the crack tip and that dissipated by fibre bridging, while $\overline{C}$ denotes the normalized crack radius at peak opening displacement. The interfacial frictional bond strength is expressed as τ, and l_f, d_f, and V_f refer to the fibre length, diameter, and volume fraction, respectively.

Considering that a substantial number of pores within ECC are not intersected by fibres, the original analytical formulation was refined by introducing a correction to the integration domain of K_L, thereby accounting for the effect of the nominal initial pore size (c_p) on the calculated cracking strength (see Figure 1). The modified model is expressed in Equation (2) and can more accurately capture the effects of pore size and crack propagation on ${\sigma }_c$.

$${\sigma }_c\left(c, c_p\right)=g{V}_f\tau \left(l_f/d_f\right)\left[{\displaystyle \frac{\sqrt{\pi }}{2}}{\displaystyle \frac{\overline{K}}{\overline{C}\sqrt{\left(c+c_p\right)/c}}}+\left({\displaystyle \frac{4}{3}}\sqrt{\overline{C}}-{\displaystyle \frac{1}{2}}\overline{C}\right)\right]/2$$

(2)

In the numerical implementation, the 80 mm gauge length of the tensile specimen is divided into n discrete segments, where the coordinate of each segment is represented by n_i (i = 1, 2, …, n). It is assumed that the failure of each segment is governed by the largest pore within that segment [24], and the pore size is measured using X-CT. The local fibre volume fraction is assumed to be linearly related to porosity. For the n-th segment, a coefficient ξ_n is introduced to quantify the relationship between the effective interfacial frictional bond strength (τ_effn) and the initial bond strength (τ₀), assuming that the interfacial bond strength decreases linearly with the reduction in fibre volume fraction (Equations (3) and (4)). Based on these assumptions, a unified link between pore structural characteristics and local mechanical parameters can be established, enabling the quantitative calculation of cracking strength σ_c for each segment.

$${\tau }_{effn}={\tau }_0·{\xi }_n$$

(3)

$${\xi }_n=-\gamma ·V_{fn}+1$$

(4)

Here, V_fn denotes the local fibre volume fraction in the n-th segment (typically not exceeding 2% in ECC), and γ represents the attenuation coefficient governing the interfacial frictional bond strength.

2.2. Bridging Stress–Crack Opening Relationship

In ECC, the fibre pullout behaviour governs the evolution of the bridging stress across the crack surface (σ_b) with respect to the crack opening displacement (δ). The pullout process consists of a debonding stage and a sliding stage. In the debonding stage, both chemical bonding and frictional resistance at the fibre–matrix interface counteract crack opening, and the pullout force P_d(δ) can be described by Equations (5) and (6). For hydrophobic polyethylene (PE) fibres, the interfacial chemical bond strength (G_d) is effectively negligible; hence, the complete debonding displacement (δ₀) primarily depends on the interfacial frictional resistance and the fibre embedment length (L_e).

$$P_d\left(\delta \right)=2\pi \sqrt{{\displaystyle \frac{{\tau }_0{E}_f{d}_f^3\left(1+\eta \right)}{2}}\delta +{\displaystyle \frac{G_d{E}_f{d}_f^3}{2}}},0\le \delta \le {\delta }_0$$

(5)

$${\delta }_0={\displaystyle \frac{2{\tau }_0{L}_e^2\left(1+V_f{E}_f/V_m{E}_m\right)}{E_f{d}_f}}$$

(6)

After entering the sliding stage, friction becomes the dominant factor. Assuming a linear relationship between friction and slip distance, a slip-hardening coefficient β can be introduced to modify the pullout force P_p(δ). The fibre inclination angle has a significant effect on the apparent bridging force P(θ), which is commonly corrected using a “snubbing effect” coefficient f [25]; the force diagram of a fully deboned, inclined short fibre is shown in Figure 2. P(0) denotes the apparent bridging force of a fibre oriented perpendicular to the crack surface. In addition, a strength reduction coefficient f’ is introduced to account for the reduction in effective strength of inclined fibres [26,27].

Under the condition of randomly distributed multiple fibres, the contributions of all individual fibres are integrated to obtain the relationship between the bridging stress σ_b(δ) and the crack opening displacement δ (Equation (7)). The spatial distribution p(z) and inclination angle distribution p(θ) of fibres are given by Equations (8) and (9), respectively [27,28,29]. This relationship provides a meso-scale mechanical basis for the strain-hardening behaviour of ECC.

$${\sigma }_b\left(\delta \right)=V_f{\int }_0^{\pi /2}{\int }_0^{\left(l_f/2\right)cos\theta }\sigma (\delta ,\theta ,z)p\left(z\right)p\left(\theta \right)dzd\theta$$

(7)

$$p\left(z\right)={\displaystyle \frac{1}{l_f}},-{\displaystyle \frac{l_f}{2}}\le z\le {\displaystyle \frac{l_f}{2}}$$

(8)

$$p\left(\theta \right)={\displaystyle \frac{{\{sin\theta \}}^{2r-1}{\{cos\theta \}}^{2q-1}}{{\int }_{{\theta }_{\mathit{min}}}^{{\theta }_{\mathit{max}}}{\{sin\theta \}}^{2r-1}{\{cos\theta \}}^{2q-1}d\theta }}$$

(9)

Here, z denotes the distance from the fibre centroid to the crack plane; r and q are experimentally derived shape parameters; and θ_min and θ_max represent the theoretical lower and upper limits of fibre inclination.

2.3. Multiple Cracking Sequence Based on Stress Transfer Mechanism

The stress transfer distance (x_d) represents the characteristic length over which the load carried by the bridging fibres across a crack is completely transferred back to the surrounding matrix through interfacial shear stress. Within this zone, the tensile stress of the matrix remains below its ultimate tensile capacity, thereby preventing the initiation of new cracks. Li et al. [30] proposed a model that incorporates fibre pullout friction, the snubbing effect, and matrix stress under force equilibrium conditions (Equation (10)), which is suitable for describing the stress transfer mechanism of randomly oriented fibres in polyethylene fibre-reinforced engineered cementitious composites (PE-ECC).

$$\int \pi d_f\tau \left(\delta \right)kp\left(z\right)p\left(\theta \right)dzd\theta +\int P\left(\delta \right)\left(e^{f\theta }-\cos \theta \right)p\left(z\right)p\left(\theta \right)dzd\theta ={\sigma }_{mu}{V}_m\times 1\times 1$$

(10)

In this model, the parameter $k=min\left\{x_d,{\displaystyle \frac{l_f}{2}}\cos \theta -z\right\}$ serves to differentiate conditions in which the fibre embedment length (L_e) exceeds or falls below the stress transfer distance (x_d), thereby governing the effective load transfer mechanism along the fibre–matrix interface. The interfacial frictional bond strength evolves with the crack opening displacement and can be expressed as $\tau \left(\delta \right)={\tau }_0\left(1+\beta \left(\delta -{\delta }_0\right)/d_f\right)$, reflecting the gradual increase in shear resistance caused by slip hardening during fibre pull-out. In practical computation, τ₀ is replaced by the effective bond strength ${\tau }_{effn}$ corresponding to each cracked region, as defined in Equation (3). Furthermore, ${\sigma }_{mu}$ denotes the tensile stress sustained by the matrix, while $V_m$ represents its volume fraction within the composite.

The above multiple-cracking model establishes a complete theoretical framework through three components: cracking strength evaluation, bridging stress constitutive behaviour, and stress transfer mechanism. Its core lies in incorporating fibre orientation, pore structure, and interfacial bonding parameters into the predictive formulations, thereby enabling meso-scale interpretation of the strain-hardening behaviour of ECC and providing a foundation for subsequent predictive modelling of 3DP-ECC based on experimentally measured microstructures.

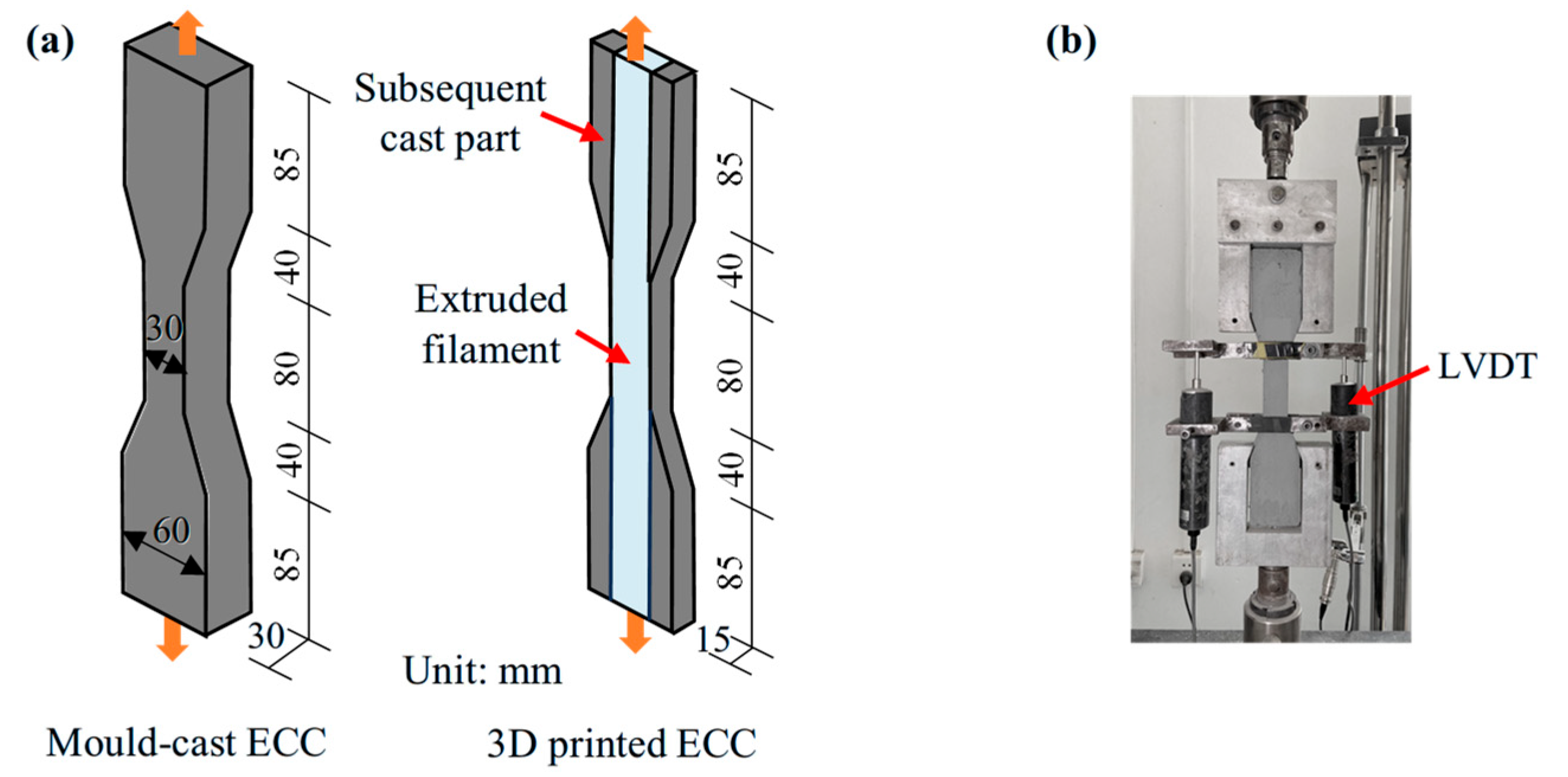
3. Uniaxial Tensile Test of 3D-Printed PE-ECC

The materials employed in this study comprised ordinary Portland cement (OPC, P·Ⅱ 52.5), sulfoaluminate cement (SAC), undensified silica fume (SF, grade 955), Class I fly ash (FA), and quartz sand with an average particle size of approximately 100 μm. Hydroxypropyl methylcellulose (HPMC, viscosity 38,000–42,000 mPa·s), water, and a polycarboxylate-based superplasticizer (water reduction ratio of 34%) were also incorporated. Short-cut ultra-high-molecular-weight polyethylene (PE) fibres served as the reinforcement phase. The binder composition followed a mass ratio of OPC:SAC:SF:FA = 0.38:0.05:0.09:0.48. The detailed mixture proportions for both the cast and 3D-printed ECC systems are listed in

Table 1. Mix design parameters for conventionally cast and 3D-printed PE-ECC (wt.%).

No.	Thickness (mm)	Binder Materials	Sand	Water	Superplasticizer	HPMC	PE Fibre
Cast-ECC	30	1	0.26	0.26	0.001	0.0004	6 mm (1.5%) and 12 mm (0.5%)
3DP-ECC	15	1	0.26	0.26	0.001	0.0004	6 mm (1.5%) and 12 mm (0.5%)

Note: Fibre content is presented as volume fraction.

. A hybrid PE fibre system comprising 6 mm and 12 mm fibres, incorporated at volume fractions of 1.5% and 0.5%, respectively, was employed to achieve an optimal balance among printability, tensile capacity, and strain-hardening behaviour. This design was mainly based on two considerations: (1) the total fibre content of normal ECC typically remains around 2% to ensure strain-hardening behaviour and uniform dispersion, and (2) in the 3D printing extrusion process, using only 12 mm fibres tends to cause nozzle blockage, while using only 6 mm fibres results in insufficient crack-bridging capacity.

The 3D-printed ECC specimens were fabricated using a gantry-based 3D concrete printing system with an overall build volume of 3 m × 2 m × 3 m. The printer was fitted with a rectangular extrusion nozzle measuring 30 mm × 16 mm, designed to ensure a stable extrusion flow and accurate layer deposition. During the printing process, the travel speed of the printhead and the material extrusion rate were maintained at 110 mm/s and 110 g/s, respectively, to achieve uniform filament continuity and prevent layer collapse or interfacial discontinuities. Both the conventionally cast and 3D-printed ECC mixtures were prepared using a 20 L planetary mixer to ensure consistent material quality. The mixing protocol was carefully controlled to promote homogeneity and avoid fibre agglomeration. Initially, the dry constituents (ordinary Portland cement, sulfoaluminate cement, silica fume, fly ash, and quartz sand) were pre-mixed at a rotational speed of 140 rpm for 2 min to achieve even dispersion of the powder phases. Subsequently, water and a polycarboxylate-based superplasticizer were gradually added to the mixture and blended at the same speed for an additional 3 min to ensure complete wetting and flowability adjustment. Hydroxypropyl methylcellulose (HPMC) was then incorporated as a viscosity-modifying agent, and mixing continued for 1 min at 140 rpm to enhance the extrusion stability of the fresh paste. Finally, short-cut ultra-high-molecular-weight polyethylene (PE) fibres were progressively introduced into the matrix and dispersed at a higher mixing speed of 420 rpm. This high-shear stage ensured uniform fibre orientation and distribution without fibre clustering, which is critical for achieving reproducible mechanical properties in both cast and printed ECC. The resulting mixtures exhibited satisfactory printability and cohesion, forming smooth, continuous filaments suitable for layer-by-layer deposition, and were either cast into moulds and compacted by vibration to produce cast ECC specimens or fed into the printer hopper to fabricate 3D-printed ECC specimens.

According to the Chinese standard JC/T 2641-2018 [31], dog-bone-shaped specimens were prepared for 28-day uniaxial tensile testing, as shown in Figure 3.

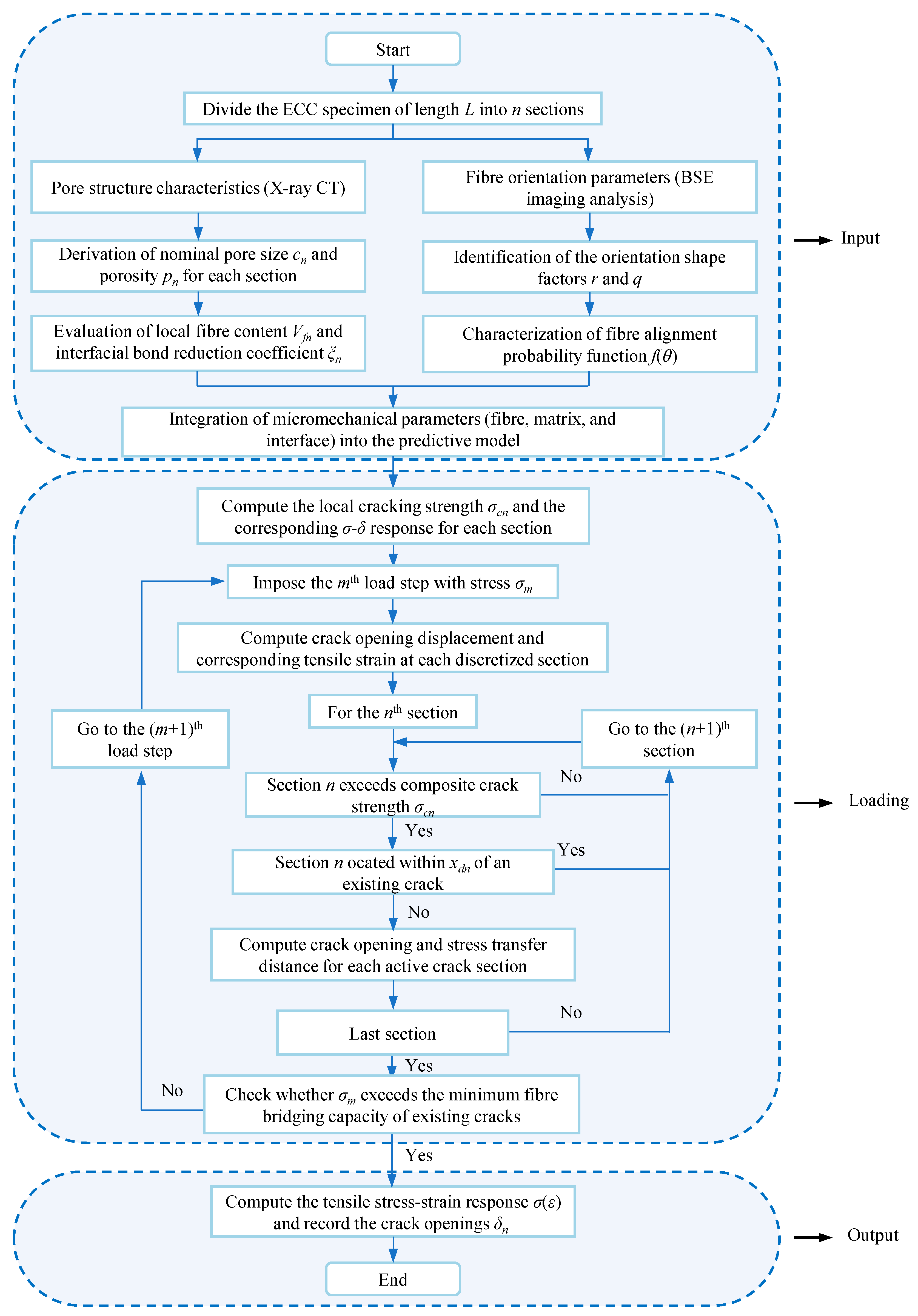
4. Quantification of Micromechanical Parameters for Model Implementation

For reliable simulation of the fibre bridging stress and crack opening displacement (σ-δ response) of 3D-printed ECC, a comprehensive set of micromechanical input parameters must be determined. These parameters collectively describe the fibre, matrix, and interfacial behaviours governing tensile response.

The cracking strength was obtained from direct tensile tests, and the matrix fracture toughness was subsequently derived. Experimental results showed that the fracture toughness of the ECC matrix was 0.118 MPa∙m^1/2, and its elastic modulus (E_m) was 18 GPa. The interfacial interaction parameters between fibre and matrix were quantified through a series of single-fibre pull-out experiments using axially aligned PE fibres. From these tests, the key micromechanical indicators, including the initial frictional bond strength (τ₀), the interfacial chemical adhesion energy (G_d), and the slip-hardening coefficient (β), were extracted by fitting the measured load–displacement curves. The experimental analysis revealed that the interfacial frictional bond strength between the PE fibres and the cementitious matrix was around 1.16 ± 0.3 MPa, whereas the corresponding slip-hardening coefficient averaged 0.004, with a standard deviation of 0.00028, indicating relatively stable interfacial performance across specimens. In addition, samples were taken from the gauge section of printed specimens after tensile testing to prepare BSE images. Based on the cross-sectional images, the fibre orientation distribution was calculated using Equation (9) (see Figure 4). The detailed experimental procedures and calculation methods are provided in [32,33]. The complete set of micromechanical parameters is listed in

Table 2. Set of micromechanical parameters.

	Preparation Method	Micromechanical Parameters	Observations
Fibre	Casting and 3D Printing	lf (mm)	6 and 12 a
	Casting and 3D Printing	df (μm)	23.86 ± 4.44 b
	Casting and 3D Printing	Elastic modulus, Ef (GPa)	110 a
	Casting and 3D Printing	Tensile strength, σfu (MPa)	3000 a
	Casting and 3D Printing	Gd (J/m2)	0 c
	Cast-ECC	(r, q)	r = 5, q = 3.8 d
	3DP-ECC	(r, q)	r = 1.7, q = 4.3 d
Matrix	Casting and 3D Printing	Em (GPa)	18 b
	Casting and 3D Printing	Ktip (MPa∙m1/2)	0.118 b
	Casting and 3D Printing	Poisson’s ratio, v	0.2 b
Interface	Cast-ECC	τ0 (MPa)	1.16 ± 0.3 b
	3DP-ECC	τ0 (MPa)	1.4 e
	Casting and 3D Printing	β	0.004 b
	Casting and 3D Printing	f	0.65 f
	Casting and 3D Printing	f’	0.50 g
	Casting and 3D Printing	γ	21 h

Note: ^a—manufacturer-specified standard fibre parameters; ^b—values determined through experimental testing; ^c—considered negligible owing to the hydrophobic surface characteristics of PE fibres; ^d—calculated using Equation (9) based on experimental data; ^e—assumed values based on experimental observations; ^f—from Li et al. [34]; ^g—from Li et al. [35]; ^h—assumed value.

.

5. Tensile Performance Prediction of 3DP-ECC

Figure 5 illustrates the analytical framework employed to simulate the multiple-cracking behaviour of 3DP-ECC based on the proposed meso-mechanical model.

5.1. Cracking Strength Calculation

Figure 6a presents the initial pore size distributions of both cast and 3D-printed ECC specimens, as determined from X-CT analysis, revealing distinct differences in their internal void structures. Utilizing the established linear correlation between total porosity and fibre dosage, the local fibre volume fraction across different cross-sectional layers was subsequently derived, as shown in Figure 6b. The two-dimensional porosity of cast ECC ranged from 0.38% to 7.99%, while that of 3D-printed ECC ranged from 0.07% to 4.58%. More cross-sections of 3D-printed ECC were found within the 1–2% porosity range. A continuous fluctuation in local fibre volume fraction was observed among adjacent cross-sections, indicating a non-uniform yet statistically stable fibre distribution. The average fibre content for both casting and printing processes remained around 2%, aligning well with the target overall fibre dosage used in material preparation. By substituting the measured parameters into Equations (2)–(4), the cracking strength of each cross-section was then calculated.

The backscattered electrons (BSE) imaging results showed that the fibre orientation parameters (r, q) of 3D-printed ECC were (1.7, 4.3), indicating a much more aligned distribution than the random distribution observed in cast ECC. The cast specimens exhibited an average fibre inclination angle of 47.7°, which was approximately 58% greater than that measured in the printed specimens (see Figure 7). This indicates that the extrusion-based printing process effectively enhances fibre alignment along the tensile loading direction. As confirmed by mechanical testing, the 3D-printed ECC achieved a higher ultimate tensile strength (5.40 ± 0.29 MPa) compared with the cast counterpart (4.35 ± 0.27 MPa). Therefore, in the prediction process, the initial interfacial frictional bond strength of printed ECC was increased from the experimentally measured average of 1.16 MPa to near the upper bound of 1.4 MPa. Based on the measured initial cracking strength of the printed specimens, the matrix fracture toughness was set to evenly spaced values of 0.100, 0.109, 0.118, and 0.127 MPa·m^1/2. The initial interfacial frictional bond strength was fixed at 1.4 MPa, while the matrix fracture toughness took the aforementioned values. The other meso-mechanical parameters are listed in Table 2.

Figure 8 shows the X-CT slices of cast ECC and interlayered 3D-printed ECC. The pores in cast ECC were randomly distributed and generally regular in shape, whereas numerous elongated strip-like pores were observed inside the printed ECC, and their volumes depended on the degree of fusion between adjacent filaments. Insufficient fusion tended to produce large through-pores, while well-fused regions contained discontinuous slender pores. Large pores at the interfacial zones were mostly aligned along the printing direction (x-axis), whereas smaller pores were predominantly distributed within the filament interiors. Figure 9 further presents the pore axial length distributions along the three principal directions, showing a consistent trend of x-axis > y-axis > z-axis. Compared with cast ECC, 3D-printed ECC exhibited more pronounced pore anisotropy, with pores elongated along the extrusion direction and thinned along the deposition direction as their volume increased. These differences highlight the significant influence of different forming processes on microstructural characteristics. Overall, the pores in both types of specimens were closer to ellipsoids rather than spheres; therefore, the semi-major axis of the 2D projected ellipse should be used as the representative pore size when predicting the cracking strength of 3D-printed PE-ECC.

Using the equivalent elliptical semi-major axis and the equivalent circular radius as pore size inputs, the initial cracking strength of 3D-printed ECC was calculated under different matrix fracture toughness values (see Figure 10). The results showed that the predicted values obtained using the elliptical semi-major axis method were consistently lower than those from the circular radius method, and the difference increased with matrix fracture toughness (from 0.20 to 0.27). Compared with the experimental results, when the fracture toughness was set to 0.1 or 0.109 MPa·m^1/2, the initial cracking strength predicted by the elliptical semi-major axis method fell within the experimental range and matched well with the measured values, verifying the validity of this method for predicting the macroscopic tensile property (initial cracking strength).

5.2. Stress–Strain Curve Prediction

Figure 11a compares the predicted and experimental uniaxial tensile stress–strain curves of 3D-printed PE-ECC. Experimentally, the ultimate tensile strength (σ_tu) of the printed PE-ECC was 5.40 ± 0.29 MPa, the ultimate tensile strain (ε_tu) was 5.22 ± 0.84%, and the crack number (Nc) was 70 ± 6.

The model predictions covered not only the initial cracking strength but also the ultimate tensile strength, ductility, and crack number under different matrix fracture toughness values. The ultimate tensile strength remained almost constant at 5.75–5.76 MPa, while the tensile ductility decreased from 6.72% (at K_m = 0.1 MPa·m^1/2) to 3.27% (at K_m = 0.127 MPa·m^1/2). Correspondingly, the crack number decreased from 123 to 58. These results indicate that, when the fibre content, fibre orientation, and initial interfacial frictional bond strength are fixed, the minimum fibre bridging capacity at the interface remains essentially unchanged, and the variation in ductility is mainly governed by the matrix fracture toughness. When τ₀ =1.4 MPa and K_m = 0.109 MPa·m^1/2, the predicted curve showed good agreement with the experimental mean values, confirming the reliability of the model.

Based on the experimentally measured meso-scale parameters of cast ECC and selected parameters of 3D-printed ECC, the modified predictive model proposed in this study can also be used to inversely estimate the feasible ranges of matrix fracture toughness and interfacial frictional bond strength for printed ECC. This approach reduces the experimental testing effort and helps validate the parameter rationality.

To quantify the uncertainty of the model predictions, a series of 10 Monte Carlo simulation runs was conducted for each set of interfacial frictional bond strength values, and the average minimum bridging strength was taken as the representative value. The variability mainly arises from the experimental determination of fibre orientation, local heterogeneity in pore morphology and matrix fracture toughness, as well as simplifications in the interfacial bond modelling. Figure 11b shows the crack patterns of a typical 3D-printed PE-ECC specimen, where variations in crack locations and widths can be observed, mainly due to the nonuniformity in pore size and local fibre distribution.

Figure 12 and Figure 13 present the crack formation sequence and crack width distribution at the ultimate tensile strength of 3D-printed PE-ECC. The results showed that the average crack width varied little (approximately 43–45 μm) across different matrix fracture toughness levels, while the crack number was strongly governed by the fracture toughness. Specifically, when the matrix fracture toughness K_tip was 0.1, 0.109, 0.118, and 0.127 MPa∙m^1/2, the predicted crack widths were 43.7 ± 7.0 μm, 43.9 ± 7.3 μm, 43.4 ± 6.4 μm, and 45.1 ± 9.6 μm, respectively, while the corresponding crack numbers were 123, 105, 75, and 58. When the fibre orientation parameters changed from (r, q) = (5, 3.8) to (1.7, 4.3), that is, the average fibre inclination angle decreased from 47.7° to 30.2°, and the number of cracks in printed ECC increased significantly. Meanwhile, the average crack width rose from 32.9 ± 7.2 μm (cast PE-ECC) to 43.7 ± 7.0 μm (printed PE-ECC, using K_m = 0.1 MPa·m^1/2 as an example), while remaining at a similar level compared with the cast specimens.

In summary, the differences in tensile performance between 3D-printed PE-ECC and cast PE-ECC primarily arise from variations in fibre orientation, interfacial frictional bond strength, and matrix toughness. The higher ductility observed in the printed specimens is not only attributed to their smaller fibre inclination angles, but also related to the enhanced interfacial frictional bonding and reduced matrix toughness induced by the extrusion process. If the matrix toughness remains constant, increasing the interfacial frictional strength alone would actually decrease ductility, resulting in lower tensile ductility in printed ECC than in cast ECC.

According to the meso-scale design principles of ECC, the coupling effect of interfacial enhancement and reduced matrix toughness prevents excessive cracking strength from suppressing crack propagation, thereby shortening the stress transfer distance, promoting the formation of more cracks, and ultimately producing a more pronounced multiple-cracking behaviour. Therefore, the strength and ductility of ECC are the combined outcomes of multiple meso-scale factors. To achieve specific design targets, performance optimization can be realized by adjusting the interfacial frictional bond strength, tailoring fibre parameters, or introducing artificial defects to modify the matrix toughness.

The present micromechanical model assumes that the effective interfacial bond strength linearly decays with decreasing local fibre content [19,36]. However, in practice, the relationship between interfacial bond and fibre content is likely nonlinear. Furthermore, the equivalent elliptical pore model statistically captures the pore anisotropy and interconnectivity induced by the 3D printing process. However, when extended to multi-layer structural elements, further improvement, such as incorporating micromechanical parameters related to interfacial pores, is required to enhance the model’s scalability and predictive accuracy. This model is thus applicable to the performance prediction of short PE fibre-reinforced 3D-printed ECC, whereas extending it to PVA, basalt, or steel fibre-reinforced composites would require recalibration of interfacial parameters and incorporation of distinct fracture mechanisms.

6. Conclusions

This study compared the fibre orientation and pore structural characteristics of mould-cast and 3D-printed PE-ECC, and predicted their tensile behaviour using experimentally measured data combined with an improved micromechanics analytical model, thereby revealing the intrinsic mechanism by which the 3D printing process enhances material ductility. The main conclusions are as follows:

(1)

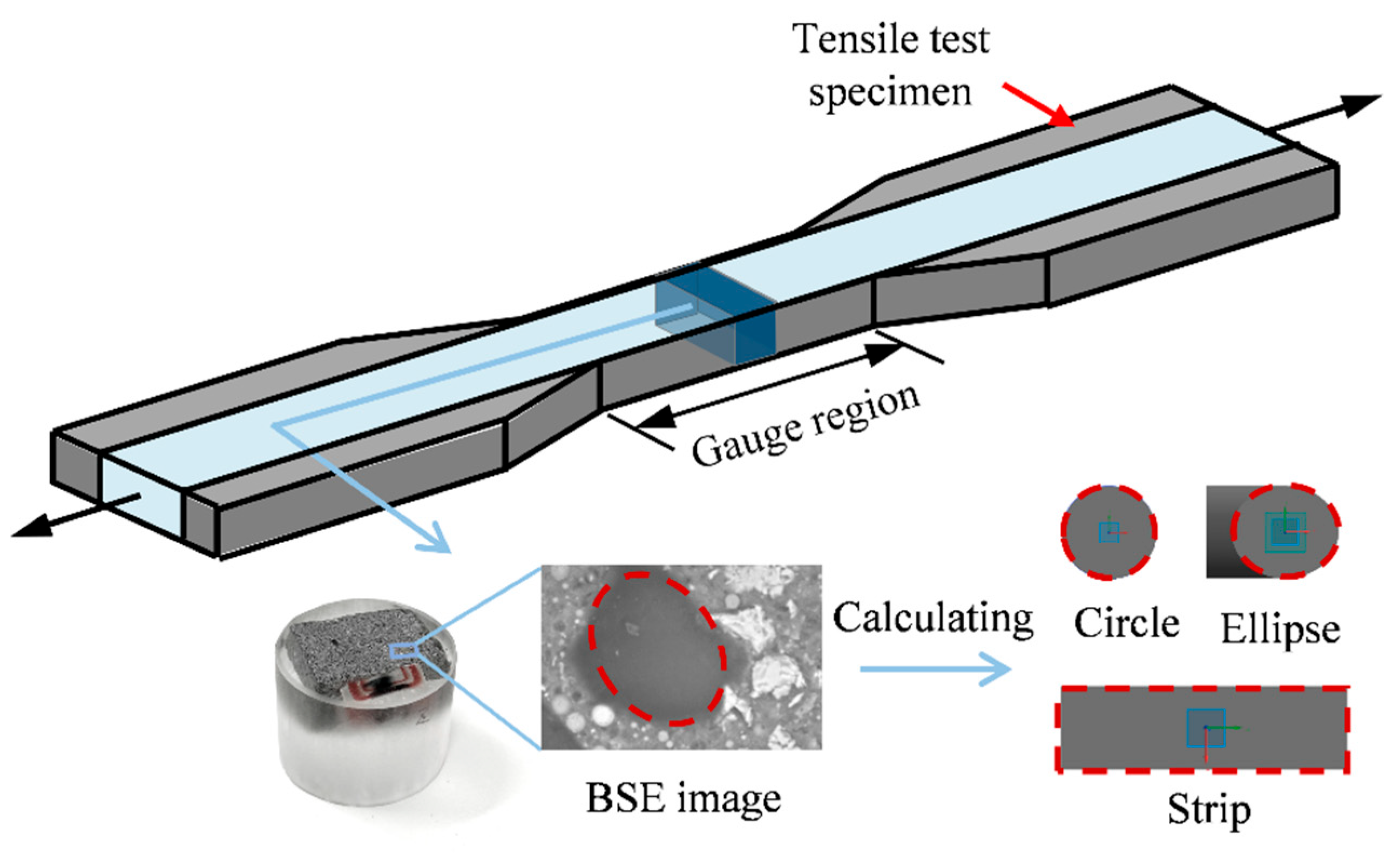
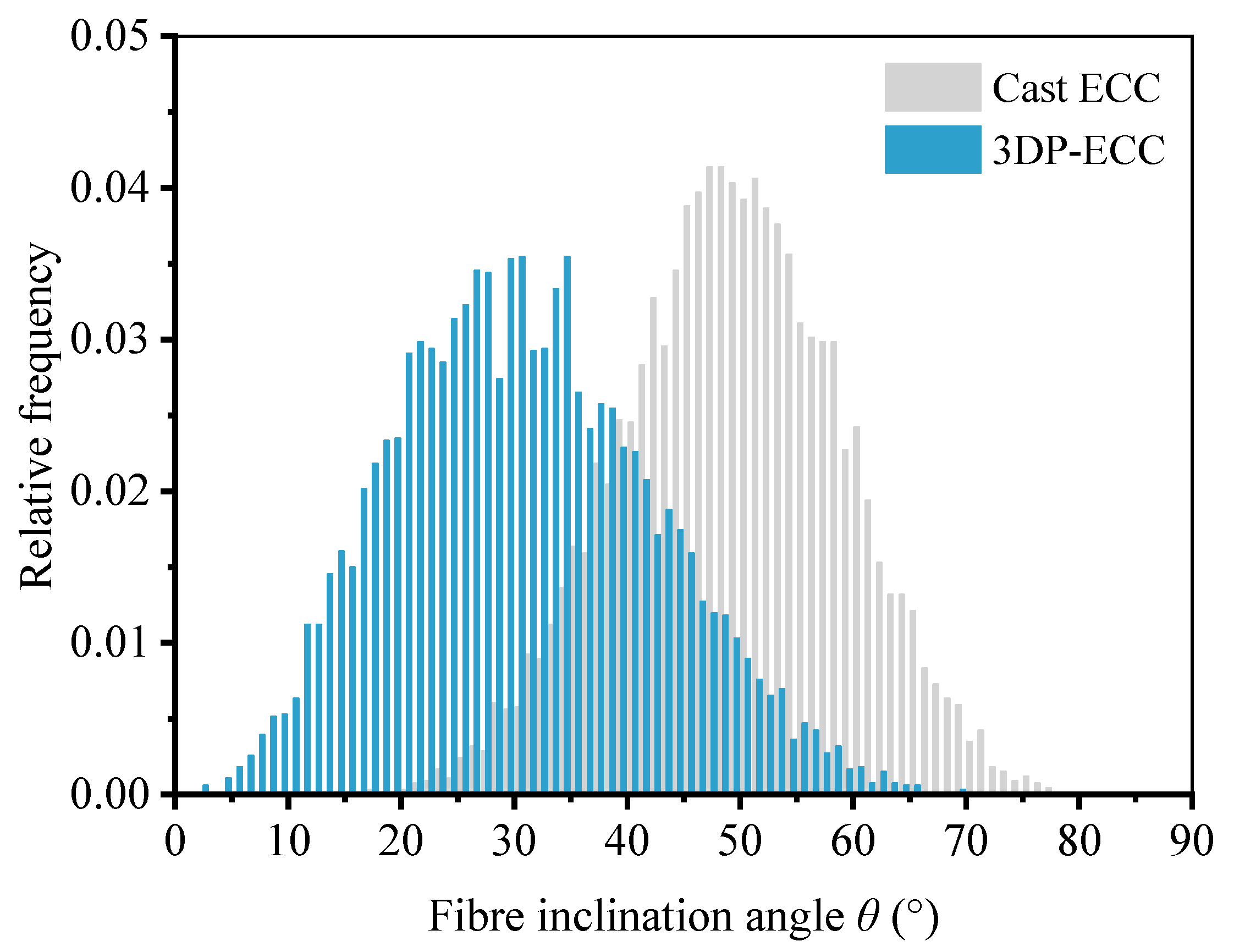
BSE image analysis showed that the average fibre inclination angle of cast ECC was 47.7°, about 58% higher than that of 3D-printed ECC, indicating that the printing process promotes fibre alignment along the loading direction, thereby improving fibre utilization efficiency.

(2)

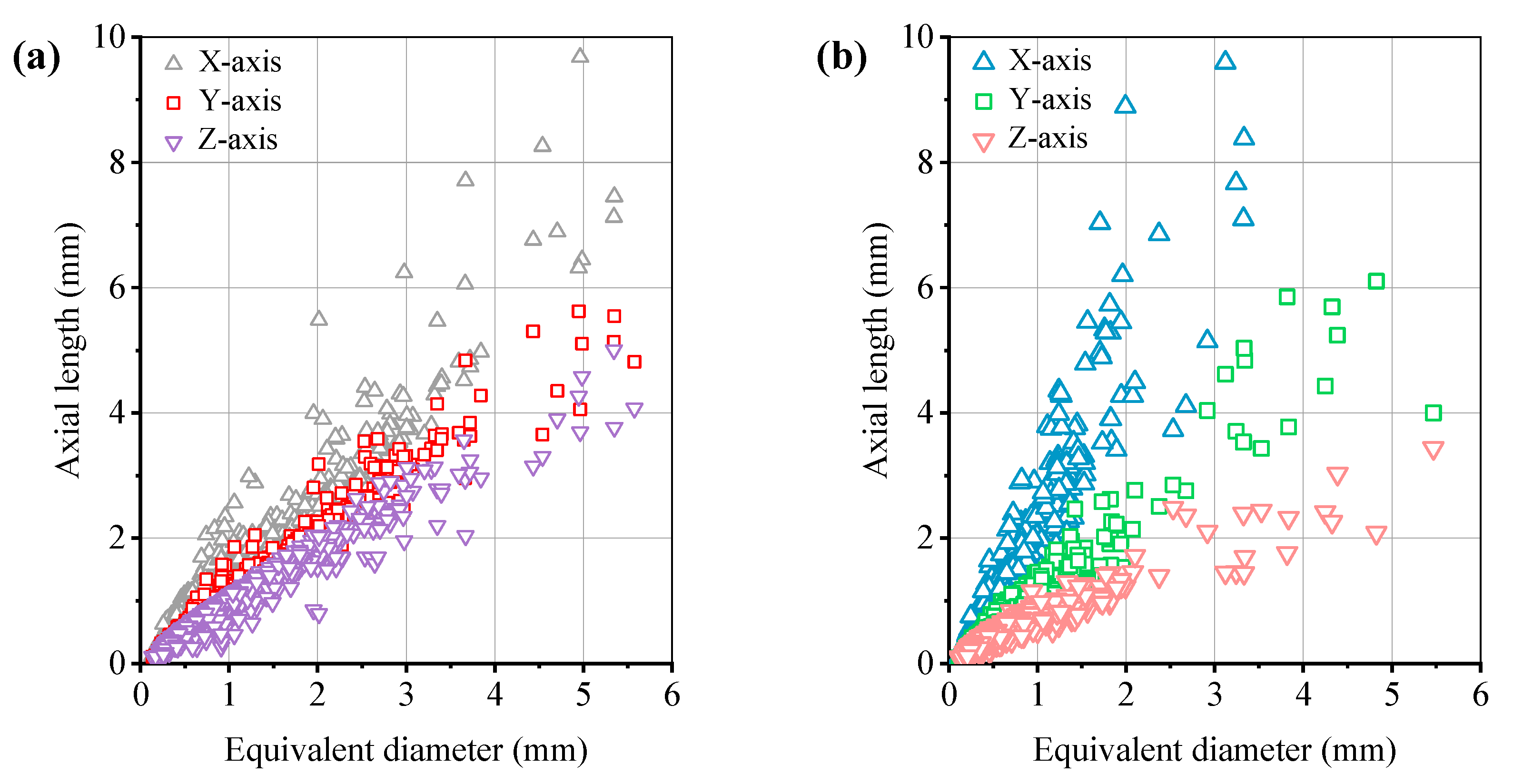
X-CT scanning revealed that the pore axial lengths in both types of ECC followed the trend x-axis > y-axis > z-axis. Compared with cast ECC, 3D-printed ECC exhibited more pronounced pore anisotropy, with pores shaped more like elongated flattened ellipsoids. Therefore, using the equivalent elliptical semi-major axis as the characteristic pore size is more appropriate for predicting tensile behaviour.

(3)

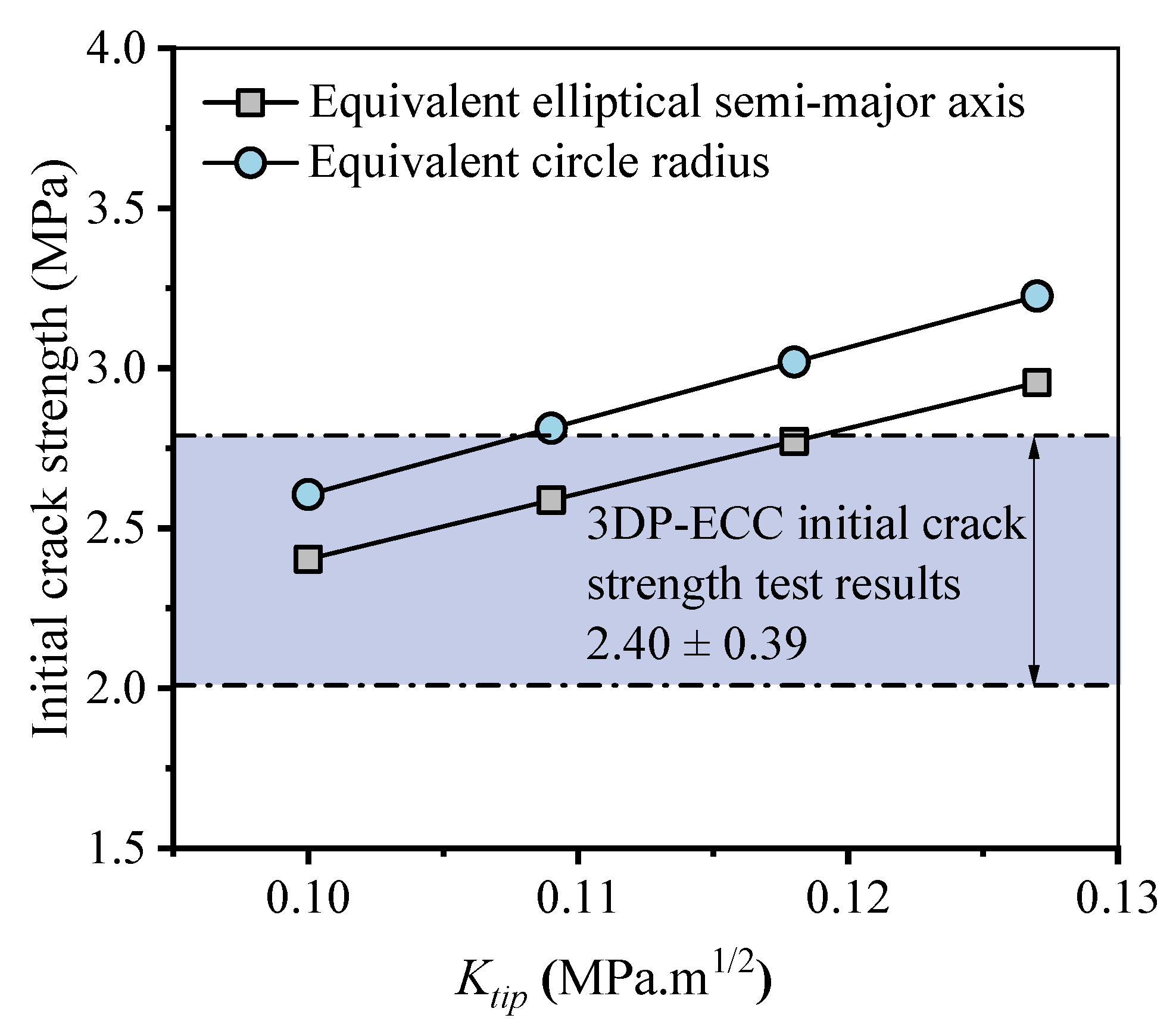
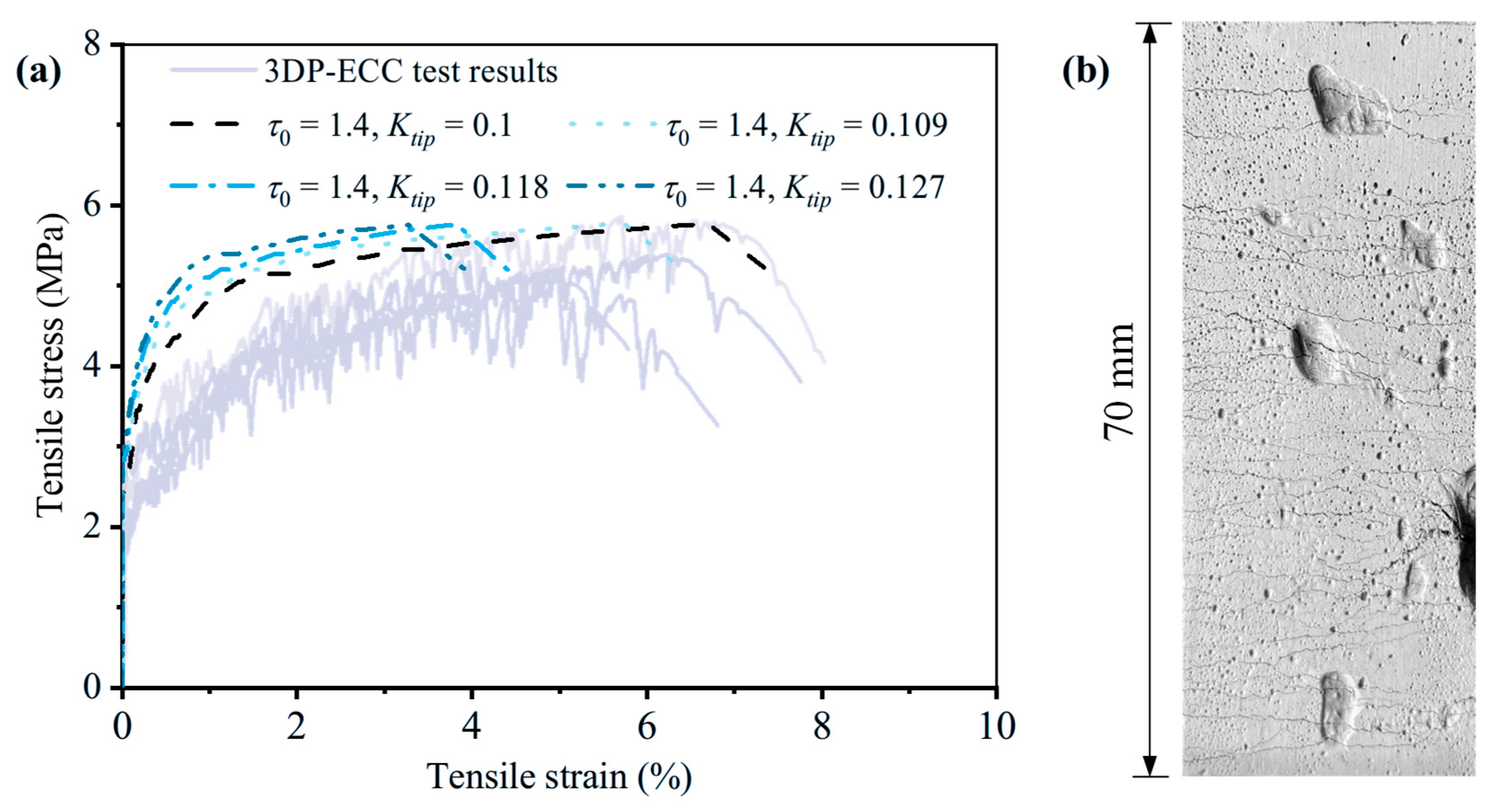
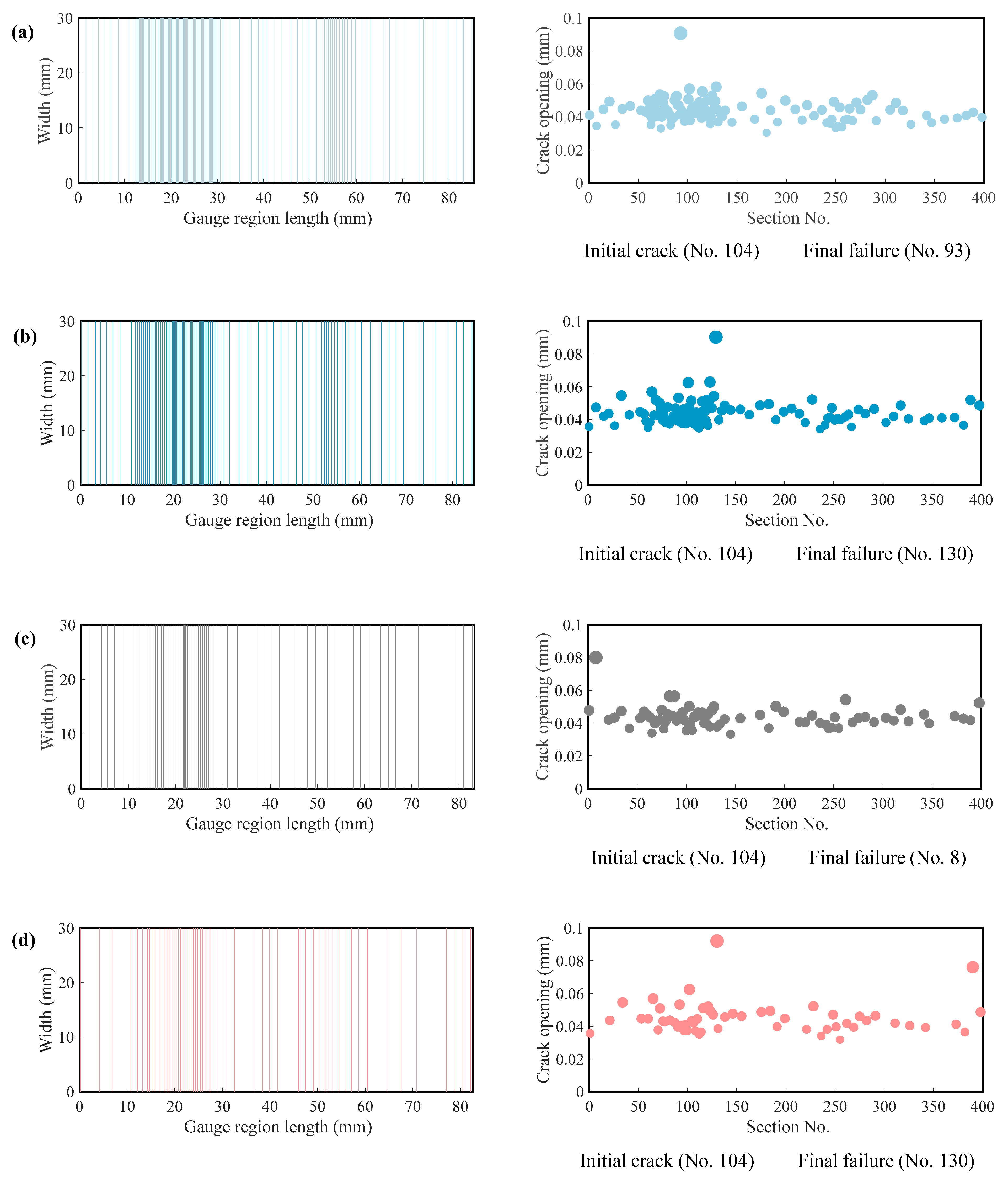
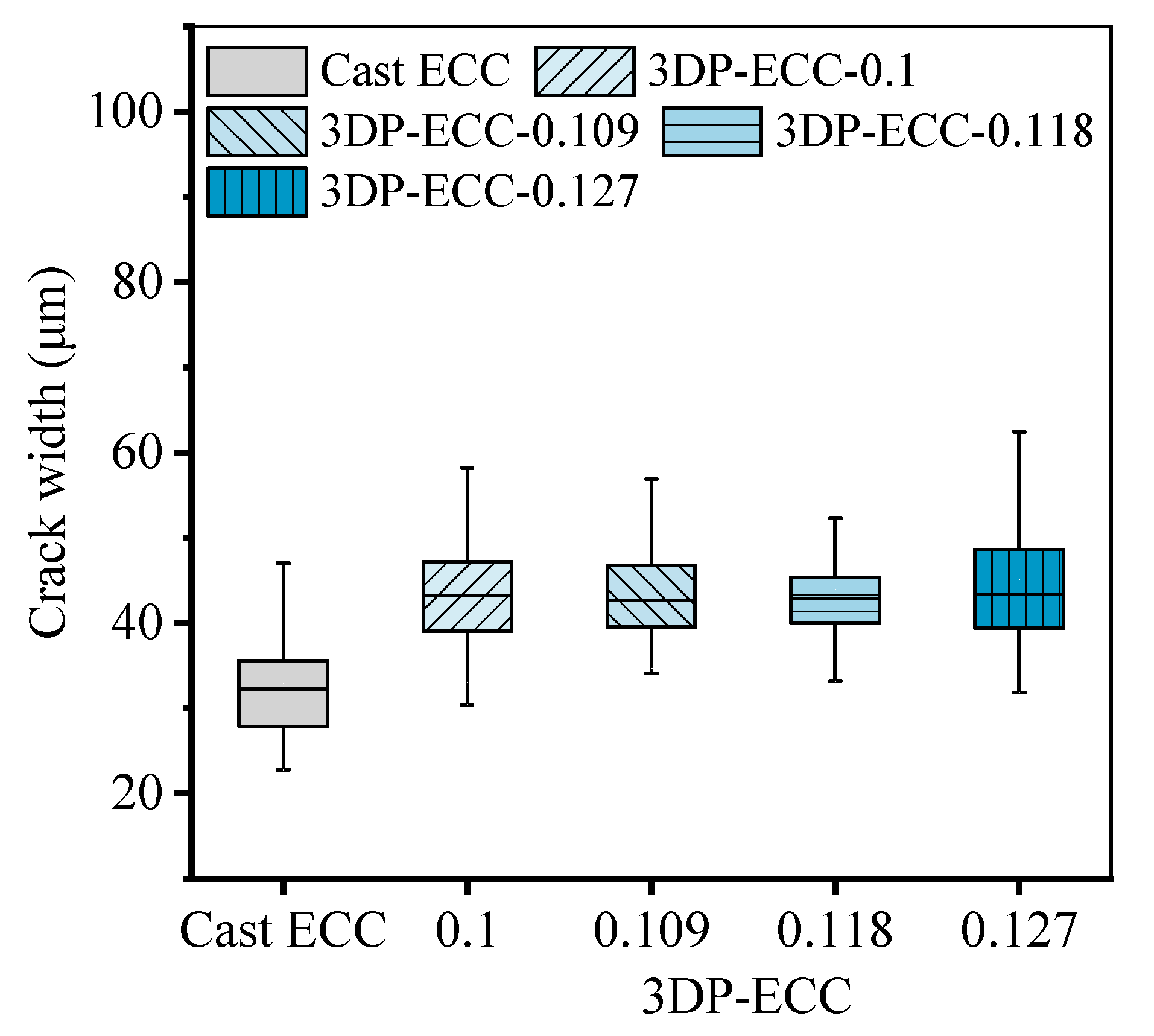
The stochastic predictive model established based on the measured microstructural parameters successfully captured the cracking sequence, stress–strain curves, and crack width distribution of 3D-printed ECC. By incorporating pore morphology into an equivalent elliptical model, the predicted cracking strength showed excellent agreement with the experimental results, validating the effectiveness of the microstructural parameters in tensile performance prediction.

(4)

The 3D printing process enhanced the interfacial bonding to some extent, which helped maintain the multiple-cracking behaviour and improve strain-hardening capacity. The superior ductility of 3D-printed ECC compared with cast ECC can be attributed to smaller fibre inclination angles and improved fibre alignment along the loading direction, increased interfacial frictional bond strength induced by the extrusion process, and reduced matrix fracture toughness caused by early moisture loss during printing.

With the fibre orientation and pore characteristics differing from those of cast ECC, the proposed model, combined with other material parameters kept consistent with the cast ECC, was still able to reasonably capture the tensile performance of 3D-printed PE-ECC. In the future, incorporating additional microstructural and meso-mechanical parameters is expected to further enhance the predictive accuracy of this method.