Experimental and Regression Modeling of Short-Term Flexural Behavior of Steel- and GFRP-Reinforced Early-Age Concrete Beams
Abstract
1. Introduction
2. Experimental Investigation
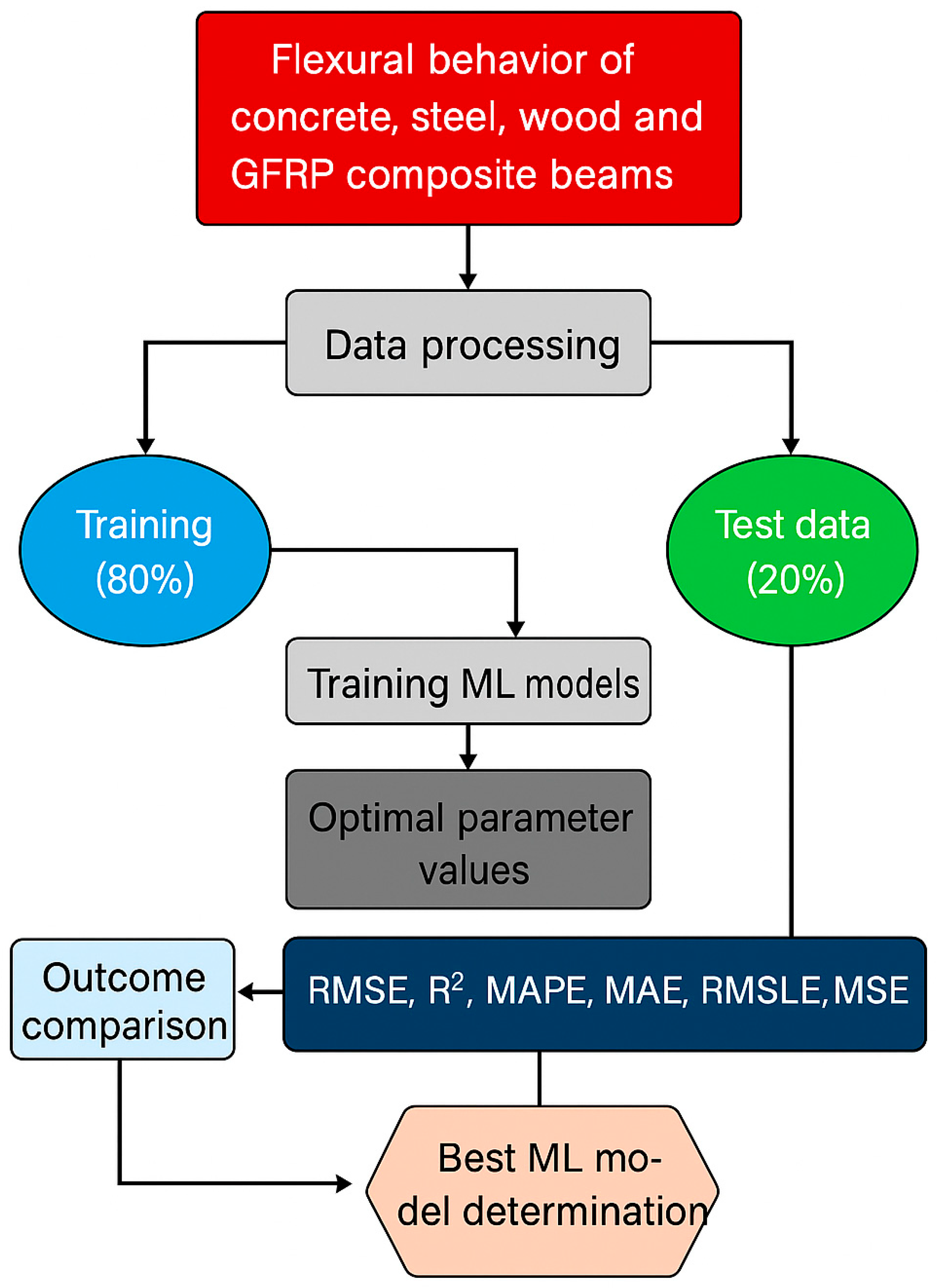
3. Artificial Intelligence Investigation
3.1. Overview of Machine Learning Algorithms
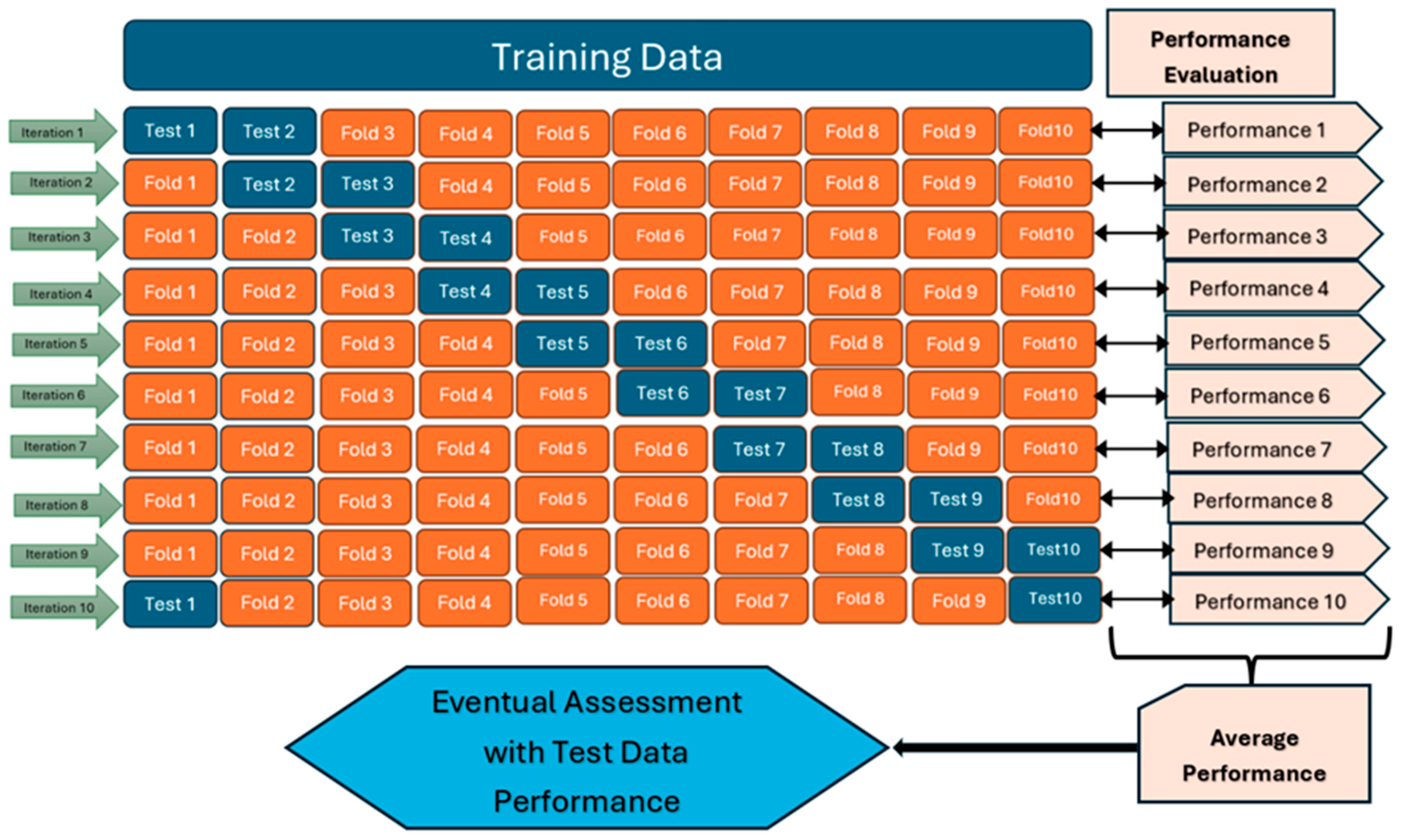
3.2. Assessment Metrics
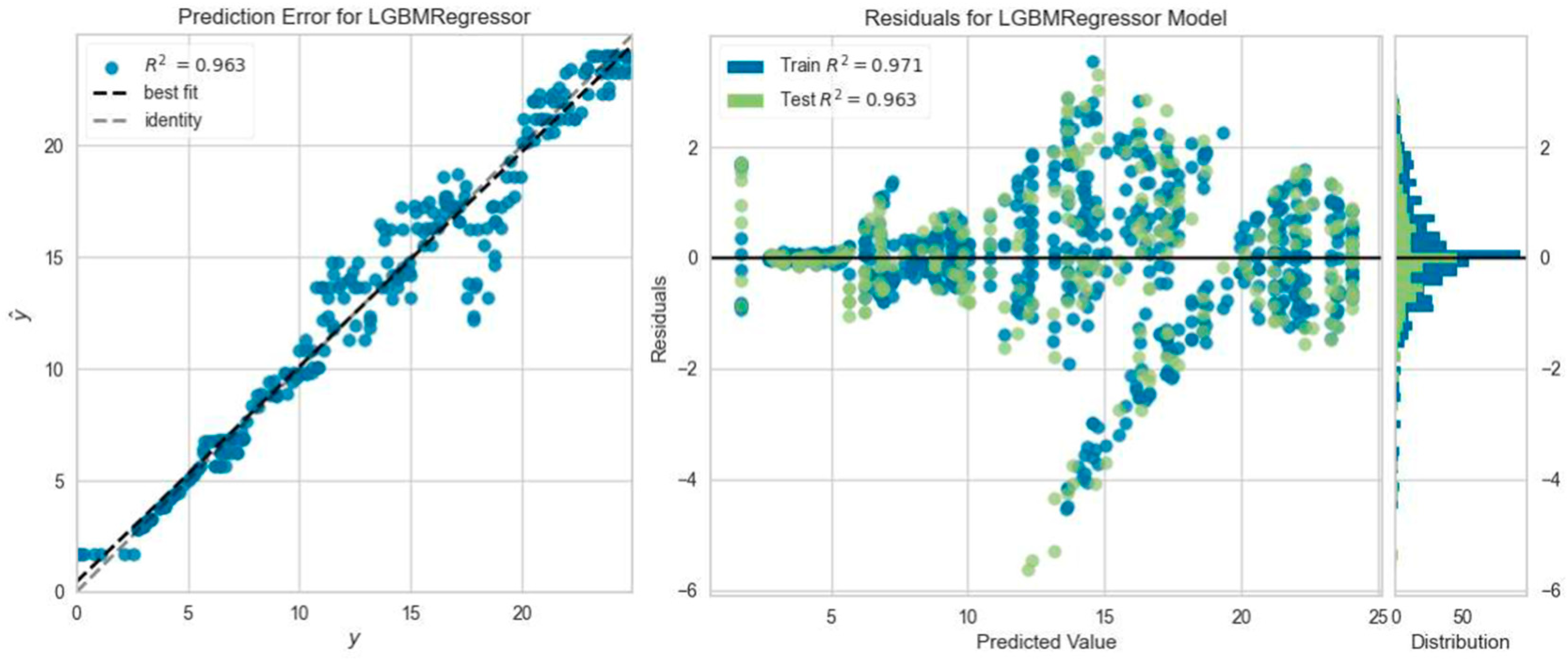
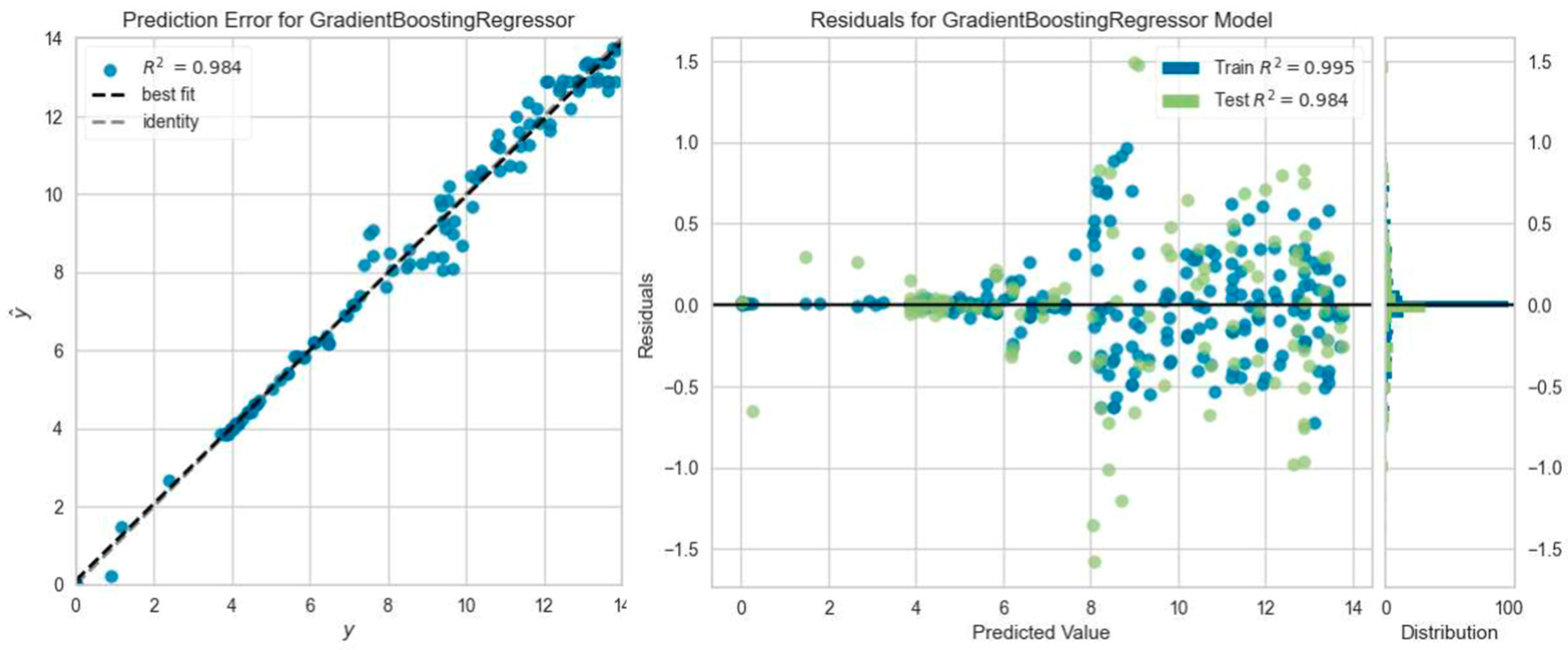
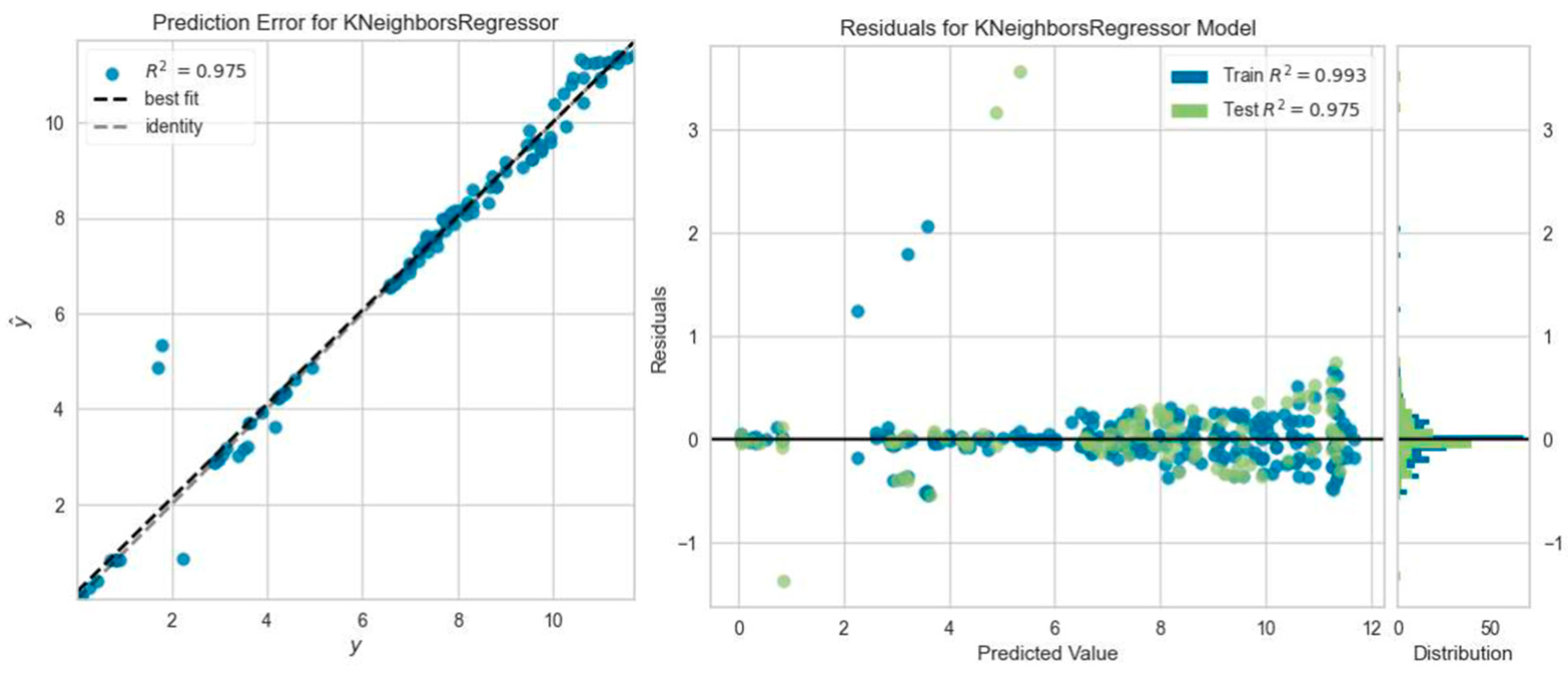
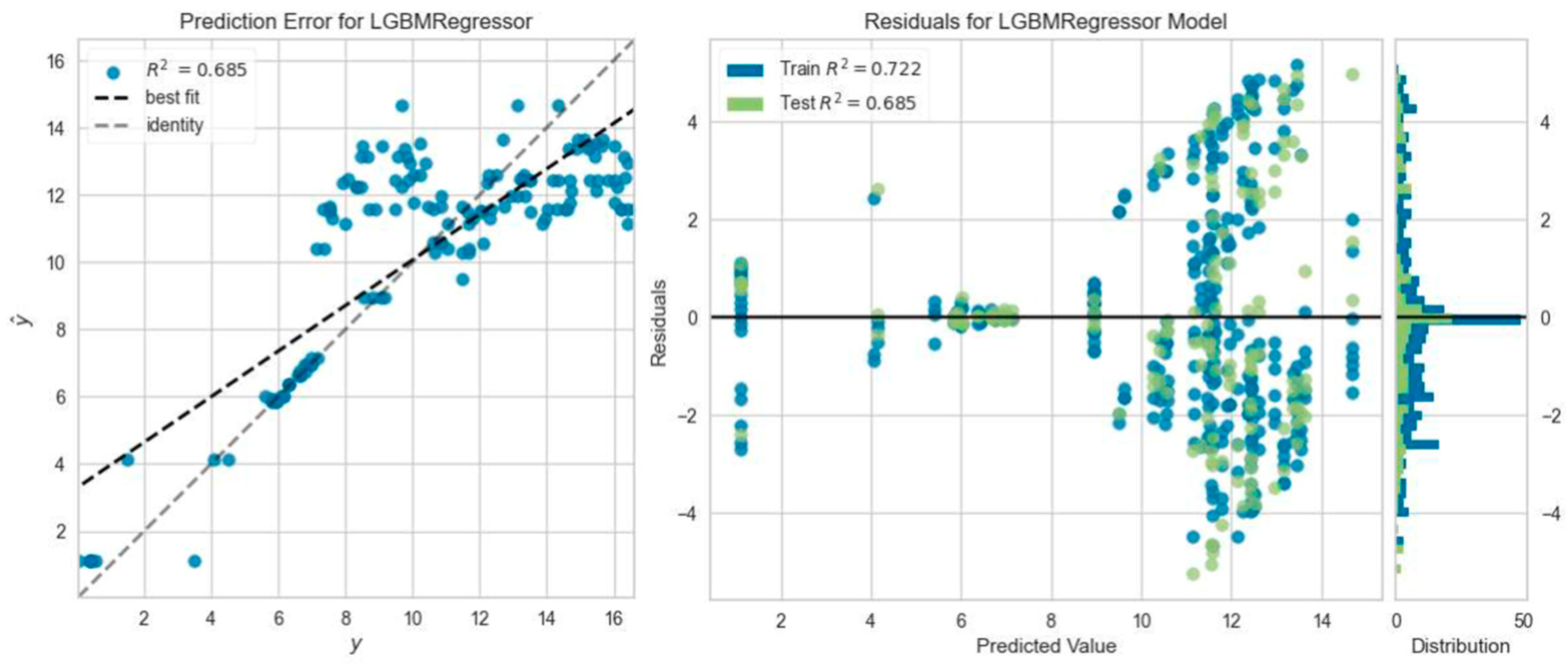
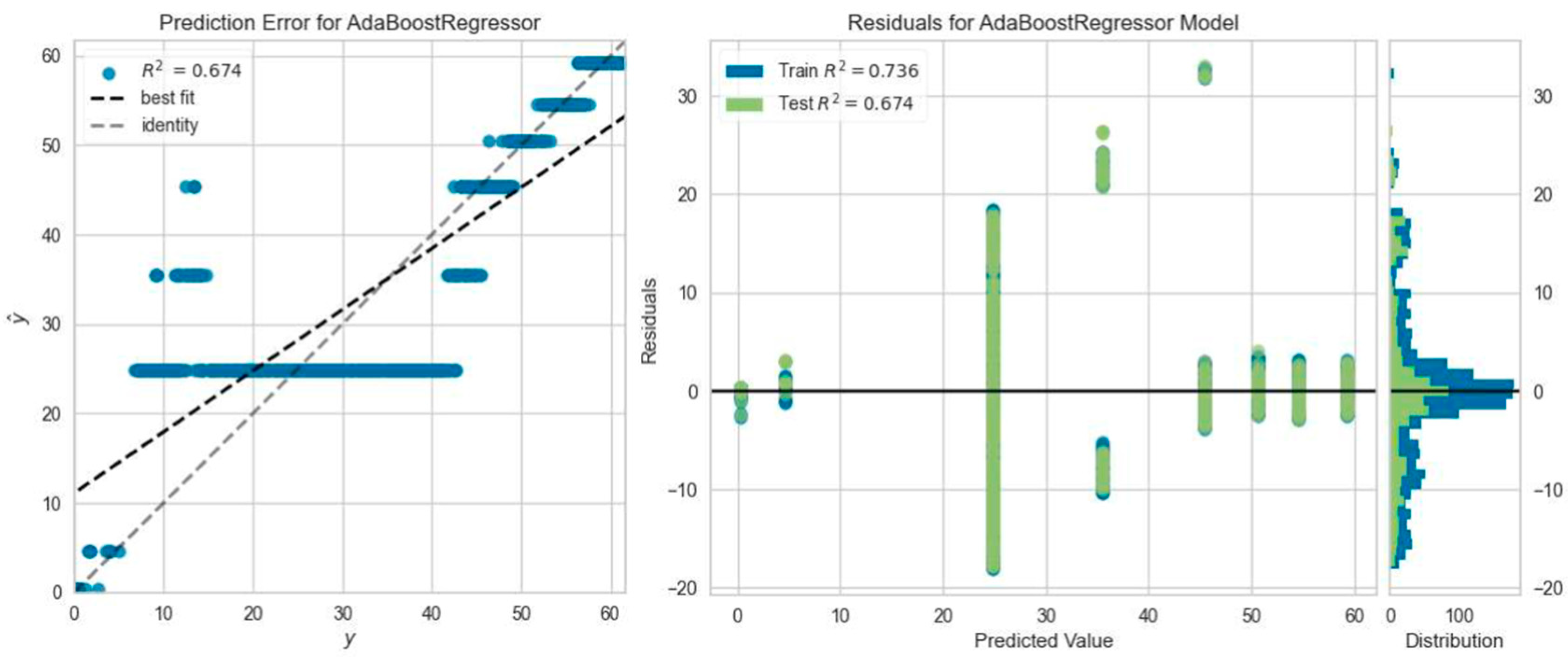
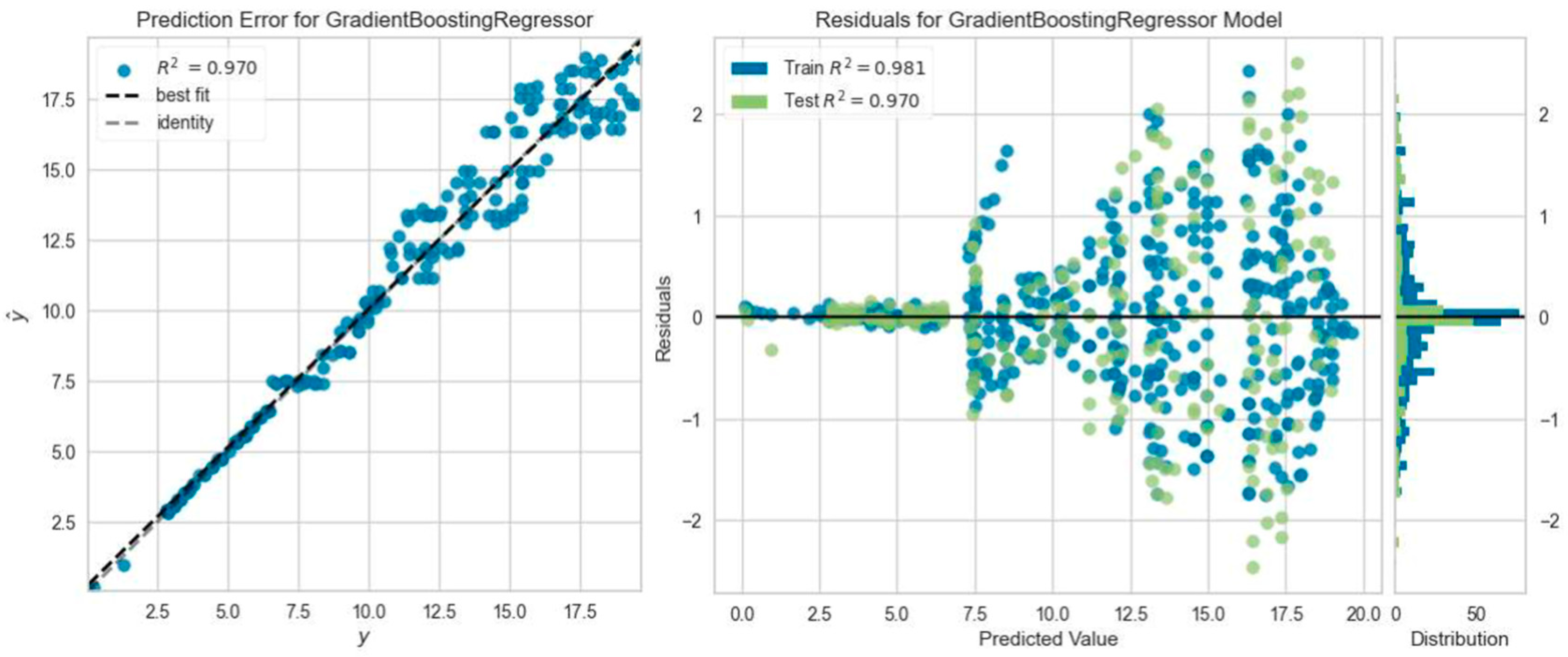
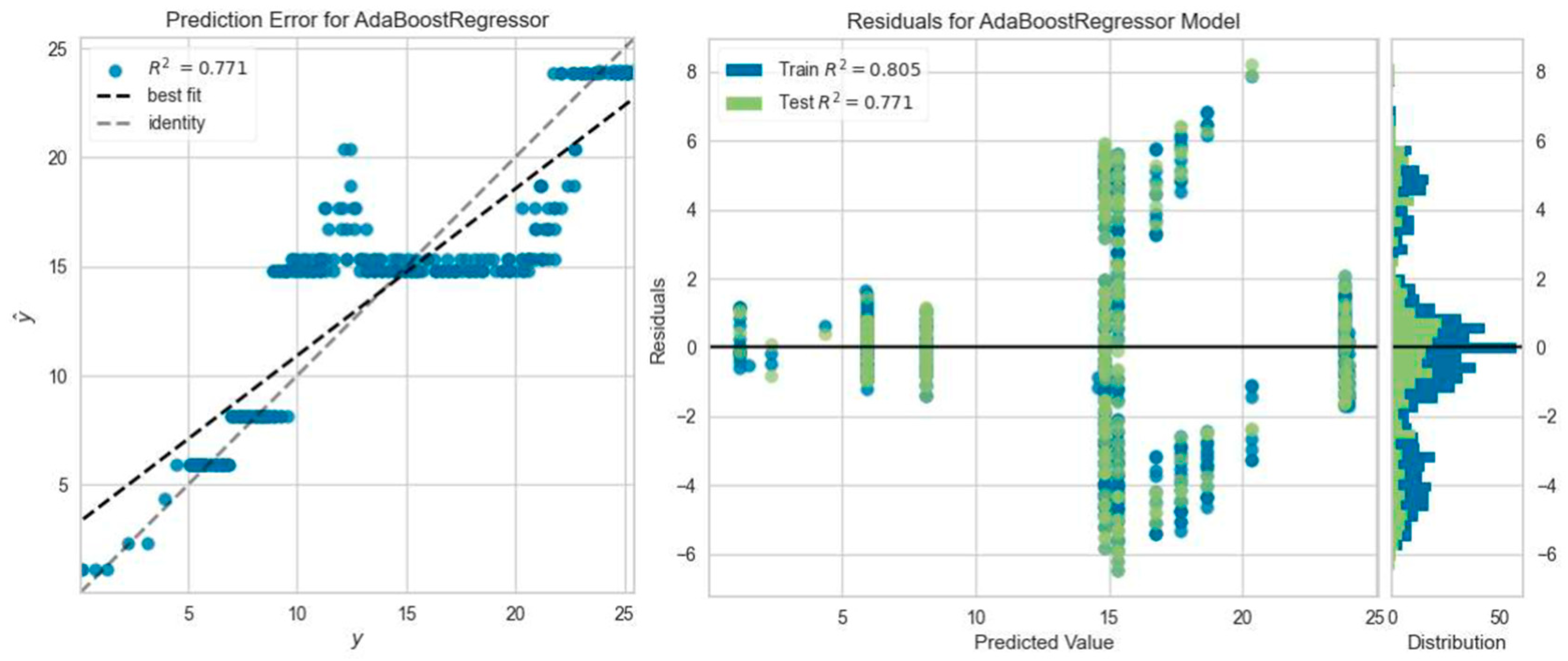
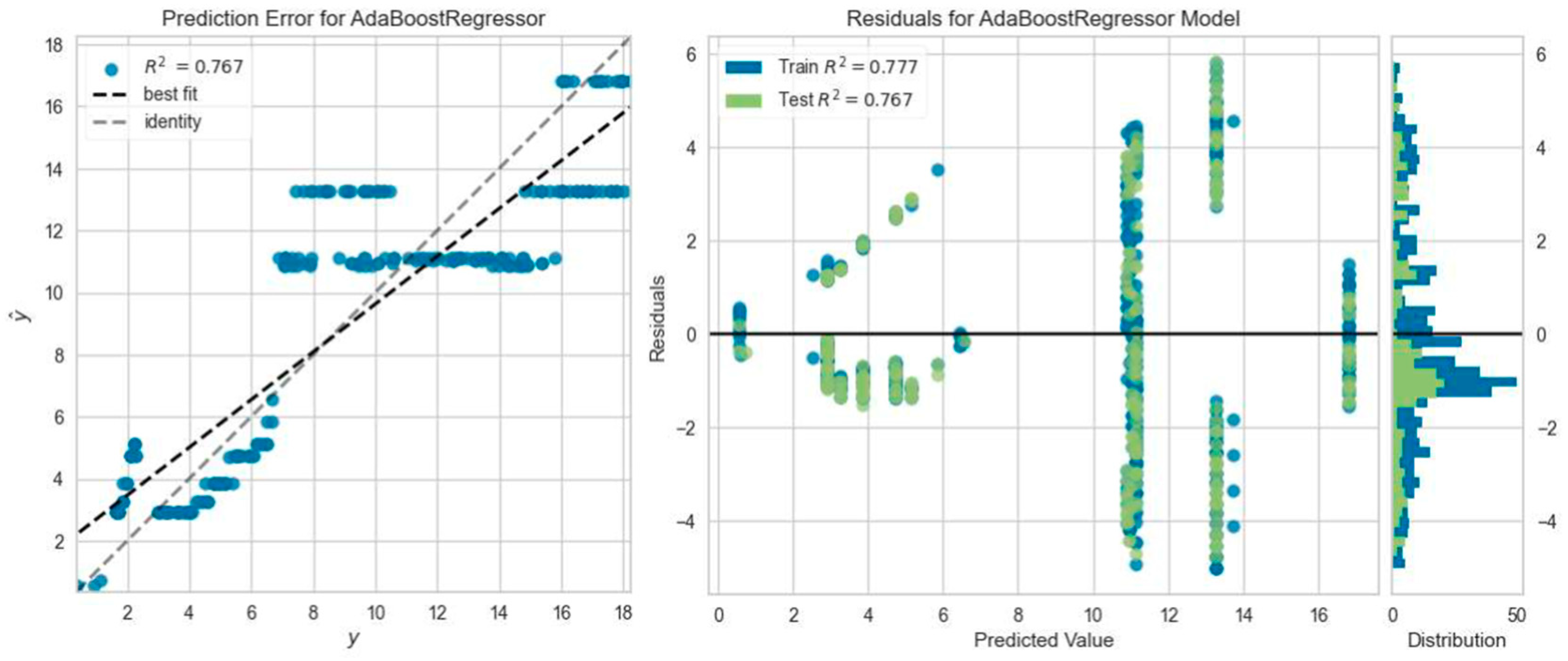
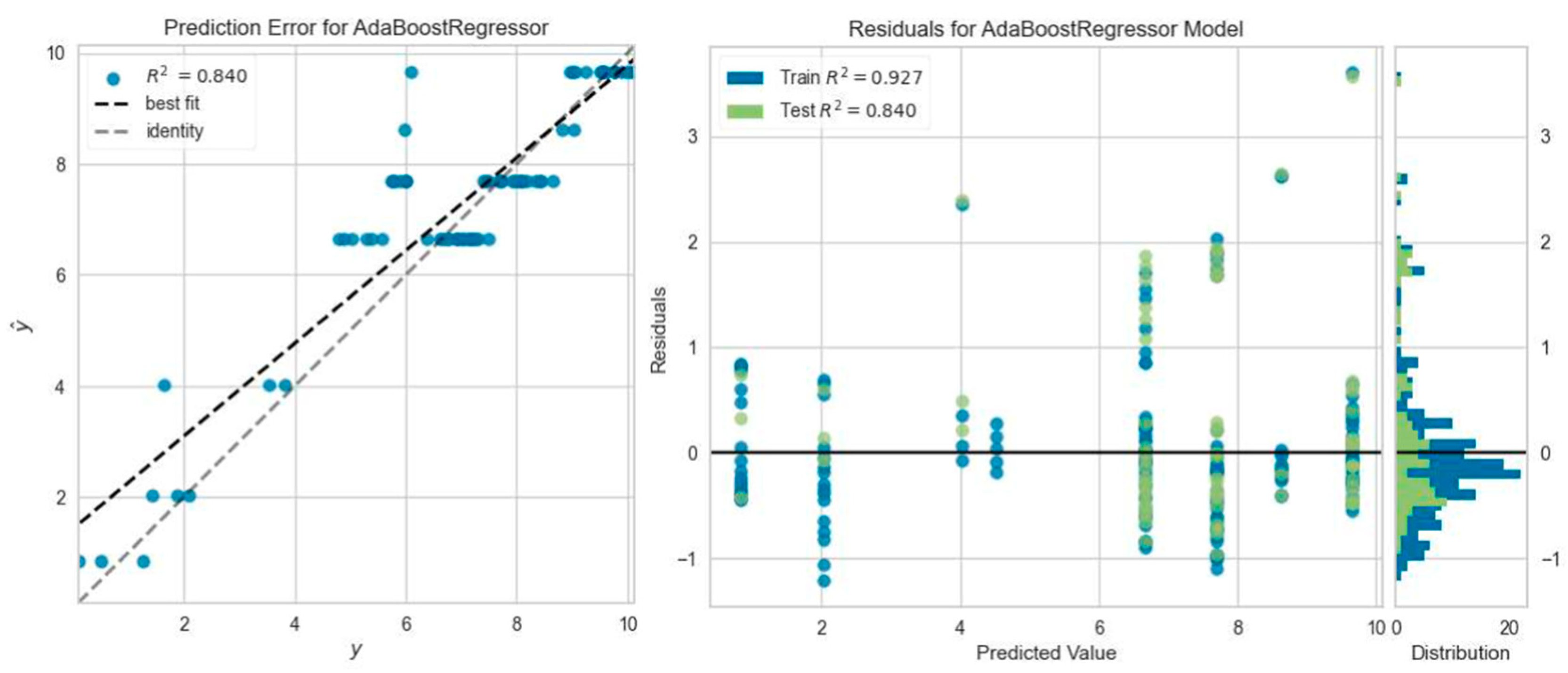
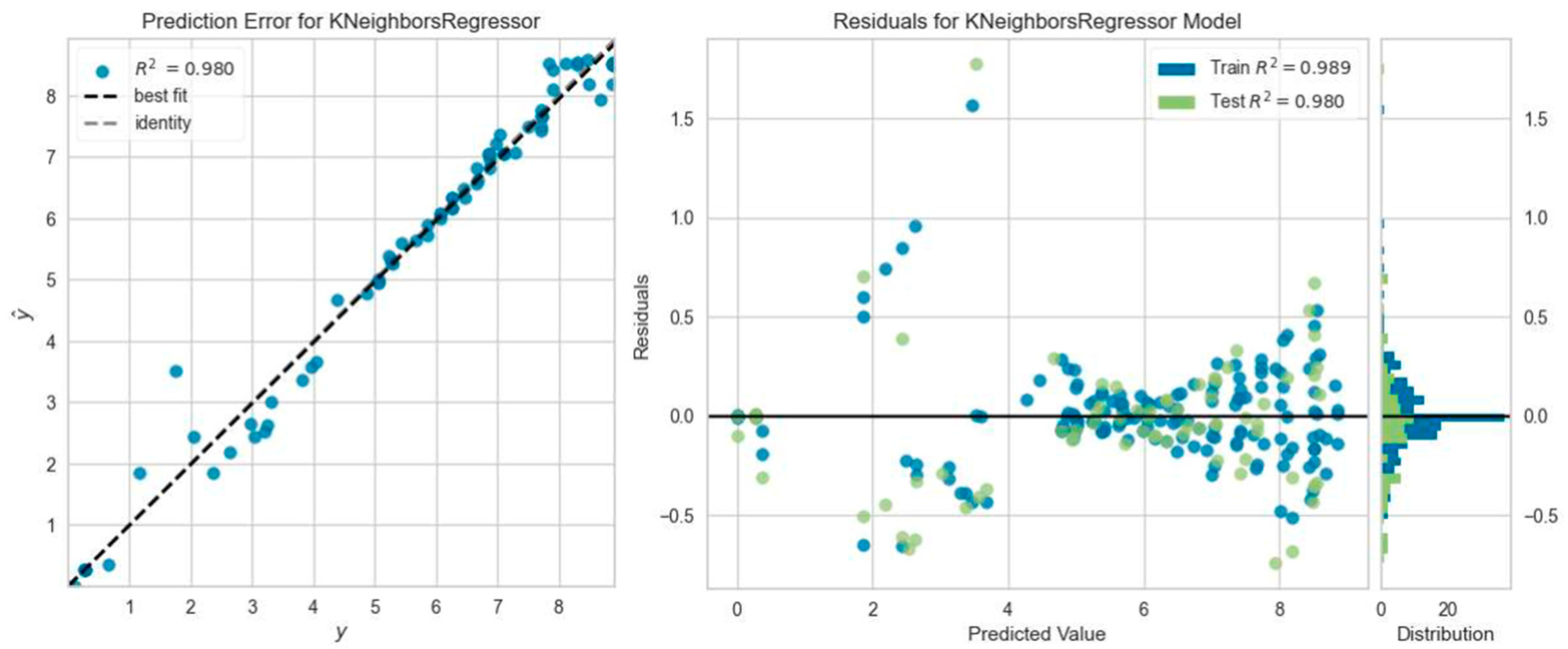
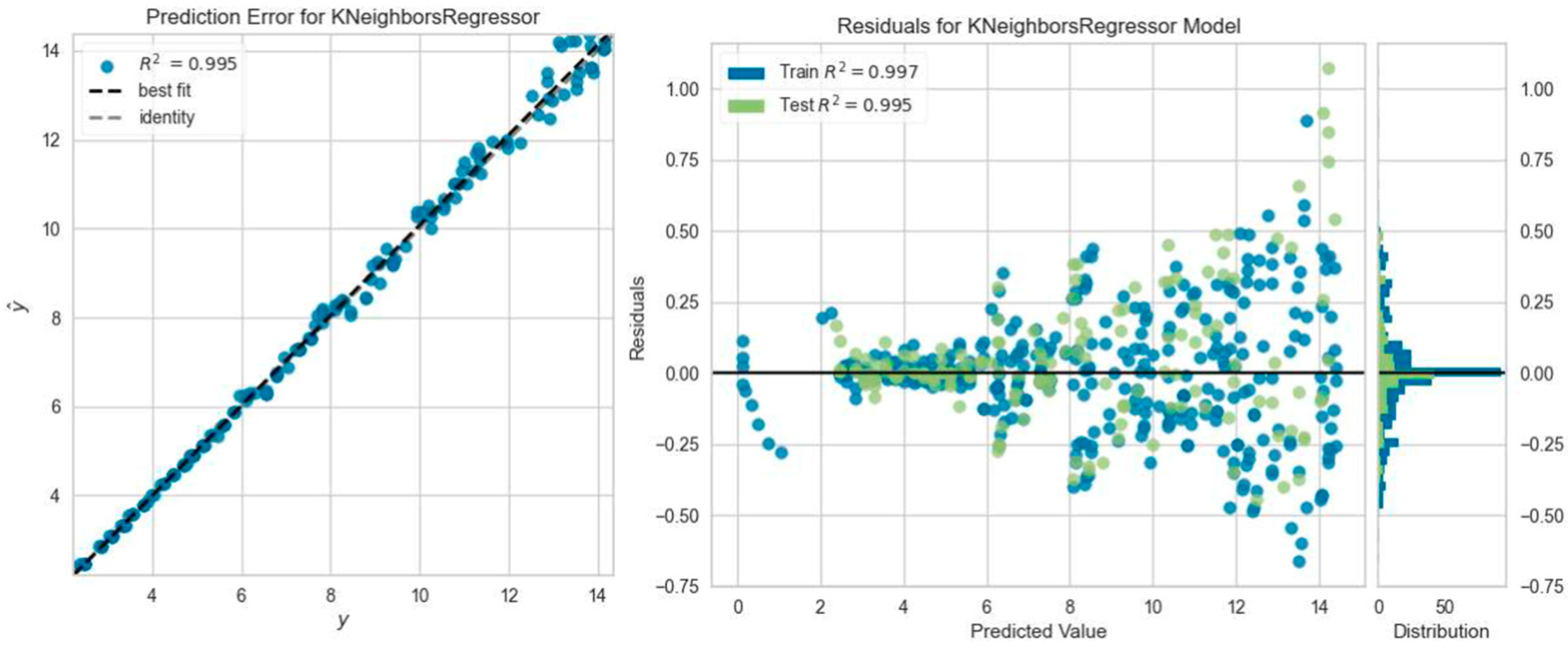
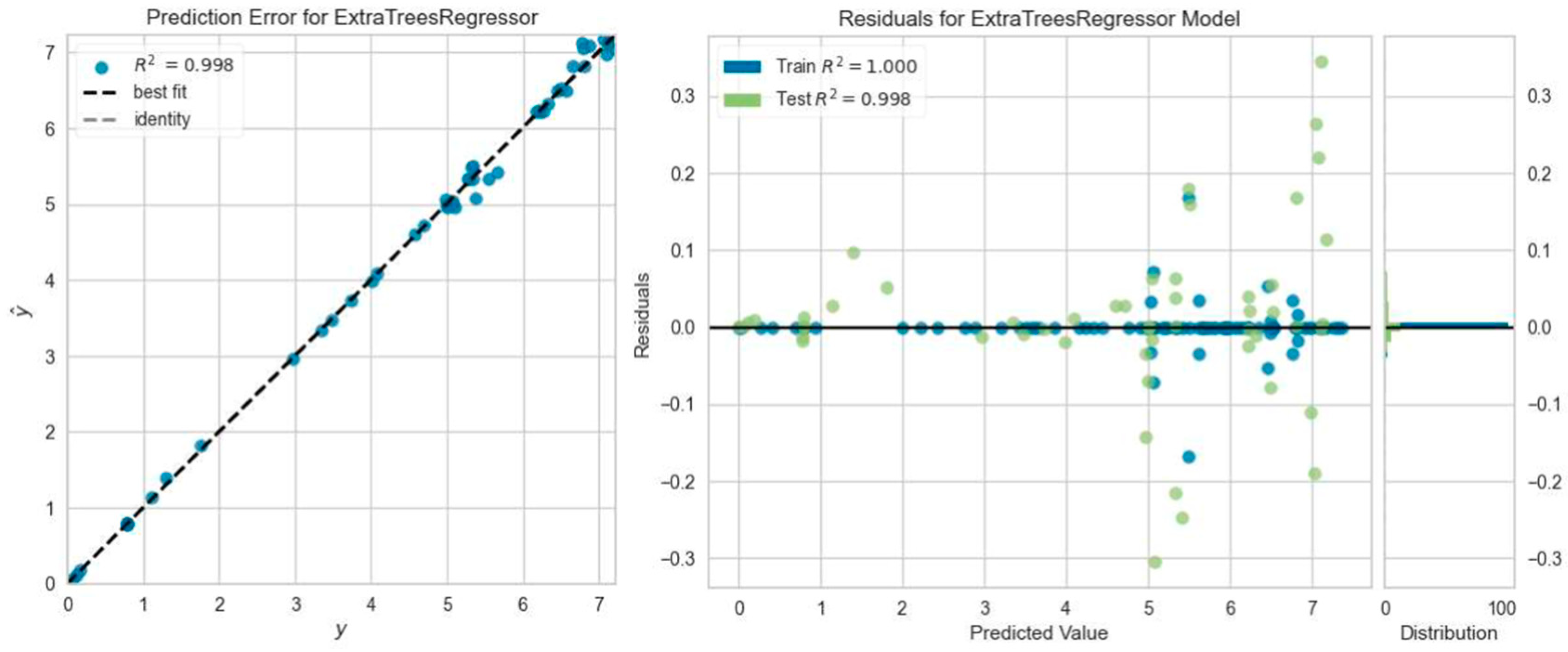
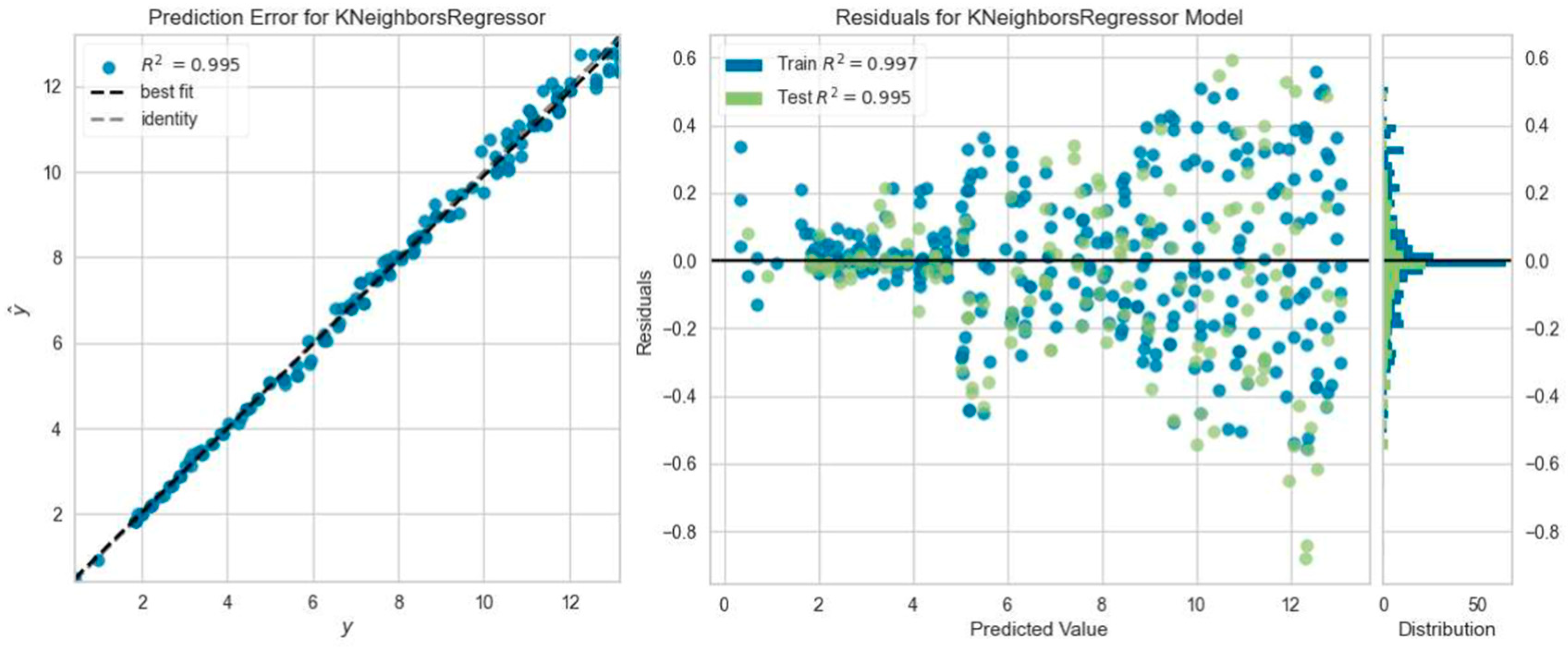
3.3. Machine Learning Analysis Results
4. Discussion
5. Conclusions
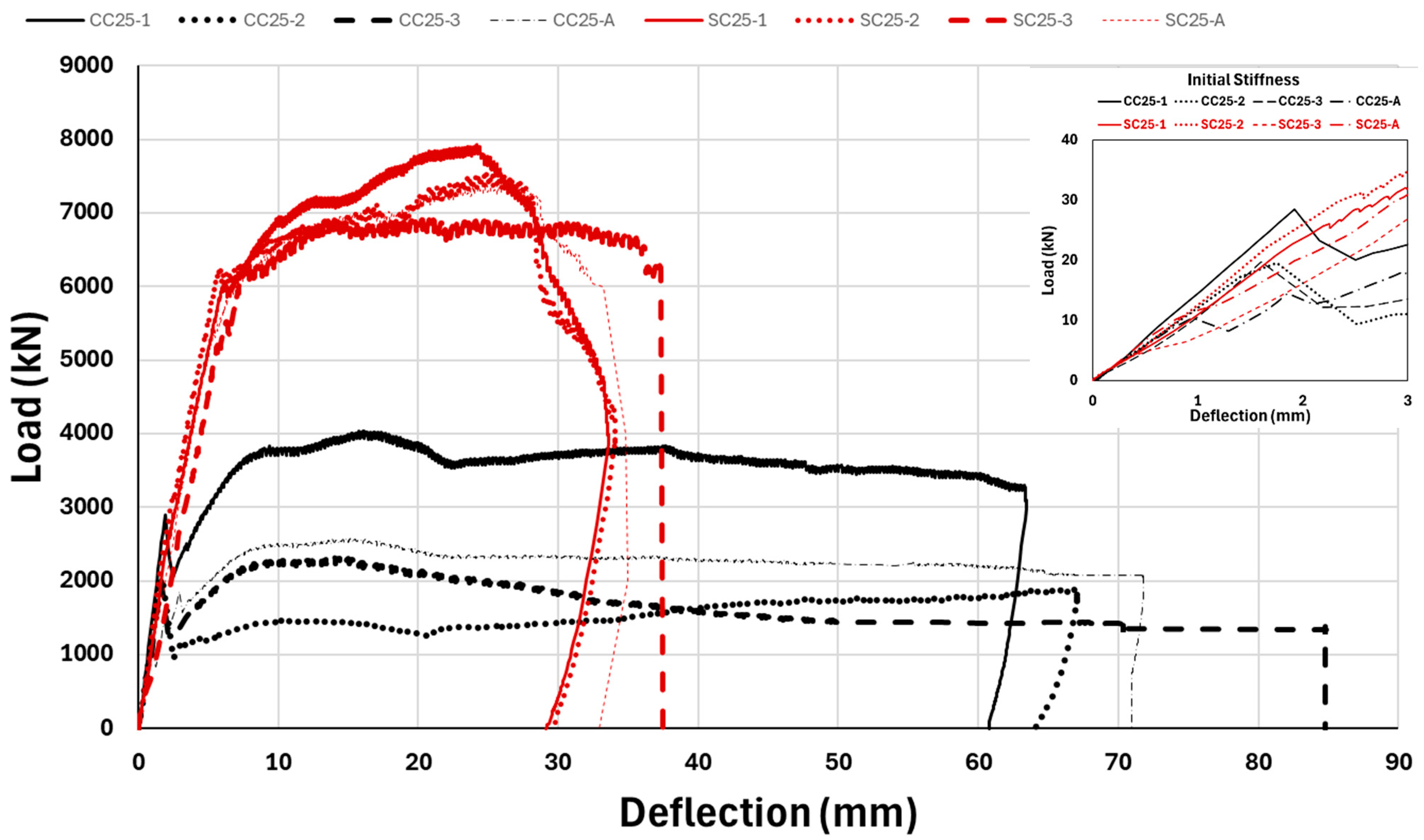
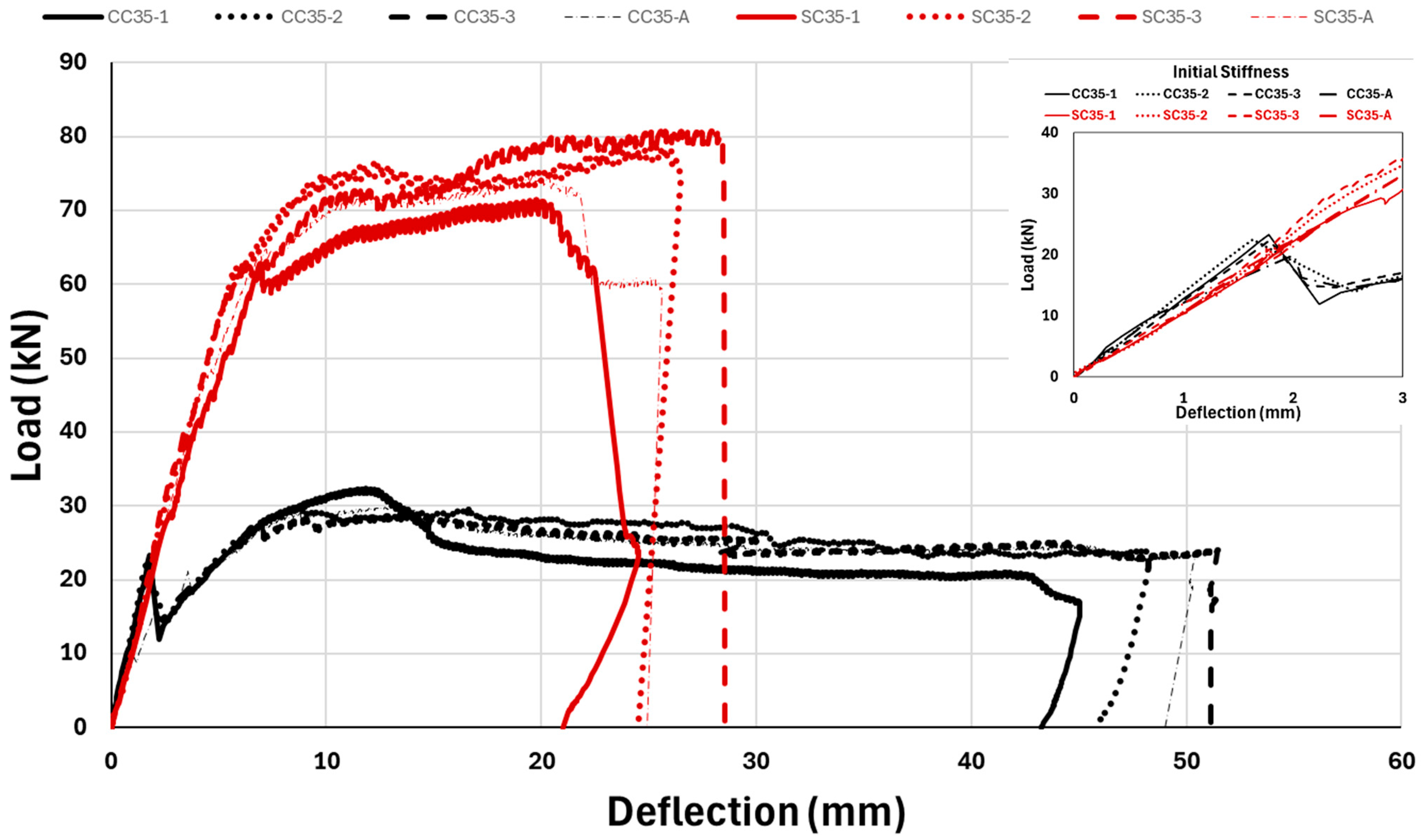
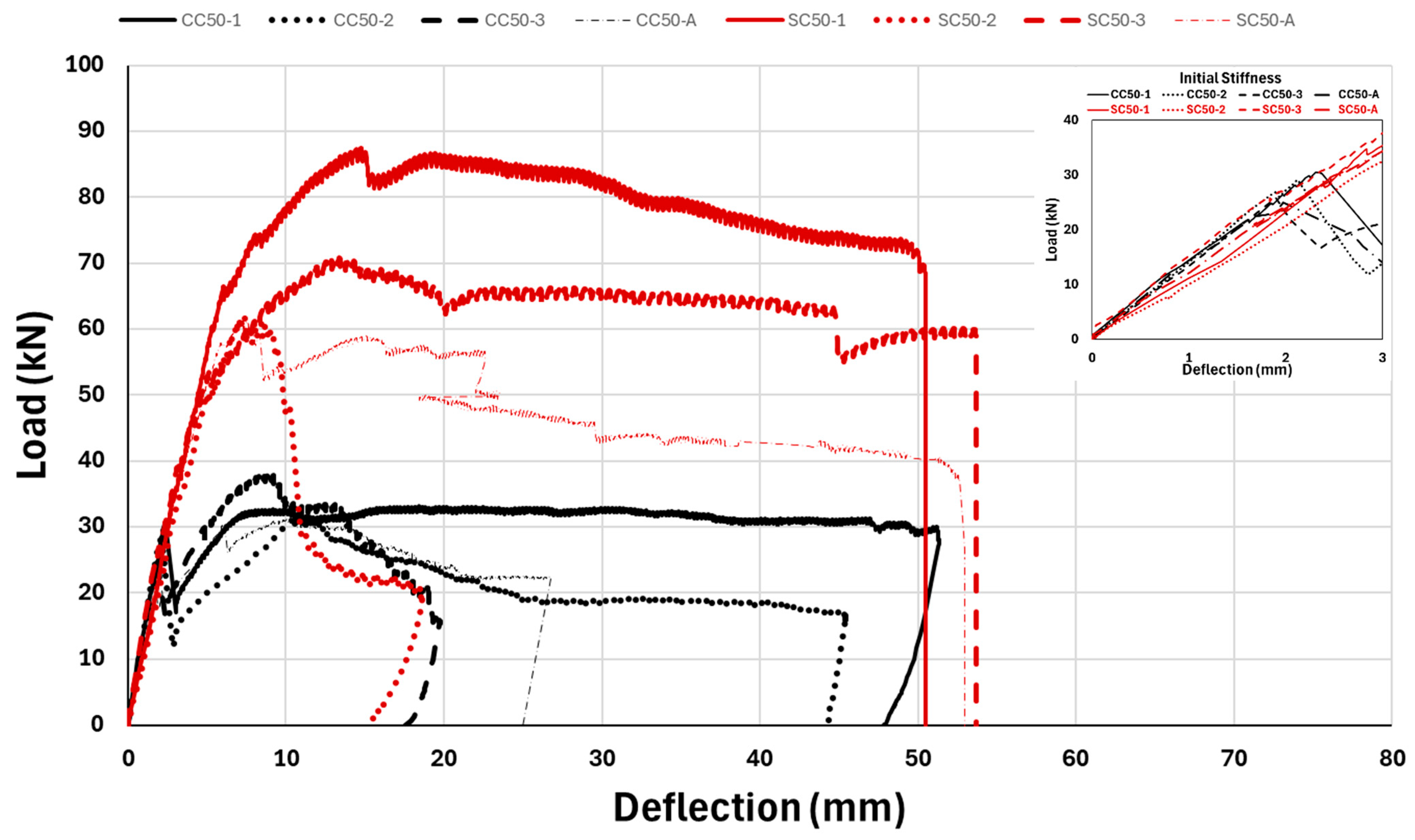
- GFRP composite bar-reinforced concrete beams indicated more ductile behavior and exhibited fracture mechanism behavior with flexural cracks.
- It was determined that fresh concrete and steel-reinforced beams exhibited very brittle behavior and failed under shear cracks.
- Although fresh concrete steel- and GFRP bar-reinforced beams generally failed under shear and flexural cracking, respectively, it was observed that different flexural behaviors could occur in the same group of beams in short-term tests due to the effect of fresh concrete.
- According to Table 4, the ultimate load-carrying capacity averages of composite GFRP rebar-reinforced concrete beams increase as the concrete compressive strength increases, but the ultimate load-carrying capacity averages of steel-reinforced beams were found to be lower in C50 concrete than in C35 concrete. This situation reveals that composite reinforcements are more compatible with the increase in concrete compressive strength levels.
- Failure and cracking behaviors of reinforced concrete beams were examined; no shear cracking and sudden rupture failure behavior occurred in composite GFRP-reinforced beams. Eight of the GFRP-reinforced concrete beams failed under flexural cracking and behavior, which represents the desired failure behavior feature in this structural element.
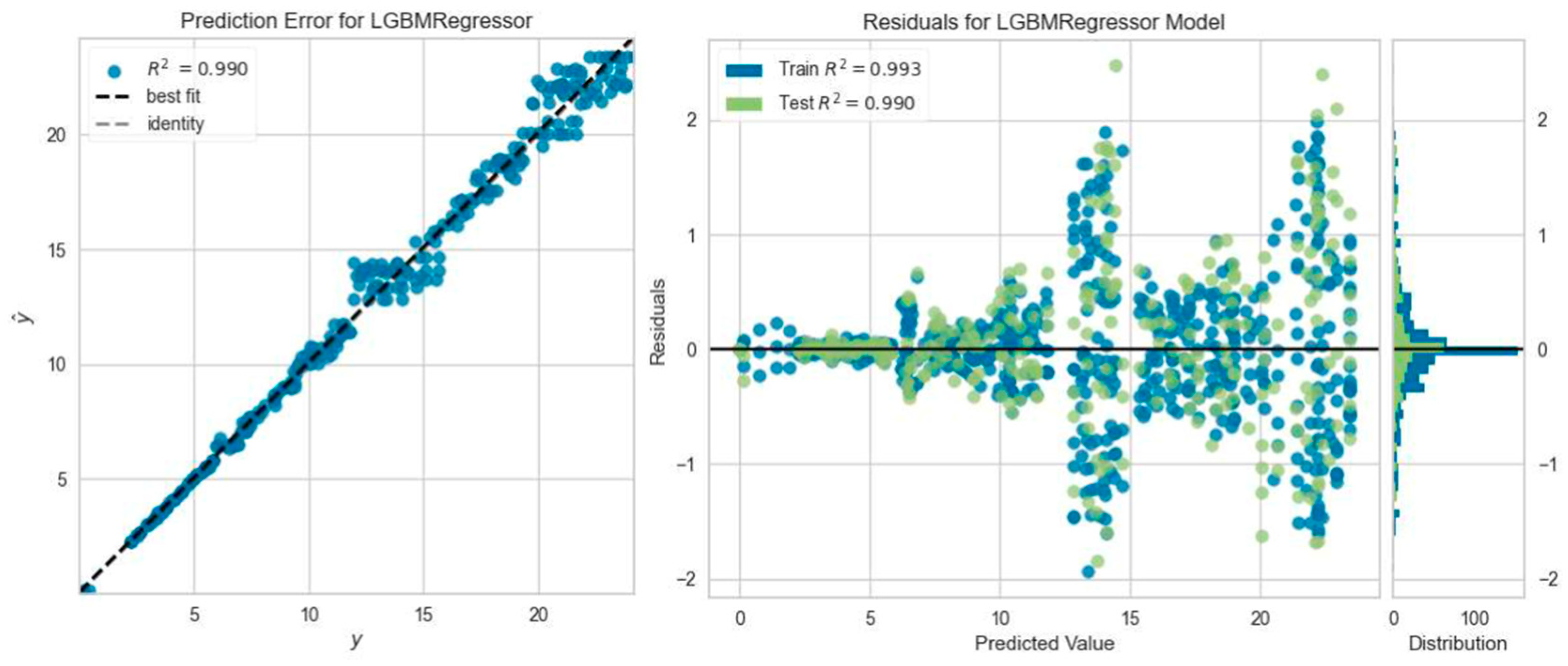
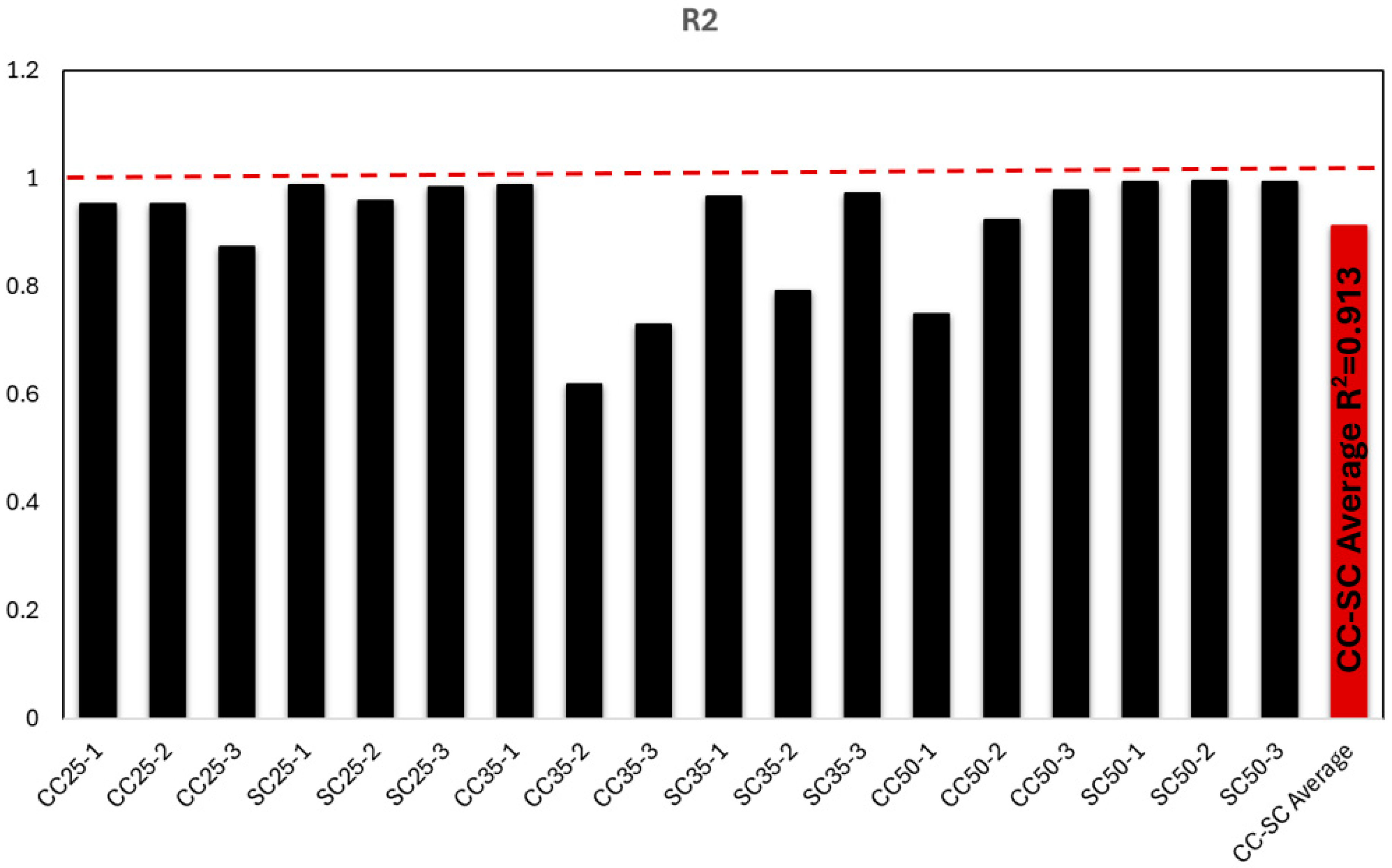
- It was found that the ML regression models predicted the deflection values of the beams under ultimate load with an average accuracy of 91.3%.
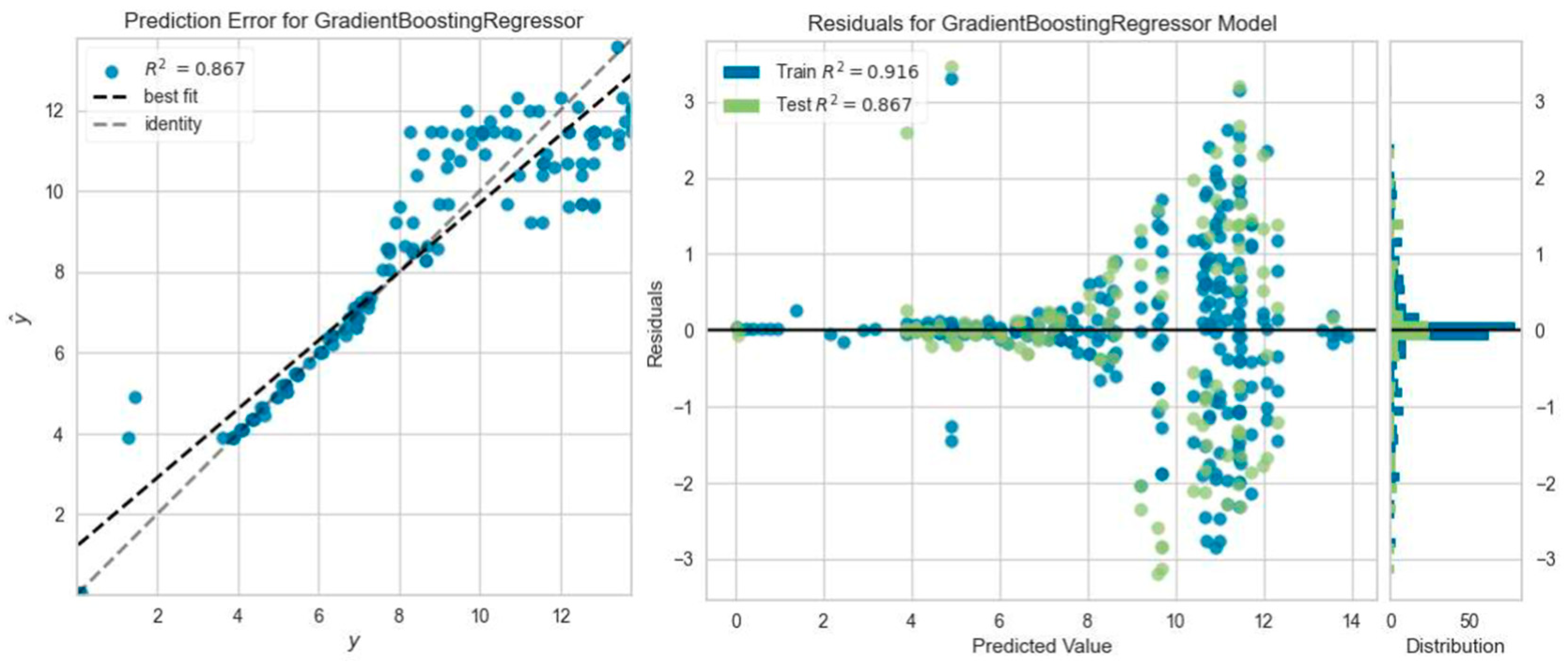
- It is seen that regression models provide higher prediction accuracy calculation capability in load–deflection curves for steel-reinforced beams. This situation is thought to be caused by the sudden rupture failure of GFRP composite reinforcement and the nonlinear behavior of the part.
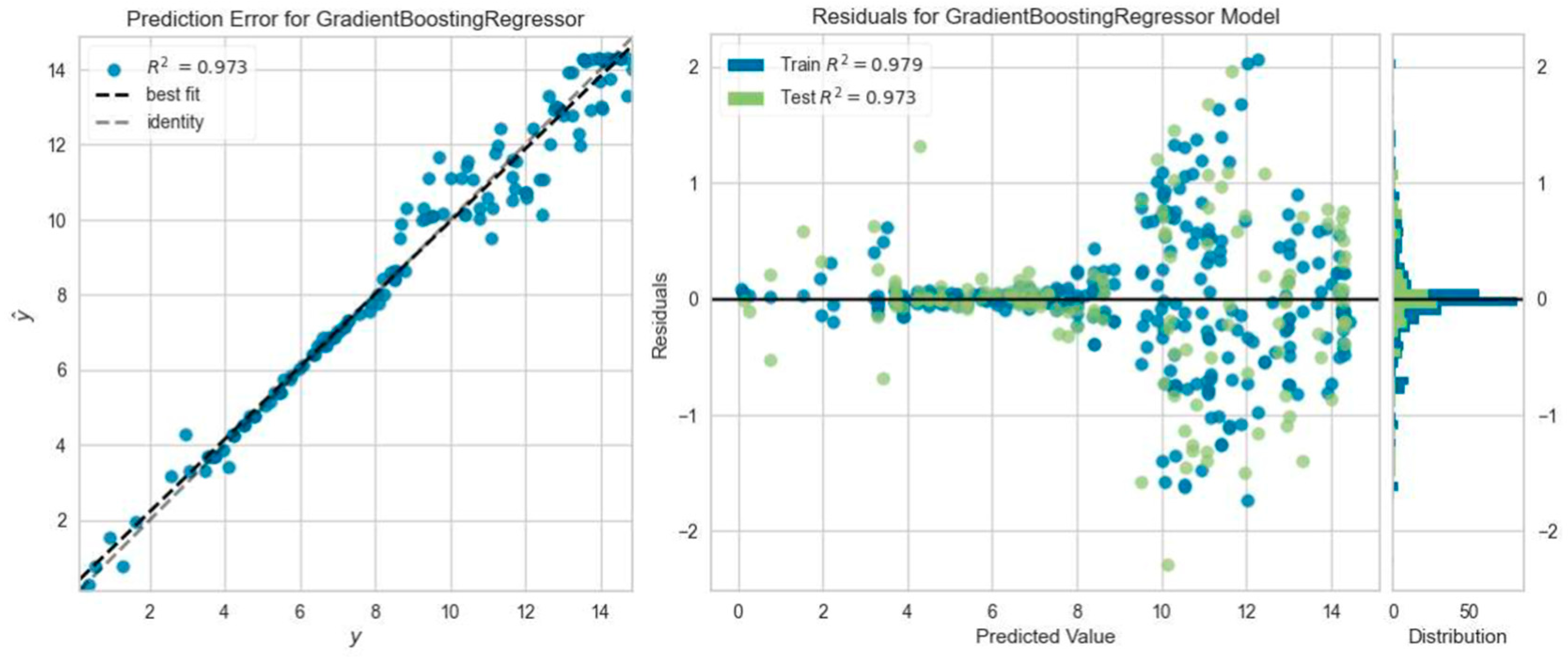
- The regression models that predicted the reinforced concrete beam deflection most accurately were the Gradient Boosting Regressor model five times, the Light Gradient Boosting Machine, K Neighbors Regressor, and Ada Boost Regressor model four times, and the Extra Trees Regressor model one time. However, among all ML analyses, the highest R2 result was obtained with Extra Trees Regressor model prediction, which was consistent with the experimental outcome of the SC50-2 beam, i.e., 0.9964.
- The Gradient Boosting Regressor model, which offers the highest number of prediction capabilities with experimental results in the load–deflection analysis calculations of reinforced concrete beams, is recommended for researchers.
- Further analysis and improvement of regression models for the prediction of deflection capacities of composite-reinforced beams are recommended based on the results of this research.
- In addition, the results of finite element analysis and machine learning regression model analysis should be compared in further studies.
- It was determined that steel rebar-reinforced concrete beams carried more loads than composite GFRP-reinforced beams, but almost all the beams indicated brittle failure behavior, which is a structurally undesirable failure mode.
- In addition, it should be considered that the ultimate load-carrying capacity of steel-reinforced structural elements will decrease significantly over time due to corrosion, and GFRP bars have a much longer service life.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| ⍴: reinforcement ratio (%) | : Max Bending Stress (MPa) |
| ⍴f: GFRP reinforcement ratio (%) | : Max Bending Moment (kNm) |
| ⍴fb: Balance GFRP reinforcement ratio (%) | : Max Shear Stress for solid section (MPa) |
| fc′: Concrete compressive strength at 7 days (MPa) | I: Moment of Inertia (mm4) |
| fc: Concrete compressive strength at 28 days (MPa) | : Load at span center (kN) |
| fy: yield strength of steel | : Bending moment (kNm) |
| ff: Tensile strength of GFRP composite | : height of specimen (mm) |
| Δ: Deflection (mm) | -width of specimen (mm) |
| Ec: Modulus of elasticity of concrete (GPa) | |
| Fcr: Initial Cracking Load, (kN) | |
| Fexp: Failure Load (kN) | |
| Mexp: Failure Moment (kNm) |
References
- Alsayed, S.H. Flexural behaviour of concrete beams reinforced with GFRP bars. Cem. Concr. Compos. 1998, 20, 1–11. [Google Scholar] [CrossRef]
- Ravindra, D.; Martyn, J. Concrete 2000: Economic and Durable Construction Through Excellence; E & FN Spon: London, UK, 1993; pp. 229–238. [Google Scholar]
- Ma, K.; Ma, Y.; Liu, B. Experimental investigation on ultra high performance fiber reinforced concrete beams. Mech. Adv. Mater. Struct. 2023, 30, 1155–1171. [Google Scholar] [CrossRef]
- Han, S.; Fan, C.; Zhou, A.; Ou, J. Shear behavior of concrete beams reinforced with corrosion-resistant and ductile longitudinal steel-FRP composite bars and FRP stirrups. Eng. Struct. 2023, 278, 115520. [Google Scholar] [CrossRef]
- Al-Hamrani, A.; Alnahhal, W.; Elahtem, A. Shear behavior of green concrete beams reinforced with basalt FRP bars and stirrups. Compos. Struct. 2021, 277, 114619. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Abdalla, J.A.; Naser, M.Z. Modeling the shear strength of concrete beams reinforced with CFRP bars under unsymmetrical loading. Mech. Adv. Mater. Struct. 2019, 26, 1290–1297. [Google Scholar] [CrossRef]
- Thomas, J.; Ramadass, S. Prediction of the load and deflection response of concrete deep beams reinforced with FRP bars. Mech. Adv. Mater. Struct. 2021, 28, 43–66. [Google Scholar] [CrossRef]
- Shabanlou, M.; Mofid, M.; Tavakoli, A. Post-fire performance of GFRP reinforced concrete deep beams: Experimental and numerical study. Struct. Infrastruct. Eng. 2024, 1–19. [Google Scholar] [CrossRef]
- Aslani, F.; Bastami, M. Relationship between deflection and crack mouth opening displacement of self-compacting concrete beams with and without fibers. Mech. Adv. Mater. Struct. 2015, 22, 956–967. [Google Scholar] [CrossRef]
- Ding, Y. Investigations into the relationship between deflection and crack mouth opening displacement of SFRC beam. Constr. Build. Mater. 2011, 25, 2432–2440. [Google Scholar] [CrossRef]
- Abdo, A.; Sharaky, I.A.; Eisa, A.; Ahmed, S. Flexural behavior of steel/GFRP reinforced concrete beams having layered sections integrated with normal and rubberized concrete. Structures 2024, 70, 107633. [Google Scholar] [CrossRef]
- Ahmed, S.; Sharaky, I.A.; El Sayed, S.; Hassan, H.; Abdo, A. Effect of rubberized concrete integrating uncoated and coated crumb rubber on the flexural behavior of the RC beams reinforced with steel and GFRP bars. Constr. Build. Mater. 2024, 426, 136192. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Hosseini, S.A.; Ozbakkaloglu, T. The combined effect of crumb rubber aggregates and steel fibers on shear behavior of GFRP bar-reinforced high-strength concrete beams. J. Build. Eng. 2021, 44, 102981. [Google Scholar] [CrossRef]
- Imjai, T.; Aosai, P.; Garcia, R.; Raman, S.N.; Chaudhary, S. Deflections of high-content recycled aggregate concrete beams reinforced with GFRP bars and steel fibres. Eng. Struct. 2024, 312, 118247. [Google Scholar] [CrossRef]
- Gouda, O.; Hassanein, A.; Galal, K. Experimental and numerical study on the crack width and deflection performance of GFRP reinforced concrete beams. Eng. Struct. 2023, 283, 115721. [Google Scholar] [CrossRef]
- Ifrahim, M.S.; Sangi, A.J.; Ahmad, S.H. Experimental and numerical investigation of flexural behaviour of concrete beams reinforced with GFRP bars. Structures 2023, 56, 104951. [Google Scholar] [CrossRef]
- Huang, J.; Wang, P.; Shi, Q.; Rong, C.; Tao, Y. Flexural behavior and numerical simulation of reinforced concrete beams with a UHPC stay-in-place formwork. Structures 2024, 69, 107254. [Google Scholar] [CrossRef]
- Huang, J.; Xing, G.; Chang, Z. Experimental and numerical investigation on flexural behavior of concrete beams strengthened by different NSM tendons. Compos. Struct. 2023, 313, 116947. [Google Scholar] [CrossRef]
- Hasan, M.A.; Sheehan, T.; Ashour, A.; Elkezza, O. Flexural behaviour of geopolymer concrete T-Beams reinforced with GFRP bars. Structures 2023, 49, 345–364. [Google Scholar] [CrossRef]
- Le, D.D.; Nguyen, H.C.; Nguyen, T.A.; Nguyen, X.H. Investigating the Influence of Transverse Reinforcement Configuration on the Torsional Behavior of GFRP-Reinforced Concrete Beams: An Experimental and Numerical Analysis. KSCE J. Civ. Eng. 2024, 28, 5793–5809. [Google Scholar] [CrossRef]
- Alam, M.S.; Hussein, A. Finite element modelling of shear critical glass fibre-reinforced polymer (GFRP) reinforced concrete beams. Int. J. Model. Simul. 2021, 41, 11–23. [Google Scholar] [CrossRef]
- Metwally, I.M. Three-dimensional nonlinear finite element analysis of concrete deep beam reinforced with GFRP bars. HBRC J. 2017, 13, 25–38. [Google Scholar] [CrossRef]
- Salem, M.; Issa, M.S. Nonlinear finite element analysis of high and ultra-high strength concrete beams reinforced with FRP bars. HBRC J. 2023, 19, 15–31. [Google Scholar] [CrossRef]
- Zhu, Z.; Abdelbaset, H.; Li, X.; Tang, Q. Flexural behavior of long-term loaded RC beams strengthened by ultra-high performance concrete. Constr. Build. Mater. 2023, 407, 133428. [Google Scholar] [CrossRef]
- Van Tran, H.; Seo, S.Y.; Hanif, M.U.; Senghong, K. Time-dependent flexural behavior of the RC beams strengthened with FRP strips using different methods. Structures 2024, 65, 106655. [Google Scholar] [CrossRef]
- Mao, J.H.; Xu, F.Y.; Jin, W.L.; Zhang, J.; Wu, X.X.; Chen, C.S. Research on the Fatigue Flexural Performance of RC Beams Attacked by Salt Spray. China Ocean Eng. 2018, 32, 179–188. [Google Scholar] [CrossRef]
- Ren, F.; Chen, Z.; Xiong, M.X. Long-Term Behavior of FRP-Bar Reinforced Seawater Sea Sand Concrete Beams Under Load Sustaining and Environment Weathering. Int. J. Civ. Eng. 2024, 22, 491–504. [Google Scholar] [CrossRef]
- Nagy, I.E.; Asadian, A.; Galal, K. Fatigue life and behaviour of ribbed GFRP reinforced concrete beams. Eng. Struct. 2024, 309, 117989. [Google Scholar] [CrossRef]
- Zhao, J.; Li, G.; Wang, Z.; Zhao, X.L. Fatigue behavior of concrete beams reinforced with glass- and carbon-fiber reinforced polymer (GFRP/CFRP) bars after exposure to elevated temperatures. Compos. Struct. 2019, 229, 111427. [Google Scholar] [CrossRef]
- Ge, Z.; Huang, M.; Wang, Y. Fatigue behaviour of asphalt concrete beams reinforced by glass fibre-reinforced plastics. Int. J. Pavement Eng. 2014, 15, 36–42. [Google Scholar] [CrossRef]
- Xing, L.; Sun, S.; Mei, K.; Guo, Y.; Yang, Z. Research progress on short-term mechanical properties of FRP bars and FRP-reinforced concrete beams. J. Traffic Transp. Eng. (Engl. Ed.) 2024, 11, 245–270. [Google Scholar] [CrossRef]
- Salman, O.; Abed, F.; Alhoubi, Y. Shear performance of GFRP reinforced UHPC short beams. Compos. Struct. 2025, 351, 118637. [Google Scholar] [CrossRef]
- Iwama, K.; Kai, M.F.; Dai, J.G.; Zhang, P.; Wang, P.; Poon, C.S.; Leung, C.K.; Maekawa, K. Physicochemical-mechanical simulation of the short- and long-term performance of FRP reinforced concrete beams under marine environments. Eng. Struct. 2024, 308, 118051. [Google Scholar] [CrossRef]
- Miàs, C.; Torres, L.; Guadagnini, M.; Turon, A. Short and long-term cracking behaviour of GFRP reinforced concrete beams. Compos. Part B Eng. 2015, 77, 223–231. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Shafighfard, T.; Jankowski, R.; Yoo, D.Y. Machine-Learning Methods for Estimating Performance of Structural Concrete Members Reinforced with Fiber-Reinforced Polymers, No. 0123456789; Springer: Dordrecht, The Netherlands, 2024. [Google Scholar]
- Mahmoudian, A.; Tajik, N.; Taleshi, M.M.; Shakiba, M.; Yekrangnia, M. Ensemble machine learning-based approach with genetic algorithm optimization for predicting bond strength and failure mode in concrete-GFRP mat anchorage interface. Structures 2023, 57, 105173. [Google Scholar] [CrossRef]
- Huang, T.; Wan, C.; Liu, T.; Hao, D.; Miao, C. Machine learning prediction method for the interface bond strength between fiber reinforced polymer bars and concrete based on multi-feature driven analysis. Mater. Today Commun. 2024, 41, 110706. [Google Scholar] [CrossRef]
- Liu, K.; Wulan, T.; Yao, Y.; Bian, M.; Bao, Y. Assessment of damage evolution of concrete beams strengthened with BFRP sheets with acoustic emission and unsupervised machine learning. Eng. Struct. 2024, 300, 117228. [Google Scholar] [CrossRef]
- Anvari, A.T.; Babanajad, S.; Gandomi, A.H. Data-Driven Prediction Models For Total Shear Strength of Reinforced Concrete Beams With Fiber Reinforced Polymers Using An Evolutionary Machine Learning Approach. Eng. Struct. 2023, 276, 115292. [Google Scholar] [CrossRef]
- Rahman, J.; Arafin, P.; Billah, A.H.M.M. Machine learning models for predicting concrete beams shear strength externally bonded with FRP. Structures 2023, 53, 514–536. [Google Scholar] [CrossRef]
- Karabulut, M. Nonlinear Load-Deflection Analysis of Steel Rebar-Reinforced Concrete Beams: Experimental, Theoretical and Machine Learning Analysis. Buildings 2025, 15, 432. [Google Scholar] [CrossRef]
- Karabulut, M. Machine Learning-Driven Flexural Performance Prediction and Experimental Investigation of Glass Fiber-Reinforced Polymer Bar-Reinforced Concrete Beams. Polymers 2025, 17, 713. [Google Scholar] [CrossRef] [PubMed]
- Ge, W.; Zhang, F.; Wang, Y.; Ashour, A.; Luo, L.; Qiu, L.; Fu, S.; Cao, D. Machine learning predictions for bending capacity of ECC-concrete composite beams hybrid reinforced with steel and FRP bars. Case Stud. Constr. Mater. 2024, 21, e03670. [Google Scholar] [CrossRef]
- Moein, M.M.; Saradar, A.; Rahmati, K.; Mousavinejad, S.H.G.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive models for concrete properties using machine learning and deep learning approaches: A review. J. Build. Eng. 2023, 63, 105444. [Google Scholar] [CrossRef]
- Karabulut, M. Investigation of the Bending Strength of Glass Fiber-Reinforced Polymer (GFRP) Bars Exposed to Thermal Stress. J. Struct. Eng. Appl. Mech. 2025, 8, 1–12. [Google Scholar] [CrossRef]
- Kina, C.; Turk, K.; Atalay, E.; Donmez, I.; Tanyildizi, H. Comparison of extreme learning machine and deep learning model in the estimation of the fresh properties of hybrid fiber-reinforced SCC. Neural Comput. Appl. 2021, 33, 11641–11659. [Google Scholar] [CrossRef]
- Tuken, A.; Abbas, Y.M.; Siddiqui, N.A. Efficient prediction of the load-carrying capacity of ECC-strengthened RC beams—An extra-gradient boosting machine learning method. Structures 2023, 56, 105053. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Al-Hamrani, A.; Ebead, U.; Alnahhal, W. Shear capacity prediction of FRP-RC beams using single and ensenble ExPlainable Machine learning models. Compos. Struct. 2022, 287, 115381. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, J.; Zhu, H.; Liu, X.; Liang, Z. Ultimate Bending Strength Evaluation of MVFT Composite Girder by using Finite Element Method and Machine Learning Regressors. Lat. Am. J. Solids Struct. 2022, 19, e438. [Google Scholar] [CrossRef]
- Le Nguyen, K.; Trinh, H.T.; Nguyen, T.T.; Nguyen, H.D. Comparative study on the performance of different machine learning techniques to predict the shear strength of RC deep beams: Model selection and industry implications. Expert Syst. Appl. 2023, 230, 120649. [Google Scholar] [CrossRef]
- Gad, M.A.; Nikbakht, E.; Ragab, M.G. Predicting the compressive strength of engineered geopolymer composites using automated machine learning. Constr. Build. Mater. 2024, 442, 137509. [Google Scholar] [CrossRef]
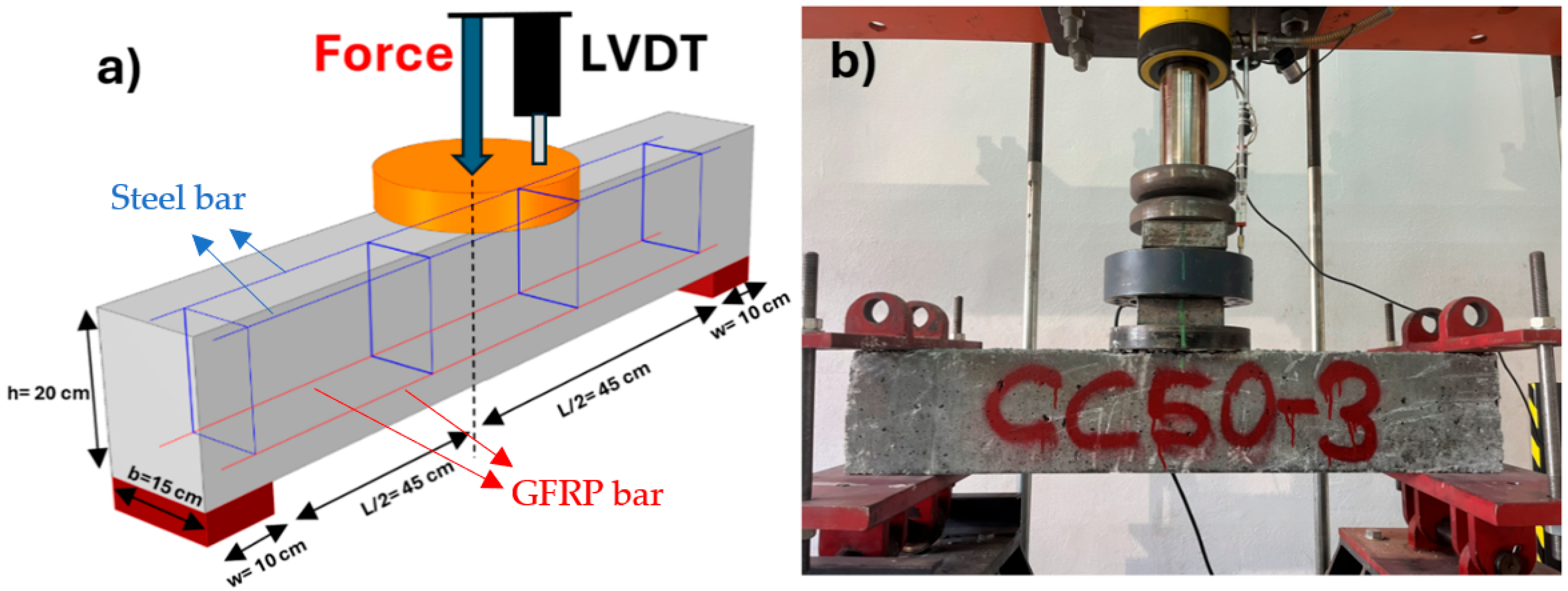









| Series | Beam No. | Cros Section (Unit: mm) | Tensile Reinforcement | Reinforcement Ratio, ⍴ (%) | Cube Sample fc′ (MPa) | a/d Ratio | |||
|---|---|---|---|---|---|---|---|---|---|
| Width, b | Height, h | Effective Depth, d | Length, l | ||||||
| C25 | CC25-1 | 150 | 200 | 162 | 1100 | 2–10 mm GFRP bars | 0.65 | 33.76 | 2.78 |
| CC25-2 | |||||||||
| CC25-3 | |||||||||
| SC25-1 | 2–10 mm steel bars | ||||||||
| SC25-2 | |||||||||
| SC25-3 | |||||||||
| C35 | CC35-1 | 150 | 200 | 162 | 1100 | 2–10 mm GFRP bars | 0.65 | 39.27 | 2.78 |
| CC35-2 | |||||||||
| CC35-3 | |||||||||
| SC35-1 | 2–10 mm steel bars | ||||||||
| SC35-2 | |||||||||
| SC35-3 | |||||||||
| C50 | CC50-1 | 150 | 200 | 162 | 1100 | 2–10 mm GFRP bars | 0.65 | 53.76 | 2.78 |
| CC50-2 | |||||||||
| CC50-3 | |||||||||
| SC50-1 | 2–10 mm steel bars | ||||||||
| SC50-2 | |||||||||
| SC50-3 | |||||||||
| Series | Beam No. | Longitudinal Reinforcement | Transverse Reinforcement | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Material | Num of Bars | Bar Dia (mm) | ⍴f-⍴b (%) | ⍴f/⍴fb or ⍴/⍴b (%) | Material | Bar Dia (mm) | Spacing (mm) | ||
| C25 | CC25-1 | GFRP | 2 | 10 | 0.60 | 107.67 | Steel bars | 8 | 300 |
| CC25-2 | |||||||||
| CC25-3 | |||||||||
| SC25-1 | Steel | 2.17 | 29.76 | Steel bars | |||||
| SC25-2 | |||||||||
| SC25-3 | |||||||||
| C35 | CC35-1 | GFRP | 2 | 10 | 0.78 | 82.82 | Steel bars | 8 | 300 |
| CC35-2 | |||||||||
| CC35-3 | |||||||||
| SC35-1 | Steel | 2.82 | 22.95 | Steel bars | |||||
| SC35-2 | |||||||||
| SC35-3 | |||||||||
| C50 | CC50-1 | GFRP | 2 | 10 | 0.99 | 65.40 | Steel bars | 8 | 300 |
| CC50-2 | |||||||||
| CC50-3 | |||||||||
| SC50-1 | Steel | 3.57 | 18.12 | Steel bars | |||||
| SC50-2 | |||||||||
| SC50-3 | |||||||||
| Test Specimen Name | GFRP Bar Diameter (mm) | Cross-Sectional Area (mm2) | GFRP Bar Sample Length (mm) | Max Tensile Strength (MPa) | Max Bending Load (kN) | Max. Bending Strength (MPa) | Ultimate Deflection Δ (mm) | Weight (gr/cm) |
|---|---|---|---|---|---|---|---|---|
| 10-1 | 10 | 78.54 | 146 | 853 | 3.150 | 40.11 | 6 | 1.61 |
| 10-2 | 10 | 78.54 | 148 | 896 | 2.900 | 36.92 | 3 | 1.57 |
| 10-3 | 10 | 78.54 | 147 | 916 | 2.950 | 37.56 | 5 | 1.58 |
| 10-A | 10 | 78.54 | 147 | 888 | 3 | 38.20 | 4.67 | 1.59 |
| Series | Beam No. | RC Beam Failure Behavior | Initial Cracking Load, Fcr (kN) | Failure Load, Fexp (kN) | Maximum Mid-Span Deflection, Δ exp (mm) | Failure Moment, Mexp (kN.m) |
|---|---|---|---|---|---|---|
| C25 | CC25-1 | FC | 28.48 | 39.58 | 63.30 | 17.81 |
| CC25-2 | FC | 17.18 | 19.57 | 67.02 | 8.81 | |
| CC25-3 | FC | 19.7 | 22.70 | 84.80 | 10.22 | |
| CC25-A | - | 21.79 | 27.28 | 71.71 | 12.28 | |
| SC25-1 | SC | 59.05 | 77.75 | 34.03 | 34.99 | |
| SC25-2 | SC | 61.51 | 73.95 | 34.02 | 33.28 | |
| SC25-3 | SC | 50.97 | 67.79 | 37.22 | 30.51 | |
| SC25-A | - | 57.18 | 73.16 | 36.62 | 32.92 | |
| C35 | CC35-1 | FC | 23.30 | 32.38 | 44.99 | 14.57 |
| CC35-2 | FC | 22.50 | 29.69 | 47.93 | 13.36 | |
| CC35-3 | FC | 22.36 | 33.32 | 62.29 | 14.99 | |
| CC35-A | - | 22.72 | 31.80 | 51.74 | 14.31 | |
| SC35-1 | SC | 62.74 | 71.52 | 24.54 | 32.18 | |
| SC35-2 | FSC | 61.77 | 78.69 | 26.47 | 35.41 | |
| SC35-3 | FSC | 62.88 | 80.91 | 27.50 | 36.41 | |
| SC35-A | - | 62.46 | 77.04 | 26.17 | 34.67 | |
| C50 | CC50-1 | FC | 30.50 | 33.09 | 51.34 | 14.89 |
| CC50-2 | FC | 28.92 | 31.37 | 45.41 | 14.12 | |
| CC50-3 | FSC | 25.80 | 37.83 | 19.74 | 17.02 | |
| CC50-A | - | 28.41 | 34.10 | 38.83 | 15.35 | |
| SC50-1 | FSC | 66.11 | 87.46 | 50.8 | 39.36 | |
| SC50-2 | SC | 49.80 | 62.04 | 18.61 | 27.92 | |
| SC50-3 | FSC | 53.60 | 70.85 | 54.3 | 31.88 | |
| SC50-A | - | 56.50 | 73.45 | 41.24 | 33.05 |
| ML Model No. | ML Regression Model Name | ML Model Name Code |
|---|---|---|
| 1 | Gradient Boosting Regressor | gbr |
| 2 | K Neighbors Regressor | knn |
| 3 | Ada Boost Regressor | ada |
| 4 | Random Forest Regressor | rf |
| 5 | Light Gradient Boosting Machine | lightgbm |
| 6 | Extra Trees Regressor | et |
| 7 | Decision Tree Regressor | dt |
| 8 | Lasso List Angle Regressor | llar |
| 9 | Ridge Regression | ridge |
| 10 | Bayesian Ridge | br |
| 11 | Orthogonal Matching Pursuit | omp |
| 12 | Elastic Net | en |
| 13 | Least Angle Regression | lar |
| 14 | Lasso Regression | lasso |
| 15 | Linear Regression | lr |
| 16 | Huber Regression | huber |
| 17 | Passive Aggressive Regressor | par |
| 18 | Dummy Regressor | dummy |
| Feature | Type | Cmin | Cmax | Ave |
|---|---|---|---|---|
| fc′ (MPa) | Input | 33.76 | 53.76 | 42.26 |
| fy (MPa) | Input | 420 | 420 | 420 |
| ff (MPa) | Input | 489 | 651 | 578 |
| b (mm) | Input | 150 | 150 | 150 |
| h (mm) | Input | 200 | 200 | 200 |
| d (mm) | Input | 162 | 162 | 162 |
| L (mm) | Input | 1100 | 1100 | 1100 |
| ⍴f (%) | Input | 0.6 | 0.99 | 0.79 |
| ⍴b (%) | Input | 2.17 | 3.57 | 2.85 |
| F (kN) | Input | 19.57 | 87.46 | 52.805 |
| Δ (mm) | Output | 18.61 | 84.80 | 44.1925 |
| Beam Name | Best Predictive ML Model | MAE | MSE | RMSE | R2 | RMSLE | MAPE |
|---|---|---|---|---|---|---|---|
| CC25-1 | Gradient Boosting Regressor | 0.5369 | 0.7003 | 0.8322 | 0.9548 | 0.0956 | 0.0767 |
| CC25-2 | Gradient Boosting Regressor | 0.4778 | 0.5605 | 0.7387 | 0.9547 | 0.0719 | 0.0657 |
| CC25-3 | Gradient Boosting Regressor | 0.7191 | 1.2556 | 1.1113 | 0.8737 | 0.1165 | 0.1535 |
| SC25-1 | Light Gradient Boosting Machine | 0.4372 | 0.4508 | 0.6650 | 0.9901 | 0.0448 | 0.2825 |
| SC25-2 | Light Gradient Boosting Machine | 0.9165 | 1.7505 | 1.3170 | 0.9595 | 0.1280 | 3.7866 |
| SC25-3 | Gradient Boosting Regressor | 0.2750 | 0.1878 | 0.4261 | 0.9855 | 0.0425 | 0.0391 |
| CC35-1 | K Neighbors Regressor | 0.1873 | 0.1021 | 0.2978 | 0.9892 | 0.0599 | 0.0676 |
| CC35-2 | Light Gradient Boosting Machine | 1.8359 | 5.7042 | 2.3812 | 0.6204 | 0.2479 | 0.5265 |
| CC35-3 | Ada Boost Regressor | 6.3675 | 76.0032 | 8.6991 | 0.7309 | 0.3919 | 0.3811 |
| SC35-1 | Gradient Boosting Regressor | 0.6270 | 0.7693 | 0.8749 | 0.9684 | 0.0632 | 0.0541 |
| SC35-2 | Ada Boost Regressor | 2.2417 | 8.7638 | 2.9504 | 0.7930 | 0.1955 | 0.8460 |
| SC35-3 | Light Gradient Boosting Machine | 0.8120 | 1.4175 | 1.1828 | 0.9738 | 0.0991 | 0.1561 |
| CC50-1 | Ada Boost Regressor | 1.9144 | 5.9810 | 2.4412 | 0.7506 | 0.2611 | 0.3005 |
| CC50-2 | Ada Boost Regressor | 0.5624 | 0.5696 | 0.7409 | 0.9243 | 0.1398 | 0.6395 |
| CC50-3 | K Neighbors Regressor | 0.1965 | 0.1007 | 0.3011 | 0.9803 | 0.0766 | 0.3933 |
| SC50-1 | K Neighbors Regressor | 0.1665 | 0.0565 | 0.2360 | 0.9959 | 0.0323 | 0.0387 |
| SC50-2 | Extra Trees Regressor | 0.0548 | 0.0071 | 0.0800 | 0.9964 | 0.0127 | 0.195 |
| SC50-3 | K Neighbors Regressor | 0.178 | 0.0591 | 0.2413 | 0.9951 | 0.0338 | 0.0312 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karabulut, M. Experimental and Regression Modeling of Short-Term Flexural Behavior of Steel- and GFRP-Reinforced Early-Age Concrete Beams. Buildings 2025, 15, 4049. https://doi.org/10.3390/buildings15224049
Karabulut M. Experimental and Regression Modeling of Short-Term Flexural Behavior of Steel- and GFRP-Reinforced Early-Age Concrete Beams. Buildings. 2025; 15(22):4049. https://doi.org/10.3390/buildings15224049
Chicago/Turabian StyleKarabulut, Muhammet. 2025. "Experimental and Regression Modeling of Short-Term Flexural Behavior of Steel- and GFRP-Reinforced Early-Age Concrete Beams" Buildings 15, no. 22: 4049. https://doi.org/10.3390/buildings15224049
APA StyleKarabulut, M. (2025). Experimental and Regression Modeling of Short-Term Flexural Behavior of Steel- and GFRP-Reinforced Early-Age Concrete Beams. Buildings, 15(22), 4049. https://doi.org/10.3390/buildings15224049





