Sensitivity Analysis of Foundation Soil Physical–Mechanical Properties on Pile Foundation Stability
Abstract
1. Introduction
2. Research Background and Study Site
2.1. Engineering Geology
2.2. Test Pile Installation
2.3. Engineering Test Data and Result Analysis
- (1)
- Under twice the characteristic load, the settlement was significantly lower than the code-specified limit (40 mm), with the pile foundation remaining in the linear elastic stage and demonstrating highly predictable behavior. This offers a reference for optimizing pile dimensions and precisely controlling settlement.
- (2)
- The results indicate favorable geological conditions of the bearing stratum at the pile tip (sandy soil) in this area. Based on an accurate assessment of the mechanical properties of the soil layers, there exists potential for optimizing pile foundation design by reducing pile length.
- (3)
- The findings reveal that the current design methodology in this region tends to be conservative in its empirical correlation between soil physical–mechanical properties and pile bearing capacity.
3. Establishment of the Pile–Soil Model
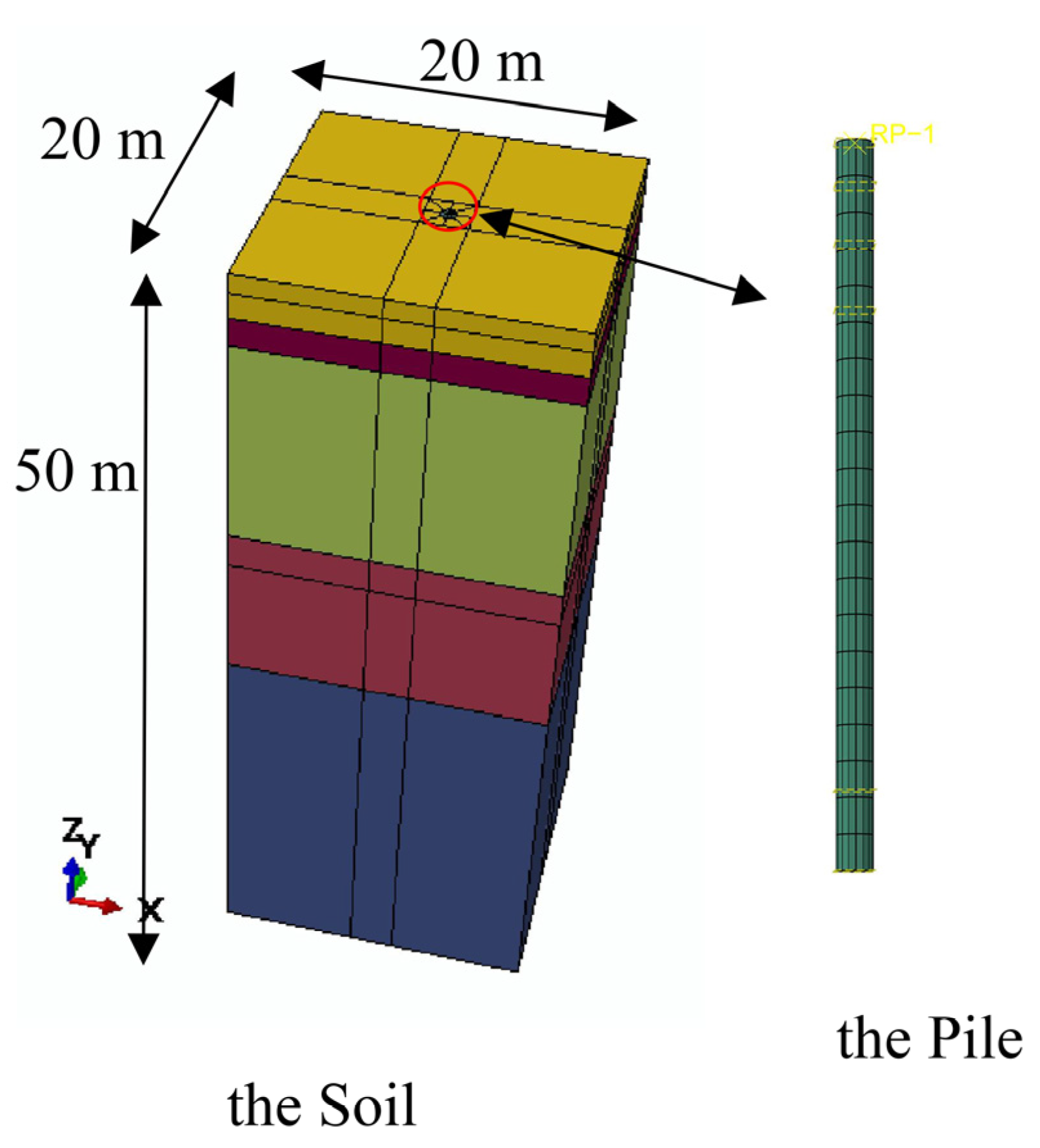
3.1. Geometric Model
3.2. Constitutive Model
3.2.1. Pile
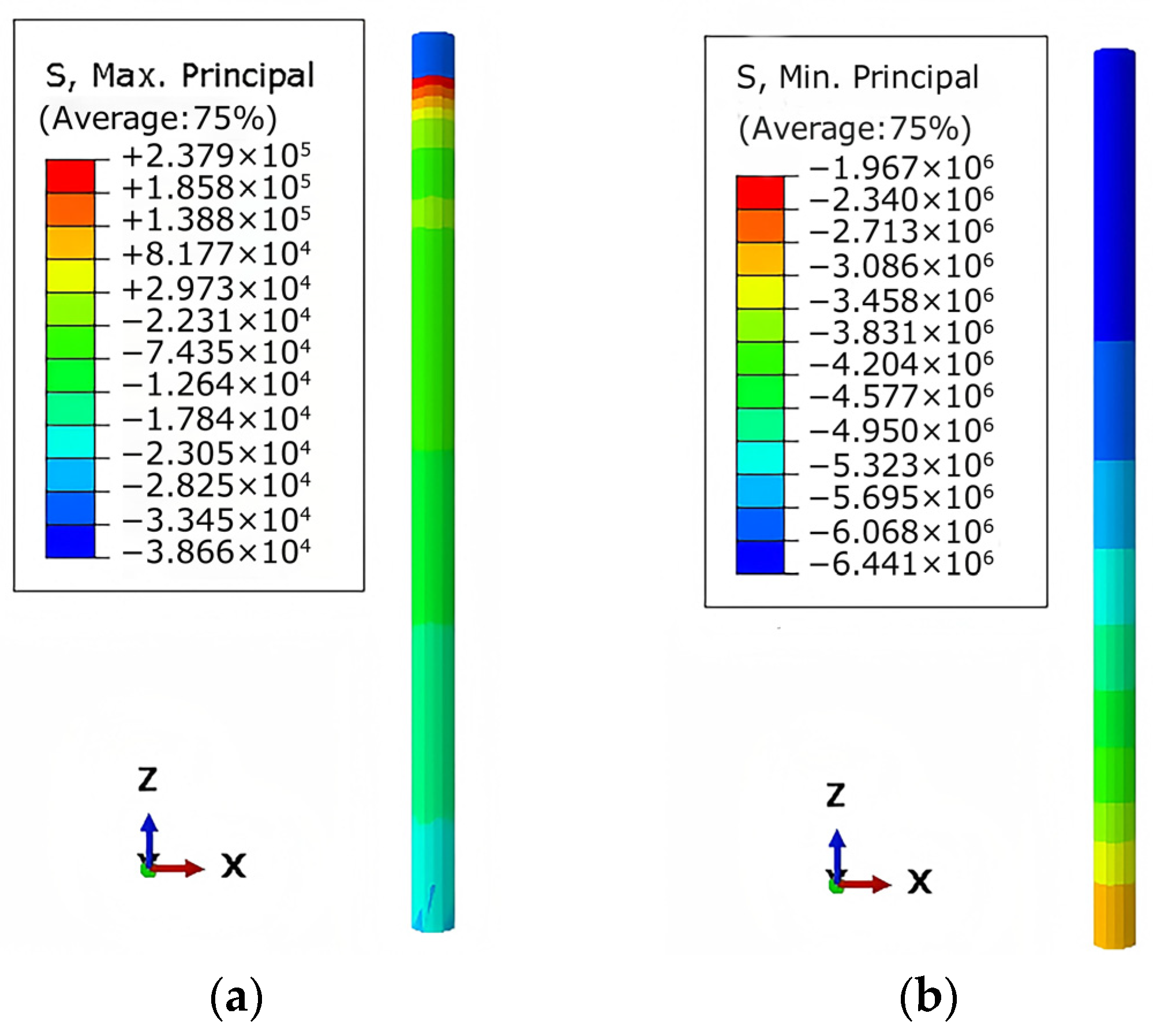
3.2.2. Soil
3.3. Contact Conditions
3.4. Boundary Conditions
- (1)
- In the soil model, all nodes on the lateral boundary planes parallel to the x-direction were constrained against displacement in the transverse direction (y-direction) [32].
- (2)
- In the soil model, all nodes on the lateral boundary planes parallel to the y-direction were constrained against displacement in the transverse direction (x-direction).
- (3)
- (4)
- At the pile–soil interface, constraints in both X and Y directions were applied to the soil prior to the activation of the pile model.
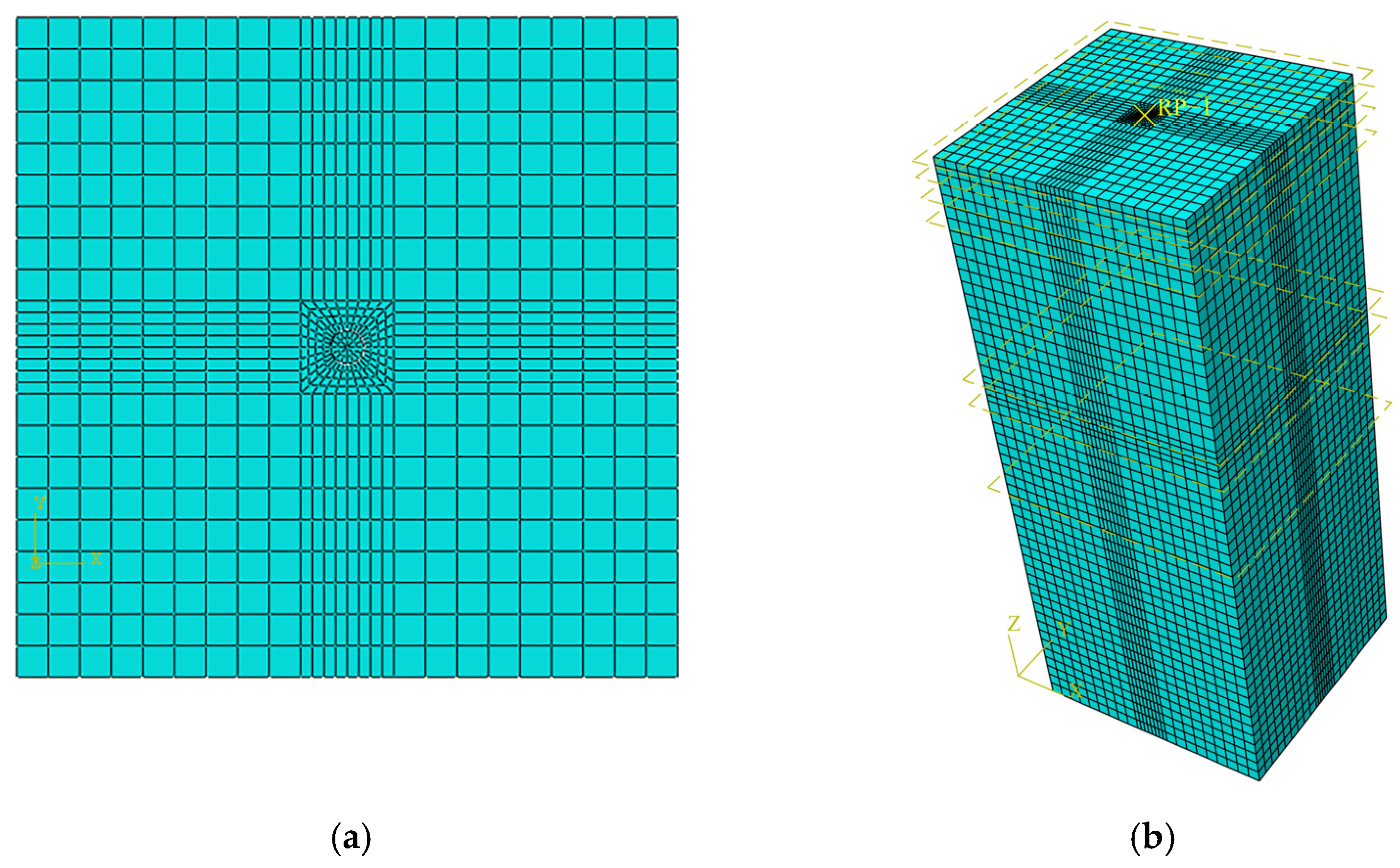
3.5. Mesh Generation and Independence Verification
3.6. Analysis Step
3.7. Comparison and Verification of Test Results
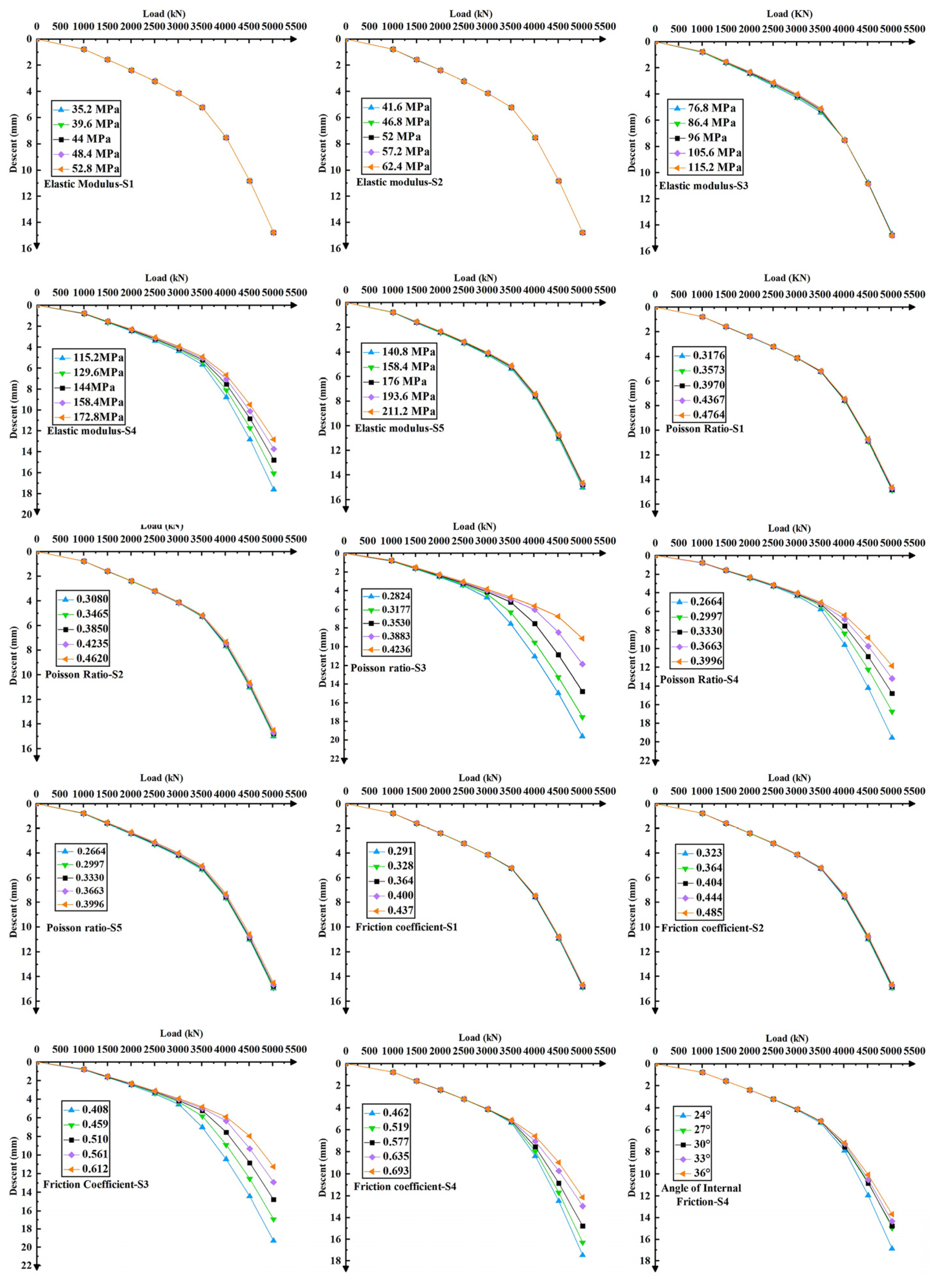
4. Sensitivity of Pile Stability to Soil Parameters
4.1. Selection of Factors and Evaluation Indicators
4.2. Variable-Control Experimental Design
- (1)
- Preliminary experiments: Each selected factor was reduced by 20% relative to its baseline value to identify insensitive variables.
- (2)
- Refined experiments: Factors deemed insensitive in the preliminary step were discarded. For the remaining factors, controlled tests were performed with baseline values taken from the engineering data and allowable fluctuations constrained within ±20%. Each experimental group included five variables, and the uniform variation rate of 10% applied to each independent variable.
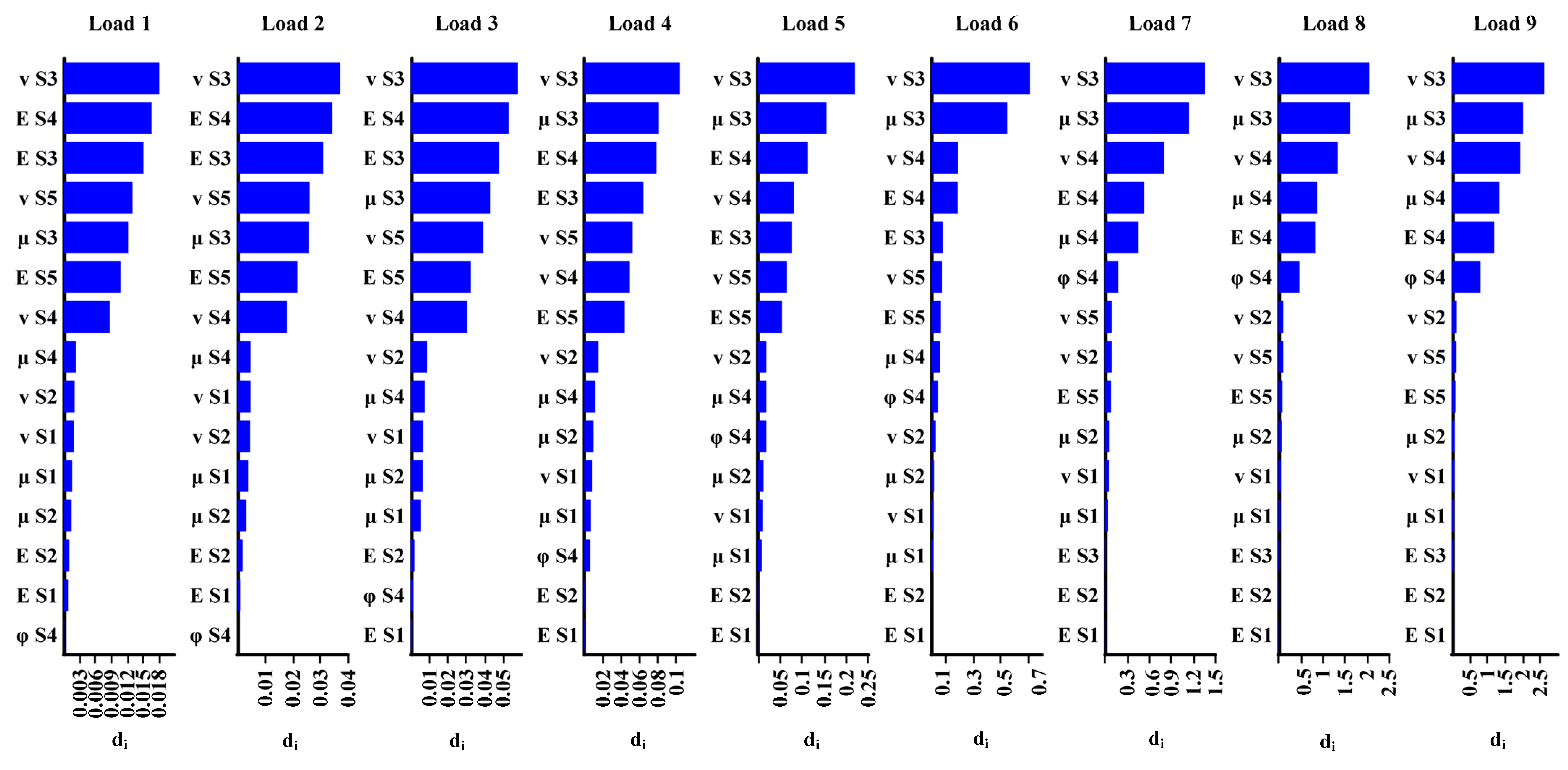
4.3. Data Processing and Results
5. Sensitivity of Soil-Property Effects on Ultimate Bearing Capacity
5.1. Pile–Soil Model Valication
5.2. Orthogonal Test Design and Result Analysis
6. Discussion
7. Conclusions
- (1)
- For the M-C model applied to sandy soils in the Kashgar region of Xinjiang, China, it is recommended to set the elastic modulus at eight times the compression modulus. Accordingly, during model optimization, priority should be given to the proportional adjustment of the friction coefficient, elastic modulus, and Poisson’s ratio of the pile-end soil.
- (2)
- The physical–mechanical properties of the pile-end soil and the adjacent strata (both above and below) exhibit relatively high sensitivity to settlement. As the load increases, the influence of the friction coefficient and Poisson’s ratio on settlement becomes more pronounced, while the sensitivity of the elastic modulus gradually decreases.
- (3)
- The sensitivity of the internal friction angle and the elastic modulus is independent for soil stratum thickness; only the values corresponding to the pile-end soil significantly affect settlement. In contrast, the sensitivity of the friction coefficient and Poisson’s ratio is influenced by the thickness of both the pile-end soil and the overlying adjacent strata.
- (4)
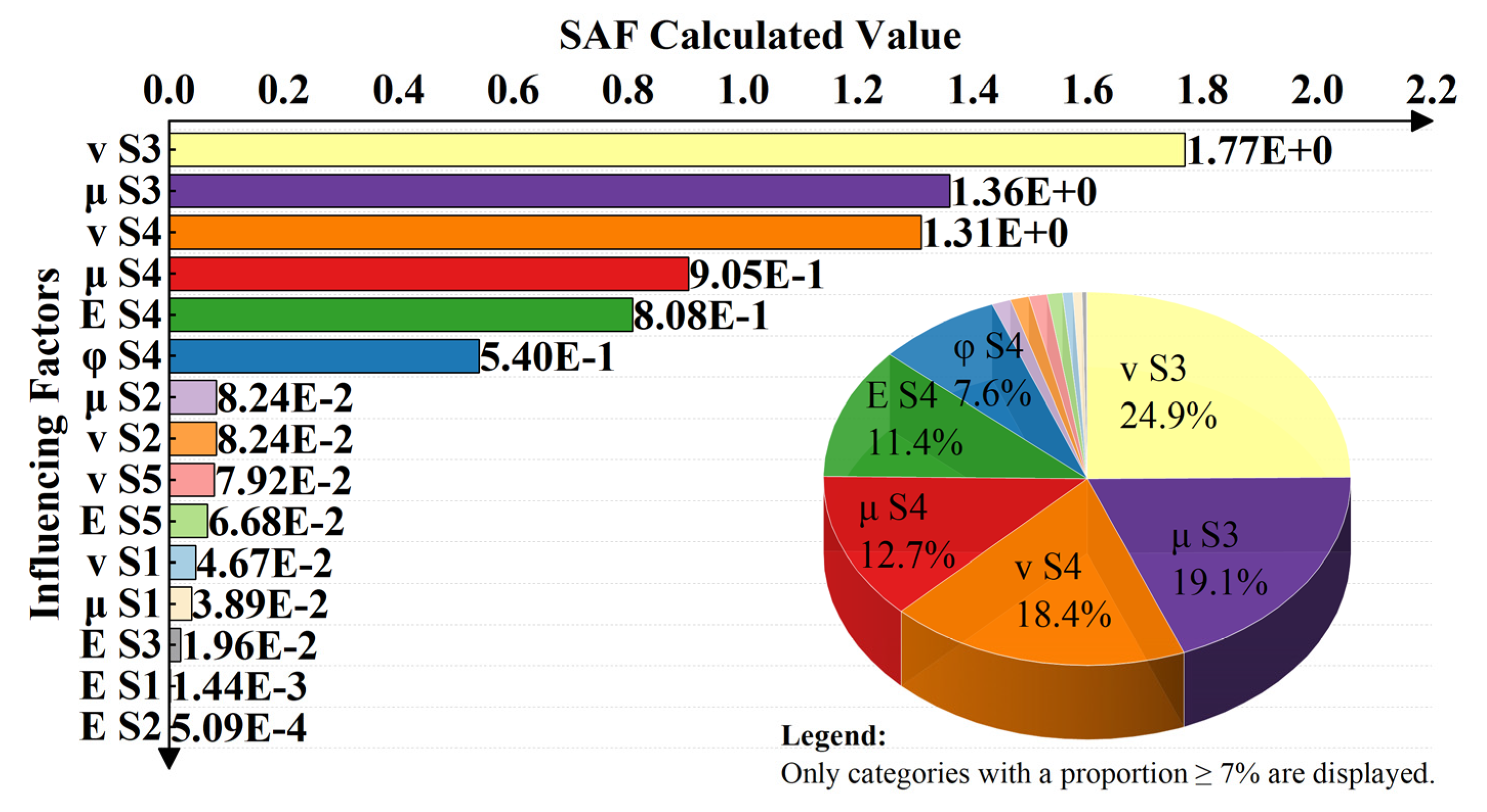
- A sensitivity analysis was conducted using orthogonal experimental design, with the ultimate bearing capacity of the pile foundation as the evaluation index. Results from multi-factor ANOVA, sensitivity analysis factor (SAF), and variance inflation factor (VIF) collinearity analysis showed that all P-values were below the 0.05 significance level, confirming the statistically significant influence of each parameter. All VIF value remained below 10, indicating an absence of serious multicollinearity between parameters. Based on the experimental outcomes, the sensitivity ranking of physical–mechanical properties affecting settlement is as follows: friction coefficient S3, Poisson’s ratio S4, Poisson’s ratio S3, friction coefficient S4, and elastic modulus S4.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.; Duan, W.; Cai, G.; Zhang, L.; Zou, H.; Liu, S. Robust geotechnical design of piles incorporating system reliability. J. Geotech. Geoenviron. Eng. 2025, 151, 04025012. [Google Scholar] [CrossRef]
- Das, S.K.; Suman, S. Prediction of lateral load capacity of pile in clay using multivariate adaptive regression spline and functional network. Arab. J. Sci. Eng. 2015, 40, 1565–1578. [Google Scholar] [CrossRef]
- Ahmed, M.N.; Amr, F.E.; Mohamed, I.A. Soil stiffness from back-analysis of pile load tests in Al burrullus. Ain Shams Eng. J. 2022, 13, 101784. [Google Scholar] [CrossRef]
- Randolph, M.F. Science and empiricism in pile foundation design. Géotechnique 2003, 53, 847–875. [Google Scholar] [CrossRef]
- Comodromos, E.M.; Papadopoulou, M.C.; Rentzeperis, I.K. Pile foundation analysis and design using experimental data and 3-D numerical analysis. Comput. Geotech. 2009, 36, 819–836. [Google Scholar] [CrossRef]
- Yan, N.; Hao, Z.; Bai, X.; Cui, L.; Yin, J.; Liu, C.; Zhang, Y. Load-bearing characteristics and optimization design for rock-socketed bored piles in sandy silty clay in coastal areas. Soil Dyn. Earthq. Eng. 2025, 190, 109207. [Google Scholar] [CrossRef]
- Liu, H.; Yan, X.; Zhang, N.; Guo, L.; Wang, Z.; Zhou, F. Bearing capacity design of strength composite piles considering dominant failure modes and calibrated adjustment coefficients. Appl. Sci. 2025, 15, 10313. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, H.; Gao, L.; Zhu, F. Experimental study on vertical loading model of single pile and group pile in sandy soil under scouring conditions. J. Civ. Environ. Eng. 2023, 280, 114672. [Google Scholar] [CrossRef]
- Qin, S.; Gao, L.; Wei, B.; QIan, J. Bearing characteristics of cast-in-place piles based on optical fiber technology and finite element calculation. Sci. Technol. Eng. 2023, 23, 5685–5692. [Google Scholar]
- Lee, C.J.; Bolton, M.D.; Al-Tabbaa, A. Numerical modelling of group effects on the distribution of dragloads in pile foundations. Géotechnique 2002, 52, 325–335. [Google Scholar] [CrossRef]
- Sun, Z.; Han, Y.; Liu, F.; Wang, Q. Safety study and analysis of the value of friction coefficient of embedded rock piles on their bearing characteristics. Ce/papers 2025, 8, 710–719. [Google Scholar] [CrossRef]
- Bai, F.; Lu, Y.; Yang, J. Multi-scale investigation on bearing capacity and load-transfer mechanism of screw pile group via model tests and DEM simulation. Buildings 2025, 15, 3581. [Google Scholar] [CrossRef]
- Fan, X. Analysis of Bearing Capacity of Large Diameter Long Pile Group in Water-Rich Sand Area. Master’s Thesis, Xi’an University of Architecture and Technology, Xian, China, 2024. [Google Scholar]
- Sun, Z.; Wang, Q.; Min, R.; Duan, Q. Sensitivity analysis of influencing factors of pile foundation stability based on field experiment. Structures 2023, 54, 14–22. [Google Scholar] [CrossRef]
- Qu, T.; Xu, J.; Shi, Y. Equivalent elastic modulus of reinforced concrete members under different stQU tiejunress states. Concrete 2016, 11, 119–122. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, F.; Han, Y.; Min, R. Prediction of ultimate bearing capacity of rock-socketed piles based on GWO-SVR algorithm. Structures 2024, 61, 106039. [Google Scholar] [CrossRef]
- Li, G.; Zhang, J.; Liu, J.; Li, H. Study on the uplift bearing capacity of rock-socketed piles. Soil Mech. Found. Eng. 2021, 58, 203–208. [Google Scholar] [CrossRef]
- Cheng, F.; Li, M.; Li, Q. Multi-method sensitivity analysis of influencing factors on the lateral displacement of retaining piles in asymmetric excavations in soft soil areas. Symmetry 2025, 17, 1525. [Google Scholar] [CrossRef]
- Li, H.; Wang, F.; Zhang, J.; Liang, R.; Wen, Y. Sensitivity analysis and determination of some parameters of the rock RHT model. Chin. J. High Press. Phys. 2025, 39, 66–76. [Google Scholar] [CrossRef]
- Basha, A.; Tayehand, B.A.; Maglad, A.M.; Mansour, W. Feasibility of improving shear performance of RC pile caps using various internal reinforcement configurations: Tests and finite element modelling. Eng. Struct. 2023, 289, 116340. [Google Scholar] [CrossRef]
- Ali, D.; Mahdy, K.; Shin, T.A.; Danial, J.A. Estimation of ultimate bearing capacity of driven piles in c-φ soil using MLP-GWO and ANFIS-GWO models: A comparative study. Soft Comput. 2020, 25, 4103. [Google Scholar] [CrossRef]
- Zhu, H.; Ding, C.; Lu, Y.; Li, G. Analysis of bearing-settlement characteristics of extra-long bored piles in URT deep soft stratum underground station. Urban. Mass. Transit. 2024, 27, 143–148. [Google Scholar] [CrossRef]
- Chopra, M.B.; Dargush, G.F. Finite-element analysis of time-dependent large-deformation problems. Int. J. Numer. Anal. Methods Geomech. 1992, 16, 101–130. [Google Scholar] [CrossRef]
- Kaur, A.; Singh, H.; Jha, J.N. Numerical study of laterally loaded piles in soft clay dense sand. Civ. Eng. J.-Tehran 2021, 7, 730–746. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Hong, Y.; He, B.; Zhu, R. Quantifying the influence of pile diameter on the load transfer curves of laterally loaded monopile in sand. Appl. Ocean Res. 2020, 101, 102196. [Google Scholar] [CrossRef]
- JGJ 106-2014; Technical Code for Testing of Buliding Foundation Piles. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2014.
- Hooman, H.; Mohammad, M.T.; Vahid, T. Application of improved ANFIS approaches to estimate bearing capacity of piles. Soft Comput. 2019, 23, 9537–9549. [Google Scholar] [CrossRef]
- Gogot, S.B.; Melisa, K.; Dewi, H.W. Bearing capacity of pile foundations embedded in clays and sands layer predicted using PDA test and static load test. Procedia Eng. 2015, 125, 406–410. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Tang, L.; Liu, Z.; Jiang, Z.; Liu, Y.; Xi, H. Modeling and computing parameters of three-dimensional voronoi models in nonlinear finite element simulation of closed-cell metallic foams. Mech. Adv. Mater. Struct. 2018, 25, 1265–1275. [Google Scholar] [CrossRef]
- Chung, S.; Yang, S. Numerical analysis of small-scale model pile in unsaturated clayey soil. Int. J. Civ. Eng. 2016, 15, 877–886. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, J.; Wang, D.; Fang, L.; Xie, M. Vertical bearing behavior of reinforced composite piles in dense sandy soils. Buildings 2025, 15, 3650. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Alisawi, A.T.; Collins, P.E.F.; Cashell, K.A. Nonlinear numerical simulation of physical shaking table test, using three different soil constitutive models. Soil. Dyn. Earthq. Eng. 2021, 143, 106617. [Google Scholar] [CrossRef]
- Zhao, H.; Tian, F.; Huang, Z.J.; Zeng, Z.R.; Qiu, J.S. Experiment study on horizontal bearing characteristics of monopile under multi-layer foundation conditions. Actaenergiae Sol. Sol. Sin. 2025, 46, 134–139. [Google Scholar] [CrossRef]
- Fei, K.; Zhang, J. Application of ABAQUS in Geotechnical Engineering; China Water & Power Press: Beijing, China, 2010. [Google Scholar]
- Du, P.; Liu, X.; Zhou, D.; Feng, C. Influence and bearing mechanisms of thorn shape on compressive characteristics of thorn piles. Buildings 2025, 15, 3328. [Google Scholar] [CrossRef]
- JGJ 138-2016; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- Kong, D.; Liu, Y.; Deng, M.; Zhao, X. Analysis of influencing factors of lateral soil resistance distribution characteristics around monopile foundation for offshore wind power. Appl. Ocean Res. 2020, 97, 102106. [Google Scholar] [CrossRef]
- Bagheri, M.; Malidarreh, N.R.; Ghaseminejad, V.; Asgari, A. Seismic resilience assessment of RC superstructures on long–short combined piled raft foundations: 3D SSI modeling with pounding effects. Structures 2025, 81, 110176. [Google Scholar] [CrossRef]



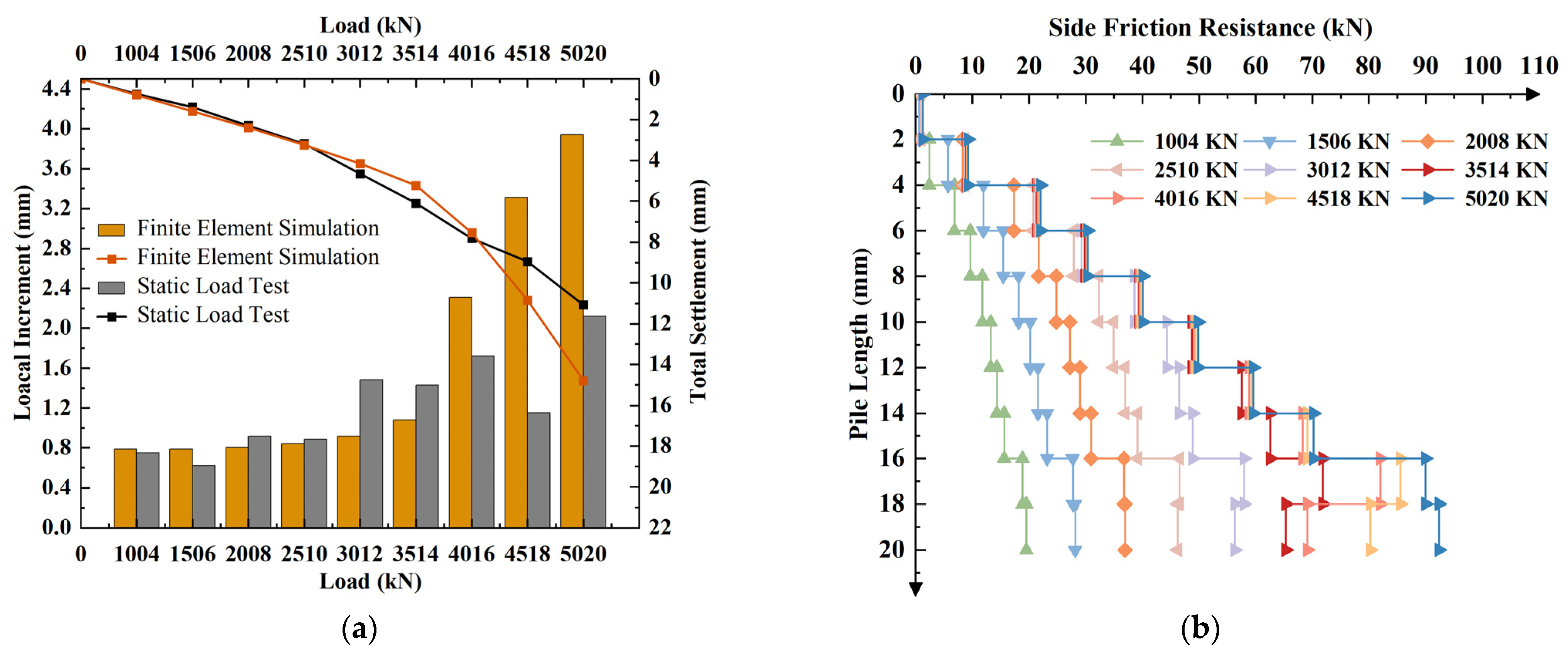
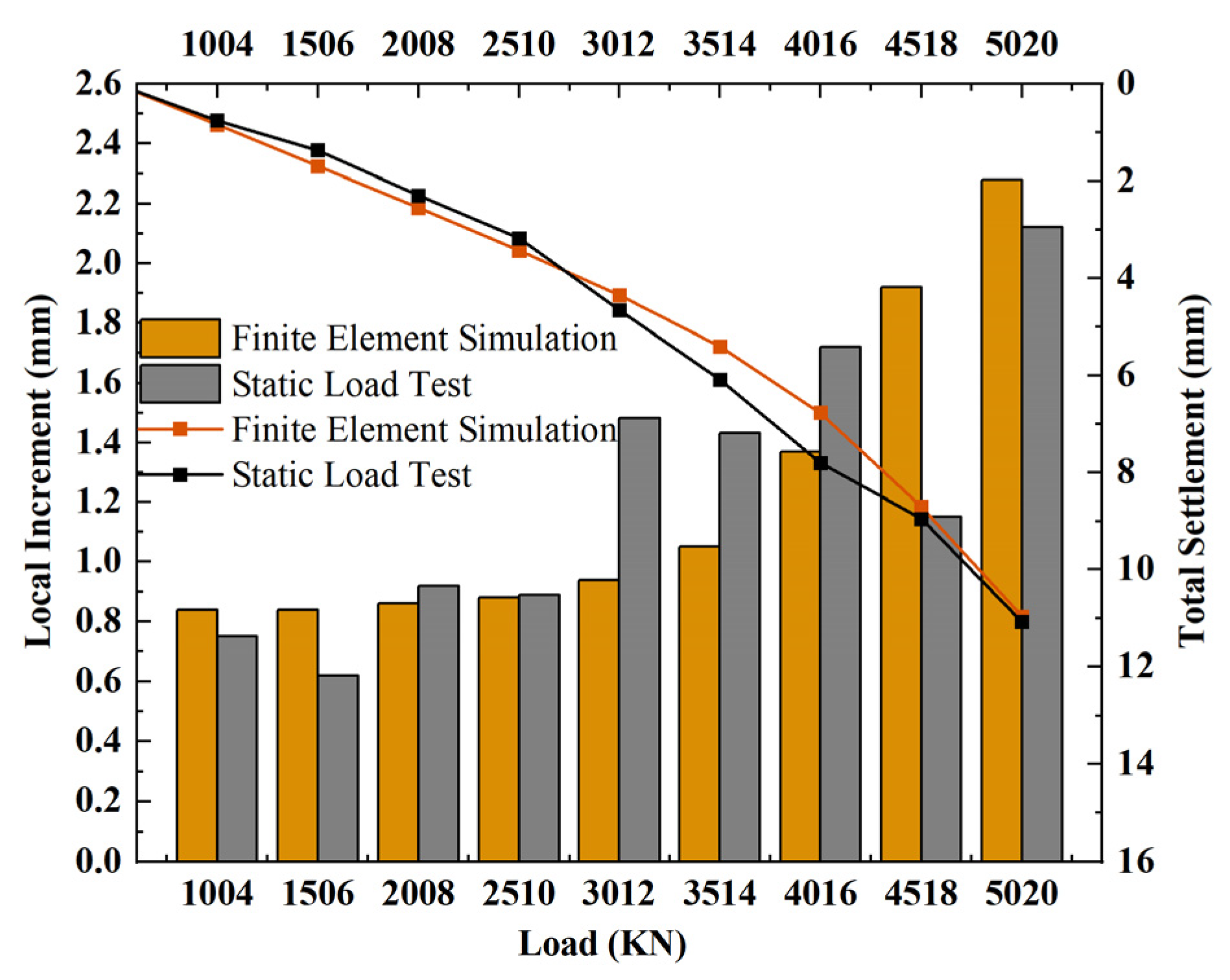
| Load: kN | Local Increment: mm | Total Settlement: mm | Load: kN | Local Increment: mm | Total Settlement: mm |
|---|---|---|---|---|---|
| 1004 | 0.75 | 0.75 | 3514 | 1.43 | 6.09 |
| 1506 | 0.62 | 1.37 | 4016 | 1.72 | 7.81 |
| 2008 | 0.92 | 2.29 | 4518 | 1.15 | 8.96 |
| 2510 | 0.89 | 3.18 | 5020 | 2.12 | 11.08 |
| 3012 | 1.48 | 4.66 |
| Soil Stratum | m−3) | (MPa) | ν | (KPa) | φ (°) | μ |
|---|---|---|---|---|---|---|
| ② silt (above 10.0 m) | 17.0 | 5.5 | 0.397 | 12 | 20 | 0.364 |
| ② silt (below 10.0 m) | 17.5 | 6.5 | 0.385 | 14 | 22 | 0.404 |
| ③ fine sand (above 25.0 m) | 18.0 | 12 | 0.353 | 0 | 27 | 0.510 |
| ③ fine sand (25.0–35.0 m) | 18.5 | 18 | 0.333 | 0 | 30 | 0.577 |
| ③ fine sand (below 35.0 m) | 19.0 | 22 | 0.333 | 0 | 30 | - |
| No | S1 | S2 | S3 | S4 | S5 | Load /kN | Settlement /mm | Difference /mm |
|---|---|---|---|---|---|---|---|---|
| K1 | 0.288 | 0.305 | 0.335 | 0.346 | 0.346 | 5020 | 29.51 | 18.43 |
| K2 | 0.268 | 0.296 | 0.369 | 0.414 | 0.414 | 5020 | 26.39 | 15.32 |
| K3 | 0.364 | 0.404 | 0.510 | 0.577 | 0.577 | 5020 | 14.80 | 3.72 |
| Element Quantity | Total Settlement (Cumulative): mm |
|---|---|
| 20,080 | 14.791 |
| 42,580 | 14.782 |
| 57,680 | 14.705 |
| Influencing Factors | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| elastic modulus | 14.8017 | 14.7952 | 14.8137 | 17.6391 | 15.0325 |
| Poisson’s ratio | 14.9142 | 15.0045 | 19.6206 | 19.5935 | 19.9884 |
| friction coefficient | 14.9085 | 14.9544 | 19.3175 | 17.4931 | - |
| internal friction angle | 14.7958 | 14.7958 | 14.7958 | 16.8978 | 14.7958 |
| Code | v-S3 | μ-S3 | v-S4 | μ-S4 | E-S4 | Code | v-S3 | μ-S3 | v-S4 | μ-S4 | E-S4 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.318 | 0.459 | 0.36 | 0.624 | 129.6 | 4 | 0.371 | 0.536 | 0.42 | 0.728 | 151.2 |
| 2 | 0.335 | 0.485 | 0.38 | 0.658 | 136.8 | 5 | 0.388 | 0.561 | 0.44 | 0.762 | 158.4 |
| 3 | 0.353 | 0.51 | 0.40 | 0.693 | 144 |
| Code | Factor | Level | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | v-S3 | μ-S3 | v-S4 | μ-S4 | E-S4 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0.318 | 0.459 | 0.36 | 0.624 | 113.4 |
| 2 | 1 | 2 | 3 | 4 | 5 | 0.318 | 0.485 | 0.40 | 0.728 | 138.6 |
| 3 | 1 | 3 | 5 | 2 | 4 | 0.318 | 0.51 | 0.44 | 0.658 | 132.3 |
| 4 | 1 | 4 | 2 | 5 | 3 | 0.318 | 0.536 | 0.38 | 0.762 | 126 |
| 5 | 1 | 5 | 4 | 3 | 2 | 0.318 | 0.561 | 0.42 | 0.693 | 119.7 |
| 6 | 2 | 1 | 5 | 4 | 3 | 0.335 | 0.459 | 0.44 | 0.728 | 126 |
| 7 | 2 | 2 | 2 | 2 | 2 | 0.335 | 0.485 | 0.38 | 0.658 | 119.7 |
| 8 | 2 | 3 | 4 | 5 | 1 | 0.335 | 0.51 | 0.42 | 0.762 | 113.4 |
| 9 | 2 | 4 | 1 | 3 | 5 | 0.335 | 0.536 | 0.36 | 0.693 | 138.6 |
| 10 | 2 | 5 | 3 | 1 | 4 | 0.335 | 0.561 | 0.40 | 0.624 | 132.3 |
| 11 | 3 | 1 | 4 | 2 | 5 | 0.353 | 0.459 | 0.42 | 0.658 | 138.6 |
| 12 | 3 | 2 | 1 | 5 | 4 | 0.353 | 0.485 | 0.36 | 0.762 | 132.3 |
| 13 | 3 | 3 | 3 | 3 | 3 | 0.353 | 0.51 | 0.40 | 0.693 | 126 |
| 14 | 3 | 4 | 5 | 1 | 2 | 0.353 | 0.536 | 0.44 | 0.624 | 119.7 |
| 15 | 3 | 5 | 2 | 4 | 1 | 0.353 | 0.561 | 0.38 | 0.728 | 113.4 |
| 16 | 4 | 1 | 3 | 5 | 2 | 0.371 | 0.459 | 0.40 | 0.762 | 119.7 |
| 17 | 4 | 2 | 5 | 3 | 1 | 0.371 | 0.485 | 0.44 | 0.693 | 113.4 |
| 18 | 4 | 3 | 2 | 1 | 5 | 0.371 | 0.51 | 0.38 | 0.624 | 138.6 |
| 19 | 4 | 4 | 4 | 4 | 4 | 0.371 | 0.536 | 0.42 | 0.728 | 132.3 |
| 20 | 4 | 5 | 1 | 2 | 3 | 0.371 | 0.561 | 0.36 | 0.658 | 126 |
| 21 | 5 | 1 | 2 | 3 | 4 | 0.388 | 0.459 | 0.38 | 0.693 | 132.3 |
| 22 | 5 | 2 | 4 | 1 | 3 | 0.388 | 0.485 | 0.42 | 0.624 | 126 |
| 23 | 5 | 3 | 1 | 4 | 2 | 0.388 | 0.51 | 0.36 | 0.728 | 119.7 |
| 24 | 5 | 4 | 3 | 2 | 1 | 0.388 | 0.536 | 0.40 | 0.658 | 113.4 |
| 25 | 5 | 5 | 5 | 5 | 5 | 0.388 | 0.561 | 0.44 | 0.762 | 138.6 |
| Code | 1004 | 1506 | 2008 | 2510 | 3012 | 3514 | 4016 | 4518 | 5020 | N-Max |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.859 | 1.724 | 2.629 | 3.670 | 5.042 | 7.678 | 10.998 | 14.813 | 19.345 | 7458 |
| 2 | 0.799 | 1.599 | 2.415 | 3.308 | 4.322 | 5.599 | 7.357 | 9.472 | 12.253 | 9540 |
| 3 | 0.786 | 1.573 | 2.375 | 3.243 | 4.223 | 5.394 | 6.986 | 9.182 | 11.386 | 10,055 |
| 4 | 0.808 | 1.616 | 2.438 | 3.317 | 4.303 | 5.498 | 7.162 | 9.345 | 12.179 | 9696 |
| 5 | 0.797 | 1.593 | 2.404 | 3.263 | 4.222 | 5.344 | 6.813 | 8.983 | 11.189 | 12,399 |
| 6 | 0.796 | 1.593 | 2.409 | 3.306 | 4.333 | 5.587 | 7.118 | 9.215 | 11.548 | 9845 |
| 7 | 0.823 | 1.649 | 2.491 | 3.412 | 4.462 | 5.851 | 8.323 | 11.080 | 14.437 | 8536 |
| 8 | 0.807 | 1.614 | 2.437 | 3.322 | 4.318 | 5.506 | 7.027 | 9.144 | 11.659 | 9626 |
| 9 | 0.792 | 1.582 | 2.384 | 3.221 | 4.138 | 5.191 | 6.720 | 8.908 | 11.700 | 9672 |
| 10 | 0.783 | 1.564 | 2.356 | 3.179 | 4.074 | 5.078 | 6.391 | 8.799 | 11.370 | 11,742 |
| 11 | 0.782 | 1.564 | 2.361 | 3.209 | 4.149 | 5.245 | 6.781 | 8.954 | 11.321 | 9687 |
| 12 | 0.800 | 1.600 | 2.413 | 3.269 | 4.215 | 5.314 | 6.831 | 9.139 | 12.220 | 9034 |
| 13 | 0.791 | 1.580 | 2.383 | 3.222 | 4.141 | 5.179 | 6.515 | 8.623 | 11.023 | 9672 |
| 14 | 0.777 | 1.553 | 2.341 | 3.160 | 4.053 | 5.053 | 6.241 | 8.205 | 10.795 | 10,114 |
| 15 | 0.802 | 1.603 | 2.415 | 3.253 | 4.161 | 5.167 | 6.376 | 8.259 | 10.672 | 12,094 |
| 16 | 0.801 | 1.602 | 2.417 | 3.280 | 4.234 | 5.326 | 6.749 | 8.817 | 11.415 | 9304 |
| 17 | 0.786 | 1.572 | 2.372 | 3.211 | 4.134 | 5.180 | 6.462 | 8.275 | 10.634 | 9881 |
| 18 | 0.776 | 1.550 | 2.334 | 3.141 | 4.007 | 4.960 | 6.094 | 8.240 | 10.914 | 9403 |
| 19 | 0.760 | 1.518 | 2.286 | 3.071 | 3.906 | 4.811 | 5.821 | 7.044 | 8.867 | 11,031 |
| 20 | 0.785 | 1.568 | 2.361 | 3.168 | 4.024 | 4.955 | 6.009 | 7.698 | 10.251 | 11,999 |
| 21 | 0.785 | 1.569 | 2.364 | 3.189 | 4.082 | 5.076 | 6.268 | 8.203 | 10.799 | 9341 |
| 22 | 0.773 | 1.545 | 2.329 | 3.136 | 4.006 | 4.958 | 6.058 | 7.815 | 10.355 | 9642 |
| 23 | 0.794 | 1.586 | 2.390 | 3.213 | 4.091 | 5.055 | 6.154 | 7.701 | 10.226 | 9303 |
| 24 | 0.785 | 1.567 | 2.361 | 3.170 | 4.031 | 4.963 | 6.006 | 7.313 | 9.884 | 10,047 |
| 25 | 0.733 | 1.463 | 2.202 | 2.951 | 3.724 | 4.548 | 5.433 | 6.404 | 7.558 | 14,305 |
| Factor | Type III Sum of Squares | Degree of Freedom | Mean Square | F | Obvious | VIF |
|---|---|---|---|---|---|---|
| v-S3 | 1,729,055.648 | 4 | 432,263.912 | 33.878 | 0.002 | 1.0 |
| μ-S3 | 37,866,578.170 | 4 | 9,466,644.543 | 741.923 | 0.000 | 1.0 |
| v-S4 | 5,672,024.188 | 4 | 1,418,006.047 | 111.132 | 0.000 | 1.0 |
| μ-S4 | 1,705,524.478 | 4 | 426,381.120 | 33.416 | 0.002 | 1.0 |
| E-S4 | 1,508,075.937 | 4 | 377,018.984 | 29.548 | 0.003 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; He, X.; Guan, Y.; Fan, D.; Gao, R.; Luo, F.; Liu, S. Sensitivity Analysis of Foundation Soil Physical–Mechanical Properties on Pile Foundation Stability. Buildings 2025, 15, 4001. https://doi.org/10.3390/buildings15214001
Ma Y, He X, Guan Y, Fan D, Gao R, Luo F, Liu S. Sensitivity Analysis of Foundation Soil Physical–Mechanical Properties on Pile Foundation Stability. Buildings. 2025; 15(21):4001. https://doi.org/10.3390/buildings15214001
Chicago/Turabian StyleMa, Yuan, Xinghong He, Yao Guan, Debao Fan, Rui Gao, Fan Luo, and Shiyuan Liu. 2025. "Sensitivity Analysis of Foundation Soil Physical–Mechanical Properties on Pile Foundation Stability" Buildings 15, no. 21: 4001. https://doi.org/10.3390/buildings15214001
APA StyleMa, Y., He, X., Guan, Y., Fan, D., Gao, R., Luo, F., & Liu, S. (2025). Sensitivity Analysis of Foundation Soil Physical–Mechanical Properties on Pile Foundation Stability. Buildings, 15(21), 4001. https://doi.org/10.3390/buildings15214001







