Damage Identification of Gas Station Double Layer Grid Structure Based on Time Domain Response Sensitivity Analysis
Abstract
1. Introduction
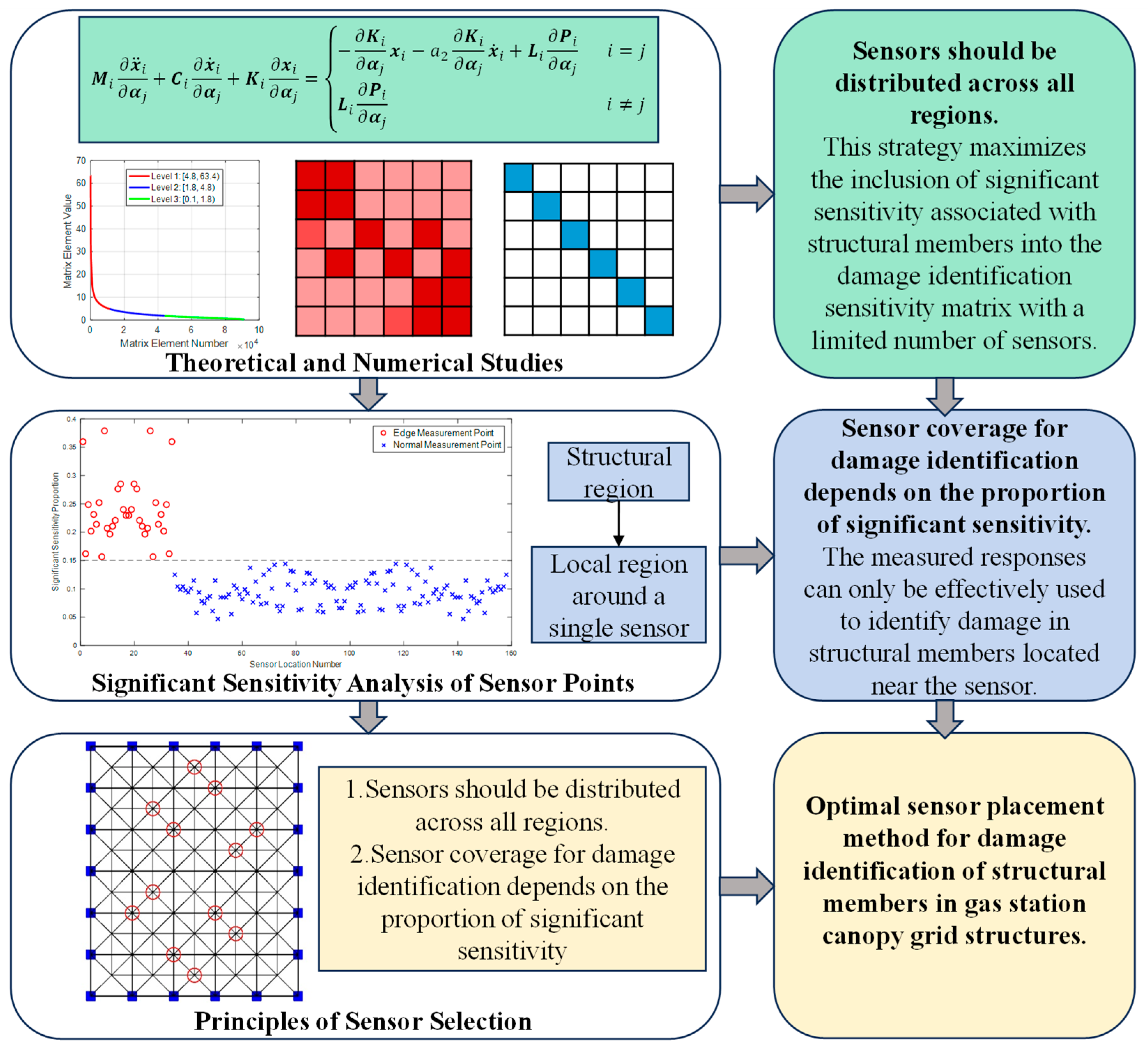
2. Sensitivity-Based Damage Identification Algorithm
3. Response Sensitivity Analysis
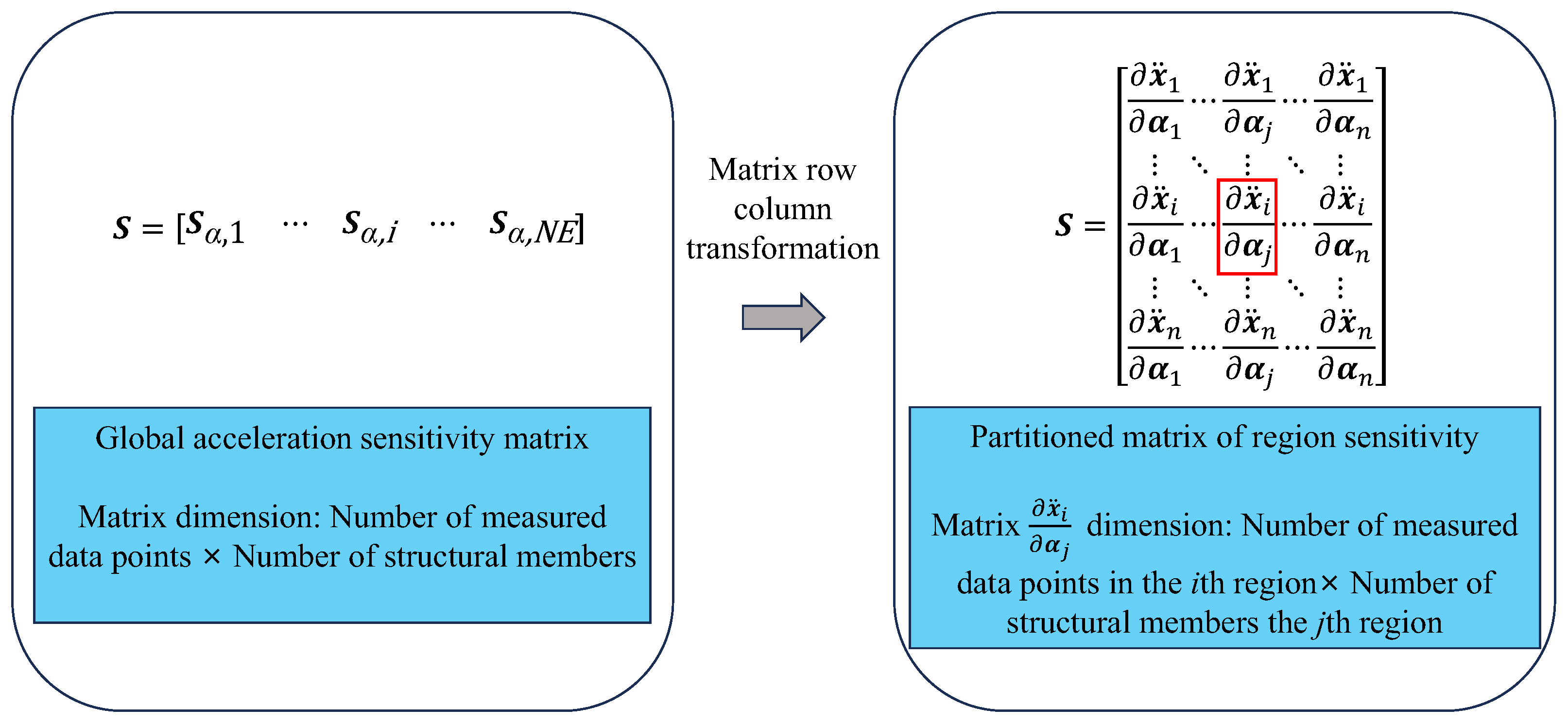
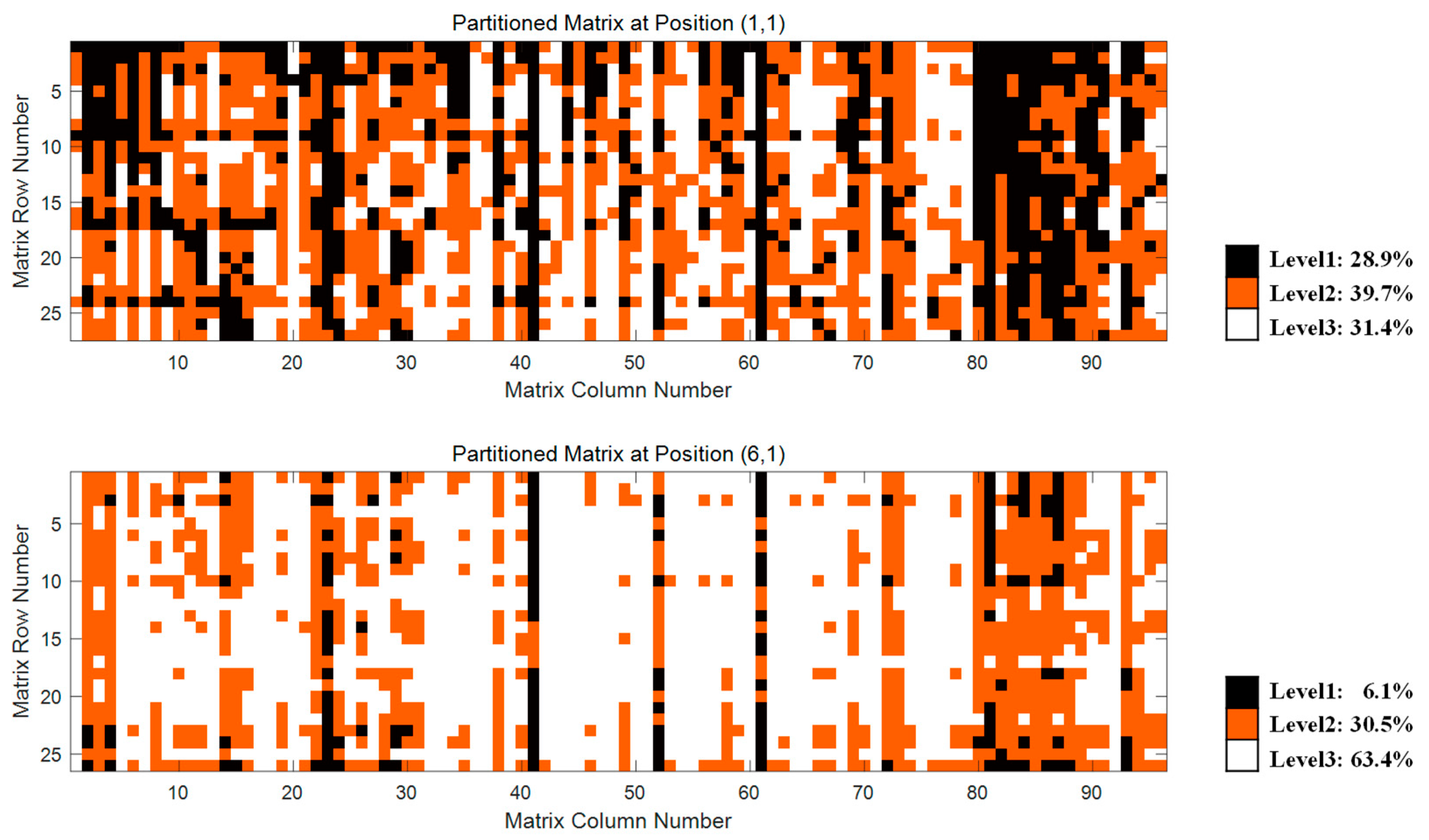
3.1. Feature Analysis of Response Sensitivity Matrix
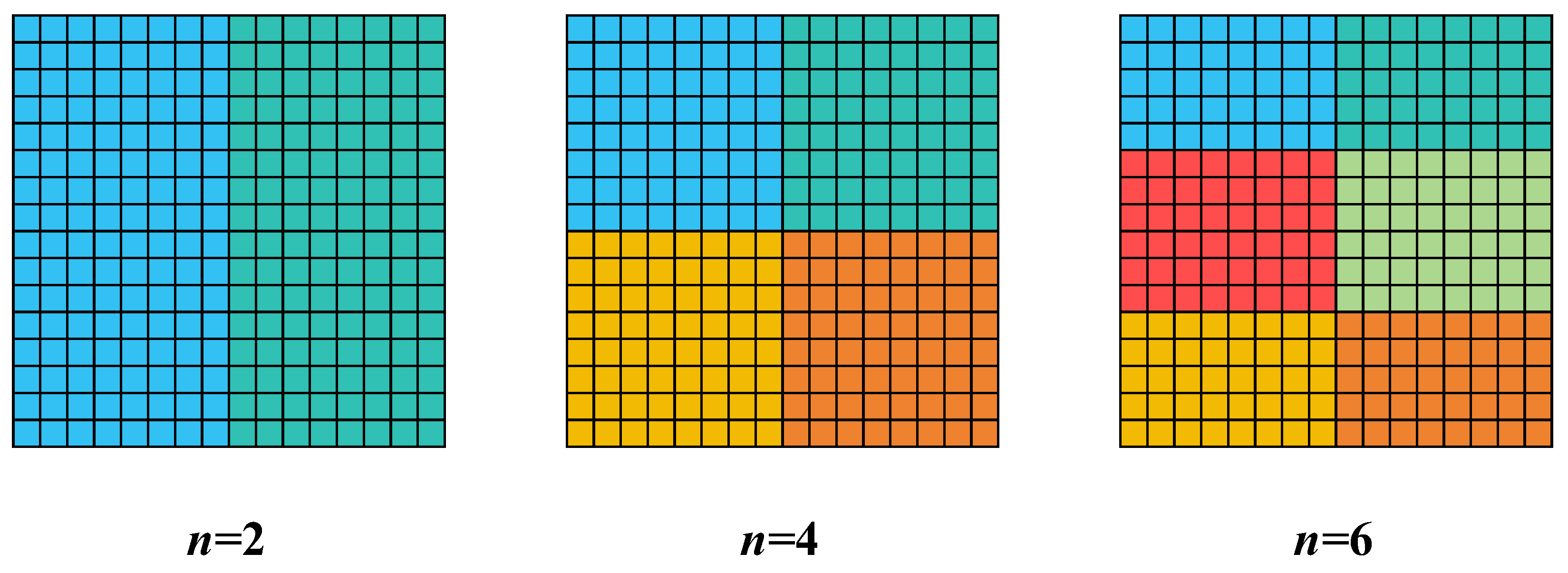
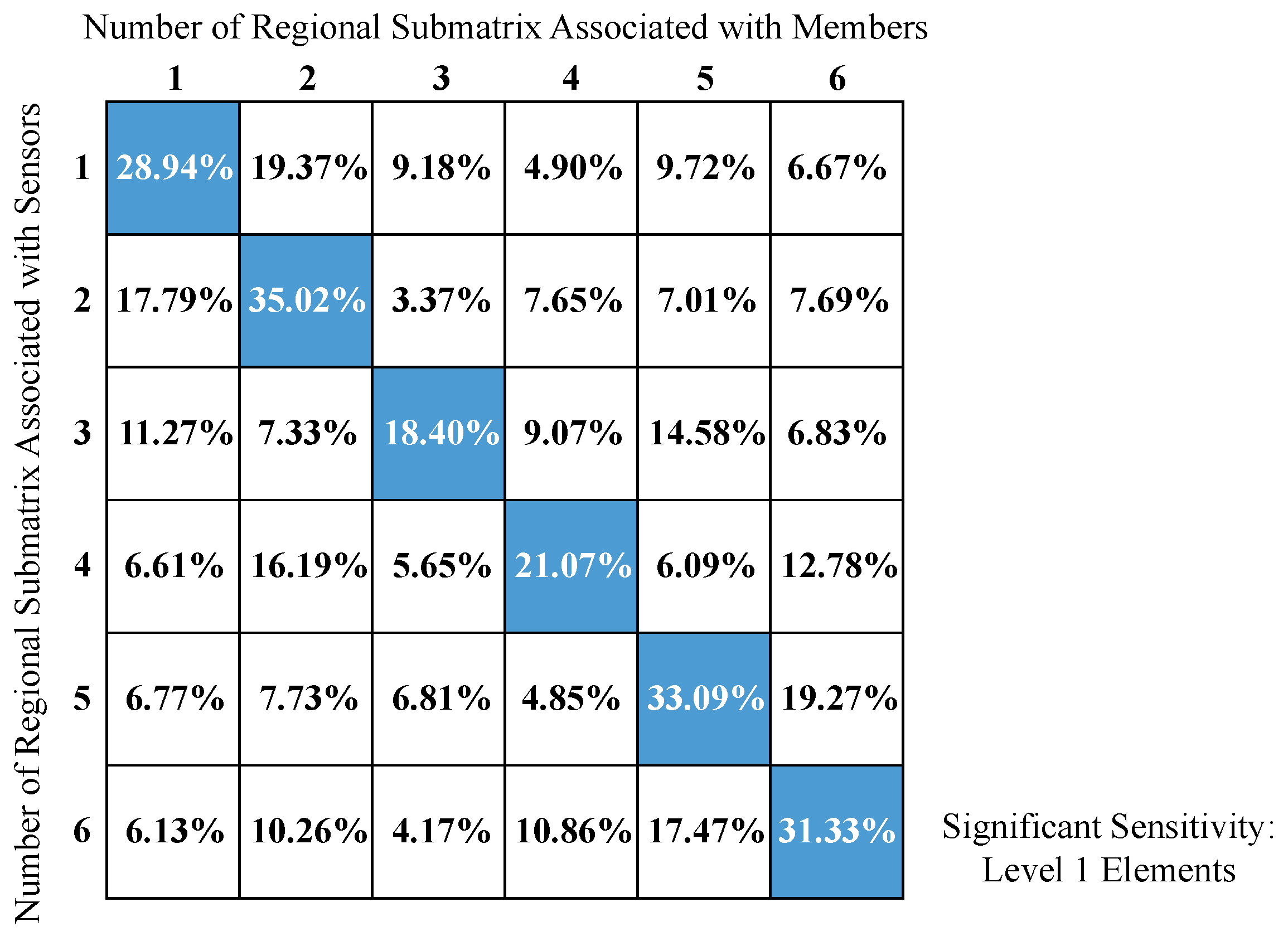
3.2. Numerical Verification for Sensitivity Matrix Features
4. Optimal Sensor Placement Based on Sensitivity
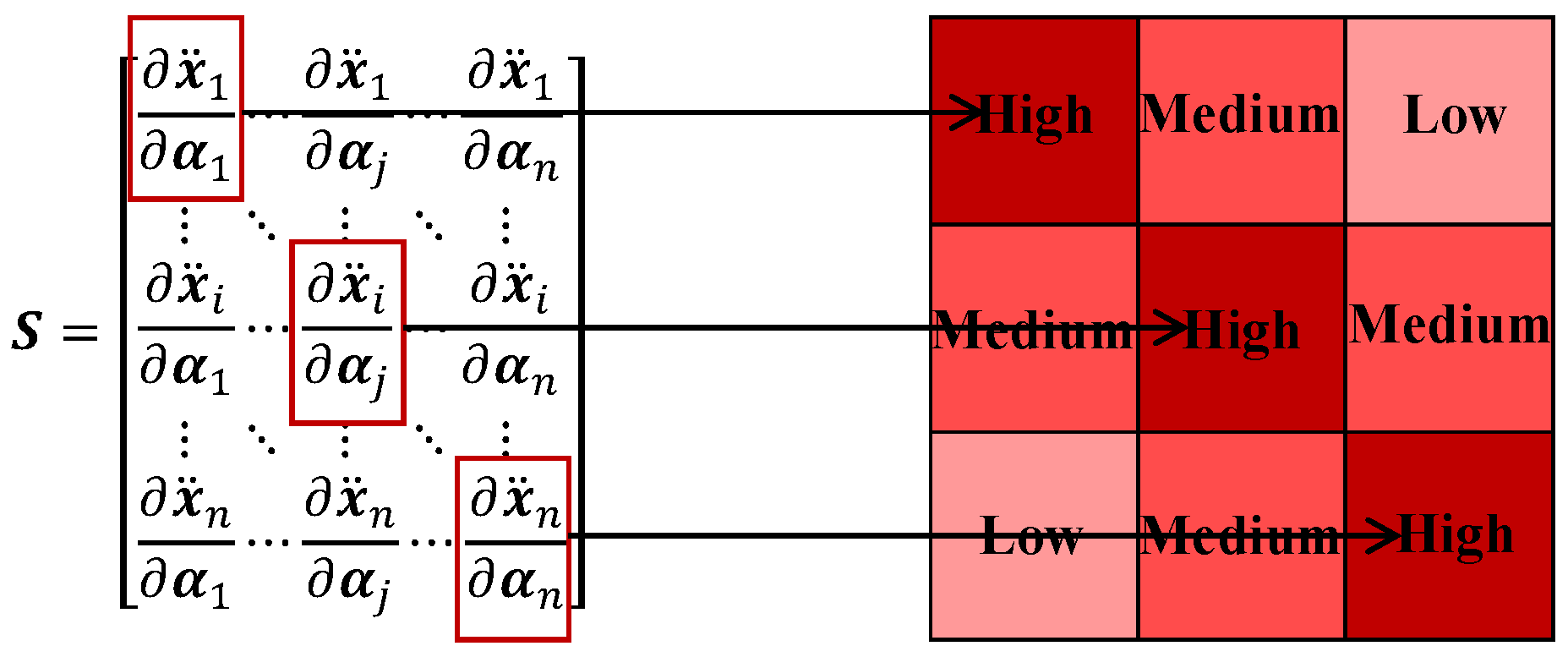
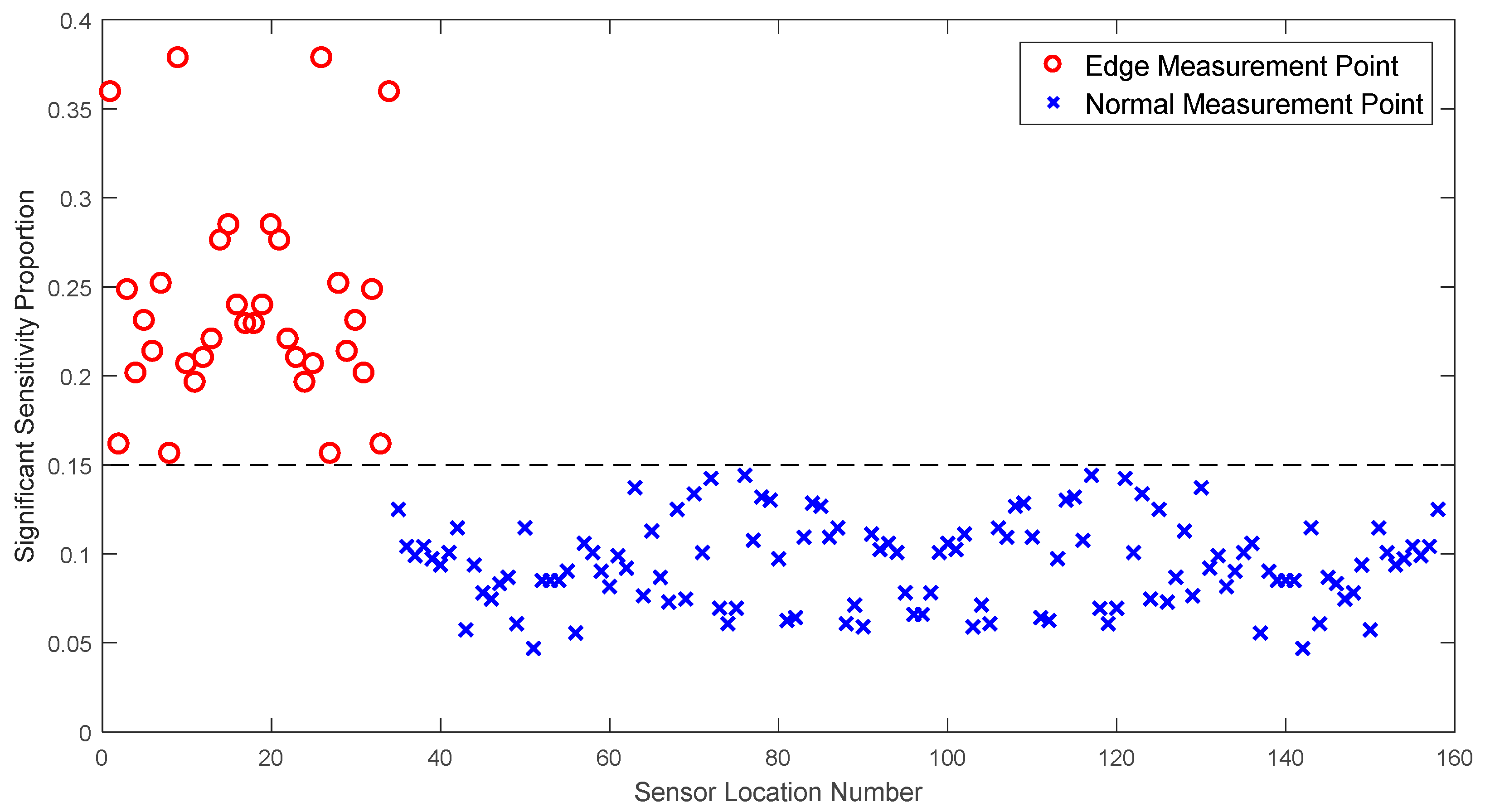
4.1. Significant Sensitivity Analysis
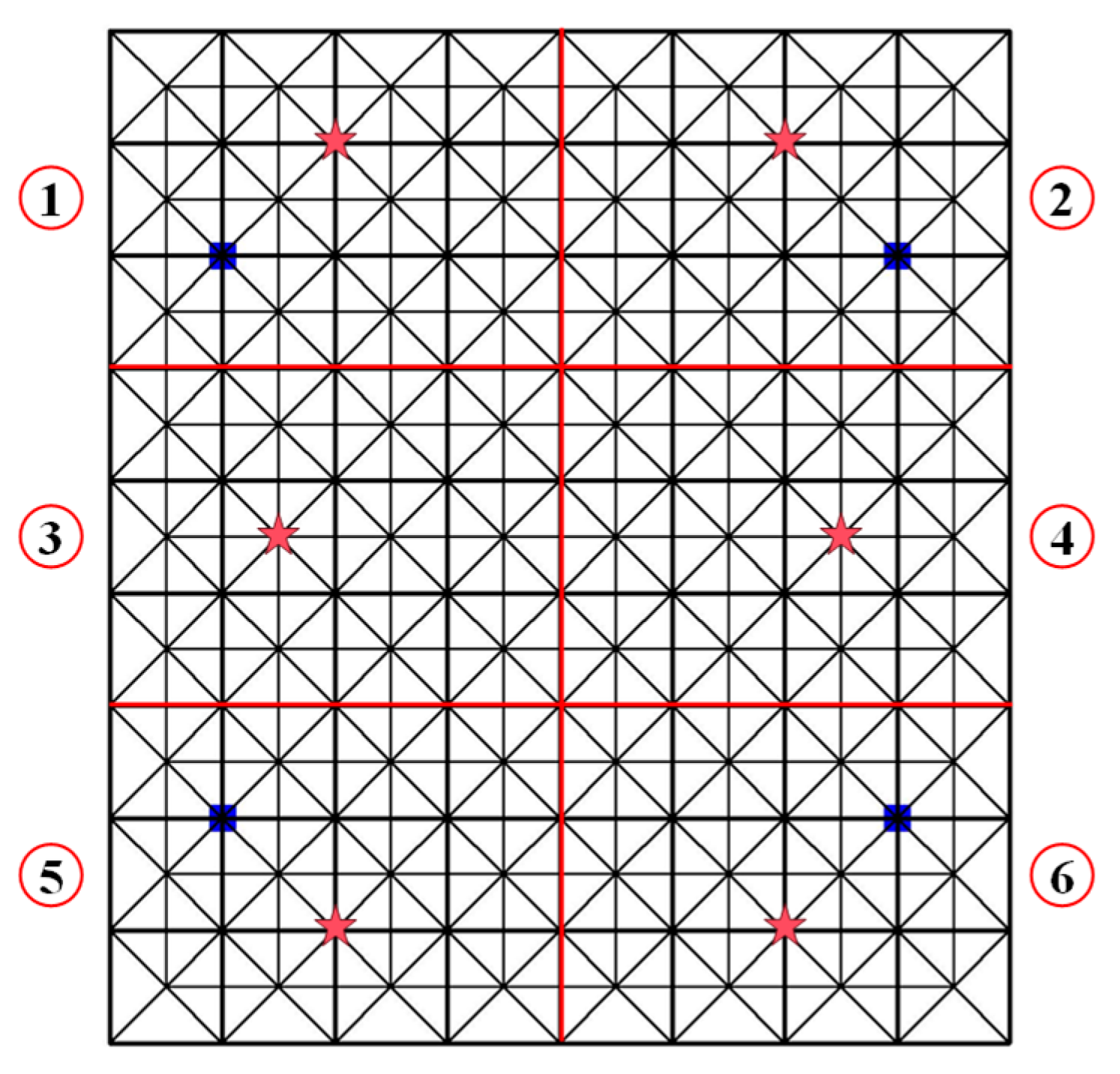
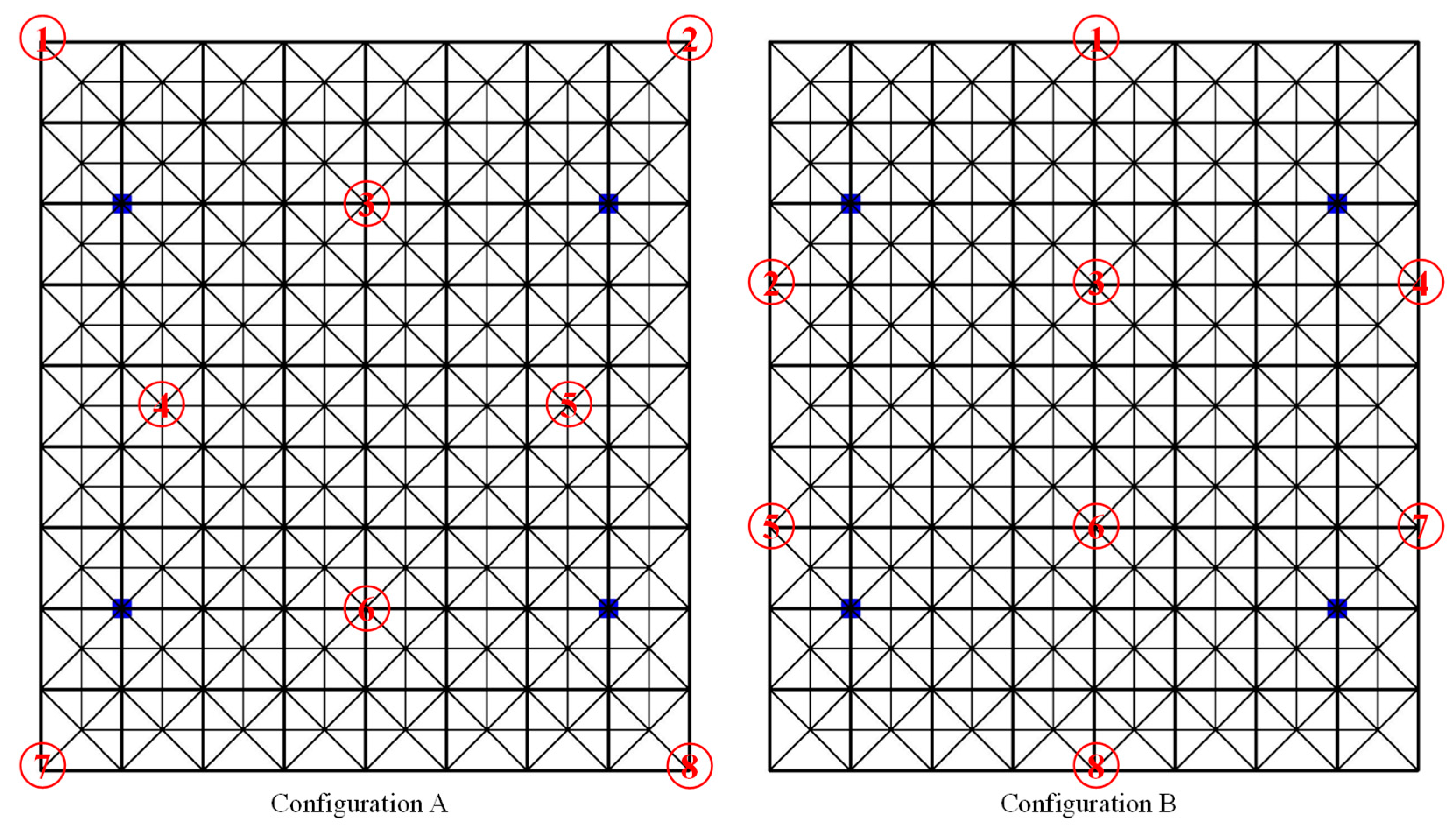
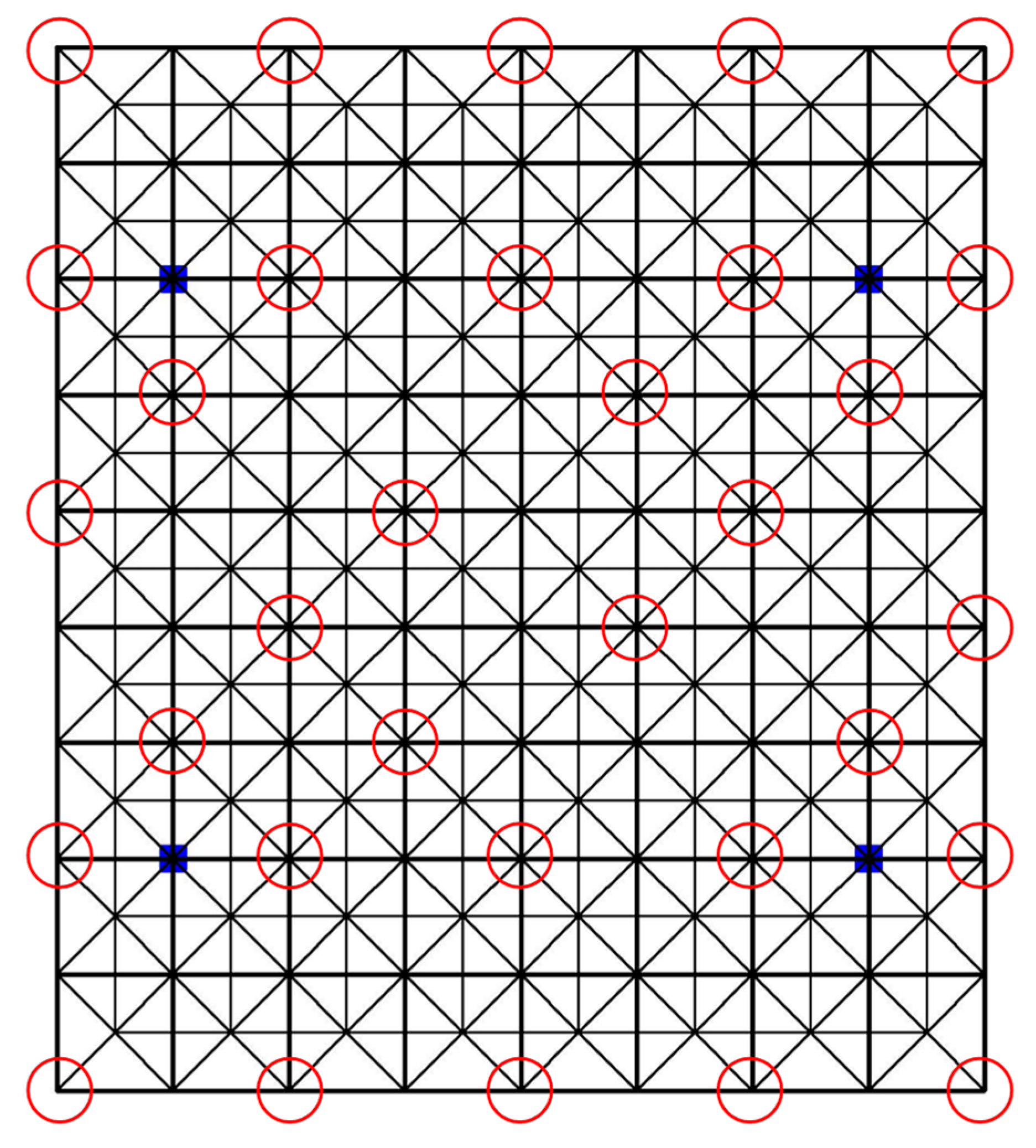
4.2. Sensor Layout Configuiation
- Sensors should be distributed across all regions.
- Sensor coverage for damage identification depends on the proportion of significant sensitivity.
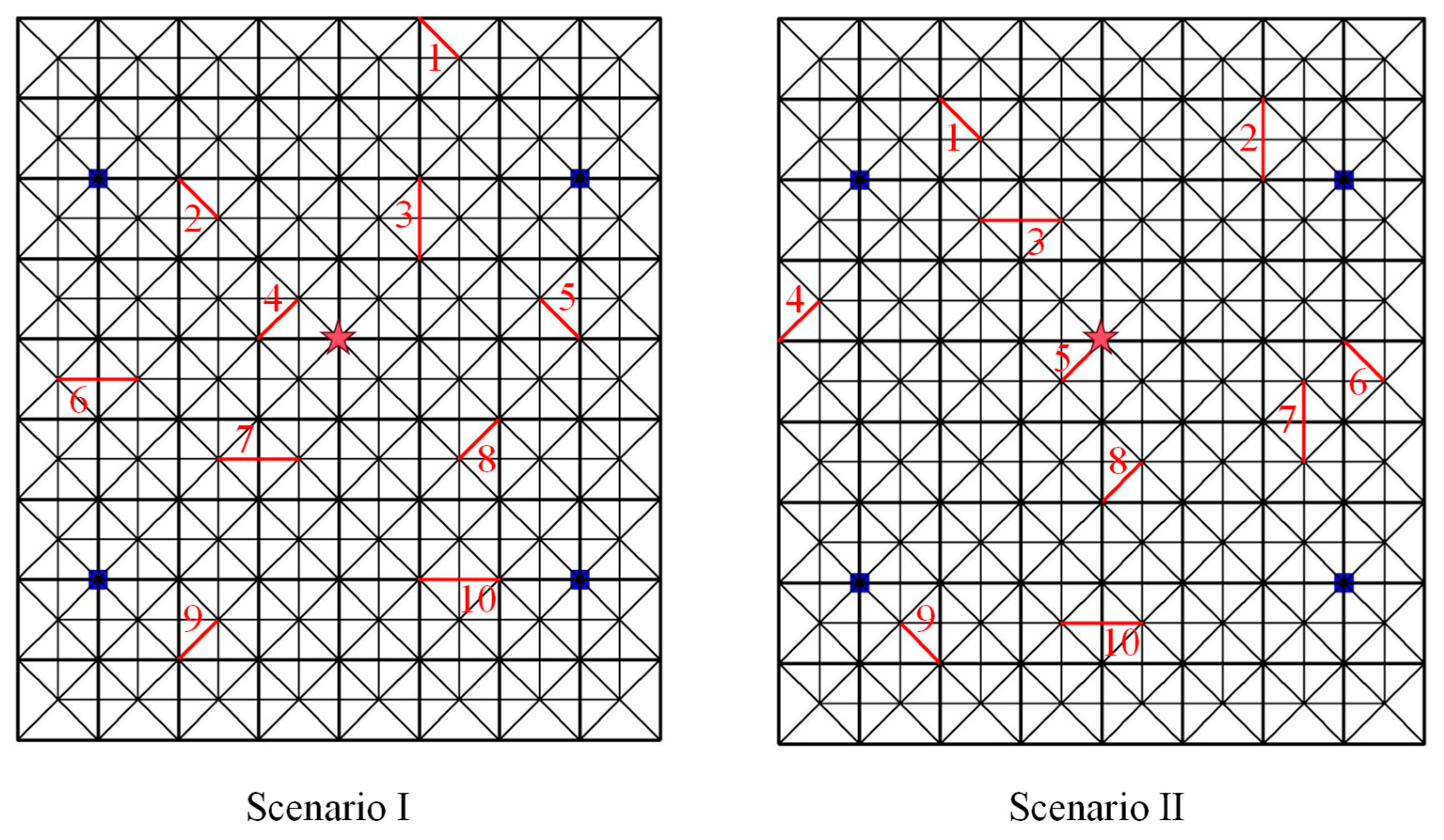
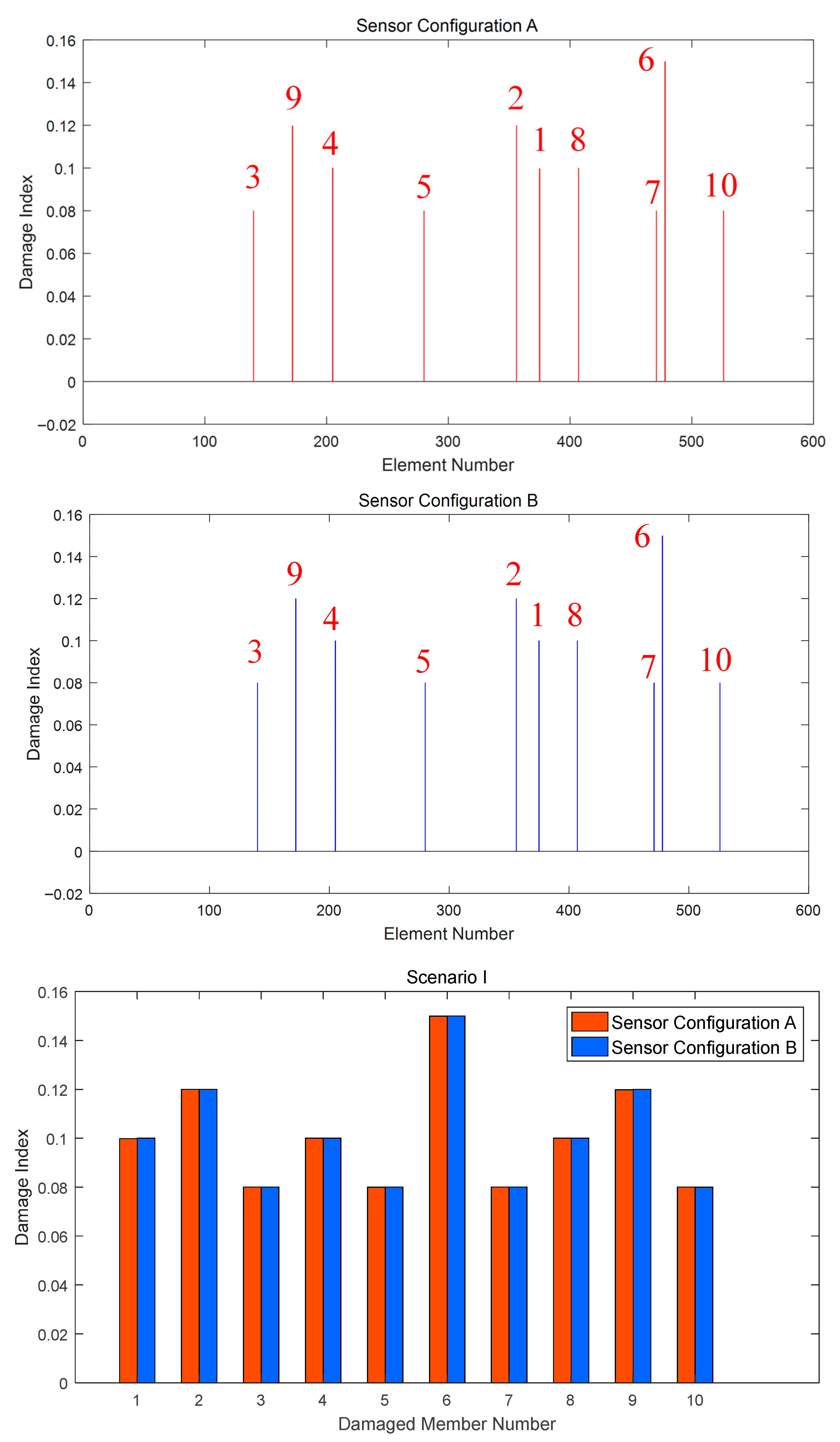
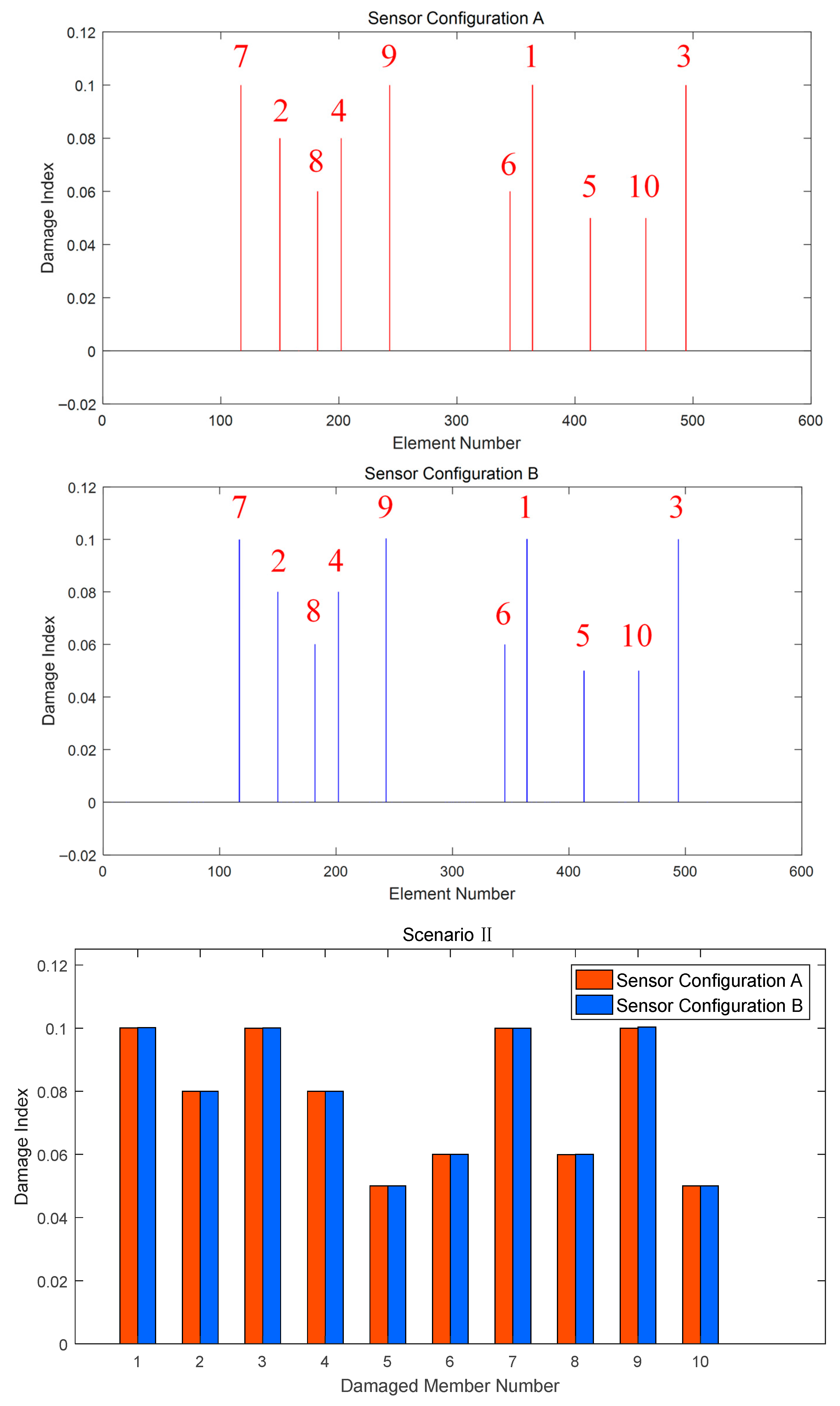
5. Numerical Simulation of Damage Identification
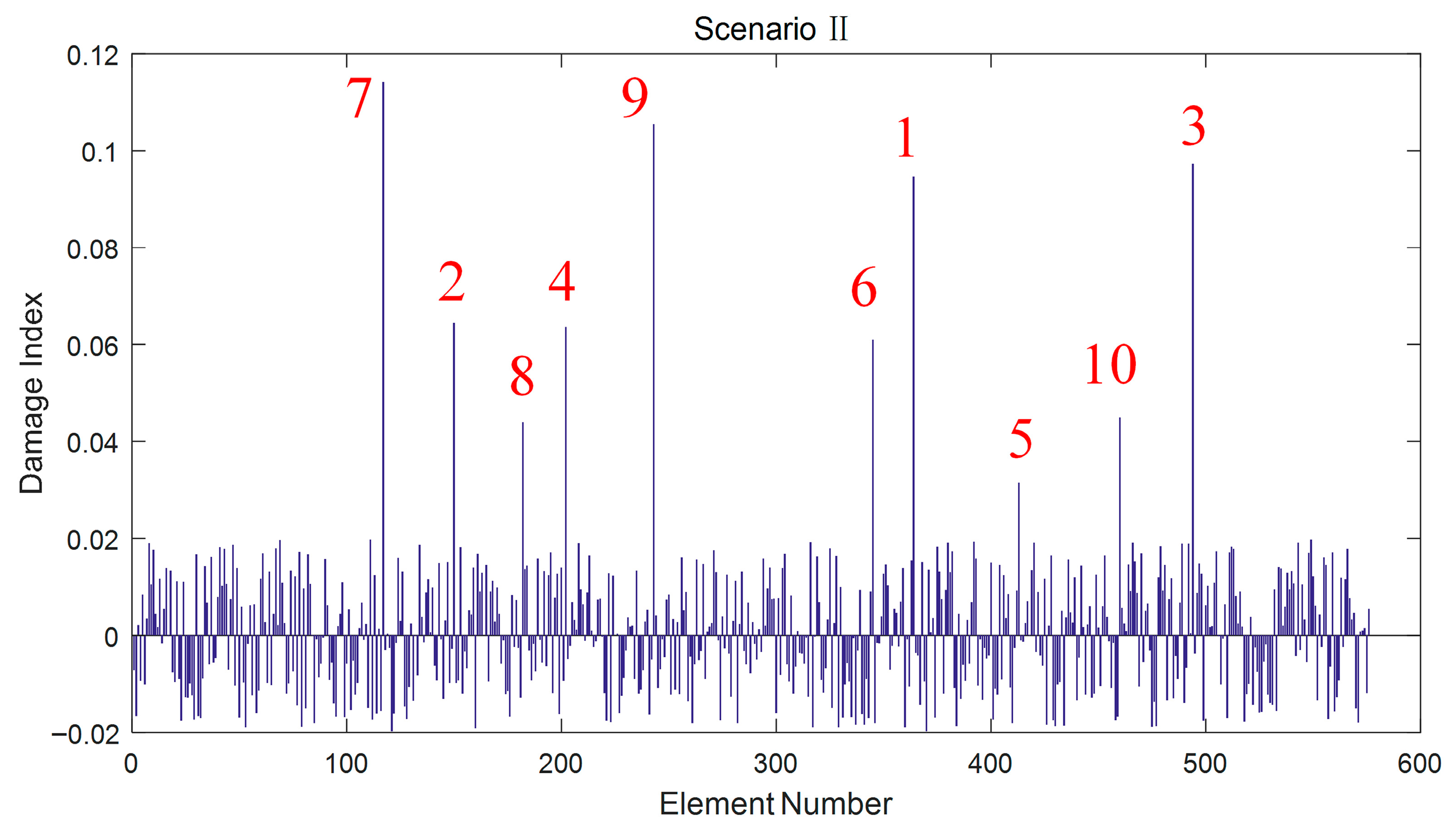
5.1. Damage Identification of Spatial Grid Structure
5.2. Uncertainty Analysis of Damage Identification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, F.C.; Feng, R.Q.; Tsavdaridis, K.D.; Yan, G.R. Designing efficient grid structures considering structural imperfection sensitivity. Eng. Struct. 2020, 204, 109910. [Google Scholar] [CrossRef]
- Roudsari, M.T.; Gordini, M. Random imperfection effect on reliability of space structures with different supports. Struct. Eng. Mech. 2015, 55, 461–472. [Google Scholar] [CrossRef]
- Zheng, X.W.; Lv, H.L.; Fan, H.; Zhou, Y.B. Physics-Based Shear-Strength Degradation Model of Stud Connector with the Fatigue Cumulative Damage. Buildings 2022, 12, 2141. [Google Scholar] [CrossRef]
- Milone, A.; Landolfo, R. A simplified approach for the corrosion fatigue assessment of steel structures in aggressive environments. Materials 2022, 15, 2210. [Google Scholar] [CrossRef]
- Almeida, J.H.S.; Ribeiro, M.L.; Tita, V.; Amico, S.C. Stacking sequence optimization in composite tubes under internal pressure based on genetic algorithm accounting for progressive damage. Compos. Struct. 2017, 178, 20–26. [Google Scholar] [CrossRef]
- Nie, G.B.; Yang, T.Y.; Zhi, X.D.; Liu, K. Damage evaluation of square steel tubes at material and component levels based on a cyclic loading experiment. Adv. Mech. Eng. 2018, 10, 1687814018797786. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; Mariani, S. Health monitoring of large-scale civil structures: An approach based on data partitioning and classical multidimensional scaling. Sensors 2021, 21, 1646. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.X.; Nie, G.B.; Dai, J.W.; Liu, K.; Zhi, X.D.; Ma, H.H. Seismic isolation research on a double-layer lattice structure using shaking table tests. Int. J. Steel Struct. 2019, 19, 1237–1248. [Google Scholar] [CrossRef]
- Nie, G.B.; Zhi, X.D.; Fan, F.; Dai, J.W. Seismic performance evaluation of single-layer reticulated dome and its fragility analysis. J. Constr. Steel Res. 2014, 100, 176–182. [Google Scholar] [CrossRef]
- Wang, W.N.; Gong, J.X.; Wu, X.Y.; Wang, X.C. A general equation for estimation of time-dependent prestress losses in prestressed concrete members. Structures 2023, 55, 278–293. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Chen, R. Strain monitoring based bridge reliability assessment using parametric Bayesian mixture model. Eng. Struct. 2021, 226, 111406. [Google Scholar] [CrossRef]
- Bojórquez, J.; Ponce, S.; Ruiz, S.E.; Bojórquez, E.; Reyes-Salazar, A.; Barraza, M.; Chávez, R.; Valenzuela, F.; Leyva, H.; Baca, V. Structural reliability of reinforced concrete buildings under earthquakes and corrosion effects. Eng. Struct. 2021, 237, 112161. [Google Scholar] [CrossRef]
- Zhang, G.L.; Zhang, Q.W.; Fan, F.; Shen, S.Z. Research on Snow Load Characteristics on a Complex Long-Span Roof Based on Snow–Wind Tunnel Tests. Appl. Sci. 2019, 9, 4369. [Google Scholar] [CrossRef]
- Li, D.; Nie, J.H.; Wang, H.; Ren, W.X. Loading condition monitoring of high-strength bolt connections based on physics-guided deep learning of acoustic emission data. Mech. Syst. Signal Process. 2024, 206, 110908. [Google Scholar] [CrossRef]
- Li, D.; Yu, T.; Wang, H.; Hu, C.X.; Nie, J.H.; Cheng, P.F.; He, W.Y. Spectral element simulation data-driven acoustic emission damage location in orthotropic steel decks. Dev. Built Environ. 2025, 22, 100676. [Google Scholar] [CrossRef]
- Qi, Y.Z.; Ding, Z.; Luo, Y.Z.; Ma, Z. A Three-Step Computer Vision-Based Framework for Concrete Crack Detection and Dimensions Identification. Buildings 2024, 14, 2360. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, Z. Research on Concrete Beam Damage Detection Using Convolutional Neural Networks and Vibrations from ABAQUS Models and Computer Vision. Buildings 2025, 15, 220. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Chen, W.L.; Ma, M.L.; Tao, D.W.; Ou, J.P. Estimation and warning of fatigue damage of FRP stay cables based on acoustic emission techniques and fractal theory. Comput.-Aided Civ. Inf. 2011, 26, 500–512. [Google Scholar] [CrossRef]
- Li, D.; Kuang, K.S.C.; Koh, C.G. Rail crack monitoring based on Tsallis synchrosqueezed wavelet entropy of acoustic emission signals: A field study. Struct. Health Monit. 2018, 17, 1410–1424. [Google Scholar] [CrossRef]
- Nie, J.H.; Li, D.; Wang, H.; Yu, T.; Kuang, K.S.C. Multi-objective optimization-based acoustic emission damage location in orthotropic steel decks considering complex wave paths. Eng. Struct. 2025, 330, 119956. [Google Scholar] [CrossRef]
- Zheng, X.W.; Hou, Y.Z.; Cheng, J.; Xu, S.; Wang, W.M. Rapid Damage Assessment and Bayesian-Based Debris Prediction for Building Clusters Against Earthquakes. Buildings 2025, 15, 1481. [Google Scholar] [CrossRef]
- Zheng, X.W.; Li, H.N.; Gardoni, P. Hybrid Bayesian-Copula-based risk assessment for tall buildings subject to wind loads considering various uncertainties. Reliab. Eng. Syst. Saf. 2023, 233, 109100. [Google Scholar] [CrossRef]
- Zheng, X.W.; Li, H.N.; Gardoni, P. Reliability-based design approach for high-rise buildings subject to earthquakes and strong winds. Eng. Struct. 2021, 244, 112771. [Google Scholar] [CrossRef]
- Xue, M.S.; Dong, J.C.; You, R.Z.; Yi, T.H. Bridge Cable Force Identification Method Under the Phenomenon of Bimodal Fundamental Frequency in Vibration. Int. J. Struct. Stab. Dyn. 2025, 2650207. [Google Scholar] [CrossRef]
- Huang, H.B.; Yi, T.H.; Li, H.N.; Liu, H. Sparse Bayesian Identification of Temperature-Displacement Model for Performance Assessment and Early Warning of Bridge Bearings. J. Struct. Eng. 2022, 148, 04022052. [Google Scholar] [CrossRef]
- Huang, H.B.; Yi, T.H.; Li, H.N. Anomaly Identification of Structural Health Monitoring Data Using Dynamic Independent Component Analysis. J. Comput. Civil. Eng. 2021, 34, 04020025. [Google Scholar] [CrossRef]
- Pei, X.Y.; Hou, Y.; Huang, H.B.; Zheng, J.X. A Multi-Objective Sensor Placement Method Considering Modal Identification Uncertainty and Damage Detection Sensitivity. Buildings 2025, 15, 821. [Google Scholar] [CrossRef]
- Pei, X.Y.; Hou, Y.; Huang, H.B.; Zheng, J.X. A Deep Learning-Based Structural Damage Identification Method Integrating CNN-BiLSTM-Attention for Multi-Order Frequency Data Analysis. Buildings 2025, 15, 763. [Google Scholar] [CrossRef]
- Mostafaei, H.; Ghamami, M. State of the Art in Automated Operational Modal Identification: Algorithms, Applications, and Future Perspectives. Machines 2025, 13, 39. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Y.; Wang, L.N.; Wang, W.N.; Yang, T.Y. Bridge Tower Warning Method Based on Improved Multi-Rate Fusion Under Strong Wind Action. Buildings 2025, 15, 2733. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Y.; Wang, L.N.; Wang, W.N.; Yang, T.Y. Bridge Cable Performance Warning Method Based on Temperature and Displacement Monitoring Data. Buildings 2025, 15, 2342. [Google Scholar] [CrossRef]
- Huang, H.B.; Yi, T.H.; Li, H.N.; Liu, H. Strain-Based Performance Warning Method for Bridge Main Girders under Variable Operating Conditions. J. Bridge Eng. 2020, 25, 04020013. [Google Scholar] [CrossRef]
- Lu, Z.R.; Law, S.S. Features of dynamic response sensitivity and its application in damage detection. J. Sound Vib. 2007, 303, 305–329. [Google Scholar] [CrossRef]
- Liu, K.; Law, S.S.; Zhu, X.Q. Sensitivity Enhancement for Structural Condition Assessment with Noisy Excitation or with Only Output. Int. J. Struct. Stab. Dyn. 2015, 15, 1450083. [Google Scholar] [CrossRef]
- Liu, K.; Law, S.S.; Zhu, X.Q. Substructural Condition Assessment Based on Force Identification and Interface Force Sensitivity. Int. J. Struct. Stab. Dyn. 2015, 15, 1450046. [Google Scholar] [CrossRef]
- Law, S.S.; Zhang, K.; Duan, Z.D. Structural damage detection from coupling forces between substructures under support excitation. Eng. Struct. 2010, 32, 2221–2228. [Google Scholar] [CrossRef]
- Li, J.; Law, S.S.; Hao, H. Improved damage identification in bridge structures subject to moving loads: Numerical and experimental studies. Int. J. Mech. Sci. 2013, 74, 99–111. [Google Scholar] [CrossRef]
- Liu, K.; Law, S.S.; Xia, Y.; Zhu, X.Q. Singular spectrum analysis for enhancing the sensitivity in structural damage detection. J. Sound Vib. 2014, 333, 2181–2182. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, L.X.; Law, S.S.; Nie, Z.H. Covariance of dynamic strain responses for structural damage detection. Mech. Syst. Signal Process. 2017, 95, 90–105. [Google Scholar] [CrossRef]
- Nabavi, S.; Gholampour, S.; Haji, M.S. Damage detection in frame elements using Grasshopper Optimization Algorithm (GOA) and time-domain responses of the structure. Evol. Syst. 2021, 13, 307–318. [Google Scholar] [CrossRef]
- Guo, L.N.; Ding, Y.; Zhang, Y.F. Seismic Damage Assessment for Isolated Buildings with a Substructure Method. Buildings 2022, 12, 1185. [Google Scholar] [CrossRef]
- Baybordi, S.; Esfandiari, A. A Novel Sensitivity-Based Finite Element Model Updating and Damage Detection using Time Domain Response. J. Sound Vib. 2023, 537, 117187. [Google Scholar] [CrossRef]
- Baybordi, S.; Esfandiari, A. Damage detection and model updating of offshore jacket platforms using a direct sensitivity relation based on structural response. Appl. Ocean Res. 2024, 149, 104068. [Google Scholar] [CrossRef]







| Load Applied Location | Proportion of Elements | ||
|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |
| Region 1 | 7.9% | 29.6% | 65.5% |
| Region 2 | 11.6% | 34.1% | 54.3% |
| All Region | 12.5% | 35.7% | 51.8% |
| Sensor Layout | Significant Sensitivity Proportion (Damage Identification Coverage) | |||
|---|---|---|---|---|
| Sensor 1 | Sensor 3 | Sensor 4 | Total | |
| Configuration A | 35.94% | 8.16% | 10.07% | 180.22% |
| Configuration B | 23.09% | 6.08% | 28.47% | 172.22% |
| Damage Scenario | Damaged Member Number and Stiffness Reduction Value | |||
|---|---|---|---|---|
| Group 1 | Group 2 | Group 3 | Group 4 | |
| Scenario I | 1, 4, 8 (−10%) | 2, 9 (−12%) | 3, 5, 7, 10 (−8%) | 6 (−15%) |
| Scenario II | 1, 3, 7, 9 (−10%) | 2, 4 (−8%) | 5, 10 (−5%) | 6, 8 (−6%) |
| Damaged Member Number | Sensor Configuration A | Sensor Configuration B | ||
|---|---|---|---|---|
| Scenario I | Scenario II | Scenario I | Scenario II | |
| 1 | 0.0170% | 0.0113% | 0.0029% | 0.0219% |
| 2 | 0.0001% | 0.0014% | 0.0001% | 0.0032% |
| 3 | 0.0029% | 0.0020% | 0.0007% | 0.0045% |
| 4 | 0.0017% | 0.0038% | 0.0002% | 0.0035% |
| 5 | 0.0013% | 0.0001% | 0.0004% | 0.0004% |
| 6 | 0.0105% | 0.0008% | 0.0007% | 0.0005% |
| 7 | 0.0012% | 0.0044% | 0.0002% | 0.0033% |
| 8 | 0.0017% | 0.0026% | 0.0002% | 0.0041% |
| 9 | 0.0198% | 0.0053% | 0.0003% | 0.0355% |
| 10 | 0.0017% | 0.0003% | 0.0007% | 0.0006% |
| Mean | 0.0045% | 0.0042% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shi, Y.; Yang, T.-Y.; Wang, W.-N.; Zhang, Y.-Q.; Xi, W. Damage Identification of Gas Station Double Layer Grid Structure Based on Time Domain Response Sensitivity Analysis. Buildings 2025, 15, 3959. https://doi.org/10.3390/buildings15213959
Wang Y, Shi Y, Yang T-Y, Wang W-N, Zhang Y-Q, Xi W. Damage Identification of Gas Station Double Layer Grid Structure Based on Time Domain Response Sensitivity Analysis. Buildings. 2025; 15(21):3959. https://doi.org/10.3390/buildings15213959
Chicago/Turabian StyleWang, Yan, Yan Shi, Tao-Yuan Yang, Wei-Nan Wang, Yu-Qi Zhang, and Wei Xi. 2025. "Damage Identification of Gas Station Double Layer Grid Structure Based on Time Domain Response Sensitivity Analysis" Buildings 15, no. 21: 3959. https://doi.org/10.3390/buildings15213959
APA StyleWang, Y., Shi, Y., Yang, T.-Y., Wang, W.-N., Zhang, Y.-Q., & Xi, W. (2025). Damage Identification of Gas Station Double Layer Grid Structure Based on Time Domain Response Sensitivity Analysis. Buildings, 15(21), 3959. https://doi.org/10.3390/buildings15213959






