Abstract
Against the backdrop of policy-driven transformation in construction industrialization, the EPC general contracting model has emerged as a core pathway for the large-scale development of prefabricated buildings. However, the EPC mode integrates the links of design, procurement, production, and transportation, construction, resulting in a complex coupling correlation among the risk factors of prefabricated construction schedule, which is easy to induce the risk contagion effect and increase the difficulty of risk control of project schedule delay. To address this, this study constructs a hybrid model integrating the “Fuzzy Interpretive Structural Model (FISM)-Coupling Degree Model-Bayesian Network (BN)” to systematically analyze risk contagion mechanisms. Taking an EPC prefabricated building project as an example, FISM is used to reveal the hierarchical structure of risk factors, while the coupling degree model quantifies interaction strengths and maps them into the BN to optimize conditional probability parameters. Through comprehensive hazard analysis, seven key causal risk factors and two critical risk propagation paths are identified. Targeted control measures are designed for the key risk factors, and BN-based simulation is applied to locate critical risk nodes and implement break-chain interventions for the risk paths, resulting in a 23% reduction in the probability of schedule delay. Engineering applications demonstrate that this model can effectively achieve the dynamic identification and blocking of risk paths, providing valuable reference for similar projects and offering informed support for managers in formulating scientific response strategies.
1. Introduction
Prefabricated construction, with its advantages such as resource efficiency, low-carbon environmental friendliness, and shortened construction periods [1], has become a technical pathway for addressing structural labor shortages and implementing the “Dual Carbon” strategy in China. In 2016, the Executive Meeting of the State Council reviewed and approved the Guiding Opinions on Vigorously Developing Prefabricated Buildings, explicitly advocating the use of the Engineering Procurement Construction (EPC) model in the development of prefabricated buildings. Owing to the inherent characteristics of prefabricated construction and disparities among different suppliers in design, production, and construction systems, close collaboration is essential across the design, production, procurement, and construction stages of prefabricated projects. Therefore, both from a policy perspective and considering the intrinsic features of prefabricated construction, adopting the EPC model is crucial for integrating the construction process into a cohesive system and maximizing its advantages [2,3]. However, under the EPC model, the entire production supply chain is interlinked, which amplifies the generalized correlation and coupling characteristics of project schedule risks [4]. This heightened interconnectivity can easily trigger a domino effect, increasing the difficulty of completing the project within the planned schedule [5]. To mitigate potential risks such as cost overruns due to delays and compromised overall project benefits, it is particularly important to manage key schedule risk factors and critical risk transmission pathways in prefabricated construction projects under the EPC model.
Currently, scholars have conducted extensive research on the EPC model, schedule management of prefabricated buildings, and associated schedule risks under their integration. In terms of EPC project schedule risk, some researchers have employed methods such as the Analytic Hierarchy Process-Extension theory [6,7] and Structural Equation Modeling [8,9] to identify and assess key schedule risk factors. However, these studies often fail to adequately account for judgment fuzziness and interdependencies among risk factors, while the weight assignment methods employed tend to be overly subjective. Habibi M. et al. [10] established a schedule risk evaluation index system from the general contractor’s perspective by optimizing weights, yet the issue of subjective bias in weighting methods remains. In contrast, Luo Q. et al. [11] emphasized that poor contract management and inadequate coordination and communication are primary causes leading to litigation and disputes, necessitating greater attention.
In the study of schedule risks in prefabricated construction, Sun et al. [12,13] applied the DEMATEL-ISM to quantitatively analyze the relationships among influencing factors, revealing complex transmission mechanisms and interaction pathways among multiple factors. However, the determination of inter-factor relationships relies heavily on subjective judgment, which affects the accuracy of evaluation results. Zhong et al. [14] used the DEMATEL-ISM-BN integrated approach to identify key risk factors affecting the schedule of prefabricated building projects and predicted the probability of schedule delay risks. Nevertheless, the Bayesian Network (BN) method depends excessively on expert experience in obtaining probability parameters and involves complicated and time-consuming computations. Luo Q. et al. [11] adopted the SAN-ISM method, taking into account the coupling characteristics of risks, to identify and analyze the propagation patterns and paths of construction schedule risks in prefabricated building projects. However, the SAN model requires substantial computational resources. In contrast, Zhao Y. et al. [15] combined System Dynamics (SD) and a BP neural network model to provide key information for controlling the impact of risk-related factors on delays in prefabricated construction progress.
Regarding schedule risk research in prefabricated construction under the EPC model, Xia, M. et al. [16] developed an evaluation model based on gray-fuzzy theory and identified construction and design as the primary factors determining project risk levels. Meanwhile, Cao, P. et al. [17] utilized structural equation modeling (SEM) to assess the impact of various risk factors on prefabricated building construction risks in EPC projects throughout the entire project lifecycle, similarly finding construction and design risks to be most influential. Further advancing this line of inquiry, Zhang, Z. et al. [18] focused on specific risks by comprehensively considering both fuzziness and randomness, employing the G1-CRITIC method and cloud model for risk assessment. Their approach quantitatively analyzed indicator weights and impact degrees, effectively evaluated safety risk management levels, helped reduce accident rates, and provided references for similar projects.
In the study of risk correlations, Wang Q. et al. [19] employed an improved Interpretative Structural Model (ISM) and Cross-Impact Matrix Multiplication Applied to Classification (MICMAC) to develop a hierarchical model and identify key risk factors. This approach addresses the issue of unreasonable judgments regarding inter-risk relationships, leading to more accurate evaluation results. Nevertheless, the magnitude of risk correlations could not be quantified. For tunnel construction safety risks, Zhang M. et al. [20] utilized the N-K model and System Dynamics (SD) to analyze risk coupling mechanisms. However, the N-K model fails to represent the hierarchical network relationships among risk factors. In contrast, the coupling degree model demonstrates significant advantages in quantifying risk correlations, enabling quantitative analysis of interaction intensities among risk factors [21]. For instance, Pan et al. [22,23] established a coupling evaluation model for tunnel collapse risks using this method, identifying primary coupled risk factors and implementing control measures that reduced accident rates. Similarly, Zhou Jun et al. [24] quantified interdependencies among schedule risk factors through the coupling degree model and converted them into weights to determine Bayesian Network (BN) probability parameters, thereby enhancing schedule risk assessment accuracy. It should be noted, however, that like the N-K model, the coupling degree model cannot reflect the hierarchical network relationships among risk factors.
2. Research Questions
2.1. Existing Problems
Based on the aforementioned research analysis, it is evident that studies on schedule risks in prefabricated construction primarily face the following issues:
(1) Existing weighting methods often overlook the fuzziness in expert judgment and exhibit excessive subjectivity, thereby undermining the accuracy of final evaluation results; (2) the hierarchical network relationships and correlation quantification of risk factors remain fragmented, making unified modeling challenging. Moreover, parameter calculations are complex, time-consuming, and lack precision, further compromising risk assessment accuracy; (3) although interactions among risk factors are considered, research still focuses on individual risks rather than thoroughly analyzing the impact of different types of risk factors on risk transmission networks; and (4) there is relatively scarce research on schedule risks specific to the integration of the EPC model and prefabricated construction.
2.2. The Limitations of Single-Model Analysis and Its Innovative Approaches
Focusing on the aforementioned issues and synthesizing the preceding literature review, existing single-model approaches demonstrate significant limitations in analyzing schedule risks for prefabricated buildings under the EPC model: although the Fuzzy Interpretative Structural Model (FISM) can effectively clarify hierarchical relationships among risk factors, it struggles to quantitatively assess uncertainties; while Bayesian Networks (BN) offer advantages in probabilistic reasoning and dynamic evolution analysis, their conditional probability parameters rely excessively on expert judgment [25] and cannot quantify coupling strength between risk factors; although the coupling degree model enables quantitative analysis of interactions between factors, it lacks the capability for systematic analysis of risk transmission paths. Therefore, to comprehensively reveal the evolution mechanism of schedule risks in EPC-based prefabricated construction and accurately identify key causal factors and critical risk propagation paths, this study innovatively proposes an integrated engineering schedule risk management methodology that combines FISM, BN, and the coupling degree model.
2.3. A Multi-Model Integration Approach for Schedule Risk Analysis in EPC Prefabricated Building Projects
Specifically, firstly, the literature research method and frequency statistics method were employed to establish a schedule risk factor index system from four dimensions: design, procurement, production and transportation, and construction. Subsequently, data was collected through questionnaire surveys and organized to form a fuzzy association matrix regarding risk factors. Secondly, the fuzzy association matrix was incorporated into the Fuzzy Interpretation Structural Model for relevant calculations, revealing complex transmission pathways among the indicators. This matrix was then mapped into a Bayesian network structure to enable reasoning and prediction of schedule delay risks, thereby identifying key causal factors and core risk transmission pathways. To address the issues of low efficiency and high error in conditional probability calculations within the Bayesian network, a modified coupling degree model was introduced. By integrating it with the fuzzy association matrix, the associations between risk factors were converted into weights that parent nodes point to child nodes, optimizing the calculation process of conditional probabilities and enhancing both their efficiency and accuracy. Finally, the proposed method was applied to the ongoing EPC prefabricated construction project at the new campus of Xinjiang Changji University. This application facilitated the probability prediction of schedule delay risks, the identification of key risk factors, and the determination of important risk pathways. Based on these findings, targeted control measures were formulated to ensure the successful completion of the project. The specific procedures are shown in Figure 1.
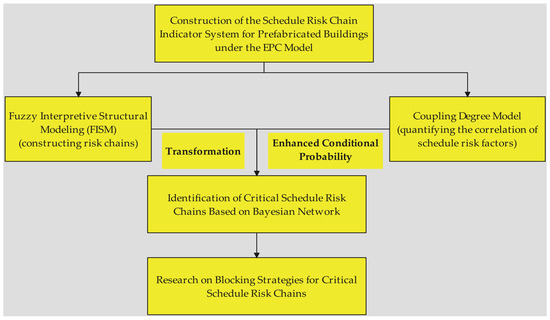
Figure 1.
Flowchart of the schedule risk chain blocking strategy.
3. Research Method
3.1. Identification of Schedule Risk Chain Factors
The schedule risk assessment for prefabricated construction projects under the EPC model requires establishing an indicator balance mechanism to avoid redundancy, increasing evaluation difficulty, and omissions leading to quantification bias. Given the limited relevant literature, the study primarily references two categories: first, the literature focusing on schedule risks in EPC-based prefabricated construction projects; second, the literature centered on schedule-related studies of prefabricated building projects. Databases such as Wan fang Data, CNKI, Elsevier Science Direct, and Web of Science were searched using keywords including “prefabricated construction” and “schedule risk” or “EPC-based prefabricated construction schedule.” Forty relevant publications were selected for statistical analysis of schedule risk factors. Key risk factors with a frequency count ≥ 6 (where conceptually similar factors were counted as one) were retained to ensure a more rational indicator system. The statistical results are shown in Figure 2.
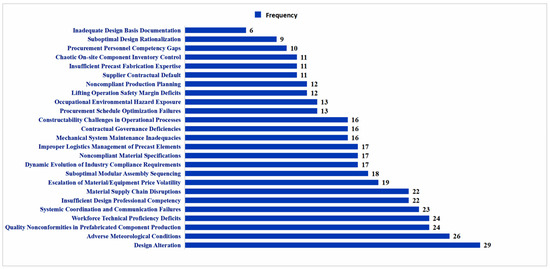
Figure 2.
Identification of schedule risk chain factors in prefabricated construction.
3.2. Construction of the Indicator System
Based on the statistical analysis results of schedule risk factors in prefabricated construction projects presented above, a schedule risk factor indicator system for EPC prefabricated buildings has been established, as detailed in Figure 3.
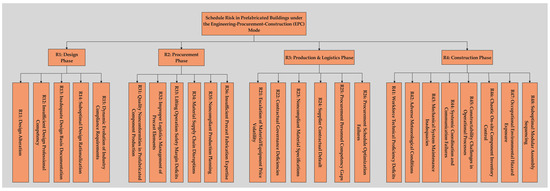
Figure 3.
Indicator system for the schedule risk chain in prefabricated construction projects.
3.3. Analysis of the Schedule Risk Chain in EPC Prefabricated Buildings
3.3.1. Construction of Schedule Risk Chain Based on FISM
While the traditional Interpretative Structural Model (ISM) can efficiently construct a hierarchical network of elements within complex systems, its reliance on the binary 0–1 judgment mechanism of classical set theory embodies a rigid, all-or-nothing logic. This fundamentally limits its ability to accurately characterize the fuzziness and gradient intensity differences in interactions between elements [26]. In highly coupled complex system scenarios, cognitive differences among experts regarding element relationships often lead to significantly dispersed judgment results, exposing the traditional model’s structural limitation in representing fuzzy associations. To address this, the Fuzzy Interpretative Structural Model (FISM) introduces fuzzy set theory. By utilizing membership functions, it transforms the discrete 0–1 relationships in ISM into continuous fuzzy relationships within the [0, 1] interval, achieving a gradient quantitative expression of interaction strength from weak to strong [27].
Compared to traditional fragmented construction models, the EPC model’s high integration of design, procurement, production, and transportation, and construction phases in prefabricated buildings causes schedule risk factors to become interlinked and intertwined, forming a complex network. In this context, FISM demonstrates significant advantages in analyzing risk interrelationships: it can not only deconstruct risk factors with complex coupling relationships into an intuitive and visual risk chain network but also provide crucial theoretical support for subsequent optimization of the Bayesian Network structure. The specific modeling process of this model is as follows:
- (1)
- Define Research Objectives and Identify Key Factors
Clearly delineate the research objectives and determine relevant influencing factors.
- (2)
- Construct Fuzzy Adjacency Matrix
Utilize questionnaire surveys to preliminarily assess inter-factor relationships, establishing the fuzzy adjacency matrix X = (xij)n×n, where xij denotes the interaction intensity between factors, with continuous values within the [0, 1] interval.
- (3)
- Select Membership Function
Develop the fuzzy interaction intensity matrix Bn = (bij)n×n for EPC prefabricated construction schedule risks based on the following Equation (1):
where bij is fuzzy interaction intensity of factor i relative to factor j, xi represents sum of elements in the i-th row of matrix X, xj is sum of elements in the j-th column of matrix X, i, j is 1, 2, …, n.
- (4)
- Determine Threshold λ
Calculate the adjacency matrix A = (aij)n×n using the following Equation (2):
where aij fuzz represents the elements in the adjacency matrix A.
- (5)
- Derive Reach ability Matrix M
Apply Boolean matrix operations to adjacency matrix A. The reachability matrix M is obtained when A satisfies the following Equation (3):
where E denotes the identity matrix.
- (6)
- Hierarchical Partitioning Based on M, compute:
Reachable Set R(Si), Antecedent Set A(Sj), Common Set Q(Si)
Iteratively eliminate identified top-level elements and allocate all factors into hierarchical tiers using the following Equations (4)–(6):
where S represents the element set.
Following these steps, the Fuzzy Interpretive Structural Model (FISM) for schedule risk factors in EPC prefabricated construction projects is systematically constructed, with computational workflows as detailed above.
3.3.2. Analysis of Critical Schedule Risk Chains Based on Bayesian Network
Bayesian network modeling involves two key steps: delineating the network structure and specifying the network parameters. Given the interdependencies among schedule risk factors, the Fuzzy Interpretive Structural Model (FISM) is adopted to construct the network topology, which is subsequently transformed into a Bayesian network model. Risk factors R11 to R48 and R are all defined with binary states: “Yes” and “No.”
Considering the scarcity of schedule delay risk data and challenges in Bayesian network-based schedule risk analysis—such as frequent expert decisions, subjectivity, computational inefficiency, and significant errors in conditional probability estimation—the mutual influence values from the fuzzy adjacency matrix F obtained in Step 2 are utilized. A modified coupling degree formula is introduced to quantify risk coupling, which is then converted into influence weights of parent nodes on child nodes in the Bayesian network. Subsequently, a probabilistic weighting method [28] is applied to estimate the conditional probabilities of non-root nodes, thereby optimizing the schedule risk evaluation process.
- (1)
- By examining the hierarchical network structure constructed through the Fuzzy Interpretive Structural Model, pairs of interacting schedule risk factors are identified. Building on the fuzzy relational matrix from the FISM, a modified coupling degree model [21] is incorporated to quantitatively calculate the coupling degree between paired risk factors.where C denotes the coupling strength, with higher values indicating stronger correlations between associated factor pairs; Ui represents the initial direct influence magnitude of individual factors. Both C and Ui are bounded within the interval [0, 1].
- (2)
- Perform normalization based on the following equation:where Wi denotes the influence weight of parent nodes on child nodes; Ci represents the coupling degree between risk factor pairs.where j denotes the node state, with j = T indicating occurrence and j = F non-occurrence; Zij represents the distance between the child node and the parent node; if the child node occurs while the parent node does not, Zij = 1; if both nodes share the same state, Zij = 0; if the child node does not occur while the parent node does, Zij = −1; Wi denotes the influence weight of the i-th parent node on the child node; Pj signifies the conditional probability of the child node being in risk state “j”; and R quantifies the expert-evaluated result distribution index.
The prior probabilities of root nodes in the Bayesian Network are determined based on expert evaluations and computed using the following triangular fuzzy numbers:
where aij denotes the minimum possible value of the node state, mij represents the most probable value of the node state, bij indicates the maximum possible value of the node state. Subsequently, the mean triangular fuzzy probability for expert-assessed values in state ii is calculated using Equation (12).
Finally, the prior probabilities of root nodes are calculated using the equation below and normalized:
where Pij denotes the probability after normalization, P′ij represents the probability before normalization.
The identification of critical risk-inducing factors and core risk transmission paths is determined by the risk impact degree of risk factors as follows [21]:
where P(Xi|A) denotes the posterior probability of each risk factor, S represents the sensitivity of the risk factor, and M indicates the impact intensity of the risk factor.
3.3.3. Research on Blocking Strategies Based on Schedule Risk Chain
Timely disruption of risk factors or propagation processes within the schedule risk chain of prefabricated construction under the EPC model can control risk transmission and prevent larger schedule delay events. Accordingly, targeting the multiple schedule risk chains identified earlier, the relevant functions of GeNIe software 4.1.3402 are utilized to comprehensively identify critical causative factors and core risk transmission paths. Chain-breaking simulations are conducted on the core risk chains to pinpoint critical risk nodes, and specific blocking strategies are proposed.
4. Empirical Analysis and Results
4.1. Overview of the EPC Prefabricated Building Project
This prefabricated building project, with a prefabrication ratio of 53%, adopts the EPC delivery system. Key specifications include the following: total floor area, 21,318.75 m2 (above-ground, 17,315.52 m2; basement, 4003.23 m2); structural system—framed structure with four above-ground floors and one basement level. Regarding the schedule, the project is planned to officially commence on 6 June 2024, and is scheduled to be completed on 2 November 2024, with a total duration of 150 days. To ensure the project can be completed smoothly according to the planned timeline and to validate the effectiveness of the hybrid model constructed earlier, the hybrid model was applied to conduct a schedule risk assessment for this project one month prior to the commencement. Through this assessment, key causal factors affecting the project schedule and critical causal risk chains were accurately identified, enabling the early implementation of targeted preventive measures, close monitoring of potential risks, and avoidance of project schedule delays.
4.2. Construction of the Schedule Risk Chain Based on the FISM
4.2.1. Determination of the Fuzzy Correlation Matrix of Factors
Questionnaires were distributed to experts actively involved in the actual construction project, requesting them to perform Step 2 of the FISM construction process by analyzing the influence relationships among the 25 factors. The fuzzy correlation matrix of factors, denoted as X, was ultimately statistically derived using the averaging method, as presented in Table 1.

Table 1.
Fuzzy correlation matrix of factors.
4.2.2. Membership Function Selection
The association strength matrix B was obtained through calculation using Equation (1). By setting a threshold value λ, the association strength matrix B was filtered. A smaller λ value results in a more refined system division, while a larger λ value leads to a coarser system division [29]. The level of refinement in system division directly affects the overall system performance, so the selection of λ must be appropriate. After multiple rounds of value analysis and filtering, a threshold value of λ = 0.482 was selected, yielding a reasonably structured risk chain network. Based on the association strength matrix B, the adjacency matrix A0 was derived using Equation (2). Building on the adjacency matrix, the reachability matrix M was calculated on the MATLAB 2023a platform using Equation (3), as shown in Table 2.

Table 2.
Reach ability matrix M.
Through Equations (4)–(6), the reachable set, antecedent set, intersection set, and hierarchy levels were computed. Finally, the prefabricated construction schedule risk factors with complex interrelationships were transformed into a clear and hierarchical directed graph, as illustrated in Figure 4.
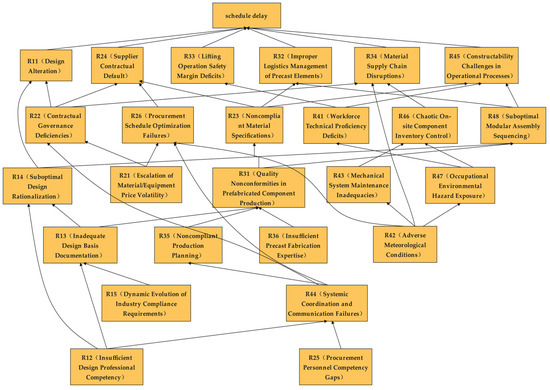
Figure 4.
Directed graph of hierarchical structure.
Starting from insufficient designer competence (R12), lack of procurement personnel experience (R25), imperfect industry standards and specifications (R15), inadequate component production experience (R36), adverse weather conditions (R42), and rising material and equipment costs (R21), all nodes were traversed along the direction of the arrows, ultimately reaching the endpoint of schedule delay (R). A total of 46 schedule risk chains were identified. To identify high-impact risk chains and key causative factors, the following figure was mapped to a Bayesian network for analysis.
4.3. Analysis of the Critical Schedule Risk Chain Based on Bayesian Network
Due to the interconnected nature of schedule risk factors, they intertwine to form risk chains. When the state of a particular risk factor changes, it triggers dynamic adjustments in other risk factors, propagating continuously [30] along the risk chain and ultimately leading to schedule delays. Accordingly, the Bayesian network model is used to analyze the state changes in schedule risk factors and predict the probability of final schedule delay risks. Through diagnostic analysis, sensitivity analysis, and impact strength analysis within the Bayesian network, critical schedule risk chains are comprehensively identified. By comparing the probability of schedule delay events before and after disrupting these risk chains, targeted schedule risk control measures are derived. These measures can disrupt the occurrence of schedule delays at the source, providing managers with proactive decision support to take preventive actions in advance.
4.3.1. Network Structure Formation
To employ Bayesian networks for reasoning about the state changes in schedule risk factors, the primary task is to establish a network topology that precisely represents the qualitative relationships. Therefore, the risk chain network model constructed earlier (Figure 4) is transformed into a Bayesian topology, where each node corresponds one-to-one to individual risk factors, enabling its use for Bayesian network inference analysis, as illustrated in Figure 5.
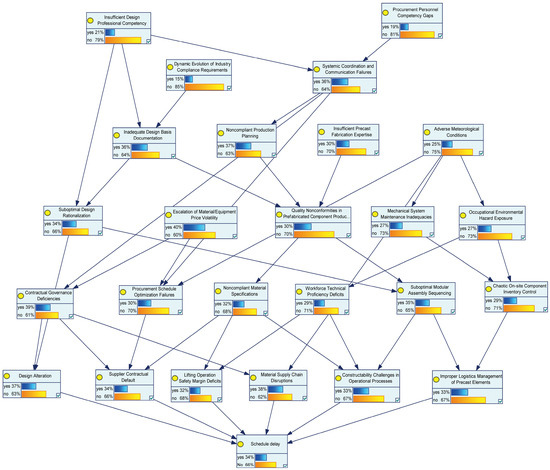
Figure 5.
Bayesian parameter learning results.
4.3.2. Probability Determination
- (1)
- Prior Probability Determination
To harmonize expert opinions and mitigate individual subjectivity, triangular fuzzy numbers were applied to calculate node prior probabilities using Equations (12) and (13). Specific calculation results are summarized in Table 3.

Table 3.
Results of prior probability calculation.
For the computation of node R (schedule delay), experts listed in Table 3 were invited to assign weights to its parent nodes, with the total weight sum constrained to unity. These weights were integrated into the probabilistic allocation method for calculation. Given space constraints, detailed derivations are omitted here.
- (2)
- Conditional Probability Determination
Using node R31 (production quality defects) as an exemplar, conditional probabilities were calculated based on Equations (7)–(10) and the fuzzy adjacency matrix (Table 4), with detailed computational outcomes presented in Table 4 and Table 5.

Table 4.
Calculation results of relevant parameters.

Table 5.
Results of conditional probability calculation.
The calculated results of each node were entered into GeNIe. Through the computational analysis of the Bayesian network model, the marginal probability distribution of each schedule risk factor was obtained, as shown in Figure 5. Further analysis revealed that the probability of construction schedule risk for this project is 34%.
4.3.3. Comprehensive Analysis
With the schedule delay risk set as the target node, three analyses were conducted sequentially: First, a sensitivity analysis was performed to investigate the amplifying effect of its probability disturbance on the risk chain, accurately identifying highly sensitive risk factors. Second, based on diagnostic analysis, the target node probability was set to 100% as observed evidence to inversely deduce the changes in posterior probabilities of input variables. Finally, impact strength analysis was introduced to reveal the multi-source synergistic mechanism of project schedule risks. All analytical data were exported via the GeNIe platform, and the risk impact degree of each factor was calculated and ranked according to Equation (14), as shown in Table 6.

Table 6.
Summary of Bayesian network reasoning analysis results.
The top 15 risk factors ranked by hazard degree were subjected to simulation analysis, yielding the most probable critical progress risk chains as follows:
- (1)
- Adverse weather (R42) → Poor construction work environment (R47) → Low technical proficiency of workers (R41) → Inadequate component lifting safety (R33) + Poor operability of construction techniques (R45) → Project delay (R);
- (2)
- Adverse weather (R42) → Insufficient maintenance of mechanical equipment (R43) → Disorganized on-site component management (R46) → Unreasonable transportation, loading/unloading, and stacking (R32) → Project delay (R).
Additionally, risk factors requiring special attention include the following: inexperienced procurement personnel (R25), poor coordination and communication (R44), inaccurate procurement schedule (R26), quality defects in supplied materials (R23), design changes (R11), supplier breach of contract (R24), and Untimely supply (R34).
4.4. Research on Blocking Strategies
Timely interruption of risk factors or propagation processes within the schedule risk chain of prefabricated buildings under the EPC mode, along with controlling risk transmission, can prevent larger schedule delay events. Therefore, the following measures are proposed based on the key causative factors and critical schedule risk chains identified earlier.
4.4.1. Management and Control Measures for Key Causative Risks
For insufficient experience of procurement personnel (R25): The Procurement Department needs to establish a structured training system and knowledge base, implement standardized procurement operation processes and decision-making checklists, and use systems to compensate for individual experience gaps.
For poor coordination and communication (R44): Build an information collaboration matrix based on BIM and project management platforms, clarify information exchange standards, institutionalize regular and specialized meeting systems, and achieve multi-party data synchronization and transparent decision-making.
For inaccurate procurement schedules (R26): Adopt the critical path method combined with buffer management, and implement dynamic rolling plans.
For quality defects in supplied materials (R23): Implement an on-site manufacturing supervision system and conduct quality witnessing of critical processes.
For design changes: Strengthen preliminary design and multi-party joint drawing review. Establish a strict change request approval process, where impact assessments (cost/schedule/technical) are mandatory before issuing change orders.
For supplier breach of contract (R24): Establish a supplier performance evaluation system and implement tiered management.
For untimely supply (R34): Develop precise transportation plans and site coordination schemes.
4.4.2. Measures for Blocking the Critical Schedule Risk Chain
Blocking Principles: Blocking is conducted based on the multiplier effect of risk values and prioritizing urgent risks in transmission paths that are close to schedule delay risk nodes [31].
Based on chain-breaking theory, chain-breaking simulations were conducted on the aforementioned two high-risk chains using GeNIe software: after fully intercepting all risk factors constituting the two risk chains, the probability of schedule delay risk decreased from 34% (unblocked) to 10%, a reduction of 24%, but with high resource consumption and when only blocking the three risk factors—“Inadequate component lifting safety (R33)”, “Poor operability of construction techniques (R45)”, and “Unreasonable transportation, loading/unloading, and stacking of components (R32)”—the schedule delay probability dropped to 11%, a 23% reduction. Compared to the full interception scheme, this strategy has lower resource consumption and similar blocking effectiveness, as shown in Figure 6.
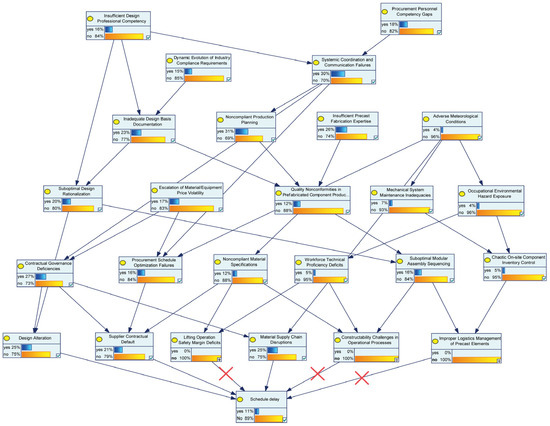
Figure 6.
Results of chain-breaking simulation for schedule delay risk.
For inadequate component lifting safety (R33): Conduct pre-mobilization annual inspection of equipment and trial lifting verification before lifting critical components; ensure operators are certified and receive regular safety briefings, with risks pre-empted through BIM simulation. During lifting, pause at 300 mm for inspection and resume only after confirming safety; no standing below is allowed, and approach is permitted only when components are within 1 m of the ground. Set warning signs, warning lines, and assign dedicated personnel for supervision. Use a total station and laser positioning instrument for double verification, control embedded part deviation within ±2 mm; and real-time monitor equipment status via an intelligent monitoring system, with adjustable slings to adapt to different component requirements.
For poor operability of construction techniques (R45): promote the “factory preassembly on-site modular installation” mode, develop adaptive grouting systems and low-support installation technologies, and optimize construction processes through BIM simulation to reduce on-site complexity. Deploy AR operation instructions and construction process BIM simulation systems, integrate AI image recognition technology for real-time monitoring of operation compliance; and establish physical process sample areas to enhance 3D visual clarification effects. Formulate construction process cards and the “three-level clarification” system, equip with electric construction tools and intelligent measuring instruments, and achieve full-process traceability of process execution via blockchain evidence storage platforms.
For unreasonable transportation, loading/unloading, and stacking of components (R32): In transportation management, precast wall panels are transported vertically, while composite floor slabs, balcony slabs, and staircases are transported horizontally; use low-bed trailers with dedicated racks and secure fixation, and confirm concrete strength meets standards before transport. For stacking specifications, strictly limit stacking layers, align and pad between layers, stack by specification, type, and lifting sequence in designated zones, and ensure the storage yard is within the crane’s working range with clear passages. Site preparation requires transport roads and storage yards to be level, firm, well-drained, and suitable for large vehicle passage; components are labeled with model, lifting sequence, and stacking requirements to avoid unloading confusion. Technologically, optimize site layout through BIM simulation of transport routes and stacking plans, and track component transport status in real-time via Internet of Things technology to ensure timely delivery.
Additionally, management decision-makers can input schedule risk events observed throughout the project into the aforementioned Bayesian network as observational evidence to dynamically predict the probability of schedule delay risk occurrence, enabling timely measures to ensure successful project completion.
5. Discussion
Although this study conducts a comparative analysis between the proposed hybrid model and existing methods. Under the EPC mode, the high integration of design, procurement, production, transportation, and construction intensifies the coupling effects among schedule risk factors in prefabricated buildings [4]. At the same time, the inherent ambiguity and uncertainty of risks further increase the difficulty of managing project schedule delays. Existing methods exhibit clear limitations in addressing different dimensions of risks: for instance, the N-K model [20] and the coupling degree model [22] mainly focus on the coupling among risk factors; the Bayesian network model [14] and Monte Carlo simulation [32] emphasize capturing the uncertainty of risks; while the Fuzzy Interpretive Structural Model [33] only analyzes risk correlations, offering a relatively narrow perspective. In contrast to these traditional single-faceted models, the hybrid model developed in this study integrates the above multidimensional characteristics, effectively overcoming the limitations of existing models and thus demonstrating higher accuracy in risk assessment and prediction.
The “23%” result indicates that after blocking key risk nodes, the overall risk occurrence probability is reduced by 23%. In construction practice, close attention should be paid to key risk nodes. Theoretically, as long as these nodes are not activated, the probability of final schedule delay risk can be effectively controlled. Engineering applications further demonstrate that the proposed model can dynamically identify and block risk paths. This not only provides a useful reference for similar projects but also offers reliable support for managers in formulating scientific decisions and response strategies.
However, the proposed hybrid model still has certain limitations. Future research should test its applicability and robustness across more types of projects and explore the incorporation of real-time data to support dynamic risk assessment. This will further enhance the model’s practical utility in complex engineering environments.
6. Conclusions
To propose effective management and control strategies for schedule delay risks in prefabricated buildings under the EPC mode, this study introduces a schedule risk chain analysis method integrating FISM, BN, and a coupling degree model from the perspective of risk correlation. The main conclusions are as follows:
- (1)
- Using the literature research method, 25 schedule risk factors for prefabricated construction under the EPC model were objectively and effectively extracted, and an indicator system was constructed after scientific classification. Considering the interrelationships among these schedule risk factors, the FISM was applied to theoretically analyze the correlation effects of risk factors, ultimately yielding a network diagram formed by the interweaving of 46 schedule delay risk chains.
- (2)
- Optimization of the Bayesian network conditional probability calculation process. Given that the hierarchical network diagram obtained from the FISM only reflects the mutual influence relationships among schedule risk factors but cannot quantify the influence intensity, a modified coupling degree model was introduced to quantify the correlation of risk factors using a fuzzy correlation matrix. To address the difficulty of weighting due to the large number of Bayesian network nodes, the coupling strength of risk factors was innovatively transformed into the influence weight of parent nodes on child nodes, calculated using the probability allocation method. This reduces the number of expert decisions, lowers error rates, and significantly improves computational efficiency and accuracy.
- (3)
- Based on the Bayesian network model, simulation analysis was conducted on the top 15 schedule risk factors by hazard degree, identifying two critical transmission paths and other potential key causal factors. For the critical transmission paths, simulations were carried out using the GeNIe platform to locate key blocking nodes, reducing the probability of schedule delay risk by 23%, avoiding the resource consumption of full-node blocking, and effectively improving engineering profits. For key causal factors, targeted control measures were formulated to block risk transmission and prevent schedule delays.
Author Contributions
Conceptualization, Y.T. (Yong Tian) and Y.T. (Yanjuan Tang); methodology, Y.T. (Yong Tian); software, Y.T. (Yong Tian); validation, Y.T. (Yanjuan Tang); formal analysis, Y.T. (Yong Tian); investigation, Y.T. (Yong Tian) and Y.T. (Yanjuan Tang); resources, Y.T. (Yanjuan Tang); data curation, Y.T. (Yong Tian); writing—original draft preparation, Y.T. (Yong Tian); writing—review and editing, Y.T. (Yong Tian) and Y.T. (Yanjuan Tang); supervision, Y.T. (Yanjuan Tang). All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Xinjiang Production and Constructior Corps Financial Science and Technology Program Project (No. 2023AB013-04).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, S.L.; Hou, Z.W.; Chen, H.B. Network model analysis of quality control factors of prefabricated buildings based on the complex network theory. Buildings 2022, 12, 1874. [Google Scholar] [CrossRef]
- Bachmann, H.; Steinle, A. Precast Concrete Structures; Ernst & Sohn: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.D.; Hu, Z.Y. Review and thinking on development of building industrialization in China. China Civ. Eng. J. 2016, 49, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.C.; Sun, R.; Ren, L.Y.; Geng, X.X.; Wang, X.M.; Lv, L. Risk Propagation Model and Simulation of an Assembled Building Supply Chain Network. Buildings 2023, 13, 981. [Google Scholar] [CrossRef]
- Huang, J.X.; Fu, X.W.; Chen, X.X.; Wen, X. Supply Chain Management for the Engineering Procurement and Construction (EPC) Model: A Review and Bibliometric Analysis. Sustainability 2024, 16, 9748. [Google Scholar] [CrossRef]
- Kim, M.H.; Lee, E.B.; Choi, H.S. A forecast and mitigation model of construction performance by assessing detailed engineering maturity at key milestones for offshore EPC mega-projects. Sustainability 2019, 11, 1256. [Google Scholar] [CrossRef]
- Li, S.Y.; Gao, S.H. Study on Factors Affecting the Progress of Engineering Projects under the EPC Model. E3S Web Conf. 2024, 565, 01015. [Google Scholar] [CrossRef]
- Aldhaheri, M.; Bakchan, A.; Sandhu, M.A. A structural equation model for enhancing effectiveness of engineering, procurement and construction (EPC) major projects: End-user’s perspective. Eng. Constr. Archit. Manag. 2018, 25, 1226–1252. [Google Scholar] [CrossRef]
- Kaming, P.F.; Koesmargono, A.; Aji, B.W. Delay model for Engineering Procurement Construction (EPC): A case of Liquefied Natural Gas (LNG) projects in Indonesia. MATEC Web Conf. EDP Sci. 2019, 270, 05010. [Google Scholar] [CrossRef]
- Habibi, M.; Kermanshachi, S.; Rouhanizadeh, B. Identifying and measuring engineering, procurement, and construction (EPC) key performance indicators and management strategies. Infrastructures 2019, 4, 14. [Google Scholar] [CrossRef]
- Luo, Q.; Sun, C.; Li, G.; Li, Y.; Xue, J.; Zhang, G. Hierarchical schedule risk structures and mitigation strategies in prefabricated building projects: An integrated SNA-ISM approach. Eng. Constr. Archit. Manag. 2025; ahead-of-print. [Google Scholar] [CrossRef]
- Sun, R.; Geng, X.; Zhao, L.; Wang, Y.; Guo, R. Research on the Risk-Inducing Factors of Prefabricated Building Design Change Based on Improved DEMATEL-ISM. Buildings 2023, 13, 3036. [Google Scholar] [CrossRef]
- Fan, C.; Binchao, D.; Yin, Y. Hierarchical structure and transfer mechanism to assess the scheduling-related risk in construction of prefabricated buildings: An integrated ISM–MICMAC approach. Eng. Constr. Archit. Manag. 2023, 30, 2991–3013. [Google Scholar] [CrossRef]
- Zhong, C.; Zhang, S. Schedule Risk Analysis of Prefabricated Building Projects Based on DEMATEL-ISM and Bayesian Networks. Buildings 2025, 15, 508. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, W.; Arashpour, M.; Yang, Z.; Shao, C.; Li, C. Predicting delays in prefabricated projects: SD-BP neural network to define effects of risk disruption. Eng. Constr. Archit. Manag. 2022, 29, 1753–1776. [Google Scholar] [CrossRef]
- Xia, M.; Zhao, L.; Zhao, L. A Comprehensive Risk-Assessment Method for Prefabricated Buildings Using EPC: A Case Study from China. Sustainability 2022, 14, 1910. [Google Scholar] [CrossRef]
- Cao, P.; Lei, X. Evaluating Risk in Prefabricated Building Construction under EPC Contracting Using Structural Equation Modeling: A Case Study of Shaanxi Province, China. Buildings 2023, 13, 1465. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, L.; Du, X. Risk Assessment of Prefabricated Building Projects Based on the G1-CRITIC Method and Cloud Model: A Case Study from China. Buildings 2025, 15, 2787. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J. Research on Key Risk Factors and Risk Transmission Path of Procurement in International Engineering Procurement Construction Project. Buildings 2022, 12, 534. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, D.; Wang, T.; Xu, C. Coupling Analysis of Tunnel Construction Safety Risks Based on N-K Model and SD Causality Diagram. Buildings 2023, 13, 1081. [Google Scholar] [CrossRef]
- Wang, S.; Kong, W.; Ren, L.; ZHI, D. Research on misuses and modification of coupling coordination degree model in China. J. Nat. Resour. 2021, 36, 793–810. [Google Scholar] [CrossRef]
- Pan, H.; Gou, H.; Wan, Z.; Ren, C.; Chen, M.; Gou, T.; Luo, Z. Research on coupling degree model of safety risk system for tunnel construction in subway shield zone. Math. Probl. Eng. 2019, 2019, 5783938. [Google Scholar] [CrossRef]
- Guo, D.; Song, Z.; Xu, T.; Zhang, Y.; Ding, L. Coupling analysis of tunnel construction risk in complex geology and construction factors. J. Constr. Eng. Manag. 2022, 148, 04022097. [Google Scholar] [CrossRef]
- Zhou, J.; Tang, Y.J.; Zhang, W.J.; Wang, H.J. Study on engineering progress risk analysis methods under perspective of risk chain. J. Hydroelectr. Eng. 2023, 42, 96–107. (In Chinese) [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, H.; Huang, P.Y.; Zhou, Z.L.; Wang, B. Safety risk evaluation of tunnel collapse based on Bayesian network of improving conditional probability. J. Cent. South Univ. (Sci. Technol.) 2023, 54, 327–340. (In Chinese) [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y.; Kou, X.; Yin, D.; Mi, R.; Li, L. Railway dangerous goods transportation system risk analysis: An Interpretive Structural Modeling and Bayesian Network combining approach. Reliab. Eng. Syst. Saf. 2020, 204, 107220. [Google Scholar] [CrossRef]
- Agarwal, N.; Seth, N. Analysis of Supply Chain Resilience Enablers and Business Outcomes Using Delphi and Fuzzy ISM for Indian Automobile Industry. Glob. J. Flex. Syst. Manag. 2024, 25, 763–783. [Google Scholar] [CrossRef]
- Roed, W.; Mosleh, A.; Vinnem, J.E.; Aven, T. On the use of the hybrid causal logic method in offshore risk analysis. Reliab. Eng. Syst. Saf. 2009, 94, 445–455. [Google Scholar] [CrossRef]
- Peng, J.L.; Zhou, J. Analysis of influence factors of prefabricated building cost based on FISMM-ANP. Chang. Univ. Sci. Technol. 2021, 18, 57–65+98. (In Chinese) [Google Scholar] [CrossRef]
- Fidan, G.; Dikemen, I.; Tanyer, A.M.; Birgonul, M.T. Ontology for relating risk and vulnerability to cost overrun in international projects. J. Comput. Civ. Eng. 2011, 25, 302–315. [Google Scholar] [CrossRef]
- Li, S.G. Key Risk Transmission Paths During the Construction Phase and Blocking Strategies of Green Retrofit Project in Public Buildings. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2024. (In Chinese). [Google Scholar] [CrossRef]
- Ichsan, M.; Isvara, W.; Karim, S. Monte Carlo Simulation for Enhancing the Schedule Completion Forecast of Jakarta Central Railway Station Construction Project. Appl. Sci. 2025, 15, 7464. [Google Scholar] [CrossRef]
- Tavakolan, M.; Etemadinia, H. Fuzzy weighted interpretive structural modeling: Improved method for identification of risk interactions in construction projects. J. Constr. Eng. Manag. 2017, 143, 04017084. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).