Applying the Enhanced Free Cooling Concept: A Case Study on Reducing Mechanical Cooling Demand
Abstract
1. Introduction
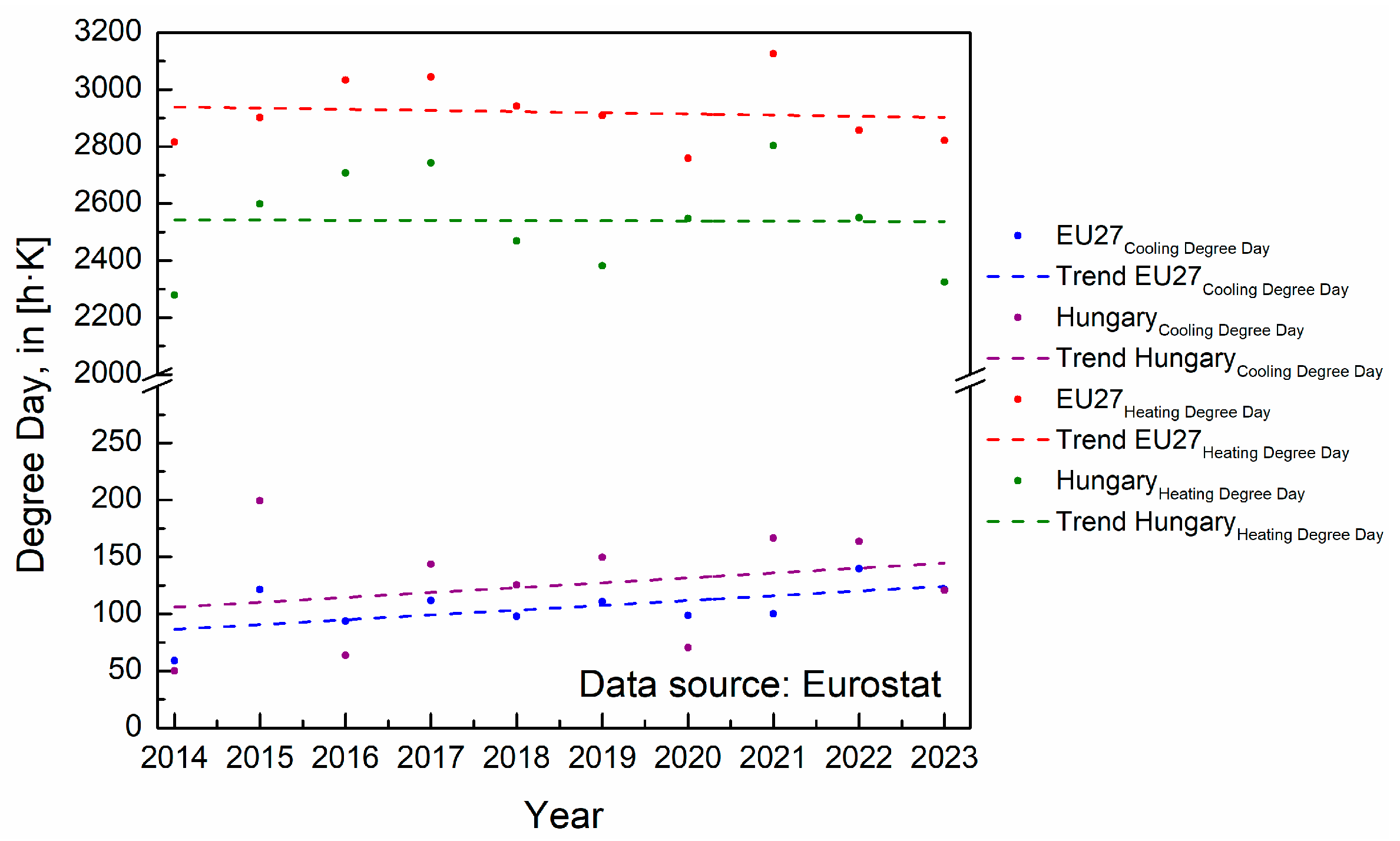
1.1. Literature Review
- Country level: construction of new power generation facilities (e.g., nuclear power plants) [11];
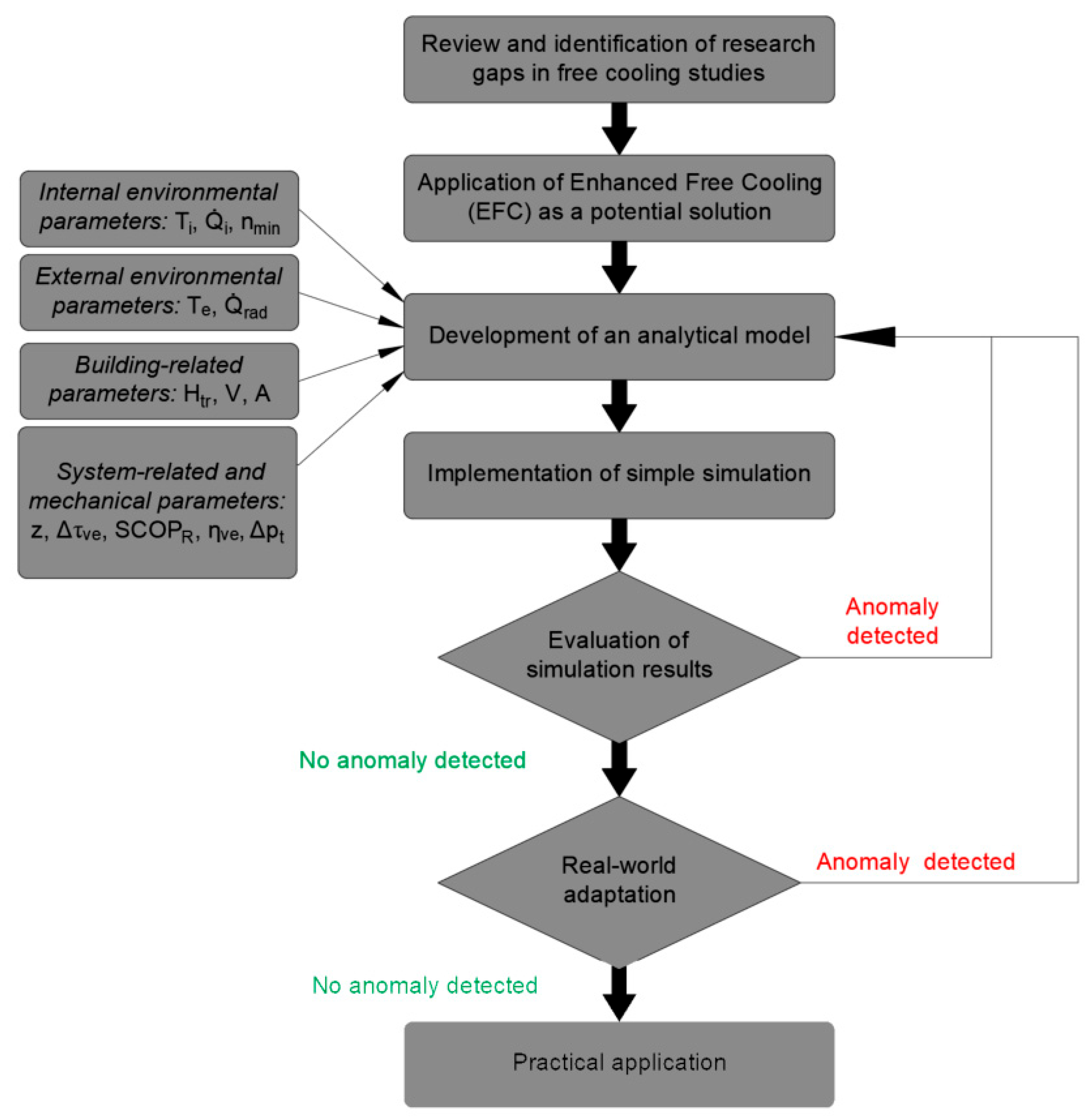
1.2. Research Gaps and Paper Structure
- Previous studies primarily focus on buildings with high cooling demand (data centres, large-scale commercial facilities), whilst smaller and low-demand facilities (residential, office, and small commercial buildings) remain underrepresented in the literature.
- Earlier research typically examined single building or system configurations, with limited systematic parametric investigation (orientation, glazing ratio, minimum air change rate, diverse meteorological day types), which restricted the generalisability of findings.
- Few studies examine how the free cooling optimum and energy-saving potential change at high air change rates (n > 10 h−1) in highly glazed buildings (modern commercial/office buildings with substantial heat gains), despite particular relevance to contemporary building designs.
- Investigation of free cooling operation extension frequently appears as mechanical chiller operation reduction, without sufficiently comprehensive impact assessment (e.g., increased air change versus increased fan energy consumption; effect of increased heat gains in highly glazed configurations).
- Few preceding studies explicitly detail how individual input parameters (minimum air change rate, orientation, glazing ratio) influence the optimal air change value and anticipated energy savings.
2. Theoretical Background and Description
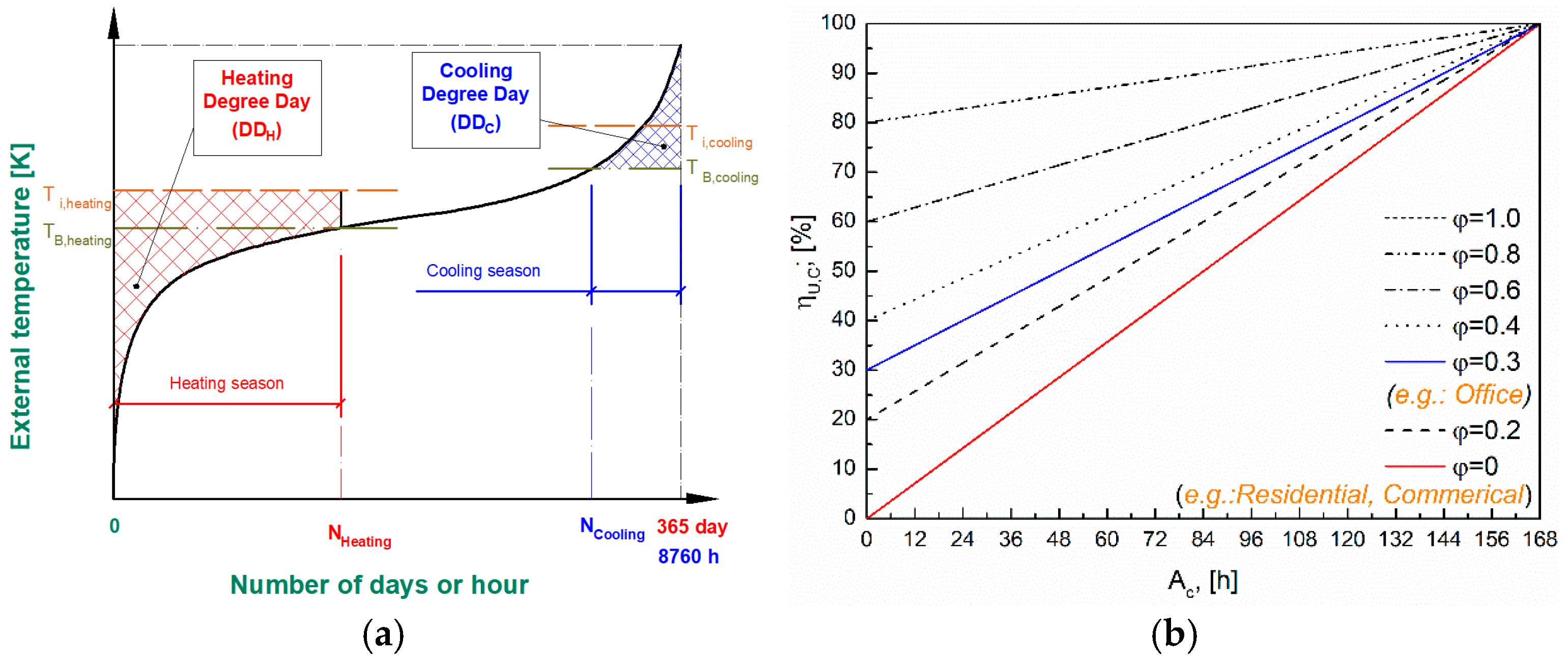
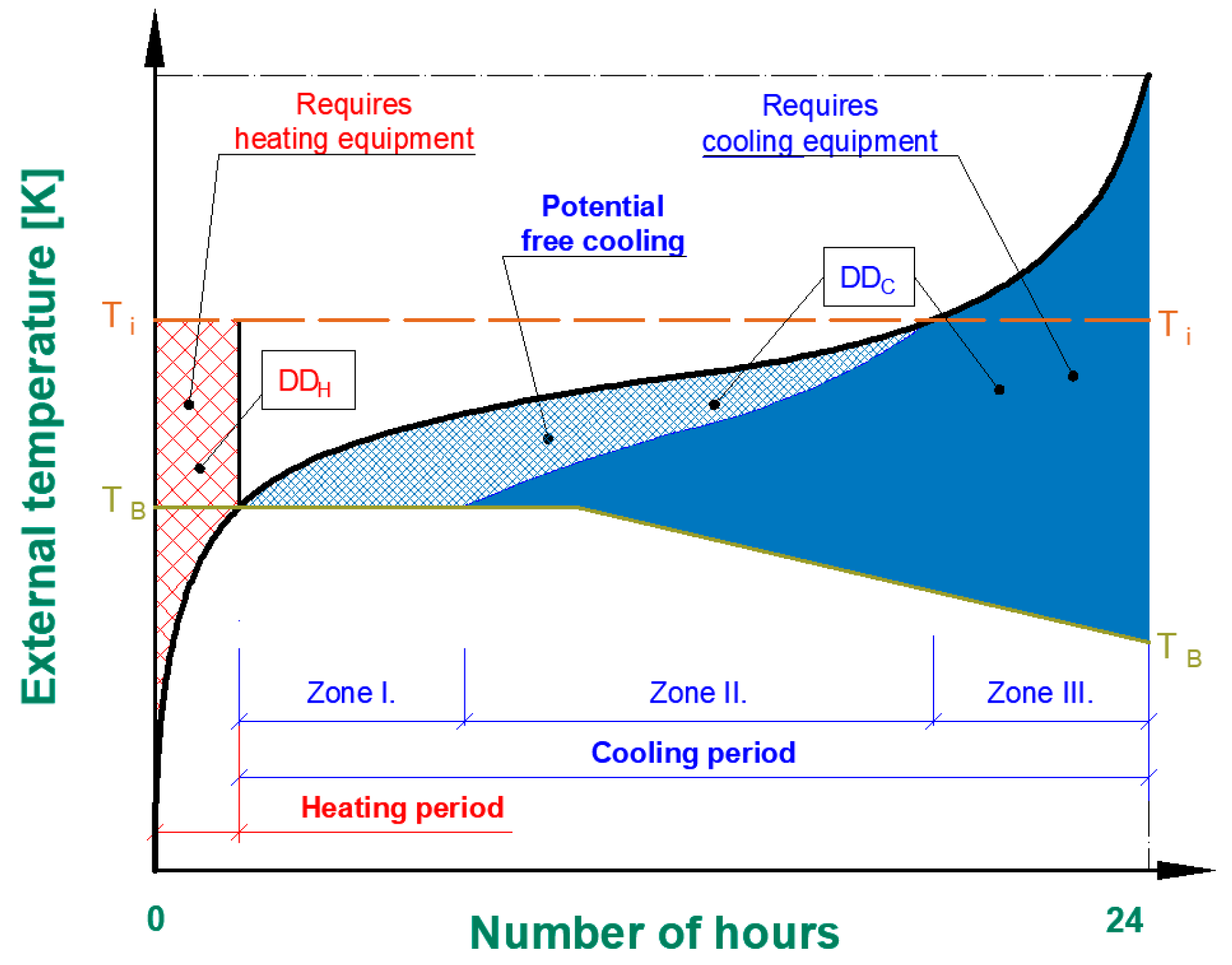
2.1. Degree-Day Curve, Degree-Day, Energy Demand
2.2. Conditions and Constraints for Equivalent Free Cooling Replacement
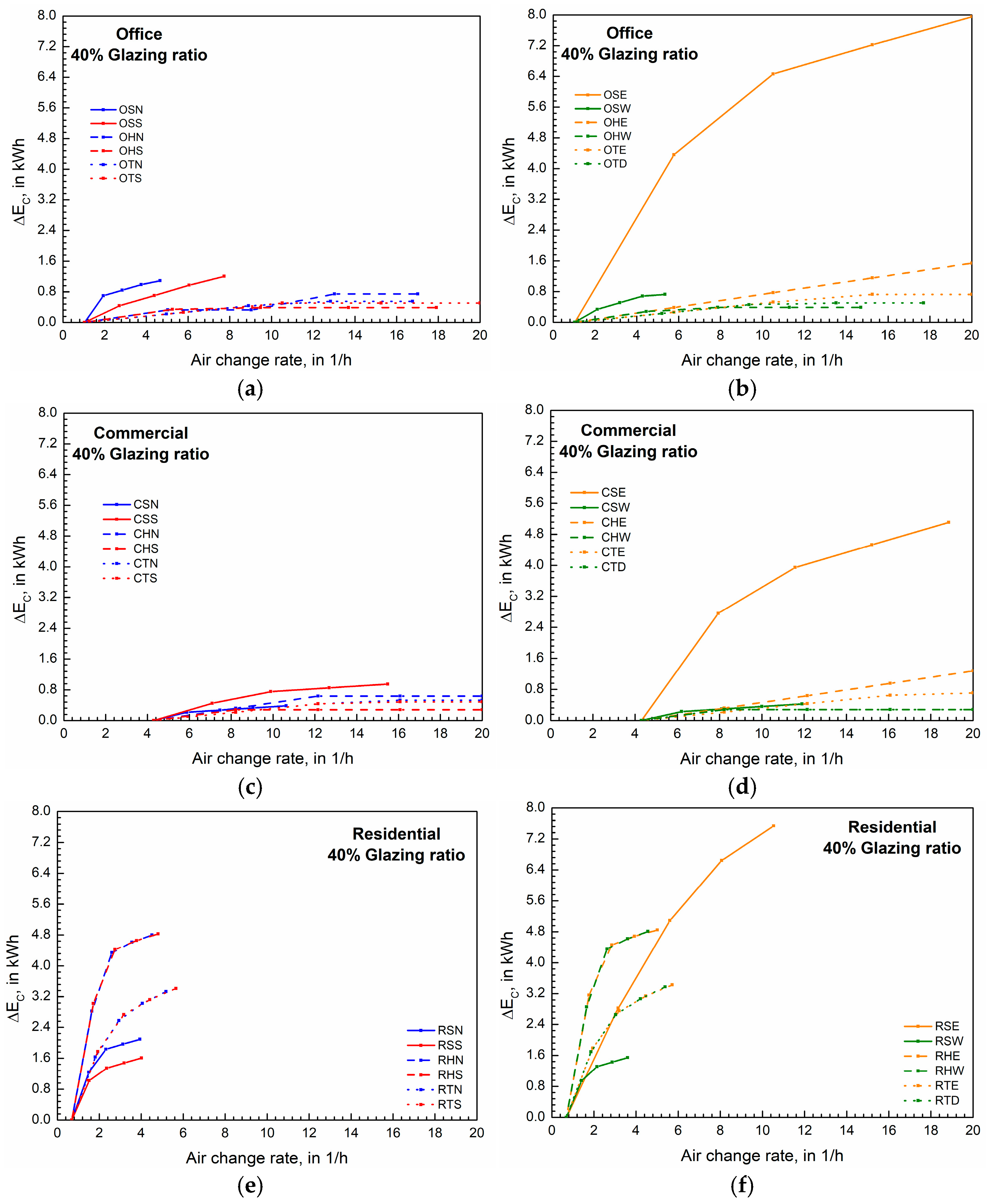
3. Results
4. Case Study and Discussion
4.1. The Analysed Room and the Changed Parameter
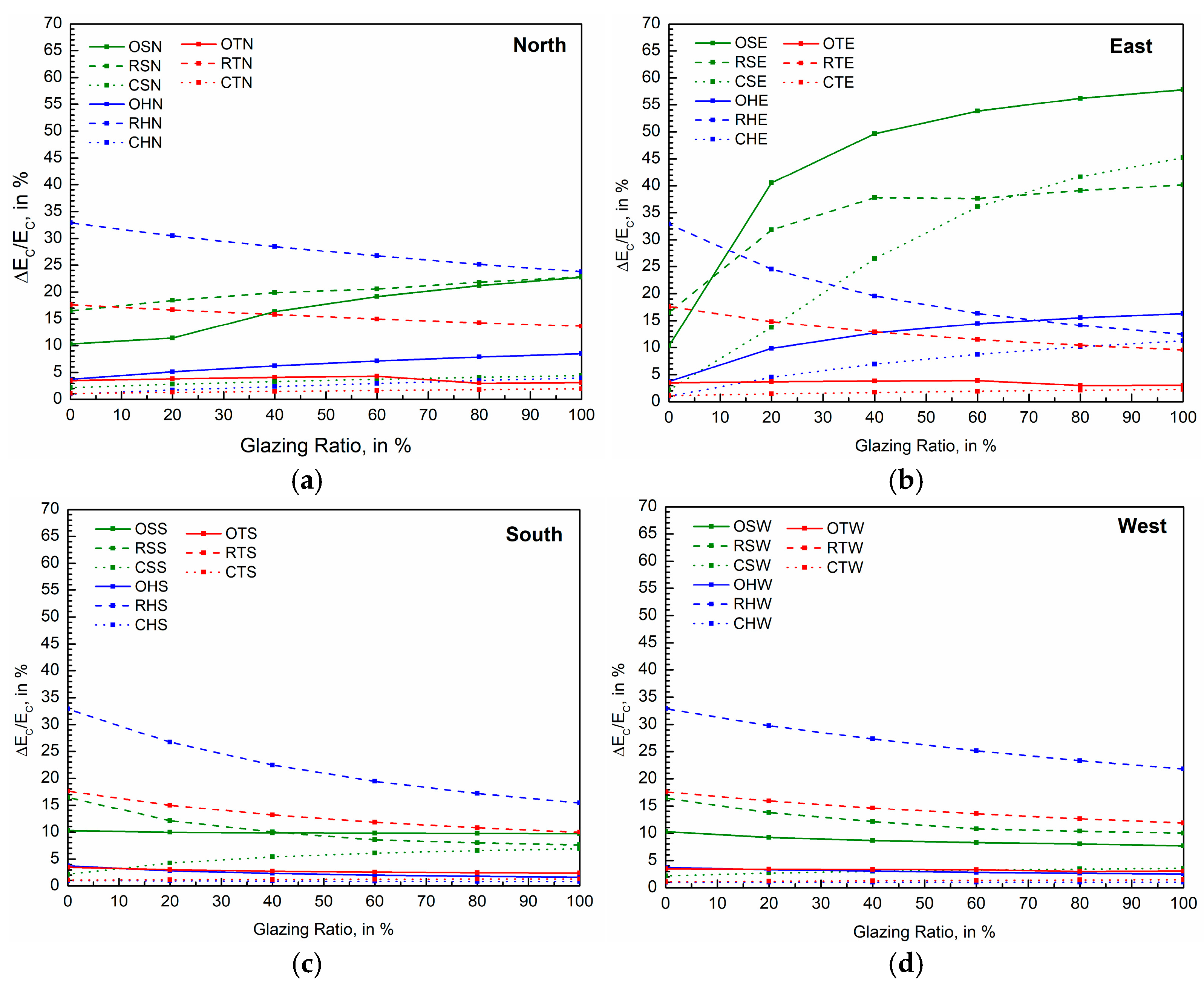
4.2. Savings Analysis with the Application of Enhanced Free Cooling
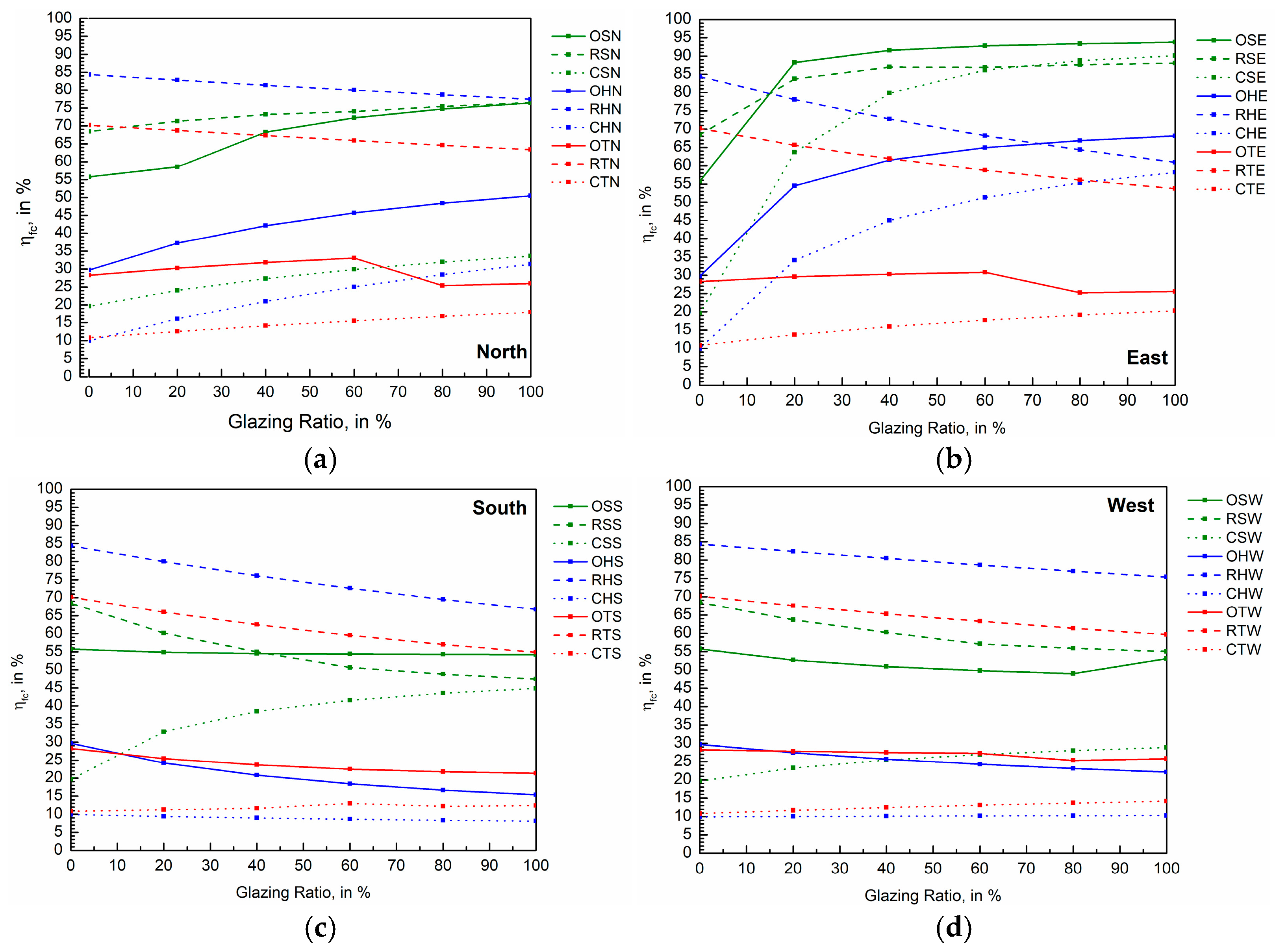
4.3. Air Exchange Rate Thresholds and EFC Resistance Points
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ‘TB’ | is the balance point temperature, in [K]. |
| ‘’ | is the solar heat gains, in [W]. |
| ‘’ | is the internal heat gains, in [W]. |
| ‘Ti’ | is the internal temperature, in [K]. |
| ‘Te’ | is the environmental temperature, in [K]. |
| ‘Htr’ | is the transmission heat loss coefficient [W∙K−1]. |
| ‘c’ | is the specific heat capacity of air, in [J·kg−1 ·K−1]. |
| ‘ρ’ | is the air density, in [kg·m−3]. |
| ‘n’ | is the air change rate, in [h−1]. |
| ‘V’ | is the volume of the examined room, in [m3]. |
| ‘DDC’ | is the cooling degree-day value, in [h·K]. |
| ‘DDH’ | is heating degree-day value, in [h·K]. |
| ‘Te’ | is the external temperature, in [K]. |
| ‘ηU,C’ | is the weekly utilisation efficiency for the building (cooling mode), in [%]. |
| ‘AC’ | is the number of active hours per week from a human usage perspective, in [h]. |
| ‘φ’ | is the passivity operating ratio during inactive periods compared to active periods, in [-]. |
| ‘EC’ | is the cooling energy demand, in [Wh]. |
| ‘nmin’ | is the air change rate based on the human fresh air requirement, in [h−1]. |
| ‘nmax’ | is the air change rate at the economic threshold and z = 1.1, in [h−1]. |
| ‘Δn’ | is the additional air change rate required to reach nmax, in [h−1] |
| ‘ΔEC’ | is the avoided mechanical cooling energy demand, in [kWh]. |
| ‘ECmax’ | is the avoided mechanical cooling energy demand upper limit, in [Wh]. |
| ‘z’ | is the HVAC system correction factor, in [-]. |
| ‘ΔWVE’ | is the additional ventilation electric work, in [kWh]. |
| ‘ΔWCU’ | is the avoided electrical work of mechanical cooling, in [kWh]. |
| ‘Δτve’ | is the operating period of EFC, in [s] |
| ‘SCOPR’ | is the Seasonal Coefficient of Performance of the cooling unit, in [-]. |
| ‘∆pt’ | is the total pressure increase created by the fan, in [Pa] |
| ‘ηve’ | is the overall efficiency of the fan, in [-]. |
| ‘ηfc’ | is the efficiency of enhanced free cooling, in [%] |
| ‘nopt’ | is the optimal air change rate, in [h−1]. |
References
- The European Parliament and the Council of the European Union. Directive 2010/30/EU of the European Parliament and of the Council; on the indication by labelling and standard product information of the consumption of energy and other resources by energy-related products (recast). Off. J. Eur. Union 2010, 153, 1–12. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32010L0030&from=EN (accessed on 20 August 2025).
- Kalmár, F.; Kalmár, T. Reduction of Energy Use for Heating in Detached Housés using Passive Technics. Int. J. Eng. Manag. Sci. 2022, 7, 64–76. [Google Scholar] [CrossRef]
- Szodrai, F.; Lakatos, Á.; Kalmár, F. Analysis of the change of the specific heat loss coefficient of buildings resulted by the variation of the geometry and the moisture load. Energy 2016, 115, 820–829. [Google Scholar] [CrossRef]
- Kostyák, A.; Szekeres, S.; Csáky, I. Assessment of the Actual and Required Cooling Demand for Buildings with Extensive Transparent Surfaces. Energies 2024, 17, 5814. [Google Scholar] [CrossRef]
- Kalmár, F.; Bodó, B.; Li, B.; Kalmár, T. Decarbonization Potential of Energy Used in Detached Houses—Case Study. Buildings 2024, 14, 1824. [Google Scholar] [CrossRef]
- Kalmár, F. Interrelation between glazing and summer operative temperature in buildings. Int. Rev. Appl. Sci. Eng. IRASE 2016, 7, 51–60. [Google Scholar] [CrossRef]
- Csáky, I.; Kalmár, T. Analysis of degree day and cooling energy demand in educational buildings. Environ. Eng. Manag. J. 2014, 13, 2765–2770. [Google Scholar] [CrossRef]
- Csáky, I. Analysis of daily energy demand for cooling in buildings with different comfort categories—Case study. Energies 2021, 14, 4694. [Google Scholar] [CrossRef]
- Santamouris, M. Cooling the buildings—Past, present and future. Energy Build. 2016, 128, 617–638. [Google Scholar] [CrossRef]
- Li, X.; Wu, W.; Yu, C.W.F. Energy demand for hot water supply for indoor environments: Problems and perspectives. Indoor Built Environ. 2015, 24, 5–10. [Google Scholar] [CrossRef]
- Akinyemi, T.; Jung, S. Power plants improve local residents’ wealth: A case study of Nigeria. Energy Econ. 2025, 142, 108131. [Google Scholar] [CrossRef]
- Prataviera, E.; Zarrella, A.; Morejohn, J.; Narayanan, V. Exploiting district cooling network and urban building energy modeling for large-scale integrated energy conservation analyses. Appl. Energy 2024, 356, 122368. [Google Scholar] [CrossRef]
- Neri, M.; Guelpa, E.; Khor, J.O.; Romagnoli, A.; Verda, V. Hierarchical model for design and operation optimization of district cooling networks. Appl. Energy 2024, 371, 123667. [Google Scholar] [CrossRef]
- Szabó, G.L. Energetic and exergetic study of a potential interconnection of a natural gas engine, heat pumps with a thermal and a mechanical compressor. Therm. Sci. Eng. Prog. 2022, 36, 101525. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X. Research progress of energy-saving technology in cold storage with/without phase change materials. J. Energy Storage 2024, 103, 114334. [Google Scholar] [CrossRef]
- Guo, Z.; Qiao, J.; Liu, X.; Lin, F.; Liu, M.; Fang, M.; Huang, Z.; Zhang, X.; Min, X. Advances in mineral-based composite phase change materials for energy storage: A review. Green Smart Min. Eng. 2024, 1, 447–473. [Google Scholar] [CrossRef]
- Lakatos, Á.; Kalmár, F.; Csáky, I. Material selection in order to minimize the heat loss of piping based on measurements and calculations. AIP Conf. Proc. 2019, 2186, 070011. [Google Scholar] [CrossRef]
- Kostyák, A.; Béres, C.; Szekeres, S.; Csáky, I. Buffer Tank Discharge Strategies in the Case of a Centrifugal Water Chiller. Energies 2023, 16, 188. [Google Scholar] [CrossRef]
- Vassiliades, C.; Barone, G.; Buonomano, A.; Forzano, C.; Giuzio, G.F.; Palombo, A. Assessment of an innovative plug and play PV/T system integrated in a prefabricated house unit: Active and passive behaviour and life cycle cost analysis. Renew. Energy 2022, 186, 845–863. [Google Scholar] [CrossRef]
- Szkordilisz, F.; Kiss, M. Passive cooling potential of alley trees and their impact on indoor comfort. Pollack Period. 2016, 11, 101–112. [Google Scholar] [CrossRef][Green Version]
- Dehwah, A.H.A.; Krarti, M. Energy performance of integrated adaptive envelope systems for residential buildings. Energy 2021, 233, 121165. [Google Scholar] [CrossRef]
- Güğül, G.N.; Gökçül, F.; Eicker, U. Sustainability analysis of zero energy consumption data centers with free cooling, waste heat reuse and renewable energy systems: A feasibility study. Energy 2023, 262, 125495. [Google Scholar] [CrossRef]
- Do, H.; Cetin, K.S. Mixed-Mode Ventilation in HVAC System for Energy and Economic Benefits in Residential Buildings. Energies 2022, 15, 4429. [Google Scholar] [CrossRef]
- Wenzel, P.M.; Mühlen, M.; Radgen, P. Free Cooling for Saving Energy: Technical Market Analysis of Dry, Wet, and Hybrid Cooling Based on Manufacturer Data. Energies 2023, 16, 3661. [Google Scholar] [CrossRef]
- Aili, A.; Long, W.; Cao, Z.; Wen, Y. Radiative free cooling for energy and water saving in data centers. Appl. Energy 2024, 359, 122672. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, B.; Zhou, Q. Air Conditioning System Design using Free Cooling Technology and Running Mode of a Data Center in Jinan. Procedia Eng. 2017, 205, 3545–3549. [Google Scholar] [CrossRef]
- Zhang, H.; Shao, S.; Xu, H.; Zou, H.; Tian, C. Free cooling of data centers: A review. Renew. Sustain. Energy Rev. 2014, 35, 171–182. [Google Scholar] [CrossRef]
- Li, J.; Li, Z. Model-based optimization of free cooling switchover temperature and cooling tower approach temperature for data center cooling system with water-side economizer. Energy Build. 2020, 227, 110407. [Google Scholar] [CrossRef]
- van Moeseke, G.; Bruyère, I.; De Herde, A. Impact of control rules on the efficiency of shading devices and free cooling for office buildings. Build. Environ. 2007, 42, 784–793. [Google Scholar] [CrossRef]
- Xu, T.; Jing, Y.; Madani, H.; Xie, X.; Jiang, Y. Applying indirect evaporative chillers for comfort cooling in Northern European commercial buildings: A case study in Sweden. Appl. Therm. Eng. 2024, 248, 123158. [Google Scholar] [CrossRef]
- Amado, E.A.; Schneider, P.S.; Bresolin, C.S. Free cooling potential for Brazilian data centers based on approach point methodology. Int. J. Refrig. 2021, 122, 171–180. [Google Scholar] [CrossRef]
- Cho, J.; Lim, T.; Kim, B.S. Viability of datacenter cooling systems for energy efficiency in temperate or subtropical regions: Case study. Energy Build. 2012, 55, 189–197. [Google Scholar] [CrossRef]
- Kwon, T.D.; Jeong, J.W. Energy advantage of cold energy recovery system using water- and air-side free cooling technologies in semiconductor fabrication plant in summer. J. Build. Eng. 2023, 69, 106277. [Google Scholar] [CrossRef]
- Mi, R.; Bai, X.; Xu, X.; Ren, F. Energy performance evaluation in a data center with water-side free cooling. Energy Build. 2023, 295, 113278. [Google Scholar] [CrossRef]
- Cai, S.; Gou, Z. Towards energy-efficient data centers: A comprehensive review of passive and active cooling strategies. Energy Built Environ. 2024; in press. [Google Scholar] [CrossRef]
- Desideri, U.; Sorbi, N.; Arcioni, L.; Leonardi, D. Feasibility study and numerical simulation of a ground source heat pump plant, applied to a residential building. Appl. Therm. Eng. 2011, 31, 3500–3511. [Google Scholar] [CrossRef]
- Lee, K.P.; Chen, H.L. Analysis of energy saving potential of air-side free cooling for data centers in worldwide climate zones. Energy Build. 2013, 64, 103–112. [Google Scholar] [CrossRef]
- Zhao, W.; Li, H.; Wang, S. A generic design optimization framework for semiconductor cleanroom air-conditioning systems integrating heat recovery and free cooling for enhanced energy performance. Energy 2024, 286, 129600. [Google Scholar] [CrossRef]
- Ljungqvist, H.M.; Risberg, M.; Toffolo, A.; Vesterlund, M. A realistic view on heat reuse from direct free air-cooled data centres. Energy Convers. Manag. X 2023, 20, 100473. [Google Scholar] [CrossRef]
- Hnayno, M.; Chehade, A.; Klaba, H.; Polidori, G.; Maalouf, C. Experimental investigation of an optimized indirect free cooling system including a dry cooler equipped with evaporative cooling pads for data center. Energy Rep. 2023, 9, 460–469. [Google Scholar] [CrossRef]
- Depoorter, V.; Oró, E.; Salom, J. The location as an energy efficiency and renewable energy supply measure for data centres in Europe. Appl. Energy 2015, 140, 338–349. [Google Scholar] [CrossRef]
- Ham, S.W.; Park, J.S.; Jeong, J.W. Optimum supply air temperature ranges of various air-side economizers in a modular data center. Appl. Therm. Eng. 2015, 77, 163–179. [Google Scholar] [CrossRef]
- Ham, S.W.; Kim, M.H.; Choi, B.N.; Jeong, J.W. Energy saving potential of various air-side economizers in a modular data center. Appl. Energy 2015, 138, 258–275. [Google Scholar] [CrossRef]
- Hellmer, B.A. Consumption Analysis of Telco and Data Center Cooling and Humidification Options. ASHRAE Trans. 2010, 116, 118–133. [Google Scholar]
- Lamptey, N.B.; Anka, S.K.; Lee, K.H.; Cho, Y.; Choi, J.W.; Choi, J.M. Comparative energy analysis of cooling energy performance between conventional and hybrid air source internet data center cooling system. Energy Build. 2024, 302, 113759. [Google Scholar] [CrossRef]
- Lubis, A.; Giannetti, N.; Alhamid, M.I.; Saito, K.; Yabase, H. Dynamic analysis of single–double-effect ab-sorption chiller with variable thermal conductance during partial-load operation. Appl. Therm. Eng. 2023, 218, 119424. [Google Scholar] [CrossRef]
- Rabczak, S.; Nowak, K. Possibilities of Adapting a Free-Cooling System in an Existing Commercial Building. Energies 2022, 15, 3350. [Google Scholar] [CrossRef]
- Jayasekara, S.; Halgamuge, S.K. Mathematical modeling and experimental verification of an absorption chiller including three dimensional temperature and concentration distributions. Appl. Energy 2013, 106, 232–242. [Google Scholar] [CrossRef]
- Boukholda, I.; Ben Ezzine, N.; Bellagi, A. Experimental investigation and simulation of commercial absorption chiller using natural refrigerant R717 and powered by Fresnel solar collector. Int. J. Thermofluids 2025, 27, 101213. [Google Scholar] [CrossRef]
- Kailkhura, G.; Mandel, R.K.; Shooshtari, A.; Ohadi, M. A 1D Reduced-Order Model (ROM) for a Novel Latent Thermal Energy Storage System. Energies 2022, 15, 5124. [Google Scholar] [CrossRef]
- Evola, G.; Costanzo, V.; Marletta, L. Exergy analysis of energy systems in buildings. Buildings 2018, 8, 180. [Google Scholar] [CrossRef]
- Dikmen, M.; Burns, C. The effects of domain knowledge on trust in explainable AI and task performance: A case of peer-to-peer lending. Int. J. Hum. Comput. Stud. 2022, 162, 102792. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, K.H.; Ha, J.W.; Song, Y.H. Research on a Plan of Free Cooling Operation Control for the Efficiency Improvement of a Water-Side Economizer. Energies 2024, 17, 2804. [Google Scholar] [CrossRef]
- Verbai, Z.; Csáky, I.; Kalmár, F. Balance point temperature for heating as a function of glazing orientation and room time constant. Energy Build. 2017, 135, 1–9. [Google Scholar] [CrossRef]
- Bodó, B.; Béni, E.; Szabó, G.L. A Facility’s Energy Demand Analysis for Different Building Functions. Buildings 2023, 13, 1905. [Google Scholar] [CrossRef]
- Szabó, G.L.; Kalmár, F. Investigation of subjective and objective thermal comfort in the case of ceiling and wall cooling systems. Int. Rev. Appl. Sci. Eng. 2017, 8, 153–162. [Google Scholar] [CrossRef]
- Hungarian Ministry of Construction and Transport. Decree No. 9/2023 (V. 25.) of the Minister of Construction and Transport on the determination of the energy performance of buildings. Magy. Közlöny 2023, 78, 3462–3492. [Google Scholar]
- Hungarian Government. Government Decree No. 176/2008 (VI. 30.) on the certification of the energy performance of buildings. Magy. Közlöny 2008, 96, 5908–5915. [Google Scholar]
- Bodó, B.; Kalmár, F. Analysis of primary energy use of typical buildings in Hungary. Environ. Eng. Manag. J. 2014, 13, 2725–2731. [Google Scholar] [CrossRef]
- ISO 7730-1994; Moderate Thermal Environments-Determination of the PMV and PPD Indices and Specification of the Conditions for Thermal Comfort. International Organization for Standardization: Geneva, Switzerland, 1994.
- EN ISO 13790:2008; Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling. European Committee for Standardization: Brussels, Belgium, 2008.
- Goia, F. Search for the optimal window-to-wall ratio in office buildings in different European climates and the implications on total energy saving potential. Sol. Energy 2016, 132, 467–492. [Google Scholar] [CrossRef]
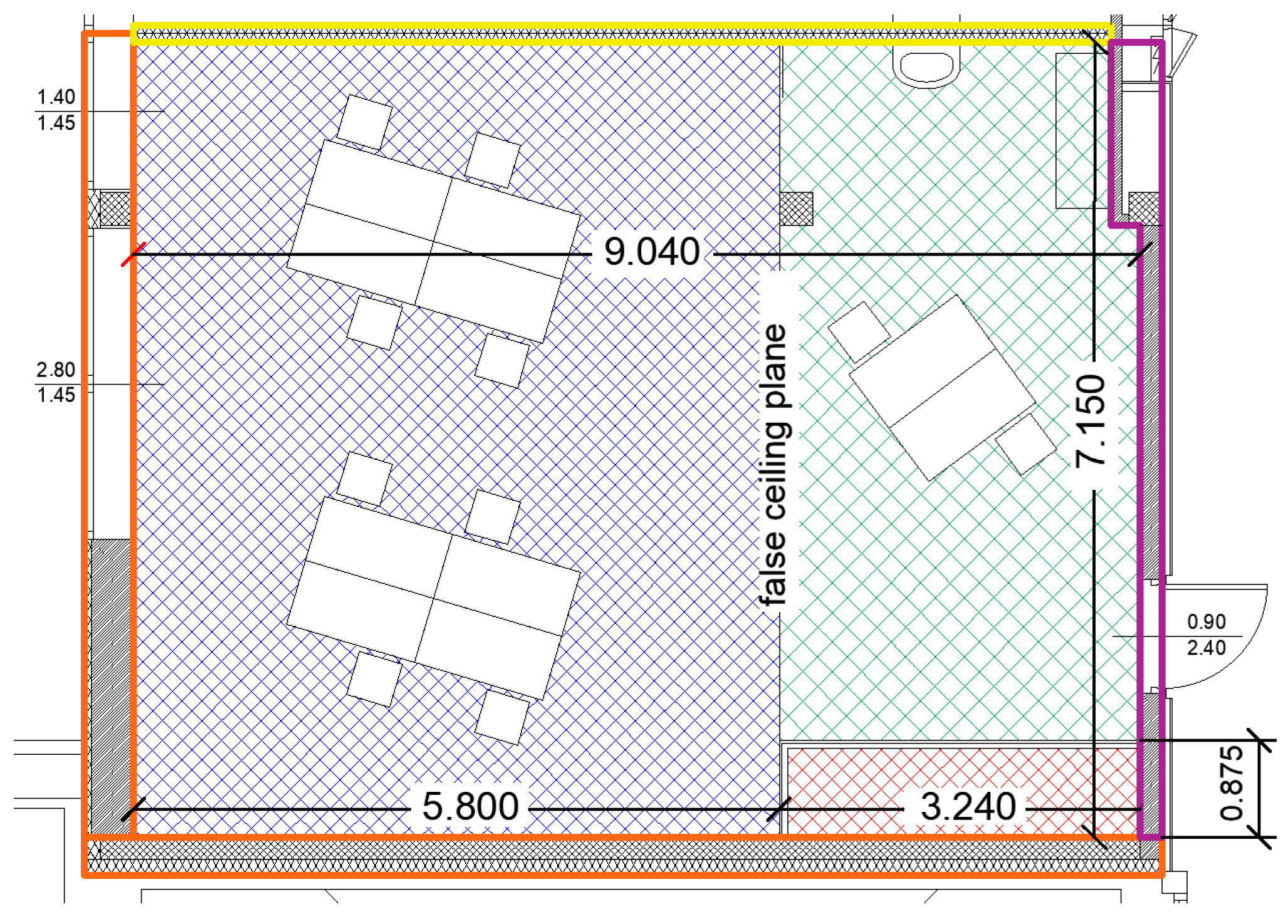
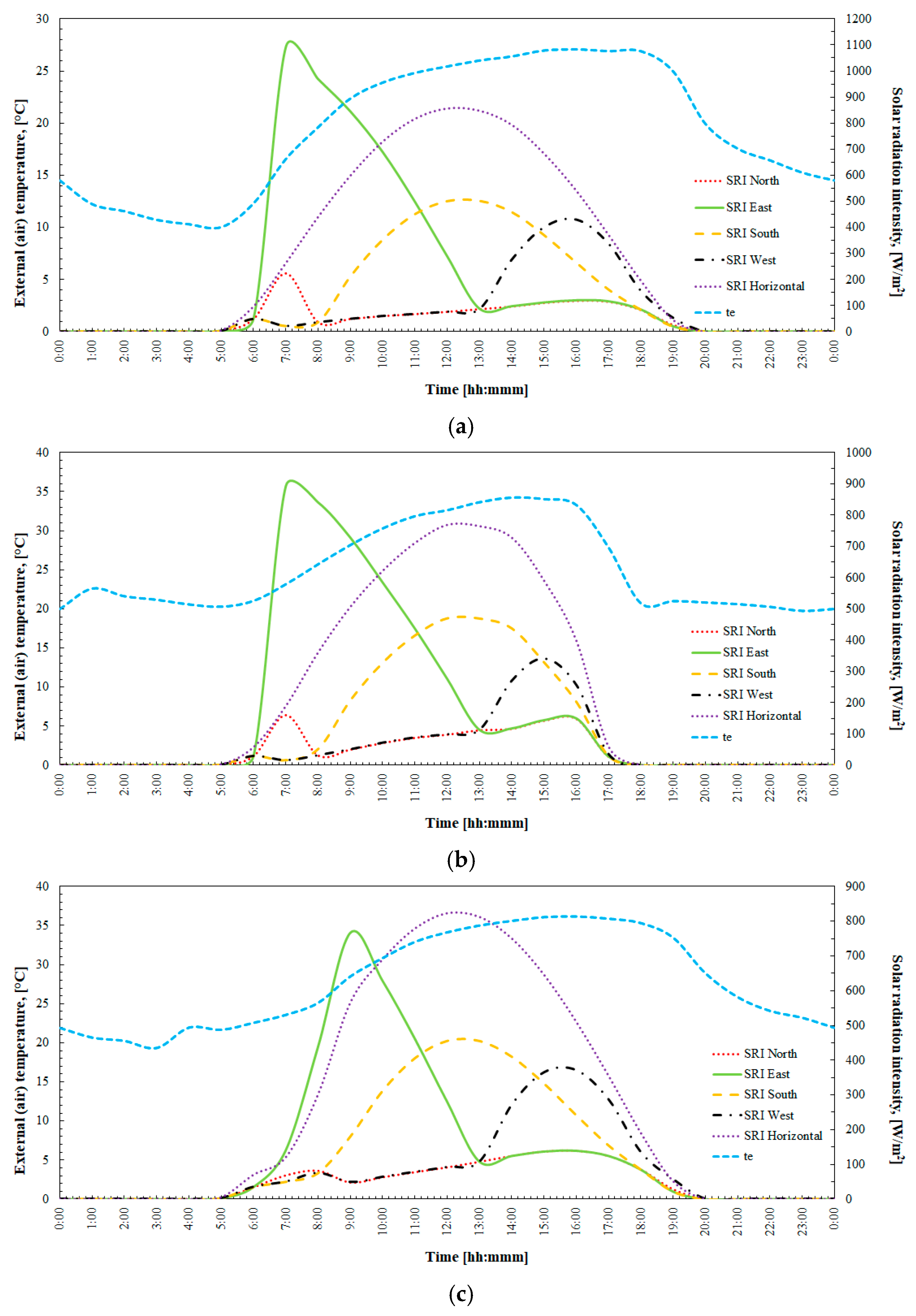

| Varied Parameter | Applied Values | |||
|---|---|---|---|---|
| Orientation | North | East | West | South |
| Glazed ratio | 0–100% (40%) | |||
| Function | Office | Commercial | Residential | |
| Meteorological parameters | Summer day (8 September 2016) | Hot day (15 August 2010) | Extremely hot day (8 April 2017) | |
| Office | Commercial | Residential | |
|---|---|---|---|
| ηve; [%] | 80% | ||
| ∆pt; [Pa] | 500 Pa | ||
| SCOPR; [-] | 4 | ||
| nmin; [h−1] | 1.0324 | 4.3017 | 0.6883 |
| AC; [h] | 7:00–17:00 (10 h) | 7:00–19:00 (12 h) | 0:00–24:00 (24 h) |
| φ; [%] | 30% | 0% | 0% |
| North | East | South | West | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ∆EC | ∆EC/EC | ∆EC | ∆EC/EC | ∆EC | ∆EC/EC | ∆EC | ∆EC/EC | ||
| in kWh | in % | in kWh | in % | in kWh | in % | in kWh | in % | ||
| Office | Summer day | 1.090 | 16.35 | 7.979 | 49.63 | 1.207 | 9.83 | 0.726 | 8.62 |
| Hot day | 0.742 | 6.22 | 2.525 | 12.71 | 0.386 | 2.33 | 0.386 | 3.04 | |
| Extremely hot day | 0.551 | 4.07 | 0.727 | 3.81 | 0.504 | 2.75 | 0.504 | 3.33 | |
| Commercial | Summer day | 0.381 | 3.31 | 5.111 | 26.45 | 0.947 | 5.39 | 0.425 | 3.01 |
| Hot day | 0.636 | 2.36 | 2.419 | 6.93 | 0.281 | 0.89 | 0.281 | 1.01 | |
| Extremely hot day | 0.530 | 1.47 | 0.706 | 1.7 | 0.484 | 1.18 | 0.484 | 1.28 | |
| Residential | Summer day | 2.094 | 19.85 | 7.539 | 37.78 | 1.60 | 9.99 | 1.543 | 12.11 |
| Hot day | 4.799 | 28.46 | 4.847 | 19.55 | 4.831 | 22.46 | 4.809 | 27.26 | |
| Extremely hot day | 3.332 | 15.79 | 3.427 | 12.86 | 3.417 | 13.16 | 3.464 | 14.61 | |
| Sort Name | 0% | 20% | 40% | 60% | 80% | 100% | |||
|---|---|---|---|---|---|---|---|---|---|
| Office | Summer day | N | OSN | 3.48 | 3.44 | 4.66 | 5.77 | 6.89 | 8.00 |
| E | OSE | 3.48 | 11.63 | 20.83 | 30.03 | 39.23 | 48.43 | ||
| S | OSS | 3.48 | 5.61 | 7.73 | 9.86 | 11.98 | 14.10 | ||
| W | OSW | 3.48 | 4.42 | 5.35 | 6.28 | 7.21 | 7.21 | ||
| Hot day | N | OHN | 11.68 | 14.35 | 17.02 | 19.68 | 22.35 | 25.01 | |
| E | OHE | 11.68 | 24.99 | 38.29 | 51.60 | 64.90 | 78.21 | ||
| S | OHS | 11.68 | 14.80 | 17.91 | 21.03 | 24.14 | 27.25 | ||
| W | OHW | 11.68 | 13.20 | 14.71 | 16.22 | 17.73 | 19.25 | ||
| Extremely hot day | N | OTN | 13.33 | 15.05 | 16.76 | 18.48 | 9.63 | 10.36 | |
| E | OTE | 13.33 | 18.07 | 22.81 | 27.54 | 15.57 | 17.79 | ||
| S | OTS | 13.33 | 16.85 | 20.37 | 23.89 | 14.25 | 16.06 | ||
| W | OTW | 13.33 | 15.51 | 17.69 | 19.87 | 11.33 | 12.49 | ||
| Commercial | Summer day | N | CSN | 9.03 | 9.83 | 10.63 | 11.43 | 12.23 | 13.03 |
| E | CSE | 9.03 | 13.09 | 18.85 | 28.49 | 37.92 | 47.16 | ||
| S | CSS | 9.03 | 12.25 | 15.48 | 18.71 | 21.93 | 25.16 | ||
| W | CSW | 9.03 | 10.46 | 11.90 | 13.33 | 14.77 | 16.21 | ||
| Hot day | N | CHN | 26.45 | 29.13 | 31.82 | 34.51 | 37.19 | 39.88 | |
| E | CHE | 26.45 | 39.77 | 53.10 | 66.42 | 79.74 | 93.07 | ||
| S | CHS | 26.45 | 29.58 | 32.72 | 35.85 | 38.99 | 42.12 | ||
| W | CHW | 26.45 | 27.99 | 29.52 | 31.06 | 32.60 | 34.13 | ||
| Extremely hot day | N | CTN | 34.69 | 36.55 | 38.40 | 40.26 | 42.11 | 43.97 | |
| E | CTE | 34.69 | 39.57 | 44.45 | 49.33 | 54.21 | 59.09 | ||
| S | CTS | 34.69 | 38.37 | 42.05 | 42.05 | 49.41 | 53.09 | ||
| W | CTW | 34.69 | 37.16 | 39.62 | 42.08 | 44.54 | 47.00 | ||
| Residential | Summer day | N | RSN | 2.80 | 3.37 | 3.94 | 4.05 | 4.62 | 5.18 |
| E | RSE | 2.80 | 6.67 | 10.53 | 12.09 | 15.23 | 18.37 | ||
| S | RSS | 2.80 | 3.41 | 4.01 | 4.15 | 4.75 | 5.34 | ||
| W | RSW | 2.80 | 3.20 | 3.60 | 3.60 | 4.02 | 4.44 | ||
| Hot day | N | RHN | 4.29 | 4.40 | 4.51 | 4.62 | 4.73 | 4.83 | |
| E | RHE | 4.29 | 4.66 | 5.01 | 5.36 | 5.71 | 6.06 | ||
| S | RHS | 4.29 | 4.56 | 4.81 | 5.06 | 5.31 | 5.55 | ||
| W | RHW | 4.29 | 4.43 | 4.57 | 4.70 | 4.83 | 4.95 | ||
| Extremely hot day | N | RTN | 4.82 | 5.01 | 5.18 | 5.35 | 5.51 | 5.67 | |
| E | RTE | 4.82 | 5.27 | 5.72 | 6.17 | 6.61 | 7.05 | ||
| S | RTS | 4.82 | 5.24 | 5.66 | 6.07 | 6.49 | 6.90 | ||
| W | RTW | 4.82 | 5.10 | 5.38 | 5.66 | 5.93 | 6.20 | ||
| Sort Name | nmin | nmax | nopt | nopt/nmax | ηfc | ΔEC |
|---|---|---|---|---|---|---|
| h−1 | h−1 | h−1 | - | % | kWh | |
| OHS | 1.0324 | 17.91 | 5.79 | 0.3233 | 67.84 | 0.386 |
| CHS | 4.3017 | 20 | 7.76 | 0.3880 | 67.37 | 0.281 |
| CHW | 4.3017 | 20 | 7.76 | 0.3880 | 67.41 | 0.281 |
| OHW | 1.0324 | 14.71 | 5.79 | 0.3936 | 68.08 | 0.386 |
| OTS | 1.0324 | 20 | 10.18 | 0.5090 | 47.03 | 0.504 |
| OTW | 1.0324 | 17.69 | 10.18 | 0.5755 | 47.35 | 0.504 |
| OHN | 1.0324 | 17.02 | 10.17 | 0.5975 | 69.12 | 0.742 |
| CHN | 4.3017 | 20 | 12.14 | 0.6070 | 67.85 | 0.636 |
| CTS | 4.3017 | 20 | 13.08 | 0.6540 | 46.18 | 0.484 |
| CTW | 4.3017 | 20 | 13.08 | 0.6540 | 46.23 | 0.484 |
| OTN | 1.0324 | 16.76 | 11.02 | 0.6575 | 47.75 | 0.551 |
| CTN | 4.3017 | 20 | 13.92 | 0.6960 | 46.34 | 0.53 |
| OTE | 1.0324 | 20 | 14.22 | 0.7110 | 47.61 | 0.727 |
| CTE | 4.3017 | 20 | 17.12 | 0.8560 | 46.46 | 0.706 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Béni, E.; Józsa, S.; L. Szabó, G. Applying the Enhanced Free Cooling Concept: A Case Study on Reducing Mechanical Cooling Demand. Buildings 2025, 15, 3929. https://doi.org/10.3390/buildings15213929
Béni E, Józsa S, L. Szabó G. Applying the Enhanced Free Cooling Concept: A Case Study on Reducing Mechanical Cooling Demand. Buildings. 2025; 15(21):3929. https://doi.org/10.3390/buildings15213929
Chicago/Turabian StyleBéni, Emese, Szabolcs Józsa, and Gábor L. Szabó. 2025. "Applying the Enhanced Free Cooling Concept: A Case Study on Reducing Mechanical Cooling Demand" Buildings 15, no. 21: 3929. https://doi.org/10.3390/buildings15213929
APA StyleBéni, E., Józsa, S., & L. Szabó, G. (2025). Applying the Enhanced Free Cooling Concept: A Case Study on Reducing Mechanical Cooling Demand. Buildings, 15(21), 3929. https://doi.org/10.3390/buildings15213929





