Effects of Near-Fault Pulse-like Ground Motions upon Seismic Performance of Large-Span Concrete-Filled Steel Tubular Arch Bridges
Abstract
1. Introduction
2. Analytical Model and Selection of Ground Motions
2.1. Modeling of Case Bridge
2.2. Selection of Near-Fault Ground Motions
3. Near-Fault Dynamic Response of the Case Bridge
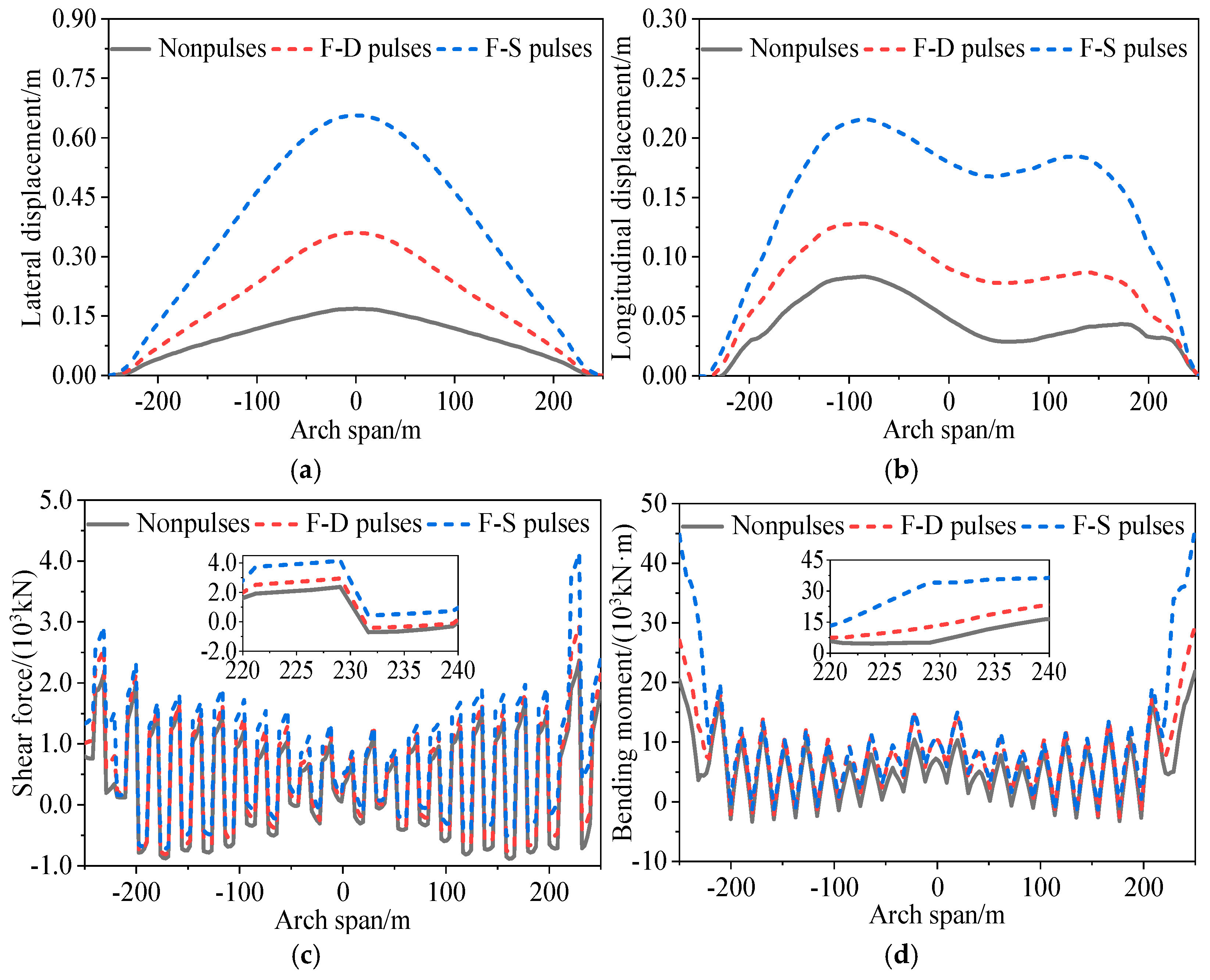
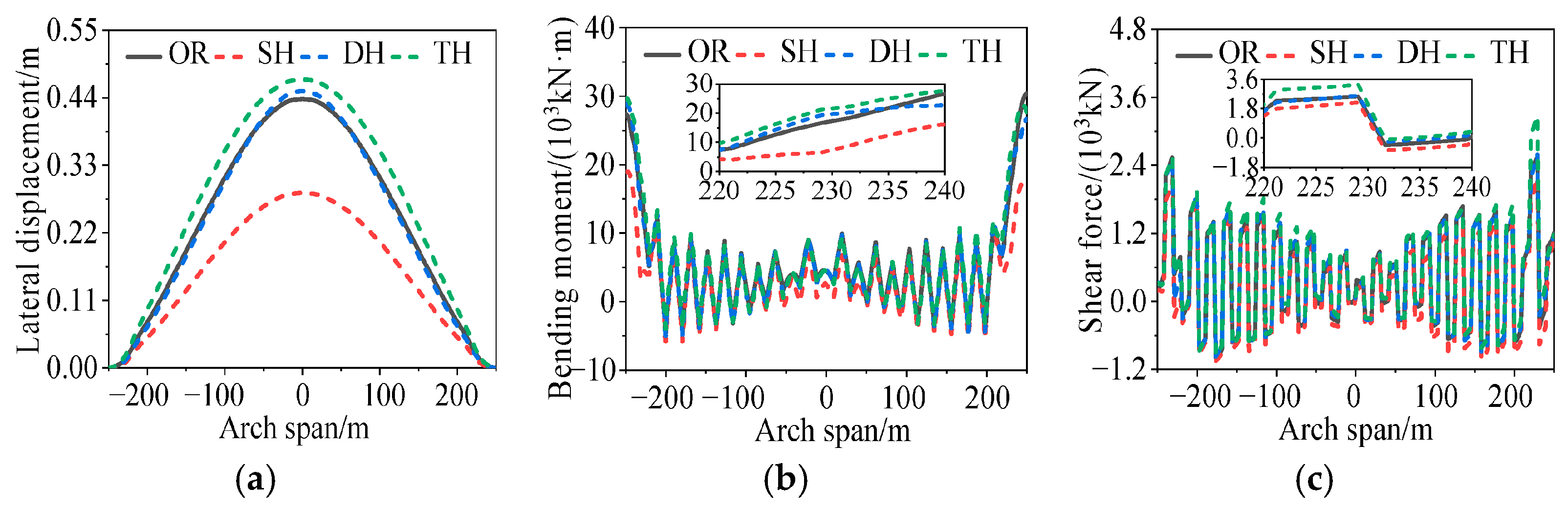
3.1. Dynamic Responses of Arch Rib
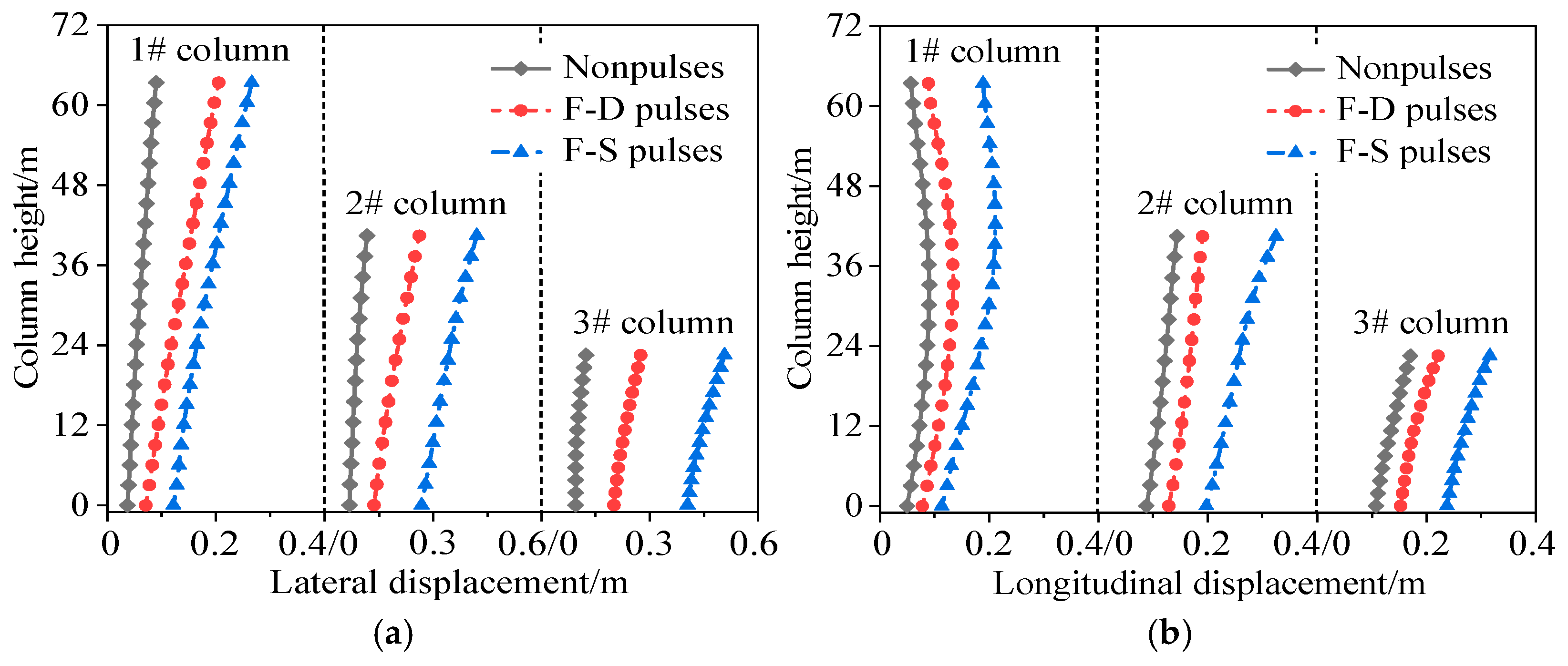
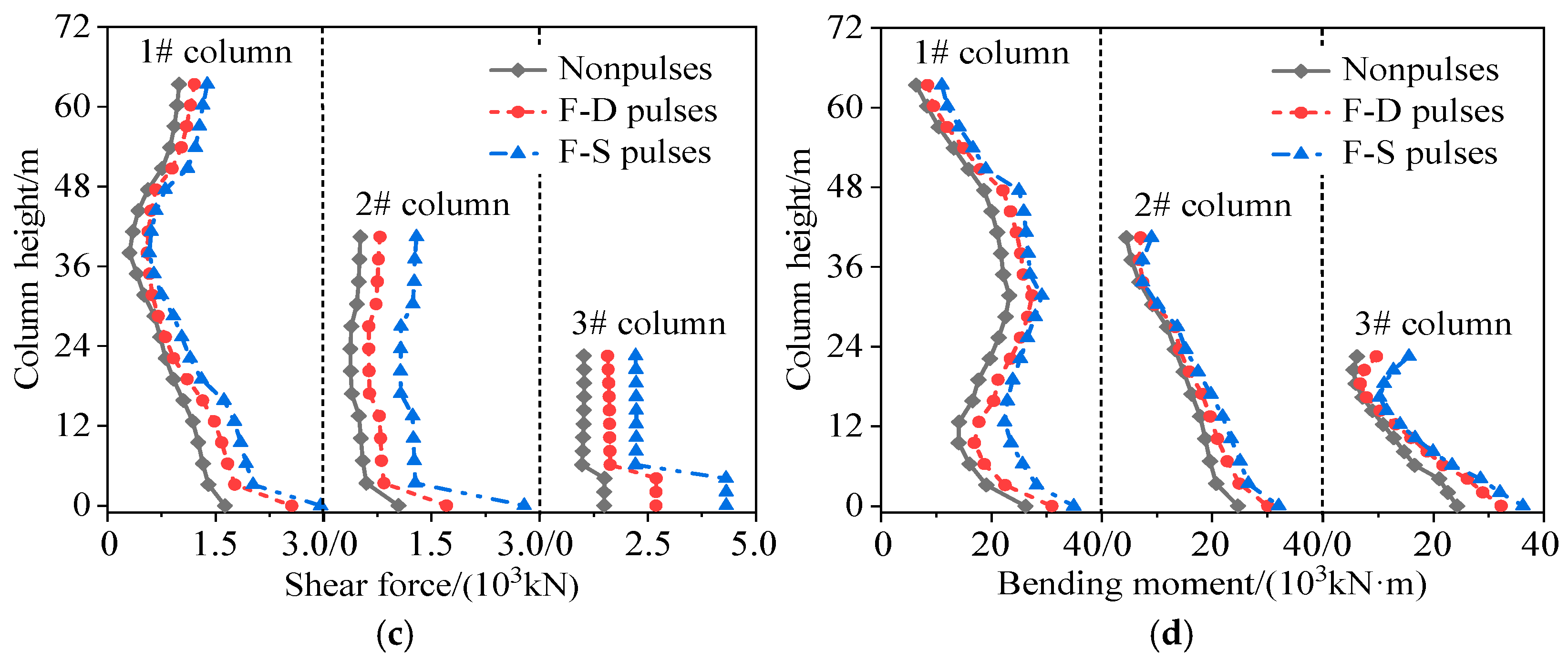
3.2. Dynamic Responses of Arch Columns
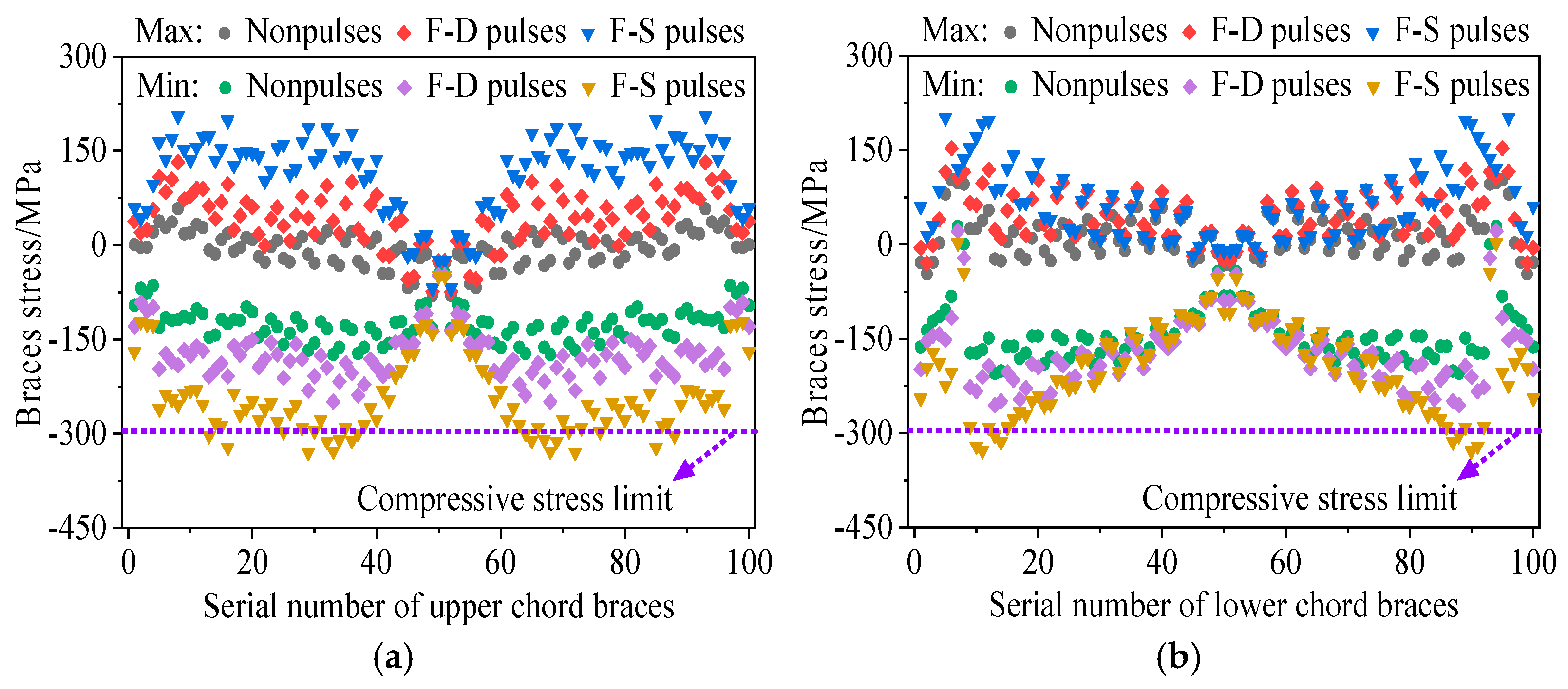
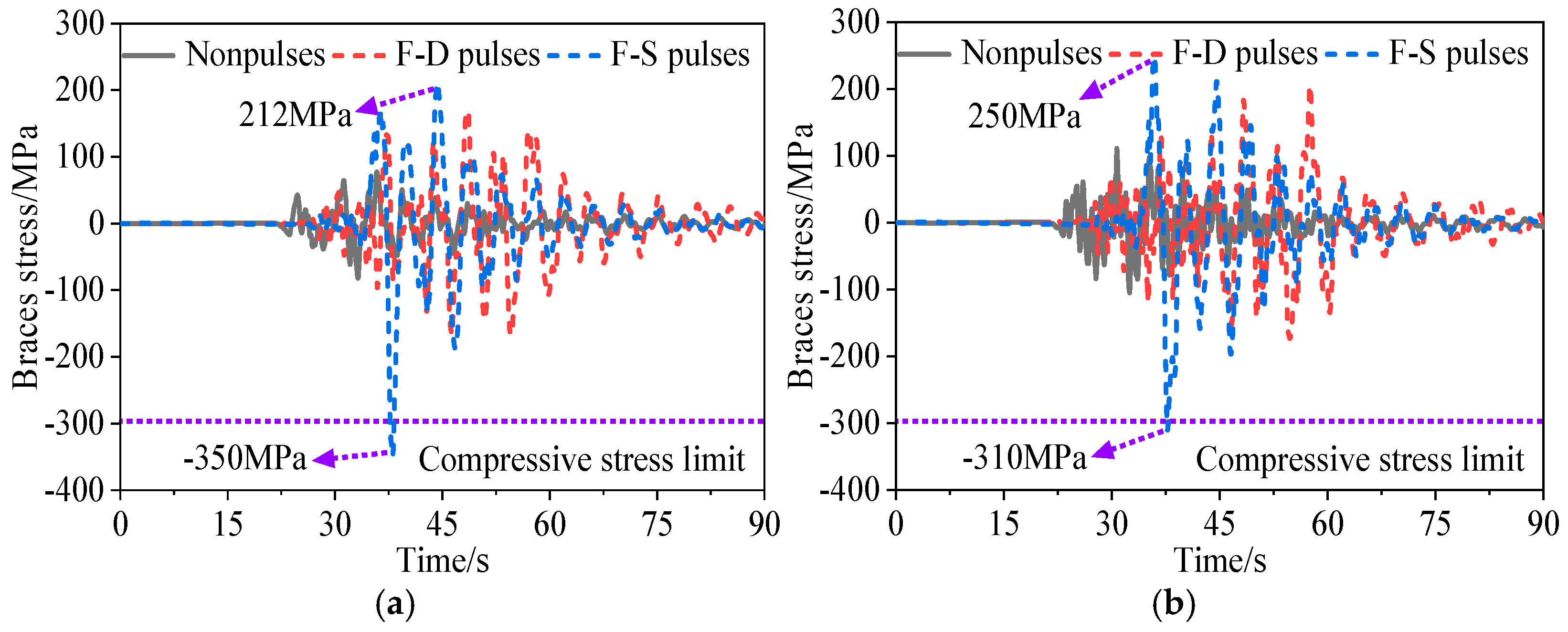
3.3. Dynamic Responses of Arch Rib Braces
4. Simulation of Near-Fault Pulse-like Ground Motions
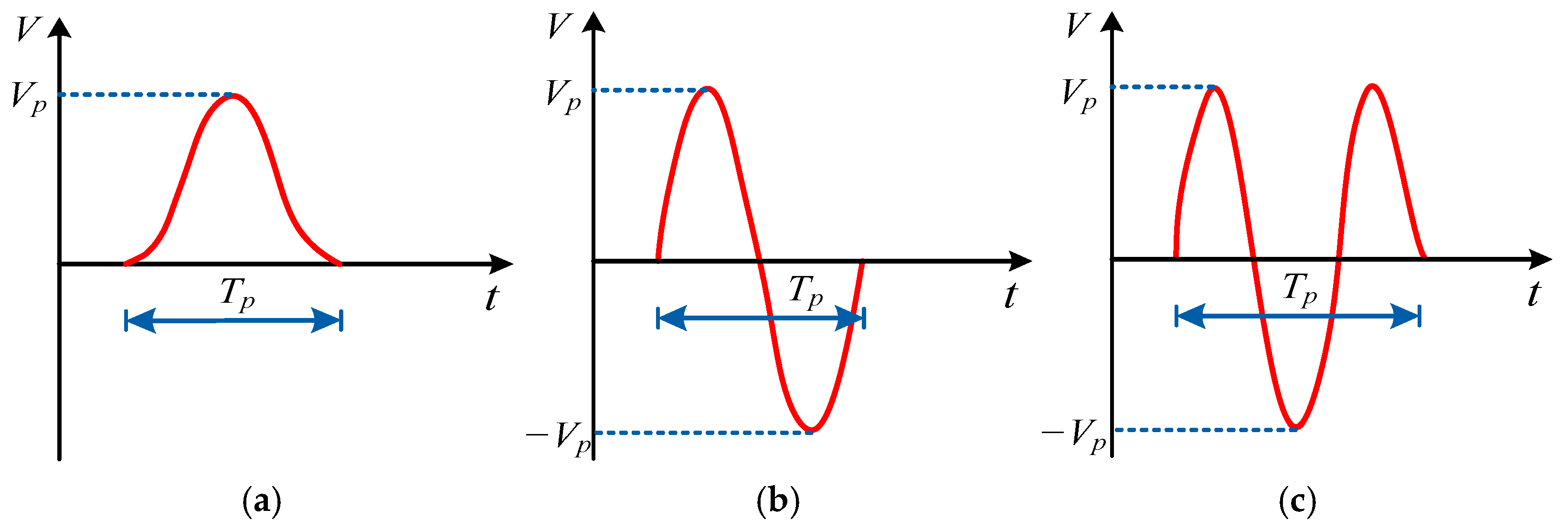
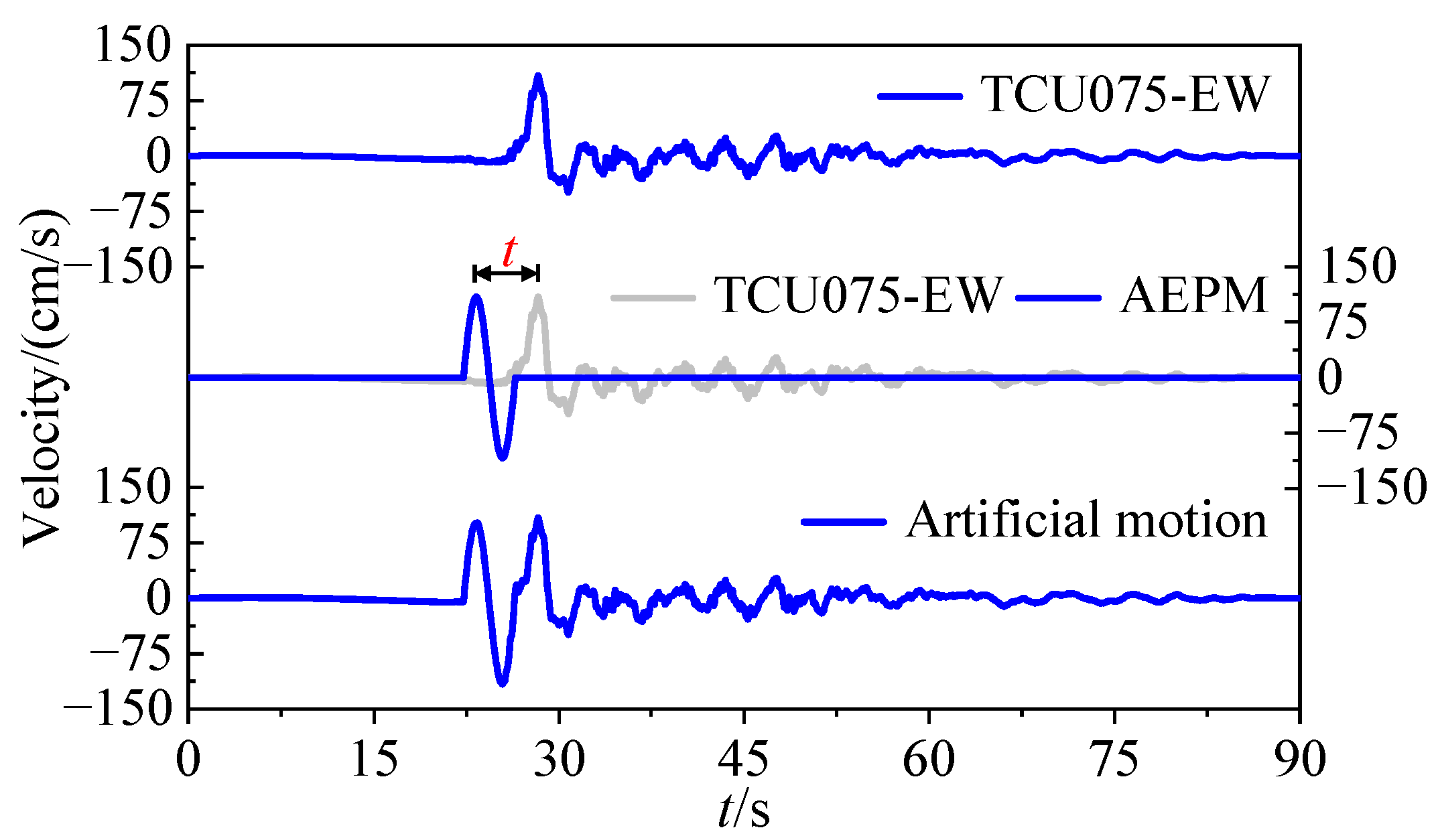
4.1. Record-Decomposition Incorporation Method
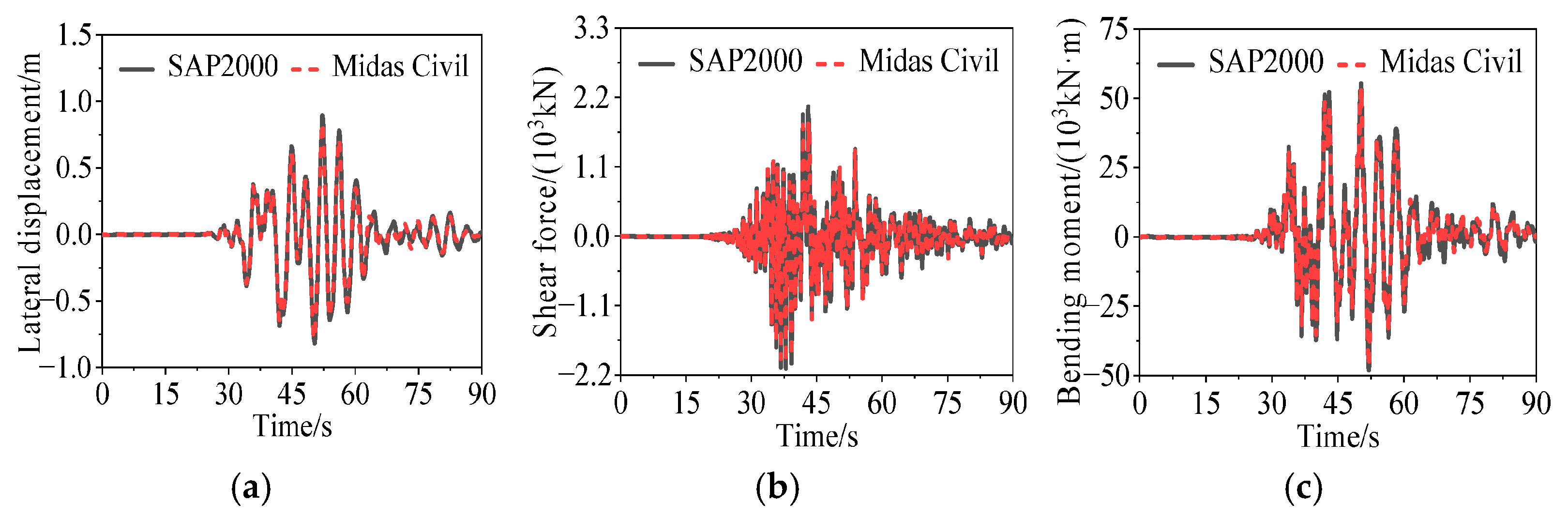
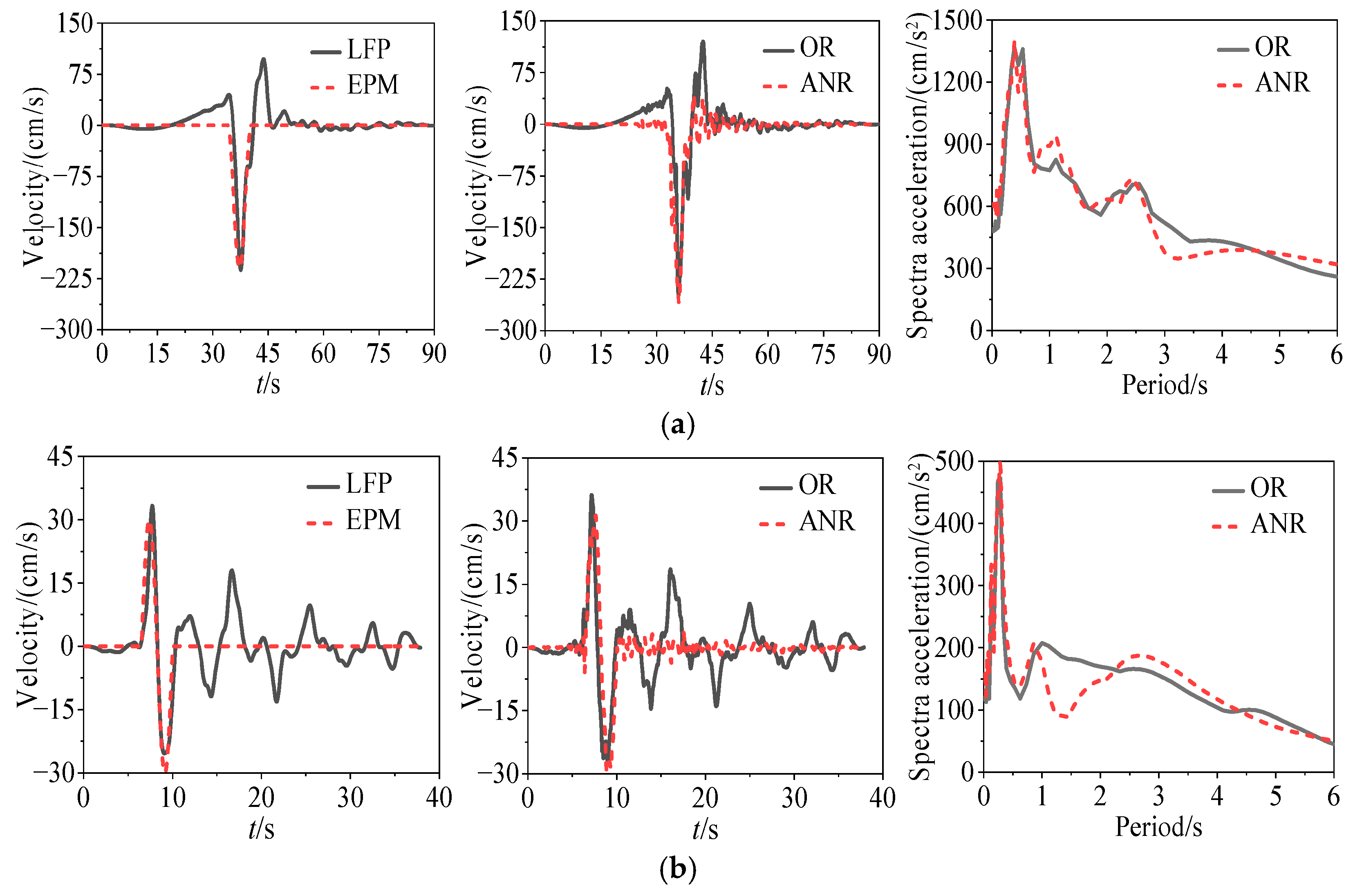
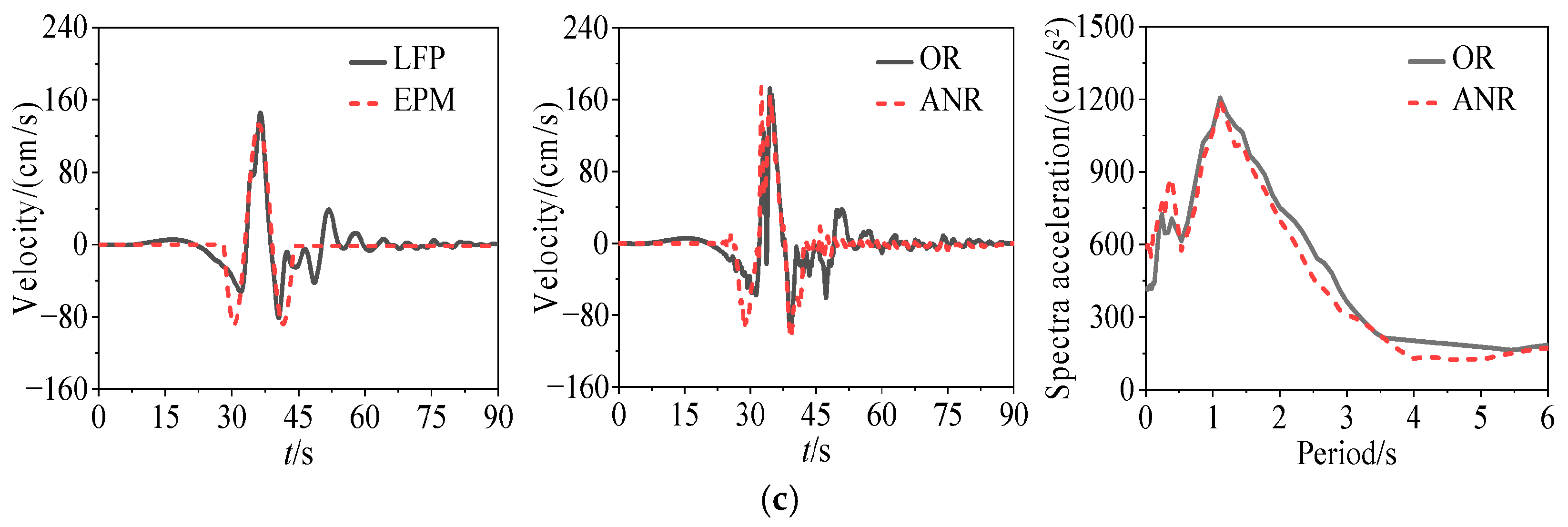
4.2. Synthesis Examples and Verification
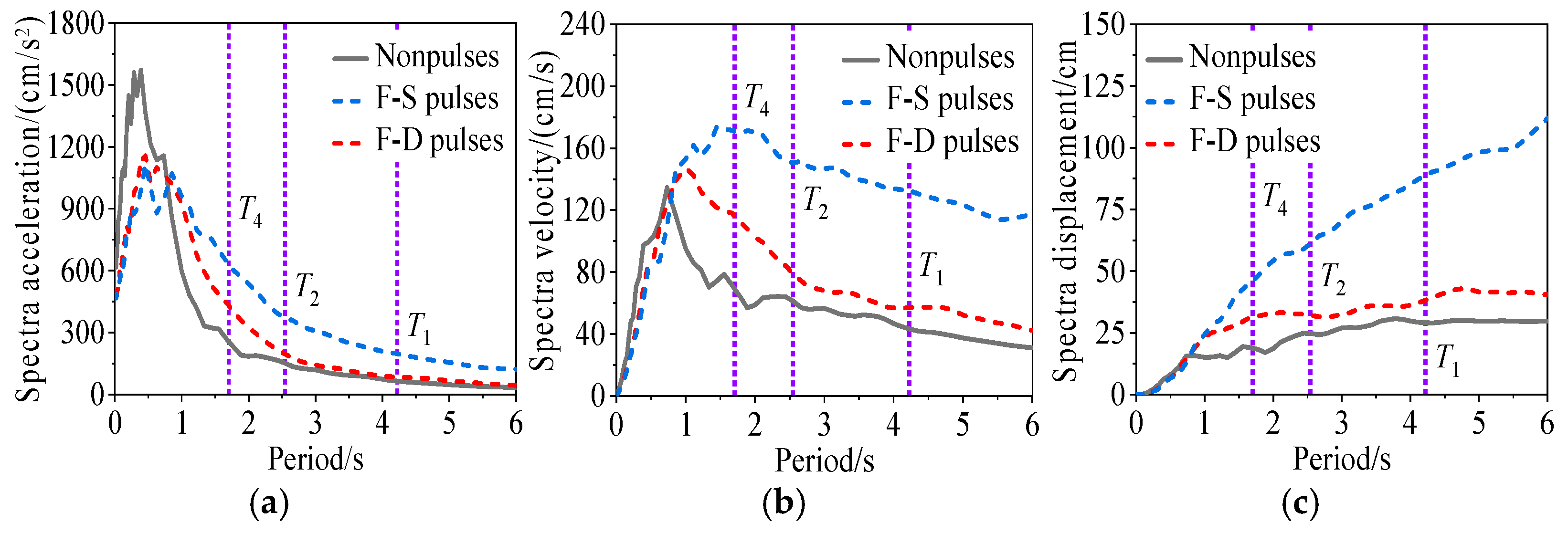
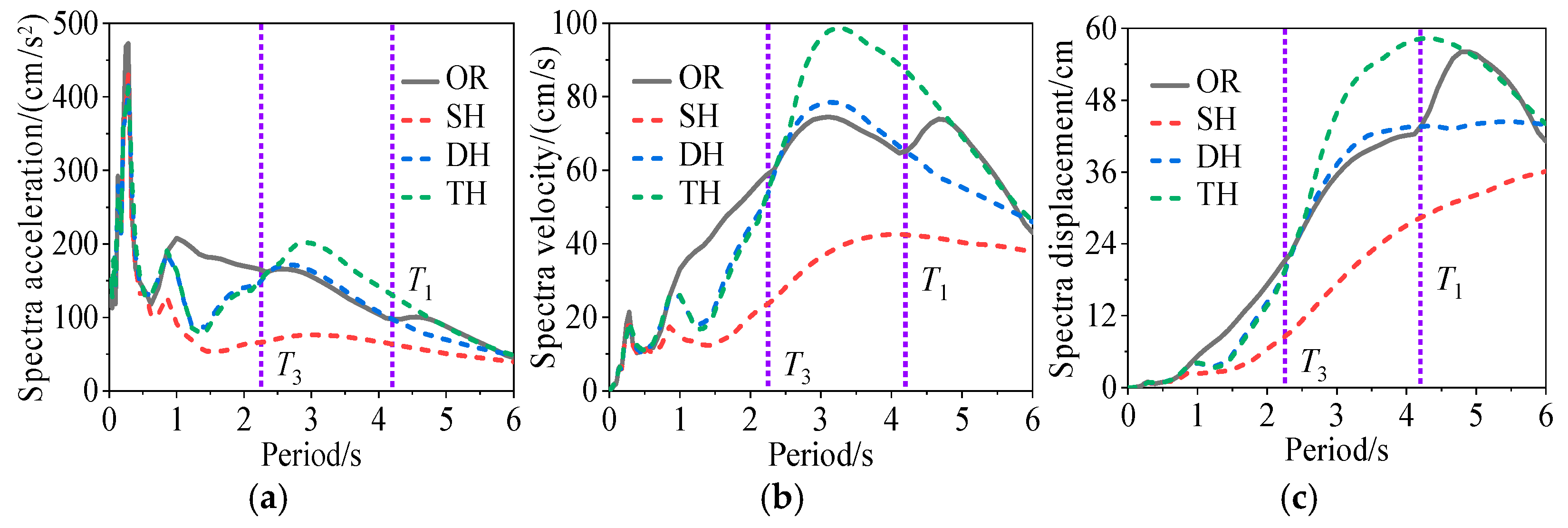
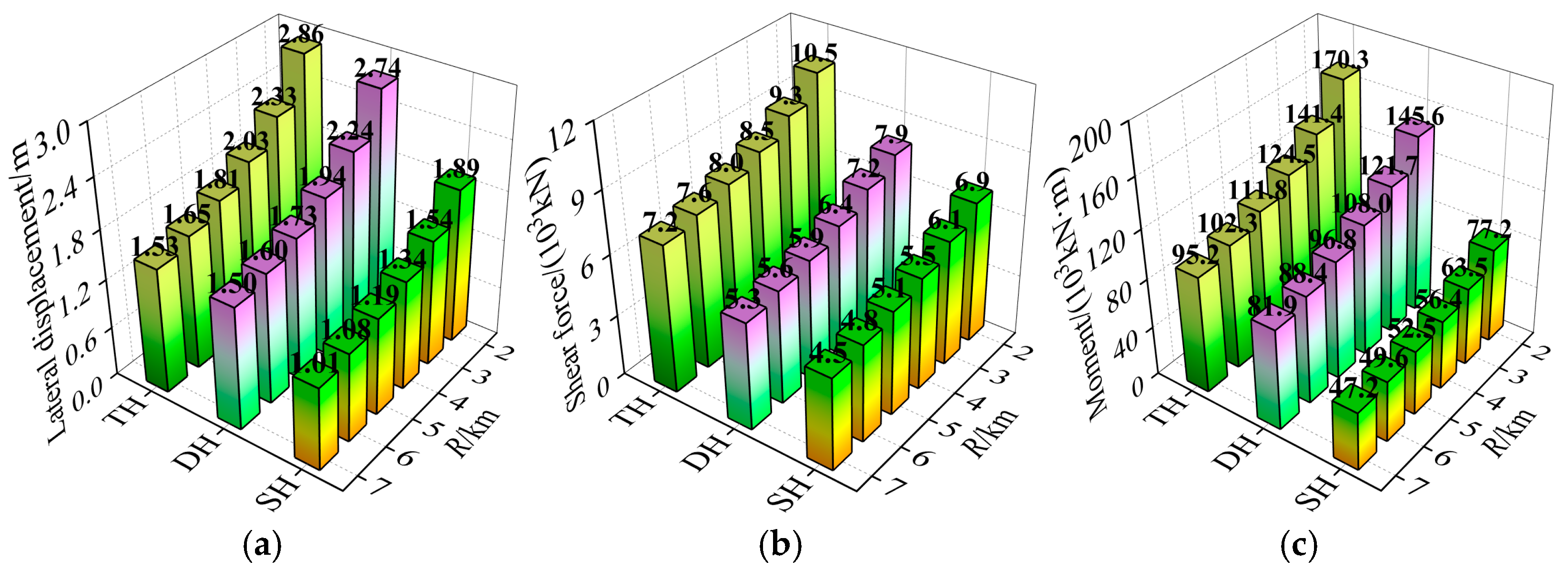
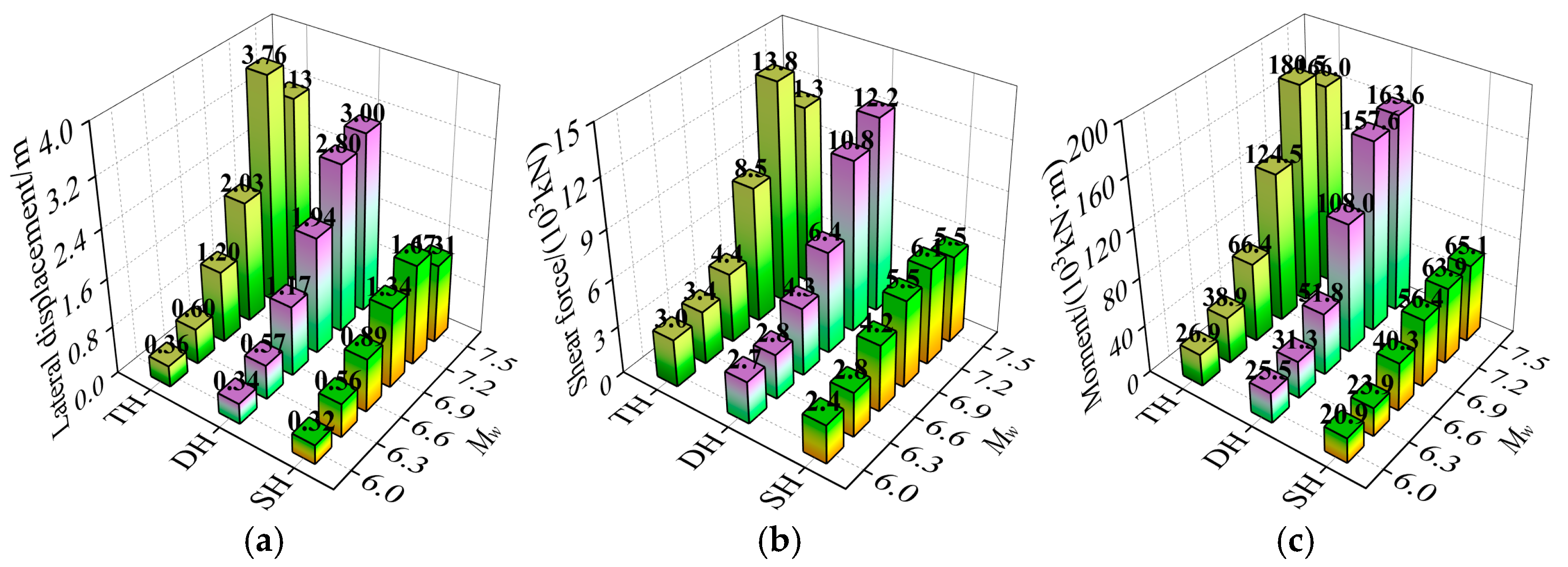
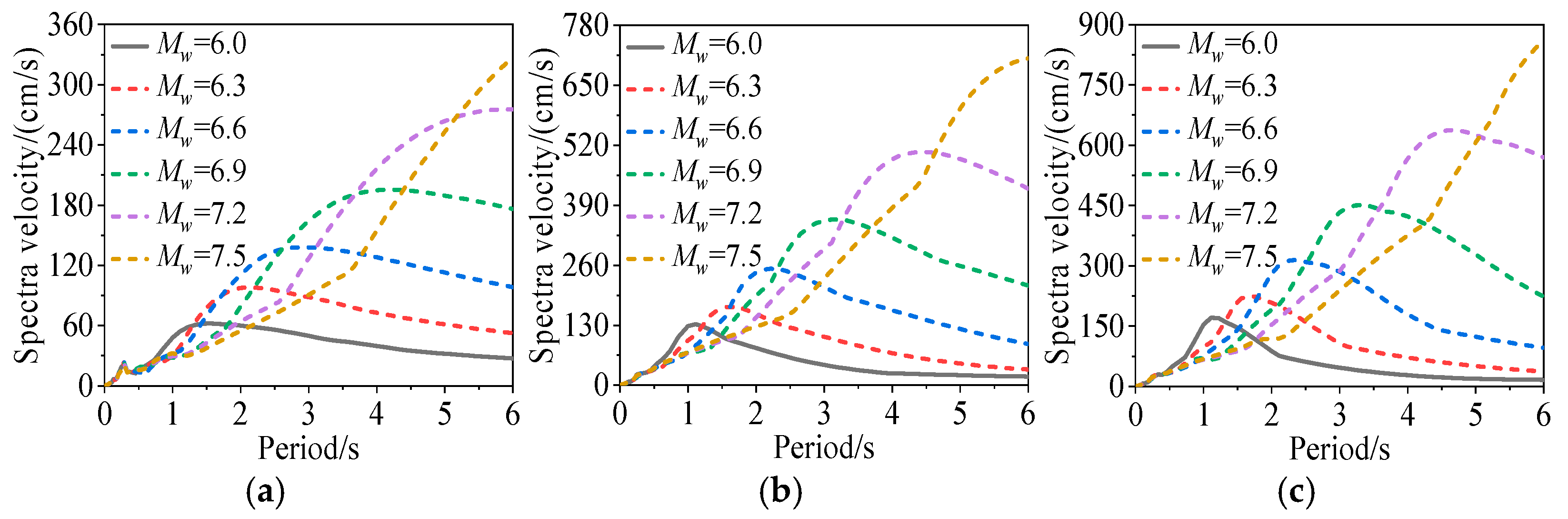
5. Analysis of Near-Fault Characteristic Parameters
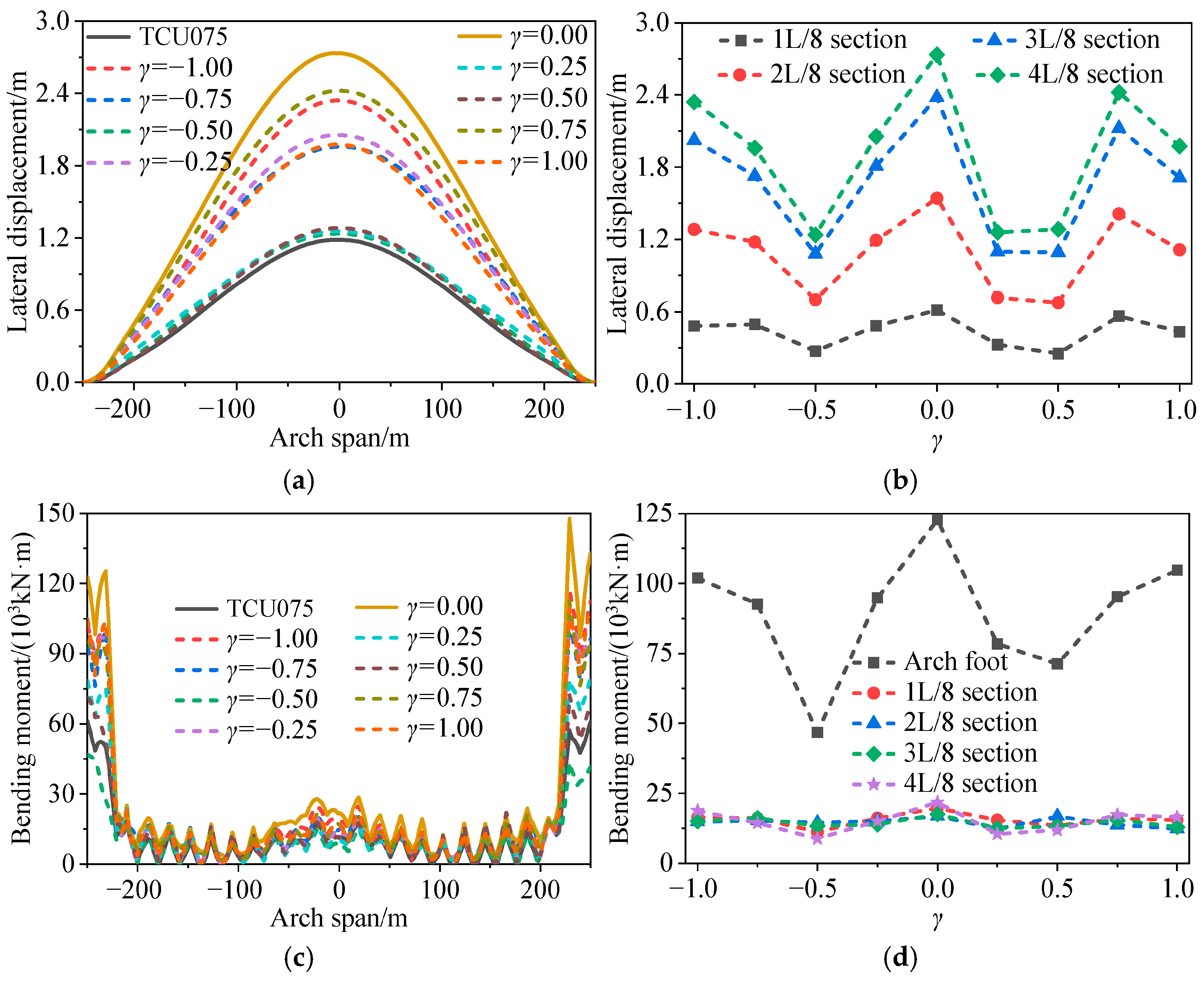
5.1. Effects of Pulse Types
5.2. Effects of Seismic Source Characteristics
5.3. Effects of Pulse Superposition Effect
6. Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, J. Recent construction technology innovations and practices for large-span arch bridges in China. Engineering 2024, 41, 110–129. [Google Scholar] [CrossRef]
- Han, X.; Han, B.; Xie, H.; Yan, W.; Yu, J.; He, Y.; Yan, L. Seismic stability analysis of the large-span concrete-filled steel tube arch bridge considering the long-term effects. Eng. Struct. 2022, 268, 114744. [Google Scholar] [CrossRef]
- Xu, L.; Xu, L.; Zhou, J.; Yuan, M.; Pan, R. Seismic analysis of large-span CFST arch bridge considering the stress accumulation effect. J. Constr. Steel. Res. 2025, 228, 109432. [Google Scholar] [CrossRef]
- Liang, X.; Xing, Y. Shaking table test on the seismic behavior of a long-span RC deck-type arch bridge under tri-directional ground motions. J. Bridge Eng. 2025, 30, 04025053. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, J.; Xu, L.; He, H.; Jin, S.; Xu, L. Seismic optimization design method of long-span concrete-filled steel tubular arch bridge based on energy-dissipation brace under near-fault ground motions. Int. J. Struct. Stab. Dyn. 2025, 2650243. [Google Scholar] [CrossRef]
- Chen, L.; Zhuang, W.; Zhao, H. Report on Highways’ Damage in the Wenchuan Earthquake: Bridge; China Communications Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Kawashima, K.; Buckle, I. Structural performance of bridges in the Tohoku-Oki earthquake. Earthq. Spectra 2013, 29, 315–338. [Google Scholar] [CrossRef]
- Kenji, K.; Hendra, S.; Masakatsu, M.; Yusuke, O.; Masaho, Y. Damage to Teluk Palu Bridge in the 2018 Sulawesi earthquake, Indonesia. MATEC Web Conf. 2020, 331, 02003. [Google Scholar] [CrossRef]
- Xin, J.; Tang, Q.; Zhou, J.; Zhou, Y.; Luo, C.; Jiang, Y. A novel method for calculating the ultimate bearing capacity of in-service RC arch bridges using sectional constitutive relation. Appl. Math. Model. 2025, 138, 115829. [Google Scholar] [CrossRef]
- Jin, S.; Ai, P.; Zhou, J.; Bai, J. Seismic performance of an assembled self-centering buckling-restrained brace and its application in arch bridge structures. J. Constr. Steel Res. 2022, 199, 107600. [Google Scholar] [CrossRef]
- Xin, J.; Tao, G.; Tang, Q.; Zou, F.; Xiang, C. Structural damage identification method based on Swin Transformer and continuous wavelet transform. Intell. Robot. 2024, 4, 200–215. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, D.; Li, X.; Tong, L.; Hui, Y.; Ge, X. Seismic performance assessment and retrofitted by buckling-restrained braces for half-through concrete-filled steel tubular arch bridge with the vertical suspended deck system. Adv. Struct. Eng. 2025, 28, 642–657. [Google Scholar] [CrossRef]
- Xin, L.; Li, X.; Zhang, Z.; Zhao, L. Seismic behavior of long-span concrete-filled steel tubular arch bridge subjected to near-fault fling-step motions. Eng. Struct. 2019, 180, 148–159. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, S. Influence of strong spatially varying near fault ground motion on steel box arch bridge. Bull. Earthq. Eng. 2021, 19, 224–255. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, L. Damage pattern analysis of large-span CFST arch bridge under near-fault earthquakes. Earthq. Eng. Eng. Dyn. 2020, 40, 204–215. Available online: https://dzgc.paperonce.org/#/digest?ArticleID=2705 (accessed on 12 September 2025).
- Zhou, T.; Jiang, L.; Xiang, P.; Lai, Z.; Zhang, Y.; Liu, X. Effects of near-fault pulse-type ground motions on high-speed railway simply supported bridge and pulse parameter analysis. Bull. Earthq. Eng. 2022, 20, 6167–6192. [Google Scholar] [CrossRef]
- Lei, H.; Feng, H.; Liu, W. Study on train safety control of high-speed railway bridge under the action of near-fault earthquake. Adv. Bridge Eng. 2024, 5, 20–47. [Google Scholar] [CrossRef]
- Makris, N.; Chang, S. Effect of viscous, viscoplastic and friction damping on the response of seismic isolated structures. Earthq. Eng. Struct. Dyn. 2000, 29, 85–107. [Google Scholar] [CrossRef]
- Menun, C.; Fu, Q. An analytical model for near-fault ground motions and the response of SDOF systems. In Proceedings of the Seventh U.S. National Conference on Earthquake Engineering: Urban Earthquake Risk, Boston, MA, USA, 21–25 July 2002. [Google Scholar]
- Hoseini, V.; Sharbatdar, M.; Ghodrati, A.; Naderpour, H.; Kheyroddin, A. Dominant pulse simulation of near fault ground motions. Earthq. Eng. Eng. Vib. 2013, 12, 267–278. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, Q.; Lu, M. Simulation method of near-fault pulse-type ground motion. Acta Seismol. Sin. 2007, 29, 77–84. [Google Scholar] [CrossRef]
- Dabaghi, M.; Kiureghian, A. Stochastic model for simulation of near-fault ground motions. Earthq. Eng. Struct. Dyn. 2017, 46, 963–984. [Google Scholar] [CrossRef]
- Panchal, V.; Jangid, R. Variable friction pendulum system for near-fault ground motions. Struct. Control Health Monit. 2008, 15, 568–584. [Google Scholar] [CrossRef]
- Zahra, M.; Seyed, R.; Ehsan, D. An approach for estimating the response of steel moment resisting frames to pulse-like ground motions. Soil Dyn. Earthq. Eng. 2021, 151, 106991. [Google Scholar] [CrossRef]
- Li, S.; Zhang, F.; Wang, J.; Alam, M.; Zhang, J. Effects of near-fault motions and artificial pulse-type ground motions on super-span cable-stayed bridge systems. J. Bridge Eng. 2017, 22, 4016128. [Google Scholar] [CrossRef]
- Xu, L.; Xu, L.; Xie, D.; Zhou, J. Seismic risk assessment methodology for large-span CFST arch bridges in near-fault areas based on fragility analysis. Struct. Saf. 2025, 118, 102656. [Google Scholar] [CrossRef]
- Han, L. Concrete Filled Steel Tubular Structures: Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Yu, J.; Zhou, W.; Jiang, L.; Yan, W.; Luo, Q.; Liang, F.; Liu, X. Amplitude response spectrum of seismic-induced track irregularity considering damping ratio. Eng. Struct. 2023, 293, 116702. [Google Scholar] [CrossRef]
- JTG/T 2231-01-2020; Specifications for Seismic Design of Highway Bridges. China Communications Press: Beijing, China, 2020. (In Chinese)
- Yazdani, M.; Jahangir, V.; Marefat, M. Seismic performance assessment of plain concrete arch bridges under near-field earthquakes using incremental dynamic analysis. Eng. Fail. Anal. 2019, 106, 104170. [Google Scholar] [CrossRef]
- Ye, D.; Zhou, J.; Zhang, R.; Xu, L.; Jin, S. Stayed buckle cable recycling for seismic upgrading of super-long-span concrete filled steel tube arch bridges. KSCE J. Civ. Eng. 2024, 28, 777–786. [Google Scholar] [CrossRef]
- Baker, W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- TB 10091-2017; Code for Design on Steel Structure of Railway Bridge. China Railway Press: Beijing, China, 2017. (In Chinese)
- Ghahari, F.; Jahankhah, H.; Ghannad, M. Study on elastic response of structures to near-fault ground motions through record decomposition. Soil Dyn. Earthq. Eng. 2010, 30, 536–546. [Google Scholar] [CrossRef]
- Zeng, C.; Jiang, H.; Song, G.; Li, C.; Zhao, X.; Ren, Y.; Xue, Z. Quantitative classification of velocity pulse-like ground motions based on an adaptive response spectrum-based decomposition method. Soil Dyn. Earthq. Eng. 2024, 177, 108419. [Google Scholar] [CrossRef]
- Somerville, P. Development of an improved representation of near fault ground motions. In Seminar on Utilization of Strong-Motion Data; SUSMD: Oakland, CA, USA, 1998. [Google Scholar]
- Mavroeidis, G. A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Xin, J.; Mo, X.; Jiang, Y.; Tang, Q.; Zhang, H.; Zhou, J. Recovery method of continuous missing data in the bridge monitoring system using SVMD-Assisted TCN-MHA-BiGRU. Struct. Control Health Monit. 2025, 2025, 8833186. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Gao, Y.; Yang, S.; Liao, Y.; Luo, B. Shaking table test of arch bridge inverted siphon considering different pulse parameters of near-fault ground motions. Eng. Struct. 2025, 327, 119619. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Bagheri, M.; Malidarreh, N.; Ghaseminejad, V.; Asgari, A. Seismic resilience assessment of RC superstructures on long-short combined piled raft foundations: 3D SSI modeling with pounding effects. Structures 2025, 81, 110176. [Google Scholar] [CrossRef]
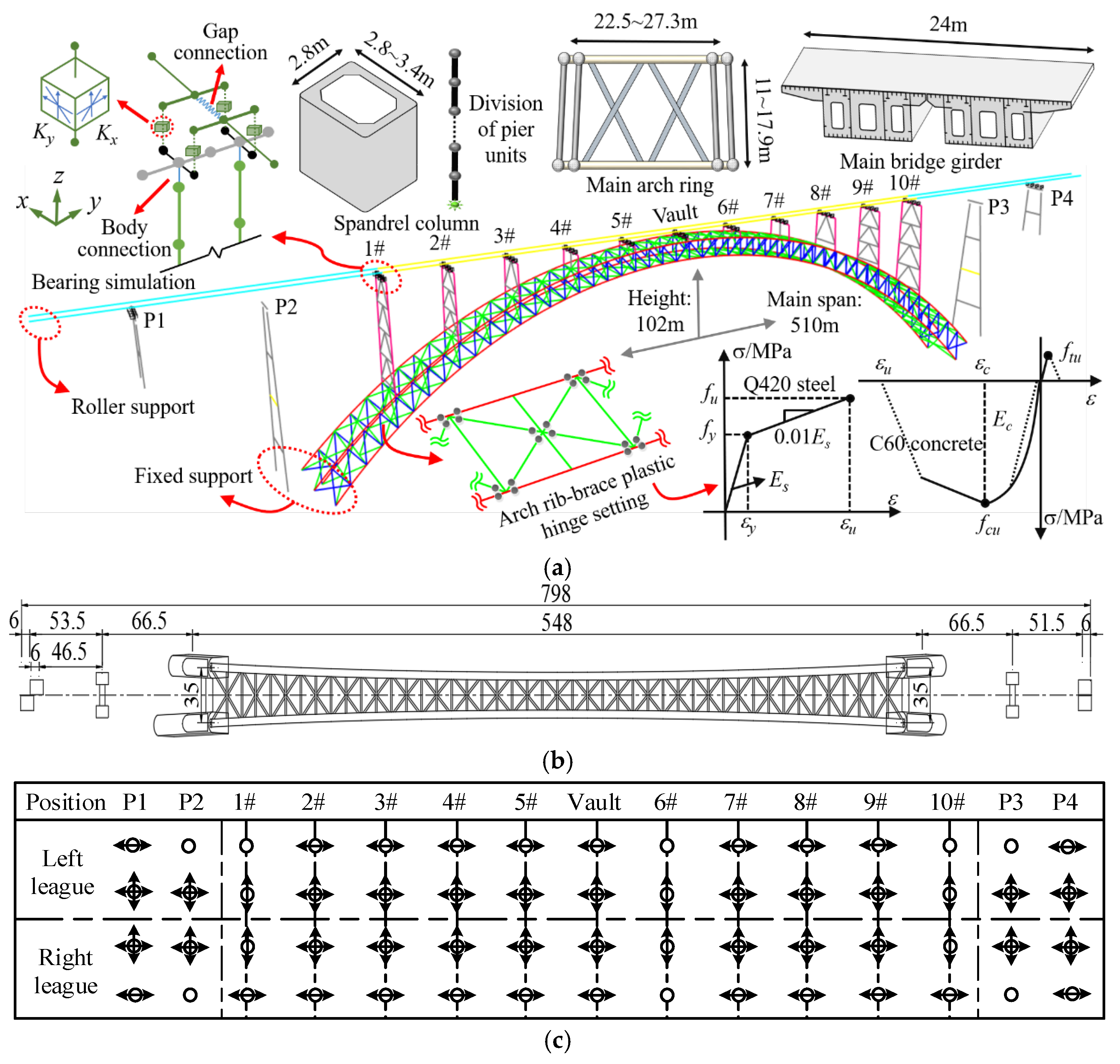


| Mode | Period/s | Effective Mass Ratio | Modal Characteristics | ||
|---|---|---|---|---|---|
| Longitudinal | Transverse | Vertical | |||
| 1 | 4.201 | 0.0% | 32.7% | 0.0% | First symmetric transverse vibration |
| 2 | 2.579 | 31.2% | 0.0% | 0.0% | First antisymmetric longitudinal vibration |
| 3 | 2.248 | 0.0% | 0.0% | 0.0% | First antisymmetric transverse vibration |
| 4 | 1.737 | 0.0% | 0.0% | 16.8% | First symmetric vertical vibration |
| 5 | 1.639 | 0.0% | 18.8% | 0.0% | Second symmetric transverse vibration |
| 6 | 1.269 | 0.3% | 0.0% | 0.0% | Second antisymmetric transverse vibration |
| 7 | 1.267 | 36.6% | 0.0% | 0.0% | Second antisymmetric longitudinal vibration |
| 8 | 1.139 | 0.0% | 6.2% | 0.0% | First symmetric transverse torsion |
| 9 | 1.074 | 0.0% | 0.0% | 1.6% | Second symmetric longitudinal vibration |
| 10 | 1.030 | 0.0% | 0.0% | 28.8% | Third symmetric vertical vibration |
| Pulse Types | Earthquake | Station | Mw | R/km | Vs30/m/s | PGA/g |
|---|---|---|---|---|---|---|
| Nonpulses | Imperial Valley | Calexico-225 | 6.53 | 10.45 | 231.23 | 0.28 |
| Northridge | KAT-90 | 6.69 | 13.42 | 557.42 | 0.8 | |
| Northridge | PKC-360 | 6.69 | 7.26 | 508.08 | 0.43 | |
| Northridge | SPV-360 | 6.69 | 8.44 | 380.06 | 0.93 | |
| Northridge | TAR-360 | 6.69 | 15.60 | 257.21 | 1.78 | |
| Chi-Chi | TCU071-EW | 7.62 | 5.80 | 624.85 | 0.65 | |
| Chi-Chi | TCU072-EW | 7.62 | 7.08 | 468.14 | 0.48 | |
| F-S pulses | Kocaeli | Yarimca YPT | 7.51 | 4.83 | 297.00 | 0.32 |
| Chi-Chi | TCU052-NS | 7.62 | 0.66 | 579.10 | 0.45 | |
| Chi-Chi | TCU068-EW | 7.62 | 0.32 | 487.34 | 0.51 | |
| Chi-Chi | TCU074-EW | 7.62 | 13.46 | 549.43 | 0.6 | |
| Chi-Chi | TCU075-EW | 7.62 | 0.89 | 573.02 | 0.33 | |
| Chi-Chi | TCU084-NS | 7.62 | 11.48 | 665.20 | 1.01 | |
| Chi-Chi | TCU087-NS | 7.62 | 6.98 | 538.69 | 0.12 | |
| F-D pulses | Cape Mendocino | Petrolia-90 | 7.01 | 8.18 | 422.17 | 0.66 |
| Imperial Valley | Brawley Airport | 6.53 | 10.42 | 208.71 | 0.16 | |
| Loma Prieta | Lexington dam | 6.93 | 5.02 | 1070.34 | 0.44 | |
| Northridge | Rinaldi | 6.69 | 6.50 | 282.25 | 0.87 | |
| Kobe | KJMA | 6.90 | 0.96 | 312.00 | 0.83 | |
| Chi-Chi | TCU051-EW | 7.62 | 7.64 | 350.06 | 0.24 | |
| Chi-Chi | TCU054-EW | 7.62 | 5.28 | 460.69 | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhang, K.; Shi, H.; Ye, D.; He, H.; Yuan, M. Effects of Near-Fault Pulse-like Ground Motions upon Seismic Performance of Large-Span Concrete-Filled Steel Tubular Arch Bridges. Buildings 2025, 15, 3923. https://doi.org/10.3390/buildings15213923
Shi J, Zhang K, Shi H, Ye D, He H, Yuan M. Effects of Near-Fault Pulse-like Ground Motions upon Seismic Performance of Large-Span Concrete-Filled Steel Tubular Arch Bridges. Buildings. 2025; 15(21):3923. https://doi.org/10.3390/buildings15213923
Chicago/Turabian StyleShi, Jun, Kai Zhang, Haoqi Shi, Dan Ye, Hongtao He, and Maojun Yuan. 2025. "Effects of Near-Fault Pulse-like Ground Motions upon Seismic Performance of Large-Span Concrete-Filled Steel Tubular Arch Bridges" Buildings 15, no. 21: 3923. https://doi.org/10.3390/buildings15213923
APA StyleShi, J., Zhang, K., Shi, H., Ye, D., He, H., & Yuan, M. (2025). Effects of Near-Fault Pulse-like Ground Motions upon Seismic Performance of Large-Span Concrete-Filled Steel Tubular Arch Bridges. Buildings, 15(21), 3923. https://doi.org/10.3390/buildings15213923





