Crack Propagation Analysis of Steels with Initial Defects by New Peridynamics
Abstract
1. Introduction
2. PD and PD-COD Theory
2.1. PD Theory
2.1.1. Ordinary State-Based PD
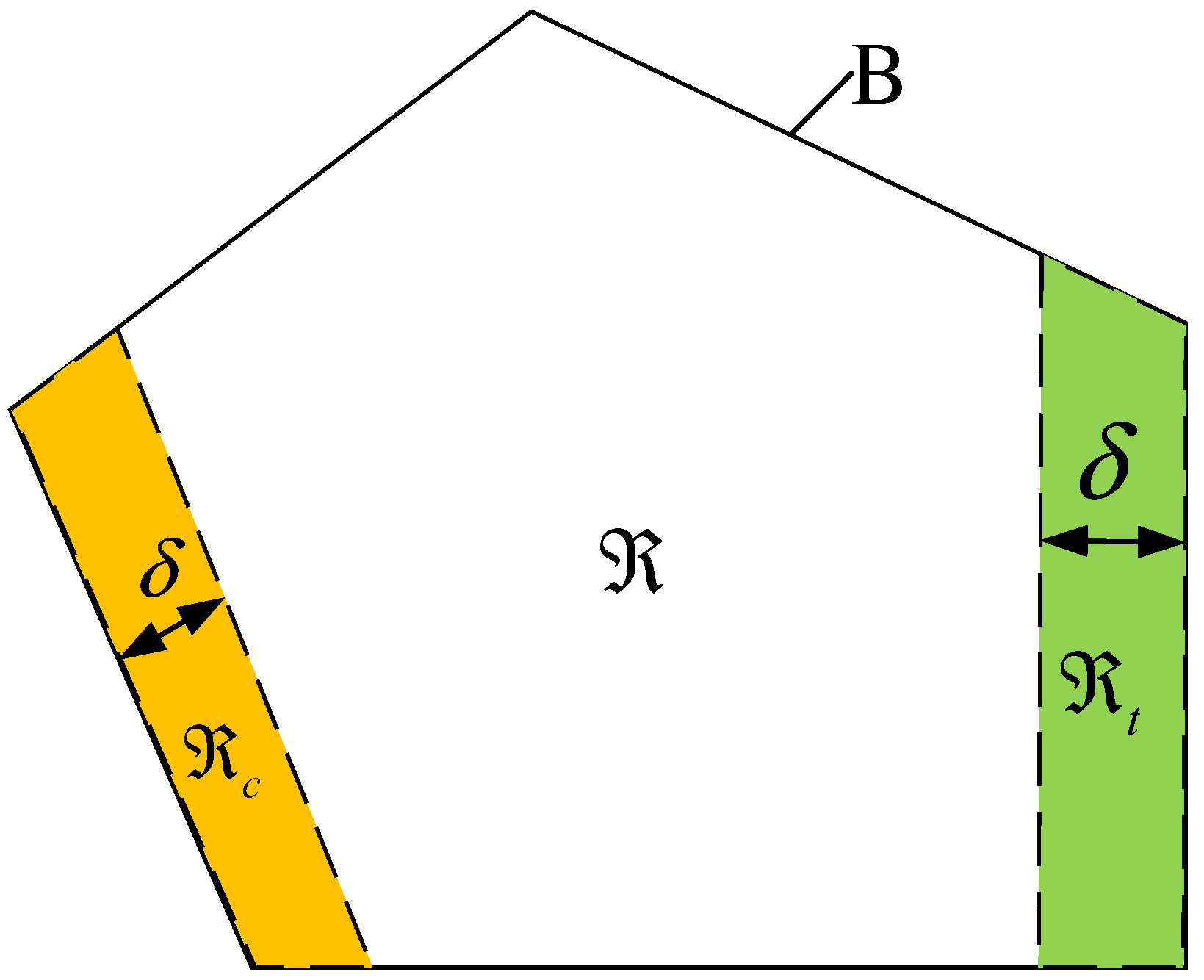
2.1.2. Boundary Conditions
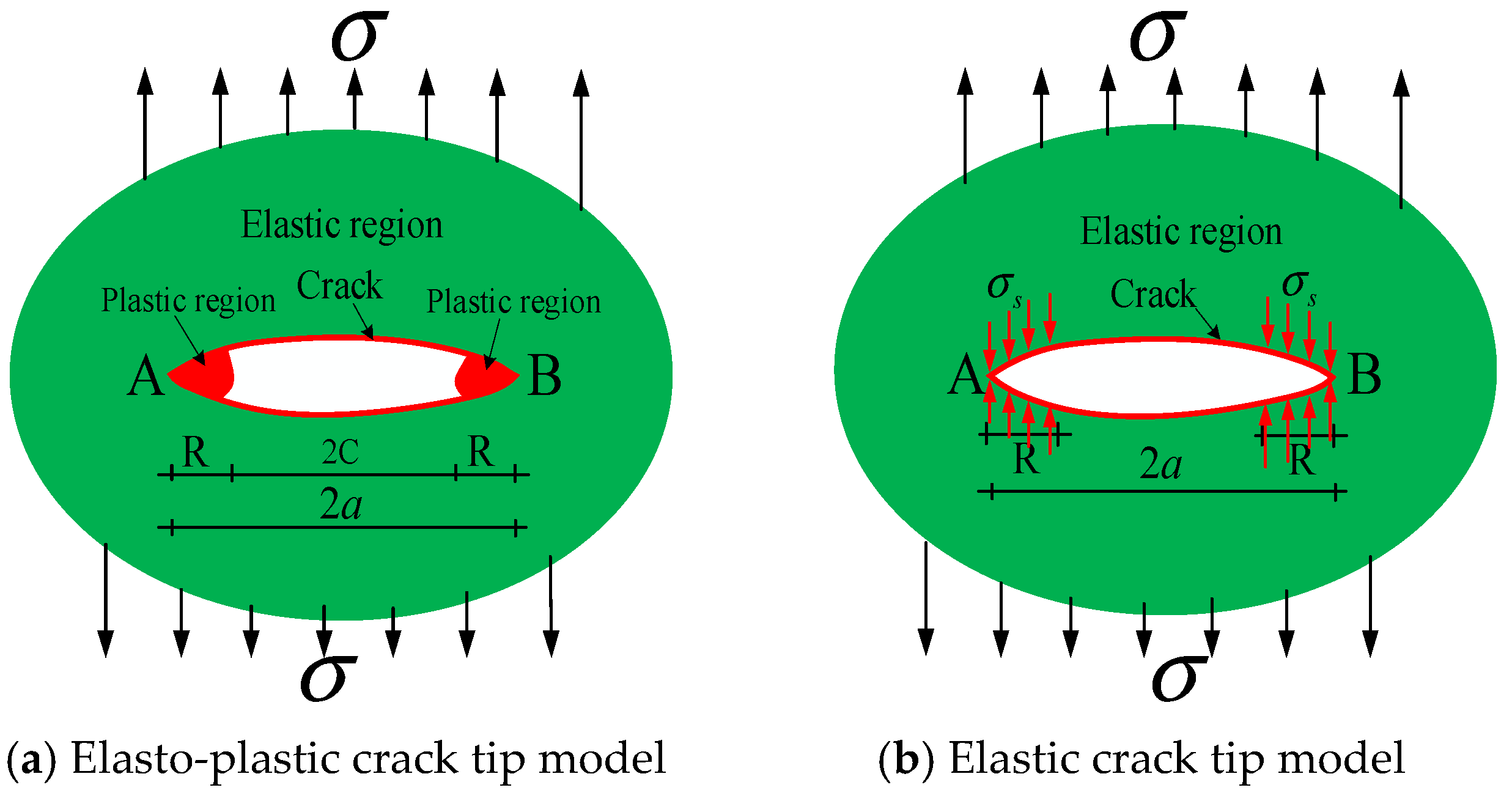
2.2. PD-COD Theory
2.3. Model Transformation
3. Crack Propagation of Steel Structure Members
3.1. Test
3.2. PD Theoretical Simulation Analysis
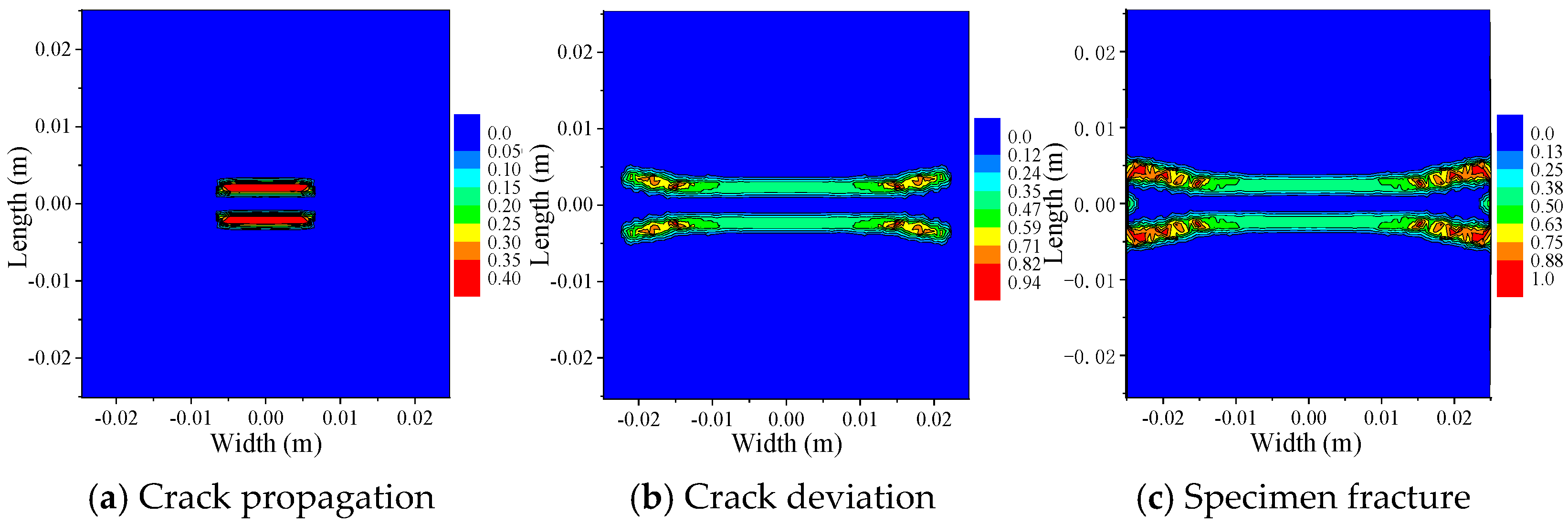
3.2.1. Simulation Analysis of Double-Sided Crack Specimens
Specimen 300X
Specimen 3010X
Specimen 3020X
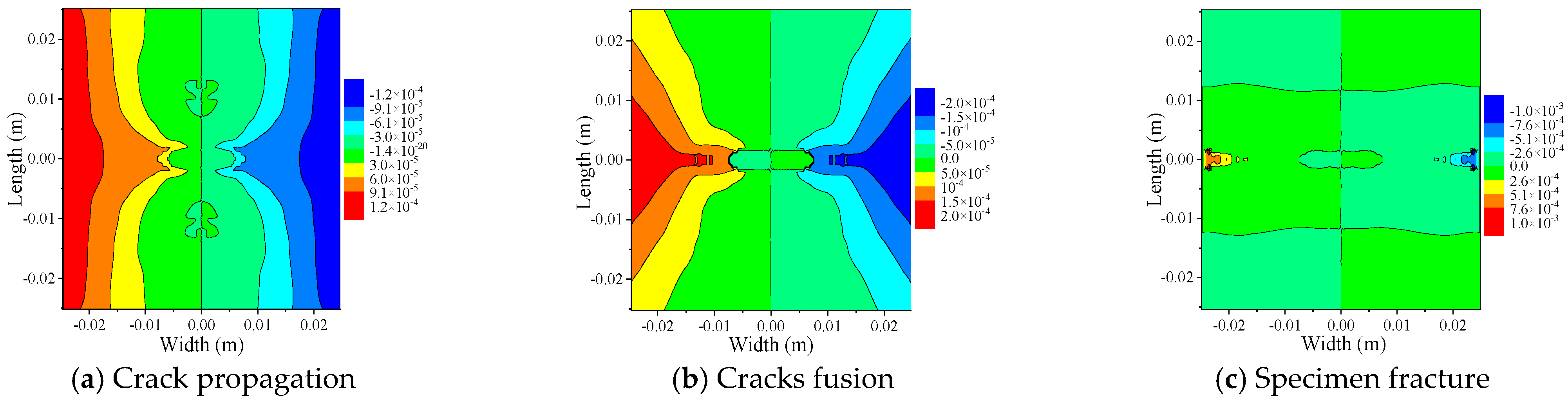
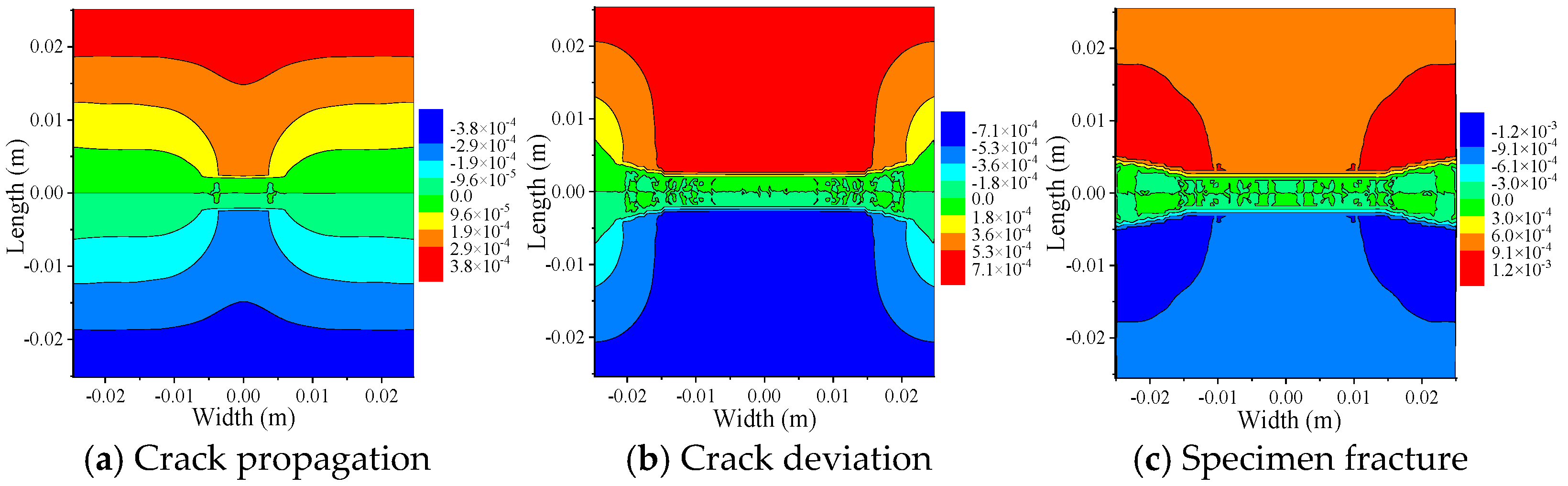
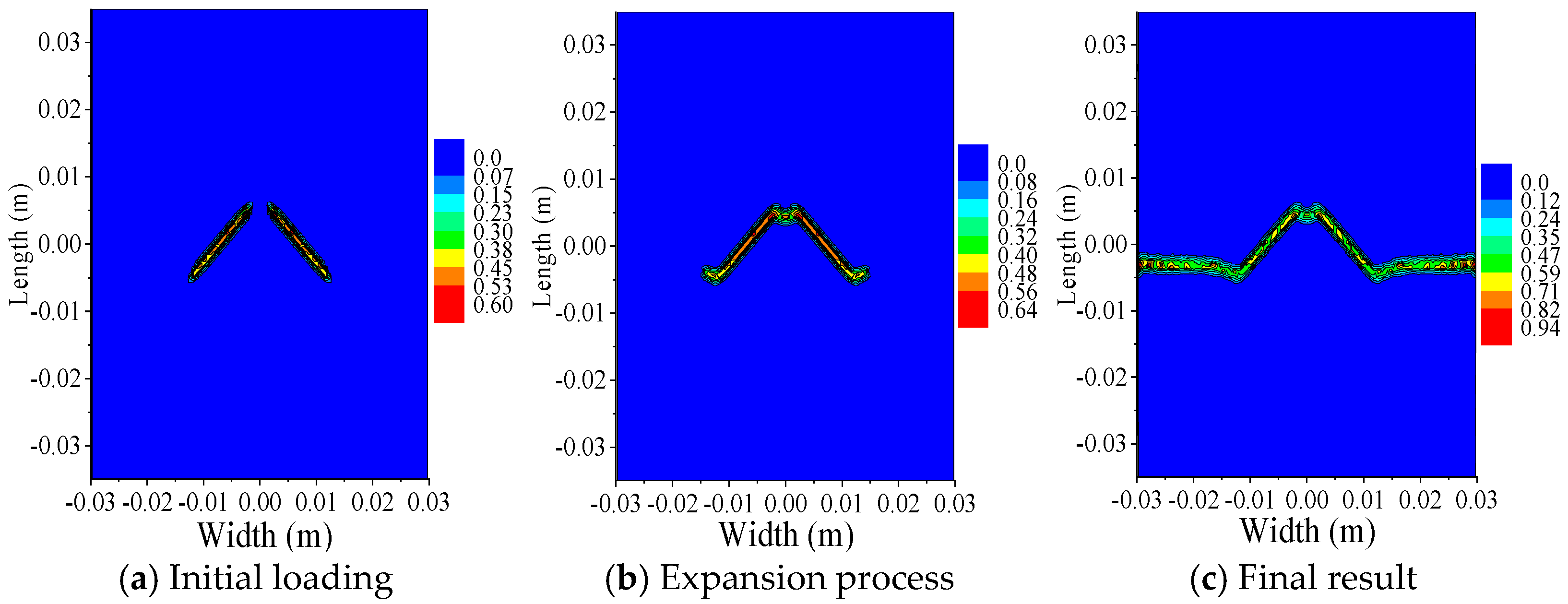
3.2.2. Central Double-Crack Growth Analysis
Specimen C02X
Specimen C03X
Specimen C04X
3.3. PD-COD Crack Propagation Analysis
4. Conclusions
- (1)
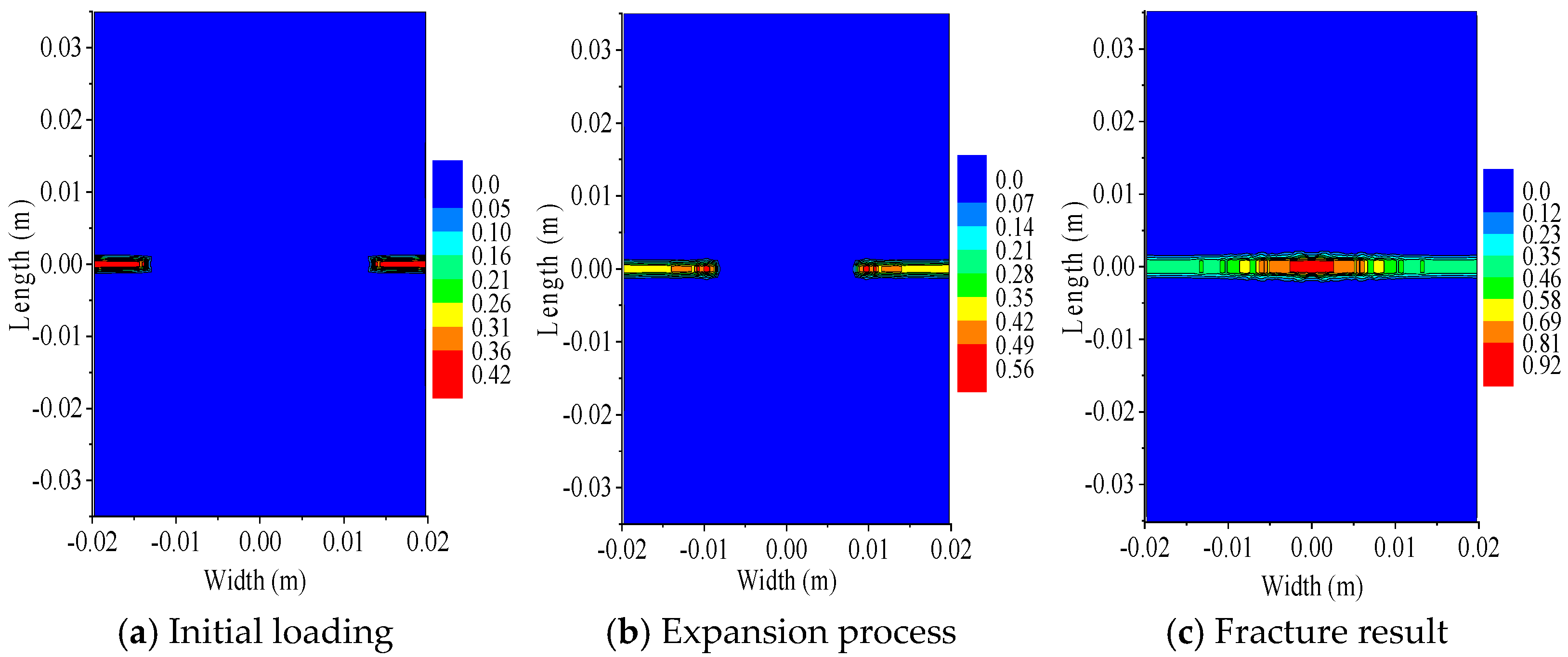
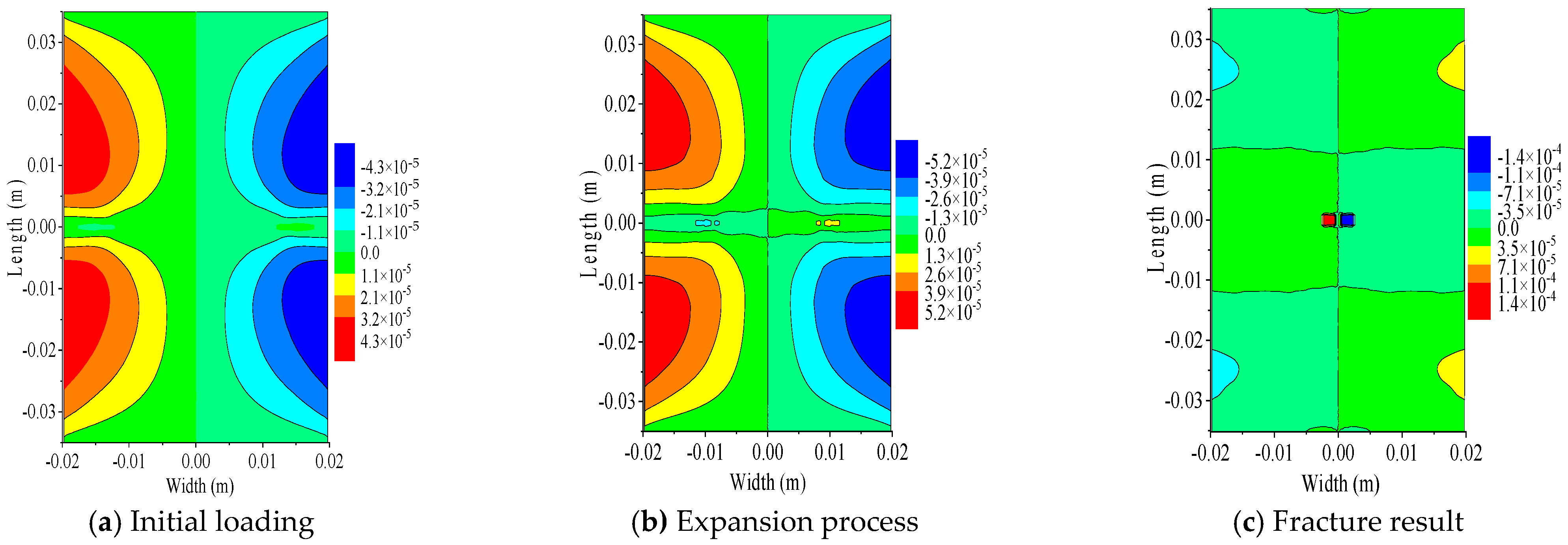
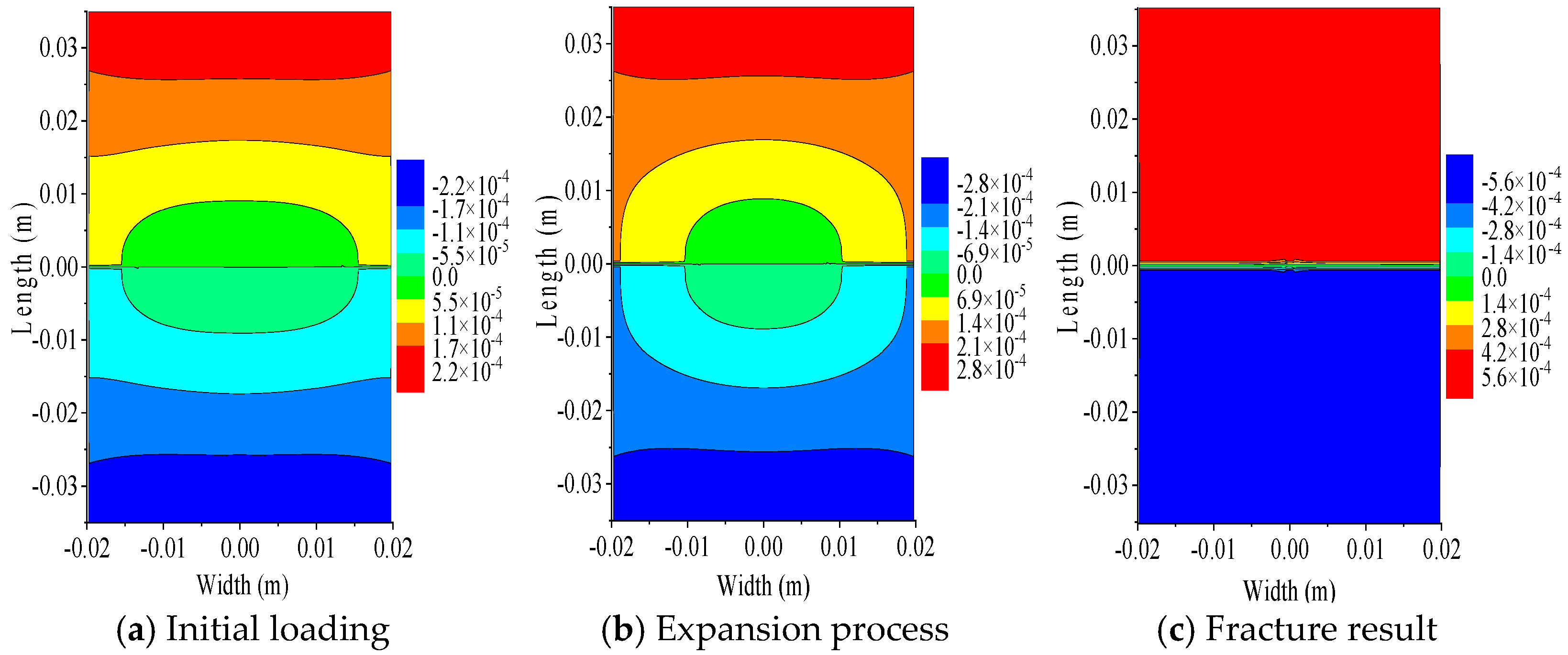
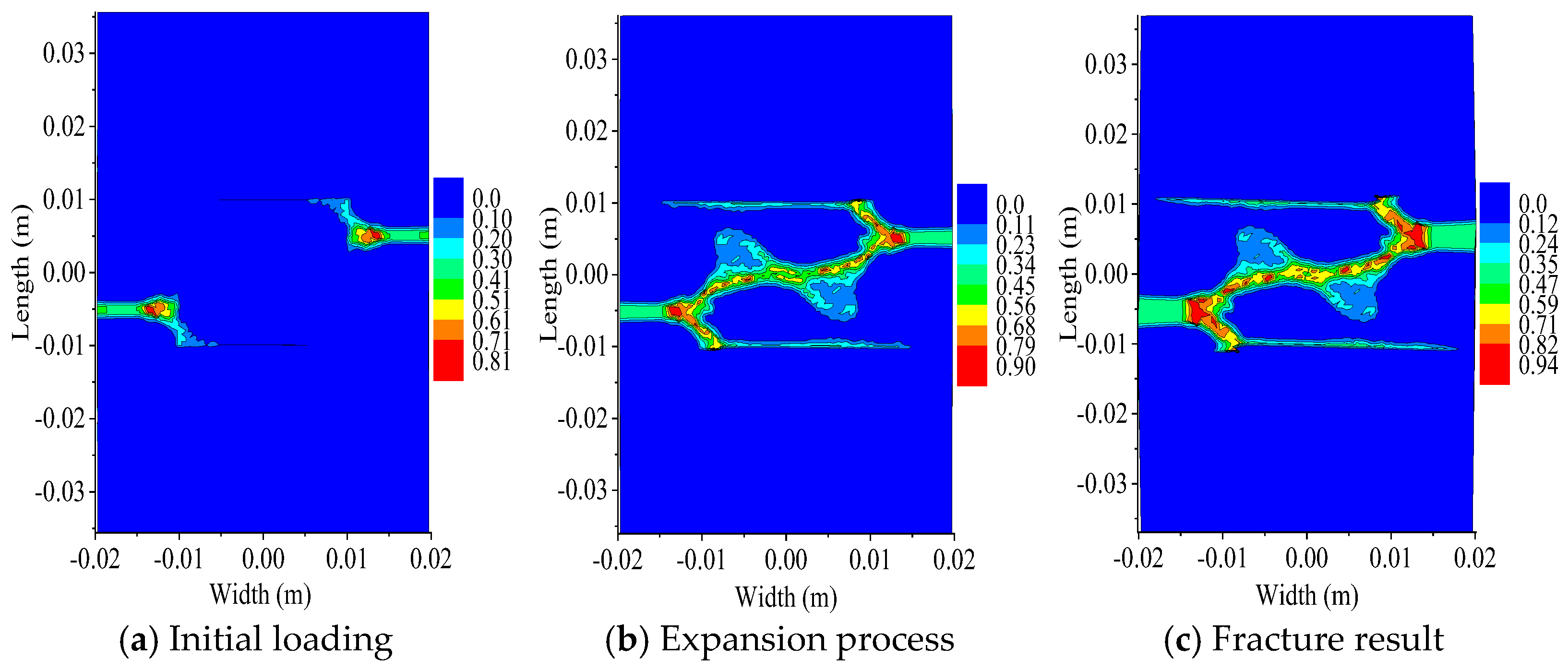
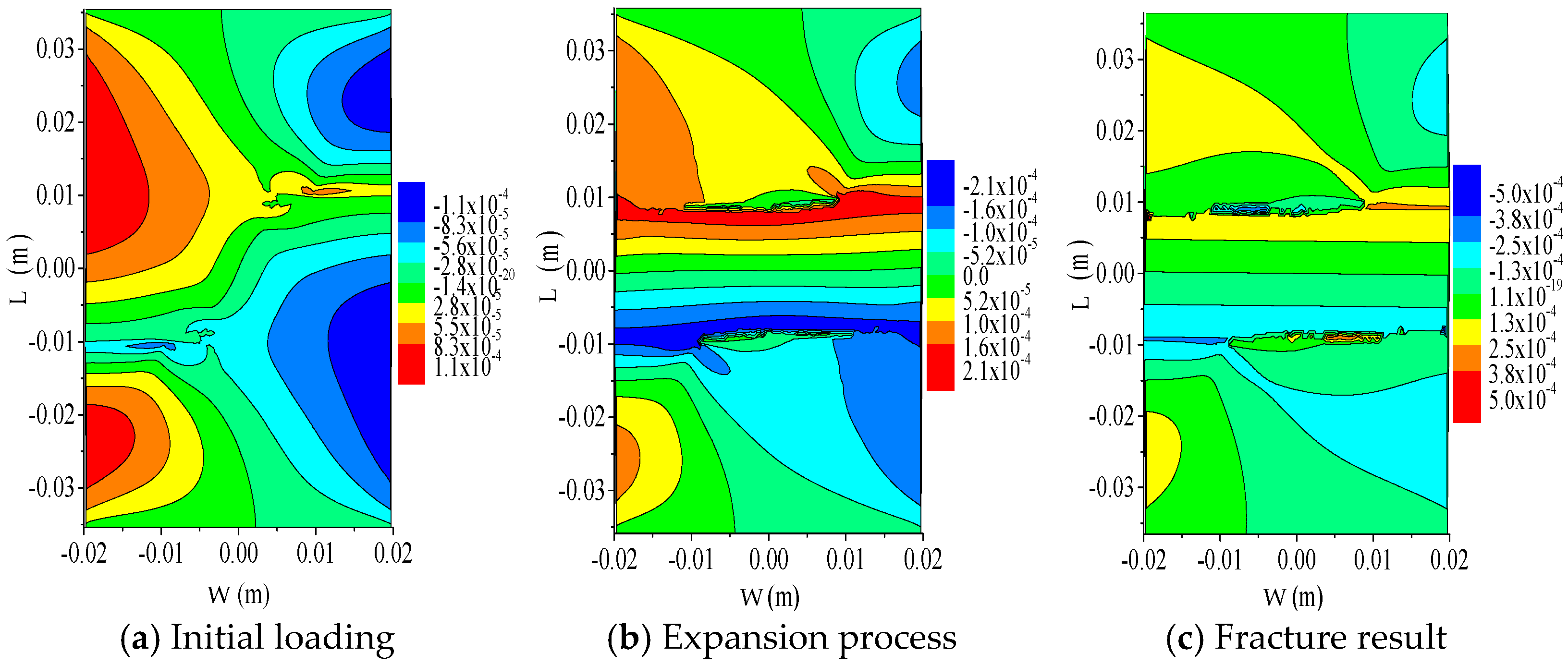
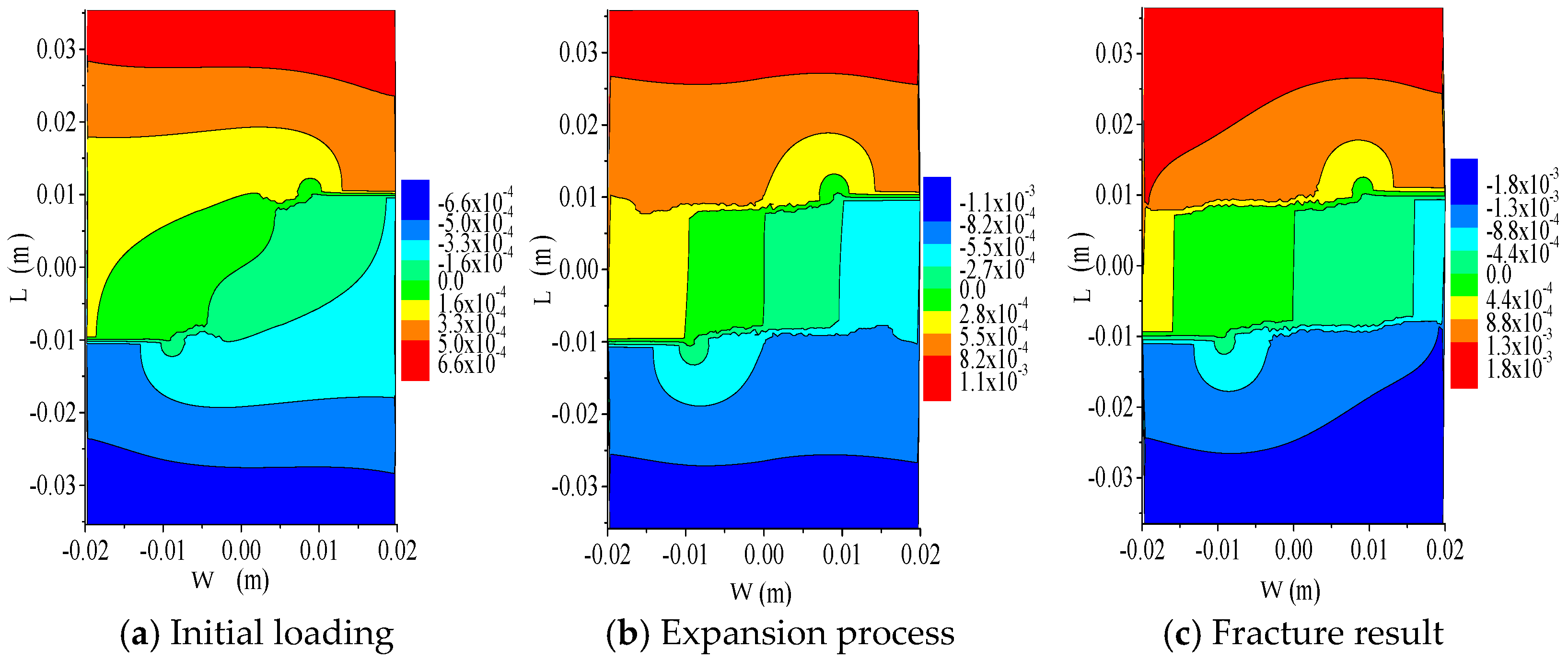
- The analysis results of bilateral crack specimens with longitudinal spacings of 0 mm, 10 mm, and 20 mm and a crack length of 5 mm show that when the longitudinal crack spacing is small, the crack growth path is significantly influenced by the spacing between the cracks; when the spacing between longitudinal cracks is sufficiently large, crack propagation remains unaffected by the crack spacing. At the onset of loading, the highest X-direction displacement values appeared on the left and right edges of the specimens, displaying an inclined symmetric pattern with respect to the specimen’s central axis. The Y-direction displacement at the upper and lower ends of the specimens was the highest. Both X- and Y-direction displacements decreased toward the center. The displacement distribution shows a symmetric pattern from the ends to the center.
- (2)
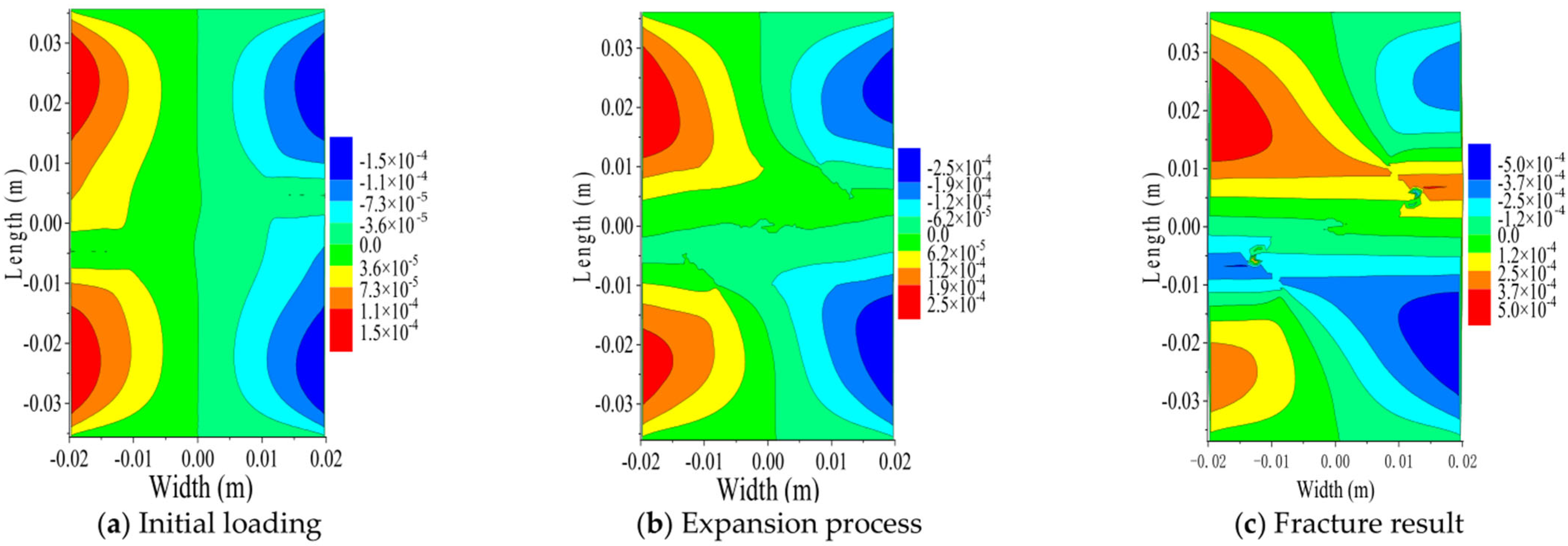
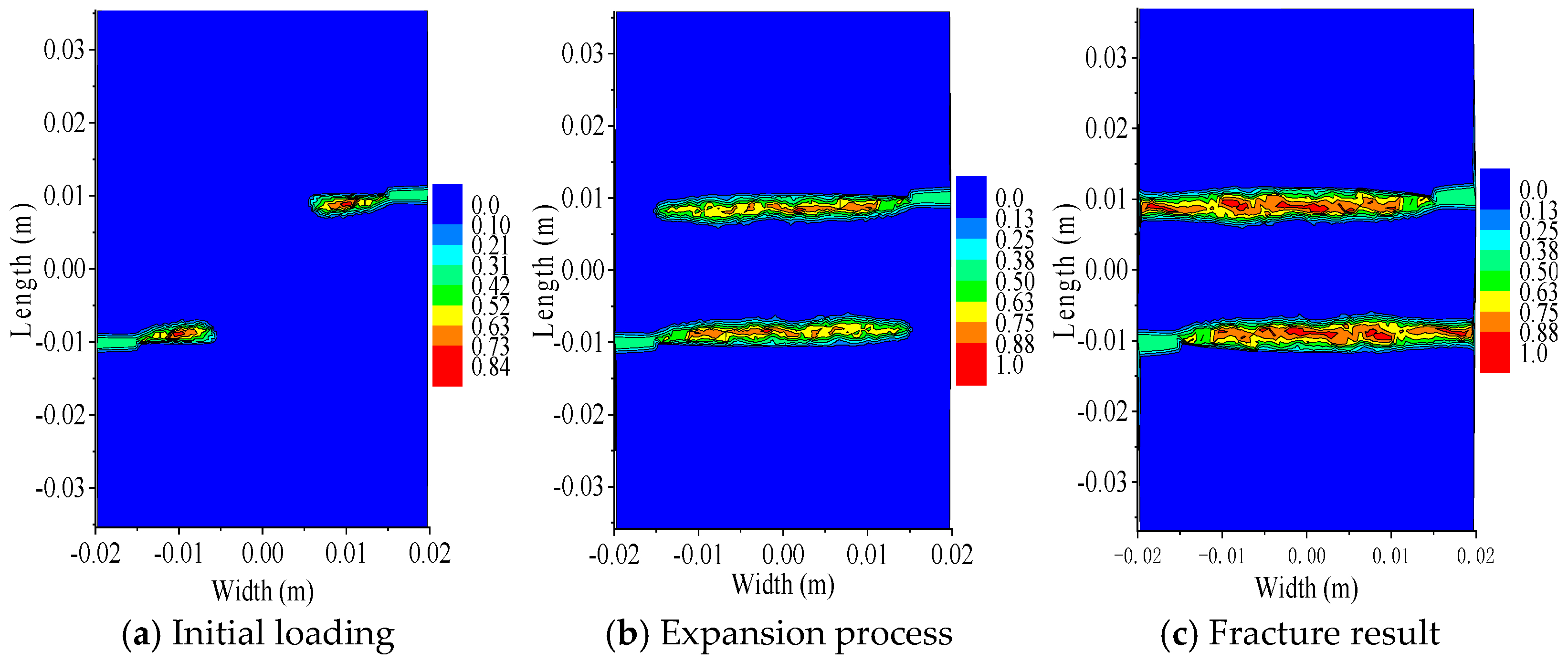
- The results obtained from analyzing the centrally located double-crack specimens with different longitudinal spacing and crack length of 10 mm show that when the longitudinal spacing is small, the two center double-crack tips first propagate a certain distance along the horizontal direction and then fuse into a horizontal crack and continue to propagate through the width direction of the specimen; when the longitudinal spacing is large, the two cracks propagate horizontally without mutual interference; after the two horizontal cracks extend a certain distance, their tips gradually diverge at a 15° angle in the opposite horizontal direction and eventually penetrate the whole specimen. The maximum X-direction displacement decreases from the left and right sides toward the Y-axis. The maximum Y-direction displacement decreases from the upper and lower regions toward the X-axis. The displacement distribution is symmetric relative to the center. Both directions show a gradient reduction from the edges inward.
- (3)
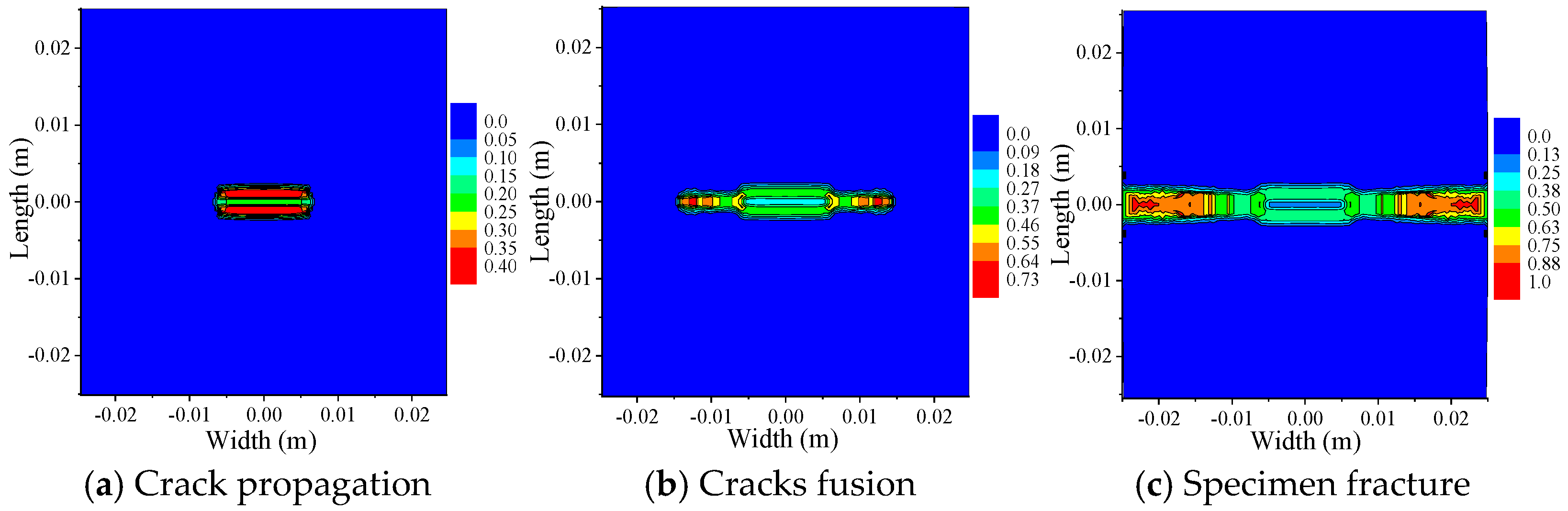
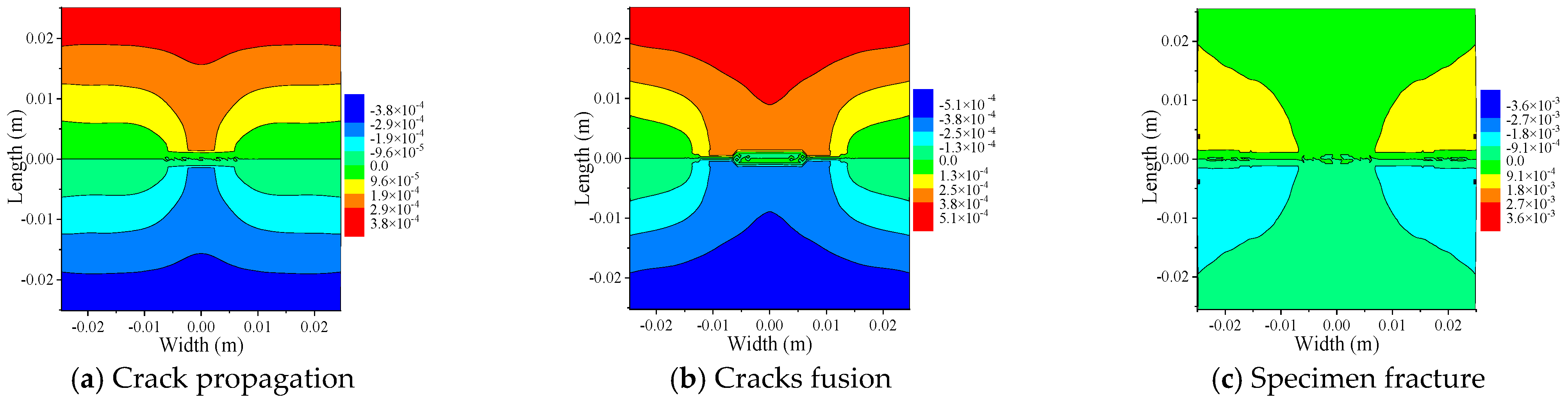
- Under the action of load, the b end of the central cross cracks first fused, and the a end of the cross cracks propagated along the direction of vertical load and penetrated the specimen. As can be observed from the damage values of the specimen during crack propagation, the damage value obtained from PD-COD analysis is slightly higher than that from PD theoretical analysis in the initial stage. When the crack permeates the specimen, the results of PD theory are basically consistent with those of PD-COD analysis. The comparison results show that the accuracy of the analysis results of PD-COD damage fracture criteria meets the requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, J.; Huang, L.; Weng, R.; Murong, Y.; Liu, L.; Zeng, H.; Jiang, H. Mechanism of chloride ion transport and associated damage in ultra-high-performance concrete subjected to hydrostatic pressure. J. Build. Eng. 2025, 112, 113700. [Google Scholar] [CrossRef]
- Weng, R.; He, Z.; Liu, J.; Lei, B.; Huang, L.; Xu, J.; Liu, L.; Xiao, J. Shear Performance of UHPC-NC Composite Structure Interface Treated with Retarder: Quantification by Fractal Dimension and Optimization of Process Parameters. Buildings 2025, 15, 2591. [Google Scholar] [CrossRef]
- Shao, H.; Shen, D.; Kang, J.; Liu, C.; Wen, C. Tensile Creep and Cracking Resistance of High-Strength Concrete with Shrinkage Reducing Admixture under Uniaxial Restrained Condition at Early Age. J. Mater. Civ. Eng. 2024, 36, 04024226. [Google Scholar] [CrossRef]
- Shi, Y.D.; Shen, H.Y.; Tan, H.M.; Ding, Y.; Li, Z.X. Research on Failure Mode Identification of High-Rise Steel Frame Structure and its Uniform Damage Pattern Control. Eng. Mech. 2025, 42, 46–59. [Google Scholar]
- Huang, X.; Zhao, J. Comparison of Different Fracture Models for Fracture Failure Prediction of Steel Structures. J. Archit. Civ. Eng. 2018, 35, 93–101. [Google Scholar]
- Wu, J. On the Unified Phase-field Theory for Damage and Failure in Solids and Structures: Theoretical and Numerical Aspects. Chin. J. Theor. Appl. Mech. 2021, 53, 301–329. [Google Scholar]
- Li, B.; Wang, X.; Lang, S. Methods for Estimating Fatigue Life of Steel Structure with Variable Cross-section. Steel Struct. 2018, 33, 18–22. [Google Scholar]
- Sun, B. Simulation and Analysis Method of Failure Process of Engineering Structures due to Trans-Scale Damage Evolution. Ph.D. Thesis, Southeast University, Nanjing, China, 2016. [Google Scholar]
- Li, Z. Micro-Mechanism Based Ansys of T-Stub Connections Failure Process Under Cyclic Loading. Ph.D. Thesis, Guangxi University, Nanning, China, 2016. [Google Scholar]
- Li, Z.; Liu, Z.; Ding, Y. Dynamic Responses and Failure Modes of Steel Structures Under Blast Loading. J. Build. Struct. 2008, 29, 106–111. [Google Scholar]
- Kulkarni, S.; Wang, X.; Tabarraei, A. Modeling the creep damage of P91 steel using peridynamics_IMECE2019 presentation. Mech. Solids Struct. Fluids 2019, 9, 11–14. [Google Scholar]
- Amani, J.; Oterkus, E.; Rabczuk, T.; Areias, P.; Zi, G.; Nguyen-Thoi, T. A non-ordinary state-based peridynamics formulation for thermoplastic fracture. Intenational J. Impact Eng. 2016, 87, 83–94. [Google Scholar] [CrossRef]
- Diyaroglu, C.; Oterkus, E.; Rabczuk, T.; Madenci, E.; Siddiq, A. Peridynamic modeling of composite laminates under explosive loading. Composite Structures 2016, 144, 14–23. [Google Scholar] [CrossRef]
- Li, Z.; Huang, D.; Rabczuk, T. Nonlocal anisotropic model for deformation and fracture using peridynamic operator method. Mech. Sci. 2024, 268, 109023. [Google Scholar] [CrossRef]
- Dorduncu, M.; Olmus, I.; Rabczuk, T. A peridynamic approach for modeling of two dimensional functionally graded plates. Compos. Struct. 2022, 279, 114743. [Google Scholar] [CrossRef]
- Dorduncu, M.; Kutlu, A.; Rabczuk, T.; Madenci, E. Nonlocal modeling of bi-material and modulus graded plates using peridynamic differential operator. Eng. Comput. 2022, 39, 893–909. [Google Scholar] [CrossRef]
- Bie, Y.; Ren, H.; Rabczuk, T.; Bui, T.Q.; Wei, Y. The fully coupled thermo-mechanical dual-horizon peridynamic correspondence damage model for homogeneous and heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2024, 420, 116730. [Google Scholar] [CrossRef]
- Zhao, J.; Tang, H.; Xue, S. Analysis of the center parallel double-crack propagation with initial casting defects by peridynamics. J. Harbin Eng. Univ. 2018, 39, 1612–1616. [Google Scholar]
- Zhao, J.; Tang, H.; Xue, S. Peridynamics versus XFEM: A comparative study for quasistatic crack problems. Front. Struct. Civ. Eng. 2018, 12, 548–557. [Google Scholar] [CrossRef]
- Zhao, J.; Li, T.; Dou, X. Crack propagation with different radius local random damage based on peridynamic theory. Front. Struct. Civ. Eng. 2021, 15, 1238–1248. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, H.; Guo, X. A numerical study of crack propagation with variable temperature in steel structures using peridynamic constitutive model. Int. J. Hydromechatronics 2021, 4, 116–141. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, H.; Zhang, X. Damage and Crack Propagation Mechanism of Q345 Specimen Based on Peridynamics with Temperature and Bolt Holes. Buildings 2024, 14, 3220. [Google Scholar] [CrossRef]
- Sun, R.; Huang, D.; Chen, D.; Zhao, J. Research on casing failure mechanisms and countermeasures in hydraulic fracture of shale reservoirs considering dynamic evolution of fault slip. Eng. Fail. Anal. 2024, 161, 108301. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, R.; He, D.; Ma, Q.; Huang, D. Analysis of compressive failure mechanism of concrete and grouting cubes by Peridynamics. Theor. Appl. Fract. Mech. 2024, 131, 104423. [Google Scholar] [CrossRef]
- Ran, X.; Qian, S.R.; Zhou, J.; Xu, Z. Crack propagation analysis of hydrogen embrittlement based on peridynamics. Int. J. Hydrogen Energy 2022, 47, 9045–9057. [Google Scholar] [CrossRef]
- Karim, M.R.; Kadau, K.; Narasimhachary, S.; Radaelli, F.; Amann, C.; Dayal, K.; Silling, S.; Germann, T.C. Crack nucleation at forging flaws studied by non-local peridynamics simulations. Math. Mech. Solids 2022, 27, 1129–1149. [Google Scholar] [CrossRef]
- Abdoh, D. Failure analysis of bolted steel plate connections with three-dimensional flexibilities. Int. J. Mech. Sci. 2024, 272, 109313. [Google Scholar] [CrossRef]
- Ahmadi, M.; Sadighi, M.; Toudeshky, H. Computational microstructural model of ordinary state-based Peridynamic theory for damage mechanisms, void nucleation, and propagation in DP600 steel. Eng. Fract. Mech. 2021, 247, 107660. [Google Scholar] [CrossRef]
- Jafarzadeh, S. Novel and Fast Peridynamic Models for Material Degradation and Failure. Ph.D. Thesis, The University of Nebraska Lincoln, Lincoln, NE, USA, 2023. [Google Scholar]
- Mossaibya, F.; Häfner, G.; Shojaei, A.; Hermann, A.; Cyron, C.; Müller, M.; Silling, S. On efficient simulation of self-assembling diblock copolymers using a peridynamic-enhanced Fourier spectral method. Comput. Methods Appl. Mech. Eng. 2025, 439, 117878. [Google Scholar] [CrossRef]
- Le, M. Dual-horizon peridynamic study of the mode-I J-integral and crack opening displacement in single-edge notched beams. Mech. Adv. Mater. Struct. 2024, 33, 5478–5485. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, S.; Ji, J.; Cui, K.; Tian, F.; Li, L. Mechanisms governing crack speed in peridynamic model. Eng. Fract. Mech. 2024, 305, 110201. [Google Scholar] [CrossRef]
- Zeng, S. Bilateral Crack Growth Behavior of Q345 Steel Under Uniaxial Thensile Load. Master’s Thesis, Guangxi University, Nanning, China, 2014. [Google Scholar]










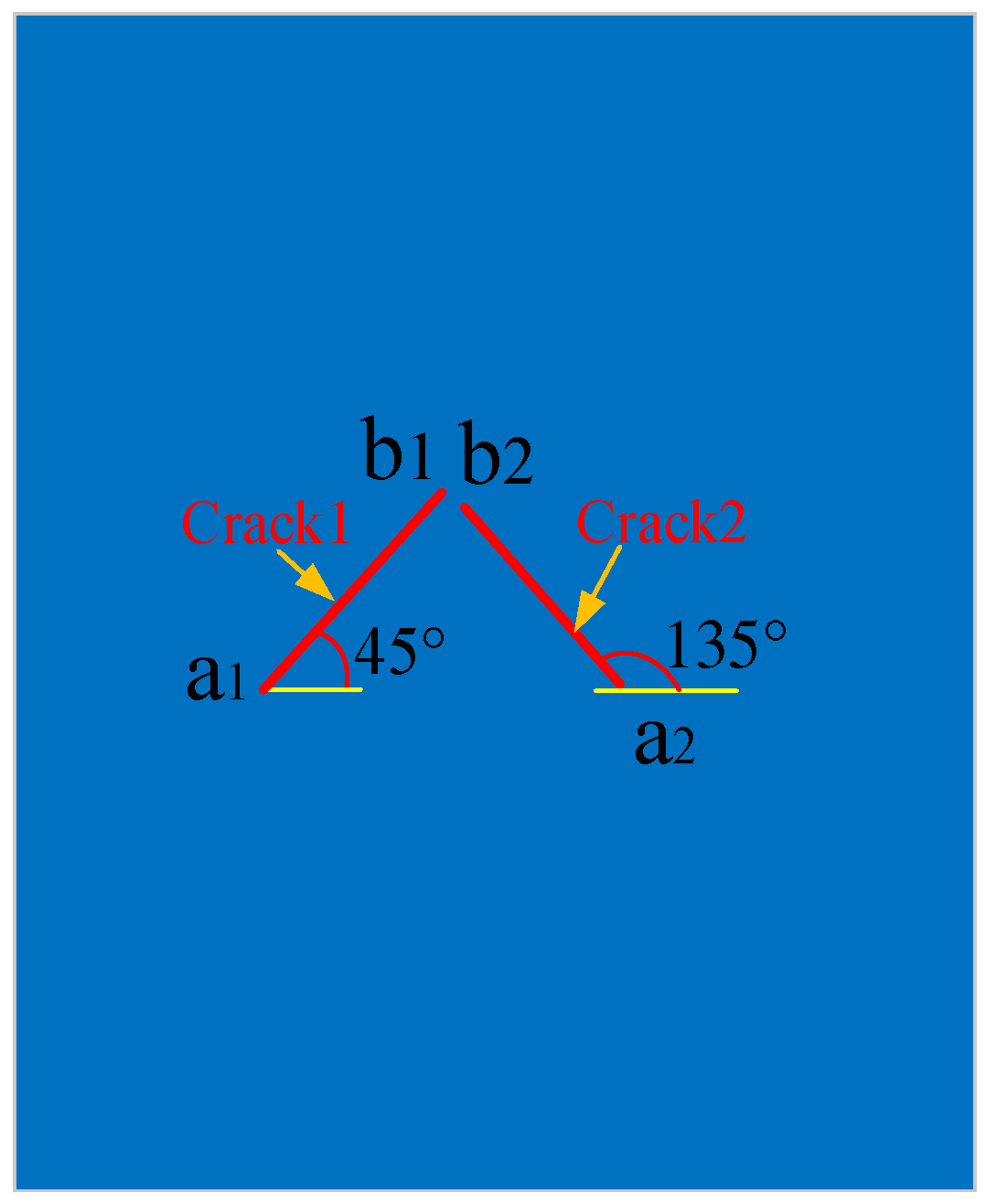

| No. | Crack Length (mm) | Longitudinal of Crack Spacing (mm) | Specimen Size (mm) | ||
|---|---|---|---|---|---|
| Left Side | Right Side | Length | Width | ||
| 300X | 5 | 5 | 0 | 70 | 40 |
| 3010X | 5 | 5 | 10 | 70 | 40 |
| 3020X | 5 | 5 | 20 | 70 | 40 |
| No. | Crack Length (mm) | Longitudinal Crack Spacing (mm) | Specimen Size (mm) | ||
|---|---|---|---|---|---|
| Top Side | Bottom Side | Length | Width | ||
| C02X | 10 | 10 | 2 | 50 | 50 |
| C03X | 10 | 10 | 3 | 50 | 50 |
| C04X | 10 | 10 | 4 | 50 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zong, G.; Zhang, S.; Ye, L.; Xiao, J.; Hu, X. Crack Propagation Analysis of Steels with Initial Defects by New Peridynamics. Buildings 2025, 15, 3911. https://doi.org/10.3390/buildings15213911
Zhao J, Zong G, Zhang S, Ye L, Xiao J, Hu X. Crack Propagation Analysis of Steels with Initial Defects by New Peridynamics. Buildings. 2025; 15(21):3911. https://doi.org/10.3390/buildings15213911
Chicago/Turabian StyleZhao, Jinhai, Gang Zong, Shimin Zhang, Lingpeng Ye, Jie Xiao, and Xinzan Hu. 2025. "Crack Propagation Analysis of Steels with Initial Defects by New Peridynamics" Buildings 15, no. 21: 3911. https://doi.org/10.3390/buildings15213911
APA StyleZhao, J., Zong, G., Zhang, S., Ye, L., Xiao, J., & Hu, X. (2025). Crack Propagation Analysis of Steels with Initial Defects by New Peridynamics. Buildings, 15(21), 3911. https://doi.org/10.3390/buildings15213911







