Optimization of Gaussian Process Regression with Intelligent Algorithms for Predicting Compacted Density of Gravel-Soil Materials
Abstract
1. Introduction
1.1. Literature Review
1.2. Contribution
1.3. Organization
2. Materials and Methods
2.1. Gradation Equation for Continuously Graded Soils
2.2. Scaled Gradation Equation Using the Parallel Gradation Method
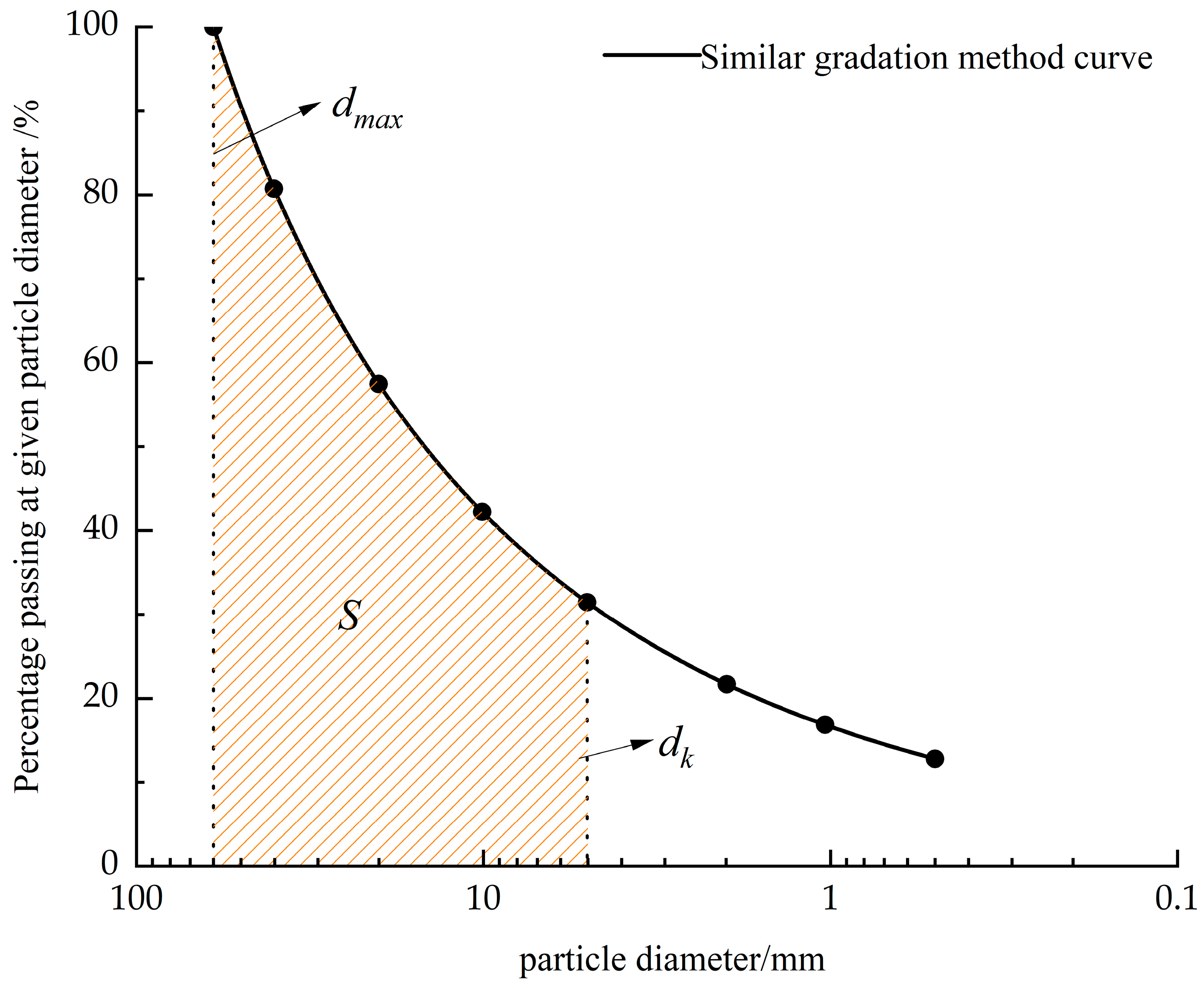
2.3. Gradation Curve Area
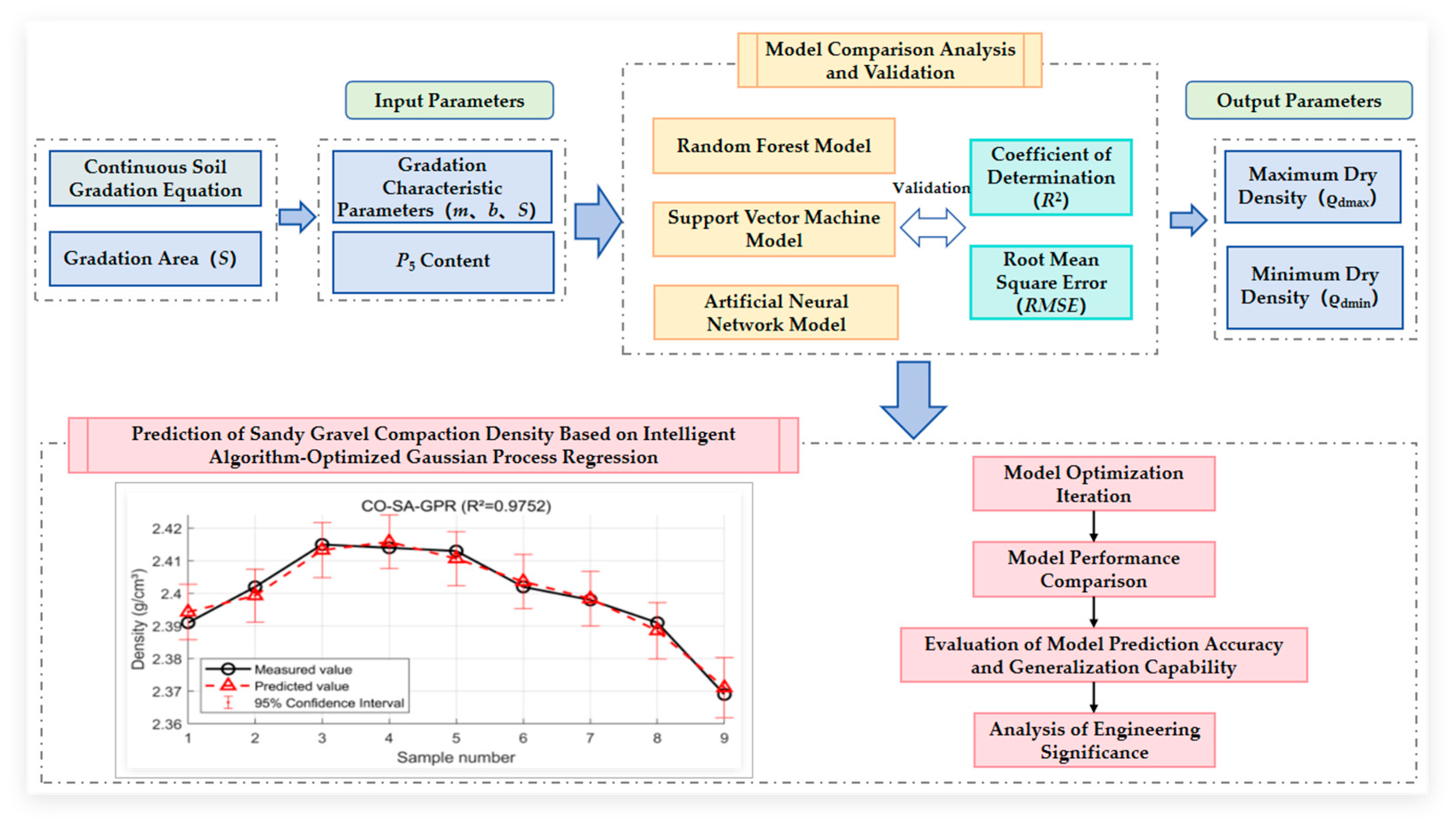
2.4. CO–SA–GPR Model
2.4.1. Gaussian Process Regression
2.4.2. Cheetah Optimizer (CO)
- (1)
- Search Strategy: Cheetahs employ two primary methods to locate prey: conducting a comprehensive scan across their entire territory or proactively searching the surrounding areas. During the hunt, depending on factors such as prey availability, terrain coverage, and the cheetah’s own physical condition, the cheetah may alternate between these two search modes. The position update formula is as follows:
- (2)
- Sitting-and-Waiting Strategy: When prey is detected but current conditions are unsuitable for an immediate attack, the cheetah will conceal itself and wait for the prey to approach or for a more opportune moment to initiate the hunt. When this strategy is adopted, the cheetah maintains its current position:
- (3)
- Attack Strategy: The attack strategy consists of two phases: sprinting and capturing. Sprinting: The cheetah rapidly closes in on the prey. When the opportunity arises, it initiates an active assault. In group hunting scenarios, each cheetah may adjust its position based on the fleeing prey and the locations of the leading or adjacent cheetahs.The mathematical formulation of the cheetah’s attack strategy is as follows:
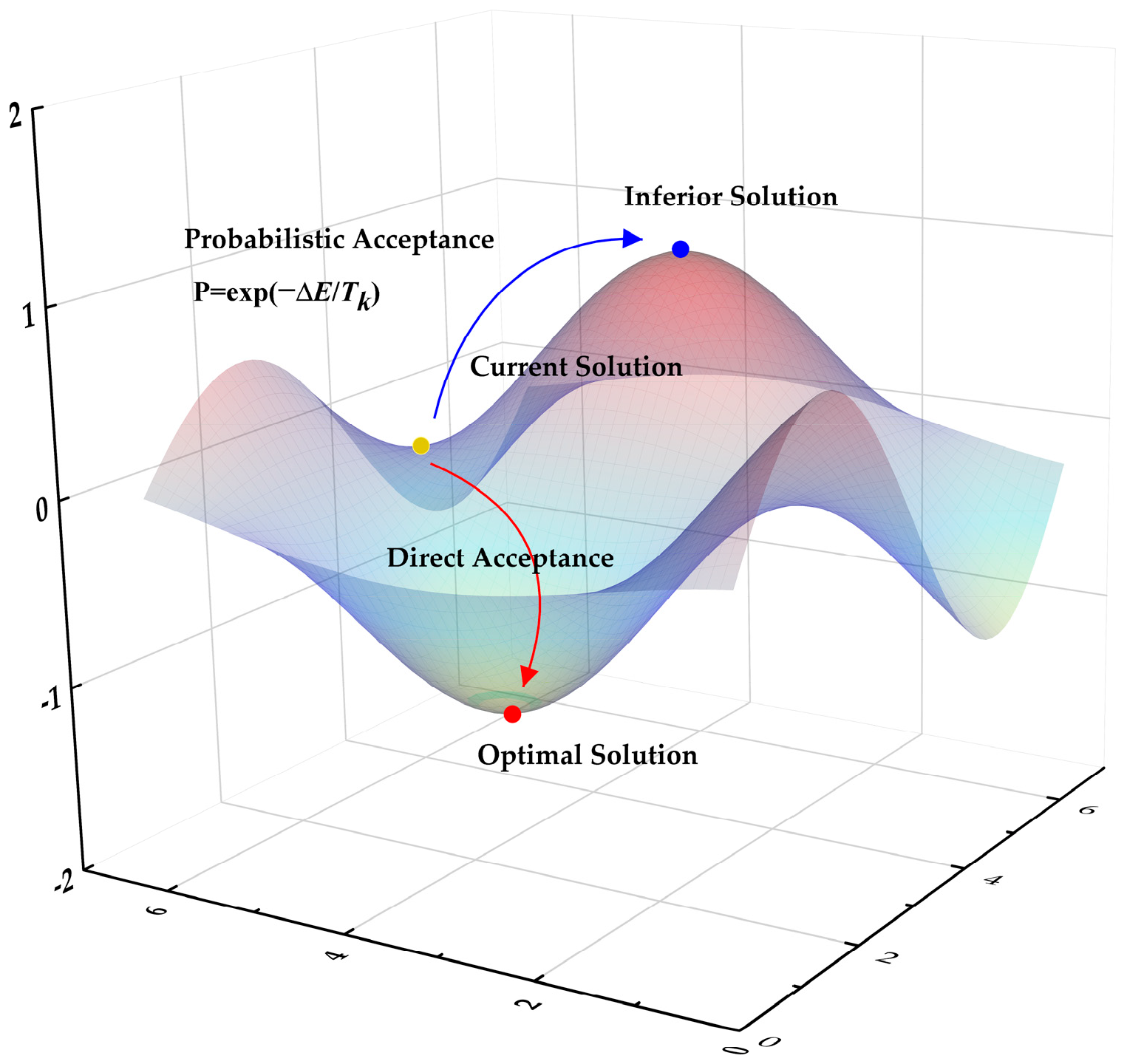
2.4.3. Simulated Annealing Algorithm
3. Development of a CO–SA–GPR-Based Model for Predicting Sandy Gravel Compaction Density and Its Engineering Application
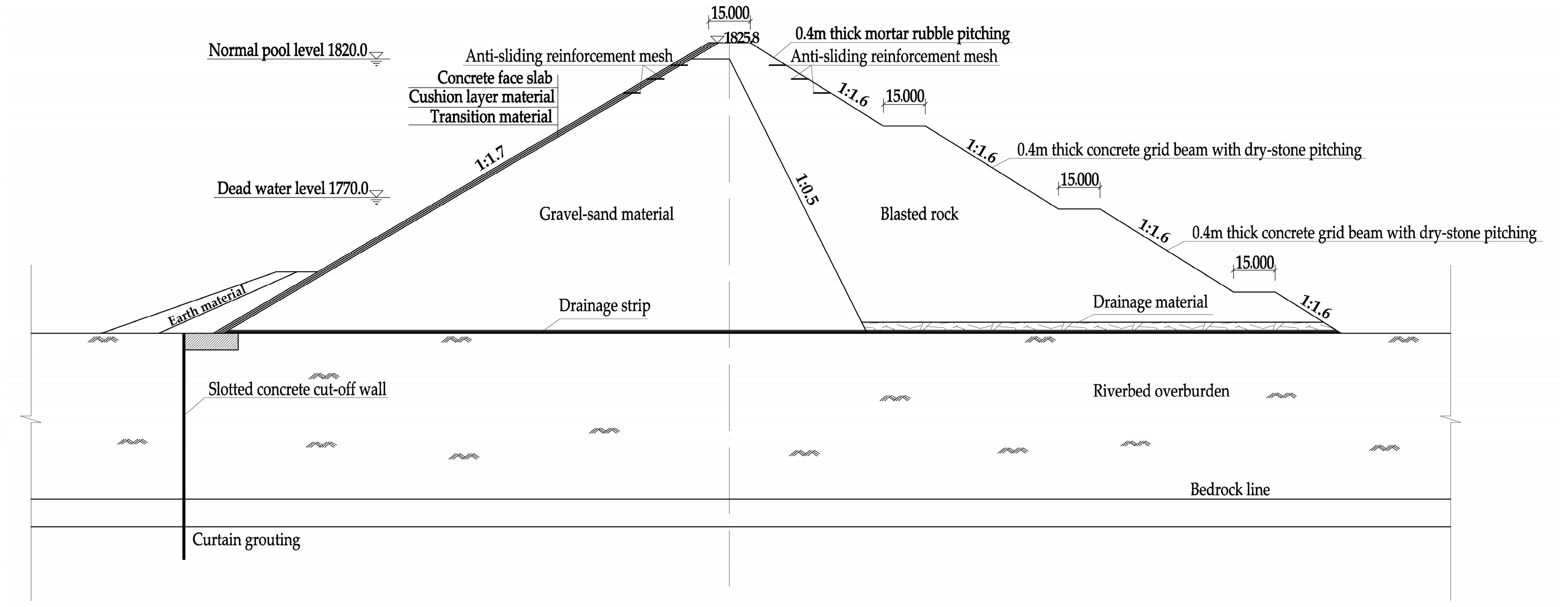
3.1. Engineering Background
3.2. Model Development and Application
4. Results and Discussion
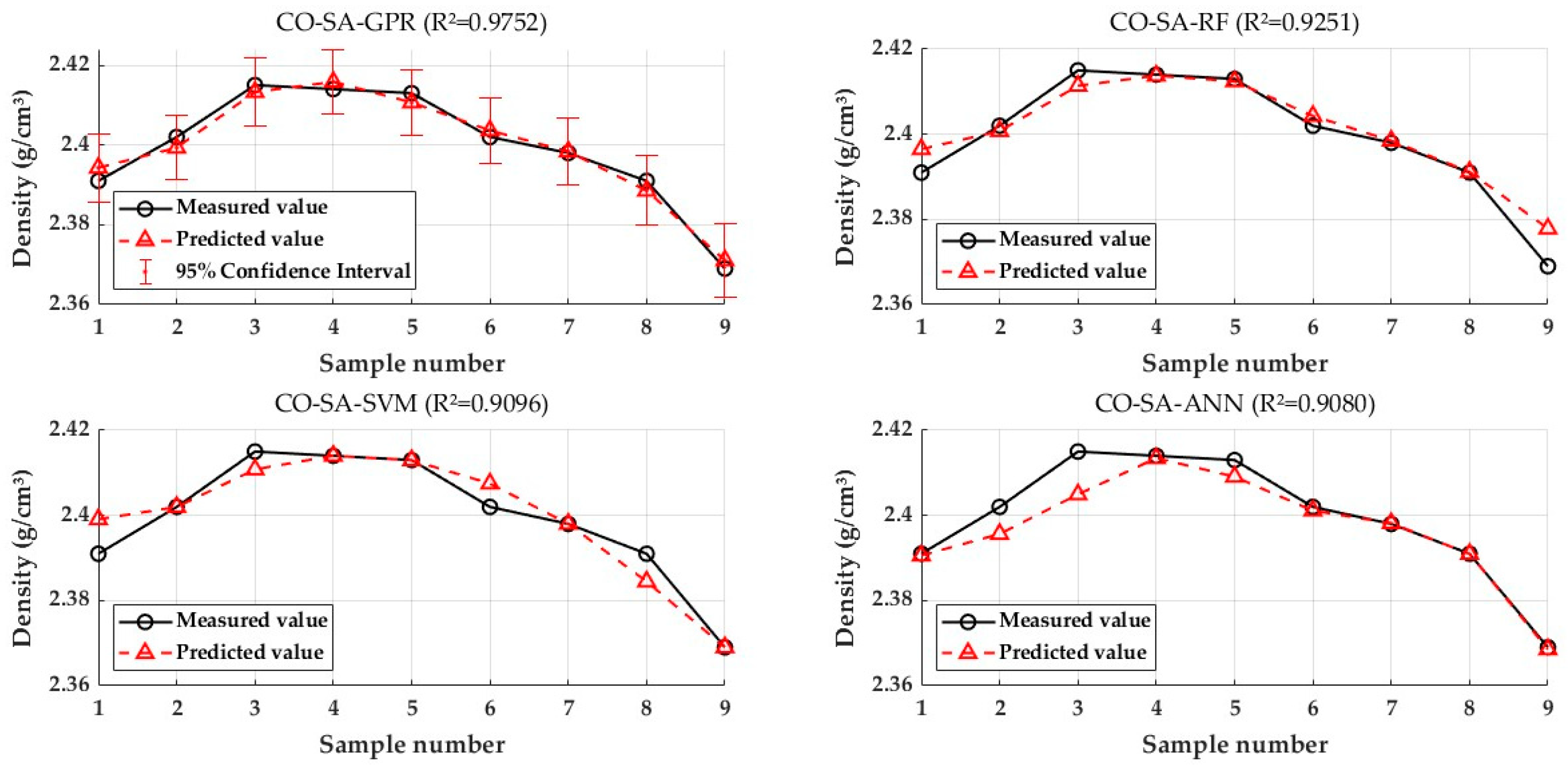
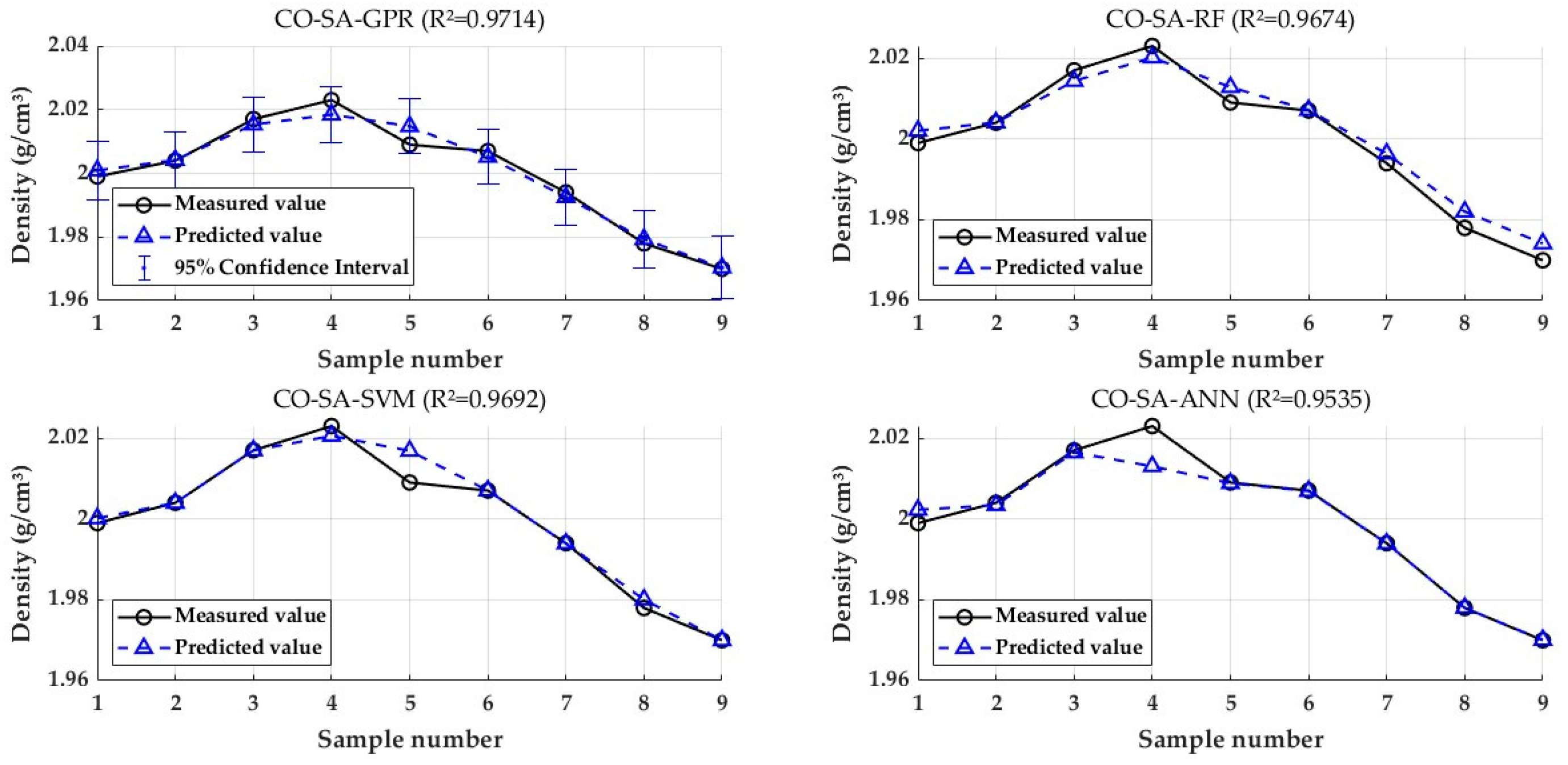
4.1. Comparison of Results from Different Evaluation Models
- (1)
- Gaussian Process Regression (GPR) describes the underlying functional relationship through a Gaussian process prior and provides a predictive probability distribution.
- (2)
- Random Forest (RF) is a Bagging ensemble learning algorithm that constructs multiple decision trees during regression modeling and aggregates their predictions to enhance overall predictive performance [40].
- (3)
- Support Vector Machine (SVM) is a supervised learning algorithm based on statistical learning theory. Its fundamental principle is to find an optimal decision boundary between data points to separate different classes, ensuring this boundary maximizes the margin to the nearest data points (support vectors). The key idea is to improve the generalization ability of the learning machine by minimizing structural risk [41].
- (4)
- An Artificial Neural Network (ANN) is a computational tool that “learns” from known sample data to establish relationships between the input and output layers [42].
4.2. Reliability Analysis of the CO–SA–GPR Model
4.3. Discussion on Model Performance Across Different Parameters and Variables
4.3.1. Influence of Input Parameters
4.3.2. Performance on Output Variables
4.3.3. Comparison with Other Models Across Variables
5. Conclusions
6. Limitations and Future Research Directions
- (1)
- Data Limitations: The predictive performance of the model relies on specific indicators such as laboratory test data and P5 content, which may be constrained by the scale and representativeness of the training dataset. Its effectiveness, particularly for materials with extreme gradations or non-typical sandy gravels, remains to be validated. Future studies could incorporate additional material parameters to enhance the model’s generalizability and interpretability across diverse materials.
- (2)
- Regarding model performance: There is potential to improve model performance by exploring alternative optimization strategies and more complex kernel functions. Furthermore, developing lightweight model architectures and embedded computing optimization strategies could reduce computational costs while maintaining prediction accuracy, thereby facilitating the integration of the model into real-time compaction monitoring systems.
- (3)
- Model Applications: This study developed an intelligently optimized Gaussian process regression model, aiming to provide a more accurate method for predicting the compaction density of gravelly soils in dam construction. The model’s output of compaction density can be used to guide on-site compaction quality control. Furthermore, these prediction results can serve as key input parameters for predictive models of the dam material’s mechanical characteristics, thereby supporting the prediction of mechanical properties and numerical analysis of long-term dam deformation. This ultimately provides data support for optimizing engineering design and informing safety operation decisions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPR | Gaussian Process Regression |
| CO | Cheetah Optimizer |
| SA | Simulated Annealing |
| RF | Random Forest |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| XGBoost | eXtreme Gradient Boosting |
References
- Guo, Q.G. Engineering Properties and Applications of Coarse-Grained Soils; Yellow River Water Conservancy Press: Zhengzhou, China, 2003. [Google Scholar]
- Deng, M.J.; Yu, H.M. Progress in Dam Construction in Xinjiang; China Water & Power Press: Beijing, China, 2011. [Google Scholar]
- Li, J.; Li, X.Q. Design and construction technology development of concrete face rockfill dams and asphalt concrete core dams under special conditions in Xinjiang. Water Resour. Hydropower Eng. 2016, 47, 2–8+20. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Huang, T. Application of key technologies in dam type selection and layout of medium-sized reservoirs in Xinjiang. Water Resour. Hydropower Eng. 2018, 49, 87–96. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Yang, Y.S.; Peng, Z.X. Filling standards and deformation control of high concrete face rockfill dams in Xinjiang. J. Hydraul. Eng. 2021, 52, 182–193. [Google Scholar] [CrossRef]
- Xu, Z.P. Key technologies and research progress of concrete face rockfill dams. J. Hydraul. Eng. 2019, 50, 62–74. [Google Scholar] [CrossRef]
- Xiao, S.; Yang, J.; Lu, X.; Zhou, H.; Cheng, L.; Ma, C.H.; Tong, F. Research progress on key technologies for safety monitoring of CFRDs considering special engineering problems of “three highs, one depth, and one narrow”. Adv. Eng. Sci. 2025, 1–19. [Google Scholar] [CrossRef]
- Zhu, J.G.; Weng, H.Y.; Wu, X.M.; Liu, H.L. Experimental study on compaction density of coarse-grained materials after particle size scaling. Rock Soil Mech. 2010, 31, 2394–2398. [Google Scholar]
- Li, P. Determination Method and Application of Filling Standards for Wide-Graded Large-Sized Coarse-Grained Soils. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2006. [Google Scholar]
- Zhu, S.; Wang, Y.M.; Weng, H.Y. Study on scale effect of compaction density of coarse dam materials. Chin. J. Rock Mech. Eng. 2011, 30, 348–357. [Google Scholar]
- Zhu, S.; Wang, J.; Zhong, C.X.; Wu, L.Q. Scale effect and sample preparation standards for dry density of rockfill materials. Chin. J. Rock Mech. Eng. 2019, 38, 1073–1080. [Google Scholar]
- Weng, H.Y.; Jing, W.H.; Li, Y.H.; Wang, G.Q. Analysis of factors influencing scale effect of coarse-grained materials. J. Water Resour. Water Eng. 2009, 20, 25–28+34. [Google Scholar]
- Fu, H.; Han, H.Q.; Ling, H. Influence of particle size scaling methods on laboratory test results of rockfill materials. Rock Soil Mech. 2012, 33, 2645–2649. [Google Scholar]
- Zhao, N.; Zuo, Y.Z.; Wang, Z.B.; Yu, S.G. Study on particle size scaling method for coarse-grained materials based on fractal theory. Rock Soil Mech. 2016, 37, 3513–3519. [Google Scholar]
- Shi, Y.W. Determination of filling standards and construction control for large-sized coarse dam materials. Chin. J. Geotech. Eng. 1982, 04, 78–93. [Google Scholar]
- Feng, G.Q.; Yang, Y.H. Study on laboratory test methods for maximum index density of rockfill materials. Chin. J. Geotech. Eng. 1992, 05, 37–45. [Google Scholar]
- Zuo, Y.Z.; Zhang, W.; Pan, J.J.; Zhao, N. Influence of particle size scaling methods on maximum dry density of coarse-grained materials. Rock Soil Mech. 2015, 36, 417–422. [Google Scholar]
- Wu, E.L.; Zhu, J.G.; Guo, W.L.; Chen, G. Experimental study on the influence of scale effect on compaction density of coarse-grained materials. Chin. J. Geotech. Eng. 2019, 41, 1767–1772. [Google Scholar]
- Wu, E.L.; Zhu, J.G.; Guo, W.L.; Lu, Y.Y. Experimental study on compaction characteristics of coarse-grained materials based on gradation equation. Rock Soil Mech. 2020, 41, 214–220. [Google Scholar]
- Sukkarak, R.; Pramthawee, P.; Jongpradist, P.; Kongkitkul, W.; Jamsawang, P. Deformation analysis of high CFRD considering the scaling effects. Geomech. Eng. 2018, 14, 211–224. [Google Scholar]
- Shibuya, S.; Uemoto, Y.; Hashimoto, Y.; Kawajiri, S. Effects of grain size distribution characteristics on compaction and deformation-strength characteristics of gravelly fill materials. In Deformation Characteristics of Geomaterials: Proceedings of the Fifth International Symposium on Deformation Characteristics of Geomaterials, IS-Seoul 2011, 1-3 September 2011, Seoul, Korea; IOS Press: Amsterdam, The Netherlands; Fairfax, VA, USA, 2011; p. 411. [Google Scholar]
- Zhou, M.; Lyu, Z.G.; Di, R.H.; Li, Y. BP neural network modeling based on small sample data. Sci. Technol. Eng. 2022, 22, 2754–2760. [Google Scholar]
- Lin, Z.X.; Ou, B.; Wang, Y.; Gao, L. Study on predicting mechanical indices of clay materials using improved RBF method. J. Yunnan Agric. Univ. (Nat. Sci.) 2011, 26, 277–279+283. [Google Scholar]
- Chen, H.C.; Zhang, X.Y.; Chen, W.L.; Qiu, W.; You, Q.S. Research on compaction quality evaluation of rockfill dams based on binary butterfly optimization algorithm and feature selection under real-time monitoring. Water Resour. Hydropower Eng. 2021, 52, 230–237. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Wang, W.; Liu, B. Compaction Density Evaluation Model of Sand-Gravel Dam Based on Elman Neural Network with Modified Particle Swarm Optimization. Front. Phys. 2022, 9, 806231. [Google Scholar] [CrossRef]
- Yao, Y.; Hu, T.; Fu, J.X.; Hu, S. Regression modeling and multi-objective optimization for small-sample dispersed data. J. Shanghai Univ. (Nat. Sci. Ed.) 2022, 28, 451–462. [Google Scholar]
- Fuller, W.B.; Thompson, S.E. The laws of proportioning concrete. Trans. Am. Soc. Civ. Eng. 1907, 59, 67–143. [Google Scholar] [CrossRef]
- Talbot, A.N.; Brown, H.A.; Richart, F.E. The Strength of Concrete: Its Relation to the Cement Aggregates and Water. Master’s Thesis, University of Illinois, Champaign, IL, USA, 1923. [Google Scholar]
- Swamee, P.K.; Ojha, C.S.P. Bed-load and suspended-load transport of nonuniform sediments. J. Hydraul. Eng. 1991, 117, 774–787. [Google Scholar] [CrossRef]
- Zhu, J.G.; Guo, W.L.; Wang, Y.L.; Wen, Y.F. Grading equation and its applicability for continuously graded soils. Chin. J. Geotech. Eng. 2015, 37, 1931–1936. [Google Scholar]
- DL/T 5356-2014; Test Code for Coarse-Grained Soils in Hydropower and Water Conservancy Engineering. China Electric Power Press: Beijing, China, 2014.
- Guo, W.L.; Zhu, J.G.; Wen, Y.F. Unified explanation of four gradation scaling methods for coarse-grained materials. Chin. J. Geotech. Eng. 2016, 38, 1473–1480. [Google Scholar]
- Huang, J.Y.; Bai, J.Q.; Xian, Y.H. DOD-LN-GPR model-based SOH estimation method for lithium-ion batteries. Acta Energiae Solaris Sin. 2025, 46, 60–69. [Google Scholar] [CrossRef]
- Akbari, M.A.; Zare, M.; Azizipanah-Abarghooee, R.; Mirjalili, S.; Deriche, M. The cheetah optimizer: A nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci. Rep. 2022, 12, 10953. [Google Scholar] [CrossRef]
- Wang, L.J.; Wang, Y.X.; Zhang, K.N.; Li, H.Y.; Zhang, W.X.; Zuo, S.K.; Lei, Z. Photovoltaic Power Prediction Based on Weather Scenario Dynamic Recognition Using CO-MHA-LSTM Model. South. Power Syst. Technol. 2025, 1–13. Available online: https://link.cnki.net/urlid/44.1643.TK.20250623.0911.012 (accessed on 21 September 2025).
- Wang, Y.X.; Cui, L.Q.; Tian, P.; Qin, K.; Zeng, X.L. Research on ECT image reconstruction method based on simulated annealing particle swarm optimization algorithm. Chin. J. Sens. Actuators 2024, 37, 484–491. [Google Scholar]
- Shao, L.S.; Wang, Z.; Li, C.M. Mine ventilation optimization algorithm based on simulated annealing and improved particle swarm optimization. J. Syst. Simul. 2021, 33, 2085–2094. [Google Scholar] [CrossRef]
- Meng, X.T.; Wang, W.; Xiang, Z. Dynamic compensation method for FOG navigation system based on particle swarm optimization and simulated annealing algorithm. Infrared Laser Eng. 2014, 43, 1555–1560. [Google Scholar]
- Hafez, A.A.; Abdelaziz, A.Y.; Hendy, M.A.; Ali, A.F. Optimal sizing of off-line microgrid via hybrid multi-objective simulated annealing particle swarm optimizer. Comput. Electr. Eng. 2021, 94, 107294. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5. [Google Scholar] [CrossRef]
- Sun, C.; Hu, R.Z.; Wu, Z.X.; Liu, N.S.; Ding, J.J. Research on Mixed Gas Detection Method Based on KNN-SVM. Spectrosc. Spectr. Anal. 2025, 45, 117–124. [Google Scholar]
- Wang, Y.; Shi, L.; Hu, X.; Song, W.; Wang, L. Multiphysics–informed neural networks for coupled soil hydrothermal modeling. Water Resour. Res. 2023, 59, e2022WR031960. [Google Scholar] [CrossRef]

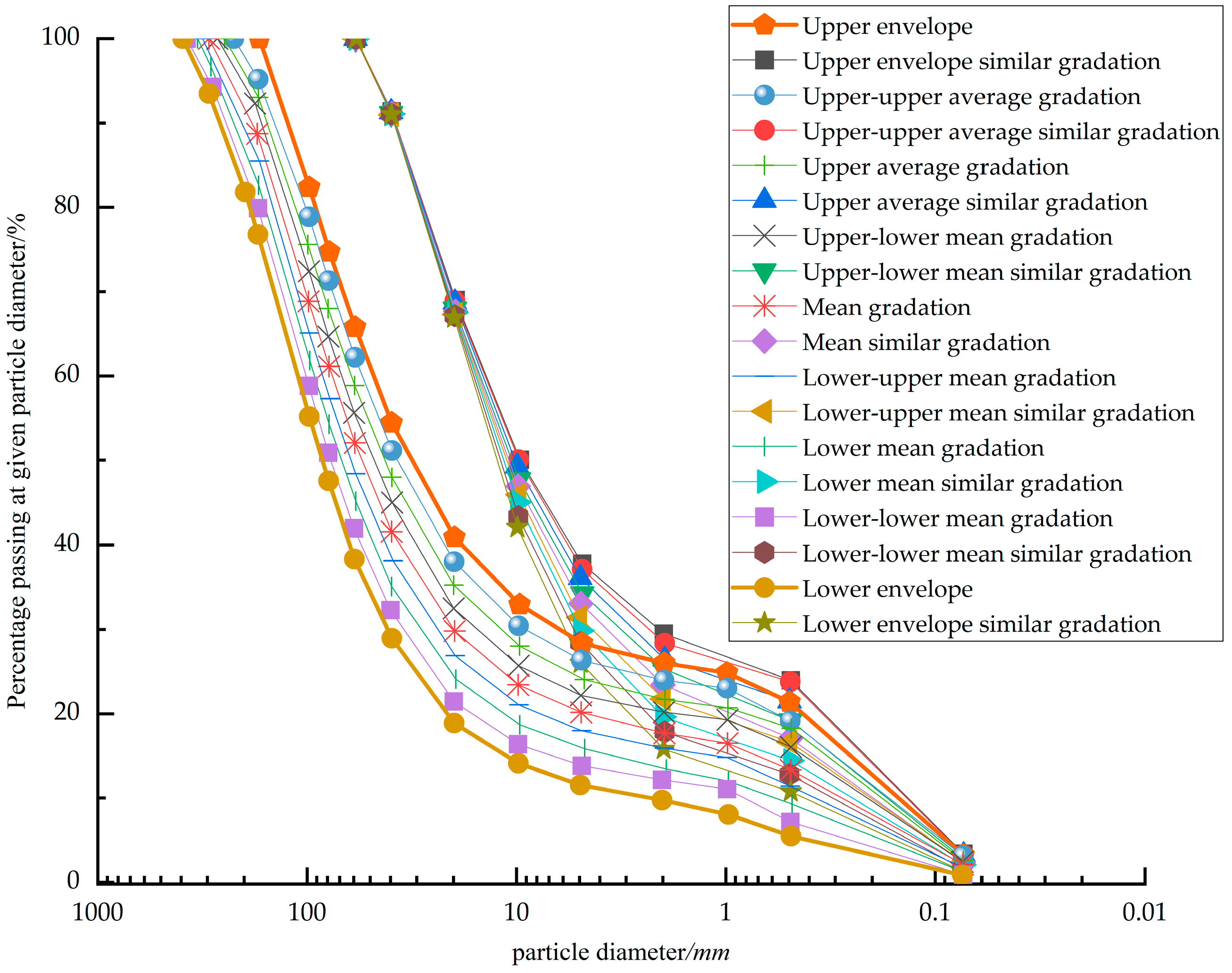

| No. | dmax /(mm) | P5 /(%) | m/(-) | b/(-) | S/(-) | ρdmax /(g·cm−3) | ρdmin /(g·cm−3) |
|---|---|---|---|---|---|---|---|
| 1 | 60 | 37.57 | 0.299 | −0.284 | 0.709 | 2.391 | 1.999 |
| 2 | 60 | 37.04 | 0.311 | −0.236 | 0.707 | 2.402 | 2.004 |
| 3 | 60 | 35.73 | 0.371 | 0.003 | 0.705 | 2.415 | 2.017 |
| 4 | 60 | 34.33 | 0.430 | 0.160 | 0.701 | 2.414 | 2.023 |
| 5 | 60 | 32.81 | 0.492 | 0.284 | 0.695 | 2.413 | 2.009 |
| 6 | 60 | 31.13 | 0.562 | 0.389 | 0.688 | 2.402 | 2.007 |
| 7 | 60 | 29.36 | 0.642 | 0.483 | 0.681 | 2.398 | 1.994 |
| 8 | 60 | 27.47 | 0.738 | 0.570 | 0.673 | 2.391 | 1.978 |
| 9 | 60 | 25.48 | 0.850 | 0.648 | 0.665 | 2.369 | 1.970 |
| Model Type | CO–SA–GPR | CO–SA–RF | CO–SA–SVM | CO–SA–ANN | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| ρdmax | 0.9752 | 0.0022 | 0.9251 | 0.0038 | 0.9096 | 0.0042 | 0.9080 | 0.0042 |
| ρdmin | 0.9714 | 0.0028 | 0.9674 | 0.0029 | 0.9692 | 0.0029 | 0.9535 | 0.0035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Li, J.; Zhao, Y.; Liu, B. Optimization of Gaussian Process Regression with Intelligent Algorithms for Predicting Compacted Density of Gravel-Soil Materials. Buildings 2025, 15, 3910. https://doi.org/10.3390/buildings15213910
Wang H, Li J, Zhao Y, Liu B. Optimization of Gaussian Process Regression with Intelligent Algorithms for Predicting Compacted Density of Gravel-Soil Materials. Buildings. 2025; 15(21):3910. https://doi.org/10.3390/buildings15213910
Chicago/Turabian StyleWang, Haijuan, Jiang Li, Yufei Zhao, and Biao Liu. 2025. "Optimization of Gaussian Process Regression with Intelligent Algorithms for Predicting Compacted Density of Gravel-Soil Materials" Buildings 15, no. 21: 3910. https://doi.org/10.3390/buildings15213910
APA StyleWang, H., Li, J., Zhao, Y., & Liu, B. (2025). Optimization of Gaussian Process Regression with Intelligent Algorithms for Predicting Compacted Density of Gravel-Soil Materials. Buildings, 15(21), 3910. https://doi.org/10.3390/buildings15213910






