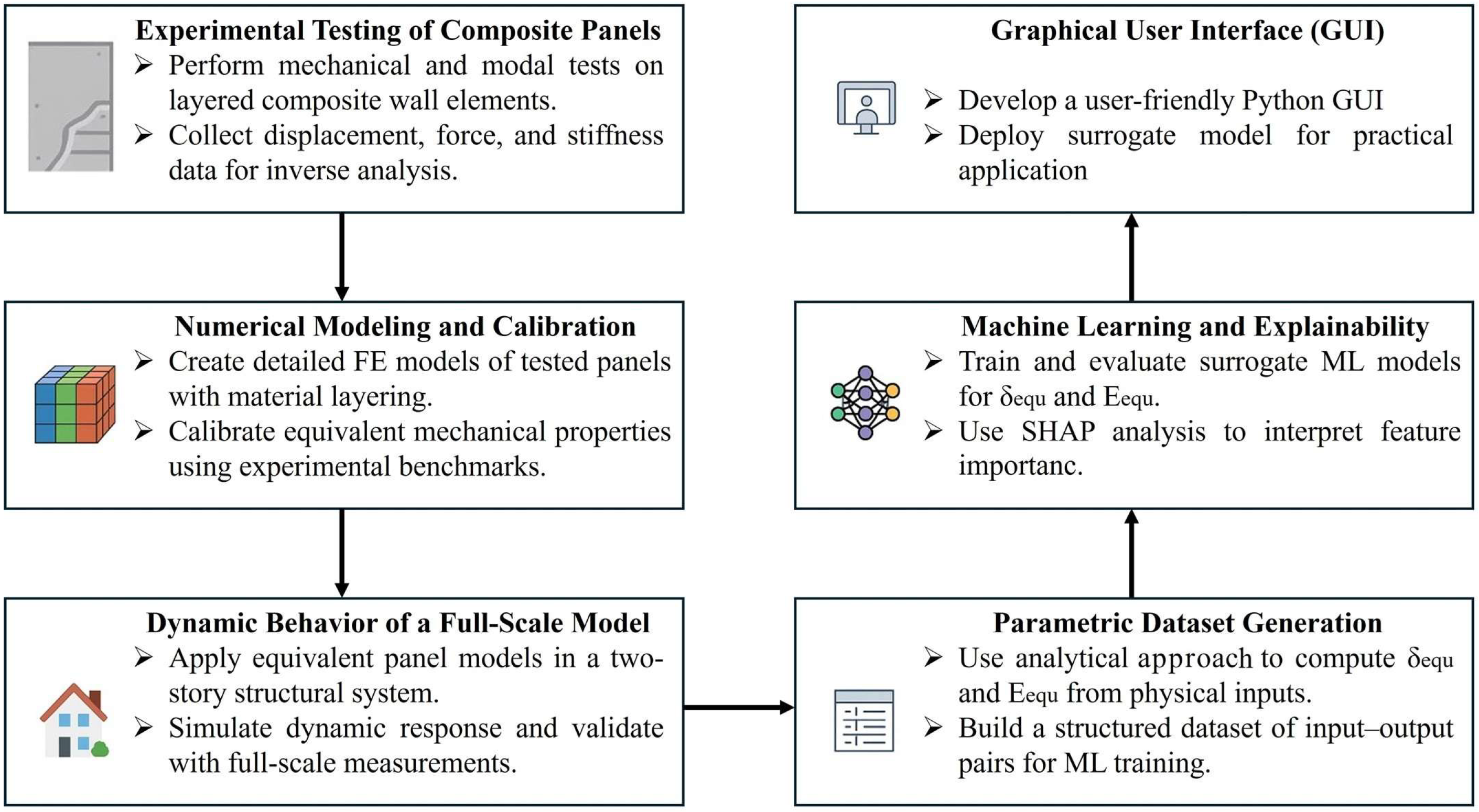
A Multi-Stage Framework Combining Experimental Testing, Numerical Calibration, and AI Surrogates for Composite Panel Characterization
Abstract
1. Introduction
Contributions and Novelty of the Study
- Integrated experimental–numerical–AI workflow: The study combines full-scale experimental testing, finite element calibration, analytical homogenization, and machine learning surrogate modeling within a single, reproducible framework.
- Closed-form homogenization formulation: A simplified analytical model is derived to compute the equivalent elastic modulus and thickness of layered concrete panels under combined bending and shear, validated against experiments and 3D FE simulations.
- Dynamic validation on a full-scale structure: The equivalent model is applied to simulate and replicate the dynamic behavior of a two-storey prototype building under vibrodyne excitation, confirming its predictive reliability.
- Surrogate modeling for design generalization: A machine learning surrogate trained on 218 parametric FE–analytical cases enables instant prediction of equivalent stiffness parameters from geometric and material inputs, reducing computational cost by several orders of magnitude.
- Deployment through an engineering-ready GUI: A user-accessible Streamlit interface translates the analytical–ML framework into a practical tool for engineers, allowing rapid prediction and data export without programming effort.
2. Experimental Characterization of Composite Panels
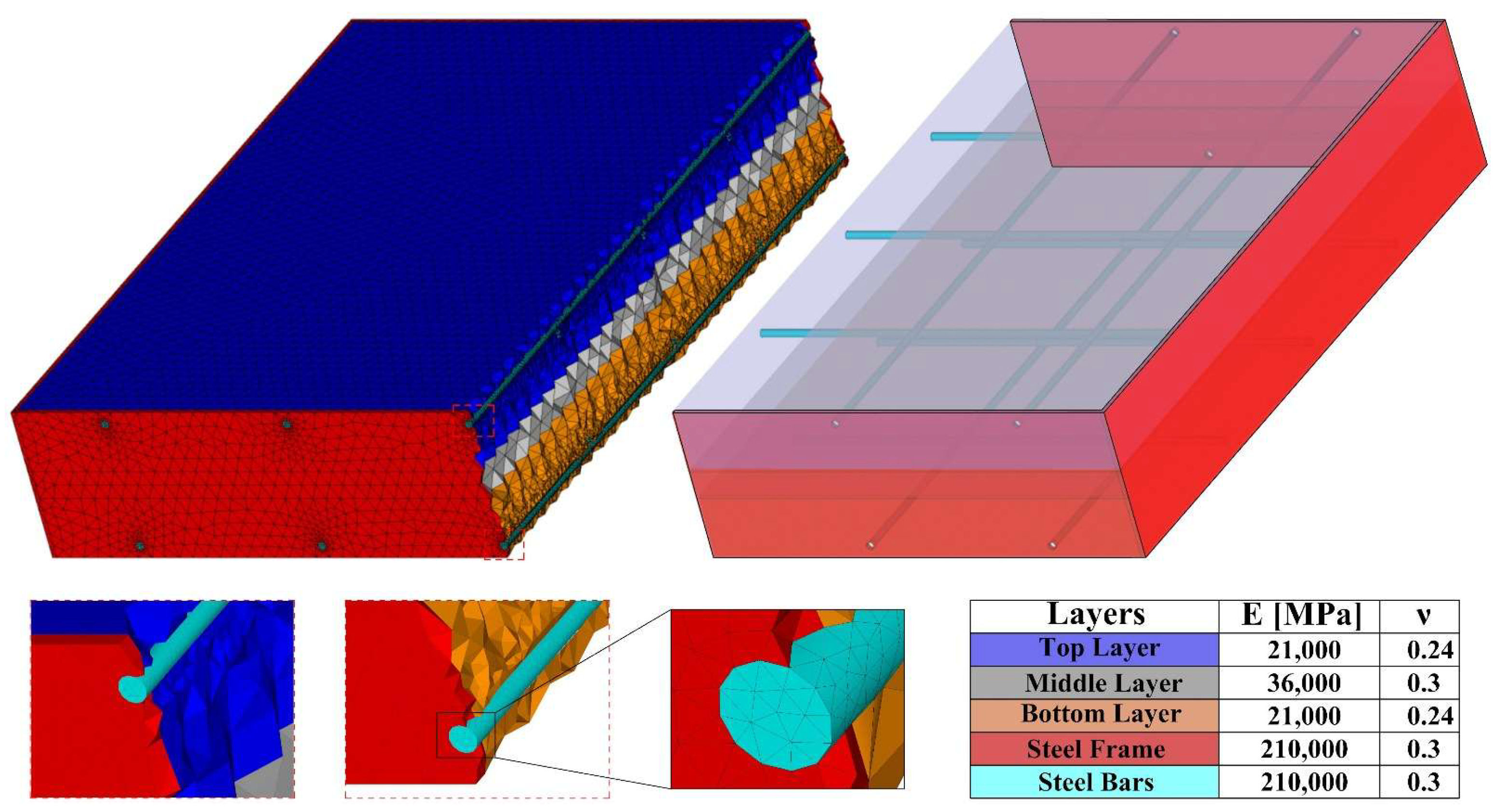
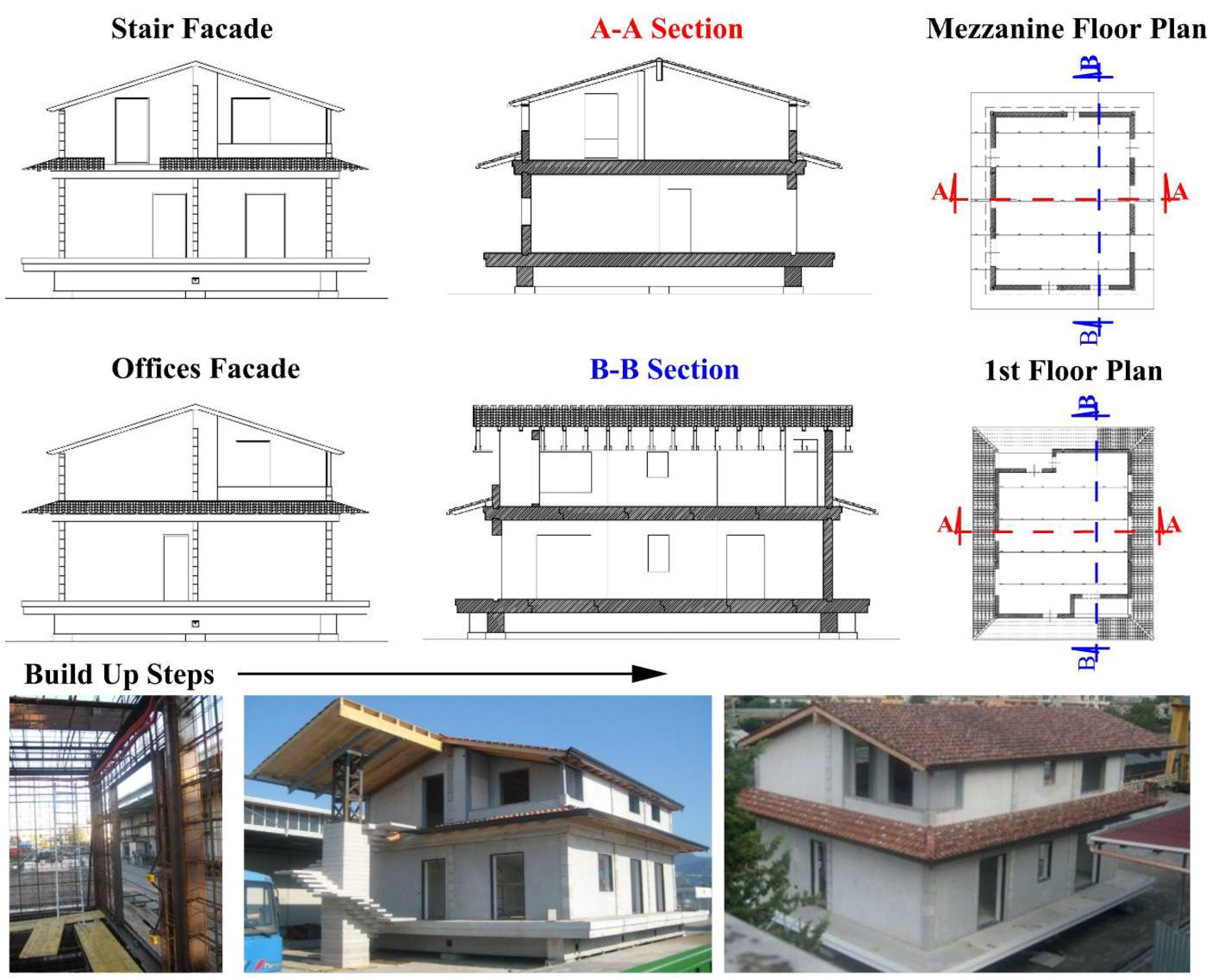
2.1. Panel Geometry and Materials
Sandwich Layer Configuration
2.2. Steel Frame and Reinforcement
- Five vertical bars (16 mm), spaced 400 mm apart (), are embedded along the height of the panel.
- Three horizontal bars (16 mm), spaced 375 mm apart (), are embedded along the panel width.
Material Properties
- Concrete: Characteristic compressive strength (), elastic modulus (), and Poisson’s ratio () for both lightweight and structural concrete layers.
- Steel: Yield strength (), elastic modulus, and Poisson’s ratio for both the perimeter frame and the embedded rebars. All materials were sourced from certified suppliers and comply with European standards for structural and prefabricated concrete components.
2.3. Experimental Setup and Instrumentation
- LVDT-1 and LVDT-2 were mounted symmetrically at the left and right support points, aligned along the panel’s mid-span. These sensors recorded the vertical movements at the supports, enabling the estimation of rigid-body displacement components due to boundary compliance or localized rotations.
- LVDT-3 was positioned at the geometric center of the panel, aligned with the loading point. This transducer measured the central deflection and served as the primary indicator of the panel’s flexural response.
2.4. Test Procedure and Key Observations
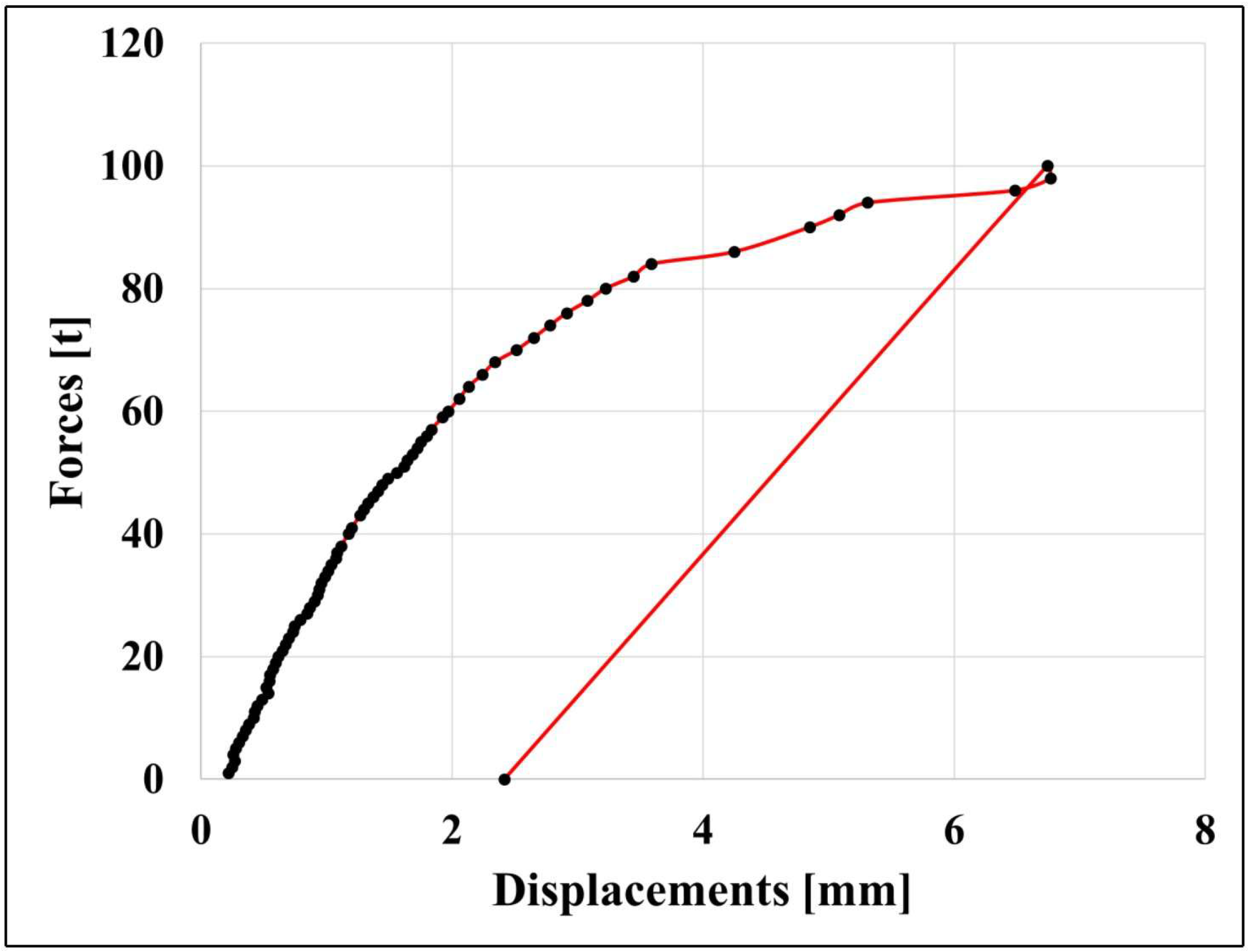
2.5. Bending Test
2.6. Shear Test
- The panel exhibited robust structural behavior under both bending and shear loads, with well-defined elastic regions and controlled post-yield deformation.
- The steel frame and internal reinforcement effectively limited excessive cracking and ensured ductility, even beyond the elastic threshold.
- The multi-layer composite design provided a favorable combination of stiffness, energy dissipation, and lightweight performance, confirming its suitability for modular structural applications.
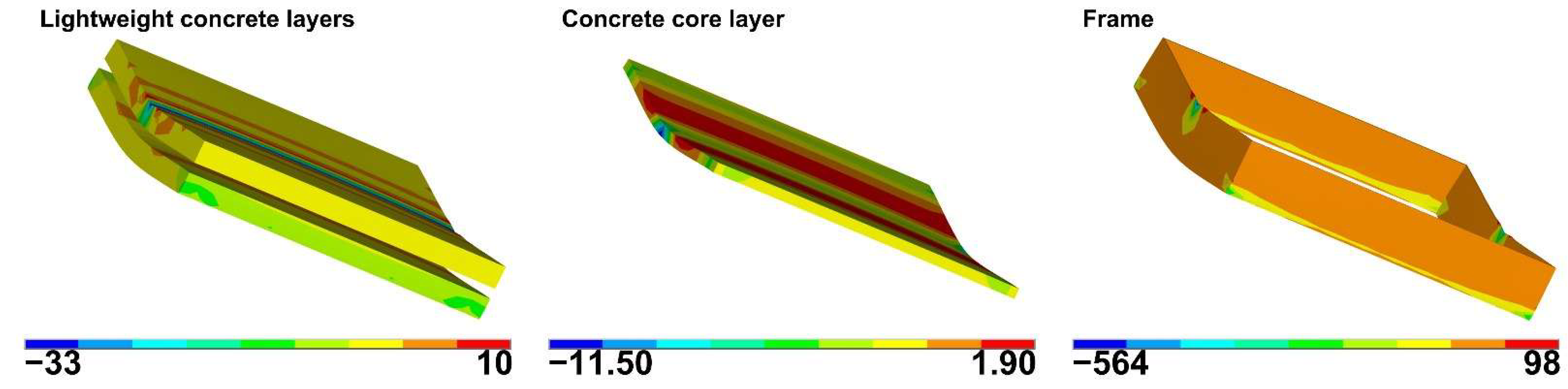
3. Numerical Modelling and Calibration
3.1. Finite Element Model Description
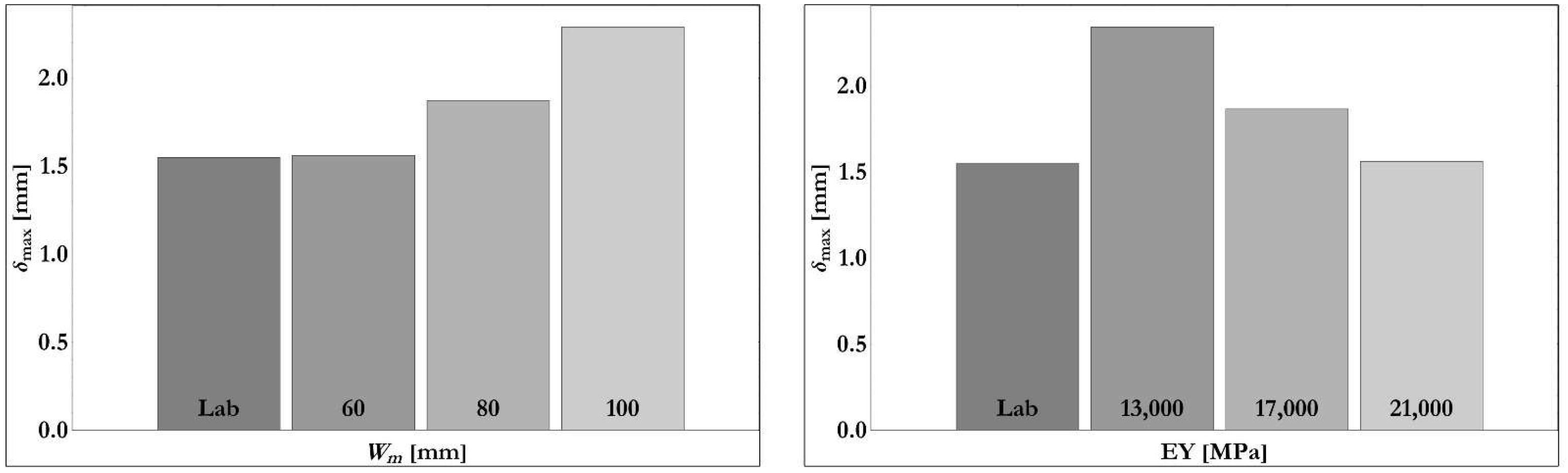
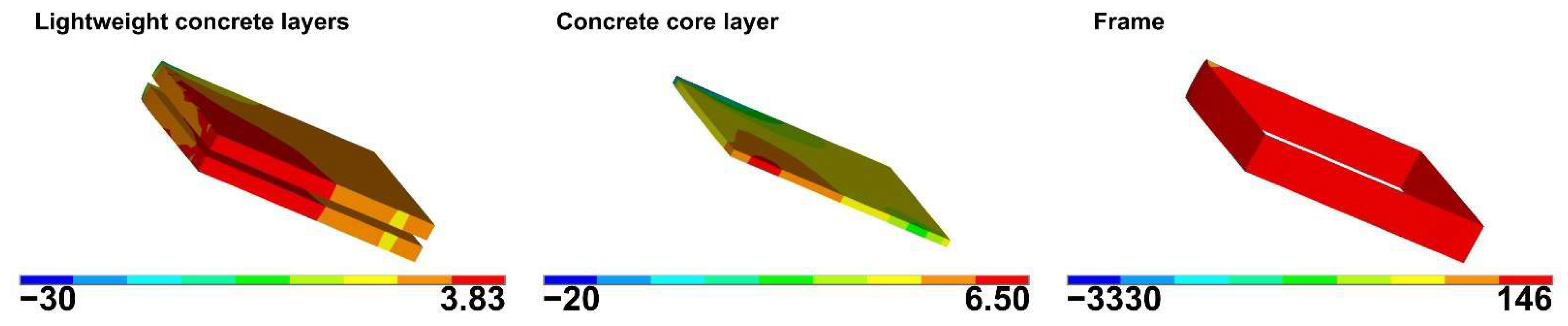
3.2. Model Calibration Using Experimental Data
3.2.1. Numerical vs. Experimental Comparison: Bending Test
- The thickness of the concrete core, Wm, from 60 mm to 100 mm in 20 mm increments;
- The Young’s modulus of the lightweight concrete layers from 13,000 MPa to 21,000 MPa in 4000 MPa increments.
3.2.2. Numerical vs. Experimental Comparison: Shear Test
3.3. Derivation of Equivalent Homogeneous Panel
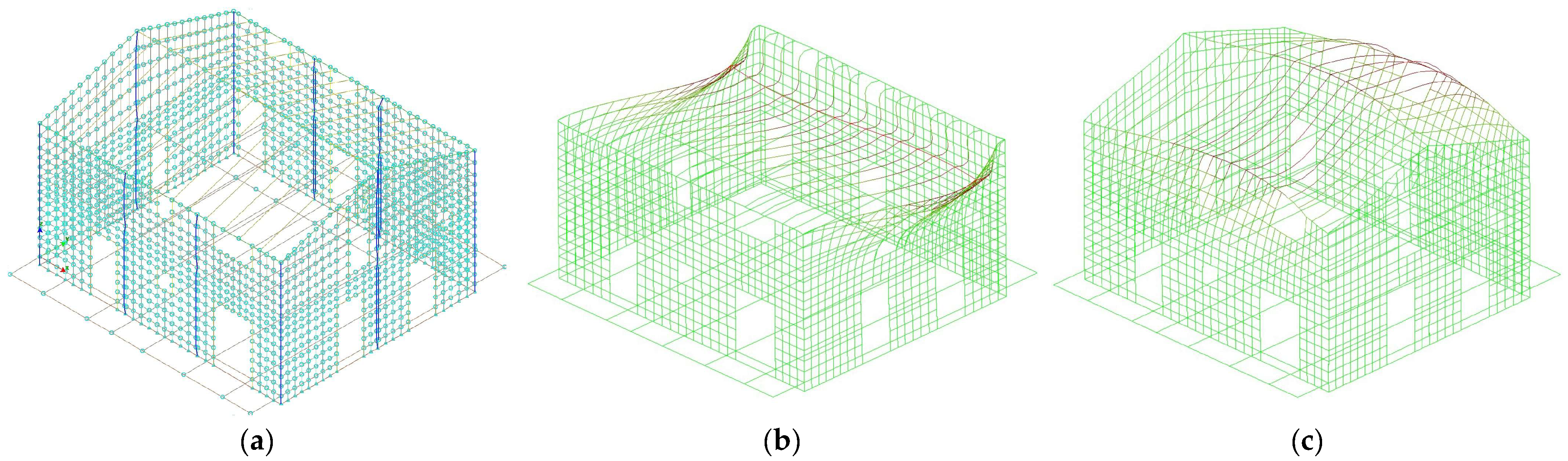
4. Dynamic Behavior of Full-Scale Building Model
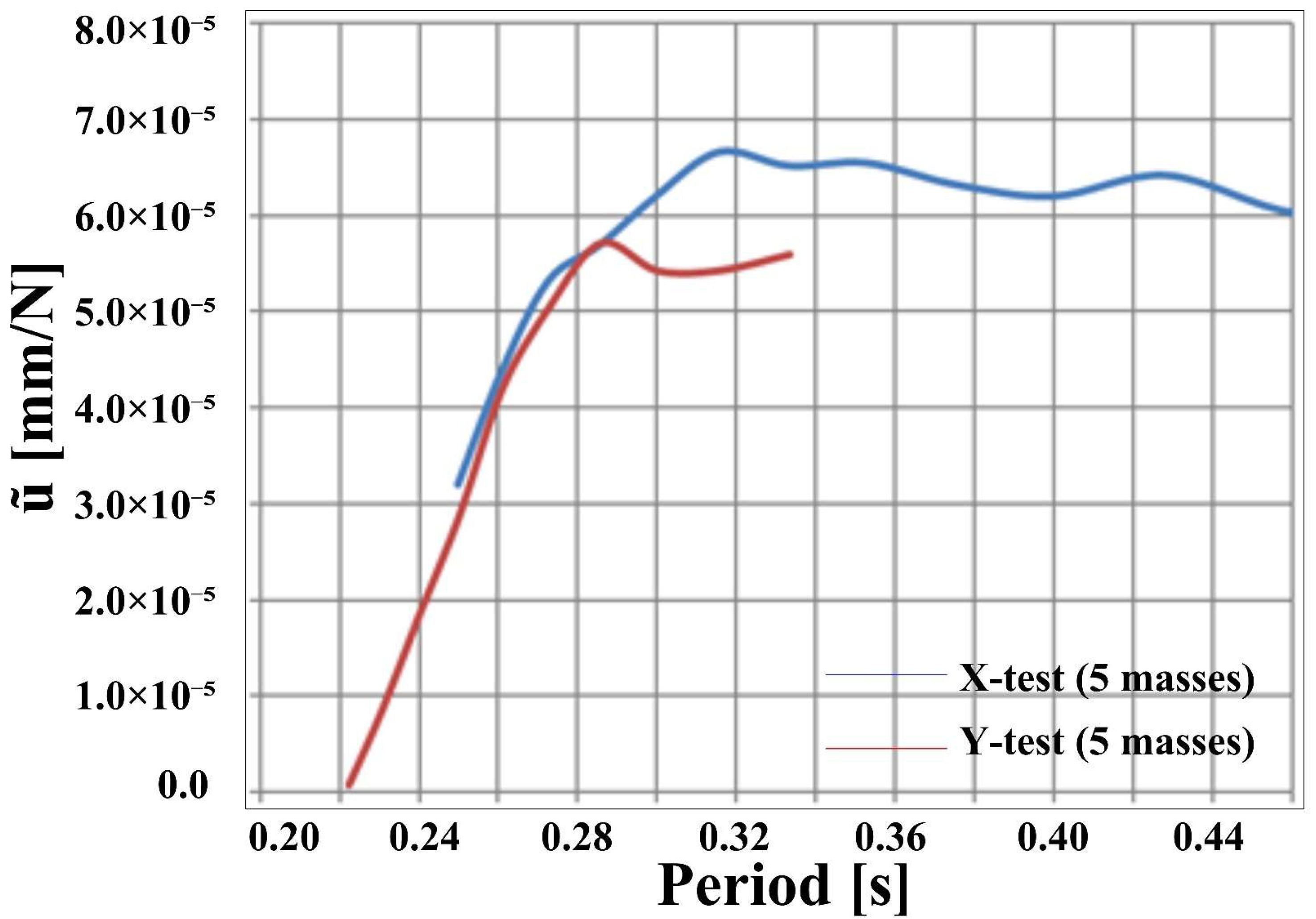
4.1. Dynamic Simulation Using Equivalent Panels
4.2. Comparison of Simulated and Experimental Response
5. Parametric Dataset Generation
6. Machine Learning Surrogate Modeling
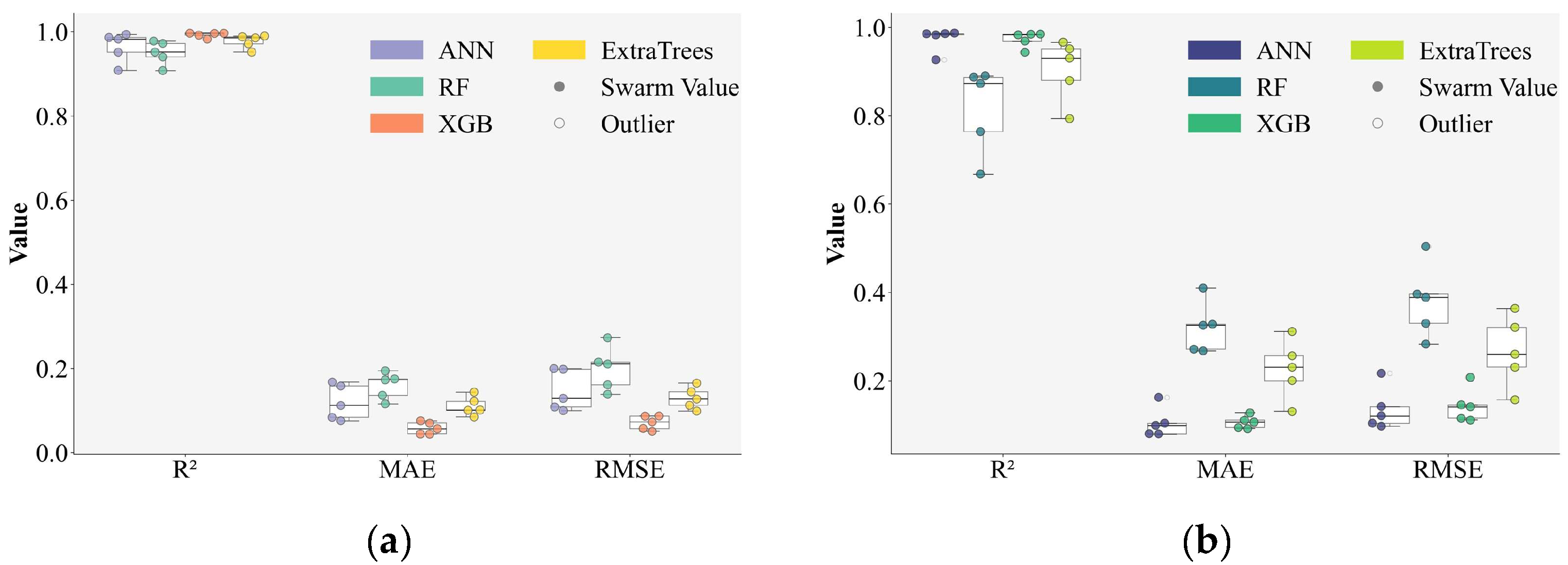
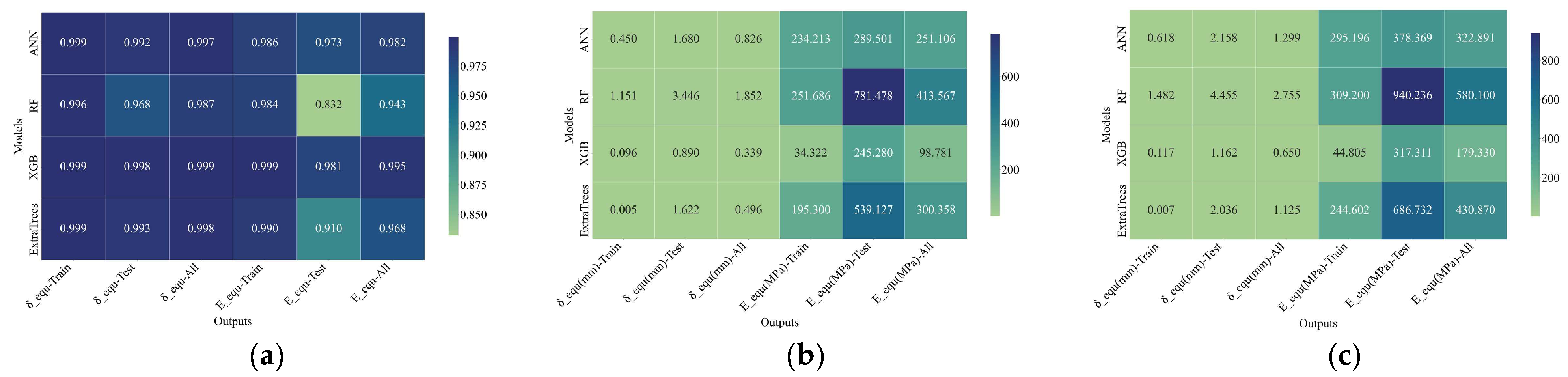
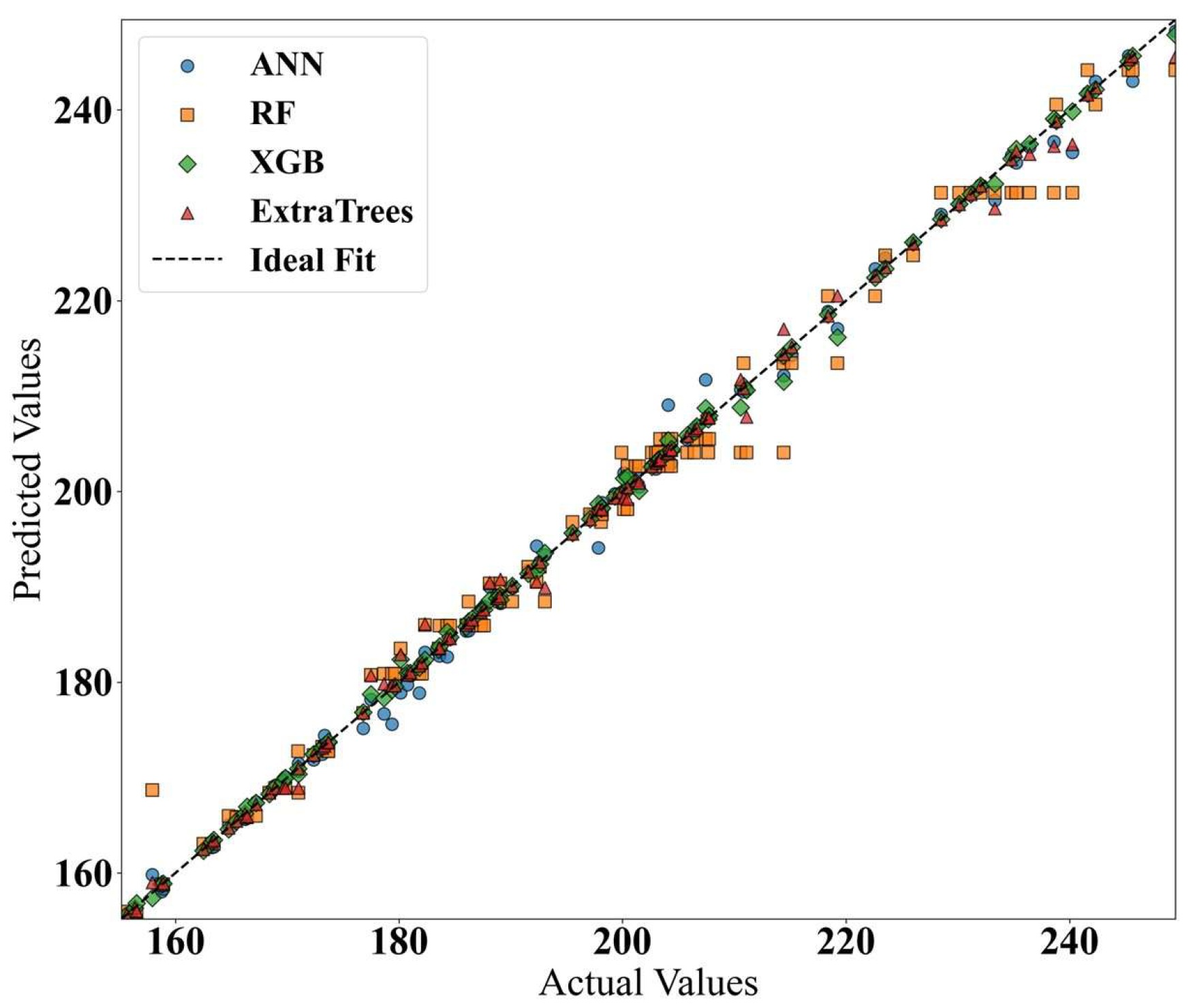
6.1. Data Preparation, Scaling, and Machine Learning Algorithms
6.2. Model Training and Evaluation Strategy
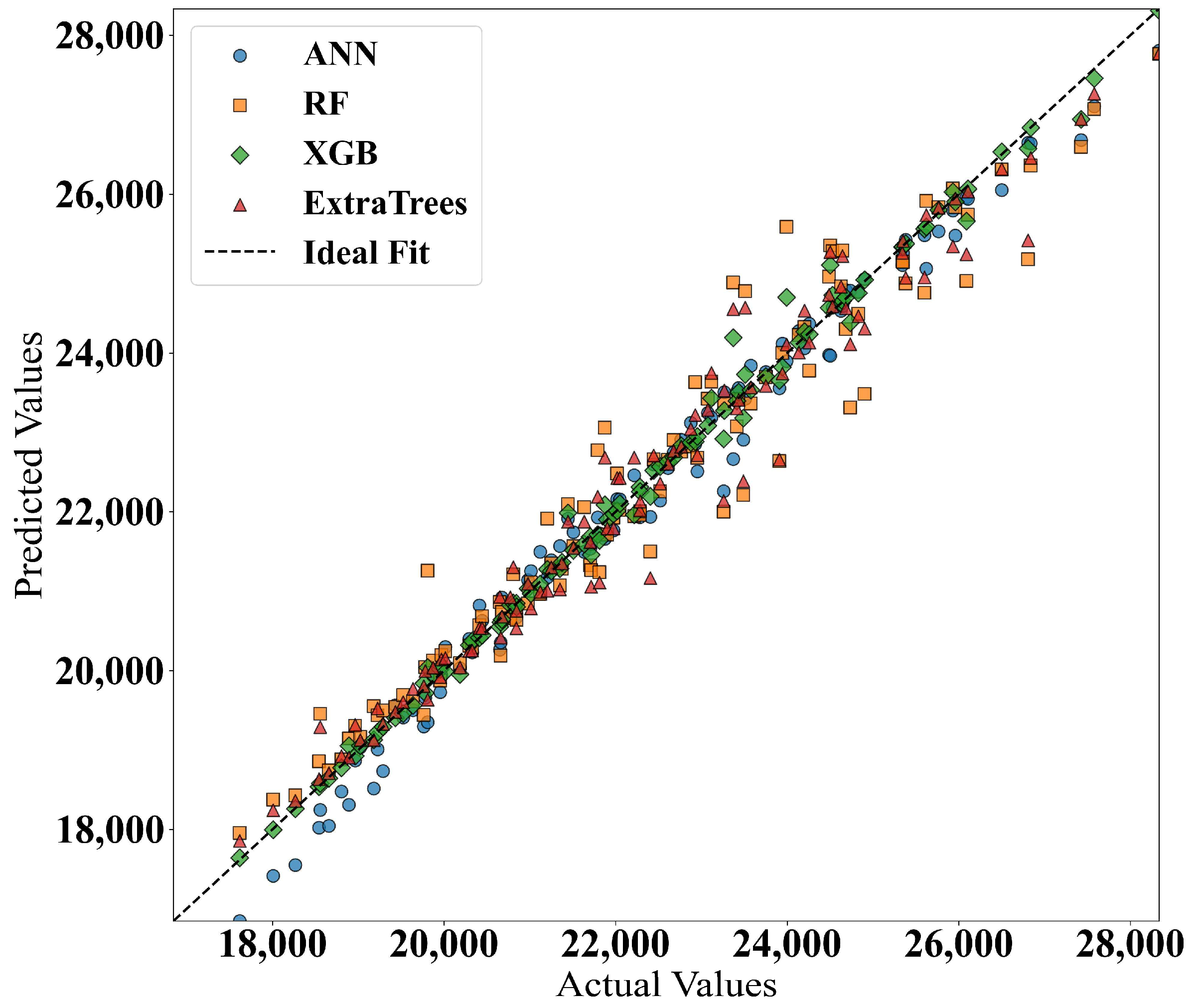
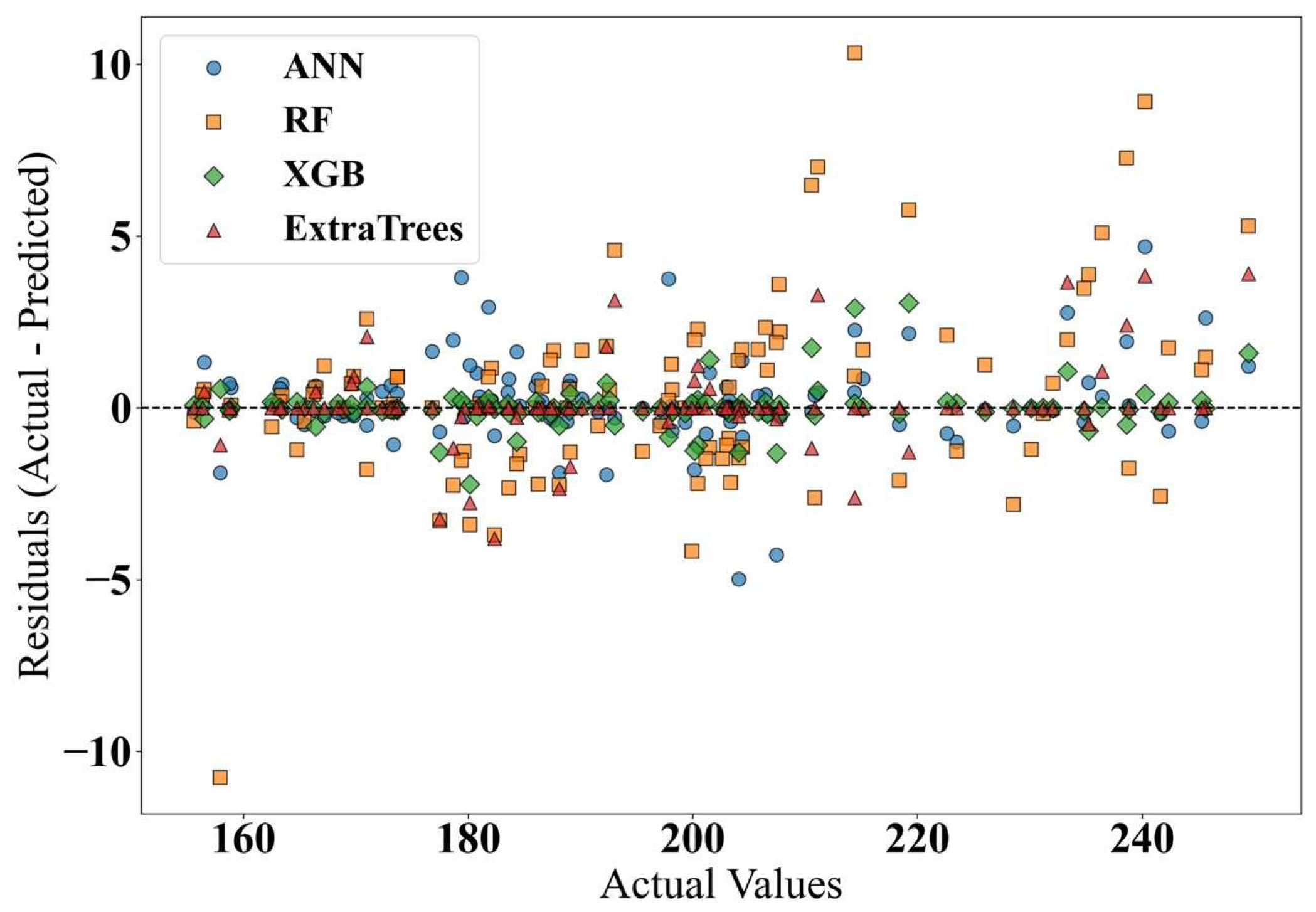
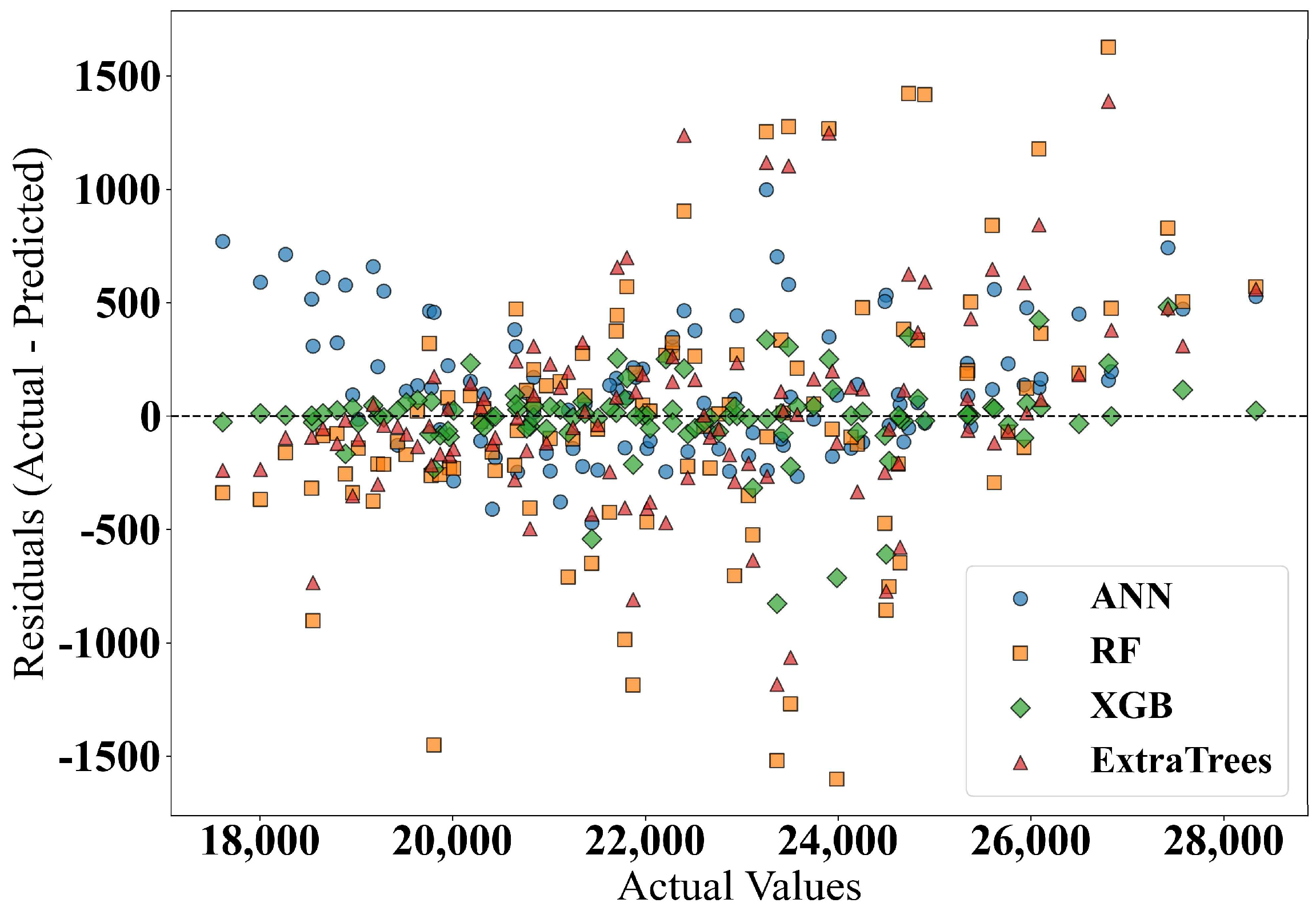
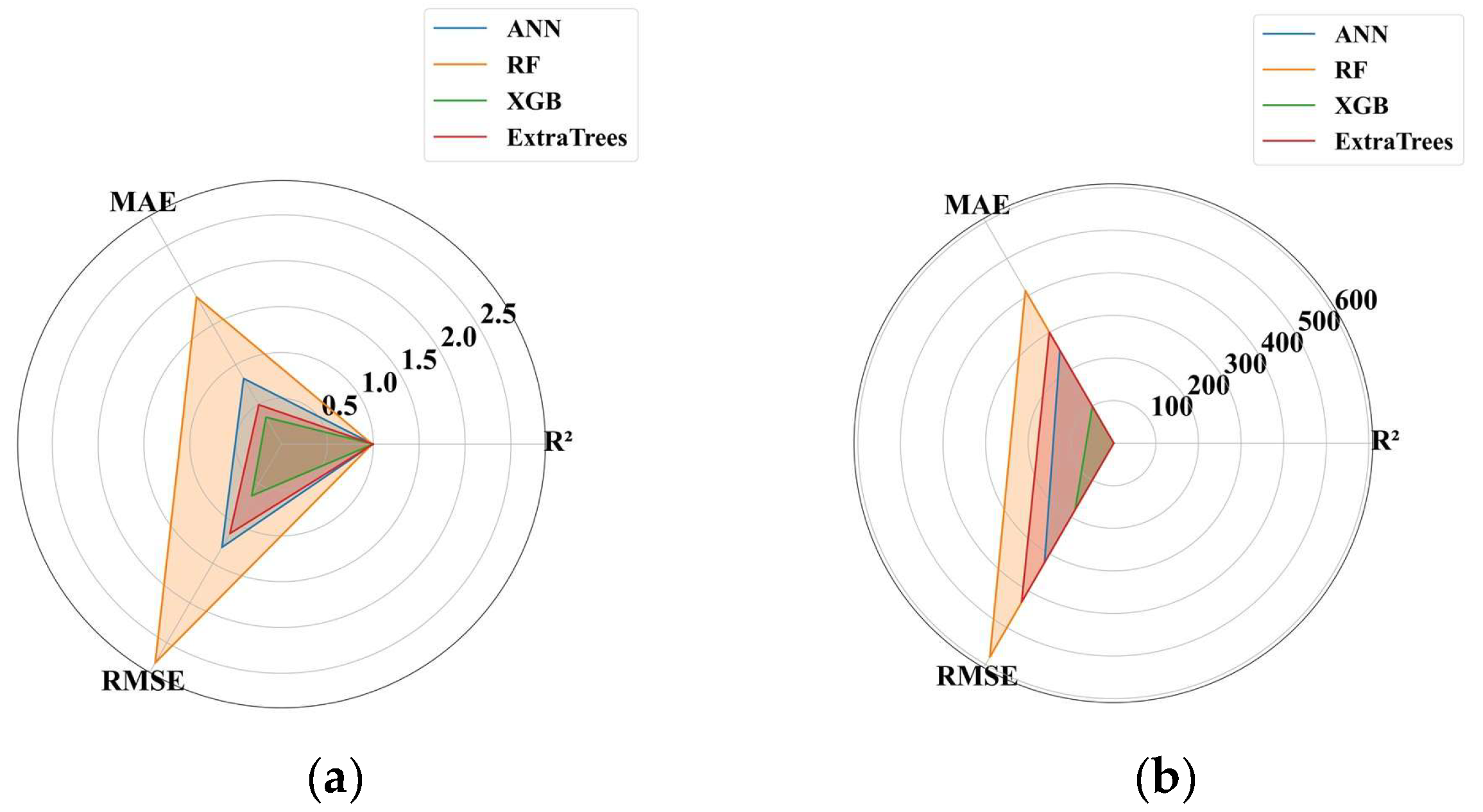
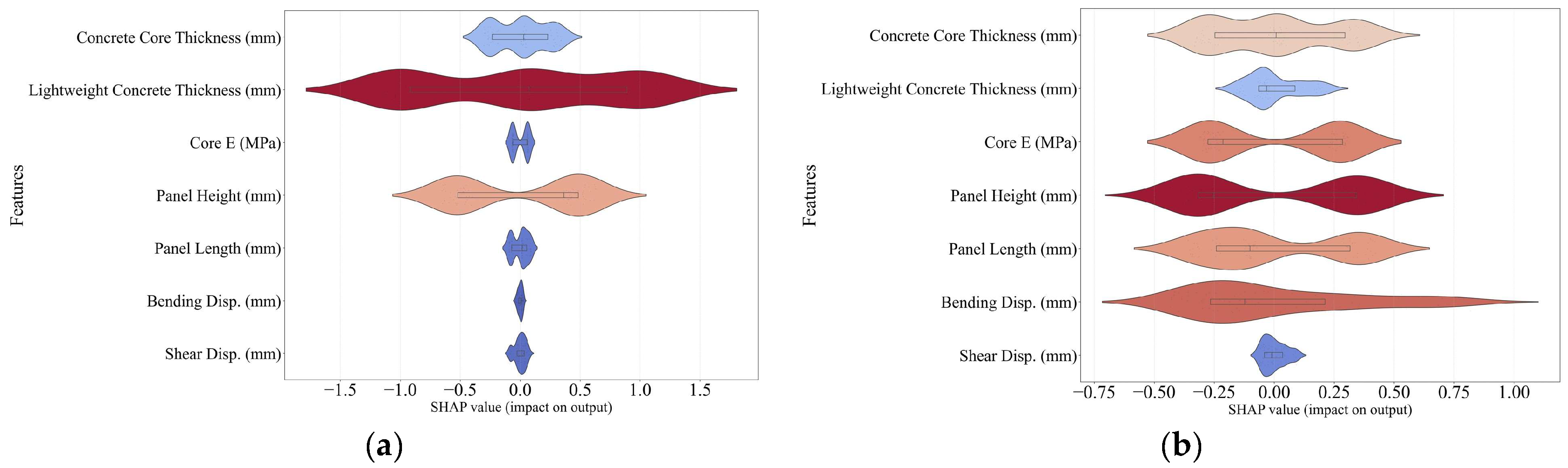
6.3. Machine Learning Analysis Results
7. Graphical Interface for Predicting Equivalent Structural Properties
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Silva, C.W. Vibration Monitoring, Testing, and Instrumentation; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Cennamo, C.; Gesualdo, A.; Monaco, M. Shear plastic constitutive behavior for near-fault ground motion. J. Eng. Mech. 2017, 143, 04017086. [Google Scholar] [CrossRef]
- Palladino, S.; Esposito, L.; Ferla, P.; Totaro, E.; Zona, R.; Minutolo, V. Experimental and numerical evaluation of residual displacement and ductility in ratcheting and shakedown of an aluminum beam. Appl. Sci. 2020, 10, 3610. [Google Scholar] [CrossRef]
- Zona, R.; Esposito, L.; Ferla, P.; Palladino, S.; Totaro, E.; Minutolo, V. Lower bound limit analysis of parabolic domes based on spherical analytical solution. Int. J. Adv. Res. Eng. Technol. 2020, 11, 59–79. [Google Scholar]
- Lalanne, C. Sinusoidal Vibration; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S.; Zhou, Y.; Wu, W.; Tu, L.; Liu, J. Calibrating nonlinearity coefficients of a nano-g accelerometer by dual-frequency excitation on a shaker. Measurement 2024, 225, 114016. [Google Scholar] [CrossRef]
- Yang, M.; Phung, B.T. Motor winding insulation degradation under repetitive voltage pulses. IEEE Access 2024, 12, 77658–77674. [Google Scholar] [CrossRef]
- Dash, B.; Mahapatra, T.R.; Mishra, P.; Mishra, D.; Mahmoud, S.R. A Review of Computational Methods for Vibroacoustic Analysis of Advanced Material Structures. Arch. Comput. Methods Eng. 2025, 32, 2187–2211. [Google Scholar] [CrossRef]
- Jefferson, A.; Sain, M.; Ramakrishna, S.; Jawaid, M.; Dhakal, H.N. Environmentally friendly fire retardant natural fibre composites: A review. Int. Mater. Rev. 2024, 69, 267–308. [Google Scholar] [CrossRef]
- Bocheński, M.; Gawryluk, J.; Kłoda, L. Experimental modal analysis of an active thin-walled composite structure. Model. Meas. Control B 2019, 88, 154–159. [Google Scholar] [CrossRef]
- Pourkamali-Anaraki, F.; Husseini, J.F.; Pineda, E.J.; Bednarcyk, B.A.; Stapleton, S.E. Two-stage surrogate modeling for data-driven design optimization with application to composite microstructure generation. Eng. Appl. Artif. Intell. 2024, 138, 109436. [Google Scholar] [CrossRef]
- Husseini, J.; Stapleton, S.; Carey, E.; Pineda, E.J. Microscale Constitutive Model Sensitivity on Multiscale Modeling of Fiber Reinforced Composites. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 1155. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G.; Cosenza, E. Automated Operational Modal Analysis as structural health monitoring tool: Theoretical and applicative aspects. Key Eng. Mater. 2007, 347, 479–484. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G.; Cosenza, E.; Manfredi, G. Implementation of OMA procedures using LabVIEW: Theory and application. In Proceedings of the 2nd International Operational Modal Analysis Conference, Copenhagen, Denmark, 30 April–2 May 2007; Volume 30, pp. 1–13. [Google Scholar]
- Esposito, L.; Palladino, S.; Minutolo, V. An effective free-meshing and linear Step-Wise procedure to predict crack initiation and propagation. Theor. Appl. Fract. Mech. 2024, 130, 104240. [Google Scholar] [CrossRef]
- Arndt, C.; Crusenberry, C.; Heng, B.; Butler, R.; TerMaath, S. Reduced-dimension surrogate modeling to characterize the damage tolerance of composite/metal structures. Modelling 2023, 4, 485–514. [Google Scholar] [CrossRef]
- Dashtgoli, D.S.; Taghizadeh, S.; Macconi, L.; Concli, F. Comparative analysis of machine learning models for predicting the mechanical behavior of bio-based cellular composite sandwich structures. Materials 2024, 17, 3493. [Google Scholar] [CrossRef] [PubMed]
- Viotti, I.D.; Gomes, G.F. Delamination identification in sandwich composite structures using machine learning techniques. Comput. Struct. 2023, 280, 106990. [Google Scholar] [CrossRef]
- Kamarian, S.; Teimouri, A.; Alinia, M.; Saber-Samandari, S.; Song, J.I. Machine learning for bending behavior of sandwich beams with 3D-printed core and natural fiber-reinforced composite face sheets. Polym. Compos. 2024, 45, 3043–3054. [Google Scholar] [CrossRef]
- Mottaghian, F.; Taheri, F. Machine learning/finite element analysis—A collaborative approach for predicting the axial impact response of adhesively bonded joints with unique sandwich composite adherends. Compos. Sci. Technol. 2023, 242, 110162. [Google Scholar] [CrossRef]
- Vaishali; Mukhopadhyay, T.; Naskar, S.; Dey, S. On machine learning assisted data-driven bridging of FSDT and HOZT for high-fidelity uncertainty quantification of laminated composite and sandwich plates. Compos. Struct. 2023, 304, 116276. [Google Scholar] [CrossRef]
- Khan, A.; Kim, N.; Shin, J.K.; Kim, H.S.; Youn, B.D. Damage assessment of smart composite structures via machine learning: A review. JMST Adv. 2019, 1, 107–124. [Google Scholar] [CrossRef]
- Ribeiro, R.F., Jr.; Gomes, G.F. On the use of machine learning for damage assessment in composite structures: A review. Appl. Compos. Mater. 2024, 31, 1–37. [Google Scholar] [CrossRef]
- Modano, M.; Albo, N.; Fulgione, M.; Spizzuoco, M. Dynamical Characterization of an Innovative Building System. In Proceedings of the GIMC-SIMAI Workshop for Young Scientists, Naples, Italy, 10–12 July 2024; Springer: Cham, Switzerland, 2024; pp. 113–122. [Google Scholar]
- Modano, M.; Fabbrocino, F.; Gesualdo, A.; Matrone, G.; Farina, I.; Fraternali, F. On the forced vibration test by vibrodyne. In Proceedings of the COMPDYN 2015—5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015; pp. 209–217. [Google Scholar]
- Modano, M.; Gesualdo, A.; Mascolo, I.; Farina, I. Dynamic testing and structural identification of innovative network structures. In Proceedings of the Atti del XXIII Convegno AIMETA, Salerno, Italy, 4–7 September 2017; Volume 3, pp. 1205–1213. [Google Scholar]
- Palladino, S.; Fraldi, M.; Minutolo, V.; Esposito, L. Steering Cracks Via Auxetic Zebra-Composites. SSRN 2025. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Fakhraddini, A.; Modaresahmadi, K. Evaluation of panel zone shear strength in cruciform columns, box-columns and double web-columns. Int. J. Struct. Civ. Eng. Res. 2016, 5, 52–56. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Saffari, H.; Fakhraddini, A. Shear Behavior of Panel Zone Considering Axial Force for Flanged Cruciform Columns. Civ. Eng. Infrastruct. J. 2020, 53, 359–377. [Google Scholar]
- Hu, X.; Yu, S.; Li, Y.; Liu, R.; Yu, J. Research on the influencing mechanisms of ice-filled fissures on the failure processes of tunnel specimens. Theor. Appl. Fract. Mech. 2025, 139, 105141. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, S.; Yu, J.; Li, Y.; Xu, H.; Huang, Q. Investigating the interaction mechanisms between fissures and layers of SCB specimens using a novel layer 3D printing technology and DEM. Theor. Appl. Fract. Mech. 2025, 139, 105044. [Google Scholar] [CrossRef]
- Mascolo, I.; Sarfarazi, S.; Modano, M. Feasible and robust optimisation of cable forces in suspended bridges: A two-stage metaheuristic approach. Mech. Res. Commun. 2025, 104, 104554. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Abdel-aziem, A.H.; Soliman, T.H.M. A multi-layer perceptron (MLP) neural networks for stellar classification: A review of methods and results. Int. J. Adv. Appl. Comput. Intell. 2023, 3, 29–37. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Mascolo, I.; Modano, M.; Guarracino, F. Application of Artificial Intelligence to Support Design and Analysis of Steel Structures. Metals 2025, 15, 408. [Google Scholar] [CrossRef]
- Sazlı, M.H. A brief review of feed-forward neural networks. Commun. Fac. Sci. Univ. Ank. Ser. A2–A3 Phys. Sci. Eng. 2006, 50. [Google Scholar] [CrossRef]
- Rabi, M.; Abarkan, I.; Sarfarazi, S.; Ferreira, F.V.; Alkherret, A.J. Automated design and optimization of concrete beams reinforced with stainless steel. Struct. Concr. 2025; early view. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Shamass, R.; Guarracino, F.; Mascolo, I.; Modano, M. Exploring the stainless-steel beam-to-column connections response: A hybrid explainable machine learning framework for characterization. Front. Struct. Civ. Eng. 2025, 19, 34–59. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Shamass, R.; Guarracino, F.; Mascolo, I.; Modano, M. Advanced predictive modeling of shear strength in stainless-steel column web panels using explainable AI insights. Results Eng. 2024, 24, 103454. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Streamlit. Streamlit Platform Documentation. 2025. Available online: https://streamlit.io (accessed on 14 July 2025).
- Sarnafazi, S. Characterization of an Innovative Composite Structural Element App. 2025. Available online: https://characterization-of-an-innovative-composite-structural-element.streamlit.app/ (accessed on 12 July 2025).
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Wang, Y.; Bwar, K.H.; Zhang, K. Review of approaches to minimise the cost of simulation-based optimisation for liquid composite moulding processes. Materials 2023, 16, 7580. [Google Scholar] [CrossRef]






| [MPa] | [MPa] | ||
|---|---|---|---|
| Top Layer | 20 | 21,000 | 0.24 |
| Middle Layer | 35 | 36,000 | 0.30 |
| Bottom Layer | 20 | 21,000 | 0.24 |
| [MPa] | [MPa] | |
|---|---|---|
| 450 | 210,000 | 0.30 |
| Parameter | Range/Value | Unit | Description |
|---|---|---|---|
| Period | 0.28–0.32 | s | Range of dominant vibration periods identified during testing |
| Main frequency | 3.15 | Hz | Fundamental excitation frequency of the vibrodyne system |
| Maximum acceleration | 0.20 | m/s2 | Peak acceleration recorded during harmonic excitation |
| Maximum displacement | 0.32 | mm | Maximum measured displacement at resonance |
| Sampling rate | 200 | Hz | Data acquisition rate of the vibrodyne sensors |
| Instrument accuracy | ±0.01 | mm | Accuracy of displacement sensors (LVDTs) |
| Category | Parameter (Symbol) | Unit | Range/Levels | Physical Role |
|---|---|---|---|---|
| Geometry | Panel height (H), length (L), core thickness (tm), face thickness (tt = tb) | mm | H: 1500–2800; L: 2000–2800; tm: 60–100; tt: 100–160 | Define global slenderness and bending–shear contribution |
| Material | Core modulus (Em), face modulus (Et = Eb) | MPa | Em: 30,000–36,000; Et: 13,000–21,000 | Control stiffness contrast and flexural rigidity |
| Reinforcement | Bar diameter (Φ), vertical spacing (iL), horizontal spacing (iH) | mm | Φ: 12–20; iL: 200–400; iH: 300–400 | Influence stiffness, ductility, and crack control |
| Outputs | Bending and shear displacements (ub, us) → Equivalent properties (Eeq, δeq) | – | Extracted from FE response | Serve as target quantities for surrogate training |
| Model | Hyperparameter | Search Space | Final Selected Value |
|---|---|---|---|
| ANN | Hidden Layers | (64, 32), (128, 64, 32), (256, 128, 64) | (256, 128, 64) |
| Learning Rate Init | 0.001, 0.01, 0.1 | 0.001 | |
| Alpha (L2 penalty) | 0.0001, 0.001, 0.01 | 0.0001 | |
| RF | n-estimators | 100, 200, 300 | 100 |
| max-depth | None, 5, 10, 20 | 10 | |
| min-samples-split | 2, 10, 20 | 10 | |
| min-samples-leaf | 1, 5, 10 | 1 | |
| Bootstrap | True, False | True | |
| XGBoost | colsample-bytree | 0.8, 1.0, 1.2 | 0.8 |
| Gamma | 0, 0.01, 0.1 | 0 | |
| learning-rate | 0.01, 0.1, 0.2, 0.3 | 0.2 | |
| max-depth | 2, 4, 6 | 2 | |
| min-child-weight | 1, 4, 7 | 4 | |
| n-estimators | 50, 100, 200 | 200 | |
| reg-alpha | 0.01, 0.1, 1.0 | 0.01 | |
| reg-lambda | 0, 0.001, 0.01, 0.1 | 0.001 | |
| Subsample | 0.8, 1.0, 1.2 | 0.8 | |
| ExtraTrees | n-estimators | 100, 200, 300 | 200 |
| max-depth | None, 10, 20, 30 | None | |
| min-samples-split | 2, 10, 20 | 2 | |
| min-samples-leaf | 1, 4, 10 | 1 | |
| Bootstrap | False, True | True |
| Metric | Formula | Description |
|---|---|---|
| Proportion of variance in the observed data explained by the model. | ||
| MAE | MAE quantifies the average absolute difference between predicted and actual values. | |
| RMSE | Reflects the square root of the average squared differences. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fulgione, M.; Palladino, S.; Esposito, L.; Sarfarazi, S.; Modano, M. A Multi-Stage Framework Combining Experimental Testing, Numerical Calibration, and AI Surrogates for Composite Panel Characterization. Buildings 2025, 15, 3900. https://doi.org/10.3390/buildings15213900
Fulgione M, Palladino S, Esposito L, Sarfarazi S, Modano M. A Multi-Stage Framework Combining Experimental Testing, Numerical Calibration, and AI Surrogates for Composite Panel Characterization. Buildings. 2025; 15(21):3900. https://doi.org/10.3390/buildings15213900
Chicago/Turabian StyleFulgione, Marcello, Simone Palladino, Luca Esposito, Sina Sarfarazi, and Mariano Modano. 2025. "A Multi-Stage Framework Combining Experimental Testing, Numerical Calibration, and AI Surrogates for Composite Panel Characterization" Buildings 15, no. 21: 3900. https://doi.org/10.3390/buildings15213900
APA StyleFulgione, M., Palladino, S., Esposito, L., Sarfarazi, S., & Modano, M. (2025). A Multi-Stage Framework Combining Experimental Testing, Numerical Calibration, and AI Surrogates for Composite Panel Characterization. Buildings, 15(21), 3900. https://doi.org/10.3390/buildings15213900







