Axial Compressive Behavior of Square Double-Skin Hybrid Concrete Bar Columns with Small-Diameter Concrete-Infilled GFRP Tubes

Abstract

With the increasing demand for lightweight, high-strength, and ductile structural systems in modern infrastructure, the hybrid composite column has emerged as a promising solution to overcome the limitations of single-material members. This paper proposes an innovative variant of double-skin tubular columns (DSTCs), termed as square double-skin hybrid concrete bar columns (SDHCBCs), composed of one square-shaped outer steel tube, small-diameter concrete-infilled glass FRP tubes (SDCFs), interstitial mortar, and an inner circular steel tube. A series of axial compression tests were conducted on eight SDHCBCs and one reference DSTC to investigate the effects of key parameters, including the thicknesses of the outer steel tube and GFRP tube, the substitution ratio of SDCFs, and their distribution patterns. As a result, significantly enhanced performance is observed in the proposed SDHCBCs, including the following: ultimate axial bearing capacity improved by 79.6%, while the ductility is increased by 328.3%, respectively, compared to the conventional DSTC. A validated finite element model was established to simulate the mechanical behavior of SDHCBCs under axial compression. The model accurately captured the stress distribution and progressive failure modes of each component, offering insights into the complex interaction mechanisms within the hybrid columns. The findings suggest that incorporating SDCFs into hybrid columns is a promising strategy to achieve superior load-carrying performance, with strong potential for application in high-rise and infrastructure engineering.

1. Introduction

In modern structural engineering, the demand for high-strength, lightweight, and large-span structures has far exceeded the capacity of conventional single-material components. Columns, as primary load-carrying members, are crucial in ensuring structural safety and functionality. Traditional reinforced concrete columns, while widely used, suffer from drawbacks such as large self-weight, limited ductility, and vulnerability to corrosion in aggressive environments; their limited ductility also increases the risk of collapse under scenarios like column removal [1,2]. Consequently, considerable research attention has shifted toward hybrid columns that integrate multiple materials to combine their respective advantages, with the aim of improving structural performance and durability. Among these, fiber-reinforced polymer (FRP) composites have emerged as highly promising due to their excellent corrosion resistance, superior tensile strength, and light weight. When used as external confining tubes for concrete columns, FRP materials effectively provide lateral confinement, creating a triaxial compressive stress state in the core concrete. This confinement greatly enhances both the compressive strength and ductility of the concrete. Early research by Harmon et al. [3,4] demonstrated the benefits of carbon FRP (CFRP) and glass FRP (GFRP) jackets, revealing that confined concrete could achieve compressive strength increases of up to seven times compared to unconfined specimens. Numerous subsequent studies have examined the behavior of FRP-confined solid concrete columns, emphasizing variables such as the FRP jacket type used for confinement [5,6,7,8], FRP thickness [9,10], the cross-section geometry of columns confined with FRP [11,12,13], and concrete strength [14,15,16].

Further advancing these hybrid columns, Teng and his group [17,18] introduced the double-skin tubular column (DSTC) concept, comprising an external FRP tube and an internal steel tube with concrete infilling the annular space between them, as schematically shown in Figure 1a. This type of hybrid columns combines the confinement effects of both the inner steel tube and the outer FRP tube. The concrete core is simultaneously confined externally by the FRP and internally by the steel tube, resulting in enhanced axial load-carrying capacity, improved ductility, and delayed local buckling of the inner steel tube. Since then, DSTCs have been extensively investigated in terms of their static and dynamic performances. For example, Wang et al. [19] incorporated UHPC as the infilling material in DSTCs. The experimental results demonstrated that the DSTCs with UHPC had good ductility under eccentric compression, indicating that it is a promising form for engineering use in practice. Similarly, Khusru et al. [20,21] used rubberized concrete as the infilling material in DSTCs, which were shown to provide a promising sustainable solution with greater compressive capacity. Qian et al. [22,23] conducted both axial compression and lateral cyclic loading tests on DSTCs. The experimental findings revealed that the sandwich concrete was effectively confined by both the inner steel tube and the outer FRP tube. In turn, the concrete delayed the local buckling of the inner steel tube. Consequently, the bearing capacity, ductility, and seismic performance of DSTCs have been significantly enhanced. Furthermore, Wong et al. [24] conducted comparative experiments involving FRP-confined solid cylinders (FCSCs), FRP-confined hollow cylinders (FCHCs), and short DSTCs. The results demonstrated that the incorporation of an inner steel tube nearly fully compensated for the reduction in FRP confinement effect attributable to the presence of the internal cavity. Yu et al. [25,26] advanced a stress–strain model specifically for concrete within DSTCs based on existing experimental data and finite element simulations considering strain gradient effect and further experimentally verified the excellent performance of DSTCs under eccentric compression. Beyond compression performance, DSTCs have also shown excellent bending [27] and seismic performance [28,29].

Based on the DSTC principle, numerous variants have been proposed to further optimize hybrid columns. For instance, Feng et al. [30] developed a type of steel–concrete-FRP–concrete columns (SCFCs) that utilized a square steel tube as the external confining layer and a circular FRP tube as the internal confinement, with concrete cast both inside and outside the FRP tube. This composite design exhibited stronger confinement effects, high ductility, and a high level of residual stress. Similarly, other scholars, such as Yu and Teng [11], Chen et al. [31], Gao et al. [32], Zakir et al. [33], Zeng et al. [34], and Li et al. [35], explored DSTC variants with diverse material configurations and cross-sectional geometries, revealing that the mechanical behavior of hybrid columns is highly dependent on the material strength and the level of confinement. Moreover, Fang et al. [36] introduced small-diameter concrete-infilled glass FRP tubes (SDCFs). Experimental results showed that SDCFs achieved compressive strengths up to 267 MPa and ultimate axial strains of 10.3%, representing 6 and 34 times, respectively, over unconfined concrete specimens. These results confirm the solid role of SDCFs as highly effective internal reinforcements for hybrid columns.

Following these innovative variants, Li et al. [37] proposed a further evolution of DSTCs, termed as FRP–concrete–steel multitube hollow columns (MTHCs), as shown in Figure 1b. In these columns, the interlayer between the inner and outer confinement tubes was partially replaced with multiple SDCFs. The outer FRP tube provided overall confinement, allowing the SDCFs to achieve high strength and exceptional deformation capacity. However, to avoid premature failure of the entire system due to fracture of the outer FRP tube, it was necessary to select an outer confinement material with fracture strain higher than that of the inner GFRP tubes. Thus, Yu et al. [38] suggested using PET-FRP as an outer confinement material, but practical constraints related to PET-FRP fabrication limited its implementation. Consequently, the use of steel tubes as the outer confining layer has been explored as a feasible alternative.

Figure 1. Typical cross-sections of hybrid columns [37].

Figure 1. Typical cross-sections of hybrid columns [37].

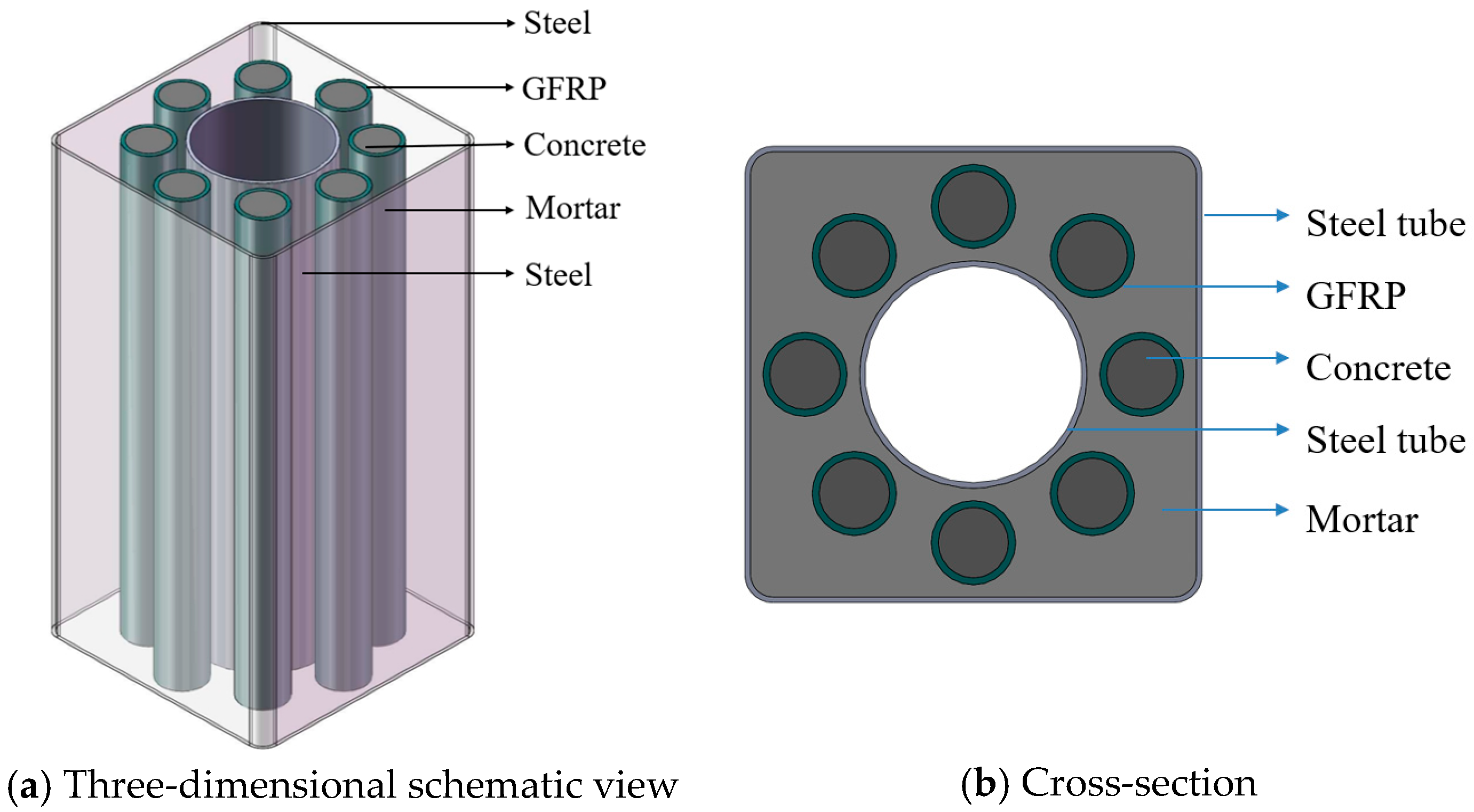
Building on these developments, this work introduces a new hybrid column type, termed square double-skin hybrid concrete bar columns (SDHCBCs), as illustrated in Figure 2. An SDHCBC is composed of a square outer steel tube, a circular inner steel tube, and multiple SDCFs, with mortar filling the interstitial spaces. This composite configuration aims to bring together the high confinement effectiveness afforded by the outer and inner steel tubes and the superior mechanical properties of SDCFs, thereby achieving excellent load-carrying capacity, ductility, and resistance to local buckling.

Notably, compared to circular outer tubes frequently used in DSTCs or MTHCs [39], the square outer steel tube is purposefully adopted to facilitate beam–column joint connections and improve construction convenience. However, in square sections, lateral confinement is inherently non-uniform: it is highest at the closed corners and lowest at the midpoints of flat sides. Under axial compression, this non-uniformity fosters earlier local softening and bulging along flats. This mechanism may result in a different failure mode of the column compared with the circular outer tube confined column. Theoretically, the non-uniform confinement of the square outer tube may result in one or both of two effects in the mechanical behavior: (1) the non-uniform confinement is a weaker confinement compared with uniform confinement of the circular tube, and earlier failure may be observed; (2) for a similar reason, the ductility of the square tube confinement column may be better than the circular tube confinement column.

Therefore, a systematic study was conducted in this paper to resolve these questions and to validate the proposed SDHCBCs. A series of axial compression tests were carried out, focusing on key parameters such as the thicknesses of the outer steel tube and the GFRP tube and the arrangement of the SDCFs. Subsequently, a finite element (FE) model was developed and validated against the experimental data. The validated model was then used to resolve spatial stress and strain fields and to characterize how the three constituent materials interact in the proposed SDHCBCs.

2. Experimental Scheme

2.1. Design of Specimens

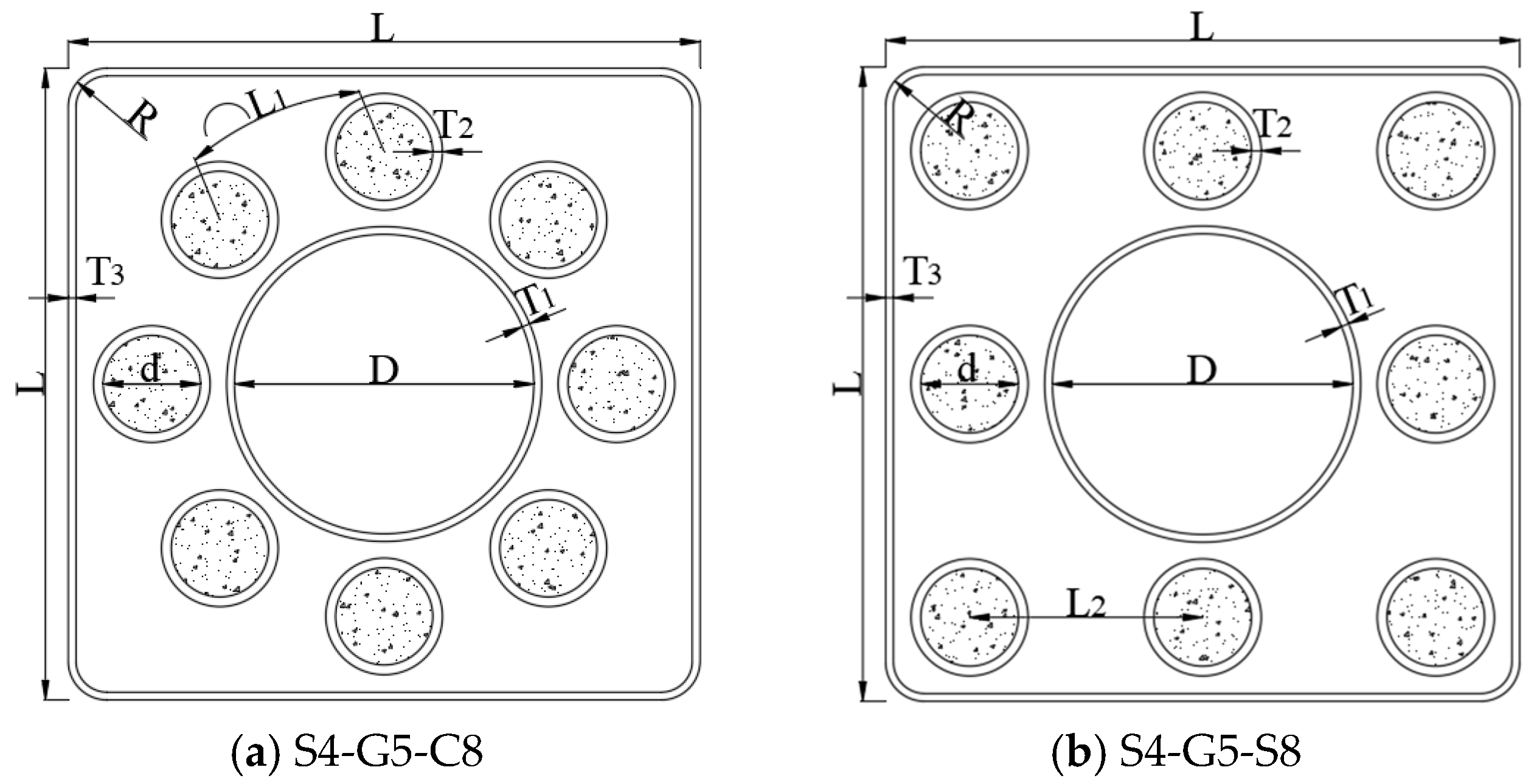
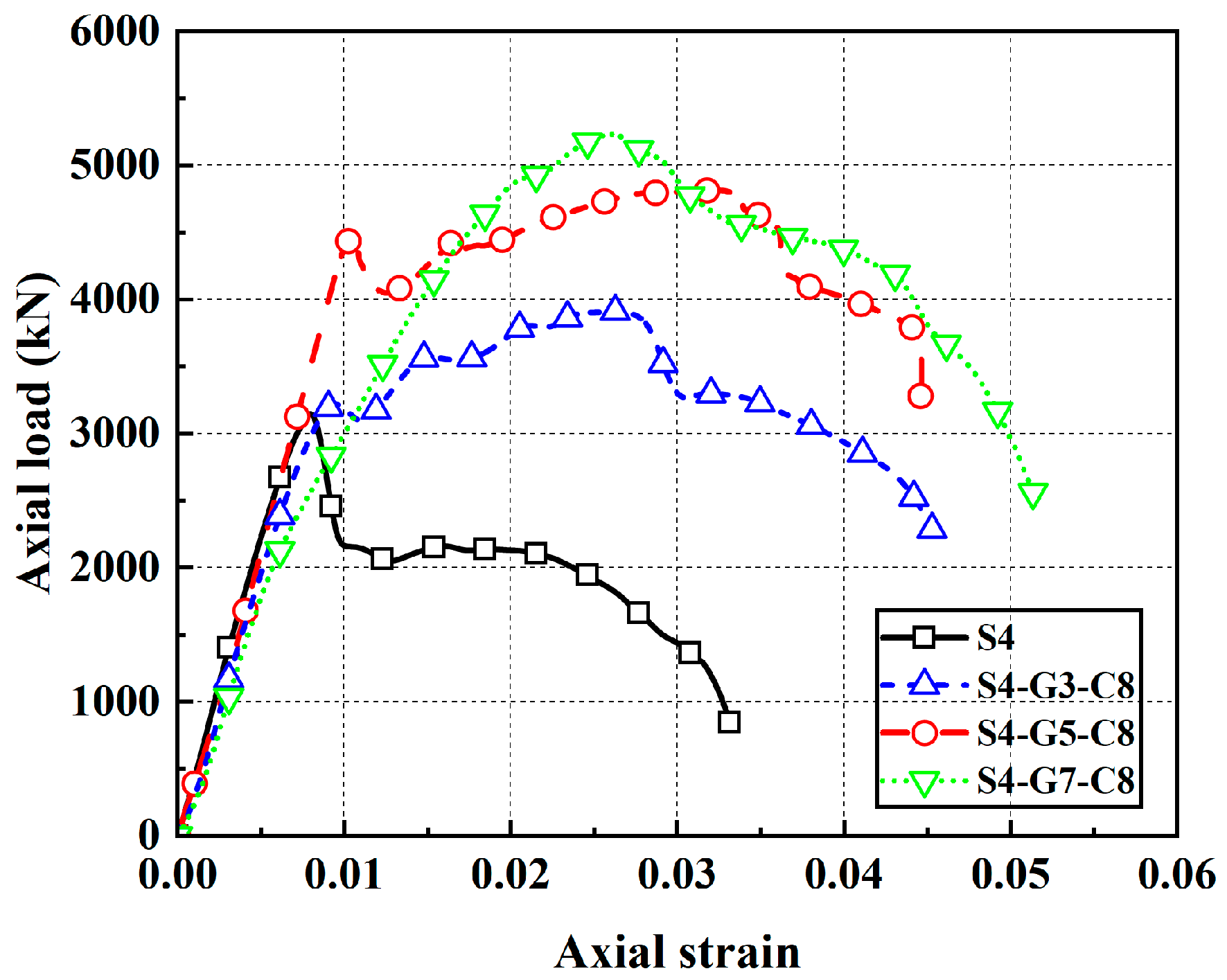
A total of nine hybrid columns were designed, comprising one specimen without SDCFs and eight SDHCBCs. The principal test variables were as follows: outer steel tube wall thickness (2, 4, and 6 mm); GFRP tube wall thickness (3.0, 5.0, and 7.0 mm); SDCF substitution ratio (0, 18.73%, 27.43%, and 38.05%); and the SDCF distribution pattern (circular or square). It should be noted that the substitution ratio is the total cross-section area of SDCFs substituted by the total cross-section area of the concrete. The default steel grade of all specimens was Q235. Detailed parameters for the specimens are presented in

Table 1. Parameters of each specimen.

Specimens	T3 (mm)	T2 (mm)	Substitution Rate (%)	Number of SDCFs
S4	4	/	/	/
S2-G5-C8	2	5	27.43%	8
S4-G5-C8	4	5	27.43%	8
S6-G5-C8	6	5	27.43%	8
S4-G5-C6	4	5	18.73%	6
S4-G5-C10	4	5	38.05%	10
S4-G3-C8	4	3	27.43%	8
S4-G7-C8	4	7	27.43%	8
S4-G5-S8	4	5	27.43%	8

Note: T₃ is the outer steel tube thickness; T₂ is the GFRP tube thickness.

and

Table 2. Specimens with the same parameters.

H (mm)	L (mm)	R (mm)	D × T1 (mm)	d (mm)
650	325	20	158 × 4	50

Note: H is the height of specimens; L is the length of the flat edge of the section and R is the radius of corner of the cross-section; D and T₁ are the inner diameter and thickness of inner tubes; d is the internal diameter of SDCFs.

, and cross-sections are illustrated in Figure 3.

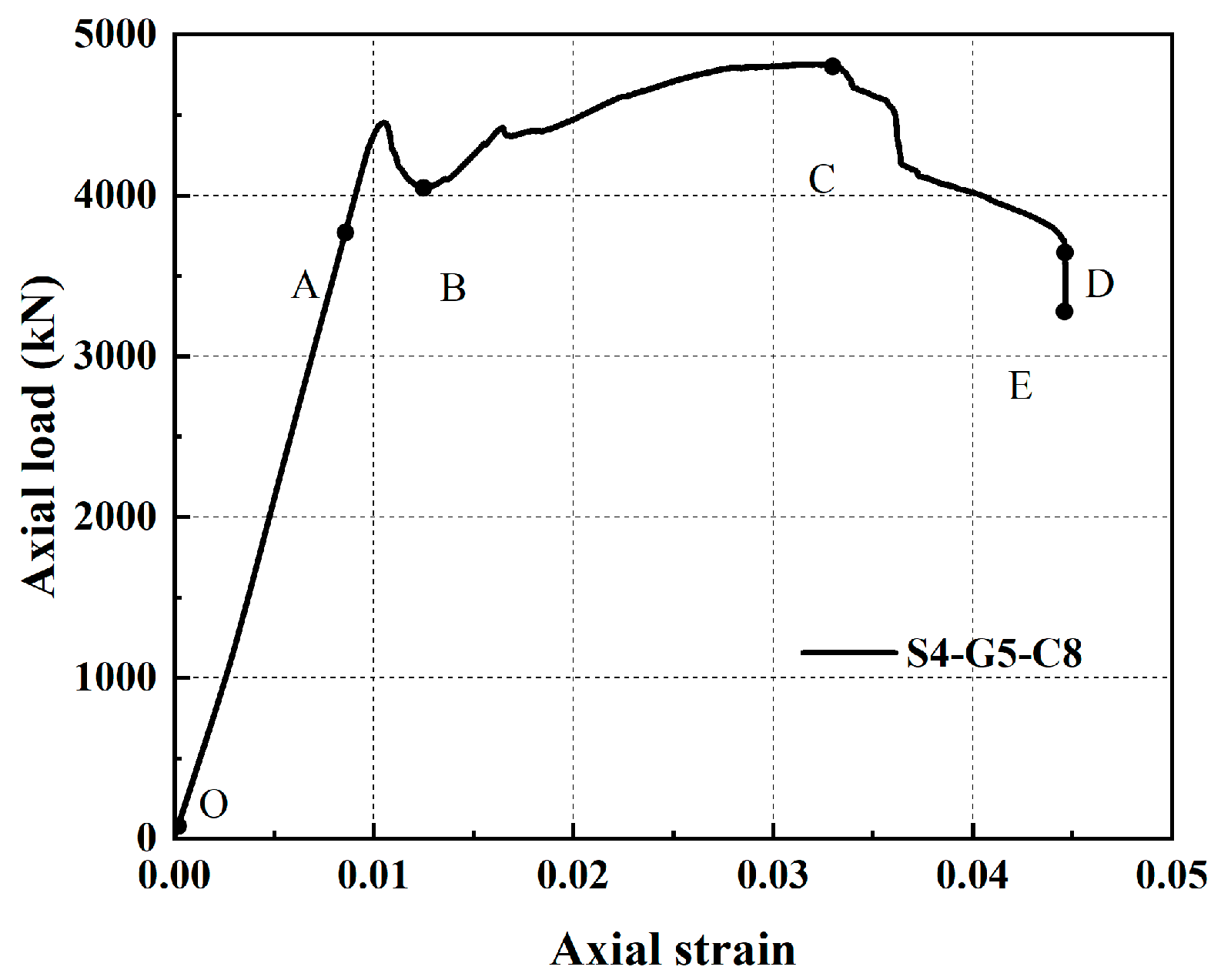
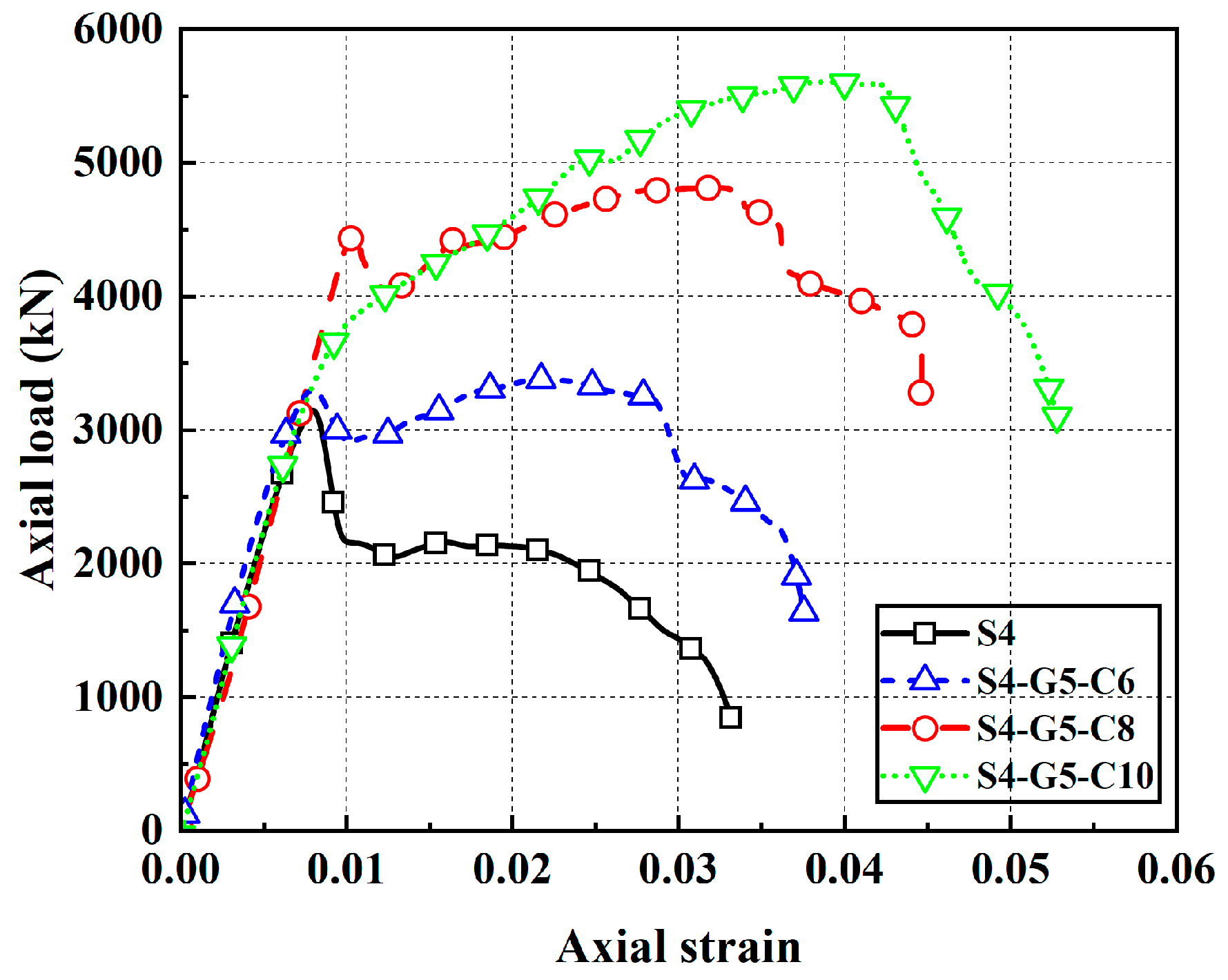
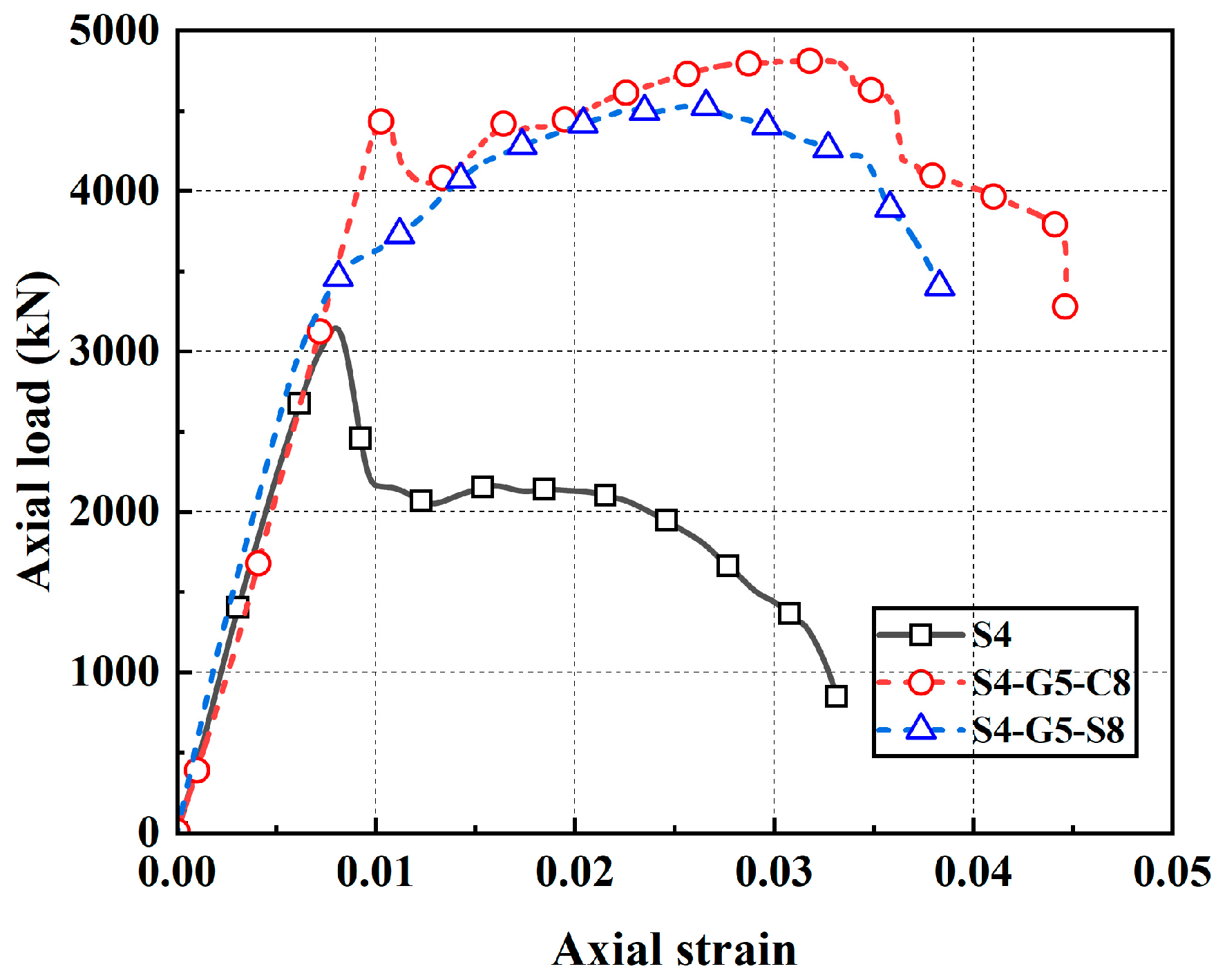
The specimen labels were assigned systematically to reflect their parameters. The first number after the letter of S (e.g., 4 in S4) denotes the thickness of outer steel tube, the middle number after “G” (e.g., 5 of G5) indicates the thickness of GFRP tube, and the ending letter and number (e.g., C8) represent the distribution pattern (C for circular and S for square) and number of SDCFs. For example, “S4-G5-C8” indicates a specimen with an outer steel tube thickness of 4 mm, a GFRP tube thickness of 5 mm, and eight SDCFs distributed in a circular pattern.

2.2. Test of Material Mechanical Properties

In this study, GFRP tubes were filled with concrete, designated herein as small-diameter concrete-infilled glass FRP tubes (SDCFs). Before filling in concrete, the GFRP tubes were manufactured in the factory, where the GFRP tubes are made by multi-layer filament winding of glass fibers, with the fiber orientation alternating at ±45° to the tube axis.

In the assembling process, SDCFs were arranged in the annular space separating the inner and outer steel tubes and grouted with mortar to promote even stress transfer among all specimen components. The mix proportions of the concrete and mortar used in this study are shown in

Table 3. Concrete and mortar mix proportions ($\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$).

Materials	Cement	Coarse Aggregate	Fine Aggregate	Water	Water Reducer
Concrete	501	1123	566	220	0.501
Mortar	796.85	/	1961.63	407.48	3.77

.

The compressive strength and elastic modulus of concrete and mortar were evaluated through mechanical tests conducted in accordance with GB/T 50081-2019 [40] and JGJ/T 70-2009 [41], respectively. The testing procedure is depicted in Figure 4, and the results are presented in

Table 4. Mechanical properties of materials for SDHCBCs.

Material	Specimen	Elastic Modulus (GPa)	Yield Stress (MPa)	Ultimate Stress (MPa)
Concrete	Cube	-	-	39.85
	Cylinder	20.5	-	33.41
Mortar	Cube	-	-	40.15
Steel tube	Coupon	206	260.82	380.87
Reinforcing confined-concrete bars	3 mm-thickness FRP tube	-	-	98.56
	5 mm-thickness FRP tube	-	-	108.45
	7 mm-thickness FRP tube	-	-	112.09

. The values presented in the table represent the averages of all data obtained from three separate batches of concrete and mortar casting.

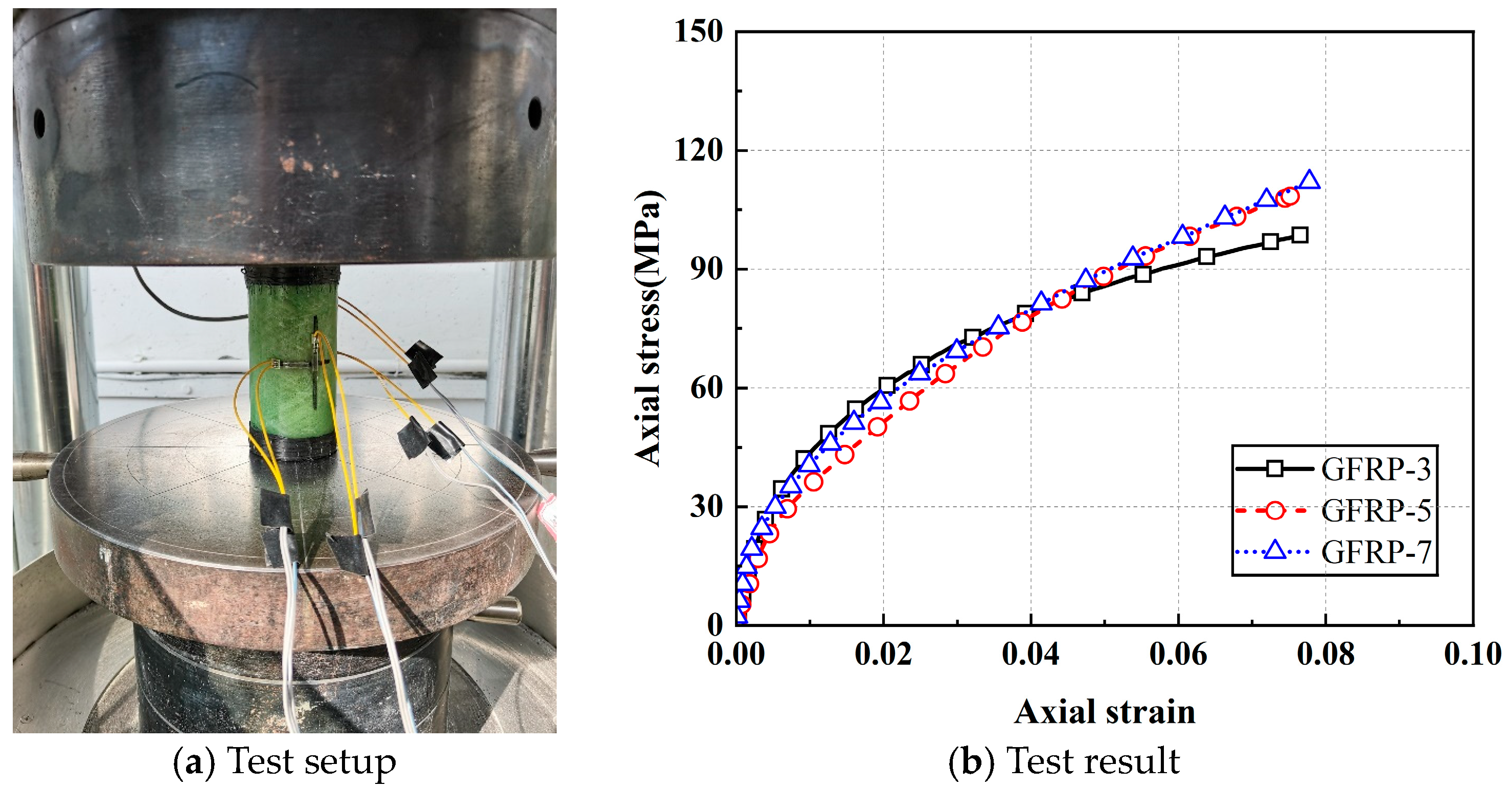
Following Reference [36], axial compression tests were performed on concrete-filled GFRP tubes, as depicted in Figure 5. Three specimens were prepared with a height of 120 mm and GFRP inner diameters of 50 mm, with thicknesses of 3 mm, 5 mm, and 7 mm, respectively. Prior to testing, the ends of concrete-infilled GFRP tubes were reinforced with CFRP fabric. The failure of the specimen was determined by the fracture of the GFRP tube. Test results are presented in Table 4.

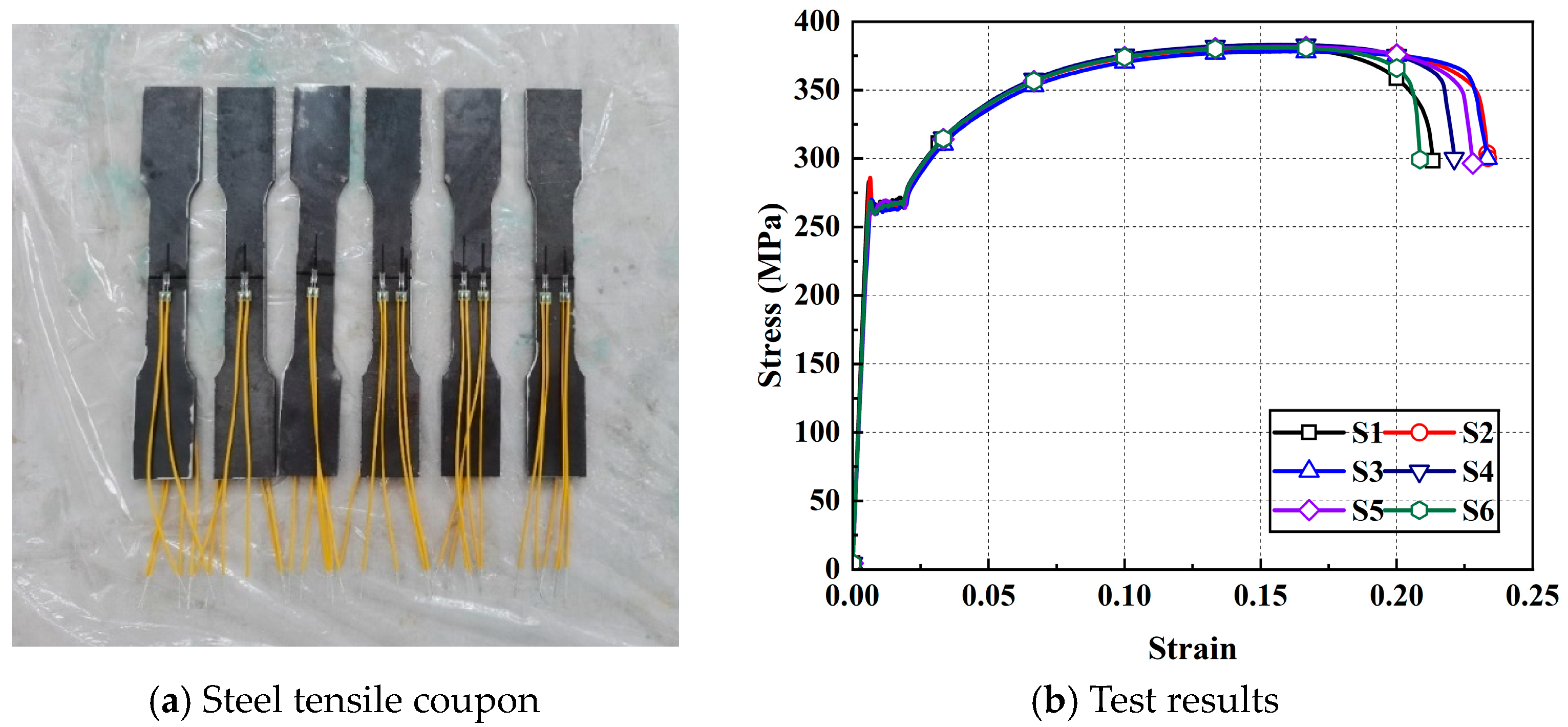
Six steel coupons sampled from different positions along the tube length were subjected to tensile testing per ASTM E8/E8M-15a [42], and the specimens are shown in Figure 6a. The results of the steel tensile test are presented in Table 4 and Figure 6b.

2.3. Specimen Preparation

The 3D-printed molds were used to position the GFRP tubes, which were then securely fixed in place. Concrete was poured in increments, with each layer approximately one-quarter of the GFRP tube’s height. Following each pour, the mixture was vibrated on a shaking table for 30 s to guarantee complete filling of the GFRP tube and adequate compaction of the concrete. Following placement, SDCFs were cured in a standard environment for 28 days. To prevent premature failure at the ends, the upper and lower ends were wrapped with three layers of 5 mm-wide CFRP cloth. The process of fabricating SDCFs is illustrated in Figure 7.

During the mortar pouring process, each part was initially secured using a 3D-printed template. A thick wooden board served as the base at the lower end, and glass adhesive was applied to the contact surfaces to prevent water seepage, which could potentially alter the mortar’s mix ratio. The pouring of the mortar was executed in three stages, with each layer being vibrated using a vibrating rod to guarantee adequate compaction. Following a 28-day curing period in a standard environment, the upper and lower ends of the specimen were wrapped with two layers of 5 mm-wide CFRP cloth to reduce the risk of premature failure due to stress concentration. Prior to testing, the ends of the specimen were flattened using a grinding machine.

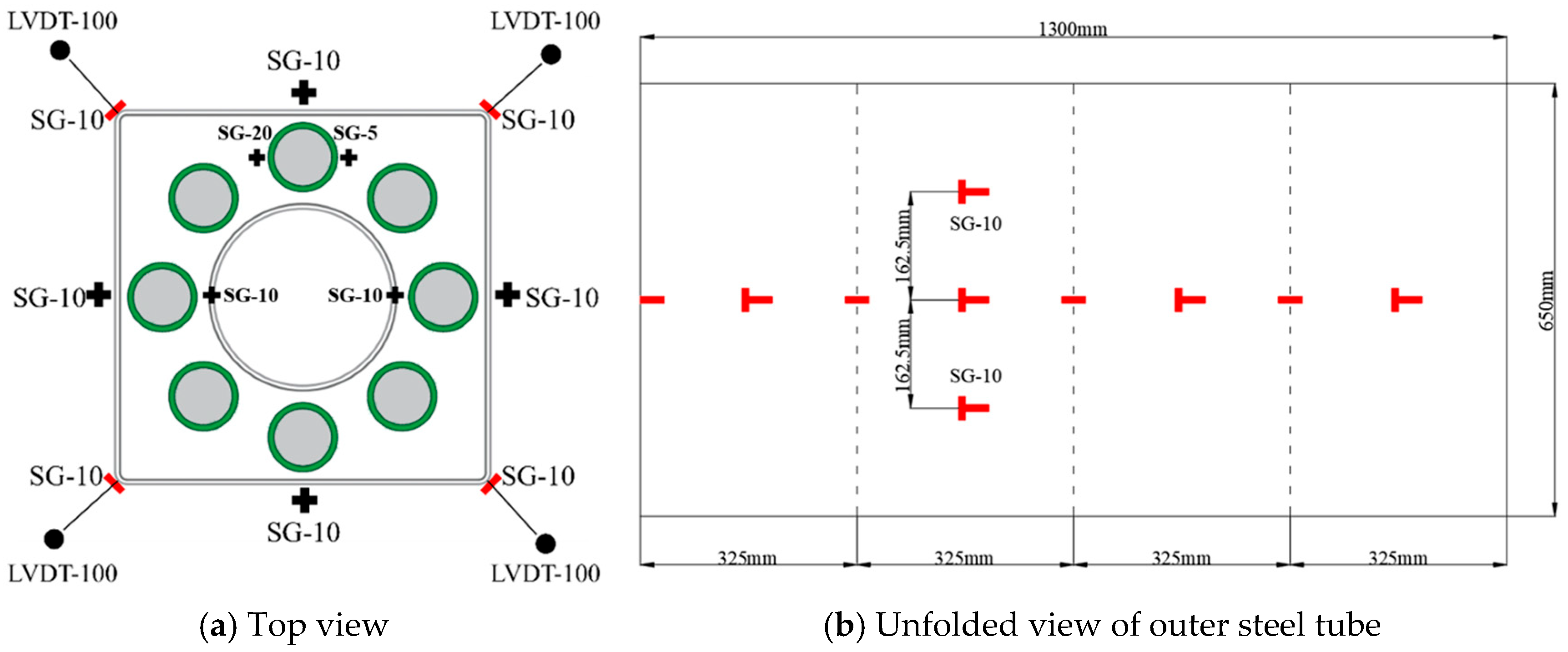
2.4. Measuring Points and Loading Scheme

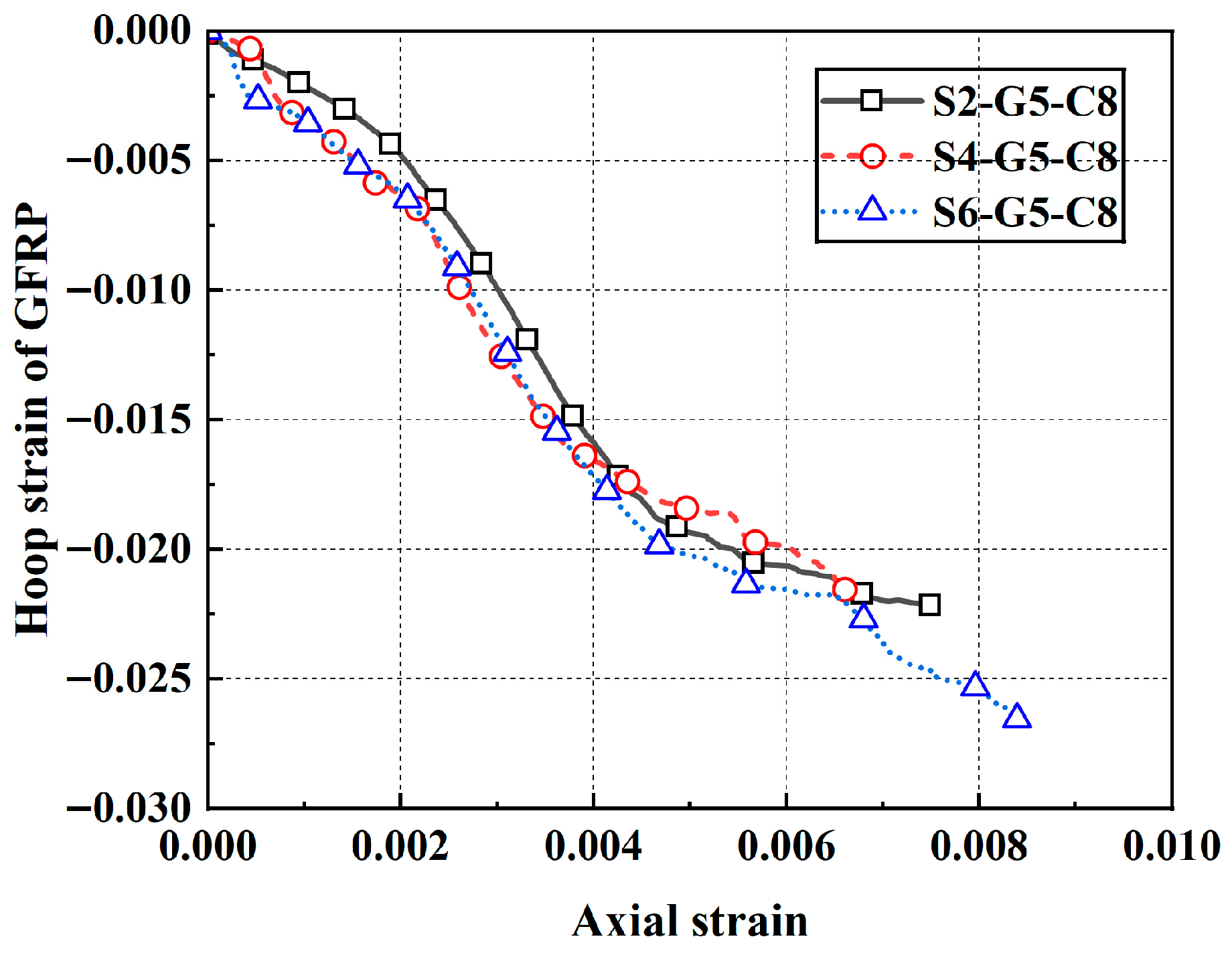
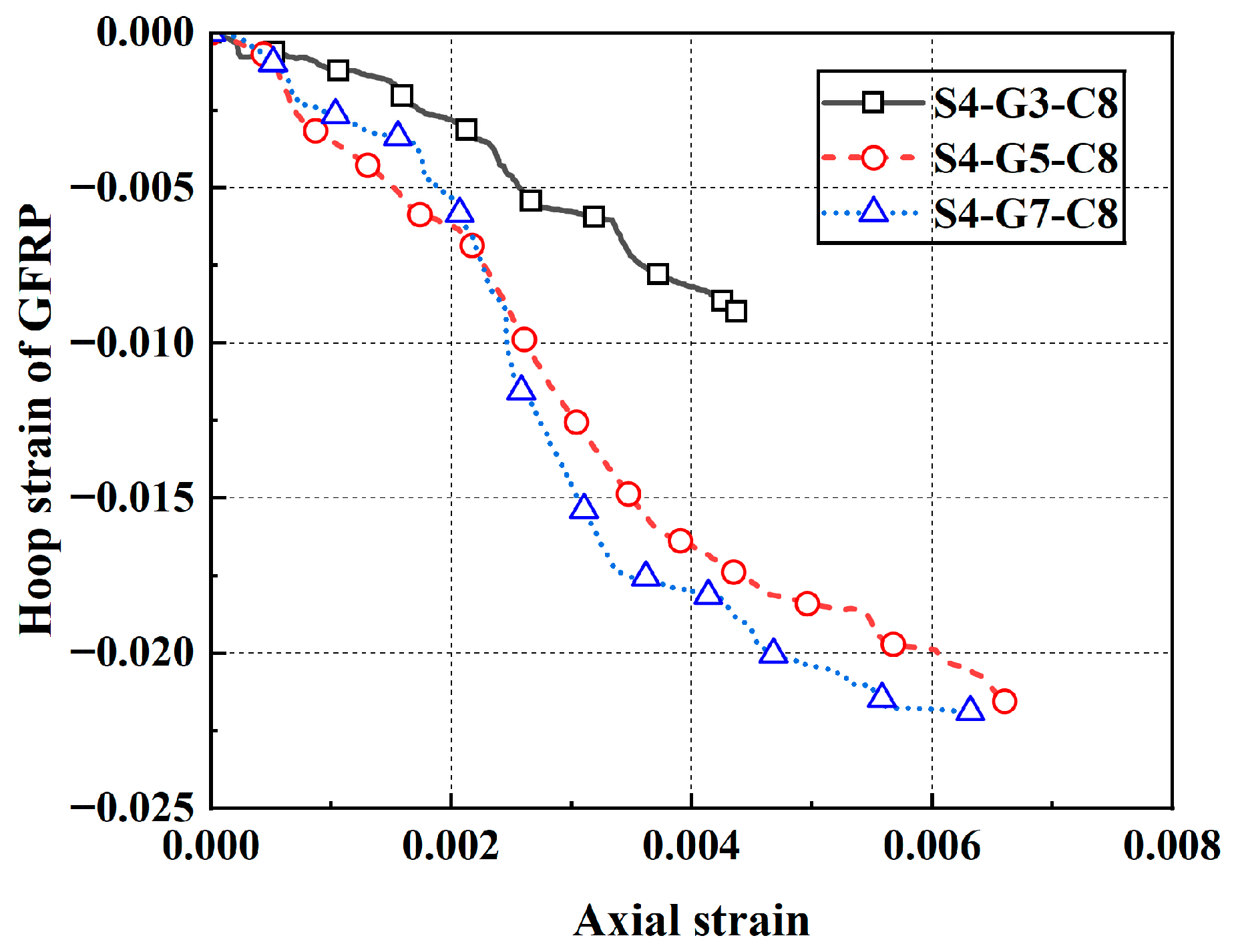
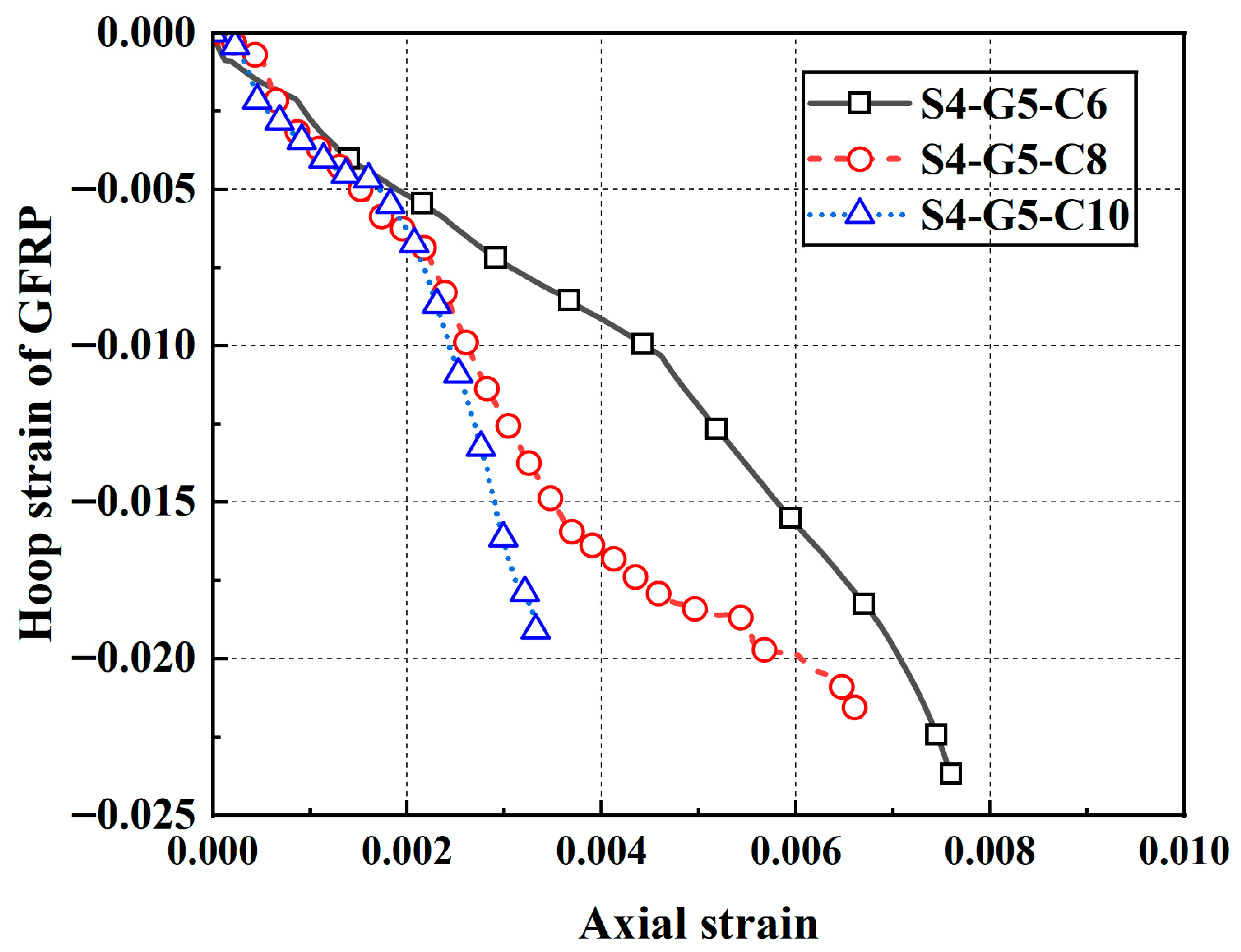
Before pouring the mortar, strain gauges of varying lengths (5 mm, 10 mm, and 20 mm) were symmetrically positioned at the mid-height of the outer surface of both the GFRP tube and the inner steel tube. To protect the gauges and ensure their waterproofing and durability, a sealant and impact-resistant paste were applied. Two mutually perpendicular strain gauges were attached at the mid-height and at distances of ±162.5 mm from the mid-height on each outer steel tube of specimens. The 10 mm-long strain gauges were positioned to measure the axial and hoop strains at the midsection, upper midsection, and lower midsection of the specimen. Additionally, one 10 mm-long hoop strain gauge was affixed at each corner to measure the circumferential strain at the corners of specimens. Furthermore, four linear variable differential transformers (LVDTs), each 100 mm in length, were positioned at the corners of the outer tube of each specimen to measure its axial displacement. The arrangement of strain gauges for specimens is shown in Figure 8.

The axial compression test on the specimens was performed using a YAW-10000F hydraulic press (manufactured by Shiji Co., Jinan, China) with a maximum capacity of 10,000 KN. Full-section loading was applied, and the test followed a displacement-controlled loading procedure.

The loading process consisted of two steps. (1) Pre-loading: An initial load of 100 KN was applied to eliminate any potential gap between the specimen and the loading machine, ensuring proper alignment before the formal loading began. (2) Formal loading: The entire loading process was conducted under displacement control at a rate of 0.6 mm/min. Data were continuously collected using a data acquisition system, and the failure process of each specimen was recorded via video.

3. Experimental Results and Analysis

3.1. Failure Modes

As shown in Figure 9, the failure of the specimens initiated at the outer steel tube (Figure 9a). In the beginning, the CFRP that wrapped at the ends of the specimen cracked, and the buckling of the outer tube started afterwards, as illustrated in Figure 9b. Following this was the crack of the weld of the outer steel tube (Figure 9c). At this stage, the failure of the inner parts is not observable.

After the compression test, the outer steel tubes of the specimens were cut to observe and document the damage to the core concrete, mortar, and inner steel tube. The failure modes of the eight SDHCBC specimens were nearly identical, in which the failure mode of S4-G5-C8 is shown in Figure 10 as an illustration. The outer steel tube exhibited significant outward bulging in the upper middle, while the welds were completely torn open. Most of the mortar was crushed and scattered, although the mortar in specimen S4 remained relatively intact, as shown in Figure 11. The SDCFs showed bending deformation in the upper middle. The GFRP tube at the bending point displayed white stripes along the fiber direction, with no shear cracks observed. The inner steel tube also buckled inward at the upper middle height. Notably, neither the inner steel tubes nor the SDCFs have shown significant deformation or damage, indicating no failure in these components. This suggests that the premature failure of the specimens is caused by cracks in the weld seams of the outer steel tube.

In our tests, the outer steel tube consistently cracked at the longitudinal weld positioned on the flat side, which then precipitated bulging and reduced lateral restraint. Concurrently, SDCFs exhibited mid-height bending and whitening of GFRP fibers (matrix cracking/fiber micro-buckling) without shear cracking, consistent with a bending-dominant demand on the bars once mortar restraint deteriorated along the flats. For comparison, the failure mode of the circular specimens is different, in which the buckling is uniformly distributed along the outer circle, and the failure mode of SDCFs is shear-dominant [39].

Figure 12 displays, for each specimen, the hoop strain–axial strain response curves for the outer steel tube, inner steel tube, and the GFRP tube. For all specimens except S4-G5-C6, the trend in circumferential strain variation under identical axial strain conditions follows a consistent order: GFRP tubes > outer steel tubes > inner steel tubes. This observation suggests that during the process of axial compression, the deformation rates of the components within SDHCBCs exhibit variations, indicative of interactions among their constituent elements.

As the primary load-bearing component, the SDCFs undergo deformation initially, leading to a higher deformation rate in the GFRP tubes. Simultaneously, the mortar experiences deformation due to both the pressure exerted by the SDCFs and its intrinsic expansive deformation, which causes it to push against the inner and outer steel tubes, ultimately resulting in their deformation.

3.2. Axial Load-Deformation Rate Relation of Specimens

Figure 13 illustrates, for all specimens, the axial load–axial strain response, with axial strain computed as the mean of four LVDT readings divided by the specimen’s overall length.

Figure 14 shows a representative axial load–axial strain curve for specimen S4-G5-C8; its response can be segmented into four phases—elastic, yield, hardening, and descending.

(1)

Elastic Stage (OA): The specimen exhibited no significant deformation, and the bonding between the internal and external steel tubes, SDCFs, and mortar was effective. The four components collaborated to support the applied load. However, the minimal lateral deformation observed in the core concrete and mortar resulted in the restraining effects of the FRP and steel tubes not being fully utilized.

(2)

Yielding Stage (AB): As the specimen initiated yielding, the upper end of the steel tube exhibited buckling, accompanied by the tearing sound of the CFRP plate. The restraining effect of the GFRP tube on the core concrete increased, while the mortar was compressed by the deformation of the GFRP tube. At this stage, the inner and outer steel tubes also provided a restraining effect.

(3)

Strengthening Stage (BC): Fracture of the CFRP plate at the end resulted in enhanced buckling of the outer steel tube and cracking of the weld. Subsequently, the collapse of the sandwich mortar was initiated. However, due to the high stiffness and ductility of the outer and inner steel tubes, the mortar was able to maintain its stabilizing effect on the SDCFs. At this point, the SDCFs performed as the primary load-bearing component.

(4)

Descending Stage (CE): As the damage in the welding progressed, the specimen’s bearing capacity gradually decreased. Upon complete cracking of the weld, the sandwich mortar was completely crushed, resulting in bending of the SDCFs and subsequent inability to sustain the applied load.

Herein, structural ductility is quantified by a ductility factor given by the following:

$$\mu ={\displaystyle \frac{{\Delta }_{\mathrm{u}}}{{\Delta }_y}}$$

(1)

where ${\Delta }_{\mathrm{u}}$ represents the ultimate displacement, which corresponds to the displacement when the structural load-bearing capacity decreases to 85% of its peak value; ${\Delta }_y$ represents the yield displacement.

The axial compression data of SDHCBCs can be found in

Table 5. Axial compression data.

Specimens	${\mathit{F}}_{\mathbf{u}}$（kN）	Yield Displacement (mm)	Ultimate Displacement (mm)	$\mathit{\mu }$
S2-G5-C8	4226	6.37	25.74	4.041
S4-G5-C8	4798	8.35	24.73	2.962
S6-G5-C8	5323	6.96	28.33	4.070
S4-G3-C8	3915	7.15	19.37	2.709
S4-G7-C8	5244	7.67	24.05	3.126
S4-G5-C6	3392	7.74	19.18	2.478
S4-G5-C10	5614	6.96	19.18	2.756
S4-G5-S8	4532	5.33	23.43	4.396
S4	3126	5.68	5.83	1.026

Note: F_u is the ultimate bearing capacity.

. Comparison of the data for each specimen reveals that the ultimate bearing capacity and ductility of the SDHCBCs significantly exceeded those of the control specimen. Specifically, S4-G5-C10 exhibited the highest value in terms of both bearing capacity and ductility. In comparison to the control specimen S4, it showed a 79.6% increase in bearing capacity. In terms of ductility, specimen S4-G5-S8 exhibits outstanding performance: its ductility coefficient is 328.3% higher than that of the control specimen S4 (i.e., $\mu$ value of 4.396 vs. 1.026), reflecting a pronounced enhancement in ductility.

By comparison with the results of circular tube confined columns, the ductility factor is largely improved from the interval of [1.5, 3.3] to [2.5, 4.4] [39]. This result quantitively reveals the improvement of applying the square-shaped outer tube.

4. Influence of Key Parameters

In this section, the influence of key parameters including outer steel tube thickness, GFRP thickness, SDCF substitution rates, and SDCF distributions are discussed in Section 4.1, Section 4.2, Section 4.3 and Section 4.4. Afterwards, a concise relation to prior work of the current study is provided in Section 4.5.

4.1. Thickness of Outer Square Steel Tube

Figure 15 presents the axial load–axial strain responses for specimens with outer steel tube wall thicknesses of 2, 4, and 6 mm, together with the control specimen. The ultimate bearing capacity and ultimate strain of the specimens improves with the increase in the outer steel tube thickness. The ultimate bearing capacity of S6-G5-C8 with the outer steel tube thickness of 6mm is 70.3% higher than that of S4 (i.e., 5323 KN vs. 3126 KN), and the ultimate strain increased by 321.4% (i.e., 0.0354 vs. 0.0084). Compared to S2-G5-C8 (2 mm outer steel tube), S6-G5-C8 exhibited 25.9% higher ultimate bearing capacity and 14.5% higher ultimate strain.

Figure 16 presents the hoop–axial strain responses of the GFRP tubes for varying outer tube thicknesses. The curves exhibit similar trends. For a given axial strain level, differences in GFRP hoop strain are minimal. Consequently, in the initial loading stage, the components largely carry load independently, with the steel tubes—inner and outer—providing only limited restraint.

4.2. Thickness of GFRP

Figure 17 illustrates the influence of GFRP thickness, plotting axial load–axial strain responses for SDHCBCs with GFRP tube thicknesses of 3, 5, and 7 mm, together with the control specimen. Increasing the GFRP thickness enhances ultimate bearing capacity. S4-G7-C8 (7 mm GFRP) attains an ultimate capacity 67.8% higher than S4 (5244 vs. 3126 kN). By contrast, S3-G5-C8 (3 mm GFRP) achieves a 33.9% increase relative to S4.

Figure 18 displays the hoop–axial strain responses for GFRP tubes with different wall thicknesses. With increasing GFRP wall thickness, concrete confinement improves. After the axial strain reaches 0.004, the response curve exhibits a progressive reduction in slope, indicating loss of stability; the slowed growth of hoop strain is attributable to GFRP tube buckling.

4.3. SDCFs Substitution Rates

The axial load–axial strain curves for SDHCBCs with different substitution rates (i.e., 0%, 18.73%, 27.43%, and 38.05%) are depicted in Figure 19. The cross-sections of the specimens at different SDCF substitution rates are shown in Figure 20. The elastic stages of the four curves are nearly identical. Following the elastic stage, the number of SDCFs has a significant impact on the ultimate bearing capacity of the specimens. The ultimate bearing capacity of S4-G5-C10 with the SDCFs of 10 is 79.6% higher than that of S4 (i.e., 5614 KN vs. 3126 KN), and the ultimate strain increased by 360.7% (i.e., 0.0387 vs. 0.0084). Compared to S4-G5-C6 with the SDCFs of 6, ultimate bearing capacity increases by 65.5% and ultimate strain increases by 68.3%. Therefore, it can be concluded that the number of SDCFs has the largest impact on the ultimate bearing capacity and ductility of SDHCBCs.

Figure 21 plots the hoop–axial strain responses of the GFRP tubes across a range of SDCF substitution ratios. Increasing the substitution ratio reduces the mortar volume, which weakens the restraining action of the SDCFs and leads to larger deformations of the GFRP tubes.

4.4. Influence of SDCFs Distributions

The axial load–axial strain curves for SDHCBCs with different distributions of SDCFs (i.e., circular and square) are depicted in Figure 22. The ultimate bearing capacity of S4-G5-C8 with the circular distribution of SDCFs is 5.9% higher than that of S4-G5-S8 (i.e., 4798 KN vs. 4532 KN), and the ultimate strain increased by 20.6% (i.e., 0.0340 vs. 0.0282). Therefore, it can be concluded that SDHCBCs with a circular distribution of SDCFs demonstrate better performance.

4.5. Relation to Prior Work of Double-Skin Tubular-Encased Confined-Concrete Bar Columns

In prior work, the double-skin tubular-encased confined-concrete bar columns (DTCBCs) were studied by means of compressive performance [39]. The systematic comparison of the DTCBCs and the proposed SDHCBCs is introduced in this sub-section for clear illustration of the improvement.

(1)

Influence of design parameters: square vs. circular outer tube

In this current study, four parameters including the thickness of outer square steel tube, the thickness of GFRP tube, the substitution ratio of SDCFs, and the distribution patterns of SDCFs are considered as the design parameters, while the first three parameters are considered in the prior work. The influence of changing these parameters to the bearing capacity and ductility factor is briefly compared with reference to the interval of parameters, and the results are shown in

Table 6. Influence of design parameters of SDHCBCs and DTCBCs.

Design Parameter	Type	Parameter Interval	Bearing Capacity Interval (kN)	Ductility Factor Interval
Thickness of outer square steel tube	SDHCBC	[2 mm, 6 mm]	[4139, 5323]	[2.962, 4.070]
	DTCBC	[2 mm, 6 mm]	[4119, 5336]	[1.549, 2.549]
Thickness of GFRP tube	SDHCBC	[3 mm, 7 mm]	[3985, 5244]	[2.709, 3.126]
	DTCBC	[2.8 mm, 5.8 mm]	[4437, 5122]	[2.033, 3.322]
Substitution ratio of SDCFs	SDHCBC	[0, 38.05%]	[3126, 5614]	[1.026, 2.962]
	DTCBC	[0, 45.91%]	[3241, 5627]	[1.833, 3.240]
Distribution pattern of SDCFs	SDHCBC	Circular, square	4798, 4532	2.962, 4.396

.

It is found that the overall influence of the design parameters on the capacity of the specimen is similar for DTCBC and SDHCBC. And the ductility factor of the SDHCBC is, in general, larger than that of the DTCBC (in some cases, the values of design parameters are not comparable).

(2)

Influence of distribution of SDCFs

The influence of the distribution pattern of SDCFs to the capacity is limited, as shown in Table 6. However, the square distribution contributes to a large increase in the ductility factor, resulting in better ductility performance in the specimen. This is a novel finding in this study since it has not been studied in prior work.

(3)

Failure modes: square vs. circular outer tube

The failure process of the proposed SDHCBC and DTCBC is different: the buckling of the outer tube of the SDHCBC is concentrated at the middle of the flat edge, and the failure of the SDCFs is bending-dominated. By comparison, the buckling of the outer tube of the DTCBC is uniformly distributed, and the failure of the SDCFs is shearing-dominated. This mechanism results in an early decreasing of the stiffness of the specimen. However, this unique failure process of the SDHCBC contributes to a larger ductility factor than that of the DTCBC.

5. Finite Element (FE) Modeling

Numerical simulations were conducted to investigate the axial loading behavior of SDHCBCs using finite element models developed in ABAQUS. In summary, a brief list of the specifications of the FE model is first given, and the details are provided afterwards for clear demonstration.

(1)

Element types: C3D8I for core concrete, mortar, steel tube components; SC8R for GFRP tube.

(2)

Constitutive model: concrete damaged plasticity for concrete; secondary plastic flow model for steel; Hashin damage constitutive model for GFRP.

(3)

Contact and boundary: Surface contact between outer steel tube, core concrete, GFRP, and inner steel tube; surface-to-surface contact with finite sliding. Both ends of the specimens: tie to rigid plates.

Details about the FE model are shown below.

The core concrete, mortar, and steel tube components were modeled using C3D8I elements (eight-node linear brick solid elements), while the GFRP tube was represented using SC8R elements (quadrilateral continuum shell elements). The meshing details for each component are presented in

Table 7. Mesh and element information of each material of SDHCBCs.

Material	Mesh Characteristic Length (mm)	Element Number	Element Name
Outer steel tube	20	1056	C3D8I
Inner steel tube	20	858	C3D8I
Core concrete	12	1080	C3D8I
Mortar	18	14508	C3D8I
GFRP tube	10	1070	SC8R
End plate	20	400	C3D8I

.

5.1. Constitutive Model of Materials

5.1.1. Concrete

The mechanical behavior of concrete was modeled using the concrete damaged plasticity (CDP) model in ABAQUS. For the GFRP-confined core, the Jiang–Teng [17] constitutive law for FRP-confined concrete was adopted; see Equation (2).

$${\displaystyle \frac{{\mathrm{\epsilon }}_c}{{\mathrm{\epsilon }}_{co}}}=0.85(1+8{\displaystyle \frac{{\sigma }_{tf}}{f_{co}}})\{{[1+0.75({\displaystyle \frac{{\mathrm{\epsilon }}_h}{{\mathrm{\epsilon }}_{co}}})]}^{0.7}-\exp [-7({\displaystyle \frac{{\mathrm{\epsilon }}_h}{{\mathrm{\epsilon }}_{co}}})]\}$$

(2)

where ${\mathrm{\sigma }}_c$ and ${\mathrm{\epsilon }}_c$ are the axial stress and axial strain of concrete, respectively; ${\epsilon }_{co}$ is the peak strain of the unconfined concrete and $f_{co}$ is the corresponding stress; ${\sigma }_{tf}$ is the confining pressure from the FRP jacket; and ${\epsilon }_h$ is the hoop strain of the FRP jacket.

The confining pressure increases with the hoop strain, and the relationship between axial strain and hoop strain is given by Equation (2):

$${\sigma }_{tf}={\displaystyle \frac{2E_f{t}_f{\mathrm{\epsilon }}_h}{D}}$$

(3)

where $E_f,t_f$ are the elastic modulus and thickness of the FRP jacket, respectively; $D$ is the diameter of the column.

5.1.2. Steel

Within the classical metal plasticity framework, the steel tube is modeled using the secondary plastic flow formulation [43], expressed as follows:

$${\sigma }_s=\left\{\begin{array}{l}{E}_s{\epsilon }_s\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\epsilon }_s\le {\epsilon }_e\\ -A{\epsilon }_s^2+B{\epsilon }_s+C {\epsilon }_e<{\epsilon }_s\le {\epsilon }_{e1}\\ f_y\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\epsilon }_{e1}<{\epsilon }_s\le {\epsilon }_{e2}\\ f_y(1+0.6{\displaystyle \frac{{\epsilon }_s-{\epsilon }_{e2}}{{\epsilon }_{e3}-{\epsilon }_{e2}}}) {\epsilon }_{e2}<{\epsilon }_s\le {\epsilon }_{e3}\\ 1.6f_y\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\epsilon }_s>{\epsilon }_{e3}\end{array}\right.$$

(4)

where $f_p$ is the proportional limit, $f_y$ denotes the yield strength, and $f_u$ represents the tensile strength; $E_s$ is the elastic modulus; and ${\mathrm{\epsilon }}_s$, ${\mathrm{\sigma }}_s$ correspondingly represent the steel strain and steel stress. The basic mechanical parameters for steel are shown in

Table 8. Applied mechanical parameters for steel.

Steel Type	Elastic Modulus (MPa)	Poisson’s Ratio	Density (kg/m3)
Q235	$2.06\times {10}^5$	0.33	7850

.

5.1.3. GFRP

The Hashin damage constitutive model [44], which was firmly grounded in the theory of damage mechanics, is adopted for GFRP. Micro-damage initiates upon the application of tensile or shear loading to the material, a phenomenon explained by this theory and leading to alterations in the material’s strength and stiffness characteristics. The effects of damage within the framework of the Hashin model are contingent upon the magnitude of the damage variable. The parameters essential for the model are detailed in

Table 9. Applied mechanical parameters for GFRP material.

Elastic Constant	$E_1$ (MPa)	$E_2$ (MPa)	$G_{12}$ (MPa)	$G_{13}$ (MPa)	$G_{23}$ (MPa)	${\nu }_{23}$
	55,000	9500	5500	5500	3000	0.33
Ultimate Strength	$X_T$ (MPa)	$X_C$ (MPa)	$Y_T$ (MPa)	$Y_C$ (MPa)	$S_L$ (MPa)	$S_T$ (MPa)
	2500	2000	50	150	50	50
Energy dissipation	$G_{ft}^c$ (N/mm)	$G_{fm}^c$ (N/mm)	$G_{mt}^c$ (N/mm)	$G_{mc}^c$ (N/mm)
	12.5	12.5	1	1

.

5.1.4. Mortar

An empirical constitutive model [45] was adopted for mortar, with Equation (5) serving as its uniaxial compressive constitutive equation.

$$y=\left\{\begin{array}{l}ax+(3-2a)x^2+(a-2)x^3 0\le x<1\\ {\displaystyle \frac{x}{b{(x-1)}^2+x}}x\ge 1\end{array}\right.$$

(5)

where a reflects the change in the deformation modulus, and b reflects the area size of the descending segment curve. According to the references, the values of a and b are determined as 2.42 and 9.76, respectively. The basic mechanical parameters for mortar are shown in

Table 10. Basic mechanical properties of the mortar.

Mortar Type	Elastic Modulus (MPa)	Poisson’s Ratio	Density (kg/m3)
M30	18,900	0.167	$1900$

.

5.2. Modeling of Bi-Material Interactions

Surface-to-surface, finite-sliding contact was used to model interactions among the outer steel tube, core concrete, the GFRP tube, and the inner steel tube. Contact behavior adopted hard contact in the normal direction with a penalty-based tangential friction law, using 0.15 as a friction coefficient. To represent weld seams, the outer steel tube—assembled from two C-shaped plates—used the same contact definitions but with the friction coefficient being 0.95. Rigid plates were attached at both ends, and tie constraints were applied to deliver uniform loading.

5.3. Boundary Conditions

The top rigid plate was constrained in all directions, with the exception of displacement loading in the z-direction. When setting the boundary conditions for the rigid plate positioned at the bottom of the specimen, it is necessary to consider two scenarios separately: the scenario with an intact outer steel tube and the scenario with a cracked weld seam. For the scenario where the outer steel tube is intact, the boundary condition was fully fixed. However, in the case of a cracked weld seam, the restraining effect of the outer steel tube undergoes a drastic diminution, which subsequently induces compressive member instability within the core concrete and ultimately results in eccentric loading of the specimen. In such circumstances, the boundary condition was designated as hinged, implying that while displacement freedom was constrained, rotational freedom remained unconstrained. The timing of these two conditions was determined through experimental observations, wherein the hybrid column fails as a result of the loss of restraining capability of the outer steel tube due to weld seam cracking, manifesting as a descending phase in the load–displacement curve.

5.4. Results and Discussions

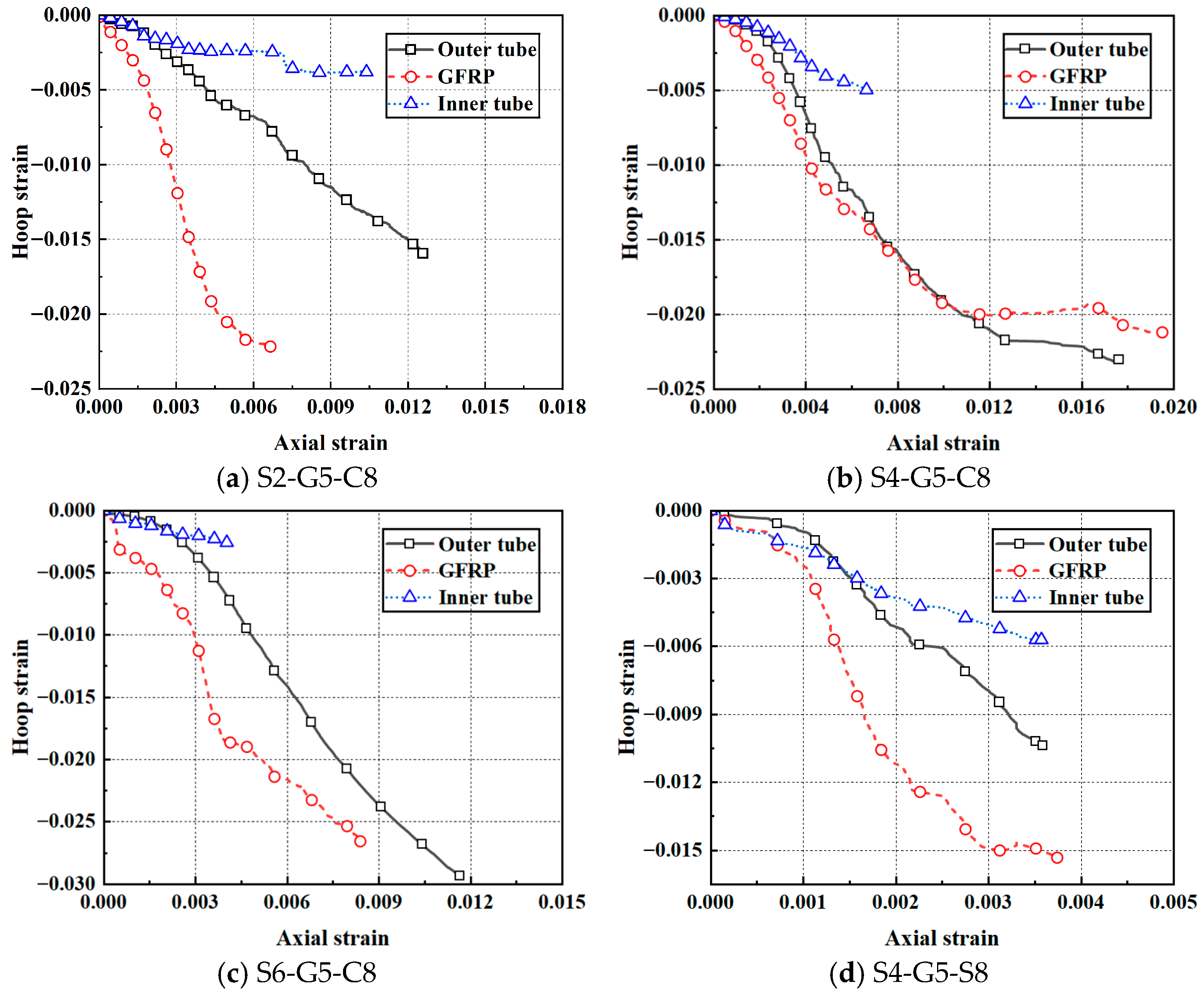
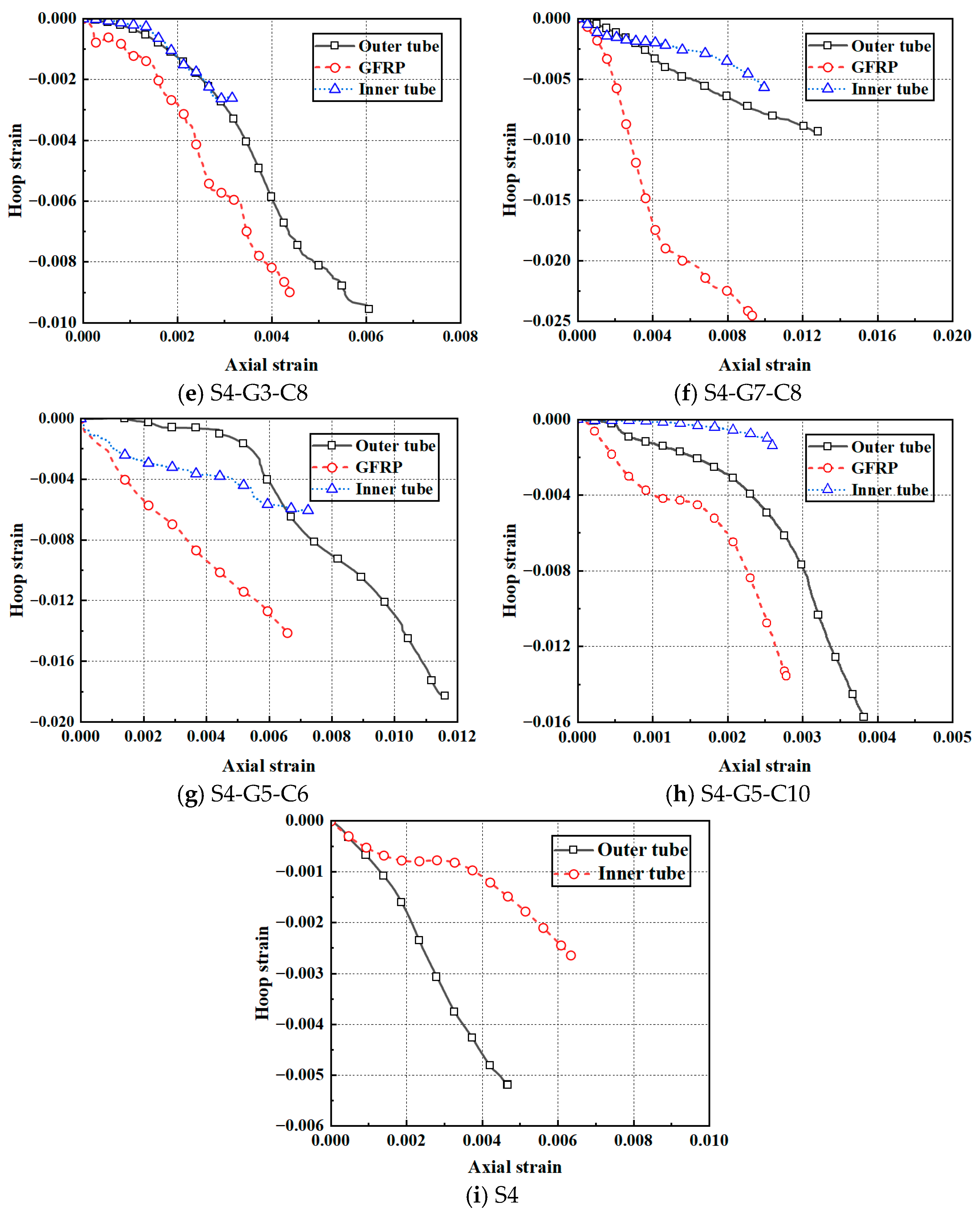
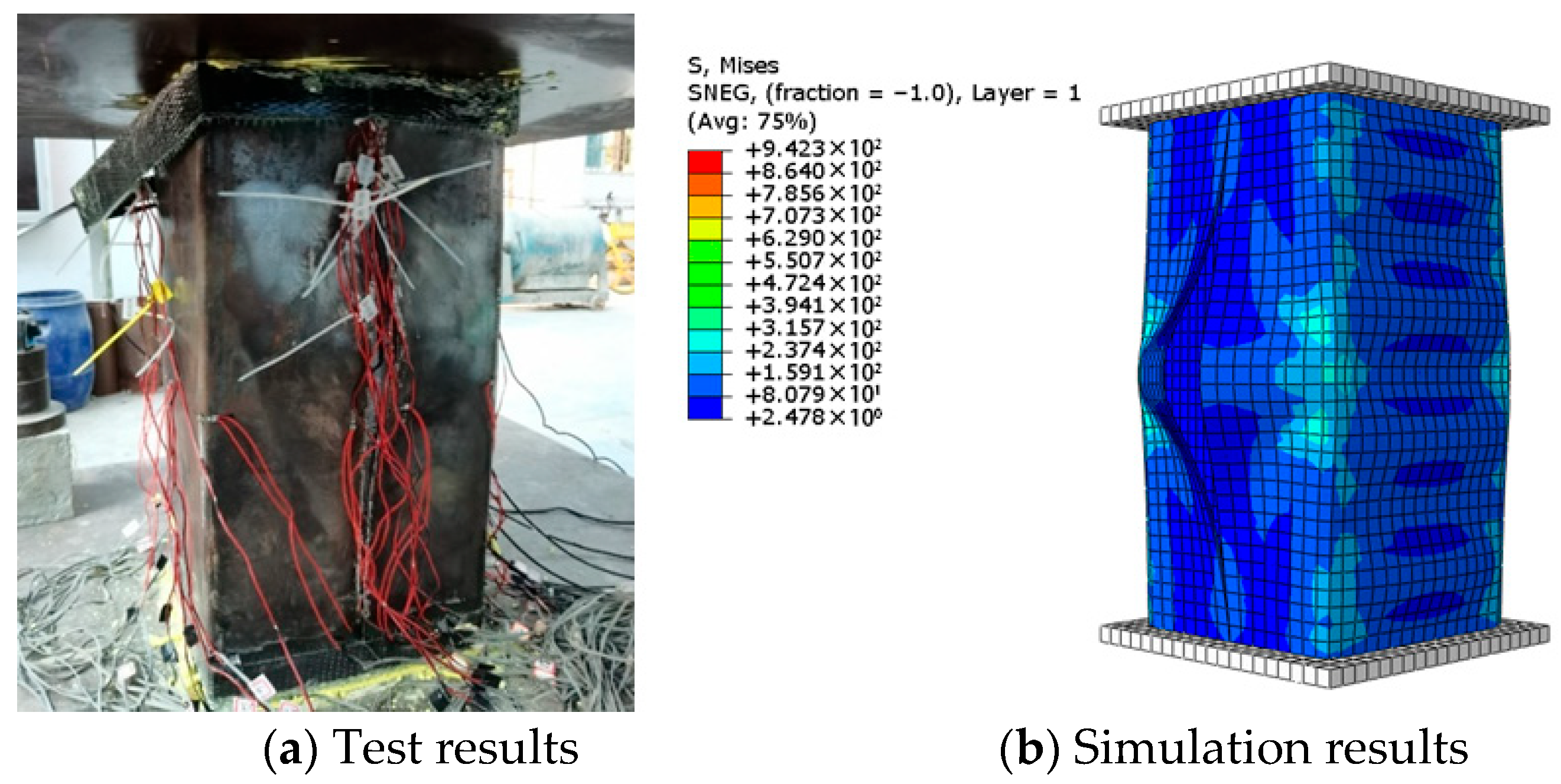
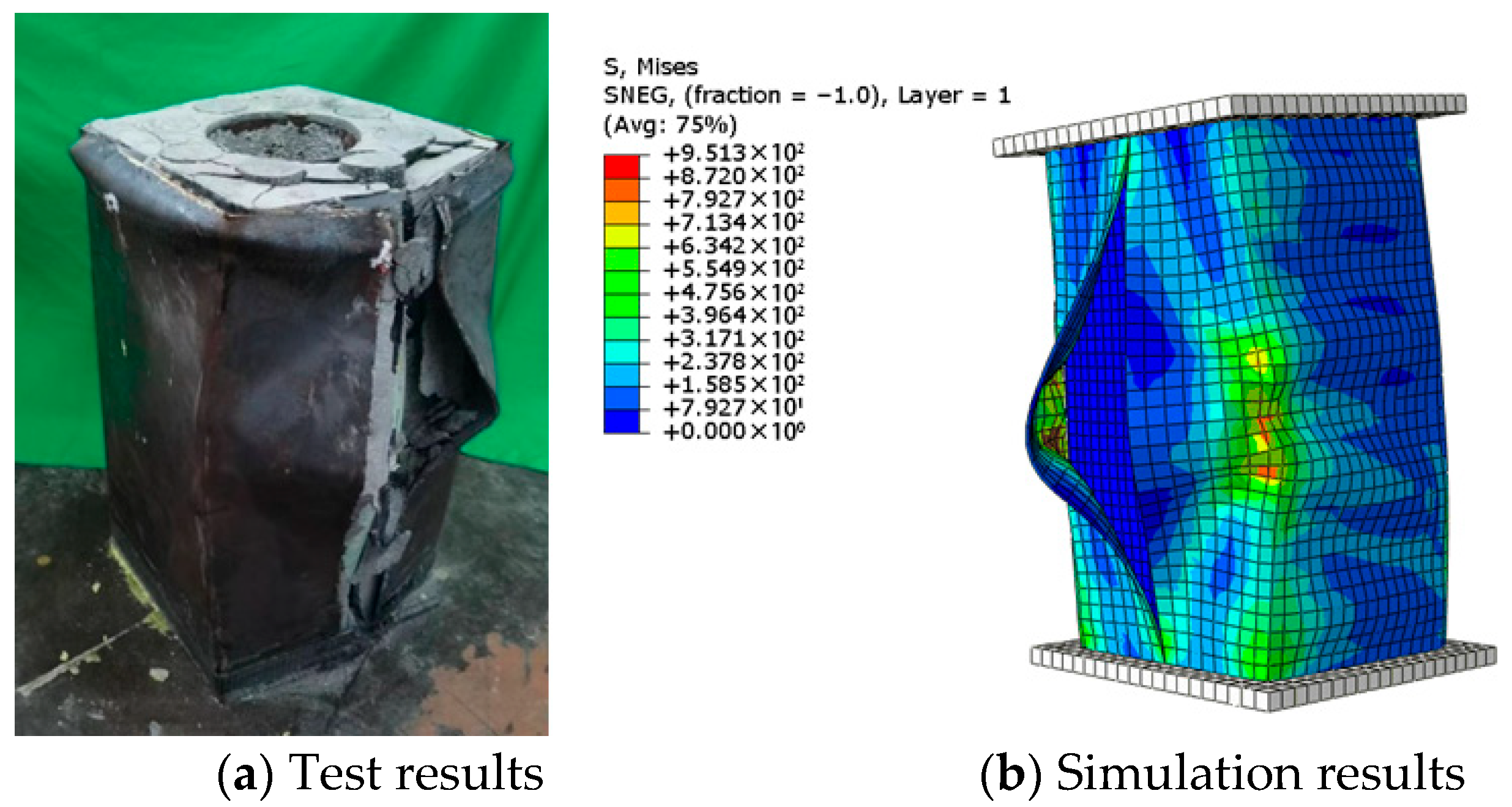
Figure 23 and Figure 24 present a comparison between FE predictions and the measured response of specimen S4-G5-C8 across the hardening and post-peak softening phases. During the hardening stage, slight welding cracks and bulging deformation of the outer steel tube were observed. During the descending stage, the ultimate bearing capacity of the specimen was reduced to below 70% of its initial value, signifying the failure of the hybrid column. At this stage, the outer steel tube exhibited complete welding cracks, along with obvious bulging deformation, and a stress concentration phenomenon was observed at the corner of steel tube. The specimen exhibited biased compression toward the weld crack, and the results of the finite element simulation were in good agreement with the experimental results.

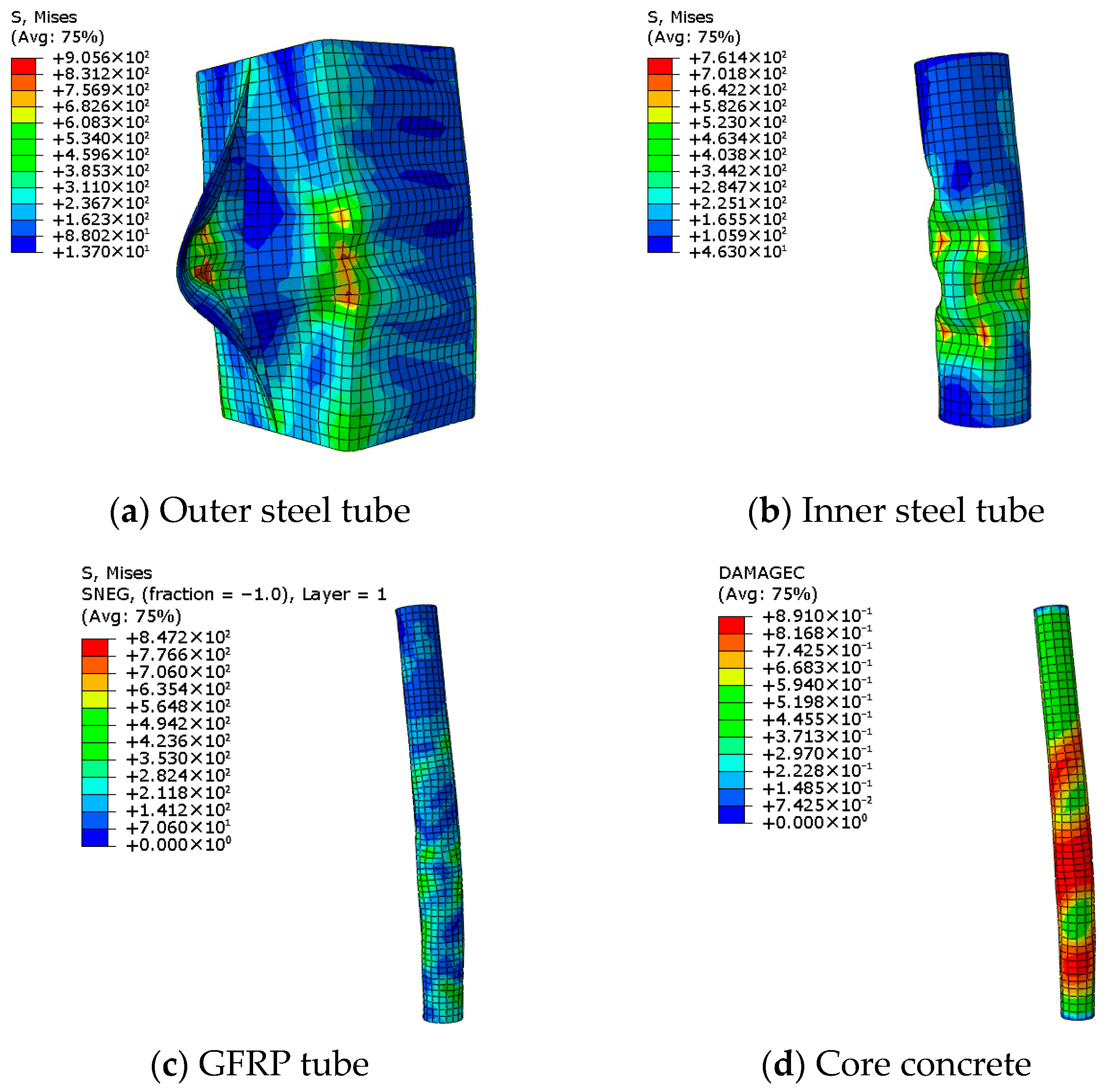
The finite element simulation results for each component, obtained when the reaction force of S4-G5-C8 was reduced to 75% of their peak values, are presented in Figure 25. Significant buckling was observed in both inner and outer steel tubes, accompanied by complete weld tearing and mortar crushing, which resulted in the loss of its restraining ability on SDCFs. The large slenderness ratio of SDCFs leads to instability of the compression bar under pressure, thereby causing the phenomenon of eccentric compression. The compressive damage to the middle and lower sections of core concrete was the most significant at this point, with a value of 0.891, accompanied by notable bending deformation. At the corresponding location within the GFRP tube, a notable bending phenomenon was also observed, accompanied by the highest stress levels. The specimen was deemed to have lost its load-bearing capacity.

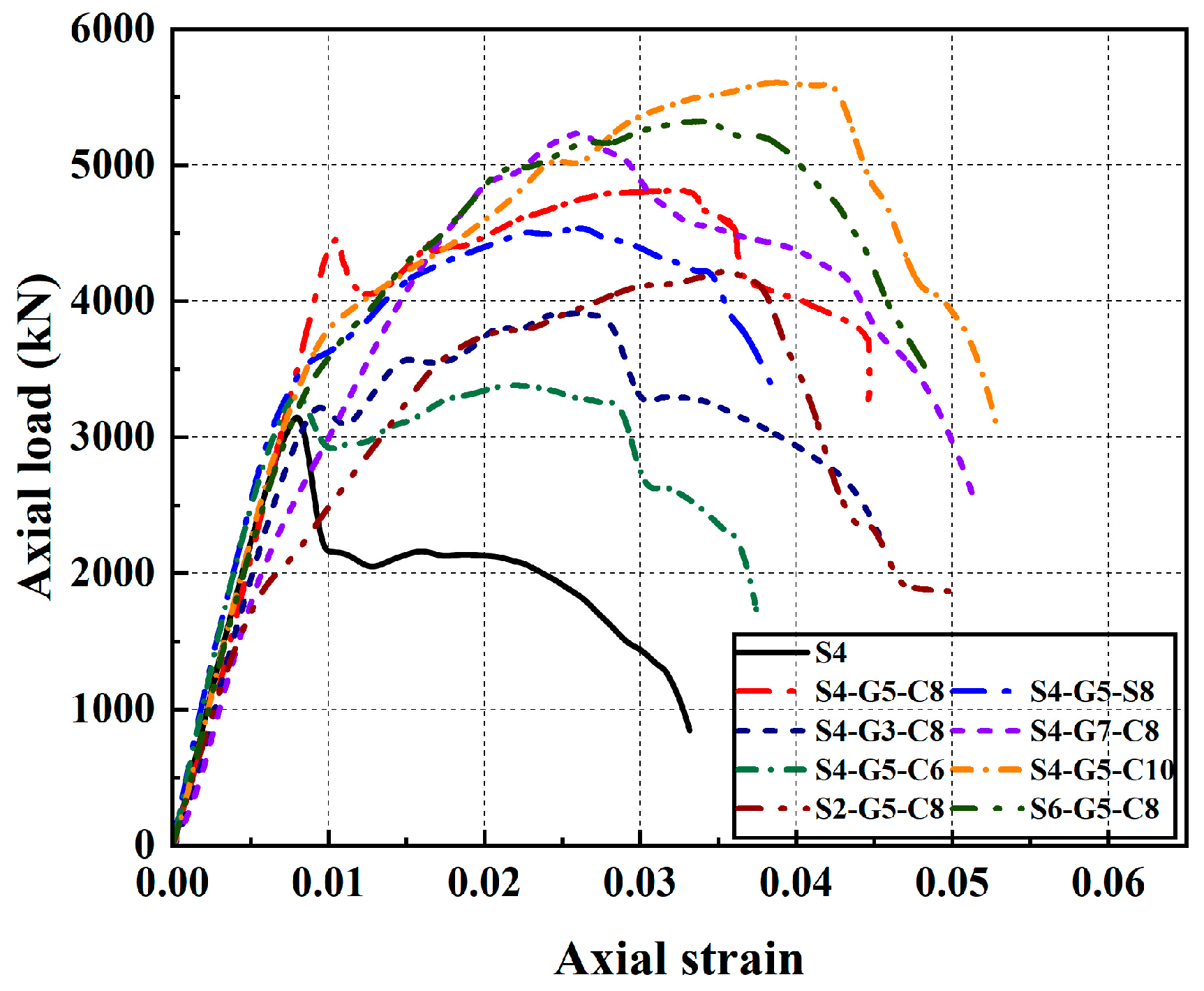
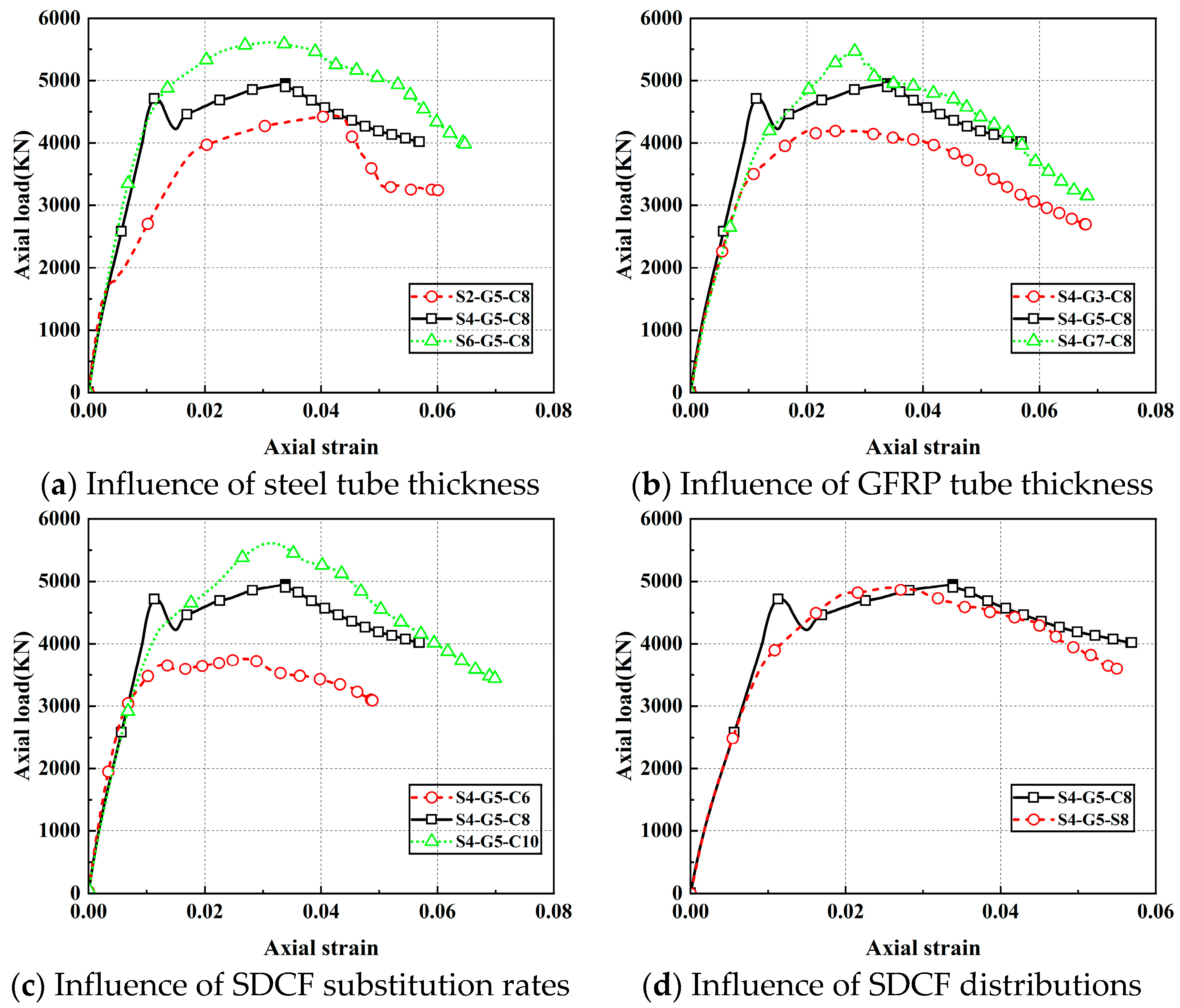
Figure 26 presents FE-simulated axial load–axial strain responses for cases with varied outer steel wall thickness, GFRP wall thickness, SDCF substitution ratio, and SDCF distribution pattern. Making the outer steel and GFRP tubes thicker, and adopting a higher substitution ratio, markedly enhances the ultimate bearing capacity and ductility of the hybrid columns. Increasing the thickness of both the outer steel tube and GFRP tube enhances the confinement on the core concrete, thereby improving the bearing capacity of the specimen. When the outer steel tube is thin, it fails to provide effective confinement to the internal components under axial load. This inadequacy leads to premature buckling and consequently shortens the elastic stage. Since the SDCF serves as the primary load-bearing component, a thicker GFRP tube enhances the bearing capacity of the SDCFs but also increases its brittleness, leading to a more pronounced post-peak decline in the hybrid column. An increase in the substitution rate results in a higher load capacity of the specimen in the strengthened section. A square GFRP tube more effectively bears the load at the specimen’s corners, ensuring a steady increase in bearing capacity and preventing a steep load drop.

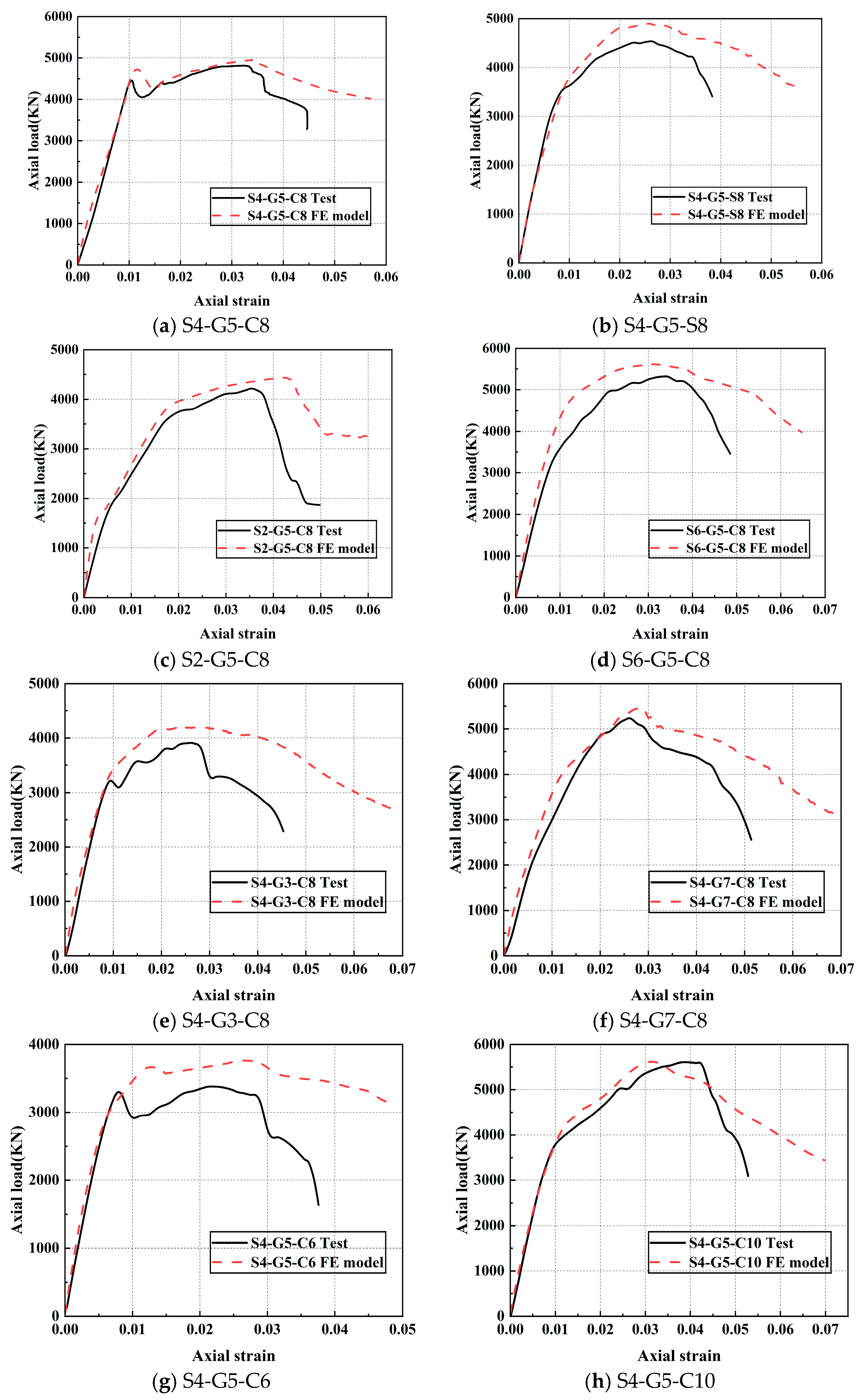
Figure 27 juxtaposes, for each specimen, the axial load–axial strain curves from experiments and FE analysis.

Table 11. The bearing capacity of the simulation and experiment.

Specimen	Experiment (KN)	Simulation (KN)	Error
S2-G5-C8	4226	4438	4.77%
S4-G5-C8	4798	4963	3.32%
S6-G5-C8	5323	5612	5.15%
S4-G3-C8	3915	4194	6.65%
S4-G7-C8	5244	5468	4.09%
S4-G5-C6	3392	3759	9.76%
S4-G5-C10	5614	5612	0.03%
S4-G5-S8	4532	4896	7.43%

compiles the ultimate capacities reported by the tests and the simulations. The numerical simulation curves closely match the experimental curves, with peak load discrepancies remaining within 10%.

The ultimate load-bearing capacity predicted by the numerical simulations exceeds that observed in the experimental curves, and the descending stage of the numerical simulation curves shows a slower rate of decline compared to the experimental results. This phenomenon was attributed to multiple factors, including the following: (1) the sedimentation and uneven distribution of aggregates in the mortar, which hindered it from achieving its optimal restraining capacity; (2) the influence of simplification of bonding condition between components; and (3) eccentricity of experimental specimens. In contrast, the numerical simulations fully accounted for the mortar’s restraining capacity. In the experiments, the hybrid column was deemed to have reached ultimate failure when the welds in the outer steel tube fully cracked, even though SDCFs had not yet completely failed. In the numerical simulations, the model was considered to have reached ultimate failure when the concrete damage exceeded 0.891, indicating the complete failure of the SDCFs. This also confirms that the SDCFs were the primary load-bearing component of the hybrid column.

6. Conclusions

The present study proposes a novel hybrid DSTC, which consists of square outer steel tubes, inner circular steel tubes, and multiple SDCFs as reinforcing confined concrete bars, with mortar filling the interstitial spaces between them. Eight SDHCBC specimens and one conventional DSTC (control) were fabricated and subjected to axial compression tests. The response of the SDHCBCs under axial load was assessed by varying key parameters—outer steel tube wall thickness, GFRP tube wall thickness, SDCF substitution ratio, and the distribution pattern of SDCFs. A complementary finite element study provided detailed stress–strain fields and clarified interactions among the constituent materials. The combined experimental and numerical investigations lead to the following principal conclusions:

(1)

The failures of all the SDHCBCs were initiated by the cracking of the outer steel tube welds, exhibiting ductile failure characteristics. The SDCFs exhibited bending deformation at the center, while the outer GFRP tube remained intact. It is believed that the SDCFs, with their large slenderness ratio, could not be effectively confined due to premature cracking of the weld, which led to instability and prevented the specimen from further bearing the load.

(2)

SDHCBCs achieved an ultimate capacity exceeding that of the DSTC control by as much as 79.6%. Increasing the outer steel and GFRP wall thicknesses and adopting a higher SDCF substitution ratio markedly boosts capacity, whereas the SDCF distribution pattern has little effect.

(3)

The ductility of SDHCBCs with square SDCF distributions exceeded that of the DSTC control by as much as 328.3%. The bearing capacity and ultimate axial strain of the core concrete were significantly enhanced due to the confinement provided by the GFRP tube. Additionally, the ductility of SDHCBCs was greatly improved by replacing part of the mortar with SDCFs.

(4)

By comparison with the previous study of the double-skin tubular-encased confined-concrete bar columns (with circular outer tubes, abbreviated as DTCBCs), the failure mode of the proposed SDHCBCs is different and the ductility is better. By means of the failure mode, the outer non-uniformly confined square tube buckled non-uniformly and the SDCFs failed in a bending-dominant way, which differ from the uniformly buckled circular tube and shearing-dominant failure of the SDCFs in the DTCBCs. As a result, the ductility of the SDHCBCs is clearly improved, which is quantitively verified by the improvement in the ductility factor from the interval of [1.5, 3.3] to [2.5, 4.4].

(5)

The simulation results of the numerical model are in good agreement with those obtained from the experiments, which validates the proposed finite element model. The finite element results indicate that when the specimen’s bearing capacity decreases to 75% of its peak load, the weld of the outer steel tube completely cracks, the damage to the core concrete reaches 0.891, the mortar fails completely, and both the inner and outer steel tubes buckle. Stress concentration occurs at the corner of the square steel tube.

(6)

Practical notes:

Practical parameter ranges tested: outer steel thickness 2–6 mm; GFRP thickness 3–7 mm; substitution ratios 18.73–38.05%; distributions tested: circular vs. square.

Common triggers for failure: weld cracking on flats as the initiator; corner stress concentration; mid-height bar bending; fiber whitening without FRP rupture.

Constructability: ensure stable mortar placement and compaction around SDCFs (vibration procedure and sealing noted in Section 2.3); end CFRP wraps to avoid premature end damage; importance of weld quality.