Calibration of Design Response Spectrum Based on Improved Particle Swarm Algorithm

Abstract

This paper proposes two improved algorithms, the DE-PSO algorithm, which combines differential evolution and phased strategy, and the hybrid particle swarm optimization algorithm integrating whale algorithm (WOAPSO), which combines the whale optimization mechanism. Compared to traditional calibration methods (such as the Newmark three- and two-parameter methods), which rely on empirical simplified models, adapting them to the complex seismic nonstationarity and multipeak characteristics is difficult. However, although intelligent optimization algorithms, such as particle swarm optimization (PSO) and differential evolution (DE) have improved calibration accuracy in recent years, insufficient convergence stability and low computational efficiency, among other problems, persist. Therefore, based on experiments, the performances of these algorithms were compared with those of standard PSO, traditional DE, and other algorithms. The results demonstrate the significant superiority of DE-PSO and WOAPSO. In 50 repeated experiments, the fitness standard deviation (STD) was significantly reduced, and the algorithms achieved rapid convergence by the mid-iteration stage, which effectively resolves the issues of premature convergence and local oscillation tendencies inherent in the standard Particle Swarm Optimization algorithm. Regarding the key parameters ($T_g$, ${\beta }_{max}$, $\gamma$) of the standard, the STD of the improved algorithm approached zero, verifying its strong adaptability to multimodal optimization problems. Furthermore, the DE-PSO algorithm had the best performance in balancing computational efficiency and stability, with a convergence speed that is three times faster than that of standard DE algorithm while maintaining the lowest parameter volatility. This study provides an efficient algorithmic tool for the rapid analysis of strong motion records and the efficient calibration of design response spectra, which has implications for the seismic optimization design of complex structures and can be guided by regulations, contributing to engineering seismic practice.

1. Introduction

The integration of optimization algorithms across various disciplines continues to drive innovation in research methodologies. In structural engineering, the study of response spectra in seismic design represents a critical area for their application. These applications can be summarized into two main pathways: in spectrum matching optimization, algorithms ensure the accuracy of ground motion inputs, thereby facilitating subsequent dynamic time-history analysis; in the development and optimization of response spectra themselves, algorithms calibrate design spectra against the response spectra derived from actual strong motion records for different conditions (such as magnitude, epicentral distance, and site characteristics), thereby providing a deeper theoretical basis for seismic design.

Various effective methods have emerged in spectrum matching optimization research. For instance, Ahmet Demir et al. [1] achieved high-precision matching of both horizontal and vertical target spectra through an improved harmony search algorithm. Another researcher, Zhijun Dai et al. [2], adopted an L1-norm minimization approach to adjust and superimpose ground motions in the time domain, generating signals compatible with multi-damping target spectra. Furthermore, Nirmal Jayaram et al. [3] utilized Monte Carlo simulation to match the target distribution of response spectra, while the work of Ali Haydar Kayhan et al. [4] further demonstrates the effectiveness of the harmony search algorithm in generating ground motion datasets that comply with the European code.

The Chinese Seismic Design Code GB 50011 [5] collects numerous strong earthquake records and converts them into impact coefficient spectra to give the standard response spectrum formulae. Under similar conditions (e.g., comparable site conditions), numerous acceleration records are processed. For a specified damping ratio, the acceleration response spectra are calculated, normalized by their respective Peak Ground Acceleration (PGA), and then subjected to statistical analysis. An averaged spectrum is obtained through this process, which is subsequently smoothed based on empirical judgment to form the “standardized response spectrum”. Finally, this normalized spectrum is multiplied by a seismic coefficient (i.e., the design ground acceleration) to yield the seismic influence coefficient curve adopted by the code—this is the seismic design spectrum. By assigning values to different parameters—such as the characteristic period $T_g$, the maximum seismic influence coefficient αmax, and the decay exponent $\gamma$—the shape of the response spectrum is adjusted to meet specific design requirements. The ability of a design spectrum to provide effective design guidance depends on a sufficient strong-motion record database, a rational classification method, an accurate target spectrum model, and an effective calibration technique. Notably, the smoothing of the response spectrum often relies on optimization algorithms to achieve its objective.

As research on earthquake engineering deepens, calibration methods for seismic design spectra are constantly evolving. Early calibration methods mainly relied on empirical formulas and simplified models, such as Newmark’s three- [6] and two-parameter methods [7]. However, these methods have certain limitations in dealing with complex seismic characteristics, making it difficult to meet the high-precision requirements of modern seismic design. With the development of optimization algorithms in recent years, calibration methods based on intelligent optimization algorithms have gradually become a research hotspot. For example, methods such as least squares [8], particle swarm optimization (PSO) [9], the differential evolution (DE) algorithm [10], the niche genetic algorithm (NGA) [11], and the Nelder Mead simplex algorithm [12] can accurately calibrate the characteristic parameters of the design spectrum through global search and multiparameter optimization.

This study utilizes the requirements of the Chinese Seismic Design Code [5] to explore several response spectrum calibration optimization methods based on particle swarm optimization improvement and compares the performance of different optimization algorithms to improve the accuracy of earthquake motion matching and optimize the representativeness of input earthquake motion. Considering factors such as the accuracy of target response spectrum matching, nonstationarity of seismic motion, and feasibility of engineering applications, several optimization algorithms are compared, and the optimal algorithm are selected. The novelty of our improved optimization algorithm lies in its ability to not only guarantee stability and accuracy but also to achieve significantly faster computational speeds. This enhanced efficiency is particularly advantageous for handling the substantial data volumes inherent in strong-motion records.

2. Design Response Spectrum

The procedure for establishing a seismic design spectrum can be summarized as the “Four Standardizations”: normalization, averaging, smoothing, and empiricism [13,14].

Normalization refers to the process of converting the absolute acceleration response spectrum of ground motion records into a normalized response spectrum or amplification factor spectrum. Averaging is the core task in developing the design spectrum. It must be conducted based on the selection and categorization of ground motion records. Factors such as the number of records, the representativeness of the selected records, the choice of classification indicators and methods, and the level of classification detail significantly influence the averaging results. These factors are also the primary source of discrepancies among different research findings. Smoothing involves processing the averaged results into smooth curves or simplified shapes according to a specific formulation. Empiricism refers to the process of finalizing the design spectrum based on expert judgment and practical experience. The target response spectra are adjusted with different correction coefficients based on site categories, magnitude, and epicentral distance. The characteristic parameters have the greatest influence on the shape of the response spectrum, which is mainly derived from the calibration of the target response spectrum, and the optimization algorithm is mostly used in calibration, which directly influences the authenticity of the characteristic values of the response spectrum.

For the purpose of analytical convenience, the dynamic amplification factor spectrum is utilized in this study. It is derived from the design response spectrum of the code and is mathematically expressed as $\beta \left(T\right)=SA\left(\mathrm{T}\right)/PGA$.

The seismic design spectrum provides important parameters for structural design, so the rationality of seismic design spectrum calibration directly affects the safety and cost of the buildings. The Chinese Seismic Design Code specifies the shape and parameters of the design spectrum, including the first inflection point period $T_0$, characteristic period $T_g$, platform value β_max, and attenuation index $\gamma$. Reasonably calibrating these parameters is the key to ensuring the accuracy of the design spectrum.

According to the Chinese Seismic Design Code GB 50011 [5], the shape of the seismic design spectrum is usually divided into ascending segment, platform segment, and descending segment, and its mathematical expression is shown in Equation (1)

$$\beta \left(T\right)=\left\{\begin{array}{c}1+T({\beta }_{max}-1)/T_0, 0<T<T_0\\ {\beta }_{max}, T_0\le T<T_g\\ {\beta }_{max}{\left(T_g/T\right)}^{\gamma },T_g\le T<T_d\\ {\beta }_{\mathit{max}\left[{0.2}^{\gamma }-0.02(T-T_d)\right]}, T_d\le T<T_m\end{array}\right.$$

(1)

$\beta \left(T\right)$ is the amplification factor spectrum, $T$ is the period, ${\beta }_{max}$ is the plateau value of the amplification factor spectrum (related to αmax), $T_0$ is the first inflection point period, $T_g$ is the characteristic period, which is determined by consulting tables in the Chinese seismic code GB 50011 based on three factors combined: Seismic Precaution Intensity, Design Earthquake Group, and Site Category. $T_d$ is the end period of the first descending segment, and $\gamma$ is the attenuation index and calculated based on the structural damping ratio (ζ). According to the GB 50011 [5], the shape of the design spectrum is also adjusted based on the site category and seismic parameters to ensure that it can reflect the seismic characteristics under different site conditions.

The calibration of seismic design spectra is not merely theoretical; it is a vital part of engineering practice. A reasonable calibration method can improve the accuracy of the design spectrum, thereby ensuring the safety of the structure under earthquake action. However, the calibration process involves overcoming many challenges, such as the complexity of seismic characteristics, the diversity of site conditions, and the sensitivity of optimization algorithm parameters.

The objective function is defined as the difference between the design response spectrum and the actual response spectrum. As shown in the following equation:

$$F\left(T_0,T_g,T_d,{\beta }_{max},\gamma \right)=\sqrt{{\displaystyle \frac{1}{T_m}}{\int }_0^{T_m}{\left[\beta \left(T\right)-{\beta }^{\prime }\left(T\right)\right]}^{2}dT}$$

(2)

A smaller value of $F$ indicates a closer match between the calibrated design response spectrum and the actual conditions. The algorithm terminates when $F$ reaches a predefined threshold, at which point the parameter values ($T_0,T_g,T_d,{\beta }_{max},\gamma$) are output as the final results.

3. PSO Algorithm and Its Improved Algorithms

PSO is an optimization algorithm based on swarm intelligence, inspired by the social behavior of biological groups, such as birds and fish. PSO searches for the optimal solution in the solution space by simulating information sharing and collaboration among individuals in a population.

The principle of the standard PSO algorithm is simple: its fewer parameters and adjustability make the algorithm easy to implement, and it has fast convergence and strong global search ability. However, its drawbacks cannot be ignored. Due to its sensitivity to parameter settings, it easily becomes stuck in local optima during computation. Therefore, standard PSO algorithms have lower search efficiency on high-dimensional problems. To improve these shortcomings, scholars have made improvements to the PSO algorithm. Liu et al. [15] introduced sine chaotic mapping and a Gaussian mutation operator to improve the convergence speed and computational accuracy of the standard PSO algorithm. Wang [16] proposed an improved simplified particle swarm algorithm based on segmented nonlinear acceleration coefficients and mean mutation strategy, as well as a hybrid multiple random mutation particle swarm differential evolution algorithm, to enhance the global and local search capabilities of the algorithm. Gong et al. [17] proposed a hybrid PSO algorithm by combining a genetic algorithm and a standard PSO algorithm. Chegini et al. [18] combined the SCA optimization algorithm, levy flight algorithm, and PSO algorithm to propose a hybrid PSO algorithm. Additionally, Wang et al. [19] combined the bee colony algorithm with the PSO algorithm to improve the optimization performance of the original PSO algorithm.

To improve the shortcomings of the standard PSO algorithm, this study proposes several improvement strategies. Specifically, by comparing the calculation results of PSO algorithms under different strategies, an optimization algorithm with fast convergence and high calculation accuracy can be achieved.

3.1. Standard PSO Algorithm

In standard PSO [20], each particle represents a candidate solution in the solution space, and its behavior is determined by two parts: the historical optimal position $p_{\mathit{best}}$ discovered by the particle itself during the search process and the global optimal position $g_{\mathit{best}}$ discovered by the entire particle swarm. The velocity and position of the particle are iteratively updated according to Equations (3) and (4).

$$v_i\left(t+1\right)=\omega ·v_i\left(t\right)+c_1·r_1·\left(p_{best}\left(i\right)-x_i\left(t\right)\right)+c_2·r_2·\left(g_{best}\left(i\right)-x_i\left(t\right)\right)$$

(3)

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$$

(4)

where $v_i\left(t\right)$ and $x_i\left(t\right)$ are the velocity and position of particle i at time t, respectively; $\omega$ is the inertial weight that controls how the particle maintains its original velocity; $c_1$ and $c_2$ are learning factors that control the degree to which particles move toward individual and global optimal solutions, respectively; $r_1$ and $r_2$ are random numbers between [0, 1].

The standard PSO algorithm involves the following steps:

(1)

Initialize particle swarm.

(2)

Calculate the fitness value of each particle.

(3)

Update the individual optimal solution and global optimal solution for each particle.

(4)

Update the velocity and position of each particle based on the velocity and position update formulae.

(5)

Repeat steps 2–4 until the termination condition is met.

3.2. Dynamically Adjusting Learning Factors

We introduced a parameter “factor” that can dynamically adjust the learning factor to improve the PSO, DE-PSO and WOAPSO algorithms. A factor is a logarithmic function that varies with the number of iterations, which can make the adjustment process change faster in the early stages and slower in the later stages. In the early stage, $c_1$ is larger and $c_2$ is smaller. Individuals tend to approach their own historical optimal solutions, enhancing their ability to develop locally. In the later stage, $c_1$ is smaller and $c_2$ is larger, and individuals tend to approach the global optimal solution, enhancing their ability to explore globally. We enabled the algorithm to dynamically balance local development and global exploration during the search process. This adjustment strategy can effectively improve the convergence speed and solution accuracy of the algorithm while preventing it from becoming stuck in local optima. The factor is shown in Equation (5), and $c_1$ and $c_2$ are calculated from Equations (6) and (7).

$$\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}=\ln \left(1+\left(e-1\right)·gen/{gen}_{max}\right)$$

(5)

$$c_1=c_{11}-\left(c_{11}-c_{12}\right)·\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}$$

(6)

$$c_2=c_{22}+\left(c_{21}-c_{22}\right)·\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}$$

(7)

where ${gen}_{max}$ is the maximum evolution generation, $gen$ is the current evolution generation. Moreover, $c_{11}$, $c_{12}$, $c_{21}$, and $c_{22}$ were set to 2, 0.5, 0.5, and 2, respectively.

3.3. Differential Particle Swarm Optimization (DE-PSO) Algorithm with Staged Strategy

Differential evolution (DE) is an optimization algorithm based on swarm intelligence that is mainly used to solve continuous optimization problems. The DE algorithm searches for the optimal solution in the solution space by simulating the mutation, crossover, and selection operations in biological evolution. Fundamentally, the DE algorithm generates new individuals by performing differential mutation and crossover operations on individuals in the population and then retains excellent individuals through selection operations, gradually approaching the optimal solution. The most critical part of the DE algorithm is the crossover, mutation, and selection of individual mutation, as the core operation of the DE algorithm generates mutated individuals by adding the difference vector between two individuals to a third individual. Crossover is the process of performing crossover operations between mutated individuals and current individuals to generate experimental individuals. The mutation vector $V_i$ can be obtained from Equation (8), and the mutated and original individuals can be crossed to obtain vector $\mathrm{Uij}$.

$$V_i=X{r}_1+f·\left(X{r}_2-X{r}_3\right)$$

(8)

$$\mathrm{Uij}=\left\{\begin{array}{c}\mathrm{V}\mathrm{i}\mathrm{j} \mathrm{i}\mathrm{f} \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(0,1\right)\le \mathrm{C}\mathrm{R}\\ \mathrm{X}\mathrm{i}\mathrm{j} \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e} \end{array}\right.$$

(9)

where $f$ is the scale factor, set to 0.8; CR is the crossover probability factor with the range of [0, 1].

After mutation and crossover, the fitness values of the experimental and current individuals are compared, and the individual with better fitness is selected to enter the next generation.

The advantages of the DE algorithm are its simple principle, easy implementation, few parameters, and adjustability, making it suitable for various complex optimization problems. This precisely compensates for the low computational efficiency of the PSO algorithm in high-dimensional complex problems. Many scholars have used the DE algorithm to calibrate the response spectra. The characteristic parameters provided by the DE algorithm for calibrating response spectra can more objectively reflect the main features of response spectra, with smaller errors and higher accuracy than those of the seismic response spectra. The DE algorithm has powerful search and optimization capabilities, but it still cannot avoid the phenomenon of search stagnation and premature convergence for specific optimization problems [21]. Moreover, the computational efficiency of the DE algorithm is relatively low.

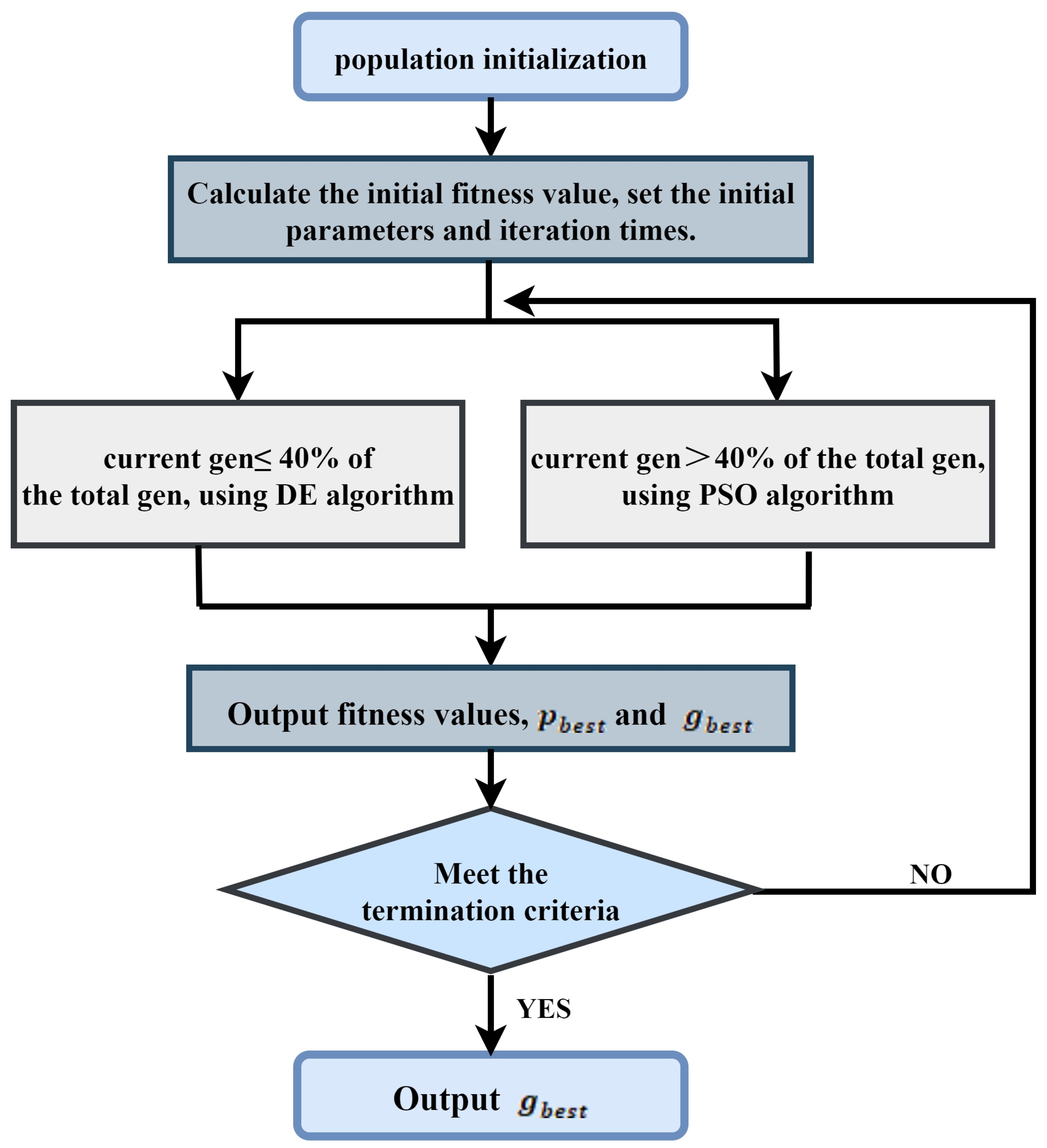
Based on the advantages and disadvantages of particle optimization algorithm and differential evolution algorithm, a phased strategy algorithm integrating DE and PSO algorithm is proposed. The algorithm employs a phased optimization strategy: during the first 40% of iterations, it utilizes Differential Evolution for global exploration, leveraging its strong global search capability; in the remaining 60% of iterations, it switches to Particle Swarm Optimization for local refinement, capitalizing on its excellent local convergence characteristics. The process of DE-PSO algorithm is shown in Figure 1. The approach employs a deterministic switch of algorithmic strategies at clearly defined generational boundaries (For the first 40% of generations), while ensuring continuity of optimization knowledge through complete inheritance of population and optimal solution information, supplemented by adaptive parameter variations to accommodate the search requirements of different phases.

3.4. Hybrid Particle Swarm Optimization Algorithm Integrating Whale Algorithm (WOAPSO)

In 2016, Mirjalili and Lewis first proposed the whale optimization algorithm [22] (WOA). This algorithm simulates the special hunting method of humpback whales. In the WOA, each whale position represents a potential optimal solution position, and the search range of the whale swarm is the entire solution space.

The WOA algorithm can be summarized into the following three calculation modes:

The first stage is the encircling prey phase. At this point, the prey’s position is the local optimal solution, and the whale approaches that position and updates its own position.

$$x_i\left(t+1\right)=x_{\ast }\left(t\right)-A·D$$

$$D=\left|C·x_{\ast }\left(t\right)-x_i\left(t\right)\right|$$

$$A=2a·r_1-a$$

(10)

$$C=2a·r_2$$

$$a=2-2t/T_{max}$$

In this equation, D represents the distance between the whale and the optimal solution, A and C are coefficient vectors, and $r_1$ and $r_2$ are random vectors that are uniformly distributed in [0, 1]. Randomness is enhanced by the random vector r₁ to prevent premature convergence, $x_{\ast }\left(t\right)$ represents the current global optimal solution position, $x_i\left(t\right)$ is the individual position, $a$ is the linearly decreasing convergence factor, and $t$ and $T_{max}$ are the current iteration times and maximum iteration times, respectively.

The subsequent phase is the bubble-net attacking stage, a simulated hunting behavior. When |A| < 1, the whale initiates the exploitation phase to narrow the encirclement. The specific updating strategy is then dictated by a probability parameter p: with a 50% chance (p < 0.5), it performs a prey-encircling motion; otherwise (p ≥ 0.5), it executes a spiral attack, and their position update formula is as follows:

$$x_i\left(t+1\right)=\mathrm{c}\left\{\begin{array}{c}{x}_{\ast }\left(t\right)-A·D,p <0.5\\ x_{\ast }\left(t\right)+D_p·e^{bl}·cos\left(2\pi l\right),p \ge 0.5\end{array}\right.$$

(11)

$$D_p=\left|x_{\ast }\left(t\right)-x_i\left(t\right)\right|$$

where $D_p$ represents the direct distance between an individual and the optimal solution that defines the radius of the spiral motion, and b is a constant vector representing the stroke line of the spiral contraction.

Furthermore, there exists a random search phase. When |A| ≥ 1, the whale population ceases to update their positions according to the current best solution. Instead, each whale updates its position based on a randomly chosen individual from the pod, with the purpose of expanding the search range.

$$x_i\left(t+1\right)=x_{rand}-A·D_d$$

(12)

$$D_d=\left|C·x_{rand}-x_i\left(t\right)\right|$$

where $x_{rand}$ is a random whale position and $D_d$ is the distance between the whale and a random location.

The spiral update mechanism of WOA simulates whales approaching prey along a spiral path, which is suitable for the fine search of local optimal solutions. Due to its early random walk and encirclement predation mechanism, it can effectively explore and avoid premature convergence, but when dealing with high-latitude problems, the convergence speed and efficiency are low.

To balance global search and local development at different stages, inertia weights are used in the WOAPSO algorithm. Shi et al. [23] first proposed the concept of inertia weight, which forms the basis of the PSO algorithm. In the PSO algorithm, the size of the inertia weight affects the iteration speed of particles. A larger inertia weight can improve the global search ability of particles, whereas a smaller inertia weight can enhance the local search ability of particles. Therefore, Shi et al. [24] proposed setting the inertia weight as a linearly decreasing coefficient from 0.9 to 0.4 to enhance the robustness of the algorithm. In this study, random inertia weights were used to improve the local search ability of particles while enhancing their global search capability in the early stage. A cosine function is used to dynamically adjust ω, which is gradually decreased as the number of iterations increases. In the initial stage, the value of ω is relatively large, and global search is emphasized; In the later stage, ω is relatively small, and the emphasis is on local development.

$$\omega ={\omega }_{min}+({{\omega }_{max}-\omega }_{min})/2·\left[1+cos\left(i-1\right)\pi /T_{max}-1\right]+\sigma ·randn$$

(13)

where ${\omega }_{min}=0.4$, ${\omega }_{max}=0.9$, $\sigma =0.3$, and $randn$ is a random number with a normal distribution.

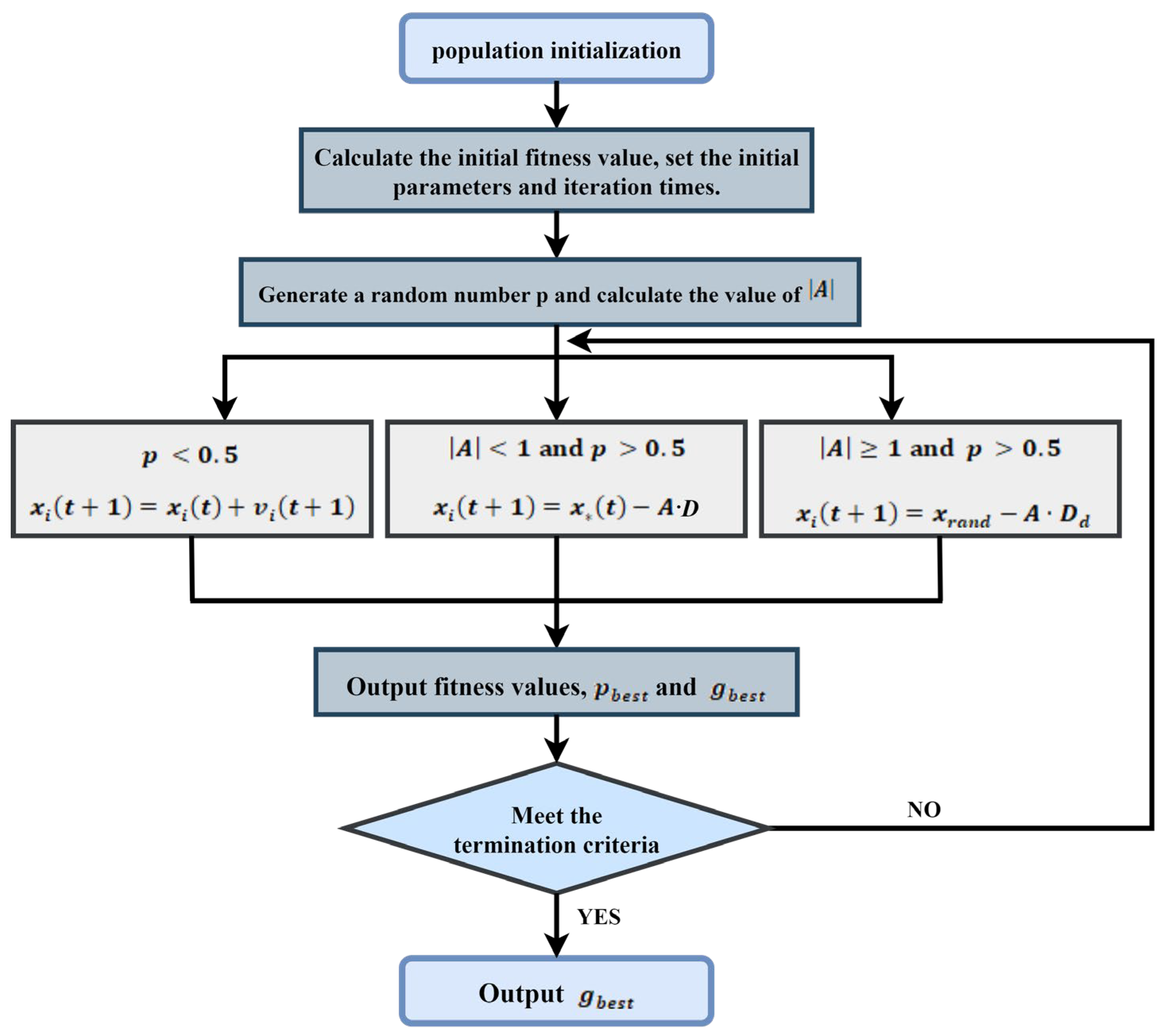
Zhang [25] combined the encirclement of prey and random search in WOA with the position update formula in the PSO algorithm, thus combining the global search ability of the PSO algorithm and the local development ability of WOA. In so doing, he introduced a random number P to increase the diversity of the algorithm. The appropriate equation of $x_i\left(t+1\right)$ is selected according to the value of P The optimization process of WOAPSO is shown in Figure 2.

4. PSO Result

This study collected a total of 50 strong earthquake records from 12 earthquakes, which were converted into amplification factor response spectra to test the calibration method. The earthquake event information is listed in

Table 1. Information of 12 earthquakes.

Seismic Event	Date	Magnitude (Ms)	Depth (km)	Strong Motion Record Count
Chi-Chi	21 September 1999	7.6	8	3
Northridge	17 January 1994	6.6	18	3
Coringa	2 May 1983	6.5	15	3
YaoAn	9 July 2009	6.3	6	4
YiLiang	7 September 2012	5.7	14	4
YingJiang	30 May 2014	6.1	12	4
LinCan	1 March 2015	5.5	11	2
MoJiang	8 September 2018	5.9	11	5
JingGu	7 October 2014	6.6	10	5
LuDian	3 August 2014	6.5	12	4
NingEr	3 June 2007	6.4	5	5
QiaoJia	18 May 2020	5.0	8	4
Yangbi	2 May 2021	6.4	8	4

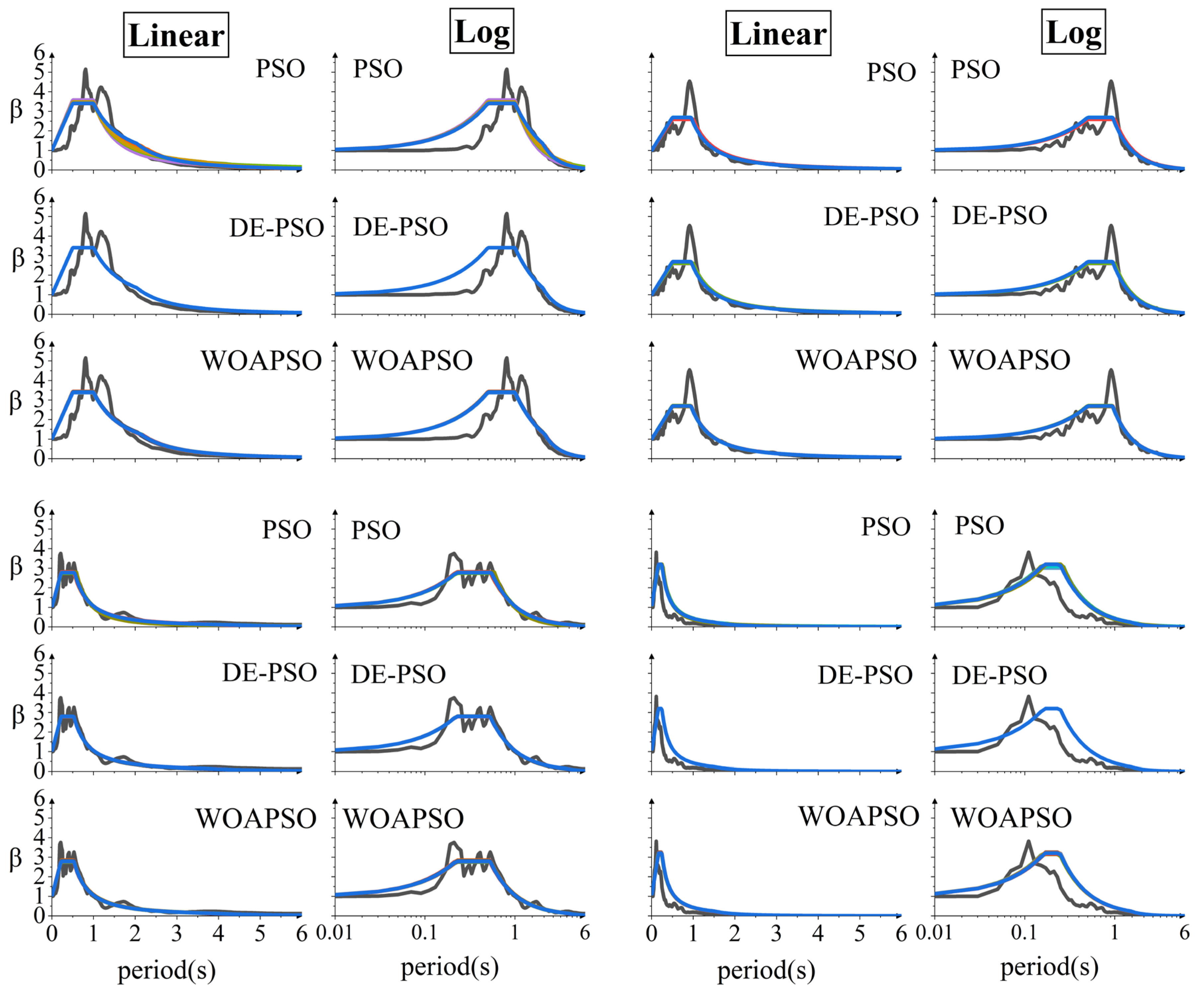
. To compare the stability of different calibration algorithms, 50 calculations with the same iteration were run for the PSO, DE-PSO, and WOAPSO algorithms. As shown in Figure 3, DE-PSO and WOAPSO maintained a high degree of consistency in their results, whereas the PSO algorithm showed differences in calibration results in some reaction spectra, indicating that the DE-PSO and WOAPSO algorithms are more stable than the standard PSO algorithm, and their calibration effects are better.

To compare their calibration effects, 10 strong earthquake records were selected from a record of 50, and the average fitness values and standard deviations were calculated. The results are listed in

Table 2. Fitness Values of the 10 Records (Mean ± SD).

Record	The Value of Fitness (Mean ± STD)
	PSO	DE-PSO	WOAPSO
1	0.384 ± 0.011	0.385 ± 0.000	0.385 ± 0.000
2	0.255 ± 0.001	0.254 ± 0.001	0.254 ± 0.000
3	0.089 ± 0.005	0.088 ± 0.000	0.088 ± 0.000
4	0.140 ± 0.004	0.138 ± 0.001	0.138 ± 0.000
5	0.170 ± 0.005	0.165 ± 0.000	0.166 ± 0.001
6	0.103 ± 0.001	0.103 ± 0.001	0.103 ± 0.001
7	0.072 ± 0.010	0.068 ± 0.003	0.067 ± 0.000
8	0.108 ± 0.011	0.105 ± 0.000	0.105 ± 0.000
9	0.132 ± 0.002	0.131 ± 0.000	0.131 ± 0.000
10	0.340 ± 0.001	0.340 ± 0.000	0.340 ± 0.000

. Comparing the fitness values of the three optimization algorithms reveals that the fitness values of all three algorithms can reach a stable minimum value after 100 iterations. However, standard deviation results indicate that the stability of the DE-PSO and WOAPSO algorithms is significantly better than that of the PSO algorithm.

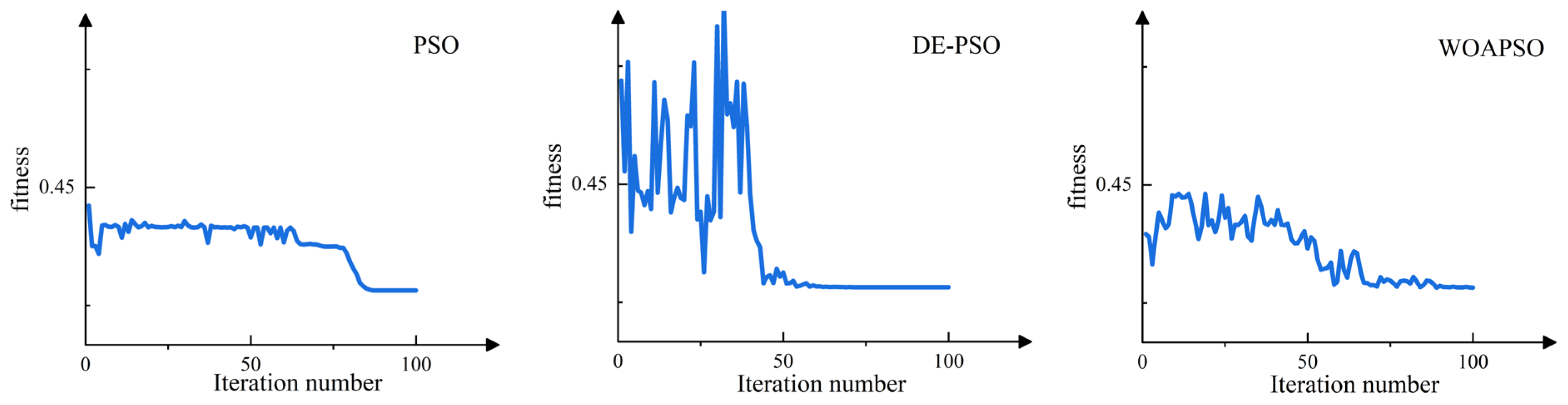
As shown in Figure 4, the PSO algorithm can only reach the minimum fitness value in the later stages of the iteration, whereas the DE-PSO and WOAPSO algorithms can identify the minimum fitness value in the middle of iteration. Specifically, the DE-PSO algorithm performs the best and has the fastest convergence. It can quickly converge and find the minimum fitness value during the alternating stage between the DE algorithm and PSO algorithm. The computation times of each algorithm for record (1) to run once are listed in

Table 3. Computation Time of Different Algorithms.

Algorithm	Time (s)	Algorithm	Time (s)
PSO	37	DE + PSO	45
DE	120	WOAPSO	40

. Compared to the DE algorithm, the PSO, DE-PSO, and WOAPSO algorithms have significantly higher computation speeds. Among them, the DE-PSO algorithm and WOAPSO algorithm can simultaneously balance computation speed and stability.

The key parameters that affect the shape of the target response spectrum are $T_g$, ${\beta }_{\mathit{max}}$, and $\gamma$. These three parameters are used as the objective function values for algorithm calibration, and the results of each parameter under different algorithms are obtained to compare the performance of different calibration methods. The objective function values, $T_g$, ${\beta }_{\mathit{max}}$, and $\gamma ,$ obtained from three optimization algorithms are listed in

Table 4. $T_g$ Values from Three Optimization Algorithms (Mean ± STD).

Record	The Value of $T_g$ (Mean ± STD)
	PSO	DE-PSO	WOAPSO
1	1.00 ± 0.000	1.00 ± 0.000	1.00 ± 0.000
2	0.97 ± 0.025	0.95 ± 0.010	0.95 ± 0.003
3	0.29 ± 0.006	0.29 ± 0.000	0.29 ± 0.002
4	0.54 ± 0.014	0.53 ± 0.007	0.53 ± 0.004
5	0.52 ± 0.002	0.52 ± 0.000	0.52 ± 0.001
6	0.32 ± 0.000	0.32 ± 0.000	0.32 ± 0.003
7	0.34 ± 0.015	0.34 ± 0.004	0.34 ± 0.003
8	0.25 ± 0.007	0.25 ± 0.000	0.25 ± 0.002
9	0.75 ± 0.007	0.75 ± 0.001	0.75 ± 0.005
10	1.00 ± 0.000	1.00 ± 0.000	1.00 ± 0.000

,

Table 5. ${\beta }_{\mathit{max}}$ Values from Three Optimization Algorithms (Mean ± STD).

Record	The Value of ${\mathit{\beta }}_{\mathit{max}}$ (Mean ± STD)
	PSO	DE-PSO	WOAPSO
1	3.42 ± 0.032	3.41 ± 0.000	3.41 ± 0.015
2	2.65 ± 0.046	2.69 ± 0.019	2.69 ± 0.011
3	2.44 ± 0.048	2.47 ± 0.000	2.45 ± 0.022
4	2.79 ± 0.011	2.80 ± 0.004	2.80 ± 0.019
5	3.13 ± 0.048	3.10 ± 0.012	3.10 ± 0.027
6	2.53 ± 0.069	2.57 ± 0.060	2.64 ± 0.071
7	1.67 ± 0.260	1.64 ± 0.003	1.64 ± 0.010
8	3.19 ± 0.044	3.20 ± 0.000	3.20 ± 0.024
9	2.17 ± 0.004	2.17 ± 0.001	2.17 ± 0.015
10	1.78 ± 0.007	1.78 ± 0.001	1.78 ± 0.013

and

Table 6. $\gamma$ Values from Three Optimization Algorithms (Mean ± STD).

Record	The Value of $\mathit{\gamma }$ (Mean ± STD)
	PSO	DE-PSO	WOAPSO
1	3.42 ± 0.032	3.41 ± 0.000	3.41 ± 0.015
2	2.65 ± 0.046	2.69 ± 0.019	2.69 ± 0.011
3	2.44 ± 0.048	2.47 ± 0.000	2.45 ± 0.022
4	2.79 ± 0.011	2.80 ± 0.004	2.80 ± 0.019
5	3.13 ± 0.048	3.10 ± 0.012	3.10 ± 0.027
6	2.53 ± 0.069	2.57 ± 0.060	2.63 ± 0.071
7	1.67 ± 0.260	1.64 ± 0.003	1.64 ± 0.010
8	3.19 ± 0.044	3.20 ± 0.000	3.20 ± 0.024
9	2.17 ± 0.004	2.17 ± 0.001	2.17 ± 0.015
10	1.78 ± 0.007	1.78 ± 0.001	1.78 ± 0.013

, respectively.

Comparing the calculation results reveals that the average value after 50 calculations is roughly the same for all three algorithms. Likewise, the comparison of the STD values for different results from the three algorithms reveals that the calculation results of the DE-PSO algorithm and WOAPSO algorithm are more stable than those of the PSO algorithm. The STD value of the DE-PSO algorithm can be stably maintained at a lower value, indicating that DE-PSO has the strongest stability.

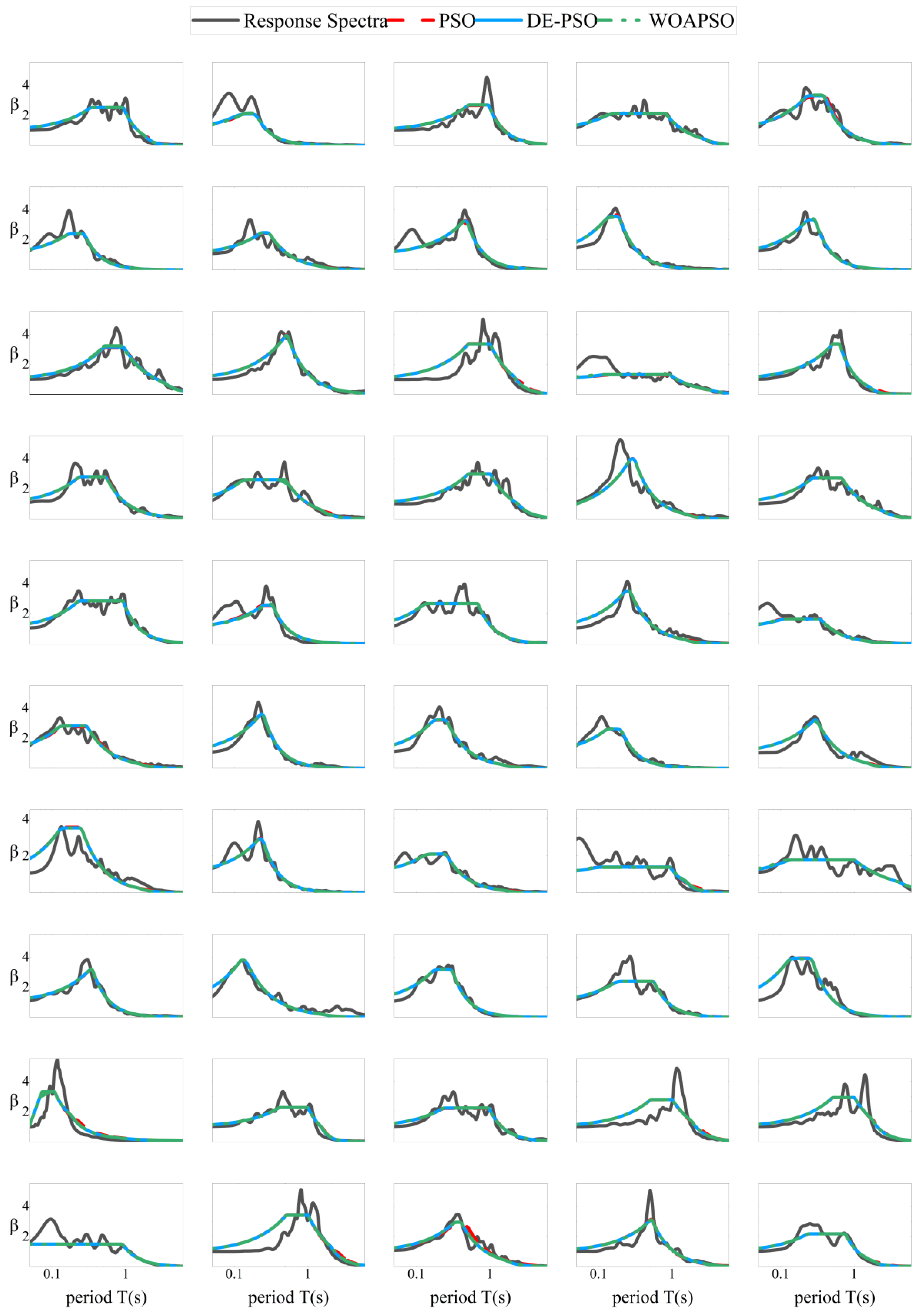
The variability in the strong earthquake records is also a major factor contributing to different shapes of response spectra. The collected records for the 50 strong earthquakes were calibrated using the PSO, DE-PSO, and WOAPSO algorithms. The calibration effect of the seismic response spectrum is plotted in Figure 5, which depicts the average value of 50 independent calibrations.

5. Discussion

Notably, the calibration results of the PSO, DE-PSO, and WOAPSO algorithms are the same in most cases. However, in some cases, the results of the PSO algorithm show significant differences, which once again demonstrates that the calibration performance and stability of the DE-PSO algorithm and WOAPSO algorithm are superior to those of the PSO algorithm.

Despite their enhanced performance, the proposed algorithms have limitations. Their hybrid switching mechanism is currently deterministic, and future work should develop adaptive strategies guided by convergence metrics. Moreover, the control parameters were set empirically, and systematically tuning these parameters to achieve the ultimate effectiveness of the algorithms is a key objective for further investigation.

For the dynamic amplification factor spectrum, the influence of site category cannot be ignored. Aicha Rouabeh et al. [26] highlighted the amplification effects in soft soils and developed site-specific prediction models for Peak Ground Acceleration (PGA) and Peak Ground Velocity (PGV), which improved the accuracy of PGA and PGV predictions. Qi et al. [27] found that site thickness and ground motion intensity have nonlinear effects on amplification, indicating that the dynamic amplification factor is not a fixed value of 2.5. In this study, the focus is on the performance of optimization algorithms in calibrating response spectra, and the influence of soft soils on $T_g$ and ${\beta }_{\mathit{max}}$ has not been considered. However, in future research, it is essential to classify and calibrate the amplification factor spectrum according to site categories.

6. Conclusions

(1)

This study applied the PSO algorithm to the calibration calculation of the design response spectra, verified its feasibility, and improved the standard PSO algorithm by proposing DE-PSO and WOAPSO. The high stability of the two improved algorithms in the calibration of response spectra was also verified.

(2)

The statistical results of 50 repeated experiments revealed that the standard deviation (STD) of the average fitness values of the DE-PSO and WOAPSO algorithms was significantly lower than that of the PSO algorithm, and they could converge to the minimum fitness value in the middle of the iteration. In fact, the STD of the fitness values for DE-PSO and WOAPSO was near zero in the majority of experiments, underscoring their remarkable convergence stability. This indicates that the improved algorithm effectively overcomes the premature convergence and local oscillation problems of standard PSO by introducing dynamic optimization strategies, such as DE and PSO, and enhances the robustness of the parameter calibration process.

(3)

For the calibration of key parameters ($T_g$, ${\beta }_{max}$, $\gamma$) in the reaction spectrum, the mean results of the three algorithms were similar, but the STD of the calibration results of DE-PSO and WOAPSO was lower than that of the PSO algorithm. Especially for the $T_g$ parameter, the STD value of DE-PSO stabilized and approached zero. This indicates that the improved algorithm can effectively suppress random fluctuations in complex multimodal optimization problems, ensure high repeatability of parameter calibration results, and provide more reliable theoretical parameter inputs for engineering seismic analysis.

(4)

Compared to traditional DE and PSO algorithms, DE-PSO and WOAPSO possess significantly higher computational speeds without sacrificing stability. Tests show that DE-PSO cuts single-run computation time by 75 s relative to DE. While the enhanced PSO versions do not greatly accelerate the standard PSO, they substantially improve its stability. This feature makes them suitable for response spectrum calibration scenarios that require high real-time performance and accuracy, such as the rapid analysis of strong earthquake records, providing an efficient algorithm tool for structural seismic optimization design.