Numerical Simulation and Model Validation of Multispiral-Reinforced Concrete Columns’ Response to Cyclic Loading
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
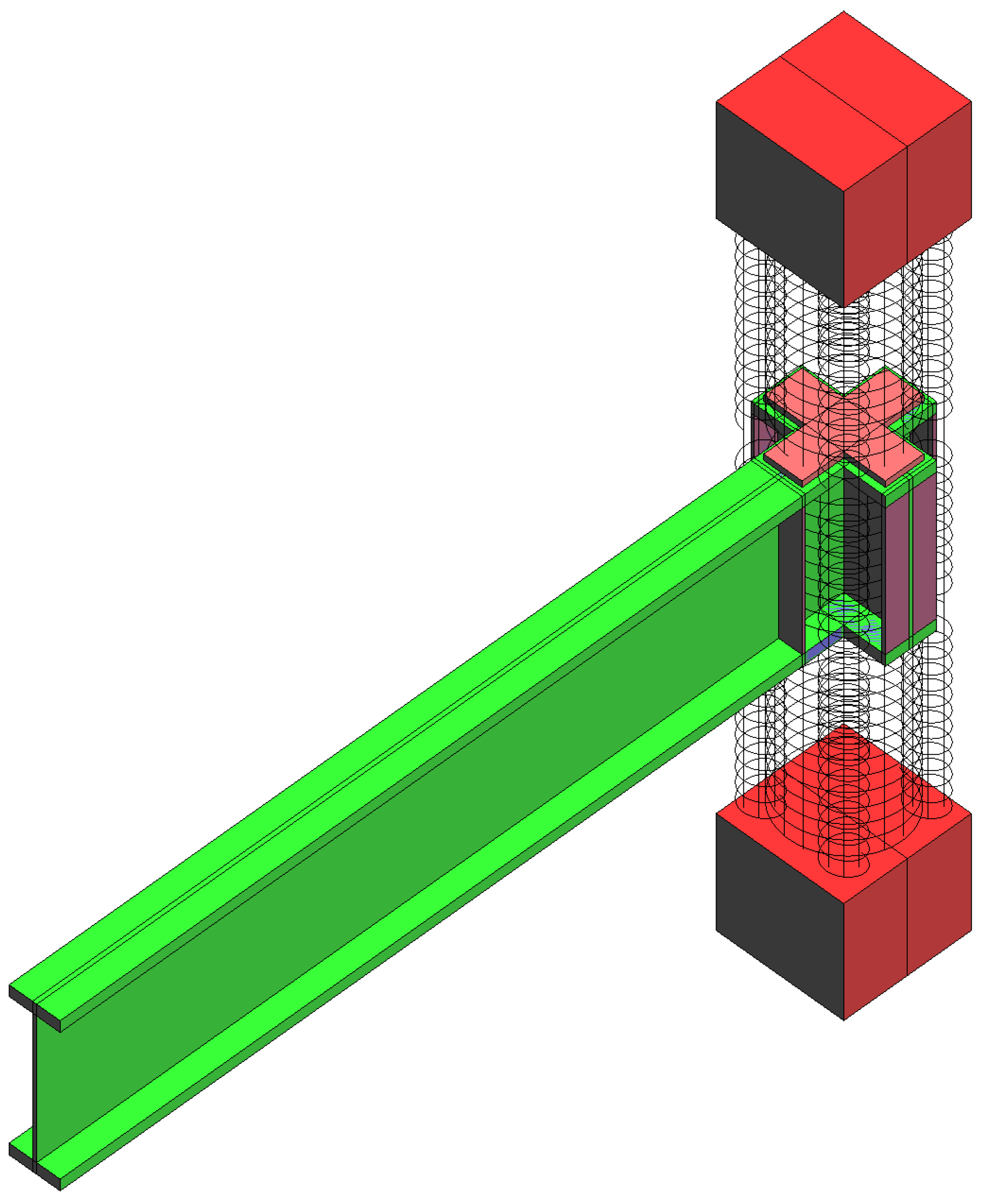
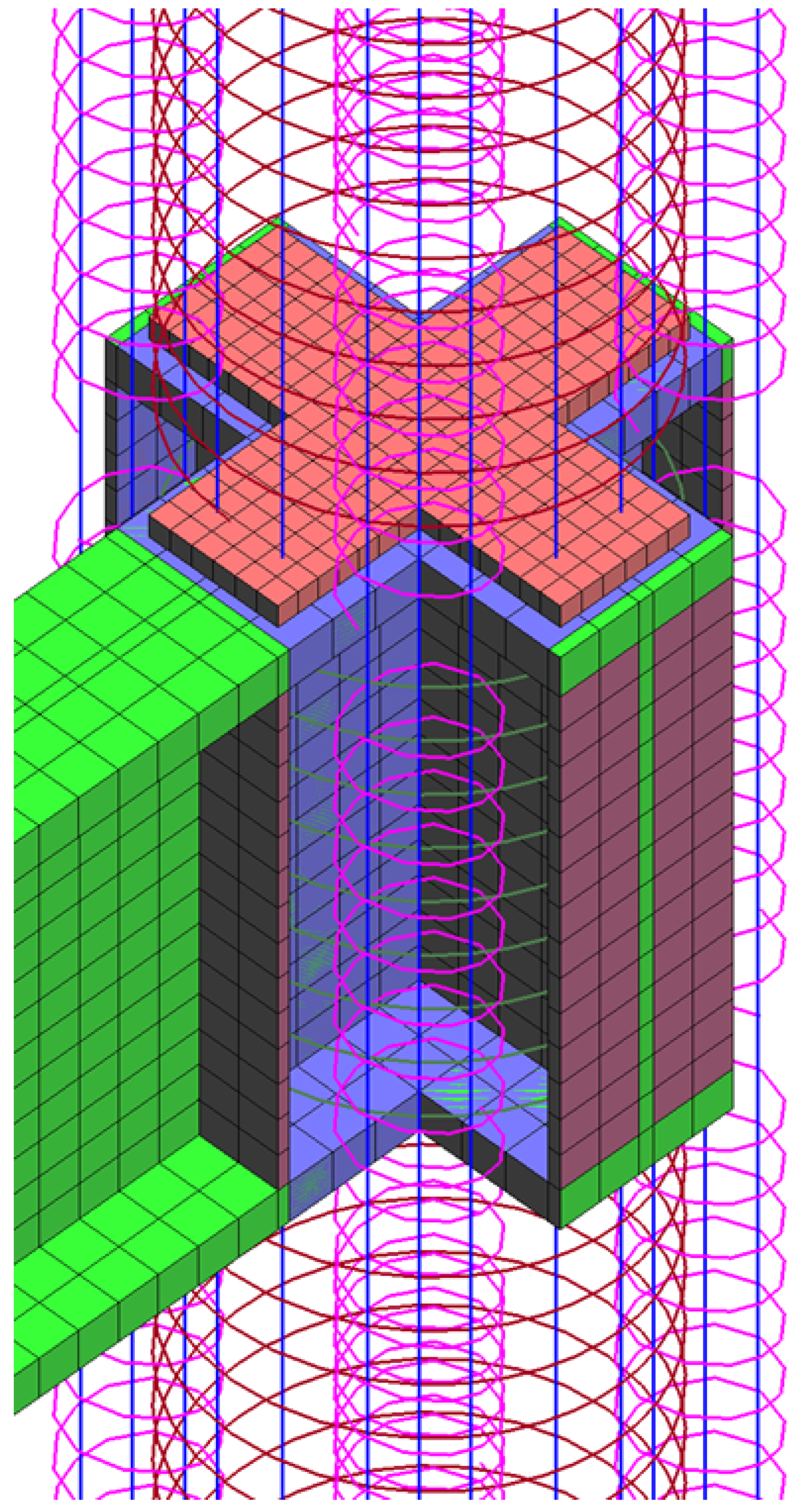
2.2. Geometrical Model
2.3. Material Models
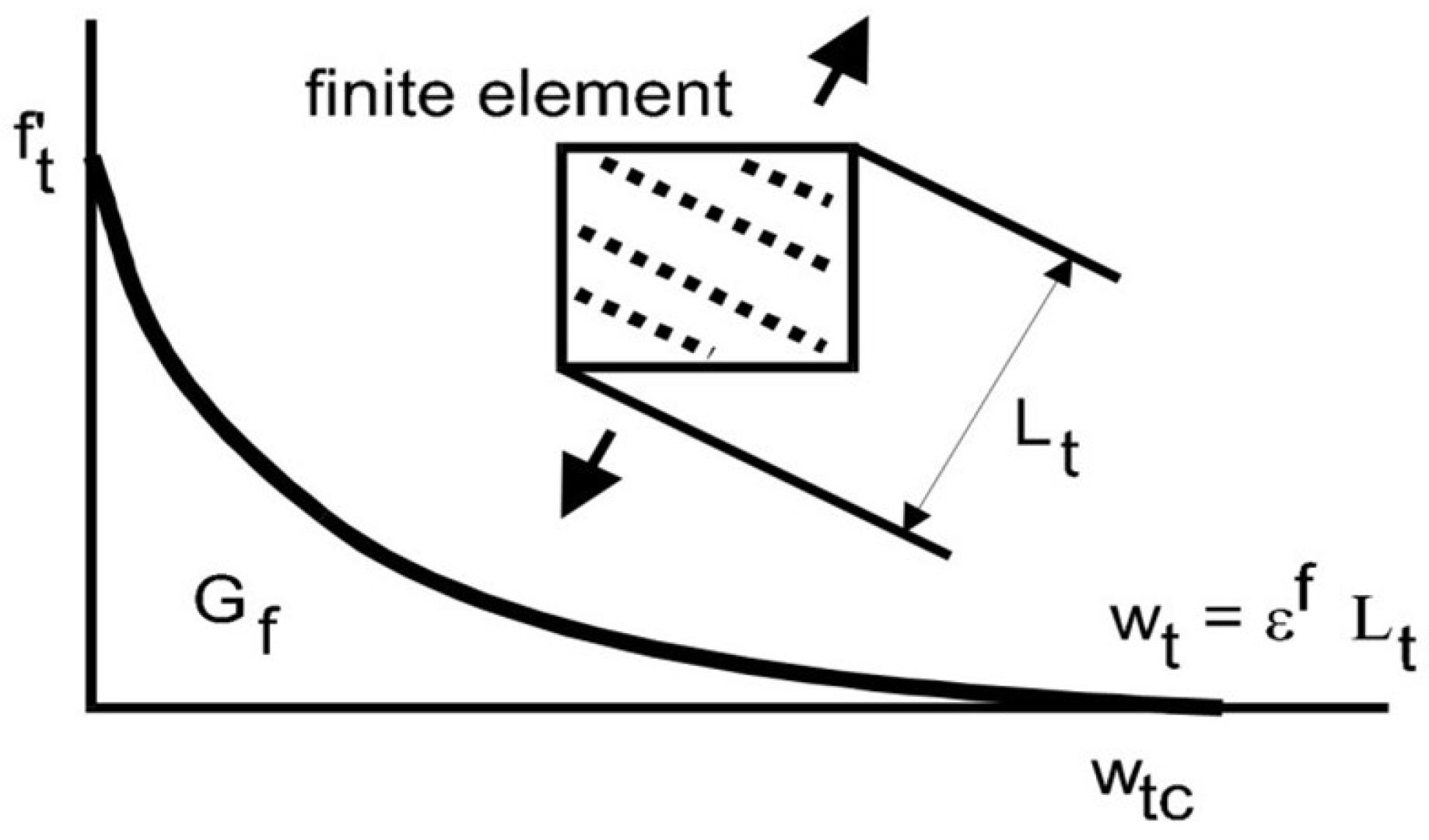
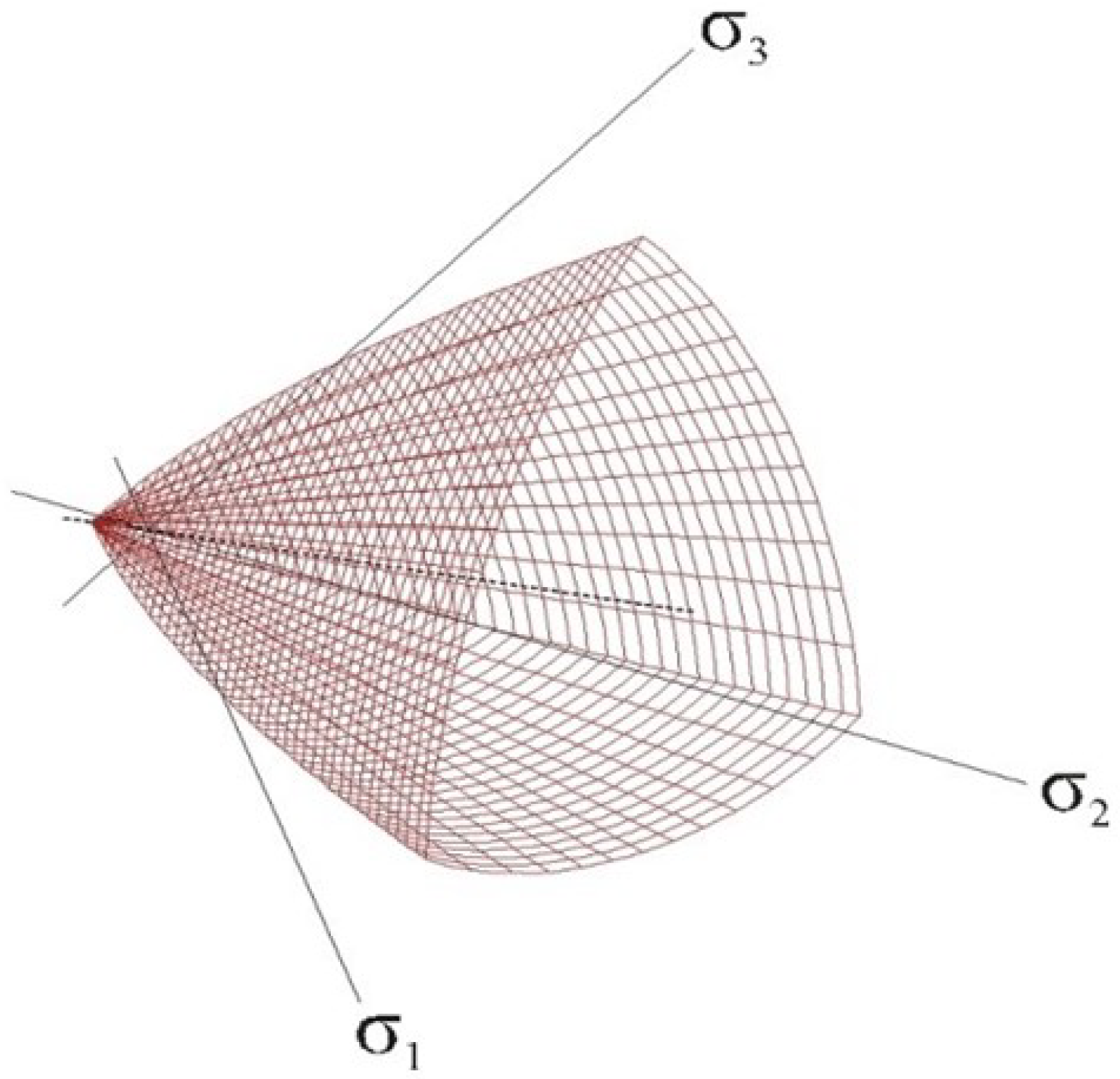
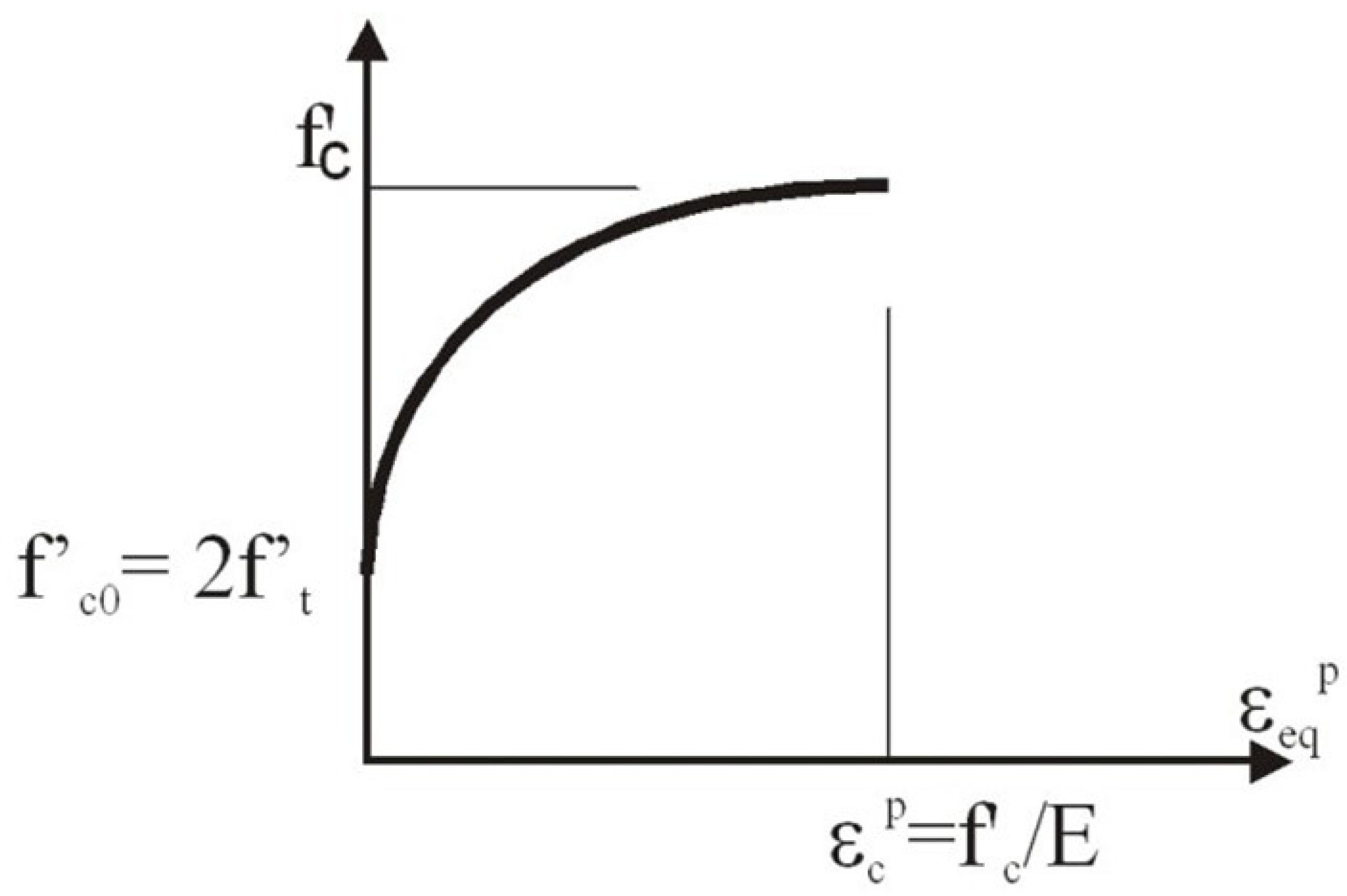
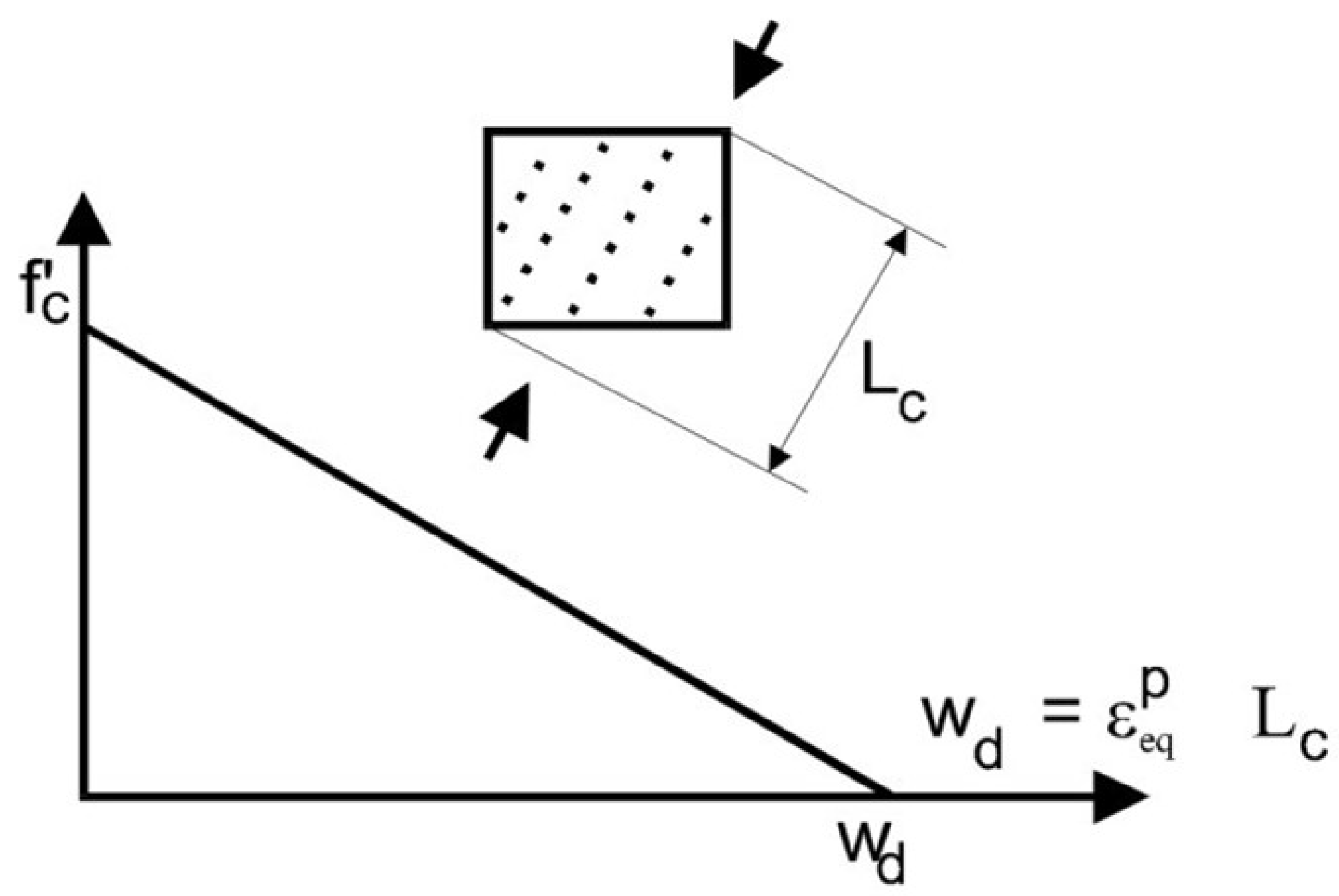
2.3.1. Concrete Material Model
- 1.
- Shear stiffness and residual stiffness of cracked concrete (aggregate interlock effect);
- 2.
- Reduction in compressive strength due to cracks perpendicular to the load;
- 3.
- Bond slip of reinforcement;
- 4.
- Tension stiffening;
- 5.
- Dowel action and bending stiffness of reinforcement;
- 6.
- Loss of bond between reinforcement and concrete.
2.3.2. Steel Material Model
2.4. Boundary Conditions and Model Properties
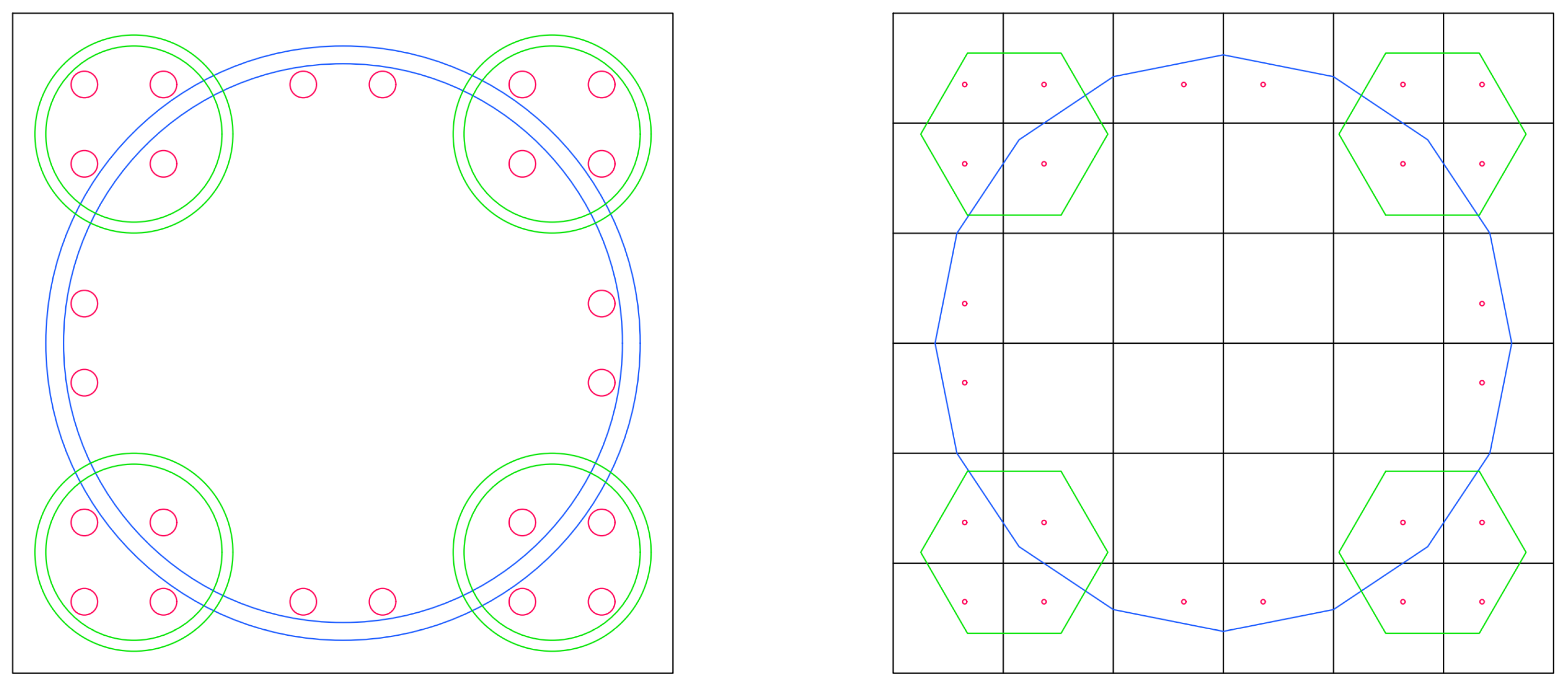
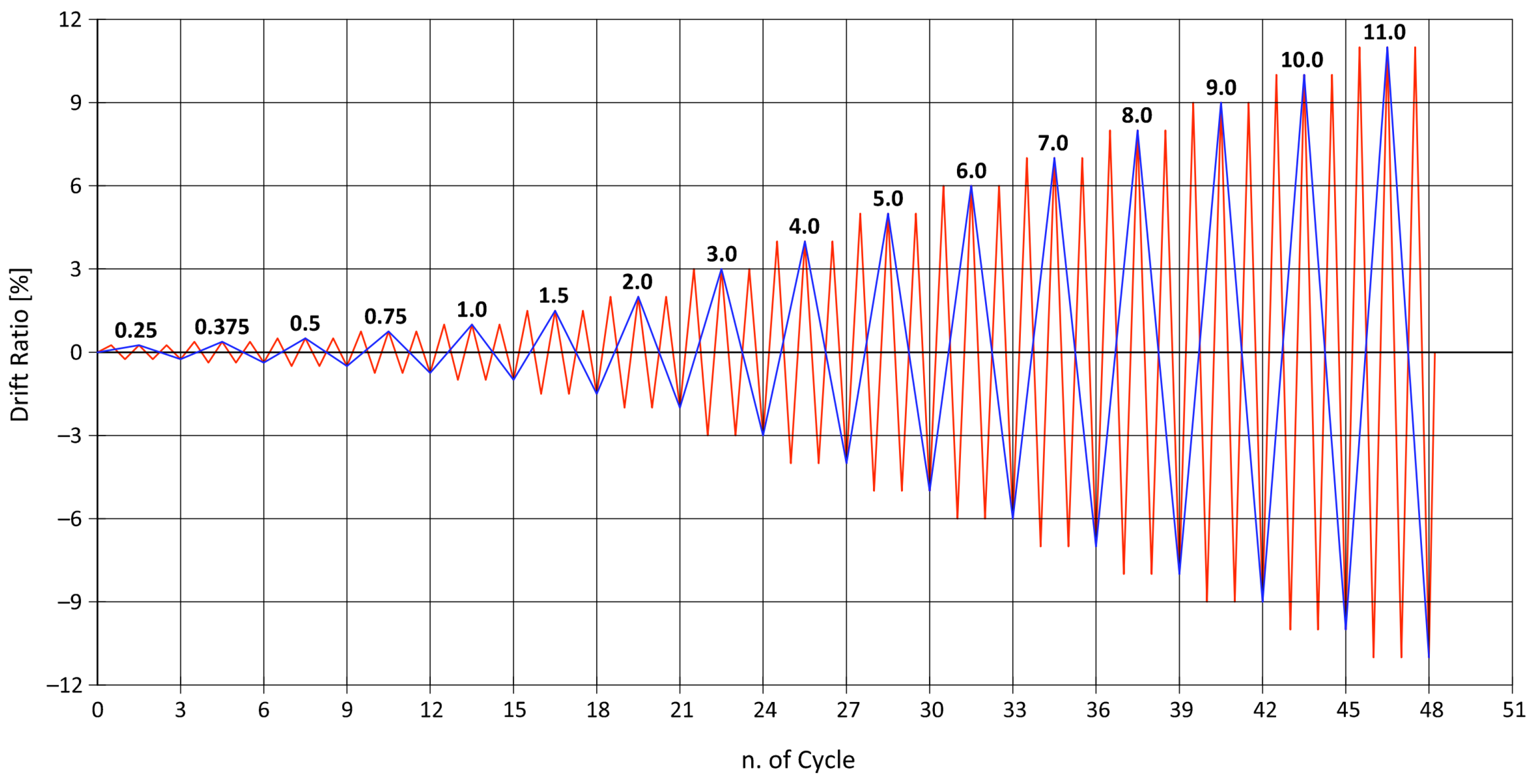
2.5. Parametric Model Generation
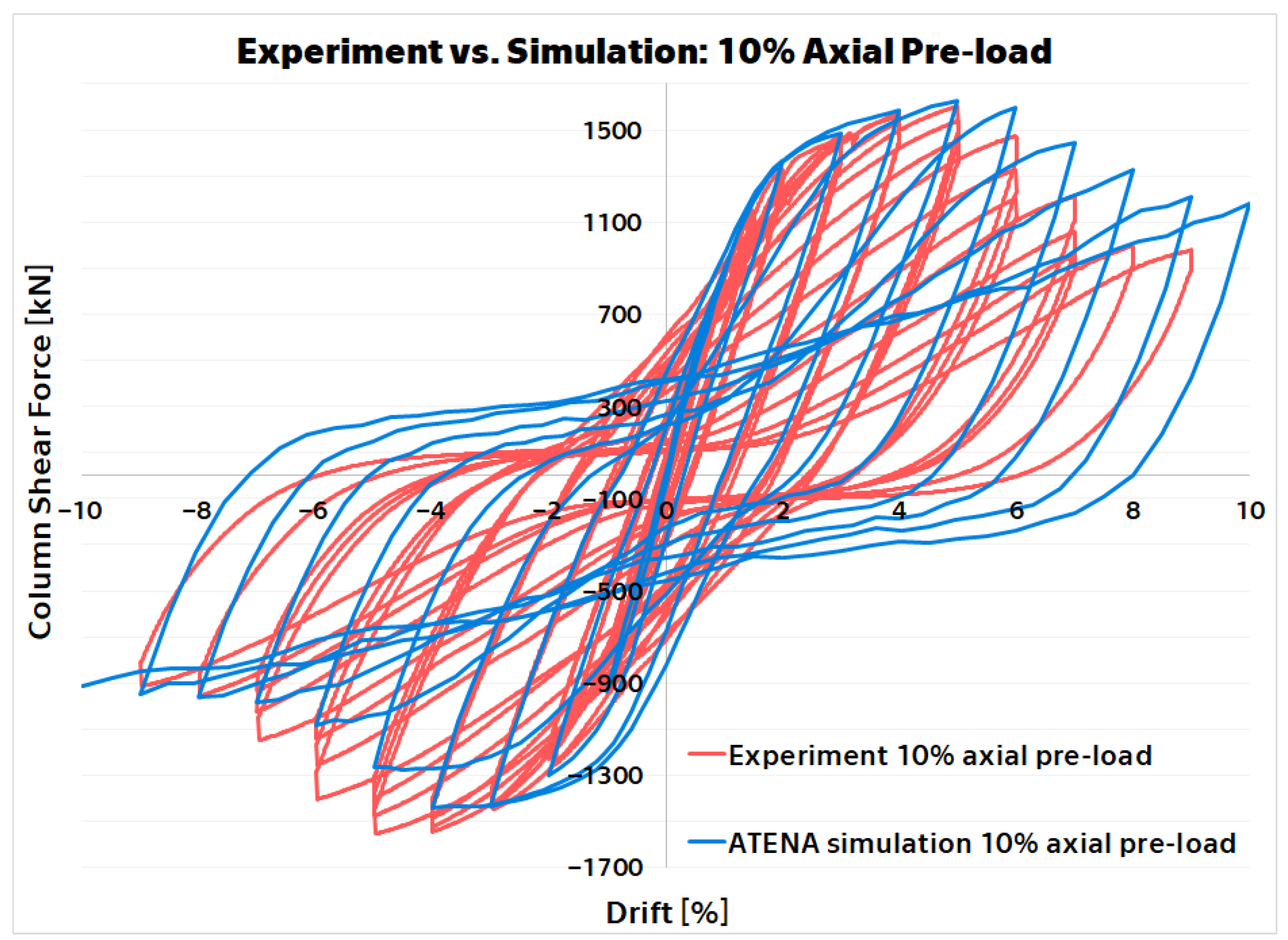
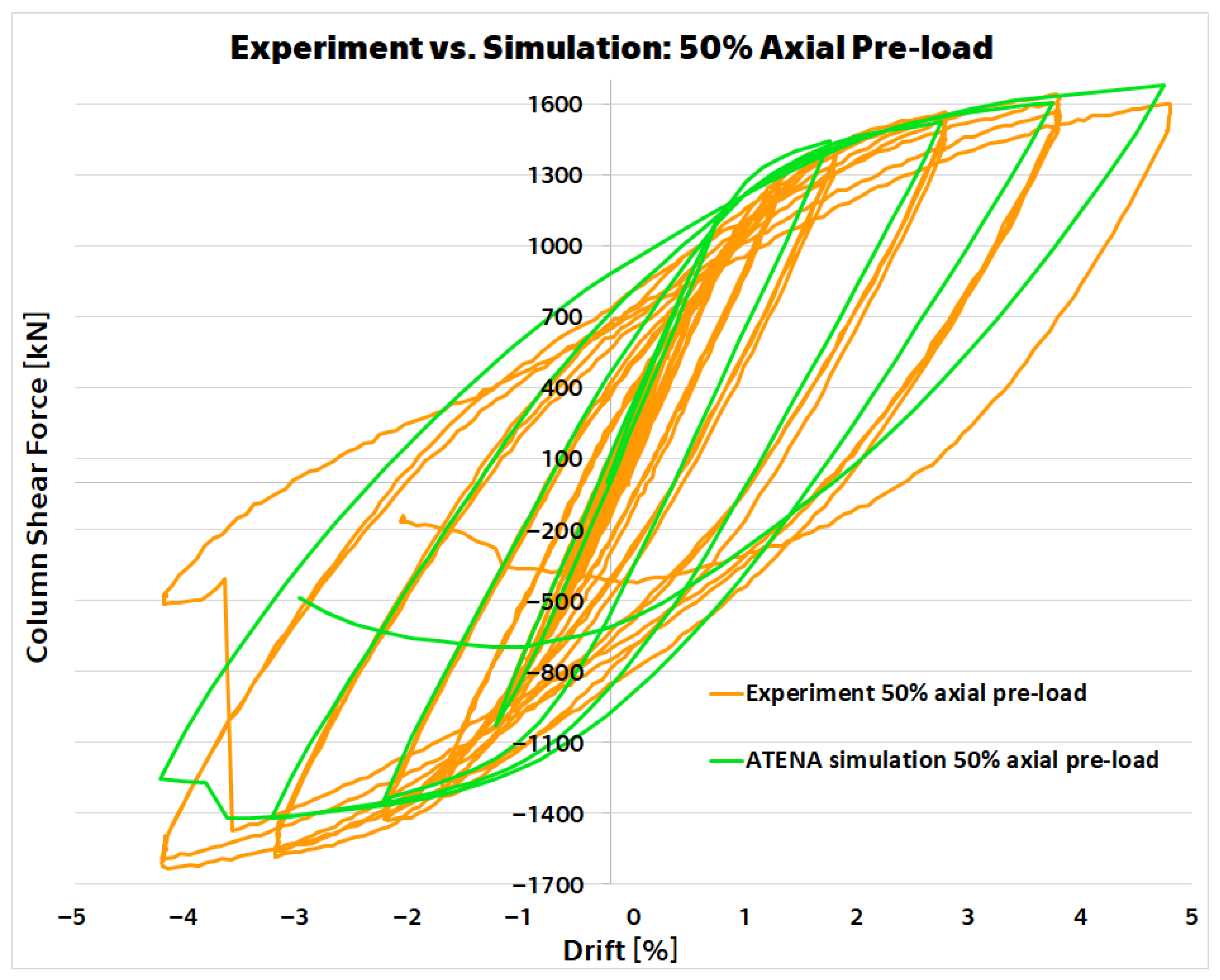
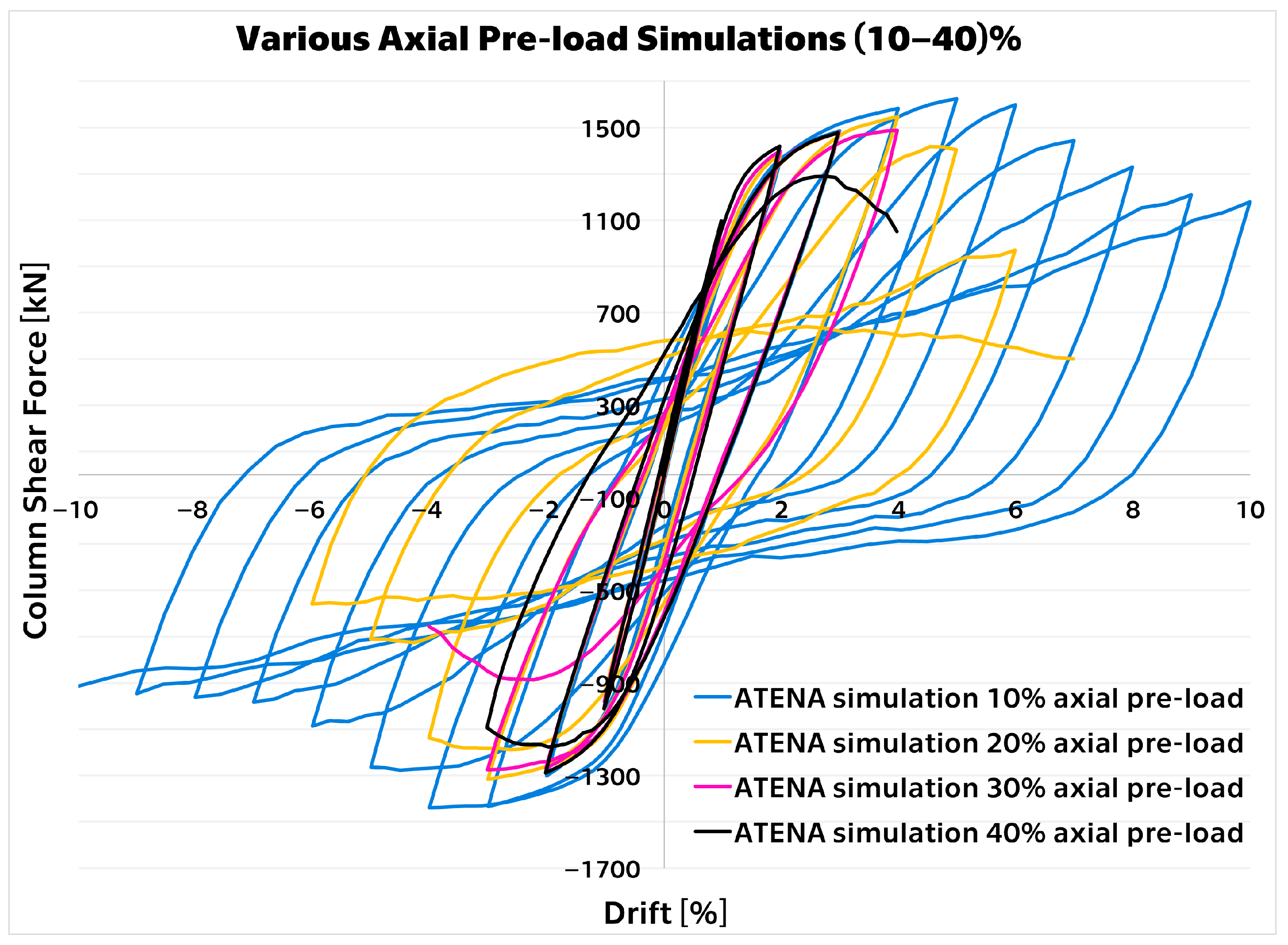
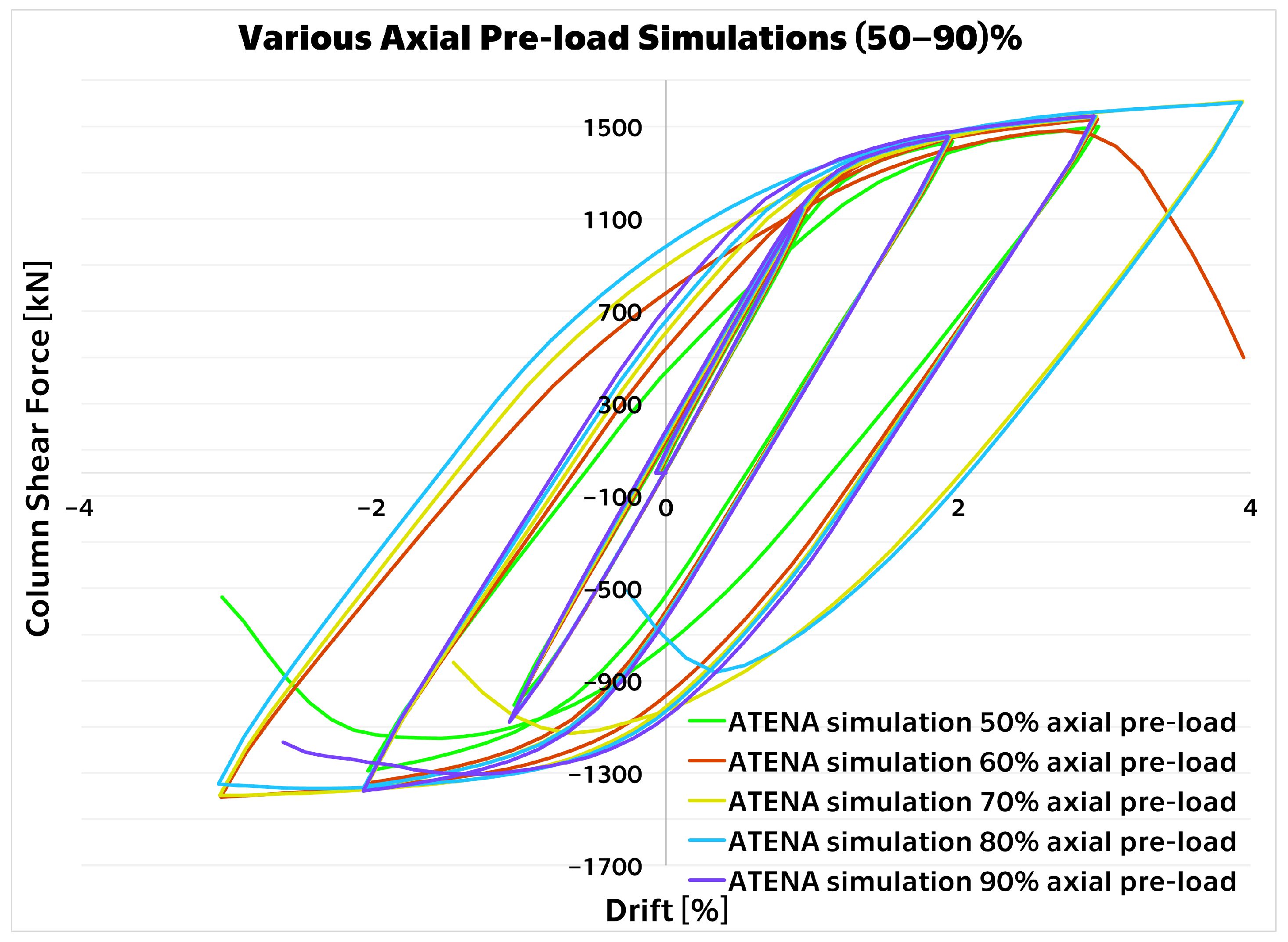
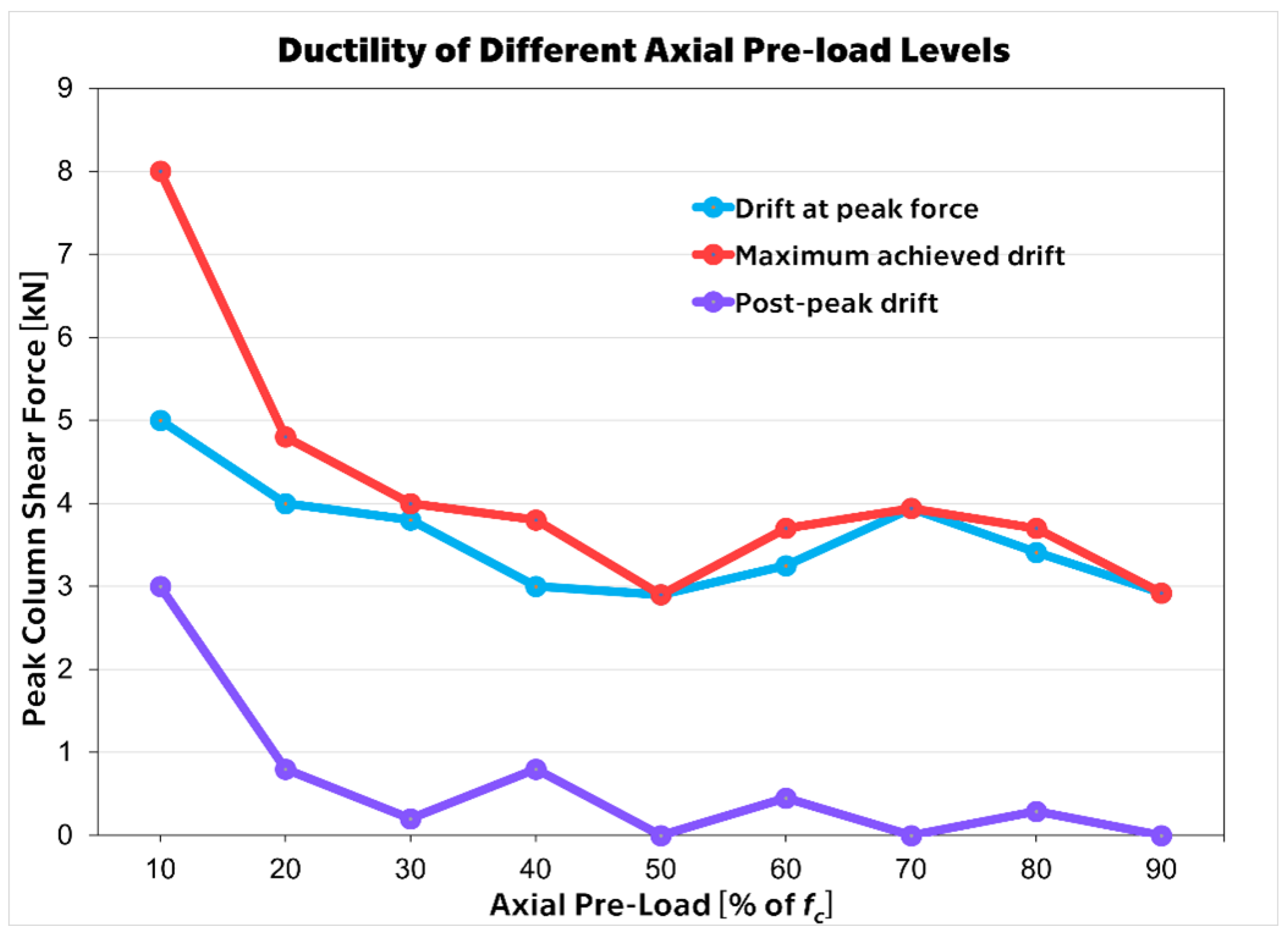
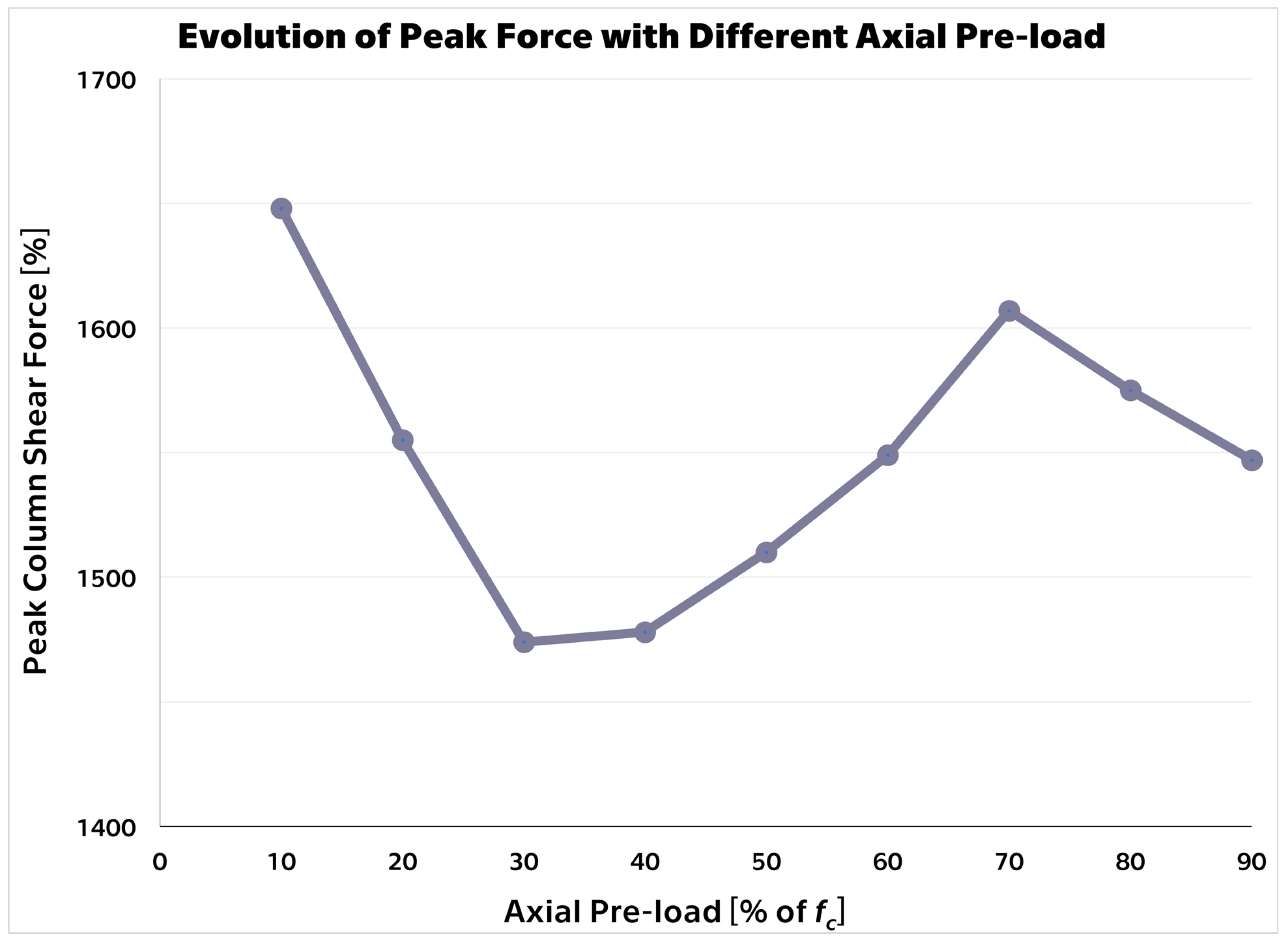
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| HP | High Pre-load |
| LP | Low Pre-load |
| MCFT | Modified Compression Field Theory |
| MRCCs | Multispiral-Reinforced Concrete Columns |
Appendix A. Code Samples
Appendix A.1. XML Part

Appendix A.2. Python Part


References
- Yin, S.Y.L.; Wang, J.C.; Wang, P.H. Development of multi-spiral confinements in rectangular columns for construction automation. J. Chin. Inst. Eng. 2012, 35, 309–320. [Google Scholar] [CrossRef]
- Kim, H.G.; Jeong, C.Y.; Kim, D.H.; Kim, K.H. Confinement effect of reinforced concrete columns with rectangular and octagon-shaped spirals. Sustainability 2020, 12, 7981. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, X.; He, L.; Zhang, X.; He, M. Behavior of large-scale concrete columns reinforced with high-strength and high-toughness steel bars under axial and eccentric compression. J. Build. Eng. 2023, 79, 107766. [Google Scholar] [CrossRef]
- Havlásek, P.; Jirásek, M.; Bittnar, Z. Modeling of precast columns with innovative multi-spiral reinforcement. In Proceedings of the fib Symposium, Krakow, Poland, 27–29 May 2019; pp. 2301–2307. [Google Scholar]
- Algamati, M.; Al-Sakkaf, A.; Bagchi, A. Energy Dissipation Technologies in Seismic Retrofitting: A Review. CivilEng 2025, 6, 23. [Google Scholar] [CrossRef]
- Hao, M.; Zheng, W.; Chang, W. Compression behavior of reinforced concrete columns jacketed with multi-spiral transverse reinforcement. Struct. Concr. 2022, 23, 2942–2967. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Yin, S. Compressive behavior of reinforced concrete columns confined by multi-spiral hoops. Comput. Concr. 2012, 9, 341–355. [Google Scholar] [CrossRef]
- Ou, Y.C.; Ngo, S.H.; Yin, S.Y.; Wang, J.C.; Wang, P.H. Shear behavior of oblong bridge columns with innovative seven-spiral transverse reinforcement. ACI Struct. J. 2014, 111, 1339. [Google Scholar] [CrossRef]
- Wang, P.H.; Chang, K.C.; Yin, S.Y.L.; Wang, J.C.; Sung, Y.C.; Hung, H.H. Seismic performance of large-scale rectangular reinforced concrete bridge columns with multi-spiral reinforcement. Earthq. Spectra 2023, 39, 1837–1858. [Google Scholar] [CrossRef]
- Liu, B.; Fan, W.; Guo, W.; Chen, B.; Liu, R. Experimental investigation and improved FE modeling of axially-loaded circular RC columns under lateral impact loading. Eng. Struct. 2017, 152, 619–642. [Google Scholar] [CrossRef]
- Fawaz, G.; Murcia-Delso, J. Three-dimensional finite element modeling of RC columns subjected to cyclic lateral loading. Eng. Struct. 2021, 239, 112291. [Google Scholar] [CrossRef]
- Cervenka, V.; Cervenka, J.; Pukl, R. ATENA—A tool for engineering analysis of fracture in concrete. Sadhana 2002, 27, 485–492. [Google Scholar] [CrossRef]
- Joju, J. Development of Composite Beam-Column Joints for New RCS Systems. Ph.D Thesis, National Taiwan University, Taiwan, China, 2024. [Google Scholar]
- CIMNE. GiD: The Personal Pre and Post Processor; Version 17.0.5; International Center for Numerical Methods in Engineering (CIMNE): Barcelona, Spain, 2025; Available online: https://www.gidhome.com/ (accessed on 25 September 2025).
- Hasan, A.M.; Torky, A.A.; Rashed, Y.F. Geometrically accurate structural analysis models in BIM-centered software. Autom. Constr. 2019, 104, 299–321. [Google Scholar] [CrossRef]
- Cervenka, V.; Jendele, L.; Cervenka, J. ATENA Program Documentation Part 1 Theory; Červenka Consulting s.r.o.: Prague, Czech Republic, 2007; Volume 231. [Google Scholar]
- Červenka, J.; Papanikolaou, V.K. Three dimensional combined fracture–plastic material model for concrete. Int. J. Plast. 2008, 24, 2192–2220. [Google Scholar] [CrossRef]
- Carol, I.; Rizzi, E.; Willam, K. A unified theory of elastic degradation and damage based on a loading surface. Int. J. Solids Struct. 1994, 31, 2835–2865. [Google Scholar] [CrossRef]
- Simo, J.; Kennedy, J.; Govindjee, S. Non-smooth multisurface plasticity and viscoplasticity. Loading/unloading conditions and numerical algorithms. Int. J. Numer. Methods Eng. 1988, 26, 2161–2185. [Google Scholar] [CrossRef]
- Červenka, J.; Kishen, J.C.; Saouma, V.E. Mixed mode fracture of cementitious bimaterial interfaces:; Part II: Numerical simulation. Eng. Fract. Mech. 1998, 60, 95–107. [Google Scholar] [CrossRef]
- Hordijk, D.A.; Reinhardt, H.W. Growth of discrete cracks in concrete under fatigue loading. In Toughening Mechanisms in Quasi-Brittle Materials; Springer: Berlin/Heidelberg, Germany, 1991; pp. 541–554. [Google Scholar]
- Červenka, V.; Jendele, L.; Červenka, J. ATENA Program Documentation–Part 1; Červenka Consulting s.r.o.: Prague, Czech Republic, 2021. [Google Scholar]
- Menetrey, P.; Willam, K.J. Triaxial failure criterion for concrete and its generalization. Struct. J. 1995, 92, 311–318. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Matériaux Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Cervenka, V. Mesh sensitivity effects in smeared finite element analysis of concrete fracture. FRAMCOS-2 1995, 2, 1387–1396. [Google Scholar]
- Solanki, H.T. Simplified Modified Compression Field Theory for Calculating Shear Strength of Reinforced Concrete Elements. Paper by Evan C. Bentz, Frank J. Vecchio, and Michael P. Collins/AUTHORS’CLOSURE. ACI Struct. J. 2007, 104, 378. [Google Scholar]
- Bai, Y.L.; Bai, S.C.; Mei, S.J.; Jia, J.F. Experimental and numerical study of PEN FRP-strengthened circular RC columns under lateral cyclic loading with high axial compression ratio. Eng. Struct. 2023, 294, 116711. [Google Scholar] [CrossRef]
- Menegotto, M. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, Lisbon, Portugal, 13–14 September 1973. [Google Scholar]




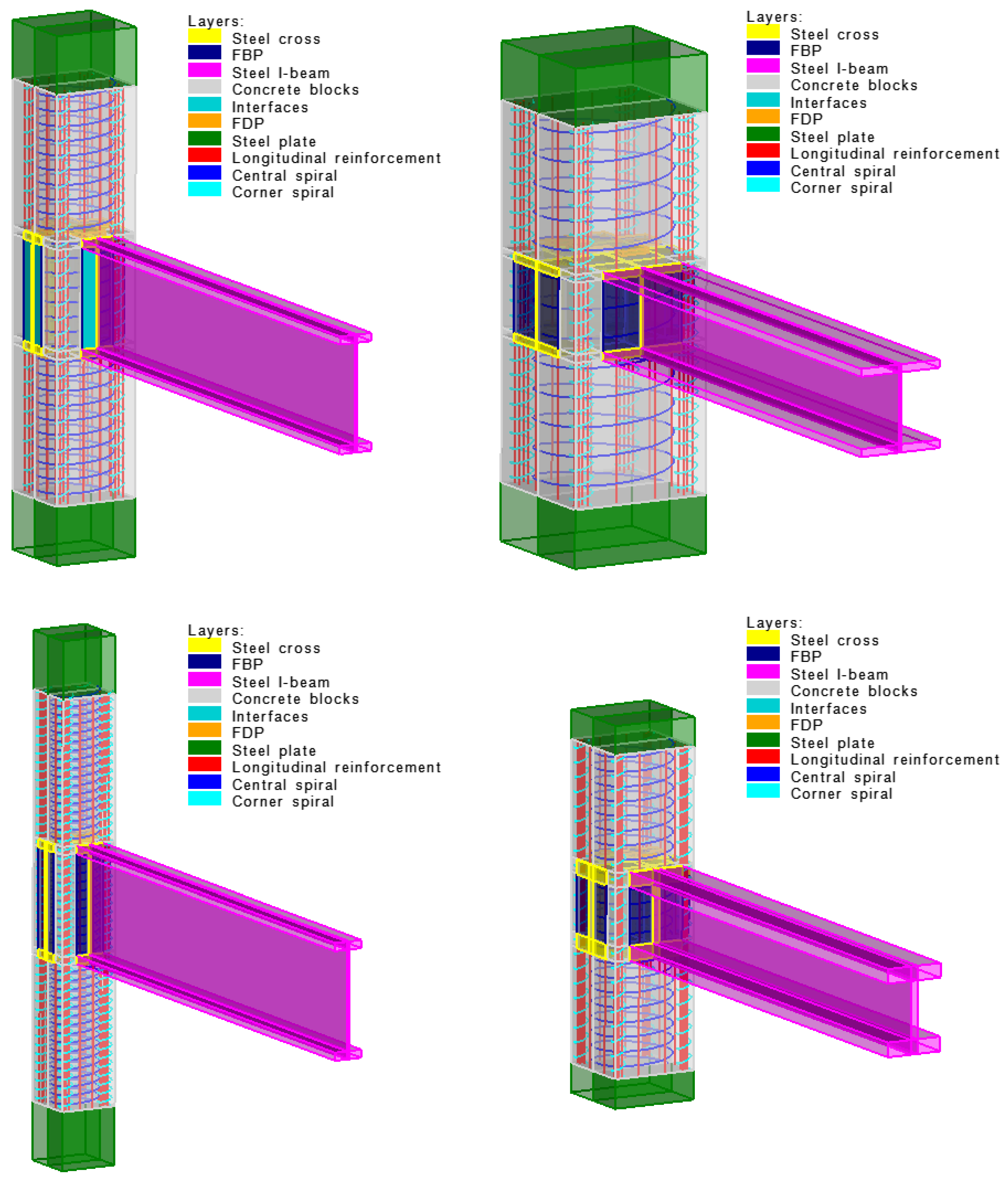
| Concrete Material Property | Units | FEA Value |
|---|---|---|
| Young’s Modulus | GPa | 42 |
| Tensile Strength | MPa | 3.4 |
| Compressive Strength | MPa | −83.8 |
| Fracture Energy 1 | MNm−1 | 8.5 |
| Plastic Strain | - | −0.0015 |
| Onset of Crushing | MPa | −7.14 |
| Critical compressive
displacement | m | −0.004 |
| Fc crack reduction | - | 1 |
| Physical Quantity | LP Experiment | LP FEA | Deviation [–] | HP Experiment | HP FEA | Deviation [–] |
|---|---|---|---|---|---|---|
| Peak Force [kN] | 1601 | 1624 | 0.014 | 1656 | 1618 | 0.023 |
| Max. Drift Force [kN] | 979 | 1209 | 0.235 | 1600 | 1676 | 0.048 |
| Max. Drift [%] | 9 | 10 | 0.1 | 5 | 5 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Řehounek, L.; Ženíšek, M. Numerical Simulation and Model Validation of Multispiral-Reinforced Concrete Columns’ Response to Cyclic Loading. Buildings 2025, 15, 3855. https://doi.org/10.3390/buildings15213855
Řehounek L, Ženíšek M. Numerical Simulation and Model Validation of Multispiral-Reinforced Concrete Columns’ Response to Cyclic Loading. Buildings. 2025; 15(21):3855. https://doi.org/10.3390/buildings15213855
Chicago/Turabian StyleŘehounek, Luboš, and Michal Ženíšek. 2025. "Numerical Simulation and Model Validation of Multispiral-Reinforced Concrete Columns’ Response to Cyclic Loading" Buildings 15, no. 21: 3855. https://doi.org/10.3390/buildings15213855
APA StyleŘehounek, L., & Ženíšek, M. (2025). Numerical Simulation and Model Validation of Multispiral-Reinforced Concrete Columns’ Response to Cyclic Loading. Buildings, 15(21), 3855. https://doi.org/10.3390/buildings15213855